Реферат на тему:
Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.
В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.
Как и любой из фундаментальных законов сохранения, закон сохранения импульса описывает одну из фундаментальных симметрий, — однородность пространства.
Рассмотрим выражение определения силы
Перепишем его для системы из N частиц:
где суммирование идет по всем силам, действующим на n-ю частицу со стороны m-ой. Согласно третьему закону Ньютона, силы вида и
будут равны по абсолютному значению и противоположны по направлению, то есть
Тогда после подстановки полученного результата в выражение (1) правая часть будет равна нулю, то есть:
или
Как известно, если производная от некоторого выражения равна нулю, то это выражение есть постоянная величина относительно переменной дифференцирования, а значит:
То есть суммарный импульс системы частиц есть величина постоянная. Нетрудно получить аналогичное выражение для одной частицы.
Следует учесть, что вышеприведенные рассуждения справедливы лишь для замкнутой системы.
Также стоит подчеркнуть, что изменение импульса зависит не только от действующей на тело силы, но и от продолжительности её действия.
Согласно теореме Нётер каждому закону сохранения ставится в соответствие некая симметрия уравнений, описывающих систему. В частности, закон сохранения импульса эквивалентен однородности пространства, то есть независимости всех законов, описывающих систему, от положения системы в пространстве. Простейший вывод этого утверждения основан на применении лагранжева подхода к описанию системы.
Рассмотрим функцию Лагранжа свободного тела зависящую от обобщённых координат
обобщённых скоростей
и времени t. Здесь точка над q обозначает дифференцирование по времени,
Выберем для рассмотрения прямоугольную декартову систему координат, тогда
для каждой
-той частицы. Используя однородность пространства, мы можем дать всем радиус-векторам частиц одинаковое приращение, которое не будет влиять на уравнения движения:
где
В случае постоянства скорости функция Лагранжа изменится следующим образом:
где суммирование идет по всем частицам системы. Так как приращение не влияет на уравнения движения, то вариация функции Лагранжа должна быть равной нулю: С учётом того, что вектор
— произвольный, последнее требование выполняется при:
Воспользуемся уравнением Лагранжа
Это означает, что сумма, стоящая под знаком дифференциала, — постоянная величина для рассматриваемой системы. Сама сумма и есть суммарный импульс системы:
Учитывая, что лагранжиан свободной частицы имеет вид: нетрудно видеть, что последнее выражение совпадает с выражением в ньютоновом формализме:
Для релятивистской свободной частицы лагранжиан имеет несколько другую форму: что приводит к релятивистскому определению импульса
В настоящее время не существует каких-либо экспериментальных фактов, свидетельствующих о невыполнении закона сохранения импульса.
Аналогично ситуации с законом сохранения энергии, при переходе к искривлённому пространству-времени закон сохранения импульса, выражаемый пространственными компонентами соотношения для тензора энергии-импульса
где точка с запятой выражает ковариантную производную, приводит лишь к локально сохраняющимся величинам. Это связано с отсутствием глобальной однородности пространства в пространстве-времени общего вида.
Можно придумать такие определения импульса гравитационного поля, что глобальный закон сохранения импульса будет выполняться при движении во времени системы тел и полей, но все такие определения содержат элемент произвола, так как вводимый импульс гравитационного поля не может быть тензорной величиной при произвольных преобразованиях координат.
wreferat.baza-referat.ru
Второй закон Ньютона \(~m \vec a = \vec F\) можно записать в иной форме, которая приведена самим Ньютоном в его главном труде «Математические начала натуральной философии».
Если на тело (материальную точку) действует постоянная сила, то постоянным является и ускорение
\(~\vec a = \frac{\vec \upsilon_2 - \vec \upsilon_1}{\Delta t}\) ,где \(~\vec \upsilon_1\) и \(~\vec \upsilon_2\) — начальное и конечное значения скорости тела.
Подставив это значение ускорения во второй закон Ньютона, получим:
\(~\frac{m \cdot (\vec \upsilon_2 - \vec \upsilon_1)}{\Delta t} = \vec F\) или \(~m \vec \upsilon_2 - m \vec \upsilon_1 = \vec F \Delta t\) . (1)В этом уравнении появляется новая физическая величина — импульс материальной точки.
Импульсом материальной точки называют величину равную произведению массы точки на ее скорость.
Обозначим импульс (его также называют иногда количеством движения) буквой \(~\vec p\) . Тогда
\(~\vec p = m \vec \upsilon\) . (2)Из формулы (2) видно, что импульс — векторная величина. Так как m > 0, то импульс имеет то же направление, что и скорость.
Единица импульса не имеет особого названия. Ее наименование получается из определения этой величины:
[p] = [m] · [υ] = 1 кг · 1 м/с = 1 кг·м/с .Обозначим через \(~\vec p_1 = m \vec \upsilon_1\) импульс материальной точки в начальный момент интервала Δt, а через \(~\vec p_2 = m \vec \upsilon_2\) — импульс в конечный момент этого интервала. Тогда \(~\vec p_2 - \vec p_1 = \Delta \vec p\) есть изменение импульса за время Δt. Теперь уравнение (1) можно записать так:
\(~\Delta \vec p = \vec F \Delta t\) . (3)Так как Δt > 0, то направления векторов \(~\Delta \vec p\) и \(~\vec F\) совпадают.
Согласно формуле (3)
изменение импульса материальной точки пропорционально приложенной к ней силе и имеет такое же направление, как и сила.
Именно так был впервые сформулирован второй закон Ньютона.
Произведение силы на время ее действия называют импульсом силы. Не надо путать импульс \(~m \vec \upsilon\) материальной точки и импульс силы \(\vec F \Delta t\) . Это совершенно разные понятия.
Уравнение (3) показывает, что одинаковые изменения импульса материальной точки могут быть получены в результате действия большой силы в течение малого интервала времени или малой силы за большой интервал времени. Когда вы прыгаете с какой-то высоты, то остановка вашего тела происходит за счет действия силы со стороны земли или пола. Чем меньше продолжительность столкновения, тем больше тормозящая сила. Для уменьшения этой силы надо, чтобы торможение происходило постепенно. Вот почему при прыжках в высоту спортсмены приземляются на мягкие маты. Прогибаясь, они постепенно тормозят спортсмена. Формула (3) может быть обобщена и на тот случай, когда сила меняется во времени. Для этого весь промежуток времени Δt действия силы надо разделить на столь малые интервалы Δti, чтобы на каждом из них значение силы без большой ошибки можно было считать постоянным. Для каждого малого интервала времени справедлива формула (3). Суммируя изменения импульсов за малые интервалы времени, получим:
\(~\Delta \vec p = \sum^{N}_{i=1}{\vec F_i \Delta t_i}\) . (4)Символ Σ (греческая буква «сигма») означает «сумма». Индексы i = 1 (внизу) и N (наверху) означают, что суммируется N слагаемых.
Для нахождения импульса тела поступают так: мысленно разбивают тело на отдельные элементы (материальные точки), находят импульсы полученных элементов, а потом их суммируют как векторы.
Импульс тела равен сумме импульсов его отдельных элементов.
При рассмотрении любой механической задачи мы интересуемся движением определенного числа тел. Совокупность тел, движение которой мы изучаем, называется механической системой или просто системой.
Рассмотрим систему, состоящую из трех тел. Это могут быть три звезды, испытывающие воздействие со стороны соседних космических тел. На тела системы действуют внешние силы \(~\vec F_i\) (i — номер тела; например, \(~\vec F_2\) — это сумма внешних сил, действующих на тело номер два). Между телами действуют силы \(~\vec F_{ik}\) называемые внутренними силами (рис. 1). Здесь первая буква i в индексе означает номер тела, на которое действует сила \(~\vec F_{ik}\) , а вторая буква k означает номер тела, со стороны которого действует данная сила. На основании третьего закона Ньютона
\(~\vec F_{ik} = - \vec F_{ki}\) . (5)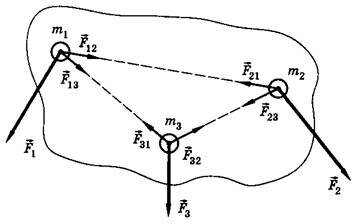
Рис. 1
Вследствие действия сил на тела системы их импульсы изменяются. Если за малый промежуток времени сила заметно не меняется, то для каждого тела системы можно записать изменение импульса в форме уравнения (3):
\(~\Delta (m_1 \vec \upsilon_1) = (\vec F_{12} + \vec F_{13} + \vec F_1) \Delta t\) , \(~\Delta (m_2 \vec \upsilon_2) = (\vec F_{21} + \vec F_{23} + \vec F_2) \Delta t\) , (6) \(~\Delta (m_3 \vec \upsilon_3) = (\vec F_{31} + \vec F_{32} + \vec F_3) \Delta t\) .Здесь в левой части каждого уравнения стоит изменение импульса тела \(~\vec p_i = m_i \vec \upsilon_i\) за малое время Δt. Более подробно\[~\Delta (m_i \vec \upsilon_i) = m_i \vec \upsilon_{ik} - m_i \vec \upsilon_{in}\] где \(~\vec \upsilon_{in}\) — скорость в начале, а \(~\vec \upsilon_{ik}\) — в конце интервала времени Δt.
Сложим левые и правые части уравнений (6) и покажем, что сумма изменений импульсов отдельных тел равна изменению суммарного импульса всех тел системы, равного
\(~\vec p_c = m_1 \vec \upsilon_1 + m_2 \vec \upsilon_2 + m_3 \vec \upsilon_3\) . (7)Действительно,
\(~\Delta (m_1 \vec \upsilon_1) + \Delta (m_2 \vec \upsilon_2) + \Delta (m_3 \vec \upsilon_3) = m_1 \vec \upsilon_{1k} - m_1 \vec \upsilon_{1n} + m_2 \vec \upsilon_{2k} - m_2 \vec \upsilon_{2n} + m_3 \vec \upsilon_{3k} - m_3 \vec \upsilon_{3n} =\) \(~=(m_1 \vec \upsilon_{1k} + m_2 \vec \upsilon_{2k} + m_3 \vec \upsilon_{3k}) -(m_1 \vec \upsilon_{1n} + m_2 \vec \upsilon_{2n} + m_3 \vec \upsilon_{3n}) = \vec p_{ck} - \vec p_{cn} = \Delta \vec p_c\) .Таким образом,
\(~\Delta \vec p_c = (\vec F_{12} + \vec F_{13} + \vec F_{21} + \vec F_{23} + \vec F_{31} + \vec F_{32} + \vec F_1 + \vec F_2 + \vec F_3) \Delta t\) . (8)Но силы взаимодействия любой пары тел в сумме дают нуль, так как согласно формуле (5)
\(~\vec F_{12} = - \vec F_{21} ; \vec F_{13} = - \vec F_{31} ; \vec F_{23} = - \vec F_{32}\) .Поэтому изменение импульса системы тел равно импульсу внешних сил:
\(~\Delta \vec p_c = (\vec F_1 + \vec F_2 + \vec F_3) \Delta t\) . (9)Мы пришли к важному выводу:
импульс системы тел могут изменить только внешние силы, причем изменение импульса системы пропорционально сумме внешних сил и совпадает с ней по направлению. Внутренние силы, изменяя импульсы отдельных тел системы, не изменяют суммарный импульс системы.
Уравнение (9) справедливо для любого интервала времени, если сумма внешних сил остается постоянной.
Из уравнения (9) вытекает чрезвычайно важное следствие. Если сумма внешних сил, действующих на систему, равна нулю, то равно нулю и изменение импульса системы\[~\Delta \vec p_c = 0\] . Это означает, что, какой бы интервал времени мы ни взяли, суммарный импульс в начале этого интервала \(~\vec p_{cn}\) и в его конце \(~\vec p_{ck}\) один и тот же\[~\vec p_{cn} = \vec p_{ck}\] . Импульс системы остается неизменным, или, как говорят, сохраняется:
\(~\vec p_c = m_1 \vec \upsilon_1 + m_2 \vec \upsilon_2 + m_3 \vec \upsilon_3 = \operatorname{const}\) . (10)Закон сохранения импульса формулируется так:
если сумма внешних сил, действующих на тела системы, равна нулю, то импульс системы сохраняется.
Тела могут только обмениваться импульсами, суммарное же значение импульса не изменяется. Надо только помнить, что сохраняется векторная сумма импульсов, а не сумма их модулей.
Как видно из проделанного нами вывода, закон сохранения импульса является следствием второго и третьего законов Ньютона. Система тел, на которую не действуют внешние силы, называется замкнутой или изолированной. В замкнутой системе тел импульс сохраняется. Но область применения закона сохранения импульса шире: если даже на тела системы действуют внешние силы, но их сумма равна нулю, импульс системы все равно сохраняется.
Полученный результат легко обобщается на случай системы, содержащей произвольное число N тел:
\(~m_1 \vec \upsilon_{1n} + m_2 \vec \upsilon_{2n} + m_3 \vec \upsilon_{3n} + \ldots + m_N \vec \upsilon_{Nn} = m_1 \vec \upsilon_{1k} + m_2 \vec \upsilon_{2k} + m_3 \vec \upsilon_{3k} + \ldots + m_N \vec \upsilon_{Nk}\) . (11)Здесь \(~\vec \upsilon_{in}\) — скорости тел в начальный момент времени, а \(~\vec \upsilon_{ik}\) — в конечный. Так как импульс — величина векторная, то уравнение (11) представляет собой компактную запись трех уравнений для проекций импульса системы на координатные оси.
Все реальные системы, конечно, не являются замкнутыми, сумма внешних сил довольно редко может оказаться равной нулю. Тем не менее в очень многих случаях закон сохранения импульса можно применять.
Если сумма внешних сил не равна нулю, но равна нулю сумма проекций сил на какое-то направление, то проекция импульса системы на это направление сохраняется. Например, система тел на Земле или вблизи ее поверхности не может быть замкнутой, так как на все тела действует сила тяжести, которая изменяет импульс по вертикали согласно уравнению (9). Однако вдоль горизонтального направления сила тяжести не может изменять импульс, и сумма проекций импульсов тел на горизонтально направленную ось будет оставаться неизменной, если действием сил сопротивления можно пренебречь.
Кроме того, при быстрых взаимодействиях (взрыв снаряда, выстрел из орудия, столкновения атомов и т. п.) изменение импульсов отдельных тел будет фактически обусловлено только внутренними силами. Импульс сис-темы сохраняется при этом с большой точностью, ибо такие внешние силы, как сила тяготения и сила трения, зависящая от скорости, заметно не изменяет импульса системы. Они малы по сравнению с внутренними силами. Так, скорость осколков снаряда при взрыве в зависимости от калибра может изменяться в пределах 600 — 1000 м/с. Интервал времени, за который сила тяжести смогла бы сообщить телам такую скорость, равен
\(~\Delta t = \frac{m \Delta \upsilon}{mg} \approx 100 c\)Внутренние же силы давления газов сообщают такие скорости за 0,01 с, т.е. в 10000 раз быстрее.
Под реактивным движением понимают движение тела, возникающее при отделении некоторой его части с определенной скоростью относительно тела,
например при истечении продуктов сгорания из сопла реактивного летательного аппарата. При этом появляется так называемая реактивная сила, сообщающая телу ускорение.
Наблюдать реактивное движение очень просто. Надуйте детский резиновый шарик и отпустите его. Шарик стремительно взовьется вверх (рис. 2). Движение, правда, будет кратковременным. Реактивная сила действует лишь до тех пор, пока продолжается истечение воздуха.

Рис. 2
Главная особенность реактивной силы состоит в том, что она возникает без какого-либо взаимодействия с внешними телами. Происходит лишь взаимодействие между ракетой и вытекающей из нее струей вещества.
Сила же, сообщающая ускорение автомобилю или пешеходу на земле, пароходу на воде или винтовому самолету в воздухе, возникает только за счет взаимодействия этих тел с землей, водой или воздухом.
При истечении продуктов сгорания топлива они за счет давления в камере сгорания приобретают некоторую скорость относительно ракеты и, следовательно, некоторый импульс. Поэтому в соответствии с законом сохранения импульса сама ракета получает такой же по модулю импульс, но направленный в противоположную сторону.
Масса ракеты с течением времени убывает. Ракета в полете является телом переменной массы. Для расчета ее движения удобно применить закон сохранения импульса.
Выведем уравнение движения ракеты и найдем выражение для реактивной силы. Будем считать, что скорость вытекающих из ракеты газов относительно ракеты постоянна и равна \(~\vec u\) . Внешние силы на ракету не действуют: она находится в космическом пространстве вдали от звезд и планет.
Пусть в некоторый момент времени скорость ракеты относительно инерциальной системы, связанной со звездами, равна \(~\vec \upsilon\) (рис. 3), а масса ракеты равна М. Через малый интервал времени Δt масса ракеты станет равной
\(~M_1 = M - \mu \Delta t\) ,где μ — расход топлива (расходом топлива называется отношение массы сгоревшего топлива ко времени его сгорания).
Рис. 3
За этот же промежуток времени скорость ракеты изменится на \(~\Delta \vec \upsilon\) и станет равной \(~\vec \upsilon_1 = \vec \upsilon + \Delta \vec \upsilon\) . Скорость истечения газов относительно выбранной инерциальной системы отсчета равна \(~\vec \upsilon + \vec u\) (рис. 4), так как до начала сгорания топливо имело ту же скорость, что и ракета.

Рис. 4
Запишем закон сохранения импульса для системы ракета — газ:
\(~M \vec \upsilon = (M - \mu \Delta t)(\vec \upsilon + \Delta \vec \upsilon) + \mu \Delta t(\vec \upsilon + \vec u)\) .Раскрыв скобки, получим:
\(~M \vec \upsilon = M \vec \upsilon - \mu \Delta t \vec \upsilon + M \Delta \vec \upsilon - \mu \Delta t \Delta \vec \upsilon + \mu \Delta t \vec \upsilon + \mu \Delta t \vec u\) .Слагаемым \(~\mu \Delta t \vec \upsilon\) можно пренебречь по сравнению с остальными, так как оно содержит произведение двух малых величин (это величина, как говорят, второго порядка малости). После приведения подобных членов будем иметь:
\(~M \Delta \vec \upsilon = - \mu \Delta t \vec u\) или \(~M \frac{\Delta \vec \upsilon}{\Delta t} = - \mu \vec u\) . (12)Это одно из уравнений Мещерского для движения тела переменной массы, полученное им в 1897 г.
Если ввести обозначение \(~\vec F_r = - \mu \vec u\) , то уравнение (12) совпадет по форме записи со вторым законом Ньютона. Однако масса тела М здесь не постоянна, а убывает со временем из-за потери вещества.
Величина \(~\vec F_r = - \mu \vec u\) носит название реактивной силы. Она появляется вследствие истечения газов из ракеты, приложена к ракете и направлена противоположно скорости газов относительно ракеты. Реактивная сила определяется лишь скоростью истечения газов относительно ракеты и расходом топлива. Существенно, что она не зависит от деталей устройства двигателя. Важно лишь, чтобы двигатель обеспечивал истечение газов из ракеты со скоростью \(~\vec u\) при расходе топлива μ. Реактивная сила космических ракет достигает 1000 кН.
Если на ракету действуют внешние силы, то ее движение определяется реактивной силой и суммой внешних сил. В этом случае уравнение (12) запишется так:
\(~M \frac{\Delta \vec \upsilon}{\Delta t} = \vec F_r + \vec F\) . (13)Широкое применение реактивные двигатели в настоящее время получили в связи с освоением космического пространства. Применяются они также для метеорологических и военных ракет различного радиуса действия. Кроме того, все современные скоростные самолеты оснащены воздушно-реактивными двигателями.
В космическом пространстве использовать какие-либо другие двигатели, кроме реактивных, невозможно: нет опоры (твердой, жидкой или газообразной), отталкиваясь от которой космический корабль мог бы получить ускорение. Применение же реактивных двигателей для самолетов и ракет, не выходящих за пределы атмосферы, связано с тем, что именно реактивные двигатели способны обеспечить максимальную скорость полета.
Реактивные двигатели делятся на два класса: ракетные и воздушно-реактивные.
В ракетных двигателях топливо и необходимый для его горения окислитель находятся непосредственно внутри двигателя или в его топливных баках.
На рисунке 5 показана схема ракетного двигателя на твердом топливе. Порох или какое-либо другое твердое топливо, способное к горению в отсутствие воздуха, помещают внутрь камеры сгорания двигателя.

Рис. 5
При горении топлива образуются газы, имеющие очень высокую температуру и оказывающие давление на стенки камеры. Сила давления на переднюю стенку камеры больше, чем на заднюю, где расположено сопло. Вытекающие через сопло газы не встречают на своем пути стенку, на которую могли бы оказывать давление. В результате появляется сила, толкающая ракету вперед.
Суженная часть камеры — сопло служит для увеличения скорости истечения продуктов сгорания, что в свою очередь повышает реактивную силу. Сужение струи газа вызывает увеличение его скорости, так как при этом через меньшее поперечное сечение в единицу времени должна пройти такая же масса газа, что и при большем поперечном сечении.
Применяются также ракетные двигатели, работающие на жидком топливе.
В жидкостно-реактивных двигателях (ЖРД) в качестве горючего можно использовать керосин, бензин, спирт, анилин, жидкий водород и др., а в качестве окислителя, необходимого для горения, — жидкий кислород, азотную кислоту, жидкий фтор, пероксид водорода и др. Горючее и окислитель хранятся отдельно в специальных баках и с помощью насосов подаются в камеру, где при сгорании топлива развивается температура до 3000 °С и давление до 50 атм (рис. 6). В остальном двигатель работает так же, как и двигатель на твердом топливе.

Рис. 6
Жидкостно-реактивные двигатели используются для запуска космических кораблей.
Воздушно-реактивные двигатели в настоящее время применяют главным образом на самолетах. Основное их отличие от ракетных двигателей состоит в том, что окислителем для горения топлива служит кислород воздуха, поступающего внутрь двигателя из атмосферы. На рисунке 7 изображена схема воздушно-реактивного двигателя турбокомпрессорного типа. В носовой части расположен компрессор, засасы-вающий и сжимающий воздух, который затем поступает в камеру сгорания. Жидкое горючее (обычно используется керосин) подается в камеру сгорания с помощью специальных форсунок.
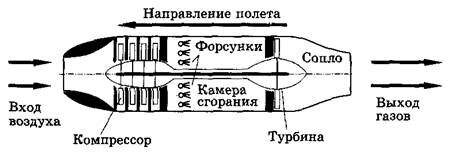
Рис. 7
Раскаленные газы (продукты сгорания), выходя через сопло, вращают газовую турбину, приводящую в движение компрессор. Турбокомпрессорные двигатели установлены в наших лайнерах Ту-134, Ил-62, Ил-86 и др.
Реактивными двигателями оснащены не только ракеты, но и большая часть современных самолетов.
Автором первого в мире проекта реактивного летательного аппарата для полета людей был русский революционер-народоволец Н.И. Кибальчич (1853—1881).
Основы теории реактивного двигателя и научное доказательство воз-можности полетов в межпланетном пространстве были впервые высказаны и разработаны русским ученым К.Э. Циолковским в работе «Исследование мировых пространств реактивными приборами».
К.Э. Циолковскому принадлежит также идея применения многоступенчатых ракет. Отдельные ступени, из которых составлена ракета, снабжаются собственными двигателями и запасом топлива. По мере выгорания топлива каждая очередная ступень отделяется от ракеты. Поэтому в дальнейшем на ускорение ее корпуса и двигателя топливо не расходуется.
Идея Циолковского о сооружении большой станции-спутника на орбите вокруг Земли, с которой будут стартовать ракеты к другим планетам Солнечной системы, еще не осуществлена, но нет сомнения в том, что рано или поздно такая станция будет создана.
В настоящее время становится реальностью пророчество Циолковского: «Человечество не останется вечно на Земле, но в погоне за светом и пространством сначала робко проникнет за пределы атмосферы, а затем завоюет себе все околосолнечное пространство».
Нашей стране принадлежит великая честь запуска 4 октября 1957 г. первого искусственного спутника Земли. Также впервые в нашей стране 12 апреля 1961 г. был осуществлен полет космического корабля с космонавтом Ю.А. Гагариным на борту.
Эти полеты были совершены на ракетах, сконструированных отечест-венными учеными и инженерами под руководством С.П. Королева. Большие заслуги в исследовании космического пространства имеют американские ученые, инженеры и астронавты. Два американских астронавта из экипажа космического корабля «Аполлон-11» — Нейл Армстронг и Эдвин Олдрин — 20 июля 1969 г. впервые совершили посадку на Луну. На космическом теле Солнечной системы человеком были сделаны первые шаги.
С выходом человека в космос не только открылись возможности исследования других планет, но и представились поистине фантастические возможности изучения природных явлений и ресурсов Земли, о которых можно было только мечтать. Возникло космическое природоведение. Раньше общая карта Земли составлялась по крупицам, как мозаичное панно. Теперь снимки с орбиты, охватывающие миллионы квадратных километров, позволяют выбирать для исследования наиболее интересные участки земной поверхности, экономя тем самым силы и средства- Из космоса лучше различаются крупные геологические структуры: плиты, глубинные разломы земной коры — места наиболее вероятного залегания полезных ископаемых. Из космоса удалось обнаружить новый тип геологических образований кольцевые структуры, подобные кратерам Луны и Марса,
Сейчас на орбитальных комплексах разработаны технологии получения материалов, которые нельзя изготовить на Земле, а только в состоянии длительной невесомости в космосе. Стоимость этих материалов (сверхчистые монокристаллы и др.) близка к затратам на запуск космических аппаратов.
www.physbook.ru
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ – МСХА имени К. А. Тимирязева»
Реферат по физике на тему «Законы сохранения энергии. Закон сохранения импульса. Закон сохранения механической энергии. Закон сохранения момента импульса. Закон сохранения и превращения энергии»
| Выполнила: | Студентка Зооинженерного факультета 104 группы Золотарева И.М. |
| Проверил: |
Москва, 2014
Закон сохранения энергии.
Закон сохранения энергии — результат обобщения многих экспериментальных данных. Идея этого закона принадлежит М. В. Ломоносову (1711—1765), изложившему закон сохранения материи и движения, а количественная формулировка закона сохранения энергии дана немецким врачом Ю. Майером (1814—1878) и немецким естествоиспытателем Г. Гельмгольцем (1821—1894).
Закон сохранения энергии утверждает, что энергия тела никогда не исчезает и не появляется вновь, она может лишь превращаться из одного вида в другой. Этот закон универсален. В различных разделах физики он имеет свою формулировку. Классическая механика рассматривает закон сохранения механической энергии.
Полная механическая энергия замкнутой системы физических тел, между которыми действуют консервативные силы, является величиной постоянной. Так формулируется закон сохранения энергии в механике Ньютона.
Замкнутой, или изолированной, принято считать физическую систему, на которую не действуют внешние силы. В ней не происходит обмена энергией с окружающим пространством, и собственная энергия, которой она обладает, остаётся неизменной, то есть сохраняется. В такой системе действуют только внутренние силы, и тела взаимодействуют друг с другом. В ней могут происходить лишь превращения потенциальной энергии в кинетическую и наоборот.
Во всех явлениях, происходящих в природе, энергия не возникает и не исчезает. Она только превращается из одного вида в другой, при этом ее значение сохраняется.

Потенциальную энергию называют энергией взаимодействия физических тел или их частей между собой. Она определяется их взаимным расположением, то есть, расстоянием между ними, и равна работе, которую нужно совершить, чтобы переместить тело из точки отсчёта в другую точку в поле действия консервативных сил.
Потенциальную энергию имеет любое неподвижное физическое тело, поднятое на какую-то высоту, так как на него действует сила тяжести, являющаяся консервативной силой. Такой энергией обладает вода на краю водопада, санки на вершине горы.
Величина потенциальной энергии тела определяется высотой, на которой находится тело относительно какого-то начального уровня. За точку отсчёту мы можем принять любую выбранную нами точку.
Если рассматривать положение тела относительно Земли, то потенциальная энергия тела на поверхности Земли равна нулю. А на высоте h она вычисляется по формуле:
Еп = mɡh,
где m – масса тела
ɡ - ускорение свободного падения
h – высота центра масс тела относительно Земли
ɡ = 9,8 м/с2
При падении тела c высоты h2 до высоты h3 сила тяжести совершает работу. Эта работа равна изменению потенциальной энергии и имеет отрицательное значение, так как величина потенциальной энергии при падении тела уменьшается.
A = - (Eп2 – Eп1) = - ∆ Eп ,
где Eп1 – потенциальная энергия тела на высоте h2 ,
Eп2 - потенциальная энергия тела на высоте h3.
Если же тело поднимают на какую-то высоту, то совершают работу против сил тяжести. В этом случае она имеет положительное значение. А величина потенциальной энергии тела увеличивается.
Потенциальной энергией обладает и упруго деформированное тело (сжатая или растянутая пружина). Её величина зависит от жёсткости пружины и от того, на какую длину её сжали или растянули, и определяется по формуле:
Еп = k·(∆x)2/2,
где k – коэффициент жёсткости,
∆x – удлинение или сжатие тела.
Потенциальная энергии пружины может совершать работу.
studfiles.net
Реферат на тему:
И́мпульс (Количество движения) — векторная физическая величина, характеризующая меру механического движения тела. В классической механике импульс тела равен произведению массы m этой точки на её скорость v, направление импульса совпадает с направлением вектора скорости:
В более общем виде, справедливом также и в релятивистской механике, определение имеет вид:
Импульс — это аддитивный интеграл движения механической системы, связанный согласно теореме Нётер с фундаментальной симметрией — однородностью пространства.
Ещё в первой половине XVII века понятие импульса введено Рене Декартом. Так как физическое понятие массы в то время отсутствовало, он определил импульс как произведение «величины тела на скорость его движения». Позже такое определение было уточнено Исааком Ньютоном. Согласно Ньютону, «количество движения есть мера такового, устанавливаемая пропорционально скорости и массе».
В классической механике полным импульсом системы материальных точек называется векторная величина, равная сумме произведений масс материальных точек на их скорости:
соответственно величина называется импульсом одной материальной точки. Это векторная величина, направленная в ту же сторону, что и скорость частицы. Единицей измерения импульса в Международной системе единиц (СИ) является килограмм-метр в секунду (кг·м/с)
Если мы имеем дело с телом конечного размера, для определения его импульса необходимо разбить тело на малые части, которые можно считать материальными точками и просуммировать по ним, в результате получим:
Импульс системы, на которую не действуют никакие внешние силы (или они скомпенсированы), сохраняется во времени:
Сохранение импульса в этом случае следует из второго и третьего закона Ньютона: написав второй закон Ньютона для каждой из составляющих систему материальных точек и просуммировав по всем материальным точкам, составляющим систему, в силу третьего закона Ньютона получим равенство (*).
В релятивистской механике трёхмерным импульсом системы невзаимодействующих материальных точек называется величина
где mi — масса покоя i-й материальной точки.
Для замкнутой системы не взаимодействующих материальных точек эта величина сохраняется. Однако трёхмерный импульс не есть релятивистски инвариантная величина, так как он зависит от системы отсчёта. Более осмысленной величиной будет четырёхмерный импульс, который для одной материальной точки определяется как
На практике часто применяются следующие соотношения между массой, импульсом и энергией частицы:
В принципе, для системы невзаимодействующих материальных точек их 4-импульсы суммируются. Однако для взаимодействующих частиц в релятивистской механике следует учитывать импульсы не только составляющих систему частиц, но и импульс поля взаимодействия между ними. Поэтому гораздо более осмысленной величиной в релятивистской механике является тензор энергии-импульса, который в полной мере удовлетворяет законам сохранения.
В теоретической механике обобщённым импульсом называется частная производная лагранжиана системы по обобщённой скорости
В случае, если лагранжиан системы не зависит от некоторой обобщённой координаты, то в силу уравнений Лагранжа .
Для свободной частицы функция Лагранжа имеет вид: , отсюда:
Независимость лагранжиана замкнутой системы от её положения в пространстве следует из свойства однородности пространства: для хорошо изолированной системы её поведение не зависит от того, в какое место пространства мы её поместим. По теореме Нётер из этой однородности следует сохранение некоторой физической величины. Эту величину и называют импульсом (обычным, не обобщённым).
В электромагнитном поле полный импульс частицы равен:
где — векторный потенциал электромагнитного поля.
Импульсом называется сохраняющаяся физическая величина, связанная с однородностью пространства (инвариант относительно трансляций).
Электромагнитное поле, как и любой другой материальный объект, обладает импульсом, который легко можно найти, проинтегрировав вектор Пойнтинга по объёму:
Существованием импульса у электромагнитного поля объясняется, например, такое явление, как давление электромагнитного излучения.
В квантовой механике оператором импульса частицы называют оператор — генератор группы трансляций. Это эрмитов оператор, собственные значения которого отождествляются с импульсом системы частиц. В координатном представлении для системы нерелятивистских частиц он имеет вид
где — оператор набла, соответствующий дифференцированию по координатам j-ой частицы. Гамильтониан системы выражается через оператор импульса:
Для замкнутой системы (U = 0) оператор импульса коммутирует с гамильтонианом и импульс сохраняется.
Формула де Бройля связывает импульс и длину волны де Бройля.
Модуль импульса обратно пропорционален длине волны λ:
В векторном виде это записывается как где
— волновой вектор, h — постоянная Планка.
wreferat.baza-referat.ru
Введение 3
1.Описание физического явления 4
2.Физический смысл закона сохранения импульса 6
3.История открытия закона сохранения импульса 10
4. Практическое применение закона сохранения импульса в жизни человека 12
Заключение 15
Список литературы 16
Содержание
Наконец, синтезировать известные законы ряд принципов, дедуктивно определить уже известные и неизвестные претензии предсказать определенные физические явления и процессы. Функция, выполняемая в соответствии с принципами симметрии, согласно Э. Вигнера наделен структурой законов природы или установлении внутренней связи между ними, так как законы природы заданной структурой или отношения в мире явлений. Это создает теорию, охватывающих широкий спектр физических явлений и процессов. Следующий этап — анализ самих принципов границ или условий и выявление тех, в которых они выполняются. Идея выявления основополагающих принципов и их последовательное применение с описанием и объяснением природных явлений впервые предложил и осуществил с использованием математического аппарата Исаак Ньютон в начале развития классической физики, и задолго до современных концепций инвариантность и симметрия.
В своей работе «Оптика», писал он, «чтобы выйти из событий двух или трех общих принципах движения, а затем объяснить, как эти четкие принципы получены свойства и действия всех вещественных предметов, так что это будет большой шаг в философии, хотя Причины этих принципов и еще не были обнаружены.
«По своей природе и месте в теории познания этих принципов являются аксиомой характер.4. Практическое применение закона сохранения импульса в жизни человекаЗакон вступил в силу в строго явлений отдачи, явление реактивного движения, взрывчатых явлений и феноменов воздействия. Закон сохранения импульса используется для платежей скоростей тел в результате взрывов и столкновений; расчеты реактивных транспортных средств; в военной промышленности в разработке оружия; Техника — при движении свай, ковки металлов и т. д.Для решения проблемы с законом сохранения импульса, а также в задачи, решаемые с помощью законов Ньютона, вы должны выбрать инерциальной системы отсчета и рассмотрим замкнутую систему органов. Для приближенного решения практических задач может быть при определенных условиях применить закон сохранения импульса и открытой системы.
Эти условия включают в себя короткую продолжительность внешних сил и небольшого количества по сравнению с внутренними силами. Кроме того, есть случаи, когда без сохранения полного импульса в открытой системе, некоторые проекция этого момента на выбранном направлении, вдоль которого сумма внешних сил равна нулю, остаются постоянными. На чертежах, иллюстрирующих задачи, необходимо представлять направление скорости проекта и импульса, а также скорость и себя (или) импульсов тел. В решении же, вместо того, чтобы законы Ньютона должны написать закон сохранения импульса, первый в векторной форме, а затем проецируется на выбранном направлении. Экспериментальное исследование взаимодействия различных органов — от планет и звезд в атомов и элементарных частиц — показали, что в любой системе взаимодействующих тел в отсутствие действий других органов за пределами системы, или равно нулю количество рабочих сил геометрическая сумма импульсов тел действительно остаются неизменными. Закон сохранения импульса является основой реактивного движения. Большая заслуга в развитии теории реактивного движения принадлежит Циолковскому. Он разработал теорию переменной массы тела полета (ракеты) в однородном гравитационном поле и рассчитаны запасы топлива, необходимого для преодоления силы тяжести; Основная теория ЖРД, а также элементов его конструкции; Теория многоступенчатых ракет, и предложил два варианта: параллельная (несколько реактивных двигателей работают одновременно) и последовательный (реактивные двигатели работают один за другим).
Циолковский строго научно доказал возможность полета в космос с ракетами с ЖРД, предложил специальную траекторию посадки космического корабля на Землю, выдвинул идею создания межпланетных космических станций и подробно рассмотрены условия жизни и средств к существованию для них. Технические идеи Циолковского используются для создания современной ракетно-космической техники. Движение с помощью струи в соответствии с законом сохранения импульса является основой гидроджет двигателя. В центре движения многих морских моллюсков (осьминогов, медуз, кальмаров, каракатица) также лежит принцип струйной. ЗаключениеЗаконы сохранения составляют основу, на основе которых непрерывность физических теорий. Действительно, рассматривая эволюцию важнейших физических концепций в области механики, электродинамики, теории теплоты, современных физических теорий, мы убеждены, что эти теории неизменно присутствуют или же классические законы сохранения (энергии, импульса и т. д.
) или в дополнение с ними, новые законы, образуя ядро, вокруг которого является интерпретация экспериментальных фактов. «Общность законов сохранения в старых и новых теорий является еще одной формой внутренней взаимосвязи последних."Принципиально важным является соотношение законов сохранения микромира с принципами симметрии. Тот факт, что с некоторых законов сохранения являются приблизительными, из-за, по-видимому, к неполноте наших знаний о свойствах симметрии субмикроскопической уровне. Связь с законами сохранения свойств симметрии был открыт на всех структурных уровнях материи, начиная и заканчивая макротела элементарных частиц. Список литературыБ.М. Яворский, А.А. Детлаф. Справочник по физике. Для инженеров и студентов ВУЗов. Издание четвертое, переработанное. Наука. М. 1968 г. Б.М Яворский, А. А Пинский. Основы физики. Том 1
1. Б.М. Яворский, А.А. Детлаф. Справочник по физике. Для инженеров и студентов ВУЗов. Издание четвертое, переработанное. Наука. М. 1968 г.
2. Б. М Яворский, А. А Пинский. Основы физики. Том 1
список литературы
referatbooks.ru
В замкнутой системе выполняется закон сохранения момента импульса.
Вращающееся вокруг своей оси тело при отсутствии тормозящих вращение сил так и будет продолжать вращаться. Физики привычно объясняют этот феномен тем, что такое вращающееся тело обладает неким количеством движения, выражающимся в форме углового момента количества движения или, кратко, момента импульса или момента вращения. Момент импульса вращающегося тела прямо пропорционален скорости вращения тела, его массе и линейной протяженности. Чем выше любая из этих величин, тем выше момент импульса. Если теперь допустить, что тело вращается не вокруг собственного центра массы, а вокруг некоего центра вращения, удаленного от него, оно всё равно будет обладать вращательным моментом импульса. В математическом представлении момент импульса L тела, вращающегося с угловой скоростью ω, равен L = Iω, где величина I, называемая моментом инерции, является аналогом инерционной массы в законе сохранения линейного импульса, и зависит она как от массы тела, так и от его конфигурации — то есть, от распределения массы внутри тела. В целом, чем дальше от оси вращения удалена основная масса тела, тем выше момент инерции.
Сохраняющейся или консервативной принято называть величину, которая не изменяется в результате рассматриваемого взаимодействия. В рамках закона сохранения момента импульса консервативной величиной как раз и является угловой момент вращения массы — он не изменяется в отсутствие приложенного момента силы или крутящего момента — проекции вектора силы на плоскость вращения, перпендикулярно радиусу вращения, помноженной на рычаг (расстояние до оси вращения). Самый расхожий пример закона сохранения момента импульса — фигуристка, выполняющая фигуру вращения с ускорением. Спортсменка входит во вращение достаточно медленно, широко раскинув руки и ноги, а затем, по мере того, как она собирает массу своего тела всё ближе к оси вращения, прижимая конечности всё ближе к туловищу, скорость вращения многократно возрастает вследствие уменьшения момента инерции при сохранении момента вращения. Тут мы и убеждаемся наглядно, что чем меньше момент инерции I, тем выше угловая скорость ω и, как следствие, короче период вращения, обратно пропорциональный ей.
Следует отметить, однако, что не любая приложенная извне сила сказывается на моменте вращения. Предположим, вы поставили свой велосипед «на попа» (колесами вверх) и сильно раскрутили одно из его колес. Понятно, что, приложив тормозящую силу трения к любой окружности колеса (нажав на ручной тормоз, приложив руку к резине или вращающимся спицам), вы, тем самым, снизите угловую скорость его вращения. Однако, сколько бы вы ни старались, вы не остановите вращения колеса, пытаясь воздействовать на ось вращения. Иными словами, для изменения момента вращения необходима не просто сила, а момент силы — то есть, сила, приложенная по направлению, отличному от направления оси вращения, и на некотором удалении от нее. Поэтому закон сохранения момента вращения можно сформулировать и несколько иначе: момент вращения тела изменяется только в присутствии момента силы, направленной на его изменение.
И тут возникает важное дополнительное замечание. До сих пор мы говорили об изменении момента вращения в плане ускорения или замедления вращения, как такового, но при этом тело продолжало вращаться всё в той же плоскости, и ось вращения не изменяла своей ориентации в пространстве. Теперь предположим, что момент силы приложен в плоскости, которая отличается от плоскости, в которой вращается тело. Такое воздействие неизбежно приведет к изменению направления оси вращения. В отсутствие же внешних воздействий закон сохранения момента импульса подразумевает, что направление оси вращения остается неизменным. Этот принцип широко используется в так называемых гироскопических навигационных приборах. В их основе лежит массивное, быстро вращающееся колесо — гироскоп, — которое не изменяет своей ориентации в пространстве, благодаря чему прибор стабильно указывает заданное направление, вне зависимости от угла поворота субмарины, самолета или спутника, на котором он установлен. С технической точки зрения гироскоп представляет собой массивный диск на осевых подшипниках низкого трения, раскрученный с очень большой скоростью. Идеальный гироскоп — это диск бесконечной массы, вращающийся с бесконечной скоростью в идеальном вакууме. В таком случае закон сохранения момента импульса подскажет нам, что направление оси такого идеального гироскопа не отклонится от исходной ни на одну угловую секунду, и он вечно будет указывать нам на изначально заданную точку. Искусственные спутники Земли, как правило, оснащаются несколькими независимыми гироскопами, вращающимися в разных плоскостях, и бортовая электроника, сопоставляя данные нескольких гироскопических компасов и усредняя поправки на возможные отклонения их показаний, безошибочно определяет координаты и ориентацию спутника в околоземном пространстве.
www.ronl.ru
Реферат на тему:
Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.
В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.
Как и любой из фундаментальных законов сохранения, закон сохранения импульса описывает одну из фундаментальных симметрий, — однородность пространства.
Рассмотрим выражение определения силы
Перепишем его для системы из N частиц:
где суммирование идет по всем силам, действующим на n-ю частицу со стороны m-ой. Согласно третьему закону Ньютона, силы вида и
будут равны по абсолютному значению и противоположны по направлению, то есть
Тогда после подстановки полученного результата в выражение (1) правая часть будет равна нулю, то есть:
или
Как известно, если производная от некоторого выражения равна нулю, то это выражение есть постоянная величина относительно переменной дифференцирования, а значит:
То есть суммарный импульс системы частиц есть величина постоянная. Нетрудно получить аналогичное выражение для одной частицы.
Следует учесть, что вышеприведенные рассуждения справедливы лишь для замкнутой системы.
Также стоит подчеркнуть, что изменение импульса зависит не только от действующей на тело силы, но и от продолжительности её действия.
Согласно теореме Нётер каждому закону сохранения ставится в соответствие некая симметрия уравнений, описывающих систему. В частности, закон сохранения импульса эквивалентен однородности пространства, то есть независимости всех законов, описывающих систему, от положения системы в пространстве. Простейший вывод этого утверждения основан на применении лагранжева подхода к описанию системы.
Рассмотрим функцию Лагранжа свободного тела зависящую от обобщённых координат
обобщённых скоростей
и времени t. Здесь точка над q обозначает дифференцирование по времени,
Выберем для рассмотрения прямоугольную декартову систему координат, тогда
для каждой
-той частицы. Используя однородность пространства, мы можем дать всем радиус-векторам частиц одинаковое приращение, которое не будет влиять на уравнения движения:
где
В случае постоянства скорости функция Лагранжа изменится следующим образом:
где суммирование идет по всем частицам системы. Так как приращение не влияет на уравнения движения, то вариация функции Лагранжа должна быть равной нулю: С учётом того, что вектор
— произвольный, последнее требование выполняется при:
Воспользуемся уравнением Лагранжа
Это означает, что сумма, стоящая под знаком дифференциала, — постоянная величина для рассматриваемой системы. Сама сумма и есть суммарный импульс системы:
Учитывая, что лагранжиан свободной частицы имеет вид: нетрудно видеть, что последнее выражение совпадает с выражением в ньютоновом формализме:
Для релятивистской свободной частицы лагранжиан имеет несколько другую форму: что приводит к релятивистскому определению импульса
В настоящее время не существует каких-либо экспериментальных фактов, свидетельствующих о невыполнении закона сохранения импульса.
Аналогично ситуации с законом сохранения энергии, при переходе к искривлённому пространству-времени закон сохранения импульса, выражаемый пространственными компонентами соотношения для тензора энергии-импульса
где точка с запятой выражает ковариантную производную, приводит лишь к локально сохраняющимся величинам. Это связано с отсутствием глобальной однородности пространства в пространстве-времени общего вида.
Можно придумать такие определения импульса гравитационного поля, что глобальный закон сохранения импульса будет выполняться при движении во времени системы тел и полей, но все такие определения содержат элемент произвола, так как вводимый импульс гравитационного поля не может быть тензорной величиной при произвольных преобразованиях координат.
www.wreferat.baza-referat.ru