
Любому, кто хоть раз задумывался в жизни о том, чтобы стать "айтишником" или системным администратором, да и просто связать судьбу с вычислительной техникой, знание о том, как происходит представление чисел в памяти компьютера, абсолютно необходимо. Ведь именно на этом основываются языки программирования низкого уровня, такие как Assembler. Поэтому сегодня мы рассмотрим представление чисел в компьютере и их размещение в ячейках памяти.
Если вы читаете данную статью, то, скорее всего, уже знаете об этом, но повторить стоит. Все данные в персональном компьютере хранятся в двоичной системе счисления. Это означает, что любое число необходимо представить в соответствующей форме, то есть состоящим из нулей и единиц.
Чтобы перевести привычные для нас десятичные числа к виду, понятному компьютеру, нужно воспользоваться описанным ниже алгоритмом. Существуют и специализированные калькуляторы.
Итак, для того чтобы перевести число в двоичную систему счисления, нужно взять выбранное нами значение и поделить его на 2. После этого мы получим результат и остаток (0 или 1). Результат опять делим 2 и запоминаем остаток. Данную процедуру нужно повторять до тех пор, пока в итоге также не окажется 0 или 1. Затем записываем конечное значение и остатки в обратном порядке, как мы их получали.
Именно так и происходит представление чисел в компьютере. Любое число записывается в двоичной форме, а потом занимает ячейку памяти.

Как вам должно быть уже известно, минимальная единица измерения информации составляет 1 бит. Как мы уже выяснили, представление чисел в компьютере происходит в двоичном формате. Таким образом, каждый бит памяти будет занят одним значением – 1 или 0.
Для хранения больших чисел используются ячейки. Каждая такая единица содержит до 8 бит информации. Поэтому можно сделать вывод, что минимальное значение в каждом отрезке памяти может составлять 1 байт или быть восьмизначным двоичным числом.
Наконец мы подобрались к непосредственному размещению данных в компьютере. Как было уже сказано, первым делом процессор переводит информацию в двоичный формат, а только затем размещает в памяти.
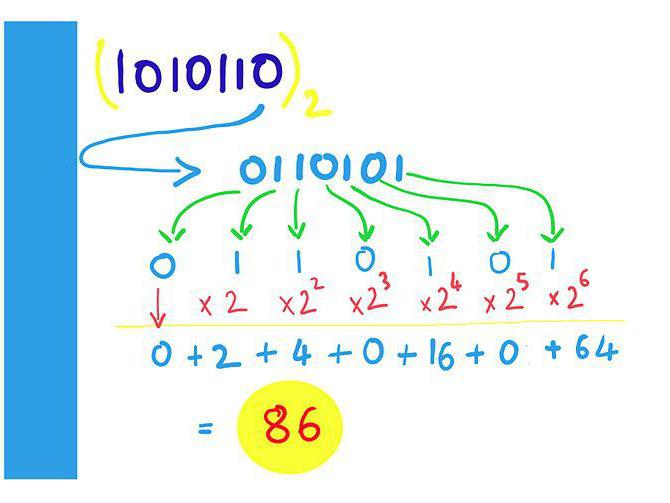
Начнем мы с самого простого варианта, коим является представление целых чисел в компьютере. Память ПК отводит под этот процесс до смешного малое количество ячеек – всего одну. Таким образом, максимум в одном слоте могут быть значения от 0 до 11111111. Давайте переведём максимальное число в привычную нам форму записи.Х = 1 × 27 + 1 × 26 + 1 × 25 + 1 × 24 + 1 × 23 + 1 × 22 + 1 × 21 + 1 × 20 = 1 × 28 - 1 = 255.
Теперь мы видим, что в одной ячейке памяти может располагаться значение от 0 до 255. Однако это относится исключительно к целым неотрицательным числам. Если же компьютеру понадобится записать отрицательное значение, всё пройдет немного по-другому.

Теперь давайте посмотрим, как происходит представление чисел в компьютере, если они являются отрицательными. Для размещения значения, которое меньше нуля, отводится две ячейки памяти, или 16 бит информации. При этом 15 уходят под само число, а первый (крайний левый) бит отдается под соответствующий знак.
Если цифра отрицательная, то записывается "1", если положительная, то "0". Для простоты запоминания можно провести такую аналогию: если знак есть, то ставим 1, если его нет, то ничего (0).
Оставшиеся 15 бит информации отводятся под число. Аналогично предыдущему случаю, в них можно поместить максимум пятнадцать единиц. Стоит отметить, что запись отрицательных и положительных чисел существенно отличается друг от друга.
Для того чтобы разместить в 2 ячейках памяти значение больше нуля или равное ему, используется так называемый прямой код. Данная операция производится так же, как и было описано, а максимальное А = 32766, если использовать десятичную систему счисления. Сразу хочется отметить, что в данном случае "0" относится к положительным.
Представление целых чисел в памяти компьютера не является такой уж трудной задачей. Хотя она немного усложняется, если речь идет об отрицательном значении. Для записи числа, которое меньше нуля, используется дополнительный код.
Чтобы его получить, машина производит ряд вспомогательных операций.
Приведем наглядный пример. Пусть у нас есть число Х = - 131. Сначала получаем его модуль |Х|= 131. Затем переводим в двоичную систему и записываем в 16 ячеек. Получим Х = 0000000010000011. После инвертирования Х=1111111101111100. Добавляем к нему "1" и получаем обратный код Х=1111111101111101. Для записи в 16-битную ячейку памяти минимальным числом является Х = - (215) = - 32767.
Как видите, представление вещественных чисел в компьютере не так уж и сложно. Однако рассмотренного диапазона может не хватать для большинства операций. Поэтому, для того чтобы разместить большие числа, компьютер выделяет из памяти 4 ячейки, или 32 бита.
Процесс записи абсолютно не отличается от представленного выше. Так что мы просто приведем диапазон чисел, которые могут храниться в данном типе.
Хмах=2 147 483 647.
Хmin=- 2 147 483 648.
Данных значений в большинстве случаев достаточно для того, чтобы записывать и проводить операции с данными.
Представление вещественных чисел в компьютере имеет свои преимущества и недостатки. С одной стороны, данная методика позволяет проще производить операции между целочисленными значениями, что значительно ускоряет работу процессора. С другой стороны, данного диапазона недостаточно для решения большинства задач экономики, физики, арифметики и других наук. Поэтому теперь мы рассмотрим очередную методику для сверхвеличин.
Это последнее, что вам необходимо знать про представление чисел в компьютере. Поскольку при записи дробей возникает проблема определения положения запятой в них, для размещения подобных цифр в компьютере используется экспоненциальная форма.
Любое число может быть представлено в следующей форме Х = m * рп. Где m – это мантисса числа, р – основание системы счисления и п – порядок числа.
Для стандартизации записи чисел с плавающей запятой используется следующее условие, согласно которому модуль мантиссы должен быть больше или равен 1/п и меньше 1.
Пусть нам дано число 666,66. Приведём его к экспоненциальной форме. Получится Х = 0,66666 * 103. Р = 10 и п = 3.
На хранение значений с плавающей запятой обычно выделяется 4 или 8 байт (32 или 64 бита). В первом случае это называется числом обычной точности, а во втором – двойной точности.
Из 4 байт, выделенных под хранение цифр, 1 (8 разрядов) отдается под данные о порядке и его знаке, а 3 байта (24 разряда) уходят на хранение мантиссы и её знака по тем же принципам, что и для целочисленных значений. Зная это, мы можем провести нехитрые расчеты.
Максимальное значение п = 11111112= 12710. Исходя из него, мы можем получить максимальный размер числа, которое может храниться в памяти компьютера. Х=2127. Теперь мы можем вычислить максимально возможную мантиссу. Она будет равна 223 – 1 ≥ 223 = 2(10 × 2,3) ≥ 10002,3 = 10(3 × 2,3) ≥ 107. В итоге, мы получили приближенное значение.
Если теперь мы объединим оба расчета, то получим значение, которое может быть записано без потерь в 4 байта памяти. Оно будет равно Х = 1,701411 * 1038. Остальные цифры были отброшены, поскольку именно такую точность позволяет иметь данный способ записи.

Поскольку все вычисления были расписаны и объяснены в предыдущем пункте, здесь мы расскажем всё очень коротко. Для чисел с двойной точностью обычно выделяется 11 разрядов для порядка и его знака, а также 53 разряда для мантиссы.
П = 11111111112= 102310.
М = 252 -1 = 2(10*5.2) = 10005.2 = 1015.6. Округляем в большую сторону и получаем максимальное число Х = 21023 с точностью до "м".
Надеемся, информация про представление целых и вещественных чисел в компьютере, которую мы предоставили, пригодится вам в обучении и будет хоть немного понятнее, чем то, что обычно пишут в учебниках.
fb.ru
План практического занятия № 13
Тема: Практическое занятие № 13 «Представление чисел в компьютере»
Преподаватель: Торчинская Е.И.
Дисциплина: Информатика
Группа: Ам 13, Св 13, АСУ 14, КСК 14, СЭЗС 14, ТОАМ 14, ТПОП 14, ТЭО 14
ЦЕЛИ УРОКА:
Обучающая: способствовать приобретению у обучающихся практических навыков применения методов кодирования и алгебраического сложения двоичных чисел.
Развивающая: развивать умение выделять главное, внимание, память учащихся, самостоятельность, умение сопоставлять полученную информацию; развивать мышление учащихся посредством анализа, сравнения и обобщения изучаемого материала.
Воспитывающая: прививать навыки самостоятельности в работе, воспитывать аккуратность, дисциплинированность; формировать интерес к предмету, навыки контроля и самоконтроля; активизировать познавательную и творческую активность учащихся.
Тип урока: комбинированный урок.
Вид урока: практическое занятие.
Предполагаемые формы работы: индивидуальная, фронтальный опрос.
Метапредметная связь: спец. дисциплины.
Средства обучения: компьютеры, проектор, доска.
Ход занятия
Организационный момент.
Приветствие. Проверка явки и готовности к занятию.
Сообщение темы и целей занятия.
Актуализация знаний.
Проверка домашнего задания.
Методические указания.
В ЭВМ в целях упрощения выполнения арифметических операций применяют специальные коды для представления чисел. Использование кодов позволяет свести операцию вычитания чисел к арифметическому сложению кодов этих чисел. Применяются прямой, обратный и дополнительный коды чисел. Прямой код используется для хранения чисел в запоминающем устройстве ЭВМ. Обратный и дополнительный коды используются для замены операции вычитания операцией сложения, что упрощает устройство арифметического блока ЭВМ.
Прямой код. Прямой код двоичного числа совпадает по изображению с записью самого числа. Значение знакового разряда для положительных чисел равно 0, а для отрицательных чисел 1.
Обратный код. Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.
Дополнительный код. Дополнительный код положительного числа совпадает с прямым кодом. Для отрицательного числа дополнительный код образуется путем получения обратного кода и добавлением к младшему разряду единицы.
Например, в однобайтовом формате числа 27 и -27 имеют вид:
| Число | Прямой код | Обратный код | Дополнительный код |
| 27 | 00011011 | 00011011 | 00011011 |
| -27 | 10011011 | 11100100 | 11100101 |
Пример 1. Найти прямой, обратный и дополнительный код представления числа 13 в однобайтном формате.
1 шаг: Переведем число 13 из десятичной системы счисления в двоичную.

2 шаг: Для представления числа в компьютере выделен 1 байт. Старший бит занимает знак числа – 0. Сам код числа должен занимать 7 бит. Таким образом прямой код числа 13
Так как для положительных чисел прямой, обратный и дополнительный код совпадает, то ответ 00001101.
Пример 2. Найти прямой, обратный и дополнительный код представления числа -23 в однобайтовом формате.
1 шаг: Переведем число -23 из десятичной системы счисления в двоичную. Получим
-2310=-101112
2 шаг: Прямой код числа в однобайтовом формате, учитывая, что старший бит занимает знак числа -1, имеет вид
3 шаг: Найдем обратный код числа -23, заменив все цифры числа на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица. Имеем,
4 шаг: Найдем дополнительный код числа -23, добавив 1 к младшему разряду обратного кода.
Ответ: прямой код – 10010111; обратный – 11101000; дополнительный – 11101001.
Инструктаж перед практической работой.
Для выполнения практической работы № 13 «Представление чисел в компьютере», необходимо воспользоваться методическими рекомендациями по выполнению практической работы.
Выполнение практической работы.
Самостоятельная работа.
Задание 1. Запишите числа в беззнаковом коде (формат 1 байт):
а) 31; б) 163; в) 65; г) 128.
Задание 2. Найдите десятичные представления чисел, записанных в беззнаковом коде: а) 0 1011000; б) 1 0011011; в) 0 1101001; г) 1 1000000.
Задание 3. Записать число в прямом, обратном и дополнительном кодах (формат 1 байт): а) 11010; б) -11101; в) -101001; г) -1001110.
Задание 4. Запишите числа в прямом коде (формат 1 байт):
а) 31; б) -63; в) 65; г) -122.
Задание 5. Запишите числа в обратном и дополнительном кодах (формат 1 байт):
а) 9; б) -15; в) -127; г) -120.
Задание 6. Найдите десятичные представления чисел, записанных в дополнительном коде: а) 1 1111000; б) 1 0011011; в) 1 1101001; г) 1 0000000.
Задание 7. Найдите десятичные представления чисел, записанных в обратном коде:
а) 1 1101000; б) 1 0011111; в) 1 0101011; г) 1 0000000.
Домашнее задание.
Информатика. Базовый уровень: учебник для 10 класса / И.Г. Семакин, Е.К. Хеннер, Т.Ю. Шеина. – 3-е изд. – М.: БИНОМ, 2014, стр. 34-38.
Подведение итогов и выводы.
Рефлексия.
Выставление оценок.
kopilkaurokov.ru
Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа. В большинстве компьютеров операция вычитания не используется. Вместо нее производится сложение обратных или дополнительных кодов уменьшаемого и вычитаемого. Это позволяет существенно упростить конструкцию АЛУ.
4.2. Арифметические действия над целыми числами
Рассмотрим кратко вопрос о выполнении арифметических действий над целыми числами. При сложении чисел А и В имеют место четыре основных случая:
1. А и В положительные. При суммировании складываются все разряды, включая разряд знака. Так как знаковые разряды положительных слагаемых равны нулю, разряд знака суммы тоже равен нулю. Например: 0 0000011 (А=3) + 0 0000111 (В=7) = 0 0001010 (10)10
Получен правильный результат
2. А положительное, B отрицательное и по абсолютной величине больше, чем А. Например: 3+(-10)=-7 0 0000011 (прямой код) + 1 1110101 (обратный код числа
-10) = 1 1111000 (обратный код числа -7) Получен правильный результат в обратном коде. При переводе в прямой код биты цифровой части результата инвертируются: 1 0000111 = –710.
3. А положительное, B отрицательное и по абсолютной величине меньше, чем А. Например: 10+(-3)=7 0 0001010 (прямой код) + 1 1111100 (обратный код числа
-3) = 1 0000110 Компьютер исправляет полученный первоначально неправильный результат (6 вместо 7). Переносом единицы из знакового разряда в младший разряд суммы и выдает правильный результат 7.
4. А и В отрицательные. Например: (-3)+(-7)=-10 1 1111100 (обратный код -3) + 1 1111000 (обратный код числа -7) = 1 1110100. Полученный первоначально неправильный результат (обратный код числа –1110 вместо обратного кода числа –1010) компьютер исправляет переносом единицы из знакового разряда в младший разряд суммы. При переводе результата в прямой код биты цифровой части числа инвертируются: 1 0001010 = –1010.
Сложение целых чисел может быть организовано с использованием дополнительных кодов. Здесь также имеют место рассмотренные выше случаи:
1. А и В положительные. Здесь нет отличий от случая 1, рассмотренного для обратного кода.
2. А положительное, B отрицательное и по абсолютной величине больше, чем А. Например: 3+(-10)=-7 0 0000011 (прямой код) + 1 1110110 (дополнительный код числа -10) = 1 1111001 (дополнительный код числа -7) Получен правильный результат в дополнительном коде. При переводе в прямой код биты цифровой части результата инвертируются и к младшему разряду прибавляется единица: 1 0000110 + 1 = 1 0000111 = –710.
3. А положительное, B отрицательное и по абсолютной величине меньше, чем А. Например: 10+(-3)=7 0 0001010 (прямой код) + 1 1111101 (дополнительный код числа -3) = 0 0000111. Получен правильный результат. Единицу переноса из знакового разряда компьютер отбрасывает.
4. А и В отрицательные. Например: : (-3)+(-7)=-10 1 1111101 (дополнительный код -3) + 1 1111001 (дополнительный код числа -7) = 1 1110110 Получен правильный результат в дополнительном коде. Единицу переноса из знакового разряда компьютер отбрасывает.
Сравнение рассмотренных форм кодирования целых чисел со знаком показывает:
на преобразование отрицательного числа в обратный код компьютер затрачивает меньше времени, чем на преобразование в дополнительный код, так как последнее состоит из двух шагов — образования обратного кода и прибавления единицы к его младшему разряду;
время выполнения сложения для дополнительных кодов чисел меньше, чем для их обратных кодов, потому что в таком сложении нет переноса единицы из знакового разряда в младший разряд результата.
При сложении может возникнуть ситуация, когда старшие разряды результата операции не помещаются в отведенной для него области памяти. Такая ситуация называется переполнением разрядной сетки формата числа. Для обнаружения переполнения и оповещения о возникшей ошибке в компьютере используются специальные средства.
Во многих компьютерах умножение производится как последовательность сложений и сдвигов. Для этого в АЛУ имеется регистр, называемый накапливающим сумматором, который до начала выполнения операции содержит число ноль. В процессе выполнения операции в нем поочередно размещаются множимое и результаты промежуточных сложений, а по завершении операции — окончательный результат.
Другой регистр АЛУ, участвующий в выполнении этой операции, вначале содержит множитель. Затем по мере выполнения сложений содержащееся в нем число уменьшается, пока не достигнет нулевого значения.
Деление для компьютера является трудной операцией. Обычно оно реализуется путем многократного прибавления к делимому дополнительного кода делителя.
4.3. Представление вещественных чисел в компьютере
Система вещественных чисел в математических вычислениях предполагается непрерывной и бесконечной, т.е. не имеющей ограничений на диапазон и точность представления чисел. Однако в компьютерах числа хранятся в регистрах и ячейках памяти с ограниченным количеством разрядов. В следствие этого система вещественных чисел, представимых в машине, является дискретной (прерывной) и конечной. При написании вещественных чисел в программах вместо привычной запятой принято ставить точку.
В ПК числа могут быть представлены в одной из двух форм:
1) с фиксированной точкой – в естественной форме (0.00345 – правильная дробь, 1.23456 – неправильная дробь)
2) с плавающей точкой (запятой) (555,55 = 55555•10-2 = 0,55555•103)
Для отображения вещественных чисел, которые могут быть как очень маленькими, так и очень большими, используется форма записи чисел с порядком основания системы счисления. Любое число А может быть представлено в экспоненциальной форме:
А = m • qn,
где m – мантисса числа, q – основание системы счисления.,n – порядок числа.
studfiles.net
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 8 классы | Планирование уроков на учебный год (ФГОС) | § 1.2. Представление чисел в компьютере
Ключевые слова:
• разряд • беззнаковое представление целых чисел • представление целых чисел со знаком • представление вещественных чисел
Оперативная память компьютера состоит из ячеек, каждая из которых представляет собой физическую систему, состоящую из некоторого числа однородных элементов. Эти элементы обладают двумя устойчивыми состояниями, одно из которых соответствует нулю, а другое — единице. Каждый такой элемент служит для хранения одного из битов — разряда двоичного числа. Именно поэтому каждый элемент ячейки называют битом или разрядом (рис. 1.2).

Рис. 1.2. Ячейка памяти
Для компьютерного представления целых чисел используется несколько различных способов, отличающихся друг от друга количеством разрядов (под целые числа обычно отводится 8, 16, 32 или 64 разряда) и наличием или отсутствием знакового разряда. Беззнаковое представление можно использовать только для неотрицательных целых чисел, отрицательные числа представляются только в знаковом виде.
Беззнаковое представление используется для таких объектов, как адреса ячеек, всевозможные счётчики (например, число символов в тексте), а также числа, обозначающие дату и время, размеры графических изображений в пикселях и т. д.
Максимальное значение целого неотрицательного числа достигается в случае, когда во всех разрядах ячейки хранятся единицы. Для n-разрядного представления оно будет равно 2n-1. Минимальное число соответствует п нулям, хранящимся в n разрядах памяти, и равно нулю.
Ниже приведены максимальные значения для беззнаковых целых n-разрядных чисел:

Для получения компьютерного представления беззнакового целого числа достаточно перевести число в двоичную систему счисления и дополнить полученный результат слева нулями до стандартной разрядности.
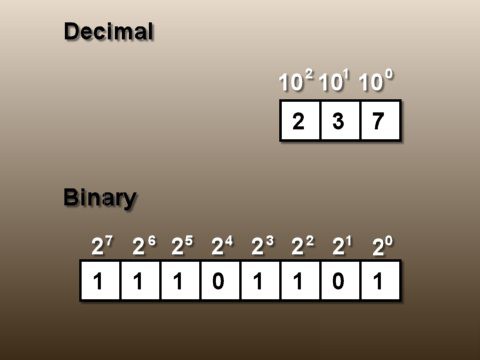
Пример 1. Число 5310 = 1101012 в восьмиразрядном представлении имеет вид:

Это же число 53 в шестнадцати разрядах будет записано следующим образом:

При представлении со знаком самый старший (левый) разряд отводится под знак числа, остальные разряды — под само число. Если число положительное, то в знаковый разряд помещается 0, если число отрицательное — 1. Такое представление чисел называется прямым кодом.
В компьютере прямые коды используются для хранения положительных чисел в запоминающих устройствах, для выполнения операций с положительными числами.
На сайте Федерального центра информационно-образовательных ресурсов (http://fcior.edu.ru/) размещён информационный модуль «Число и его компьютерный код». С помощью этого ресурса вы можете получить дополнительную информацию по изучаемой теме.
Для выполнения операций с отрицательными числами используется дополнительный код, позволяющий заменить операцию вычитания сложением. Узнать алгоритм образования дополнительного кода вы можете с помощью информационного модуля «Дополнительный код», размещённого на сайте Федерального центра информационно-образовательных ресурсов (http://fcior.edu.ru/).
Любое вещественное число А может быть записано в экспоненциальной форме:
 где:
где:
m — мантисса числа; q — основание системы счисления; p — порядок числа.
Например, число 472 ООО ООО может быть представлено так: 4,72 • 108, 47,2 • 107, 472,0 • 106 и т. д.
С экспоненциальной формой записи чисел вы могли встречаться при выполнении вычислений с помощью калькулятора, когда в качестве ответа получали записи следующего вида: 4.72Е+8.
Здесь знак «Е» обозначает основание десятичной системы счисления и читается как «умножить на десять в степени».
Из приведённого выше примера видно, что положение запятой в записи числа может изменяться.
Для единообразия мантиссу обычно записывают как правильную дробь, имеющую после запятой цифру, отличную от нуля. В этом случае число 472 ООО ООО будет представлено как 0,472 • 109.
Вещественное число может занимать в памяти компьютера 32 или 64 разряда. При этом выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.
Пример:

Диапазон представления вещественных чисел определяется количеством разрядов, отведённых для хранения порядка числа, а точность определяется количеством разрядов, отведённых для хранения мантиссы.
Максимальное значение порядка числа для приведённого выше примера составляет 11111112 = 12710, и, следовательно, максимальное значение числа:
0,11111111111111111111111 • 101111111
Попытайтесь самостоятельно выяснить, каков десятичный эквивалент этой величины.
Широкий диапазон представления вещественных чисел важен для решения научных и инженерных задач. Вместе с тем следует понимать, что алгоритмы обработки таких чисел более трудоёмки по сравнению с алгоритмами обработки целых чисел.
Для компьютерного представления целых чисел используются несколько различных способов, отличающихся друг от друга количеством разрядов (8, 16, 32 или 64) и наличием или отсутствием знакового разряда.
Для представления беззнакового целого числа его следует перевести в двоичную систему счисления и дополнить полученный результат слева нулями до стандартной разрядности.
При представлении со знаком самый старший разряд отводится под знак числа, остальные разряды — под само число. Бели число положительное, то в знаковый разряд помещается 0, если число отрицательное, то 1. Положительные числа хранятся в компьютере в прямом коде, отрицательные — в дополнительном.
При хранении в компьютере вещественных чисел выделяются разряды на хранение знака порядка числа, самого порядка, знака мантиссы и мантиссы. При этом любое число записывается так:
 где:
где:
m — мантисса числа; q — основание системы счисления; p — порядок числа.
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Используйте эти материалы при подготовке ответов на вопросы и выполнении заданий.
2. Как в памяти компьютера представляются целые положительные и отрицательные числа?
3. Любое целое число можно рассматривать как вещественное, но с нулевой дробной частью. Обоснуйте целесообразность наличия особых способов компьютерного представления целых чисел.
4. Представьте число 6310 в беззнаковом 8-разрядном формате.
5. Найдите десятичные эквиваленты чисел по их прямым кодам, записанным в 8-разрядном формате со знаком:
а) 01001100; б) 00010101.
6. Какие из чисел 4438, 1010102, 25610 можно сохранить в 8-разрядном формате?
7. Запишите следующие числа в естественной форме:
а) 0,3800456 • 102; б) 0,245 • 10-3; в) 1,256900Е+5; г) 9,569120Е-3.
8. Запишите число 2010,010210 пятью различными способами в экспоненциальной форме.
9. Запишите следующие числа в экспоненциальной форме с нормализованной мантиссой — правильной дробью, имеющей после запятой цифру, отличную от нуля:
а) 217,93410; б) 7532110; в) 0,0010110.
10. Изобразите схему, связывающую основные понятия, рассмотренные в данном параграфе.

 |  |  | ||
| Презентации, плакаты, текстовые файлы | Вернуться к материалам урока | Ресурсы ЭОР |

Cкачать материалы урока
xn----7sbbfb7a7aej.xn--p1ai