Числа Фибоначчи. Реферат на тему числа фибоначчи
Числа Фибоначчи. История. Интересные факты. Использование в повседневной жизни
Золотое сечение в теле человека
 Краевая научно-практическая конференция учебно-исследовательских и проектных работ учащихся 6-11 классов «Прикладные и фундаментальные вопросы математики» Прикладные вопросы математики Золотое сечение
Краевая научно-практическая конференция учебно-исследовательских и проектных работ учащихся 6-11 классов «Прикладные и фундаментальные вопросы математики» Прикладные вопросы математики Золотое сечение
Подробнее Числа Фибоначчи и золотое сечение
 МОУ «Малыгинская средняя общеобразовательная школа» Числа Фибоначчи и золотое сечение Выполнила ученица 9 «а» класса Кузнецова Юлия под руководством учителя математики Большаковой О.К. «Числа не управляют
МОУ «Малыгинская средняя общеобразовательная школа» Числа Фибоначчи и золотое сечение Выполнила ученица 9 «а» класса Кузнецова Юлия под руководством учителя математики Большаковой О.К. «Числа не управляют
Подробнее Рис. 1.Золотой квадрат.
 УДК 517.8 ЗОЛОТОЕ СЕЧЕНИЕ В ПРИРОДЕ А.А. Куликов, студент группы ЭЭб-152, I курс Научный руководитель: А.В. Чередниченко, ассистент Кузбасский государственный технический университет г. Кемерово Что общего
УДК 517.8 ЗОЛОТОЕ СЕЧЕНИЕ В ПРИРОДЕ А.А. Куликов, студент группы ЭЭб-152, I курс Научный руководитель: А.В. Чередниченко, ассистент Кузбасский государственный технический университет г. Кемерово Что общего
Подробнее Уровни Фибоначчи В XIII веке Леонардо Фибоначчи, известный итальянский математик обнаружил простую последовательность чисел 1, 1, 2, 3, 5, 8, 13, 21,
 Уровни Фибоначчи В XIII веке Леонардо Фибоначчи, известный итальянский математик обнаружил простую последовательность чисел 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144... Такая зависимость получилась в результате
Уровни Фибоначчи В XIII веке Леонардо Фибоначчи, известный итальянский математик обнаружил простую последовательность чисел 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144... Такая зависимость получилась в результате
Подробнее Темы проектов по математике для 5 класса
 Темы проектов по математике для 5 класса Алгебраические дроби. В мире процентов. В стране рыцарей и лжецов. Виды уравнений, решаемые в 5-м классе. Возникновение чисел. Вокруг обыкновенных дробей. Графический
Темы проектов по математике для 5 класса Алгебраические дроби. В мире процентов. В стране рыцарей и лжецов. Виды уравнений, решаемые в 5-м классе. Возникновение чисел. Вокруг обыкновенных дробей. Графический
Подробнее Золотое сечение и строение человека
 1 Городское соревнование юных исследователей «Шаг в будущее Юниор» Золотое сечение и строение человека Россия, г.сургут, Ульянова Виктория Александровна Муниципальное бюджетное общеобразовательное учреждение
1 Городское соревнование юных исследователей «Шаг в будущее Юниор» Золотое сечение и строение человека Россия, г.сургут, Ульянова Виктория Александровна Муниципальное бюджетное общеобразовательное учреждение
Подробнее Древнекитайский символ
 Древнекитайский символ Сравните Некоторые современные здания Золотое сечение «Красота и гармония стали важнейшими категориями познания, в определенной степени даже его целью, ибо в конечном итоге художник
Древнекитайский символ Сравните Некоторые современные здания Золотое сечение «Красота и гармония стали важнейшими категориями познания, в определенной степени даже его целью, ибо в конечном итоге художник
Подробнее Глава 4.2. Технический анализ: Фибоначчи
 Глава 4.2 Технический анализ: Фибоначчи ТЕХНИЧЕСКИЙ АНАЛИЗ: ФИБОНАЧЧИ Анализ Фибоначчи - это инструмент, позволяющий выявить потенциальные уровни поддержки и сопротивления, основываясь на прошлых ценовых
Глава 4.2 Технический анализ: Фибоначчи ТЕХНИЧЕСКИЙ АНАЛИЗ: ФИБОНАЧЧИ Анализ Фибоначчи - это инструмент, позволяющий выявить потенциальные уровни поддержки и сопротивления, основываясь на прошлых ценовых
Подробнее Математическая гармония человеческого тела
 Краевая научно-практическая конференция учебно-исследовательских работ учащихся 9-11 классов «Прикладные и фундаментальные вопросы математики» Прикладные вопросы математики Математическая гармония человеческого
Краевая научно-практическая конференция учебно-исследовательских работ учащихся 9-11 классов «Прикладные и фундаментальные вопросы математики» Прикладные вопросы математики Математическая гармония человеческого
Подробнее Числа Фибоначчи. Формула красоты.
 Научно исследовательская работа Числа Фибоначчи. Формула красоты. Автор: ученик10 класс Шроо Артур Муниципального бюджетного образовательного учреждения Катановской средней общеобразовательной школы Руководитель:
Научно исследовательская работа Числа Фибоначчи. Формула красоты. Автор: ученик10 класс Шроо Артур Муниципального бюджетного образовательного учреждения Катановской средней общеобразовательной школы Руководитель:
Подробнее Страничка для влюбленных в математику
 Страничка для влюбленных в математику Страницу подготовила учитель математики, директор школы Шмелькова Наталья Александровна Если учитель имеет только любовь к делу, он будет хороший учитель. Если учитель
Страничка для влюбленных в математику Страницу подготовила учитель математики, директор школы Шмелькова Наталья Александровна Если учитель имеет только любовь к делу, он будет хороший учитель. Если учитель
Подробнее Проект для учеников 8 классов
 Проект для учеников 8 классов «Геометрия владеет двумя сокровищами - теоремой Пифагора и золотым сечением. И если первое из этих двух сокровищ можно сравнить с мерой золота, то второе с драгоценным камнем.
Проект для учеников 8 классов «Геометрия владеет двумя сокровищами - теоремой Пифагора и золотым сечением. И если первое из этих двух сокровищ можно сравнить с мерой золота, то второе с драгоценным камнем.
Подробнее Учебный проект «Золотое сечение» Часть I
 Муниципальное бюджетное общеобразовательное учреждение Лицей 7 г. Химки Учебный проект «Золотое сечение» Часть I «Человек венец творения природы» Автор исследования: Мизеровская Анна ученица 10 «А» класса
Муниципальное бюджетное общеобразовательное учреждение Лицей 7 г. Химки Учебный проект «Золотое сечение» Часть I «Человек венец творения природы» Автор исследования: Мизеровская Анна ученица 10 «А» класса
Подробнее АСТРОНОМИЯ А С Т Р О Н О М И Я. Кеплер
 А С Т Р О Н О М И Я Кеплер 243 Золотое сечение в строении Солнечной системы и Вселенной У каждой планеты имеется минимальный радиус орбиты, но есть и максимальный как у всякого эллипса. Если рассмотреть
А С Т Р О Н О М И Я Кеплер 243 Золотое сечение в строении Солнечной системы и Вселенной У каждой планеты имеется минимальный радиус орбиты, но есть и максимальный как у всякого эллипса. Если рассмотреть
Подробнее Содержание курса математики в 5 6 классах
 Содержание курса математики в 5 6 классах Натуральные числа и нуль Натуральный ряд чисел и его свойства Натуральное число, множество натуральных чисел и его свойства, изображение натуральных чисел точками
Содержание курса математики в 5 6 классах Натуральные числа и нуль Натуральный ряд чисел и его свойства Натуральное число, множество натуральных чисел и его свойства, изображение натуральных чисел точками
Подробнее Буква слово, цифра число?
 1 Буква слово, цифра число? Нина Коптюг, кандидат филологических наук, лауреат 1 Всероссийского конкурса «Дистанционный учитель года РФ», победитель конкурса ПНПО «Лучший учитель РФ», представитель РФ
1 Буква слово, цифра число? Нина Коптюг, кандидат филологических наук, лауреат 1 Всероссийского конкурса «Дистанционный учитель года РФ», победитель конкурса ПНПО «Лучший учитель РФ», представитель РФ
Подробнее МЕДИЦИНА ЭПОХИ ВОЗРОЖДЕНИЯ
 ВГУЗУ «Украинская медицинская стоматологическая академия» Кафедра социальной медицины, организации и экономики здравоохранения с биостатистикой и медицинским правоведением МЕДИЦИНА ЭПОХИ ВОЗРОЖДЕНИЯ Лектор:
ВГУЗУ «Украинская медицинская стоматологическая академия» Кафедра социальной медицины, организации и экономики здравоохранения с биостатистикой и медицинским правоведением МЕДИЦИНА ЭПОХИ ВОЗРОЖДЕНИЯ Лектор:
Подробнее ОСНОВНЫЕ АЛГОРИТМИЧЕСКИЕ КОНСТРУКЦИИ
 ОСНОВНЫЕ АЛГОРИТМИЧЕСКИЕ КОНСТРУКЦИИ ЭТАПЫ РЕШЕНИЯ ЗАДАЧ НА ЭВМ : постановка задачи; математическое описание задачи; выбор и обоснование метода решения; алгоритмизация вычислительного процесса; составление
ОСНОВНЫЕ АЛГОРИТМИЧЕСКИЕ КОНСТРУКЦИИ ЭТАПЫ РЕШЕНИЯ ЗАДАЧ НА ЭВМ : постановка задачи; математическое описание задачи; выбор и обоснование метода решения; алгоритмизация вычислительного процесса; составление
Подробнее Урок-игра по теме «Системы счисления»
 Урок-игра по теме «Системы счисления» Предмет: информатика и ИКТ Класс: 9 класс Тема учебного занятия: Урок-игра «Системы счисления. Перевод из одной системы счисления в другие, арифметические операции
Урок-игра по теме «Системы счисления» Предмет: информатика и ИКТ Класс: 9 класс Тема учебного занятия: Урок-игра «Системы счисления. Перевод из одной системы счисления в другие, арифметические операции
Подробнее Создание собственной линейки фэн-шуй
 Создание собственной линейки фэн-шуй Ко мне часто обращаются с вопросом: есть ли общие корни у архитектурных и дизайнерских принципов, используемых китайскими мастерами, и священной геометрии масонов и
Создание собственной линейки фэн-шуй Ко мне часто обращаются с вопросом: есть ли общие корни у архитектурных и дизайнерских принципов, используемых китайскими мастерами, и священной геометрии масонов и
Подробнее ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ В КОМПЬЮТЕРЕ
 ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ В КОМПЬЮТЕРЕ Информация в ЭВМ кодируется, как правило, в двоичной или в двоично-десятичной системе счисления. Система счисления это способ наименования и изображения чисел с помощью
ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ В КОМПЬЮТЕРЕ Информация в ЭВМ кодируется, как правило, в двоичной или в двоично-десятичной системе счисления. Система счисления это способ наименования и изображения чисел с помощью
Подробнее S = {1, 1, 1, } (1) N = (N раз). (2)
 7.5. Новое геометрическое определение числа Что такое число? «Ливийский» период моей жизни, который продолжался с февраля 1995 по август 1997 г., был своеобразным и сознательным «заточением», кода я у
7.5. Новое геометрическое определение числа Что такое число? «Ливийский» период моей жизни, который продолжался с февраля 1995 по август 1997 г., был своеобразным и сознательным «заточением», кода я у
Подробнее «Золотое сечение» Часть I
 Учебный проект «Золотое сечение» Часть I «Человек венец творения природы» Автор исследования Мизеровская Анна, ученица 10 «А» класса МБОУ Лицей 7 г. Химки Провести исследования по теме «Золотое сечение
Учебный проект «Золотое сечение» Часть I «Человек венец творения природы» Автор исследования Мизеровская Анна, ученица 10 «А» класса МБОУ Лицей 7 г. Химки Провести исследования по теме «Золотое сечение
Подробнее Пояснительная записка
 Пояснительная записка Программа по математике разработана, в соответствии с Федеральными государственными образовательными стандартами основного общего образования 2-го поколения, Фундаментального ядра
Пояснительная записка Программа по математике разработана, в соответствии с Федеральными государственными образовательными стандартами основного общего образования 2-го поколения, Фундаментального ядра
Подробнее Анкета для индивидуального пошива
 01 РОСТ Измеряется в сантиметрах от пола до макушки. 02 ОБХВАТ ГОЛОВЫ Измеряется в самом широком месте головы: Горизонтально, по кругу, над ушами и бровями 02-А ДЛИНА ГОЛОВЫ ОТ 7 ШЕЙНОГО ПОЗВОНКА ДО НАДБРОВНЫХ
01 РОСТ Измеряется в сантиметрах от пола до макушки. 02 ОБХВАТ ГОЛОВЫ Измеряется в самом широком месте головы: Горизонтально, по кругу, над ушами и бровями 02-А ДЛИНА ГОЛОВЫ ОТ 7 ШЕЙНОГО ПОЗВОНКА ДО НАДБРОВНЫХ
Подробнее Семинар 7 Модели динамики популяций
 Семинар 7 Модели динамики популяций Модель Мальтуса Модель Ферхюльста Модели Моно и Базыкина Модели с запаздыванием Возрастное распределение Модель смертности Где применяется Главное отличие от физики
Семинар 7 Модели динамики популяций Модель Мальтуса Модель Ферхюльста Модели Моно и Базыкина Модели с запаздыванием Возрастное распределение Модель смертности Где применяется Главное отличие от физики
Подробнее Рабочая программа по алгебре
 Муниципальное казенное общеобразовательное учреждение средняя общеобразовательная школа 3 города Пудожа Рассмотрено на заседании МО математики и информатики Протокол 1 от 29.08.2016 Руководитель МО Купцова
Муниципальное казенное общеобразовательное учреждение средняя общеобразовательная школа 3 города Пудожа Рассмотрено на заседании МО математики и информатики Протокол 1 от 29.08.2016 Руководитель МО Купцова
Подробнее по математике для 6 классов
 УТВЕРЖДЕНО приказом директора МБОУ «СОШ 32» 153/01-10 от 28.08.2014 СОГЛАСОВАНО с заместителем директора МБОУ «СОШ 32» 27.08.2014 РАССМОТРЕНО на заседании МО учителей математики 27.08.2014, протокол 1
УТВЕРЖДЕНО приказом директора МБОУ «СОШ 32» 153/01-10 от 28.08.2014 СОГЛАСОВАНО с заместителем директора МБОУ «СОШ 32» 27.08.2014 РАССМОТРЕНО на заседании МО учителей математики 27.08.2014, протокол 1
Подробнее Великая математика
 Великая математика 0011 0010 1010 1101 0001 0100 1011 «Математика царица наук, арифметика царица математики» МОУ Яринская ООШ Учитель математики Быстрова И.А. К. Ф. Гаусс Физика Математика-это язык,на
Великая математика 0011 0010 1010 1101 0001 0100 1011 «Математика царица наук, арифметика царица математики» МОУ Яринская ООШ Учитель математики Быстрова И.А. К. Ф. Гаусс Физика Математика-это язык,на
Подробнее docplayer.ru
Реферат Числа Фибоначчи
 Опубликовать Опубликовать | скачать Реферат на тему: План: Введение- 1 Происхождение
- 2 Формула Бине
- 3 Тождества
- 4 Свойства
- 5 Вариации и обобщения
- 6 В других областях
- 6.1 В природе
- 6.2 В культуре
ЛитератураПримечания ВведениеЧи́сла Фибона́ччи — элементы числовой последовательности 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946,… (последовательность A000045 в OEIS) в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (известного как Фибоначчи)[1]. Иногда число 0 не рассматривается как член последовательности. Более формально, последовательность чисел Фибоначчи  задается линейным рекуррентным соотношением: задается линейным рекуррентным соотношением:  Иногда числа Фибоначчи рассматривают и для отрицательных номеров n как двусторонне бесконечную последовательность, удовлетворяющую тому же рекуррентному соотношению. Члены с такими номерами легко получить с помощью эквивалентной формулы «назад»: Fn = Fn + 2 − Fn + 1: n | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Fn | −55 | 34 | −21 | 13 | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
Легко заметить, что  . . 1. Происхождение Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении), намного раньше, чем она стала известна в Европе. Образец длиной n может быть построен путём добавления S к образцу длиной n-1, либо L к образцу длиной n-2; и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования». На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая что: - В «нулевом» месяце имеется пара кроликов (1 новая пара).
- В первом месяце первая пара производит на свет другую пару (1 новая пара).
- Во втором месяце обе пары кроликов порождают другие пары и первая пара погибает (2 новые пары).
- В третьем месяце вторая пара и две новые пары порождают в общем три новые пары, а старая вторая пара погибает (3 новые пары).
Закономерным является тот факт, что каждая пара кроликов порождает ещё две пары на протяжении жизни, а затем погибает. Пусть популяция за месяц n будет равна F(n). В это время только те кролики, которые жили в месяце n-2, являются способными к размножению и производят потомков, тогда F(n-2) пар прибавится к текущей популяции F(n-1). Таким образом общее количество пар будет равно F(n) = F(n-1) + F(n-2). 2. Формула Бине Формула Бине выражает в явном виде значение Fn как функцию от n:  , , где  — золотое сечение. При этом — золотое сечение. При этом  и и  являются корнями характеристического уравнения являются корнями характеристического уравнения  . . Из формулы Бине следует, что для всех  , Fn есть ближайшее к , Fn есть ближайшее к  целое число, то есть целое число, то есть  . В частности, при . В частности, при  справедлива асимптотика справедлива асимптотика  . . Формула Бине может быть аналитически продолжена следующим образом:  При этом соотношение Fz + 2 = Fz + 1 + Fz выполняется для любого комплексного числа z. 3. Тождества И более общие формулы: - Числа Фибоначчи представляются значениями континуант на наборе единиц:
 , то есть , то есть
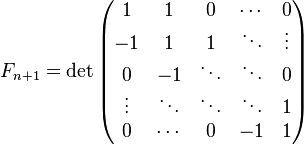 , а также , а также  , где матрицы имеют размер , где матрицы имеют размер  , i — мнимая единица. , i — мнимая единица. - Числа Фибоначчи можно выразить через многочлены Чебышева:
  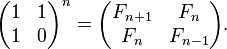 - Следствие. Подсчёт определителей даёт
 4. Свойства - Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, т. е. (Fm,Fn) = F(m,n). Следствия:
- Fm делится на Fn тогда и только тогда, когда m делится на n (за исключением n = 2). В частности, Fm делится на F3 = 2 (то есть является чётным) только для m = 3k; Fm делится на F4 = 3 только для m = 4k; Fm делится на F5 = 5 только для m = 5k и т. д.
- Fm может быть простым только для простых m (с единственным исключением m = 4). Например, число F13 = 233 простое, и его индекс 13 также прост. Обратное не верно, наименьший контрпример —
 . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми. . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
- Последовательность чисел Фибоначчи является частным случаем возвратной последовательности, её характеристический многочлен x2 - x - 1 имеет корни
 и и  . .
- Отношения
 являются подходящими дробями золотого сечения φ и, в частности, являются подходящими дробями золотого сечения φ и, в частности,  - Суммы биномиальных коэффициентов на диагоналях треугольника Паскаля являются числами Фибоначчи ввиду формулы
 . .
- В 1964 году Дж. Кон (J. H. E. Cohn) доказал,[2] что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12: F0 = 02 = 0, F1 = 12 = 1, F2 = 12 = 1, F12 = 122 = 144.
- Производящей функцией последовательности чисел Фибоначчи является:

- Множество чисел Фибоначчи совпадает с множеством неотрицательных значений многочлена z(x,y) = 2xy4 + x2y3 − 2x3y2 − y5 − x4y + 2y,
на множестве неотрицательных целых чисел x и y.[3] - Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.
- Период чисел Фибоначчи по модулю натурального числа n называется периодом Писано[убрать шаблон] и обозначается π(n). Периоды Писано π(n) образуют последовательность: 1, 3, 8, 6, 20, 24, 16, 12, 24, 60, 10, 24, 28, 48, 40, 24, 36, … (последовательность A001175 в OEIS)
- В частности, последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом π(10)=60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом π(100)=300, последние три цифры — с периодом π(1000)=1500, последние четыре — с периодом π(10000)=15000, последние пять — с периодом π(100000)=150000 и т. д.
- Натуральное число N является числом Фибоначчи тогда и только тогда, когда 5N2 + 4 или 5N2 − 4 является квадратом.[4]
- Не существует арифметической прогрессии длиной больше 3, состоящей из чисел Фибоначчи.[5]
5. Вариации и обобщения - Числа трибоначчи
- Числа Фибоначчи являются частным случаем последовательностей Люка
 , при этом их дополнением являются числа Люка , при этом их дополнением являются числа Люка  . .
6. В других областях 6.1. В природе - Филлотаксис (листорасположение) у растений описывается последовательностью Фибоначчи. Зерна подсолнуха, сосновые шишки, лепестки цветков, ячейки ананаса также располагаются согласно последовательности Фибоначчи.[6]
[7][8][9] - Длины фаланг пальцев человека относятся примерно как числа Фибоначчи.[6][10]
- Молекулу ДНК составляют две вертикально переплетенные спирали длиной 34 ангстрема и шириной 21 ангстрема. Числа 21 и 34 следуют друг за другом в последовательности Фибоначчи.[11]
6.2. В культуре - Американский писатель-фантаст Дэн Браун в книге «Код да Винчи» описал последовательность Фибоначчи как «лжешифр».
- Светящиеся числа Фибоначчи от 1 до 55 прикреплены на дымовой трубе Turku Energia в Турку[12] и главном вокзале Цюриха[13].
Литература - Н. Н. Воробьёв Числа Фибоначчи. — Наука, 1978. — Т. 39. — (Популярные лекции по математике).
- А. И. Маркушевич Возвратные последовательности. — Гос. Издательство Технико-Теоретической Литературы, 1950. — Т. 1. — (Популярные лекции по математике).
- А. Н. Рудаков Числа Фибоначчи и простота числа 2127-1 // Математическое Просвещение, третья серия. — 2000. — Т. 4.
- Дональд Кнут Искусство программирования, том 1. Основные алгоритмы = The Art of Computer Programming, vol.1. Fundamental Algorithms. — 3-е изд. — М.: «Вильямс», 2006. — С. 720. — ISBN 0-201-89683-4
- Дональд Кнут, Роналд Грэхем, Орен Паташник Конкретная математика. Основание информатики = Concrete Mathematics. A Foundation for Computer Science. — М.: Мир; Бином. Лаборатория знаний, 2006. — С. 703. — ISBN 5-94774-560-7
Примечания - Числа Фибоначчи - slovari.yandex.ru/dict/bse/article/00083/91300.htm — статья из Большой советской энциклопедии
- J H E Cohn. Square Fibonacci Numbers Etc - math.la.asu.edu/~checkman/SquareFibonacci.html, стр. 109–113.
- P. Ribenboim The New Book of Prime Number Records - books.google.com/books?id=72eg8bFw40kC&pg=PA193. — Springer, 1996. — С. 193.
- Ira Gessel Problem H-187 // Fibonacci Quarterly. — 1972. — Т. 10. — С. 417–419.
- В. Серпинский Задача 66 // 250 задач по элементарной теории чисел - ilib.mccme.ru/djvu/serp-250-tch.htm. — М.: Просвещение, 1968. — 168 с.
- ↑ 12 Золотое сечение в природе - himekoscho.ucoz.ru/load/16-1-0-92
- Числа Фибоначчи - elementy.ru/trefil/21136
- Числа Фибоначчи - www.diary.ru/~Organon/p19280903.htm
- Глава из книги О.Е.Акимова "Конец науки" - kompot.soneta.ru/O-chislah-Fibonachchi-fillotaksise-i-ZS
- Г. Манукян. ПОЭЗИЯ ЧИСЕЛ ФИБОНАЧЧИ - www.21mm.ru/item/291/
- Г. Манукян.ПОЭЗИЯ ЧИСЕЛ ФИБОНАЧЧИ - www.21mm.ru/item/291/
- Марио Мерц Fibonacci Sequence 1-55 - www.turku.fi/public/default.aspx?contentid=57923&nodeid=13067 (фин.)
- Based in Villigen: Fibonacci sequence at the Zürich Hauptbahnhof - basedinvilligen.blogspot.com/2007/02/fibonacci-sequence-at-zrich.html
скачатьДанный реферат составлен на основе статьи из русской Википедии. Синхронизация выполнена 12.07.11 19:26:18Похожие рефераты: Фибоначчи, Код Фибоначчи, Кодирование Фибоначчи, Дерево Фибоначчи, Метод Фибоначчи с запаздываниями, Метод чисел Фибоначчи.Категории: Теория чисел, Золотое сечение, Целочисленные последовательности. Текст доступен по лицензии Creative Commons Attribution-ShareAlike. | | www.wreferat.baza-referat.ru
Реферат Число Фибоначчи
 Опубликовать Опубликовать | скачать Реферат на тему: План: Введение- 1 Происхождение
- 2 Формула Бине
- 3 Тождества
- 4 Свойства
- 5 Вариации и обобщения
- 6 В других областях
- 6.1 В природе
- 6.2 В культуре
ЛитератураПримечания ВведениеЧи́сла Фибона́ччи — элементы числовой последовательности 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946,… (последовательность A000045 в OEIS) в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (известного как Фибоначчи)[1]. Иногда число 0 не рассматривается как член последовательности. Более формально, последовательность чисел Фибоначчи  задается линейным рекуррентным соотношением: задается линейным рекуррентным соотношением:  Иногда числа Фибоначчи рассматривают и для отрицательных номеров n как двусторонне бесконечную последовательность, удовлетворяющую тому же рекуррентному соотношению. Члены с такими номерами легко получить с помощью эквивалентной формулы «назад»: Fn = Fn + 2 − Fn + 1: n | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Fn | −55 | 34 | −21 | 13 | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
Легко заметить, что  . . 1. Происхождение Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении), намного раньше, чем она стала известна в Европе. Образец длиной n может быть построен путём добавления S к образцу длиной n-1, либо L к образцу длиной n-2; и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования». На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая что: - В «нулевом» месяце имеется пара кроликов (1 новая пара).
- В первом месяце первая пара производит на свет другую пару (1 новая пара).
- Во втором месяце обе пары кроликов порождают другие пары и первая пара погибает (2 новые пары).
- В третьем месяце вторая пара и две новые пары порождают в общем три новые пары, а старая вторая пара погибает (3 новые пары).
Закономерным является тот факт, что каждая пара кроликов порождает ещё две пары на протяжении жизни, а затем погибает. Пусть популяция за месяц n будет равна F(n). В это время только те кролики, которые жили в месяце n-2, являются способными к размножению и производят потомков, тогда F(n-2) пар прибавится к текущей популяции F(n-1). Таким образом общее количество пар будет равно F(n) = F(n-1) + F(n-2). 2. Формула Бине Формула Бине выражает в явном виде значение Fn как функцию от n:  , , где  — золотое сечение. При этом — золотое сечение. При этом  и и  являются корнями характеристического уравнения являются корнями характеристического уравнения  . . Из формулы Бине следует, что для всех  , Fn есть ближайшее к , Fn есть ближайшее к  целое число, то есть целое число, то есть  . В частности, при . В частности, при  справедлива асимптотика справедлива асимптотика  . . Формула Бине может быть аналитически продолжена следующим образом:  При этом соотношение Fz + 2 = Fz + 1 + Fz выполняется для любого комплексного числа z. 3. Тождества И более общие формулы: - Числа Фибоначчи представляются значениями континуант на наборе единиц:
 , то есть , то есть
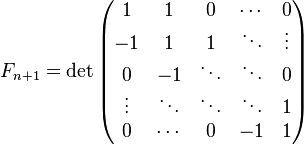 , а также , а также  , где матрицы имеют размер , где матрицы имеют размер  , i — мнимая единица. , i — мнимая единица. - Числа Фибоначчи можно выразить через многочлены Чебышева:
  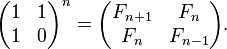 - Следствие. Подсчёт определителей даёт
 4. Свойства - Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, т. е. (Fm,Fn) = F(m,n). Следствия:
- Fm делится на Fn тогда и только тогда, когда m делится на n (за исключением n = 2). В частности, Fm делится на F3 = 2 (то есть является чётным) только для m = 3k; Fm делится на F4 = 3 только для m = 4k; Fm делится на F5 = 5 только для m = 5k и т. д.
- Fm может быть простым только для простых m (с единственным исключением m = 4). Например, число F13 = 233 простое, и его индекс 13 также прост. Обратное не верно, наименьший контрпример —
 . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми. . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
- Последовательность чисел Фибоначчи является частным случаем возвратной последовательности, её характеристический многочлен x2 - x - 1 имеет корни
 и и  . .
- Отношения
 являются подходящими дробями золотого сечения φ и, в частности, являются подходящими дробями золотого сечения φ и, в частности,  - Суммы биномиальных коэффициентов на диагоналях треугольника Паскаля являются числами Фибоначчи ввиду формулы
 . .
- В 1964 году Дж. Кон (J. H. E. Cohn) доказал,[2] что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12: F0 = 02 = 0, F1 = 12 = 1, F2 = 12 = 1, F12 = 122 = 144.
- Производящей функцией последовательности чисел Фибоначчи является:

- Множество чисел Фибоначчи совпадает с множеством неотрицательных значений многочлена z(x,y) = 2xy4 + x2y3 − 2x3y2 − y5 − x4y + 2y,
на множестве неотрицательных целых чисел x и y.[3] - Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.
- Период чисел Фибоначчи по модулю натурального числа n называется периодом Писано[убрать шаблон] и обозначается π(n). Периоды Писано π(n) образуют последовательность: 1, 3, 8, 6, 20, 24, 16, 12, 24, 60, 10, 24, 28, 48, 40, 24, 36, … (последовательность A001175 в OEIS)
- В частности, последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом π(10)=60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом π(100)=300, последние три цифры — с периодом π(1000)=1500, последние четыре — с периодом π(10000)=15000, последние пять — с периодом π(100000)=150000 и т. д.
- Натуральное число N является числом Фибоначчи тогда и только тогда, когда 5N2 + 4 или 5N2 − 4 является квадратом.[4]
- Не существует арифметической прогрессии длиной больше 3, состоящей из чисел Фибоначчи.[5]
5. Вариации и обобщения - Числа трибоначчи
- Числа Фибоначчи являются частным случаем последовательностей Люка
 , при этом их дополнением являются числа Люка , при этом их дополнением являются числа Люка  . .
6. В других областях 6.1. В природе - Филлотаксис (листорасположение) у растений описывается последовательностью Фибоначчи. Зерна подсолнуха, сосновые шишки, лепестки цветков, ячейки ананаса также располагаются согласно последовательности Фибоначчи.[6]
[7][8][9] - Длины фаланг пальцев человека относятся примерно как числа Фибоначчи.[6][10]
- Молекулу ДНК составляют две вертикально переплетенные спирали длиной 34 ангстрема и шириной 21 ангстрема. Числа 21 и 34 следуют друг за другом в последовательности Фибоначчи.[11]
6.2. В культуре - Американский писатель-фантаст Дэн Браун в книге «Код да Винчи» описал последовательность Фибоначчи как «лжешифр».
- Светящиеся числа Фибоначчи от 1 до 55 прикреплены на дымовой трубе Turku Energia в Турку[12] и главном вокзале Цюриха[13].
Литература - Н. Н. Воробьёв Числа Фибоначчи. — Наука, 1978. — Т. 39. — (Популярные лекции по математике).
- А. И. Маркушевич Возвратные последовательности. — Гос. Издательство Технико-Теоретической Литературы, 1950. — Т. 1. — (Популярные лекции по математике).
- А. Н. Рудаков Числа Фибоначчи и простота числа 2127-1 // Математическое Просвещение, третья серия. — 2000. — Т. 4.
- Дональд Кнут Искусство программирования, том 1. Основные алгоритмы = The Art of Computer Programming, vol.1. Fundamental Algorithms. — 3-е изд. — М.: «Вильямс», 2006. — С. 720. — ISBN 0-201-89683-4
- Дональд Кнут, Роналд Грэхем, Орен Паташник Конкретная математика. Основание информатики = Concrete Mathematics. A Foundation for Computer Science. — М.: Мир; Бином. Лаборатория знаний, 2006. — С. 703. — ISBN 5-94774-560-7
Примечания - Числа Фибоначчи - slovari.yandex.ru/dict/bse/article/00083/91300.htm — статья из Большой советской энциклопедии
- J H E Cohn. Square Fibonacci Numbers Etc - math.la.asu.edu/~checkman/SquareFibonacci.html, стр. 109–113.
- P. Ribenboim The New Book of Prime Number Records - books.google.com/books?id=72eg8bFw40kC&pg=PA193. — Springer, 1996. — С. 193.
- Ira Gessel Problem H-187 // Fibonacci Quarterly. — 1972. — Т. 10. — С. 417–419.
- В. Серпинский Задача 66 // 250 задач по элементарной теории чисел - ilib.mccme.ru/djvu/serp-250-tch.htm. — М.: Просвещение, 1968. — 168 с.
- ↑ 12 Золотое сечение в природе - himekoscho.ucoz.ru/load/16-1-0-92
- Числа Фибоначчи - elementy.ru/trefil/21136
- Числа Фибоначчи - www.diary.ru/~Organon/p19280903.htm
- Глава из книги О.Е.Акимова "Конец науки" - kompot.soneta.ru/O-chislah-Fibonachchi-fillotaksise-i-ZS
- Г. Манукян. ПОЭЗИЯ ЧИСЕЛ ФИБОНАЧЧИ - www.21mm.ru/item/291/
- Г. Манукян.ПОЭЗИЯ ЧИСЕЛ ФИБОНАЧЧИ - www.21mm.ru/item/291/
- Марио Мерц Fibonacci Sequence 1-55 - www.turku.fi/public/default.aspx?contentid=57923&nodeid=13067 (фин.)
- Based in Villigen: Fibonacci sequence at the Zürich Hauptbahnhof - basedinvilligen.blogspot.com/2007/02/fibonacci-sequence-at-zrich.html
скачатьДанный реферат составлен на основе статьи из русской Википедии. Синхронизация выполнена 12.07.11 19:26:18Похожие рефераты: Фибоначчи, Код Фибоначчи, Кодирование Фибоначчи, Дерево Фибоначчи, Метод Фибоначчи с запаздываниями, Метод чисел Фибоначчи.Категории: Теория чисел, Золотое сечение, Целочисленные последовательности. Текст доступен по лицензии Creative Commons Attribution-ShareAlike. | | wreferat.baza-referat.ru
 Краевая научно-практическая конференция учебно-исследовательских и проектных работ учащихся 6-11 классов «Прикладные и фундаментальные вопросы математики» Прикладные вопросы математики Золотое сечение
Краевая научно-практическая конференция учебно-исследовательских и проектных работ учащихся 6-11 классов «Прикладные и фундаментальные вопросы математики» Прикладные вопросы математики Золотое сечение  Краевая научно-практическая конференция учебно-исследовательских и проектных работ учащихся 6-11 классов «Прикладные и фундаментальные вопросы математики» Прикладные вопросы математики Золотое сечение
Краевая научно-практическая конференция учебно-исследовательских и проектных работ учащихся 6-11 классов «Прикладные и фундаментальные вопросы математики» Прикладные вопросы математики Золотое сечение  МОУ «Малыгинская средняя общеобразовательная школа» Числа Фибоначчи и золотое сечение Выполнила ученица 9 «а» класса Кузнецова Юлия под руководством учителя математики Большаковой О.К. «Числа не управляют
МОУ «Малыгинская средняя общеобразовательная школа» Числа Фибоначчи и золотое сечение Выполнила ученица 9 «а» класса Кузнецова Юлия под руководством учителя математики Большаковой О.К. «Числа не управляют  УДК 517.8 ЗОЛОТОЕ СЕЧЕНИЕ В ПРИРОДЕ А.А. Куликов, студент группы ЭЭб-152, I курс Научный руководитель: А.В. Чередниченко, ассистент Кузбасский государственный технический университет г. Кемерово Что общего
УДК 517.8 ЗОЛОТОЕ СЕЧЕНИЕ В ПРИРОДЕ А.А. Куликов, студент группы ЭЭб-152, I курс Научный руководитель: А.В. Чередниченко, ассистент Кузбасский государственный технический университет г. Кемерово Что общего  Уровни Фибоначчи В XIII веке Леонардо Фибоначчи, известный итальянский математик обнаружил простую последовательность чисел 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144... Такая зависимость получилась в результате
Уровни Фибоначчи В XIII веке Леонардо Фибоначчи, известный итальянский математик обнаружил простую последовательность чисел 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144... Такая зависимость получилась в результате  Темы проектов по математике для 5 класса Алгебраические дроби. В мире процентов. В стране рыцарей и лжецов. Виды уравнений, решаемые в 5-м классе. Возникновение чисел. Вокруг обыкновенных дробей. Графический
Темы проектов по математике для 5 класса Алгебраические дроби. В мире процентов. В стране рыцарей и лжецов. Виды уравнений, решаемые в 5-м классе. Возникновение чисел. Вокруг обыкновенных дробей. Графический  1 Городское соревнование юных исследователей «Шаг в будущее Юниор» Золотое сечение и строение человека Россия, г.сургут, Ульянова Виктория Александровна Муниципальное бюджетное общеобразовательное учреждение
1 Городское соревнование юных исследователей «Шаг в будущее Юниор» Золотое сечение и строение человека Россия, г.сургут, Ульянова Виктория Александровна Муниципальное бюджетное общеобразовательное учреждение  Древнекитайский символ Сравните Некоторые современные здания Золотое сечение «Красота и гармония стали важнейшими категориями познания, в определенной степени даже его целью, ибо в конечном итоге художник
Древнекитайский символ Сравните Некоторые современные здания Золотое сечение «Красота и гармония стали важнейшими категориями познания, в определенной степени даже его целью, ибо в конечном итоге художник  Глава 4.2 Технический анализ: Фибоначчи ТЕХНИЧЕСКИЙ АНАЛИЗ: ФИБОНАЧЧИ Анализ Фибоначчи - это инструмент, позволяющий выявить потенциальные уровни поддержки и сопротивления, основываясь на прошлых ценовых
Глава 4.2 Технический анализ: Фибоначчи ТЕХНИЧЕСКИЙ АНАЛИЗ: ФИБОНАЧЧИ Анализ Фибоначчи - это инструмент, позволяющий выявить потенциальные уровни поддержки и сопротивления, основываясь на прошлых ценовых  Краевая научно-практическая конференция учебно-исследовательских работ учащихся 9-11 классов «Прикладные и фундаментальные вопросы математики» Прикладные вопросы математики Математическая гармония человеческого
Краевая научно-практическая конференция учебно-исследовательских работ учащихся 9-11 классов «Прикладные и фундаментальные вопросы математики» Прикладные вопросы математики Математическая гармония человеческого  Научно исследовательская работа Числа Фибоначчи. Формула красоты. Автор: ученик10 класс Шроо Артур Муниципального бюджетного образовательного учреждения Катановской средней общеобразовательной школы Руководитель:
Научно исследовательская работа Числа Фибоначчи. Формула красоты. Автор: ученик10 класс Шроо Артур Муниципального бюджетного образовательного учреждения Катановской средней общеобразовательной школы Руководитель:  Страничка для влюбленных в математику Страницу подготовила учитель математики, директор школы Шмелькова Наталья Александровна Если учитель имеет только любовь к делу, он будет хороший учитель. Если учитель
Страничка для влюбленных в математику Страницу подготовила учитель математики, директор школы Шмелькова Наталья Александровна Если учитель имеет только любовь к делу, он будет хороший учитель. Если учитель  Проект для учеников 8 классов «Геометрия владеет двумя сокровищами - теоремой Пифагора и золотым сечением. И если первое из этих двух сокровищ можно сравнить с мерой золота, то второе с драгоценным камнем.
Проект для учеников 8 классов «Геометрия владеет двумя сокровищами - теоремой Пифагора и золотым сечением. И если первое из этих двух сокровищ можно сравнить с мерой золота, то второе с драгоценным камнем.  Муниципальное бюджетное общеобразовательное учреждение Лицей 7 г. Химки Учебный проект «Золотое сечение» Часть I «Человек венец творения природы» Автор исследования: Мизеровская Анна ученица 10 «А» класса
Муниципальное бюджетное общеобразовательное учреждение Лицей 7 г. Химки Учебный проект «Золотое сечение» Часть I «Человек венец творения природы» Автор исследования: Мизеровская Анна ученица 10 «А» класса  А С Т Р О Н О М И Я Кеплер 243 Золотое сечение в строении Солнечной системы и Вселенной У каждой планеты имеется минимальный радиус орбиты, но есть и максимальный как у всякого эллипса. Если рассмотреть
А С Т Р О Н О М И Я Кеплер 243 Золотое сечение в строении Солнечной системы и Вселенной У каждой планеты имеется минимальный радиус орбиты, но есть и максимальный как у всякого эллипса. Если рассмотреть  Содержание курса математики в 5 6 классах Натуральные числа и нуль Натуральный ряд чисел и его свойства Натуральное число, множество натуральных чисел и его свойства, изображение натуральных чисел точками
Содержание курса математики в 5 6 классах Натуральные числа и нуль Натуральный ряд чисел и его свойства Натуральное число, множество натуральных чисел и его свойства, изображение натуральных чисел точками  1 Буква слово, цифра число? Нина Коптюг, кандидат филологических наук, лауреат 1 Всероссийского конкурса «Дистанционный учитель года РФ», победитель конкурса ПНПО «Лучший учитель РФ», представитель РФ
1 Буква слово, цифра число? Нина Коптюг, кандидат филологических наук, лауреат 1 Всероссийского конкурса «Дистанционный учитель года РФ», победитель конкурса ПНПО «Лучший учитель РФ», представитель РФ  ВГУЗУ «Украинская медицинская стоматологическая академия» Кафедра социальной медицины, организации и экономики здравоохранения с биостатистикой и медицинским правоведением МЕДИЦИНА ЭПОХИ ВОЗРОЖДЕНИЯ Лектор:
ВГУЗУ «Украинская медицинская стоматологическая академия» Кафедра социальной медицины, организации и экономики здравоохранения с биостатистикой и медицинским правоведением МЕДИЦИНА ЭПОХИ ВОЗРОЖДЕНИЯ Лектор:  ОСНОВНЫЕ АЛГОРИТМИЧЕСКИЕ КОНСТРУКЦИИ ЭТАПЫ РЕШЕНИЯ ЗАДАЧ НА ЭВМ : постановка задачи; математическое описание задачи; выбор и обоснование метода решения; алгоритмизация вычислительного процесса; составление
ОСНОВНЫЕ АЛГОРИТМИЧЕСКИЕ КОНСТРУКЦИИ ЭТАПЫ РЕШЕНИЯ ЗАДАЧ НА ЭВМ : постановка задачи; математическое описание задачи; выбор и обоснование метода решения; алгоритмизация вычислительного процесса; составление  Урок-игра по теме «Системы счисления» Предмет: информатика и ИКТ Класс: 9 класс Тема учебного занятия: Урок-игра «Системы счисления. Перевод из одной системы счисления в другие, арифметические операции
Урок-игра по теме «Системы счисления» Предмет: информатика и ИКТ Класс: 9 класс Тема учебного занятия: Урок-игра «Системы счисления. Перевод из одной системы счисления в другие, арифметические операции  Создание собственной линейки фэн-шуй Ко мне часто обращаются с вопросом: есть ли общие корни у архитектурных и дизайнерских принципов, используемых китайскими мастерами, и священной геометрии масонов и
Создание собственной линейки фэн-шуй Ко мне часто обращаются с вопросом: есть ли общие корни у архитектурных и дизайнерских принципов, используемых китайскими мастерами, и священной геометрии масонов и  ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ В КОМПЬЮТЕРЕ Информация в ЭВМ кодируется, как правило, в двоичной или в двоично-десятичной системе счисления. Система счисления это способ наименования и изображения чисел с помощью
ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ В КОМПЬЮТЕРЕ Информация в ЭВМ кодируется, как правило, в двоичной или в двоично-десятичной системе счисления. Система счисления это способ наименования и изображения чисел с помощью  7.5. Новое геометрическое определение числа Что такое число? «Ливийский» период моей жизни, который продолжался с февраля 1995 по август 1997 г., был своеобразным и сознательным «заточением», кода я у
7.5. Новое геометрическое определение числа Что такое число? «Ливийский» период моей жизни, который продолжался с февраля 1995 по август 1997 г., был своеобразным и сознательным «заточением», кода я у  Учебный проект «Золотое сечение» Часть I «Человек венец творения природы» Автор исследования Мизеровская Анна, ученица 10 «А» класса МБОУ Лицей 7 г. Химки Провести исследования по теме «Золотое сечение
Учебный проект «Золотое сечение» Часть I «Человек венец творения природы» Автор исследования Мизеровская Анна, ученица 10 «А» класса МБОУ Лицей 7 г. Химки Провести исследования по теме «Золотое сечение  Пояснительная записка Программа по математике разработана, в соответствии с Федеральными государственными образовательными стандартами основного общего образования 2-го поколения, Фундаментального ядра
Пояснительная записка Программа по математике разработана, в соответствии с Федеральными государственными образовательными стандартами основного общего образования 2-го поколения, Фундаментального ядра  01 РОСТ Измеряется в сантиметрах от пола до макушки. 02 ОБХВАТ ГОЛОВЫ Измеряется в самом широком месте головы: Горизонтально, по кругу, над ушами и бровями 02-А ДЛИНА ГОЛОВЫ ОТ 7 ШЕЙНОГО ПОЗВОНКА ДО НАДБРОВНЫХ
01 РОСТ Измеряется в сантиметрах от пола до макушки. 02 ОБХВАТ ГОЛОВЫ Измеряется в самом широком месте головы: Горизонтально, по кругу, над ушами и бровями 02-А ДЛИНА ГОЛОВЫ ОТ 7 ШЕЙНОГО ПОЗВОНКА ДО НАДБРОВНЫХ  Семинар 7 Модели динамики популяций Модель Мальтуса Модель Ферхюльста Модели Моно и Базыкина Модели с запаздыванием Возрастное распределение Модель смертности Где применяется Главное отличие от физики
Семинар 7 Модели динамики популяций Модель Мальтуса Модель Ферхюльста Модели Моно и Базыкина Модели с запаздыванием Возрастное распределение Модель смертности Где применяется Главное отличие от физики  Муниципальное казенное общеобразовательное учреждение средняя общеобразовательная школа 3 города Пудожа Рассмотрено на заседании МО математики и информатики Протокол 1 от 29.08.2016 Руководитель МО Купцова
Муниципальное казенное общеобразовательное учреждение средняя общеобразовательная школа 3 города Пудожа Рассмотрено на заседании МО математики и информатики Протокол 1 от 29.08.2016 Руководитель МО Купцова  УТВЕРЖДЕНО приказом директора МБОУ «СОШ 32» 153/01-10 от 28.08.2014 СОГЛАСОВАНО с заместителем директора МБОУ «СОШ 32» 27.08.2014 РАССМОТРЕНО на заседании МО учителей математики 27.08.2014, протокол 1
УТВЕРЖДЕНО приказом директора МБОУ «СОШ 32» 153/01-10 от 28.08.2014 СОГЛАСОВАНО с заместителем директора МБОУ «СОШ 32» 27.08.2014 РАССМОТРЕНО на заседании МО учителей математики 27.08.2014, протокол 1  Великая математика 0011 0010 1010 1101 0001 0100 1011 «Математика царица наук, арифметика царица математики» МОУ Яринская ООШ Учитель математики Быстрова И.А. К. Ф. Гаусс Физика Математика-это язык,на
Великая математика 0011 0010 1010 1101 0001 0100 1011 «Математика царица наук, арифметика царица математики» МОУ Яринская ООШ Учитель математики Быстрова И.А. К. Ф. Гаусс Физика Математика-это язык,на  Опубликовать
Опубликовать задается линейным рекуррентным соотношением:
.
— золотое сечение. При этом
и
являются корнями характеристического уравнения
.
, Fn есть ближайшее к
целое число, то есть
. В частности, при
справедлива асимптотика
.
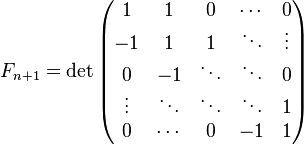 , а также
, а также  , где матрицы имеют размер
, где матрицы имеют размер 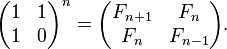
 Опубликовать
Опубликовать задается линейным рекуррентным соотношением:
.
— золотое сечение. При этом
и
являются корнями характеристического уравнения
.
, Fn есть ближайшее к
целое число, то есть
. В частности, при
справедлива асимптотика
.
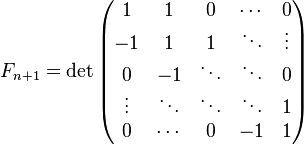 , а также
, а также  , где матрицы имеют размер
, где матрицы имеют размер