Как сделать из точек числа?
Если речь идет о точках на прямой – это просто. Выбрав начало отсчета и масштабс направлением, можно получить из прямой числовую ось и тем самым превратить каждуюточку в действительное число – ее координату.
С точками на плоскости сложнее. Выбираем две оси и начало отсчета. Для каждойточки плоскости сопоставляем ее координаты (x; y). Эта парабудет называться дуплетом. Чтобы сделать дуплет числом, нужнонаучиться “складывать” и “умножать” их в соответствии со свойствами сложения иумножения.
Дуплеты складываются как векторы – покоординатно:
(x; y) + (x’; y’) = (x + x’; y + y’).(1)
Дляумножения существует иная формула:
(x; y) /> (x’; y’)= (xx’ - yy’; xy’ + x’y). (2)
Умножениеи сложение (1), (2) дуплетов подчиняются привычным свойствам сложения иумножения. Следовательно, множество дуплетов с операциями (1), (2) можносчитать полноценным числовым множеством.
На самом деле дуплеты – это комплексные числа. Их записывают так:x + yi, где i –мнимая единица (дуплет (0; 1)). Ее квадрат равен />. Это позволяет извлекатьквадратные корни из отрицательных чисел.
Но встает проблема превращения точек пространствав числа.Здесь снова введем систему координат и запишем точки в виде набора уже трехкоординат (x; y; z). Эти так называемые триплетытожескладываются покоординатно:
(x; y; z) + (x’; y’; z’) = (x + x’; y + y’; z + z’). (3)
Триплетыможно будет считать числами, если научиться их умножать, обладая, вместе сосвойствами сложения, обычными способами умножения этих операций.
В 1833 г. умножением триплетов занимался ирландский математик У. Р. Гамильтон(1805 – 1865). О нем мы расскажем особо.
Уильям Роуан ГамильтонГамильтон был человеком многосторонне развитым. В четырнадцать лет владелдевятью языками, в 1824 г. опубликовал в трудах Королевской Ирландской Академииработу, посвященную геометрической оптике, в 1828 г. получил званиекоролевского астронома Ирландии.
К 1833 г. Гамильтон занимал пост директора обсерватории в Денсинке и былизвестен работами по оптике и аналитической механики. Он предсказал эффектдвойной конической рефракции в двуосных кристаллах.
В течение долгих десяти лет Гамильтон безуспешно пытался придумать правилоумножения триплетов.
Векторное произведениеЗадача поначалу казалась несложной. Складывать векторы следовало по формуле(3). Оставалось найти формулу умножения, подобную формуле (2). Но Гамильтонбезуспешно пытался подбирать формулы для умножения триплетов.
В то время было известно правило векторного произведения:
векторнымпроизведением /> ненулевыхвекторов /> называется вектор,перпендикулярный плоскости, проходящей через векторы /> имеющий направление,определяемое правилом “правой руки”, и длину ê/>ê/> ê/>ê/>.Если для данных векторов заданы координаты в прямоугольной системе координат:
/>
/>
то/> (4)
Нооперация векторного произведения не годилась Гамильтону, поскольку она не имеетобратной. Например, если /> то угол(/>) между векторами равеннулю. Значит, длина векторного произведения /> равнанулю, т.е. и сам вектор /> нулевой.
Но несмотря на неудачи, Гамильтон пытался решить поставленную перед собойзадачу. Но эта задача не могла быть решена (объяснение следует ниже). Но трудне пропал даром. В 1843 г. Гамильтон вдруг решил, что для определения умножениянужно рассматривать не триплеты (тройки чисел), а четверки, или кватернионы.Вот история их создания.
Случай на Брогемском мосту/>
В одном из писем к своему сыну Гамильтон писал: “Это был 16-й день октября,который случился в понедельник, в день заседания Совета Королевской ИрландскойАкадемии, где я должен был председательствовать. Я направлялся туда с твоейматерью вдоль Королевского канала; и, хотя она говорила мне какие-то отдельныефразы, я их почти не воспринимал, так как в моем сознании подспудно что-тотворилось. Неожиданно как будто бы замкнулся электрический контур; блеснулаискра, предвещающая многие длительные годы определенно направленной мысли итруда, моего – если доведется, или труда других, если мне будет дарованодостаточно сознательной жизни, чтобы сообщить о своем открытии. Я оказался не всостоянии удержаться от желания высечь ножом на мягком камне Брогемского мостафундаментальную формулу о символах i, j, k,
/>,
содержащуюрешение проблемы, но, конечно, эта запись с тех пор стерлась. Однако болеепрочное упоминание осталось в Книге записей Совета Академии за этот день, гдезасвидетельствовано, что я попросил и получил разрешение на доклад окватернионах на первом заседании сессии, который и был прочитан соответственнов Понедельник 13-го следующего месяца – ноября”.
Определениекватернионов
Кватернионы – это четверки действительных чисел (x; y; u; v),которые удобно записывать в виде q = x + yi + uj + vk, где i, j, k– новые числа, являющиеся аналогом мнимой единицы в комплексных числах.Требуется, чтобы числа i, j, k удовлетворяли следующим соотношениям:
/> (5)
/> /> (6)
которыеудобно записать в виде “таблицы умножения”.
x i j k
i -1 k j
j -k -1 i
k -j -i -1
По определению операции сложения и умножения кватернионов производятся пообычным правилам раскрытия скобок и приведения подобных членов с учетом правил(5) – (6).
Согласно этому определению, если /> и /> – два кватерниона, то
/>/> (7)
Это,разумеется, привычное нам “покоординатное” сложение. Далее, произведениекватернионов /> и /> вычисляется так:
/>
Длинная,но совершенно автоматическая проверка показывает, что умножение кватернионовобладает сочетательным свойством:
/>
Естественносчитать, что действительные и комплексные числа являются частным случаемкватернионов. Так, действительное число x – это кватернион вида
/>
Комплексноечисло z = x + yi представляется как кватернион
/>
У операции сложения кватернионов, очевидно, имеется обратная операция–вычитание. Именно, разность двух кватернионов /> и/> определяется формулой:
/>
Если/>, то разность кватернионов –это нулевой кватернион.
Деление кватернионовПерейдем теперь к операции деления кватернионов, обратной к операции умножения.Вообще, что мы понимаем под частным от деления числа a на число b,не равное нулю? Это такое число c, что
bc = a. (10)
Такопределяется частное от деления для действительных и комплексных чисел. Ксожалению, для кватерниона применить непосредственно это определение мы неможем. Для того чтобы формула (10) “корректно” определяла частное, нужно, чтобыпроизведение не зависело от порядка сомножителей. В противном случае наряду счастным /> определенным формулой (10),существует вполне равноправное “левое” частное” с’, определяемое формулой
c’b = a,
котороеможет отличаться от “правого частного” c из (10). Вот здесь, кроменеобходимости выйти за пределы трехмерного пространства, Гамильтону пришлосьпринести еще одну жертву.
Оказывается, определенные им новые числа – кватернионы – потеряли еще однопривычное качество: произведение кватернионов зависит от порядка сомножителей.Действительно, уже в формулах (6) при изменении порядка сомножителейпроизведение меняет знак.
Таким образом, можно говорить лишь о “делении справа” и “делении слева”. Какреально найти, скажем, “левое частное” от деления кватерниона /> на кватернион />?
Обозначим искомое частное через q = x + yi + uj + vk. Тогда, используяправило умножения для кватернионов и определение левого частного, получимследующее равенство кватернионов:
/>,
или
/>
Полученное равенство равносильно системе четырех линейных уравнений спеременными x, y, u, v:
/>
Аналогичным образом находится “правое частное” от деления /> на />.
Рассмотрим частный случай, когда делимое /> равноединице. В этом случае частное от деления />=1на кватернион /> (и “слева” и“справа”) равно одному и тому же кватерниону
/>
Поэтомукватернион p обозначается через />.Тогда “правое частное” от деления кватерниона /> на/> выражается формулой
/>,
а“левое частное” от деления кватерниона /> на/> – формулой
/>
Практически частное от деления двух кватернионов ищется другим путем. Для этогонам потребуются
Скалярные и векторные кватернионыТак же как комплексные числа разлагаются в сумму своей действительной и мнимойчастей, кватернион тоже можно разложить в сумму q = x + (yi + uj + vk). Первоеслагаемое в этом разложении называется скалярной частью кватерниона,а второе – векторной частью. Скалярная часть х – это простодействительное число, а векторная часть может быть изображена вектором r =yi + uj + vk в трехмерном пространстве, где i, j, k мы теперьрассматриваем как единичные вектора прямоугольной системы координат.
Таким образом, каждый кватернион q представляется в виде суммы q = x+ r, где x – скалярная часть кватерниона q, а r –векторная часть. Если r = 0, то q = x и кватернион q называетсяскалярным кватернионом. Если же x = 0, то q = r и qназывается векторным кватернионом.
При сложении кватернионов независимо складываются их скалярные и векторныечасти.
При умножении дело обстоит сложнее. Если /> и/> – скалярные кватернионы, тоих произведение тоже скалярный кватернион. В случае, когда />= х – скалярныйкватернион, а /> = r –векторный кватернион, произведение /> являетсявекторным кватернионом, и операция умножения совпадает с умножением вектора rв пространстве на действительное число x.
И, наконец, если оба кватерниона векторные, то
/>
Каквидно из последней формулы, скалярная часть произведения />/> равна скалярномупроизведению /> векторов /> и /> с обратным знаком.Векторная же часть />/> – это наш старый знакомый –векторное произведение />, записанное вкоординатах.
/> Объединяя все рассмотренные случаи, получим общую формулу для умножениякватернионов. Если /> и/>, то
/>
А как же триплеты?Почему же Гамильтону не удалось найти способа умножения триплетов? Раньше ужебыло отмечено, что эту задачу решить нельзя. Доказано, что попросту несуществует способа умножения точек пространства, удовлетворяющего нашимтребованиям (ассоциативности, дистрибутивности относительно покоординатногосложения, возможности деления на ненулевые элементы). Сейчас, к тому же,известны все случаи, когда можно вести такое умножение. Это доказал немецкийматематик Ф. Г. Фробениус (1849 – 1917). По его словам, этих случаев три: вразмерности один (действительные числа), в размерности два (комплексные числа)и в “размерности четыре” (кватернионы).
Что было дальшеГамильтон и его последователи возлагали большие надежды на кватернионы. Откватернионов ожидали таких же результатов, как от комплексных чисел, и дажебольше. И действительно, с помощью исчисления кватернионов были обнаруженысовершенные в их математической красоте формулы, описывающие ряд важныхфизических явлений. Но дальнейшие надежды на развитие алгебраического ифункционального исчисления кватернионов не оправдались.
Для кватернионов не имеет места основная теорема алгебры о существовании корнейу многочлена с кватернионными коэффициентами, а, с другой стороны, существуеттакой многочлен с кватернионными коэффициентами от одной переменной, длякоторого любой кватернион является корнем.
Оптимизм сменился скепсисом. В начале нашего века математики пересталиинтересоваться кватернионами. Но время шло, и физики упорно искалиматематический формализм для некоторых эффектов, связанных с так называемым спиномэлементарных частиц. Кватернионы снова получили признание, когда была понята ихроль в построении различных геометрических преобразований пространства, используемыхв квантовой физике. Геометрические свойства кватернионов – это особая большаятема.
Дляэтого будет посвящен другой реферат.
Использованнаялитература:
Квант.Изд. “Наука”. Главная редакция физико-математической литературы, Москва,1983(9).
www.ronl.ru
Как сделать из точек числа?
Если речь идет о точках на прямой – это просто. Выбрав начало отсчета и масштаб с направлением, можно получить из прямой числовую ось и тем самым превратить каждую точку в действительное число – ее координату.
С точками на плоскости сложнее. Выбираем две оси и начало отсчета. Для каждой точки плоскости сопоставляем ее координаты (x; y ). Эта пара будет называться дуплетом . Чтобы сделать дуплет числом, нужно научиться “складывать” и “умножать” их в соответствии со свойствами сложения и умножения.
Дуплеты складываются как векторы – покоординатно:
(x; y) + (x’; y’) = (x + x’; y + y’). (1)
Для умножения существует иная формула:
(x; y) (x’; y’) = (xx’ — yy’; xy’ + x’y). (2)
Умножение и сложение (1), (2) дуплетов подчиняются привычным свойствам сложения и умножения. Следовательно, множество дуплетов с операциями (1), (2) можно считать полноценным числовым множеством.
На самом деле дуплеты – это комплексные числа. Их записывают так: x + yi, где i –мнимая единица (дуплет (0; 1)). Ее квадрат равен. Это позволяет извлекать квадратные корни из отрицательных чисел.
Но встает проблема превращения точек пространства в числа. Здесь снова введем систему координат и запишем точки в виде набора уже трех координат (x; y; z ). Эти так называемые триплеты тоже складываются покоординатно:
(x; y; z) + (x’; y’; z’) = (x + x’; y + y’; z + z’). (3)
Триплеты можно будет считать числами, если научиться их умножать, обладая, вместе со свойствами сложения, обычными способами умножения этих операций.
В 1833 г. умножением триплетов занимался ирландский математик У. Р. Гамильтон (1805 – 1865). О нем мы расскажем особо.
Уильям Роуан Гамильтон
Гамильтон был человеком многосторонне развитым. В четырнадцать лет владел девятью языками, в 1824 г. опубликовал в трудах Королевской Ирландской Академии работу, посвященную геометрической оптике, в 1828 г. получил звание королевского астронома Ирландии.
К 1833 г. Гамильтон занимал пост директора обсерватории в Денсинке и был известен работами по оптике и аналитической механики. Он предсказал эффект двойной конической рефракции в двуосных кристаллах.
В течение долгих десяти лет Гамильтон безуспешно пытался придумать правило умножения триплетов.
Векторное произведение
Задача поначалу казалась несложной. Складывать векторы следовало по формуле (3). Оставалось найти формулу умножения, подобную формуле (2). Но Гамильтон безуспешно пытался подбирать формулы для умножения триплетов.
В то время было известно правило векторного произведения:
векторным произведением ненулевых векторов называется вектор, перпендикулярный плоскости, проходящей через векторы имеющий направление, определяемое правилом “правой руки”, и длину êê êê. Если для данных векторов заданы координаты в прямоугольной системе координат:
то (4)
Но операция векторного произведения не годилась Гамильтону, поскольку она не имеет обратной. Например, если то угол () между векторами равен нулю. Значит, длина векторного произведения равна нулю, т.е. и сам вектор нулевой.
Но несмотря на неудачи, Гамильтон пытался решить поставленную перед собой задачу. Но эта задача не могла быть решена (объяснение следует ниже). Но труд не пропал даром. В 1843 г. Гамильтон вдруг решил, что для определения умножения нужно рассматривать не триплеты (тройки чисел), а четверки, или кватернионы. Вот история их создания.
Случай на Брогемском мосту
В одном из писем к своему сыну Гамильтон писал: “Это был 16-й день октября, который случился в понедельник, в день заседания Совета Королевской Ирландской Академии, где я должен был председательствовать. Я направлялся туда с твоей матерью вдоль Королевского канала; и, хотя она говорила мне какие-то отдельные фразы, я их почти не воспринимал, так как в моем сознании подспудно что-то творилось. Неожиданно как будто бы замкнулся электрический контур; блеснула искра, предвещающая многие длительные годы определенно направленной мысли и труда, моего – если доведется, или труда других, если мне будет даровано достаточно сознательной жизни, чтобы сообщить о своем открытии. Я оказался не в состоянии удержаться от желания высечь ножом на мягком камне Брогемского моста фундаментальную формулу о символах i, j, k,
,
содержащую решение проблемы, но, конечно, эта запись с тех пор стерлась. Однако более прочное упоминание осталось в Книге записей Совета Академии за этот день, где засвидетельствовано, что я попросил и получил разрешение на доклад о кватернионах на первом заседании сессии, который и был прочитан соответственно в Понедельник 13-го следующего месяца – ноября”.
Определение кватернионов
Кватернионы – это четверки действительных чисел (x; y; u; v), которые удобно записывать в виде q = x + yi + uj + vk, где i, j, k – новые числа, являющиеся аналогом мнимой единицы в комплексных числах. Требуется, чтобы числа i, j, k удовлетворяли следующим соотношениям:
(5)
(6)
которые удобно записать в виде “таблицы умножения”.
x i j k
i -1 k j
j -k -1 i
k -j -i -1
По определению операции сложения и умножения кватернионов производятся по обычным правилам раскрытия скобок и приведения подобных членов с учетом правил (5) – (6).
Согласно этому определению, если и – два кватерниона, то
(7)
Это, разумеется, привычное нам “покоординатное” сложение. Далее, произведение кватернионов и вычисляется так:
Длинная, но совершенно автоматическая проверка показывает, что умножение кватернионов обладает сочетательным свойством:
Естественно считать, что действительные и комплексные числа являются частным случаем кватернионов. Так, действительное число x – это кватернион вида
Комплексное число z = x + yi представляется как кватернион
У операции сложения кватернионов, очевидно, имеется обратная операция –вычитание. Именно, разность двух кватернионов и определяется формулой:
Если, то разность кватернионов – это нулевой кватернион.
Деление кватернионов
Перейдем теперь к операции деления кватернионов, обратной к операции умножения. Вообще, что мы понимаем под частным от деления числа a на число b, не равное нулю? Это такое число c, что
bc = a. (10)
Так определяется частное от деления для действительных и комплексных чисел. К сожалению, для кватерниона применить непосредственно это определение мы не можем. Для того чтобы формула (10) “корректно” определяла частное, нужно, чтобы произведение не зависело от порядка сомножителей. В противном случае наряду с частным определенным формулой (10), существует вполне равноправное “левое” частное” с’, определяемое формулой
c’b = a,
которое может отличаться от “правого частного” c из (10). Вот здесь, кроме необходимости выйти за пределы трехмерного пространства, Гамильтону пришлось принести еще одну жертву.
Оказывается, определенные им новые числа – кватернионы – потеряли еще одно привычное качество: произведение кватернионов зависит от порядка сомножителей. Действительно, уже в формулах (6) при изменении порядка сомножителей произведение меняет знак.
Таким образом, можно говорить лишь о “делении справа” и “делении слева”. Как реально найти, скажем, “левое частное” от деления кватерниона на кватернион ?
Обозначим искомое частное через q = x + yi + uj + vk. Тогда, используя правило умножения для кватернионов и определение левого частного, получим следующее равенство кватернионов:
,
или
Полученное равенство равносильно системе четырех линейных уравнений с переменными x, y, u, v :
Аналогичным образом находится “правое частное” от деления на .
Рассмотрим частный случай, когда делимое равно единице. В этом случае частное от деления =1 на кватернион (и “слева” и “справа”) равно одному и тому же кватерниону
Поэтому кватернион p обозначается через. Тогда “правое частное” от деления кватерниона на выражается формулой
,
а “левое частное” от деления кватерниона на – формулой
Практически частное от деления двух кватернионов ищется другим путем. Для этого нам потребуются
Скалярные и векторные кватернионы
Так же как комплексные числа разлагаются в сумму своей действительной и мнимой частей, кватернион тоже можно разложить в сумму q = x + (yi + uj + vk). Первое слагаемое в этом разложении называется скалярной частью кватерниона, а второе – векторной частью. Скалярная часть х – это просто действительное число, а векторная часть может быть изображена вектором r = yi + uj + vk в трехмерном пространстве, где i, j, k мы теперь рассматриваем как единичные вектора прямоугольной системы координат.
Таким образом, каждый кватернион q представляется в виде суммы q = x + r, где x – скалярная часть кватерниона q, а r – векторная часть. Если r = 0, то q = x и кватернион q называется скалярным кватернионом . Если же x = 0, то q = r и q называется векторным кватернионом .
При сложении кватернионов независимо складываются их скалярные и векторные части.
При умножении дело обстоит сложнее. Если и – скалярные кватернионы, то их произведение тоже скалярный кватернион. В случае, когда = х – скалярный кватернион, а = r – векторный кватернион, произведение является векторным кватернионом, и операция умножения совпадает с умножением вектора r в пространстве на действительное число x .
И, наконец, если оба кватерниона векторные, то
Как видно из последней формулы, скалярная часть произведения равна скалярному произведению векторов и с обратным знаком. Векторная же часть – это наш старый знакомый – векторное произведение, записанное в координатах.
Объединяя все рассмотренные случаи, получим общую формулу для умножения кватернионов. Если и, то
А как же триплеты?
Почему же Гамильтону не удалось найти способа умножения триплетов? Раньше уже было отмечено, что эту задачу решить нельзя. Доказано, что попросту не существует способа умножения точек пространства, удовлетворяющего нашим требованиям (ассоциативности, дистрибутивности относительно покоординатного сложения, возможности деления на ненулевые элементы). Сейчас, к тому же, известны все случаи, когда можно вести такое умножение. Это доказал немецкий математик Ф. Г. Фробениус (1849 – 1917). По его словам, этих случаев три: в размерности один (действительные числа), в размерности два (комплексные числа) и в “размерности четыре” (кватернионы).
Что было дальше
Гамильтон и его последователи возлагали большие надежды на кватернионы. От кватернионов ожидали таких же результатов, как от комплексных чисел, и даже больше. И действительно, с помощью исчисления кватернионов были обнаружены совершенные в их математической красоте формулы, описывающие ряд важных физических явлений. Но дальнейшие надежды на развитие алгебраического и функционального исчисления кватернионов не оправдались.
Для кватернионов не имеет места основная теорема алгебры о существовании корней у многочлена с кватернионными коэффициентами, а, с другой стороны, существует такой многочлен с кватернионными коэффициентами от одной переменной, для которого любой кватернион является корнем.
Оптимизм сменился скепсисом. В начале нашего века математики перестали интересоваться кватернионами. Но время шло, и физики упорно искали математический формализм для некоторых эффектов, связанных с так называемым спином элементарных частиц. Кватернионы снова получили признание, когда была понята их роль в построении различных геометрических преобразований пространства, используемых в квантовой физике. Геометрические свойства кватернионов – это особая большая тема.
Для этого будет посвящен другой реферат.
Использованная литература:
Квант. Изд. “Наука”. Главная редакция физико-математической литературы, Москва, 1983(9).
www.ronl.ru
Как сделать из точек числа?
Если речь идет о точках на прямой – это просто. Выбрав начало отсчета и масштабс направлением, можно получить из прямой числовую ось и тем самым превратить каждуюточку в действительное число – ее координату.
С точками на плоскости сложнее. Выбираем две оси и начало отсчета. Для каждойточки плоскости сопоставляем ее координаты (x; y). Эта парабудет называться дуплетом. Чтобы сделать дуплет числом, нужнонаучиться “складывать” и “умножать” их в соответствии со свойствами сложения иумножения.
Дуплеты складываются как векторы – покоординатно:
(x; y) + (x’; y’) = (x + x’; y + y’).(1)
Дляумножения существует иная формула:
(x; y) /> (x’; y’)= (xx’ - yy’; xy’ + x’y). (2)
Умножениеи сложение (1), (2) дуплетов подчиняются привычным свойствам сложения иумножения. Следовательно, множество дуплетов с операциями (1), (2) можносчитать полноценным числовым множеством.
На самом деле дуплеты – это комплексные числа. Их записывают так:x + yi, где i –мнимая единица (дуплет (0; 1)). Ее квадрат равен />. Это позволяет извлекатьквадратные корни из отрицательных чисел.
Но встает проблема превращения точек пространствав числа.Здесь снова введем систему координат и запишем точки в виде набора уже трехкоординат (x; y; z). Эти так называемые триплетытожескладываются покоординатно:
(x; y; z) + (x’; y’; z’) = (x + x’; y + y’; z + z’). (3)
Триплетыможно будет считать числами, если научиться их умножать, обладая, вместе сосвойствами сложения, обычными способами умножения этих операций.
В 1833 г. умножением триплетов занимался ирландский математик У. Р. Гамильтон(1805 – 1865). О нем мы расскажем особо.
Уильям Роуан ГамильтонГамильтон был человеком многосторонне развитым. В четырнадцать лет владелдевятью языками, в 1824 г. опубликовал в трудах Королевской Ирландской Академииработу, посвященную геометрической оптике, в 1828 г. получил званиекоролевского астронома Ирландии.
К 1833 г. Гамильтон занимал пост директора обсерватории в Денсинке и былизвестен работами по оптике и аналитической механики. Он предсказал эффектдвойной конической рефракции в двуосных кристаллах.
В течение долгих десяти лет Гамильтон безуспешно пытался придумать правилоумножения триплетов.
Векторное произведениеЗадача поначалу казалась несложной. Складывать векторы следовало по формуле(3). Оставалось найти формулу умножения, подобную формуле (2). Но Гамильтонбезуспешно пытался подбирать формулы для умножения триплетов.
В то время было известно правило векторного произведения:
векторнымпроизведением /> ненулевыхвекторов /> называется вектор,перпендикулярный плоскости, проходящей через векторы /> имеющий направление,определяемое правилом “правой руки”, и длину ê/>ê/> ê/>ê/>.Если для данных векторов заданы координаты в прямоугольной системе координат:
/>
/>
то/> (4)
Нооперация векторного произведения не годилась Гамильтону, поскольку она не имеетобратной. Например, если /> то угол(/>) между векторами равеннулю. Значит, длина векторного произведения /> равнанулю, т.е. и сам вектор /> нулевой.
Но несмотря на неудачи, Гамильтон пытался решить поставленную перед собойзадачу. Но эта задача не могла быть решена (объяснение следует ниже). Но трудне пропал даром. В 1843 г. Гамильтон вдруг решил, что для определения умножениянужно рассматривать не триплеты (тройки чисел), а четверки, или кватернионы.Вот история их создания.
Случай на Брогемском мосту/>
В одном из писем к своему сыну Гамильтон писал: “Это был 16-й день октября,который случился в понедельник, в день заседания Совета Королевской ИрландскойАкадемии, где я должен был председательствовать. Я направлялся туда с твоейматерью вдоль Королевского канала; и, хотя она говорила мне какие-то отдельныефразы, я их почти не воспринимал, так как в моем сознании подспудно что-тотворилось. Неожиданно как будто бы замкнулся электрический контур; блеснулаискра, предвещающая многие длительные годы определенно направленной мысли итруда, моего – если доведется, или труда других, если мне будет дарованодостаточно сознательной жизни, чтобы сообщить о своем открытии. Я оказался не всостоянии удержаться от желания высечь ножом на мягком камне Брогемского мостафундаментальную формулу о символах i, j, k,
/>,
содержащуюрешение проблемы, но, конечно, эта запись с тех пор стерлась. Однако болеепрочное упоминание осталось в Книге записей Совета Академии за этот день, гдезасвидетельствовано, что я попросил и получил разрешение на доклад окватернионах на первом заседании сессии, который и был прочитан соответственнов Понедельник 13-го следующего месяца – ноября”.
Определениекватернионов
Кватернионы – это четверки действительных чисел (x; y; u; v),которые удобно записывать в виде q = x + yi + uj + vk, где i, j, k– новые числа, являющиеся аналогом мнимой единицы в комплексных числах.Требуется, чтобы числа i, j, k удовлетворяли следующим соотношениям:
/> (5)
/> /> (6)
которыеудобно записать в виде “таблицы умножения”.
x i j k
i -1 k j
j -k -1 i
k -j -i -1
По определению операции сложения и умножения кватернионов производятся пообычным правилам раскрытия скобок и приведения подобных членов с учетом правил(5) – (6).
Согласно этому определению, если /> и /> – два кватерниона, то
/>/> (7)
Это,разумеется, привычное нам “покоординатное” сложение. Далее, произведениекватернионов /> и /> вычисляется так:
/>
Длинная,но совершенно автоматическая проверка показывает, что умножение кватернионовобладает сочетательным свойством:
/>
Естественносчитать, что действительные и комплексные числа являются частным случаемкватернионов. Так, действительное число x – это кватернион вида
/>
Комплексноечисло z = x + yi представляется как кватернион
/>
У операции сложения кватернионов, очевидно, имеется обратная операция–вычитание. Именно, разность двух кватернионов /> и/> определяется формулой:
/>
Если/>, то разность кватернионов –это нулевой кватернион.
Деление кватернионовПерейдем теперь к операции деления кватернионов, обратной к операции умножения.Вообще, что мы понимаем под частным от деления числа a на число b,не равное нулю? Это такое число c, что
bc = a. (10)
Такопределяется частное от деления для действительных и комплексных чисел. Ксожалению, для кватерниона применить непосредственно это определение мы неможем. Для того чтобы формула (10) “корректно” определяла частное, нужно, чтобыпроизведение не зависело от порядка сомножителей. В противном случае наряду счастным /> определенным формулой (10),существует вполне равноправное “левое” частное” с’, определяемое формулой
c’b = a,
котороеможет отличаться от “правого частного” c из (10). Вот здесь, кроменеобходимости выйти за пределы трехмерного пространства, Гамильтону пришлосьпринести еще одну жертву.
Оказывается, определенные им новые числа – кватернионы – потеряли еще однопривычное качество: произведение кватернионов зависит от порядка сомножителей.Действительно, уже в формулах (6) при изменении порядка сомножителейпроизведение меняет знак.
Таким образом, можно говорить лишь о “делении справа” и “делении слева”. Какреально найти, скажем, “левое частное” от деления кватерниона /> на кватернион />?
Обозначим искомое частное через q = x + yi + uj + vk. Тогда, используяправило умножения для кватернионов и определение левого частного, получимследующее равенство кватернионов:
/>,
или
/>
Полученное равенство равносильно системе четырех линейных уравнений спеременными x, y, u, v:
/>
Аналогичным образом находится “правое частное” от деления /> на />.
Рассмотрим частный случай, когда делимое /> равноединице. В этом случае частное от деления />=1на кватернион /> (и “слева” и“справа”) равно одному и тому же кватерниону
/>
Поэтомукватернион p обозначается через />.Тогда “правое частное” от деления кватерниона /> на/> выражается формулой
/>,
а“левое частное” от деления кватерниона /> на/> – формулой
/>
Практически частное от деления двух кватернионов ищется другим путем. Для этогонам потребуются
Скалярные и векторные кватернионыТак же как комплексные числа разлагаются в сумму своей действительной и мнимойчастей, кватернион тоже можно разложить в сумму q = x + (yi + uj + vk). Первоеслагаемое в этом разложении называется скалярной частью кватерниона,а второе – векторной частью. Скалярная часть х – это простодействительное число, а векторная часть может быть изображена вектором r =yi + uj + vk в трехмерном пространстве, где i, j, k мы теперьрассматриваем как единичные вектора прямоугольной системы координат.
Таким образом, каждый кватернион q представляется в виде суммы q = x+ r, где x – скалярная часть кватерниона q, а r –векторная часть. Если r = 0, то q = x и кватернион q называетсяскалярным кватернионом. Если же x = 0, то q = r и qназывается векторным кватернионом.
При сложении кватернионов независимо складываются их скалярные и векторныечасти.
При умножении дело обстоит сложнее. Если /> и/> – скалярные кватернионы, тоих произведение тоже скалярный кватернион. В случае, когда />= х – скалярныйкватернион, а /> = r –векторный кватернион, произведение /> являетсявекторным кватернионом, и операция умножения совпадает с умножением вектора rв пространстве на действительное число x.
И, наконец, если оба кватерниона векторные, то
/>
Каквидно из последней формулы, скалярная часть произведения />/> равна скалярномупроизведению /> векторов /> и /> с обратным знаком.Векторная же часть />/> – это наш старый знакомый –векторное произведение />, записанное вкоординатах.
/> Объединяя все рассмотренные случаи, получим общую формулу для умножениякватернионов. Если /> и/>, то
/>
А как же триплеты?Почему же Гамильтону не удалось найти способа умножения триплетов? Раньше ужебыло отмечено, что эту задачу решить нельзя. Доказано, что попросту несуществует способа умножения точек пространства, удовлетворяющего нашимтребованиям (ассоциативности, дистрибутивности относительно покоординатногосложения, возможности деления на ненулевые элементы). Сейчас, к тому же,известны все случаи, когда можно вести такое умножение. Это доказал немецкийматематик Ф. Г. Фробениус (1849 – 1917). По его словам, этих случаев три: вразмерности один (действительные числа), в размерности два (комплексные числа)и в “размерности четыре” (кватернионы).
Что было дальшеГамильтон и его последователи возлагали большие надежды на кватернионы. Откватернионов ожидали таких же результатов, как от комплексных чисел, и дажебольше. И действительно, с помощью исчисления кватернионов были обнаруженысовершенные в их математической красоте формулы, описывающие ряд важныхфизических явлений. Но дальнейшие надежды на развитие алгебраического ифункционального исчисления кватернионов не оправдались.
Для кватернионов не имеет места основная теорема алгебры о существовании корнейу многочлена с кватернионными коэффициентами, а, с другой стороны, существуеттакой многочлен с кватернионными коэффициентами от одной переменной, длякоторого любой кватернион является корнем.
Оптимизм сменился скепсисом. В начале нашего века математики пересталиинтересоваться кватернионами. Но время шло, и физики упорно искалиматематический формализм для некоторых эффектов, связанных с так называемым спиномэлементарных частиц. Кватернионы снова получили признание, когда была понята ихроль в построении различных геометрических преобразований пространства, используемыхв квантовой физике. Геометрические свойства кватернионов – это особая большаятема.
Дляэтого будет посвящен другой реферат.
Использованнаялитература:
Квант.Изд. “Наука”. Главная редакция физико-математической литературы, Москва,1983(9).
www.ronl.ru
Уже сейчас на сайте вы можете воспользоваться более чем 20 000 рефератами, докладами, шпаргалками, курсовыми и дипломными работами.Присылайте нам свои новые работы и мы их обязательно опубликуем. Давайте продолжим создавать нашу коллекцию рефератов вместе!!!
Вы согласны передать свой реферат (диплом, курсовую работу и т.п.), а также дальнейшие права на хранение, и распространение данного документа администрации сервера "mcvouo.ru"?
Дата добавления: март 2006г.
Как сделать из точек числа?
Если речь идет о точках на прямой –это просто. Выбрав начало отсчета и масштаб с направлением, можно получить из прямой числовую ось и тем самым превратить каждую точку вдействительное число – ее координату. С точками на плоскости сложнее. Выбираем две оси и начало отсчета. Для каждой точки плоскости сопоставляем ее координаты (x; y). Эта пара будет называться дуплетом. Чтобы сделать дуплет числом, нужно научиться “складывать” и “умножать” их в соответствии со свойствами сложения и умножения.
Дуплеты складываются как векторы – покоординатно: (x; y) + (x’; y’) = (x + x’; y + y’). (1) Для умножения существует иная формула: (x; y) (x’; y’) = (xx’ - yy’; xy’ + x’y). (2)
Умножение и сложение (1), (2) дуплетов подчиняются привычным свойствам сложения и умножения. Следовательно, множество дуплетов с операциями (1), (2) можно считать полноценным числовым множеством.
На самом деле дуплеты – это комплексные числа. Их записывают так: x + yi, где i –мнимая единица (дуплет (0; 1)). Ее квадрат равен . Это позволяет извлекать квадратные корни из отрицательных чисел. Но встает проблема превращения точек пространства в числа. Здесь снова введем систему координат и запишем точки в виде набора уже трех координат(x; y; z). Эти так называемые триплеты тоже складываются покоординатно:
(x; y; z) + (x’; y’; z’) = (x + x’; y + y’; z + z’). (3)
Триплеты можно будет считать числами, если научиться их умножать, обладая, вместе со свойствами сложения, обычными способами умножения этих операций. В 1833 г. умножением триплетов занимался ирландский математик У. Р. Гамильтон (1805– 1865). О нем мы расскажем особо.
Уильям Роуан Гамильтон
Гамильтон был человеком многосторонне развитым. В четырнадцать лет владел девятью языками, в 1824 г. опубликовал в трудах Королевской Ирландской Академии работу, посвященную геометрической оптике, в 1828 г. получил звание королевского астронома Ирландии.
К 1833 г. Гамильтон занимал пост директора обсерватории в Денсинке и был известен работами по оптике и аналитической механики. Он предсказал эффект двойной конической рефракции в двуосных кристаллах.
В течение долгих десяти лет Гамильтон безуспешно пытался придумать правило умножения триплетов.
Векторное произведение
Задача поначалу казалась несложной. Складывать векторы следовало по формуле (3). Оставалось найти формулу умножения, подобную формуле (2). Но Гамильтон безуспешно пытался подбирать формулы для умножения триплетов. В то время было известно правило векторного произведения:
векторным произведением ненулевых векторов называется вектор, перпендикулярный плоскости, проходящей через векторы имеющий направление, определяемое правилом “правой руки”, и длину кк кк. Если для данных векторов заданы координаты в прямоугольной системе координат:
то (4)
Но операция векторного произведения не годилась Гамильтону, поскольку она не имеет обратной. Например, если то угол () между векторами равен нулю. Значит, длина векторного произведения равна нулю, т. е. и сам вектор нулевой. Но несмотря на неудачи, Гамильтон пытался решить поставленную перед собой задачу. Но эта задача не могла быть решена (объяснение следует ниже). Но труд не пропал даром. В 1843 г. Гамильтон вдруг решил, что для определения умножения нужно рассматривать не триплеты (тройки чисел), а четверки, или кватернионы. Вот история их создания.
Случай на Брогемском мосту
В одном из писем к своему сыну Гамильтон писал: “Это был 16-й день октября, который случился в понедельник, в день заседания Совета Королевской Ирландской Академии, где я должен был председательствовать. Я направлялся туда с твоей матерью вдоль Королевского канала; и, хотя она говорила мне какие-то отдельные фразы, я их почти не воспринимал, так как в моем сознании подспудно что-то творилось. Неожиданно как будто бы замкнулся электрический контур; блеснула искра, предвещающая многие длительные годы определенно направленной мысли и труда, моего–если доведется, или труда других, если мне будет даровано достаточно сознательной жизни, чтобы сообщить о своем открытии. Я оказался не в состоянии удержаться от желания высечь ножом на мягком камне Брогемского моста фундаментальную формулу о символахi, j, k,
,
содержащую решение проблемы, но, конечно, эта запись с тех пор стерлась. Однако более прочное упоминание осталось в Книге записей Совета Академии за этот день, где засвидетельствовано, что я попросил и получил разрешение на доклад о кватернионах на первом заседании сессии, который и был прочитан соответственно в Понедельник 13-го следующего месяца– ноября”.
Определение кватернионов
Кватернионы – это четверки действительных чисел (x; y; u; v), которые удобно записывать в виде q = x + yi + uj + vk, где i, j, k –новые числа, являющиеся аналогом мнимой единицы в комплексных числах. Требуется, чтобы числаi, j, k удовлетворяли следующим соотношениям:
(5) (6) которые удобно записать в виде “таблицы умножения”. x i j k i -1 k j j -k -1 i k -j -i -1
По определению операции сложения и умножения кватернионов производятся по обычным правилам раскрытия скобок и приведения подобных членов с учетом правил (5)– (6).
Согласно этому определению, если и – два кватерниона, то (7)
Это, разумеется, привычное нам “покоординатное” сложение. Далее, произведение кватернионов и вычисляется так:
Длинная, но совершенно автоматическая проверка показывает, что умножение кватернионов обладает сочетательным свойством:
Естественно считать, что действительные и комплексные числа являются частным случаем кватернионов. Так, действительное числоx – это кватернион вида
Комплексное число z = x + yi представляется как кватернион
У операции сложения кватернионов, очевидно, имеется обратная операция –вычитание. Именно, разность двух кватернионов и определяется формулой:
Если , то разность кватернионов – это нулевой кватернион. Деление кватернионов
Перейдем теперь к операции деления кватернионов, обратной к операции умножения. Вообще, что мы понимаем под частным от деления числаa на число b, не равное нулю? Это такое число c, что
bc = a. (10)
Так определяется частное от деления для действительных и комплексных чисел. К сожалению, для кватерниона применить непосредственно это определение мы не можем. Для того чтобы формула (10) “корректно” определяла частное, нужно, чтобы произведение не зависело от порядка сомножителей. В противном случае наряду с частным определенным формулой (10), существует вполне равноправное “левое” частное” с’, определяемое формулой
c’b = a,
которое может отличаться от “правого частного” cиз (10). Вот здесь, кроме необходимости выйти за пределы трехмерного пространства, Гамильтону пришлось принести еще одну жертву. Оказывается, определенные им новые числа – кватернионы –потеряли еще одно привычное качество: произведение кватернионов зависит от порядка сомножителей. Действительно, уже в формулах (6) при изменении порядка сомножителей произведение меняет знак.
Таким образом, можно говорить лишь о “делении справа” и “делении слева”. Как реально найти, скажем, “левое частное” от деления кватерниона на кватернион ? Обозначим искомое частное через q = x + yi + uj + vk. Тогда, используя правило умножения для кватернионов и определение левого частного, получим следующее равенство кватернионов:
, или
Полученное равенство равносильно системе четырех линейных уравнений с переменнымиx, y, u, v:
Аналогичным образом находится “правое частное” от деления на . Рассмотрим частный случай, когда делимое равно единице. В этом случае частное от деления =1 на кватернион (и “слева” и “справа”) равно одному и тому же кватерниону
Поэтому кватернион p обозначается через . Тогда “правое частное” от деления кватерниона на выражается формулой
, а “левое частное” от деления кватерниона на – формулой
Практически частное от деления двух кватернионов ищется другим путем. Для этого нам потребуются
Скалярные и векторные кватернионы
Так же как комплексные числа разлагаются в сумму своей действительной и мнимой частей, кватернион тоже можно разложить в суммуq = x + (yi + uj + vk). Первое слагаемое в этом разложении называется скалярной частью кватерниона, а второе – векторной частью. Скалярная часть х –это просто действительное число, а векторная часть может быть изображена векторомr = yi + uj + vk в трехмерном пространстве, где i, j, k мы теперь рассматриваем как единичные вектора прямоугольной системы координат. Таким образом, каждый кватернион q представляется в виде суммы q = x + r, где x – скалярная часть кватерниона q, а r – векторная часть. Если r = 0, то q = x и кватернион q называется скалярным кватернионом. Если же x = 0, то q = r и q называется векторным кватернионом. При сложении кватернионов независимо складываются их скалярные и векторные части.
При умножении дело обстоит сложнее. Если и –скалярные кватернионы, то их произведение тоже скалярный кватернион. В случае, когда= х – скалярный кватернион, а = r – векторный кватернион, произведение является векторным кватернионом, и операция умножения совпадает с умножением вектораr в пространстве на действительное число x.
И, наконец, если оба кватерниона векторные, то
Как видно из последней формулы, скалярная часть произведения равна скалярному произведению векторов и с обратным знаком. Векторная же часть – это наш старый знакомый – векторное произведение , записанное в координатах. Объединяя все рассмотренные случаи, получим общую формулу для умножения кватернионов. Если и , то
А как же триплеты?
Почему же Гамильтону не удалось найти способа умножения триплетов? Раньше уже было отмечено, что эту задачу решить нельзя. Доказано, что попростуне существуетспособа умножения точек пространства, удовлетворяющего нашим требованиям (ассоциативности, дистрибутивности относительно покоординатного сложения, возможности деления на ненулевые элементы). Сейчас, к тому же, известны все случаи, когда можно вести такое умножение. Это доказал немецкий математик Ф. Г. Фробениус (1849–1917). По его словам, этих случаев три: в размерности один (действительные числа), в размерности два (комплексные числа) и в “размерности четыре” (кватернионы).
Что было дальше
Гамильтон и его последователи возлагали большие надежды на кватернионы. От кватернионов ожидали таких же результатов, как от комплексных чисел, и даже больше. И действительно, с помощью исчисления кватернионов были обнаружены совершенные в их математической красоте формулы, описывающие ряд важных физических явлений. Но дальнейшие надежды на развитие алгебраического и функционального исчисления кватернионов не оправдались.
Для кватернионов не имеет места основная теорема алгебры о существовании корней у многочлена с кватернионными коэффициентами, а, с другой стороны, существует такой многочлен с кватернионными коэффициентами от одной переменной, для которого любой кватернион является корнем.
Оптимизм сменился скепсисом. В начале нашего века математики перестали интересоваться кватернионами. Но время шло, и физики упорно искали математический формализм для некоторых эффектов, связанных с так называемымспиномэлементарных частиц. Кватернионы снова получили признание, когда была понята их роль в построении различных геометрических преобразований пространства, используемых в квантовой физике. Геометрические свойства кватернионов– это особая большая тема. Для этого будет посвящен другой реферат.
Использованная литература:
Квант. Изд. “Наука”. Главная редакция физико-математической литературы, Москва, 1983(9).
Скачен 330 раз.
mcvouo.ru
Реферат на тему:
Кватернио́ны (от лат. quaterni, по четыре) — система гиперкомплексных чисел, предложенная Гамильтоном в 1843 году.
Умножение кватернионов некоммутативно; они образуют тело, которое обычно обозначается .
Кватернионы очень удобны для описания изометрий трёхмерного и четырёхмерного Евклидовых пространств, и поэтому получили широкое распространение в механике. Также их используют в вычислительной математике, например при создании трёхмерной графики.[1]
Кватернион представляет собой пару где
— вектор трёхмерного пространства, а
— скаляр, то есть вещественное число. Операции сложения определены следующим образом:
Произведение определяется следующим образом:
где обозначает скалярное произведение, а
— векторное произведение.
В частности,
Заметим, что
Кватернионы можно определить как формальную сумму где
— вещественные числа, а
— мнимые единицы со следующим свойством: i2 = j2 = k2 = ijk = − 1. Таким образом, таблица умножения базисных кватернионов —
— выглядит так:
например, , a
.
Кватернионы также можно определить как вещественные матрицы следующего вида с обычными матричными произведением и суммой:

При такой записи:
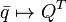 ;
; 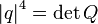 .
. Кватернион можно представить как пару комплексных чисел. Пусть 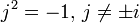 и
и 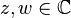 . Тогда кватернион можно записать в виде q = z + wj = a + bi + cj + dij.
. Тогда кватернион можно записать в виде q = z + wj = a + bi + cj + dij.
Альтернативно, кватернионы можно определить как комплексные матрицы следующего вида с обычными матричными произведением и суммой:
здесь и
обозначают комплексно-сопряжённые числа к
и
.
Такое представление имеет несколько замечательных свойств:
 ;
;  .
. Для кватерниона
кватернион называется скалярной частью
а кватернион
— векторной частью. Если
то кватернион называется чисто скалярным, а при
— чисто векторным.
Кватернион
называется сопряжённым к
Сопряжённое произведение есть произведение сопряжённых в обратном порядке:

Для кватернионов справедливо равенство

Так же, как и для комплексных чисел,
называется модулем . Если
то
называется единичным кватернионом.
В качестве нормы кватерниона обычно рассматривают его модуль: 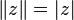 .
.
Таким образом, на множестве кватернионов можно ввести метрику. Кватернионы образуют метрическое пространство, изоморфное с евклидовой метрикой.
Кватернионы с модулем в качестве нормы образуют банахову алгебру.
Из тождества четырёх квадратов вытекает, что иными словами, кватернионы обладают мультипликативной нормой и образуют ассоциативную алгебру с делением.
Кватернион, обратный по умножению к q, вычисляется так:
 .
. Четыре базисных кватерниона и четыре противоположных им по знаку образуют по умножению группу кватернионов (порядка 8). Обозначается:
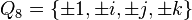 .
. Множество кватернионов является примером кольца с делением.
Множество кватернионов образует четырёхмерную ассоциативную алгебру с делением над полем вещественных (но не комплексных) чисел. Вообще ,
,
являются единственными конечномерными ассоциативными алгебрами с делением над полем вещественных чисел.[2]
Некоммутативность умножения кватернионов приводит к неожиданным последствиям. Например, количество различных корней полиномиального уравнения над множеством кватернионов может быть больше, чем степень уравнения. В частности, уравнение q2 + 1 = 0 имеет бесконечно много решений — это все единичные чисто векторные кватернионы.
Организация всех трёх степеней свободы, однако окончательная свобода наименьшего кольца зависит от положения старших колец
Кватернионы, рассматриваемые как алгебра над , образуют четырёхмерное вещественное векторное пространство. Любой поворот этого пространства относительно
может быть записан в виде
, где
и
— пара единичных кватернионов, при этом пара
определяется с точностью до знака, то есть один поворот определяют в точности две пары —
и
. Из этого следует, что группа Ли
поворотов
есть факторгруппа
, где
обозначает мультипликативную группу единичных кватернионов.
Чисто векторные кватернионы образуют трёхмерное вещественно векторное пространство. Любой поворот пространства чисто векторных кватернионов относительно может быть записан в виде
, где
— некоторый единичный кватернион. Соответственно,
, в частности,
диффеоморфно
.
В качестве нормы кватерниона выберем квадрат его модуля:  .
.
Целыми принято называть кватернионы a + bi + cj + dk такие, что все 2a,2b,2c,2d — целые и одинаковой чётности.
Целый кватернион называется
если таким же свойством обладает его норма.
Целый кватернион называется примитивным, если он не делится ни на какое натуральное число, кроме 1, нацело (иными словами, 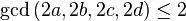 ).
).
Существует 24 целых единичных кватерниона:
 ,
,  ,
,  ,
,  ,
,  .
. Они образуют группу по умножению и лежат в вершинах правильного четырёхмерного многогранника — кубооктаэдра (не путать с трёхмерным многогранником-кубооктаэдром).
Для примитивных кватернионов верен аналог основной теоремы арифметики.
Теорема.[3] Для любого фиксированного порядка множителей в разложении нормы кватерниона N(q) в произведение простых целых положительных чисел N(q) = p1p2...pn существует разложение кватерниона q в произведение простых кватернионов q = q1q2...qn такое, что N(qi) = pi. Причём данное разложение единственно по модулю домножения на единицы — это значит, что любое другое разложение будет иметь вид
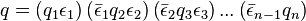 ,
, где ε1, ε2, ε3, … εn − 1 — целые единичные кватернионы.
Например, примитивный кватернион q = (1 + i)2(1 + i + j)(2 + i) имеет норму 60, значит, по модулю домножения на единицы он имеет ровно 12 разложений в произведение простых кватернионов, отвечающих 12 разложениям числа 60 в произведений простых:
Общее число разложений такого кватерниона равно
Знак кватерниона вычисляется так:
 .
. Аргумент кватерниона — это угол поворота четырёхмерного вектора, который отсчитывается от вещественной единицы:
 .
. В дальнейшем используется представление заданного кватерниона q в виде
Здесь a — вещественная часть кватерниона, . При этом i2 = − 1, поэтому проходящая через q и вещественную прямую плоскость имеет структуру алгебры комплексных чисел, что позволяет перенести на случай кватернионов произвольные аналитические функции. Они удовлетворяют стандартным соотношениям, если все аргументы имеют вид a + bi для фиксированного единичного вектора i. В случае если требуется рассматривать кватернионы с разным направлением, формулы значительно усложняются, в силу некоммутативности алгебры кватернионов.
Стандартное определение аналитических функций на ассоциативной нормированной алгебре основано на разложении этих функций в степенные ряды. Рассуждения, доказывающие корректность определения таких функций, полностью аналогичны комплексному случаю и основаны на вычислении радиуса сходимости соответствующих степенных рядов. Учитывая указанное выше «комплексное» представление для заданного кватерниона, соответствующие ряды можно привести к указанной ниже компактной форме. Здесь приведены лишь некоторые наиболее употребительные аналитические функции, аналогично можно вычислить любую аналитическую функцию. Общее правило таково: если f(a + bi) = c + di для комплексных чисел, то , где кватернион q рассматривается в «комплексном» представлении
.

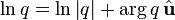
Отметим, что, как обычно в комплексном анализе, логарифм оказывается определён лишь с точностью до .

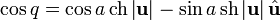

Существуют разные способы определения регулярных функций кватернионного переменного. Самый явный — рассмотрение кватернионно дифференцируемых функций, при этом можно рассматривать праводифференцируемые и леводифференцируемые функции, не совпадающие в силу некоммутативности умножения кватернионов. Очевидно, что их теория полностью аналогична. Определим кватернионно леводифференцируемую функцию f как имеющую предел
Оказывается, что все такие функции имеют в некоторой окрестности точки q вид
f = a + qbгде a,b — постоянные кватернионы. Другой способ основан на использовании операторов
и рассмотрении таких кватернионных функций f, для которых[4]
что полностью аналогично использованию операторов и
в комплексном случае. При этом получаются аналоги интегральной теоремы Коши, теории вычетов, гармонических функций и рядов Лорана для кватернионных функций[5].
Производная Гато функции кватернионного переменного определена согласно формуле
Производная Гато является аддитивным отображением приращения аргумента и может быть представлена в виде[6]

Здесь предполагается суммирование по индексу s. Число слагаемых зависит от выбора функции f. Выражения и
называются компонентами производной.
Так по-другому называется общепринятое умножение кватернионов (pq).
Отличается от общепринятого тем, что вместо первого сомножителя берется сопряжённый к нему: . Оно также некоммутативно.
Аналогично одноимённой операции для векторов:
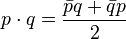 .
. Эту операцию можно использовать для выделения одного из коэффициентов, например, 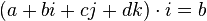 .
.
Определение модуля кватерниона можно видоизменить:
 .
. Используется не очень часто, тем не менее рассматривается в дополнение к скалярному произведению.
Аналогично одноимённой операции для векторов. Результатом является тоже вектор:
 .
. Система кватернионов была впервые опубликована Гамильтоном в 1843 году. Историки науки также обнаружили наброски по этой теме в неопубликованных рукописях Гаусса, относящихся к 1819—1820 годам.[8]
Бурное и чрезвычайно плодотворное развитие комплексного анализа в XIX веке стимулировало у математиков интерес к следующей задаче: найти новый вид чисел, аналогичный по свойствам комплексным, но содержащий не одну, а две мнимые единицы. Предполагалось, что такая модель будет полезна при решении пространственных задач математической физики. Однако работа в этом направлении оказалась безуспешной.
Новый вид чисел был обнаружен ирландским математиком Уильямом Гамильтоном в 1843 году, и он содержал не две, как ожидалось, а три мнимые единицы. Гамильтон назвал эти числа кватернионами. Позднее Фробениус строго доказал (1877) теорему, согласно которой расширить комплексное поле до поля или тела с двумя мнимыми единицами невозможно.
Несмотря на необычные свойства новых чисел (их некоммутативность), эта модель довольно быстро принесла практическую пользу. Максвелл использовал компактную кватернионную запись для формулировки своих уравнений электромагнитного поля.[9] Позднее на основе алгебры кватернионов был создан трёхмерный векторный анализ (Гиббс, Хевисайд).
Как алгебра над , кватернионы образуют вещественное векторное пространство
, снабжённое тензором третьего ранга S типа (1,2), иногда называемого структурным тензором. Как всякий тензор такого типа, S отображает каждую 1-форму t на
и пару векторов
из
в вещественное число
. Для любой фиксированной 1-формы t S превращается в ковариантный тензор второго ранга, который, в случае его симметрии, становится скалярным произведением на
. Поскольку каждое вещественное векторное пространство является также вещественным линейным многообразием, такое скалярное произведение порождает тензорное поле, которое, при условии его невырожденности, становится (псевдо- или собственно-)евклидовой метрикой на
. В случае кватернионов это скалярное произведение индефинитно, его сигнатура не зависит от 1-формы t, а соответствующая псевдоевклидова метрика есть метрика Минковского [10]. Эта метрика автоматически продолжается на группу Ли ненулевых кватернионов вдоль её левоинвариантных векторных полей, образуя так называемую закрытую ФЛРУ (Фридман — Леметр — Робертсон — Уолкер) метрику[11] — важное решение уравнений Эйнштейна. Эти результаты проясняют некоторые аспекты проблемы совместимости квантовой механики и общей теории относительности в рамках теории квантовой гравитации[12].
wreferat.baza-referat.ru
Реферат на тему:
Кватернио́ны (от лат. quaterni, по четыре) — система гиперкомплексных чисел, предложенная Гамильтоном в 1843 году.
Умножение кватернионов некоммутативно; они образуют тело, которое обычно обозначается .
Кватернионы очень удобны для описания изометрий трёхмерного и четырёхмерного Евклидовых пространств, и поэтому получили широкое распространение в механике. Также их используют в вычислительной математике, например при создании трёхмерной графики.[1]
Кватернион представляет собой пару где
— вектор трёхмерного пространства, а
— скаляр, то есть вещественное число. Операции сложения определены следующим образом:
Произведение определяется следующим образом:
где обозначает скалярное произведение, а
— векторное произведение.
В частности,
Заметим, что
Кватернионы можно определить как формальную сумму где
— вещественные числа, а
— мнимые единицы со следующим свойством: i2 = j2 = k2 = ijk = − 1. Таким образом, таблица умножения базисных кватернионов —
— выглядит так:
например, , a
.
Кватернионы также можно определить как вещественные матрицы следующего вида с обычными матричными произведением и суммой:

При такой записи:
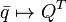 ;
; 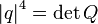 .
. Кватернион можно представить как пару комплексных чисел. Пусть 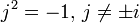 и
и 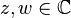 . Тогда кватернион можно записать в виде q = z + wj = a + bi + cj + dij.
. Тогда кватернион можно записать в виде q = z + wj = a + bi + cj + dij.
Альтернативно, кватернионы можно определить как комплексные матрицы следующего вида с обычными матричными произведением и суммой:
здесь и
обозначают комплексно-сопряжённые числа к
и
.
Такое представление имеет несколько замечательных свойств:
 ;
;  .
. Для кватерниона
кватернион называется скалярной частью
а кватернион
— векторной частью. Если
то кватернион называется чисто скалярным, а при
— чисто векторным.
Кватернион
называется сопряжённым к
Сопряжённое произведение есть произведение сопряжённых в обратном порядке:

Для кватернионов справедливо равенство

Так же, как и для комплексных чисел,
называется модулем . Если
то
называется единичным кватернионом.
В качестве нормы кватерниона обычно рассматривают его модуль: 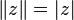 .
.
Таким образом, на множестве кватернионов можно ввести метрику. Кватернионы образуют метрическое пространство, изоморфное с евклидовой метрикой.
Кватернионы с модулем в качестве нормы образуют банахову алгебру.
Из тождества четырёх квадратов вытекает, что иными словами, кватернионы обладают мультипликативной нормой и образуют ассоциативную алгебру с делением.
Кватернион, обратный по умножению к q, вычисляется так:
 .
. Четыре базисных кватерниона и четыре противоположных им по знаку образуют по умножению группу кватернионов (порядка 8). Обозначается:
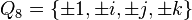 .
. Множество кватернионов является примером кольца с делением.
Множество кватернионов образует четырёхмерную ассоциативную алгебру с делением над полем вещественных (но не комплексных) чисел. Вообще ,
,
являются единственными конечномерными ассоциативными алгебрами с делением над полем вещественных чисел.[2]
Некоммутативность умножения кватернионов приводит к неожиданным последствиям. Например, количество различных корней полиномиального уравнения над множеством кватернионов может быть больше, чем степень уравнения. В частности, уравнение q2 + 1 = 0 имеет бесконечно много решений — это все единичные чисто векторные кватернионы.
Организация всех трёх степеней свободы, однако окончательная свобода наименьшего кольца зависит от положения старших колец
Кватернионы, рассматриваемые как алгебра над , образуют четырёхмерное вещественное векторное пространство. Любой поворот этого пространства относительно
может быть записан в виде
, где
и
— пара единичных кватернионов, при этом пара
определяется с точностью до знака, то есть один поворот определяют в точности две пары —
и
. Из этого следует, что группа Ли
поворотов
есть факторгруппа
, где
обозначает мультипликативную группу единичных кватернионов.
Чисто векторные кватернионы образуют трёхмерное вещественно векторное пространство. Любой поворот пространства чисто векторных кватернионов относительно может быть записан в виде
, где
— некоторый единичный кватернион. Соответственно,
, в частности,
диффеоморфно
.
В качестве нормы кватерниона выберем квадрат его модуля:  .
.
Целыми принято называть кватернионы a + bi + cj + dk такие, что все 2a,2b,2c,2d — целые и одинаковой чётности.
Целый кватернион называется
если таким же свойством обладает его норма.
Целый кватернион называется примитивным, если он не делится ни на какое натуральное число, кроме 1, нацело (иными словами, 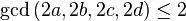 ).
).
Существует 24 целых единичных кватерниона:
 ,
,  ,
,  ,
,  ,
,  .
. Они образуют группу по умножению и лежат в вершинах правильного четырёхмерного многогранника — кубооктаэдра (не путать с трёхмерным многогранником-кубооктаэдром).
Для примитивных кватернионов верен аналог основной теоремы арифметики.
Теорема.[3] Для любого фиксированного порядка множителей в разложении нормы кватерниона N(q) в произведение простых целых положительных чисел N(q) = p1p2...pn существует разложение кватерниона q в произведение простых кватернионов q = q1q2...qn такое, что N(qi) = pi. Причём данное разложение единственно по модулю домножения на единицы — это значит, что любое другое разложение будет иметь вид
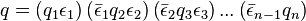 ,
, где ε1, ε2, ε3, … εn − 1 — целые единичные кватернионы.
Например, примитивный кватернион q = (1 + i)2(1 + i + j)(2 + i) имеет норму 60, значит, по модулю домножения на единицы он имеет ровно 12 разложений в произведение простых кватернионов, отвечающих 12 разложениям числа 60 в произведений простых:
Общее число разложений такого кватерниона равно
Знак кватерниона вычисляется так:
 .
. Аргумент кватерниона — это угол поворота четырёхмерного вектора, который отсчитывается от вещественной единицы:
 .
. В дальнейшем используется представление заданного кватерниона q в виде
Здесь a — вещественная часть кватерниона, . При этом i2 = − 1, поэтому проходящая через q и вещественную прямую плоскость имеет структуру алгебры комплексных чисел, что позволяет перенести на случай кватернионов произвольные аналитические функции. Они удовлетворяют стандартным соотношениям, если все аргументы имеют вид a + bi для фиксированного единичного вектора i. В случае если требуется рассматривать кватернионы с разным направлением, формулы значительно усложняются, в силу некоммутативности алгебры кватернионов.
Стандартное определение аналитических функций на ассоциативной нормированной алгебре основано на разложении этих функций в степенные ряды. Рассуждения, доказывающие корректность определения таких функций, полностью аналогичны комплексному случаю и основаны на вычислении радиуса сходимости соответствующих степенных рядов. Учитывая указанное выше «комплексное» представление для заданного кватерниона, соответствующие ряды можно привести к указанной ниже компактной форме. Здесь приведены лишь некоторые наиболее употребительные аналитические функции, аналогично можно вычислить любую аналитическую функцию. Общее правило таково: если f(a + bi) = c + di для комплексных чисел, то , где кватернион q рассматривается в «комплексном» представлении
.

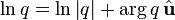
Отметим, что, как обычно в комплексном анализе, логарифм оказывается определён лишь с точностью до .

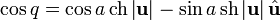

Существуют разные способы определения регулярных функций кватернионного переменного. Самый явный — рассмотрение кватернионно дифференцируемых функций, при этом можно рассматривать праводифференцируемые и леводифференцируемые функции, не совпадающие в силу некоммутативности умножения кватернионов. Очевидно, что их теория полностью аналогична. Определим кватернионно леводифференцируемую функцию f как имеющую предел
Оказывается, что все такие функции имеют в некоторой окрестности точки q вид
f = a + qbгде a,b — постоянные кватернионы. Другой способ основан на использовании операторов
и рассмотрении таких кватернионных функций f, для которых[4]
что полностью аналогично использованию операторов и
в комплексном случае. При этом получаются аналоги интегральной теоремы Коши, теории вычетов, гармонических функций и рядов Лорана для кватернионных функций[5].
Производная Гато функции кватернионного переменного определена согласно формуле
Производная Гато является аддитивным отображением приращения аргумента и может быть представлена в виде[6]

Здесь предполагается суммирование по индексу s. Число слагаемых зависит от выбора функции f. Выражения и
называются компонентами производной.
Так по-другому называется общепринятое умножение кватернионов (pq).
Отличается от общепринятого тем, что вместо первого сомножителя берется сопряжённый к нему: . Оно также некоммутативно.
Аналогично одноимённой операции для векторов:
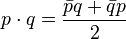 .
. Эту операцию можно использовать для выделения одного из коэффициентов, например, 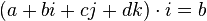 .
.
Определение модуля кватерниона можно видоизменить:
 .
. Используется не очень часто, тем не менее рассматривается в дополнение к скалярному произведению.
Аналогично одноимённой операции для векторов. Результатом является тоже вектор:
 .
. Система кватернионов была впервые опубликована Гамильтоном в 1843 году. Историки науки также обнаружили наброски по этой теме в неопубликованных рукописях Гаусса, относящихся к 1819—1820 годам.[8]
Бурное и чрезвычайно плодотворное развитие комплексного анализа в XIX веке стимулировало у математиков интерес к следующей задаче: найти новый вид чисел, аналогичный по свойствам комплексным, но содержащий не одну, а две мнимые единицы. Предполагалось, что такая модель будет полезна при решении пространственных задач математической физики. Однако работа в этом направлении оказалась безуспешной.
Новый вид чисел был обнаружен ирландским математиком Уильямом Гамильтоном в 1843 году, и он содержал не две, как ожидалось, а три мнимые единицы. Гамильтон назвал эти числа кватернионами. Позднее Фробениус строго доказал (1877) теорему, согласно которой расширить комплексное поле до поля или тела с двумя мнимыми единицами невозможно.
Несмотря на необычные свойства новых чисел (их некоммутативность), эта модель довольно быстро принесла практическую пользу. Максвелл использовал компактную кватернионную запись для формулировки своих уравнений электромагнитного поля.[9] Позднее на основе алгебры кватернионов был создан трёхмерный векторный анализ (Гиббс, Хевисайд).
Как алгебра над , кватернионы образуют вещественное векторное пространство
, снабжённое тензором третьего ранга S типа (1,2), иногда называемого структурным тензором. Как всякий тензор такого типа, S отображает каждую 1-форму t на
и пару векторов
из
в вещественное число
. Для любой фиксированной 1-формы t S превращается в ковариантный тензор второго ранга, который, в случае его симметрии, становится скалярным произведением на
. Поскольку каждое вещественное векторное пространство является также вещественным линейным многообразием, такое скалярное произведение порождает тензорное поле, которое, при условии его невырожденности, становится (псевдо- или собственно-)евклидовой метрикой на
. В случае кватернионов это скалярное произведение индефинитно, его сигнатура не зависит от 1-формы t, а соответствующая псевдоевклидова метрика есть метрика Минковского [10]. Эта метрика автоматически продолжается на группу Ли ненулевых кватернионов вдоль её левоинвариантных векторных полей, образуя так называемую закрытую ФЛРУ (Фридман — Леметр — Робертсон — Уолкер) метрику[11] — важное решение уравнений Эйнштейна. Эти результаты проясняют некоторые аспекты проблемы совместимости квантовой механики и общей теории относительности в рамках теории квантовой гравитации[12].
www.wreferat.baza-referat.ru
Реферат на тему:
Кватернио́ны (от лат. quaterni, по четыре) — система гиперкомплексных чисел, предложенная Гамильтоном в 1843 году.
Умножение кватернионов некоммутативно; они образуют тело, которое обычно обозначается .
Кватернионы очень удобны для описания изометрий трёхмерного и четырёхмерного Евклидовых пространств, и поэтому получили широкое распространение в механике. Также их используют в вычислительной математике, например при создании трёхмерной графики.[1]
Кватернион представляет собой пару где
— вектор трёхмерного пространства, а
— скаляр, то есть вещественное число. Операции сложения определены следующим образом:
Произведение определяется следующим образом:
где обозначает скалярное произведение, а
— векторное произведение.
В частности,
Заметим, что
Кватернионы можно определить как формальную сумму где
— вещественные числа, а
— мнимые единицы со следующим свойством: i2 = j2 = k2 = ijk = − 1. Таким образом, таблица умножения базисных кватернионов —
— выглядит так:
например, , a
.
Кватернионы также можно определить как вещественные матрицы следующего вида с обычными матричными произведением и суммой:

При такой записи:
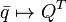 ;
; 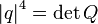 .
. Кватернион можно представить как пару комплексных чисел. Пусть 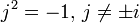 и
и 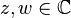 . Тогда кватернион можно записать в виде q = z + wj = a + bi + cj + dij.
. Тогда кватернион можно записать в виде q = z + wj = a + bi + cj + dij.
Альтернативно, кватернионы можно определить как комплексные матрицы следующего вида с обычными матричными произведением и суммой:
здесь и
обозначают комплексно-сопряжённые числа к
и
.
Такое представление имеет несколько замечательных свойств:
 ;
;  .
. Для кватерниона
кватернион называется скалярной частью
а кватернион
— векторной частью. Если
то кватернион называется чисто скалярным, а при
— чисто векторным.
Кватернион
называется сопряжённым к
Сопряжённое произведение есть произведение сопряжённых в обратном порядке:

Для кватернионов справедливо равенство

Так же, как и для комплексных чисел,
называется модулем . Если
то
называется единичным кватернионом.
В качестве нормы кватерниона обычно рассматривают его модуль: 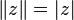 .
.
Таким образом, на множестве кватернионов можно ввести метрику. Кватернионы образуют метрическое пространство, изоморфное с евклидовой метрикой.
Кватернионы с модулем в качестве нормы образуют банахову алгебру.
Из тождества четырёх квадратов вытекает, что иными словами, кватернионы обладают мультипликативной нормой и образуют ассоциативную алгебру с делением.
Кватернион, обратный по умножению к q, вычисляется так:
 .
. Четыре базисных кватерниона и четыре противоположных им по знаку образуют по умножению группу кватернионов (порядка 8). Обозначается:
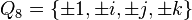 .
. Множество кватернионов является примером кольца с делением.
Множество кватернионов образует четырёхмерную ассоциативную алгебру с делением над полем вещественных (но не комплексных) чисел. Вообще ,
,
являются единственными конечномерными ассоциативными алгебрами с делением над полем вещественных чисел.[2]
Некоммутативность умножения кватернионов приводит к неожиданным последствиям. Например, количество различных корней полиномиального уравнения над множеством кватернионов может быть больше, чем степень уравнения. В частности, уравнение q2 + 1 = 0 имеет бесконечно много решений — это все единичные чисто векторные кватернионы.
Организация всех трёх степеней свободы, однако окончательная свобода наименьшего кольца зависит от положения старших колец
Кватернионы, рассматриваемые как алгебра над , образуют четырёхмерное вещественное векторное пространство. Любой поворот этого пространства относительно
может быть записан в виде
, где
и
— пара единичных кватернионов, при этом пара
определяется с точностью до знака, то есть один поворот определяют в точности две пары —
и
. Из этого следует, что группа Ли
поворотов
есть факторгруппа
, где
обозначает мультипликативную группу единичных кватернионов.
Чисто векторные кватернионы образуют трёхмерное вещественно векторное пространство. Любой поворот пространства чисто векторных кватернионов относительно может быть записан в виде
, где
— некоторый единичный кватернион. Соответственно,
, в частности,
диффеоморфно
.
В качестве нормы кватерниона выберем квадрат его модуля:  .
.
Целыми принято называть кватернионы a + bi + cj + dk такие, что все 2a,2b,2c,2d — целые и одинаковой чётности.
Целый кватернион называется
если таким же свойством обладает его норма.
Целый кватернион называется примитивным, если он не делится ни на какое натуральное число, кроме 1, нацело (иными словами, 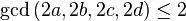 ).
).
Существует 24 целых единичных кватерниона:
 ,
,  ,
,  ,
,  ,
,  .
. Они образуют группу по умножению и лежат в вершинах правильного четырёхмерного многогранника — кубооктаэдра (не путать с трёхмерным многогранником-кубооктаэдром).
Для примитивных кватернионов верен аналог основной теоремы арифметики.
Теорема.[3] Для любого фиксированного порядка множителей в разложении нормы кватерниона N(q) в произведение простых целых положительных чисел N(q) = p1p2...pn существует разложение кватерниона q в произведение простых кватернионов q = q1q2...qn такое, что N(qi) = pi. Причём данное разложение единственно по модулю домножения на единицы — это значит, что любое другое разложение будет иметь вид
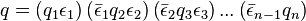 ,
, где ε1, ε2, ε3, … εn − 1 — целые единичные кватернионы.
Например, примитивный кватернион q = (1 + i)2(1 + i + j)(2 + i) имеет норму 60, значит, по модулю домножения на единицы он имеет ровно 12 разложений в произведение простых кватернионов, отвечающих 12 разложениям числа 60 в произведений простых:
Общее число разложений такого кватерниона равно
Знак кватерниона вычисляется так:
 .
. Аргумент кватерниона — это угол поворота четырёхмерного вектора, который отсчитывается от вещественной единицы:
 .
. В дальнейшем используется представление заданного кватерниона q в виде
Здесь a — вещественная часть кватерниона, . При этом i2 = − 1, поэтому проходящая через q и вещественную прямую плоскость имеет структуру алгебры комплексных чисел, что позволяет перенести на случай кватернионов произвольные аналитические функции. Они удовлетворяют стандартным соотношениям, если все аргументы имеют вид a + bi для фиксированного единичного вектора i. В случае если требуется рассматривать кватернионы с разным направлением, формулы значительно усложняются, в силу некоммутативности алгебры кватернионов.
Стандартное определение аналитических функций на ассоциативной нормированной алгебре основано на разложении этих функций в степенные ряды. Рассуждения, доказывающие корректность определения таких функций, полностью аналогичны комплексному случаю и основаны на вычислении радиуса сходимости соответствующих степенных рядов. Учитывая указанное выше «комплексное» представление для заданного кватерниона, соответствующие ряды можно привести к указанной ниже компактной форме. Здесь приведены лишь некоторые наиболее употребительные аналитические функции, аналогично можно вычислить любую аналитическую функцию. Общее правило таково: если f(a + bi) = c + di для комплексных чисел, то , где кватернион q рассматривается в «комплексном» представлении
.

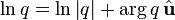
Отметим, что, как обычно в комплексном анализе, логарифм оказывается определён лишь с точностью до .

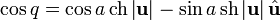

Существуют разные способы определения регулярных функций кватернионного переменного. Самый явный — рассмотрение кватернионно дифференцируемых функций, при этом можно рассматривать праводифференцируемые и леводифференцируемые функции, не совпадающие в силу некоммутативности умножения кватернионов. Очевидно, что их теория полностью аналогична. Определим кватернионно леводифференцируемую функцию f как имеющую предел
Оказывается, что все такие функции имеют в некоторой окрестности точки q вид
f = a + qbгде a,b — постоянные кватернионы. Другой способ основан на использовании операторов
и рассмотрении таких кватернионных функций f, для которых[4]
что полностью аналогично использованию операторов и
в комплексном случае. При этом получаются аналоги интегральной теоремы Коши, теории вычетов, гармонических функций и рядов Лорана для кватернионных функций[5].
Производная Гато функции кватернионного переменного определена согласно формуле
Производная Гато является аддитивным отображением приращения аргумента и может быть представлена в виде[6]

Здесь предполагается суммирование по индексу s. Число слагаемых зависит от выбора функции f. Выражения и
называются компонентами производной.
Так по-другому называется общепринятое умножение кватернионов (pq).
Отличается от общепринятого тем, что вместо первого сомножителя берется сопряжённый к нему: . Оно также некоммутативно.
Аналогично одноимённой операции для векторов:
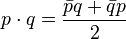 .
. Эту операцию можно использовать для выделения одного из коэффициентов, например, 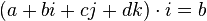 .
.
Определение модуля кватерниона можно видоизменить:
 .
. Используется не очень часто, тем не менее рассматривается в дополнение к скалярному произведению.
Аналогично одноимённой операции для векторов. Результатом является тоже вектор:
 .
. Система кватернионов была впервые опубликована Гамильтоном в 1843 году. Историки науки также обнаружили наброски по этой теме в неопубликованных рукописях Гаусса, относящихся к 1819—1820 годам.[8]
Бурное и чрезвычайно плодотворное развитие комплексного анализа в XIX веке стимулировало у математиков интерес к следующей задаче: найти новый вид чисел, аналогичный по свойствам комплексным, но содержащий не одну, а две мнимые единицы. Предполагалось, что такая модель будет полезна при решении пространственных задач математической физики. Однако работа в этом направлении оказалась безуспешной.
Новый вид чисел был обнаружен ирландским математиком Уильямом Гамильтоном в 1843 году, и он содержал не две, как ожидалось, а три мнимые единицы. Гамильтон назвал эти числа кватернионами. Позднее Фробениус строго доказал (1877) теорему, согласно которой расширить комплексное поле до поля или тела с двумя мнимыми единицами невозможно.
Несмотря на необычные свойства новых чисел (их некоммутативность), эта модель довольно быстро принесла практическую пользу. Максвелл использовал компактную кватернионную запись для формулировки своих уравнений электромагнитного поля.[9] Позднее на основе алгебры кватернионов был создан трёхмерный векторный анализ (Гиббс, Хевисайд).
Как алгебра над , кватернионы образуют вещественное векторное пространство
, снабжённое тензором третьего ранга S типа (1,2), иногда называемого структурным тензором. Как всякий тензор такого типа, S отображает каждую 1-форму t на
и пару векторов
из
в вещественное число
. Для любой фиксированной 1-формы t S превращается в ковариантный тензор второго ранга, который, в случае его симметрии, становится скалярным произведением на
. Поскольку каждое вещественное векторное пространство является также вещественным линейным многообразием, такое скалярное произведение порождает тензорное поле, которое, при условии его невырожденности, становится (псевдо- или собственно-)евклидовой метрикой на
. В случае кватернионов это скалярное произведение индефинитно, его сигнатура не зависит от 1-формы t, а соответствующая псевдоевклидова метрика есть метрика Минковского [10]. Эта метрика автоматически продолжается на группу Ли ненулевых кватернионов вдоль её левоинвариантных векторных полей, образуя так называемую закрытую ФЛРУ (Фридман — Леметр — Робертсон — Уолкер) метрику[11] — важное решение уравнений Эйнштейна. Эти результаты проясняют некоторые аспекты проблемы совместимости квантовой механики и общей теории относительности в рамках теории квантовой гравитации[12].
wreferat.baza-referat.ru