

Разделы: Математика
В курсе изучения геометрии основной школы рассматриваются задачи, связанные с практическим применением изученных знаний: измерительные работы на местности, измерительные инструменты. Практические работы на местности являются одной из наиболее активных форм связи обучения с жизнью, теории с практикой. Учащиеся учатся пользоваться справочниками, применять необходимые формулы, овладевают практическими приёмами геометрических измерений и построений.
Практические работы с использованием измерительных инструментов повышают интерес учащихся к математике, а решение задач на измерение ширины реки, высоты предмета и определение расстояния до недоступной точки позволяют применить их в практической деятельности, увидеть масштаб применения математики в жизни человека.
По мере изучения материала способы решения этих задач изменяются, одну и ту же задачу можно решить многими способами. При этом используются следующие вопросы геометрии: равенство и подобие треугольников, соотношения в прямоугольном треугольнике, теорема синусов и теорема косинусов, теорема Пифагора, свойства прямоугольных треугольников и т.д.
Цели проведения уроков “Измерение на местности”:
Задачи:
При отборе содержания каждого урока по данной теме и форм деятельности учащихся используются принципы:
Критерии оценки достижения ожидаемых результатов:
Подготовка и проведение таких уроков позволяют в результате:
Одной из наиболее активных форм связи обучения с жизнью, теории с практикой является выполнение учащимися на уроках геометрии практических работ, связанных с измерением, построением, изображением. В курсе изучения геометрии основной школы рассматриваются задачи, связанные с практическим применением изученных знаний: измерительные работы на местности, измерительные инструменты. На уроках математики параллельно с изучением теоретического материала учащиеся должны научиться производить измерения, пользоваться справочниками и таблицами, свободно владеть чертёжными и измерительными инструментами. Работа проводится как на местности, так и решение задач в классе различными способами на нахождение высоты предмета и определение расстояния до недоступной точки. По программе в курсе геометрии рассматриваются следующие вопросы:
7 класс
8 класс.
9 класс.
Практические работы на уроках геометрии позволяют решать педагогические задачи: ставить перед учащимися познавательную математическую проблему, актуализировать их знания и готовить к усвоению нового материала, формировать практически умения и навыки в обращении с различными приборами, инструментами, вычислительной техникой, справочниками и таблицами.. Они позволяют реализовать в обучении важнейшие принципы взаимосвязи теории и практики: практика выступает в качестве исходного звена развития теории и служит важнейшим стимулом её изучения учащимися, она является средством проверки теории и областью её применения.
Система проведения уроков “Измерение на местности” ставит цели:
Предусматривает выполнение следующих задач:
При отборе содержания каждого урока по данной теме и форм деятельности учащихся используются принципы:
Критерии оценки достижения ожидаемых результатов:
Подготовка и проведение таких уроков позволяют в результате:
Измерительные инструменты, используемые при измерении на местности:
Экер представляет собой два бруска, расположенных под прямым углом и укреплённых на треножнике. На концах брусков вбиты гвозди так, что прямые, проходящие через них, взаимно перпендикулярны.

Экер
Устройство: астролябия состоит из двух частей: диска (лимб), разделённого на градусы, и вращающейся вокруг центра линейки (алидады). При измерении угла на местности она наводится на предметы, лежащие на его сторонах. Наведение алидады называется визированием. Для визирования служат диоптры. Это металлические пластинки с прорезами. Диоптров два: один с прорезом в виде узкой щели, другой с широким прорезом, посередине которого натянут волосок. При визировании к узкому прорезу прикладывается глаз наблюдателя, поэтому диоптр с таким прорезом называется глазным. Диоптр с волоском направляется к предмету, лежащему на стороне измеряемого; он называется предметным. В середине алидады прикреплён к ней компас.

астролябия
1. Построение прямой на местности (провешивание прямой линии)
Отрезки на местности обозначают с помощью вех. Чтобы вешка стояла прямо, применяют отвес (какой – либо грузик, подвешенный на нитке). Ряд вбитых в землю вех и обозначает отрезок прямой линии на местности. В выбранном направлении ставят две вехи на расстоянии друг от друга, между ними другие вехи, так, чтобы глядя через одну, другие прикрывались друг другом.
Практическая работа: построение прямой на местности.
Задание: отметьте на ней отрезок в 20 м, 36 м, 42 м.

2. Измерение средней длины шага.
Считается некоторое число шагов (например, 50), измеряется данное расстояние и вычисляется средняя длина шага. Опыт удобнее провести несколько раз и сосчитать среднее арифметическое.
Практическая работа: измерение средней длины шага.
Задание: зная среднюю длину шага, отложите на местности отрезок 20 м, проверьте с помощью рулетки.
3. Построение прямых углов на местности.
Чтобы построить на местности прямой угол АОВ с заданной стороной ОА, устанавливают треножник с экером так, чтобы отвес находился точно над точкой О, а направление одного бруска совпало с направлением луча ОА. Совмещение этих направлений можно осуществить с помощью вехи, поставленной на луче. Затем провешивают прямую линию по направлению другого бруска (ОВ).
Практическая работа: построение прямого угла на местности, прямоугольника, квадрата.
Задание: измерьте периметр и площадь прямоугольника, квадрата.

4. Построение и измерение углов с помощью астролябии.
Астролябию устанавливают в вершине измерительного угла так, чтобы лимб её был расположен в горизонтальной плоскости, а отвес, подвешенный под центром лимба, проектировался бы в точку, принимаемую за вершину угла на поверхности земли. Затем визируют алидадой по направлению одной стороны измеряемого угла и отсчитывают на лимбе градусные деления против метки предметного диоптра. Повёртывают алидаду по ходу часовой стрелки в направлении второй стороны угла и делают второй отсчёт. Искомый угол равен разности показаний при втором и первом отсчётах.
Практическая работа:
Задание: измерить градусные меры заданных углов.
5. Построение окружности на местности.
На местности устанавливается колышек, к которому привязывается верёвка. Держась за свободный конец верёвки, двигаясь вокруг колышка, можно описать окружность.
Практическая работа: построение окружности.
Задание: измерение радиуса, диаметра; вычисление площади круга, длины окружности.

6. Определение высоты предмета.
а) С помощью вращающейся планки.
Предположим, что нам нужно определить высоту какого – нибудь предмета, например высоту столба А1С1 (задача № 579). Для этого поставим на некотором расстоянии от столба шест АС с вращающейся планкой и направим планку на верхнюю точку С1 столба. Отметим на поверхности земли точку В, в которой прямая А1А пересекается с поверхностью земли. Прямоугольные треугольники А1С1В и АСВ подобны по первому признаку подобия треугольников ( угол А1 = углу А = 90о, угол В – общий). Из подобия треугольников следует;

Измерив расстояния ВА1 и ВА (расстояние от точки В до основания столба и расстояние до шеста с вращающейся планкой), зная длину АС шеста, по полученной формуле определяем высоту А1С1 столба.

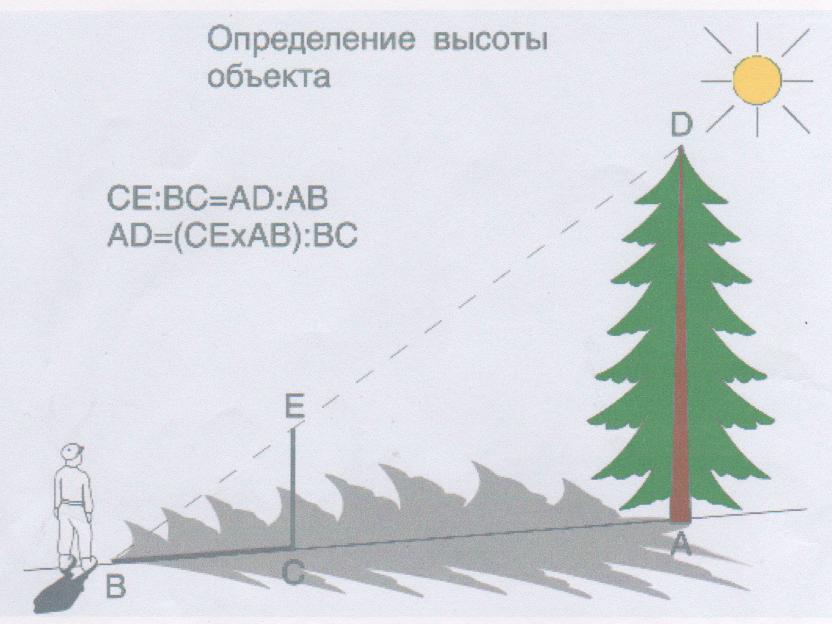
б) С помощью тени.
Измерение следует проводить в солнечную погоду. Измерим длину тени дерева и длину тени человека. Построим два прямоугольных треугольника, они подобны. Используя подобие треугольников составим пропорцию (отношение соответственных сторон), из которой и найдём высоту дерева (задача №580). Можно таким образом определить высоту дерева и в 6 кл, используя построение прямоугольных треугольников в выбранном масштабе.

в) С помощью зеркала.
Для определения высоты предмета можно использовать зеркало, расположенное на земле горизонтально (задача №581). Луч света, отражаясь от зеркала попадает в глаз человека. Используя подобие треугольников можно найти высоту предмета, зная рост человека (до глаз), расстояние от глаз до макушки человека и измеряя расстояние от человека до зеркала, расстояние от зеркала до предмета (учитывая, что угол падения луча равен углу отражения).

г) С помощью чертёжного прямоугольного треугольника.
На уровне глаз расположим прямоугольный треугольник, направив один катет горизонтально поверхности земли, другой катет направив на предмет, высоту которого измеряем. Отходим от предмета на такое расстояние, чтобы второй катет “прикрыл” дерево. Если треугольник ещё и равнобедренный, то высота предмета равна расстоянию от человека до основания предмета (прибавив рост человека). Если треугольник не равнобедренный, то используется снова подобие треугольников, измеряя катеты треугольника и расстояние от человека до предмета (используется и построение прямоугольных треугольников в выбранном масштабе). Если треугольник имеет угол в 300, то используется свойство прямоугольного треугольника: против угла в 300 лежит катет вдвое меньше гипотенузы.
д) Во время игры “ Зарница” учащимся не разрешается использовать измерительные приборы, поэтому можно предложить следующий способ:
один ложится на землю и направляет глаза на макушку другого, находящегося от него на расстоянии своего роста, так чтобы прямая проходила через макушку товарища и верхушку предмета. Тогда треугольник получается равнобедренным и высота предмета равна расстоянию от лежавшего до основания предмета, которое измеряется, зная среднюю длину шага учащегося. Если же треугольник не равнобедренный, то зная среднюю длину шага измеряется расстояние от лежавшего на земле до стоявшего и до предмета, рост стоявшего заведомо известен. А далее по признаку подобия треугольников вычисляется высота предмета (или построение прямоугольных треугольников в выбранном масштабе).
7. Определение расстояния до недоступной точки.
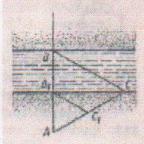
а) Предположим, что нам нужно найти расстояние от пункта А до недоступного пункта В. Для этого на местности выбираем точку С, провешиваем отрезок АС и измеряем его. Затем с помощью астролябии измеряем углы А и С. На листке бумаги строим какой – нибудь треугольник А1В1С1, у которого угол А1 = угол А, угол С! = угол С и измеряем длины сторон А1В1 и А1С1 этого треугольника. Так как треугольник АВС подобен треугольнику А1В1С1, то АВ: А1В1 = АС : А1С1, откуда находим АВ по известным расстояниям АС, А1С1, А1В1.. Для удобства вычислений удобно построить треугольник А1В1С1 так, чтобы А1С1 : АС = 1 : 1000

б) Для измерения ширины реки на берегу измеряем расстояние АС, с помощью астролябии устанавливаем угол А = 900 (направив на объект В на противоположном берегу), измеряем угол С. На листке бумаги строим подобный треугольник (удобнее в масштабе 1: 1000) и вычисляем АВ (ширину реки).
в) Ширину реки можно определить и так: рассматривая два подобных треугольника АВС и АВ1С1. Точка А выбрана на берегу реки, В1 и С у кромки поверхности воды, ВВ1 – ширина реки (зад №583, рис 204 учебника), измеряя при этом АС, АС1, АВ1.
Практическая работа: определить высоту дерева, ширину реки.

В 9 классе в пункте 100 тоже рассматриваются измерительные работы на местности, но используется тема “Решение треугольников”, при этом применяется теорема синусов и теорема косинусов. Рассматриваются задачи с конкретными данными, решая которые можно увидеть различные способы нахождения и высоты предмета и определить расстояние до недоступной точки, что можно применить в будущем практически.
1. Измерение высоты предмета.
Предположим, что требуется определить высоту АН какого – то предмета. Для этого отметим точку В на определённом расстоянии а от основания Н предмета и измерим угол АВН. По этим данным из прямоугольного треугольника АНВ находим высоту предмета: АН = НВ tgАВН.
Если основание предмета недоступно, то можно поступить так: на прямой, проходящей через основание Н предмета, отметим две точки В и С на определенном расстоянии а друг от друга и измерим углы АВН и АСВ: угол АВН = a , угол АСВ = b, угол ВАС = a – b. Эти данные позволяют определить все элементы треугольника АВС; по теореме синусов находим АВ:

АВ = sin (a – b). Из прямоугольного треугольника АВН находим высоту АН предмета:
АН = АВ sin a.
№ 1036
Наблюдатель находится на расстоянии 50 м от башни, высоту которой хочет определить. Основание башни он видит под углом 100 к горизонту, а вершину – под углом 450 к горизонту. Какова высота башни? (рис.298 учебника)
Решение

Рассмотрим треугольник АВС – прямоугольный и равнобедренный, т.к угол СВА =450, то и угол ВСА =450, значит СА=50м.
Рассмотрим треугольник АВН – прямоугольный, tg (АВН) = АН/ АВ, отсюда
АН = АВ tg (АВН), т.е АН = 50tg 100, отсюда АН =9м. СН= СА+АН =50+9 = 59(м)

№ 1038
На горе находится башня, высота которой равна 100м. Некоторый предмет А у подножия горы наблюдают сначала с вершины В башни под углом 600 к горизонту, а потом с её основания С под углом 300. Найдите высоту Н горы (рисунок 299 учебника).
Решение:


Дано:
СВ = 100 м
угол ЕВА = 600
угол КСА =300
Найти СР.
Решение:
Угол СВК = 300, т.к. угол ЕВС =900 и угол ЕВА =600, отсюда угол СКА =600, значит уголСКА = 1800 – 600 = 1200.
В треугольнике СКА видим, что угол АСК = 300, уголСКА = 1200, то уголСАК = 300, получим, что треугольник ВСА равнобедренный с основанием АВ, т.к. уголСВК = 300 и уголВАС = 300, значит АС = 100м (ВС = АС).
Рассмотрим треугольник АСР, прямоугольный с острым углом в 300 (РАС = АСК, накрест лежащие углы при пересечении параллельных прямых СК и АР секущей АС), а против угла в 300 лежит катет вдвое меньше гипотенузы, поэтому РС = 50м.
2. Измерение расстояния до недоступной точки ( измерение ширины реки).
Случай 1. Измерение расстояния между точками Аи В, разделёнными препятствием (рекой).
Выберем на берегу реки две доступные точки А и В, расстояние между которыми может быть измерено. Из точки А видны и точка В и точка С, взятая на противоположном берегу. Измерим расстояние АВ, с помощью астролябии измеряем углы А и В, угол АСВ = 1800 - угол А - угол В
Зная одну сторону треугольника и все углы, по теореме синусов находим искомое расстояние.


2 случай.
Измерение расстояния между точками А и В, разделёнными препятствием (озером). Точки А и В доступны.
Выбирают третью точку С, из которой видны точки А и В и могут быть непосредственны измерены расстояния до них. Получается треугольник, у которого даны угол АСВ (измеряется с помощью астролябии) и стороны АС и ВС. На основании этих данных по теореме косинусов можно определить величину стороны АВ – искомое расстояние. АВ2 = АС2 + ВС2 – 2 АС * ВС cos угла С.

3 случай:
Измерение расстояния между точками А и В, разделёнными препятствием (лесом) и недоступными определяющему расстояние (точки находятся по ту сторону реки).
Выбирают две доступные точки С и К, расстояние между которыми может быть измерено и из которых видны как точка А, так т точка В.
Устанавливают астролябию в точке С и измеряют углы АСК и ВСК. Затем измеряют расстояние СК и переносят астролябию в т. К, из которой измеряют углы АКС и АКВ. На бумаге по стороне СК, взятой в определённом масштабе и двум прилежащим углам строят треугольники АСК и ВСК и вычисляют элементы этих треугольников. Проведя на чертеже линию АВ, определяют длину её непосредственно по чертежу или путём вычисления (решают треугольники АВС и АВК, в которые входит определяемая линия АВ).
Практическая работа в 9 кл на уроках геометрии:
Работу провести и через подобие треугольников и через тему “Решение треугольников”.
Задание: сравнить полученные результаты.
В результате проведения цикла уроков по вопросам рассмотрения практического применения геометрии, учащиеся убеждаются в непосредственном применении математики в практической жизни человека (измерение расстояния до недоступной точки, определение высоты предмета различными способами к концу обучения в основной школе, использование измерительных приборов). Решение задач этого типа вызывает заинтересованность учащихся, которые с нетерпением ждут уроков, связанных с непосредственным измерением на местности. А задачи, предложенные в учебнике, знакомят с различными способами решения этих задач.
Литература:
xn--i1abbnckbmcl9fb.xn--p1ai
Подготовил
ученик 7 б класса
Егошин Роман
2012 год
Угол.
Плоский угол —неограниченная геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки(вершины угла).
Углом также называют фигуру образованную всеми точками плоскости, заключёнными между этими лучами (Вообще говоря, двум таким лучам соответствуют два угла, так как они делят плоскость на две части. Один из этих углов условно называют внутренним, а другой — внешним. Иногда, для краткости, углом называют угловую меру.
Угол измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги к длине окружности , в радианах — отношение длины дуги к радиусу ; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется.
Угол называется острым, если он меньше 90°. Угол называется тупым, если он больше 90°, но меньше 180°.Угол равный 90°, называется прямым. Угол называется развернутым, если он равен 180°, т.е. двум прямым углам.
Углы бывают вертикальными и смежными. В геометрии, два угла называются вертикальными, если они созданы пересечением двух прямых и не являются прилегающими. Такие углы имеют общую вершину. Они имеют одинаковую градусную меру и могут рассматриваться как равные. Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой . Сумма смежных углов равна 180°.
Вертикальный угол Смежный угол
Измерение углов на местности.
Углы на местности можно измерять несколькими способами: Живой угломер, Посох Якова, Грабельный угломер, угол артиллериста.
Живой угломер.
Изготовить самому угломерный прибор простого устройства не очень трудно, особенно если воспользоваться транспортиром. Но и самодельный угломер не всегда бывает под рукою во время загородной прогулки. В таких случаях можно пользоваться услугами того «живого угломера», который всегда при нас. Это - наши собственные пальцы. Чтобы пользоваться ими для приблизительной оценки углов зрения, нужно лишь произвести предварительно несколько измерений и расчетов.
Прежде всего, надо установить, под каким углом зрения видим мы ноготь указательного пальца своей вытянутой вперед руки. Обычная ширина ногтя - 1 см, а расстояние его от глаза в таком положении - около 60 см; поэтому мы видим его примерно под углом в 1° (немного менее, потому что угол в 1° получился бы при расстоянии в 67 см). У подростков ноготь меньше, но и рука короче, так что угол зрения для них примерно тот же - 1°. Читатель хорошо сделает, если, не полагаясь на книжные данные, выполнит для себя это измерение и расчет, чтобы убедиться, не слишком ли отступает результат от 1°; если уклонение велико, надо испытать другой палец.
Зная это, вы располагаете способом оценивать малые углы зрения буквально голыми руками. Каждый отдаленный предмет, который как раз покрывается ногтем указательного пальца вытянутой руки, виден вами под углом в 1° и, следовательно! отодвинут в 57 раз дальше своего поперечника. Если ноготь покрывает половину предмета, значит, угловая величина его 2°, а расстояние равно 28 поперечникам.
Полная Луна покрывает только половину ногтя, т. е. видна под углом в полградуса, и значит, отстоит от нас на 114 своих поперечников; вот ценное астрономическое измерение, выполненное буквально голыми руками!
Для углов побольше воспользуйтесь ногтевым суставом вашего большого пальца, держа его согнутым на вытянутой руке. У взрослого человека длина (заметьте: длина, а их ширина) этого сустава около 3 ½ см, а расстояние от глаза при вытянутой руке - около 55 см. Легко рассчитать, что угловая величина его в таком положении должна равняться 4°. Это дает средство оценивать углы зрения в 4° (а значит и в 8°).
Сюда надо присоединить еще два угла, которые могут быть измерены пальцами, - именно те, под которыми нам представляются на вытянутой руке промежутки 1) между средним и указательным пальцами, расставленными возможно шире; 2) между большим и указательным, также раздвинутыми в наибольшей степени. Нетрудно вычислить, что первый угол равен примерно 7-8°, второй 15-16°.
Случаев применить ваш живой угломер во время прогулок по открытой местности может представиться множество. Пусть вдалеке виден товарный вагон, который покрывается примерно половиною сустава большого пальца вашей вытянутой руки, т. е. виден под углом около 2°. Так как длина товарного; вагона известна (около 6 м), то вы легко находите, какое расстояние вас от него отделяет: 6х28=170 м или около того. Измерение, конечно, грубо приближенное, но все же более надежное, чем необоснованная оценка просто на глаз.
Заодно укажем также способ проводить на местности прямые углы, пользуясь лишь своим собственным телом.
Если вам нужно провести через некоторую точку перпендикуляр к данному направлению, то, став на эту точку лицом в направлении данной линии, вы, не поворачивая пока головы, свободно протягиваете руку в ту сторону, куда желаете провести перпендикуляр. Сделав это, приподнимите большой палец своей вытянутой руки, поверните к нему голову и заметьте, какой предмет-камешек, кустик и т. п.-• покрывается большим пальцем, если на него смотреть соответствующим глазом (т. е. правым, когда вытянута правая рука, и левым - когда левая).
Вам остается лишь отметить на земле прямую линию от места, где вы стояли, к замеченному предмету, - это и будет искомый перпендикуляр.
Рисунок. Съемка озера на план.
Способ, как будто не обещающий хороших результатов, но после недолгих упражнений вы научитесь ценить услуги этого «живого эккера»1) не ниже настоящего, крестообразного.
Далее пользуясь «живым угломером», вы можете, при отсутствии всяких приспособлений, измерять угловую высоту светил над горизонтом, взаимное удаление звезд в градусной мерз, видимые размеры огненного пути метеора и т. п. Наконец, умея без приборов проводить прямые углы на местности, вы можете снять план небольшого участка по способу, сущность которого ясна из рисунке, например, при съемке озера измеряют прямоугольник ABCD, а также длины перпендикуляров, опущенных из приметных точек берега, и расстояния их оснований от вершин прямоугольника. Словом, в положении Робинзона уменье пользоваться собственными руками для измерения углов (и ногами для измерения расстояний) могло бы пригодиться для самых разнообразных надобностей.
Посох Якова.
При желании располагать более точными измерителями углов, нежели сейчас описанный нами природный «живой угломер», вы можете изготовить себе простой и удобный прибор, некогда служивший нашим предкам. Это - названный по имени изобретателя «посох Якова»-прибор, бывший в широком употреблении у мореплавателей до XVIII века (рисунок), до того как его постепенно вытеснили еще бол*е удобные и точные угломеры (секстанты).
Рисунок Посох Якова и схема его употребления.
Он состоит из длинной линейки АВ в 70-100 см, по которой может скользить перпендикулярный к ней брусок CD; обе части СО и OD скользящего бруска равны между собою. Если вы желаете при помощи этого бруска определить угловое расстояние между звездами S и S' (рисунок), то приставляете к глазу конец А линейки (где для удобства наблюдения приделана просверленная пластинка) и направляете линейку так, чтобы звезда S' была видна у конца В линейки; затем двигаете поперечину CD вдоль линейки до тех пор, пока звезда 5 не будет видна как раз у конца С (рисунок). Теперь остается лишь измерить расстояние АО, чтобы, зная длину СО, вычислить величину угла
Грабельный угломер.
Главная часть его- дощечка любой формы, у одного края которого укреплена просверленная пластинка; её отверстие наблюдатель приставляет к глазу. У противоположного края дощечки втыкают ряд тонких булавок (употребляемых для коллекций насекомых), промежутки между которыми составляют 57-ю долю их расстояния от отверстия просверленной пластинки!). Мы уже знаем, что при этом каждый промежуток усматривается под углом в один градус. Можно разместить булавки также следующим приемом, дающим более точный результат; на стене чертят две параллельные линии в расстоянии одного метра одну от другой н, отойдя от стены
Рисунок . Грабельный угломер.
по перпендикуляру к ней на 57 м, рассматривают эти линии в отверстии просверленной пластинки; булавки втыкают в дощечку так, чтобы каждая пара смежных булавок покрывала начерченные на стене линии.
Когда булавки поставлены, можно некоторые из них снять, чтобы получить углы в 2°, в 3°, в 5°. Способ употребления этого угломера, конечно, понятен читателю и без объяснений. Пользуясь этим угломером, можно измерять углы зрения с довольно большою точностью, не меньше чем 1/4°.
Угол артиллериста.
Артиллерист не стреляет вслепую. Зная высоту цели, он определяет ее угловую величину и вычисляет расстояние до цели; в другом случае определяет, артиллериста какой угол ему надо повернуть орудие для переноса огня с одной цели на другую.
Подобного рода задачи он решает быстро и в уме. Каким образом?
Посмотрите на рис, 72. АВ- это дуга окружности радиуса OA = D) ab-дуга окружности радиуса Оа =r.
Рисунок, Схема угломера артиллериста.
Из подобия двух секторов АОВ и аb следует: = или AB=D
Отношение характеризует величину угла зрения AОВ;
зная это отношение, легко вычислить АВ по известному D или D по известному АB.
Артиллеристы облегчают себе расчет тем, что делят окружность не на 360 частей, как обычно, а на 6000 равных дуг, тогда длина каждого деления составляет примерно радиуса окружности.
freepapers.ru
Местоположение объекта (цели) определяется обычно по отношению к тому ориентиру, который находится ближе всего к объекту (цели). Достаточно знать две координаты объекта (цели): дальность, то есть расстояние от наблюдателя до объекта (цели), и угол (правее или левее ориентира), на который объект (цель) видна нам, и тогда местоположение объекта (цели) будет определено вполне точно.
Если расстояния до объекта (цели) определяются непосредственным промером или расчетом по формуле «тысячной», то угловые величины могут измеряться с помощью подручных предметов, линейки, бинокля, компаса, башенного угломера, приборов наблюдения и прицеливания и других измерительных приборов.
Измерение на местности углов с помощью подручных предметов
Не имея измерительных приборов, для приблизительного измерения на местности углов в тысячных, можно использовать подручные предметы, размеры которых (в миллиметрах) заранее известны. Это могут быть: карандаш, патрон, спичечный коробок, мушка и магазин автомата и т.п.
Ладонь, кулак и пальцы рук могут также стать неплохим угломерным прибором, если знать, сколько в них заключается «тысячных», однако в этом случае необходимо помнить, что разные люди имеют разную длину руки и разную ширину ладони, кулака и пальцев. Поэтому, прежде чем использовать для измерения углов свою ладонь, кулак и пальцы, каждый военнослужащий должен заранее определить их «цену».
Чтобы определить угловую величину, надо знать, что отрезку в 1 мм, удаленному от глаза на 50 см, соответствует угол в две тысячных (записывается: 0-02).
Например, ширина кулака равна 100 мм, следовательно, его «цена» в угловых величинах равна 2-00 (двести тысячных), а если, например, ширина карандаша равна 6 мм, то его «цена» в угловых величинах будет равна 0-12 (двенадцать тысячных).
При измерении углов в тысячных принято называть и записывать вначале число сотен, а затем десятков и единиц тысячных. Если при этом сотен или десятков не окажется, вместо них называют и записывают нули, например: (см. таблицу).

«Цена» пальцев, кулака, карандаша и спичечной коробки в тысячных («цена» пальцев и кулака у каждого военнослужащего индивидуальная)
| Угол втысячных | Записывается | Читается |
| 1250 | 12-50 | Двенадцать пятьдесят |
| 156 | 1-56 | Один пятьдесят шесть |
| 35 | 0-35 | Ноль тридцать пять |
| 1 | 0-01 | Ноль ноль одни |
Измерение на местности углов с помощью линейки
Для измерения углов в тысячных с помощью линейки необходимо держать ее перед собой, на расстоянии 50 см от глаза, тогда одно ее деление (1 мм) будет соответствовать 0-02. При измерении угла необходимо подсчитать на линейке число миллиметров между предметами (ориентирами) и умножить на 0-02.
Полученный результат будет соответствовать величине измеряемого угла в тысячных.
Например (см. рисунок), для отрезка в 32 мм угловая величина будет составлять 64 тысячных (0-64), для отрезка в 21 мм - 42 тысячных (0-42).
Помните, что точность измерения углов с помощью линейки зависит от навыка в вынесении линейки точно на 50 см от глаза. Для этого можно потренироваться, а лучше и проводить замеры, с помощью веревки (нитки) с двумя узелками, расстояние между которыми равно 50 см. При выносе линейки (руки) на 50 см один узелок (веревки) нитки зажимается в зубах, а другой – прижимается пальцем руки к линейке.
Для измерения угла в градусах линейка выносится перед собой на расстояние 60 см. В этом случае 1 см на линейке будет соответствовать 1°.

Измерение углов с помощью линейки с миллиметровыми делениями
Измерение на местности углов с помощью биноклем
В поле зрения бинокля имеются две взаимно перпендикулярные угломерные шкалы (сетки). Одна из них служит для измерения горизонтальных углов, другая - для измерения вертикальных.
Величина одного большого деления соответствует 0-10 (десяти тысячным), а величина малого деления соответствует 0-05 (пяти тысячным).
Для определения на местности углов до объекта (цели) при помощи бинокля необходимо поместить объект (цель) между делениями шкалы бинокля, подсчитать количество делений шкалы и узнать его угловую величину.
Чтобы измерить угол между двумя предметами (например, между ориентиром и целью), надо совместить какой-либо штрих шкалы с одним из них и подсчитать число делений против изображения второго. Умножив число делений на цену одного деления, получим величину измеряемого угла в тысячных.

Измерение углов с помощью бинокля
Измерение на местности углов с помощью компаса
Шкала компаса может быть проградуирована в градусах и делениях угломера. Не ошибитесь с цифрами. Градусов в окружности - 360; делений угломера - 6000.
Измерение углов в тысячных с помощью компаса осуществляется следующим образом. Вначале мушку визирного устройства компаса устанавливают на нулевой отсчет шкалы. Затем поворотом компаса в горизонтальной плоскости совмещают через целик и мушку линию визирования с направлением на правый предмет (ориентир).
После этого, не меняя положения компаса, визирное устройство переводят в направление на левый предмет и снимают по шкале отсчет, который будет соответствовать величине измеряемого угла в тысячных. Показания снимают по шкале компаса, проградуированной в делениях угломера.
При измерении угла в градусах линию визирования совмещают сначала с направлением на левый предмет (ориентир), так как счет градусов возрастает по ходу часовой стрелки, а показания снимают по шкале компаса, проградуированной в градусах.
Измерение на местности углов с помощью башенного угломера
На танках и боевых машинах для измерения угла поворота башенки имеется угломерное устройство.
Оно состоит из основной шкалы 1, расположенной на погоне по всей длине ее окружности, и отчетной шкалы 2, укрепленной на вращающемся колпаке башенки. Основная шкала разбита на 600 делений (цена деления 0-10). Отчетная, шкала имеет 10 делений и позволяет отсчитывать углы с точностью 0-01.
В некоторых машинах башенка механически связана со стрелками азимутального указателя, на котором имеются шкалы грубого и точного отсчетов углов. Азимутальный указатель также позволяет отсчитывать угол с точностью до 0-01.
Для наведения на наблюдаемый предмет используется оптический визир, в поле зрения, которого имеется перекрестие или угольник. Оптический визир установлен на вращающейся башенке таким образом, что в положении 0-00 его оптическая ось параллельна продольной оси машины.
Для определения угла между продольной осью машины и направлением, на предмет необходимо повернуть вращающийся колпак башенки в направлении на этот предмет до совмещения перекрестия (угольника) с предметом и на угломерной шкале прочитать отсчет.
Горизонтальный угол между направлениями на два каких-нибудь предмета будет равен разности отсчетом по шкале на эти предметы.
 Угломерное устройство башенки: 1 – угломерное кольцо; 2 - визир; 3 – прицел
Угломерное устройство башенки: 1 – угломерное кольцо; 2 - визир; 3 – прицел Измерение на местности углов с помощью приборов наблюдения и прицеливания
Приборы наблюдения и прицеливания имеют шкалы, подобные шкалам бинокля, поэтому углы с помощью этих приборов измеряют так же, как и с помощью бинокля.
Определение на местности расстояний по степени видимости предметов
Невооруженным глазом можно приблизительно определить расстояние до объектов (целей) по степени их видимости.
Военнослужащий с нормальной остротой зрения может увидеть и различить некоторые предметы со следующих предельных расстояний, указанных в таблице.
Определение расстояния по видимости (различимости) некоторых объектов
| Объекты и признаки | Предельнаявидимость (км) |
| Колокольни, башни, большие дома на фоне неба | 15-18 |
| Населенные пункты | 10-12 |
| Ветряные мельницы и их крылья | 11 |
| Деревни и отдельные большие дома | 8 |
| Заводские трубы | 6 |
| Отдельные небольшие дома | 5 |
| Окна в домах (без деталей) | 4 |
| Трубы на крышах | 3 |
| Самолеты на земле, танки на месте | 1,2-1,5 |
| Стволы деревьев, столбы линий связи, люди (в виде точки), повозки на дороге | 1,5 |
| Движение ног идущего человека (лошади) | 0,7 |
| Станковый пулемет, миномет, переносная ПУ, ПТУР, колья проволочных заграждений, переплеты в окнах | 0,5 |
| Движение рук, выделяется голова человека | 0,4 |
| Ручной пулемет, цвет и части одежды, овал лица | 0,25-0,3 |
| Черепица на крышах, листья деревьев, проволока на кольях | 0,2 |
| Пуговицы и пряжки, подробности вооружения солдата | 0,15-0,17 |
| Черты лица, кисти рук, детали стрелкового оружия | 0,1 |
| Глаза человека в виде точки | 0,07 |
| Белки глаз | 0,02 |
Надо иметь в виду, что в таблице указаны предельные расстояния, с которых начинают быть видны те или иные предметы. Например, если военнослужащий увидел трубу на крыше дома, то это означает, что до дома не более 3 км, а не ровно 3 км. Пользоваться данной таблицей как справочной не рекомендуется. Каждый военнослужащий должен индивидуально для себя уточнить эти данные.
Определение на местности расстояний по степени слышимости предметов
Ночью и в туман, когда наблюдение ограничено или вообще невозможно (а на сильно пересеченной местности и в лесу, как ночью, так и днем) на помощь зрению приходит слух.
Военнослужащие обязательно должны учиться определять характер звуков (то есть что они означают), расстояние до источников звуков и направление, откуда они исходят. Если слышны различные звуки, военнослужащий должен уметь отличать их один от другого. Развитие такой способности достигается длительной тренировкой.
Почти все звуки, означающие опасность, производятся человеком. Поэтому если военнослужащий слышит даже самый слабый подозрительный шум, он должен замереть на месте и слушать. Возможно, что недалеко от него затаился враг. Если противник начнет двигаться первым, выдав тем самым свое месторасположение, то он первым и погибнет. Если это сделает разведчик, такая участь постигнет его.
В тихую летнюю ночь даже обычный человеческий голос на открытом пространстве слышно далеко, иногда на полкилометра. В морозную осеннюю или зимнюю ночь всевозможные звуки и шумы слышны очень далеко. Это касается и речи, и шагов, и звяканья посуды либо оружия. В туманную погоду звуки тоже слышны далеко, но их направление определить трудно. По поверхности спокойной воды и в лесу, когда нет ветра, звуки разносятся на очень большое расстояние. А вот дождь сильно глушит звуки. Ветер, дующий в сторону военнослужащего, приближает звуки, а от него - удаляет. Он также относит звук в сторону, создавая искаженное представление о местонахождении его источника. Горы, леса, здания, овраги, ущелья и глубокие лощины изменяют направление звука, создавая эхо. Порождают эхо и водные пространства, способствуя его распространению на большие дальности.
Звук меняется, когда источник его передвигается по мягкой, мокрой или жесткой почве, по улице, по проселочной или полевой дороге, по мостовой или покрытой листьями почве. Необходимо учитывать, что сухая земля лучше передает звуки, чем воздух. Ночью звуки особенно хорошо передаются через землю. Потому часто прислушиваются, приложив ухо к земле или к стволам деревьев.
Средняя дальность слышимости различных звуков днем на ровной местности, км (летом)
| Источник звука (действия противника) | Слышимость звука | Характерныезвуковые признаки |
| Шум двигающегося поезда | 10 |
|
| Паровозный или пароходный гудок, заводская сирена | 7-10 |
|
| Стрельба очередями из винтовок и пулеметов | 5 |
|
| Выстрел из охотничьего ружья | 3,0 |
|
| Автомобильный сигнал | 2-3 |
|
| Топот лошадей на рыси по мягкому грунту | 0,6 |
|
| Топот лошадей на рыси по шоссе | 1,0 |
|
| Крик человека | 1-1,5 |
|
| Ржание лошадей, лай собак | 2-3 |
|
| Разговорная речь | 0,1-0,2 |
|
| Всплеск воды от весел | 0,25-0,5 |
|
| Звяканье котелков, ложек | 0,5 |
|
| Переползание | 0,02 |
|
| Шаги | 0,03 |
|
| Кашель | 0,04-0,05 |
|
| Резкая команда голосом | 0,5-1 |
|
| Движение пехоты в строю по грунту | 0,3 | Ровный глухой шум |
| Движение пехоты в строю по шоссе | 0,6 | |
| Стук весел о борт лодки | 1-1,5 |
|
| Отрывка окопов вручную | 0,5-1 | Удары лопаты по камням |
| Вбивание деревянных колье вручную | 0,3-0,6 | Глухой звук равномерно чередующихся ударов |
| Вбивание деревянных колье механическим способом | 0,8 | |
| Рубка и спиливание деревьев ручным способом (топором, ручной пилой) | 0,3-0,4 | Резкий стук топора, визг пилы, прерывистый звук бензинового двигателя, глухой удар о землю спиленного дерева |
| Спиливание деревьев бензопилой | 0,7-0,9 | |
| Падение дерева | 0,8-1,0 | |
| Движение автомобилей по грунтовой дороге | 0,5 | Ровный шум моторов |
| Движение автомобилей по шоссе | 1-1,5 | |
| Движение танков, САУ, БМП по грунту | 2-3 | Резкий шум двигателей одновременно с резким металлическим лязгом гусениц |
| Движение танков, САУ, БМП по шоссе | 3-4 | |
| Шум двигателя стоящего танка, БМП | 1-1,5 |
|
| Движение буксируемой артиллерии по грунту | 1-2 | Резкий отрывистый грохот металла и шум двигателей |
| Движение буксируемой артиллерии по шоссе | 2-3 | |
| Стрельба артиллерийской батареи (дивизиона) | 10-15 |
|
| Выстрел из орудия | 6 |
|
| Стрельба из минометов | 3-5 |
|
| Стрельба из крупнокалиберных пулеметов | 3 |
|
| Стрельба из автоматов | 2 |
|
| Одиночный выстрел из винтовки | 1,2 |
|
Существуют определенные способы, помогающие слушать ночью, а именно:- лежа: приложить ухо к земле;- стоя: один конец палки прислонить к уху, другой конец упереть в землю;- стоять, слегка наклонившись вперед, перенеся центр тяжести тела на одну ногу, с полуоткрытым ртом, - зубы являются проводником звука.
Обученный военнослужащий при подкрадывании, ложится на живот и слушает лежа, стараясь определить направление звуков. Это легче сделать, повернув одно ухо в ту сторону, откуда доносится подозрительный шум. Для улучшения слышимости рекомендуется при этом приложить к ушной раковине согнутые ладони, котелок, отрезок трубы.
Для лучшего прослушивания звуков военнослужащий может приложить ухо к положенной на землю сухой доске, которая выполняет роль собирателя звука, или к сухому бревну, вкопанному в землю.
При необходимости можно изготовить самодельный водяной стетоскоп. Для этого используется стеклянная бутылка (либо металлическая фляга), заполненная водой до горловины, которую зарывают в грунт до уровня воды в ней. В пробку плотно вставляют трубку (пластмассовую), на которую одевают резиновую трубку. Другой конец резиновой трубки, снабженный наконечником, вставляют в ухо. Для проверки чувствительности прибора необходимо ударить пальцем землю на расстоянии 4 м от него (звук от удара ясно слышен через резиновую трубку).
При обучении распознаванию звуков необходимо воспроизводить с учебной целью следующее:- Отрывку траншей.- Сбрасывание мешков с песком.- Ходьбу по дощатому настилу.- Забивание металлического штыря.- Звук при работе затвором автомата (при открывании и закрывании его).- Постановку часового на пост.- Часовой зажигает спичку и закуривает сигарету.- Нормальный разговор и шепот.- Сморканье и кашель.- Треск ломающихся веток и кустарника.- Трение ствола оружия о стальную каску.- Хождение по металлической поверхности.- Перерезание колючей проволоки.- Перемешивание бетона.- Стрельбу из пистолета, автомата, пулемета одиночными выстрелами и очередями.- Шум двигателя танка, БМП, БТР, автомобиля на месте.- Шум при их движении по грунтовой дороге и по шоссе.- Движение небольших воинских подразделений (отделение, взвод) строем.- Лай и повизгивание собак.- Шум вертолета, летящего на различной высоте.- Резкие команды голосом и т.п. звуки.
Определение на местности расстояний по линейным размерам предметов
Определение расстояний по линейным размерам предметов заключается в следующем: с помощью линейки, расположенной на расстоянии 50 см от глаза, измеряют в миллиметрах высоту (ширину) наблюдаемого предмета. Затем действительную высоту (ширину) предмета в сантиметрах делят на измеренную по линейке в миллиметрах, результат умножают на постоянное число 5 и получают искомую высоту (ширину) предмета в метрах.
Например, телеграфный столб высотой 6 м (см. рисунок) закрывает на линейке отрезок 10 мм. Следовательно, расстояние до него:

Определение расстояний по линейным размерам предмета
Точность определения расстояний по линейным величинам составляет 5-10% длины измеряемого расстояния.
Определение на местности расстояний по угловым размерам предметов
Для применения этого способа надо знать линейную величину наблюдаемого предмета (его высоту, длину либо ширину) и тот угол (в тысячных), под которым виден данный предмет. Угловые размеры предметов измеряют с помощью бинокля, приборов наблюдения и прицеливания и подручными средствами.
Расстояние до предметов в метрах определяют по формуле: где В - высота (ширина) предмета в метрах: У - угловая величина предмета в тысячных.
где В - высота (ширина) предмета в метрах: У - угловая величина предмета в тысячных.
Например, высота железнодорожной будки составляет 4 метра, военнослужащий видит ее под углом 25 тысячных. Тогда расстояние до будки составит:  .
.
Или военнослужащий видит танк «Леопард-2» под прямым углом сбоку. Длина этого танка - 7 метров 66 сантиметров. Предположим, что угол наблюдения составляет 40 тысячных. Следовательно, расстояние до танка - 191,5 метров.
Чтобы определить угловую величину подручными средствами, надо знать, что отрезку в 1 мм, удаленному от глаза на 50 см, соответствует угол в две тысячных (записывается 0-02). Отсюда легко определить угловую величину для любых отрезков.
Например, для отрезка в 0,5 см угловая величина будет 10 тысячных (0-10), для отрезка в 1 см - 20 тысячных (0-20) и т.д. Проще всего выучить наизусть стандартные значения тысячных.
Угловые величины (в тысячных долях дистанции)
| Наименование предметов | Размерв тысячных |
| Патрон по ширине дульца гильзы (7,62 мм) | 12 |
| Гильза по ширине корпуса | 18 |
| Карандаш простой | 10-11 |
| Спичечная коробка по длине | 60 |
| Спичечная коробка по ширине | 50 |
| Спичечная коробка по высоте | 30 |
| Толщина спички | 2 |
Точность определения расстояний по угловым величинам составляет 5-10% длины измеряемого расстояния.
Для определения расстояний по угловым и линейным размерам предметов рекомендуется запомнить величины (ширину, высоту, длину) некоторых из них, либо иметь эти данные под рукой (на планшете, в записной книжке). Размеры наиболее часто встречаемых объектов приведены в таблице.
Линейные размеры некоторых предметов
| Наименование предметов | Высота | Длина | Ширина |
| Рост среднего человека (в обуви) | 1,65-1,75 |
|
|
| Стрелок с колена | 1,05-1,20 |
|
|
| Телеграфный столб | 6,00 |
|
|
| Обычный смешанный лес | 6,50-8,40 |
|
|
| Железнодорожная будка | 4,00 |
|
|
| Одноэтажный дом с крышей | 6-8 |
|
|
| Всадник верхом | 2,20-2,30 |
|
|
| Танки | 2,30-2,70 | 6,8-7,7 | 3,1-3,7 |
| БТР и БМП | 1,8-2,0 | 4,6-6,5 | 2,5-2,7 |
| Один этаж жилого капитального дома | 3-4 |
|
|
| Один этаж промышленного строения | 5-6 |
|
|
| Расстояние между столбами линии связи |
| 50-60 |
|
| Расстояние между опорами электросети высокого напряжения |
| 100 |
|
| Заводская труба | 30 |
|
|
| Вагон пассажирский цельнометаллический | 4,25 | 24-25 | 2,75 |
| Вагоны товарные двухосные | 3,8 | 7,2 | 2,75 |
| Вагоны товарные многоосные | 4 | 13,6 | 2,75 |
| Железнодорожные цистерны двухосные | 3 | 6,75 | 2,75 |
| Железнодорожные цистерны четырехосные | 3 | 9 | 2,75 |
| Железнодорожные платформы двухосные | 1,6 | 9,2 | 2,75 |
| Железнодорожные платформы четырехосные | 1,6 | 13 | 2,75 |
| Автомобили грузовые двухосные | 2 | 5-6 | 2-2,5 |
| Автомобили легковые | 1,5-1,8 | 4-5 | 1,5 |
| Тяжелый крупнокалиберный пулемет | 0,75 | 1,65 | 0,75 |
| Станковый пулемет | 0,5 | 1,5 | 0,5 |
| Мотоциклист на мотоцикле с коляской | 1,5 | 2 | 1,2 |
Определение на местности расстояний по соотношению скоростей звука и света
Звук распространяется в воздухе со скоростью 330 м/с, т. е. округленно 1 км за 3 с, а свет - практически мгновенно (300000 км/ч).
Таким образом, например, расстояние в километрах до места вспышки выстрела (взрыва) равно числу секунд, прошедших от момента вспышки до момента, когда был услышан звук выстрела (взрыва), деленному на 3.
Например, наблюдатель услышал звук взрыва через 11 с после вспышки. Расстояние до места вспышки будет равно: 
Определение на местности расстояний по времени и скорости движения
Этот способ применяется для приближенного определения величины пройденного расстояния, для чего среднюю скорость умножают на время движения. Средняя скорость пешехода около 5, а при движении на лыжах 8-10 км/ч.
Например, если разведывательный дозор двигался на лыжах 3 ч, то он прошел около 30 км.
Определение на местности расстояний шагами
Этот способ применяется обычно при движении по азимуту, составлении схем местности, нанесении на карту (схему) отдельных объектов и ориентиров и в других случаях. Счет шагов ведется, как правило, парами. При измерении расстоянии большой протяженности шаги более удобно считать тройками попеременно под левую и правую ногу. После каждой сотни пар или троек шагов делается отметка каким-нибудь способом и отсчет начинается снова. При переводе измеренного расстояния шагами в метры число пар или троек шагов умножают на длину одной пары или тройки шагов.
Например, между точками поворота на маршруте пройдено 254 пары шагов. Длина одной пары шагов равна 1,6 м. Тогда: 
Обычно шаг человека среднего роста равен 0,7-0,8 м. Длину своего шага достаточно точно можно определить по формуле:  где Д-длина одного шага в метрах; Р - рост человека в метрах; 0,37 – постоянная величина.
где Д-длина одного шага в метрах; Р - рост человека в метрах; 0,37 – постоянная величина.
Например, если рост человека 1,72 м, то длина его шага будет: 
Более точно длина шага определяется промером какого-нибудь ровного линейного участка местности, например дороги, протяженностью 200-300 м, который заранее измеряется мерной лентой (рулеткой, дальномером и т. п.).
При приближенном измерении расстояний длину пары шагов принимают равной 1,5 м.
Средняя ошибка измерения расстояний шагами в зависимости от условий движения составляет около 2-5% пройденного расстояния.
Счет шагов может выполняться с помощью шагомера. Он имеет вид и размеры карманных часов. Внутри прибора помещен тяжелый молоточек, который при встряхивании опускается, а под воздействием пружины возвращается в первоначальное положение.
При этом пружина перескакивает по зубцам колесика, вращение которого передается на стрелки.
На большой шкале циферблата стрелка показывает число единиц и десятков шагов, на правой малой - сотни, а на левой малой - тысячи.
Шагомер подвешивают отвесно к одежде. При ходьбе вследствие колебания его механизм приходит в действие и отсчитывает каждый шаг.

Шагомер
Определение на местности расстояний с помощью прицела

Фрагмент дневной сетки прицела
Дневной режим
Подготовить прицел к работе в дневном режиме. По дальномерной шкале определить дальность до выбранной цели, для чего:
Подъемным и поворотным механизмами подвести дальномерную шкалу так, чтобы цель высотой 2,7 м вписывалась между сплошной горизонтальной линией и одним из верхних горизонтальных коротких штрихов. При этом на дальность до цели (в гектометрах) будет указывать цифра, стоящая над этим штрихом, слева на прицельной сетке.
В том случае, когда есть время для производства несложных расчетов, можно определить дальность до цели при помощи прицельной сетки.
Для этого нужно:- навести прицел на предмет, размеры которого известны, и определить угол, под которым виден этот предмет. Следует помнить, что цена деления боковых поправок равна 0-05, а горизонтальный и вертикальный размеры верхнего креста соответствуют 0-02;- разделить известный размер цели (в метрах) на полученный угол (в тысячных дистанции) и частное умножить на 1000.
Пример 1. Определить дальность до цели (высота 2,5 м), если размер верхнего креста сетки уложится по высоте машины три раза.Решение: Дальность до цели будет равна:  Пример 2. Движущаяся вдоль фронта цель видна под углом равным 0-05 (цель укладывается в промежутке между двумя боковыми штрихами). Определить дальность до цели, если длина ее 6 метров.Решение: Дальность до цели будет равна:
Пример 2. Движущаяся вдоль фронта цель видна под углом равным 0-05 (цель укладывается в промежутке между двумя боковыми штрихами). Определить дальность до цели, если длина ее 6 метров.Решение: Дальность до цели будет равна: 
voenservice.ru
Количество просмотров публикации Измерение углов на местности - 205
При ориентировании и целеуказании на местности горизонтальные (вертикальные) углы между направлениями на местные предметы и цели измеряют с помощью приборов наблюдения или глазомерно. Многие приборы, применяемые в войсках, имеют шкалы, оцифрованные в делениях угломера. Окружность разделена на 60 больших или 6000 малых делений угломера. Одно малое деление угломера называют тысячной. Такое название объясняется тем, что длина отрезка дуги окружности, соответствующего одному малому делению, равна тысячной доле радиуса этой окружности. Единицей измерения угла здесь служит линейный отрезок, равный тысячной доле дистанции. Это позволяет быстро и легко посредством простейших арифметических действий переходить от угловых измерений к линейным и обратно.
При измерении углов в тысячных принято называть и записывать сначала число сотен, а затем десятков и единиц тысячных. В случае если при этом сотен или десятков не окажется, вместо них называют и записывают нули (табл. 2).
Таблица 2
| Угол в тысячных | Записывается | Читается |
| 12-50 1-55 0-35 0-01 | Двенадцать пятьдесят Один пятьдесят пять Ноль тридцать пять Ноль ноль один |
Для перехода от делений угломера к градусной мере угла пользуются соотношениями: одно малое деление (0-01) равно 3,6', а одно большое (1-00)-6°.
Рассмотрим некоторые способы измерения углов.
Измерение углов с помощью башенного угломера. На танках и боевых машинах для измерения угла поворота башенки имеется угломерное устройство (рис. 16, а). Основная шкала 1 устройства разбита на 600 делений, цена деления равна 0-10. Отсчетная шкала 2 имеет 10 делений по 0-01. Устройство позволяет снимать отсчеты угла поворота башенки с точностью до 0-01.
Оптический визир 3 установлен таким образом, что при отсчете 0-00 или 30-00 его оптическая ось параллельна продольной оси машины. На рис. 16,б отсчет угломерного устройства равен 8-33. Это значит, что оптическая ось визира отклонена от продольной оси машины на угол, равный данному отсчету. При измерении горизонтального угла между направлениями на два местных предмета (объекта) вначале наводят имеющийся в поле зрения визира угольник или перекрестие на один предмет и снимают отсчет, затем визируют на второй предмет и снимают отсчет. Величина угла между направлениями на предметы (объекты) равна разности двух отсчетов.
Измерение углов с помощью приборов наблюдения и прицеливания. В зрительной трубе бинокля имеются две взаимно перпендикулярные шкалы (сетки) для измерения горизонтальных и вертикальных углов с ценой большого деления 0-10, а малого 0-05. Чтобы измерить угол между двумя предметами, нужно совместить какой-либо штрих шкалы с одним из них и подсчитать число делений против изображения второго. Умножив число делений на цену одного деления, получим величину измеряемого угла в тысячных. На рис. 17 горизонтальный угол (Между двумя отдельными деревьями равен 0-45, а вертикальный угол между основанием и вершиной отдельного дерева -0-15.
Приборы наблюдения и прицеливания имеют шкалы, подобные шкалам бинокля, в связи с этим углы с помощью этих приборов измеряют аналогично тому, как и с помощью бинокля.
Измерение углов с помощью компаса. Вначале мушку визирного устройства компаса устанавливают на нулевой отсчет шкалы. Далее поворотом компаса в горизонтальной плоскости совмещают через целик и мушку линию визирования с направлением на левый предмет (ориентир). После этого, не меняя положения компаса, визирное устройство переводят в направление на правый предмет и снимают по шкале отсчет, который будет соответствовать величине измеряемого угла в градусах.
При измерении угла в тысячных линию визирования совмещают сначала с направлением на правый предмет (ориентир), так как счёт тысячных возрастает против хода часовой стрелки.
Измерение углов с помощью линейки. С помощью линейки с миллиметровыми делениями можно измерять углы в делениях угломера и градусах. В случае если линейку держать перед собой на расстоянии 59 см от глаза (рис. 18), то один миллиметр на линейке будет соответствовать двум тысячным (0-02). При измерении угла крайне важно подсчитать на линейке число миллиметров между предметами (ориентирами) и умножить на 0-02. Полученный результат будет соответствовать величине измеряемого угла в тысячных. На рис. 18 угол между столбами равен 0-32, а высота дерева--0-21.
Для измерения угла в градусах линейка выносится перед собой на расстояние 60 см. В этом случае 1 см на линейке будет соответствовать 1°.
Точность измерения углов с помощью линейки зависит от точности выноса ее на расстояние 50 см перед собой.
Измерение углов с помощью подручных предметов. Для измерения углов можно пользоваться небольшими подручными предметами (спичечная коробка, карандаш, патрон и т. п.), размеры которых в миллиметрах, а следовательно, и в тысячных на расстоянии 50 см от глаза известны.
Для приближенного измерения углов на местности могут служить пальцы руки, вытянутой на расстояние 50 см от глаза. Угол между линиями визирования на сомкнутые указательный, средний и безымянный пальцы равен 1-00 (рис. 19), а на разведенные до отказа большой и указательный пальцы-2-50.
referatwork.ru
Муниципальное образовательное учреждение
«Великодворская основная общеобразовательная школа»
Измерительные работы на местности
Работу выполнил:
Анфалов Сергей Васильевич, 8
класс
Великодворская ООШ Бабушкинского
района
Дата рождения: 16.06.1995
Домашний адрес: 161344, Вологодская
область, Бабушкинский р-н, д. Великий
Двор, д.76.
Руководитель:
Беляева Елена Васильевна,
учитель физики и математики
МОУ «Великодворская основная
общеобразовательная школа»
Адрес школы: 161344, Вологодская
область Бабушкинский р-н, д. Великий
Двор, д.72
д. Великий Двор
2009
ВВЕДЕНИЕ. В курсе изучения геометрии основной школы рассматриваются задачи, связанные с практическим применением изученных знаний: измерительные работы на местности, измерительные инструменты. Практические работы на местности являются одной из наиболее активных форм связи обучения с жизнью, теории с практикой. Мы учимся пользоваться справочниками, применять необходимые формулы, овладевать практическими приёмами геометрических измерений и построений. Практические работы с использованием измерительных инструментов повышают интерес к математике, а решение задач на измерение ширины реки, высоты предмета и определение расстояния до недоступной точки позволяют применить их в практической деятельности, увидеть масштаб применения математике в жизни человека. По мере изучения материала способы решения этих задач изменяются, одну и ту же задачу можно решить многими способами. При этом используются следующие вопросы геометрии: равенство и подобие треугольников, соотношения в прямоугольном треугольнике, теорема синусов и теорема косинусов(9 кл.), теорема Пифагора, свойства прямоугольных треугольников и т. д. В школе мы довольно подробно геометрические построения с помощью циркуля и линейки и решаем много задач. А как решить такие же задачи на местности? Ведь возможно вообразить себе такой огромный циркуль, который мог бы очертить окружность школьного стадиона или линейку для разметки дорожек парка. На практике картографам для составления карт, геодезистам для того, чтобы размечать участки на местности, например, для закладки фундамента дома, приходится использовать специальные методы.
Тема нашего реферата: Измерительные работы на местности.Цель: изучение некоторых методов решения геометрических задач на местности.
Для реализации поставленной цели мы определили следующие задачи:
● Изучить теоретическую и методическую литературу по данному вопросу.
● Показать взаимосвязь математики и основ безопасности жизнедеятельности.
● Применить на практике теоретические знания.
Объектом моих наблюдений стали:
● Определение высоты предмета.
● Расстояние до недоступной точки.
ОСНОВНАЯ ЧАСТЬ.
Одной из наиболее активных форм связи обучения с жизнью, теории с практикой является выполнение на уроках геометрии практических работ, связанных с измерением, построением, изображением. Эти же вопросы рассматриваются и в курсе основ безопасности жизнедеятельности, но все измерения проходят без специальных приборов. Работа проводится как на местности, так и решение задач в классе различными способами на нахождение высоты предмета и определение расстояния до недоступной точки. По программе в курсе геометрии рассматриваются следующие вопросы:7 класс● «Провешивание прямой на местности» (п.2).● «Измерительные инструменты» (п.8).● «Измерение углов на местности» (п.10).● «Построение прямых углов на местности» (п.13) ● « Задачи на построение. Окружность» (п.21). ● « Практические способы построения параллельных прямых» (п.26). ● «Уголовный отражатель» (п.36).● «Расстояние между параллельными прямыми» (п.37 – рейсмус). ● «Построение треугольника по трём элементам» (п.38). 8 класс● «Практические приложения подобия треугольников» (п.64 – измерение высоты предмета, определение расстояния до недоступной точки).9 класс● "Измерительные работы» (п.100 - измерение высоты предмета, определение расстояния до недоступной точки).
Измерительные инструменты, используемые при измерении на местности:
● РУЛЕТКА – лента, с нанесёнными на ней делениями, предназначена для построения прямых углов на местности.● ЭКЕР – прибор для измерения прямых углов на местности.● АСТРОЛЯБИЯ – прибор измерения углов на местности.● ВЕХИ (ВЕШКИ) – колья, которые вбивают в землю.● ЗЕМЛЯНОЙ ЦИРКУЛЬ (ПОЛЕВОЙ ЦИРКУЛЬ – САЖЕНЬ) – инструмент в виде буквы А высотой 1,37 м. и шириной 2 м. для измерения на местности.
ЭКЕР. Экер представляет собой два бруска, расположенных под прямым углом и укреплённых на треножнике. На концах брусков вбиты гвозди так, что прямые, проходящие через них взаимно перпендикулярны.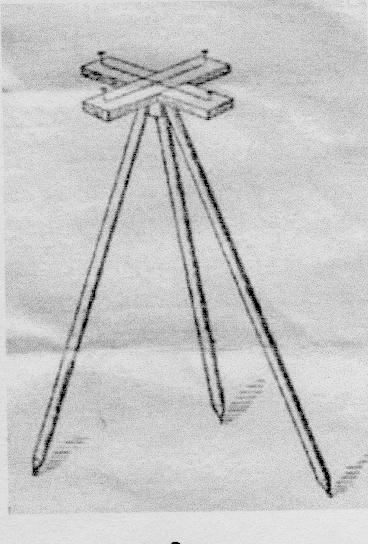 АСТРОЛЯБИЯ.
АСТРОЛЯБИЯ.
Устройство астролябия состоит из двух частей: диска (лимб), разделённого на градусы, и вращающейся вокруг центра линейки (алидады). При измерении угла на местности она наводится на предметы, лежащие на его сторонах. Наведение алидады называется визированием. Для визирования служат диоптры. Это металлические пластинки с прорезами. Диоптров два: один с прорезом в виде узкой щели, другой с широким прорезом, посередине которого натянут волосок. При визировании к узкому прорезу прикладывается глаз наблюдателя, поэтому диоптр с таким прорезом называется глазным. Диоптр с волоском направляется к предмету, лежащему на стороне измеряемого; он называется предметным. В середине алидады прикреплён к ней компас. 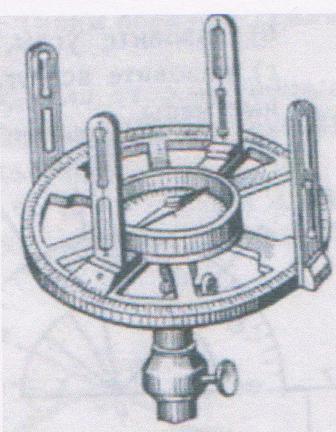
ПОСТРОЕНИЕ ОКРУЖНОСТИ НА МЕСТНОСТИ.На местности устанавливается колышек, к которому привязывается верёвка. Держась за свободный конец верёвки, двигаясь вокруг колышка, можно описать окружность.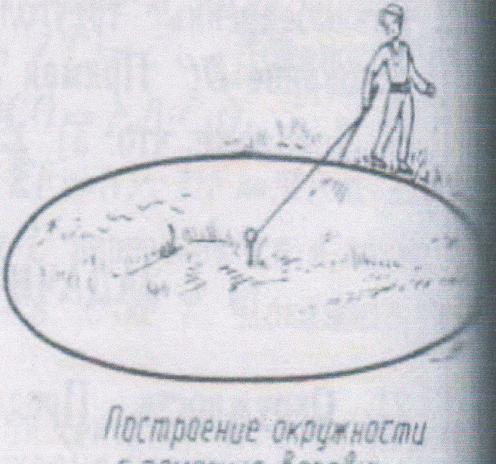 ПРАКТИЧЕСКАЯ РАБОТА.
ПРАКТИЧЕСКАЯ РАБОТА.
І. Измерение высоты объекта.
Способы:
1 Измерение высоты столба при помощи плоского зеркала.
Согласно законам отражения (оптика, физика), угол падения солнечного луча равен углу отражения этого луча от зеркала.
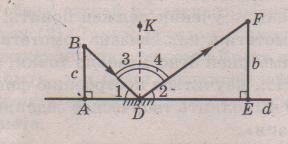
∟3 = ∟4, где DK ┴ d, d – горизонтальная плоскость.
С – человек; b – предмет; а – зеркало.
∟ADB=∟FDF, так как углы падения и отражения солнечного луча равны, а ∟1 = ∟2 = 90º-∟3, ∟A = ∟E = 90º, значит, треугольники ABD и EFD подобны по двум углам.
Из подобия треугольников следует AB:AD = FE:DE EF = (AB·DE):AD, где AB – «рост» человека – расстояние от земли до глаз, EF – измеряемая высота, AD и DE – соответственно расстояния от человека, отражённого в зеркале до измеряемого предмета.
2. Измерение высоты предмета при помощи тени.
С

N





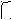
В М А

СВ – высота телеграфного столба.
МN – рост человека (1,6м.).
АМ – тень человека (3,35м.).
АВ – тень столба (15,3м.).
Человек встаёт в область тени столба так, что тень его макушки головы совпадала с концом тени от столба.
Рассмотрим треугольники АВС и АМN.
∟
 АВС =∟АМN = 90º. По двум равным
АВС =∟АМN = 90º. По двум равным
∟ВАС – общий. углам.


Треугольники АВС и АМN подобны.
Можно записать соотношение сторон AB:AM = CB:MN
CB = (AB·MN):AM
СВ = (15,3 · 1,6) : 3,35
СВ = 7,3м.
3. Измерение высоты предмета при помощи вехи.
Используем способ, основанный на измерении тени, отбрасываемой объектом.
● Измерить расстояние от дерева до точки, где заканчивается его тень.
● Взять веху и, наблюдая за её тенью, двигаться обратно к дереву до точки полного перекрытия их теней.
● Установить в этом месте веху, измерить расстояние до неё.
●Из подобия треугольников следует, что длина вехи относится к длине своей тени также как и высота дерева к своей.
● Определяем высоту дерева по формуле:
СЕ:BC = AD:AB, отсюда AD = (CE·AB):BC.
4. Измерение высоты предмета при помощи отсутствии тени.
При отсутствии тени высота вертикальных предметов определяется следующим образом.
Рядом с измеряемым предметом установить вертикально палку известной длины и отойти на 25 – 30 шагов. В вытянутой руке держать перед глазами вертикально карандаш или ровную палочку. Отметить на карандаше высоту вертикальной палки и измерить это расстояние. Мысленно умножить это расстояние на измеренный предмет. Умножив полученное количество раз на длину палки, можно получить искомую величину. На этом опыте мы определили, что высота столба равна 6,89 м.


II. Измерение расстояния до недоступной точки.
Способы:
1. Измерение расстояния до недоступной точки при помощи глазомера.
Отчётливо видны:
● на расстоянии 2 – 3 км – очертания больших деревьев;
● на расстоянии 1 км – стволы деревьев;
● на расстоянии 0,5 км – большие сучья;
● на расстоянии 300 м – можно различить листья на деревьях.
2. Измерение расстояния до недоступной точки с помощью подобия треугольников.
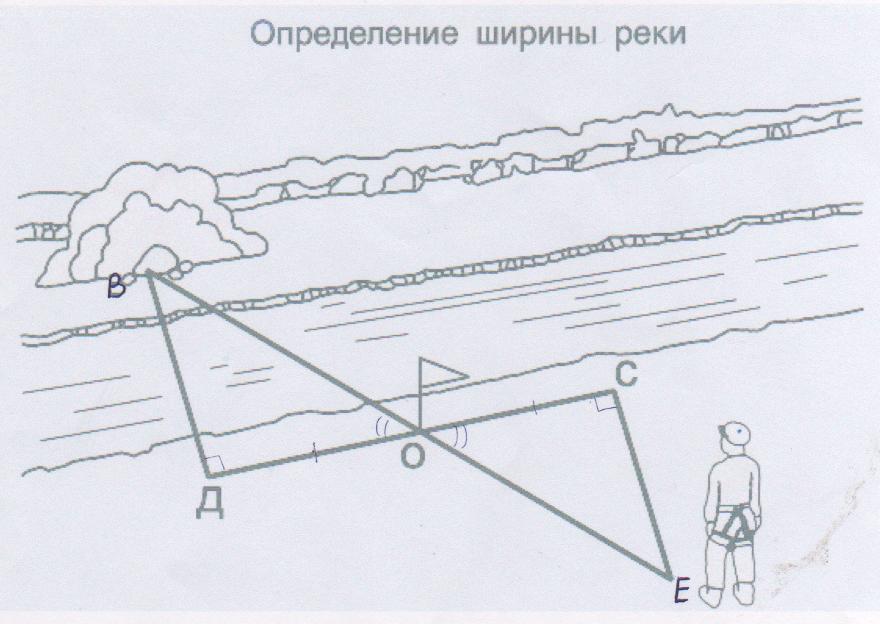
А) Для измерения ширины реки на берегу измеряем расстояние АС, с помощью астролябии устанавливаем угол А = 90˚ (направив на объект В на противоположном берегу), измеряем угол С. На листке бумаги строим подобный треугольник в масштабе 1:1000 и вычисляем АВ (ширину реки).
В 1
1
А1 С1
Запишем отношение сторон АВ: А1В1 = АС: А1С1
АВ = (АС·АВ1) : А1С1
Б) Ширину реки можно определить и так: рассматривая два подобных треугольника АВС и АВ1С1. Точка А выбрана на берегу реки, В1 и С у кромки поверхности воды, ВВ1 – ширина реки.
3. Измерение расстояния до недоступной точки способом «кепки».
Для определения ширины реки (оврага) необходимо встать на берег и надвинуть кепку на лоб так, чтобы из-под козырька был виден только обрез воды на противоположном берегу. Далее не меняя наклона головы и положения кепки, следует повернуть голову вправо (влево), заметить предмет, который находится на том же берегу, что и наблюдатель, и виден из-под края козырька. Расстояние до этого предмета равно ширине реки. На опыте мы определили, что ширина реки равна 6 м.


5. Измерение расстояния до недоступной точки с помощью равенства треугольников.
Один из способов определения расстояния до недоступной точки связан с законами геометрии и основан на равенстве треугольников.
● Встать напротив предмета на противоположном берегу реки.
● Повернувшись на 90˚, пройти вдоль берега 20 метров и поставить веху О.
● В том же направлении пройти ещё столько же.
● Повернувшись на 90˚, идти пока веха О и предмет на противоположном берегу не будут на одной линии.
● Расстояние СЕ равно ширине реки ВD.
ВD равно 5,78 м.


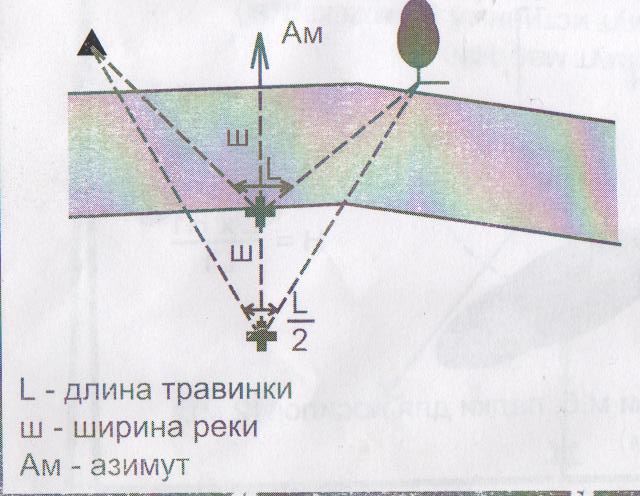
6. Измерение расстояния до недоступной точки способом «травинки».
Наблюдатель стоит в точке А и выбирает на противоположном берегу около воды два неподвижных предмета (ориентира), затем, держа в руке травинку (проволоку), которая закрывает промежуток между ориентирами, складывают её пополам и отходят от реки до тех пор, пока расстояние между ориентирами не уложится в сложенную пополам травинку В. Расстояние от А до В равно ширине реки. АВ равно 5,96 м.


ЗАКЛЮЧЕНИЕ.
В этом реферате рассмотрены наиболее актуальные задачи, связанные с геометрическими построениями на местности – измерением высоты предмета, определения расстояния до недоступной точки. Приведённые задачи имеют значительный практический интерес, закрепляют полученные знания по геометрии и могут использоваться для практических работ.
Литература
Атанасян Л. С. Геометрия 7-9. – М.: Просвещение, 2003.
Юрченко О. Методы мотивации и стимулирования деятельности учащихся. // Математика в школе, №1, 2005
СD-диск «Школа безопасности».
infourok.ru
Геометрические построения на местности
Исполнитель: ученица 8 класса Корепанова Наталья Владимировна
Министерство общего и профессионального образования Свердловской области МОУО г. Екатеринбурга
Образовательное учреждение – гимназия № 47
г. Екатеринбург, 2000г.
Введение
В школе мы довольно подробно изучаем геометрические построения с помощью циркуля и линейки и решаем много задач. А как решить такие же задачи на местности? Ведь невозможно вообразить себе такой огромный циркуль, который мог бы очертить окружность школьного стадиона или линейку для разметки дорожек парка.
На практике картографам для составления карт, геодезистам для того, чтобы размечать участки на местности, например, для закладки фундамента дома, приходится использовать специальные методы.
Цель настоящего реферата – изучение некоторых методов решения геометрических задач на местности. Кроме того, мечтая в будущем работать в области конструирования, я поставила себе дополнительную задачу – освоить приемы конструирования на компьютере. Для этого я изучаю многие программы – текстовый редактор Word, графический редактор PhotoShop, редактор Web-страниц FrontPage и др.
Реферат докладывался на районной научно-практической конференции школьников г. Екатеринбурга, проходившей 12 февраля 2000 г. в Уральском государственном техническом университете (секция математика, 7 – 8 классы) и занял третье место.
Построения на местности
Знание геометрии и умение применять эти знания на практике полезно в любой профессии. Традиционно построения на местности производят геодезисты для съемки плана земельного участка и строители для закладки фундаментов. Однако, такие знания бывают довольно часто нужны и в других областях деятельности. Всемирно известный писатель Артур Конан Дойль был врачом. Но он очень хорошо, видимо, знал геометрию. В рассказе «Обряд дома Месгрейвов» он описал, как Шерлоку Холмсу нужно было определить, где будут конец тени от вяза, который срубили. Он знал высоту этого дерева ранее. Шерлок Холмс так объяснил свои действия: «… я связал вместе два удилища, что дало мне шесть футов, и мы с моим клиентом отправились к тому месту, где когда-то рос вяз. Я воткнул свой шест в землю, отметил направление тени и измерил ее. В ней было девять футов.
Дальнейшие мои вычисления были уж совсем несложны. Если палка высотой в шесть футов отбрасывает тень в девять футов, то дерево высотой в шестьдесят четыре фута отбросит тень в девяносто шесть футов, и направление той и другой, разумеется, будет совпадать».
Можно подумать, что работа на местности ничем существенно не отличается от работы циркулем и линейкой на обыкновенной бумаге. Но это не так. На местности расстояния между точками довольно велики и нет таких линеек и циркулей, которые могли бы помочь нам. Да и вообще чертить на земле какие-либо линии затруднительно. Таким образом, построения на местности, основываясь на геометрических законах, имеют свою специфику:
Во – первых, все прямые не проводятся на земле, а прокладываются, т. е. отмечается на них, например, колышками, достаточно густая сеть точек. Обычно прокладку прямых на местности называют провешиванием прямых.
Во – вторых, запрещается при построениях проводить какие–либо дуги. Поэтому, циркуля у нас фактически нет. Все, что остается от циркуля — это возможность откладывать на данных (проложенных) прямых конкретные расстояния, которые должны быть заданы не численно, а с помощью двух точек, уже обозначенных колышками, где-то на местности. Сами расстояния будут измеряться шагами, ступнями, пальцами рук, или любыми подходящими для этой цели предметами.
При геодезических работах используются специальные колышки длиной 15-20 см и диаметром 2-3 см, в торец которых забиваются гвоздики для более точного обозначения концов отмеряемого отрезка, и вехи – деревянные заостренные шесты длиной 1,5-2 м и диаметром 2-4 см.
Как правило, участки местности представляют собой не идеально ровную поверхность, как тетрадный лист, на земле есть возвышения и углубления. Чтобы они не искажали геометрические образы прокладываемых линий, на местности строят не наклонные отрезки, а их ортогональные проекции на горизонтальную плоскость – горизонтальные проложения. Их можно определить, зная угол наклон – угол, образованный линией местности и ее проекцией на горизонтальную плоскость. Эти углы измеряются специальными приборами эклиметрами.
Поскольку в настоящем реферате ставится не задача изучения основ геодезии, а применения знаний по геометрии к решению практических задач, мы не будем пользоваться никакими приборами — ни рулеткой, ни астролябией, ни экером, ни теодолитом. Работать так, конечно, трудно, но всё же попробуем решить предложенные ниже задачи только с помощью колышек или вех и неотградуированного измерительного устройства, например, веревки, хотя принципиально можно обойтись и без нее.
Решение задач
Задача 1. Проложить прямую
На местности колышками обозначены две удалённые друг от друга точки. Как проложить через них прямую и, в частности, как можно без помощника устанавливать колышки на прямой между данными точками?
Решение!
Пользуясь зрительным эффектом, состоящим в загораживание двух колышков третьим, стоящим на общей с ними прямой, нетрудно установить ещё один колышек в некоторой точке С на продолжении отрезка с концами в двух данных точках А и В. после этого точки отрезка АВ можно построить с помощью того же эффекта, поскольку они будут лежать на продолжении либо отрезка АС, либо ВС (в зависимости от того, какая из точек — А или В — находятся ближе к точке С). Вообще, любая точка прямой АВ будет лежать на продолжении хотя бы одного из отрезков АВ, АС или ВС.
/>/>/>
Задача 2. Точка пересечения прямых
На местности колышками обозначены две точки одной прямой и две точки другой прямой. Как найти точку пересечения этих прямых?
Решение!
Пользуясь зрительным эффектом, указанным в решении задачи 1, легко найти точку пересечения прямых в том случае, если сразу ясно, что она лежит на продолжениях обоих отрезков с концами в данных точках. В противном случае достаточно сначала проложить одну или обе прямые так, чтобы на каждой из них с одной стороны от предполагаемой точки пересечения были отмечены по две точки.
/>/>/>
Задача 3. Симметрия относительно точки
На местности обозначены точки А и В. Найдите точку С, симметричную точке А относительно точки В.
Решение!
Продолжим прямую АВ за точку В и отложим на ней точку С на расстоянии АВ от точки В. Для этого понадобится измерить в подходящих единицах длины расстояние между точками А и В.
/>/>/>
Задача 4. Параллельная прямая
На местности обозначены три данные точки: А, В и С, не лежащие на одной прямой. Через точку А проложите прямую, параллельную прямой ВС.
Решение!
Продолжим прямую АВ за точку В и отложим на ней точку Dна расстоянии АВ от точки В. Продолжим прямую СDза точку С и отложим на ней точку Е на расстоянии СDот точки С. Тогда отрезок АЕ будет параллелен отрезку ВС, являющемуся средней линией треугольника АDЕ. Заметим, что предложенный способ выгодно отличается от множества других способов, опирающихся на измерение углов или на деление отрезка пополам.
/>/>/>
Задача 5. Нахождение середины отрезка.
Найдите середину отрезка АВ, заданного на местности двумя точками А и В.
Решение!
Возьмём какую-либо точку С, не лежащую на прямой АВ. Продолжим прямую CВ за точку С и отложим на ней точку Dна расстоянии 2ВС от точки С. Продолжим прямую АDза точку А и отложим на ней точку Е на расстоянии АDот точки А. Искомая середина Fотрезка АВ лежит на его пересечении с прямой ЕС. Действительно, отрезок СЕ параллелен отрезку AG— средней линии треугольника CDE(здесь G— середина отрезка CD). Так как, кроме того, BC= CG, то CF— средняя линия треугольника ABG, откуда AF= FB.
/>/>/>
Задача 6. Деление отрезка в данном отношении
Отрезок, заданный на местности двумя точками А и В, требуется разделить в отношении, в котором находятся длины двух отрезков KLи MN, заданных на местности точками K, Lи M, N. Как это сделать?
/>/>/>
Решение!
Построение точки F, делящей отрезок АВ в отношении AF:BF=KL: MN, произведём аналогично построению середины отрезка АВ, описанному в решении задачи 5. Отличие будет состоять в том, что точку С выберем на расстоянии KLот точки В, а точку D— на расстоянии 2MNот точки С. В этом случае прямая ECпо-прежнему будет параллельна отрезку AG, а значит, разделит отрезок АВ в том же отношении, в котором она делит отрезок BG.
Задача 7. Построение биссектрисы угла
На местности обозначены три точки A, Mи N, не лежащие на одной прямой. Проложите биссектрису угла MAN.
Решение!
Выберем на стороне данного угла точки В и С, а на другой — точки Dи Е так, чтобы выполнялись равенства
AB= BC= AD= DE.
Найдём точку О пересечения прямых ВЕ и CD. Тогда прямая АО будет искомой биссектрисой, поскольку в равнобедренном треугольнике ACEбиссектриса AFявляется одновременно и медианой, а значит, проходит через точку О пересечения медиан EBи CD.
/>/>/>
Задача 8. Построение перпендикуляра к прямой
Проложите на местности какую-нибудь прямую, перпендикулярную прямой, проходящей через заданные точки А и В. Как проложить перпендикуляр к прямой АВ, проходящей через данную точку H?
Решение!
Продолжим прямую АВ за точку В и отложим на ней точку С на расстоянии АВ от точки В. Кроме того, отложим на том же расстоянии от точки В ещё две точки Dи Eв двух разных, но не противоположных направлениях. Найдём точку Fпересечения прямых AEи CD, а также точку Gпересечения прямых ADи CE. Прямая FGперпендикулярна прямой АВ. Действительно, точка А, Е,Dи С равноудалены от точки В, т.е. лежат на одной окружности с центром В и диаметром АС. Следовательно, вписанные углы ADCи AECпрямые, поэтому ADи CE– высоты треугольника AFC. Так как все три высоты этого треугольника пересекаются в одной точке G, то прямая FGперпендикулярна стороне АС. Для того чтобы проложить перпендикуляр к прямой АВ через данную точку H, достаточно теперь проложить через эту точку прямую, параллельную прямой FG.
/>/>/>
Задача 9. Построения под заданным углом
На местности обозначены точки А и В. Найдите точки C, Dи E, для которых выполнены равенства />BAC=45°,/>BAD=6O,°/>BAE=3O°.
Решение!
Проложим перпендикуляр к прямой АВ, пересекающий в какой–то точке луч АВ. Без ограничения общности считаем для удобства, что эта точка пересечения и есть точка В. На перпендикуляре по разные стороны от точки В отложить точки С и F, удалённые от точки В на расстояние АВ. Тогда угол ВАС равен 45°(из равнобедренного прямоугольного треугольника АВС). На прямой AFотложим точку Gна расстоянии АВ от точки А, а затем на прямой ВС отложим точку Dна расстоянии CGот точки В. Тогда угол ВАDравен 6О°, так как по теореме Пифагора для прямоугольного треугольников АВС, ACGи ABDимеют место равенства
/>
Для построения точки Е теперь остаётся проложить биссектрису угла BAD.
/>/>/>
Задача 10. Измерение высоты дерева.
Высоту деревьев можно определить при помощи шеста. Этот способ состоит в следующем.
Запасшись шестом выше своего роста, воткните его в землю отвесно на некотором расстоянии от измеряемого дерева. Отойдите от шеста назад, по продолжению Ddдо того места А, с которого, глядя на вершину дерева, вы увидите на одной линии с ней верхнюю точку bшеста. Затем, не меняя положения головы, смотрите по направлению горизонтальной прямой aC, замечая точки с и С, в которых луч зрения встречает шест и ствол. Попросите помощника сделать в этих местах пометки, и наблюдение окончено. Остаётся только на основании подобия треугольников adcи aBCвычислить ВС из пропорции
ВС: bc= aC: ас,
Расстояния bc, aCлегко измерить непосредственно. К полученной величине ВС нужно прибавить расстояние CD(которое также измеряется непосредственно), чтобы узнать искомую высоту дерева.
/>
--PAGE_BREAK--ЗаключениеВ настоящем реферате рассмотрены наиболее актуальные задачи, связанные с геометрическими построениями на местности – провешиванием прямых, делением отрезков и углов, измерением высоты предмета. Приведено большое количество задач и даны их решения. Приведенные задачи имеют значительный практический интерес, закрепляют полученные знания по геометрии и могут использоваться для практических работ. Ценно то, что для их решения не требуется знаний больших, чем в объеме 8 классов.
Кроме того, при работе над рефератом освоен текстовый редактор Word, графический редактор PhotoShop, редактор Web — страниц FrontPage.
Таким образом, цель реферата – изучение методов геометрических построений на местности – достигнута, задачи реферата – ознакомиться с конструированием на компьютере и изучить редакторы, применяющиеся для этого – выполнены.
Список литературы
1. Сергеев И.Н., Олехник С.Н., Гашков С.Б. «Примени математику», М., Наука, 1989.
2. Балк М.Б., Балк Г.Д. «Математика после уроков», М., Просвещение, 1971.
3. Четверухин Н.Ф. «Методы геометрических построений», М., Учпедгиз, 1952.
4. Косякин А.С., Никулин А.С., Смирнов А.С. «Землеустроительные работы», М., Недра, 1988.
www.ronl.ru
Региональная научно-практическая конференция обучающихся
«К вершинам знаний – 2017»
Секция: математика
Тема: Измерение углов.
Автор:
Коняева Полина Геннадьевна
Научный руководитель:
Дуб Оксана Владимировна
Место выполнения работы:
МБОУ СОШ с. Становое
2017
Содержание:
Введение…………………………………………..3
Цель и задачи проекта……………………………3
Угол………………………………..………………4
Виды углов..………………………………………4
Транспортир…………………………..………..…5
Виды транспортиров……………………………..6
Измерение и построение углов………………….6
Единицы измерения углов……………………….7
Измерение углов…………………………………8
10. Результаты исследования и основные выводы…8
11. Литература……………………………………….9
Введение:
Математика великая наука, она нужна каждому, и каждый день мы применяем знания математики в жизни. Вся наша жизнь – это вычисления и подсчеты. Без знаний математики мы не можем вычислить время, подсчитать деньги, построить дом. Мы не можем сравнить предметы, расстояния. Математика развивает интеллект и помогает найти решения в сложной задаче. Также в этой науке есть геометрические фигуры. Одна из них – угол. Это очень важно знать, как строить углы и как измерять их. В своей работе я хотела бы показать это.
1 слайд:
В математических вопросах нельзя пренебрегать даже с самыми мелкими ошибками.И. Ньютон
2 слайд:
Как построить, как измерить,
Биссектрису провести,
Как сравнить и как отметить
И в тетрадку занести,
Чтоб уметь решать задачи,
Выполнять и чертежи,
На десятку не иначе
Всё усвоить мы должны,
Астроном ты, иль конструктор,
Архитектор иль портной,
Всюду угол очень нужен,Всюду важно знать о том,
Где развёрнутый, где острый,
Где прямой, а где тупой,
Разобраться очень просто -Самому или со мной!
3 слайд:
Цель работы:
Задачи:
Изучить вопрос о происхождении угла и транспортира.
Научиться измерять углы с помощью транспортира.
Узнать, какие бывают углы и как их различать.
Обобщить и систематизировать научный материал по данному вопросу.
В наиболее простой и интересной форме преподнести данный материал слушателям для развития у них интереса к математике.
4 слайд:
Угол.
Углом называют фигуру, образованную двумя лучами, выходящими из одной точки.
5 слайд:
Угол в повседневной жизни
6 слайд:
Историческая справка
Знак ∠ для обозначения угла ввёл в 18 веке французский математик Пьер Эригон. Эригон применял для обозначения прямого угла знак ∟.
7 слайд:
Равные углы:
∠ А=∠В
8 слайд:
Вывод:
Равные углы при наложении совпадают.
Или
Если один угол наложить на другой, и они совпадут, то это равные углы.
9 слайд:
Виды углов
Острый прямой
тупой развёрнутый
10 слайд:
Два дополнительных друг другу луча образуют развёрнутый угол.
11 слайд:
Пример развёрнутого угла.
12слайд:
Прямой угол – это половина развёрнутого угла.
13 слайд:
Виды углов
Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус. Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля.
В зависимости от градусной меры углы делятся на несколько групп.
1. Острый угол - градусная мера от 0 до 90 градусов.
2. Прямой угол - градусная мера 90 градусов.
3. Тупой угол - градусная мера больше 90 градусов.
14 слайд:
Виды углов
Следует отметить, что любой угол, разделяет плоскость на две части. Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла.
В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла, может находиться на одной из его сторон, либо может лежать внутри угла.
15 слайд:
Транспортир
Транспортир – инструмент для построения и измерения углов.
16 слайд:
Что такое транспортир?
17 слайд:
Но древние ученые производили измерения не только транспортиром – ведь этот инструмент был неудобен для измерений на местности и решения задач прикладного характера. А именно прикладные задачи и являлись главным предметом интереса древних геометров. Изобретение первого инструмента, позволяющего измерять углы на местности, связывают с именем древнегреческого ученого Герона Александрийского(I в. до н.э.). Он описал инструмент диоптр, позволяющий измерять углы на местности и решать множество прикладных задач.
18 слайд:
Первые транспортиры возникли много тысяч лет тому назад. Предполагают, что это было связано с созданием первого календаря. Древние математики нарисовали круг и разделили его на столько частей, сколько дней в году. Но они думали, что в году не 365 или 366 дней, а 360. Поэтому круг, обозначающий год, разделили на 36 равных частей. Такое изображение было очень полезным, на нём можно было каждый прошедший день, и видеть, сколько дней осталось до конца года. Каждой части дали название – градус. Градусная мера сохранилась и до наших дней. Картинку с древним календарём легко сделать с помощью транспортира.
19 слайд:
Виды транспортира
Полукруговые (180 градусов) — наиболее простые и древние транспортиры.
Круговые (360 градусов).
Геодезические, которые бывают двух типов: ТГ-А — для построения и измерения углов на планах и картах; ТГ-Б — для нанесения точек на чертежной основе по известным углам и расстояниям. Цена деления угломерной шкалы — 0,5°, прямолинейной — 1 миллиметр.
Улучшенные типы транспортиров, которые необходимы для более точных построений и измерений. Например, существуют специальные транспортиры с прозрачной линейкой с угломерным нониусом, которая вращается вокруг центра.
20 слайд:
Картинки
21 слайд:
Алгоритм измерения углов с помощью транспортира
1) Нужно вершину угла совместить с центром транспортира.
2) Одна сторона угла должна проходить через нулевую отметку (0о по шкале).
3) Вторая сторона угла должна пересекать шкалу. Нужно посмотреть, через какую отметку проходит вторая сторона угла. Это и есть величина этого угла.
Если у транспортира есть две шкалы, то надо смотреть на отметку той шкалы, через ноль которой проходит одна из сторон угла.
22 слайд:
Измерение углов
23 слайд:
Измерение углов
24 слайд:
Алгоритм построения угла:
Начертить луч.
Совместить центр транспортира с началом луча так, чтобы луч проходил через начало отсчёта на шкале транспортира.
Найти на нужном ряду необходимое значение угла и поставить на бумаге точку.
Соединить начало луча с отмеченной точкой.
Проверить вид угла, который нужно построить.
Искомый угол построен.
25 слайд:
Построение углов
26 слайд:
Построение углов
27 слайд:
Построение углов
28 слайд:
В чём измеряются углы.
Градус, минута, секунда — общепринятые единицы измерения плоских углов. Также эти величины используются в картографии для определения координат произвольной точки земной поверхности, в том числе для определения азимута.
Град (гон), метрическая минута, метрическая секунда — единицы измерения плоских углов.
29 слайд:
Что такое градус?
1 градус – одна сто восьмидесятая часть развёрнутого угла
Градус – единица измерения углов
30 слайд:
Кроме градуса, были введены такие единицы измерения, как минута( часть градуса) и секунда( часть минуты). Названия минута и секунда произошли от partes minutae primae и partes minutae sekundae, что в переводе означает "части меньшие первые" и "части меньшие вторые". В истории науки эти единицы измерения сохранились благодаря Клавдию Птолемею, жившему во II веке.
31 слайд:
Угловая секунда (обозначается ) используется в астрономии при измерении плоских углов в градусных мерах. При измерении углов в часовых мерах (в частности, для определения прямого восхождения) используется единица измерения «секунда» (обозначается с). Соотношение между этими величинами определяется формулой 1c = 15.Иногда угловую секунду (и производные от неё дольные единицы) ошибочно называют арксекундой, что является простой транслитерацией с англ. arcsecond.
32 слайд:
Радиа́н (обозначение: рад, rad; от лат. radius луч, радиус) - основная единица измерения плоских углов в современной математике и физике. Радиан определяется как угловая величина дуги, длина которой равна её радиусу. Таким образом, величина полного угла равна 2π радиан.
33 слайд:
Измерение углов
Измерение углов основано на сравнении их с углом, принятым за единицу измерения. Обычно за единицу измерения углов принимают градус — угол, равный 1/180 части развернутого угла.
Транспортир
Рис.1
Положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле, называется градусной мерой угла. Для измерения углов используется транспортир (рис.1).
∠AOB = 150°
Рис.2
На рисунке 2 изображен угол АОВ, градусная мера которого равна 150°. Обычно говорят кратко: «Угол АОВ равен 150°» — и пишут: Z АОВ = 150°.
1/60 часть градуса называется минутой, а 1/60 часть минуты — секундой. Минуты обозначают знаком «′», а секунды — знаком «″». Например, угол в 68 градусов, 32 минуты и 27 секунд обозначается так: 68°32′27″.
34 слайд:
РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ И ОСНОВНЫЕ ВЫВОДЫ:
В результате проведенного исследования я пришла к выводу, что угол - это очень интересная геометрическая фигура.
35слайд:
Литература.
1.Бунимович Е.А. Математика. Арифметика. Геометрия. 5 класс: учебник для общеобразовательных учреждений/ Е.А. Бунимович , Г.В. Дорофеев, С.Б.Суворова и др. – М.: Просвещение, 2012.
2.Шеврин Л.Н., Гейн А. Г., Коряков И.О. Математика: учебник – собеседник для 5 кл ./ Л.Н. Шеврин , А.Г. Гейн , И.О.Коряков и др. – М.: Просвещение, 1994.
3.http://images.yandex.ru/ F688952.jpg
4.http://images.yandex.ru/ Goniometro.jpg
5.http://images.yandex.ru/ 462158.jpg
6.http://ru.wikipedia.org/wiki /
7. http :// images.yandex.ru/2F6333429_18c50e4f.gif
8. http :// images.yandex.ru/Fmatematik_galerisi4.jpg
9. http :// images.yandex.ru/F039126.jpg
10. http :// images.yandex.ru/Fmuha.gif
11. http :// images.yandex.ru/07610885.jpg
36 слайд:
СПАСИБО ЗА ВНИМАНИЕ!
infourok.ru