Опубликовать ОпубликоватьРеферат на тему:
Египетская дробь — в математике сумма нескольких дробей вида (так называемых аликвотных дробей). Другими словами, каждая дробь суммы имеет числитель, равный единице, и знаменатель, представляющий собой натуральное число.
Пример: .
Египетская дробь представляет собой положительное рациональное число вида a/b; к примеру, египетская дробь, записанная выше, может быть записана в виде дроби 43/48. Можно показать, что каждое положительное рациональное число может быть представлено в виде египетской дроби. Сумма такого типа использовалась математиками как определение для дробей начиная со времён древнего Египта до средневековья. В современной математике вместо египетских дробей используются простые и десятичные дроби, однако египетские дроби продолжают изучаться в теории чисел и истории математики.
Египетские дроби были изобретены и впервые использованы в древнем Египте. Одним из первых известных упоминаний о египетских дробях является Математический папирус Ринда. Три более древних текста, в которых упоминаются египетские дроби — это Египетский математический кожаный свиток, Московский математический папирус и Деревянная табличка Ахмима. Папирус Ринда был написан Ахмесом в эпоху Второго переходного периода; он включает таблицу египетских дробей для рациональных чисел вида 2/n, а также 84 математических задачи, их решения и ответы, записанные в виде египетских дробей.
Египтяне ставили иероглиф
(ер, «[один] из» или ре, рот) над числом для обозначения единичной дроби в обычной записи, а в священных текстах использовали линию. К примеру:
У них также были специальные символы для дробей 1/2, 2/3 и 3/4, которыми можно было записывать также другие дроби (большие чем 1/2).
Египтяне использовали также и другие формы записи, основанные на иероглифе Глаз Хора для представления специального набора дробей вида 1/2k (для k = 1, 2, …, 6), то есть, двухэлементных рациональных чисел. Такие дроби использовались вместе с другими формами записи египетских дробей для того, чтобы поделить хекат, основную меру объёма в Древнем Египте. Эта комбинированная запись также использовалась для измерения объёма зерна, хлеба и пива. Если после записи количества в виде дроби Глаза Хора оставался какой-то остаток, его записывали в обычном виде кратно ро, единице измерения, равной 1/320 хеката.
При этом "рот" помещался перед всеми иероглифами.
Египетские дроби продолжались использоваться в древней Греции и впоследствии математиками всего мира до средних веков, несмотря на имеющиеся к ним замечания древних математиков (к примеру, Клавдий Птолемей говорил о неудобстве использования египетских дробей по сравнению с Вавилонской системой). Важную работу по исследованию египетских дробей провёл математик XIII века Фибоначчи в своём труде «Liber Abaci».
Основная тема «Liber Abaci» — вычисления, использующие десятичные и обычные дроби, вытеснившие со временем египетские дроби. Фибоначчи использовал сложную запись дробей, включавшую запись чисел со смешанным основанием и запись в виде сумм дробей, часто использовались и египетские дроби. Также в книге были приведены алгоритмы перевода из обычных дробей в египетские.
Категории: Теория чисел, История математики, Элементарная математика, Наука в Древнем Египте, Математические головоломки и досуг.
Текст доступен по лицензии Creative Commons Attribution-ShareAlike.wreferat.baza-referat.ru
ОпубликоватьРеферат на тему:
Египетская дробь — в математике сумма нескольких дробей вида (так называемых аликвотных дробей). Другими словами, каждая дробь суммы имеет числитель, равный единице, и знаменатель, представляющий собой натуральное число.
Пример: .
Египетская дробь представляет собой положительное рациональное число вида a/b; к примеру, египетская дробь, записанная выше, может быть записана в виде дроби 43/48. Можно показать, что каждое положительное рациональное число может быть представлено в виде египетской дроби. Сумма такого типа использовалась математиками как определение для дробей начиная со времён древнего Египта до средневековья. В современной математике вместо египетских дробей используются простые и десятичные дроби, однако египетские дроби продолжают изучаться в теории чисел и истории математики.
Египетские дроби были изобретены и впервые использованы в древнем Египте. Одним из первых известных упоминаний о египетских дробях является Математический папирус Ринда. Три более древних текста, в которых упоминаются египетские дроби — это Египетский математический кожаный свиток, Московский математический папирус и Деревянная табличка Ахмима. Папирус Ринда был написан Ахмесом в эпоху Второго переходного периода; он включает таблицу египетских дробей для рациональных чисел вида 2/n, а также 84 математических задачи, их решения и ответы, записанные в виде египетских дробей.
Египтяне ставили иероглиф
(ер, «[один] из» или ре, рот) над числом для обозначения единичной дроби в обычной записи, а в священных текстах использовали линию. К примеру:
У них также были специальные символы для дробей 1/2, 2/3 и 3/4, которыми можно было записывать также другие дроби (большие чем 1/2).
Египтяне использовали также и другие формы записи, основанные на иероглифе Глаз Хора для представления специального набора дробей вида 1/2k (для k = 1, 2, …, 6), то есть, двухэлементных рациональных чисел. Такие дроби использовались вместе с другими формами записи египетских дробей для того, чтобы поделить хекат, основную меру объёма в Древнем Египте. Эта комбинированная запись также использовалась для измерения объёма зерна, хлеба и пива. Если после записи количества в виде дроби Глаза Хора оставался какой-то остаток, его записывали в обычном виде кратно ро, единице измерения, равной 1/320 хеката.
При этом "рот" помещался перед всеми иероглифами.
Египетские дроби продолжались использоваться в древней Греции и впоследствии математиками всего мира до средних веков, несмотря на имеющиеся к ним замечания древних математиков (к примеру, Клавдий Птолемей говорил о неудобстве использования египетских дробей по сравнению с Вавилонской системой). Важную работу по исследованию египетских дробей провёл математик XIII века Фибоначчи в своём труде «Liber Abaci».
Основная тема «Liber Abaci» — вычисления, использующие десятичные и обычные дроби, вытеснившие со временем египетские дроби. Фибоначчи использовал сложную запись дробей, включавшую запись чисел со смешанным основанием и запись в виде сумм дробей, часто использовались и египетские дроби. Также в книге были приведены алгоритмы перевода из обычных дробей в египетские.
Категории: Теория чисел, История математики, Элементарная математика, Наука в Древнем Египте, Математические головоломки и досуг.
Текст доступен по лицензии Creative Commons Attribution-ShareAlike.www.wreferat.baza-referat.ru
Введение
В результате практической деятельности человека, при дележе добычи после охоты возникла потребность в нахождении долей. Другой существенной причиной появления дробных чисел можно считать измерение величин при помощи выбранной единицы измерения.
Первые дроби, с которыми нас знакомит история, это дроби вида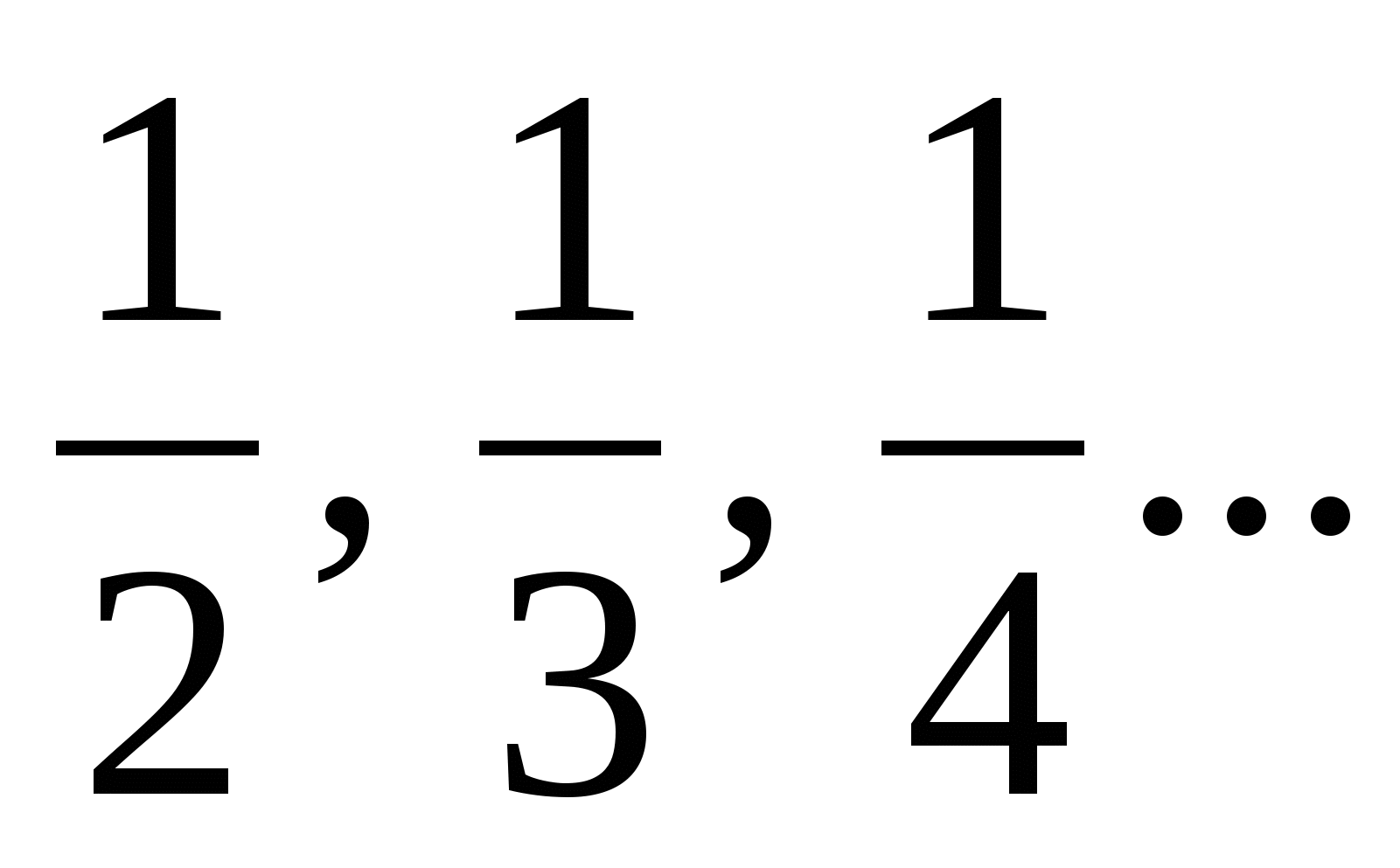 
– так называемые единичные дроби или аликвотные (от лат. aliquot – «несколько»).
Египетская дробь — в математике сумма нескольких дробей вида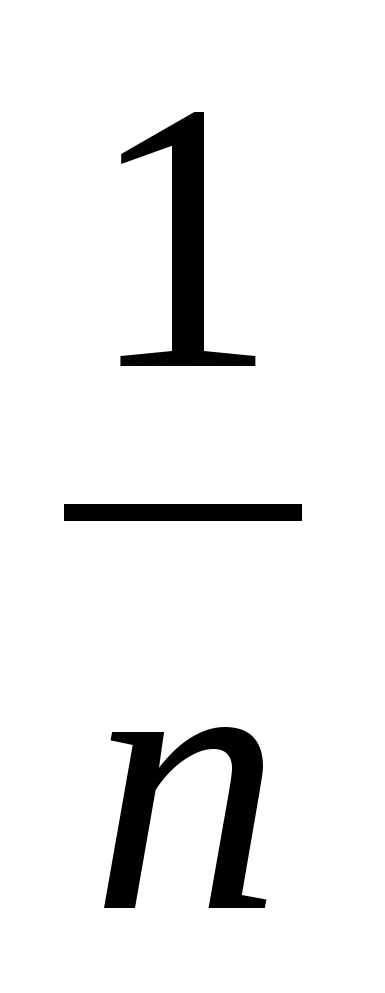 
(так называемых аликвотных дробей). Другими словами, каждая дробь суммы имеет числитель, равный единице, и знаменатель, представляющий собой натуральное число.
Задачи с использованием в решении аликвотных дробей составляют обширный класс нестандартных задач. Сюда относятся, прежде, всего, задачи, в которых требуется разделить какие либо ресурсы на несколько частей с наименьшим количеством действий для этого.
Цель: Выяснить, какое значение имеют аликвотные дроби в нашей жизни
Задачи:
Узнать происхождение аликвотных дробей.
Рассмотреть основные операции с аликвотными дробями.
Решать олимпиадные задачи с помощью аликвотных дробей.
Составлять и решать задачи практического содержания.
I Теоретическая часть
1 Происхождение аликвотных дробей
В Древнем Египте «настоящими» математики считали только аликвотные дроби. Поэтому каждую дробь стремились представить в виде суммы аликвотных дробей, причём с разными знаменателями.
Таким образом, первые дроби, с которыми нас знакомит история, это дроби вида 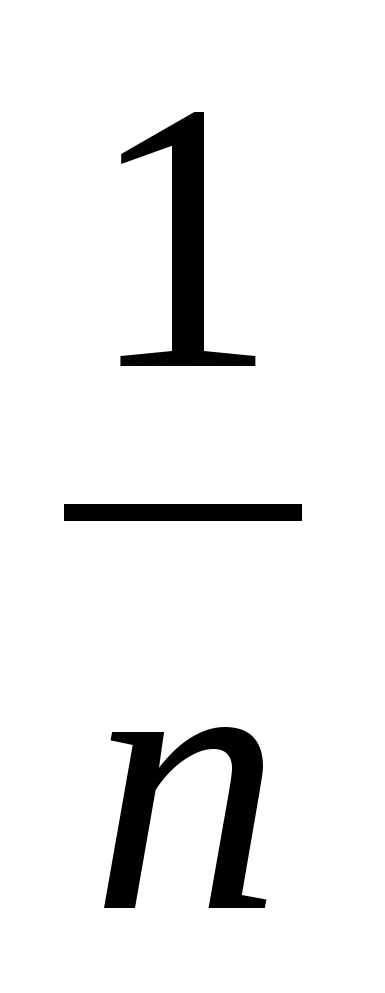так называемые единичные дроби или аликвотные. То есть аликвотными дробями называются дроби с числителем 1.
И даже сами аликвотные дроби они часто стремились представить в виде суммы меньших аликвотных дробей. Например,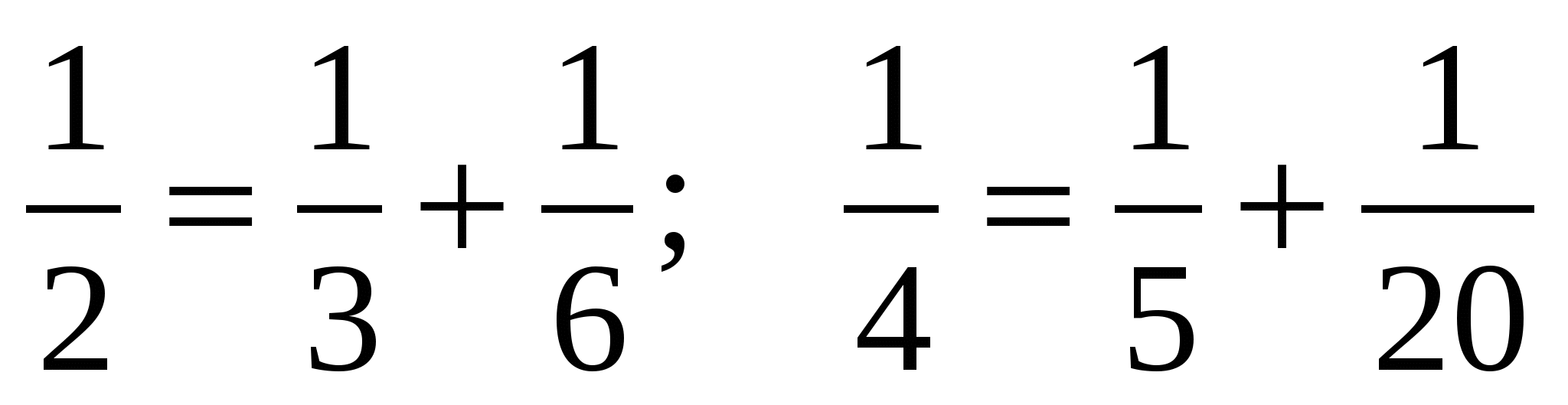 
.
Такие дроби использовались вместе с другими формами записи египетских дробей для того, чтобы поделить «хекат», основную меру объёма в Древнем Египте, т.е. аликвотные дроби нужны были египтянам в практических целях.
Египтяне широко использовали дроби. Египетская дробь представляла собой сумму нескольких единичных (или аликвотных) дробей вида 1/n. Например, 8/15=1/3+1/5. Часто сами аликвотные дроби они представляли в виде суммы меньших аликвотных дробей. Например, 1/4=1/5+1/20.
Для обозначения единичной дроби египтяне над обычным числом ставили специальный иероглиф "рот" 
. Например дроби 1/3 и 1/10 выглядели так:
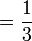и 
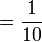
В папирусе Ахмеса есть задача:.«Как разделить 7 хлебов между 8 людьми?».
Египтяне решали эту задачу так: 7/8 = 1/2 + 1/4 + 1/8.
Значит, каждому человеку надо дать полхлеба, четверть хлеба и восьмушку хлеба.
С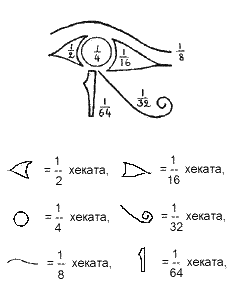
уществовали и другие способы записи дробей, например, для написания дробей от 1/2 до 1/64 использовались составные части глаза Гора.
Египетские дроби продолжались использоваться в древней Греции и впоследствии математиками всего мира до средних веков, несмотря на имеющиеся к ним замечания древних математиков . К примеру, Клавдий Птолемей говорил о неудобстве использования египетских дробей по сравнению с Вавилонской системой(позиционная система исчисления)
Важную работу по исследованию египетских дробей провёл математик XIII века Фибоначчи в своём труде «Liber Abaci» – это вычисления, использующие десятичные и обычные дроби, вытеснившие со временем египетские дроби. Фибоначчи использовал сложную запись дробей, включавшую запись чисел со смешанным основанием и запись в виде сумм дробей, часто использовались и египетские дроби. Также в книге были приведены алгоритмы перевода из обычных дробей в египетские.
2 Основные операции над аликвотными дробями
Чтобы представить какое либо число в виде суммы аликвотных дробей, порой приходится проявлять, незаурядную изобретательность. Скажем, число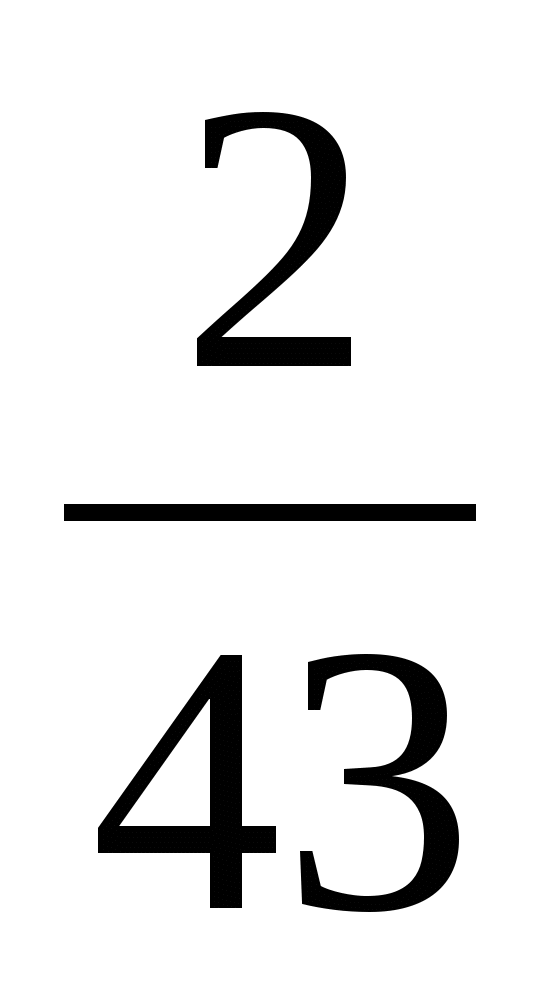 
выражается так:
.
Производить арифметические действия над числами, раскладывая их в сумму долей единицы, очень неудобно.
Начиная решение задач для разложения аликвотных дробей в виде суммы меньших аликвотных дробей, как, например
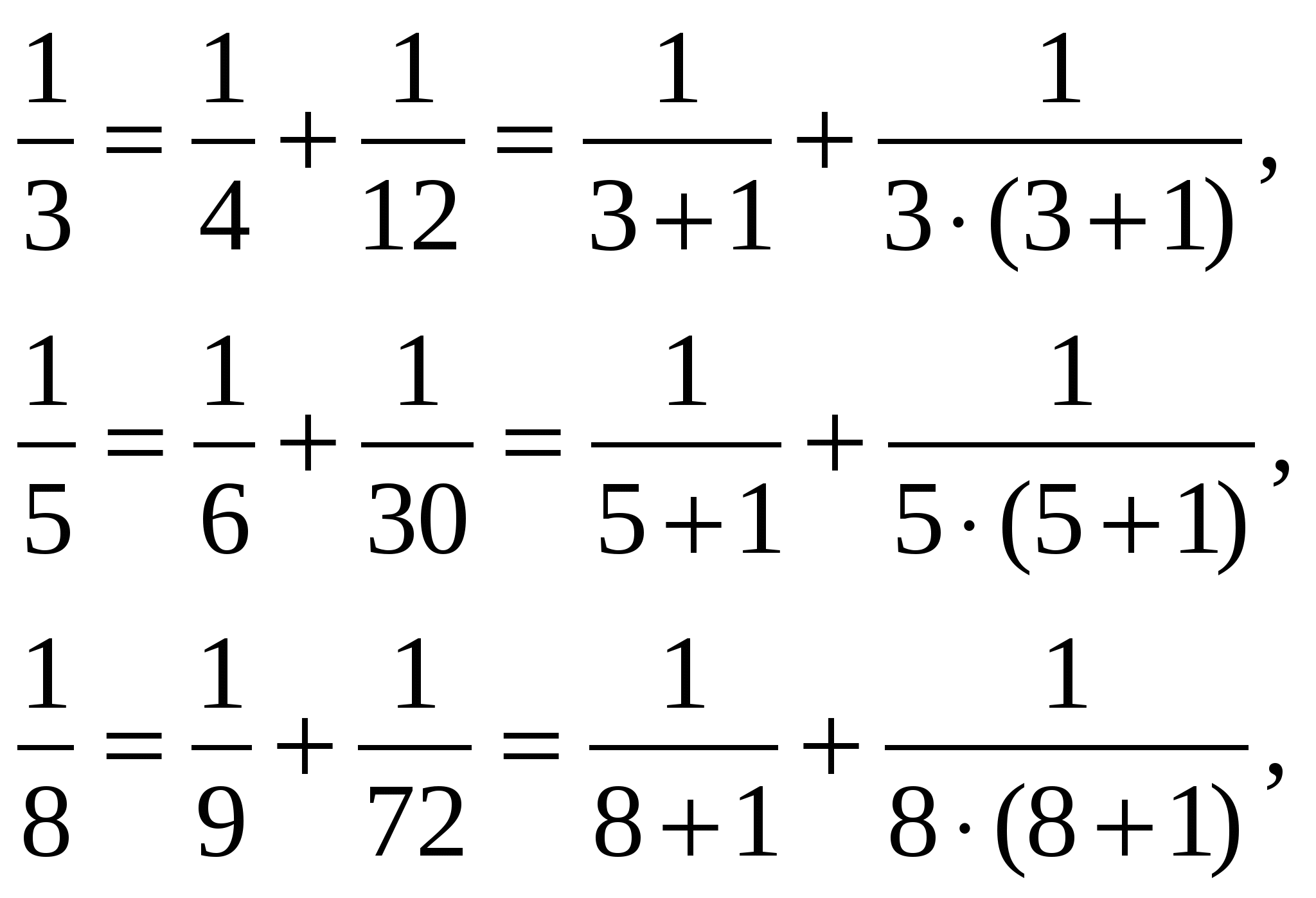
мы выявили закономерность, которую записали в виде формулы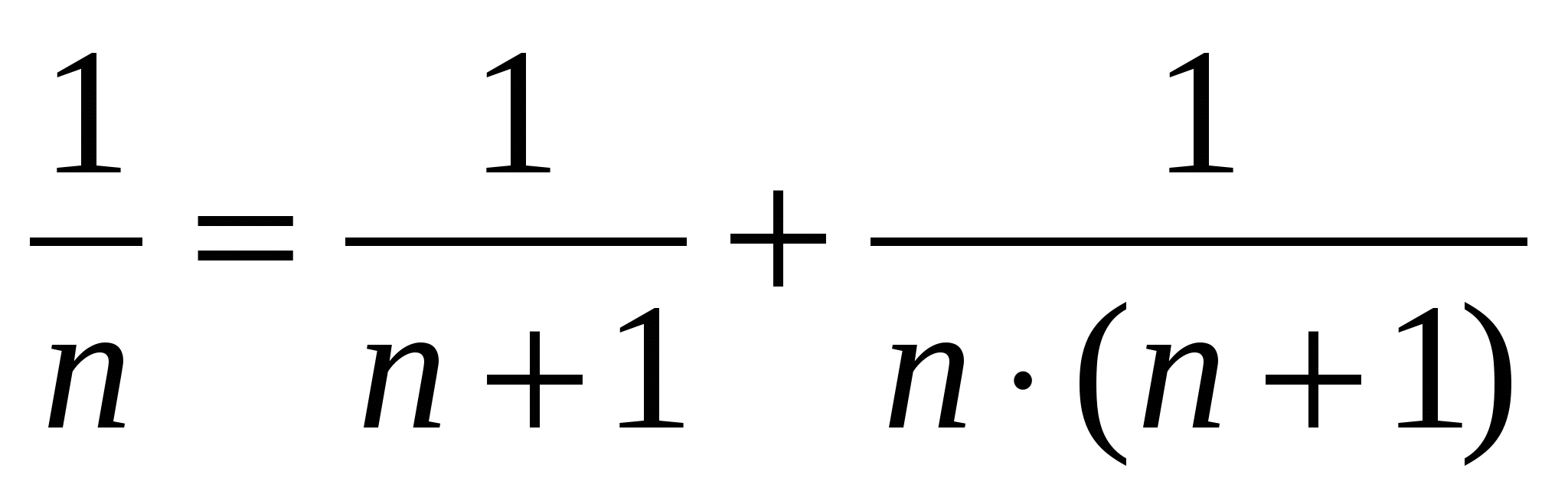
. Эта формула действует, если требуется разложение аликвотной дроби на две аликвотные дроби.
Докажем это равенство:
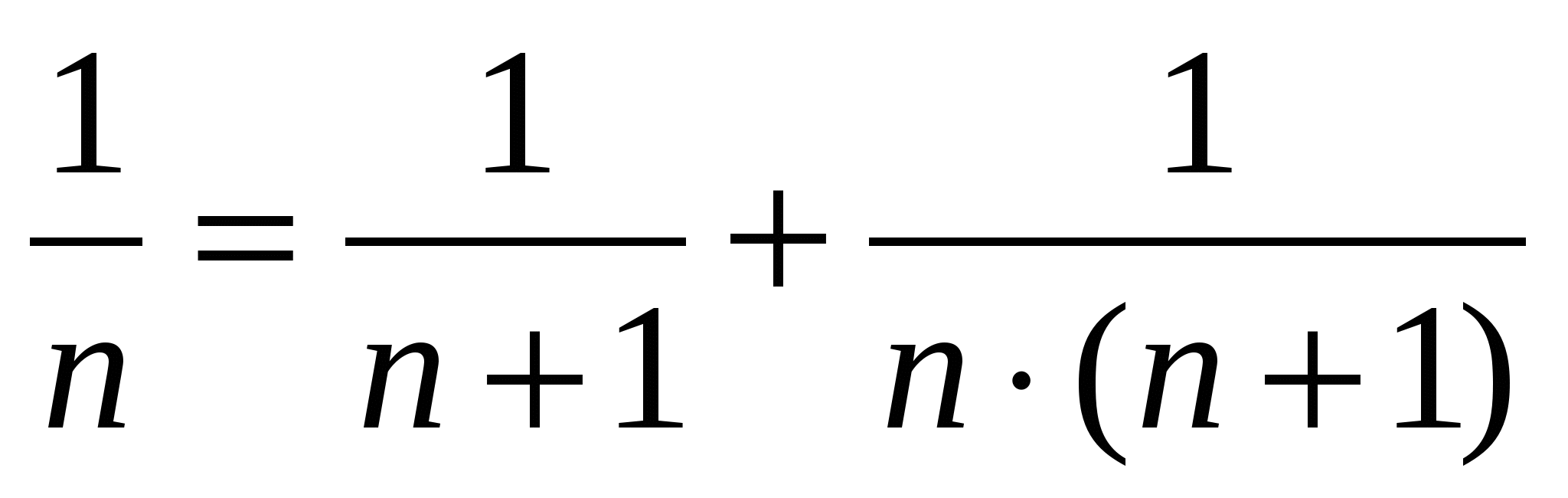(1)
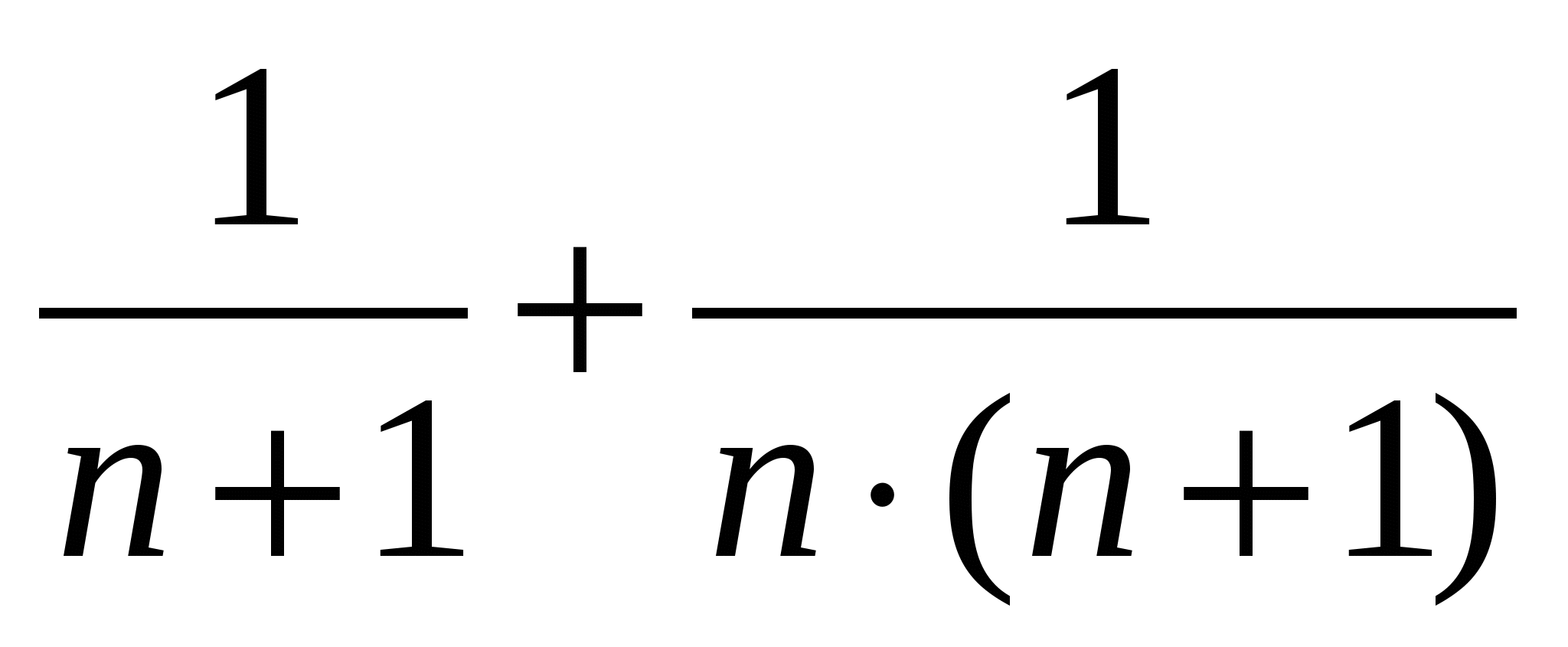, приведя дроби к общему знаменателю, получаем:
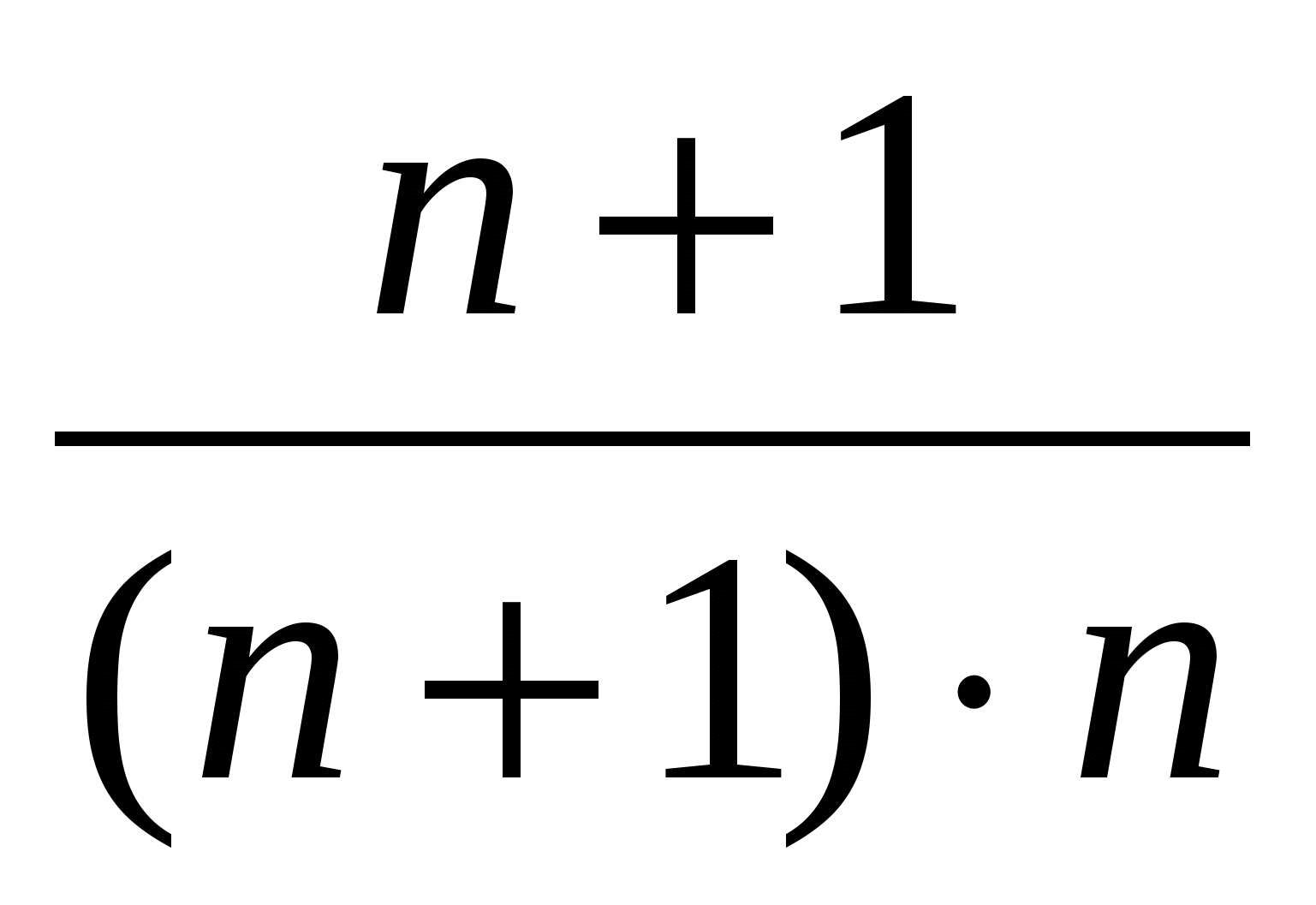после сокращения получаем .
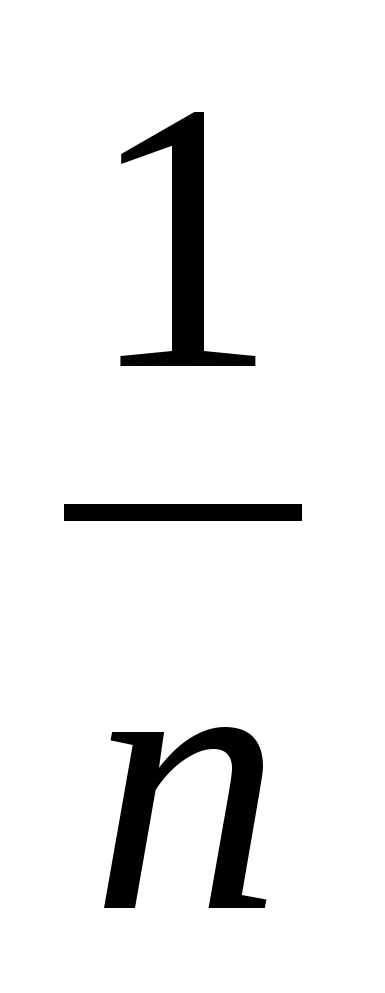Итак, получается, что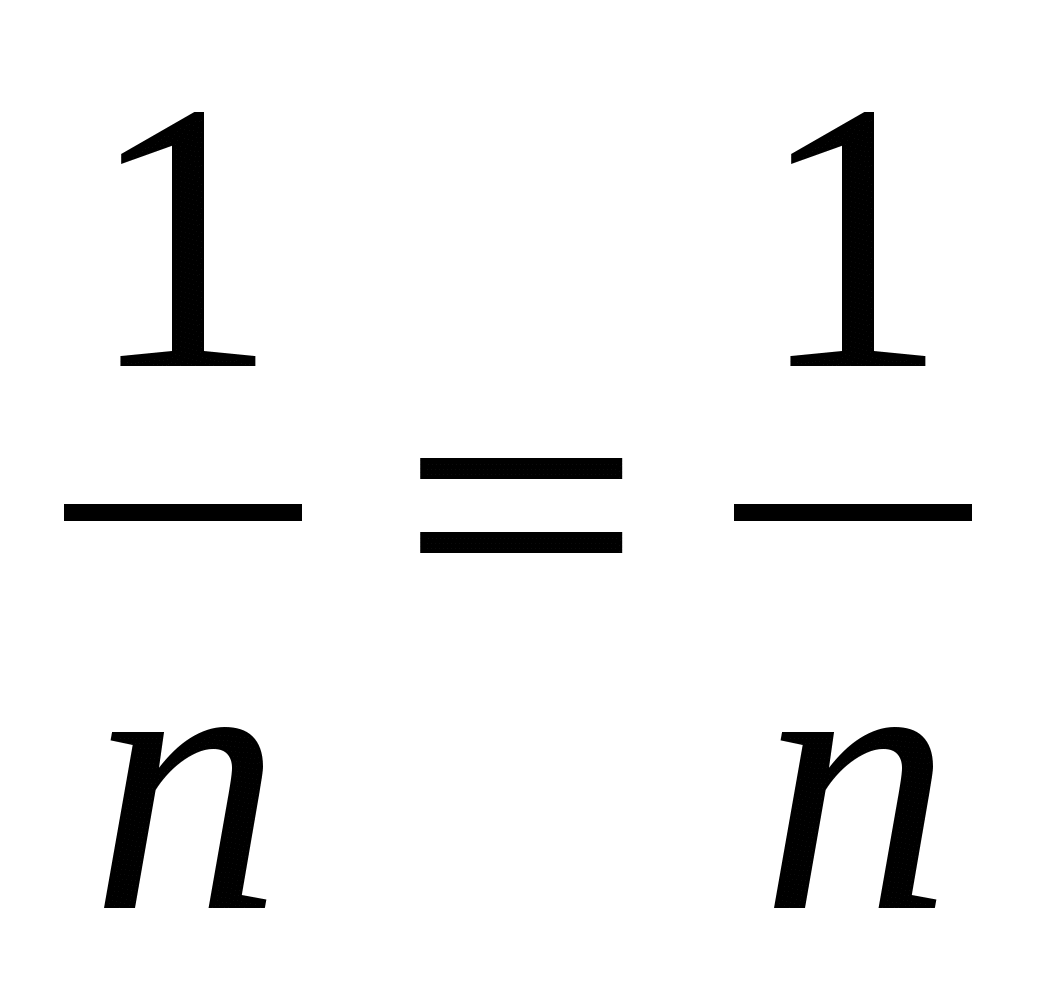 
. Наша формула верна.
Но если преобразовать нашу формулу, то получим следующее полезное равенство:
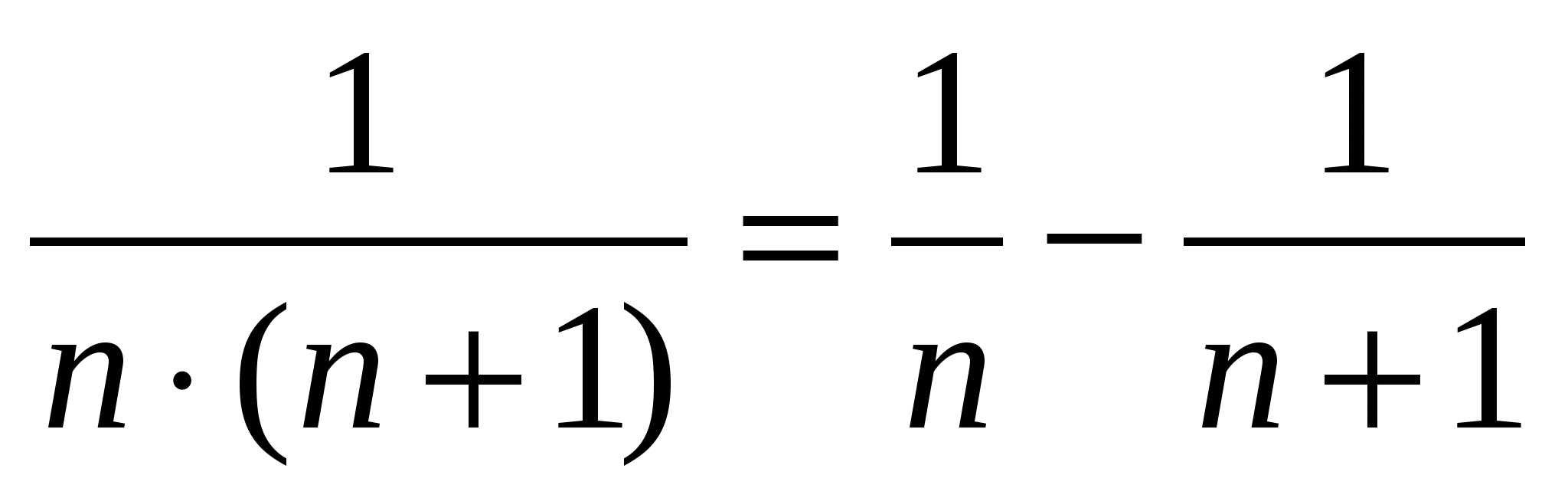. (2)
3 Решение задач
3.1 Решение задач из учебника
Простейшими задачами – разложение дроби на сумму аликвотных дробей. Эти разделить на две категории:
1. в знаменателе простое число,
2. в знаменателе составное число.
Рассмотрим решение задач первого типа:
Для того, чтобы выполнить это задание, нужно умножить числитель и знаменатель дроби на такое число, чтобы числитель получившейся дроби можно было разложить на слагаемые, каждый из которых будет делителем знаменателя (так как при сокращении в числители получится 1). После решения многих таких задач мы сделали вывод, что таким «удобным» числом является число 6.
.
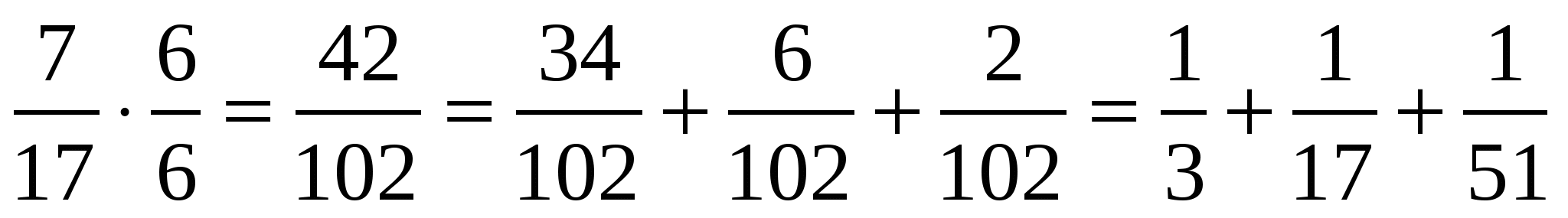Задачи второго типа также можно разделить на три вида:
1) числитель сразу можно предс2тавить в виде суммы делителей знаменателя, например
;
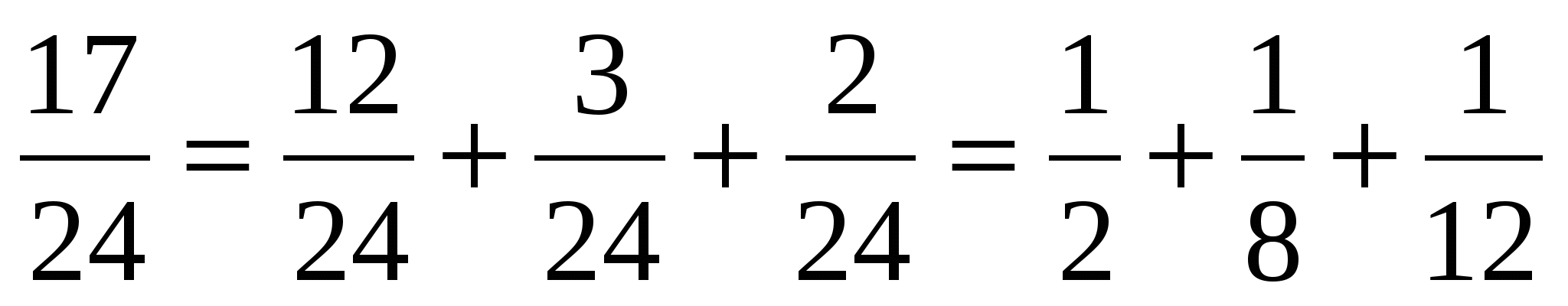2) в числителе число меньшее наименьшего делителя знаменателя:
решение совпадает с решением первого типа
;
3) числитель можно разложить на сумму чисел, среди которых есть как делители знаменателя, так и числа не являющиеся таковыми:
.
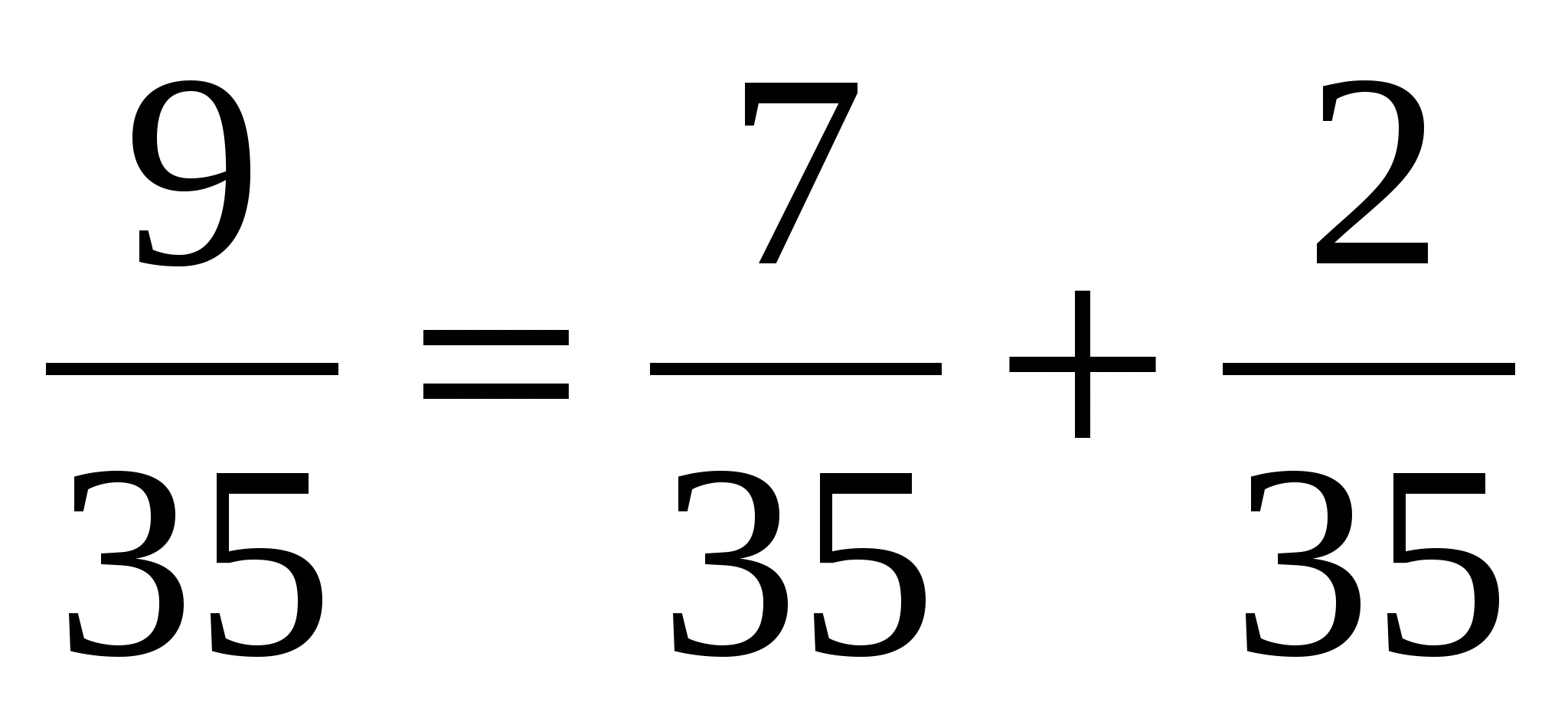Для того чтобы разложить дробь
на сумму аликвотных дробей, воспользуемся алгоритмом пункта 1.
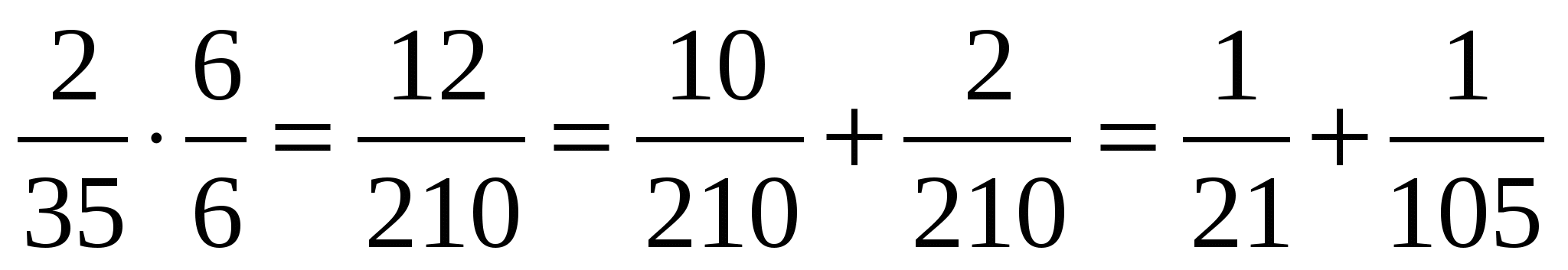
Тогда конечный результат будет таким: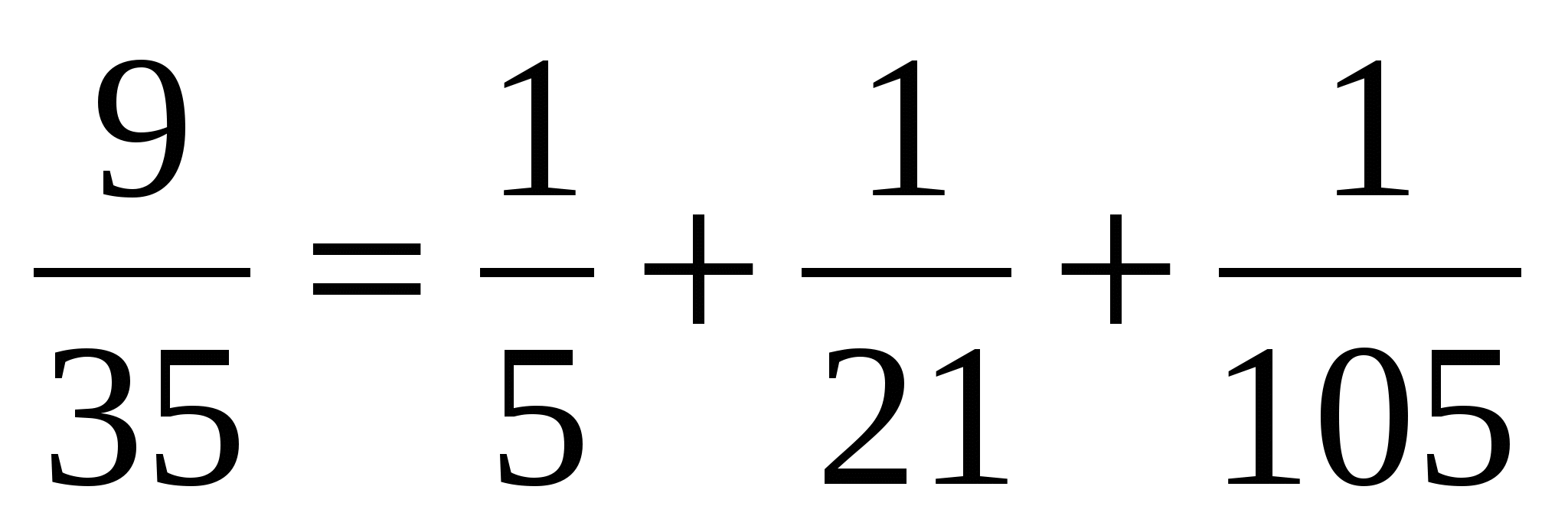 
.
К следующей разновидности задач, относятся задачи подобные задаче о 7 хлебах (рассмотренная выше). Приведем пример из учебника [2]:
№ 730. Олжас, Нуртас и Алмас купили 2 дыни. Как не разрезая каждую дыню на 3 доли, мальчики разделят их поровну?
Решение: По условию задачи 2 дыни нужно разделить на 3 равные части.
.
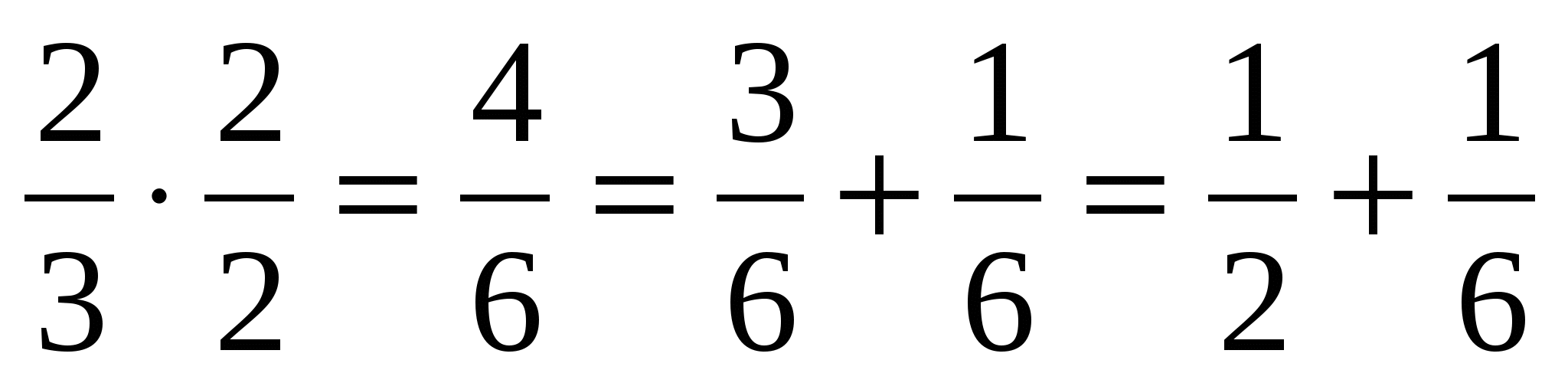Каждый мальчик взял по половинке дыни, а когда оставшуюся половину дыни разделили на три равные части, то каждый мальчик получил еще по 
дыни.
Ответ: половинка дыни и дыни.
Подобных задач можно придумать очень много. И над этим мы планируем поработать в дальнейшем. Рассмотрим одну из таких придуманных нами задач.
Задача.
3.2 Решение олимпиадных задач
1. Найдите сумму: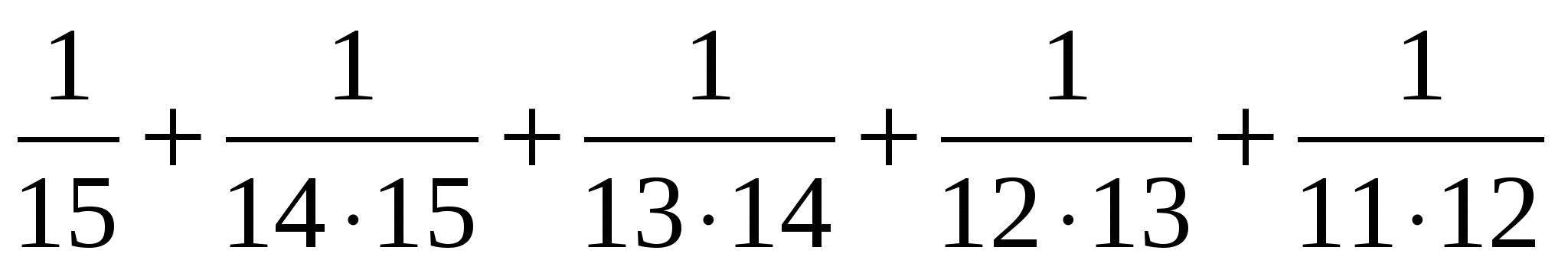 
.
Решение: Для решения воспользуемся формулой (2)
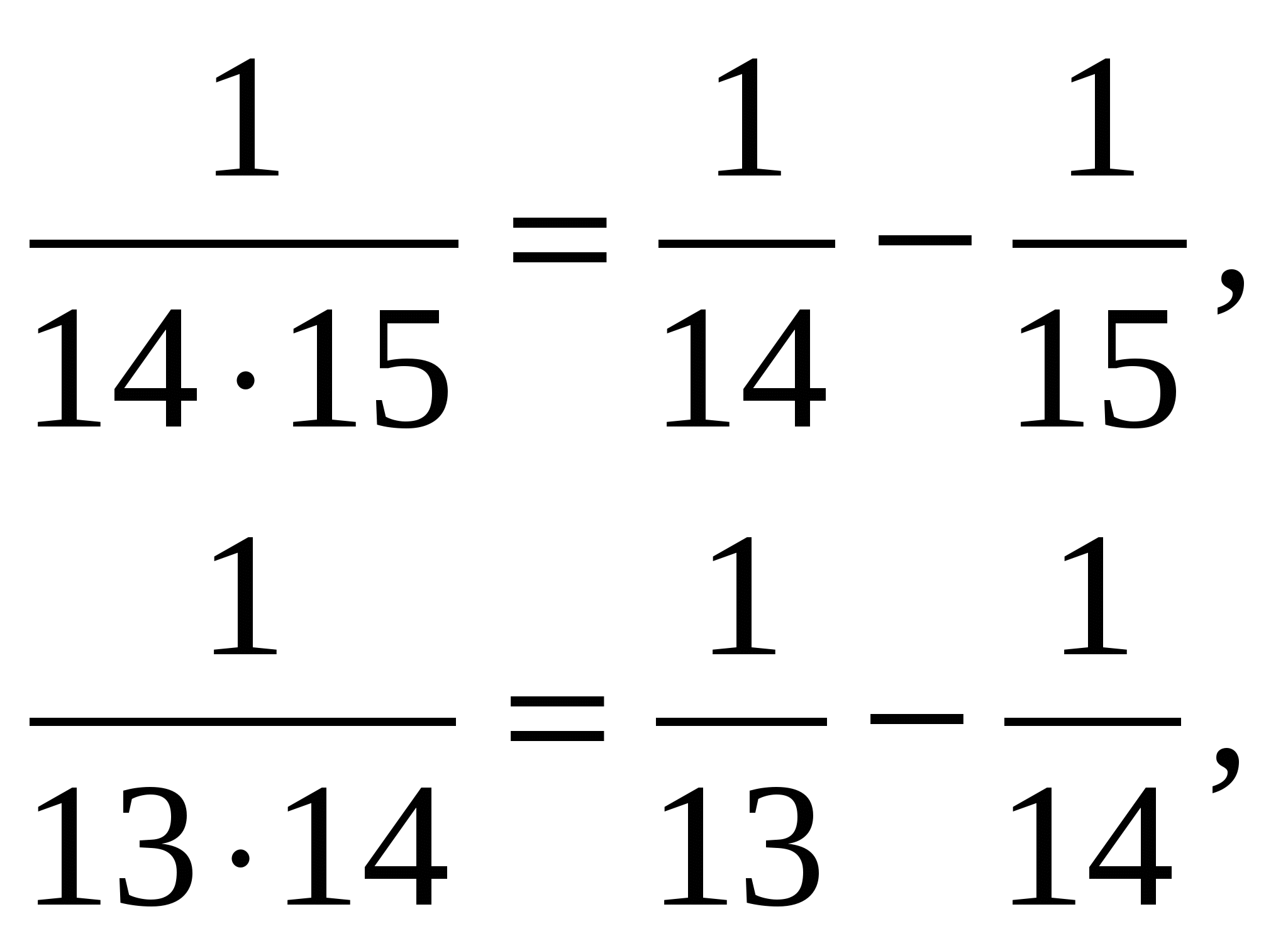
и т. д.
т. е. получим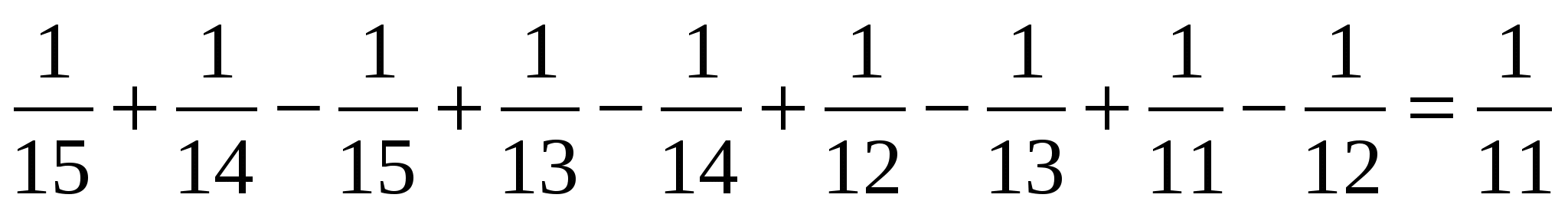 
.
2. Найти сумму: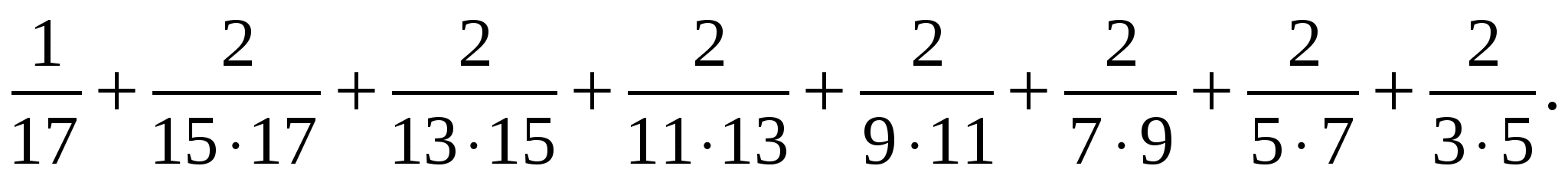 
Решение: Для решения воспользуемся решением предыдущей задачи.
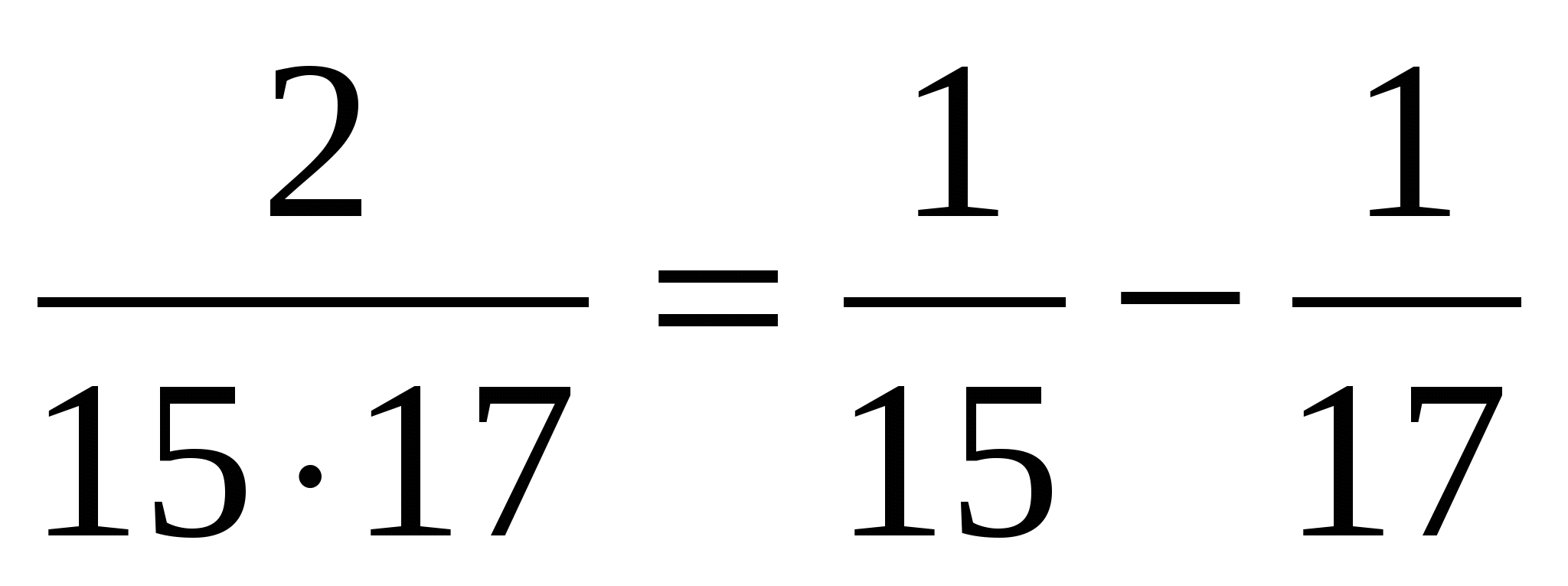, и т. д.
Рассуждая аналогично решению предыдущей задачи, получаем ответ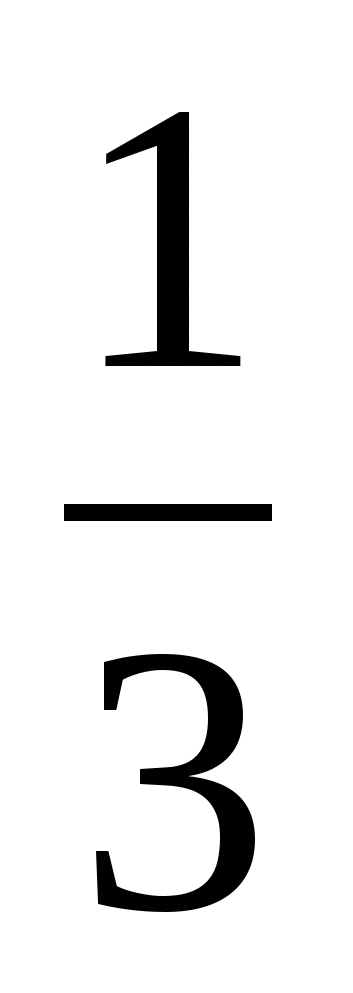 
.
4 Авторская задача
Хотим предложить свою задачу для решения в олимпиадах.
Чтобы узнать в каком году в Астане будет проводиться международная ярмарка EXPO нужно сумму аликвотных дробей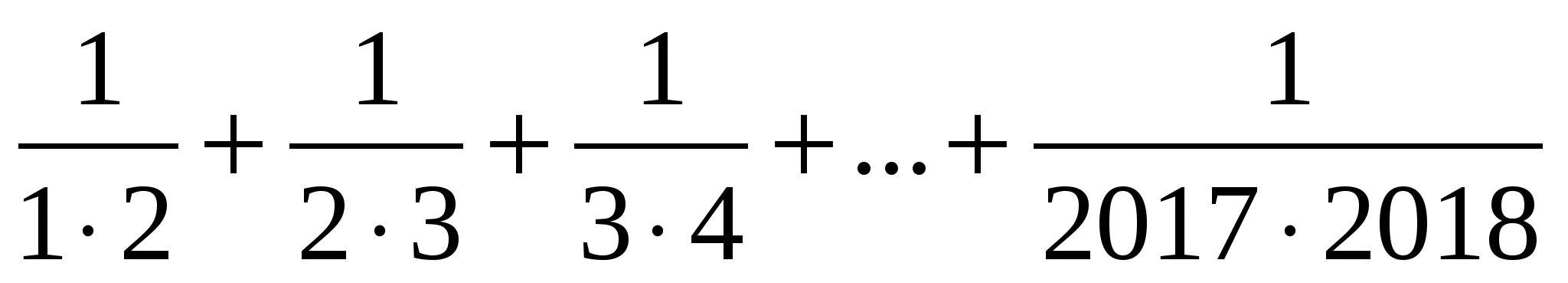 
умножить на год, когда Н. А. Назарбаеву исполнится лет.
Решение: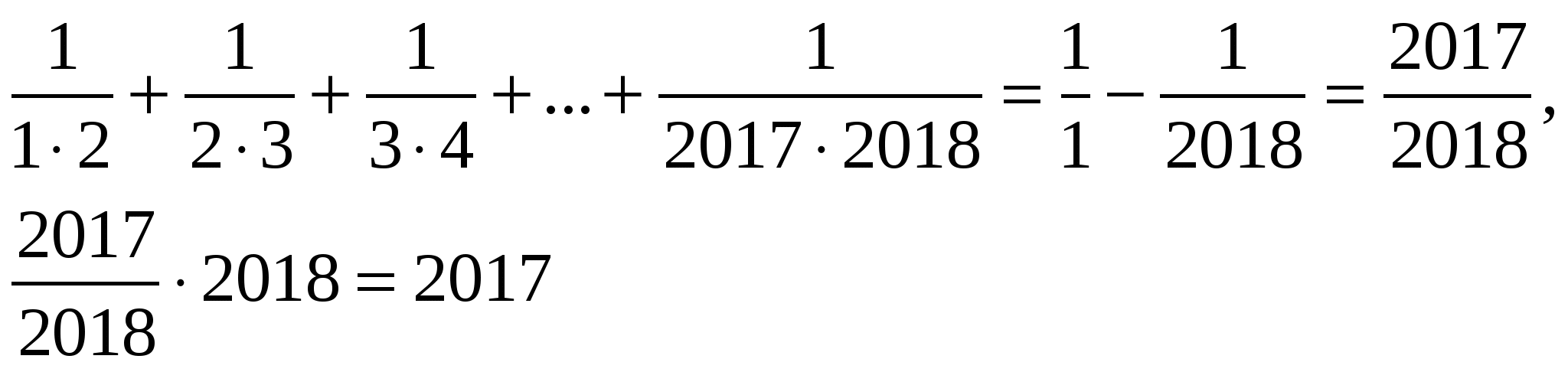 
Ответ: 2017 год.
Заключение
При разработке данной темы, мы узнали, что первыми дробями, которыми оперировали люди, были аликвотные дроби. Выяснили, что любая правильная дробь может быть разложено на единичные дроби. В современной математике вместо египетских дробей используются простые и десятичные дроби, однако египетские дроби продолжают изучаться в теории чисел и истории математики. Аликвотные дроби долгое время были единственными дробями, с которыми как-то умел оперировать человек, а правила действий с произвольными дробями разработаны «сравнительно недавно».
Задачи с использованием аликвотных дробей составляют обширный класс нестандартных задач. Аликвотные дроби используются тогда, когда требуется что-то разделить на несколько частей с наименьшим количеством действий для этого. Мы выяснили, что точного алгоритма решения подобных задач нет, но мы составили приближенный алгоритм решения для различных дробей. Мы рассмотрели решение некоторых олимпиадных задач, а также составили свою.
На этом работа над данной темой не заканчивается. Нам бы хотелось рассмотреть, как можно разложит любое рациональное число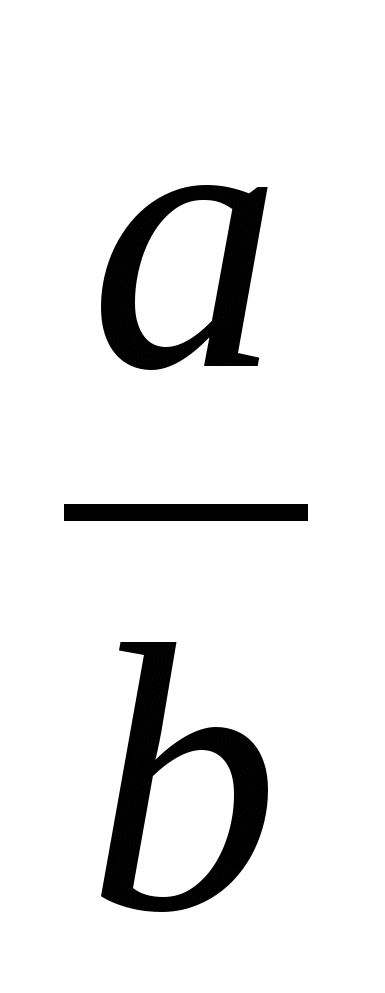 
. А так же составить сборник задач.
infourok.ru
Раменское (Раменский муниципальный район МО, Московская область)
Проектная работа на тему:
«Аликвотные дроби»
Выполнила ученица 7 класса «В»
МОУ СОШ 19
Строилова Валерия
Руководитель: учитель
Капин Артем Витальевич
Город Раменское 2017год
Объект исследования: аликвотные дроби
Цель исследования: выяснить, какое значение имеют аликвотные дроби в нашей жизни.
Задачи исследования:
Узнать происхождение аликвотных дробей.
Рассмотреть основные операции с аликвотными дробями.
Решать олимпиадные задачи с помощью аликвотных дробей.
Составлять и решать задачи практического содержания.
Методы исследования:
Анализ математической литературы по данной теме;
Отбор конкретных задач прикладного характера по данной теме;
Оглавление
Введение……………………………………………………………………4
История аликвотных дробей………………………………………4
1.1 Аликвотные дроби в Древнем Египте………………………5
1.2. Значение аликвотных дробей в истории………...…………6
Аликвотные струны……………………………………...………...7
Формулы аликвотных дробей. ……………………………………7
Открытые проблемы…………………………………….…………8
Решение задач ………………………………………….…………..8
5.1. Из учебника…………………………………….…………….8
5.2.Авторская задача……………………………….……………..9
Заключение …………………………………………………..……………10
Список литературы……………………………………………………….11
Введение
Тема «Аликвотные дроби» является интересной темой для исследования дробей. Столкнувшись с этим термином впервые, понимаешь, почему в Древнем Египте математики «настоящими» дробями считали только аликвотные дроби.
Почему же я выбрала эту тему? В седьмом классе наша любимая математика разделилась на составляющие, а именно Алгебру и Геометрию. Сначала мы в классе подразумевали эти два предмета как совершенно новые, но оказалось, что в алгебре изучается теория чисел, а в геометрии различные фигуры. И при решении разнообразных олимпиадных задач по алгебре, я пришла к выводу, что часть этих задач решается с использованием аликвотных дробей.
История аликвотных дробей
Аликвота - (лат. aliquoties, «несколько раз;несколько частей»)
Аликвотная дробь- дробь, числитель которой равен единице.
Аликвотные дроби начали использоваться ещё в древности. Необходимость в дробных числах возникла в результате практической деятельности человека. Потребность в нахождении долей единицы появилась у наших предков при дележе добычи после охоты. Второй существенной причиной появления дробных чисел следует считать измерение величин при помощи выбранной единицы измерения.
Первой дробью, с которой познакомились люди, была половина. Хотя названия всех следующих дробей связаны с названиями их знаменателей (три – «треть», четыре – «четверть» и т. д.), для половины это не так – ее название во всех языках не имеет ничего общего со словом «два». Следующей дробью была треть.
1.1 Аликвотные дроби в Древнем Египте
Аликвотные дроби появились раньше других дробей. В Древнем Египте математики “ настоящими “ считали только аликвотные дроби. Это дроби вида 1/n.
Египтяне все дроби записывали как суммы долей. Например: 8/15=1/3+1/5. Дроби 1/n ( где n - натуральные число ), которым египтяне отдавали предпочтение, в современной математике именуются аликвотными ( от латинского aliguot- " несколько''). То есть аликвотными дробями называются дроби с числителем 1. И даже сами аликвотные дроби они часто стремились представить в виде суммы меньших аликвотных дробей. Например,
1/2=1/3+1/6, 1/4=1/5+1/20
Египтяне ставили иероглиф «Глаз Хора» - единица для измерения ёмкостей и объемов,
представляла собой дробь 
, так как согласно мифам глаз Хора был выбит, а затем восстановлен на . Каждая часть глаза соответствовала определённой дроби и была представлена в виде суммы аликвотных дробей таким образом: 
+ 
+ 
+ 
+ 
+ 
= .
Причиной появления этих дробей являлась необходимость разбить единицу на доли. Это нужно было для того:
1. чтобы разделить добычу после охоты, ведь, нужно было знать, сколько частей составляет целое и кому какая часть добычи станет принадлежать.
2. чтобы поделить основную меру объёма в Древнем Египте - «хекат».
Египетская дробь — в математике сумма нескольких аликвотных дробей вида 1/n. Другими словами, каждая дробь суммы имеет числитель, равный единице, и знаменатель, представляющий собой натуральное число.
Пример : ½ +1/3+1/16.
Египетская дробь представляет собой положительное вида a/b; к примеру, египетская дробь, записанная выше, может быть записана в виде дроби 43/48. Можно показать, что каждое положительное рациональное число может быть представлено в виде египетской дроби. Важную работу по исследованию египетских дробей провёл математик XIII века Фибоначчи в своём труде «Liber Abaci» - это вычисления, использующие десятичные и обычные дроби, вытеснившие со временем египетские дроби. Фибоначчи использовал сложную запись дробей, включавшую запись чисел со смешанным основанием и запись в виде сумм дробей, часто использовались и египетские дроби. Также в книге были приведены алгоритмы перевода из обычных дробей в египетские.
1.2. Значение аликвотных дробей в истории
Основная мысль Алгоритма Фибоначчи
Первый дошедший до нас общий метод разложения произвольной дроби на египетские составляющие описал Фибоначчи в XIII веке. В современной записи его алгоритм можно изложить следующим образом.
1. Дробь разлагается на 2 слагаемых:
Здесь — частное от деления n на m, округлённое до целого в бо́льшую сторону, а — (положительный) остаток от деления -n на m.
2. Первое слагаемое в правой части уже имеет вид египетской дроби. Из формулы видно, что числитель второго слагаемого строго меньше, чем у исходной дроби. Аналогично, по той же формуле, разложим второе слагаемое и продолжим этот процесс, пока не получим слагаемое с числителем 1.
Метод Фибоначчи всегда сходится после конечного числа шагов и даёт искомое разложение. Пример:
Однако полученное таким методом разложение может оказаться не самым коротким. Пример его неудачного применения: в то время как более совершенные алгоритмы приводят к разложению:
Новейшее время
Современные математики продолжают исследовать ряд задач, связанных с египетскими дробями и достигли больших успехов в этом направлении.
Аликвотные струны
Аликвотные дроби применятся и в жизни. В ходе работы я узнала, что бывают аликвотные струны, чаще всего их называют резонансовыми струнами. Это дополнительные струны, к которым исполнитель не прикасается во время игры. Резонансовые струны само возбуждаются от колебания игровых струн, служат для усиления их звучания и для обогащения тембровых возможностей инструмента. Эти струны размещаются под грифом, сбоку или под игровыми струнами. Встречаются у многих индийских инструментов, у хардингфеле, у некоторых виолончелей.
Формулы аликвотных дробей.
Чтобы представить какое либо число в виде суммы аликвотных дробей, порой приходится проявлять, незаурядную изобретательность. Скажем, число 2/43 выражается так: 2/43= 1/42 +1/86 +1/129 +1/301.Производить арифметические действия над числами, раскладывая их в сумму долей единицы, очень неудобно.
Поэтому в процессе решения задач для разложения аликвотных дробей в виде суммы меньших аликвотных дробей возникла идея систематизировать разложение дробей в виде формулы. Эта формула действует, если требуется разложение аликвотной дроби на две аликвотные дроби.
Формула выглядит следующим образом:
1/n=(1/(n+1)) +(1/n*(n+1))
Но если преобразовать нашу формулу, то получим следующее полезное равенство:
1/(n*(n+1))=1/n -1/(n+1)
Т.е. аликвотную дробь можно представить разностью двух аликвотных дробей, или разность двух аликвотных, знаменателями которых, являются последовательные числа равна их произведению.
Вернемся к формуле и докажем это равенство:
1/n=(1/(n+1)) +(1/n*(n+1))
(1/(n+1)) +(1/n*(n+1)) , приведя дроби к общему знаменателю, получаем:
( n+1 )/((n+1)*n) после сокращения получаем: 1/n.
Итак, получается, что 1/n=1/n. Наша формула верна.
Открытые проблемы
Гипотеза Эрдёша-Страуса утверждает , что для всякого целого числа
n ≥ 2, существуют положительные целые x, y и z такие, что
4/n=1/x+ 1/y+ 1/z
Компьютерные эксперименты показывают, что гипотеза верна для всех n ≤ 1014, но доказательство пока не найдено. Обобщение этой гипотезы утверждает, что для всякого положительного k существует N такое, что для всех n ≥ N существует разложение
k/n=1/x+1/y+1/z
Решение задач
Из учебника
Из математического сборника олимпиады, я нашла интересную задачу, в которой требуются знания по аликвотным дробям.
Петя тратит 1/3 часть своего времени на занятия в школе, ¼ часть – на игру футбол, 1/5 – на прослушивание пластинок, 1/6 – на телевизор, 1/7 – на решение задач по математике. Можно ли так жить?
Разделить 7 хлебов между 8 людьми. Если разрезать каждый хлеб на 8 частей, придется провести 49 разрезов. А по-египетски эта задача решалась так: 7/8= 1/2 +1/4 +1/8. Значит, каждому человеку нужно дать полхлеба, четверть хлеба и восьмушку хлеба. Придется сделать почти в три раза меньше разрезов.
Авторская задача
В рамках подготовки к участию по проектной работе на тему «аликвотные дроби», авторскую задачу я связала именно с этим числом.
Чтобы узнать в каком году Фибоначчи со дня рождения исполнится 845 лет, нужно сумму аликвотных дробей 1/(1*2)+1/(2*3)+1(3*4)+…+1(1169*1170)+1(1170*1171) умножить на число, когда Фибоначчи исполнилось 1 год, если он родился в 1170 году, и
прибавить возраст Фибоначчи.
Решение: 1/(1*2)+1/(2*3)+1(3*4)+…+1(1169*1170)+1(1170*1171) = 1170/1171*1171+845=2015
Ответ: Фибоначчи в 2015 году исполняется 845 лет.
Заключение
Таким образом, при разработке данной темы, я узнала, что первыми дробями, которыми оперировали люди, были аликвотные дроби.
Задачи с использованием аликвотных дробей составляют обширный класс нестандартных задач. Аликвотные дроби используются тогда, когда требуется что-то разделить на несколько частей с наименьшим количеством действий для этого.
Разложение дробей на две аликвотные дроби систематизировали в виде формулы, преобразовав которую, легко решили олимпиадные задачи по математике разных лет.
Решив проблему разложения аликвотных дробей на две аликвотные дроби, мы пришли к выводу, что разложение на три, четыре, пять и т.д. аликвотных дробей можно произвести , разложив одно из слагаемых на две дроби, следующее слагаемое еще на две аликвотные дроби и т.д.
Таким образом, аликвотные дроби (с числителем 1) долгое время были единственными дробями, с которыми как-то умел оперировать человек. И я считаю, что на эти дроби в школьном курсе нужно обращать как можно больше внимания, ведь в учебниках даже нет понятия «аликвотные дроби». С Древних времен тема «Дроби» считалась одной из самых сложных, поэтому, когда человек попадал в трудное положение, говорили «Попал в дроби». Для того чтобы не в жизни у вас все получалось, нужно знать и изучать дроби! Спасибо за внимание!
Список литературы
Энциклопедический словарь юного математика для среднего и старшего школьного возраста. М.: Педагогика,1989.
Левитас Г. Г. Нестандартные задачи по математике.– М.: ИЛЕКСА,2007.
Баженов И.И., Порошкин А.Г. и др. Задачи для школьных математических кружков. Сыктывкар, 1994.
Гаврилова Т. Д. «Занимательная математика». 5-11класс. Волгоград: Учитель, 2008.
Фарков А. В. Математические олимпиады в школе. 5-11класс. – М.: Айрис-пресс, 2005.
Петерсон Л. Г. Математика. 5класс. – М.:Ювента, 2009.
Приложение
Задачи из журнала «Квант». Решение задач.
Представить число 1 в виде сумм различных аликвотных дробей
А) трёх слагаемых:
1 = 
.
Б) четырёх слагаемых:
1 = = 
.
В) пяти слагаемых:
1 = = 
+ 
+ 
.
Г) шести слагаемых:
1 = = + + = 
+ 
Представьте дробь 
в виде аликвотных дробей.
Существует 2 способа представления дроби в виде суммы и один - в виде разности аликвотных дробей. Это, опять-таки, из-за простоты числа 2011.
3. Верно ли равенство?
Равенство верно.
4. Верно ли равенство?
Равенство верно.
5. Верно ли равенство?
Равенство верно.
6. Решить пример.
compedu.ru
1.Введение
Необходимость в дробных числах возникла в результате практической деятельности человека. Потребность в нахождении долей единицы появилась наших предков при дележе добычи после охоты. Второй существенной причиной появления дробных чисел следует считать измерение величин при помощи выбранной единицы измерения.
Первой дробью, с которой познакомились люди, была половина. Хотя названия всех следующих дробей связаны с названиями их знаменателей (три – «треть», четыре – «четверть» и т. д.), для половины это не так – ее название во всех языках не имеет ничего общего со словом «два». Следующей дробью была треть.
Таким образом, первые дроби, с которыми нас знакомит история, это дроби вида – – так называемые единичные дроби или аликвотные (от лат. aliquot – «несколько»).
Единичные дроби встречаются в древнейших дошедших до нас математических текстах, составленных более 5000 лет тому назад, – древнеегипетских папирусах и вавилонских клинописных табличках. Египетская дробь — в ìатематике сумма нескольких äрîбей вида (так называемых аликвотных дробей). Другими словами, каждая дробь суммы имеет ÷ислитель, равный единице, и çнаменатель, представляющий собой íаòуральное число.
Пример: .
Египетская дробь представляет собой положительное ðаöиональное число вида a/b; к примеру, египетская дробь, записанная выше, может быть записана в виде дроби 43/48. Можно показать, что каждое положительное рациональное число может быть представлено в виде египетской дроби. Сумма такого типа использовалась ìатематиками, как определение, для дробей начиная со времён äрåвнего Египта до ñредневековья.
Задачи с использованием в решении аликвотных дробей составляют обширный класс нестандартных задач. Сюда относятся, прежде, всего, задачи, в которых требуется разделить какие либо ресурсы на несколько частей с наименьшим количеством действий для этого.
Цель исследования:
Выяснить, какое значение имеют аликвотные дроби в нашей жизни
Задачи исследования:
Узнать происхождение аликвотных дробей.
Рассмотреть основные операции с аликвотными дробями.
Решать олимпиадные задачи с помощью аликвотных дробей.
Составлять и решать задачи практического содержания.
2.Основная часть. Происхождение аликвотных дробей.
Тема «Аликвотные дроби» является интересной темой для исследования дробей. Столкнувшись с этим термином впервые, понимаешь, почему в Древнем Египте математики «настоящими» дробями считали только аликвотные дроби.
Итак, Египтяне все дроби записывали как суммы долей, то есть дробей вида 1/n. Например: 8/15=1/3+1/5. Дроби 1/n ( где n - натуральные число ), которым египтяне отдавали предпочтение, в современной математике именуются аликвотными ( от латинского aliguot- " несколько''). То есть аликвотными дробями называются дроби с числителем 1. И даже сами аликвотные дроби они часто стремились представить в виде суммы меньших аликвотных дробей. Например,
1/2=1/3+1/6, 1/4=1/5+1/20
Åгиптяне ставили èеðоглиф «Глаз Хора»
Такие дроби использовались вместе с другими формами записи египетских дробей для того, чтобы поделить «хекат», основную меру объёма в Древнем Египте, т.е.аликвотные дроби нужны были египтянам в практических целях.
Рассмотрим такую задачу: ,,Разделить 7 хлебов между 8 людьми.,, Если разрезать каждый хлеб на 8 частей, придется провести 49 разрезов. А по-египетски эта задача решалась так: 7/8= 1/2 +1/4 +1/8. Значит, каждому человеку дать полхлеба, четверть хлеба и восьмушку хлеба. Придется сделать почти в три раза меньше разрезов.
Египетские дроби продолжались использоваться в древней Греции и впоследствии математиками всего мира до средних веков, несмотря на имеющиеся к ним замечания древних математиков . К примеру, Клавдий Птолемей говорил о неудобстве использования египетских дробей по сравнению с Вавилонской системой(позиционная система исчисления)
Важную работу по исследованию египетских дробей провёл математик XIII века Фибоначчи в своём труде «Liber Abaci» - это
вычисления, использующие десятичные и обычные дроби, вытеснившие со временем египетские дроби. Фибоначчи использовал сложную запись дробей, включавшую запись чисел со смешанным основанием и запись в виде сумм дробей, часто использовались и египетские дроби. Также в книге были приведены алгоритмы перевода из обычных дробей в египетские.
2.2 Основные операции над аликвотными дробями
Чтобы представить какое либо число в виде суммы аликвотных дробей, порой приходится проявлять, незаурядную изобретательность. Скажем, число 2/43 выражается так: 2/43= 1/42 +1/86 +1/129 +1/301.Производить арифметические действия над числами, раскладывая их в сумму долей единицы, очень неудобно.
Поэтому в процессе решения задач для разложения аликвотных дробей в виде суммы меньших аликвотных дробей возникла идея систематизировать разложение дробей в виде формулы. Эта формула действует, если требуется разложение аликвотной дроби на две аликвотные дроби.
Формула выглядит следующим образом:
1/n=(1/(n+1)) +(1/n*(n+1))
Примеры разложения дробей:
1/3=1/(3+1)+1/3*(3+1)=1/4 +1/12;
1/5=1/(5+1)+1/5*(5+1)=1/6 +1/30;
1/8=1/(8+1)+1/8*(8+1)=1/9+ 1/72.
Но если преобразовать нашу формулу, то получим следующее полезное равенство:
1/(n*(n+1))=1/n -1/(n+1)
1/6=1/(2*3)=1/2 -1/3
½=1/(1*2)=1/1 -1/2
Т.е. аликвотную дробь можно представить разностью двух аликвотных дробей, или разность двух аликвотных, знаменателями которых являются последовательные числа равна их произведению.
Вернемся к формуле и докажем это равенство:
1/n=(1/(n+1)) +(1/n*(n+1))
(1/(n+1)) +(1/n*(n+1)) , приведя дроби к общему знаменателю, получаем:
( n+1 )/((n+1)*n) после сокращения получаем:
1/n.
Итак, получается, что 1/n=1/n. Наша формула верна.
Но мы пойдем дальше, и на основании разности аликвотных дробей решим, на первый взгляд, трудноразрешимую для обычного человека задачу:
1/2+1/(2*3)+1/(3*4)+1/(4*5)+…….+1/(19*20) =????
Воспользуемся нашей формулой для разложения аликвотной дроби в виде разности:
½=1/(1*2)=1/1 -1/2
1/6=1/(2*3)=1/2-1/3
1/12=1/(3*4)=1/3-1/4
1/20=1/(4*5)=1/4-1/5 и т.д.
Подставив, уже разложенные выражения в наш пример, получаем:
1/1-1/2+1/2-1/3+1/3-1/4+1/4-1/5……..+1/19-1/19-1/20=1/1-1/20=19/20.
Мы представили формулу, как удобство при разложении аликвотной дроби на 2 слагаемых. При разложении 1 на два слагаемых получается:
1=1/2+1/2 (Наша формула действует!). Чтобы разложить 1 на 3 слагаемых, мы возьмем одну аликвотную дробь и по формуле разложим ее еще на две аликвотные дроби:
½=1/3+1/6 =½=1/3+1/6 => 1=1/2+1/3+1/6;
Чтобы разделить на 4 слагаемых, делим еще одну дробь на две аликвотные дроби:
1/3=1/4+1/12 => 1=1/2+1/4+1/12+1/6;
На 5 слагаемых: 1/6=1/7+1/42 => 1=1/2+1/4+1/12+1/7+1/42.
2.3 Решение задач из учебника
2.3.1.Представить число 1 в виде сумм различных аликвотных дробей
А) трех слагаемых
1=1/2+1/2=1/2+(1/3+1/6)=1/2+1/3+1/6
Б) четырех слагаемых
1=1/2+1/2=1/2+(1/3+1/6)=1/2+1/3+1/6=1/2+1/3+(1/7+1/42)= 1/2+1/3+1/7+1/42
B) 5-и слагаемых
1=1/2+1/2=1/2+(1/3+1/6)=1/2+1/3+1/6=1/2+1/3+(1/7+1/42)=
1/2+1/3+1/7+1/42=1/2+(1/4+1/12) +1/7+1/42=
1/2+1/4+1/12 +1/7+1/42
2.3.2.Митя обнаружил, что 1/n часть класса написала работу лучше него, а 1/(n-1) часть класса – хуже него. Сколько учеников в классе?
Если 1/n написало лучше, а 1/(n-1) хуже. В идеале никто не написал работу также как и он, но с таким же результатом могло быть и большее количество учеников.
За нескольких сказать ничего не могу, а за одного: Мы можем взять число всех учеников классе за 1. И тогда получается что мы должны разложить число 1 на 3-и аликвотные дроби.
1=1/n+1/(n-1)+1/x
1/x=1/n*(n-1) тогда получается что в классе n*(n-1) учеников.
1=1/(n-1)+1/n+1/(n*(n-1))
Методом подбора мы видим что 1 раскладывается на аликвотные дроби только следующим образом :
1=1/2+1/2=1/2+1/3+1/6 во всех других случаях мы не сможем получить из суммы других аликвотных дробей 1.
Так что, в случае , если он один написал работу с таким результатом, можно утверждать, что в классе 6 человек.
А если таких учеников было несколько, то задача имеет множество решений.
1/x=(n*(n-1)-n –n+1)/(n*(n-1))
2.4 Решение олимпиадных задач
2.4.1.Найди сумму
1/(10*11)+1/(11*12)+…+1/(98*99)+1/(99*100)=?
Чтобы найти решение данной задачи необходимо найти сумму
1/(1*2)+1/(2*3)+…+1/(98*99)+1/(99*100)=99/100
И вычесть из нее сумму
1/(1*2)+1/(2*3)+…+1/(8*9)+1/(9*10)=9/10
99/100-9/10=(99-90)/100=9/100=0.09
2.4.2.Найти сумму
½+1/6+1/12+1/20+1/30+1/42+1/56+1/72+1/90=
1, b) 10/11, c) 4/5, d) 8/9, e) 9/10
1/(1*2)+1/(2*3)+1/(3*4)+1/(5*6)+1/(6*7)+1/(7*8)+1/(8*9)+1/(9*10) =9/10
Ответ e)
2.5 Авторская задача
Чтобы узнать в каком году в Казани будет проводиться Универсиада нужно сумму аликвотных дробей
1/(1*2)+1/(2*3)+1/(3*4)+…+1/(2013*2014) умножить на год проведения зимних олимпийских игр в городе Сочи.
Решение :
1/(1*2)+1/(2*3)+1/(3*4)+…+1/(2013*2014)=2013/2014
2013/2014 * 2014 = 2013
Ответ : Универсиада будет проводиться в 2013 году.
3.Заключение.
Таким образом, при разработке данной темы, мы узнали, что первыми дробями, которыми оперировали люди, были аликвотные дроби. Выяснили, что каждое рациональное число вида a/b может быть разложено на единичные дроби.
Задачи с использованием аликвотных дробей составляют обширный класс нестандартных задач. Аликвотные дроби используются тогда, когда требуется что-то разделить на несколько частей с наименьшим количеством действий для этого.
Разложение дробей на две аликвотные дроби систематизировали в виде формулы, преобразовав которую, легко решили олимпиадные задачи по математике разных лет.
Решив проблему разложения аликвотных дробей на две аликвотные дроби, мы пришли к выводу, что разложение на три, четыре, пять и т.д. аликвотных дробей можно произвести , разложив одно из слагаемых на две дроби, следующее слагаемое еще на две аликвотные дроби и т.д.
Таким образом, аликвотные дроби (с числителем 1) долгое время были единственными дробями, с которыми как-то умел оперировать человек, а правила действий с произвольными дробями разработаны «сравнительно недавно».
В современной математике вместо египетских дробей используются простые и äеñятичные дроби, однако египетские дроби продолжают изучаться в òеîрии чисел и èсòории математики.
4.Используемая литература:
Энциклопедический словарь юного математика для среднего и старшего школьного возраста. М.: Педагогика,1989.
Левитас Г. Г. Нестандартные задачи по математике.– М.: ИЛЕКСА,2007.
Баженов И.И., Порошкин А.Г. и др. Задачи для школьных математических кружков. Сыктывкар, 1994.
Гаврилова Т. Д. «Занимательная математика». 5-11класс. Волгоград: Учитель, 2008.
Фарков А. В. Математические олимпиады в школе. 5-11класс. – М.: Айрис-пресс, 2005.
Петерсон Л. Г. Математика. 5класс. – М.:Ювента, 2009.
cendomzn.ucoz.ru
