
 Контрольная работа по теме: Тригонометрические функции
Контрольная работа по теме: Тригонометрические функции 
 Контрольная работа по теме: Тригонометрические функции
Контрольная работа по теме: Тригонометрические функции
Вариант 1
№1. Вычислите :
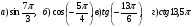 .
.
№2. Решите уравнение: 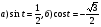 .
.
№3. Найдите заданную точку на числовой окружности: 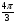 ,
, 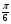 ; -3,5; 240˚,180˚
; -3,5; 240˚,180˚
№4. Известно, что 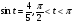 . Вычислите:
. Вычислите: 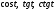 .
.
№5. Решить однородное уравнение первой степени:
а) 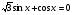 ; б)
; б) 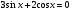 .
.
№6. Решить однородное уравнение второй степени:
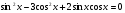 .
.
№7. Вычислите 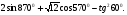
№8. Упростите выражение: 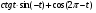
Контрольная работа по теме: Тригонометрические функции
Вариант 2
№1. Вычислите:
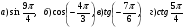
№2. Решите уравнение: 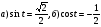 .
.
№3 Найдите заданную точку на числовой окружности: 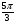 ,
, 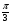 ; -1,5; 340˚,270˚
; -1,5; 340˚,270˚
№4. Известно, что 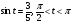 . Вычислите:
. Вычислите: 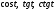 .
.
№5. . Решить однородное уравнение первой степени:
а) 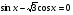 ; б)
; б) 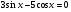 .
.
№6. Решить однородное уравнение второй степени:
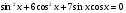 .
.
№7. Вычислите: 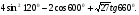
№8. Упростите выражение: 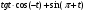 .
.
Контрольная работа по теме: Тригонометрические функции
Вариант 3
№1. Вычислите: а) 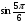 ; б)
; б) 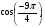 в)
в) 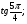 г)
г) 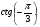
№2. Решите уравнение: а) 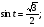 б)
б) 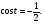
№3. Найдите заданную точку на числовой окружности: 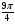 ,
, 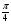 ; -2,5; 140˚,90˚
; -2,5; 140˚,90˚
№4. Известно, что 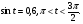 Вычислите:
Вычислите: 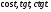
№5. . Решить однородное уравнение первой степени:
а) 3 sin x — √3 cos x = 0.; б) 2 cos x — √2 sin x = 0.
№6. Решить однородное уравнение второй степени:
 .
.
№7. Вычислите: 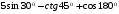
№8. Упростите выражение: sin * cos * ctg – 1.
Контрольная работа по теме: Тригонометрические функции
Вариант 4
№1. Вычислите: а) 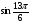 ; б)
; б) 
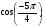 в)
в) 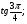 г)
г) 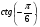
№2. Решите уравнение: а) 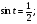 б)
б) 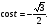
№3. Найдите заданную точку на числовой окружности: 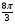 , -
, - 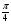 ; 1,5; -340˚,180˚
; 1,5; -340˚,180˚
№4. Известно, что 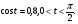 Вычислите:
Вычислите: 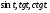

№5. . Решить однородное уравнение первой степени:
а) 2 sin x – 3 cos x= 0; б) sin х — cos х = 0;
№6. Решить однородное уравнение второй степени:
sin2 x — 4 sin x cos x + 3 cos2 x = 0.
№7. Вычислите: 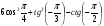
№8. Упростите выражение: 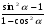 .
.
infourok.ru
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К МАТЕРИАЛАМ контрольной работы
ПО АЛГЕБРЕ в 10 КЛ
Разработала: учитель математики МБОУ СОШ №31 Шевчук В.С.
Тема «Тригонометрические функции»
Назначение материала – выявить степень усвоения знаний, умений, навыков учащихся 10 класса
по темам «Тригонометрические функции числового аргумента», «Основные свойства функций»,
«Решение тригонометрических уравнений». Материал контрольной работы позволяет выяснить владение
формально-оперативным алгебраическим аппаратом, способным к интеграции знаний из различных тем
школьного курса.
Учащиеся должны знать: алгоритм вычисления значений функции, область определения и область
значения тригонометрических функций, тригонометрические тождества, формулы двойного угла, свойства
периодической функции, свойства четной функции, формулы для решения тригонометрических уравнений,
определение модуля, алгоритм решения тригонометрических уравнений, алгоритм нахождения области
допустимых значений
Учащиеся должны уметь: определять значение функции по значению аргумента, решать
тригонометрические уравнения; извлекать информацию представленную графиком, выполнять действия с
функциями, использовать приобретенные знания и умения в практической деятельности,
Содержание экзаменационной работы определяется на основе следующих документов:
1) Федеральный компонент государственного стандарта общего образования. Математика: Приказ
Минобразования России №1089 от 5.03.2004 г «Об утверждении Федерального компонента государственного
стандарта основного общего образования»;
Содержание контрольной работы рассчитано на учащихся 10 класса, ориентировано на использование
УМК по алгебре 10 класса под редакцией Колмогорова (Алгебра и начала математического анализа: учеб.
Для 10-11 кл. общеобразоват. учреждений / [А.Н.Колмогоров, А.М. Абрамов и др] – 17 изд. –М.:
Просвещение, 2008. – 384с.
Вид К\Р : административный
Дата: конец 1 полугодия
Структура работы. Работа состоит из 7 заданий. А1, А2, А3 – задания базового уровня с выбором
ответа. В1, В2, – задания базового уровня с кратким ответом, В3 – задания повышенного уровня с
развернутым ответом, задание С1 – высокого уровня сложности с полной записью решения с обоснованием
выполняемых действий. При выполнении заданий учащиеся должны продемонстрировать умение
математически грамотно записать решение, приводя при этом необходимые пояснения и обоснования.
Обозначение
задания в
работе
Проверяемые умения
Уметь выполнять вычисления и преобразования, используя основные
тригонометрические тождества
Уметь решать простейшие тригонометрические уравнения
Уметь описывать по графику поведение и свойства функции
Уметь определять значение функции по значению аргумента
Уметь выполнять действия с функциями, определять значения функции
используя свойства функции (периодичность, четность)
Уметь выполнять преобразования тригонометрических выражений,
применять метод введения новой переменной для решения
тригонометрических уравнений,
Уметь решать уравнения, проводить доказательные рассуждения при
решении, определять ограниченность
Время выполнения работы
На выполнение работы отводится 40 минут.
uchitelya.com
Вариант1
1.Найти область определения и множество
значений функции у=5 cos х .
2. Выяснить является функция у=2sin x – tg x
четной или нечетной?
3.Изобразить график функции у= sin x на
интервале ( - 2п; 2п) и решить уравнение
sin x = 0,5.
4.Найти наибольшее и наименьшее значения
функции у= 6sin x cos х + 3
5. Построить график функции у= cos х + 2.
При каких значениях функция убывает;
возрастает?
Вариант2
1.Найти область определения и множество
значений функции у=0,5 sin х .
2. Выяснить является функция у=2cos x – x
четной или нечетной?
3.Изобразить график функции у= cos x на
интервале ( - 2п; 2п) и решить уравнение
cos x = -0,5.
4.Найти наибольшее и наименьшее значения
функции у= 6cos x - 6sin
x - 6sin х + 3
х + 3
5. Построить график функции у= sin х + 2.
При каких значениях функция убывает;
возрастает?
Вариант3
1.Найти область определения и множество
значений функции у= cos х + 4
2. Выяснить является функция у = 3sin x + tg x
четной или нечетной?
3.Изобразить график функции у= sin x на
интервале ( - 2п; 2п) и решить уравнение
sin x = -1.
4.Найти наибольшее и наименьшее значения
функции у= 8sin x cos х - 2
5. Построить график функции у= cos х - 1.
При каких значениях функция убывает;
возрастает?
Вариант6
1.Найти область определения и множество
значений функции у=sin х - 3
2. Выяснить является функция у = cos x +3 x
четной или нечетной?
3.Изобразить график функции у= cos x на
интервале ( - 2п; 2п) и решить уравнение
cos x = -1.
4.Найти наибольшее и наименьшее значения
функции у= 5cos x - 5sin
x - 5sin х + 2
х + 2
5. Построить график функции у= sin х - 1.
При каких значениях функция убывает;
возрастает?
Вариант5
1.Найти область определения и множество
значений функции у= 5cos х .
2. Выяснить является функция у=sin x –5 tg x
четной или нечетной?
3.Изобразить график функции у= sin x на
интервале ( - 2п; 2п) и решить уравнение
sin x = 1.
4.Найти наибольшее и наименьшее значения
функции у= 10sin x cos х + 2 .
5. Построить график функции у= cos х + 1.
При каких значениях функция убывает;
возрастает?
Вариант6
1.Найти область определения и множество
значений функции у=sin х + 2
2. Выяснить является функция у=2cos x – x
четной или нечетной?
3.Изобразить график функции у= cos x на
интервале ( - 2п; 2п) и решить уравнение
cos x = 1.
4.Найти наибольшее и наименьшее значения
функции у= 8cos x - 8sin
x - 8sin х + 3
х + 3
5. Построить график функции у= sin х + 1.
При каких значениях функция убывает;
возрастает?
Вариант7
1.Найти область определения и множество
значений функции у=cos х + 11
2. Выяснить является функция у=sin x –2tg x
четной или нечетной?
3.Изобразить график функции у= sin x на
интервале ( - 2п; 2п) и решить уравнение
sin x = 1.
4.Найти наибольшее и наименьшее значения
функции у= 6sin x cos х + 3
5. Построить график функции у= cos х + 3.
При каких значениях функция убывает;
возрастает?
Вариант8
1.Найти область определения и множество
значений функции у=0,5 sin х .
2. Выяснить является функция у=2cos x – x
четной или нечетной?
3.Изобразить график функции у= cos x на
интервале ( - 2п; 2п) и решить уравнение
cos x = -1.
4.Найти наибольшее и наименьшее значения
функции у= 6cos x - 6sin
x - 6sin х + 3
х + 3
5. Построить график функции у= sin х +3.
При каких значениях функция убывает;
возрастает?
kopilkaurokov.ru
Контрольная работа № 1 ВАРИАНТ 1 А 11
Найти область определения и множество значений функции y = sin x + 2.
Выяснить, является ли функция
y = x2 + cos x чётной или нечётной.
Доказать, что наименьший положительный период функции y = cos 2 x равен π.
Найти принадлежащие отрезку [- π; π] корни уравнения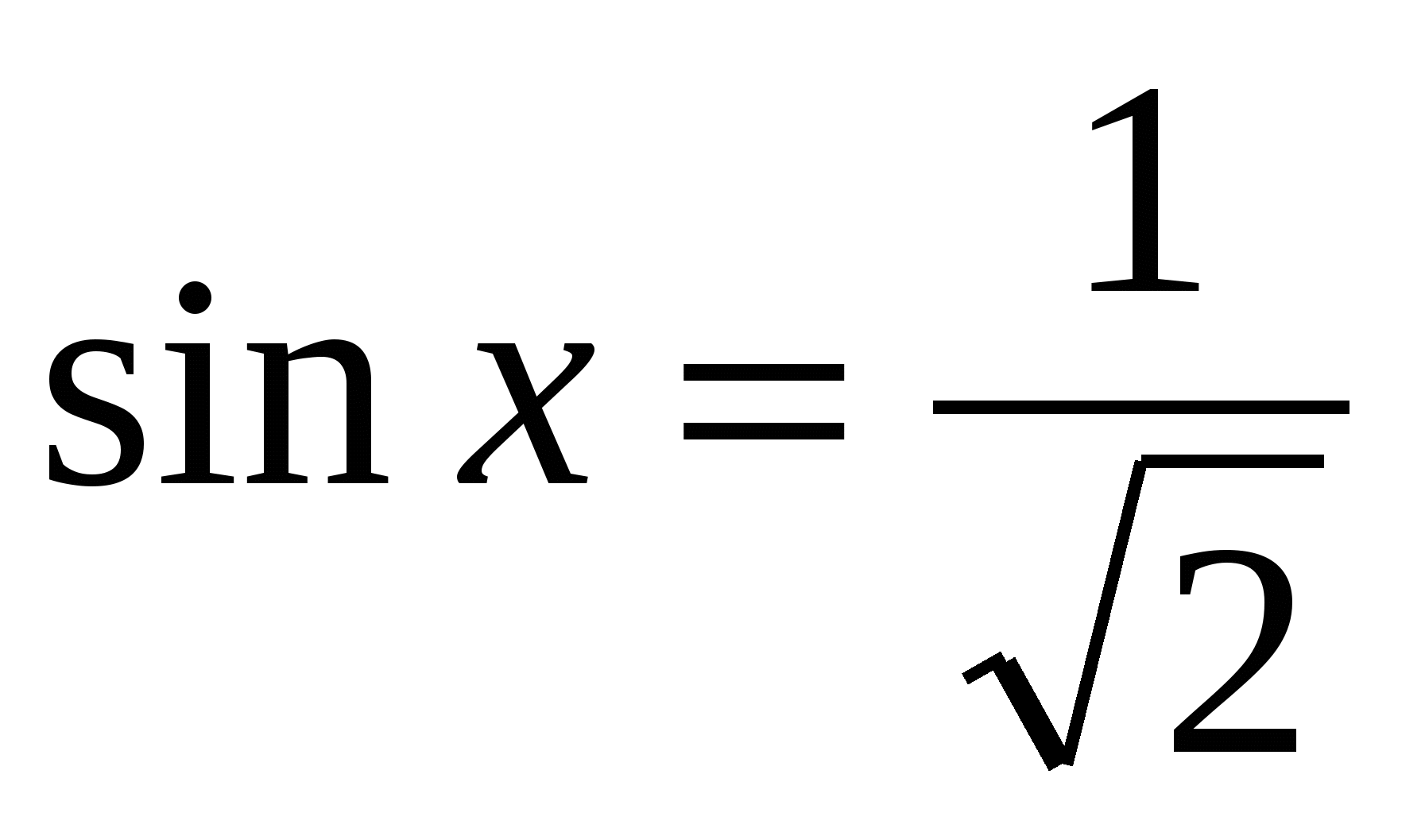 с помощью графика функции.
с помощью графика функции.
Построить график функции y = cos x - 1 и найти значение аргумента, при которых функция возрастает, принимает наибольшее значение.
_________________________________________
Контрольная работа № 1 ВАРИАНТ 2 А 11
Найти область определения и множество значений функции y = 3 cos x.
Выяснить, является ли функция y = x3 sin x чётной или нечётной.
Доказать, что наименьший положительный период функции 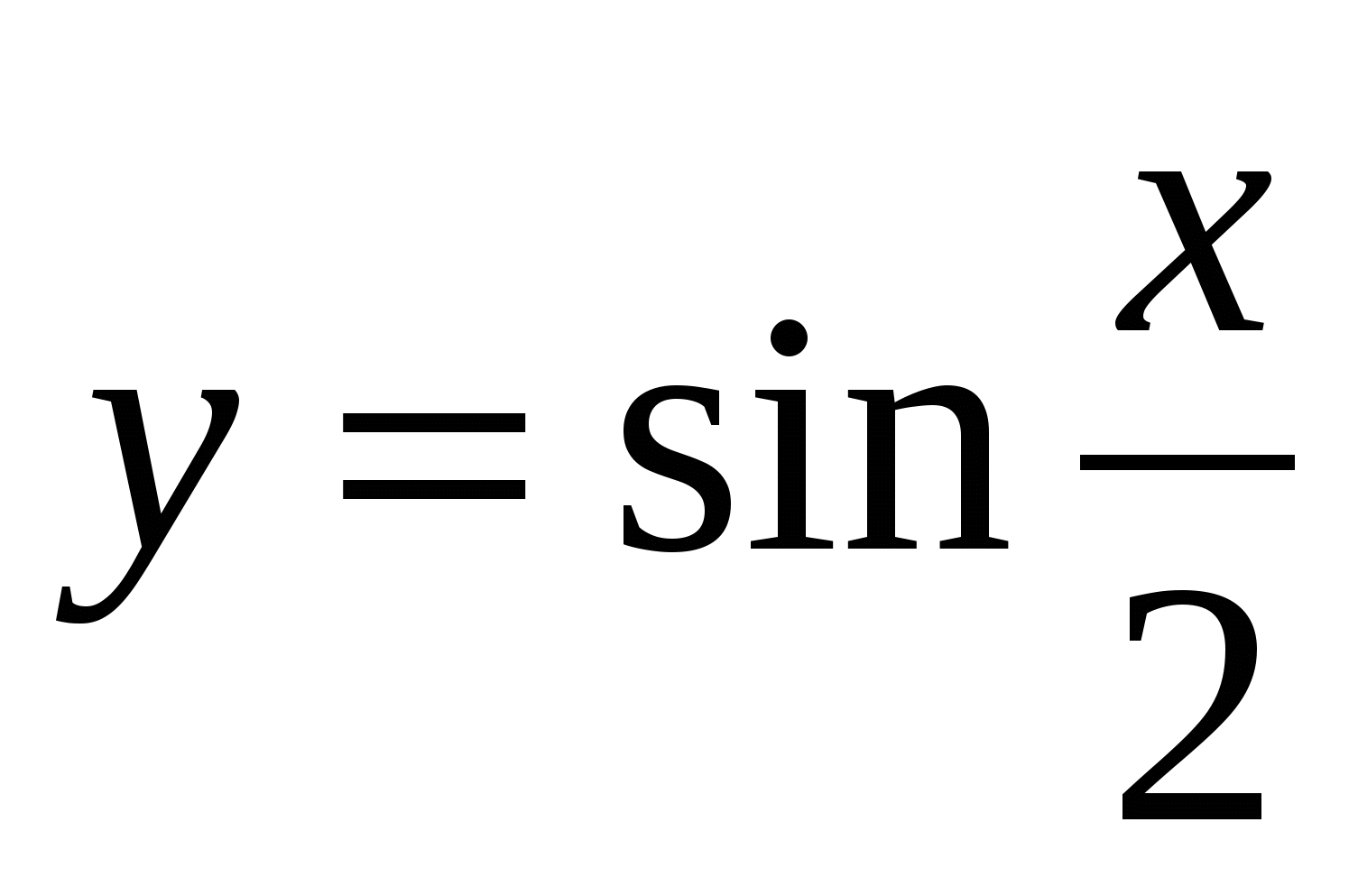 равен 4π.
равен 4π.
Найти принадлежащие отрезку [0; 2,5π] корни уравнения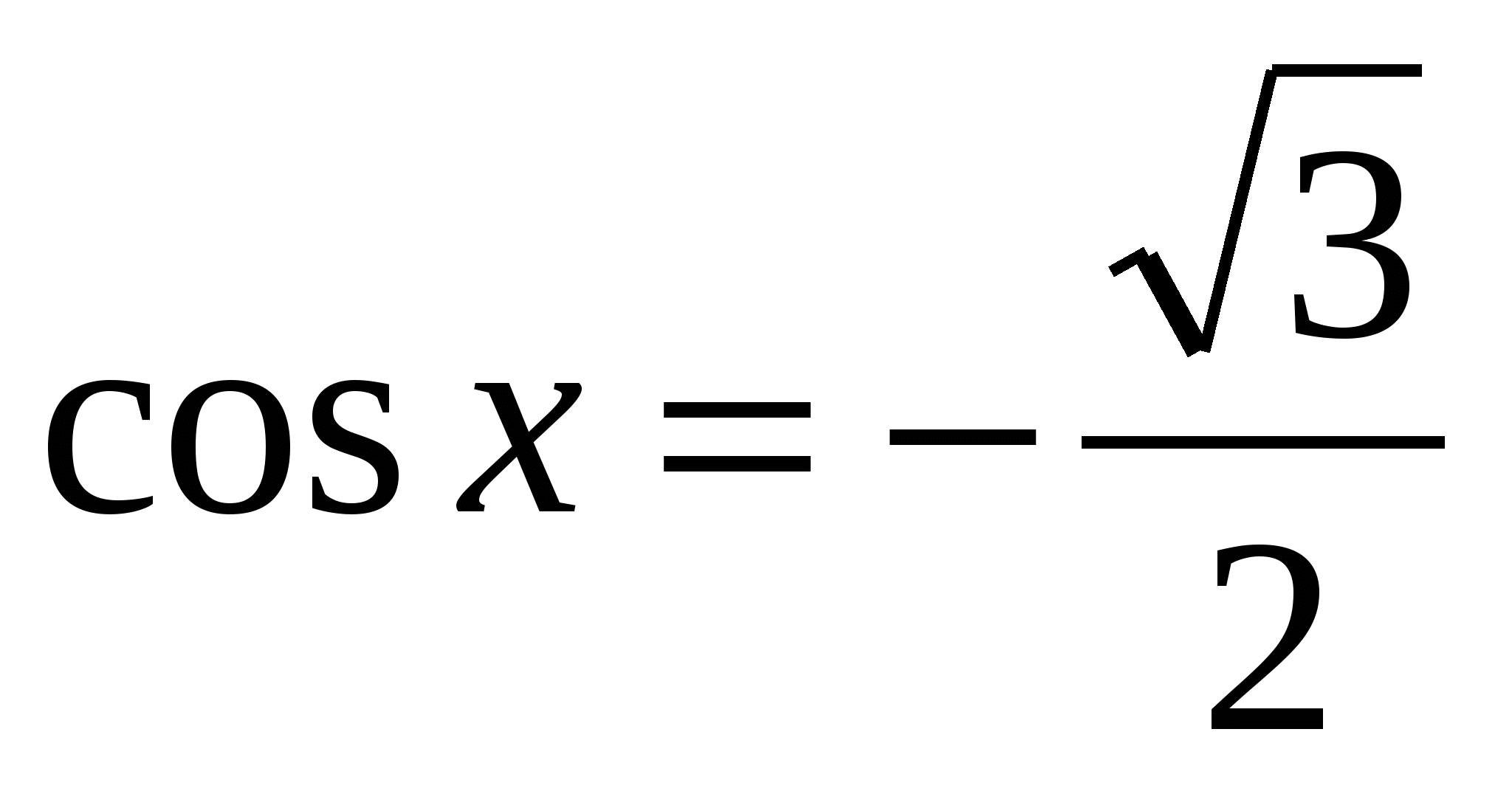 с помощью графика функции.
с помощью графика функции.
Построить график функции 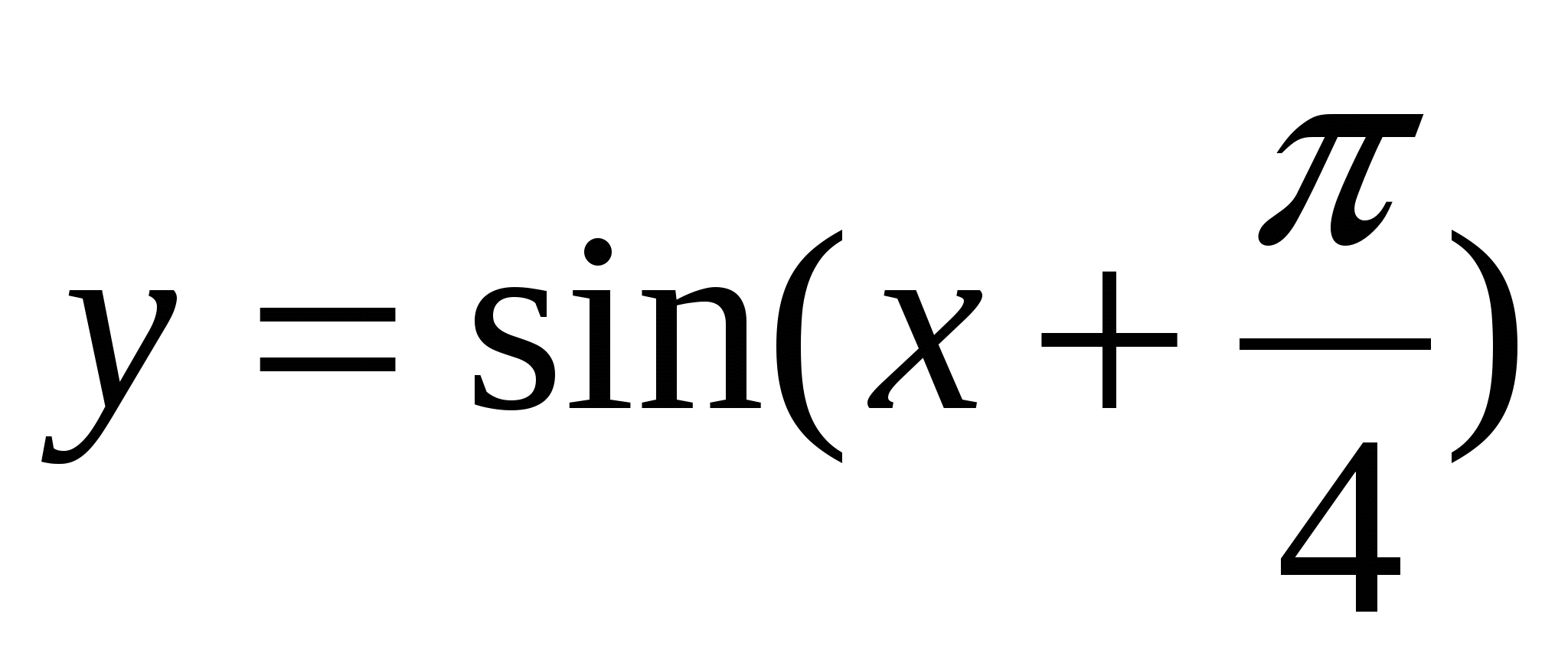 и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.
и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.
_________________________________________
Контрольная работа № 1 ВАРИАНТ 3 А 11
Найти область определения и множество значений функции y = - sin x +3.
Выяснить, является ли функция
y = x - cos x чётной или нечётной.
Доказать, что наименьший положительный период функции y = sin 2x равен π.
Найти принадлежащие отрезку [- π/2; π] корни уравнения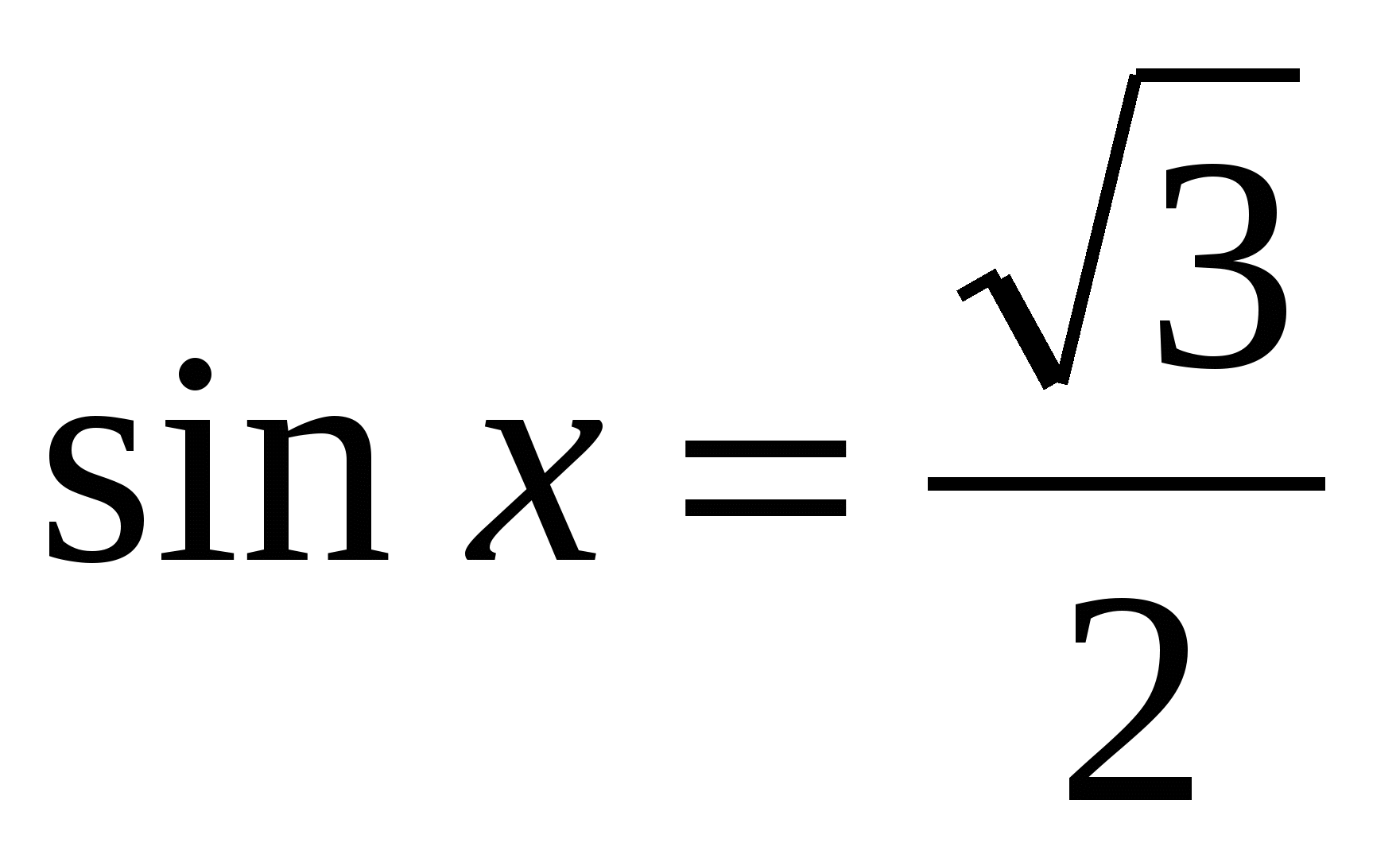 с помощью графика функции.
с помощью графика функции.
Построить график функции y = cos x +2 и найти значение аргумента, при которых функция возрастает, принимает наибольшее значение.
_________________________________________
Контрольная работа № 1 ВАРИАНТ 4 А 11
Найти область определения и множество значений функции y = -5 cos x.
Выяснить, является ли функция y = -x2 + sin x чётной или нечётной.
Доказать, что наименьший положительный период функции 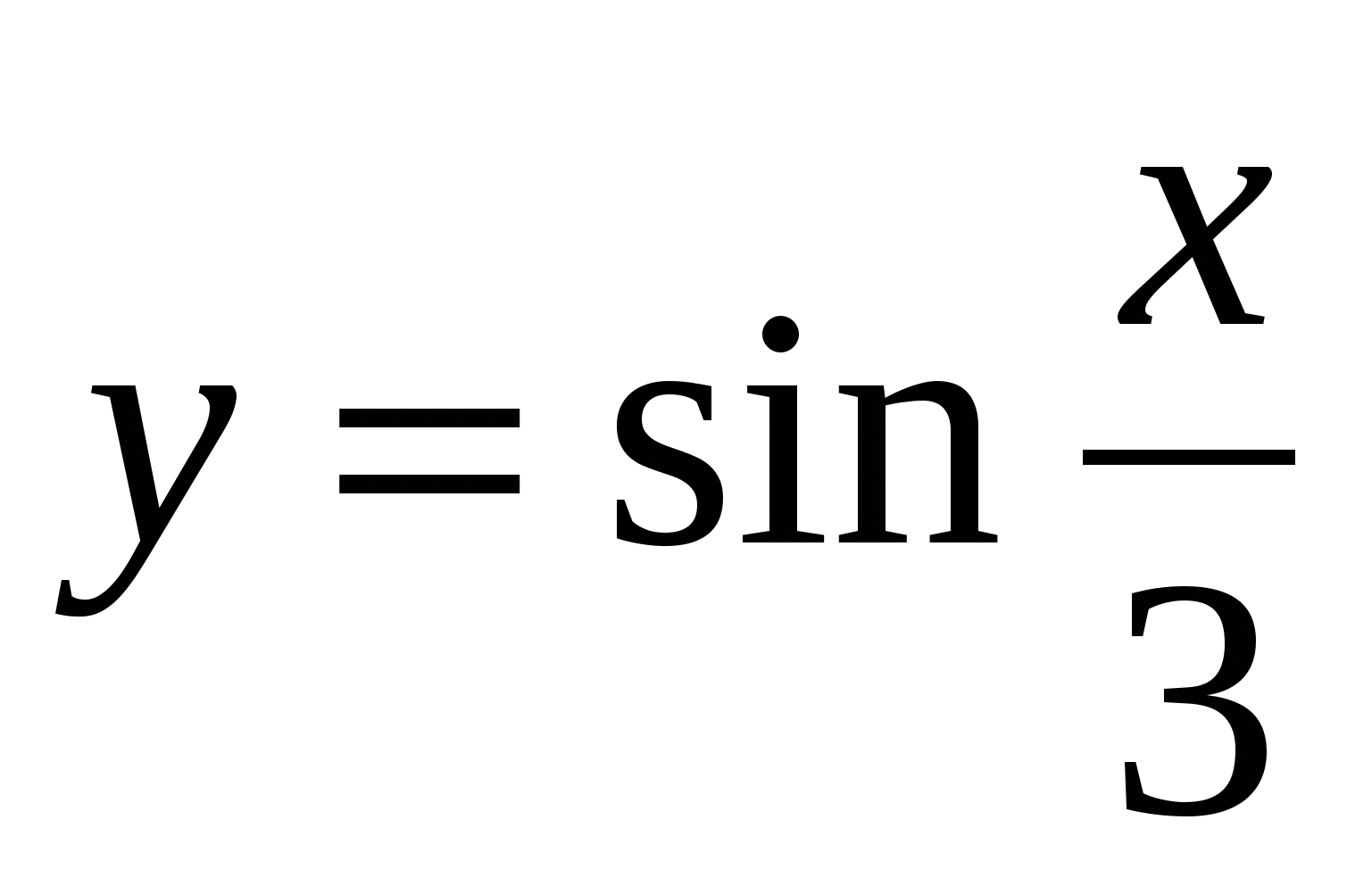 равен 6π.
равен 6π.
Найти принадлежащие отрезку [- π/2; 2,5π] корни уравнения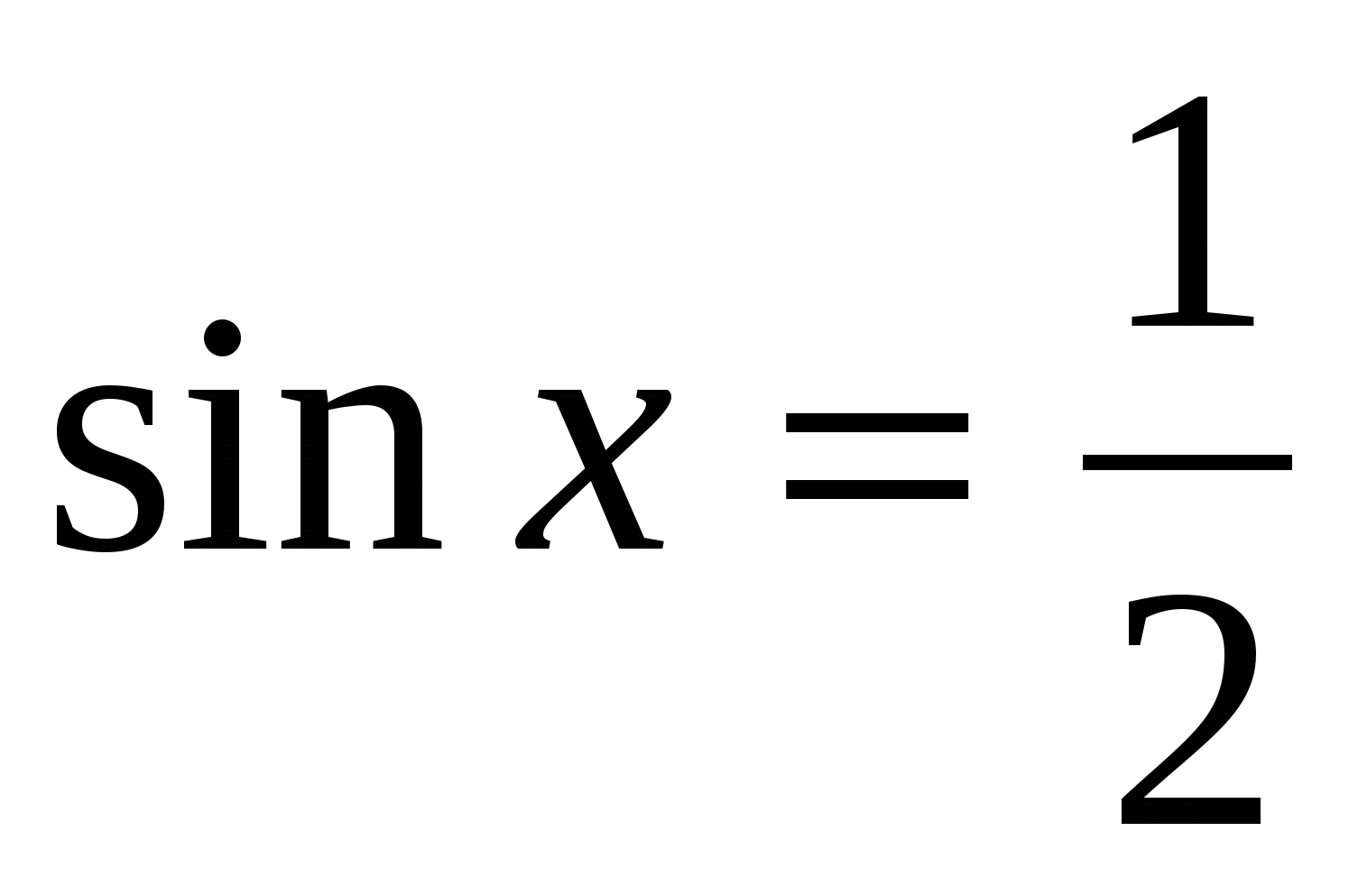 с помощью графика функции.
с помощью графика функции.
Построить график функции 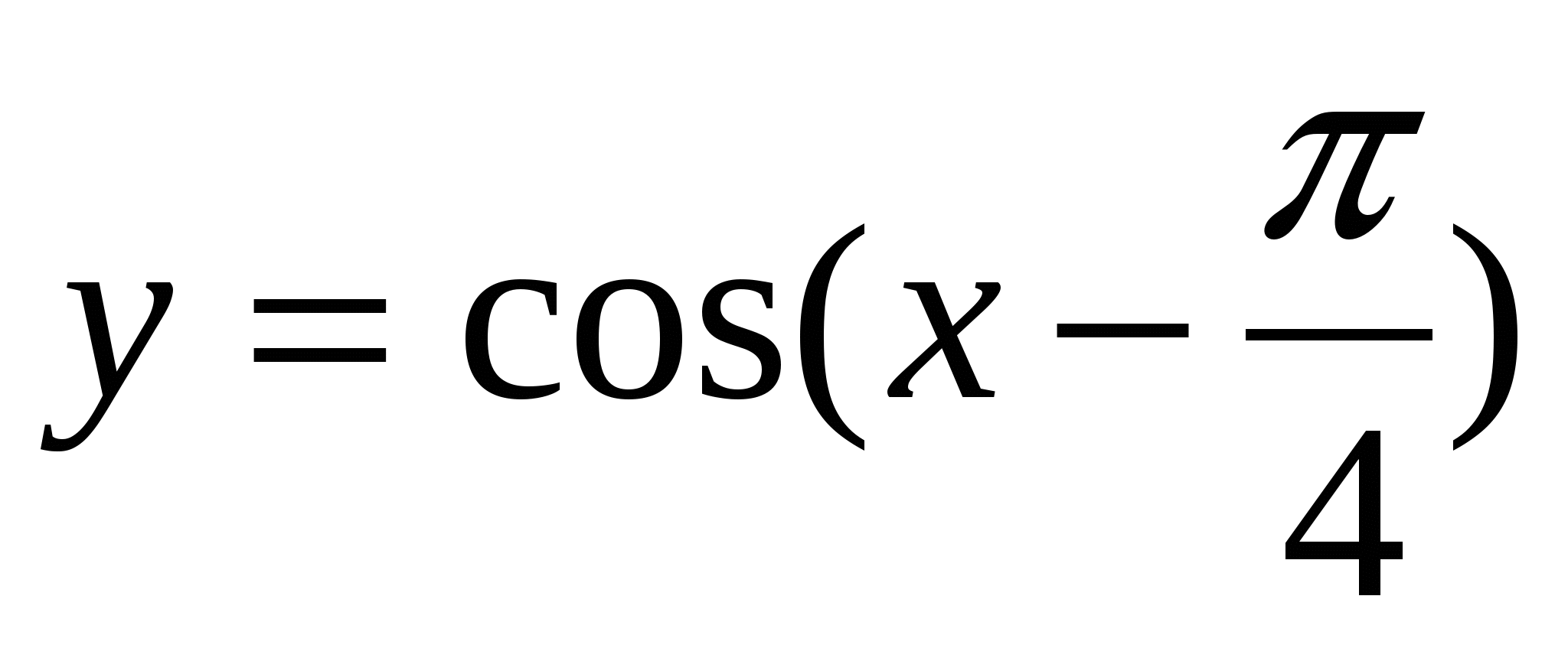 и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.
и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.
_________________________________________
Контрольная работа № 1 ВАРИАНТ 5 А 11
Найти область определения и множество значений функции y = cos x -1.
Выяснить, является ли функция
y = sin x –x2 чётной или нечётной.
Доказать, что наименьший положительный период функции 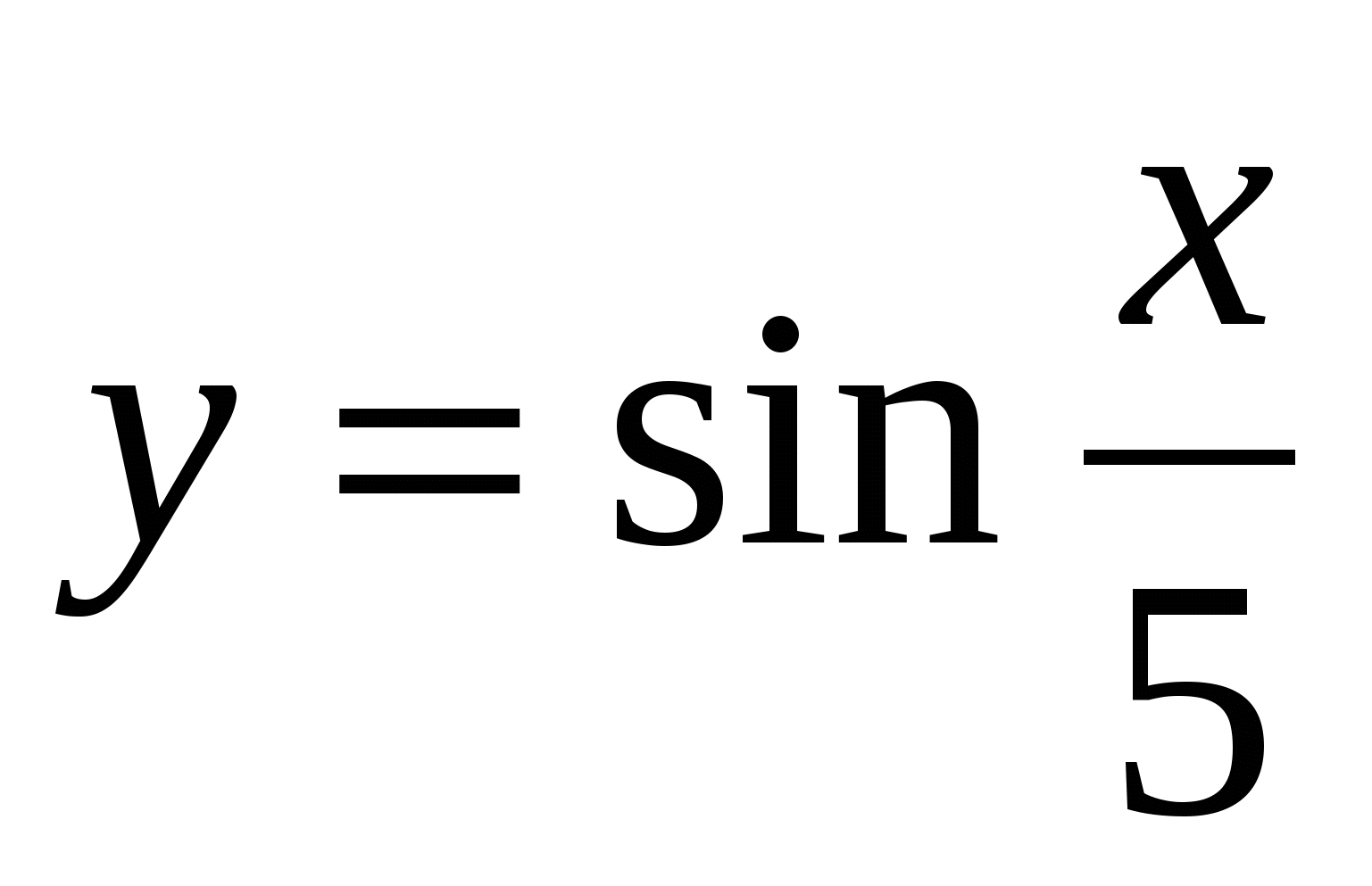 равен 10π.
равен 10π.
Найти принадлежащие отрезку [0; 2π] корни уравнения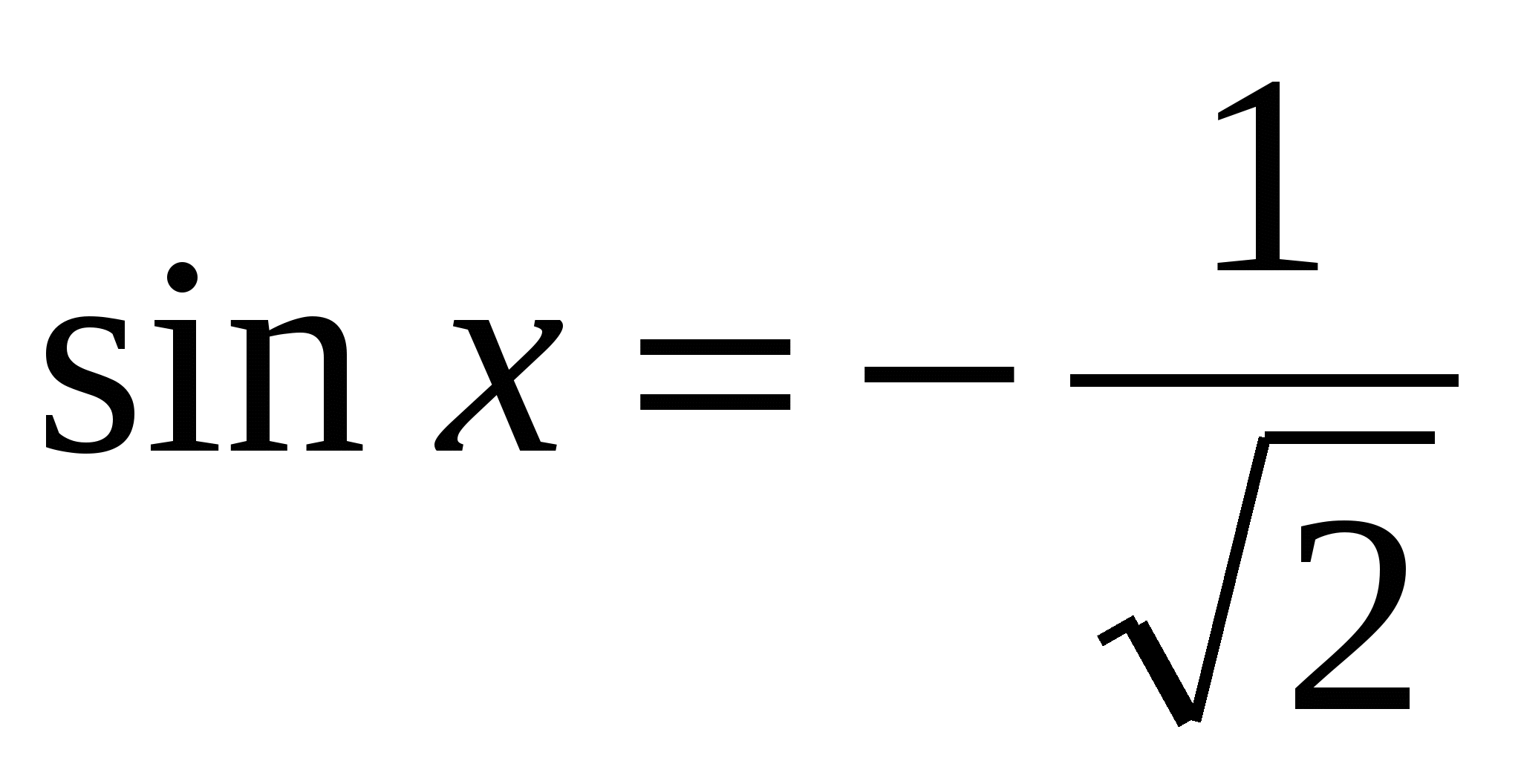 с помощью графика функции.
с помощью графика функции.
Построить график функции y = cos x +3 и найти значение аргумента, при которых функция возрастает, принимает наибольшее значение.
_________________________________________
Контрольная работа № 1 ВАРИАНТ 6 А 11
Найти область определения и множество значений функции y = -2 sin x.
Выяснить, является ли функция y = -x4 cos x чётной или нечётной.
Доказать, что наименьший положительный период функции 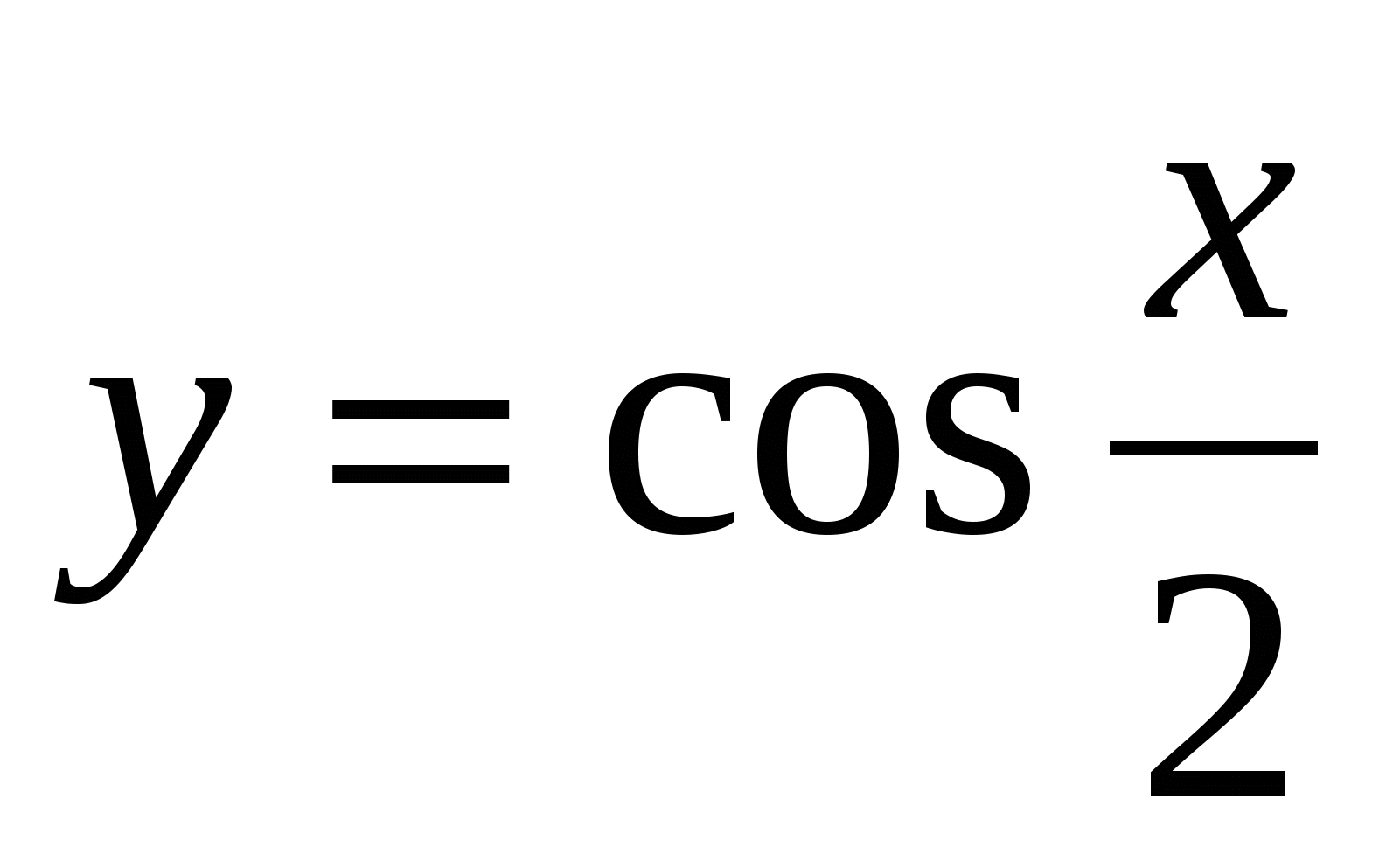 равен 4π.
равен 4π.
Найти принадлежащие отрезку [- π/2; π] корни уравнения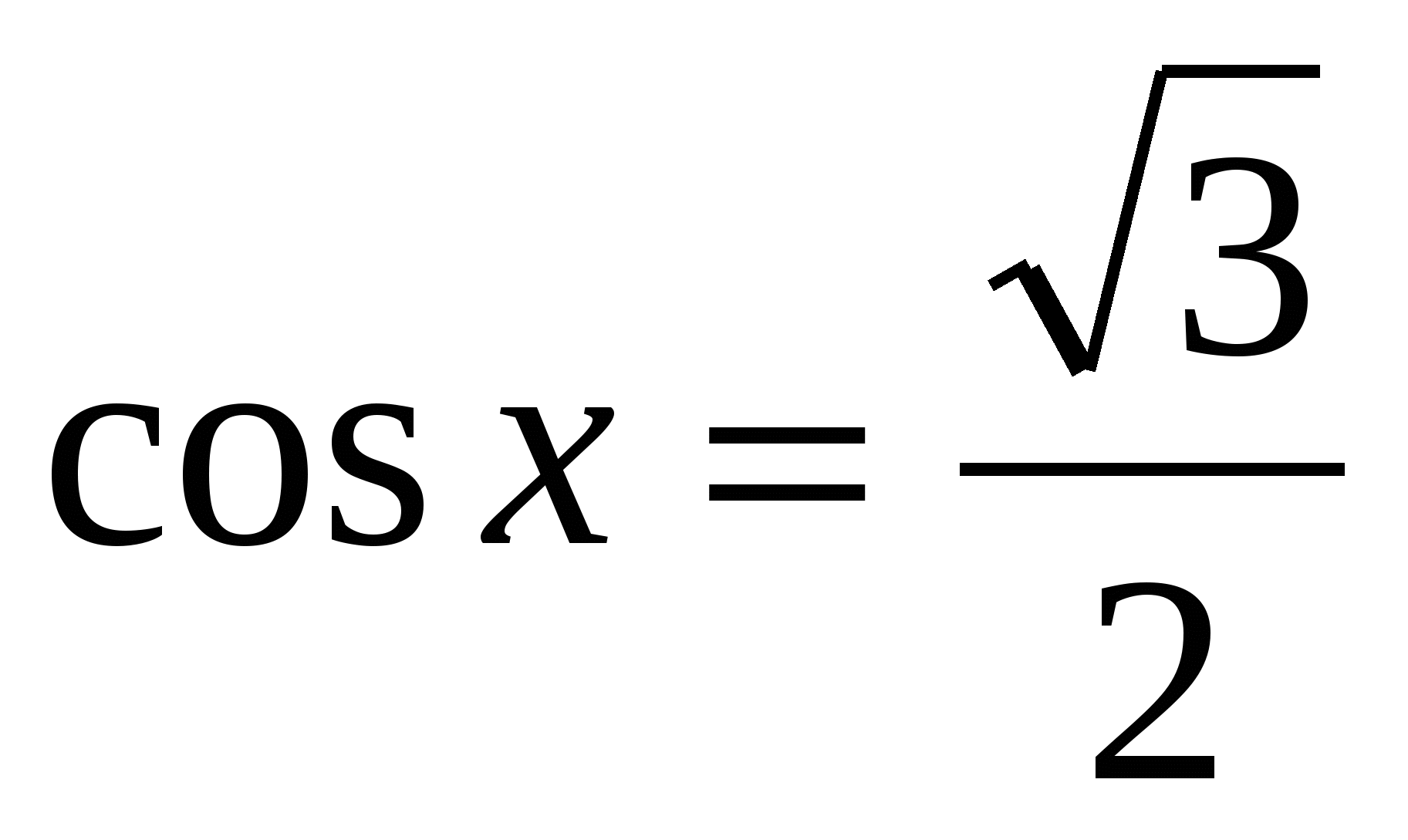 с помощью графика функции.
с помощью графика функции.
Построить график функции 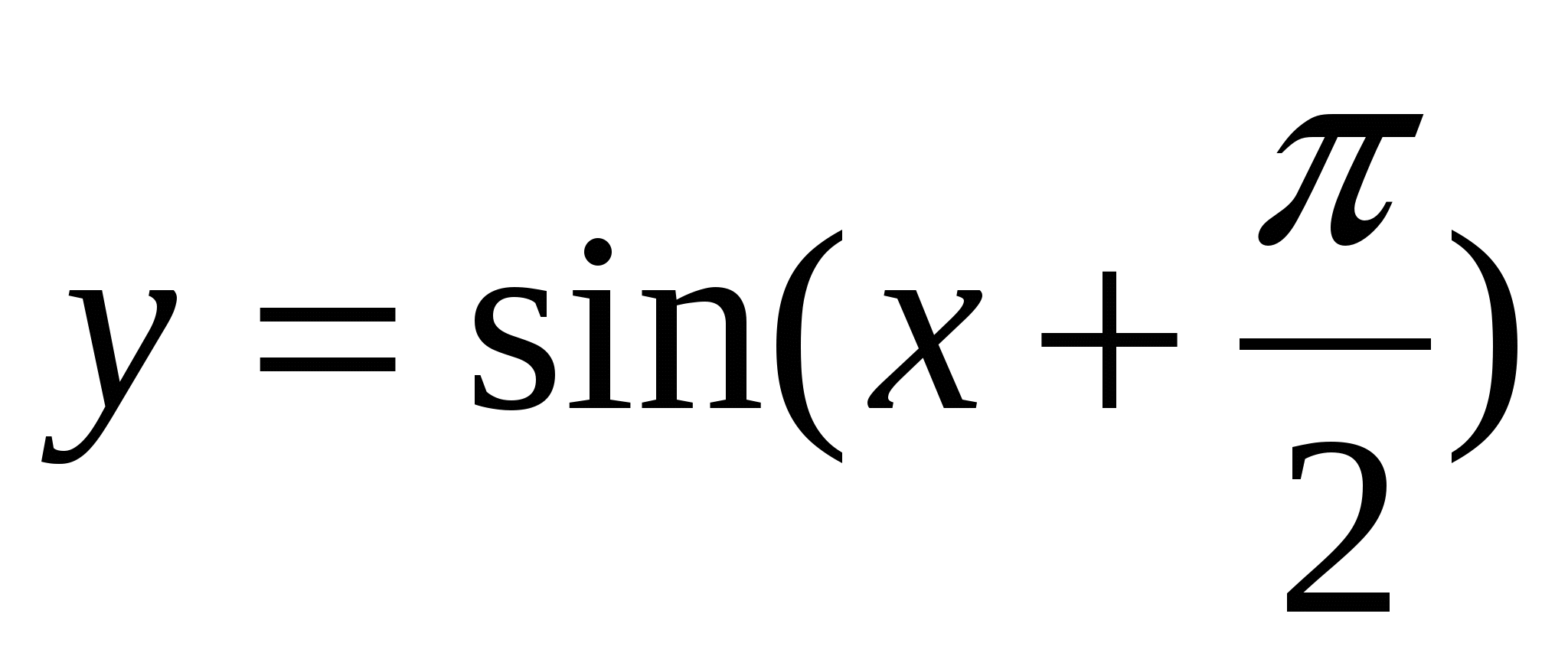 и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.
и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.
_________________________________________
Контрольная работа № 1 ВАРИАНТ 7 А 11
Найти область определения и множество значений функции y = - cos x -2.
Выяснить, является ли функция
y = x3 + cos x чётной или нечётной.
Доказать, что наименьший положительный период функции y = sin 4 x равен π.
Найти принадлежащие отрезку [- π; π/2] корни уравнения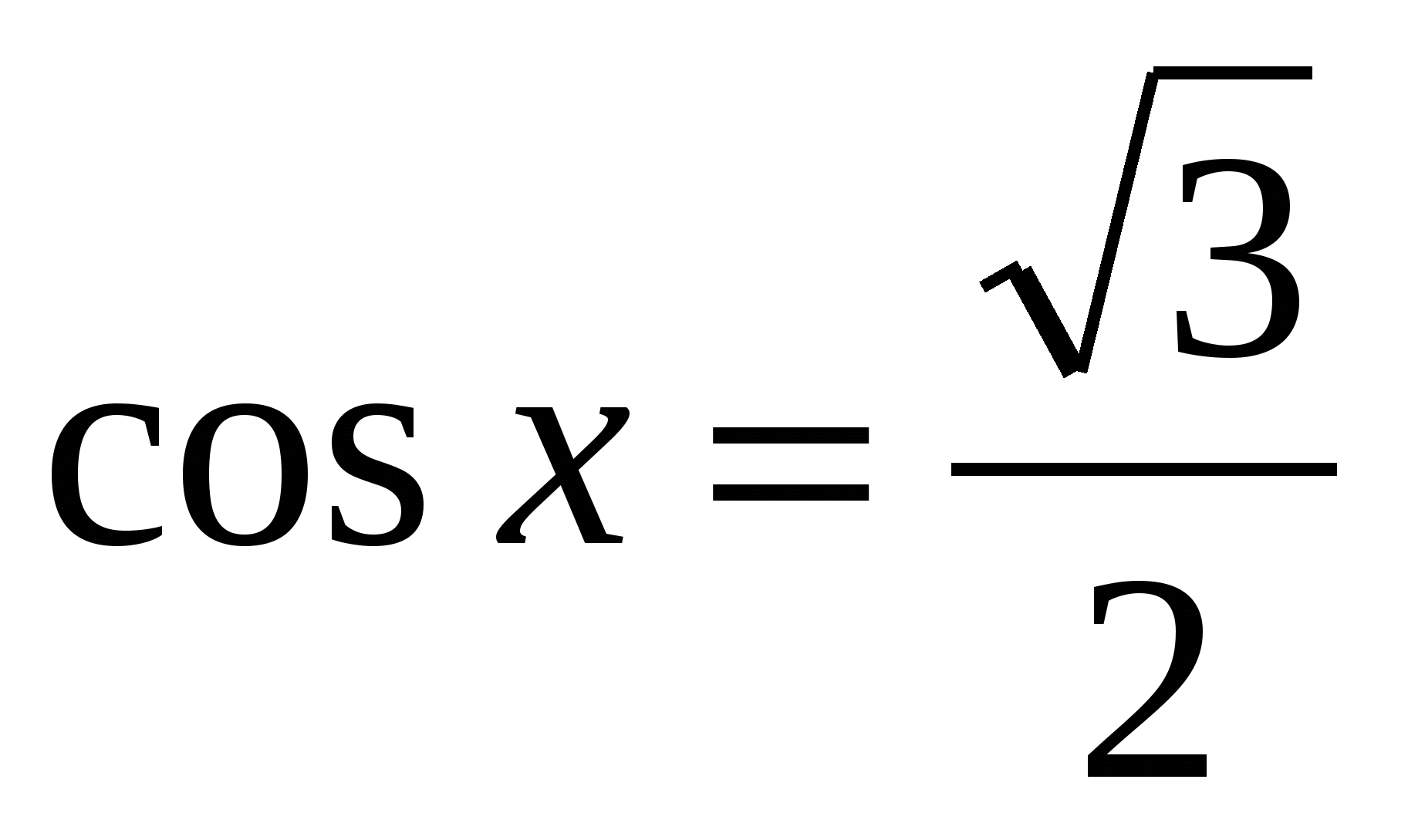 с помощью графика функции.
с помощью графика функции.
Построить график функции y = sin x +2 и найти значение аргумента, при которых функция возрастает, принимает наибольшее значение.
_________________________________________
Контрольная работа № 1 ВАРИАНТ 8 А 11
Найти область определения и множество значений функции y = -5 sin x.
Выяснить, является ли функция y = x2 +sin x чётной или нечётной.
Доказать, что наименьший положительный период функции 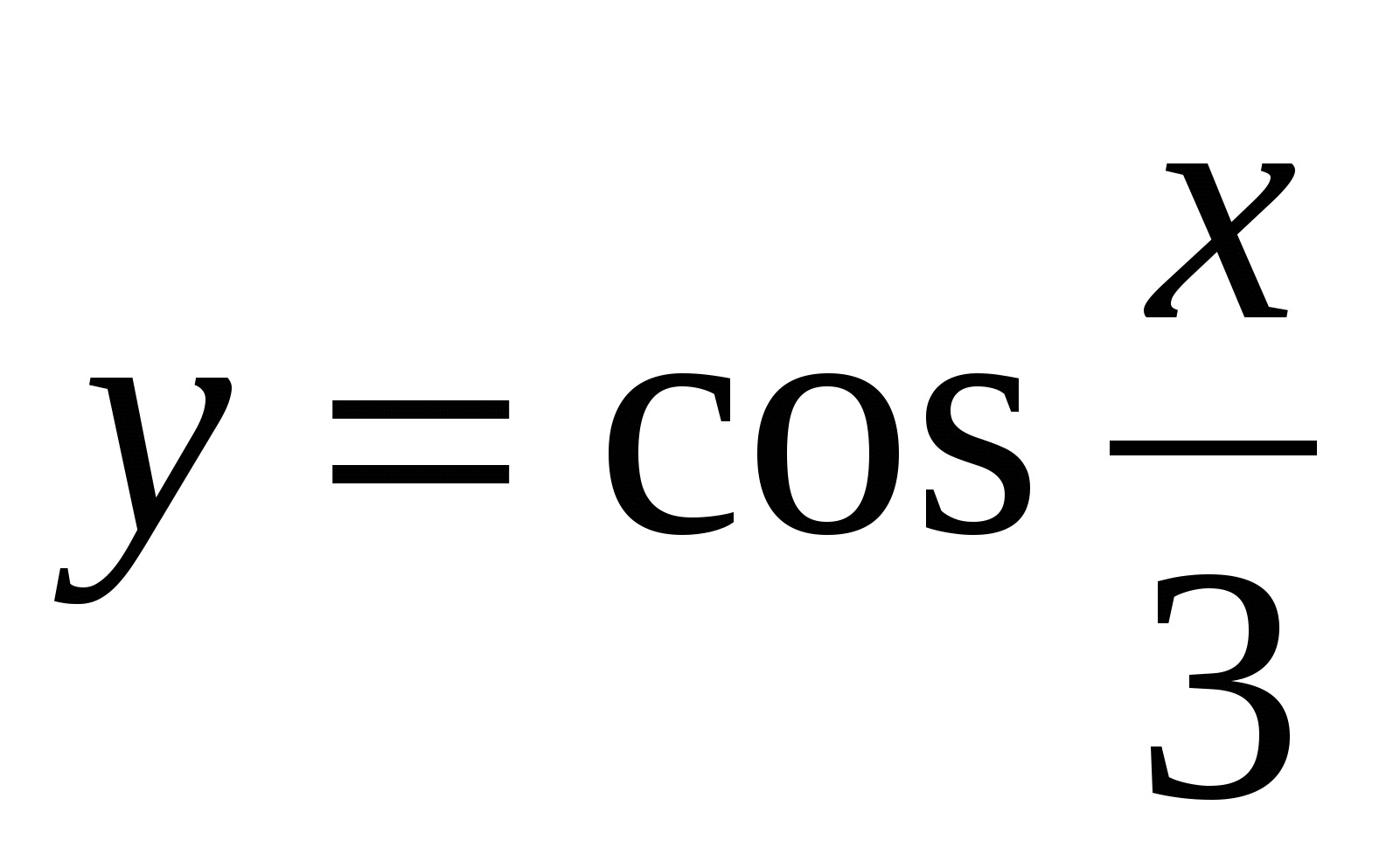 равен 6π.
равен 6π.
Найти принадлежащие отрезку [- π/2; 2,5π] корни уравнения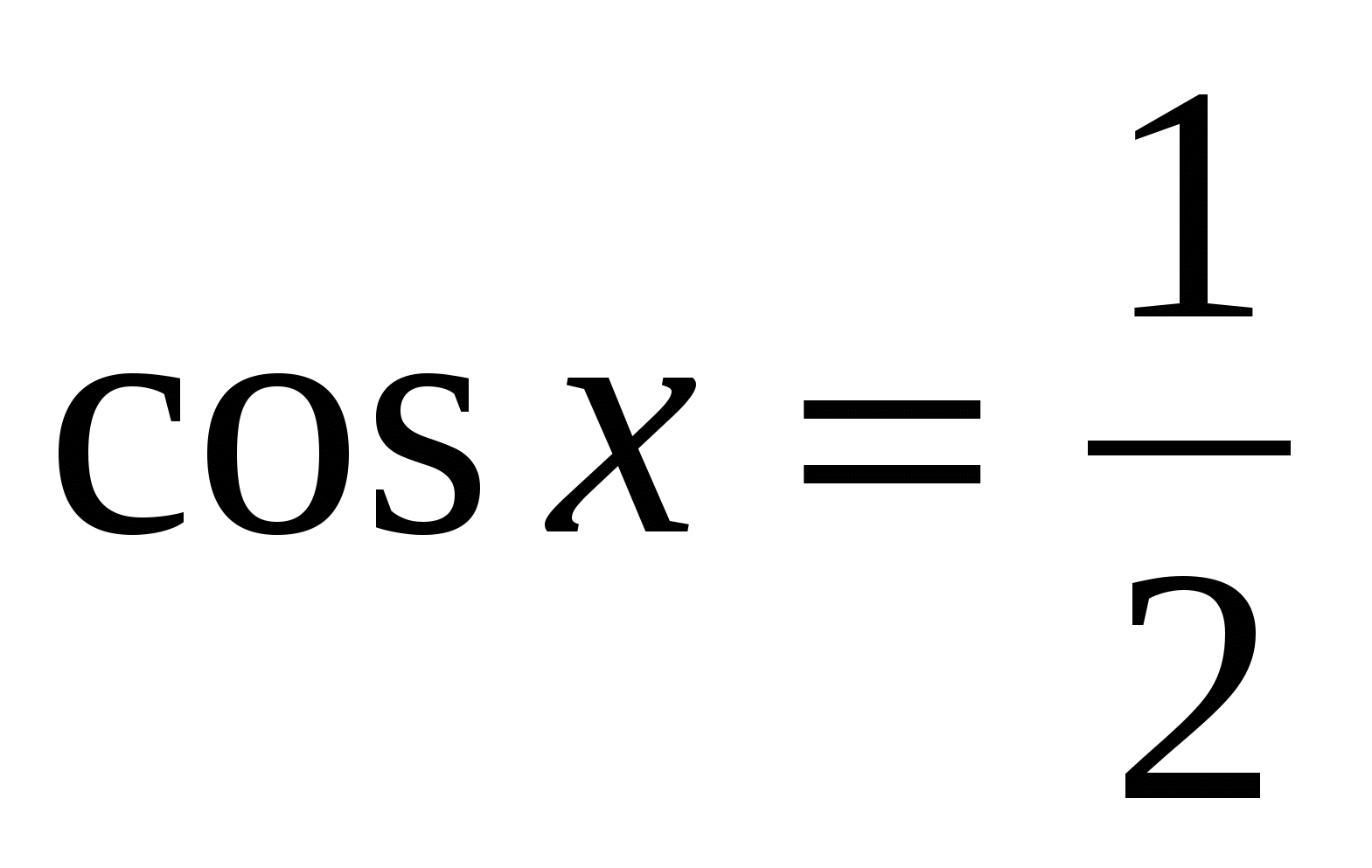 с помощью графика функции.
с помощью графика функции.
Построить график функции 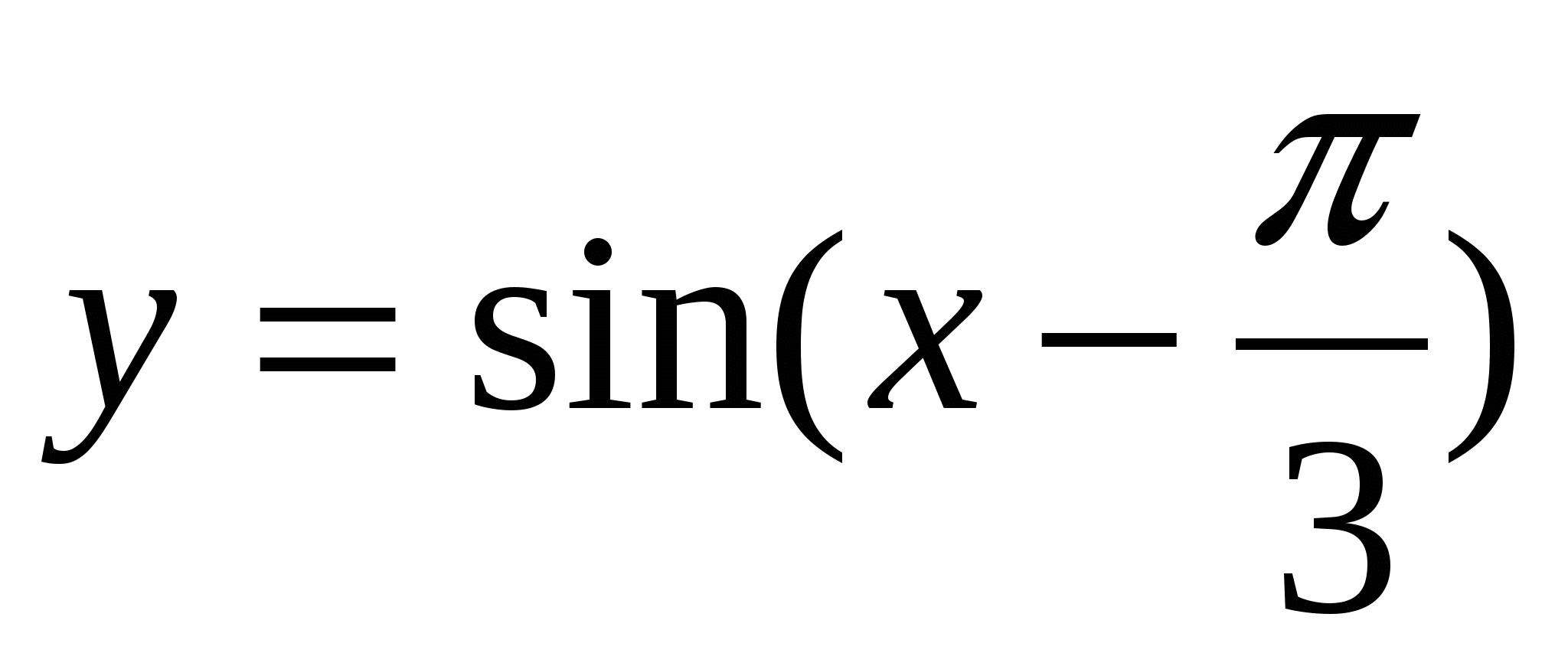 и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.
и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.
_________________________________________
infourok.ru
Контрольная работа № 1
Тригонометрические функции
Вариант 1
А1. Найдите область определения функции 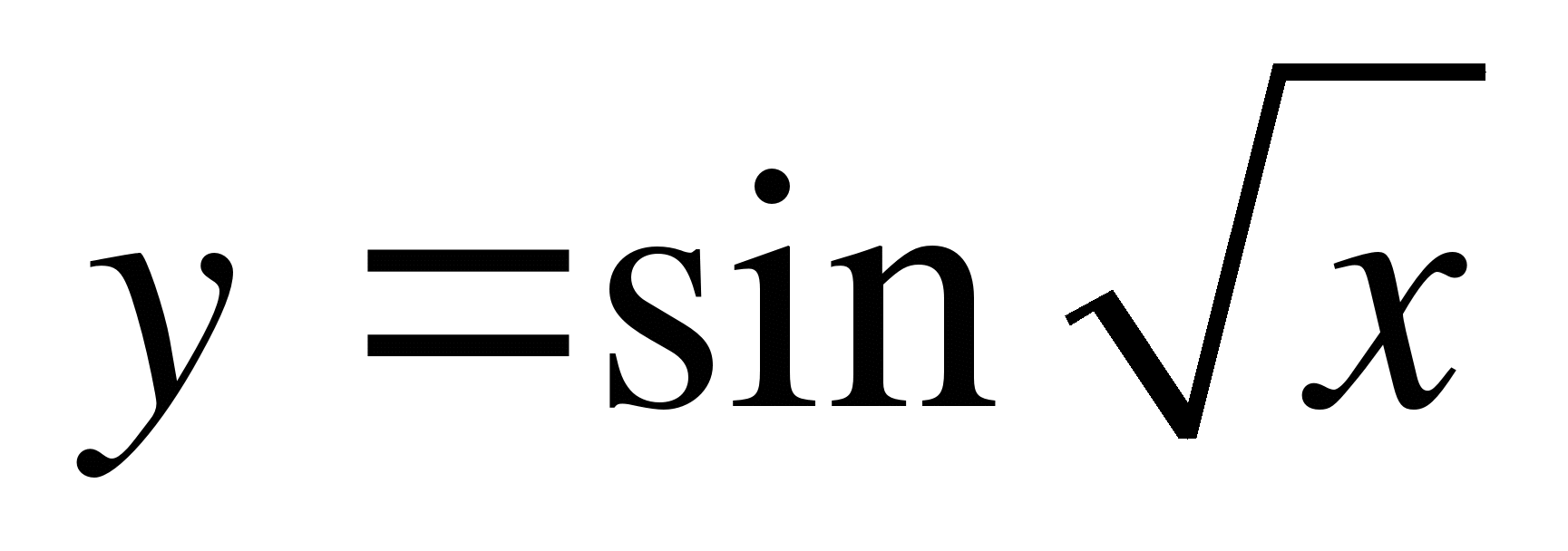 .
.
А2. Найдите множество значений функции 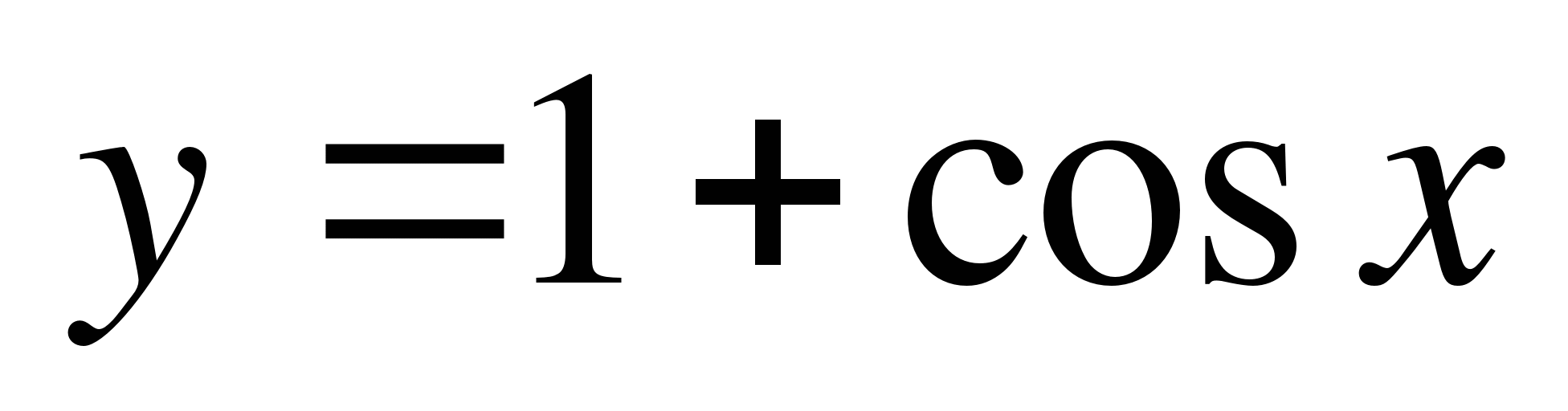 .
.
А3. Выяснить, является ли данная функция четной или нечетной: 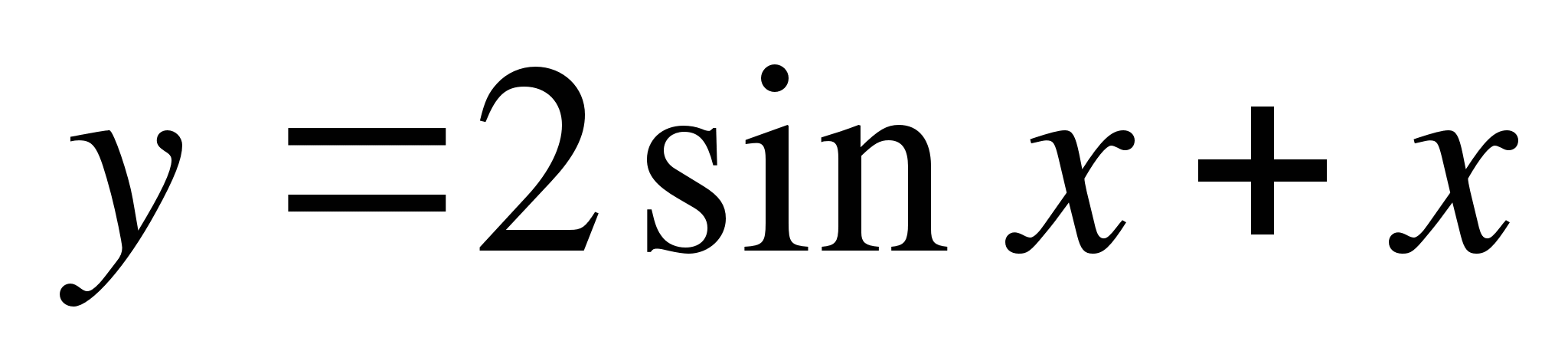
А4. Докажите, что функция 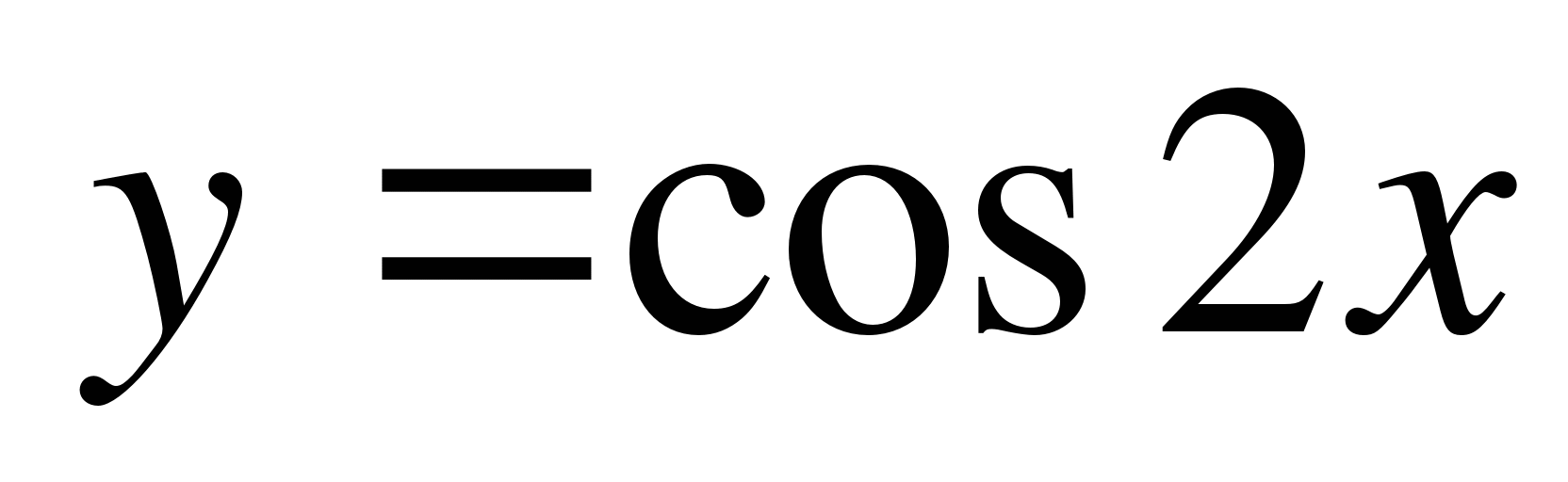 является периодической с периодом Т = p.
является периодической с периодом Т = p.
А5. Сравните числа: 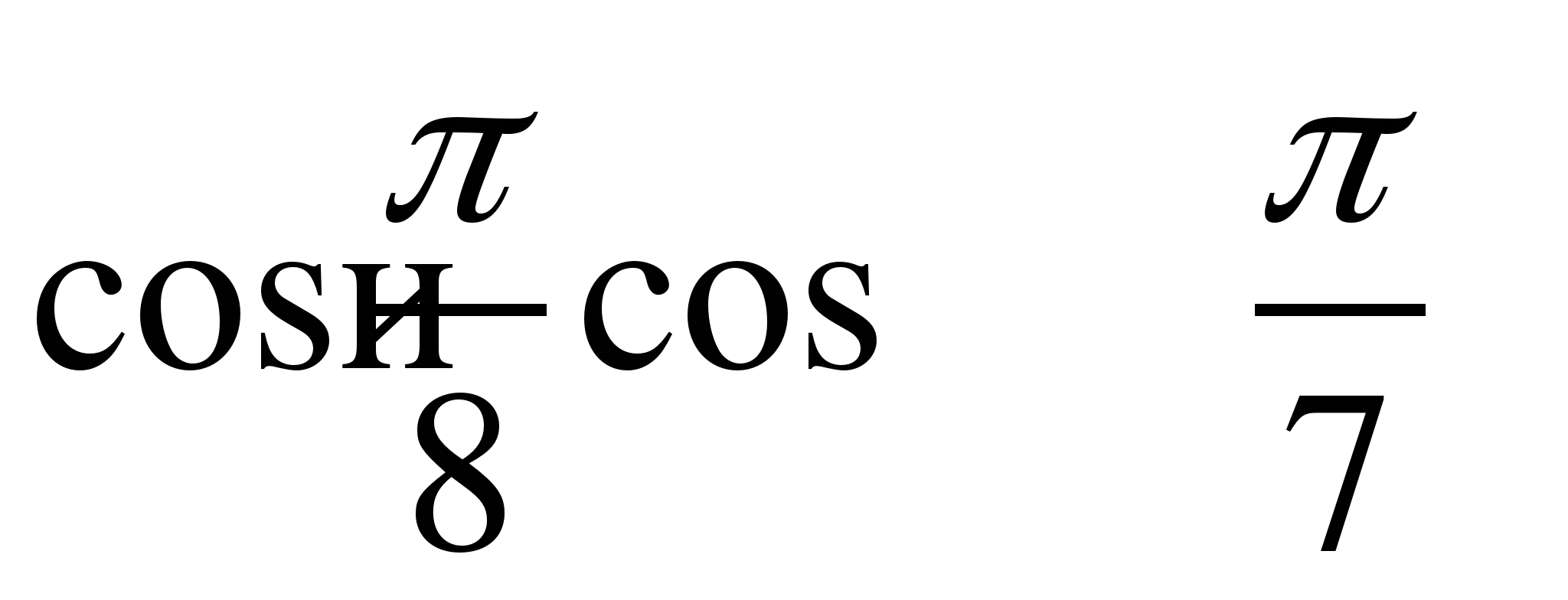 .
.
A6. Найдите значение функции 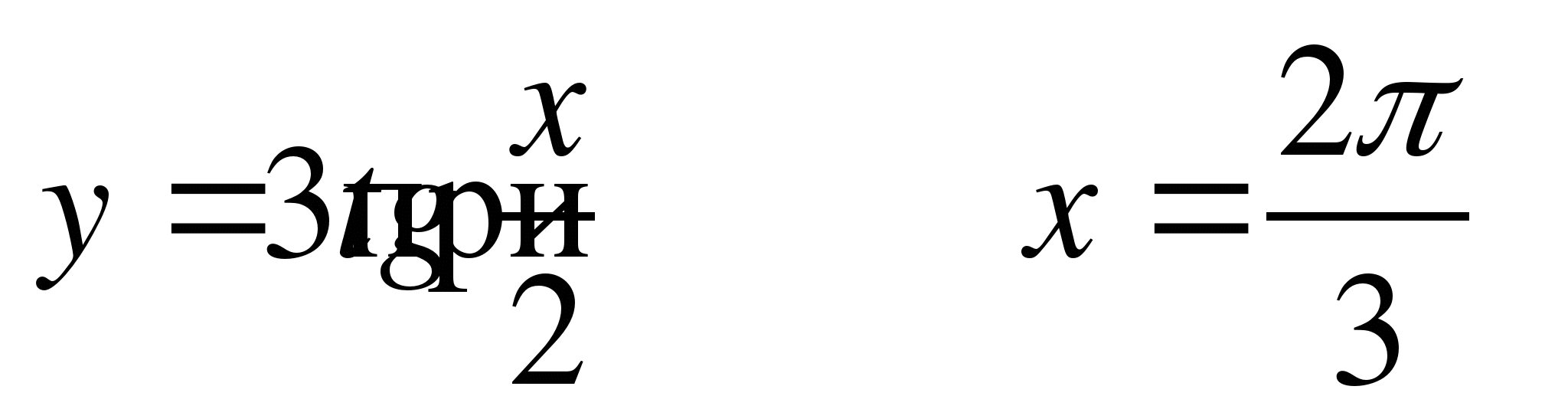 .
.
В1. Сравните числа:  .
.
В2. Найдите все корни уравнения 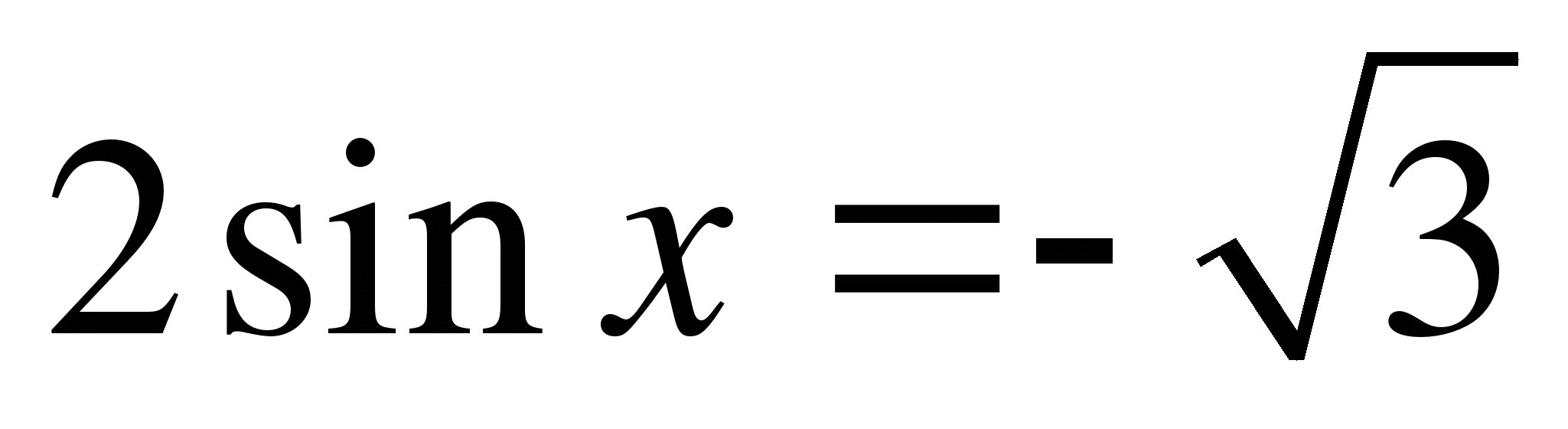 , принадлежащие промежутку [0;2p].
, принадлежащие промежутку [0;2p].
С1. Найдите наибольшее и наименьшее значение функции 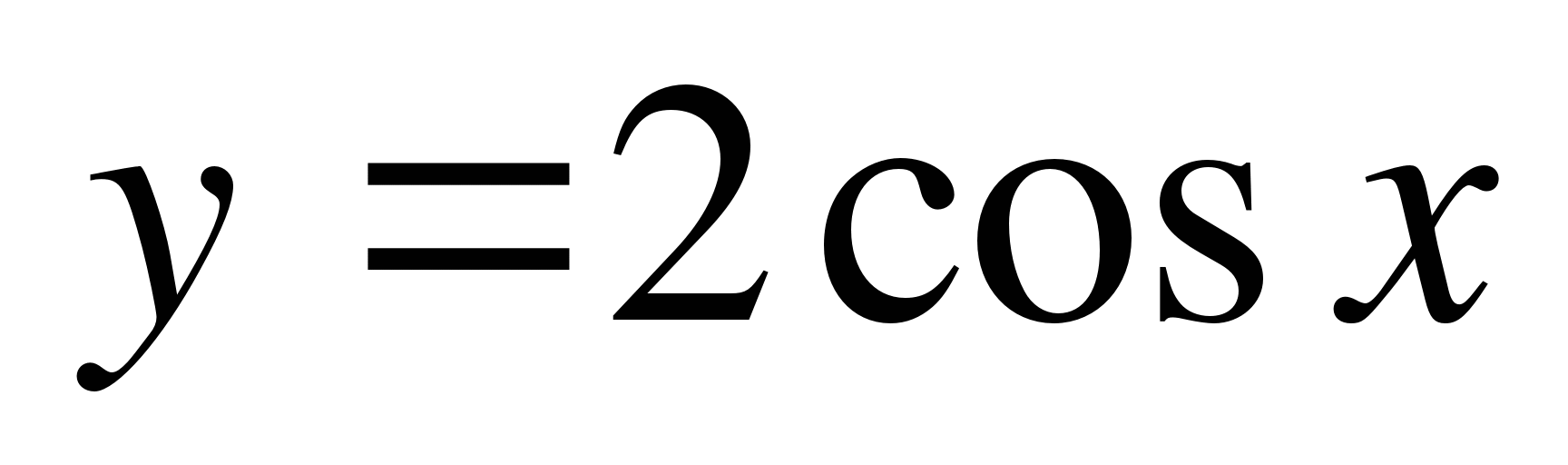 на отрезке
на отрезке 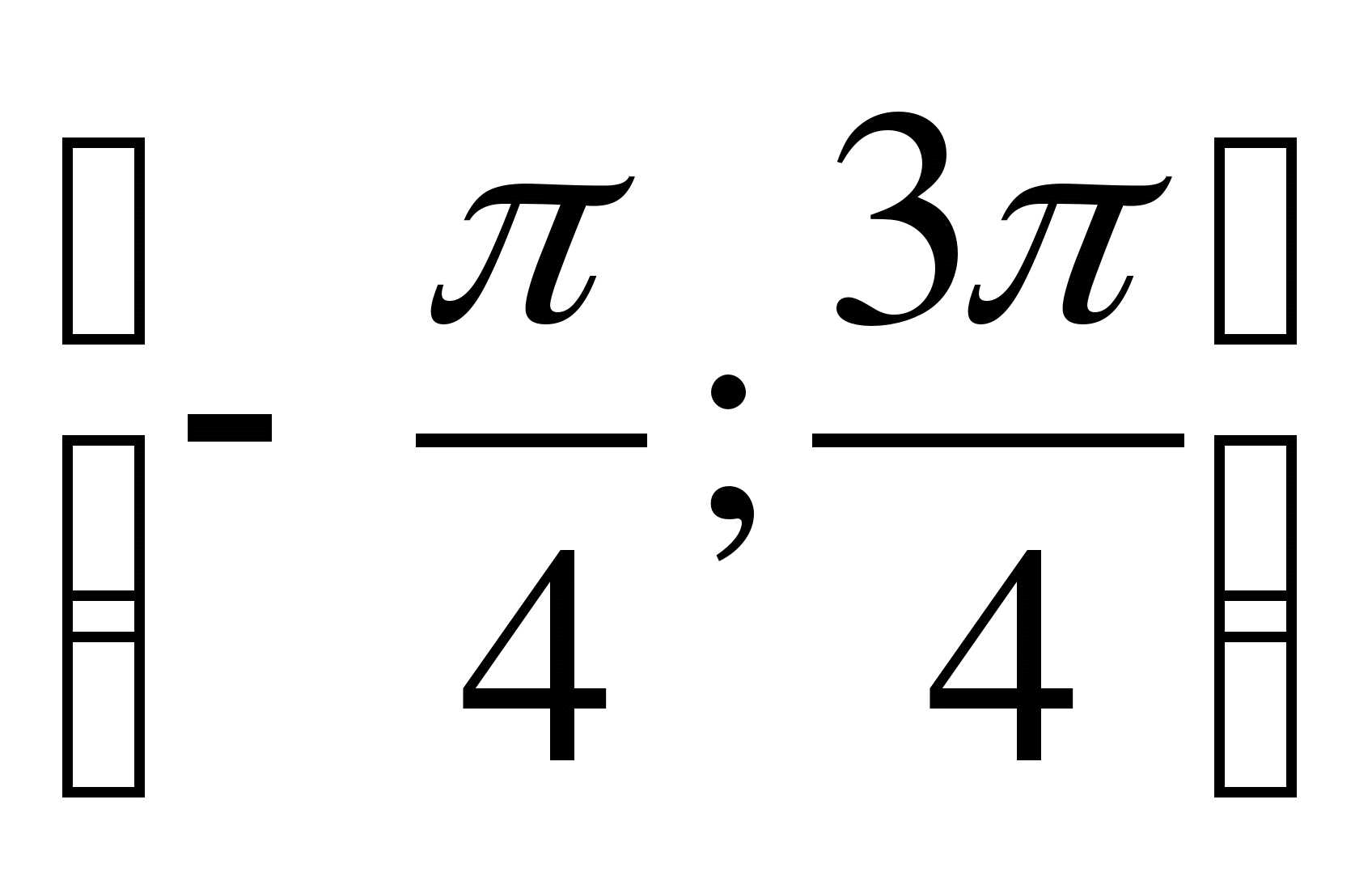 .
.
С2. Постройте график функции 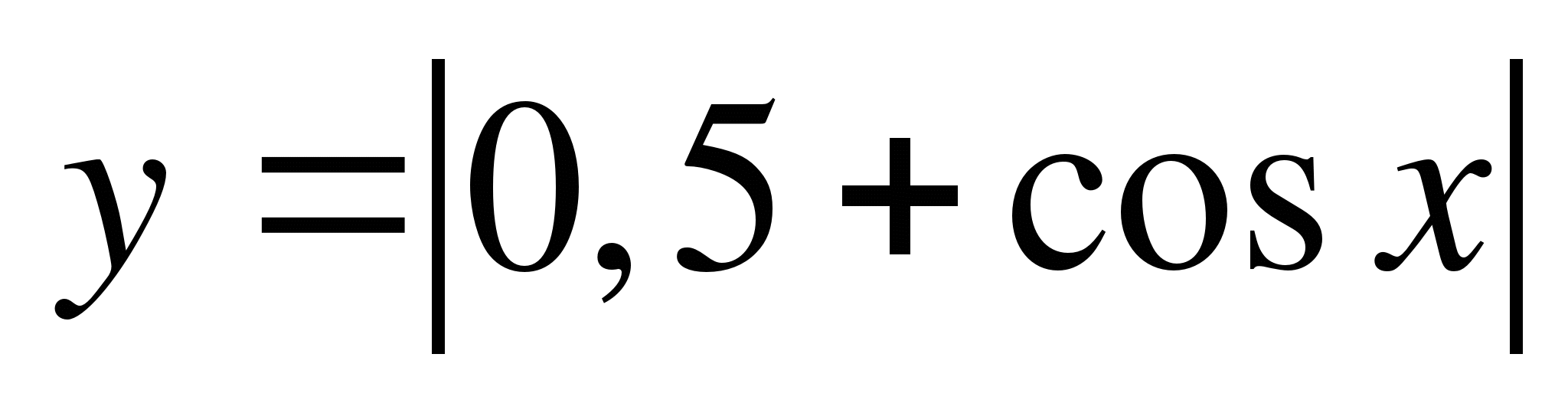 .
.
Нормы оценок: «3» - 5А, «4» - 4А + 1В, «5» - 3А + 1В +1С или 2А + 2В + 1С.
_________________________________________________________________
Контрольная работа № 1.
Тригонометрические функции
Вариант 2
А1. Найдите область определения функции 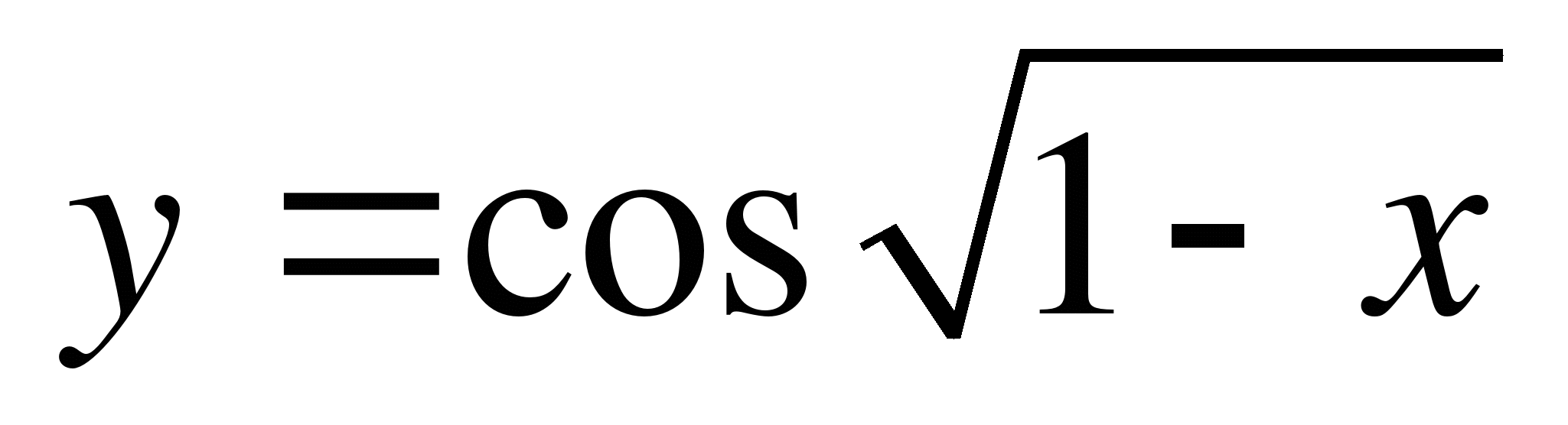 .
.
А2. Найдите множество значений функции 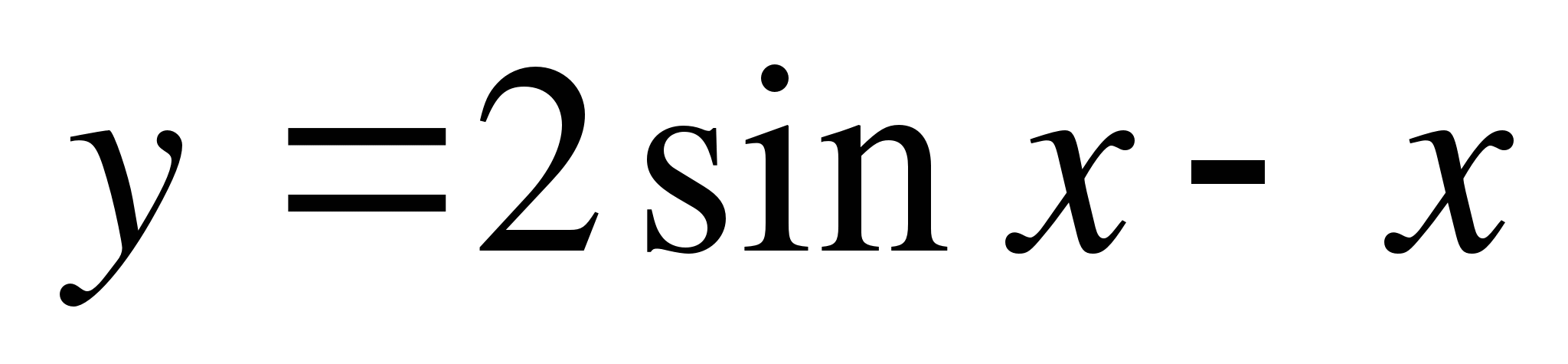 .
.
А3. Выясните, является ли данная функция четной или нечетной: 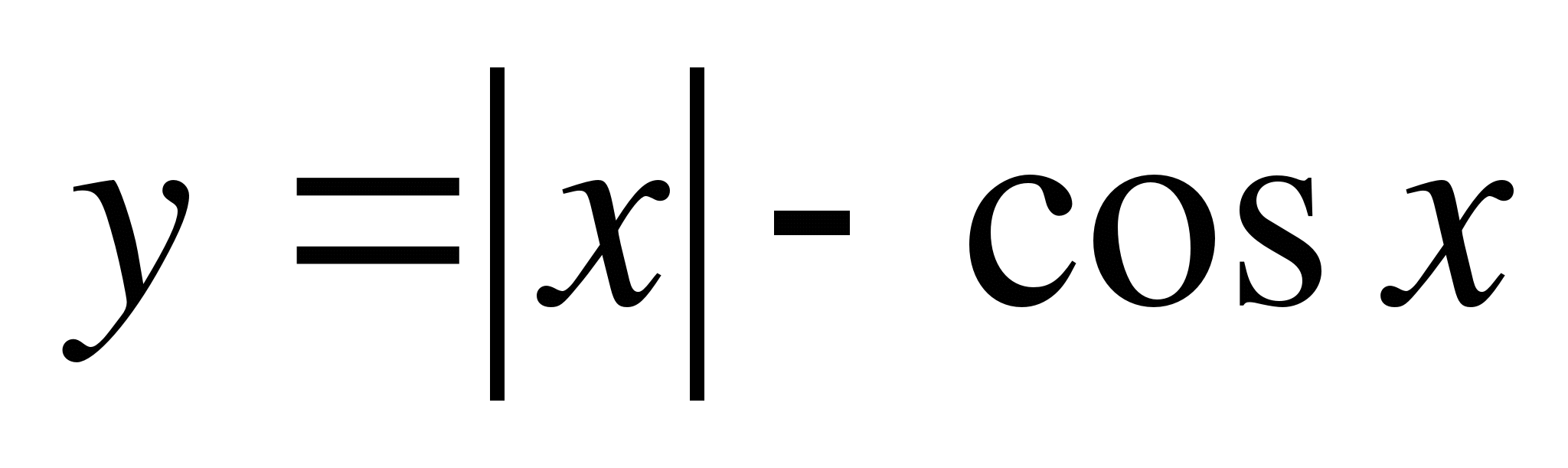 .
.
А4. Докажите, что функция у = tg 3x является периодической с периодом Т = 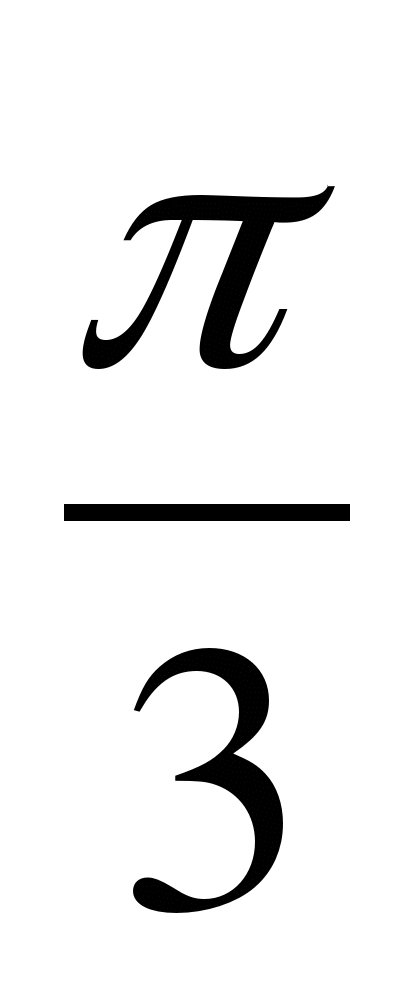 .
.
А5. Сравните числа: sin 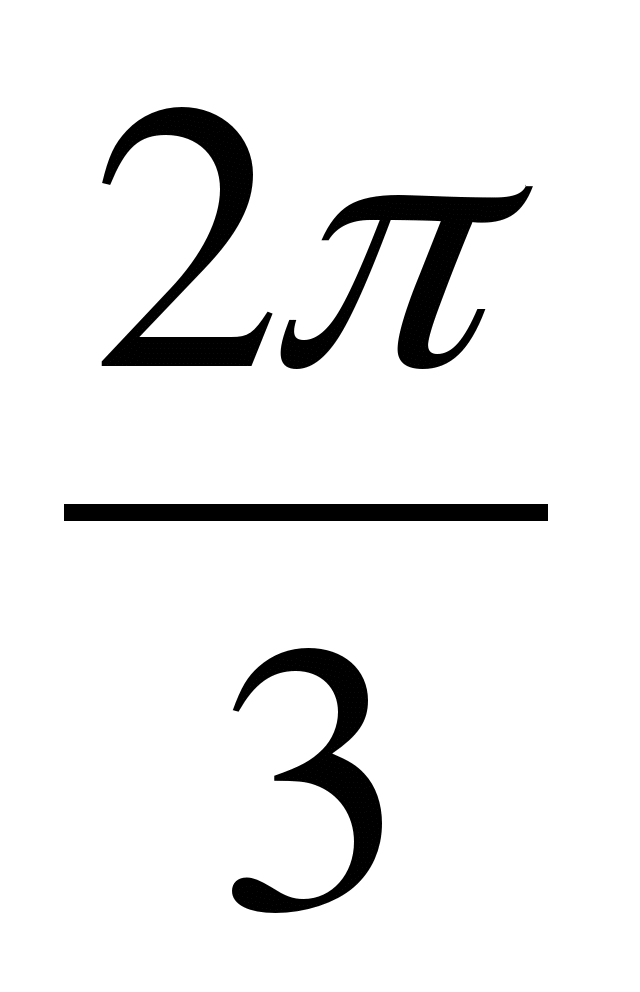 и sin
и sin 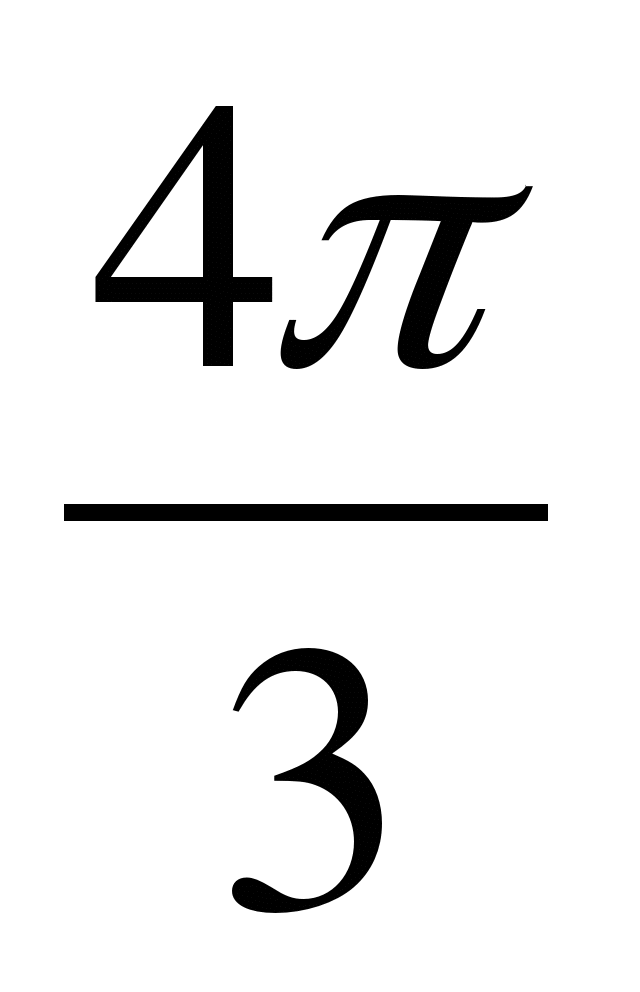 .
.
A6. Найдите значение функции 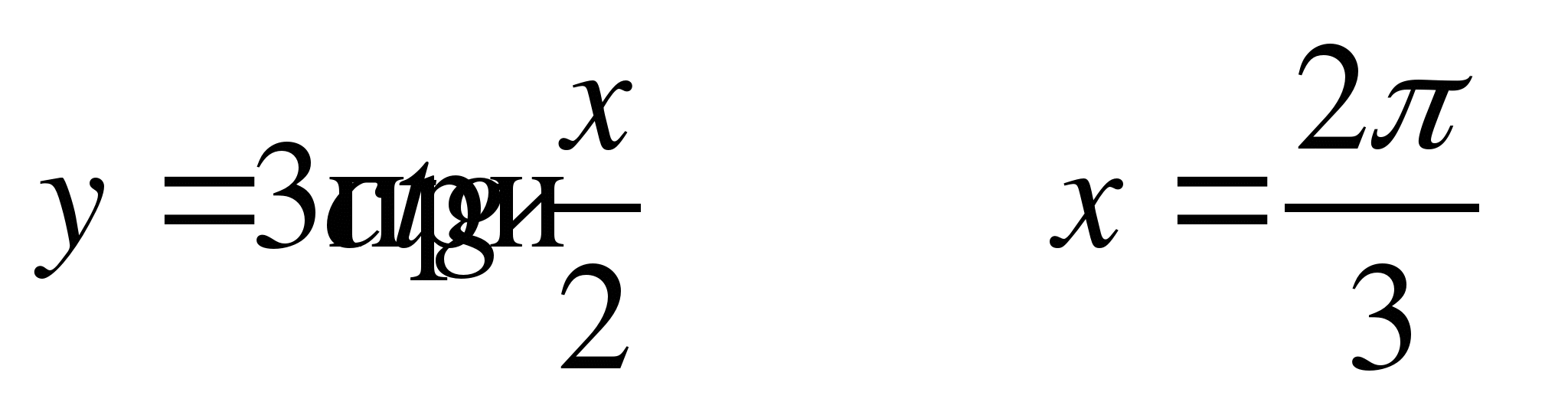 .
.
В1. Сравните числа: 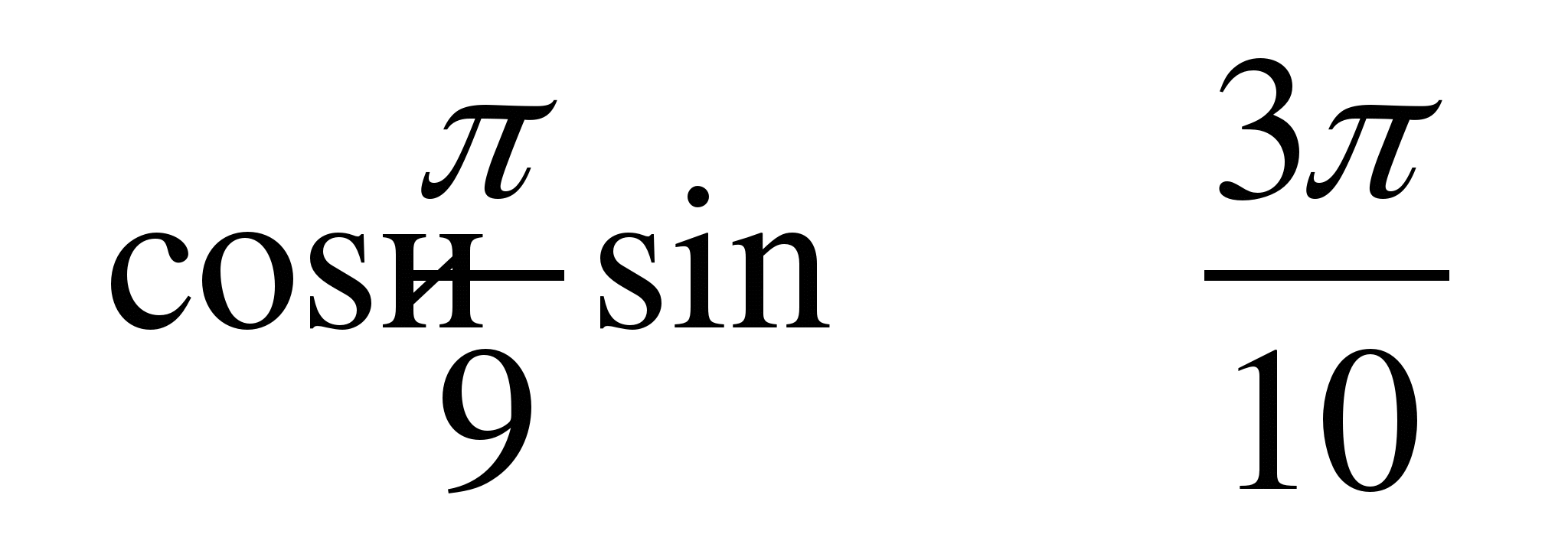 .
.
В2.Найти все корни уравнения 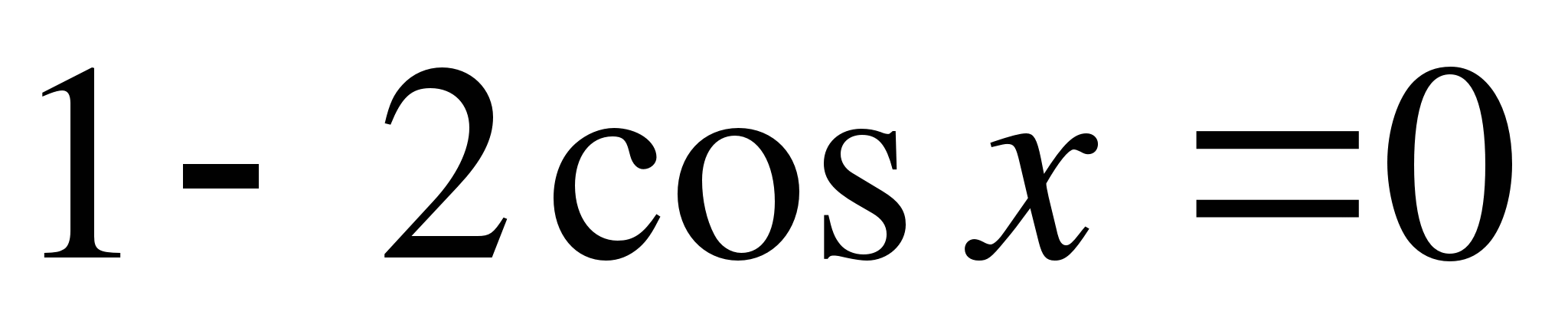 , принадлежащие промежутку [-p;p].
, принадлежащие промежутку [-p;p].
С1. Найдите наибольшее и наименьшее значение функции 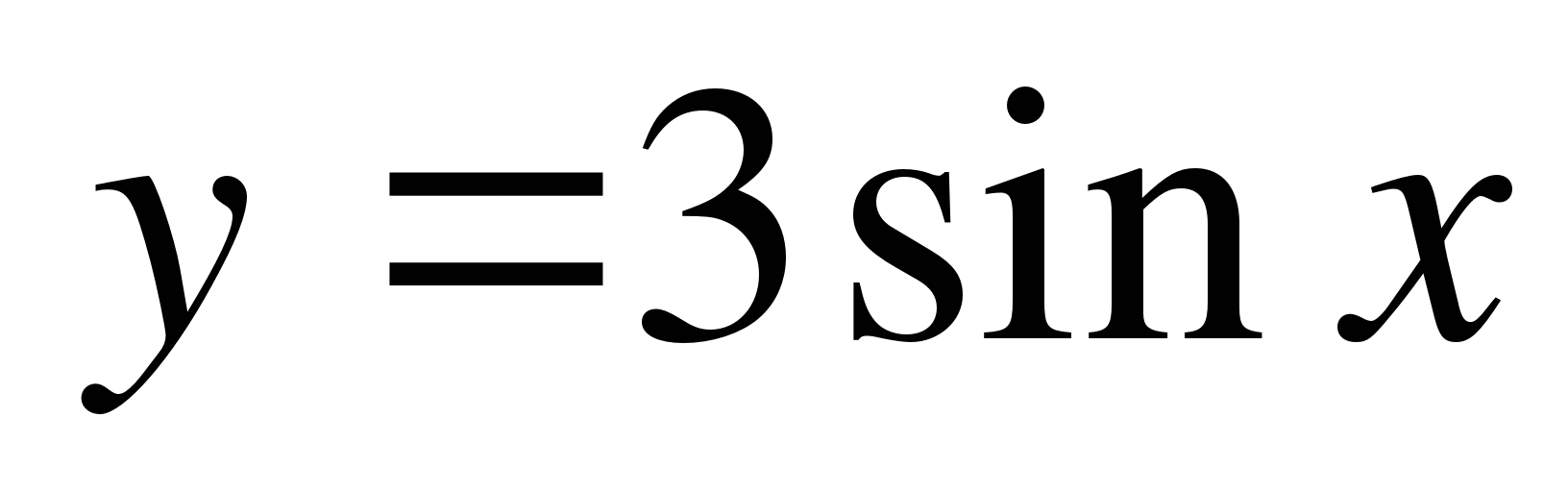 на отрезке
на отрезке 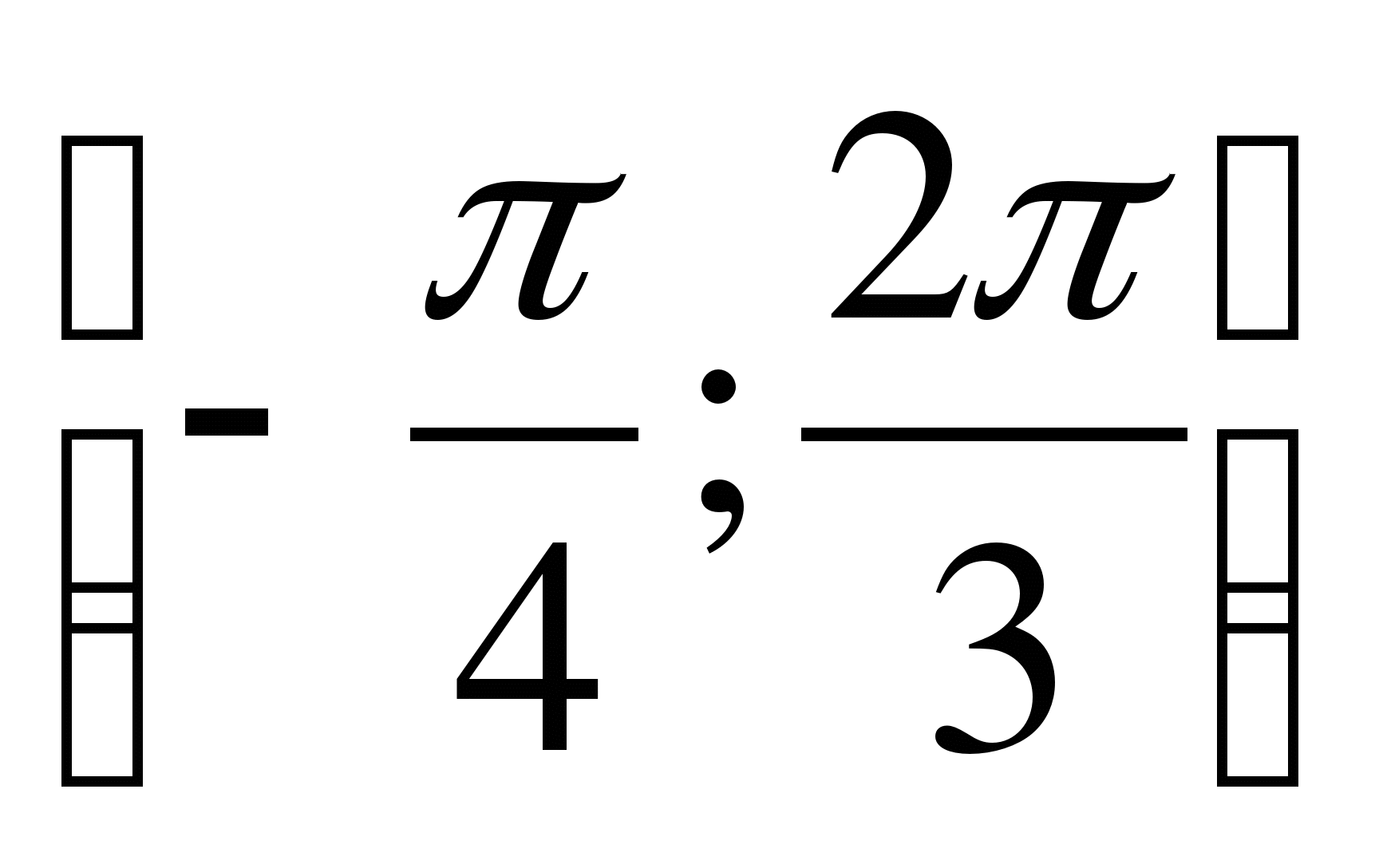 .
.
С2. Построить график функции 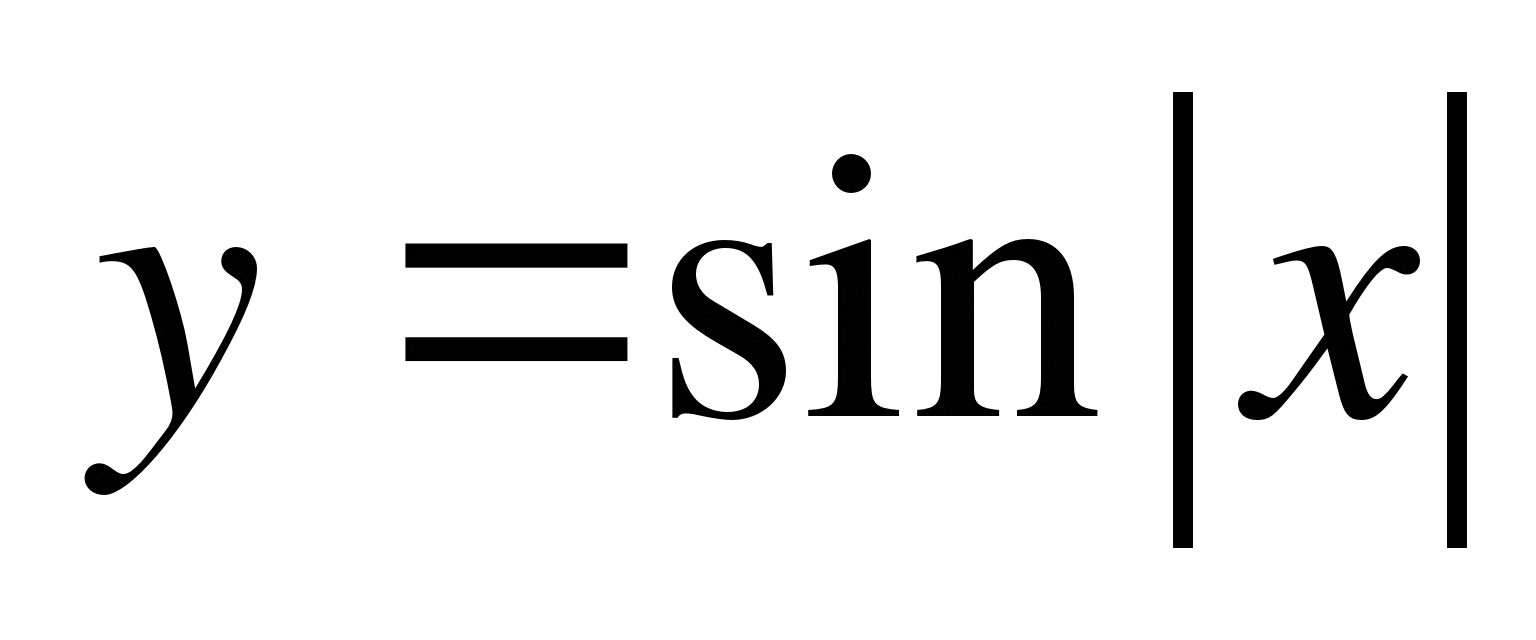 .
.
Нормы оценок: «3» - 5А, «4» - 4А + 1В, «5» - 3А + 1В +1С или 2А + 2В + 1С.
Контрольная работа № 1
Тригонометрические функции
Вариант 3
А1. Найдите область определения функции у = sin 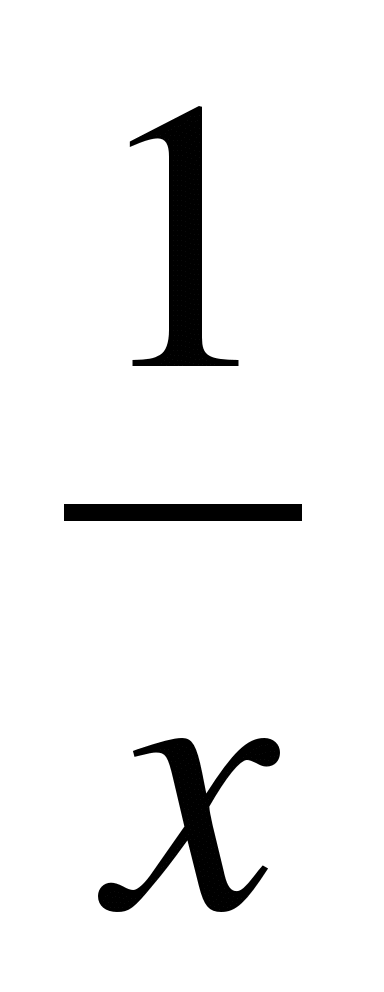 .
.
А2. Найдите множество значений функции у = 1 –2sin x.
А3. Выяснить, является ли данная функция четной или нечетной: у = 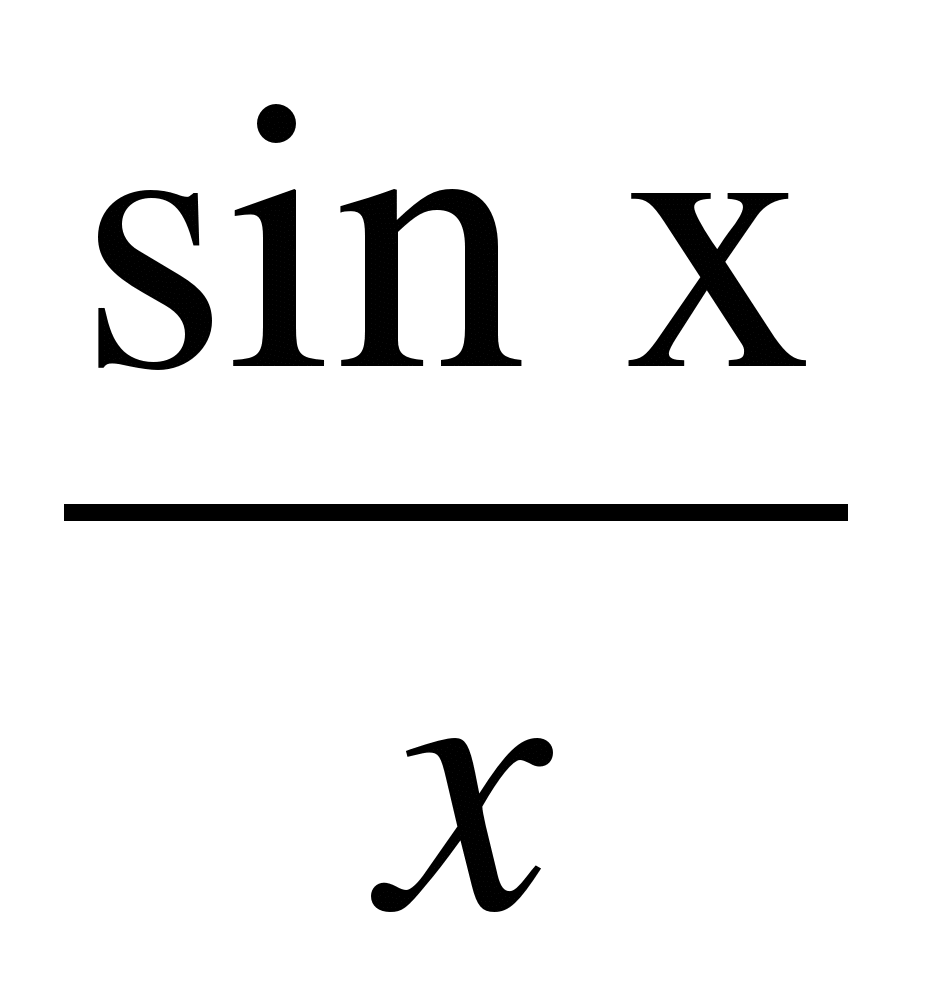 .
.
А4. Докажите, что функция у = cos 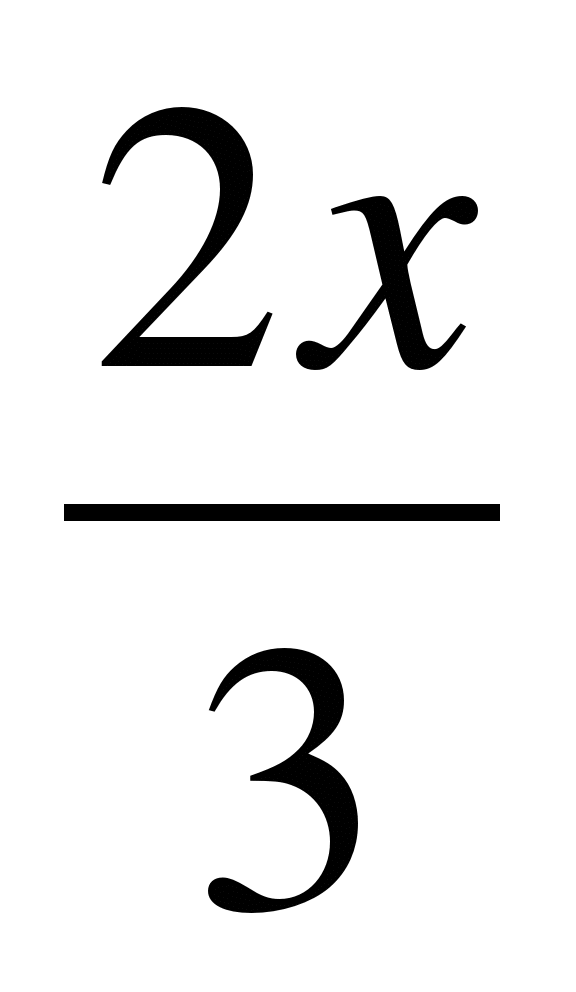 является периодической с периодом Т=3p.
является периодической с периодом Т=3p.
А5. Сравните числа: tg 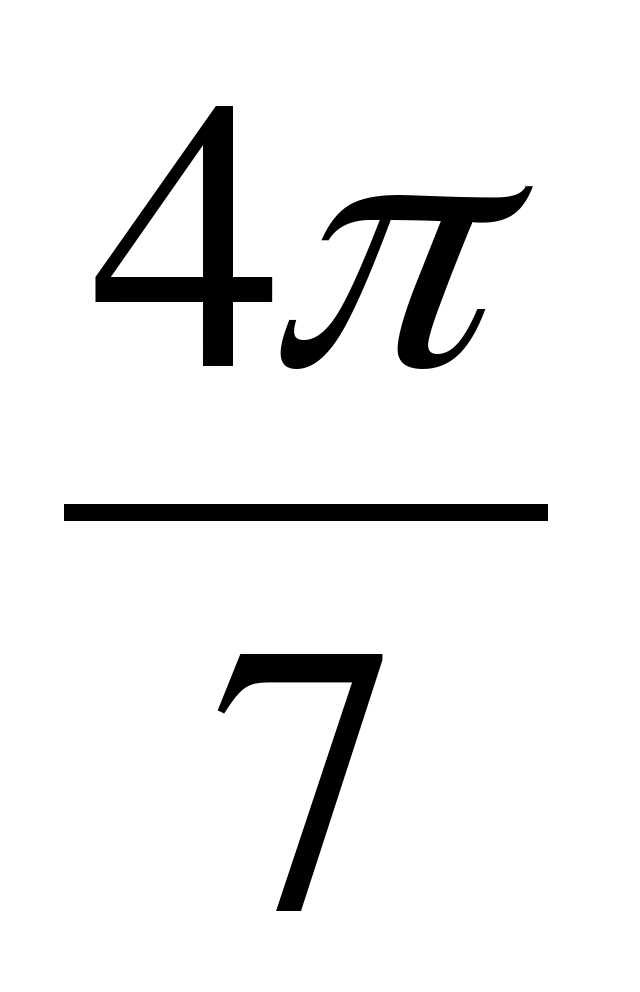 и tg
и tg 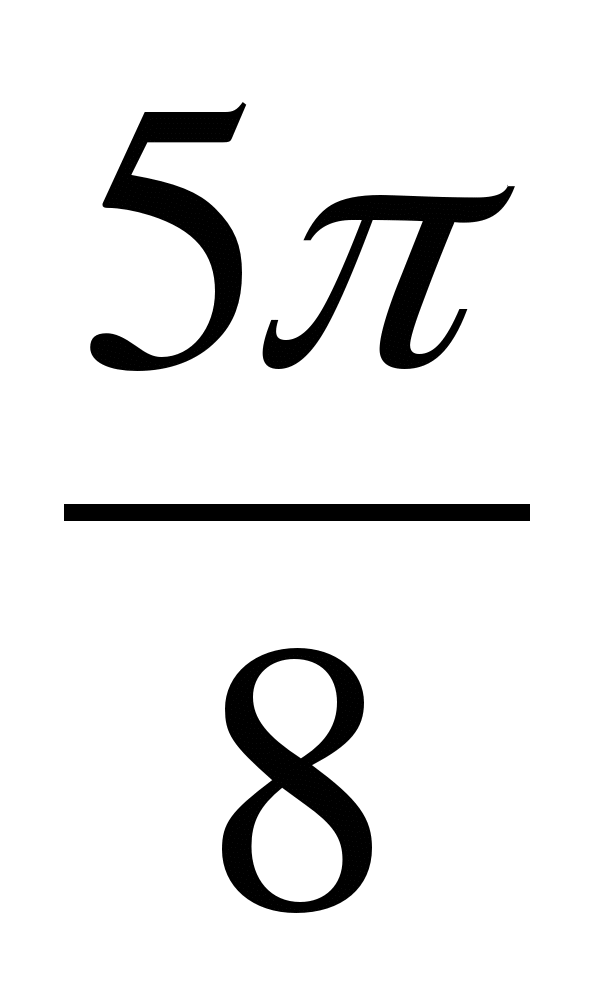 .
.
A6. Найдите значение функции у=3cos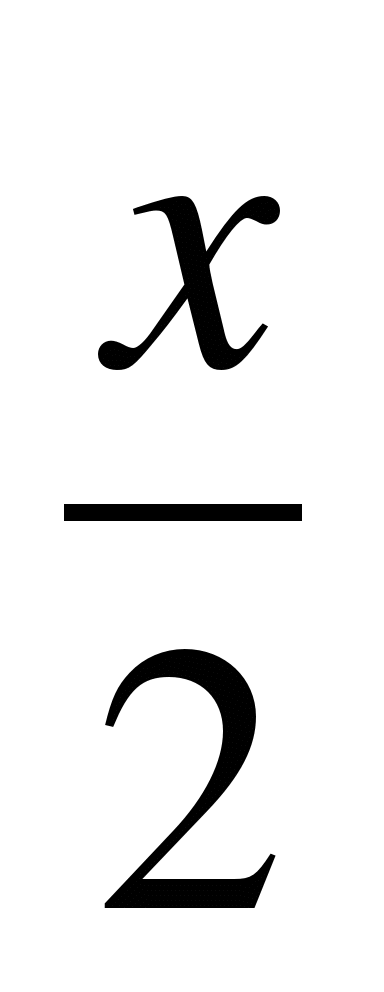 при х =
при х = 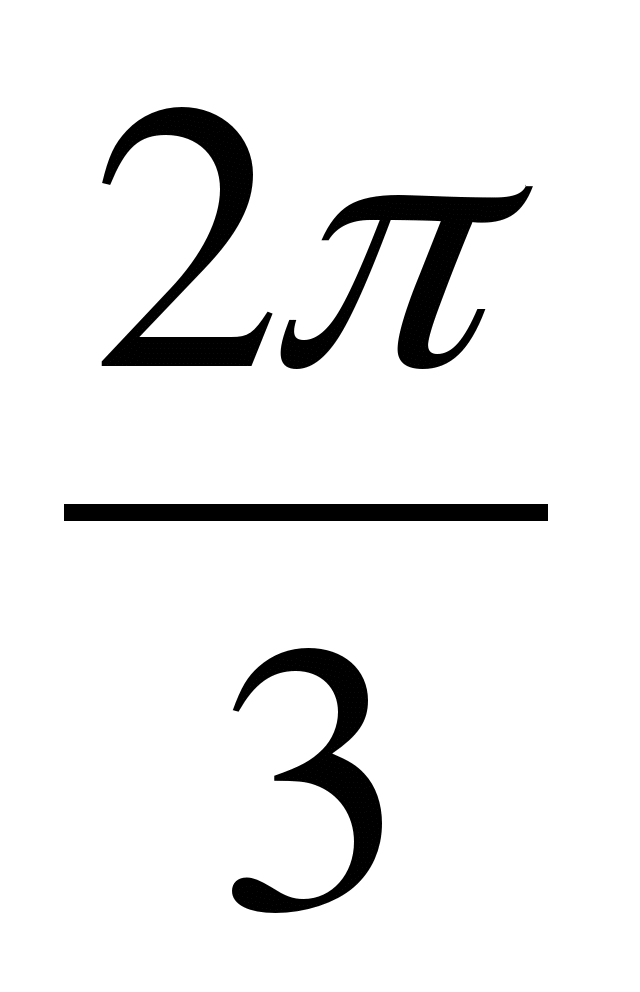 .
.
В1. Сравните числа: sin 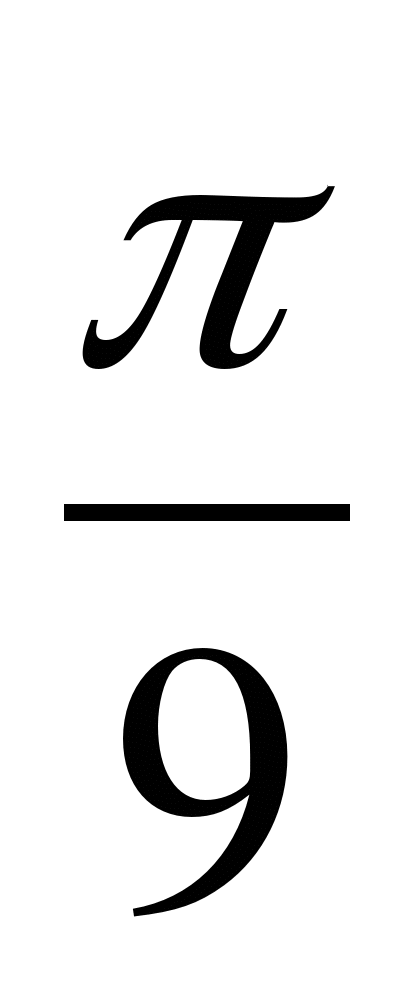 и cos
и cos 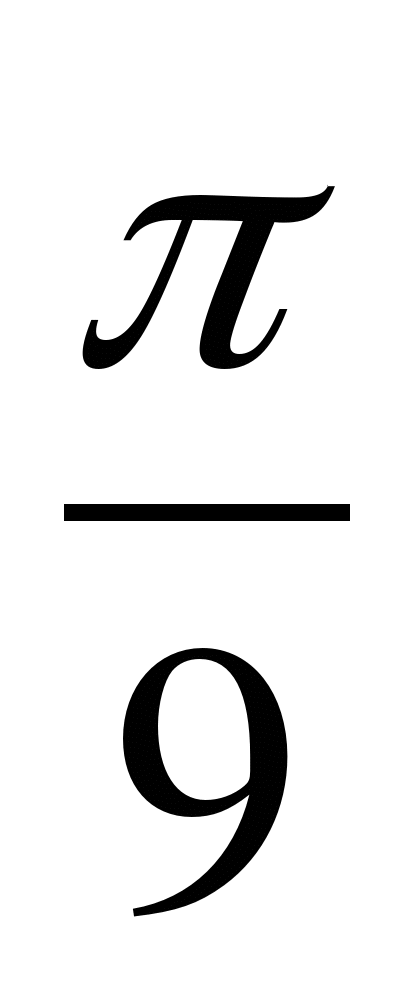 .
.
В2. Найдите все корни уравнения 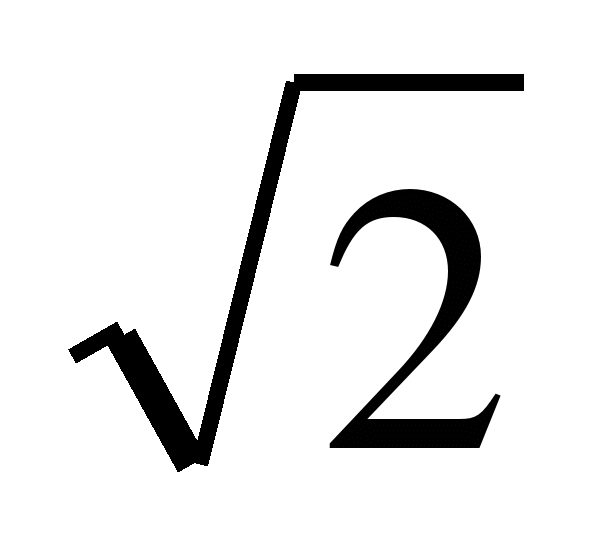 sin x = 1, принадлежащие промежутку [-p;p].
sin x = 1, принадлежащие промежутку [-p;p].
С1. Найдите наибольшее и наименьшее значение функции у=4tgx на отрезке 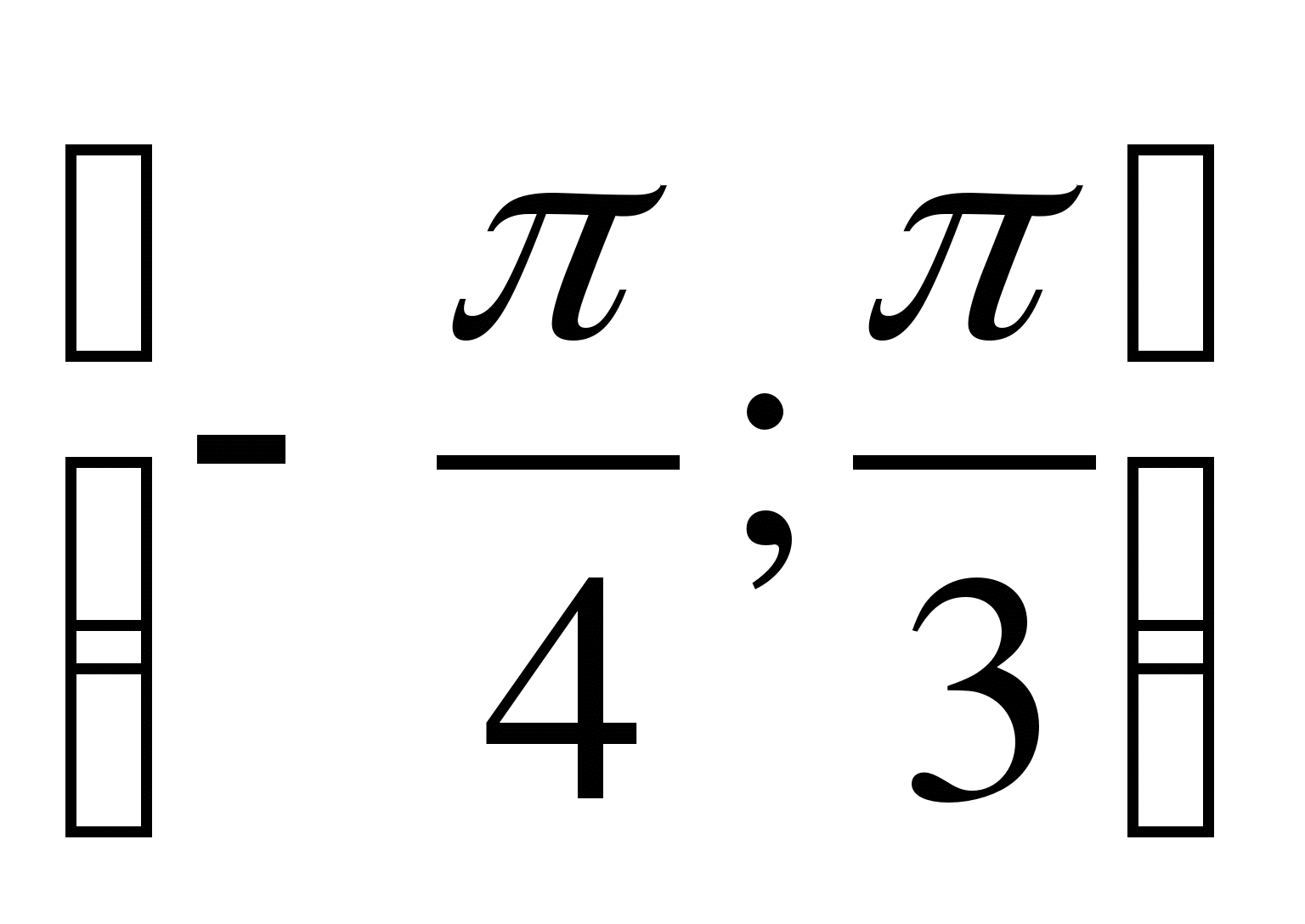 .
.
С2. Построить график функции 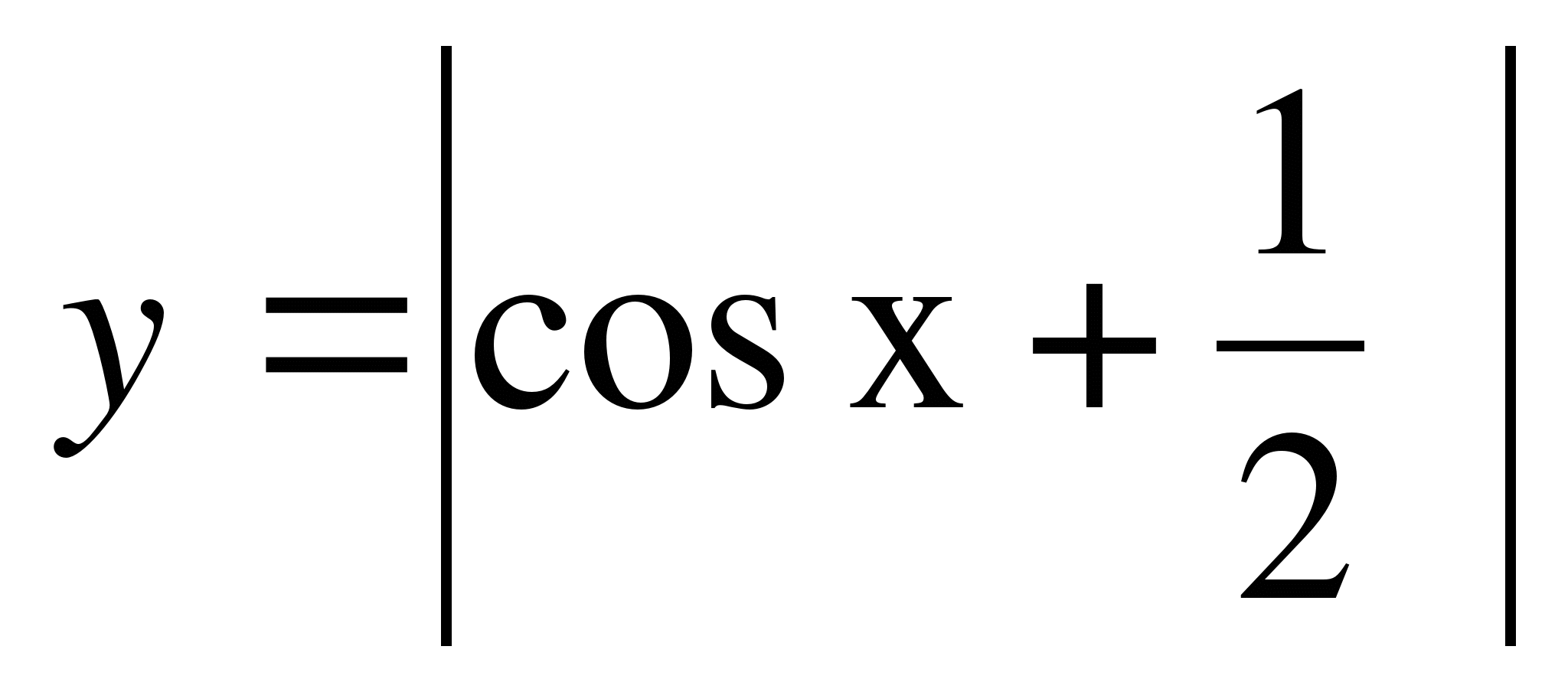 .
.
Нормы оценок: «3» - 5А, «4» - 4А + 1В, «5» - 3А + 1В +1С или 2А + 2В + 1С.
Контрольная работа № 1
Тригонометрические функции
Вариант 4
А1. Найти область определения функции у = cos 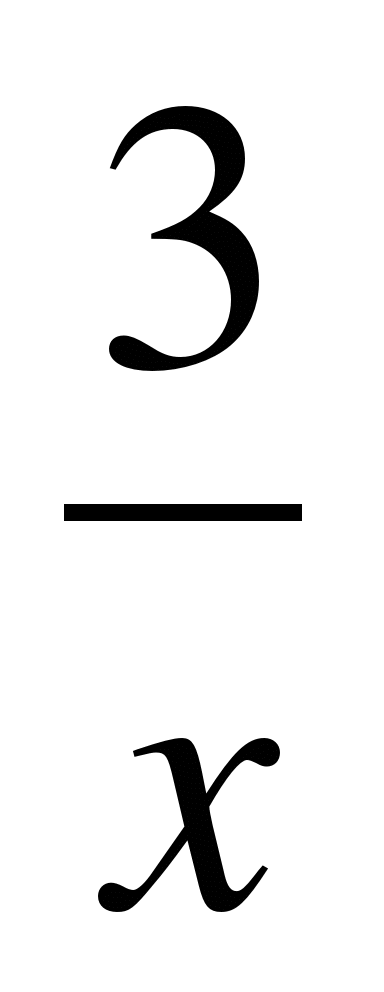 .
.
А2. Найти множество значений функции у = 3sin x.
А3. Выяснить, является ли данная функция четной или нечетной: у = tg x – x3.
А4. Доказать, что функция у = cos 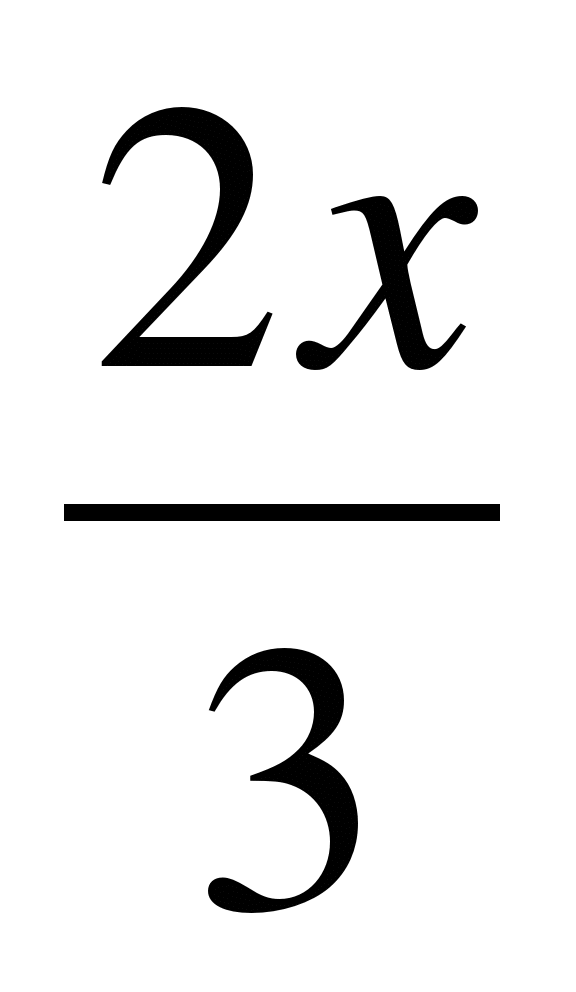 является периодической с периодом Т=3p.
является периодической с периодом Т=3p.
А5. Возрастает или убывает функция у = sin x на отрезке 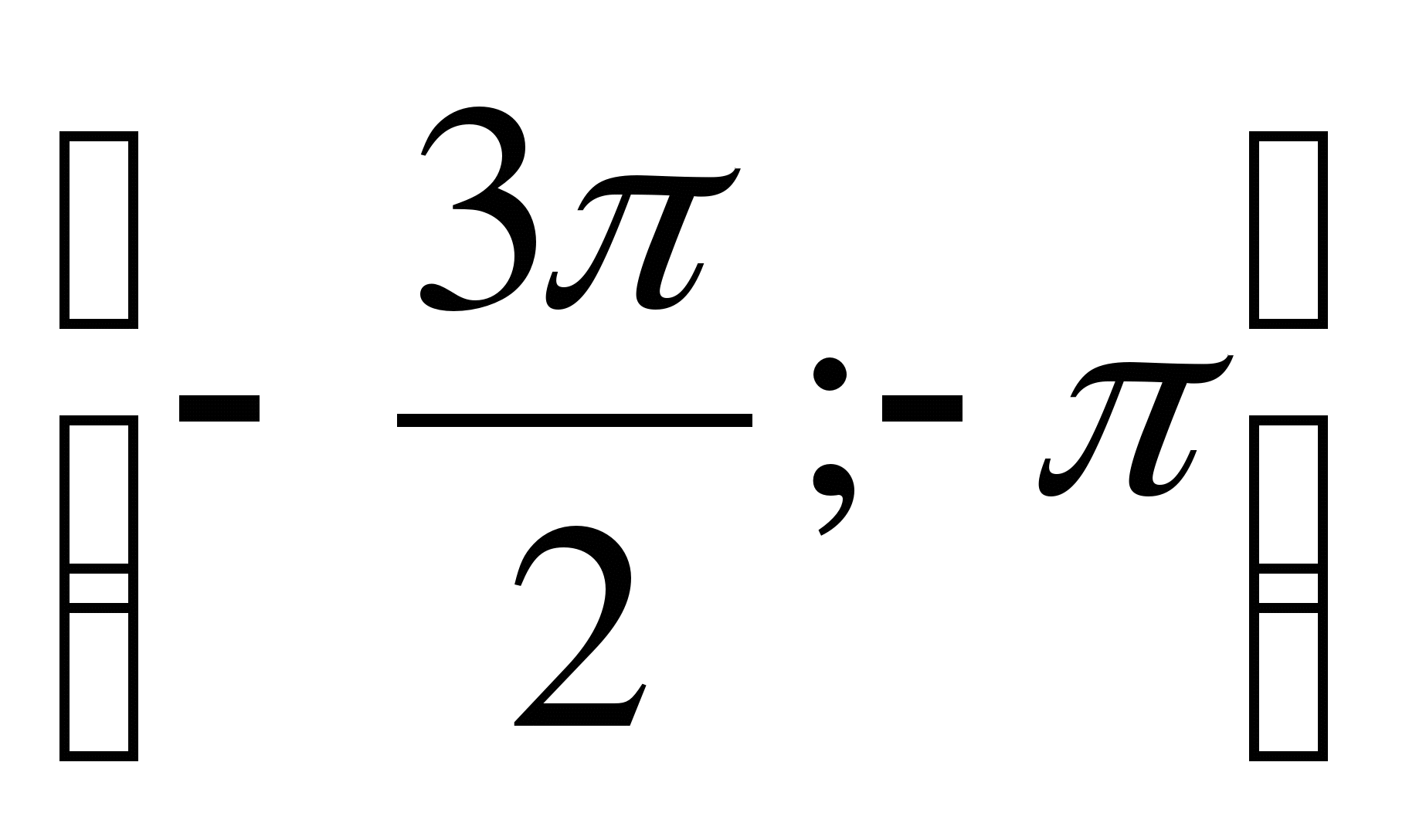 ?
?
A6. Найдите значение функции у=4sin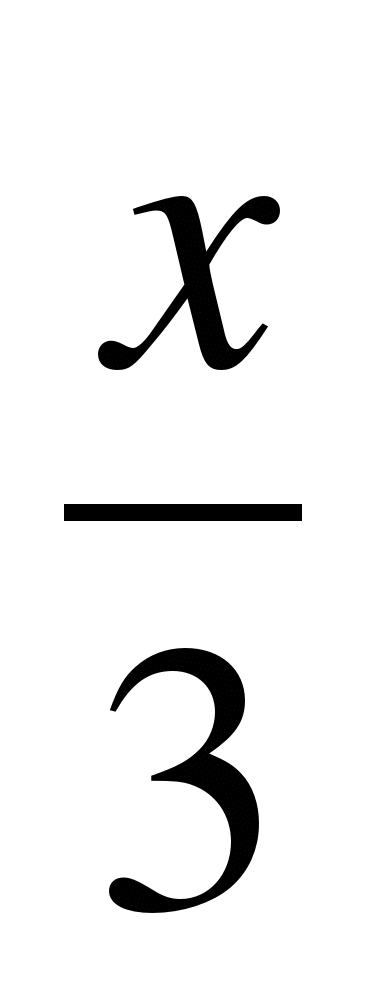 при х =
при х = 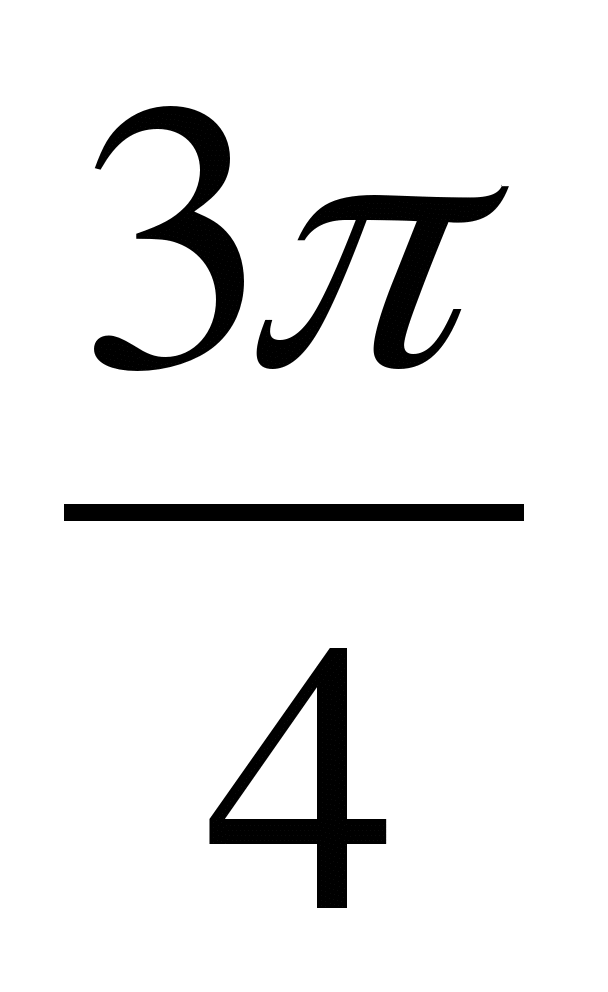 .
.
В1. Сравните числа: cos 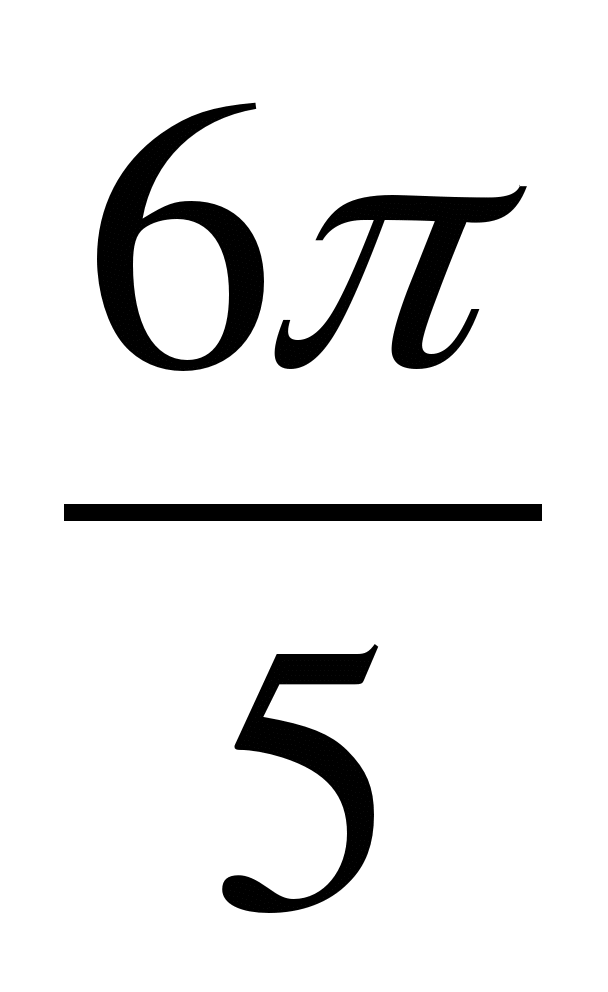 и sin
и sin 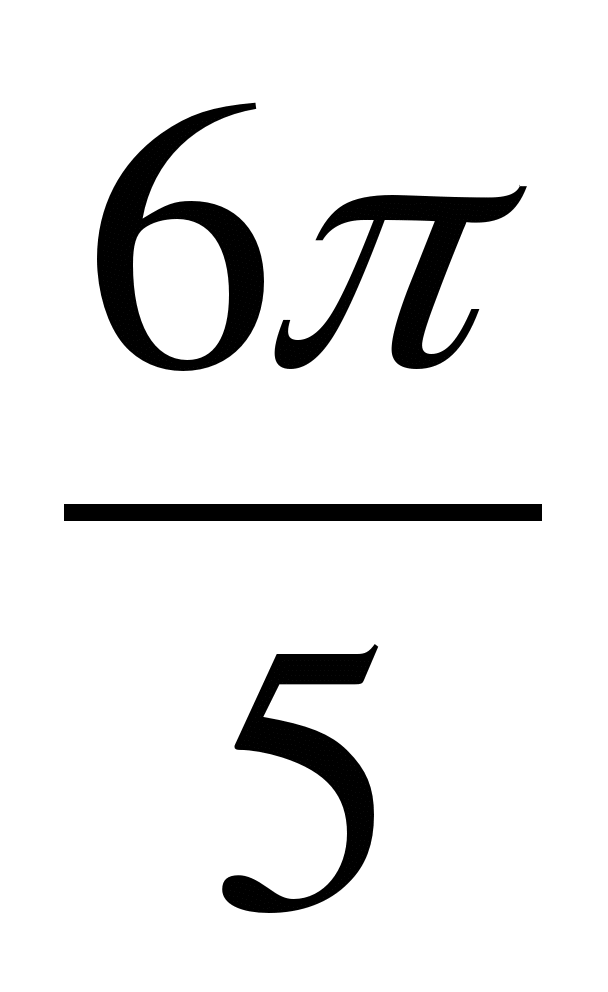 .
.
В2. Найдите все корни уравнения 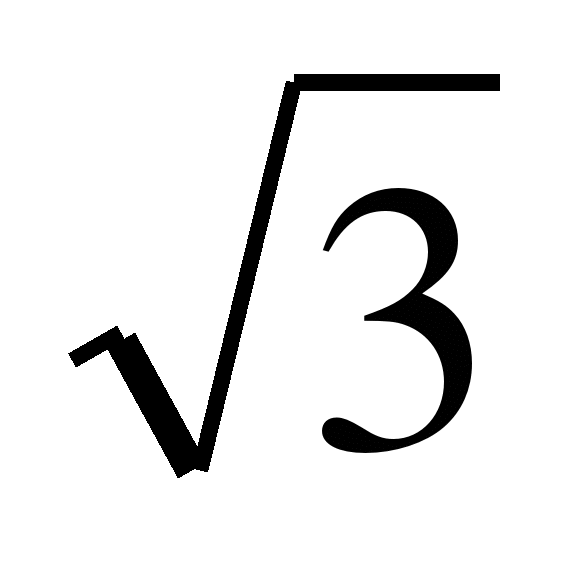 + 2cos x = 0, принадлежащие промежутку
+ 2cos x = 0, принадлежащие промежутку
[0; 2p].
С1. Найдите наибольшее и наименьшее значение функции у=4cosx на отрезке 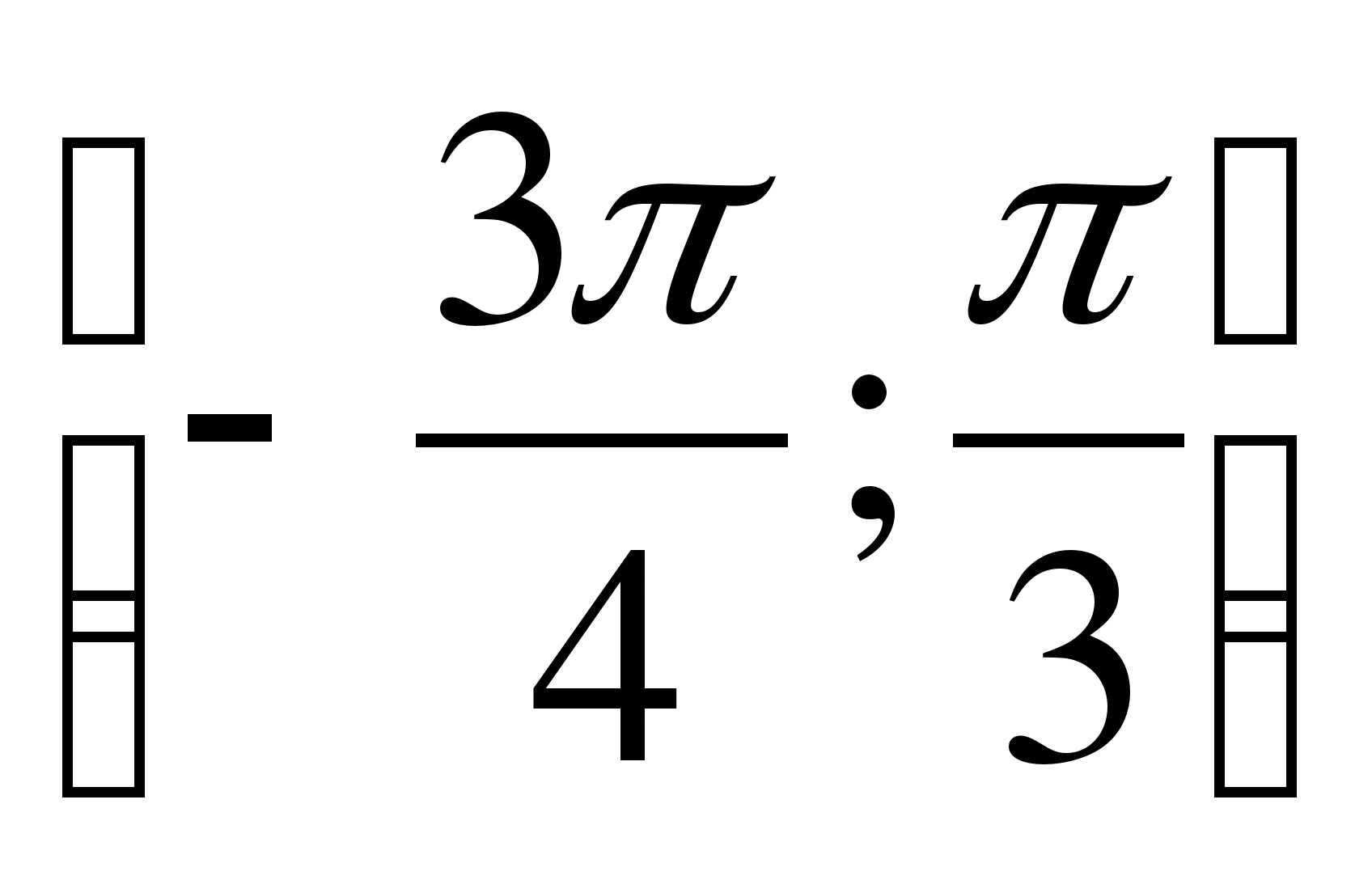 .
.
С2. Построить график функции у = |sin x| +1
Нормы оценок: «3» - 5А, «4» - 4А + 1В, «5» - 3А + 1В +1С или 2А + 2В + 1С.
infourok.ru
1 вариант
№ 1 Найти область определения и
множество значений функции
У=
У=2
№2 Исследовать функцию на четность
или нечетность
У=
У=
№3 Доказать, что функция у=
периодическая и найти ее
наименьший положительный период.
№4 Найти все принадлежащие
отрезку корни уравнения
№5 Найти все принадлежащие
отрезку-π;2π решения неравенства
соs≥
2 вариант
№ 1 Найти область определения и
множество значений функции
У=
У=3
№2 Исследовать функцию на четность
или нечетность
У=
У=
№3 Доказать, что функция у=
периодическая и найти ее
наименьший положительный период.
№4 Найти все принадлежащие
отрезку корни уравнения
№5 Найти все принадлежащие
отрезку-3π;0 решения неравенства
соs≤
3 вариант
№ 1 Найти область определения и
множество значений функции
У=
У=2
№2 Исследовать функцию на четность
или нечетность
У=
У=
№3 Доказать, что функция у=
периодическая и найти ее
наименьший положительный период.
№4 Найти все принадлежащие
отрезку корни уравнения
№5 Найти все принадлежащие
отрезку-2π;π решения неравенства
соs≥
4 вариант
№1 Найти область определения и
множество значений функции
У=
У=
№2 Исследовать функцию на четность
или нечетность
У=
У=
№3 Доказать, что функция у=
периодическая и найти ее
наименьший положительный период.
№4 Найти все принадлежащие
отрезку корни уравнения
№5 Найти все принадлежащие
отрезку-0.5π;2.5π решения
неравенства sin≤
5 вариант
№1 Найти область определения и
множество значений функции
У=
У=2
№2 Исследовать функцию на четность
или нечетность
У=
У=
№3 Доказать, что функция у=
периодическая и найти ее
наименьший положительный период.
№4 Найти все принадлежащие
отрезку корни уравнения
№5 Найти все принадлежащие
отрезку-π;2π решения неравенства
соs≥
6 вариант
№1 Найти область определения и
множество значений функции
У=
У=2
№2 Исследовать функцию на четность
или нечетность
У=
У=
№3 Доказать, что функция у=
периодическая и найти ее
наименьший положительный период.
№4 Найти все принадлежащие
отрезку корни уравнения
№5 Найти все принадлежащие
отрезку-2π;π решения неравенства
tg≥1
7 вариант
№1 Найти область определения и
множество значений функции
У=
У=
№2 Исследовать функцию на четность
или нечетность
У=
У=
№3 Доказать, что функция у=
периодическая и найти ее
наименьший положительный период.
№4 Найти все принадлежащие
отрезку корни уравнения
№5 Найти все принадлежащие
отрезку-π;2π решения неравенства
8 вариант
№1 Найти область определения и
множество значений функции
У=
У=2
№2 Исследовать функцию на четность
или нечетность
У=
У=
№3 Доказать, что функция у=
периодическая и найти ее
наименьший положительный период.
№4 Найти все принадлежащие
отрезку корни уравнения
№5 Найти все принадлежащие
отрезку-2π;π решения неравенства
соs≤
uchitelya.com
Контрольная работа
По теме «Тригонометрические функции и их свойства».
Выполнил ученик 9 класса ___________________________________
Вариант I
Результаты:
1-1
1-2
1-3
1-4
1-5
2а
2б
2в
2а
2б
3в
4а
4б
4в
5а
5б
5в
6а
6б
6в
6г
7а
7б
⅀
оц
№1 (по 1 баллу) Отметьте данный угол на тригонометрической окружности:
1) 600 2) 1575 3) -750 4)-1020 5) 810




№2 Найдите значение выражения (по 1 баллу)
а)  б)
б)  . в)
. в)  .
.
Отв: Отв:
Отв: Отв:
Отв:
№3 Найдите значение выражения (по 2 балла)
а) 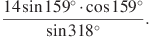 б)
б) 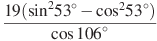 . в)
. в) 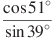
Отв: Отв:
Отв: Отв:
Отв:
№4 Найдите значение выражения (по 2 балла)
а) 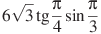 б)
б) 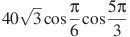 в)
в) 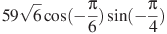 ..
..
Отв: Отв:
Отв: Отв:
Отв:
№5 Найдите значение выражения (по 2 балла)
а) 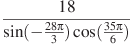 . б)
. б) 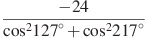 . в)
. в) 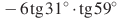
Отв: Отв:
Отв: Отв:
Отв:
№6 Найдите (по 2 балла)
а) 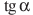 , если
, если 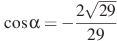 и
и  .б)
.б) 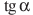 , если
, если 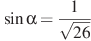 и
и 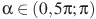


Отв: Отв:
Отв:
в) , если
, если 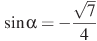 и
и 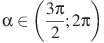 .г)
.г)  , если
, если  .
.


Отв: Отв:
Отв:
№7 Найдите значение выражения (по 3 балла)
а) 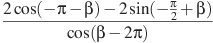 . б)
. б) 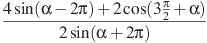 .
.


Отв: Отв:
Отв:
Контрольная работа
По теме «Тригонометрические функции и их свойства».
Выполнил ученик 9 класса ___________________________________
Вариант II
Результаты:
1-1
1-2
1-3
1-4
1-5
2а
2б
2в
2а
2б
3в
4а
4б
4в
5а
5б
5в
6а
6б
6в
6г
7а
7б
⅀
оц
№1 (1 балл) Отметьте данный угол на тригонометрической окружности:
1) -495 2) -1650 3) 1020 4)690 5) 990





№2 Найдите значение выражения (по 1 баллу)
а)  . б)
. б)  в)
в) 
Отв: Отв:
Отв: Отв:
Отв:
№3 Найдите значение выражения (по 2 балла)
а) 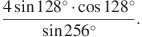 б)
б) 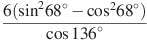 в)
в)  .
.
Отв: Отв:
Отв: Отв:
Отв:
№4 Найдите значение выражения (по 2 балла)
а)  . б)
. б) 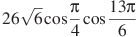 . в)
. в) 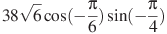 .
.
Отв: Отв:
Отв: Отв:
Отв:
№5 Найдите значение выражения (по 2 балла)
а) 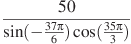 . б)
. б) 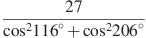 . в)
. в) 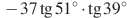 .
.
Отв: Отв:
Отв: Отв:
Отв:
№6 Найдите (по 2 балла)
а) 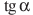 , если
, если 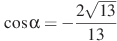 и
и  .б)
.б) 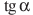 , если
, если 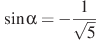 и
и 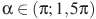 .
.


Отв: Отв:
Отв:
в) , если
, если 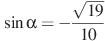 и
и 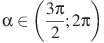 .г)
.г)  , если
, если  .
.


Отв: Отв:
Отв:
№7 Найдите значение выражения (по 3 балла)
а) 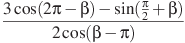 . б)
. б) 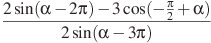 ..
..


Отв: Отв:
Отв:
doc4web.ru