
Какая бы задача не стояла перед системой, объединяющей последовательность применения статистических методов, всегда начинают со сбора исходных данных, на базе которых затем применяют тот или иной инструмент. Контрольный листок (или лист) — это инструмент для сбора данных и автоматического их упорядочения для облегчения дальнейшего использования собранной информации.
Обычно контрольный листок представляет собой бумажный бланк, на котором заранее напечатаны контролируемые параметры, согласно которым можно заносить в листок данные с помощью пометок или простых символов. Он позволяет автоматически упорядочить данные без их последующего переписывания. Таким образом, контрольный листок — хорошее средство регистрации данных.
Число различных контрольных листков исчисляется сотнями, и в принципе для каждой конкретной цели может быть разработан свой листок. Но принцип их оформления остается неизменным. Например, график температуры больного — один из возможных типов контрольных листков. В качестве другого примера можно привести контрольный листок, применяемый для фиксирования отказавших деталей в телевизорах (рисунок 1).

Рисунок 1. — Пример контрольного листка
На основании собранных с помощью этих контрольных листков данных не представляет труда составить таблицу суммарных отказов (таблица 1):
Таблица 1 — суммарные отказы
| По всем моделям | Число отказов | Процент от общего числа отказов |
| Интегральные схемы | 8 | 6,8 |
| Конденсаторы | 77 | 65,2 |
| Сопротивления | 4 | 3,4 |
| Трансформаторы | 8 | 6,8 |
| Переключатели | 19 | 15,3 |
| Трубки | 3 | 2,5 |
| Итого | 119 | 100 |
При составлении контрольных листков следует обратить внимание на то, чтобы было указано, кто, на каком этапе процесса и в течение какого времен собирал данные, а также чтобы форма листка была простой и понятной без дополнительных пояснений. Важно и то, чтобы все данные добросовестно фиксировались, и собранная в контрольном листке информация могла быть использована для анализа процесса.
Для наглядного представления тенденции изменения наблюдаемых значений применяют графическое изображение статистического материала. Наиболее распространенным графиком, к которому прибегают при анализе распределения случайной величины при проведении контроля качества, является гистограмма.
Гистограмма — это инструмент, позволяющий зрительно оценить закон распределения статистических данных.
Гистограмма распределения обычно строится для интервального изменения значения параметра. Для этого на интервалах, отложенных на оси абсцисс, строят прямоугольники (столбики), высоты которых пропорциональны частотам интервалов. По оси ординат откладывают абсолютные значения частот (см. рисунок). Аналогичную форму гистограммы можно получить, если по оси ординат отложить соответствующие значения относительных частот. При этом сумма площадей всех столбиков будет равна единице, что оказывается удобно. Гистограмма также очень удобна для визуальной оценки расположения статистических данных в пределах допуска. Чтобы оценить адекватность процесса требованиям потребителя, мы должны сравнить качество процесса с полем допуска, установленным пользователем. Если имеется допуск, то на гистограмму наносят верхнюю (SU) и нижнюю (SL) его границы в виде линий, перпендикулярных оси абсцисс, чтобы сравнить распределение параметра качества процесса с этими границами. Тогда можно увидеть, хорошо ли располагается гистограмма внутри этих границ.
Пример построения гистограммы.
На рисунке 2 в качестве примера приведена гистограмма значений коэффициентов усиления 120 проверенных усилителей. В ТУ на эти усилители указано номинальное значение коэффициента SN на этот тип усилителей, равное 10дБ. В ТУ также установлены допустимые значения коэффициента усиления: нижняя граница допуска SL = 7,75 дБ, а верхняя SU = 12,25 дБ. При этом ширина поля допуска Т равна разности значений верхней и нижней границ допуска Т = SU – SL.
Если расположить все значения коэффициентов усиления в ранжированный ряд, все они будут находиться в пределах поля допуска, что создаст иллюзию отсутствия проблем. При построении гистограммы сразу становится очевидным, что распределение коэффициентов усиления хотя и находится в пределах допуска, но явно сдвинуто в сторону нижней границы и у большинства усилителей значение этого параметра качества меньше номинала. Это, в свою очередь, дает дополнительную информацию для дальнейшего анализа проблем.
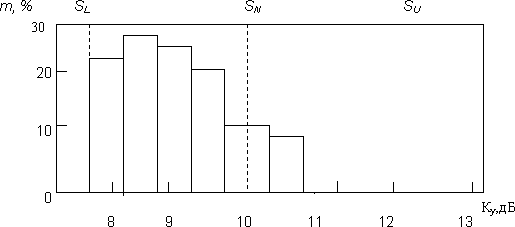
Рисунок 2 — Пример построения гистограммы
studfiles.net
Для анализа результатов контроля качества при крупносерийном и массовом производстве широкое распространение получили методы статистического контроля качества (Statistical Quality Control - SQC). Наиболее известными среди них стали «семь инструментов контроля качества», которые сначала широко применялись в кружках качества в Японии, а затем и в других странах благодаря своей эффективности и доступности для рядовых работников предприятий. В состав «семи инструментов» входят: диаграмма Парето, причинно-следственная диаграмма, контрольные карты, гистограммы, метод расслоения, графики, диаграмма разброса.
Контрольный листок (или лист) — это инструмент для сбора данных и автоматического их упорядочения для облегчения дальнейшего использования собранной информации. Обычно контрольный листок представляет собой бумажный бланк, на котором заранее напечатаны контролируемые параметры, согласно которым можно заносить в листок данные с помощью пометок или простых символов. Он позволяет автоматически упорядочить данные без их последующего переписывания. Таким образом, контрольный листок - хорошее средство регистрации данных. Число различных контрольных листков исчисляется сотнями, и в принципе для каждой конкретной цели может быть разработан свой листок. Но принцип их оформления остается неизменным. Например, график температуры больного - один из возможных типов контрольных листков. При составлении контрольных листков следует обратить внимание на то, чтобы было указано, кто, на каком этапе процесса и в течение какого времен собирал данные, а также чтобы форма листка была простой и понятной без дополнительных пояснений. Важно и то, чтобы все данные добросовестно фиксировались, и собранная в контрольном листке информация могла быть использована для анализа процесса.
Для наглядного представления тенденции изменения наблюдаемых значений применяют графическое изображение статистического материала. Наиболее распространенным графиком, к которому прибегают при анализе распределения случайной величины при проведении контроля качества, является гистограмма.
Гистограмма — это инструмент, позволяющий зрительно оценить закон распределения статистических данных. Гистограмма распределения обычно строится для интервального изменения значения параметра. Для этого на интервалах, отложенных на оси абсцисс, строят прямоугольники (столбики), высоты которых пропорциональны частотам интервалов. По оси ординат откладывают абсолютные значения частот. Аналогичную форму гистограммы можно получить, если по оси ординат отложить соответствующие значения относительных частот. При этом сумма площадей всех столбиков будет равна единице, что оказывается удобно.
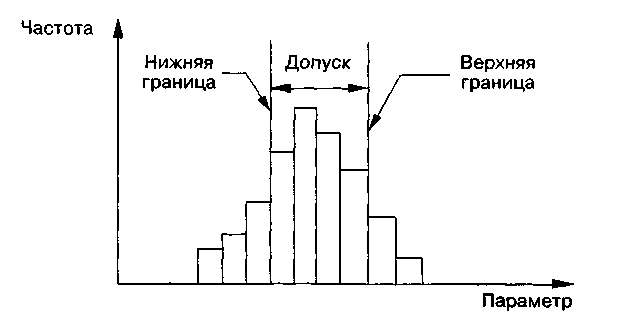
Гистограмма также очень удобна для визуальной оценки расположения статистических данных в пределах допуска. Чтобы оценить адекватность процесса требованиям потребителя, мы должны сравнить качество процесса с полем допуска, установленным пользователем. Если имеется допуск, то на гистограмму наносят верхнюю (SU) и нижнюю (SL) его границы в виде линий, перпендикулярных оси абсцисс, чтобы сравнить распределение параметра качества процесса с этими границами. Тогда можно увидеть, хорошо ли располагается гистограмма внутри этих границ.
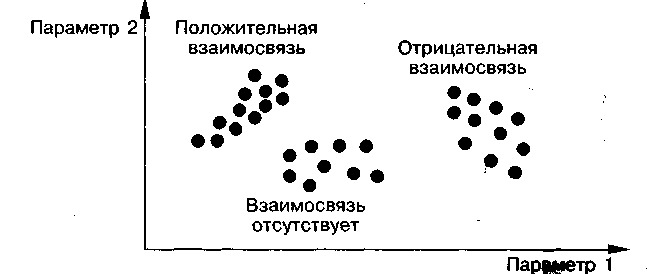
Диаграмма разброса — инструмент, позволяющий определить вид и тесноту связи между парами соответствующих переменных. Эти две переменные могут относиться к:
o характеристике качества и влияющему на нее фактору;
o двум различным характеристикам качества;
o двум факторам, влияющим на одну характеристику качества.
Для выявления связи между ними и служит диаграмма разброса, которую также называют полем корреляции. Использование диаграммы разброса в процессе контроля качества не ограничивается только выявлением вида и тесноты связи между парами переменных. Диаграмма разброса используется также для выявления причинно-следственных связей показателей качества и влияющих факторов.
Построение диаграммы разброса выполняется в следующей последовательности:
Этап 1. Соберите парные данные (х, у), между которыми вы хотите исследовать зависимость, и расположите их в таблицу. Желательно не менее 25-30 пар данных.
Этап 2. Найдите максимальные и минимальные значения для х и y. Выберите шкалы на горизонтальной и вертикальной осях так, чтобы обе длины рабочих частей получились приблизительно одинаковыми, тогда диаграмму будет легче читать. Возьмите на каждой оси от 3 до 10 градаций и используйте для облегчения чтения круглые числа. Если одна переменная - фактор, а вторая - характеристика качества, то выберите для фактора горизонтальную ось х, а для характеристики качества - вертикальную ось у.
Этап 3. На отдельном листе бумаги начертите график и нанесите на него данные. Если в разных наблюдениях получаются одинаковые значения, покажите эти точки, либо рисуя концентрические кружки, либо нанося вторую точку рядом с первой.
Этап 4. Сделайте все необходимые обозначения. Убедитесь, что нижеперечисленные данные, отраженные на диаграмме, понятны любому человеку, а не только тому, кто делал диаграмму:
название диаграммы;
интервал времени;
число пар данных;
названия и единицы измерения для каждой оси;
имя (и другие данные) человека, который делал эту диаграмму.
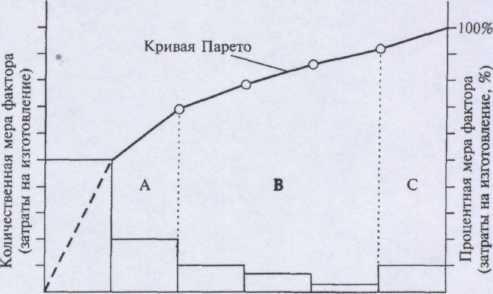
В 1897 г. итальянский экономист В. Парето предложил формулу, показывающую, что общественные блага распределяются неравномерно. Эта же теория была проиллюстрирована на диаграмме американским экономистом М. Лоренцом. Оба ученых показали, что в большинстве случаев наибольшая доля доходов или благ (80%) принадлежит небольшому числу людей (20%). Д. Джуран применил диаграмму М. Лоренца в сфере контроля качества для классификации проблем качества на немногочисленные, но существенно важные и многочисленные, но несущественные и назвал этот метод анализом Парето. Он указал, что в большинстве случаев подавляющее число дефектов и связанных с ними потерь возникают из-за относительно небольшого числа причин. При этом он иллюстрировал свои выводы с помощью диаграммы, которая получила название диаграммы Парето.
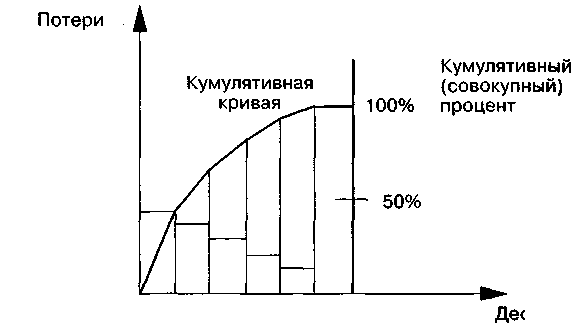
Диаграмма Парето — инструмент, позволяющий распределить усилия для разрешения возникающих проблем и выявить основные причины, с которых нужно начинать действовать. В повседневной деятельности по контролю и управлению качеством постоянно возникают всевозможные проблемы, связанные, например, с появлением брака, неполадками оборудования, увеличением времени от выпуска партии изделий до ее сбыта, наличием на складе нереализованной продукции, поступлением рекламаций. Диаграмма Парето позволяет распределить усилия для разрешения возникающих проблем и установить основные факторы, с которых нужно начинать действовать с целью преодоления возникающих проблем.
Различают два вида диаграмм Парето:
1. Диаграмма Парето по результатам деятельности. Эта диаграмма предназначена для выявления главной проблемы и отражает следующие нежелательные результаты деятельности:
качество: дефекты, поломки, ошибки, отказы, рекламации, ремонты, возвраты продукции
себестоимость: объем потерь, затраты
сроки поставок: нехватка запасов, ошибки в составлении счетов, срыв сроков поставок
безопасность: несчастные случаи, трагические ошибки, аварии.
2. Диаграмма Парето по причинам. Эта диаграмма отражает причины проблем, возникающих в ходе производства, и используется для выявления главной из них:
исполнитель работы: смена, бригада, возраст, опыт работы, квалификация, индивидуальные характеристики;
оборудование: станки, агрегаты, инструменты, оснастка, организация использования, модели, штампы;
сырье: изготовитель, вид сырья, завод-поставщик, партия;
метод работы: условия производства, заказы-наряды, приемы работы, последовательность операций;
измерения: точность (указаний, чтения, приборная), верность и повторяемость (умение дать одинаковое указание в последующих измерениях одного и того же значения), стабильность (повторяемость в течение длительного периода), совместная точность, т.е. вместе с приборной точностью и тарированием прибора, тип измерительного прибора (аналоговый или цифровой).
Построение диаграммы Парето состоит из следующих этапов.
Этап 1. Решите, какие проблемы надлежит исследовать и как собирать данные.
1. Какого типа проблемы вы хотите исследовать? Например, дефектные изделия, потери в деньгах, несчастные случаи.
2. Какие данные надо собрать и как их классифицировать? Например, по видам дефектов, по месту их появления, по процессам, по станкам, по рабочим, по технологическим причинам, по оборудованию, по методам измерения и применяемым измерительным средствам.
Примечание. Суммируйте остальные нечасто встречающиеся признаки под общим заголовком «прочие».
3. Установите метод и период сбора данных.
Примечание. Если это рекомендуется, используйте специальный бланк.
Этап 2. Разработайте контрольный листок для регистрации данных с перечнем видов собираемой информации. В нем надо предусмотреть место для графической регистрации данных проверок.
Этап 3. Заполните листок регистрации данных и подсчитайте итоги.
Этап 4. Для построения диаграммы Парето разработайте бланк таблицы для проверок данных, предусмотрев в нем графы для итогов по каждому проверяемому признаку в отдельности, накопленной суммы числа дефектов, процентов к общему итогу и накопленных процентов.
Этап 5. Расположите данные, полученные по каждому проверяемому признаку, в порядке значимости и заполните таблицу.
Примечание. Группу «прочие» надо поместить в последнюю строку независимо от того, насколько большим получилось число, так как ее составляет совокупность признаков, числовой результат по каждому из которых меньше, чем самое маленькое значение, полученное для признака, выделенного в отдельную строку.
Этап 6. Начертите одну горизонтальную и две вертикальные оси.
1. Вертикальные оси. Нанесите на левую ось шкалу с интервалами от 0 до числа, соответствующего общему итогу. На правую ось наносится шкала с интервалами от 0 до 100%.
2. Горизонтальная ось. Разделите эту ось на интервалы в соответствии с числом контролируемых признаков.
Этап 7. Постройте столбиковую диаграмму
Этап 8. Начертите кривую Парето. Для этого на вертикалях, соответствующих правым концам каждого интервала на горизонтальной оси, нанесите точки накопленных сумм (результатов или процентов) и соедините их между собой отрезками прямых.
Этап 9. Нанесите на диаграмму все обозначения и надписи.
1. Надписи, касающиеся диаграммы (название, разметка числовых значений на осях, наименование контролируемого изделия, имя составителя диаграммы).
2. Надписи, касающиеся данных (период сбора информации, объект исследования и место его проведения, общее число объектов контроля).
Одним из наиболее эффективных статистических методов, широко используемых в системе управления качеством, является метод стратификации или расслаивания. В соответствии с этим методом водят расслаивание статистических данных, т.е. группируют данные в зависимости от условий их получения и производят обработку каждой группы данных в отдельности.
Данные, разделенные на группы в соответствии с их особенностями, называют слоями (стратами), а сам процесс разделения на слои (страты) - расслаиванием (стратификацией).
Метод расслаивания исследуемых статистических данных - это инструмент, позволяющий произвести селекцию данных, отражающую требуемую информацию о процессе. Существуют различные методы расслаивания, применение которых зависит от конкретных задач. Например, данные, относящиеся к изделию, производимому в цехе на рабочем месте, могут в какой-то мере различаться в зависимости от исполнителя, используемого оборудования, методов проведения рабочих операций, температурных условий и т.д. Все эти отличия могут быть факторами расслаивания. В производственных процессах часто используется метод 5М, учитывающий факторы, зависящие от человека (man), машины machine), материала (material), метода (method), измерения (measurement).
Расслаивание может осуществляться по следующим критериям:
расслаивание по исполнителям - по квалификации, полу, стажу работы и т.д.;
расслаивание по машинам и оборудованию - по новому и старому оборудованию, марке, конструкции, выпускающей фирме и т.д.;
расслаивание по материалу - по месту производства, фирме - производителю, партии, качеству сырья и т.д.;
расслаивание по способу производства - по температуре, технологическому приему, месту производства и т.д.;
расслаивание по измерению - по методу, измерения, типу измерительных средств или их точности и т.д.
Однако пользоваться этим методом не так просто. Иногда расслаивание по, казалось бы, очевидному параметру не дает ожидаемого результата. В этом случае нужно продолжить анализ данных по другим возможным параметрам в поисках решения возникшей проблемы.
Результат процесса зависит от многочисленных факторов, между которыми существуют отношения типа причина - следствие (результат). Диаграмма причин и следствий - средство, позволяющее выразить эти отношения в простой и доступной форме. В 1953 г. профессор Токийского Университета Каору Исикава, обсуждая проблему качества на одном заводе, суммировал мнение инженеров в форме диаграммы причин и результатов. Когда диаграмму начали применять на практике, она оказалась весьма полезной и скоро стала широко использоваться во многих компаниях Японии, получив название диаграммы Исикавы. Она была включена в японский промышленный стандарт (JIS) на терминологию в области контроля качества и определяется в нем следующим образом: диаграмма причин и результатов - диаграмма, которая показывает отношение между показателем качества и воздействующими на него факторами.
Причинно-следственная диаграмма - инструмент, позволяющий выявить наиболее существенные факторы (причины), влияющие на конечный результат следствие). Если в результате процесса качество изделия оказалось неудовлетворительным, значит, в системе причин, т.е. в какой-то точке процесса, произошло отклонение от заданных условий. Если эта причина может быть обнаружена и устранена, то будут производиться изделия только высокого качества. Более того, если постоянно поддерживать заданные условия процесса, то можно обеспечить формирование высокого качества выпускаемых изделий.
В настоящее время причинно-следственная диаграмма, являясь одним из семи инструментов контроля качества, используется во всем мире применительно не только к показателям качества продукции, но и к другим областям диаграмм. Можно предложить процедуру ее построения, состоящую из следующих основных этапов.
Этап 1. Определите показатель качества, т.е. тот результат, который вы хотели бы достичь.
Этап 2. Напишите выбранный показатель качества в середине правого края чистого листа бумаги. Слева направо проведите прямую линию («хребет»), а записанный показатель заключите в прямоугольник. Далее напишите главные причины, которые влияют на показатель качества, заключите их в прямоугольники и соедините с «хребтом» стрелками в виде «больших костей хребта» (главных причин).
Этап 3. Напишите (вторичные) причины,, влияющие на главные причины («большие кости») и расположите их в виде «средних костей», примыкающих к «большим». Напишите причины третичного порядка, которые влияют на вторичные причины, и расположите их в виде «мелких костей», примыкающих к «средним».
Этап 4. Проранжируйте причины (факторы) по их значимости, используя для этого диаграмму Парето, и выделите особо важные, которые предположительно оказывают наибольшее влияние на показатель качества.
Этап 5. Нанесите на диаграмму всю необходимую информацию: ее название; наименование изделия, процесса или группы процессов; имена участников процесса; дату и т.д.
После того как вы завершили построение диаграммы, следующий шаг - распределение причин по степени их важности. Не обязательно все причины, включенные в диаграмму, будут оказывать сильное влияние на показатель качества. Обозначьте только те, которые, на ваш взгляд, оказывают наибольшее воздействие.
Все вышеописанные статистические методы дают возможность зафиксировать состояние процесса в определенный момент времени. В отличие от них метод контрольных карт позволяет отслеживать состояние процесса во времени и более того — воздействовать на процесс до того, как он выйдет из-под контроля.
Контрольные карты — инструмент, позволяющий отслеживать ход протекания процесса и воздействовать на него (с помощью соответствующей обратной связи), предупреждая его отклонения от предъявляемых к процессу требований. Использование контрольных карт преследует следующие цели:
держать под контролем значение определенной характеристики;
проверять стабильность процессов;
немедленно принимать корректировочные меры;
проверять эффективность принятых мер.
Однако следует отметить, что перечисленные цели являются характерными для действующего процесса. В период же запуска процесса контрольные карты используют для проверки возможностей процесса, т.е. его возможностей стабильно выдерживать установленные допуски.
Контрольная карта (Control chart) - это разновидность графика, который отличается наличием контрольных границ, обозначающих допустимый диапазон разброса характеристик в обычных условиях течения процесса. Выход характеристик за пределы контрольных границ означает нарушение стабильности процесса и требует проведения анализа причин и принятия соответствующих мер.
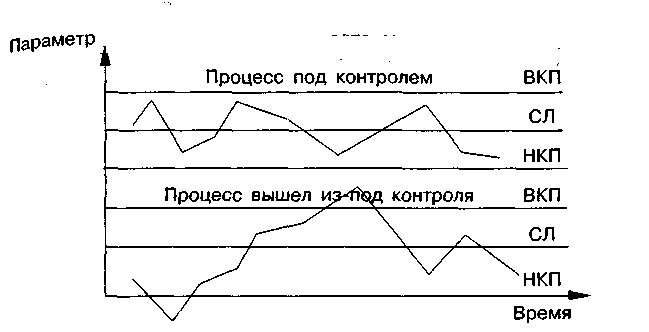
При построении контрольных карт на оси ординат откладываются значения контролируемого параметра, а на оси абсцисс - время t взятия выборки (или ее номер). Всякая контрольная карта состоит обычно из трех линий. Центральная линия представляет собой требуемое среднее значение характеристики контролируемого параметра качества. Две другие линии, одна из которых находится над центральной — верхний контрольный предел (Кв или UCL — Upper Control Level), а другая под ней — нижний контрольный предел ( К н или LCL — Lower Control Level), представляют собой максимально допустимые пределы изменения значений контролируемой характеристики (показателя качества), чтобы считать процесс удовлетворяющим предъявляемым к нему требованиям.
Если все точки соответствуют выборочным средним значениям контролируемого параметра и его изменчивости, полученные по результатам обследования выборок, оказываются внутри контрольных пределов, не проявляя каких бы то ни было тенденций, то процесс рассматривается как находящийся в контролируемом состоянии. Если же, напротив, они попадут за контрольные пределы или примут какую-нибудь необычную форму расположения, то процесс считается вышедшим из-под контроля. Процесс считается контролируемым, если систематические составляющие его погрешности регулярно выявляются и устраняются, а остаются только случайные составляющие погрешностей, которые, как правило, распределяются в соответствии с нормальным (гауссовским) законом распределения.
studfiles.net
Краткие теоретические сведения
В комплексной системе управления качеством продукции статистические методы контроля относятся к наиболее прогрессивным методам. Они основаны на применении методов математической статистики к систематическому контролю за качеством изделий и состоянием технологического процесса с целью поддержания его устойчивости и обеспечения заданного уровня качества выпускаемой продукции.
Семь основных инструментов качества - набор инструментов, позволяющих облегчить задачу контроля протекающих процессов и предоставить различного рода факты для анализа, корректировки и улучшения качества процессов.
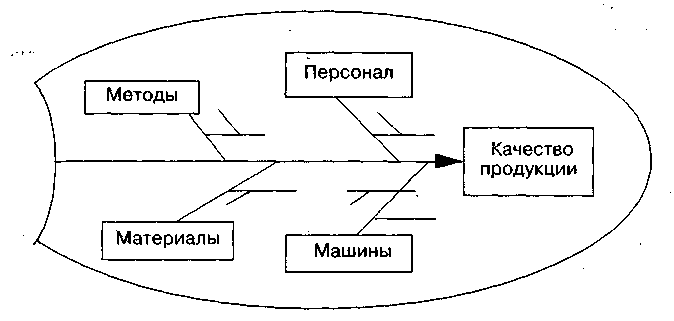
Причинно-следственная диаграмма. Данная диаграмма представляет собой наиболее эффективный метод проверки различных гипотез о потенциальных причинах проблемы качества. Идея диаграммы состоит в установлении взаимосвязей между показателями качества – следствием – и воздействующими на него факторами – причинами. При этом следствие, результат или проблема обозначаются на правой стороне диаграммы, а главные воздействующие факторы или причины перечисляются на левой стороне. Главные причины при построении диаграммы Исикавы группируются по следующим факторам: «человек», «машина», «метод», «контроль, управление (менеджмент)», «среда», «материал».
Алгоритм построения диаграммы Исикавы с целью определения причин, влияющих на качество:
1. Определить показатель качества и написать его в середине правого края чистого листа бумаги.
2. Слева направо провести центральную прямую линию, записанный показатель заключить в прямоугольник.
3. Написать главные причины, влияющие на показатель качества, заключить их в прямоугольники и соединить с центральной линией стрелками.
4. Написать причины (вторичные), влияющие на главные причины, и расположить их в виде "стрелок", примыкающих к стрелкам главных причин.
5. Написать причины третичного порядка, влияющие на «вторичные» причины, и расположить их в виде «стрелок», примыкающих к стрелкам вторичных причин.
6. Проранжировать факторы по их значимости и выделить особо важные, оказывающие предположительно наибольшее влияние на показатель качества.
Наглядно Диаграмма Исикавы представлена на рис.
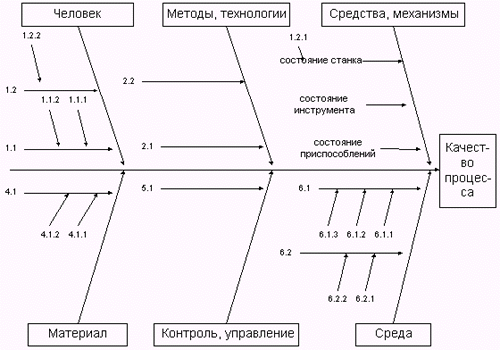
Рис. Диаграмма Исикавы
Контрольный листок. Контрольный листок - инструмент для сбора данных и их автоматического упорядочения для дальнейшего использования собранной информации.
Порядок составления контрольного листка:
Определение типа данных и очередности сбора информации.
Определение периода времени сбора информации.
Формулировка заголовка контрольного листка, отражающего тип собираемой информации.
Определение и составление перечня контролируемых характеристик продукции или процесса.
Разработка бланка контрольного листка, максимально удобного для заполнения в соответствии с принятыми правилами.
При заполнении контрольного листка обязательно должна быть предусмотрена адресная часть, в которой указывается название листка, измеряемый (контролируемый) параметр, название и номер детали, цех, участок, станок, смена, материал, режим обработки и другие данные, представляющие интерес для контроля. Кроме этого ставится дата заполнения, указывается фамилия и подпись лица, проводившего заполнения литка, или соответствующие расчеты.
Пример. Составьте форму контрольного листка по сбору информации и данных о качестве для анализа видов дефектов промышленной продукции.
Таблица
Контрольный листок
| Наименование документа | Контрольный листок по видам дефектов | Дата: 23 мая 200__ г. |
| Предприятие: ЗАО «ЛИТ» Цех: формовочный Участок: 2____ | Изделие _формовка___ Операция _изготовление___ Контролер ___Иванов И.И.___ | |
| Типы дефектов | Данные контроля | Кол-во деталей |
| Деформация | ////////////////// | 20 |
| Царапины | //////////// | 16 |
| Трещины | //////////// | 12 |
| Сколы | ////// | 6 |
| Раковины | //////////////////// | 23 |
| Разрыв | ///////// | 9 |
| Пятна | //////////////// | 18 |
| Прочие | ////////// | 10 |
| ИТОГО | 114 |
Гистограмма
Гистограмма - инструмент, позволяющий зрительно оценить распределение статистических данных, сгруппированных по частоте попадания данных в определенный (заранее заданный) интервал. Для статистических данных часто строят гистограмму распределения. При простоте построения гистограммы дает много полезной аналитической информации о разбросе (рассеивании) качественных показателей, средних значениях, о точности и стабильности технологических процессов.
Последовательность построения гистограммы:
Собрать исходные данные (или произвести измерение 50 -200 значений).
Из совокупности полученных результатов определить наибольшее (Хmax) и наименьшее (Хmin) значения параметра, а также его диапазон (размах): R = Хmax – Хmin.
Полученный диапазон (размах) разделить на интервалы, предварительно определив их число (обычно от 6 до 20 интервалов в зависимости от числа показателей) и определить ширину интервала. В табл. представлено рекомендуемое число интервалов гистограммы.
Таблица
Рекомендуемое число интервалов гистограммы
| Количество наблюдаемых значений в выборке | Число интервалов |
| 40 – 50 | 6 |
| 51 – 100 | 7 |
| 101 – 200 | 8 |
| 201 – 500 | 9 |
| 501 – 1000 | 10 |
| Более 1000 | 11 - 20 |
Все данные распределить по интервалам в порядке возрастания. При этом наименьшие и наибольшие значения измеренных величин должны находиться не на границе интервала, а внутри его, в центре интервала.
Подсчитать частоту каждого интервала.
Вычислить относительную частоту попадания данных в каждый из интервалов (для этого необходимо частоту каждого интервала разделить на общее количество измерений).
По полученным данным построить гистограмму (высота столбиков соответствует частоте или относительной частоте попадания данных в каждый из интервалов). При этом на горизонтальной оси выбирается масштаб, и откладываются соответствующие интервалы, а на вертикальной оси - соответствующие им значения частот.
Пример 1. Имеются следующие значения измеряемой величины. Построить гистограмму.
| 8,5 | 9,5 | 10,5 | 8,75 | 11,0 | 9,75 | 9,75 | 8,75 | 10,5 | 9,75 |
| 9,5 | 8,75 | 9,25 | 10,25 | 9,0 | 10,0 | 10,0 | 9,75 | 11,0 | 9,5 |
| 9,25 | 10,25 | 9,0 | 10,0 | 9,25 | 9,0 | 9,0 | 10,00 | 10,75 | 9,5 |
| 10,0 | 9,75 | 10,0 | 10,0 | 10,0 | 9,5 | 10,5 | 8,75 | 10,25 | 8,75 |
| 9,75 | 10,75 | 9,5 | 9,75 | 9,75 | 10,25 | 9,75 | 9,75 | 9,75 | 10,0 |
| 9,0 | 9,0 | 10,0 | 10,5 | 10,5 | 10,0 | 9,0 | 10,00 | 9,5 | 10,0 |
| 10,75 | 8,25 | 9,0 | 9,0 | 9,0 | 10,5 | 10,25 | 10,0 | 9,5 | 10,25 |
| 10,5 | 10,0 | 8,75 | 11,0 | 11,0 | 9,75 | 10,0 | 10,25 | 9,75 | 10,25 |
| 11,0 | 8,75 | 11,25 | 9,5 | 9,5 | 9,5 | 8,75 | 9,75 | 10,0 | 11,0 |
| 10,25 | 9,25 | 9,75 | 9,0 | 9,00 | 10,0 | 9,5 | 10,0 | 10,0 | 11,75 |
Х мах = 12.00, Х мин = 8.25, Размах = 2,75 , ширина интервала составляет 8 (округлили до ближайшего целого числа).
Определим границы интервалов и произведем подсчет частот. Представим полученные данные в виде таблицы.
| Границы интервалов | Середина интервала | Подсчет частот | Частота в интервале | Относительная частота |
| 8,00-8,50 | 8,25 | // | 2 | 0,02 |
| 8,50-9,00 | 8,75 | ///…./// | 20 | 0,2 |
| 9,00-9,50 | 9,25 | ///…/// | 16 | 0,16 |
| 9,50-10,00 | 9,75 | ///…..//// | 35 | 0,35 |
| 10,00-10,50 | 10,25 | ///…/// | 16 | 0,16 |
| 10,50-11,00 | 10,75 | /////// | 9 | 0,09 |
| 11,00-11,50 | 11,25 | / | 1 | 0,01 |
| 11,50-12,00 | 11,75 | / | 1 | 0,01 |
| 100 | 1,00 |
Используя данные таблицы, построим гистограмму.
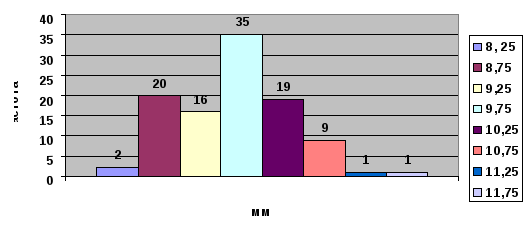
Рис. Пример гистограммы
Пример 2. Постройте гистограмму по результатам 30 наблюдений контроля показателя качества – содержание жира в сметане. Данные наблюдений представлены в таблице
| 14 | 14 | 12 | 13 | 15 | 16 | 17 | 14 | 16 | 16 | 15 | 15 | 15 | 15 | 14 |
| 16 | 16 | 14 | 15 | 18 | 17 | 15 | 15 | 13 | 14 | 15 | 15 | 14 | 16 | 16 |
Решение (поэтапный алгоритм)
| № п/п | Алгоритм | Конкретное соответствие данной ситуации предложенному алгоритму |
| 1 | Определить границы интервалов и их количество | Номера границы и количество интервалов: 1) 12-13 2) 13-14 3) 14-15 4) 15-16 5) 16-17 6) 17-18 Итого: 6 интервалов |
| 2 | Определить частоты интервалов (см. исходную таблицу) | Частоты интервалов: 1) 3 2) 7 3) 10 4) 7 5) 2 6) 1 Итого: 30 |
| 3 | Нанести на ось ординат интервалы группировок данных Выбрать масштаб оси ординат и нанести последовательное количество частот интервалов Соединить отмеченные точки в виде столбцов |
|
| 4 | Сформулировать вывод о наиболее часто встречающихся интервалах | Наиболее часто встречается сметана с содержанием жира 15% |
Диаграмма Парето. Диаграмма Парето - инструмент, позволяющий объективно представить и выявить основные факторы, влияющие на исследуемую проблему, и распределить усилия для ее эффективного разрешения
Порядок построения диаграммы Парето:
Решить, какие проблемы (причины проблем) необходимо исследовать ; как и какие данные собирать и осуществлять их классификацию.
Разработать формы для регистрации исходных данных (например, контрольный листок с перечнем видов собираемой информации).
Собрать данные, заполнить формы регистрации данных и подсчитать итоги по каждому исследуемому фактору (показателю, признаку за заданный промежуток времени).
Для построения диаграммы Парето подготовить (или разработать) бланк таблицы, предусмотрев в ней графы для итогов по каждому проверяемому факторы (признаку) в отдельности, накопленной суммы числа проявлений соответствующего фактора, процентов к общему итогу и накопленных процентов.
Заполнить таблицу, расположив в ней данные, полученные по проверяемому фактору, в порядке убывания значимости. При этом «прочие» поместить в последнюю строку таблицы.
Подготовить оси (одну горизонтальную и две вертикальные линии) для построения диаграммы. Нанести на левую ось ординат шкалу с интервалами от 0 до общей суммы числа выявленных факторов, а на правую ось ординат – шкалу с интервалами от 0 до 100, отражающую процентную меру фактора. Ось абсцисс необходимо разделить на интервалы в соответствии с числом исследуемых факторов или относительной частотой.
Построить столбчатую диаграмму. Высота откладывается по левой шкале и равна числу появлений соответствующего фактора. При этом столбцы располагаются в порядке убывания (уменьшения) значимости фактора. Последний столбец характеризует прочие (т.е. малозначимые факторы) и может быть выше других.
Построить кумулятивную кривую (кривую Парето) – ломаную линию, соединяющую точки накопленных сумм (количественной меры факторов или процентов). Каждую точку ставят над соответствующим столбцом столбчатой диаграммы, ориентируясь на его правую сторону.
Нанести на диаграмму все обозначения и надписи.
Провести анализ диаграммы Парето.
На рис. представлен пример диаграммы Парето.
studfiles.net
Статистические методы признаются важным условием рентабельного управления качеством. Методы, основанные на статистическом подходе, используются на всех этапах жизненного цикла изделий и наиболее часто применяются следующие:
- гистограммы;- временные ряды;- диаграммы Парето;- причинно-следственные диаграммы;- контрольные листки;- контрольные карты;- диаграммы рассеяния.Эти методы получили название «Семь инструментов качества» [32].Гистограммы используются в случае необходимости представить распределение данных о параметрах изделия с помощью столбикового графика. Аналогом гистограммы в теории вероятностей и математической статистике служит функция плотности вероятности, которая показывает частоту появления того или иного события. С помощью гистограммы можно получить информацию о категоризации измеряемых параметров изделия, оценить степень симметрии разброса данных относительно среднего значения, подобрать аппроксимирующее теоретическое распределение.Временные ряды применяются для оценки изменения хода наблюдаемого события за определенный период времени. Такие ряды обладают большой наглядностью и очень просты при построении и использовании. Точки наносятся на график в том порядке, в котором они были получены. Построенная кривая в виде линейного графика иллюстрирует временной ход процесса и позволяет выявить существенные отклонения данного процесса, к примеру, от среднего значения или границ допусков. Типичный вид временного графика показан на рис. 4.5.Диаграммы Парето используются в ситуациях, когда требуется представить относительную важность всех проблем или условий с целью выбора отправной точки для решения проблемы. ДиаграммаПарето представляет собой вертикальный столбиковый график, с помощью которого определяются рассматриваемые проблемы и порядок их решения. Построение таких диаграмм помогает привлечь внимание к действительно важным проблемам. Порядок построения диаграммы состоит из следующих этапов:1) выбор сравниваемых проблем;2) определение критериев для сравнения единиц измерения;3) выбор периода времени для изучения;4) группирование данных по категориям и сравнение критериев каждой группы;5) перечисление категорий слева направо на горизонтальной оси в порядке уменьшения значения критерия.Причинно-следственные диаграммы применяются для исследования и анализа всех возможных причин или условий. Такая диаграмма была разработана с целью представления соотношений между следствием, результатом и всеми возможными причинами, влияющими на них. Следствие, результат или проблема обычно обозначаются на правой стороне схемы, а главные воздействия (причины) - на левой. Такая диаграмма носит еще название диаграммы К. Исикавы, в честь японского ученого, ее разработавшего.
Контрольные листки (таблицы проверок) используются для сбора данных с целью изучения выборки наблюдений
Контрольные карты представляют собой нанесенные на график временные ряды с указанными верхними и нижними границами. На графике наносятся три линии, позволяющие понять происходящий процесс. Эти горизонтальные линии называются верхним контрольным пределом (ВКП), центральной линией (ЦЛ) и нижним контрольным пределом (НКП). С помощью этих линий можно проследить следующие зависимости:- если слишком большое количество экспериментальных точек находится выше ВКП (ниже НКП), это означает, что с процессом происходит что-то неладное;- если ряд экспериментальных точек находится между ЦЛ и ВКП (или ЦЛ и НКП), это также означает, что процесс требует вмешательства;- если ряд экспериментальных точек имеет тенденцию повышения к ВКП, следует сделать вывод, что протекание процесса затруднено.Контрольные карты бывают двух видов: одни отображают средние показатели процесса (х-диаграммы), а другие - стандартное отклонение (s-диаграммы). С помощью диаграмм можно определить причину возникшей проблемы: возможно, изменение параметров процесса происходит всякий раз при изменении штата работников (например, при пересменке). Причиной также может служить переход на зимнее время (или обратно), при котором служащие в течение нескольких дней привыкают к новому режиму работы.Параметр ЦЛ является двойным средним значением. В х-диаграм- мах каждая точка представляет конкретный день, а среднее значение этой точки определяется на основе всех данных наблюдений, зафиксированных в этот день. Средние значения всех дней затем применяются для вычисления общего среднего - это и есть ЦЛ х-диаг- раммы. Центральная линия для s-диаграммы строится таким же образом, за исключением того, что вычисления начинаются со стандартного отклонения на каждый день, а затем определяется среднее значение всех этих показателей.Диаграмма рассеяния применяется для оценки возможной связи между двумя переменными величинами. По диаграмме рассеяния можно установить корреляционную и регрессионную форму связи между параметрами процесса. Корреляция показывает, как в среднем изменяется поведение одной из переменных при возрастании (убывании) другой. Наиболее распространенной оценкой этого вида связи является выборочный коэффициент корреляции с пределами изменений от -1 до + 1. При высокой положительной связи (величина коэффициента корреляции составляет 0,8-1,0) можно считать, что увеличение одной из переменных приводит к возрастанию другой. В противном случае следует предположить, что возрастание одной из переменных дает уменьшение другой. При значениях коэффициента корреляции, близких к нулю, изменение одного из параметров не оказывает влияния на другой. При построении диаграмм рассеяния по одной из осей откладывают числовые значения первого параметра, по второй оси - значения другого параметра. Полученное «облако» рассеяния числовых данных позволяет визуально установить характер взаимосвязи между двумя переменными.Регрессионный анализ, примененный к тем же самым данным, позволяет подобрать аппроксимирующую кривую, которая лучше всего описывает экспериментальные точки. В основе такого подбора лежит метод наименьших квадратов, минимизирующий сумму квадратов отклонений между опытными данными и значениями теоретической кривой. Построенная теоретическая зависимость дает возможность экстраполировать поведение оцениваемой зависимости за пределы наблюдений.Перечисленные методы, относящиеся к статистическим, в настоящее время стандартизированы и рекомендуются для использования в работе по повышению качества. Кроме того, на начальной стадии работы часто применяются еще два метода: мозговая атака и схема процесса.Мозговая атака (МА) - один из наиболее распространенных методов раскрепощения и активизации творческого мышления. Впервые этот метод был использован еще в 1939 г. в США как способ получения новых идей в условиях запрещения критики. Основная цель МА - это отделение процедуры генерирования идей в замкнутой группе специалистов от процесса анализа и оценки высказанных идей. Как правило, МА длится недолго (около 40 минут). Участникам предлагается высказывать любые идеи на заданную тему при регламенте до двух минут на выступление. Самый интересный момент МА - это наступление пика, когда идеи начинают «фонтанировать», т. е. происходит непроизвольная генерация гипотез участниками. При последующем анализе всего лишь 10-15 % идей оказываются значимыми, но среди них бывают весьма оригинальные. Оценивает результаты группа экспертов, не участвовавшая в генерации идей.Схема процесса представляет собой графическое изображение последовательных стадий какого-либо процесса. Этот метод применяется в ситуациях, когда требуется проследить действительные или мысленные стадии процесса, через которые проходят изделие или услуга. При изучении схем различных процессов можно обнаружить те места, где на практике наиболее вероятно возникновение помех и сбоев. Группа специалистов, обладающих наибольшими знаниями о протекающем процессе, например, технологи, должны выполнить следующие действия:- построить последовательную схему действующего процесса;- построить такую же схему процесса, который должен протекать, если все будет работать нормально;- сравнить две схемы, чтобы найти места различий, которые определяют точку с возможными отклонениями процесса.
megaobuchalka.ru
Если данные из какой либо выборки сгруппировать по частоте попадания в тот или иной интервал значений и представить это распределение графически в виде столбиков соответствующей высоты, получим график, называемый гистограммой (или столбчатой диаграммой). Гистограмма способна дать много информации, если сравнить полученное распределение данных с контрольными нормативами. Полезность информации увеличится, если по полученному распределению частоты определить среднее арифметическое и стандартное отклонение.
При измерении в течение определённого периода свойств изделий или полуфабрикатов, например, размеров листовых стеклоизделий, влажность шихты, светопропускание стекла, содержание оксидов в стекле и т.д., и последующем графическом представлении распределения частотности этих данных, получим колоколообразную гистограмму, соответствующую нормальномураспределению (Гаусса) – см. рис. 5.
Типичная гистограмма нормального распределения характерна для процесса, колебания параметров в котором в основном зависят от случайных причин. Если в процесс вмешиваются не случайные влияния, то характер распределения измерений параметров меняется – гистограмма «деформируется» (примеры этого на рис. 6).
Характер гистограммы отражает условия технологического процесса:
а) гистограмма с двухсторонней симметрией (нормальное распределение) указывает на стабильность процесса;
б) гистограммы с прогалами (одним – «с вырванным зубом», несколькими – «гребёнка») получаются, когда ширина участка не кратна единице измерения (не выражается целым числом в выбранной единице измерения), когда оператор ошибается в считывании показаний прибора и другие;
Таблица 8
|
| Диапазон | Частота попадания в диапазон, % | Частота попадания за пределы диа- пазона, % |
| μ ± 1 σ | 68,2 | 31,74 | |
| μ ± 2 σ | 95,44 | 4,56 | |
| μ ± 3 σ | 99,73 | 0,27 | |
| μ ± 4 σ | 99,994 | 0,006 | |
| Рис. 5. Гистограмма нормального распределения |
в) гистограмма в форме обрыва, у которой как бы обрезан один край (или оба). Она представляет случаи, когда, например, отобраны и исключены из партии все изделия с параметрами ниже (или выше, или и те и другие). После исследования причин отклонения значений параметров от нормы и стабилизации процесса можно прекратить отбор всех изделий с параметрами, отличающимися от нормальных.
д) гистограмма, не имеющая высокой центральной части («плато») получается, когда объединяются несколько распределений, в которых средние значения имеют небольшую разницу между собой. Анализ такой гистограммы следует проводить, используя метод расслоения
е) и ж) двугорбые гистограммы отражают случаи объединения двух распределений с разными средними значениями, напрмер, в случае наличия разницы между двумя станками, между двумя видами материалов (или комплектующих), между двумя операторами и т.д. В этом случае надо провести расслоение по двум видам фактора, исследовать причины различия и принять соответствующие меры для его устранения. Вариант разделения гистограмм после расслоения представлен на рис. 7.
В некоторых случаях данные выборок подчиняются иным законам распределения. Например, при задании диапазона скоростей выработки листового стекла персонал стремится работать на скоростях, близких к верхнему пределу задания; при нормативном задании диапазона допуска
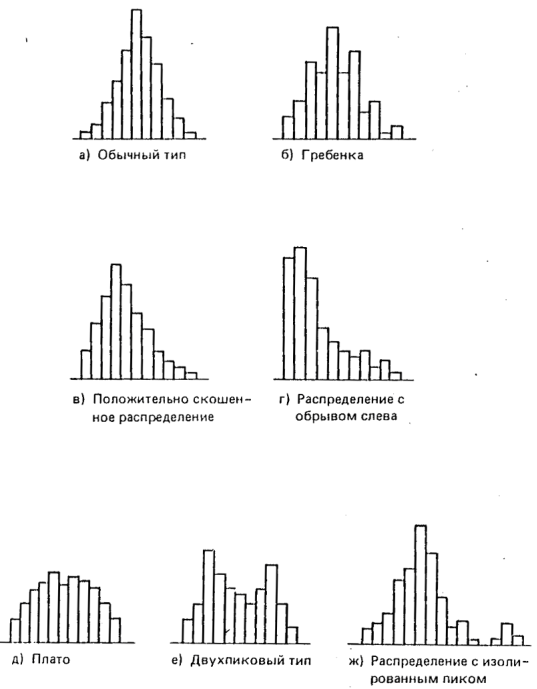
Рис. 6. Виды гистограмм
по толщине вырабатываемого стекла персонал стремится работать ближе к нижнему пределу допуска. И это понятно, в обоих случаях преобладают экономические интересы.
В этом случае в выборке больше будет данных, скопившихся в начале или в конце диапазона, чем в его середине. Такие выборки характеризуются биноминальнымраспределением или распределениемПуассона(см. рис. 8. и 9.). При подобном распределении, как видно из графиков, мода и медиана выборки заметно не совпадают со средним арифметическим, поэтому для анализа выборок используются иные критерии и оценки доверительной вероятности.
Так, при систематизации количественных данных, полученных в результате контроля, можно увидеть, что число дефектных изделий pnи доля дефектных изделийpподчиняются биноминальному распределению, а суммарное число дефектовСподчиняется закону распределения Пуассона.
Оба эти распределения чётко проявляются при небольших выборках данных – до 10 точек. Если число данных в выборке велико (pn ≥ 5;m≥5), то распределение их приближается к нормальному. Поэтому при построе-

Рис. 7. Расслоение выборки на основе гистограммы
нии контрольных карт как биноминальное распределение, так и распределение Пуассона можно представлять как нормальное распределение.
На производстве гистограммы в основном используются в системе контроля качества продукции, причём для сравнения действительного разброса данных с контрольными (нормативными) допусками на колебание параметров (рис. 10) При взгляде на гистограмму (см.рис. 11)
сразу видно, попадает ли гистограмма внутрь допуска, смещена ли в какую-либо сторону допуска (к верхней или нижней границе допуска), не выходит ли за пределы допуска, а если выходит, то насколько; насколько
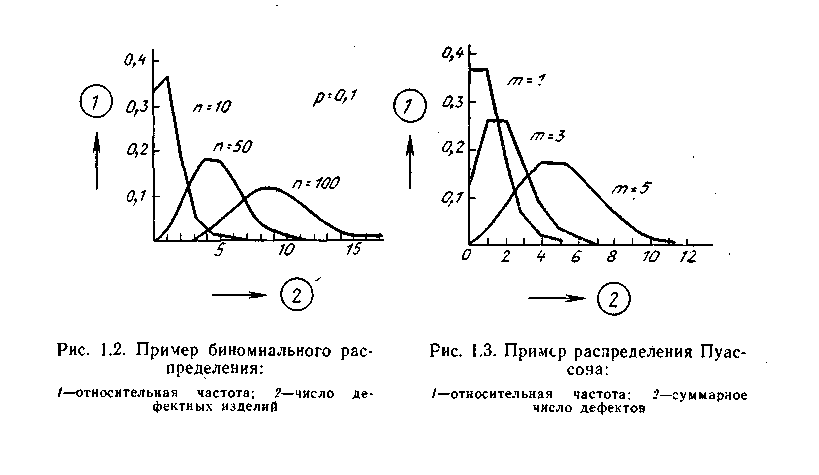
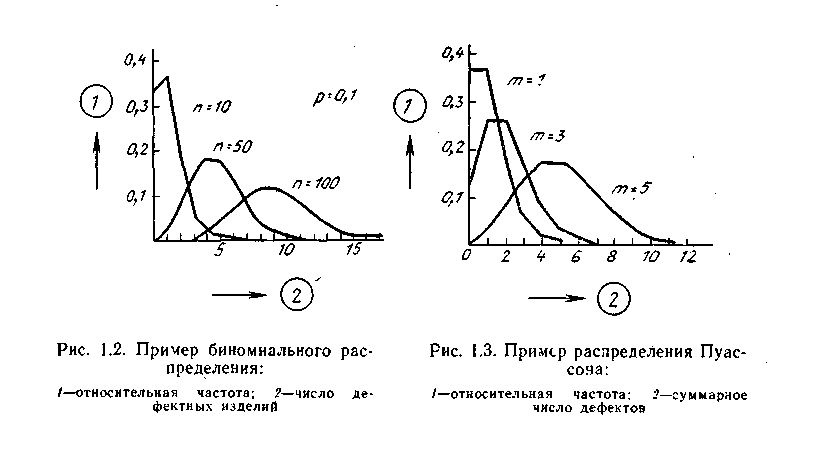
Рис. 8. Рис. 9.
Биноминальное распределение Распределение Пуассона
( 1 - относительная частота, 2 - ( 1 – относительная частота, 2 –
число дефектных изделий – pn ) суммарное число дефектов, m –
cреднее число дефектов на еди-
ницу площади)
середина гистограммы не совпадает с серединой допуска. Выяснив эти вопросы, можно составить более обоснованный план мероприятий по усовершенствованию производства данной продукции.
При сравнении гистограммы с нормой – допуском, предусмотренным стандартом, регламентом производства, договором с поставщиком или потребителем – возможны разные варианты их соотношения:
Среднее значение 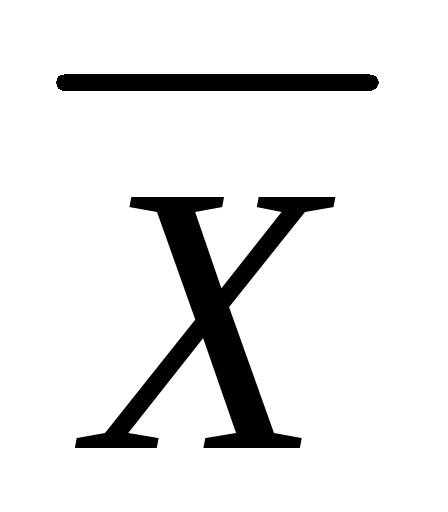 распределения находится посредине между
распределения находится посредине между
верхней и нижней границами допуска, разброс (ширина гистограммы) не выходит за пределы нормы (допуска). Наилучшее положение, когда стандартное отклонение σвыборки примерно в 8 раз меньше допуска.
Гистограмма полностью входит в границы допуска, но разброс
велик, края гистограммы находятся почти на границах допуска (стандартное отклонение в этом случае лишь в 6 раз меньше допуска). А это значит, что возможно появления брака (0,27%), поэтому нужны меры для уменьшения разброса.
Среднее значение 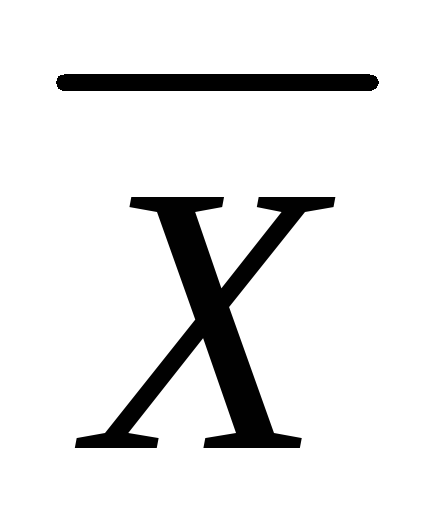 распределения находится посредине допус-
распределения находится посредине допус-
ка, однако края гистограммы намного не доходят до границ допуска. Значит стандартное отклонение σ выборки боле чем в 10 раз меньше допуска. С одной стороны это положение не должно вызывать беспокойства, поскольку явно есть гарантия против появления брака. С другой стороны, если сузить допуск, т.е. сделать норматив на изделие менее строгим, можно повысить мощность производства и эффективность с точки зрения сбыта продукции; или если несколько увеличить разброс, т.е. сделать менее строгими нормативы на технологические операции и на сырьё, материалы и комплектующие, можно повысить производительность производства и понизить стоимость исходных материалов.
4. Разброс невелик по сравнению с допуском, но среднее значение 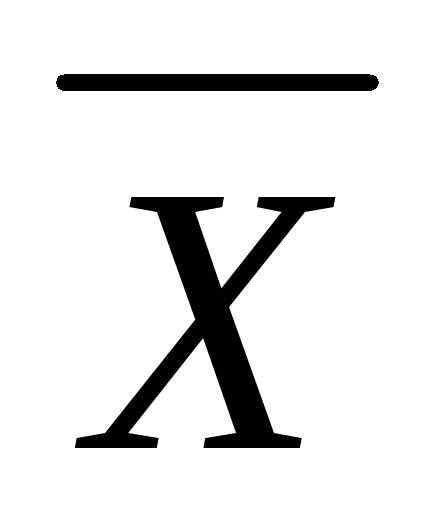 сместилось в сторону какой-либо из границ допуска так, что край гистограммы находится на этой границе. Значит существует возможность появления брака, и необходимы меры, обеспечивающие перемещение среднего значения в середину допуска.
сместилось в сторону какой-либо из границ допуска так, что край гистограммы находится на этой границе. Значит существует возможность появления брака, и необходимы меры, обеспечивающие перемещение среднего значения в середину допуска.
5. Среднее значение выборки находится посредине допуска, а края гистограммы выходят за его границы, т.е. явно какая-то часть продукции выпускается бракованной. Необходимы меры по уменьшению разброса.
6. И среднее значение смещено относительно центра допуска, и разброс велик (края гистограммы за границами допуска). Вероятность выпуска брака весьма существенна. Необходимы меры по перемещению среднего значения выборки в середину допуска и сокращению разброса.
Существует индекс возможностей(или показатель мощности) процесса, по значению которого можно делать заключение о состоянии разброса по отношению к допуску; о том, достаточен ли допуск.
В том случае, когда есть и верхняя, и нижняя границы допуска и гистограмма выборки расположена между ними, индекс возможностей процесса С ропределяется по формуле:
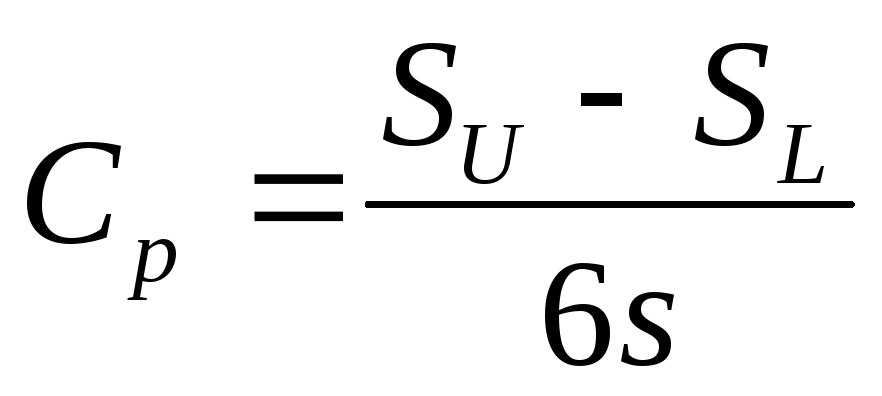 ,
,
где SU- верхняя граница допуска,
SL- нижняя граница допуска,
s- стандартное отклонение выборки.
Если сложно отрегулировать среднее значение параметра, степень отклонения можно оценить по индексу возможностей процесса С ркпо восстановлению отклонения:
С рк= ( 1 – К ) (SU–SL) / 6s,
где К – степень отклонения:
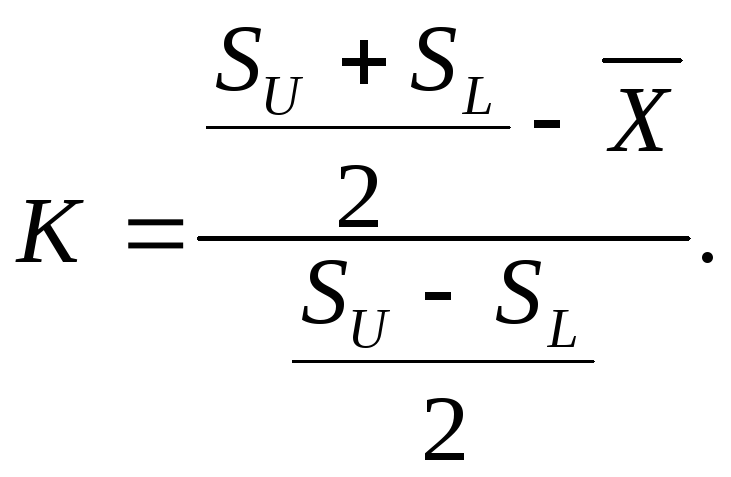
(в числителе берётся абсолютная величина).
В том случае, когда имеется только одна граница допуска, индекс возможностей процесса определяется по одной из следующих формул, смотря какая задана граница (см.рис. 11.):
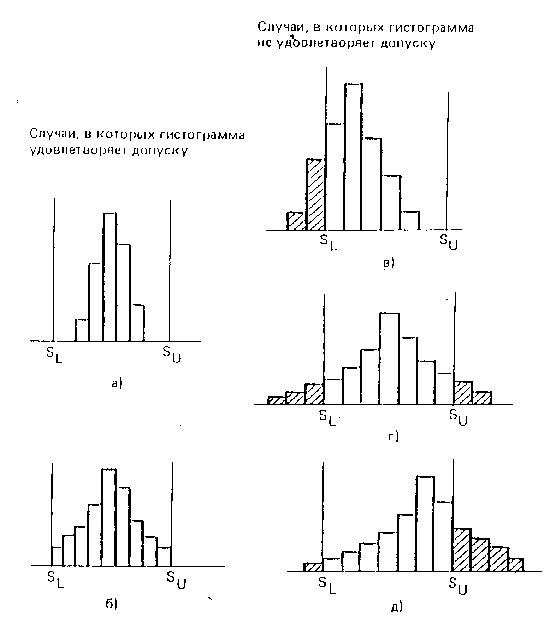
Рис. 10.
Примеры соотношения гистограммы
и допуска на колебание параметра
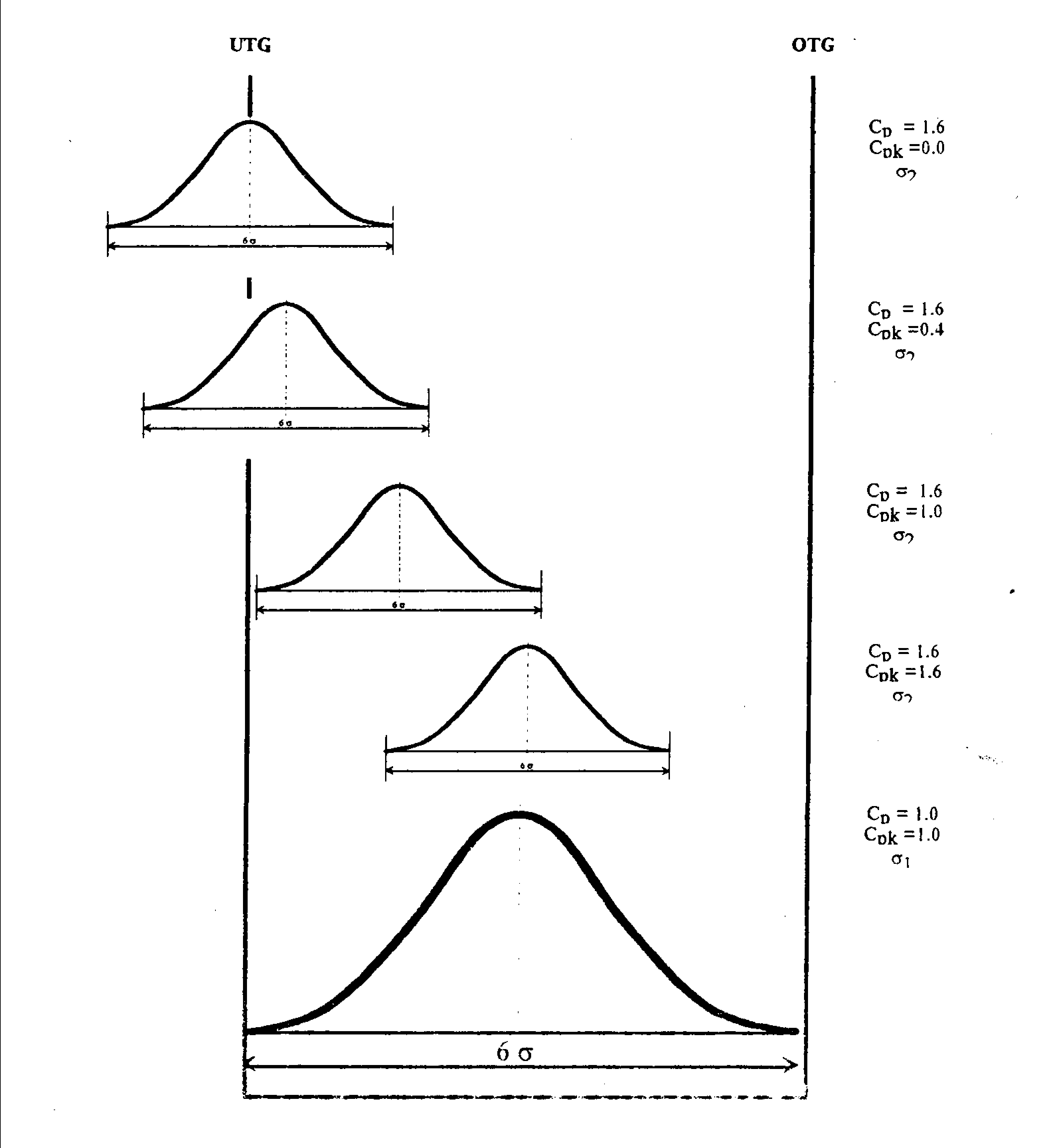
Рис. 11.
Варианты соотношения гистограммы и допуска
к расчёту индекса возможностей процесса
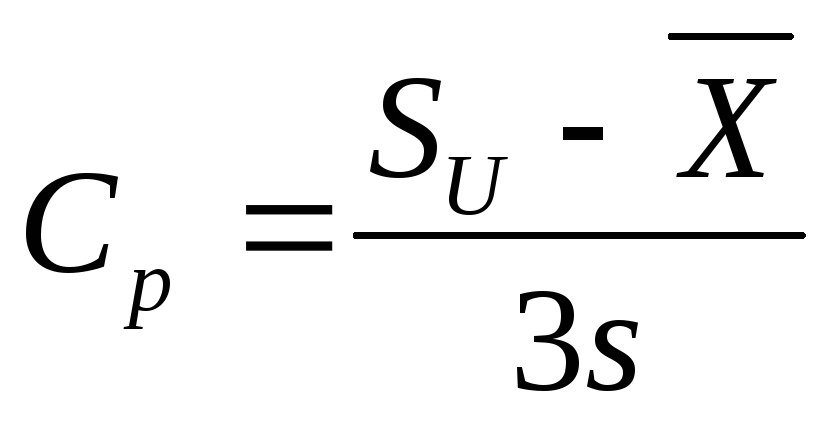 или
или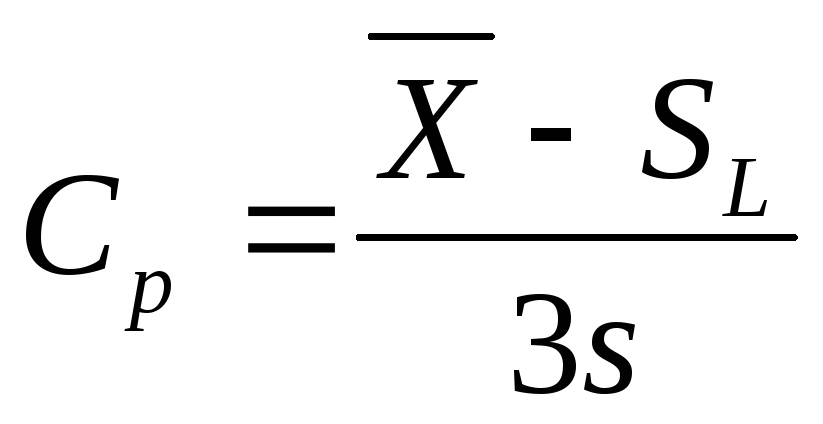 .
.
Например, при вырезке листов стекла длиной 1 м стандартное отклонение выборки из 20 листов составило 0,0918 мм при среднем значении, равном 1000,47 мм. Допуск на длину листов предусмотрен в ± 1 мм. Оценим процесс резки с точки зрения его возможностей.
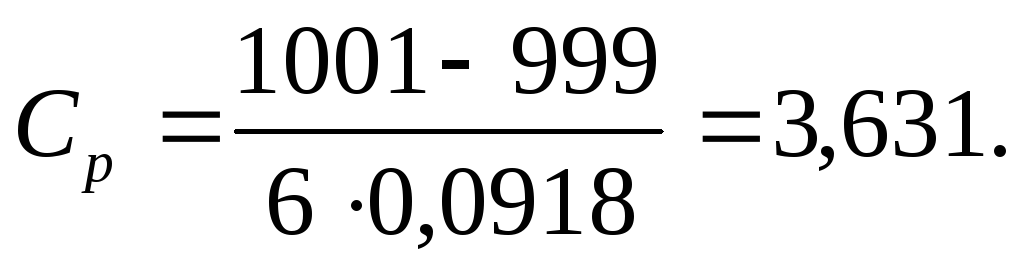
Степень отклонения будет равна
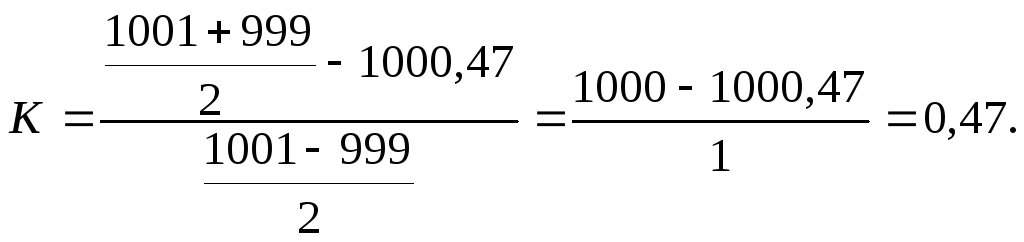
Тогда индекс возможностей процесса по восстановлению отклонения оказывается равным
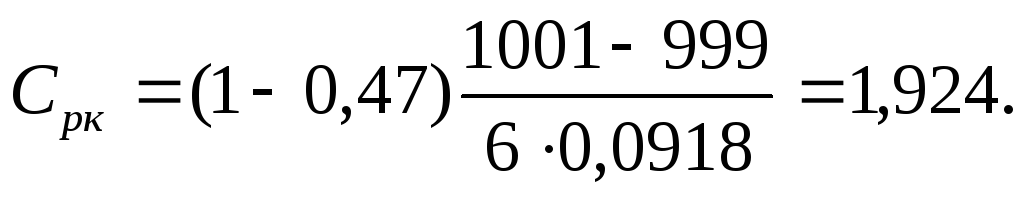
Как оценивается числовое значение индекса возможностей процесса ? См. рис. 11 и 12.
Когда С р(или С рк) > 1,67 , значит допуск не менее чем в 10 раз превышает стандартное отклонение; разброс параметра изделия невелик, появление брака не угрожает. В этом случае можно упростить контроль процесса, что приведёт к снижению себестоимости продукции; можно уменьшить допуск, что будет способствовать улучшению стратегии сбыта
Когда 1,67 > С р> 1,33 , значит допуск в 8 – 10 раз превышает стандартное отклонение выборки. Состояние процесса считается идеальным.
Если 1,33 > С р> 1,00 , значит допуск в 6 – 8 раз превышает стандартное отклонение. Когда индекс С рблизок к 1 , вероятность появления брака составляет 0,27 % (см.табл. 8). Поэтому контроль за процессом необходимо усилить, проанализировать, какие факторы и как влияют на разброс, провести соответствующие мероприятия по улучшению состояния процесса.
В случае когда 1,00 > С р> 0,67 , значит допуск лишь в 4 – 6 раз превышает стандартное отклонение выборки. Приближение С рк 0,67 указывает на вероятность появления брака в количестве 4,56 %. Это означает, что контроль процесса неудовлетворителен. Необходимо наладить его, провести сплошной контроль с целью недопущения брака. Вместе с тем нужно немедленно исследовать факторы, влияющие на разброс, и принять меры к улучшению состояния процесса.
Если С р< 0,67 , значит допуск не превышает 4-х стандартных отклонений. Процент брака превышает 4,56 %. О таком процессе надо говорить, что он неконтролируем. Необходимо провести сплошной контроль продукции, чтобы не выдавать потребителю
|
| Рис. 12. Примеры связи гистограмм, допусков и индекса возможностей процесса |
бракованных изделий, и одновременно принять меры к повышению качества, выяснив причины появления брака. Иногда приходится заново проводить изучение потребностей потребителей, а также пересматривать допуски.
Анализ состояния процесса по индексу его возможностей целесообразно проводить в комбинации с применением карт контроля (см. раздел Б.9.).
Взаимосвязь параметров гистограмм хорошо иллюстрируется нижеследующей таблицей 2 (по Ремезову Н.И.):
Таблица 2.
Взаимосвязь параметров гистограмм
(стрелки указывают направление изменения параметра:
↑ - увеличение, ↓ - уменьшение )
| | σ | С р | С рк | Снрк | Сврк | |
|
| ↓ | ↑ | ↓ | |||
|
| ↓ | ↓ | ↑ | |||
| σ ↑ | ↓ | ↓ | ||||
| σ ↓ | ↑ | ↑ | ||||
| С р ↑ | ↓ | |||||
| С р↓ | ↑ | |||||
| Срк↑ | → к середи- не допуска | ↓ | ||||
| Срк↓ | → к грани- цам допуска | ↑ | ||||
| Снрк↑ | ↑ | ↓ | ||||
| Снрк↓ | ↓ | ↑ | ||||
| Сврк↑ | ↓ | ↓ | ||||
| Сврк↓ | ↑ | ↑ |
studfiles.net
Инструменты контроля качества
Контроль качества — это деятельность, включающая проведение измерений, экспертизы, испытаний или оценки параметров объекта и сравнение полученных величин с установленными требованиями к этим параметрам (показателями качества).
Современные инструменты контроля качества — это методы, которые используются для решения задачи количественной оценки параметров качества. Такая оценка необходима для объективного выбора и принятия управленческих решений при стандартизации и сертификации продукции, планировании повышения ее качества и т. д.
Применение статистических методов — весьма действенный путь разработки новых технологий и контроля качества процессов.
Какова роль контроля в процессе управления качеством?
Современные подходы к управлению качеством предполагают внедрение системы контроля показателей качества продукта на всех этапах его жизненного цикла, начиная от проектирования, и заканчивая послепродажным обслуживанием. Основная задача контроля качества — не допустить появления брака. Поэтому в ходе контроля проводится постоянный анализ заданных отклонений параметров продукции от установленных требований. В том случае, если параметры продукции не соответствуют заданным показателям качества, система контроля качества поможет Вам оперативно выявить наиболее вероятные причины несоответствия и устранить их.
Нужно ли контролировать всю продукцию, которую выпускает наше предприятие?
Все зависит от специфики Вашего производства. Если оно носит единичный или мелкосерийный характер, Вы можете подвергнуть продукцию сплошному т.е. 100-процентному контролю. Сплошной контроль, как правило, является довольно трудоемким и дорогостоящим, поэтому в крупносерийном и массовом производстве обычно применяют так называемый выборочный контроль, подвергая проверке лишь часть партии продукции (выборку). Если качество продукции в выборке отвечает установленным требованиям, то вся партия считается качественной, если нет — вся партия бракуется. Однако при таком методе контроля сохраняется вероятность ошибочного бракования (риск Поставщика) или, наоборот, признания партии изделий годной (риск Заказчика). Поэтому при выборочном контроле, заключая контракт на поставку своей продукции, Вы должны будете оговорить обе возможные ошибки, выразив их в процентах.
Какие методы чаще всего используют в процессе контроля качества?
Существуют различные методы контроля качества продукции, среди которых особое место занимают статистические методы.
Многие из современных методов математической статистики довольно сложны для восприятия, а тем более для широкого применения всеми участниками процесса управления качеством. Поэтому японские ученые отобрали из всего множества семь методов, которые наиболее применимы в процессах контроля качества . Заслуга японцев состоит в том, что они обеспечили простоту, наглядность, визуализацию этих методов, превратив их в инструменты контроля качества , которые можно понять и эффективно использовать без специальной математической подготовки. В то же время, при всей своей простоте эти методы позволяют сохранить связь со статистикой и дают возможность профессионалам при необходимости совершенствовать их.
Итак, к семи основным методам или инструментам контроля качества относятся следующие статистические методы:
контрольный листок
гистограмма
диаграмма разброса
диаграмма Парето
стратификация (расслоение)
диаграмма Исикавы (причинно-следственная диаграмма)
контрольная карта
Перечисленные инструменты контроля качества можно рассматривать и как отдельные методы, и как систему методов, обеспечивающую комплексный контроль показателей качества. Они — наиболее важная составляющая комплексной системы контроля Всеобщего Управления Качеством.
В чем заключаются особенности применения инструментов контроля качества на практике?
Внедрение семи инструментов контроля качества должно нaчинaться с обучения этим методам всех участников процесса. Например, успешному внедрению инструментов контроля качества в Японии способствовало обучение руководства и сотрудников компаний методикам контроля качества. Большую роль в обучении статистическим методам в Японии сыграли Кружки контроля качества (см. Главу 2), в которых прошли обучение рабочие и инженеры большинства японских компаний.
Говоря о семи простых статистических методах контроля качества , следует подчеркнуть, что основное их назначение — контроль протекающего процесса и предоставление участнику процесса фактов для корректировки и улучшения процесса. Знание и применение на практике семи инструментов контроля качества лежат в основе одного из важнейших требований TQM — постоянного самоконтроля.
Статистические методы контроля качества в настоящее время применяются не только в производстве, но и в планировании, проектировании маркетинге, материально-техническом снабжении и т.д. Последовательность применения семи методов может быть различной в зависимости от цели, которая поставлена перед системой. Точно так же применяемая система контроля качества не обязательно должна включать все семь методов. Их может быть меньше, а может быть и больше, так как существуют и другие статистические методы.
Однако можно с полной уверенностью сказать, что семь инструментов контроля качества являются необходимыми и достаточными статистическими методами, применение которых помогает решить 95 % всех проблем, возникающих на производстве.
Что такое контрольный листок и как им пользуются?
Какая бы задача не стояла перед системой, объединяющей последовательность применения статистических методов, всегда начинают со сбора исходных данных, на базе которых затем применяют тот или иной инструмент.
Контрольный листок (или лист) — это инструмент для сбора данных и автоматического их упорядочения для облегчения дальнейшего использования собранной информации.
Обычно контрольный листок представляет собой бумажный бланк, на котором заранее напечатаны контролируемые параметры, согласно которым можно заносить в листок данные с помощью пометок или простых символов. Он позволяет автоматически упорядочить данные без их последующего переписывания. Таким образом, контрольный листок — хорошее средство регистрации данных.
Число различных контрольных листков исчисляется сотнями, и в принципе для каждой конкретной цели может быть разработан свой листок. Но принцип их оформления остается неизменным. Например, график температуры больного — один из возможных типов контрольных листков. В качестве другого примера можно привести контрольный листок, применяемый для фиксирования отказавших деталей в телевизорах (см. рисунок 3.2.).
На основании собранных с помощью этих контрольных листков данных не представляет труда составить таблицу суммарных отказов:
| По всем моделям | Число отказов | Процент от общего числа отказов |
| Интегральные схемы | 8 | 6,8 |
| Конденсаторы | 77 | 65,2 |
| Сопротивления | 4 | 3,4 |
| Трансформаторы | 8 | 6,8 |
| Переключатели | 19 | 15,3 |
| Трубки | 3 | 2,5 |
| Итого | 119 | 100 |
При составлении контрольных листков следует обратить внимание на то, чтобы было указано, кто, на каком этапе процесса и в течение какого времен собирал данные, а также чтобы форма листка была простой и понятной без дополнительных пояснений. Важно и то, чтобы все данные добросовестно фиксировались, и собранная в контрольном листке информация могла быть использована для анализа процесса.
Для каких целей в практике контроля качества используется гистограмма?
Для наглядного представления тенденции изменения наблюдаемых значений применяют графическое изображение статистического материала. Наиболее распространенным графиком, к которому прибегают при анализе распределения случайной величины при проведении контроля качества, является гистограмма.
Гистограмма — это инструмент, позволяющий зрительно оценить закон распределения статистических данных.
Гистограмма распределения обычно строится для интервального изменения значения параметра. Для этого на интервалах, отложенных на оси абсцисс, строят прямоугольники (столбики), высоты которых пропорциональны частотам интервалов. По оси ординат откладывают абсолютные значения частот (см. рисунок). Аналогичную форму гистограммы можно получить, если по оси ординат отложить соответствующие значения относительных частот. При этом сумма площадей всех столбиков будет равна единице, что оказывается удобно. Гистограмма также очень удобна для визуальной оценки расположения статистических данных в пределах допуска. Чтобы оценить адекватность процесса требованиям потребителя, мы должны сравнить качество процесса с полем допуска, установленным пользователем. Если имеется допуск, то на гистограмму наносят верхнюю (SU) и нижнюю (SL) его границы в виде линий, перпендикулярных оси абсцисс, чтобы сравнить распределение параметра качества процесса с этими границами. Тогда можно увидеть, хорошо ли располагается гистограмма внутри этих границ.
Пример построения гистограммы.
На рисунке в качестве примера приведена гистограмма значений коэффициентов усиления 120 проверенных усилителей. В ТУ на эти усилители указано номинальное значение коэффициента SN на этот тип усилителей, равное 10дБ. В ТУ также установлены допустимые значения коэффициента усиления: нижняя граница допуска SL = 7,75 дБ, а верхняя SU = 12,25 дБ. При этом ширина поля допуска Т равна разности значений верхней и нижней границ допуска Т = SU – SL.
Если расположить все значения коэффициентов усиления в ранжированный ряд, все они будут находиться в пределах поля допуска, что создаст иллюзию отсутствия проблем. При построении гистограммы сразу становится очевидным, что распределение коэффициентов усиления хотя и находится в пределах допуска, но явно сдвинуто в сторону нижней границы и у большинства усилителей значение этого параметра качества меньше номинала. Это, в свою очередь, дает дополнительную информацию для дальнейшего анализа проблем.
Что собой представляет диаграмма разброса для чего она используется?
Диаграмма разброса — инструмент, позволяющий определить вид и тесноту связи между парами соответствующих переменных.
Эти две переменные могут относиться к:
характеристике качества и влияющему на нее фактору
двум различным характеристикам качества
двум факторам, влияющим на одну характеристику качества
Для выявления связи между ними и служит диаграмма разброса, которую также называют полем корреляции.
Использование диаграммы разброса в процессе контроля качества не ограничивается только выявлением вида и тесноты связи между парами переменных. Диаграмма разброса используется также для выявления причинно-следственных связей показателей качества и влияющих факторов.
Как построить диаграмму разброса?
Построение диаграммы разброса выполняется в следующей последовательности:
Этап 1.
Соберите парные данные (х, у), между которыми вы хотите исследовать зависимость, и расположите их в таблицу. Желательно не менее 25—30 пар данных.
Этап 2.
Найдите максимальные и минимальные значения для х и y. Выберите шкалы на горизонтальной и вертикальной осях так, чтобы обе длины рабочих частей получились приблизительно одинаковыми, тогда диаграмму будет легче читать. Возьмите на каждой оси от 3 до 10 градаций и используйте для облегчения чтения круглые числа. Если одна переменная — фактор, а вторая — характеристика качества, то выберите для фактора горизонтальную ось х, а для характеристики качества — вертикальную ось у.
Этап 3.
На отдельном листе бумаги начертите график и нанесите на него данные. Если в разных наблюдениях получаются одинаковые значения, покажите эти точки, либо рисуя концентрические кружки, либо нанося вторую точку рядом с первой.
Этап 4.
Сделайте все необходимые обозначения. Убедитесь, что нижеперечисленные данные, отраженные на диаграмме, понятны любому человеку, а не только тому, кто делал диаграмму:
название диаграммы
интервал времени
число пар данных
названия и единицы измерения для каждой оси
имя (и другие данные) человека, который делал эту диаграмму
Пример построения диаграммы разброса.
Требуется выяснить влияние термообработки интегральных схем при Т = 120° С в течение времени t= 24 ч на уменьшение обратного тока p-n-перехода (Iобр. ). Для эксперимента было взято 25 интегральных схем (n = 25) и замерены значения Iобр, которые приведены в таблице.
| Номер интегральной схемы | До термообработки, X | После термообработки, Y |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | 68 71 65 78 75 85 86 84 74 65 78 92 60 75 73 69 73 73 83 70 68 79 78 78 73 | 61 67 63 70 74 76 82 70 68 60 68 88 57 71 70 68 73 69 76 73 70 69 71 71 69 |
По таблице находят максимальные и минимальные значения х и у: максимальные значения х = 92, у = 88; минимальные значения х = 60, у = 57.
На графике на оси абсцисс откладывают значения х, на оси ординат — значения у. При этом длину осей делают почти равной разности между их максимальными и минимальными значениями и наносят на оси деления шкалы. На вид график приближается к квадрату. Действительно, в рассматриваемом случае разность между максимальными и минимальными значениями равна 92—60 = 32 для х и 88- 57 = 31 для у, поэтому промежутки между делениями шкалы можно делать одинаковыми.
На график наносятся данные в порядке измерений и точки диаграммы разброса.
На графике указываются число данных, цель, наименование изделия, название процесса, исполнитель, дата составления графика и т.д. Желательно также, чтобы при регистрации данных во время измерений приводилась и сопровождающая информация, необходимая ддя дальнейших исследований и анализа: наименование объекта измерения, характеристики, способ выборки, дата, время измерения, температура, влажность, метод измерения, тип измерительного прибора, имя оператора, проводившего измерения (для данной выборки), и др.
Диаграмма разброса позволяет наглядно показать характер изменения параметра качества во времени. Для этого проведем из начала координат биссектрису. Если все точки лягут на биссектрису, то это означает, что значения данного параметра не изменились в процессе эксперимента. Следовательно, рассматриваемый фактор (или факторы) не влияет на параметр качества. Если основная масса точек лежит под биссектрисой, то это значит, что значения параметров качества за прошедшее время уменьшилось. Если же точки ложатся выше биссектрисы, то значения параметра за рассматриваемое время возросли. Проведя лучи из начала координат, соответствующие уменьшению увеличению параметра на 10, 20, 30, 50 %, можно путем подсчета точек между прямыми выяснить частоту значений параметра в интервалах 0…: %, 10…20 % и т.д. Что такое диаграмма Парето и как она используется для контроля качества?
В 1897 г. итальянский экономист В. Парето предложил формулу, показывающую, что общественные блага распределяются неравномерно. Эта же теория была проиллюстрирована на диаграмме американским экономистом М. Лоренцом. Оба ученых показали, что в большинстве случаев наибольшая доля доходов или благ (80%) принадлежит небольшому числу людей (20%).
Доктор Д. Джуран применил диаграмму М. Лоренца в сфере контроля качества для классификации проблем качества на немногочисленные, но существенно важные и многочисленные, но несущественные и назвал этот метод анализом Парето. Он указал, что в большинстве случаев подавляющее число дефектов и связанных с ними потерь возникают из-за относительно небольшого числа причин. При этом он иллюстрировал свои выводы с помощью диаграммы, которая получила название диаграммы Парето.
Диаграмма Парето — инструмент, позволяющий распределить усилия для разрешения возникающих проблем и выявить основные причины, с которых нужно начинать действовать.
В повседневной деятельности по контролю и управлению качеством постоянно возникают всевозможные проблемы, связанные, например, с появлением брака, неполадками оборудования, увеличением времени от выпуска партии изделий до ее сбыта, наличием на складе нереализованной продукции, поступлением рекламаций. Диаграмма Парето позволяет распределить усилия для разрешения возникающих проблем и установить основные факторы, с которых нужно начинать действовать с целью преодоления возникающих проблем.
Различают два вида диаграмм Парето:
1. Диаграмма Парето по результатам деятельности. Эта диаграмма предназначена для выявления главной проблемы и отражает следующие нежелательные результаты деятельности:
качество: дефекты, поломки, ошибки, отказы, рекламации, ремонты, возвраты продукции
себестоимость: объем потерь, затраты
сроки поставок: нехватка запасов, ошибки в составлении счетов, срыв сроков поставок
безопасность: несчастные случаи, трагические ошибки, аварии.
2. Диаграмма Парето по причинам. Эта диаграмма отражает причины проблем, возникающих в ходе производства, и используется для выявления главной из них:
исполнитель работы: смена, бригада, возраст, опыт работы, квалификация, индивидуальные характеристики;
оборудование: станки, агрегаты, инструменты, оснастка, организация использования, модели, штампы;
сырье: изготовитель, вид сырья, завод-поставщик, партия;
метод работы: условия производства, заказы-наряды, приемы работы, последовательность операций;
измерения: точность (указаний, чтения, приборная), верность и повторяемость (умение дать одинаковое указание в последующих измерениях одного и того же значения), стабильность (повторяемость в течение длительного периода), совместная точность, т.е. вместе с приборной точностью и тарированием прибора, тип измерительного прибора (аналоговый или цифровой).
Как построить диаграмму Парето?
Построение диаграммы Парето состоит из следующих этапов.
Этап 1. Решите, какие проблемы надлежит исследовать и как собирать данные.
1. Какого типа проблемы вы хотите исследовать? Например, дефектные изделия, потери в деньгах, несчастные случаи.
2. Какие данные надо собрать и как их классифицировать? Например, по видам дефектов, по месту их появления, по процессам, по станкам, по рабочим, по технологическим причинам, по оборудованию, по методам измерения и применяемым измерительным средствам.
Примечание. Суммируйте остальные нечасто встречающиеся признаки под общим заголовком «прочие».
3. Установите метод и период сбора данных.
Примечание. Если это рекомендуется, используйте специальный бланк.
Этап 2. Разработайте контрольный листок для регистрации данных с перечнем видов собираемой информации. В нем надо предусмотреть место для графической регистрации данных проверок .
Этап 3. Заполните листок регистрации данных и подсчитайте итоги.
Этап 4. Для построения диаграммы Парето разработайте бланк таблицы для проверок данных, предусмотрев в нем графы для итогов по каждому проверяемому признаку в отдельности, накопленной суммы числа дефектов, процентов к общему итогу и накопленных процентов.
Этап 5. Расположите данные, полученные по каждому проверяемому признаку, в порядке значимости и заполните таблицу.
Примечание. Группу «прочие» надо поместить в последнюю строку независимо от того, насколько большим получилось число, так как ее составляет совокупность признаков, числовой результат по каждому из которых меньше, чем самое маленькое значение, полученное для признака, выделенного в отдельную строку.
Этап 6. Начертите одну горизонтальную и две вертикальные оси.
1. Вертикальные оси. Нанесите на левую ось шкалу с интервалами от 0 до числа, соответствующего общему итогу. На правую ось наносится шкала с интервалами от 0 до 100%.
2. Горизонтальная ось. Разделите эту ось на интервалы в соответствии с числом контролируемых признаков.
Этап 7. Постройте столбиковую диаграмму
Этап 8. Начертите кривую Парето. Для этого на вертикалях, соответствующих правым концам каждого интервала на горизонтальной оси, нанесите точки накопленных сумм (результатов или процентов) и соедините их между собой отрезками прямых.
Этап 9. Нанесите на диаграмму все обозначения и надписи.
1. Надписи, касающиеся диаграммы (название, разметка числовых значений на осях, наименование контролируемого изделия, имя составителя диаграммы).
3. Надписи, касающиеся данных (период сбора информации, объект исследования и место его проведения, общее число объектов контроля).
Как с помощью диаграммы Парето можно проанализировать проблемы качества, возникающие на предприятии?
При использовании диаграммы Парето наиболее распространенным методом анализа является так называемый АВС-анализ, сущность которого мы рассмотрим на примере.
Пример построения и анализа диаграммы Парето.
Допустим, на складе Вашего предприятия скопилось большое количество готовой продукции разных типов. При этом вся продукция, вне зависимости от ее вида и стоимости, подвергается сплошному выходному контролю. Из-за длительного времени контроля реализация продукции задерживается, а Ваше предприятие несет убытки в связи с задержкой поставок.
Разделим всю готовую продукцию, хранящуюся на складе, по группам в зависимости от стоимости каждого продукта.
| Стоимость продукта, USD | Число образцов, тыс. шт. |
| 90 — 100 | 0,2 |
| 80 — 90 | 0,3 |
| 70 — 80 | 0,5 |
| 60 — 70 | 0,5 |
| 50 — 60 | 0,8 |
| 40 — 50 | 1,2 |
| 30 — 40 | 1,5 |
| 20 — 30 | 2,5 |
| 10 — 20 | 5,0 |
| До 10 | 12,5 |
| Итого | 25 |
Для построения диаграммы Парето и проведения АВС-анализа построим таблицу с накоплением до 100%.
| Стоимость продукта, USD | Число образцов, тыс. шт. | Стоимость продукции, хранящейся на складе | Число образцов, хранящихся на складе | ||
| Накопленная стоимость, тыс. USD | Относительная стоимость, % | Накопленное число продукта, тыс.шт | Относительная частота продукта ni/N,% | ||
| 1 | 2 | 3 | 4 | 5 | 6 |
| 95 85 75 65 55 45 35 25 15 5 | 0,2 0,3 0,5 0,5 0,8 1,2 1,5 2,5 5,0 12,5 | 19,0 44,5 82,0 114,5 158,5 212,5 265,0 327,5 402,5 465,0 | 4,1 9,6 17,6 24,5 34,0 45,5 56,7 70,2 86,7 100,0 | 0,2 0,5 1,0 1,5 2,3 3,5 5,0 7,5 12,5 25,0 | 0,8 2,0 4,0 6,0 9,2 14,0 20,0 30.0 50,0 100,0 |
Построение таблицы накопленных частот осуществляется следующим образом.
Сначала находят общую стоимость изделий как сумму произведений для значений центров классов и числа образцов, перемножая значения столбцов 1 и 2, т.е. общая стоимость равна
95 × 200 = 85 × 300 + 75 × 500 + …+ 15 × 5000 + 5 × 12500 = 465,0 тыс. долл.
Затем составляют данные столбца 3. Например, значение из первой строки 19,0 тыс. долл. определяется следующим образом: 95 × 200 = 19 тыс. долл. Значение из второй строки, равное 44,5 тыс. долл., определяется так: 95 × 200 + 85 × 300 = 44,5 тыс. долл. и т.д.
Затем находят значение столбца 4, который показывает, сколько процентов от общей стоимости составляют данные каждой строки.
Данные столбца 6 образуются следующим образом. Значение 0,8 из первой строки представляет собой число процентов, приходящихся на накопленный запас продукции (200) от всего количества образцов (25000). Значение 2,0 из второй строки представляет собой число процентов, приходящихся на накопленный запас продукции (200 + 300), от всего ее количества.
После проведения этой подготовительной работы несложно построить диаграмму Парето. В прямоугольной системе координат по оси абсцисс отложим относительную частоту продукта ni/N,% (данные столбца 6), а по оси ординат — относительную стоимость этой продукции Стi/Cт, % (данные столбца 4). Соединив полученные точки прямыми, получим кривую Парето (или диаграмму Парето), как это показано на рисунке.
Кривая Парето получилась сравнительно плавной в результате большого числа классов. При уменьшении числа классов она становится более ломаной.
Из анализа диаграммы Парето видно, что на долю наиболее дорогой продукции (первые 7 строк таблицы), которая составляет 20% от общего числа хранящихся на складе образцов, приходится более 50% общей стоимости всей готовой продукции, а на долю самой дешевой продукции, расположенной в последней строке таблицы и составляющей 50% от общего количества продукции на складе, приходится всего 13,3% от общей стоимости.
Назовем группу «дорогой» продукции группой А, группу дешевой продукции (до 10 долл.) — группой С, и промежуточную группу — группой В. Построим таблицу АВС — анализа полученных результатов.
| Группа | Относительная частота количества образцов в группе, % | Относительная стоимость образцов в группе, % |
| А В С | 20 30 50 | 56,7 30 13,3 |
Теперь ясно, что контроль продукции на складе будет эффективнее в том случае, если контроль образцов группы А будет самым жестким (сплошным), а контроль образцов группы С — выборочным.
Что такое стратификация?
Одним из наиболее эффективных статистических методов, широко используемых в системе управления качеством, является метод стратификации или расслаивания. В соответствии с этим методом водят расслаивание статистических данных, т.е. группируют данные в зависимости от условий их получения и производят обработку каждой группы данных в отдельности. Данные, разделенные на группы в соответствии с их особенностями, называют слоями (стратами), а сам процесс разделения на слои (страты) — расслаиванием (стратификацией).
Метод расслаивания исследуемых статистических данных — это инструмент, позволяющий произвести селекцию данных, отражающую требуемую информацию о процессе.
studfiles.net