Вариант 1
1.
2.
3.
4.
Вариант 2
1.
2.
3.
4.
Вариант 3
1.
2.
3.
4.
Вариант 4
1.
2.
3.
4.
Вариант 5
1.
2.
3.
4.
Вариант 6
1.
2.
3.
4.
Контрольная работа по теме «Векторы» 10 класс
1. Распределение задач по уровням сложности соответствует современной классификации уровней владения знаниями:
задания части А – вопросы, тестовые задания в которых преобладает
Узнавание. Для правильного решения учащийся должен сопоставить собственные знания с информацией, содержащейся в вопросе ,которые являются самыми легкими и выполняемыми, так как даже учащиеся, уделяющие недостаточное внимание домашней подготовке, находят в своей памяти образ информации, соответствующий вопросу.
Воспроизведение. Этот уровень требует от учащихся восстановления имеющейся в памяти информации. Задания такого типа требуют от тестируемого закончить определение, сопоставить формулу и ее словесное прочтение и т. д.
задания части В – задачи в 1 – 2 действия, в которых предполагается использование выученных формул, законов, определений из данной темы. Такие задачи в большом количестве рассматриваются на уроках применения знаний, повторения и обобщения.
задания части С – задачи, требующие применения знаний по данной теме в измененной ситуации. Для решения задач данного типа кроме знаний из текущей темы, учащийся должен применить знания их других разделов физики, математические знания, сведения из других смежных наук.
2. Соответствие №задания, уровня и необходимых знаний и умений
| № задания | Уровень | необходимые знания и умения |
| А1
А2 А3 А4 А5 | узнавание материала
вопросы с выбором ответа | Коллинеарность и компланарность векторов Равные векторы формулы нахождение длины вектора сложения векторов умножение вектора на число скалярное произведение векторов |
| А6 | применение знаний | Вычисление длины вектора |
| А7 | воспроизведение знаний | Вычисление координат вектора полученного при сложении векторов и умножении вектора на число |
| В1 | применение знаний | Вычисление неизвестной координаты вектора исходя из коллинеарности векторов при известной длине вектора |
| В2 | применение знаний | Вычисление угла между векторами |
| С | применение знаний | Разложение вектора Нахождение высот и медиан треугольника Задачи на доказательство
|
Подбор заданий.
| Вариант 1 | |
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| Вариант 2 | |
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| Вариант 3 | |
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| Вариант 4 | |
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| Вариант 5 | |
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| Вариант 6 | |
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| | |
| Вариант 1 | |
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| Вариант 2 | |
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| Вариант 3 | |
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| Вариант 4 | |
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| Вариант 5 | |
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| Вариант 6 | |
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| Вариант 7 | |
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| Вариант 8 | |
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| Вариант 9 | |
| 1. | |
| 2. | |
| 3. | |
| 4. | |
xn--j1ahfl.xn--p1ai
1 вариант.
1. Начертите два неколлинеарных вектора 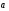 и
и 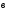 . Постройте векторы, равные:
. Постройте векторы, равные:
а) 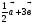 ; б)
; б) 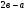
2. На стороне ВС ромба АВСD лежит точкаК такая, что ВК = КС, О – точка пересечения диагоналей. Выразите векторы 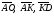 через векторы
через векторы 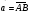 и
и 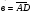 .
.
3. В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 и 12 см. Найдите среднюю линию трапеции.
4.* В треугольнике АВС О – точка пересечения медиан. Выразите вектор 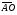 через векторы
через векторы 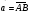 и
и 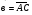 .
.
2 вариант
1. Начертите два неколлинеарных вектора 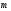 и
и 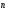 . Постройте векторы, равные:
. Постройте векторы, равные:
а) 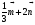 ; б)
; б) 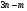
2. На стороне СD квадрата АВСD лежит точка Р такая, что СР = РD , О – точка пересечения диагоналей. Выразите векторы 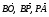 через векторы
через векторы 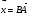 и
и 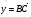
3. В равнобедренной трапеции один из углов равен 600, боковая сторона равна 8 см, а меньшее основание 7 см. Найдите среднюю линию трапеции.
4. * В треугольнике МNK О – точка пересечения медиан, 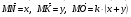 . Найдите число k.
. Найдите число k.
1 вариант.
1. Найдите координаты и длину вектора 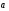 , если
, если 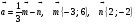 .
.
2. Напишите уравнение окружности с центром в точкеА (- 3;2), проходящей через точку В (0; - 2).
3. Треугольник МNK задан координатами своих вершин: М (- 6; 1), N (2; 4), К (2; - 2).
а) Докажите, что Δ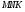 - равнобедренный;
- равнобедренный;
б) Найдите высоту, проведённую из вершины М.
4. * Найдите координаты точки N, лежащей на оси абсцисс и равноудалённой от точек Р и К, если Р( - 1; 3 ) и К( 0; 2 ).
2 вариант.
1). Найдите координаты и длину вектора 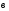 , если
, если 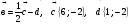 .
.
2). Напишите уравнение окружности с центром в точке С ( 2; 1 ), проходящей через точку D ( 5; 5 ).
3). Треугольник СDЕ задан координатами своих вершин: С (2; 2), D (6; 5), Е (5; - 2).
а) Докажите, что Δ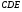 - равнобедренный;
- равнобедренный;
б) Найдите биссектрису, проведённую из вершины С.
4. * Найдите координаты точки А, лежащей на оси ординат и равноудалённой от точек В и С, если В( 1; - 3 ) и С( 2; 0 ).
1 вариант
В треугольнике АВС 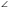 А = 450,
А = 450,
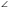 В = 600, ВС =
В = 600, ВС = 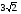 Найдите АС.
Найдите АС.
Две стороны треугольника равны
7 см и 8 см, а угол между ними равен 1200. Найдите третью сторону треугольника.
Определите вид треугольника АВС, если
А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).
* В ΔАВС АВ = ВС, 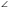 САВ = 300, АЕ – биссектриса, ВЕ = 8 см. Найдите площадь треугольника АВС.
САВ = 300, АЕ – биссектриса, ВЕ = 8 см. Найдите площадь треугольника АВС.
2 вариант
В треугольнике СDE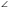 С = 300,
С = 300,
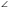 D = 450, СЕ =
D = 450, СЕ =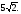 Найдите DE.
Найдите DE.
Две стороны треугольника равны
5 см и 7 см, а угол между ними равен 600. Найдите третью сторону треугольника.
Определите вид треугольника АВС, если
А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).
* В ромбе АВСD АК – биссектриса угла САВ, 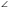 ВАD = 600, ВК = 12 см. Найдите площадь ромба.
ВАD = 600, ВК = 12 см. Найдите площадь ромба.
1 вариант
1. Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна 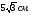
2. Вычислите длину дуги окружности с радиусом 4 см, если её градусная мера равна 1200. Чему равна площадь соответствующего данной дуге кругового сектора?
3. Периметр правильного треугольника, вписанного в окружность, равен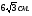 Найдите периметр правильного шестиугольника, описанного около той же окружности.
Найдите периметр правильного шестиугольника, описанного около той же окружности.
2 вариант
1. Найдите площадь круга и длину ограничивающей его окружности, если сторона квадрата, описанного около него, равна 6 см.
2. Вычислите длину дуги окружности с радиусом 10 см, если её градусная мера равна 1500. Чему равна площадь соответствующего данной дуге кругового сектора?
3. Периметр квадрата, описанного около окружности, равен 16 дм. Найдите периметр правильного пятиугольника, вписанного в эту же окружность.
1 вариант
1. Начертите ромб АВСD. Постройте образ этого ромба:
а) при симметрии относительно точки С;
б) при симметрии относительно прямой АВ;
в) при параллельном переносе на вектор 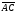 ;
;
г) при повороте вокруг точки D на 600 по часовой стрелке.
2. Докажите, что прямая, содержащая середины двух параллельных хорд окружности, проходит через её центр.
3. * Начертите два параллельных отрезка, длины которых равны.начертите точку, являющуюся центром симметрии, при котором один отрезок отображается на другой.
2 вариант
1. Начертите параллелограмм АВСD. Постройте образ этого параллелограмма:
а) при симметрии относительно точки D;
б) при симметрии относительно прямой CD;
в) при параллельном переносе на вектор 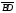 ;
;
г) при повороте вокруг точки А на 450 против часовой стрелки.
2. Докажите, что прямая, содержащая середины противоположных сторон параллелограмма, проходит через точку пересечения его диагоналей.
3.* Начертите два параллельных отрезка, длины которых равны. Постройте центр поворота, при котором один отрезок отображается на другой.
doc4web.ru
Контрольная работа № 1 «Векторы»
Вариант 1
Закончи предложение.
1. Вектором называется направленный ....
2. Векторы называются равными, если они сонаправлены и ...
3. Дан треугольник АВС.
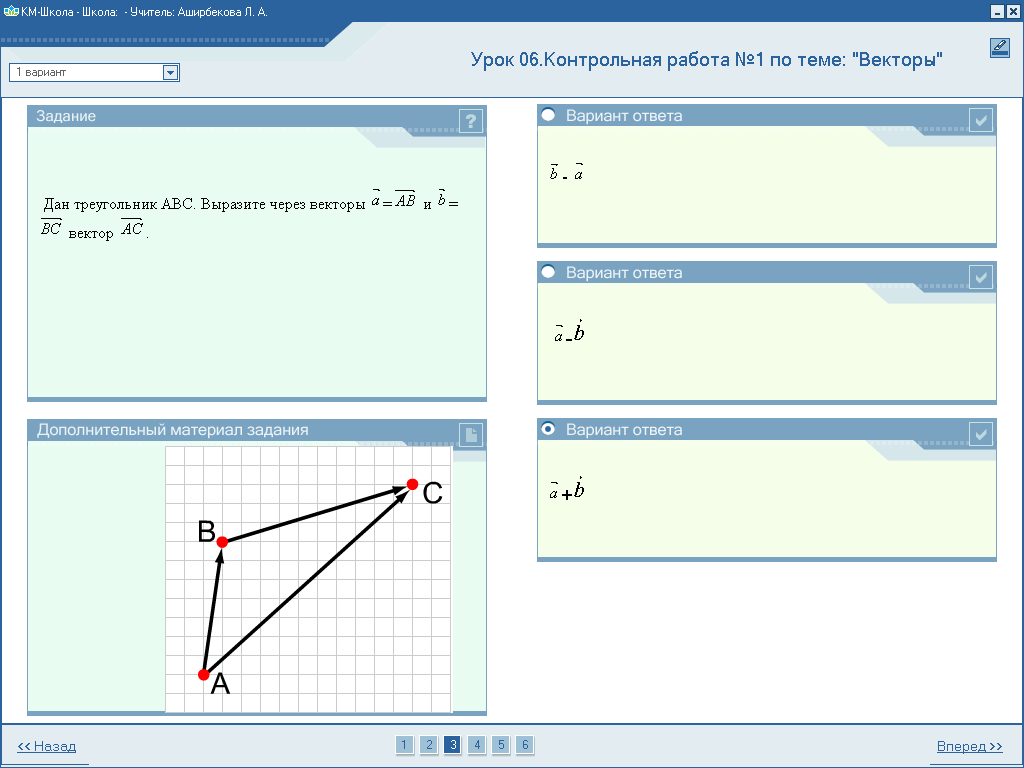 Выразите через векторы
Выразите через векторы  =
= и
и  =
= вектор
вектор 
А)  -
-  ; б)
; б)  -
- ; в)
; в)  +
+
4.ABCD - трапеция. Найдите сумму векторов  +
+ +
+ ; разность векторов
; разность векторов  -
-
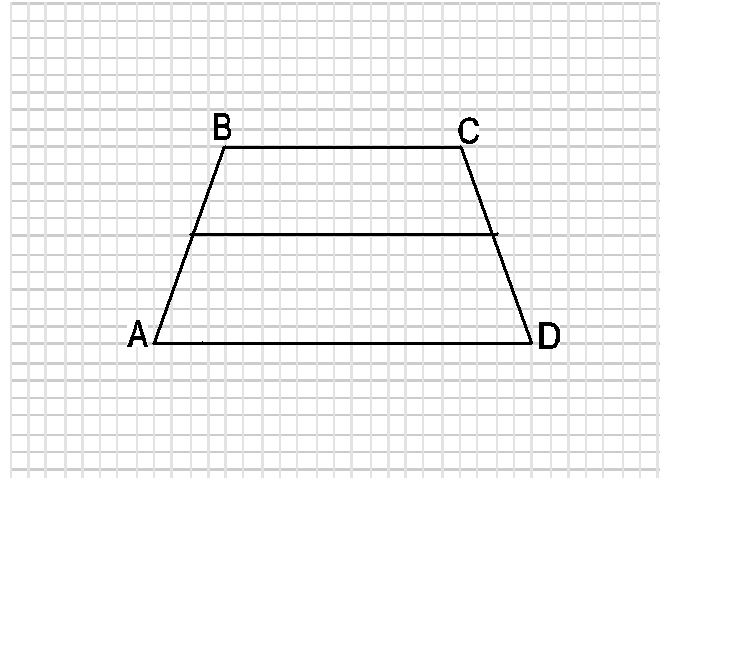
А)  +
+ +
+ =
= ,
,  -
- =
=
Б)  +
+ +
+ =
= ,
,  -
- =
=
В)  +
+ +
+ =
= ,
,  -
- =
=
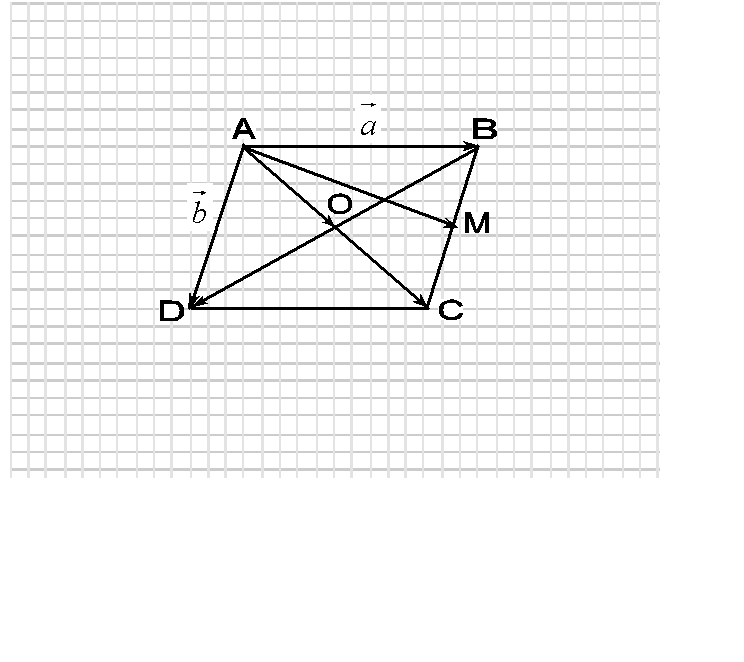
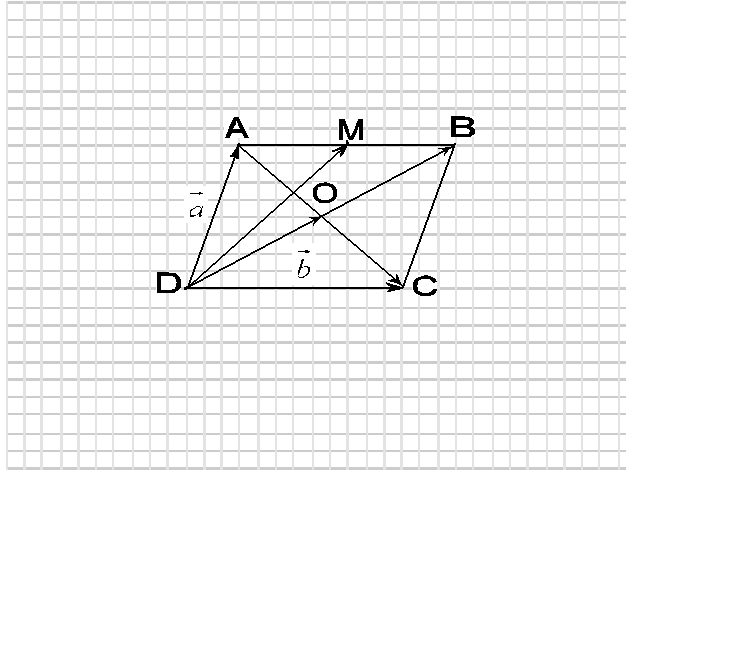
5. ABCD - параллелограмм, О - точка пересечения диагоналей, М - середина ВС,  =
= ,
,  =
=  . Выразите через векторы
. Выразите через векторы  и
и  следующие векторы:
следующие векторы:
а)  , б)
, б)  , в)
, в)  , г)
, г) 
6. Одно основание трапеции на 4 см больше другого, а средняя линия равна 8 см. Найдите основания трапеции.
7. В треугольнике АВС: ВА=а, ВС=в. Выразите через векторы а и в следующие векторы: АС, АС1, АС2, АС3, если точки С1, С2, С3 взяты на стороне ВС так, что СС1=С1 С2=С 2С3=С 3В.
8. В треугольнике АВС точка О-середина медианы АМ. Выразите вектор ВО через векторы АВ =а и АС =с.
Вариант 2
Закончи предложение.
1. От любой точки М можно отложить вектор, равный данному вектору, и притом только...
2. Ненулевые векторы называются коллинеарными, если они лежат на одной прямой, либо на ... прямых
3. Дан треугольник АВС. Выразите через векторы  =
= и
и  =
=  вектор
вектор  .
.

А)  -
-
Б)  +
+
В)  -
- 
4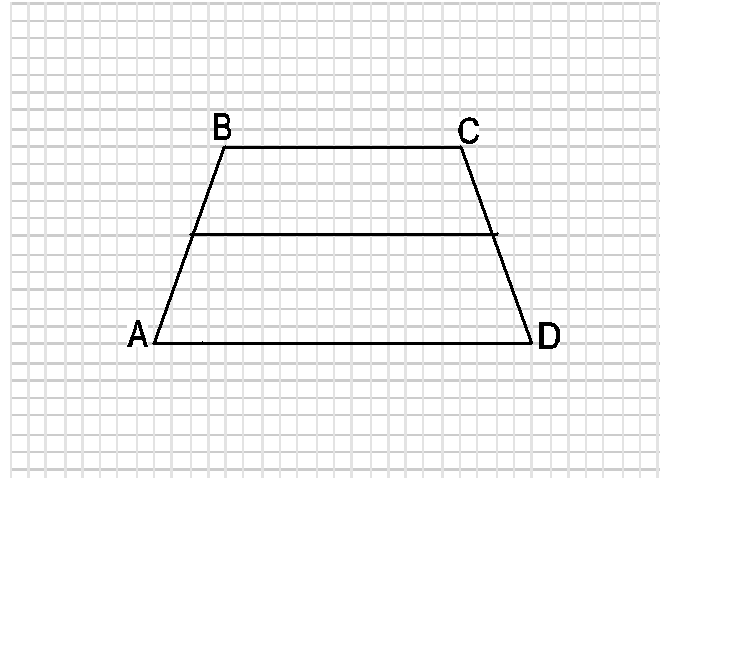 . ABCD - трапеция. Найдите сумму векторов
. ABCD - трапеция. Найдите сумму векторов  +
+ ; разность векторов
; разность векторов  -
-
а)  +
+ =
= ,
,  -
- =
=
б)  +
+ =
= ,
,  -
- =
=
в)  +
+ =
= ,
,  -
- =
= 
5. ABCD - параллелограмм, О - точка пересечения диагоналей, М - середина АВ,  =
= ,
,  =
= . Выразите через векторы
. Выразите через векторы  и
и  следующие векторы: А)
следующие векторы: А)  , б)
, б)  , в)
, в)  , г)
, г)
6. Одно основание трапеции на 2 см меньше другого, а средняя линия равна 10 см. Найдите основания трапеции.
7. В треугольнике АВС: ВА=а, ВС=в. Выразите через векторы а и в следующие векторы: СА, С А1, СА2, СА3, если точки А1, А2, А3 взяты на стороне АВ так, что АА1=А1 А2=
А 2А3=А 3В.
8. В треугольнике АВС точка О-середина медианы АМ. Выразите вектор ВО через векторы АВ =а и АС =с.
infourok.ru
Контрольная работа по геометрии №1 (9 класс)
Вариант I
1. В параллелограмме ABCD точка M – середина стороны CD; N – точка на стороне AD, такая, что AN : ND = 3 : 4. Выразите векторы  и
и  , через векторы
, через векторы  и .
и .
2. Упростите выражение:
а) 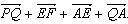
б) 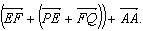
в)
г)
д)
3. Высота, проведенная из вершины тупого угла равнобедренной трапеции, делит среднюю линию трапеции на отрезки, равные 2 см и 6 см. Найдите основания трапеции
4* В прямоугольной трапеции один из углов равен 120°. Найдите ее среднюю линию, если меньшая диагональ и большая боковая сторона трапеции равна b.
Контрольная работа по геометрии №1 (9 класс)
Вариант II
1. Четырехугольник KMNP – параллелограмм. Выразите через векторы и  векторы
векторы  ,
,  , где А – точка на стороне PN, такая, что PA : AN = 2 : 5, B – середина отрезка MN.
, где А – точка на стороне PN, такая, что PA : AN = 2 : 5, B – середина отрезка MN.
2. Упростите выражение:
а)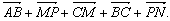
б) 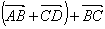
в)
г)
д)
3. Высота, проведенная из вершины тупого угла равнобедренной трапеции, делит большее основание трапеции на два отрезка, меньший из которых равен 2 см. Найдите большее основание трапеции, если ее средняя линия равна 8 см.
4* В прямоугольной трапеции один из углов равен 120°. Найдите ее среднюю линию, если меньшая диагональ и большая боковая сторона трапеции равна b.
Контрольная работа по геометрии №1 (9 класс)
Вариант I
1. В параллелограмме ABCD точка M – середина стороны CD; N – точка на стороне AD, такая, что AN : ND = 3 : 4. Выразите векторы  и
и  , через векторы
, через векторы  и .
и .
2. Упростите выражение:
а) 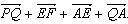
б) 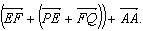
в)
г)
д)
3. Высота, проведенная из вершины тупого угла равнобедренной трапеции, делит среднюю линию трапеции на отрезки, равные 2 см и 6 см. Найдите основания трапеции
4* В прямоугольной трапеции один из углов равен 120°. Найдите ее среднюю линию, если меньшая диагональ и большая боковая сторона трапеции равна b.
Контрольная работа по геометрии №1 (9 класс)
Вариант II
1. Четырехугольник KMNP – параллелограмм. Выразите через векторы и  векторы
векторы  ,
,  , где А – точка на стороне PN, такая, что PA : AN = 2 : 5, B – середина отрезка MN.
, где А – точка на стороне PN, такая, что PA : AN = 2 : 5, B – середина отрезка MN.
2. Упростите выражение:
а)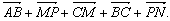
б) 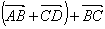
в)
г)
д)
3. Высота, проведенная из вершины тупого угла равнобедренной трапеции, делит большее основание трапеции на два отрезка, меньший из которых равен 2 см. Найдите большее основание трапеции, если ее средняя линия равна 8 см.
4* В прямоугольной трапеции один из углов равен 120°. Найдите ее среднюю линию, если меньшая диагональ и большая боковая сторона трапеции равна b.
infourok.ru
Муниципальное бюджетное общеобразовательное учреждение «Гимназия №2 г. Владивостока»
КОНТРОЛЬНАЯ РАБОТА
«ВЕКТОРЫ, СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ»
ВАРИАНТ №1
№1. Даны точки А (–3; 5; –6), В(5; –2; 4), С(0; 4; 3), D(–6; –3; 0). Найти: 1) координаты 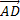
2) расстояние между точками B и D
3) координаты середины М отрезка АВ
4) 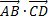 5) угол между векторами
5) угол между векторами 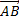 и
и 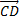
6) угол между прямыми AD и ВС 7) 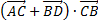
8) коллинеарны ли векторы 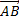 и
и 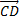 ? (ответ обосновать)
? (ответ обосновать)
№2. Даны векторы  и
и  , причем
, причем  Найти
Найти  .
.
№3. Даны точки А(2; –1; 0), В(–3; 2; 1), С(1; 1,4). Найдите координаты точки D, если 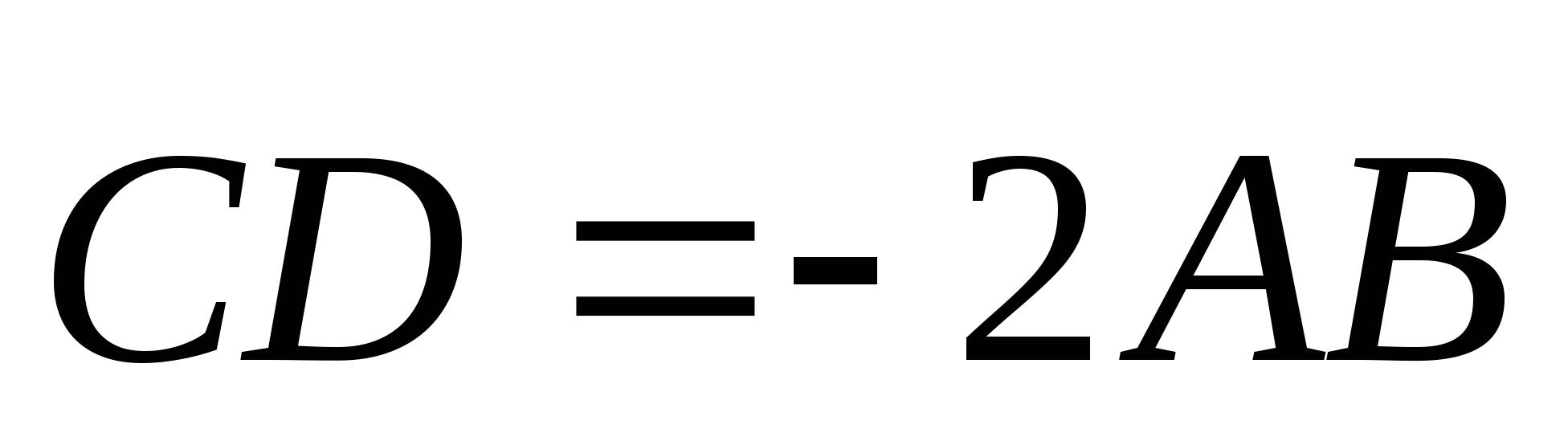 .
.
№4. Векторы 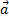 и
и 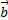 образуют угол 150º,
образуют угол 150º, 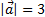 ,
, 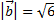 . Найти
. Найти 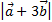
КОНТРОЛЬНАЯ РАБОТА
«ВЕКТОРЫ, СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ»
ВАРИАНТ №3
№1. Даны точки А(4; –6; 3), В(–5; 2; –5), С(0; –3; –4),D(–6; –3; 0). Найти: 1) координаты 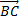
2) расстояние между точками А и D
3) координаты середины Х отрезка СВ
4) 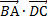 5) угол между векторами
5) угол между векторами 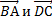
6) угол между прямыми DА и СВ 7) 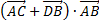
8) коллинеарны ли векторы 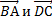 ? (ответ обосновать)
? (ответ обосновать)
№2. Даны векторы  и
и  , причем
, причем 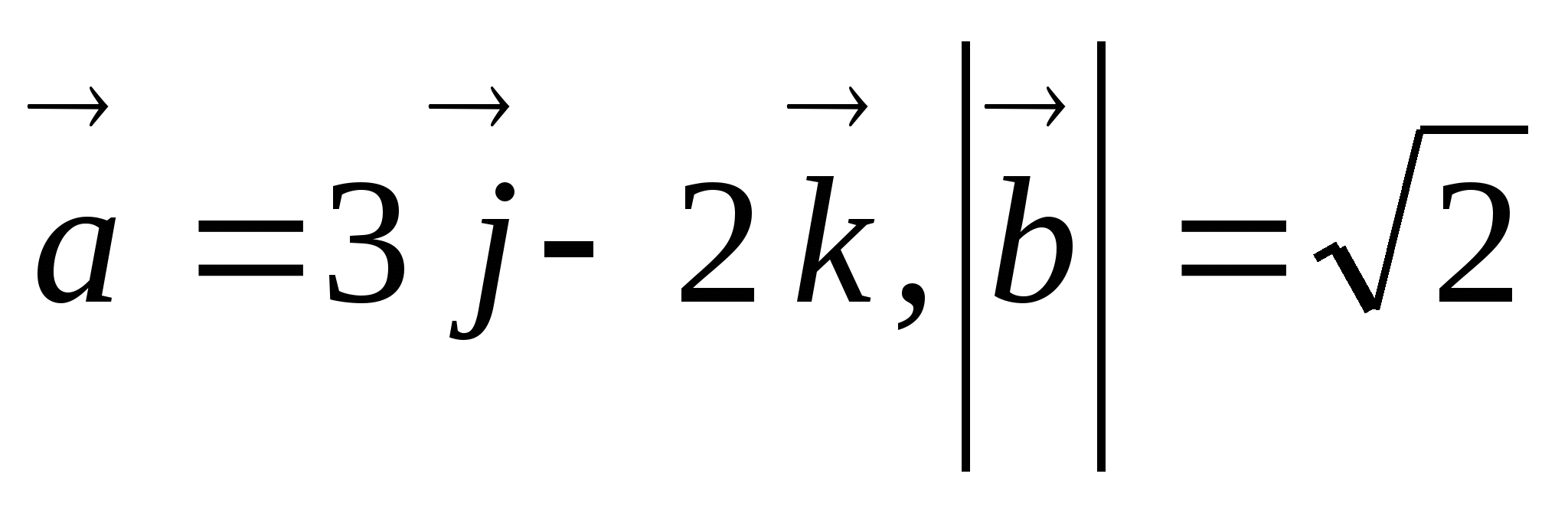 . Векторы
. Векторы 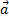 и
и 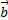 образуют угол 135º . Найти
образуют угол 135º . Найти  .
.
№3. Даны точки А(2; 1; 0), В(3; –2; 1), С(1; 1, –4). Найдите координаты точки D, если 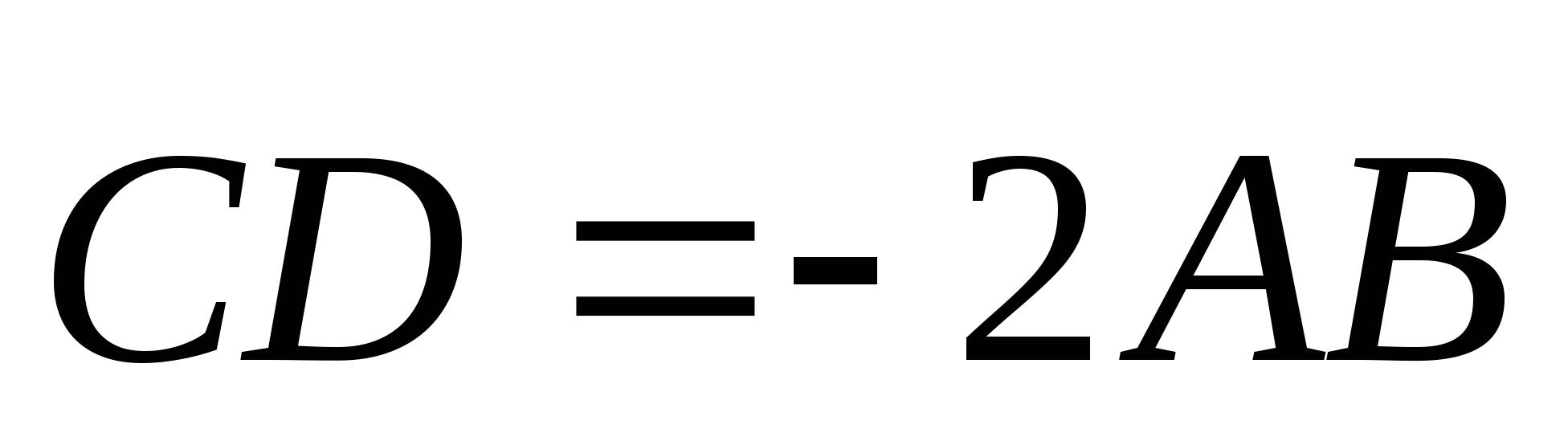 .
.
№4. Векторы 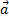 и
и 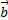 образуют угол 150º,
образуют угол 150º, 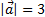 ,
, 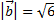 . Найти
. Найти 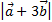
КОНТРОЛЬНАЯ РАБОТА
«ВЕКТОРЫ, СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ»
ВАРИАНТ №2
№1. Даны точки А(3; –5; 6), В(–3; 1; –4), С(–4; 0; 3), D(0; –3; –5). Найти: 1) координаты 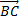
2) расстояние между точками С и D
3) координаты середины К отрезка АС
4) 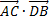 5) угол между векторами
5) угол между векторами 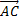 и
и 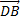
6) угол между прямыми DС и АВ 7) 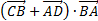
8) коллинеарны ли векторы 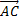 и
и 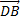 ? (ответ обосновать)
? (ответ обосновать)
№2. Даны векторы  и
и  , причем
, причем  Найти
Найти  . №3. Даны точки А(2; –1; 0), В(–3; 2; 1), С(1; 1,4). Найдите координаты точки D, если
. №3. Даны точки А(2; –1; 0), В(–3; 2; 1), С(1; 1,4). Найдите координаты точки D, если 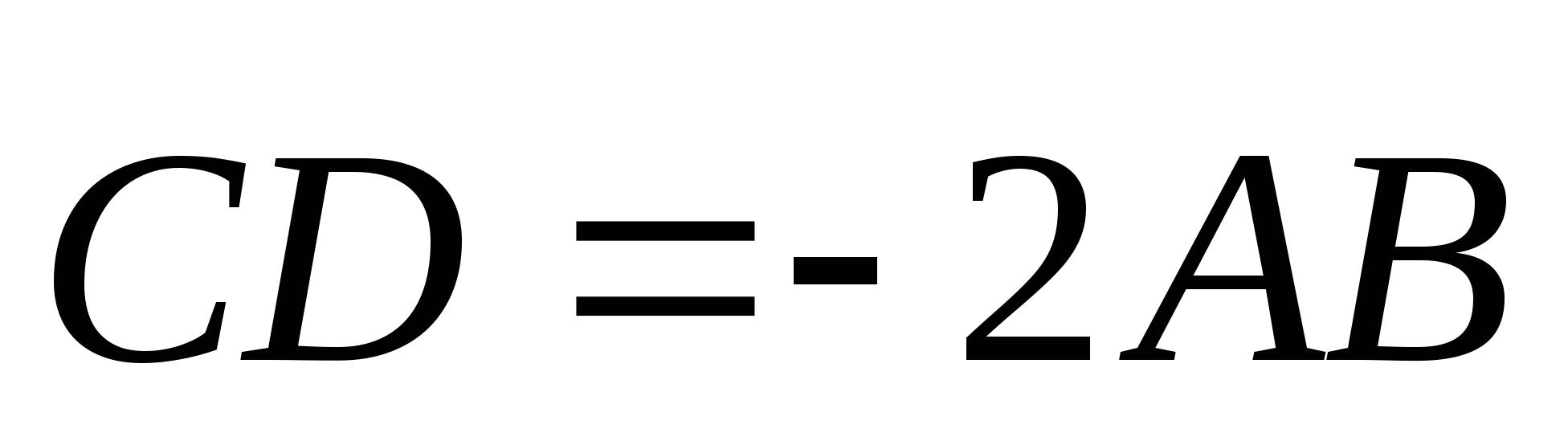 .
.
№4. Векторы 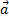 и
и 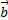 образуют угол 120º,
образуют угол 120º, 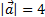 ,
, 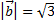 . Найти
. Найти 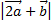
infourok.ru
Контрольная работа по геометрии, 8 класс.
1 уровень.
ВАРИАНТ 1.
ВАРИАНТ 2.
II уровень.
ВАРИАНТ 1.
1.
Начертите неколлинеарные векторы  ,
, . Постройте векторы, равные: а)
; б) -
 +
+ + 0,5
2.
На сторонах ВС и СD параллелограмма АВСD отмечены точки К и Е так, что ВК = КС, СЕ : ЕD = 2 : 3. Выразите векторы  ,
, ,
через векторы
 =
=  и
и  =
=  .
.
3.
В трапеции АВСD ∠A = 600, ∠D = 450, боковые стороны равны 10 см и 12 см, а меньшее основание 8 см. Найдите среднюю линию трапеции.
4.
В треугольнике АВС В1 - середина стороны АС, точка А1 лежит на стороне ВС так, что ВА1 : А1С = 1 : 2. Используя векторы, докажите, что середина ВВ1 лежит на прямой АА1
ВАРИАНТ 2.
1.
Начертите неколлинеарные векторы ,
. Постройте векторы, равные: а)
; б) 0,2
-
+
2.
На сторонах AB и AD параллелограмма АВСD отмечены точки M и N так, что AM = MB, AN : ND = 3 : 4. Выразите векторы ,
,
через векторы
=
и
=
.
3.
В трапеции MNKP ∠M = 450, ∠P = 300, боковые стороны равны 8 см и 10 см, а меньшее основание 5 см. Найдите среднюю линию трапеции.
4.
В трапеции АВСD ВС : АD = 1 : 2, Е - середина боковой стороны СВ, точка М лежит на стороне АЕ так, что АМ : МЕ = 4 : 1. Используя векторы, докажите, что точка М лежит на диагонали ВD.
III уровень.
ВАРИАНТ 1.
ВАРИАНТ 2.
1.
ABCD и CFED - параллелограммы, имеющие общую сторону, Постройте вектор такой, что
 +
+ -
- +
+
=

2.
На стороне AB и диагонали BD параллелограмма АВСD лежат точки N и M так, AN : NB = 3 : 2, BM : MD = 5 : 2. Выразите вектор через векторы
=
и
=
.
3.
В прямоугольной трапеции меньшее основание в два раза меньше меньшей боковой стороны, один из углов 1350, а средняя линия 14 см. Найти периметр трапеции.
4.
В параллелограмме АВСD точка Р - середина отрезка СD, М - середина стороны ВС, отрезки ВD и АМ пересекаются в точке О. Докажите, что ОР АD + АВ.
multiurok.ru
1 вариант
Найдите координаты и длину вектора  , если
, если 
Найдите координаты вектора  , если A(1,-3), B(0,-6)
, если A(1,-3), B(0,-6)
Начертите два неколлинеарных вектора  и
и  . Постройте
. Постройте 
Найдите координаты вектора  , если
, если  , если
, если 
В трапеции основания равны 9 и 14. Найдите среднюю линию трапеции
Напишите уравнение окружности с центром A(-1,2), проходящей через точку B(0,1)
2 вариант
Найдите координаты и длину вектора  , если
, если 
Найдите координаты вектора  , если A(6,-4), B(1,-6)
, если A(6,-4), B(1,-6)
Начертите два неколлинеарных вектора  и
и  . Постройте
. Постройте 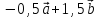
Найдите координаты вектора  , если
, если  , если
, если 
В трапеции основания равны 12 и 7. Найдите среднюю линию трапеции
Напишите уравнение окружности с центром A(2,-3), проходящей через точку B(-1,-2)
1 вариант
Найдите координаты и длину вектора  , если
, если 
Найдите координаты вектора  , если A(1,-3), B(0,-6)
, если A(1,-3), B(0,-6)
Начертите два неколлинеарных вектора  и
и  . Постройте
. Постройте 
Найдите координаты вектора  , если
, если  , если
, если 
В трапеции основания равны 9 и 14. Найдите среднюю линию трапеции
Напишите уравнение окружности с центром A(-1,2), проходящей через точку B(0,1)
2 вариант
Найдите координаты и длину вектора  , если
, если 
Найдите координаты вектора  , если A(6,-4), B(1,-6)
, если A(6,-4), B(1,-6)
Начертите два неколлинеарных вектора  и
и  . Постройте
. Постройте 
Найдите координаты вектора  , если
, если  , если
, если 
В трапеции основания равны 12 и 7. Найдите среднюю линию трапеции
Напишите уравнение окружности с центром A(2,-3), проходящей через точку B(-1,-2)
1 вариант
Найдите координаты и длину вектора  , если
, если 
Найдите координаты вектора  , если A(1,-3), B(0,-6)
, если A(1,-3), B(0,-6)
Начертите два неколлинеарных вектора  и
и  . Постройте
. Постройте 
Найдите координаты вектора  , если
, если  , если
, если 
В трапеции основания равны 9 и 14. Найдите среднюю линию трапеции
Напишите уравнение окружности с центром A(-1,2), проходящей через точку B(0,1)
2 вариант
Найдите координаты и длину вектора  , если
, если 
Найдите координаты вектора  , если A(6,-4), B(1,-6)
, если A(6,-4), B(1,-6)
Начертите два неколлинеарных вектора  и
и  . Постройте
. Постройте 
Найдите координаты вектора  , если
, если  , если
, если 
В трапеции основания равны 12 и 7. Найдите среднюю линию трапеции
Напишите уравнение окружности с центром A(2,-3), проходящей через точку B(-1,-2)
xn--j1ahfl.xn--p1ai