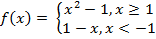
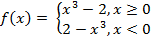
Контрольная работа № 1
по теме «Функции и их свойства»
Цель: проверить уровень усвоение ГОСО
- умение находить значение функции в точке;
- умение находить область определения функции;
- умения строить эскиз графика функции и находить по эскизу промежутки
возрастания и убывания , экстремумы функции, точки пересечения с осями
координат;
- знания свойств четных и нечетных функций.
1. Вычислите:
y = f(x) является нечетной y = f(x) является четной
2 f(-4) + f(3) f(-3) + 2 f(1)
eсли f(4)=1, f(-3)=2 eсли f(3)=4, f(-1)=2
2. Найдите значение функции в точке X0.
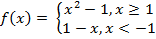
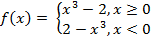
X0 = -2 и X0 = 4 X0 = -3 и X0 = 1
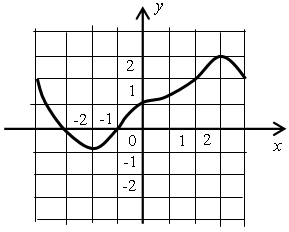
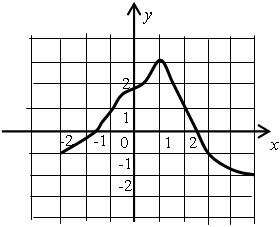
3. Постройте эскиз функции и найдите координаты точек его пересечения с осями координат.
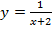
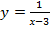
4. Найдите область определения функции
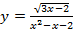
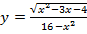
5. Найдите промежутки возрастания и убывания и экстремумы функции.
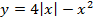
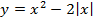
Критерии оценки.
0-10 баллов – «2»
11-14баллов – «3»
15-19 баллов – «4»
20-21 баллов – «5»
Распределение заданий по содержанию и видам деятельности.
Содержательные линии
Воспроизведение знаний
Применение знаний
Интеграция знаний
Процентное
Соотношение в тексте
Четные и нечетные функции.
№1
20%
Значения функции в точке
№2
20%
График функции и ее свойства
№3,4
№5
40%
Процентное
Соотношение в тексте
40%
40%
20%
100%
Критерии оценивания
№
задания
Характеристика задания
Проверяемые элементы
Балл за выполнение проверяемого элемента
Балл за выполнение задания
1
Свойства четных и нечетных функций.
Знания свойств четных и нечетных функций
2
3
Запись ответа
1
2
Значение функции в точке
Правильно подставил
2
3
Вычисления
1
3
График функции и ее свойства
Построение эскиза графика
2
5
Пересечение с осью абсцисс
1
Пересечение с осью ординат
2
Запись ответа
1
4
Область определения функции
Составление условий для нахождения области определения
2
5
Решение неравенства
1
Запись ответа
2
5
Промежутки возрастания , убывания и экстремумы функции
Вершина параболы
1
5
Свойства модуля
1
Эскиз графика
2
Запись ответа
1
infourok.ru
Контрольная работа по алгебре №1
Вариант 2
1. Найдите значение х, при котором функция, заданная формулой f (х) = х + 2, принимает значение, равное 1.
2. Найдите область определения функции, заданной формулой:
а) f (х) = 16 – 8х; в) γ (х) =  ;
;
б) g (х) = ; г) у = х2– 4
3. Укажите область значений функции:
а) у = 37х + 1; в) у = ;
б) у = – 23; г) у = | х |
4. Перечислите свойства функции:
5. Разложите на множители квадратный трехчлен:
а) х2– 7х + 12; б) 10х2+ 19х – 2.
6. Сократите дробь:
а)  ; б)
; б)  .
.
Контрольная работа по алгебре №1
Вариант 1
1.Найдите значение х, при котором функция, заданная формулой f (х) = х + 9, принимает значение, равное 10.
2. Найдите область определения функции, заданной формулой:
а) f (х) = 5х – 7; в) g (х) =  ;
;
б) у = –; г) γ (х) = 5 – х2
3. Укажите область значений функции:
а) у = –29х + 5; в) у =  ;
;
б) у = 41; г) у = –
4. Перечислите свойства функции:
5. Разложите на множители квадратный трехчлен:
а) х2+ х – 72; б) 5х2+ 2х – 3.
6. Сократите дробь:
а)  ; б)
; б)  .
.
Контрольная работа по алгебре №1
Вариант 2
1. Найдите значение х, при котором функция, заданная формулой f (х) = х + 2, принимает значение, равное 1.
2. Найдите область определения функции, заданной формулой:
а) f (х) = 16 – 8х; в) γ (х) =  ;
;
б) g (х) = ; г) у = х2– 4.
3. Укажите область значений функции:
а) у = 37х + 1; в) у = ;
б) у = –23; г) у = | х |.
4. Перечислите свойства функции:

5. Разложите на множители квадратный трехчлен:
а) х2– 7х + 12; б) 10х2+ 19х – 2.
6. Сократите дробь:
а)  ; б)
; б)  .
.
Контрольная работа по алгебре №1
Вариант 1
1.Найдите значение х, при котором функция, заданная формулой f (х) = х + 9, принимает значение, равное 10.
2. Найдите область определения функции, заданной формулой:
а) f (х) = 5х – 7; в) g (х) =  ;
;
б) у = –; г) γ (х) = 5 – х2.
3. Укажите область значений функции:
а) у = – 29х + 5; в) у =  ;
;
б) у = 41; г) у = –.
4. Перечислите свойства функции:

5. Разложите на множители квадратный трехчлен:
а) х2+ х – 72; б) 5х2+ 2х – 3.
6. Сократите дробь:
а)  ; б)
; б)  .
.
infourok.ru









































 Вариант 1.
Вариант 1.
Описать свойства функции по графику.
5
-5 6
-4
С помощью преобразования графика функции 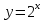 постройте графики функций:
постройте графики функций:
а) 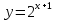 б)
б) 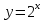 в)
в)  .
.
3. Построить график функции 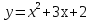 . Непрерывна ли эта функция на [0;2]. Найдите предел функции
. Непрерывна ли эта функция на [0;2]. Найдите предел функции 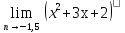 .
.
4. Найти предел функций:
а) 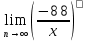 б)
б) 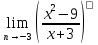 в)
в) 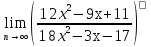
г) 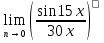 д)
д) 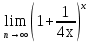 е)
е) 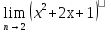
5. Найти функцию, обратную к функции 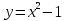 на (-∞; 0] и постройте графики обеих функций в одной системе координат.
на (-∞; 0] и постройте графики обеих функций в одной системе координат.
6. Найти область определения функции 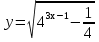 .
.
Вариант 2.
Описать свойства функции по графику.
4
-6 4
-4
С помощью преобразования графика функции 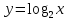 постройте графики функций:
постройте графики функций:
а) 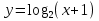 б)
б) 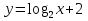 в)
в) 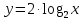
3. Построить график функции 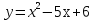 . Непрерывна ли эта функция на [-1;2]. Найдите предел функции
. Непрерывна ли эта функция на [-1;2]. Найдите предел функции 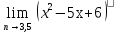 .
.
4. Найти предел функций:
а) 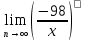 б)
б) 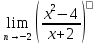 в)
в) 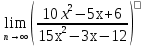
г) 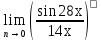 д)
д) 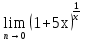 е)
е) 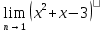
5. Найти функцию, обратную к функции 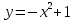 на (-∞; 0] и постройте графики обеих функций в одной системе координат.
на (-∞; 0] и постройте графики обеих функций в одной системе координат.
6. Найти область определения функции 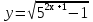 .
.
infourok.ru