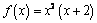
8. Определите абсциссы точек, в которых угловой коэффициент касательной к графику функции
sin равен 2.
9. Решите неравенство где
Вопросыск зачету:
1. Применение непрерывности, метод интервалов.
2. Геометрический смысл производной.
3. Уравнение касательной
4. Производная в физике
5. Признак возрастания, убывания функции, критические точки.
6. Исследование функции, построение графиков.
7. Наибольшее, наименьшее значение функции.
КРИТЕРИИ ОЦЕНКИ:«3» - наличие контрольной работы, ответов на вопросы зачета письменно.
«4»- наличие контрольной работы, выполнить тест, знание всех основных формул.
«5»-наличие контрольных работ, выполнить тест, устно отвечать на вопросы зачета, уметь доказывать теоремы и применять теоретический материал при решении задач.
Справочный материал
Производная
Определение производной
Физический смысл производной – скорость изменения функции в точке .
Геометрический смысл производной – существование производной функции в точке равносильно существованию касательной в точке , при этом угловой коэффициент равен .
Формулы
Производная сложной функции. Если функция сложная, то с начала берется производная внешней функции, а потом умножается на производную внутренней функции.
Правила производной:
Уравнение касательной
Уравнение касательной –
, где – абсцисса точки касания, – ордината точки касания, – производная функции в точке
Формула Лагранжа
Урок 91. Зачет по теме «Производная»
1 группа
2 группа
1. Найдите производную функции
А
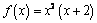
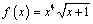
В
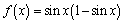
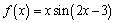
С
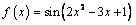
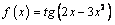
2. Решите уравнение 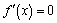
А
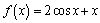
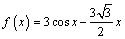
В
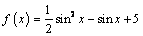
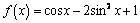
С
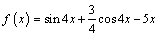
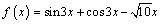
3. Составьте уравнение касательной к графику
А
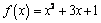 ,
, 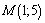
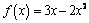 ,
, 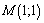
В
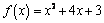 ,
, 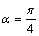
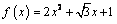 ,
, 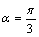
С
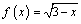 ,
, 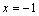
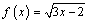 ,
, 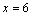
4. Исследуйте функцию и постройте график
А
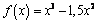

В
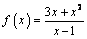
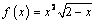
С
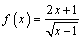
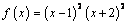
3 группа
4 группа
1. Найдите производную функции
А
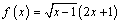
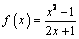
В
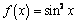
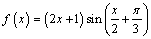
С
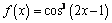
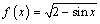
2. Решите уравнение 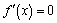
А
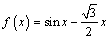
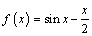
В
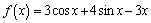
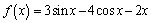
С
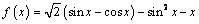
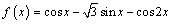
3. Составьте уравнение касательной к графику
А
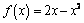 ,
, 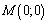
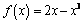 ,
, 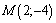
В
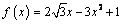 ,
, 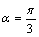
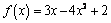 ,
, 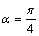
С
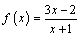 ,
, 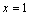
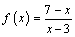 ,
, 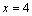
4. Исследуйте функцию и постройте график
А
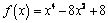
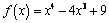
В
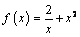
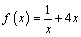
С
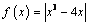
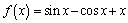
Домашнее задание: 1) Найдите промежутки возрастания и убывания функции 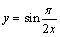 , если
, если 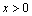 . 2) Найдите наибольшее и наименьшее значения функции
. 2) Найдите наибольшее и наименьшее значения функции 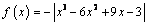 на
на 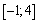 . 3) Найдите уравнение прямой, проходящей через точку
. 3) Найдите уравнение прямой, проходящей через точку 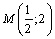 , касающейся графика функции
, касающейся графика функции 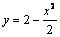 и пересекающей в двух различных точках график функции
и пересекающей в двух различных точках график функции 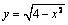 .
.
Государственная инспекция по надзору и контролю в сфере образования
Пермского края
ТЕСТ ПО алгебре и началам анализа, 10 класс
Тема: «Производная функции»
Цель: Проверка усвоения учащимися темы «Производная функции», умение применять полученные знания на конкретных примерах и задачам физики и геометрии.
Уровень сложности: базовый
Время на выполнение одного тестового задания: 1-4 мин.
Инструкция по выполнению работы
На выполнение работы дается 2 часа (120 минут). Работа содержит 30 заданий с выбором ответа (один верный ответ из четырех предложенных). Содержание, проверяемое заданиями, включает: геометрический смысл производной, физический смысл производной, таблица производных, исследование функции с помощью производной. С помощью заданий с выбором ответа проверяется базовый уровень подготовки по теме.
В бланке теста отмечать правильный ответ запрещено. Выбранный ответ необходимо отметить на отдельном бланке ответов.
Выполняйте задания в том порядке, в котором они даны. Если какое-то задание вызывает у вас затруднения, пропустите его. К пропущенным заданиям можно будет вернуться, если у вас останется время.
infourok.ru
Контрольная работа по теме «Производная и ее приложение»
Вариант – 1
1. Вычислить пределы
а) y =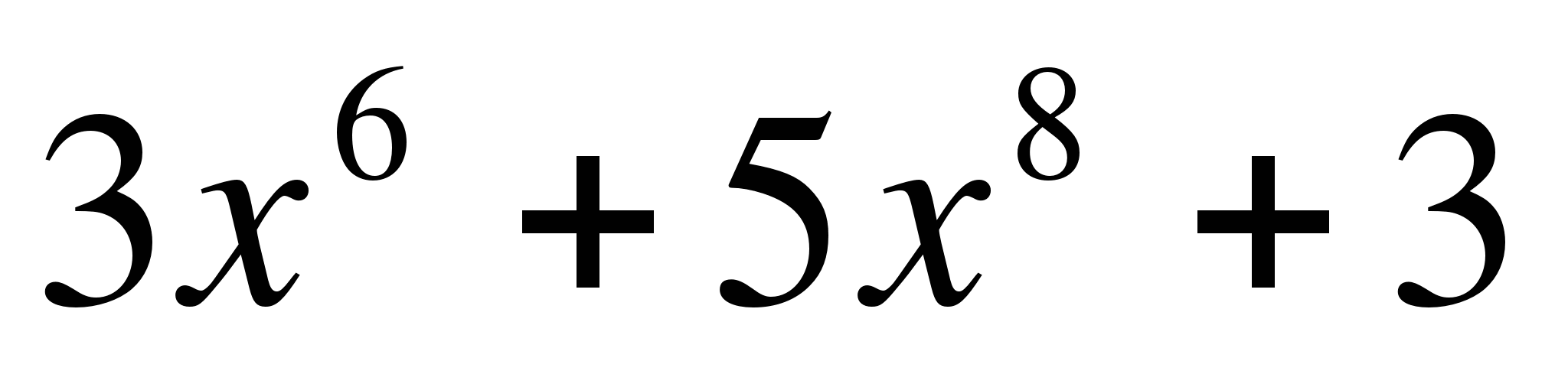 б) y =
б) y = 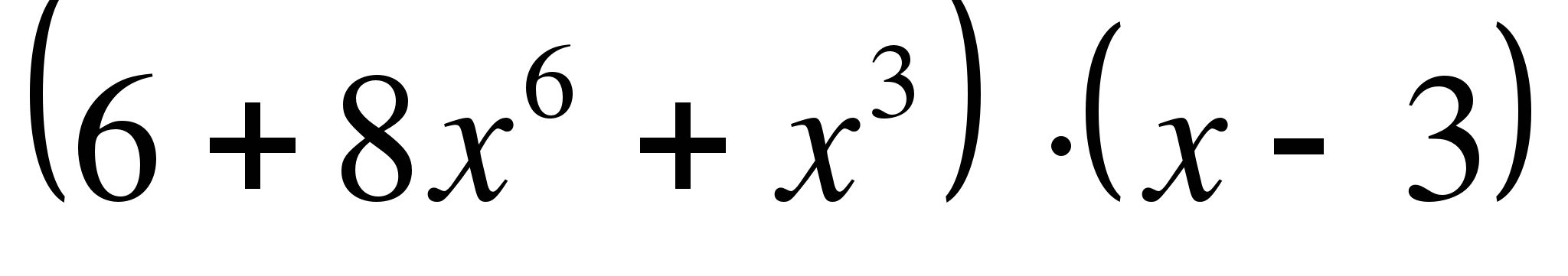
в) y = 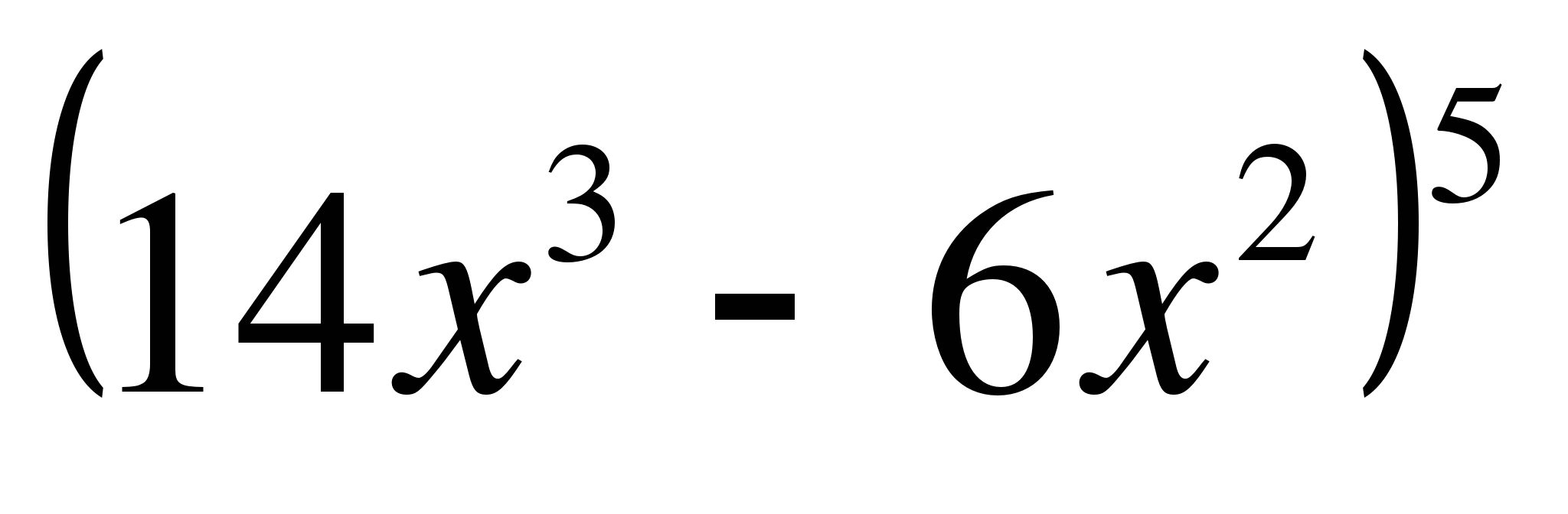 г) y =
г) y = 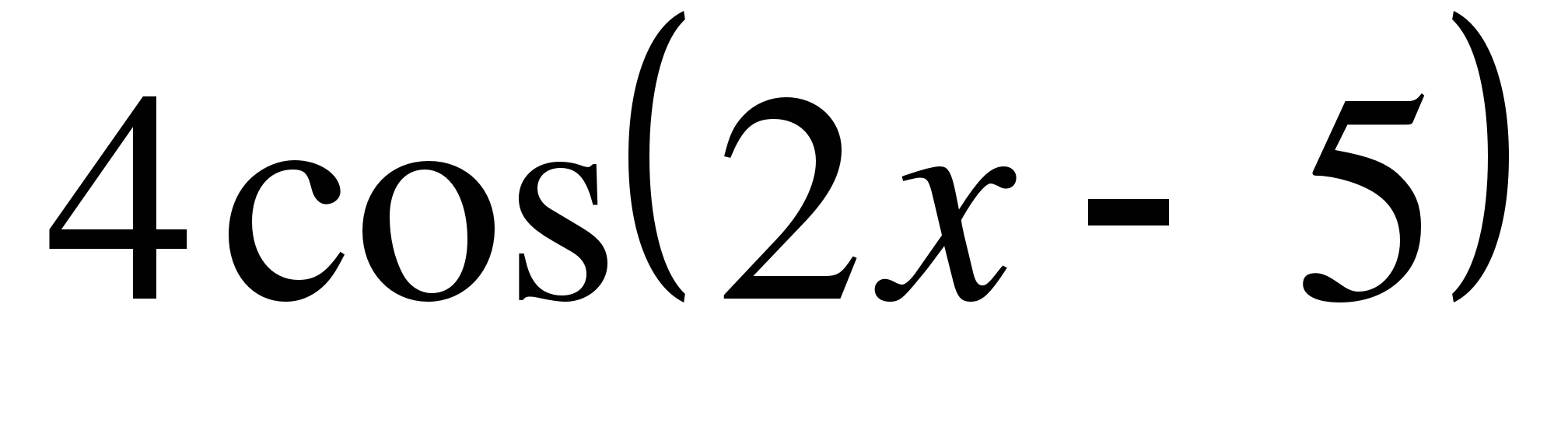 д) y =
д) y = 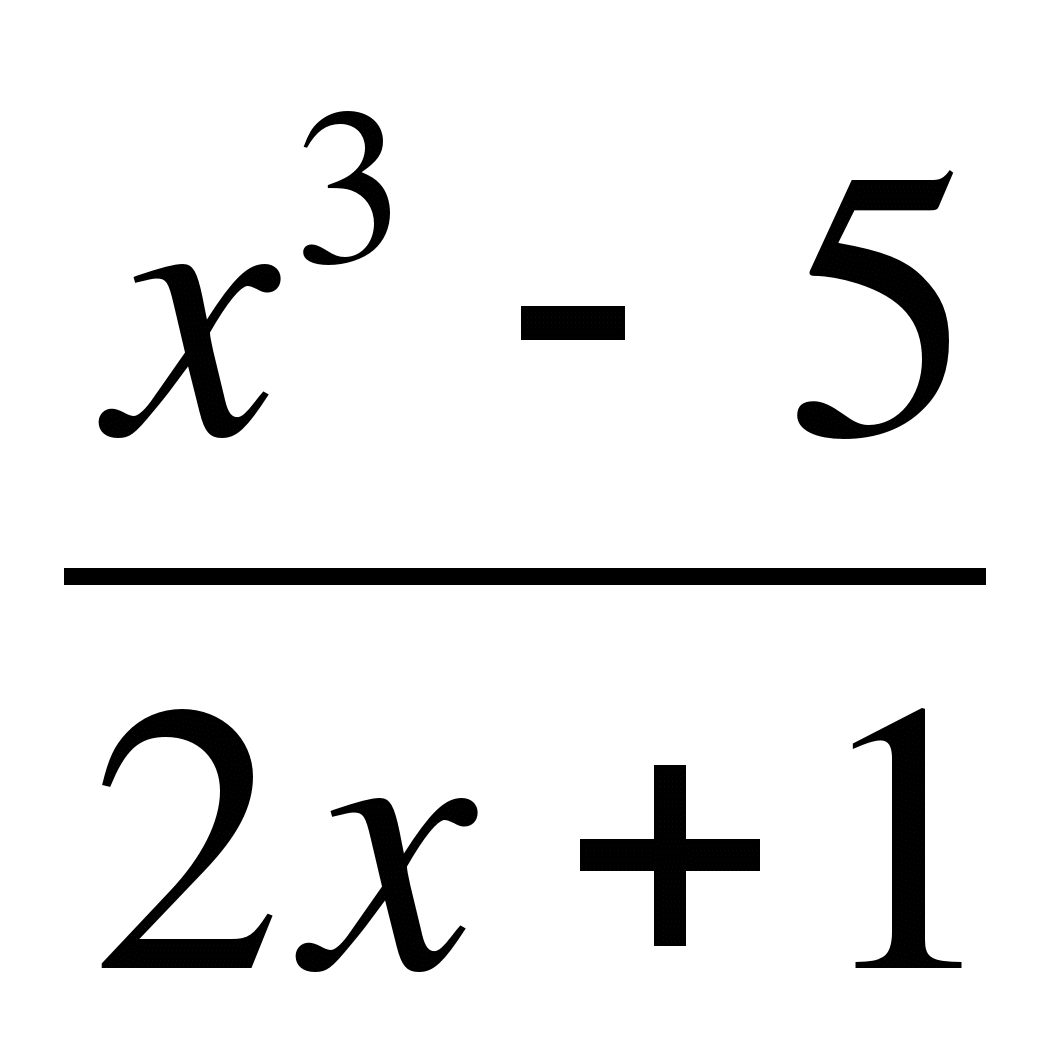
3. Найти скорость и ускорение материальной точки в момент времени t
4. Найти наибольшее и наименьшее значения функции y = f(x) на интервале [a; b] с помощью производной:5. Исследовать функцию на экстремумы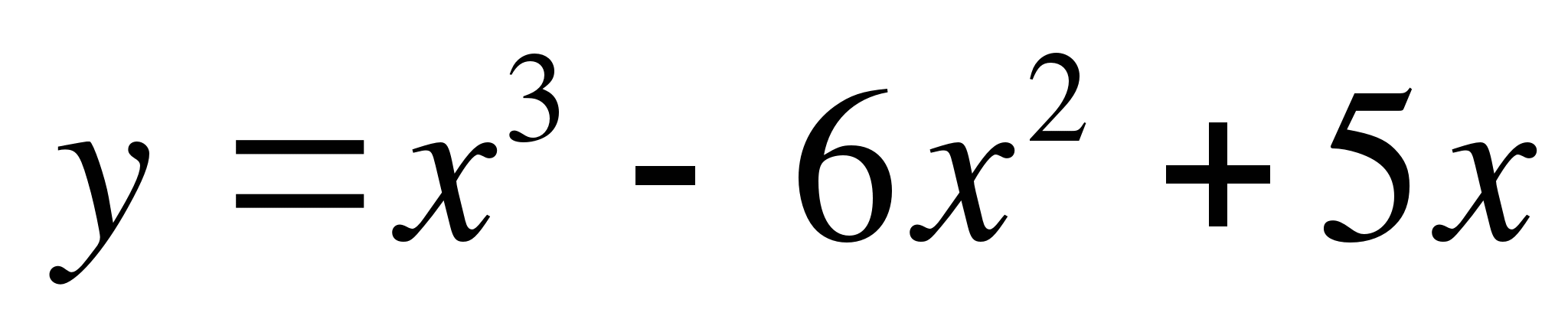
6. Найти вторую производную функции у = 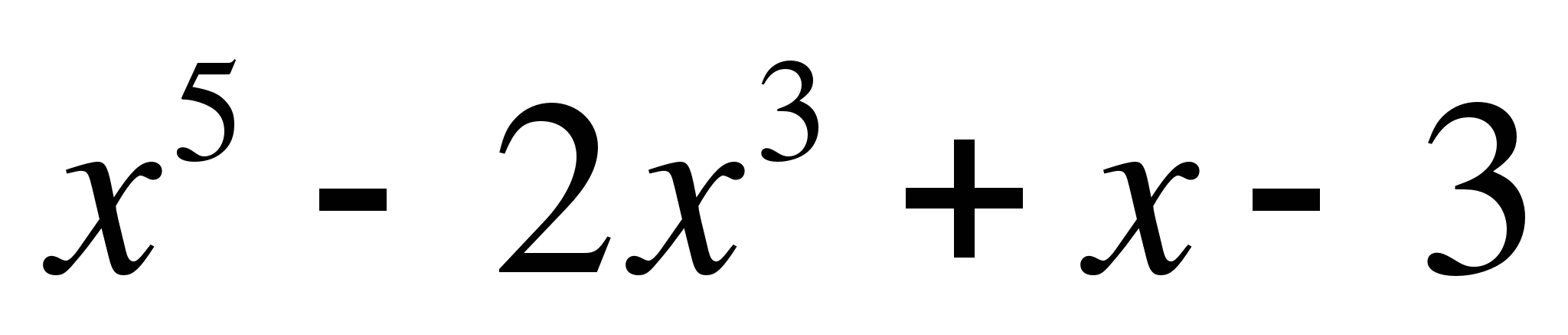
7. Найдите тангенс угла между касательной к графику функции 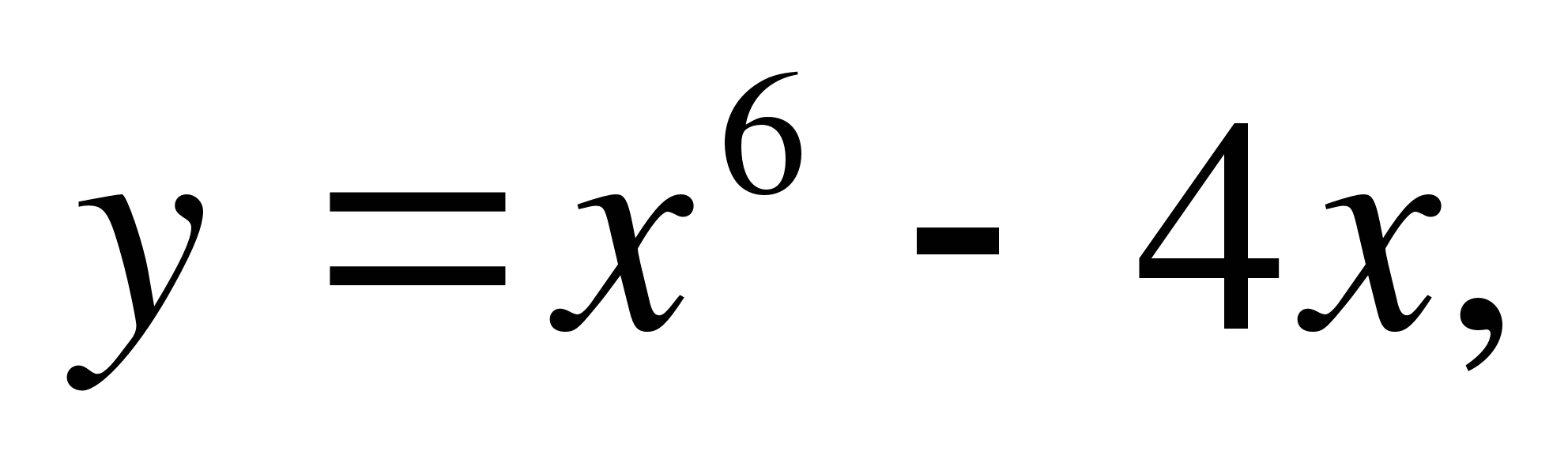 в точке x0= 1
в точке x0= 1
8. 
Контрольная работа по теме «Производная и ее приложение»
Вариант – 2
1. Вычислить пределы
а) у =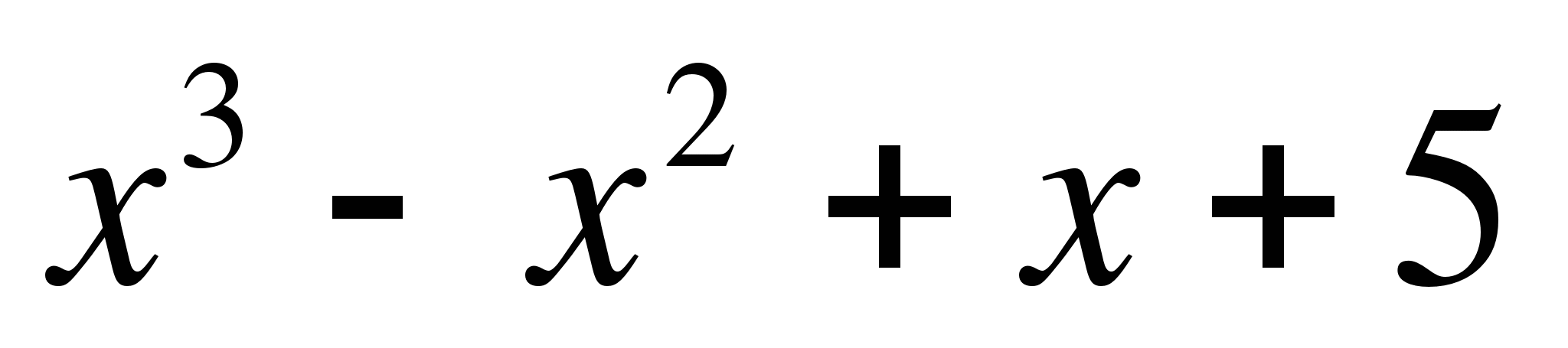 б) у =
б) у = 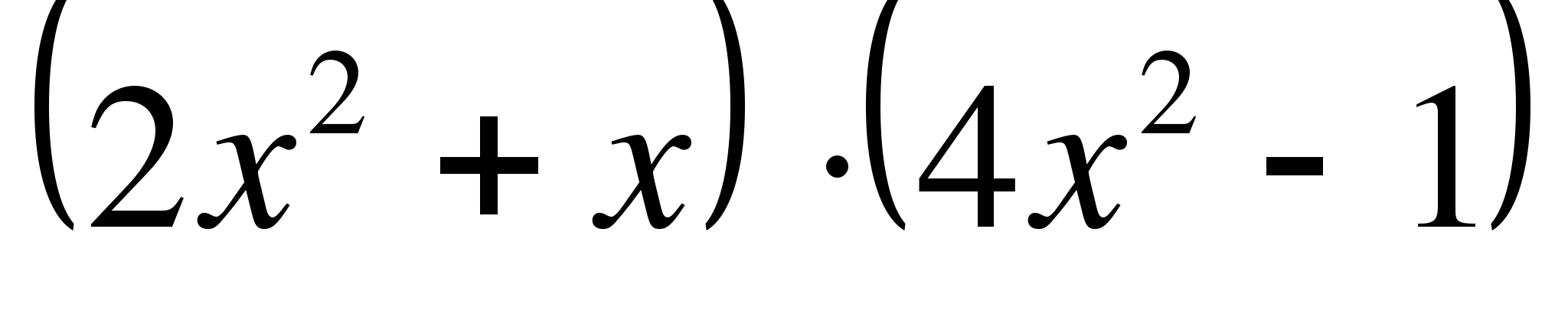
в) у = 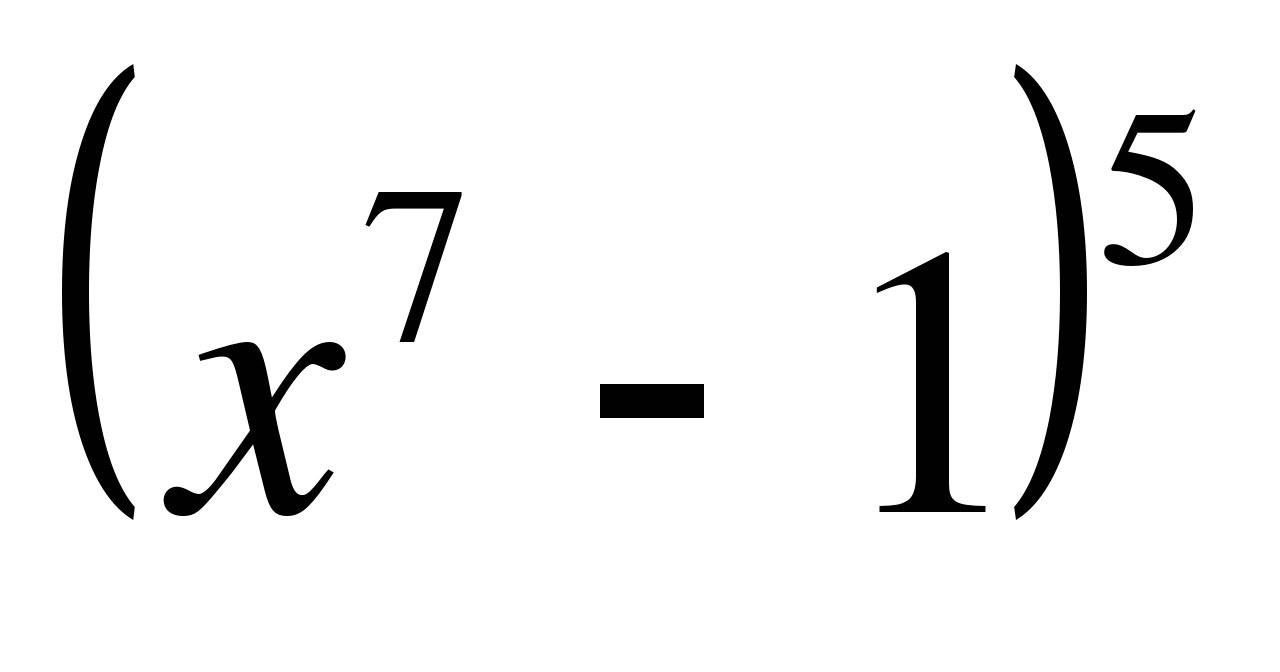 г) у =
г) у = 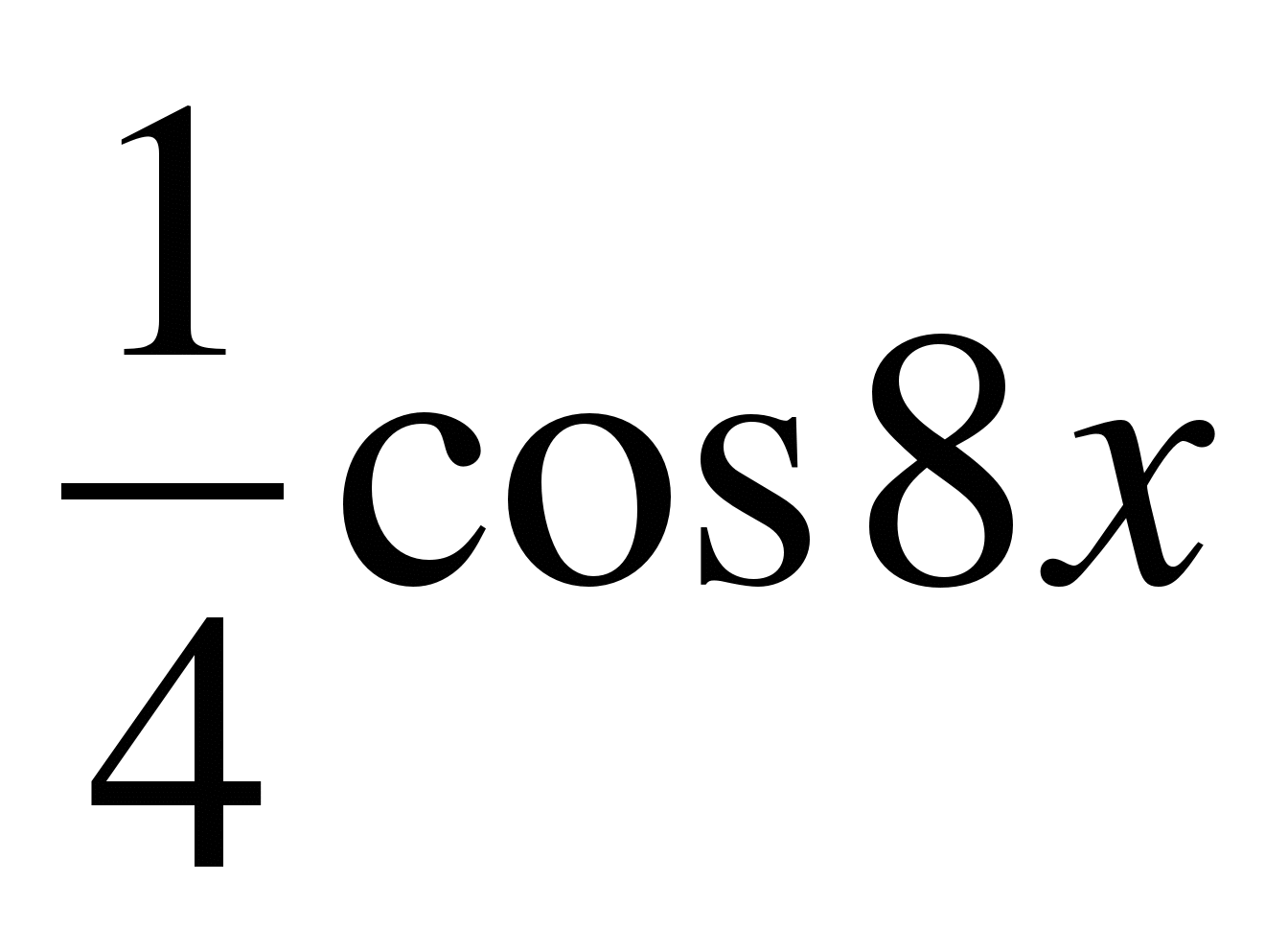 д) у =
д) у = 
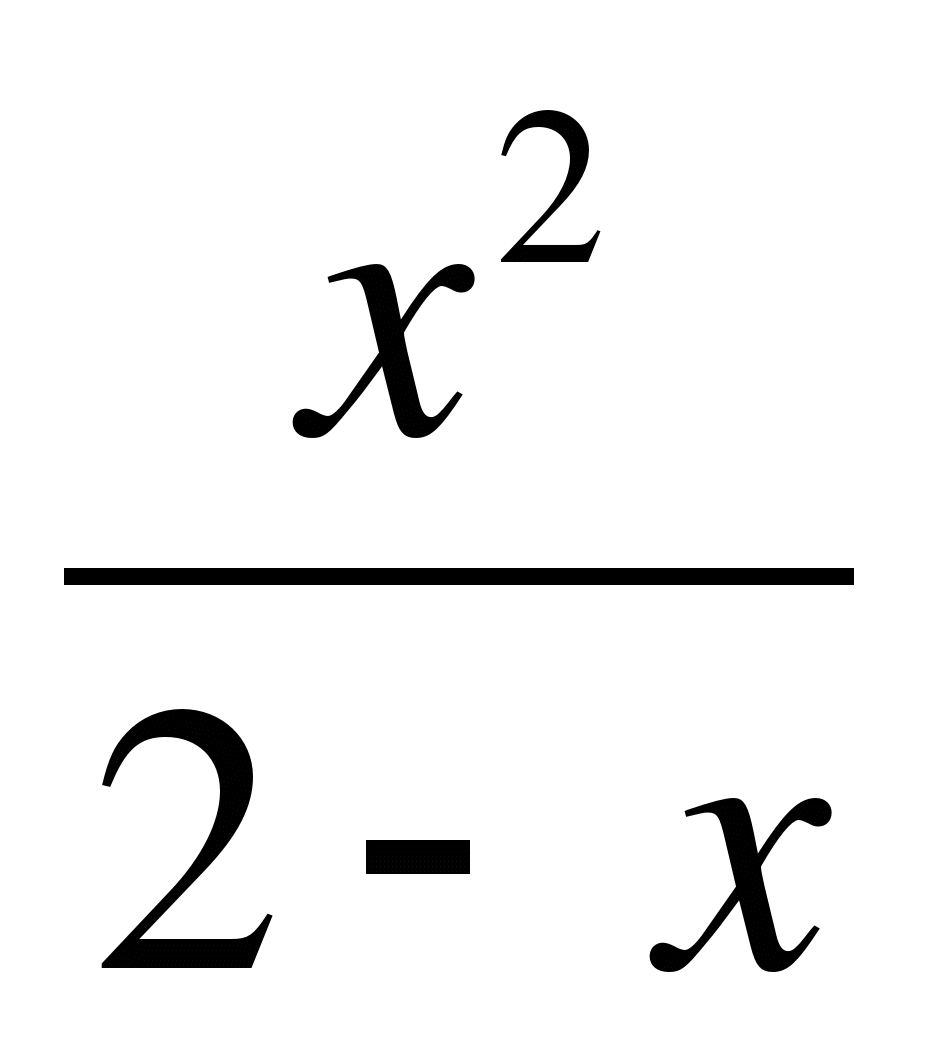
3. Найти скорость и ускорение материальной точки в момент времени t
4. Найти наибольшее и наименьшее значения функции y = f(x) на интервале [a; b] с помощью производной:5. Исследовать функцию на экстремумы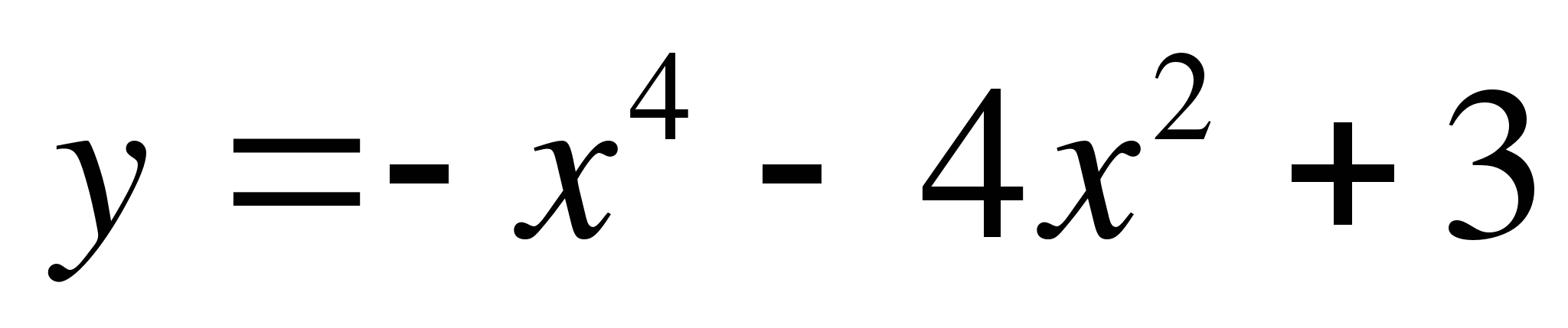
6. Найти вторую производную функции 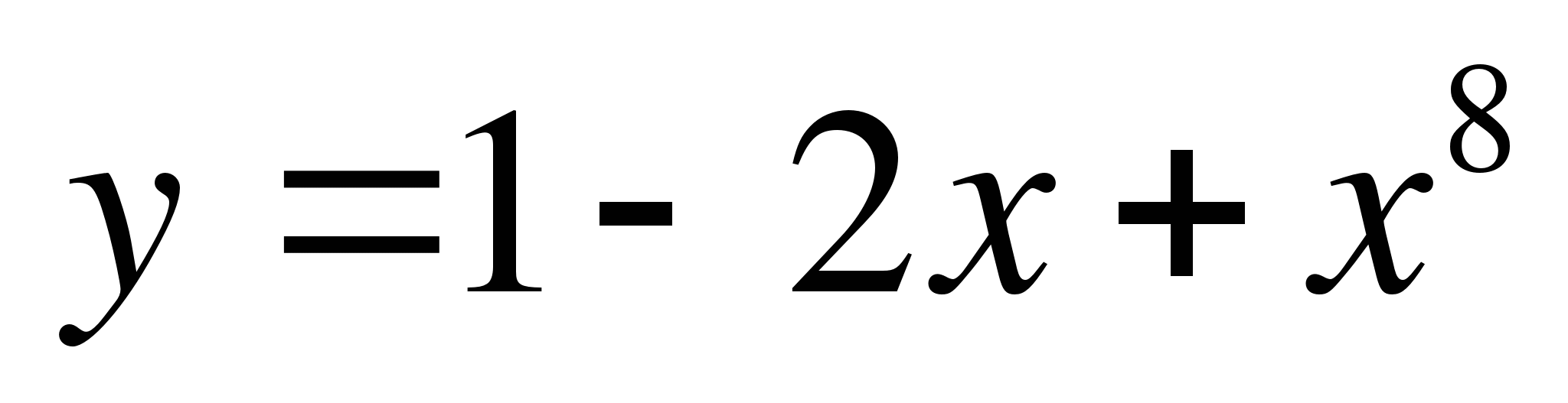
7. Найдите тангенс угла между касательной к графику функции 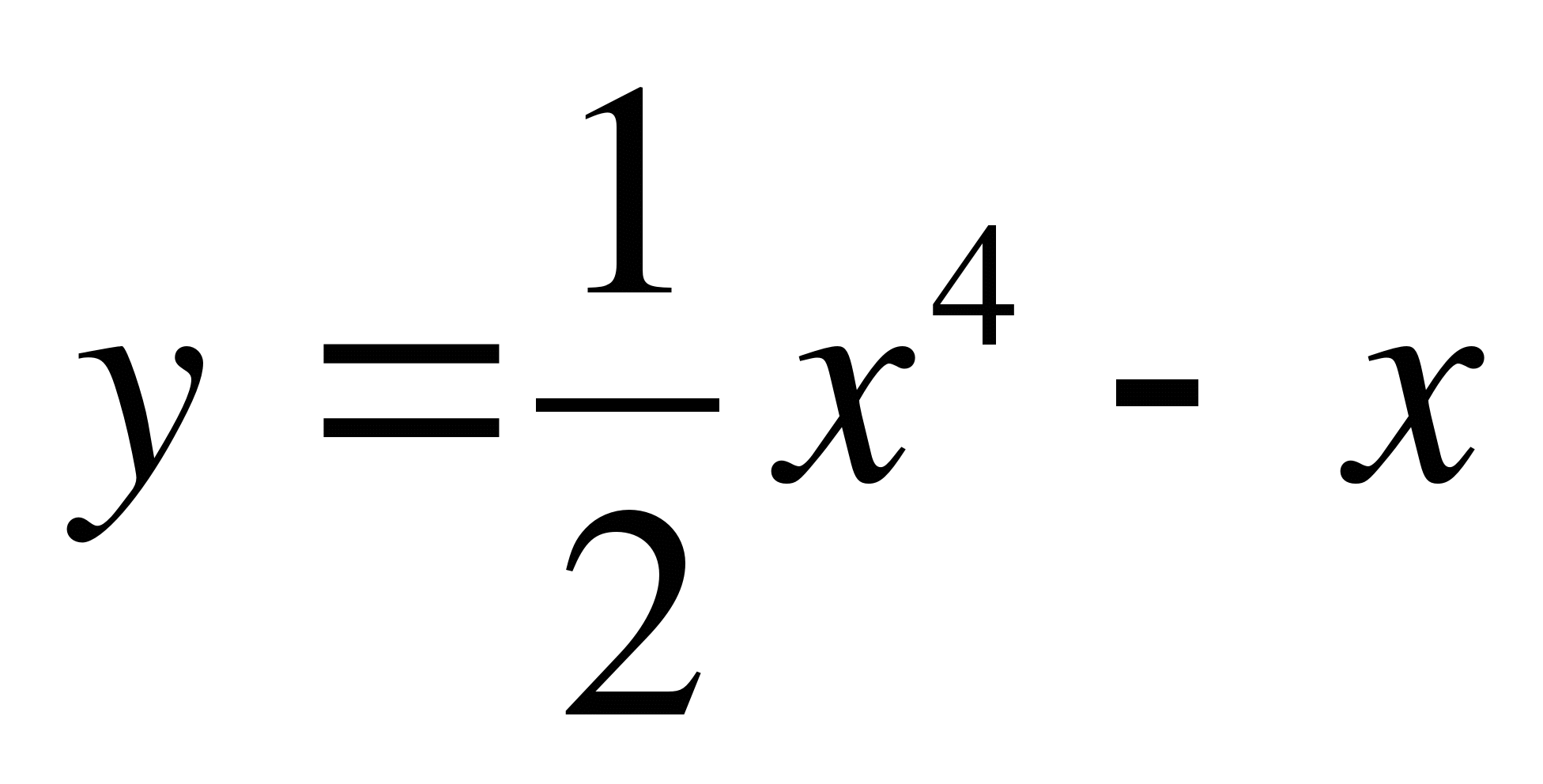 в точке x0= 2
в точке x0= 2
8. 
Контрольная работа по теме «Производная и ее приложение»
Вариант – 3
1. Вычислить пределы
вариант а)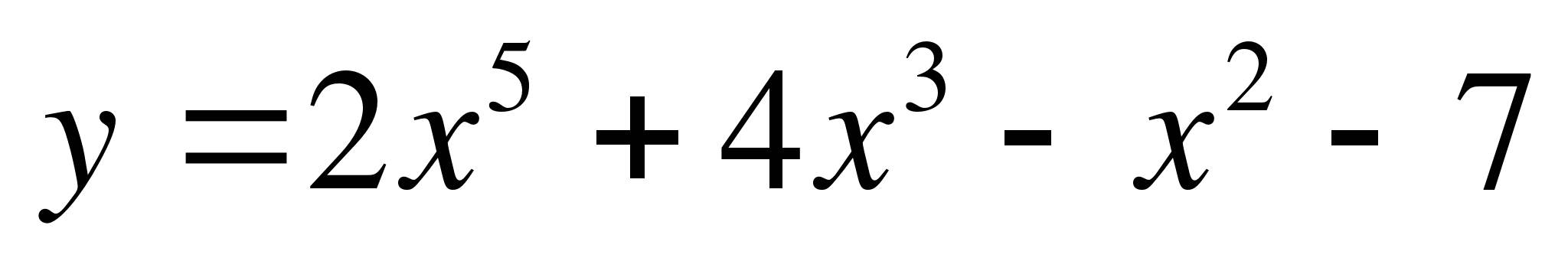 б)
б) 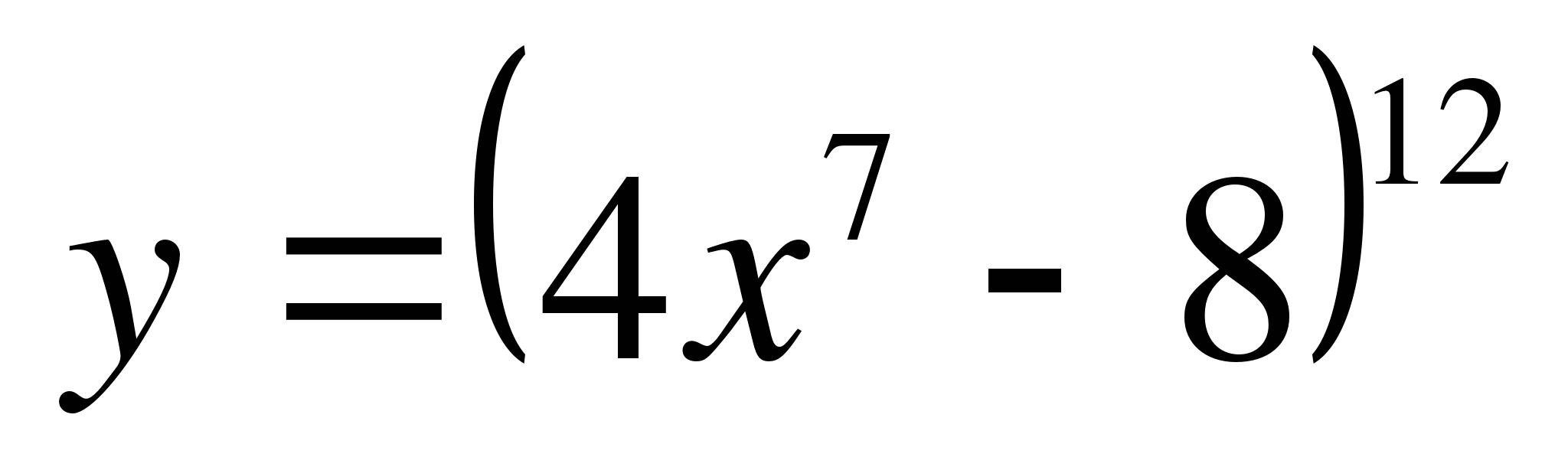
в) 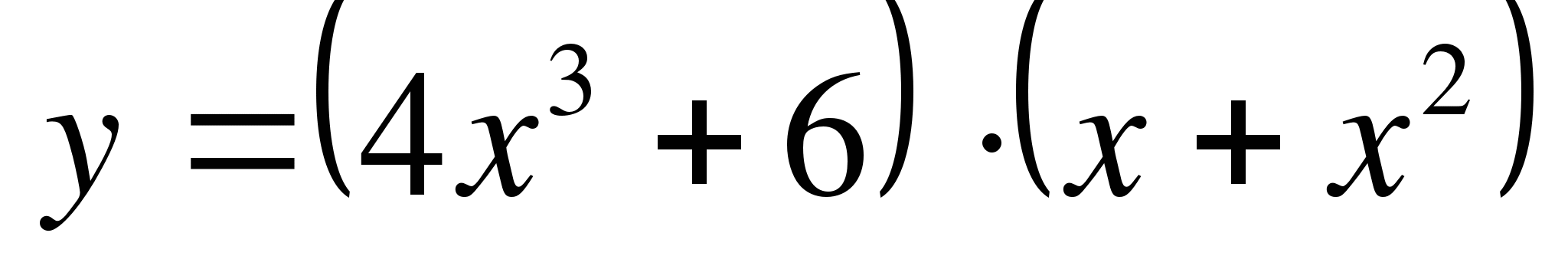 г)
г)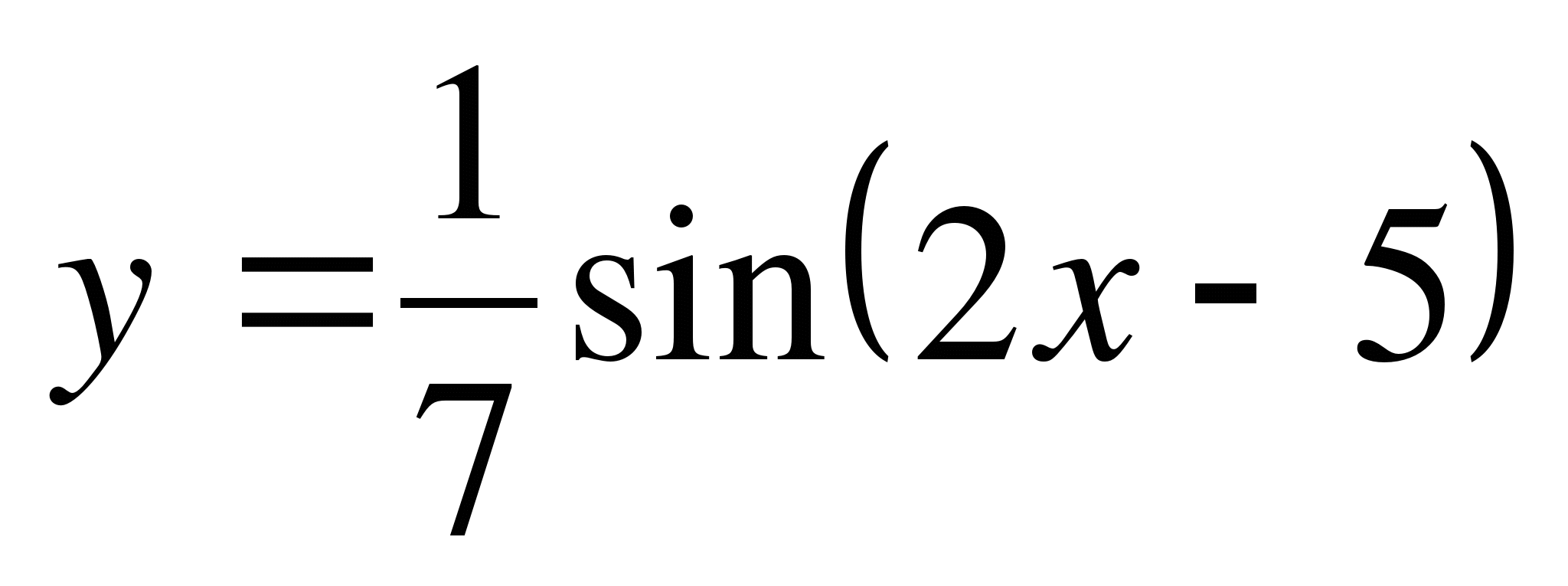 д)
д) 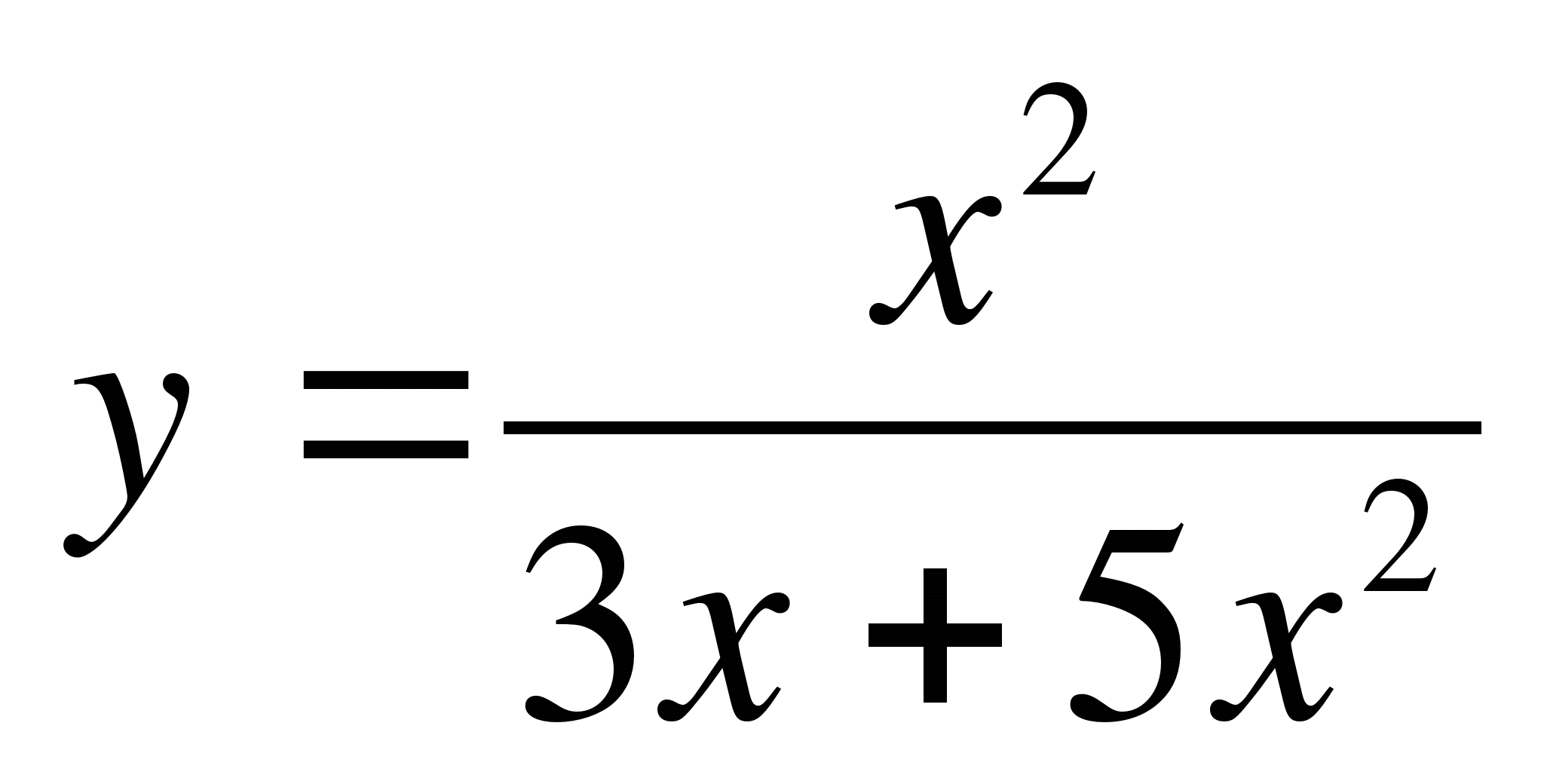
3. Найти скорость и ускорение материальной точки в момент времени t
4. Найти наибольшее и наименьшее значения функции y = f(x) на интервале [a; b] с помощью производной:5. Исследовать функцию на экстремумы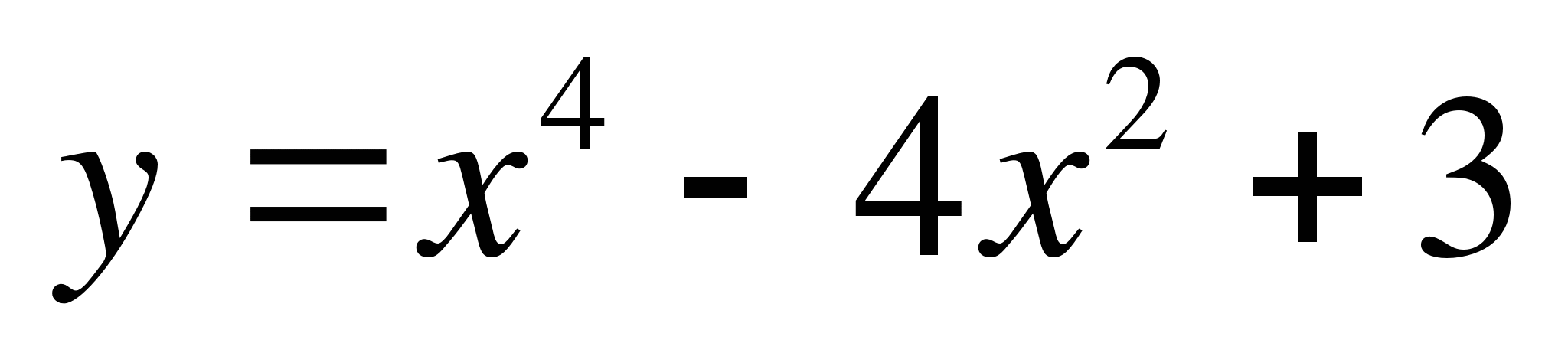
6. Найти вторую производную функции 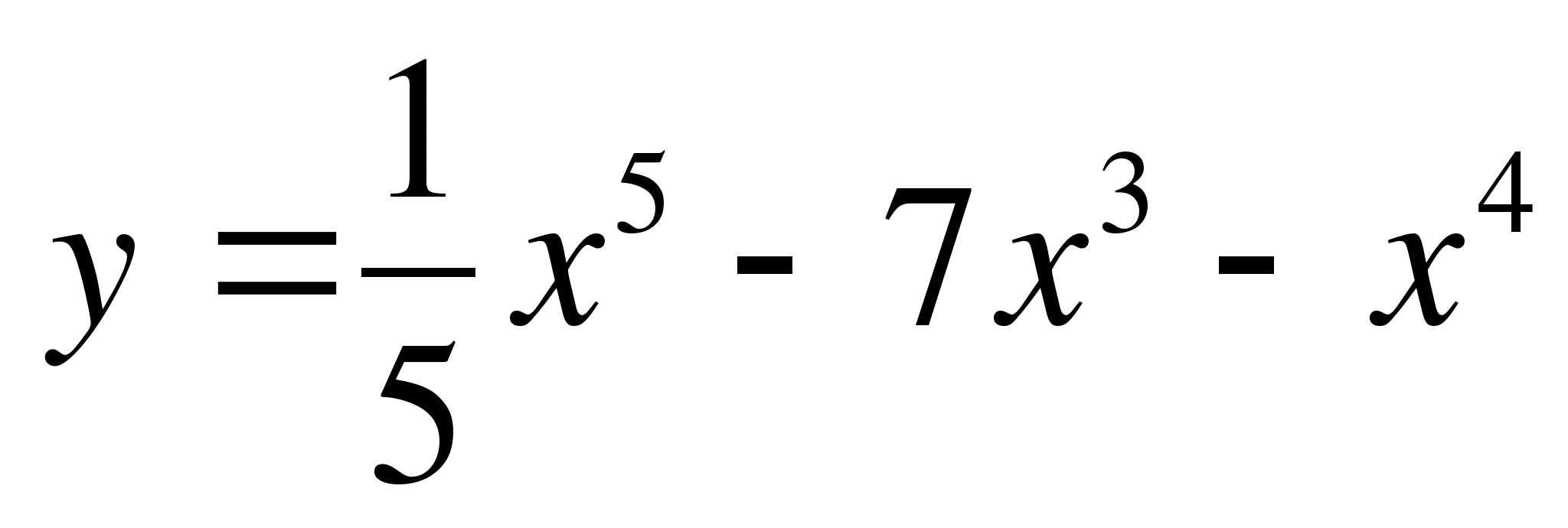
7. Найдите тангенс угла между касательной к графику функции 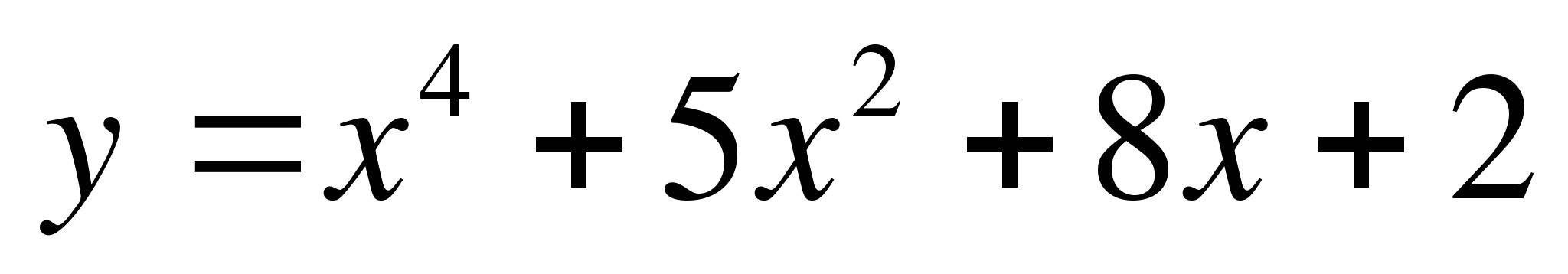 в точке x0= 1
в точке x0= 1
8. 
Контрольная работа по теме «Производная и ее приложение»
Вариант – 4
1. Вычислить пределы
вариант а)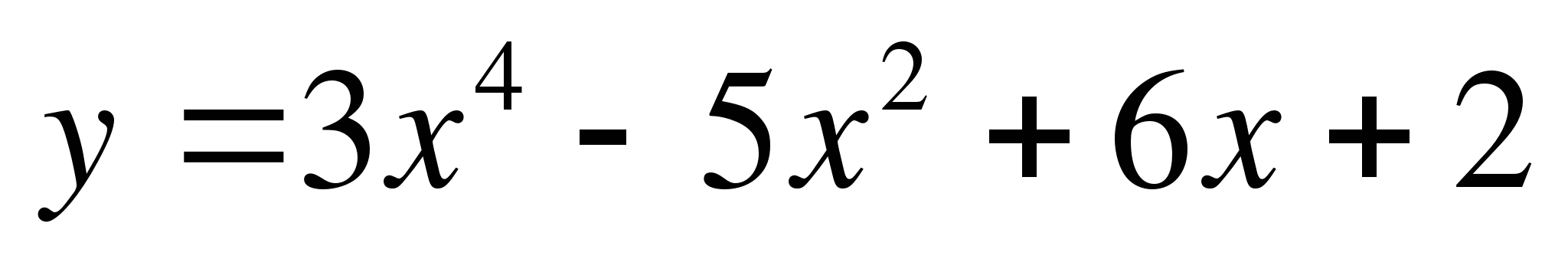 б)
б) 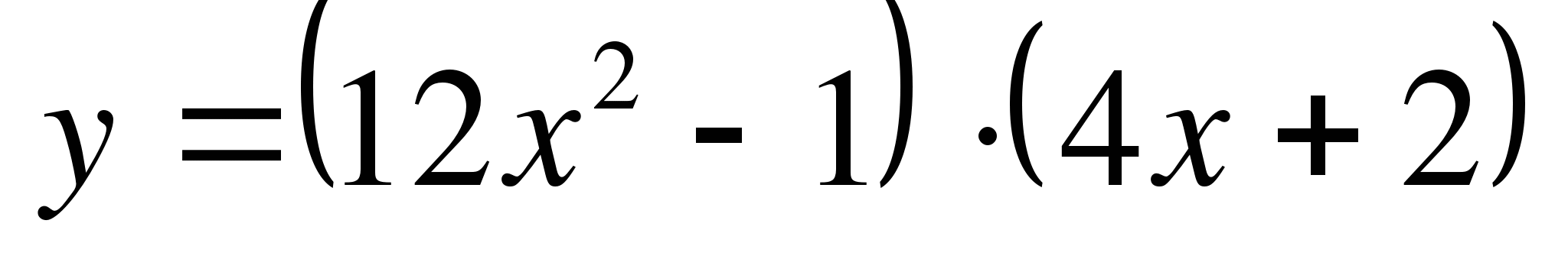
в) 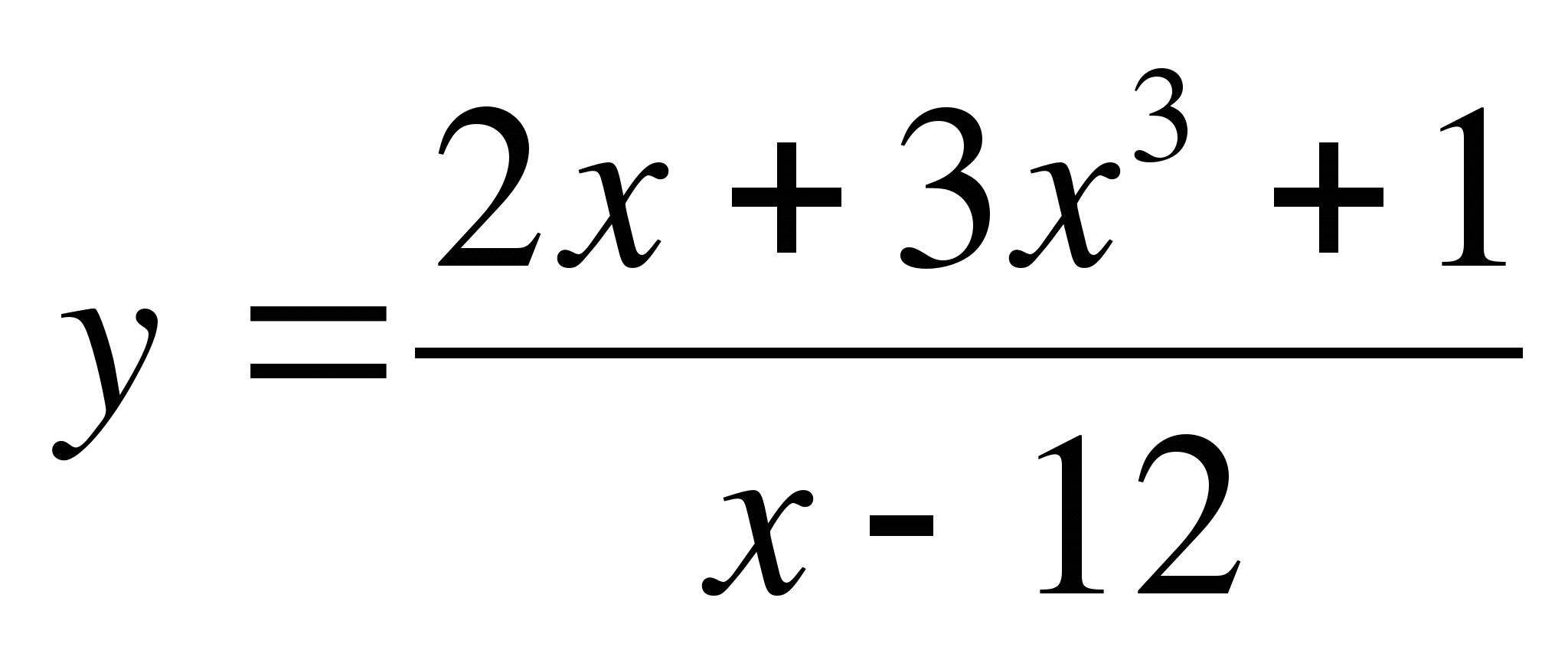 г)
г) 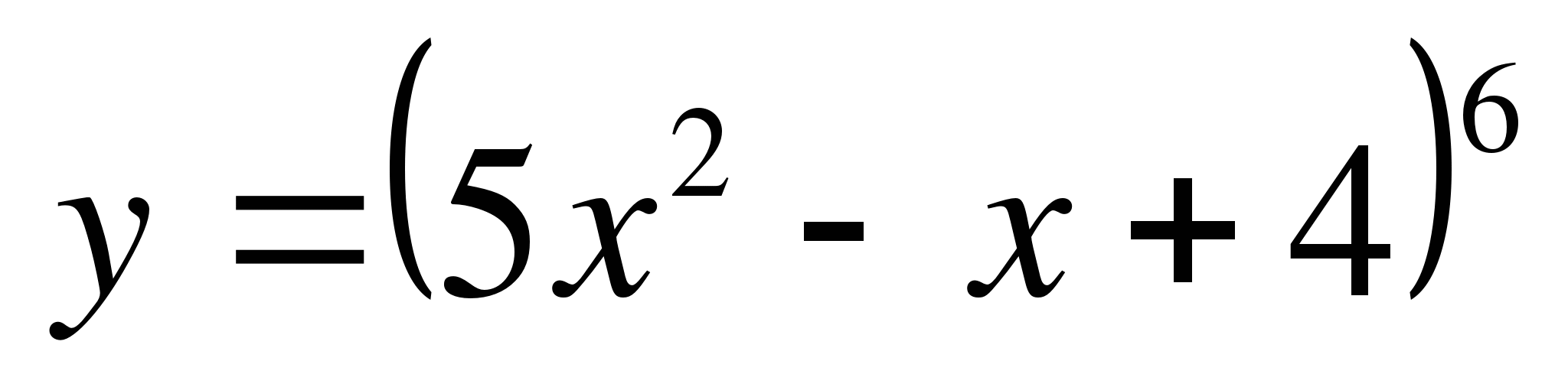 д)
д) 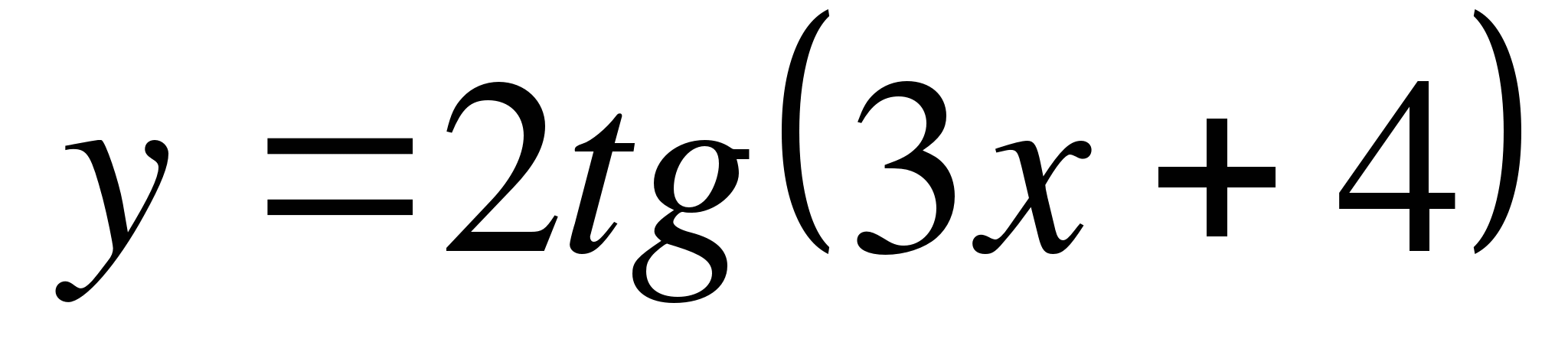
3. Найти скорость и ускорение материальной точки в момент времени t
4. Найти наибольшее и наименьшее значения функции y = f(x) на интервале [a; b] с помощью производной:5. Исследовать функцию на экстремумы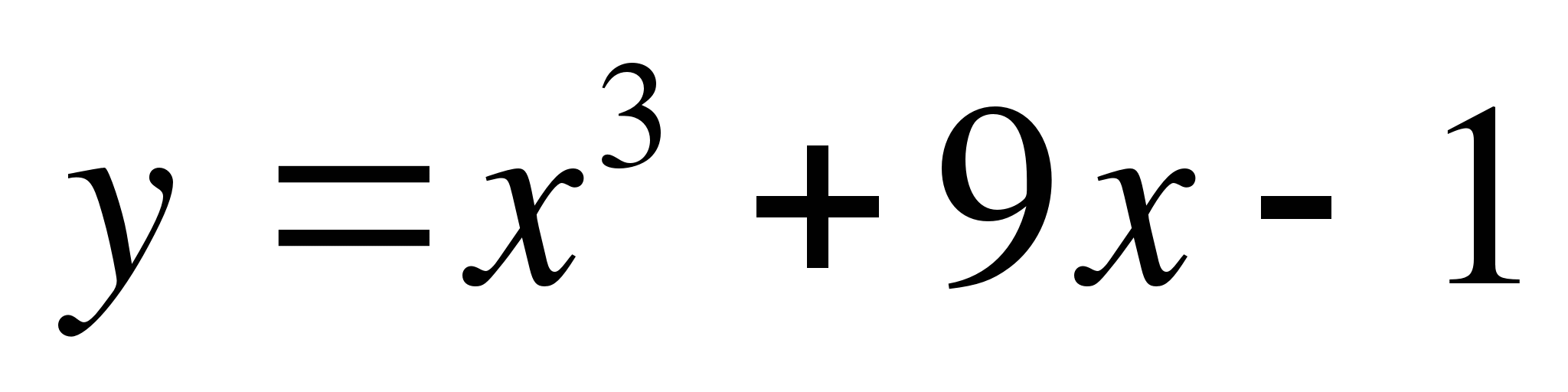
6. Найти вторую производную функции 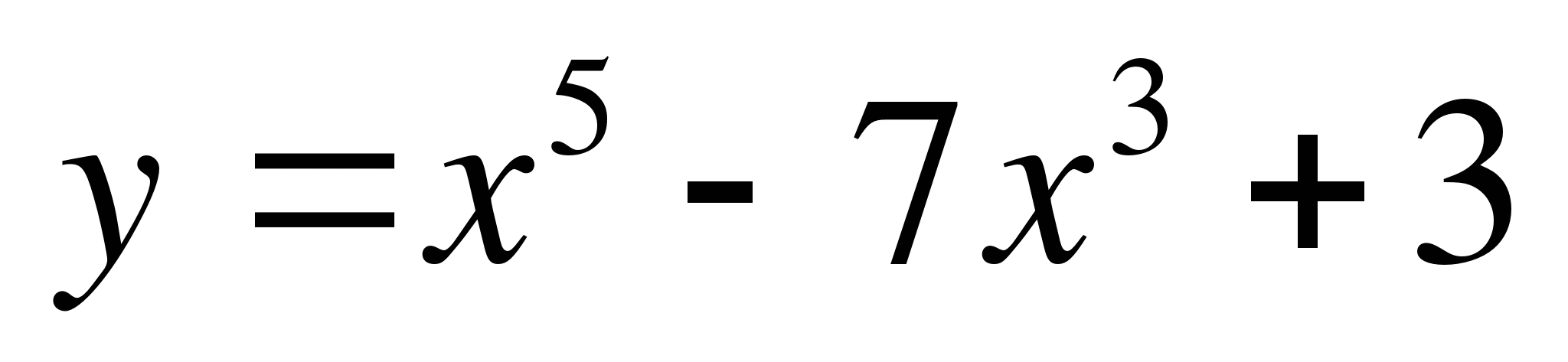
7. Найдите тангенс угла между касательной к графику функции 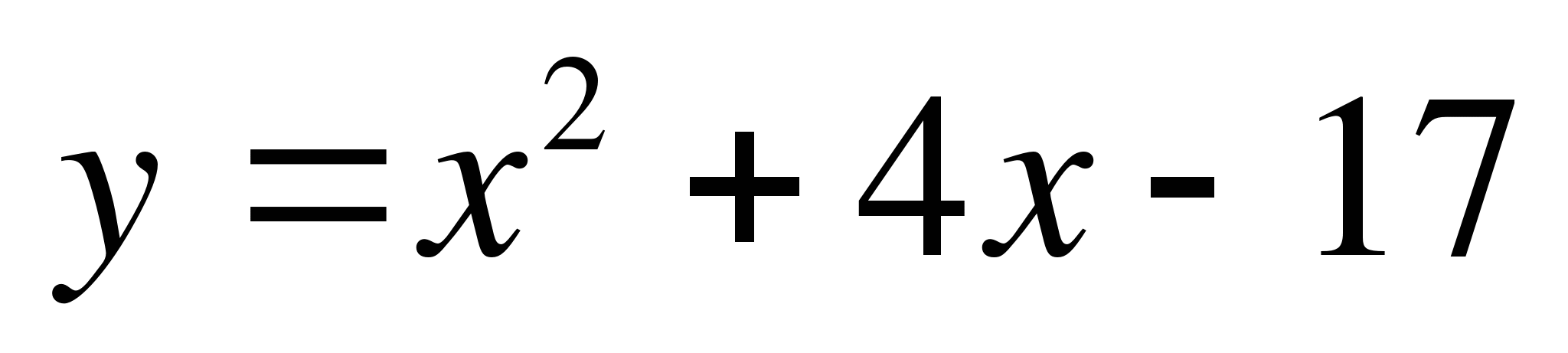 в точке x0= 0
в точке x0= 0
8. 
infourok.ru
Контрольная работа по теме : « Производная и ее применение»
1 вариант
1. Используя правила дифференцирования, найдите производные следующих функций:
а) у = х4 -2х -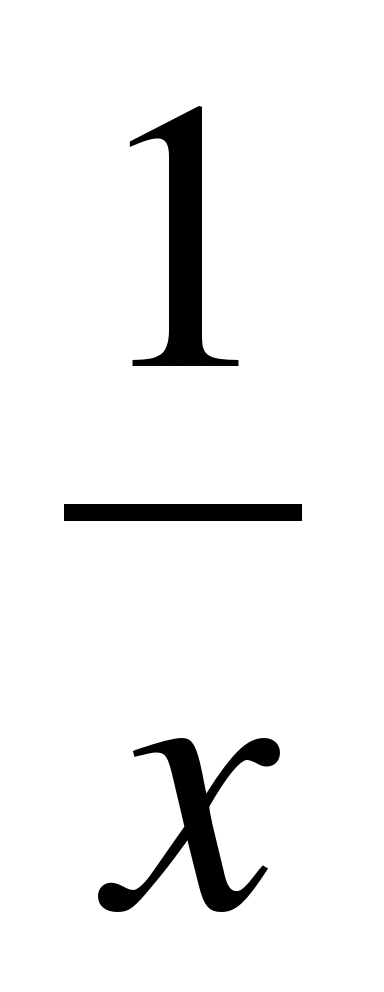
б) у = 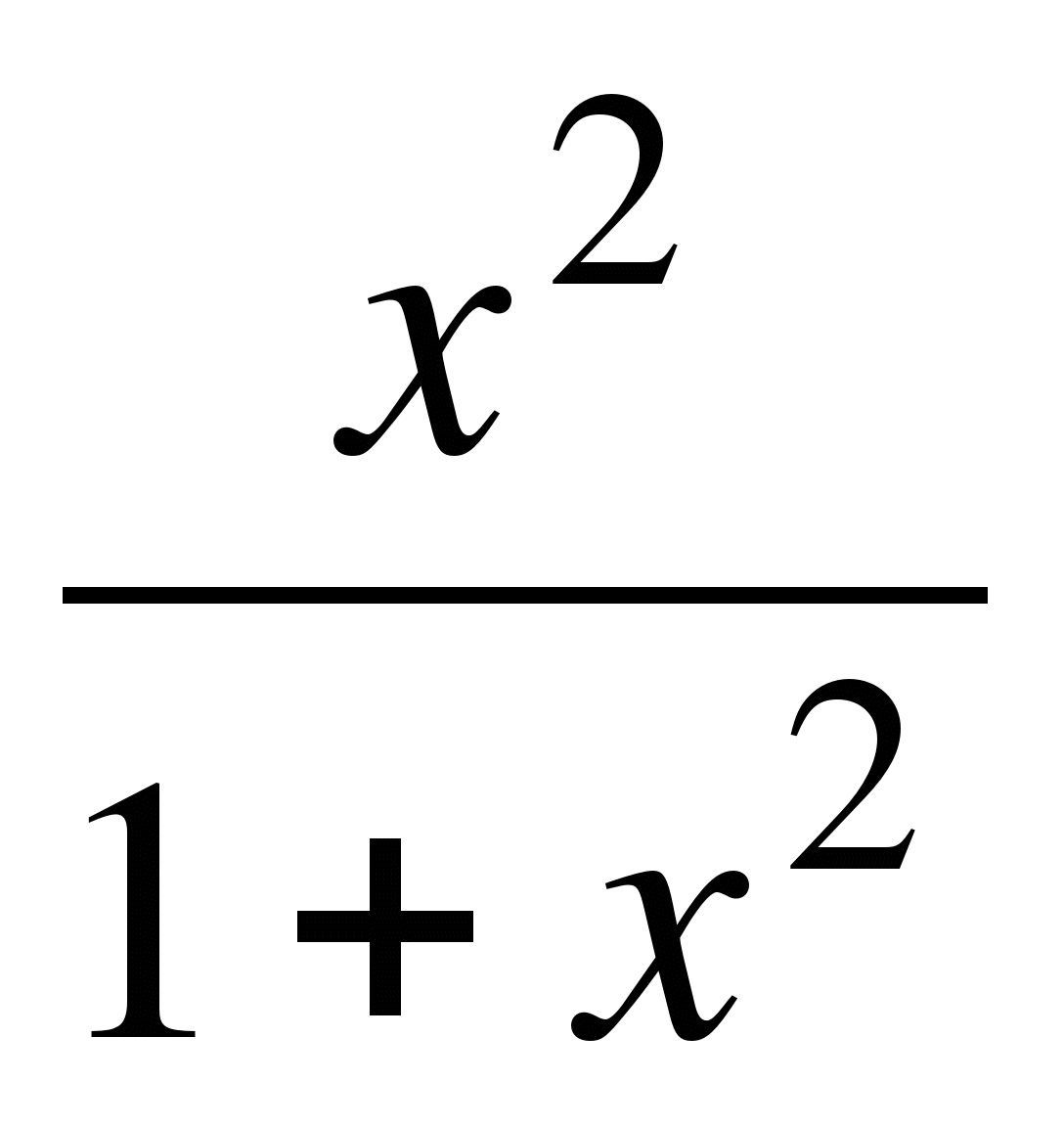 ,
,
в) у = (х2 – х – 1)8,
г) у = tg2 х.
2. Укажите промежутки возрастания и убывания функции
y = x3– 5x2– 32x +9
3. Исследуйте функцию f (х) = х3-3х 2 + 2 и постройте ее график.
4. Найдите наибольшее значение функции f(x) = 2x-x2 на отрезке [-2;0].
Контрольная работа по теме : « Производная и ее применение».
2 вариант
1. Используя правила дифференцирования, найдите производные следующих функций:
а) у = х2 -5х +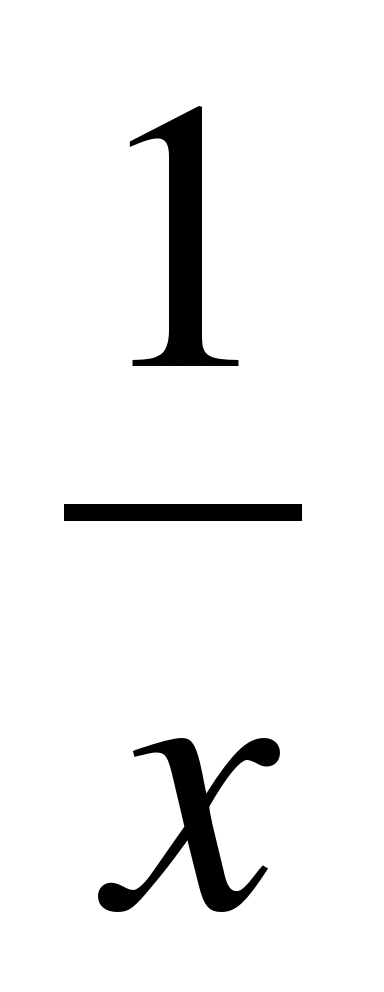
б) у = 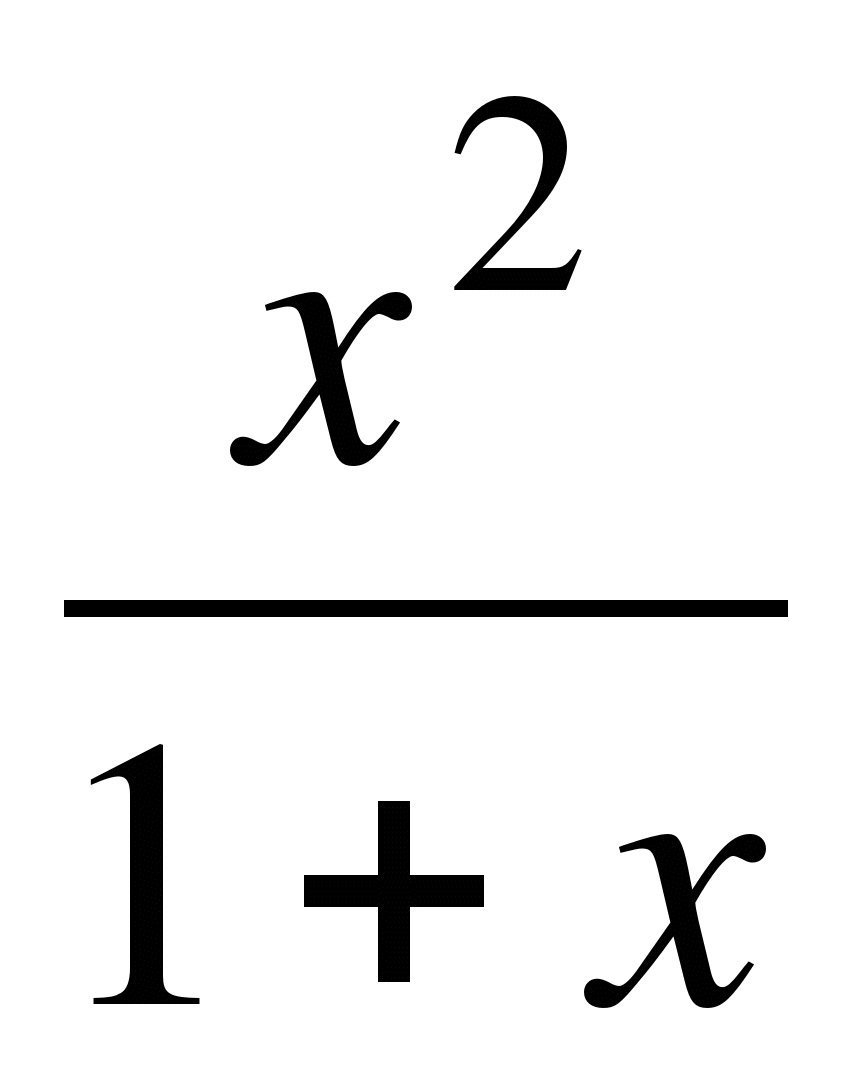 ,
,
в) у = (х2 – 3х + 1)7,
г) у = cos2 х.
2. Укажите промежутки возрастания и убывания функции
y = 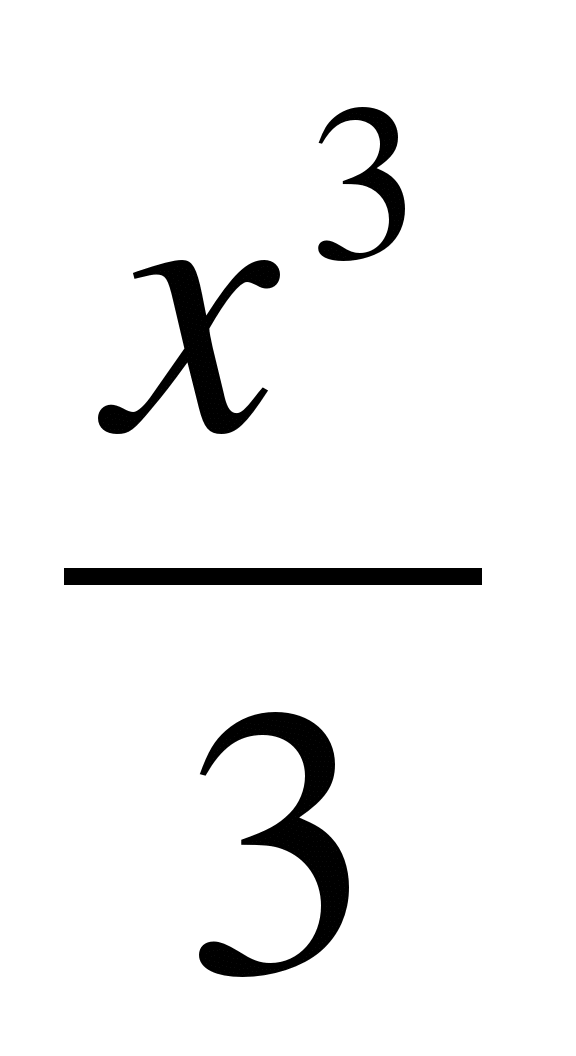 – x2– 3x +9
– x2– 3x +9
3. Исследуйте функцию f (х) = 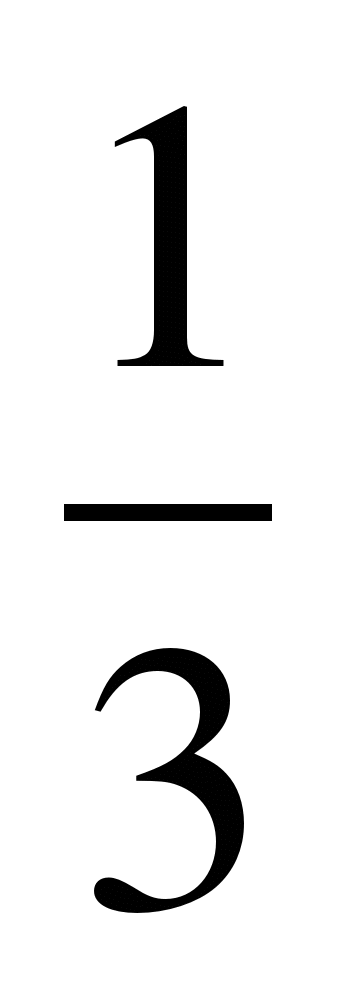 х3- 4х -3 и постройте ее график.
х3- 4х -3 и постройте ее график.
4. Найдите наименьшее значение функции f(x) = x2 -3 x на отрезке [-3;0].
Контрольная работа по теме : « Производная и ее применение».
2 вариант
1. Используя правила дифференцирования, найдите производные следующих функций:
а) у = х2 -5х +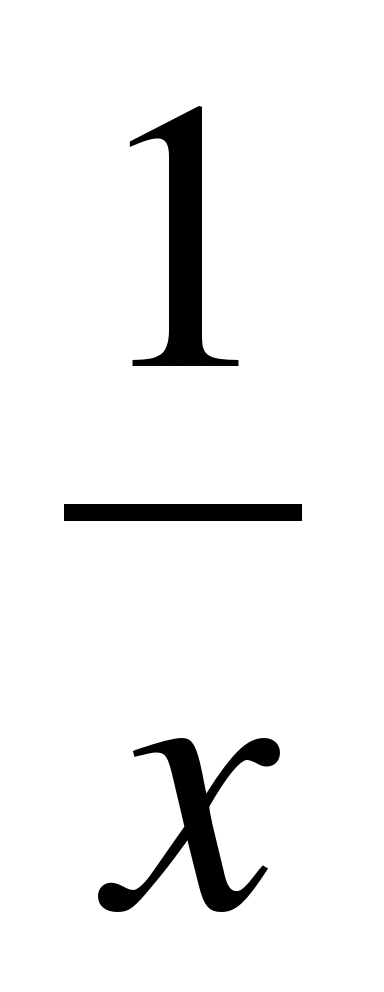
б) у = 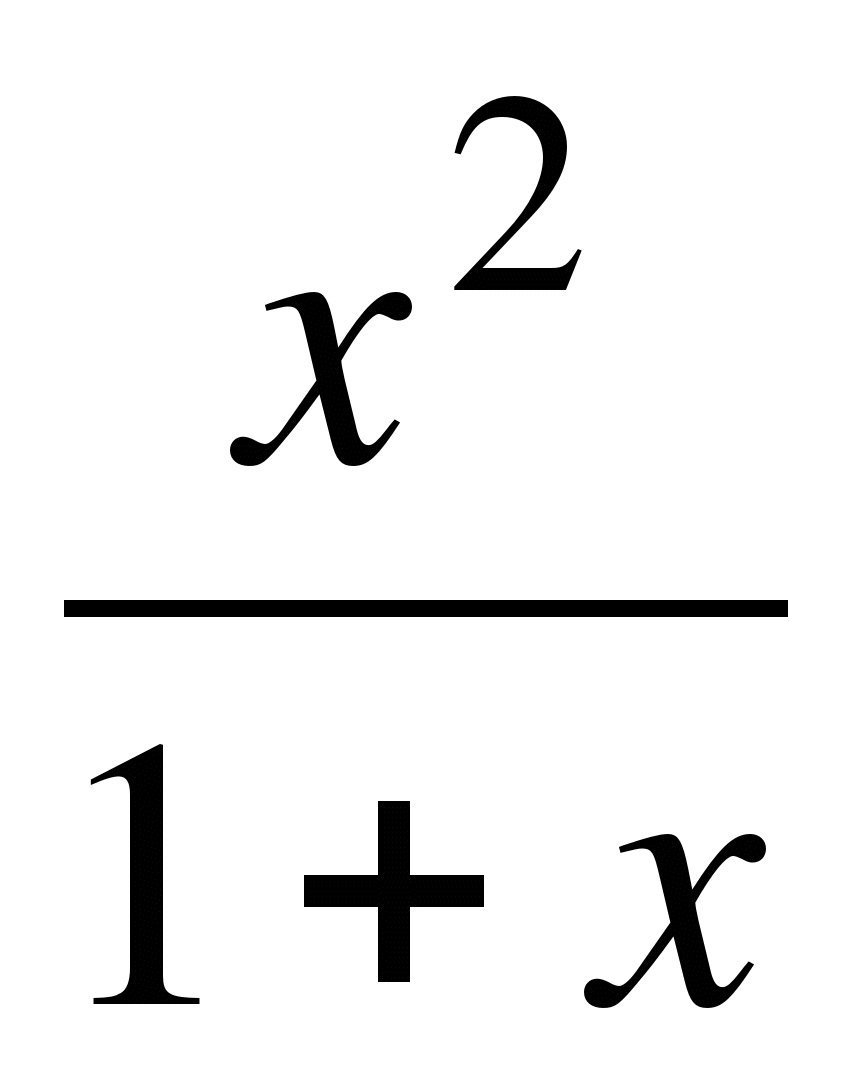 ,
,
в) у = (х2 – 3х + 1)7,
г) у = cos2 х.
2. Укажите промежутки возрастания и убывания функции
y = 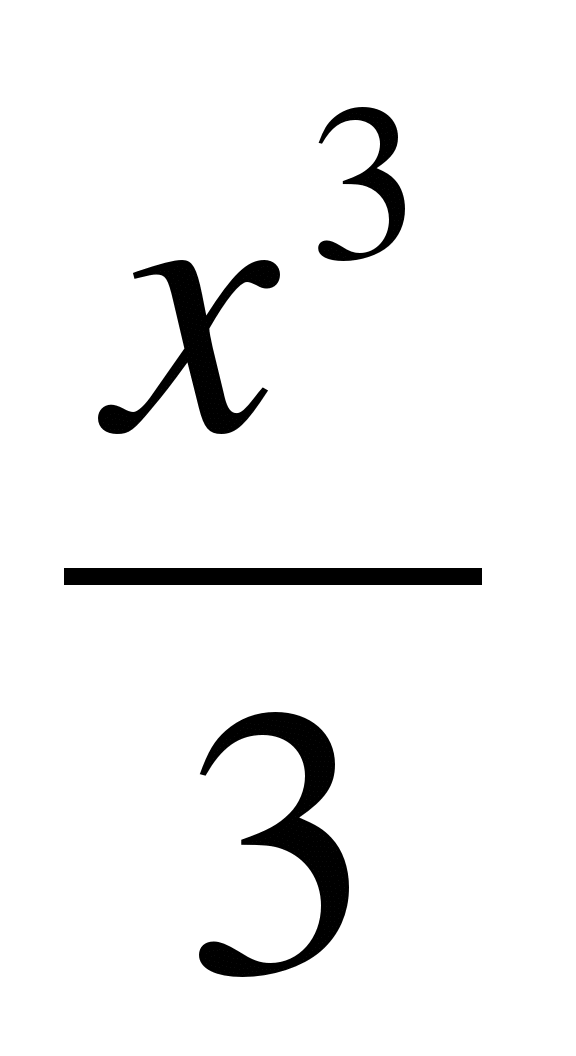 – x2– 3x +9
– x2– 3x +9
3. Исследуйте функцию f (х) = 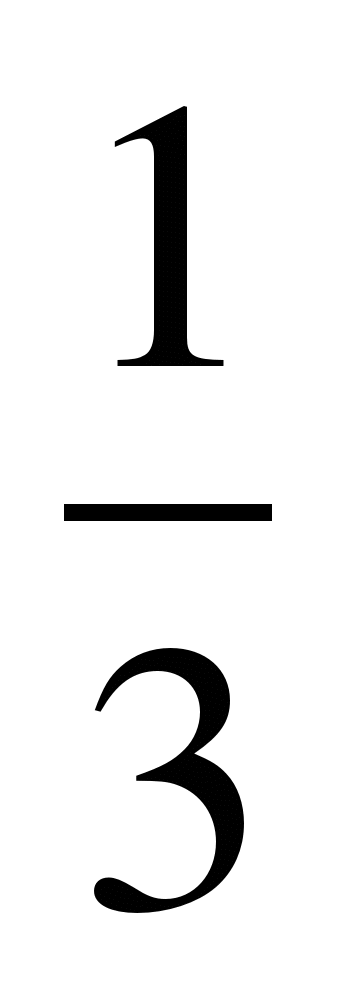 х3- 4х -3 и постройте ее график.
х3- 4х -3 и постройте ее график.
4. Найдите наименьшее значение функции f(x) = x2 -3 x на отрезке [-3;0].
Контрольная работа по теме : « Производная и ее применение».
1 вариант
1. Используя правила дифференцирования, найдите производные следующих функций:
а) у = х4 -2х -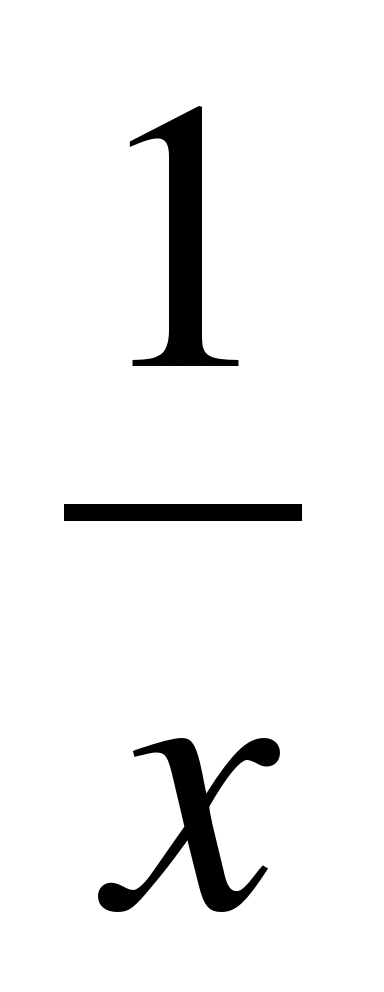
б) у = 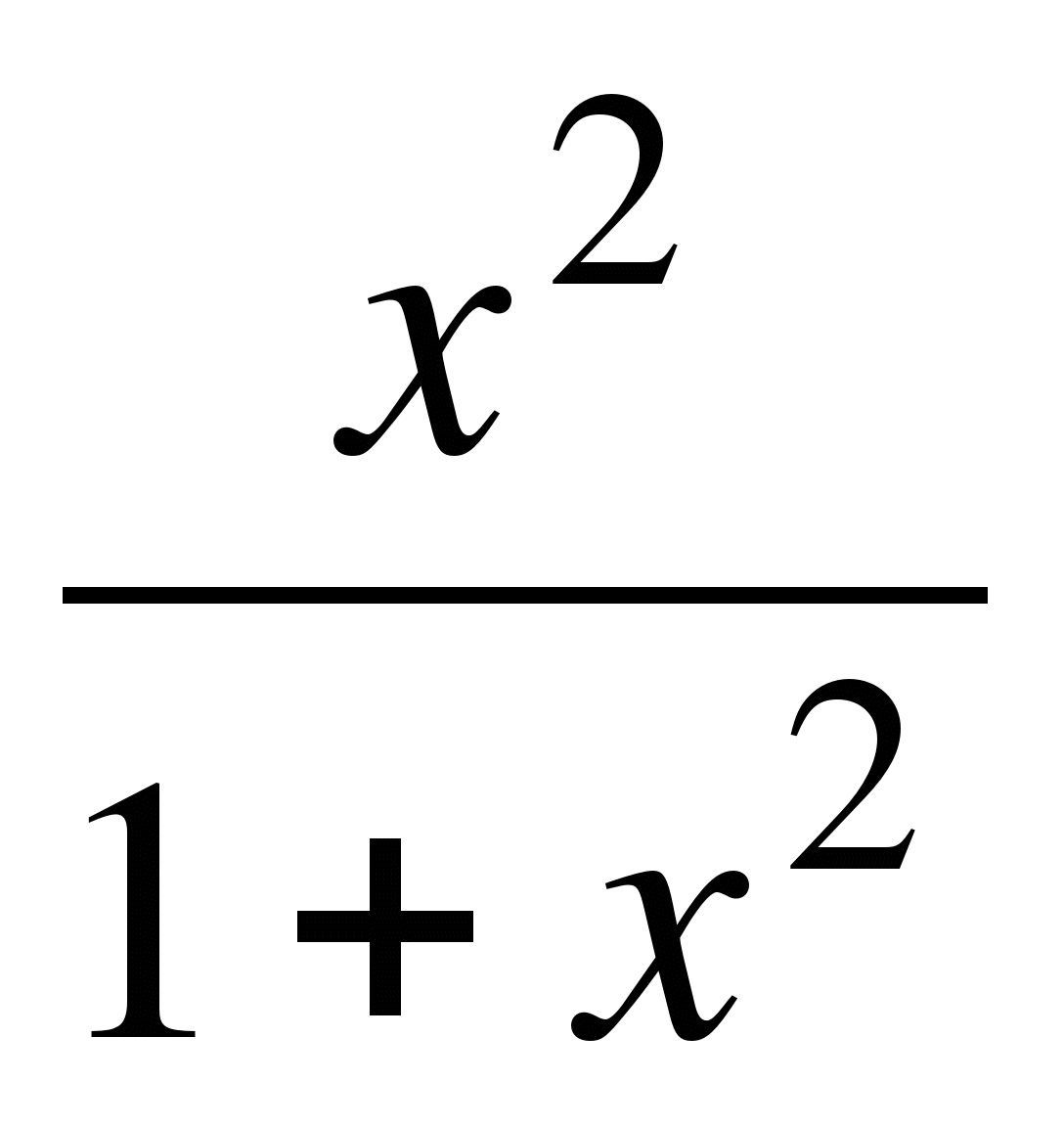 ,
,
в) у = (х2 – х – 1)8,
г) у = tg2 х.
2. Укажите промежутки возрастания и убывания функции
y = x3– 5x2– 32x +9
3. Исследуйте функцию f (х) = х3-3х 2 + 2 и постройте ее график.
4. Найдите наибольшее значение функции f(x) = 2x-x2 на отрезке [-2;0].
Контрольная работа по теме : « Производная и ее применение».
1 вариант
1. Используя правила дифференцирования, найдите производные следующих функций:
а) у = х4 -2х -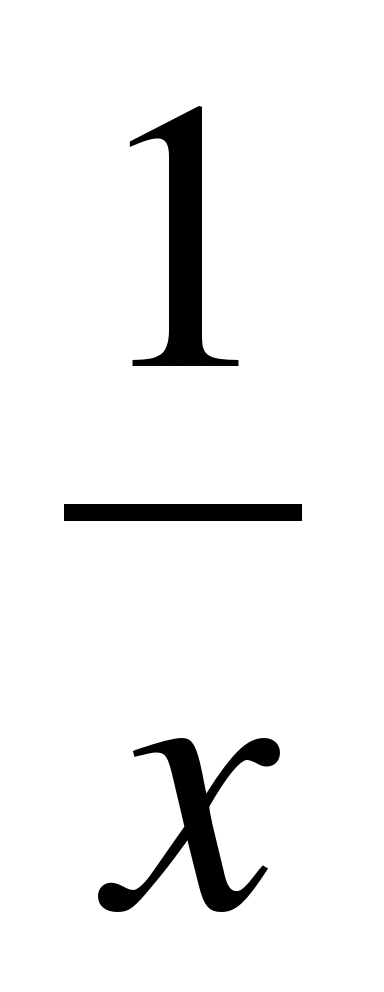
б) у = 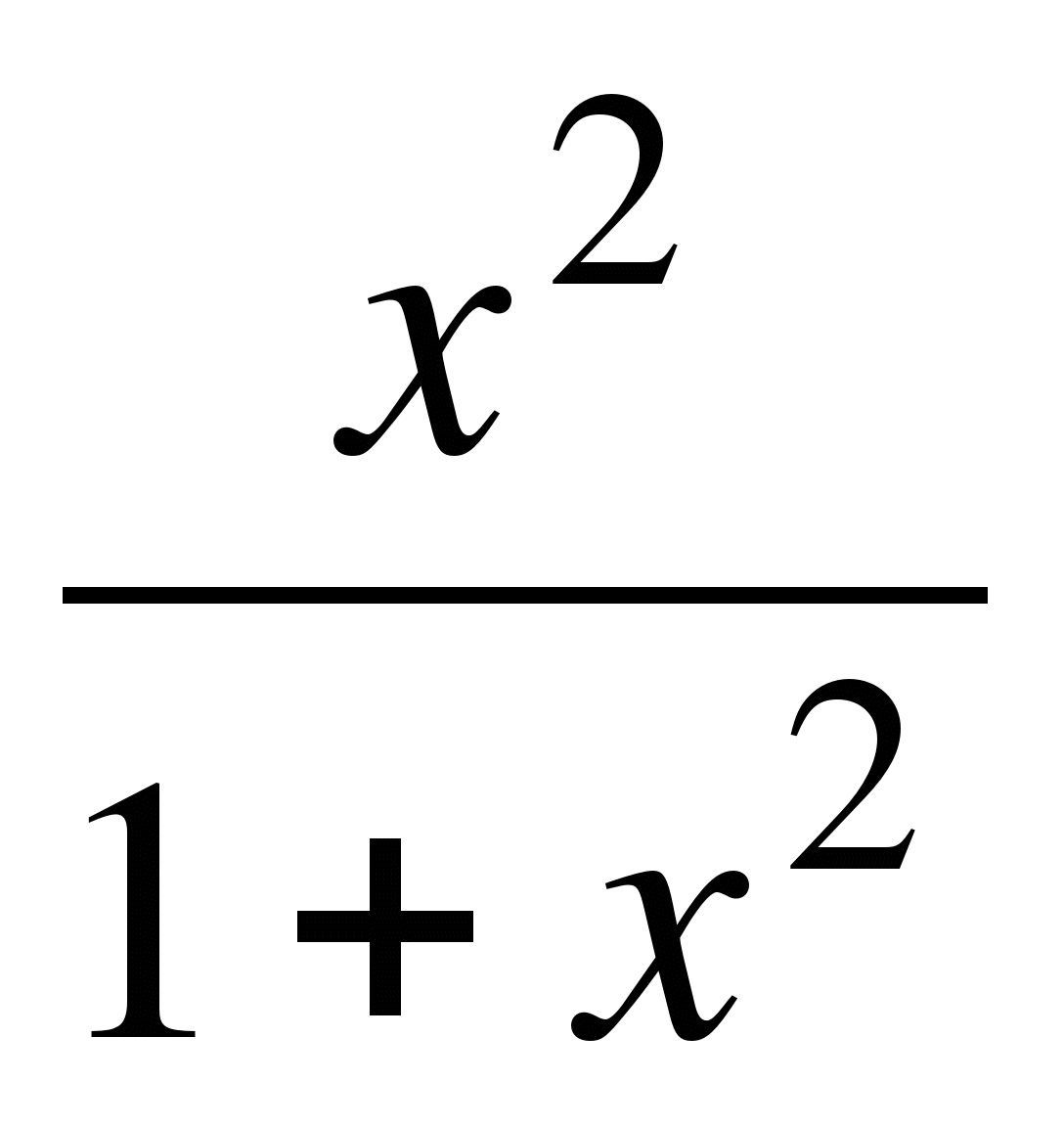 ,
,
в) у = (х2 – х – 1)8,
г) у = tg2 х.
2. Укажите промежутки возрастания и убывания функции
y = x3– 5x2– 32x +9
3. Исследуйте функцию f (х) = х3-3х 2 + 2 и постройте ее график.
4. Найдите наибольшее значение функции f(x) = 2x-x2 на отрезке [-2;0].
Контрольная работа по теме : « Производная и ее применение».
2 вариант
1. Используя правила дифференцирования, найдите производные следующих функций:
а) у = х2 -5х +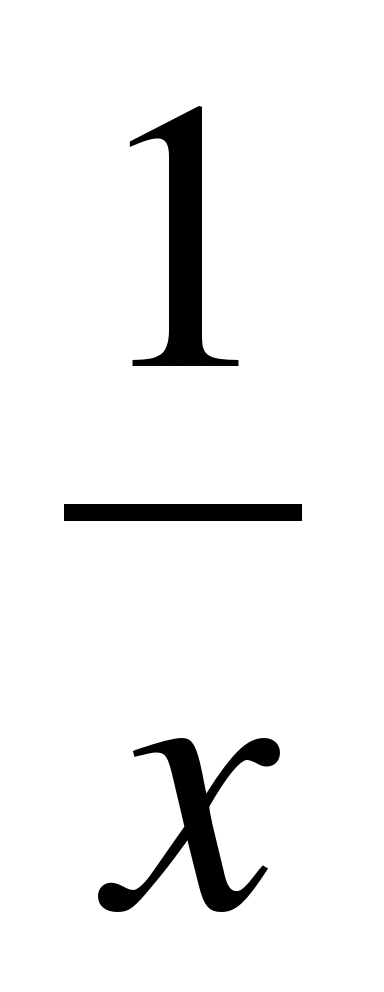
б) у = 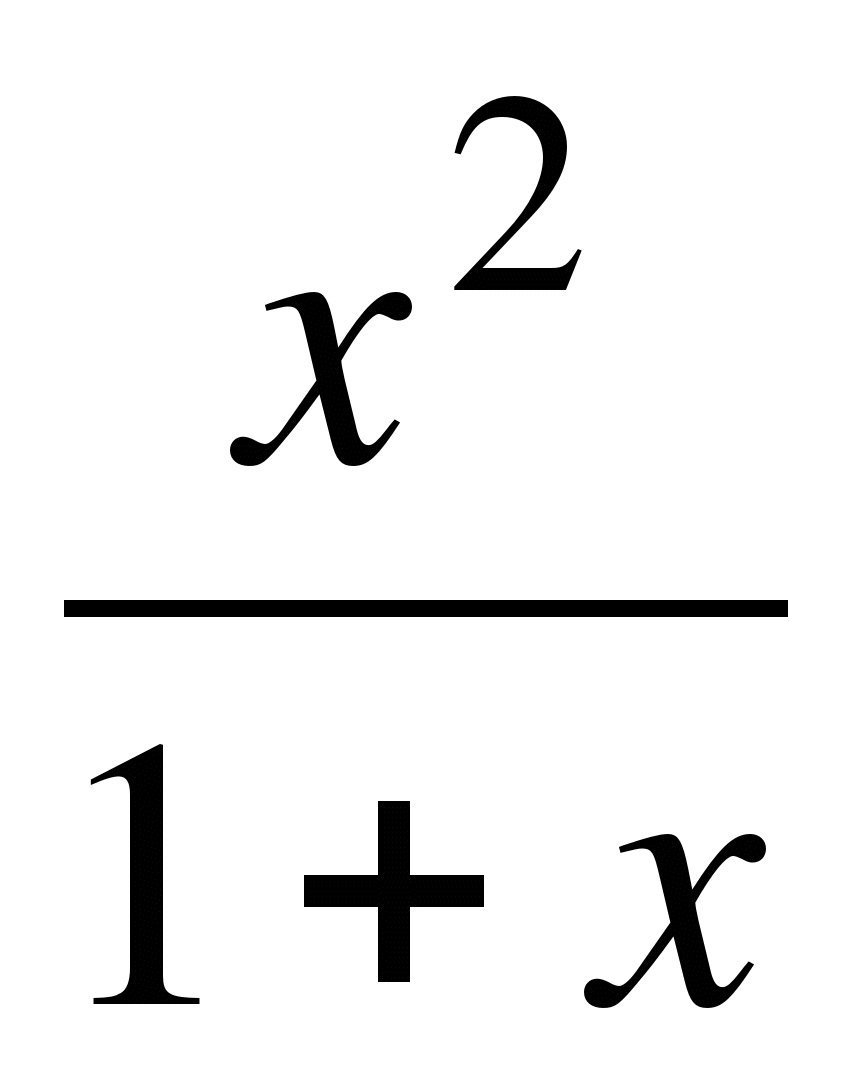 ,
,
в) у = (х2 – 3х + 1)7,
г) у = cos2 х.
2. Укажите промежутки возрастания и убывания функции
y = 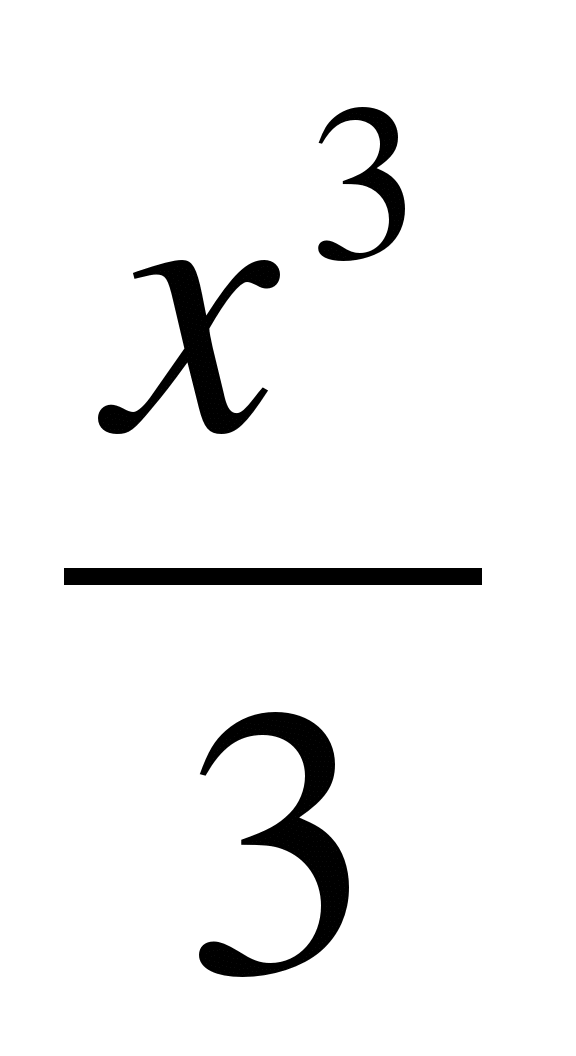 – x2– 3x +9
– x2– 3x +9
3. Исследуйте функцию f (х) = 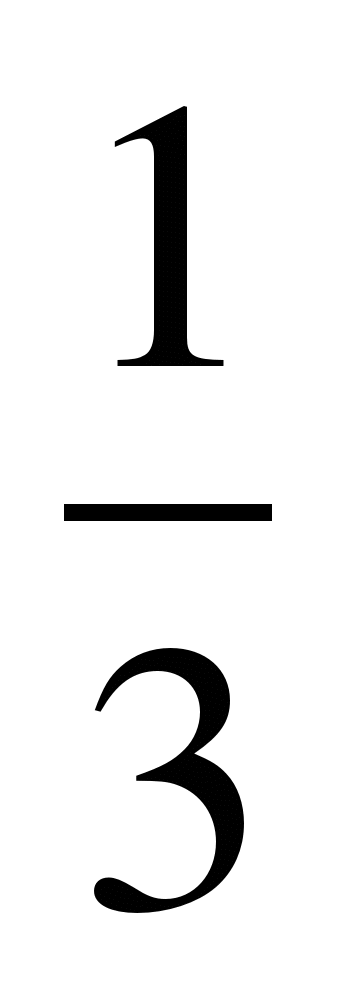 х3- 4х -3 и постройте ее график.
х3- 4х -3 и постройте ее график.
4. Найдите наименьшее значение функции f(x) = x2 -3 x на отрезке [-3;0].
infourok.ru
За выполнение заданий дается один балл. Баллы, полученные вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Желаем успеха!
1. Производную функции равна :
1) 12х22) 12х 3) 4х24) 12х3
2. Укажите производную функции .
1) -5 2) 11 3) 6 4) 6х
3. Определите производную функции .
1) 2) 3) 4)
4. Найдите производную функции .
1) 2) 3) 4)
5. Значение производной функции равно:
1) 2) 3) 4)
6. Значение производной функции в точке хо=2 равно :
1) 10 2) 12 3) 8 4) 6
7. Определите производную функции .
1) 2) 3) 4)
8. Вычислите значение производной функции в точке хо= 4.
1) 21 2) 24 3) 0 4) 3,5
9. Значение производной функции
в точке равно:
1) 2 2) 3) 4 4)
10. Найдите производную функции .
2) 3) 4)
11.Корень уравнение f ´(x)=0, если f(x)=(x-1)(x²+1)(x+1) равен:
1)-1 2)1 3)±1 4)0
12. Решите неравенство f ´(x)>0, если f(x)=-x²-4x-2006
1) (-∞; -2) 2) (-2;+∞) 3) (-∞;2) 4) (2;+∞)
13.Какой угол образует с осью абсцисс касательная к графику функции y=x2-x в начале координат?
1)45° 2)135° 3)60° 4)115°
14. Уравнение касательной к графику функции у=-1/х, проведенной в точке(1;1), имеет вид;
у=х 2) у = - х-2 3)у=х+2 4) у=-х+2
15. Определите угловой коэффициент касательной, проведенной к графику функции у=sin2x в его точке с абсциссой 0.
2 2) 1 3)0 4) -1
16. Тангенс угла наклона касательной, проведенной к графику функции у=6х-2/х в его точке с абсциссой (-1) равен:
1) -4 2) 1 3)0 4)-1
17. Укажите промежуток, на котором функция f(x) =5x²-4x-7 только возрастает.
1) (-1;+∞) 2) 3) 4) (0;+∞)
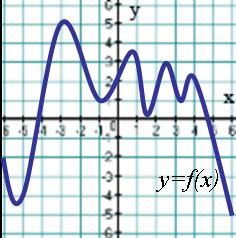
18. На рисунке изображен график функции . Сколько точек минимума имеет функция?
1) 4 2) 5 3) 2 4) 1
19. Точка максимума функции равна:
1) -4 2) -2 3) 4 4) 2
20. Сколько критических точек имеет функция f(x)=2x³+x²+5?
1) 2 2) 1 3) 4 4) 3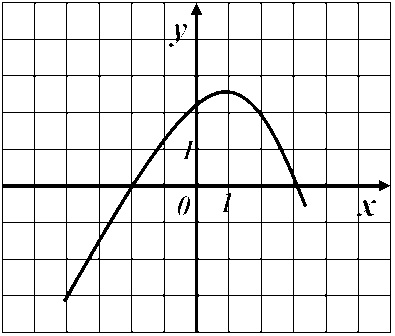
21. На рисунке изображен график производной у =f ´(x).
Найдите точку максимума функции у =f(x).
1) 1 2) 3 3) 2 4) -2
22. Точка минимума функции равна:
1) -2 2) -0,5 3) 0,5 4) 2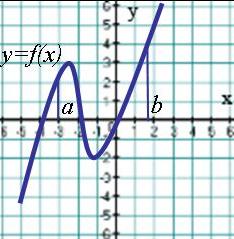
23. График функции у=f(x) изображен на рисунке. Укажите наибольшее значение этой функции на отрезке
1) 2 2) 3 3) 4 4) 6
24. Определите наименьшее значение функции на отрезке
2) 3 3) 1 4) -
25. Какая из функций возрастает на всей координатной прямой?
1)y=x³+x 2)y=x³-x 3)y=-x³+3 4)y=x²+1
26. Функция y=4x²+ 23 на отрезке [-2006; 2006] имеет наименьшее значение при х, равном...
-2005 2)0 3) 23 4)2005
27.Укажите точку максимума функции f(x), если f´ (x)=(x+6)(x-4)
-5 2)6 3)-6 4)-5
28.Тело движется по прямой так, что расстояние S( в метрах) от него до точки В этой прямой изменяется по закону S(t)=2t³-12t²+7 ( t-время движения в секундах). Через сколько секунд после начала движения ускорение тела будет равно 36 м/с²?
1) 3 2) 6 3)4 4)5
29.Тело движется по прямой так, что расстояние от начальной точки изменяется по закону S=5t+0,2t³-6 (м), где t- время движения в секундах. Найдите скорость тела через 5 секунд после начала движения.
1)10 2) 18 3) 20 4)26
30.Прямая, проходящая через начало координат, касается графика функции y=f(x) в точке (-2;10). Вычислите f ´(-2).
infourok.ru