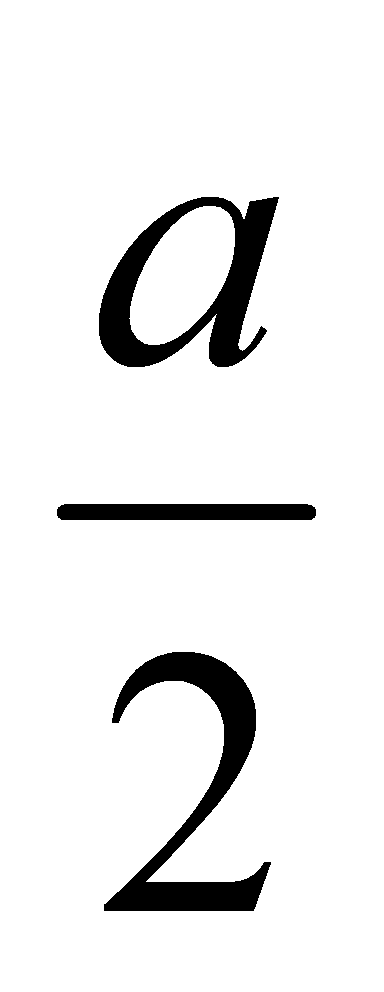 от точки D.
от точки D.Контрольная работа № 1
1 вариант
1). Основание АD трапеции АВСD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно.
а). Каково взаимное расположение прямых
ЕF и АВ?
б). Чему равен угол между прямыми ЕF и АВ,
если АВС = 1500?
Ответ обоснуйте.
2). Дан пространственный четырехугольник АВСD, в котором диагонали АС и ВD равны. Середины сторон этого четырехугольника соединены последовательно отрезками.
а). Выполните рисунок к задаче;
б). Докажите, что полученный четырех –
угольник – ромб.
2 вариант
1). Треугольники АВС и АDС лежат в разных плоскостях и имеют общую сторону АС. Точка Р – середина стороны АD, точка К – середина DС.
а). Каково взаимное расположение прямых
РК и АВ?
б). Чему равен угол между прямыми РК и
АВ, если АВС = 400 и ВСА = 80?
Ответ обоснуйте.
2). Дан пространственный четырехугольник АВСD, М и N – середины сторон АВ и ВС соответственно, Е СD, К D, DА : ЕС = 1 : 2, DК : КА = 1 : 2.
а). Выполните рисунок к задаче;
б). докажите, что четырехугольник МNЕК –
трапеция.
Контрольная работа № 2
1 вариант
1). Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть:
а). Параллельными;
б). Скрещивающимися?
Сделайте рисунок для каждого возможного случая.
2). Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А2В2, если А1В1 = 12 см, В1О : ОВ2 = 3 : 4.
3). Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через точки M, N и K, являющиеся серединами ребер АВ, ВС и DD1.
2 вариант
1). Прямые a и b лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть:
а). Параллельными;
б). Скрещивающимися?
Сделайте рисунок для каждого возможного случая.
2). Через точку О, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А1В1, если А2В2 = 15 см, ОВ1 : ОВ2 = 3 : 5.
3). Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N, являющиеся серединами ребер DC и BC, и точку K, такую, что K DA, АK : KD = 1 : 3.
Контрольная работа № 3
1 вариант
1). Диагональ куба равна 6 см. Найдите:
а). Ребро куба;
б). Косинус угла между диагональю куба и
плоскостью одной из его граней.
2). Сторона АВ ромба ABCD равна a, один из углов равен 60°. Через сторону АВ проведена плоскость α на расстоянии 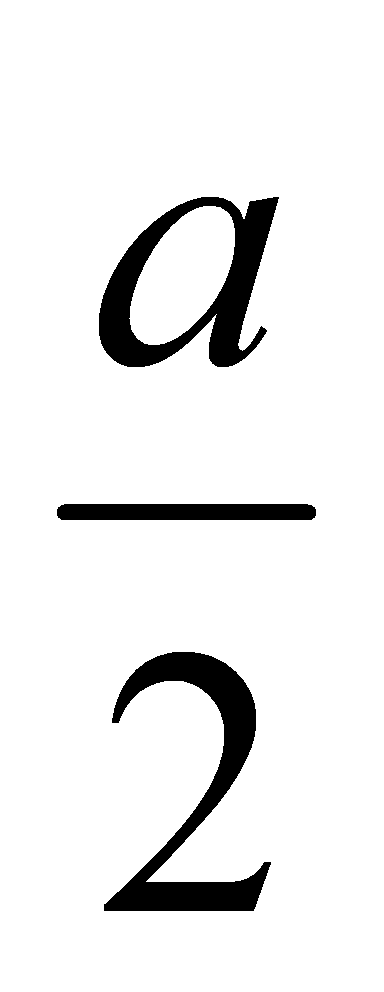 от точки D.
от точки D.
а). Найдите расстояние от точки С до плоскости α;
б). Покажите на рисунке линейный угол двугранного угла DABM, М α.
в) Найдите синус угла между плоскостью ромба и плоскостью α.
2 вариант
1). Основанием прямоугольного параллелепипеда служит квадрат, диагональ параллелепипеда равна 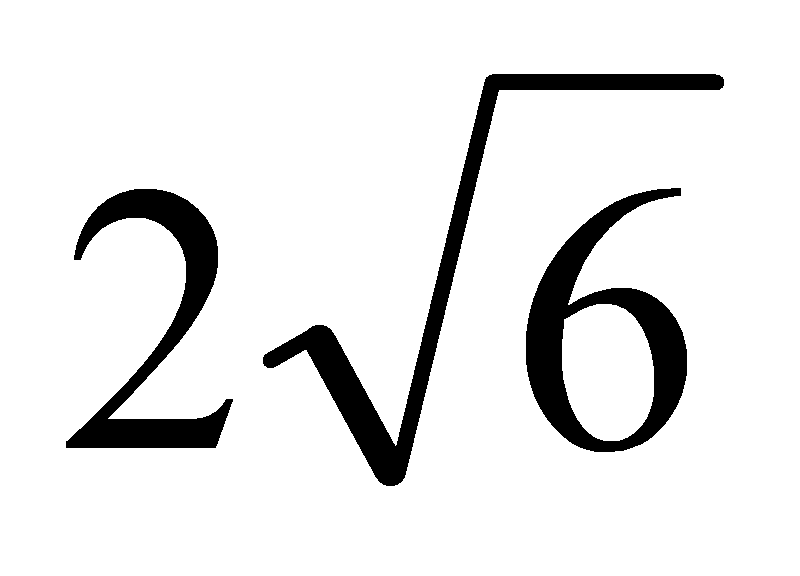 см, а его измерения относятся как 1:1:2. Найдите:
см, а его измерения относятся как 1:1:2. Найдите:
а). Измерения параллелепипеда;
б). Синус угла между диагональю параллеле –
пипеда и плоскостью его основания.
2). Сторона квадрата ABCD равна а. Через сторону AD проведена плоскость α на расстоянии 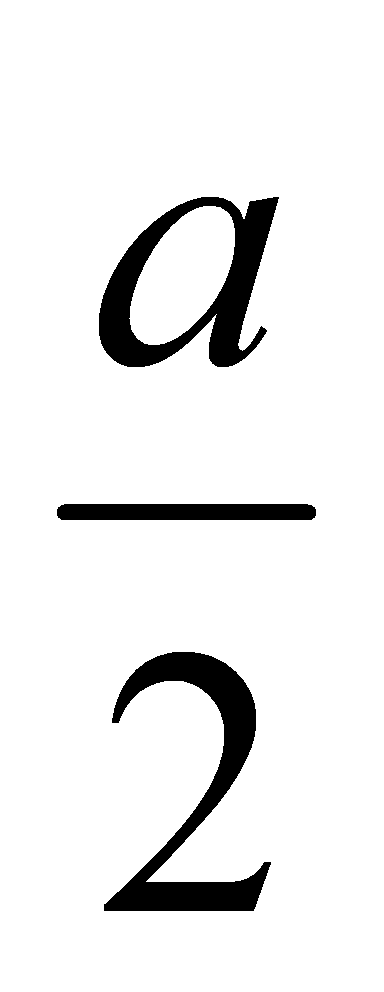 от точки В.
от точки В.
а). Найдите расстояние от точки С до плоскости α.
б). Покажите на рисунке линейный угол
двугранного угла BADM, М α.
в). Найдите синус угла между плоскостью
квадрата и плоскостью α.
Контрольная работа № 4
1 вариант
1). Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площадь боковой поверхности пирамиды.
2). Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб ABCD, сторона которого равна а и угол равен 60°. Плоскость AD1C1 составляет с плоскостью основания угол в 60°. Найдите:
а) высоту ромба;
б) высоту параллелепипеда;
в) площадь боковой поверхности параллелепипеда;
г) площадь поверхности параллелепипеда.
2 вариант
1). Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды.
2). Основанием прямого параллелепипеда ABCDA1B1C1D1 является параллелограмм ABCD, стороны которого равны 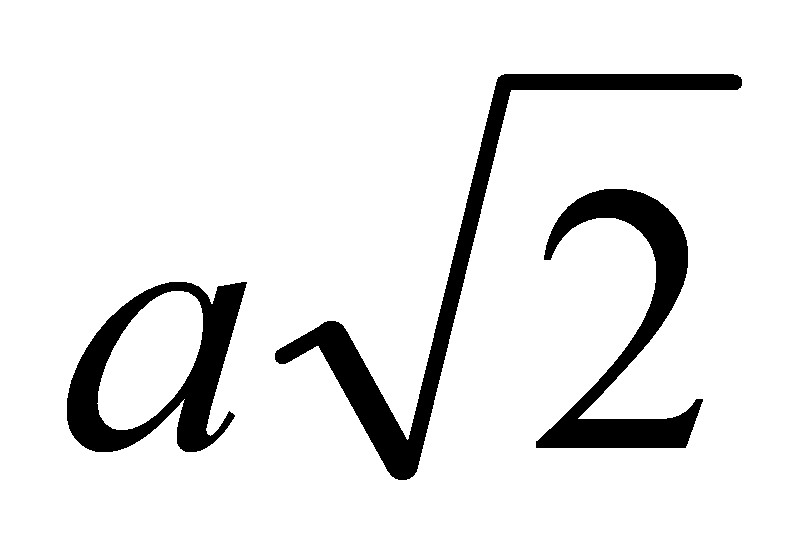 и 2а, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:
и 2а, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:
а). меньшую высоту параллелограмма;
б). угол между плоскостью АВС1 и плоскостью основания;
в). площадь боковой поверхности параллелепипеда;
г). площадь поверхности параллелепипеда.
infourok.ru
Пояснительная записка
Данная контрольная работа содержит темы курса алгебры и начал анализа курса 10 класса (учебник А.Г. Мордкович). Содержание контрольной работы находится в рамках Обязательного минимума содержания образования по математике. Тест составлен из заданий ЕГЭ по математике разных лет.
Этот же тест можно использовать и в сентябре, как вводный контроль для учащихся 11 класса.
Контрольная работа составлена в 4-х вариантах.
Время выполнения 60 минут.
Вариант 1
Часть 1
1. Найдите значение выражения
2. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой . Найдите значение производной функции f(x) в точке
.
3. Найдите
4. Найдите множество значений функции
5. Решите уравнение
6. Найдите наибольшее значение функции на отрезке
.
7. Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9 с.
8. Найдите угловой коэффициент касательной, проведённой к графику функции
f(x)= в его точке с абсциссой
=2.
9. На рисунке изображен график производной функции , определенной на интервале
. Найдите количество точек минимума функции
на отрезке
.
Часть 2
Задание с развернутым решением
10. а) Решите уравнение
б) Укажите корни, принадлежащие отрезку
Вариант 2
Часть 1
1. Найдите значение выражения
2. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой . Найдите значение производной функции f(x) в точке
.
3. Найдите
4. Найдите множество значений функции
5. Решите уравнение .
6. Найдите наименьшее значение функции на отрезке
.
7. Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени t = 6 с.
8. Найдите угловой коэффициент касательной, проведённой к графику функции
в точке с абсциссой
.
9. На рисунке изображен график производной функции, определенной на интервале . Найдите промежутки убывания функции. В ответе укажите длину наибольшего из них.
Часть 2
Задание с развернутым решением
10. а) Решите уравнение
б) Найдите корни, принадлежащие отрезку
Вариант 3
Часть 1
1. Найдите значение выражения
2. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой . Найдите значение производной функции f(x) в точке
.
3. Найдите
4. Укажите множество значений функции
5. Решите уравнение
6. Найдите наибольшее значение функции на отрезке
.
7. Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени
8. Найдите угловой коэффициент касательной, проведённой к графику функции в его точке с абсциссой
=1.
9. На рисунке изображен график производной функции , определенной на интервале
. Найдите количество точек максимума функции
на отрезке
.
Часть 2
Задание с развернутым решением
10. а) Решите уравнение
б) Найдите корни, принадлежащие отрезку
Вариант 4
Часть 1
1. Найдите значение выражения
2. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой . Найдите значение производной функции f(x) в точке
.
3. Найдите
4. Найдите множество значений функции
5. Решите уравнение
6. Найдите наименьшее значение функции на отрезке
.
7. Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 3 м/с?
8. Найдите угловой коэффициент касательной, проведённой к графику функции
f(x)= в его точке с абсциссой
=2.
9. На рисунке изображен график производной функции , определенной на интервале
. Найдите промежутки возрастания функции
. В ответе укажите длину наибольшего из них.
Часть 2
Задание с развернутым решением
10. а) Решите уравнение
б) Найдите корни, принадлежащие отрезку
итоговая контрольная работа по алгебре, 10 классDOCX / 363.99 Кб
xn--j1ahfl.xn--p1ai
Контрольная работа №1 по теме «Действительные числа» (1ч)
Вариант 1
Найдите остаток от деления на 11 числа 437.
Запишите периодическую дробь 0,(87) в виде обыкновенной дроби.
Сравните числа 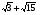 и
и 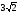 .
.
Решите уравнение 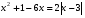 .
.
_____________________________________________
5. Решите неравенство 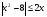 .
.
______________________________________
6. Постройте график функции 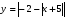 .
.
Вариант 2
Найдите остаток от деления на 19 числа 671.
Запишите периодическую дробь 0,(35) в виде обыкновенной дроби.
Сравните числа 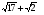 и
и 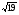 .
.
Решите уравнение 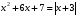 .
.
________________________________________
5. Решите неравенство 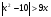 .
.
________________________________________
6. Постройте график функции 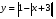 .
.
Контрольная работа №1 по теме «Действительные числа» (1ч)
Вариант 3
Найдите остаток от деления на 13 числа 371.
Запишите периодическую дробь 0,21(8) в виде обыкновенной дроби.
Расположите следующие числа в порядке возрастания: 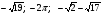 .
.
Решите уравнение 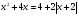 .
.
_____________________________________________
5. Найдите все двузначные нечетные делители числа 2184. ______________________________________________
6. Постройте график функции 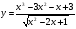 .
.
Вариант 4
Найдите остаток от деления на 17 числа 392.
Запишите периодическую дробь 2,35(7) в виде обыкновенной дроби.
Расположите следующие числа в порядке убывания: 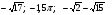 .
.
Решите уравнение 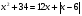 .
.
______________________________________________
5. Найдите все двузначные четные делители числа 2772
_______________________________________________
6.Постройте график функции 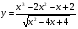 .
.
Контрольная работа № 2 по теме «Числовые функции». (2ч)
Вариант 1
Задает ли указанное правило функцию 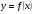 , если:
, если:
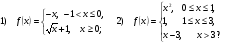
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках ─ 2; 1; 5;
в) постройте график функции;
г) найдите промежутки монотонности функции.
Исследуйте функцию 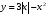 на четность.
на четность.
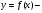 периодическая функция с периодом Т = 3. Известно, что
периодическая функция с периодом Т = 3. Известно, что
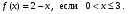
а) Постройте график функции; б) найдите нули функции;
в) найдите ее наибольшее и наименьшее значения.
Придумайте пример аналитически заданной функции, определенной на открытом луче 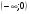 .
.
Известно, что функция 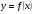 возрастает на R. Решите неравенство
возрастает на R. Решите неравенство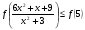 .
.
______________________________________________________________
6. Найдите функцию, обратную функции 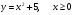 . Постройте на одном чертеже графики указанных двух взаимно обратных функций.
. Постройте на одном чертеже графики указанных двух взаимно обратных функций.
______________________________________
7. Вычислите: 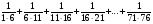 .
.
Контрольная работа № 2 по теме «Числовые функции». (2ч)
Вариант 2
Задает ли указанное правило функцию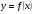 , если:
, если:
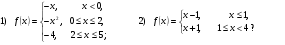
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках 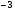 ; 2; 6;
; 2; 6;
в) постройте график функции;
г) найдите промежутки монотонности функции.
Исследуйте функцию 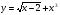 на четность.
на четность.
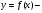 периодическая функция с периодом Т = 2. Известно, что
периодическая функция с периодом Т = 2. Известно, что 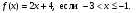
а) Постройте ее график функции;
б) найдите нули функции;
в) найдите ее наибольшее и наименьшее значения.
Придумайте пример аналитически заданной функции, определенной на луче 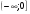 .
.
Известно, что функция 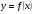 убывает на R. Решите неравенство
убывает на R. Решите неравенство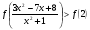 .
.
_______________________________________________________________________
6. Найдите функцию, обратную функции 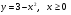 . Постройте на одном чертеже графики указанных двух взаимно обратных функций.
. Постройте на одном чертеже графики указанных двух взаимно обратных функций.
__________________________________________________
7. Вычислите: 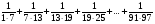 .
.
Контрольная работа № 2 по теме «Числовые функции». (2ч)
Вариант 3
Задает ли указанное правило функцию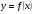 , если:
, если:
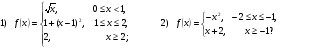
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках 0; 1,5; 10;
в) постройте график функции;
г) найдите промежутки монотонности функции.
Исследуйте функцию 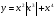 на четность.
на четность.
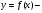 периодическая функция с периодом Т = 4. Известно, что
периодическая функция с периодом Т = 4. Известно, что
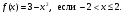
а) Постройте график функции; б) найдите нули функции;
в) найдите ее наибольшее и наименьшее значения.
Придумайте пример аналитически заданной функции 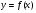 , определенной при всех
, определенной при всех 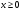 , кроме точки x = 2.
, кроме точки x = 2.
Известно, что функция 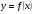 возрастает на R. Решите неравенство
возрастает на R. Решите неравенство 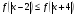 .
.
_______________________________________________________________
6. Найдите функцию, обратную функции 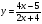 . Постройте на одном чертеже графики указанных двух взаимно обратных функций.
. Постройте на одном чертеже графики указанных двух взаимно обратных функций.
______________________________________
7. Докажите, что для любого 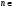 N справедливо равенство
N справедливо равенство 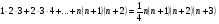 .
.
Контрольная работа № 2 по теме «Числовые функции». (2ч)
Вариант 4
Задает ли указанное правило функцию 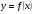 :
:
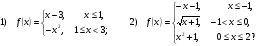
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках -0,75; 0; 3.
в) постройте график функции;
г) найдите промежутки монотонности функции.
Исследуйте функцию 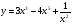 на четность.
на четность.
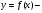 периодическая функция с периодом Т = 2. Известно, что
периодическая функция с периодом Т = 2. Известно, что 
а) Постройте график функции;
б) найдите нули функции;
в) найдите ее наибольшее и наименьшее значения.
Придумайте пример аналитически заданной функции 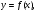 определенной при всех
определенной при всех 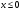 , кроме точки
, кроме точки 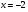 .
.
Известно, что функция 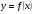 убывает на R. Решите неравенство
убывает на R. Решите неравенство 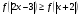 .
.
______________________________________________________________
6. Найдите функцию, обратную функции 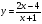 . Постройте на одном чертеже графики указанных двух взаимно обратных функций.
. Постройте на одном чертеже графики указанных двух взаимно обратных функций.
______________________________________________________________
7. Докажите, что для любого 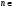 N справедливо равенство
N справедливо равенство 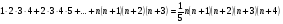 .
.
Контрольная работа № 3 по теме «Тригонометрические функции». (1ч)
Вариант 1
Центр окружности единичного радиуса совпадает с началом координат плоскости хОу. Принадлежат ли дуге 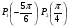 точки М1(-1; 0), М2 (0; -1), М3
точки М1(-1; 0), М2 (0; -1), М3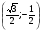 , М4
, М4 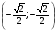 ?
?
Вычислите: 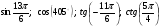 .
.
Вычислите 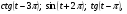 если
если 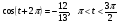 .
.
Решите неравенство: а) 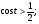 б)
б) 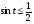 .
.
Постройте график функции 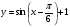 .
.
Исследуйте функцию на четность и периодичность; укажите основной период, если он существует:
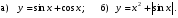
__________________________________________________
7. Сравните числа 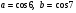 .
.
______________________________________
8. Решите неравенство 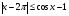 .
.
Вариант 2
Центр окружности единичного радиуса совпадает с началом координат плоскости хОу. Принадлежат ли дуге 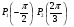 точки М1
точки М1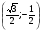 , М2 (0; 1), М3
, М2 (0; 1), М3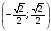 , М4
, М4 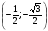 ?
?
Вычислите: 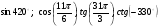 .
.
Вычислите 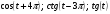 , если
, если 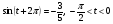 .
.
Решите неравенство: а) 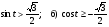
Постройте график функции 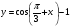 .
.
Исследуйте функцию на четность и периодичность; укажите основной период, если он существует:
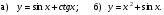
___________________________________________
7. Сравните числа 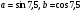 .
.
__________________________________________
8. Решите неравенство 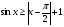 .
.
Контрольная работа № 3 по теме «Тригонометрические функции». (1ч)
Вариант 3
Центр окружности единичного радиуса совпадает с началом координат плоскости хОу. Принадлежат ли дуге 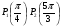 точки М1 (1; 0), М2
точки М1 (1; 0), М2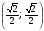 , М3
, М3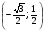 , М4
, М4 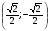 ?
?
Вычислите: 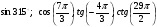 .
.
Вычислите 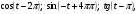 если
если 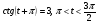 .
.
Решите неравенство: а) 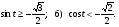
Постройте график функции 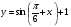 .
.
Исследуйте функцию на четность и периодичность; укажите основной период, если он существует:
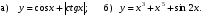
_________________________________________________
7. Расположите в порядке возрастания следующие числа: 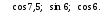
_____________________________________
8. При каком значении параметра 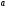 уравнение
уравнение 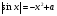 имеет единственный корень? Чему он равен?
имеет единственный корень? Чему он равен?
Вариант 4
Центр окружности единичного радиуса совпадает с началом координат плоскости XOY. Принадлежат ли дуге 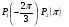 точки М1 (1; 0), М2
точки М1 (1; 0), М2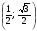 , М3
, М3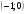 , М4
, М4 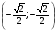 ?
?
Вычислите: 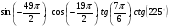 .
.
Вычислите: 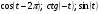 , если
, если 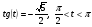 .
.
Решите неравенство: а) 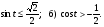
Постройте график функции 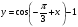 .
.
Исследуйте функцию на четность и периодичность; укажите основной период, если он существует:
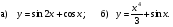
______________________________________________
7. Расположите в порядке возрастания следующие числа: 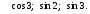 .
.
_____________________________________
8. При каком значении параметра 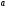 уравнение
уравнение 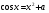 имеет единственный корень? Чему он равен?
имеет единственный корень? Чему он равен?
Контрольная работа № 4 « Аксиомы стереометрии».
Вариант 1
Точки К, М, Р, Т не лежат в одной плоскости. Могут ли прямые КМ и РТ пересекаться?
Через точки А, В и середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А1, В1, М1 соответственно. Найдите длину отрезка ММ1, если АА1 = 13 м, ВВ1 = 7 м, причем отрезок АВ не пересекает плоскость α.
Точка Р не лежит в плоскости трапеции ABCD с основаниями AD и ВС. Докажите, что прямая, проходящая через середины отрезков РВ и PC, параллельна средней линии трапеции.
Вариант 2
Прямые EN и КМ не лежат на одной плоскости. Могут ли прямые ЕМ и NK пересекаться? (Ответ обоснуйте.)
Через точки А, В и середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А1, В1, М1 соответственно. Найдите длину отрезка ММ1, если АА1 = 3 м, ВВ1 = 17 м, причем отрезок АВ не пересекает плоскость α.
Точка Е не лежит в плоскости параллелограмма ABCD. Докажите, что прямая, проходящая через середины отрезков ЕА и ЕВ, параллельна стороне CD.
Контрольная работа № 5 по теме «Простейшие тригонометрические уравнения и неравенства». (2ч)
Вариант 1
Вычислите: 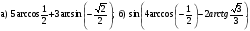
Постройте график функции 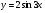 .
.
Решите уравнение: а) 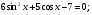
б) 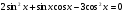 .
.
Найдите корни уравнения 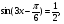 принадлежащие промежутку
принадлежащие промежутку 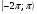 .
.
Постройте график функции 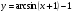 .
.
__________________________________________________
6. Решите систему неравенств:
а) 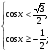 б)
б) 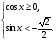
___________________________________
7. Решите уравнение 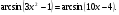 .
.
Вариант 2
1. Вычислите: 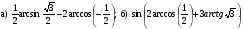
2. Постройте график функции 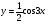 .
.
3. Решите уравнение: а) 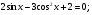
б) 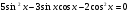 .
.
4. Найдите корни уравнения 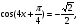 принадлежащие промежутку
принадлежащие промежутку 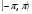 .
. 
5. Постройте график функции 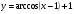 .
.
__________________________________________________
6. Решите систему неравенств:
а) 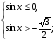 б)
б) 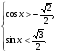
___________________________________
7. Решите уравнение 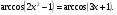 .
.
Контрольная работа № 5 по теме «Простейшие тригонометрические уравнения и неравенства». (2ч)
Вариант 3
1. Вычислите: 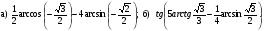
2. Постройте график функции 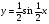 .
.
3. Решите уравнение: а) 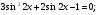
б) 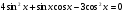 .
.
4. Найдите корни уравнения 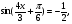 принадлежащие промежутку
принадлежащие промежутку 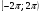 .
.
5. Постройте график функции 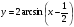 .
.
_______________________________________________
6. Решите систему неравенств:
а) 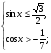 б)
б) 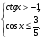
___________________________________
7. Решите уравнение 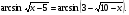 .
.
Вариант 4
1. Вычислите: 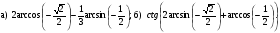
2. Постройте график функции 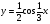 .
.
3. Решите уравнения: а) 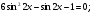
б) 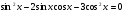 .
.
4. Найдите корни уравнения 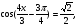 принадлежащие промежутку
принадлежащие промежутку 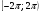 .
.
 5. Постройте график функции
5. Постройте график функции 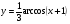 .
.
__________________________________________________
6. Решите систему неравенств:
а) 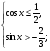 б)
б) 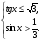
___________________________________
7. Решите уравнение 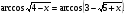 .
.
Контрольная работа №6 по теме «Параллельность в пространстве». (1ч)
Вариант 1
Плоскости α и β параллельны, причем плоскость α пересекает некоторую прямую а. Докажите, что и плоскость β пересекает прямую а.
2. Точки А, В, С, D не лежат в одной плоскости, точки К, М, Р — середины отрезков АВ, ВС, CD. Докажите, что плоскость КМР параллельна прямым АС и BD.
3. Даны две параллельные плоскости и не лежащая между ними точка Р. Две прямые, проходящие через точку Р, пересекают ближнюю к точке Р плоскость в точках А1 и А2, а дальнюю — в точках В1 и В2 соответственно. Найдите длину отрезка B1B2, если
А1А2 = 6 см и РА1 : А1В1 = 3:2.
4. Постройте проекцию квадрата ABCD, зная проекции его вершин А, B и точки пересечения диагоналей О: точки A1, B1 и О1.
Вариант 2
1. Прямые а и b параллельны, причем прямая а пересекает некоторую плоскость α. Докажите, что и прямая b пересекает плоскость α.
2. Точки А, В, С, D не лежат в одной плоскости, точки К, М, Р — середины отрезков АВ, AC, AD. Докажите, что плоскости КМР и BCD параллельны.
3. Даны две параллельные плоскости и не лежащая между ними точка К. Две прямые, проходящие через точку К, пересекают ближнюю к точке К плоскость в точках А1 и А2, а дальнюю — в точках В1 и В2 соответственно. Найдите длину отрезка В1В2, если А1А2 = 10 см и КА1 : А1В1 = 2:3.
4. Постройте проекцию правильного треугольника, зная проекции его вершины А и середин К, М сторон АВ и ВС: точки А1, К1 и М1.
Контрольная работа №7 по теме « Преобразование тригонометрических выражений». (2ч)
Вариант 1
Докажите тождество:
а) 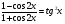 ,
,
б) 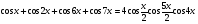 .
.
Упростите выражение 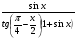 .
.
Вычислите 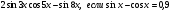 .
.
Найдите 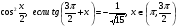 .
.
Найдите корни уравнения 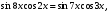 принадлежащие промежутку
принадлежащие промежутку 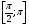 .
.
Решите уравнение:
а) 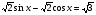 , б)
, б) 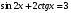 .
.
_________________________________________
7. Вычислите 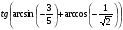 .
.
___________________________________
8. Решите уравнение 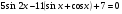 .
.
Вариант 2
1. Докажите тождество:
а) 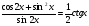 ,
,
б) 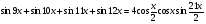 .
.
2. Упростите выражение 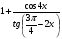 .
.
3. Вычислите 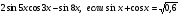 .
.
4. Найдите 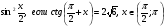 .
.
5. Найдите корни уравнения 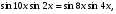
принадлежащие промежутку 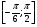 .
.
6. Решите уравнение:
а) 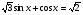 ; б)
; б) 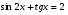 .
.
_____________________________________
7. Вычислите 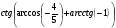 .
.
___________________________________
8. Решите уравнение 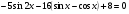 .
.
Контрольная работа №7 по теме « Преобразование тригонометрических выражений». (2ч)
Вариант 3
Докажите тождество:
а) 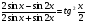 ,
,
б) 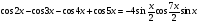 .
.
Упростите выражение 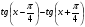 .
.
Вычислите 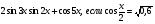 .
.
Найдите 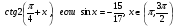 .
.
Найдите корни уравнения 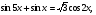 принадлежащие промежутку
принадлежащие промежутку 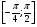 .
.
Решите уравнение: а) 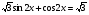 ;
;
б) 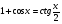 .
.
____________________________________
7. Вычислите 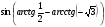 .
.
___________________________________
8. Решите уравнение 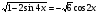 .
.
Вариант 4
Докажите тождество:
а) 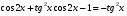 ,
,
б) 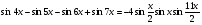 .
.
Упростите выражение 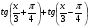 .
.
Вычислите 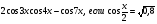 .
.
Найдите 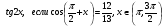 .
.
Найдите корни уравнения 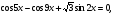 принадлежащие промежутку
принадлежащие промежутку 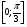 .
.
Решите уравнение:
а) 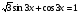 ; б)
; б) 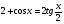 .
.
__________________________________________________
7. Вычислите 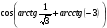 .
.
___________________________________
8. Решите уравнение 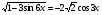 .
.
Контрольная работа №8 по теме «Перпендикулярность прямой и плоскости». (1ч)
1 вариант
Концы отрезка АВ, не пересекающего плоскость, удалены от нее на расстояния 2,4м и 7,6м. Найдите расстояние от середины М отрезка АВ до этой плоскости.
Перекладина длиной 5м своими концами лежит на двух вертикальных столбах высотой 3м и 6м. Каково расстояние между основаниями столбов?
Из точки к плоскости проведены две наклонные, равные 17см и 15 см. Проекция одной из них на 4 см больше проекции другой. Найдите проекции наклонных.
Из вершины равностороннего треугольника АВС проведен перпендикуляр АМ к плоскости треугольника. Чему равно расстояние от точки М до прямой ВС, если АМ =1м, ВС = 8м?
2 вариант
Точка А лежит в плоскости, точка В - на расстоянии 12,5м от нее. Найдите расстояние от плоскости до точки М, делящей отрезок АВ в отношении АМ : МВ = 2 : 3.
Какой длины нужно взять перекладину, чтобы ее можно было положить концами на два вертикальных столба высотой 4м и 8м, поставленные на расстоянии 3м один от другого?
Из точки к плоскости проведены две наклонные, одна из которых на 6см длиннее другой. Проекции наклонных равны 17см и 7см. Найдите наклонные.
Из вершины квадрата АВСК проведен перпендикуляр АМ к плоскости квадрата. Чему равно расстояние от точки М до прямой ВК, если АМ =2м, АВ = 8м?
Контрольная работа № 9 по теме «Комплексные числа». (1ч)
Вариант 1
Вычислите:
а)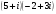 , б)
, б)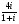 .
.
Изобразите на комплексной плоскости:
а) середину отрезка, соединяющего точки 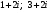 ;
;
б) множество точек z, удовлетворяющих условию 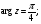
в) множество точек z, удовлетворяющих условию 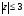 .
.
Запишите комплексное число в стандартной тригонометрической форме: а)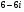 , б)
, б)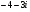 .
.
Решите уравнение 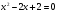 .
.
Вычислите 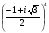 .
.
____________________________________
6. Решите уравнение 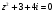 .
.
___________________________________
7. Найдите множество точек, изображающих комплексные числа, удовлетворяющие условиям: 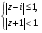
Вариант 2
Вычислите:
а)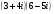 , б)
, б)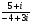 .
.
Изобразите на комплексной плоскости:
а) середину отрезка, соединяющего точки 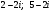 ;
;
б) множество точек z, удовлетворяющих условию 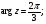
в) множество точек z, удовлетворяющих условию 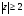 .
.
Запишите комплексное число в стандартной тригонометрической форме: а)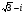 , б)
, б)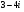 .
.
Решите уравнение 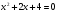 .
.
Вычислите 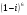 .
.
__________________________________________________
6. Решите уравнение 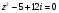 .
.
___________________________________
7. Найдите множество точек, изображающих комплексные числа, удовлетворяющие условиям: 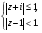
Контрольная работа № 9 по теме «Комплексные числа». (1ч)
Вариант 3
Вычислите: а)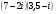 , б)
, б)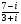 .
.
Изобразите на комплексной плоскости:
а) середину отрезка, соединяющего точки 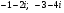 ;
;
б) множество точек z, удовлетворяющих условию
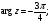
в) множество точек z, удовлетворяющих условию 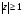 .
.
Запишите комплексное число в стандартной тригонометрической форме: а)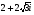 , б)
, б)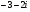 .
.
Решите уравнение 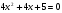 .
.
Вычислите 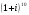 .
.
____________________________________
6. Решите уравнение 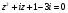 .
.
___________________________________
7.Найдите множество точек, изображающих
комплексные числа, удовлетворяющие условиям: 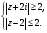
Вариант 4
Вычислите: а)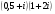 , б)
, б)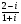 .
.
Изобразите на комплексной плоскости:
а) середину отрезка, соединяющего точки 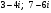 ;
;
б) множество точек z, удовлетворяющих условию 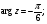
в) множество точек z, удовлетворяющих условию 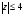 .
.
Запишите комплексное число в стандартной тригонометрической форме: а)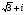 , б)
, б)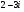 .
.
Решите уравнение 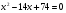 .
.
Вычислите 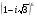 .
.
____________________________________
6. Решите уравнение 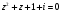 .
.
___________________________________
7. Найдите множество точек, изображающих комплексные числа, удовлетворяющие условиям: 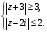
Контрольная работа № 10 по теме «Перпендикулярность плоскостей». (1ч)
Вариант 1.
Отрезок АМ перпендикулярен плоскости квадрата АВСD со стороной 3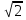 см. Найдите расстояние от точки М до диагонали ВD квадрата, если АМ=4см.
см. Найдите расстояние от точки М до диагонали ВD квадрата, если АМ=4см.
Перпендикулярные плоскости α и β пересекаются по прямой m. Точка А лежит в плоскости α, точка В – в плоскости β. АА1 перпендикулярен m, ВВ1 перпендикулярен m. Найти АВ, если АА1= 8см, ВВ1=12 см, А1В1=4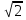 см.
см.
Плоскости равностороннего треугольника АВС и квадрата ВСDЕ перпендикулярны. Найти расстояние от точки А до стороны DЕ, если
АВ = 4 см.
Вариант 2.
Отрезок ВК перпендикулярен плоскости квадрата АВСD. Периметр квадрата равен 16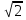 см. Найдите длину отрезка ВК, если расстояние от точки К до диагонали АС квадрата равно 5см.
см. Найдите длину отрезка ВК, если расстояние от точки К до диагонали АС квадрата равно 5см.
Перпендикулярные плоскости α и β пересекаются по прямой n. Точка А лежит в плоскости α, точка В – в плоскости β. АМ перпендикулярен n, ВК перпендикулярен n. Найти МК, если АМ= 4см, ВК=6см, АВ=10см.
Плоскости равнобедренного треугольника АВС и квадрата АВDЕ перпендикулярны. Найдите расстояние от точки С до стороны DЕ, если АВ = 6см, < АВС=90°.
Контрольная работа №11 по теме «Декартовы координаты». (1ч)
Вариант 1
Даны точки А (0; 0; 2) и В(1; 1; -2), О — начало координат. На оси у найдите точку М (0; у; 0), равноудаленную от точек А и В.
В плоскости ху найдите точку С (х; у; 0), такую, чтобы векторы 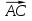 и
и 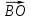 были коллинеарными.
были коллинеарными.
При каком значении х вектор 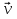 (х; 2; 1) будет перпендикулярен вектору
(х; 2; 1) будет перпендикулярен вектору 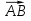 ?
?
Вариант 2
Даны точки А (0; -2; 0) и В (1; 2; -1), О — начало координат. На оси z найдите точку М (0; 0; z), равноудаленную от точек А и В.
Найдите точку С (х; у; z), такую, чтобы векторы 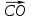 и
и 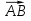 были равными.
были равными.
При каком значении х вектор 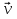 (х; 1; 2) будет перпендикулярен вектору
(х; 1; 2) будет перпендикулярен вектору 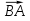 ?
?
Контрольная работа № 12 по теме « Вычисление производных». (2ч)
Вариант 1
Напишите первый, тридцатый и сотый члены последовательности, если ее n-й член задается формулой 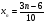 .
.
Исследуйте последовательность 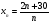 на ограниченность и на монотонность.
на ограниченность и на монотонность.
Вычислите: а) 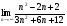 ; б)
; б) 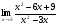 .
.
Пользуясь определением, выведите формулу дифференцирования функции 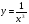 .
.
Пользуясь правилами и формулами дифференцирования, найдите производную функции:
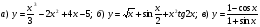 .
.
Напишите уравнение касательной к графику функции 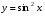 в точке
в точке 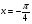 .
.
__________________________________________________________________
Докажите, что функция 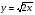 удовлетворяет соотношению
удовлетворяет соотношению 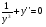 .
.
_____________________________________________________________________
8. Найдите площадь треугольника, образованного осями координат и касательной к графику функции 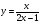 в точке
в точке 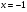 .
.
Вариант 2
Напишите первый, тридцатый и сотый члены последовательности, если ее n-й член задается формулой 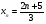 .
.
Исследуйте последовательность 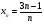 на ограниченность и на монотонность.
на ограниченность и на монотонность.
Вычислите: а) 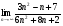 ; б)
; б) 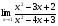 .
.
Пользуясь определением, выведите формулу дифференцирования функции 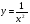 .
.
Пользуясь правилами и формулами дифференцирования, найдите производную функции:
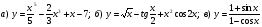 6.Напишите уравнение касательной к графику функции
6.Напишите уравнение касательной к графику функции 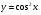 в точке
в точке 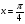 .
.
__________________________________________________________________
7. Докажите, что функция 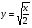 удовлетворяет соотношению
удовлетворяет соотношению 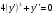 .
.
______________________________________________________________________
8. Найдите площадь треугольника, образованного осями координат и касательной к графику функции 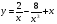 в точке
в точке 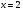 .
.
Контрольная работа № 12 по теме « Вычисление производных». (2ч)
Вариант 3
1. Вычислите первый, тридцатый и сотый члены последовательности, если ее n-й член задается формулой 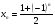 .
.
2. Исследуйте последовательность 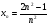 на ограниченность и на монотонность.
на ограниченность и на монотонность.
3. Вычислите: 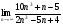 ; б)
; б) 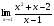 .
.
4. Пользуясь определением, выведите формулу дифференцирования функции 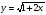 .
.
5. Пользуясь правилами и формулами дифференцирования, найдите производную функции:
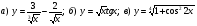 .
.
6. Найдите угол, образованный касательной к графику функции 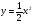 в точке с абсциссой
в точке с абсциссой 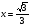 , с осью абсцисс.
, с осью абсцисс.
____________________________________________________________________________
7. Докажите, что функция 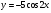 удовлетворяет соотношению
удовлетворяет соотношению 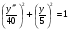 .
.
__________________________________________________________________________
8. Найдите значение параметра 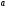 , при котором касательная к графику функции
, при котором касательная к графику функции 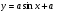 в точке с абсциссой
в точке с абсциссой 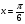 параллельна прямой
параллельна прямой 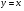 . Напишите уравнение этой касательной.
. Напишите уравнение этой касательной.
Вариант 4
1. Напишите первый, тридцатый и сотый члены последовательности, если ее n-й член задается формулой 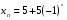 .
.
2. Исследуйте последовательность 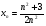 на ограниченность и на монотонность.
на ограниченность и на монотонность.
3. Вычислите: а) 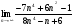 ; б)
; б) 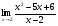 .
.
4. Пользуясь определением, выведите формулу дифференцирования функции 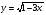 .
.
5. Пользуясь правилами и формулами дифференцирования, найдите производную функции:
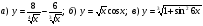 .
.
Найдите угол, образованный касательной к графику функции 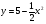 в точке с абсциссой
в точке с абсциссой 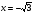 , с осью абсцисс.
, с осью абсцисс.
____________________________________
Докажите, что функция 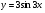 удовлетворяет соотношению
удовлетворяет соотношению 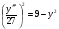
___________________________________
8. Найдите значения параметра 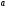 , при которых касательная к графику функции
, при которых касательная к графику функции 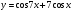 в точке с абсциссой
в точке с абсциссой 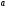 параллельна касательной к этому графику в точке с абсциссой
параллельна касательной к этому графику в точке с абсциссой 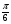 .
.
Контрольная работа № 13 по теме «Применения производной». (2ч)
Вариант 1
Исследуйте функцию у = 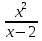 на монотонность и экстремумы.
на монотонность и экстремумы.
Постройте график функции у = 3x2 – х3.
Найдите наименьшее и наибольшее значения функции у = 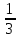 х3 -
х3 - 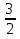 х2 + 1 на отрезке [-1; 1].
х2 + 1 на отрезке [-1; 1].
В полукруг радиуса 6 см вписан прямоугольник. Чему равна наибольшая площадь прямоугольника?
________________________________________
Докажите, что при х ϵ (0;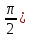 справедливо неравенство cos х + х sin х > 1.
справедливо неравенство cos х + х sin х > 1.
___________________________________________
При каких значениях параметра а функция у = 2 ах3 + 9х2 + 54 ах + 66 убывает на всей числовой прямой?
Вариант 2
Исследуйте функцию у = 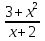 на монотонность и экстремумы.
на монотонность и экстремумы.
Постройте график функции у = х3 - х2.
Найдите наименьшее и наибольшее значения функции у = 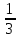 х3 - х2 + 1 на отрезке [-1; 3].
х3 - х2 + 1 на отрезке [-1; 3].
В прямоугольный треугольник с гипотенузой 8 см и углом 60° вписан прямоугольник так, что одна из его сторон лежит на гипотенузе. Чему равна наибольшая площадь такого прямоугольника?
______________________________________
Докажите, что при х ϵ (0;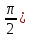 справедливо неравенство sin х > х cos х.
справедливо неравенство sin х > х cos х.
__________________________________________
При каких значениях параметра а функция у = 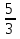 ах3 - 30х2 + 5(а+9)х - 7 возрастает на всей числовой прямой?
ах3 - 30х2 + 5(а+9)х - 7 возрастает на всей числовой прямой?
Контрольная работа № 13 по теме «Применения производной». (2ч)
Вариант 3
Исследуйте функцию у = 4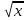 (2 - х) на монотонность и экстремумы.
(2 - х) на монотонность и экстремумы.
Постройте график функции у = 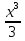 + 4х2 - 15х.
+ 4х2 - 15х.
Найдите наименьшее и наибольшее значения функции у = х - cos 2х на отрезке [-л; 0].
Периметр параллелограмма с острым углом 60° равен 8 см. Чему равна наибольшая площадь такого параллелограмма?
__________________________________________
Докажите, что при х > 0 справедливо неравенство cos х > 1 - 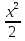
___________________________________
При каких значениях параметра а наименьшее на отрезке [0; 2] значение функции
у = 4х2 - 4ах + а2 - 2а + 2 равно 3?
Вариант 4
Исследуйте функцию у = 2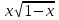 на монотонность и экстремумы.
на монотонность и экстремумы.
Постройте график функции у =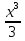 +х2+3х
+х2+3х
Найдите наименьшее и наибольшее значения функции у = 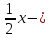 sin х на отрезке [-
sin х на отрезке [- 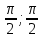 ].
].
В треугольник с основанием а и высотой h вписан прямоугольник так, что одна его сторона принадлежит основанию треугольника. Чему равна наибольшая площадь такого прямоугольника?
____________________________________________
Докажите, что при х 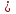 3 справедливо неравенство 4х(х2 + 6) > 15(х2 + 3).
3 справедливо неравенство 4х(х2 + 6) > 15(х2 + 3).
___________________________________________
При каких значениях параметра а наименьшее на отрезке [0; 2] значение функции у = х2 + (а + 4)х + 2а + 3 равно - 4?
Контрольная работа № 14 по теме « Комбинаторика и вероятность». (1ч)
Вариант 1
Сколькими способами можно составить трехцветный полосатый флаг, если имеется материал 5 различных цветов?
Сколько четырехзначных чисел можно составить из цифр 1,2,3,4 при условии, что каждая цифра может содержаться в записи числа лишь нечетное число раз?
3. Решите уравнение 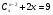 .
.
4. Из колоды в 36 карт вытаскивают две карты. Какова вероятность извлечь при этом 2 туза?
__________________________________________________
На прямой взяты 8 точек, а на параллельной ей прямой – 5 точек. Сколько существует треугольников, вершинами которых являются данные точки?
В разложении бинома 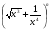 коэффициент третьего члена на 44 больше коэффициента второго члена. Найдите член, не зависящий от
коэффициент третьего члена на 44 больше коэффициента второго члена. Найдите член, не зависящий от 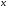 .
.
Вариант 2
1. В яхт-клубе состоит 9 человек. Из них надо выбрать председателя, заместителя, секретаря и казначея. Сколькими способами это можно сделать?
Сколько четырехзначных чисел можно составить из цифр 1,2,3,0 при условии, что каждая цифра может содержаться в записи числа лишь 1 раз?
Решите уравнение 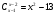 .
.
Из колоды в 36 карт вытаскивают три карты. Какова вероятность того, что все они тузы?
________________________________________________
5. Сколько существует треугольников, у которых вершины являются вершинами данного выпуклого 8-угольника, но стороны не совпадают со сторонами этого n-угольника?
6.Сумма биномиальных коэффициентов разложения бинома 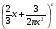 равна 64. Найдите член, не зависящий от x.
равна 64. Найдите член, не зависящий от x.
Контрольная работа № 9 (1 час)
Вариант 3
Из 30 членов спортивного клуба надо не только составить команду из 4 человек для участия в четырехэтапной эстафете, но и определить порядок выхода спортсменов на этапы. Сколькими способами это можно сделать?
Сколько трехзначных чисел можно составить из цифр 1,2,3 при условии, что цифры могут повторяться?
Решите уравнение 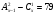 .
.
В урне находится 3 белых и 4 черных шара. Какова вероятность того, что вынутые из нее наудачу два шара окажутся белыми?
____________________________________________
На прямой взяты 6 точек, а на параллельной ей прямой – 7 точек. Сколько существует треугольников, вершинами которых являются данные точки?
В разложении бинома 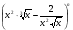 биномиальный коэффициент пятого члена относится к биномиальному коэффициенту третьего члена, как 1:2. Найдите член, не зависящий от х.
биномиальный коэффициент пятого члена относится к биномиальному коэффициенту третьего члена, как 1:2. Найдите член, не зависящий от х.
Вариант 4
В городской думе 30 человек. Из них надо выбрать председателя и трех его заместителей. Сколькими способами это можно сделать?
Сколько трехзначных чисел можно составить из цифр 1,2,3,4,0 при условии, что каждая цифра может содержаться в записи числа лишь 1 раз?
Решите уравнение 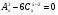 .
.
В урне находится 2 белых, 3 красных и 16 черных шаров. Какова вероятность того, что из вынутых из нее наудачу двух шаров один окажется белым, а другой красным?
_____________________________________________
Сколько существует треугольников, у которых вершины являются вершинами данного выпуклого 10-угольника?
_______________________________________
В разложении бинома 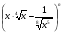 сумма биномиальных коэффициентов второго члена от начала и третьего члена от конца равна 78.
сумма биномиальных коэффициентов второго члена от начала и третьего члена от конца равна 78.
Найдите член, не зависящий от х.
Контрольная работа №15 по теме «Векторы». (1ч)
Вариант 1
Найдите координаты вектора 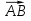 , если А(5; -1; 3), В(2; -2; 4).
, если А(5; -1; 3), В(2; -2; 4).
Даны векторы 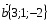 и
и 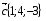 . Найдите
. Найдите 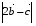 .
.
Изобразите систему координат Охуz и постройте точку А(1; -2; -4). Найдите расстояние от этой точки до координатных плоскостей.
Вычислите скалярное произведение векторов 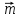 и
и 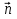 , если
, если 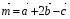 ,
, 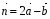 ,
, 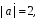
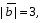
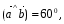
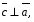
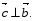
Вариант 2
Найдите координаты вектора 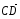 , если С(6; 3; -2), D(2; 4; -5).
, если С(6; 3; -2), D(2; 4; -5).
Даны векторы 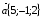 и
и 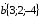 . Найдите
. Найдите 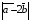 .
.
Изобразите систему координат Охуz и постройте точку B(-2; -3; 4). Найдите расстояние от этой точки до координатных плоскостей.
Вычислите скалярное произведение векторов 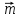 и
и 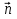 , если
, если 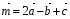 ,
, 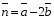 ,
, 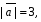
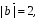
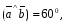
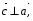
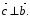
infourok.ru