МБОУ СОШ №3 им. К.А.Москаленко
Реферат по математике
ЗОЛОТОЕ СЕЧЕНИЕ
Авторы: Межов Илья Сергеевич,
Банных Даниил Дмитриевич
МБОУ СОШ№3 6В класс
Научный руководитель: Чеботарева Марина Викторовна
Липецк 2013
ОГЛАВЛЕНИЕ
Введение…………………………………………………………………2
Понятие о «золотом» сечении……………………………………2-4
Пентаграмма………………………………………………………4-5
«Золотой» прямоугольник…………………………………….....5
«Золотое» сечение в живописи…………………………………..5-7
«Золотое» сечение в архитектуре………………………………..7-11
«Золотое» сечение в природе…………………………………….11-14
«Золотое» сечение в анатомии…………………………………...14-15
«Золотое» сечение в скульптуре…………………………………15
Заключение……………………………………………………………….15
Список литературы……………………………………………………….16
Введение
При подготовке к данному реферату мы изучили много научной литературы не только по математике, но и использовали информацию из других наук: биологии, истории, анатомии. Для начала мы бы хотели привести пример из практики.
Если вы подходите к пустой скамейке и садитесь на неё, то вы сядете не посередине скамейки и, конечно, не на самый край. Если вы незаметно замерите длины, на которые своим телом разделили скамейку, то обнаружите, что отношение большего отрезка к меньшему равно отношению всей длины к большему отрезку. Это число, называется золотым сечением.
1. Понятие «золотого» сечения
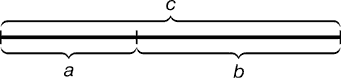
Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему.
с: b = b: а или a: b = b: c. Первое отношение приблизительно равно 1.6, а второе- 0.6.

Принято считать, что понятие о золотом сечении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян.
В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипосикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне.
Золотое отношение обычно обозначают буквой F – прописной буквой греческого алфавита. Такое обозначение принято в честь древнегреческого скульптора Фидия, жившего в V в. до н.э. Он руководил строительством храма Парфенон в Афинах; в пропорциях этого храма многократно присутствует число F. Его фасад вписывается в прямоугольник, отношение сторон которого равно F.
2. Пентаграмма
Замечательный пример «золотого» сечения представляет собой правильный пятиугольник - выпуклый и звездчатый. В звездчатом пятиугольнике каждая из пяти линий, составляющих эту фигуру, делит другую в отношении золотого сечения, а концы звезды являются золотыми треугольниками. Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.
infourok.ru
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Муниципальное общеобразовательное учреждение средняя общеобразовательная школа №2
РЕФЕРАТ
Тема
Выполнил Ткачев Дмитрий, ученик 7кл.
Руководитель Балакирева Елена Викторовна
п.Октябрьский
2011 год
ПЛАН:
«Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением и если первое можно сравнить с мерой золота, то второе – с драгоценным камнем.»
Иоганн Кеплер
С давних пор ученые занимались поисками гармонии и совершенства. Одним из таких вопросов был деление отрезка таким образом, чтобы отношение частей было совершенным. Задолго до нашей эры, в различных точках мира, разные ученые, независимо друг от друга, находили это отношение, и у всех это отношение было одним и тем же.
Золотым сечением, гармоническим делением и даже “божественной пропорцией” называли математики древности и средневековья деление отрезка, при котором длина всего отрезка так относится к длине его большей части, как длина большей части к меньшей. Это отношение приближенно равно 0,618 или 5/8.
Эту пропорцию принято обозначать греческой буквой φ (встречается также обозначение τ) .
В дошедшей до нас античной литературе золотое сечение впервые встречается в «Началах» Евклида (3 в. до н.э.).
В эпоху Возрождения математическое понятие – золотая пропорция было возведено в ранг главного эстетического принципа. Леонардо да Винчи именовал ее Sectio aurea, откуда и получил начало термин “золотое сечение”.
Леонардо да Винчи, использовал золотое сечение как пропорции «идеального человеческого тела». Золотое сечение имеет множество замечательных свойств, но ещё больше свойств вымышленных, следуя Леонардо да Винчи, многие люди «стремятся найти» золотое сечение во всём что между полутора и двумя.
В геометрии “золотым сечением” называется также деление отрезка в среднем и крайнем отношениях, при котором длина большего отрезка есть среднее геометрическое, или, как часто говорят, среднее пропорциональное длин всего отрезка и его меньшей части. “Золотое сечение” отрезка можно определить, достроив его до прямоугольного треугольника, в котором данный отрезок будет гипотенузой. Доказательство можно провести с помощью теоремы Пифагора. Эта задача очень древняя, она присутствует в “Началах” Евклида, который решил ее геометрически.
Замечательный пример “золотого сечения” представляет собой правильный пятиугольник – выпуклый и звездчатый, который называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и опознавательным знаком.
Отношение частей его диагоналей, названное золотым сечением, и приближенно равное 0,6, а более точно 0,618, считалось идеальным. Пентаграмма была хорошо известна в Древнем Египте. Но непосредственно как эмблема здоровья она была принята в Древней Греции. Существует гипотеза, что пентаграмма – первичное понятие, а “золотое сечение” вторично. Пентаграмму никто не изобретал, ее лишь скопировали с натуры. Красоту этой фигуры можно обосновать с помощью математики.
Золотое сечение отрезка AB можно построить следующим образом: в точке B восстанавливается перпендикуляр к AB, откладывают на нём отрезок BC, равный половине AB, на отрезке AC откладывают отрезок CD, равный CB, и наконец, на отрезке AB откладывают отрезок AE, равный AD.
Принято считать, что объекты, содержащие в себе «золотое сечение», воспринимаются людьми как наиболее гармоничные. Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона якобы свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании. Архитектор Ле Корбюзье «нашёл», что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого сечения. Зодчий Хесира, изображённый на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого сечения. В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления, и т. д. и т. п.
Ко всем этим утверждениям следует относиться с осторожностью, поскольку во многих случаях это может оказаться результатом подгонки или совпадения.
«Золотое сечение» в архитектуре.
«Архитектура – главнейшие имеет три предмета: красоту, спокойность и прочность здания... К достижению сего служит руководством знание пропорции, перспектива, механика или вообще физика, а всем им общим вождем является рассудок». В. Баженов
Профессия архитектора вовсе не чужда точных дисциплин. По своей сути архитектура стоит на грани искусства и техники. Без первого - архитектура превращается в ремесленничество, без второго - в бесплотные абстракции, которые невозможно реализовать. Не случайно один из создателей теории архитектуры Витрувий Поллион заложил в ее основу три основных принципа - польза, прочность и красота. Тесная связь архитектуры и математики известна давно. В одной из колыбелей современной цивилизации - Древней Греции - геометрия считалась одним из разделов архитектуры. Не исчезла связь архитектуры с математикой и в дальнейшем, чему можно привести множество примеров. "Золотым сечением" - соотношением, определяющим оптимальные с точки зрения зрительного восприятия пропорции архитектурного сооружения.
Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.). Он по праву считается одним из величайших образцов античного зодчества, шедевром мирового искусства и пластики. Здание соединяет в себе гармоничность и точность золотого сечения.
Другим примером из архитектуры древности является Пантеон. Пантеон представляет собой огромную круглую постройку с величественным куполом. С точки зрения архитектурных решений Пантеон является единственным в мире монументальным сооружением, в котором естественно и гармонично сочетается величественность с изящностью линий.
«Золотое сечение» в природе.
Пропорциональность в природе, означает соблюдение соотношений между размерами отдельных частей растения, и является непременным условием правильного и красивого изображения.
Рассматривая расположение листьев на общем стебле растений, можно заметить, что между каждыми двумя из листьев третье расположено в месте золотого сечения. Это исследовали на традесканции и разновидностях плюща.
Расположение листьев на деревьях не случайно, а подчиняется определенным математическим законам. Если рассмотреть веточку с листьями, то можно заметить, что основания черешков располагаются по винтовой линии, каждый следующий лист прикреплен выше и в сторону от предыдущего. Если соединить последовательно основания листьев ниткой, то она обовьется вокруг стебля по правильной винтовой линии. Проследив за расположением листьев по этой спирали, можно заметить, что листья расположены одни над другими. Часть спирали, заключенная между двумя такими листьями, называется в ботанике “циклом”. Листорасположение обозначают в виде дроби, в числителе которой число оборотов одного цикла спирали, а в знаменателе – число листьев в одном цикле. Наиболее распространенные типы листорасположений: ?, 1/3, 2/5, 3/8,5/13 и т.д.
Ботаники давно заметили, что этот ряд отличается одной любопытной и довольно неожиданной особенностью: каждая из этих дробей, начиная с третьей, получается из предыдущих путем сложения их числителей и знаменателей. Числители и знаменатели дают ряд Фибоначчи: 1, 2, 3, 5, 8… и 2, 3, 5, 8, 13…. Все эти дроби дают точные приближения к числу 0,62,числу Золотого сечения.
«Золотое сечение» и человек
"Необходимо прекрасному зданию быть построенным подобно хорошо сложенному человеку"
(Павел Флоренский)
Знаменитый зодчий Ле Корбюзье нашел золотое сечение во многих пропорциях человеческой фигуры. Если высоту хорошо сложенной фигуры разделить в крайнем и среднем отношении, то линия раздела окажется на высоте талии. Особенно хорошо удовлетворяет этой пропорции мужская фигура, и художники давно знают, что вопреки общему мнению, мужчины сложены красивее, чем женщины.
Каждую отдельно взятую часть тела (голову, руку, кисть) также можно разделить на естественные части по закону золотого сечения.
Рука, например, при рассмотрении согласно принципу золотого деления распадется на “свои анатомические части – плечо, предплечье, кисть. Разделение кисти руки также отвечает этому принципу.
Правильно! И, когда человек узнал, что его тело делится в таком отношении, он назвал это отношение “божественным”, а Леонардо да Винчи назвал его золотым, в смысле “идеальным”. Золотое сечение дано человеку самой природой в пропорциях своего тела, поэтому золотое сечение стало для человека эталоном красоты.
«Золотое сечение» в живописи..
Еще в эпоху Возрождения художники открыли, что любая картина имеет определенные точки, невольно приковывающие наше внимание, так называемые зрительные центры. При этом абсолютно неважно, какой формат имеет картина - горизонтальный или вертикальный. Таких точек всего четыре, и расположены они на расстоянии 3/8 и 5/8 от соответствующих краев плоскости.
Данное открытие у художников того времени получило название "золотое сечение" картины. Поэтому, для того чтобы привлечь внимание к главному элементу фотографии, необходимо совместить этот элемент с одним из зрительных центров.
Переходя к примерам «золотого сечения» в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды».
Он снискал славу непревзойденного художника, великого ученого, гения, предвосхитившего многие изобретения, которые не были осуществлены вплоть доXXв.Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника. Существует очень много версий об истории этого портрета.
Начиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения».
Размеры холста для картин художники нередко выбирали в соответствии с этой пропорцией.
Проверьте это! Ярко освещенная солнцем сосна, стоящая на переднем плане, делит длину картины по горизонтали в золотом отношении.
Справа от сосны, освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по вертикали. Так же можно найти мотивы золотого сечения и в других частях картины. Наличие в картине ярких деталей, делящих ее по золотому сечению, придает картине уравновешенность, чувство спокойствия и гармонии.
Картины великих художников, вызывающие непонятную, притягательную силу, запоминающиеся, написаны с применением золотого сечения. Чтобы создать шедевр, даже в искусстве необходима математика!
«Золотое сечение» в скульптуре.
Скульптурные сооружения, памятники воздвигаются, чтобы увековечить знаменательные события, сохранить в памяти потомков имена прославленных людей, их подвиги и деяния.
Известно, что еще в древности основу скульптуры составляла теория пропорций. Отношения частей человеческого тела связывались с формулой золотого сечения.
Пропорции «золотого сечения» создают впечатление гармонии красоты, поэтому скульпторы использовали их в своих произведениях.
Скульпторы утверждают, что талия делит совершенное человеческое тело в отношении «золотого сечения». Так, например, знаменитая статуя Аполлона Бельведерского состоит из частей, делящихся по золотым отношениям.
Великий древнегреческий скульптор Фидий часто использовал «золотое сечение» в своих произведениях. Самыми знаменитыми из них были статуя Зевса Олимпийского (которая считалась одним из чудес света) и Афины Парфенос.
«Золотое сечение» и кинематограф..
Так, известно, что Сергей Эйзенштейн искусственно построил фильм Броненосец Потёмкин по правилам «золотого сечения». Он разбил ленту на пять частей. В первых трёх действие разворачивается на корабле. В двух последних — в Одессе, где разворачивается восстание. Этот переход в город происходит точно в точке золотого сечения. Да и в каждой части есть свой перелом, происходящий по закону золотого сечения[источник?]. В кадре, сцене, эпизоде происходит некий скачок в развитии темы: сюжета, настроения. Эйзенштейн считал, что так как такой переход близок к точке золотого сечения, он воспринимается как наиболее закономерный и естественный.
Заключение.
Можно ли “поверить алгеброй гармонию”? “Да”, – считал Леонардо и указал, как это сделать. “Золотое сечение” – не середина, а пропорция – несложное математическое соотношение, содержащее в себе “закон звезды и формулу цветка”, рисунок на хитиновом покрове животных, длину ветвей дерева, пропорции человеческого тела. Видишь гармоничную композицию, пропорциональное телосложение или здание, радующее глаз, – измерь и придешь к одной и той же формуле.
Психологи утверждают, что человек, живущий в комнате, имеющей форму золотого прямоугольника, более спокойный, уравновешенный.
И лист бумаги, и почтовая открытка, и карманный календарь, и проездной билет, даже шоколадка, являются золотым прямоугольником. А золотое сечение встречается в жизни в самых неожиданных местах. Это и окрас шкуры некоторых животных, и размер ящерицы, и даже куриное яйцо, присутствует в паутине, в раковине улитке, в расположении семян подсолнуха, и даже в нашей галактике!
Литература.
nsportal.ru
Муниципальное Общеобразовательное учреждение
Средняя Общеобразовательная школа №6
Реферат по геометрии
Тема: «Золотое сечение пропорции»
Ученик:
Вахромеев Андрей
Учитель:
Трошина Людмила Ивановна
2011 год
План работы:
1. Введение
2.История золотого сечения.
3.Математическая сущность золотого сечения.
4.Золотое сечение в совершенной науке.
5.Заключение.
6.Список литературы.
Введение
«Геометрия обладает двумя великими
сокровищами. Первое — это теорема Пифагора,
второе — деления отрезка в крайнем и среднем
отношении»
Иоганн Кеплер
Вопрос о математических предпосылках прекрасного, о роли математики в искусстве волновал еще древних греков, причем свой интерес они унаследовали от предшествующих цивилизаций.
Воплощение математических законов просматривается в загадочном величии египетских пирамид. Пространственные формы пирамид настолько правильны, и геометричны, что они вот уже пятое тысячелетие видятся скорее не плодом вдохновенного порыва художника, а результатом скрупулезных построений древнеегипетского математика.
Другим интересным проявлением поисков математических закономерностей в области ваяния и зодчества является существование в древности так называемых канонов, т. е. совокупности правил изображения человеческой фигуры. Создателем первого канона считается древнеегипетский архитектор и скульптор Имхотеп (28 в. до н. э.), а Древняя Греция подарила миру великого ваятеля и теоретика искусства Поликлета (V в. до н.э.)
А вот систематическое приложение к искусству математика нашла, конечно, в музыке, в трудах древнегреческого математика Пифагора, его многочисленных учеников и последователей..
«Числа правят миром» — знаменитый пифагорейский лозунг.
В основе объективных законов красоты лежат два фундаментальных принципа: качественный принцип гармонии и количественный принцип симметрии. Оба принципа – гармонии и симметрии – воплощают в природе и искусстве идею порядка.
Под гармонией понимается наиболее оптимальное сочетание противоречивых сторон в едином целом. В состоянии гармонии заложена изначальная противоречивость мира. Многочисленные исследования показывают, что состояние гармонии достигается, когда соотношение порядка в поведении элементов системы и хаоса (непредсказуемого, свободы выбора) тяготеет к «Золотой» пропорции (=0,618).
Поэтому моя работа посвящена теме «Золотая пропорция».
Цель работы:
Как из чисто геометрического понятия, Золотая Пропорция превращается в фундаментальное понятие, что она не только то, что можно видеть глазами, что Золотая Пропорция – вокруг нас, что, более того, она — в основе всего.
Если законы природы управляют явлениями, то Золотая пропорция управляет законами природы, и как мера гармонии – тождества противоположностей – лежит в основе метода аналогий (отыскание общих свойств в различных объектах, явлениях и распространение этой общности на другие свойства).
Задачи:
1.Узнать, что такое Золотое сечение.
2.Отобразить Золотое сечение в аспектах деятельности человека.
3.Сделать вывод.
История золотого сечения
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамсеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.
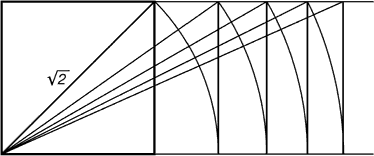
Греки же были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.
Динамические прямоугольники
Платон (427...347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.
Парфенон
Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по «золотому сечению», то получим те или иные выступы фасада.
При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.
В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др… В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.
В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением, как в геометрии, так и в искусстве, особенно в архитектуре. Леонардо да Винчи, художник и ученый, видел, что в итальянских художниках большой эмпирический опыт, но недостаток знаний. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем.
Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства: бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок — бога отца, а весь отрезок — бога духа святого).
Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.
В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет: «Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать».
Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица — ртом и т.д. Известен пропорциональный циркуль Дюрера.
Построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).
Если на прямой произвольной длины, отложить отрезок m(φ), рядом откладываем отрезок M. На основании этих двух отрезков выстраиваем шкалу отрезков золотой пропорции восходящего и нисходящего рядов
Построение шкалы отрезков золотой пропорции
В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы «вместе с водой выплеснули и ребенка». Вновь «открыто» золотое сечение было в середине XIX в. В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». С Цейзингом произошло именно то, что и должно было неминуемо произойти с исследователем, который рассматривает явление как таковое, без связи с другими явлениями. Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях «математической эстетикой».
Построение пропорции.
Здесь приводится построение точки Е, делящий отрезок прямой в пропорции золотое сечение.
Деление отрезка прямой по золотому сечению. BC = 1/2 AB ; CD = BC
Из точки В восстанавливается перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D . Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.
Именно эти отрезки использовал Евклид при построении правильного пятиугольника, т.к. каждая из сторон пятиугольной звезды делится другими именно в такой пропорции.
Таким образом, звездчатый пятиугольник также обладает «золотым сечением». Интересно, что внутри пятиугольника можно продолжить строить пятиугольники, и это отношение будет сохраняться.
Звездчатый пятиугольник называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком.
В настоящее время существует гипотеза, что пентаграмма – первичное понятие, а «золотое сечение» вторично. Пентаграмму никто не изобретал, ее только скопировали с натуры. Вид пятиконечной звезды имеют пяти-лепестковые цветы плодовых деревьев и кустарников, морские звезды. Те и другие создания природы человек наблюдает уже тысячи лет. Поэтому естественно предположить, что геометрический образ этих объектов – пентаграмма – стала известна раньше, чем «золотая» пропорция.
Математическая сущность
Золотой прямоугольник:
Если построить квадрат со стороной АВ=а, найти середину М отрезка АВ и провести дугу окружности радиусом МС с центром в точке М до пересечения с продолжением стороны АВ в точке Е, то точка В разделит отрезок АЕ в крайнем и среднем отношении.
Чтобы убедиться в этом, заметим, что по теореме Пифагора
МС2 =а2 +(а/2)2=5а2 /4
В силу чего
АЕ=а/2 +МЕ=(√5+1)а/2= φ АВ
Прямоугольник АЕ FD со сторонами АЕ= φ А D называется золотым прямоугольником. Четырехугольник АВС D — квадрат. Нетрудно видеть, что прямоугольник ВЕ F С также золотой, поскольку BC = a = φ ВЕ. Это обстоятельство сразу наводит на мысль о дальнейшем разбиении прямоугольника ВЕ F С .
Можно ли считать, что прямоугольник с отношением сторон, равным φ, выглядит изящнее, чем прямоугольники с отношением сторон, скажем, 2:1, 3:2 или 5:7? Чтобы ответить на этот вопрос, были проведены специальные эксперименты. Результаты их не вполне убедительны, но все же свидетельствуют о некотором предпочтении, отдаваемом золотому сечению. Впрочем, может ли прямоугольник сам по себе быть захватывающе прекрасным или отталкивающе безобразным?
Золотой треугольник:
Проводим прямую АВ. От точки А откладываем на ней три раза отрезок О произвольной величины, через полученную точку Р проводим перпендикуляр к линии АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1 откладываем на линию Ad1, получая точку С. Она разделила линию Ad1 в пропорции золотого сечения. Линиями Ad1 и dd1 пользуются для построения «золотого» прямоугольника.
Золотой пятиугольник; построение Евклида.
Замечательный пример «золотого сечения» представляет собой правильный пятиугольник – выпуклый и звездчатый .
Построение правильного пятиугольника и пентаграммы.
Для построения пентаграммы необходимо построить правильный пятиугольник.
Пусть О — центр окружности, А — точка на окружности и Е — середина отрезка ОА. Перпендикуляр к радиусу ОА, восстановленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.
Есть и золотой кубоид- это прямоугольный параллелепипед с ребрами, имеющими длины 1.618, 1 и 0.618.
Теперь рассмотрим доказательство, предложенное Евклидом в «Началах».
Посмотрим теперь, как Евклид использует золотое сечение для того, чтобы построить угол в 72 градуса – именно под таким углом видна сторона правильного пятиугольника
из центра описанной окружности. Начнем с отрезка АВЕ, разделенного в среднем и крайнем отношении точкой В. Проведем далее дуги окружностей с центрами в точках В и Е и радиусах АВ, пересекающиеся в точке С. Чуть ниже докажем, что АС=АЕ, а пока примем это на веру.
Итак, пусть АС=АЕ. Обозначим через a равные углы ЕВС и СЕВ. Так как АС=АЕ, то угол АСЕ также равен a. Теорема о том, что сумма углов треугольника равна 180 градусов, позволяет найти угол ВСЕ: он равен 180-2a, а угол ЕАС — 3a — 180. Но тогда угол АВС равен 180-a. Суммируя углы треугольника АВС получаем,
180=(3a -180) + (3a-180) + (180 — a)
Откуда 5a=360, значит a=72.
Итак, каждый из углов при основании треугольника ВЕС вдвое больше угла при вершине, равного 36 градусов. Следовательно, чтобы построить правильный пятиугольник, необходимо лишь провести любую окружность с центром в точке Е, пересекающую ЕС в точке Х и сторону ЕВ в точке Y: отрезок XY служит одной из сторон вписанного в окружность правильного пятиугольника; Обойдя вокруг всей окружности, можно найти и все остальные стороны.
Докажем теперь, что АС=АЕ. Предположим, что вершина С соединена отрезком прямой с серединой N отрезка ВЕ. Заметим, что поскольку СВ=СЕ, то угол СNЕ прямой. По теореме Пифагора:
CN2 = а2 – (а/2j) 2= а2 (1-4j 2)
Отсюда имеем (АС/а) 2 = (1+1/2j) 2 + (1-1/4j 2) = 2+1/j = 1 + j =j 2
Итак, АС = jа = jАВ = АЕ, что и требовалось доказать
Золотое сечение в совершенной науке
Золотое сечение в живописи.
Переходя к примерам «золотого сечения» в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды».
Нет сомнений, что Леонардо да Винчи был великим художником, это признавали уже его современники, но его личность и деятельность останутся покрытыми тайной, так как он оставил потомкам не связное изложение своих идей, а лишь многочисленные рукописные наброски, заметки, в которых говорится «обо всем на свете».
Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника..
Также пропорция золотого сечения проявляется в картине Шишкина. На этой знаменитой картине И. И. Шишкина с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны — освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали.
В картине Рафаэля «Избиение младенцев» просматривается другой элемент золотой пропорции — золотая спираль. На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции — точки, где пальцы воина сомкнулись вокруг лодыжки ребенка — вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Неизвестно, строил ли Рафаэль золотую спираль или чувствовал её.
Т.Кук использовал при анализе картины Сандро Боттичелли «рождение Венеры» золотое сечение.
Джоконда построена на золотых треугольниках, золотая спираль присутствует на картине Рафаэля «Избиение младенцев».
Пропорция обнаружена в картине Сандро Боттичелли «Рождение Венеры»
Загадки египетских пирамид.
Все на свете страшится времени
А время страшится пирамид.
Арабская пословица
О египетских пирамидах с восхищением писал греческий историк Геродот. Первым европейцем, спустившимся в глубь пирамиды, был римский ученый Плиний Старший. Согласно многим описаниям, эти гигантские монолиты имели совсем иной вид, чем в наше время. Они сияли на солнце белой глазурью отполированных известняковых плит на фоне многоколонных прилегающих храмов. Рядом с царскими пирамидами стояли малые пирамиды жен и членов семьи фараонов.
Среди грандиозных пирамид Египта особое место занимает великая пирамида фараона Хеопса. Она самая крупная и наиболее хорошо изученная. Чего только не находили в ее пропорциях! Число «пи» и золотую пропорцию, число дней в году, расстояние до Солнца, диаметр Земли и т.п. Однако при расчете этих величин получались неточности, возникали недоразумения, в результате чего подвергались сомнению даже простейшие пропорции в размерах пирамиды и все сообщения о скрытых в геометрии пирамиды математических сведениях объявлялись выдумкой.
Правильная четырехгранная пирамида является одной из хорошо изученных геометрических фигур, символизирующих простоту и гармонию формы, олицетворяющую устойчивость, надежность, устремление вверх.
Очевидно, размеры пирамиды: площадь ее основания и высота — не были выбраны случайно, а должны нести какие-то геометрические, математические идеи, информацию об уровне знаний египетских жрецов. Причем следует напомнить, что эти знания составляли тайну и были доступны лишь ограниченному числу лиц, поэтому и в геометрии пирамиды они должны быть воплощены не в явной, а в скрытой форме.
Методической ошибкой многих исследователей является то, что они использовали размеры пирамид, выраженные в метрической системе мер. Но ведь египтяне пользовались другой системой мер! Из этой системы и следует исходить при анализе размерных отношений в пирамидах.
Прежде чем приступить к анализу формы и размеров пирамиды Хеопса, следует учесть уровень знаний тех времен, психологию создателей пирамиды. У египтян было три единицы длины: локоть (466 мм), равнявшийся семи ладоням (66,5 мм), которая, в свою очередь, равнялась четырем пальцам (16,6 мм).
Трудно допустить, что строители пирамиды пользовались исходными размерами, выраженными в долях локтя; более очевидно, что основные исходные размеры были определены в целых единицах длины – локтях.
Рассмотрим размеры пирамиды Хеопса.
Длина стороны основания пирамиды (L) принята равной 233,16 м. Эта величина отвечает почти точно 500 локтям. Очевидно, размер основания пирамиды при ее строительстве и был определен в 500 локтей.
Высота пирамиды (H) оценивается исследователями различно от 146,6 до 148,2 м. И в зависимости от принятой высоты пирамиды изменяются и все отношения ее геометрических элементов. Поэтому на этой величине следует остановиться особо. Одним из чудес великой пирамиды является очень точная подгонка ее каменных блоков и плит; между ними буквально нигде не просунешь лезвия бритвы (0,1 мм). Но никакого чуда здесь не оказалось. В процессе строительства каменные блоки не могли быть изготовлены столь точно: для этого у древних египтян просто не было средств – ни обрабатывающих, ни измерительных. Но за длительное время под воздействием колоссального давления (достигающего 500 тонн на 1 м2 нижней поверхности) произошла «усадка» конструкции, пластическая деформация строительных блоков, вследствие чего они и оказались так тесно подогнанными. В результате усадки высота пирамиды стала меньше, чем она была в период завершения строительства. Какой же она была первоначально? Ее можно воссоздать, если найти основную «геометрическую идею», положенную в основу сооружения.
Угол наклона граней пирамиды еще в 1837 году определил английский полковник Г.Вайз: он равен . Указанному значению угла отвечает тангенс, равный 1,272. Эта величина, отвечающая отношению высот пирамиды к половине ее основания, очень близка к корню квадратному из золотой пропорции = 1,27202 и является иррациональной величиной. Поэтому, скорее всего, в основу треугольника OMN пирамиды Хеопса и было заложено отношение OM/MN, равное .
Итак, примем отношение катетов, т.е. высоты пирамиды H к половине ее основания, равным 1,272. При этом высота пирамиды Хеопса будет равна точно 318 локтей, или 148,28 м. Такую высоту, очевидно, имела пирамида Хеопса при завершении ее сооружения ( или должна была иметь по проекту).
Таким образом, основные элементы конструкции пирамиды имели следующие размеры: сторона основания – 500 локтей, высота – 318 локтей. Отсюда следует, что апофема боковой грани ON равна 404,5 локтя.
А теперь посмотрим, какие интересные соотношения следуют из этих геометрических размеров. Отношения сторон в треугольнике OMN пирамиды равно: OM/MN=ON/OM=1,272=; ON/MN=Ф.
Рассмотрим теперь поверхность пирамиды. Она состоит из четырех треугольников и квадрата основания. Основание треугольника BOC равно 500 локтям, высота его равна 404,5 локтя. По теореме Пифагора можно рассчитать длину боковых ребер OB и OC. Они равны 475,5 локтя.
Площадь основания пирамиды равна 250000 кв. локтей, площадь боковой грани 101125 кв. локтей, а площадь четырех граней пирамиды равна 404500 кв. локтей. Отношение поверхности граней к площади основания также равно золотой пропорции.
Еще Геродот, основываясь на рассказах египетских жрецов, писал, что площадь квадрата, построенного на высоте пирамиды, равна площади каждой из его боковых граней. По нашим расчетам, квадрат высоты равен 3182 = 101127 кв. локтей, что почти точно отвечает площади боковой грани (101125 кв. локтей).
Многие исследователи указывают, что отношение удвоенной стороны основания 2L к высоте пирамиды H отвечает числу «пи». Однако в связи с тем, что высота пирамиды принималась равной современной и не всегда однозначной, число «пи» получалось разным: 3,16-3,18. На почве этого возникали сомнения, предпринимались различные подгонки, стали говорить даже о некоем «египетском p», равном 3,16. Если принять высоту пирамиды равной 318 локтям, то отношение 2L/H=1000/318 будет равно 3,144. Эта величина очень близка к современному значению числа «пи» (3,14159…).
Интересно сравнить два основных отношения, установленных нами при изучении геометрических пропорций пирамиды: 2H/L=и 2L/H=p. Отсюда получаем простую и красивую формулу, связывающую число «пи» и золотую пропорцию: 4/p=.
Гениальные создатели пирамиды Хеопса стремились поразить далеких потомков глубиной своих знаний, и они достигли этого. Следует лишь удивляться высокому знанию и искусству древних математиков и архитекторов Египта, которые смогли воплотить в пирамиде две иррациональные (т.е. неизмеримые) величины – p и Ф со столь поразительной точностью, оперируя исходными отношениями целых чисел – стороной основания и высотой пирамиды, выраженных в локтях.
Золотая пропорция в искусстве Древней Греции.
Великолепные памятники архитектуры оставили нам зодчие Древней Греции. И среди них первое место по праву принадлежит Парфенону.
Всю вторую половину V в. до н.э. на Акрополе шло строительство храмов, пропилей (преддверий), алтаря и статуи Афины Воительницы. В 447 году начались работы над храмом Афины – Парфеноном и продолжались до 434 года до н.э. Для создания гармонической композиции на холме его строители даже увеличили холм в южной части, соорудив для этого мощную насыпь.
Как указывает исследователь Г. И. Соколов, протяженность холма перед Парфеноном, длины храма Афины и участка Акрополя за Парфеноном относятся как отрезки золотой пропорции. При взгляде на Парфенон от места расположения пропилей отношения массива скалы и храма также соответствуют золотой пропорции. Таким образом, золотая пропорция была использована уже при создании композиции храмов на священном холме.
Размеры Парфенона хорошо изучены, но приводимые замеры не всегда однозначны. Следует учесть, о чем сказано ниже, что геометрия архитектуры храма очень непростая – в ней почти отсутствуют прямые линии, поэтому определение размеров затруднено. Известно, что фасад Парфенона вписан в прямоугольник со сторонами 1: 2, а план образует прямоугольник со сторонами 1 и . Известно, что диагональ прямоугольника 1:2 имеет размер , следовательно, прямоугольник фасада и является исходным в построении геометрии Парфенона.
Ширина Парфенона оценена в 100 греческих футов (3089 см), а размер высоты несколько варьирует у различных авторов. Так, по данным Н. Бруно, высота Парфенона 61,8, высота трех ступеней основания и колонны – 38,2, высота перекрытия и фронтона – 23,6 футов. Указанные размеры образуют ряд золотой пропорции: 100: 61,8 = 61,8: 38,2 = 38,2 :23,6 = Ф.
Многие исследователи, стремившиеся раскрыть секрет гармонии Парфенона, искали и находили в соотношениях его частей золотую пропорцию. В работе В.Смоляка, посвященной изучению пропорций Парфенона, установлен закономерный ряд золотых пропорций. Приняв за единицу ширину торцового фасада храма, Смоляк получил прогрессию, состоящую из 8 членов ряда: 1: j: j2: j3: j4: j5: j6. Указанным членам ряда отвечают основные пропорции фасада Парфенона (рис.8).
В некоторых сооружениях древнего мира золотая пропорция выражена не в пропорциях формы зданий, а в деталях внутренней композиции, даже в числе мест для зрителей. Интересные данные приводит Э.Сороко. Построенный Поликлетом-младшим театр был рассчитан на 15 тысяч зрителей. Места для зрителей (театроп) имели 2 яруса: первый- 34 ряда мест, а второй – 21 ряд (числа Фибоначчи). Раствор угла, охватывающего пространство между театропом и скемой (пристройка для переодевания актеров и хранения реквизита), делит окружность основания амфитеатра
в отношении : , что равно 1: 1,618…. Это соотношение углов реализовано практически во всех античных театрах. Театр Диониса в Афинах трехъярусный. Первый ярус имеет 13 секторов, второй – 21 сектор.
Древние скульпторы знали и использовали золотую пропорцию как критерий гармонии, канон красоты, корни которой лежат в пропорциях человеческого тела. “Человеческое тело – лучшая красота на земле”, — утверждал Н.Чернышевский. Эталонами красоты человеческого тела, образцами гармонического телосложения издавна и по праву считаются великие творения греческих скульпторов: Фидия, Поликлета, Мирона, Праксителя. В создании своих творений греческие мастера использовали принцип золотой пропорции. Центр золотой пропорции строения человеческого тела располагался точно на месте пупка. И не случайно величину золотой пропорции принято обозначать буквой Ф; это сделано в честь Фидия – творца бессмертных скульптурных произведений.
Одним из высших достижений классического греческого искусства может служить статуя “Дорифор”, изваянная Поликлетом. Фигура юноши выражает единство прекрасного и доблестного, лежащих в основе греческих принципов искусства. Широкие плечи почти равны высоте туловища, высота головы восемь раз укладывается в высоте тела, а золотой пропорции отвечает положение пупка на теле атлета.
Но проанализируем другие пропорции знаменитой статуи. Расстояние от подошвы копьеносца до его колена равна j3, высота шеи вместе с головой — j4, длина шеи до уха — j5, а расстояние от уха до макушки — j6 . Таким образом, в этой статуе мы видим геометрическую прогрессию со знаменателем j: 1, j, j2, j3, j4, j5, j6. (рис.9).
Таким образом, золотое сечение – один из основополагающих принципов в искусстве античной Греции.
Алгебра музыки.
В композиции многих музыкальных произведений отмечается наличие некоторого «кульминационного взлета», высшей точки, причем такое построение характерно не только для произведения в целом, но и для его отдельных частей. Такая высшая точка крайне редко расположена в центре произведения или его композиционной части, обычно она смещена, асимметрична. Изучая восьмитактные мелодии Бетховена, Шопена, Скрябина, советский музыковед Л.Мазель установил, что во многих из них вершина, или высшая точка, приходится на сильную долю шестого такта или на последнюю мелкую долю пятого такта, т.е. находится в точке золотого сечения. По мнению Л.Мазеля, число подобных восьмитактов, где подъем мелодии занимает пять тактов, а последующий спуск – три, необычайно велико. Их можно без труда найти почти у каждого автора, сочинявшего музыку в гармоническом стиле.
Очевидно, такое расположение кульминационных моментов музыкальной мелодии является важным элементом ее гармонической композиции, придающим художественную выразительность и эстетическую эмоциональность мелодии.
Характерно, что в некоторых случаях авторы музыкальных произведений смещали их вершину от точки золотого сечения, что придавало мелодиям неустойчивый характер. По мнению Л.Мазеля, это входило в намерения авторов, например, при сочинении скерцо, рондообразных финалов.
Наиболее обширное исследование проявлений золотого сечения в музыке было предпринято Л.Сабанеевым. Им было изучено две тысячи произведений различных композиторов. По его мнению, временное протяжение музыкального произведения делится «некоторыми вехами», которые выделяются при восприятии музыки и облегчают созерцание формы целого. Все эти музыкальные вехи делят целое на части, как правило, по закону золотого сечения.
По наблюдениям Л.Сабанеева, в музыкальных произведениях различных композиторов обычно констатируется не одно золотое сечение, а целая серия подобных сечений. Каждое такое сечение отражает свое музыкальное событие, качественный скачок в развитии музыкальной темы. В изученных им 1770 сочинениях 42 композиторов наблюдалось 3275 золотых сечений. Количество произведений, в которых наблюдалось хотя бы одно золотое сечение, составило 1338. Наибольшее количество музыкальных произведений, в которых имеется золотое сечение, у Аренского (95%), Бетховена (97%), Гайдна (97%), Моцарта (91%), Скрябина (90%), Шопена (92%), Шуберта (91%).
Наиболее детально были изучены все 27 этюдов Шопена. В них обнаружено 154 золотых сечения; всего в трех этюдах золотое сечение отсутствовало. В некоторых случаях строение музыкального произведения сочетало в себе симметричность и золотое сечение одновременно; в этих случаях оно делилось на несколько симметричных частей, в каждой из которых проявляется золотое сечение. У Бетховена также сочинения делятся на две симметричные части, а внутри каждой из них наблюдаются проявления золотой пропорции.
Характерно, что наиболее часто золотое сечение обнаруживается в произведениях высокохудожественных, принадлежащих гениальным авторам. Может быть, частота проявлений золотой пропорции является одним из объективных критериев оценки гениальности музыкальных произведений и их авторов?
Итак, можно признать, что золотая пропорция является критерием гармонии композиции музыкального произведения.
Музыка стихов.
Многое в структуре произведений поэзии роднит этот вид искусства с музыкой. Каждый стих обладает своей музыкальной формой – своей ритмикой и мелодией. Можно ожидать, что в строении стихотворений проявятся некоторые черты музыкальных композиций, закономерности музыкальной гармонии, а следовательно, и золотая пропорция, и числа Фибоначчи.
Исследования поэтических произведений с этих позиций только начинаются. И начинать нужно с поэзии А.С.Пушкина. Ведь его произведения — образец наиболее выдающихся творений русской культуры, образец высочайшего уровня гармонии. С поэзии А.С.Пушкина мы и начнем поиски золотой пропорции – мерила гармонии и красоты.
Для анализа метрики стихотворений А.С.Пушкина рассмотрены его произведения периода 1829-1836 г.г., периода создания наиболее совершенных стихов. Сюда вошло 109 стихов. Число строк в стихотворениях этого периода изменялось от 4 до 116. Однако большие стихотворные формы встречаются редко; число стихотворений с количеством строк более 60 составило всего 9 штук. Средний размер этих стихотворений составил 88 строк.
Казалось бы, величина стихотворения, определяемая числом строк, может изменяться произвольно и непрерывно от самой малой в четыре строки до самых больших. Однако оказалось, что это не так. Размеры стихов распределены совсем не равномерно; выделяются предпочтительные и редко встречающиеся размеры. На графике распределения стихотворений А.С.Пушкина по числу строк в них отчетливо выделяется несколько максимумов — наиболее встречающихся размеров (рис.10). Они явно тяготеют к числам 5, 8, 13, 21, 34. Проявляется вполне закономерная тенденция в творческой манере поэта – он явно предпочитает стихотворения, размер которых близок к числам ряда Фибоначчи.
Только ли стихотворения А.С. Пушкина тяготеют в своих размерах к числам Фибоначчи?
Конечно, нет. И у других поэтов проявляется тяготение размера стихов к 8,13,21 строчкам, но ни у одного из русских поэтов эта тенденция не выражена так отчетливо, как у А.С.Пушкина. Стихотворения В.Брюсова отличаются совершенством своих форм. И неудивительно, что в их размерности также проявляются числа Фибоначчи. Было проанализировано 360 стихотворений поэта из его двухтомника; эти стихи охватывали период от 1882 до 1912 года. Только в трех стихотворениях число строк составило 70, 85, 90 (что в среднем близко к числу Фибоначчи 89). Остальные стихотворения содержали значительно меньше строк – от 8 до 36 и крайне редко несколько больше.
Среди рассмотренных стихотворений В.Брюсова явно преобладают те, в которых число строчек равно или близко к числам Фибоначчи. Они распределены следующим образом:
стихотворения с числом строк 8 25 шт. 7%
стихотворения с числом строк 131 77 шт. 21,5%
стихотворения с числом строк 211 70 шт. 19,6% стихотворения с числом строк 342 36 шт. 10,0%
Общее число этих стихотворений составило 208 шт. или 58%. К остальным относятся стихотворения с числом строчек 10, 14, 16, 18, 24, 26, 28, 31, 32 и т.д. Поэт явно предпочитал стихотворения с числом строк 8, 131, 211 как наиболее оптимальные для выражения мыслей и чувств.
Обратимся вновь к произведениям А.С.Пушкина. Рассмотрим композицию «Пиковой дамы». В этой повести кульминационным моментом является сцена в спальне графини, куда проник Германн в надежде узнать тайну трех карт, сцена, которая оканчивается смертью графини в повести 853 строки. Кульминационный момент повести – это смерть графини. Ему отвечает 535 –я строка. Эта строка расположена в повести почти точно в месте золотого сечения, т.к. 853:535=1,6 .
Повесть «Пиковая дама» состоит из шести глав. Посмотрим, не проявляется ли в композиции глав золотая пропорция? В первой главе золотому сечению отвечает 68 строчка (всего в главе 110 строк). Но ведь это же узловая точка повествования, в ней переломный момент всей главы: откроет ли Сен — Жермен свою тайну графине!
Вторая глава повести содержит 219 строк. Золотое сечение здесь приходится на 135 строку. Но ведь это кульминационный момент главы, Лиза увидела в окне стоящего на улице Германа! Отсюда начался для нее новый отсчет времени, начались события, определившие всю ее дальнейшую судьбу. А.С.Пушкин совершенно точно определил это место во второй главе: ведь 219:135 = 1,62.
Третья глава повести описывает усилия Германа попасть в дом старой графини, выведать у нее тайну трех карт. Это место начинает новый отсчет времени для Германа. Эта ситуация приходится на 131 строку третьей главы, а всего в ней 212 строк. Разделив 212 на 131, мы получим точно золотую пропорцию 1,618!
В четвертой главе размером 113 строк золотая пропорция приходится на 70 строку. Это также переломный, трагический момент в жизни Лизы.
В пятой главе описано посещение Германа похорон графини. 46 строка пятой главы разделила повествование на две части: первая — похороны графини и вторая – сон Германа. Эта 46 строка также отвечает золотой пропорции, ведь всего в этой главе 75 строк (75:46=1,63).
В последней главе повести золотая пропорция приходится на 77 строчку, которая завершает описание первого дня игры Германа в карты и первого его выигрыша. Как видим, и в композиции последней главы повести присутствует золотая пропорция.
Золотая пропорция присутствует и в композиции других произведений Пушкина. В рассказе «Станционный смотритель» 377 строк. Кульминационный момент рассказа – это известие о том, что дочь смотрителя уехала с гусаром. Этот момент отражен во фразе, которая является 214 строкой. Здесь почти точное соответствие золотой пропорции.
В маленьком рассказе «Гробовщик» всего 229 строк. Со 139 строки начинается описание страшного сна гробовщика. И здесь переломный момент рассказа приходится почти точно на золотую пропорцию (229:1,618=141 строка).
Совпадение кульминационных моментов в произведениях А.С.Пушкина с золотой пропорцией удивительно близкое, в пределах 1-3 строк. Чувство гармонии у него было развито необыкновенно, что объективно подтверждает гениальность великого поэта и писателя.
Заключение:
Красота природных форм рождается во взаимодействии двух физических сил – тяготения и инерции. «Золотая пропорция» — символ этого взаимодействия, поскольку диктуемое ею отношение большей части целого к самому целому выражает основные моменты живого роста: стремительный взлет легкого юного побега до зрелости и замедленный рост « по инерции» до момента цветения, когда достигшее полной силы растение готовится дать жизнь новому побегу.
Человеческие представления о красивом формируются явно под влиянием того, какие воплощения порядка и гармонии человек видит в живой природе. А природа, как известно, любит повторения. В различных своих творениях, казалось бы очень далеких друг от друга, она может использовать одни и те же принципы.
«Золотое сечение» — один из основополагающих принципов природы.
Литература:
1. Д. Пидоу. Геометрия и искусство. – М.: Мир, 1979.
2. Журнал «Наука и техника»
3. Журнал «Квант», 1973, № 8.
4. Журнал «Математика в школе», 1994, № 2; № 3.
5. Ковалев Ф.В. Золотое сечение в живописи. К.: Выща школа, 1989.
6. Стахов А. Коды золотой пропорции.
7. «Математика. Я познаю мир». – М.: Аванта + 1998
8. «Математика — Энциклопедия для детей» М.: Аванта +, 1998
9. Мурутаев. «Вопросы философии» 1994г. №6 стр. 71 (О гармонии мира).
10. Информация из интернета: www.yandex.ru & www.km.ru
www.ronl.ru
Реферат выполнила ученица 8 класса МОУ гимназия №9 Вьюшина Вероника
Екатеринбург
2002
1. Введение. Пропорция золотого сечения. Ф и φ.
"Геометрия обладает двумя великими сокровищами. Первое - это теорема Пифагора, второе - деления отрезка в крайнем и среднем отношении"
Иоганн Кеплер
Правильные многоугольники привлекали внимание древнегреческих учёных ещё задолго да Архимеда. Пифагорейцы, выбравшие эмблемой своего союза пентаграмму - пятиконечную звезду, придавали очень большое значение задаче о делении окружности на равные части, то есть о построении правильного вписанного многоугольника. Альбрехт Дюрер (1471-1527гг), ставший олицетворением Возрождения в Германии приводит теоретически точный способ построения правильного пятиугольника, заимствованный из великого сочинения Птолемея "Альмагест".
Интерес Дюрера к построению правильных многоугольников отражает использование их в Средние века в арабских и готических орнаментах, а после изобретения огнестрельного оружия - в планировке крепостей.
Средневековые способы построения правильных многоугольников носили приближенный характер, но были (или не могли не быть) простыми: предпочтение отдавалось способам построения, не требующим даже изменять раствор циркуля. Леонардо да Винчи также много писал о многоугольниках, но именно Дюрер, а не Леонардо, передал средневековые способы построения потомкам. Дюрер, конечно, был знаком с " Началами" Евклида, но не привел в своем "Руководстве к измерению" (о построениях при помощи циркуля и линейки) предложенный Евклидом способ построения правильного пятиугольника, теоретически точный, как и все евклидовы построения. Евклид не пытается разделить заданную дугу окружности на три равные части, и Дюрер знал, хотя доказательство было найдено лишь в XIX веке, что эта задача неразрешима.
Предложенное Евклидом построение правильного пятиугольника включает в себя деление отрезка прямой в среднем и крайнем отношении, названное впоследствии золотым сечением и привлекавшим к себе внимание художников и архитекторов на протяжении нескольких столетий.
Точка В делит отрезок АВЕ в среднем и крайнем отношении или образует золотое сечение, если отношение большей части отрезка к меньшей равно отношению всего отрезка к большей части.
Записанное в виде равенства отношений золотое сечение имеет вид
АВ/ВЕ= АВ/АЕ
Если положить АВ=а, а ВЕ=а/Ф так, чтобы золотое отношение было равно АВ/ВЕ=Ф, то получается соотношение
Ф = 1+1/Ф
То есть Ф удовлетворяет уравнению
Ф2- Ф-1=0
Это уравнение имеет один положительный корень
Ф=(√5+1)/2=1.618034….
Заметим, что 1/Ф = (√5 -1 )/2, так как (√5-1)(√5+1) =5-1=4. За 1/Ф принято считать φ=0.618034….
Ф и φ - прописная и строчная формы греческой буквы "фи".
Такое обозначение принято в честь древнегреческого скульптора Фидия (V век до н. э.) Фидий руководил строительством храма Парфенон в Афинах. В пропорциях этого храма многократно присутствует число φ .
2.История золотого сечения
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамсеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

 |
Платон (427...347гг. до н.э.) также знал о золотом делении. Его диалог "Тимей" посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.

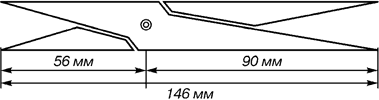
Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по «золотому сечению», то получим те или иные выступы фасада. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.
 |

В дошедшей до нас античной литературе золотое деление впервые упоминается в "Началах" Евклида. Во 2-й книге "Начал" дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др.. В средневековой Европе с золотым делением познакомились по арабским переводам "Начал" Евклида. Переводчик Дж.Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.
В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением, как в геометрии, так и в искусстве, особенно в архитектуре. Леонардо да Винчи, художник и ученый, видел, что в итальянских художниках большой эмпирический опыт, но недостаток знаний. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем.
Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509г. в Венеции была издана книга Луки Пачоли "Божественная пропорция" с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее "божественную суть" как выражение божественного триединства: бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок - бога отца, а весь отрезок - бога духа святого).
Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.
В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет: "Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать".
Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица - ртом и т.д. Известен пропорциональный циркуль Дюрера.
Построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).
Если на прямой произвольной длины, отложить отрезок m(φ), рядом откладываем отрезок M. На основании этих двух отрезков выстраиваем шкалу отрезков золотой пропорции восходящего и нисходящего рядов
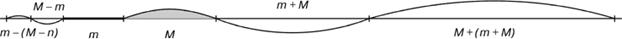

В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы "вместе с водой выплеснули и ребенка". Вновь "открыто" золотое сечение было в середине XIX в. В 1855г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд "Эстетические исследования". С Цейзингом произошло именно то, что и должно было неминуемо произойти с исследователем, который рассматривает явление как таковое, без связи с другими явлениями. Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях "математической эстетикой".
3. Построение пропорции.
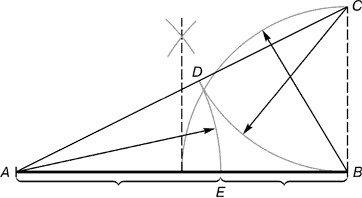 |
| Рис. 1. Деление отрезка прямой по золотому сечению. BC = 1/2 AB; CD = BC |
Из точки В восстанавливается перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.
Именно эти отрезки использовал Евклид при построении правильного пятиугольника, т.к. каждая из сторон пятиугольной звезды делится другими именно в такой пропорции.
Таким образом, звездчатый пятиугольник также обладает «золотым сечением». Интересно, что внутри пятиугольника можно продолжить строить пятиугольники, и это отношение будет сохраняться.
Звездчатый пятиугольник называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком.
В настоящее время существует гипотеза, что пентаграмма – первичное понятие, а «золотое сечение» вторично. Пентаграмму никто не изобретал, ее только скопировали с натуры. Вид пятиконечной звезды имеют пяти-лепестковые цветы плодовых деревьев и кустарников, морские звезды. Те и другие создания природы человек наблюдает уже тысячи лет. Поэтому естественно предположить, что геометрический образ этих объектов – пентаграмма – стала известна раньше, чем «золотая» пропорция.
4. Второе золотое сечение.
Болгарский журнал «Отечество» (№10, 1983 г.) опубликовал статью Цветана Цекова-Карандаша «О втором золотом сечении», которое вытекает из основного сечения и дает другое отношение 44 : 56.
Такая пропорция обнаружена в архитектуре, а также имеет место при построении композиций изображений удлиненного горизонтального формата.
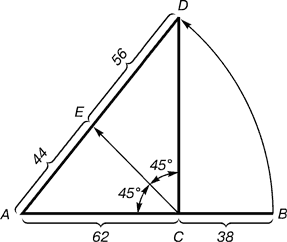
| Рис. 2. Построение второго золотого сечения |
Деление осуществляется следующим образом. Отрезок АВ делится в пропорции золотого сечения. Из точки С восставляется перпендикуляр СD. Радиусом АВ находится точка D, которая соединяется линией с точкой А. Прямой угол АСD делится пополам. Из точки С проводится линия до пересечения с линией AD. Точка Е делит отрезок AD в отношении 56:44.
На рисунке показано положение линии второго золотого сечения. Она находится посередине между линией золотого сечения и средней линией прямоугольника.
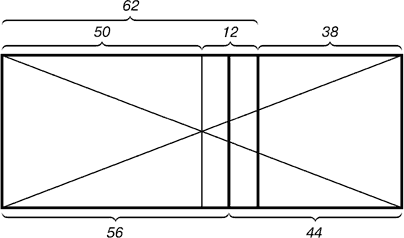
| Рис. 3. Деление прямоугольника линией второго золотого сечения |
Таким образом было доказано, что разделить отрезок в крайнем и среднем отношении можно не единственным способом.
5. "Золотые" фигуры.
5.1.Золотой прямоугольник:
Если построить квадрат со стороной АВ=а, найти середину М отрезка АВ и провести дугу окружности радиусом МС с центром в точке М до пересечения с продолжением стороны АВ в точке Е, то точка В разделит отрезок АЕ в крайнем и среднем отношении.
Чтобы убедиться в этом, заметим, что по теореме Пифагора
МС2=а2+(а/2)2=5а2/4
В силу чего
АЕ=а/2 +МЕ=(√5+1)а/2=φАВПрямоугольник АЕFD со сторонами АЕ=φАD называется золотым прямоугольником. Четырехугольник АВСD - квадрат. Нетрудно видеть, что прямоугольник ВЕFС также золотой, поскольку BC=a=φВЕ. Это обстоятельство сразу наводит на мысль о дальнейшем разбиении прямоугольника ВЕFС.
Можно ли считать, что прямоугольник с отношением сторон, равным φ, выглядит изящнее, чем прямоугольники с отношением сторон, скажем, 2:1, 3:2 или 5:7? Чтобы ответить на этот вопрос, были проведены специальные эксперименты. Результаты их не вполне убедительны, но все же свидетельствуют о некотором предпочтении, отдаваемом золотому сечению. Впрочем, может ли прямоугольник сам по себе быть захватывающе прекрасным или отталкивающе безобразным?
5.2.Золотой треугольник:
Проводим прямую АВ. От точки А
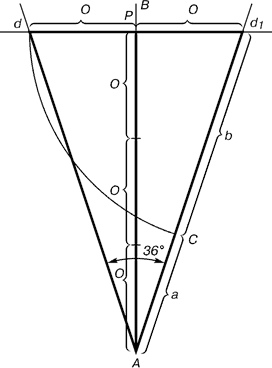 откладываем на ней три раза отрезок О
откладываем на ней три раза отрезок О
произвольной величины, через
полученную точку Р проводим перпендикуляр к линии
АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1
откладываем на линию Ad1, получая точку С. Она разделила линию Ad1 в пропорции золотого сечения. Линиями Ad1 и dd1 пользуются для построения «золотого»
прямоугольника.
5.3. Золотой пятиугольник; построение Евклида.
Замечательный пример «золотого сечения» представляет собой правильный пятиугольник – выпуклый и звездчатый (рис.5).
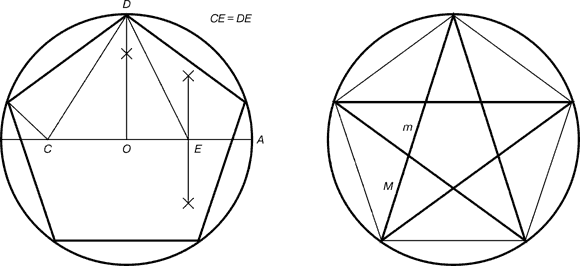
| Рис.6. Построение правильного пятиугольника и пентаграммы. |
Для построения пентаграммы необходимо построить правильный пятиугольник.
Пусть О - центр окружности, А - точка на окружности и Е - середина отрезка ОА. Перпендикуляр к радиусу ОА, восстановленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.
Есть и золотой кубоид- это прямоугольный параллелепипед с ребрами, имеющими длины 1.618, 1 и 0.618.
Теперь рассмотрим доказательство, предложенное Евклидом в «Началах».
Посмотрим теперь, как Евклид использует золотое сечение для того, чтобы построить угол в 72 градуса – именно под таким углом видна сторона правильного пятиугольникаиз центра описанной окружности. Начнем с
отрезка АВЕ, разделенного в среднем и
крайнем отношении точкой В. Проведем далее дуги окружностей с центрами в точках В и Е и радиусах АВ, пересекающиеся в точке С. Чуть ниже докажем, что АС=АЕ, а пока примем это на веру.
Итак, пусть АС=АЕ. Обозначим через a равные углы ЕВС и СЕВ. Так как АС=АЕ, то угол АСЕ также равен a. Теорема о том, что сумма углов треугольника равна 180 градусов, позволяет найти угол ВСЕ: он равен 180-2a, а угол ЕАС - 3a - 180. Но тогда угол АВС равен 180-a. Суммируя углы треугольника АВС получаем,
180=(3a -180) + (3a-180) + (180 - a)
Откуда 5a=360, значит a=72.
Итак, каждый из углов при основании треугольника ВЕС вдвое больше угла при вершине, равного 36 градусов. Следовательно, чтобы построить правильный пятиугольник, необходимо лишь провести любую окружность с центром в точке Е, пересекающую ЕС в точке Х и сторону ЕВ в точке Y: отрезок XY служит одной из сторон вписанного в окружность правильного пятиугольника; Обойдя вокруг всей окружности, можно найти и все остальные стороны.
Докажем теперь, что АС=АЕ. Предположим, что вершина С соединена отрезком прямой с серединой N отрезка ВЕ. Заметим, что поскольку СВ=СЕ, то угол СNЕ прямой. По теореме Пифагора:
CN2 = а2 – (а/2j) 2= а2 (1-4j 2)
Отсюда имеем (АС/а) 2 = (1+1/2j) 2 + (1-1/4j 2) = 2+1/j = 1 + j =j 2
Итак, АС = jа = jАВ = АЕ, что и требовалось доказать
5.4.Спираль Архимеда.
Последовательно отсекая от золотых прямоугольников квадраты до бесконечности, каждый раз соединяя противоположные точки четвертью окружности, мы получим довольно изящную кривую. Первым внимание на неё обратил древнегреческий ученый Архимед, имя которого она и носит. Он изучал её и вывел уравнение этой спирали.
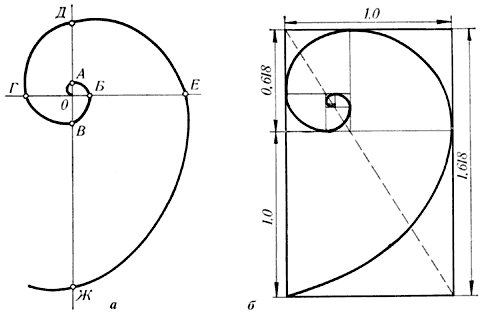
В настоящее время спираль Архимеда широко используется в технике.
6.Числа Фибоначчи.
С золотым сечением косвенно связано имя итальянского математика Леонардо из Пизы, который известен больше по своему прозвищу Фибоначчи (Fibonacci - сокращенное filius Bonacci, то есть сын Боначчи)
В 1202г. им была написана книга "Liber abacci", то есть "Книга об абаке" . "Liber abacci" представляет собой объемистый труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший заметную роль в развитии математики в Западной Европе в течение нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими ("арабскими") цифрами.
Сообщаемый в книге материал поясняется на большом числе задач, составляющих значительную часть этого трактата.
Рассмотрим одну такую задачу:
"Сколько пар кроликов в один год от одной пары рождается?
Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, дабы узнать, сколько пар кроликов родится в течение этого года, если природа кроликов такова, что через месяц пара кроликов воспроизведет другую, а рождают кролики со второго месяца после своего рождения"
| Месяцы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Пары кроликов | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 |
| Табл.1 Ряд Фибоначчи при u1=1 |
Перейдем теперь от кроликов к числам и рассмотрим следующую числовую последовательность:
u1, u2 … un
в которой каждый член равен сумме двух предыдущих, т.е. при всяком n>2
un=un-1+un-2.
Данная последовательность асимптотически (приближаясь все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.
Если какой-либо член последовательности Фибоначчи разделить на предшествующий ему (например, 13:8), результатом будет величина, колеблющаяся около иррационального значения 1.61803398875... и через раз то превосходящая, то не достигающая его.
Асимптотическое поведение последовательности, затухающие колебания ее соотношения около иррационального числа Ф могут стать более понятными, если показать отношения нескольких пеpвых членов последовательности. В этом примере приведены отношения второго члена к первому, третьего ко второму, четвертого к третьему, и так далее:
1:1 = 1.0000, что меньше фи на 0.6180
2:1 = 2.0000, что больше фи на 0.3820
3:2 = 1.5000, что меньше фи на 0.1180
5:3 = 1.6667, что больше фи на 0.0486
8:5 = 1.6000, что меньше фи на 0.0180
По мере продвижения по суммационной последовательности Фибоначчи каждый новый член будет делить следующий со все большим и большим приближением к недостижимому Ф.
Человек подсознательно ищет Божественную пропорцию: она нужна для удовлетворения его потребности в комфорте.
Пpи делении любого члена последовательности Фибоначчи на следующий за ним получается просто обратная к 1.618 величина (1 : 1.618=0.618). Hо это тоже весьма необычное, даже замечательное явление. Поскольку пеpвоначальное соотношение – бесконечная дpобь, у этого соотношения также не должно быть конца.
При делении каждого числа на следующее за ним через одно, получаем число 0.382
1:0.382=2.618
Подбирая таким образом соотношения, получаем основной набор коэффициентов Фибоначчи: 4.235 ,2.618 ,1.618,0.618,0.382,0.236.Упомянем также 0.5.Все они играют особую роль в природе и в частности в техническом анализе.
Тут необходимо отметить, что Фибоначчи лишь напомнил свою последовательность человечеству, так как она была известна еще в древнейшие времена под названием Золотое сечение.
Золотое сечение, как мы видели, возникает в связи с правильным пятиугольником, поэтому и числа Фибоначчи играют роль во всем, что имеет отношение к правильным пятиугольникам - выпуклым и звездчатым.
Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления. Ученые продолжали активно развивать теорию чисел Фибоначчи и золотого сечения. Ю. Матиясевич с использованием чисел Фибоначчи решает 10-ю проблему Гильберта (о решении Диофантовых уравнений). Возникают изящные методы решения ряда кибернетических задач (теории поиска, игр, программирования) с использованием чисел Фибоначчи и золотого сечения. В США создается даже Математическая Фибоначчи-ассоциация, которая с 1963 года выпускает специальный журнал.
Одним из достижений в этой области является открытие обобщенных чисел Фибоначчи и обобщенных золотых сечений. Ряд Фибоначчи (1, 1, 2, 3, 5, 8) и открытый им же «двоичный» ряд чисел 1, 2, 4, 8, 16...(то есть ряд чисел до n , где любое натуральное число, меньшее n можно представить суммой некоторых чисел этого ряда) на первый взгляд совершенно разные. Но алгоритмы их построения весьма похожи друг на друга: в первом случае каждое число есть сумма предыдущего числа с самим собой 2 = 1 + 1; 4 = 2 + 2..., во втором – это сумма двух предыдущих чисел 2 =1 + 1, 3 = 2 + 1, 5 = 3 + 2.... Нельзя ли отыскать общую математическую формулу, из которой получаются и «двоичный» ряд, и ряд Фибоначчи?
Действительно, зададимся числовым параметром S, который может принимать любые значения: 0, 1, 2, 3, 4, 5... Рассмотрим числовой ряд, S + 1 первых членов которого – единицы, а каждый из последующих равен сумме двух членов предыдущего и отстоящего от предыдущего на S шагов. Если n-й член этого ряда мы обозначим через S (n), то получим общую формулу S (n) = S (n – 1) + S (n – S – 1).
Очевидно, что при S = 0 из этой формулы мы получим «двоичный» ряд, при S = 1 –ряд Фибоначчи, при S = 2, 3, 4. новые ряды чисел, которые получили название S-чисел Фибоначчи.
В общем виде золотая S-пропорция есть положительный корень уравнения золотого S-сечения xS+1 – xS – 1 = 0.
Нетрудно показать, что при S = 0 получается деление отрезка пополам, а при S = 1 – знакомое классическое золотое сечение.
Отношения соседних S-чисел Фибоначчи с абсолютной математической точностью совпадают в пределе с золотыми S-пропорциями! То есть золотые S-сечения являются числовыми инвариантами S-чисел Фибоначчи.
7.Золотое сечение в искусстве.
7.1. Золотое сечение в живописи.
Переходя к примерам «золотого сечения» в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды».
 Нет сомнений, что Леонардо да Винчи был великим художником, это признавали уже его современники, но его личность и деятельность останутся покрытыми тайной, так как он оставил потомкам не связное изложение своих идей, а лишь многочисленные рукописные наброски, заметки, в которых говорится «обо всем на свете».
Нет сомнений, что Леонардо да Винчи был великим художником, это признавали уже его современники, но его личность и деятельность останутся покрытыми тайной, так как он оставил потомкам не связное изложение своих идей, а лишь многочисленные рукописные наброски, заметки, в которых говорится «обо всем на свете».
Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника..
Также пропорция золотого сечения проявляется в картине Шишкина. На этой знаменитой картине И. И. Шишкина с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны - освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали.
В картине Рафаэля "Избиение младенцев" просматривается другой элемент золотой пропорции - золотая спираль. На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции - точки, где пальцы воина сомкнулись вокруг лодыжки ребенка - вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Неизвестно, строил ли Рафаэль золотую спираль или чувствовал её.
Т.Кук использовал при анализе картины Сандро Боттичелли «рождение Венеры» золотое сеченеие .
7.2. Пирамиды золотого сечения.
Широко известны медицинские свойства пирамид, особенно золотого сечения. По некоторым наиболее распространенным мнениям, комната, в которой находится такая пирамида, кажется больше, а воздух - прозрачнее. Сны начинают запоминаться лучше. Также известно, что золотое сечение широко применялась в архитектуре и скульптуре. Примером тому стали: Пантеон и Парфенон в Греции, здания архитекторов Баженова и Малевича
8. Заключение.
 Необходимо сказать, что золотое сечение имеет большое применение в нашей жизни.
Необходимо сказать, что золотое сечение имеет большое применение в нашей жизни.
Было доказано, что человеческое тело делится в пропорции золотого сечения линией пояса.
Раковина наутилуса закручена подобно золотой спирали.
Благодаря золотому сечению был открыт пояс астероидов между Марсом и Юпитером – по пропорции там должна находиться ещё одна планета.
Возбуждение струны в точке , делящей её в отношении золотого деления, не вызовет колебаний струны, то есть это точка компенсации.
На летательных аппаратах с электромагнитными источниками энергии создаются прямоугольные ячейки с пропорцией золотого сечения.
Джоконда построена на золотых треугольниках, золотая спираль присутствует на картине Рафаэля «Избиение младенцев».
Пропорция обнаружена в картине Сандро Боттичелли «Рождение Венеры»
Известно много памятников архитектуры, построенных с использованием золотой пропорции, в том числе Пантеон и Парфенон в Афинах, здания архитекторов Баженова и Малевича.
Иоанну Кеплеру, жившему пять веков назад, принадлежит высказывание: "Геометрия обладает двумя великими сокровищами. Первое - это теорема Пифагора, второе - деления отрезка в крайнем и среднем отношении"
Список литературы
1. Д. Пидоу. Геометрия и искусство. – М.: Мир, 1979.
2. Журнал "Наука и техника"
3. Журнал «Квант», 1973, № 8.
4. Журнал «Математика в школе», 1994, № 2; № 3.
5. Ковалев Ф.В. Золотое сечение в живописи. К.: Выща школа, 1989.
6. Стахов А. Коды золотой пропорции.
7.Воробьев Н.Н. "Числа Фибоначчи" - М.: Наука 1964
8. "Математика - Энциклопедия для детей" М.: Аванта +, 1998
9. Информация из интернета.
Дата добавления: 19.01.2005
www.km.ru
Золотое сечение
Реферат выполнила ученица 8 класса МОУ гимназия №9 Вьюшина Вероника
Екатеринбург
2002
1. Введение. Пропорция золотого сечения. Ф и φ.
"Геометрия обладает двумя великими сокровищами. Первое - это теорема Пифагора, второе - деления отрезка в крайнем и среднем отношении"
Иоганн Кеплер
Правильные многоугольники привлекали внимание древнегреческих учёных ещё задолго да Архимеда. Пифагорейцы, выбравшие эмблемой своего союза пентаграмму - пятиконечную звезду, придавали очень большое значение задаче о делении окружности на равные части, то есть о построении правильного вписанного многоугольника. Альбрехт Дюрер (1471-1527гг), ставший олицетворением Возрождения в Германии приводит теоретически точный способ построения правильного пятиугольника, заимствованный из великого сочинения Птолемея "Альмагест".
Интерес Дюрера к построению правильных многоугольников отражает использование их в Средние века в арабских и готических орнаментах, а после изобретения огнестрельного оружия - в планировке крепостей.
Средневековые способы построения правильных многоугольников носили приближенный характер, но были (или не могли не быть) простыми: предпочтение отдавалось способам построения, не требующим даже изменять раствор циркуля. Леонардо да Винчи также много писал о многоугольниках, но именно Дюрер, а не Леонардо, передал средневековые способы построения потомкам. Дюрер, конечно, был знаком с " Началами" Евклида, но не привел в своем "Руководстве к измерению" (о построениях при помощи циркуля и линейки) предложенный Евклидом способ построения правильного пятиугольника, теоретически точный, как и все евклидовы построения. Евклид не пытается разделить заданную дугу окружности на три равные части, и Дюрер знал, хотя доказательство было найдено лишь в XIX веке, что эта задача неразрешима.
Предложенное Евклидом построение правильного пятиугольника включает в себя деление отрезка прямой в среднем и крайнем отношении, названное впоследствии золотым сечением и привлекавшим к себе внимание художников и архитекторов на протяжении нескольких столетий.
Точка В делит отрезок АВЕ в среднем и крайнем отношении или образует золотое сечение, если отношение большей части отрезка к меньшей равно отношению всего отрезка к большей части.
Записанное в виде равенства отношений золотое сечение имеет вид
АВ/ВЕ= АВ/АЕ
Если положить АВ=а, а ВЕ=а/Ф так, чтобы золотое отношение было равно АВ/ВЕ=Ф, то получается соотношение
Ф = 1+1/Ф
То есть Ф удовлетворяет уравнению
Ф2- Ф-1=0
Это уравнение имеет один положительный корень
Ф=(√5+1)/2=1.618034….
Заметим, что 1/Ф = (√5 -1 )/2, так как (√5-1)(√5+1) =5-1=4. За 1/Ф принято считать φ=0.618034….
Ф и φ - прописная и строчная формы греческой буквы "фи".
Такое обозначение принято в честь древнегреческого скульптора Фидия (V век до н. э.) Фидий руководил строительством храма Парфенон в Афинах. В пропорциях этого храма многократно присутствует число φ .
2.История золотого сечения
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамсеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

 |
Платон (427...347 гг. до н.э.) также знал о золотом делении. Его диалог "Тимей" посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.

Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по «золотому сечению», то получим те или иные выступы фасада. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.
 |

В дошедшей до нас античной литературе золотое деление впервые упоминается в "Началах" Евклида. Во 2-й книге "Начал" дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др.. В средневековой Европе с золотым делением познакомились по арабским переводам "Начал" Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.
В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением, как в геометрии, так и в искусстве, особенно в архитектуре. Леонардо да Винчи, художник и ученый, видел, что в итальянских художниках большой эмпирический опыт, но недостаток знаний. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем.
Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли "Божественная пропорция" с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее "божественную суть" как выражение божественного триединства: бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок - бога отца, а весь отрезок - бога духа святого).
Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.
В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет: "Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать".
Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица - ртом и т.д. Известен пропорциональный циркуль Дюрера.
Построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).
Если на прямой произвольной длины, отложить отрезок m(φ), рядом откладываем отрезок M. На основании этих двух отрезков выстраиваем шкалу отрезков золотой пропорции восходящего и нисходящего рядов


В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы "вместе с водой выплеснули и ребенка". Вновь "открыто" золотое сечение было в середине XIX в. В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд "Эстетические исследования". С Цейзингом произошло именно то, что и должно было неминуемо произойти с исследователем, который рассматривает явление как таковое, без связи с другими явлениями. Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях "математической эстетикой".
3. Построение пропорции.
 |
|
Из точки В восстанавливается перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.
Именно эти отрезки использовал Евклид при построении правильного пятиугольника, т.к. каждая из сторон пятиугольной звезды делится другими именно в такой пропорции.
Таким образом, звездчатый пятиугольник также обладает «золотым сечением». Интересно, что внутри пятиугольника можно продолжить строить пятиугольники, и это отношение будет сохраняться.
Звездчатый пятиугольник называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком.
В настоящее время существует гипотеза, что пентаграмма – первичное понятие, а «золотое сечение» вторично. Пентаграмму никто не изобретал, ее только скопировали с натуры. Вид пятиконечной звезды имеют пяти-лепестковые цветы плодовых деревьев и кустарников, морские звезды. Те и другие создания природы человек наблюдает уже тысячи лет. Поэтому естественно предположить, что геометрический образ этих объектов – пентаграмма – стала известна раньше, чем «золотая» пропорция.
4. Второе золотое сечение.
Болгарский журнал «Отечество» (№10, 1983 г.) опубликовал статью Цветана Цекова-Карандаша «О втором золотом сечении», которое вытекает из основного сечения и дает другое отношение 44 : 56.
Такая пропорция обнаружена в архитектуре, а также имеет место при построении композиций изображений удлиненного горизонтального формата.

|
Деление осуществляется следующим образом. Отрезок АВ делится в пропорции золотого сечения. Из точки С восставляется перпендикуляр СD. Радиусом АВ находится точка D, которая соединяется линией с точкой А. Прямой угол АСD делится пополам. Из точки С проводится линия до пересечения с линией AD. Точка Е делит отрезок AD в отношении 56 : 44.
На рисунке показано положение линии второго золотого сечения. Она находится посередине между линией золотого сечения и средней линией прямоугольника.

|
Таким образом было доказано, что разделить отрезок в крайнем и среднем отношении можно не единственным способом.
5. "Золотые" фигуры.
5.1.Золотой прямоугольник:
Если построить квадрат со стороной АВ=а, найти середину М отрезка АВ и провести дугу окружности радиусом МС с центром в точке М до пересечения с продолжением стороны АВ в точке Е, то точка В разделит отрезок АЕ в крайнем и среднем отношении.
Чтобы убедиться в этом, заметим, что по теореме Пифагора
МС2=а2+(а/2)2=5а2/4
В силу чего
АЕ=а/2 +МЕ=(√5+1)а/2=φАВ
Прямоугольник АЕFD со сторонами АЕ=φАD называется золотым прямоугольником. Четырехугольник АВСD - квадрат. Нетрудно видеть, что прямоугольник ВЕFС также золотой, поскольку BC=a=φВЕ. Это обстоятельство сразу наводит на мысль о дальнейшем разбиении прямоугольника ВЕFС.
Можно ли считать, что прямоугольник с отношением сторон, равным φ, выглядит изящнее, чем прямоугольники с отношением сторон, скажем, 2:1, 3:2 или 5:7? Чтобы ответить на этот вопрос, были проведены специальные эксперименты. Результаты их не вполне убедительны, но все же свидетельствуют о некотором предпочтении, отдаваемом золотому сечению. Впрочем, может ли прямоугольник сам по себе быть захватывающе прекрасным или отталкивающе безобразным?
5.2.Золотой треугольник:
Проводим прямую АВ. От точки А
 откладываем на ней три раза отрезок О
откладываем на ней три раза отрезок О
произвольной величины, через
полученную точку Р проводим перпендикуляр к линии
АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1
откладываем на линию Ad1, получая точку С. Она разделила линию Ad1 в пропорции золотого сечения. Линиями Ad1 и dd1 пользуются для построения «золотого»
прямоугольника.
5.3. Золотой пятиугольник; построение Евклида.
Замечательный пример «золотого сечения» представляет собой правильный пятиугольник – выпуклый и звездчатый (рис. 5).

|
Для построения пентаграммы необходимо построить правильный пятиугольник.
Пусть О - центр окружности, А - точка на окружности и Е - середина отрезка ОА. Перпендикуляр к радиусу ОА, восстановленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.
Есть и золотой кубоид- это прямоугольный параллелепипед с ребрами, имеющими длины 1.618, 1 и 0.618.
Теперь рассмотрим доказательство, предложенное Евклидом в «Началах».
Посмотрим теперь, как Евклид использует золотое сечение для того, чтобы построить угол в 72 градуса – именно под таким углом видна сторона правильного пятиугольника
из центра описанной окружности. Начнем с
отрезка АВЕ, разделенного в среднем и
крайнем отношении точкой В. Проведем далее дуги окружностей с центрами в точках В и Е и радиусах АВ, пересекающиеся в точке С. Чуть ниже докажем, что АС=АЕ, а пока примем это на веру.
Итак, пусть АС=АЕ. Обозначим через a равные углы ЕВС и СЕВ. Так как АС=АЕ, то угол АСЕ также равен a. Теорема о том, что сумма углов треугольника равна 180 градусов, позволяет найти угол ВСЕ: он равен 180-2a, а угол ЕАС - 3a - 180. Но тогда угол АВС равен 180-a. Суммируя углы треугольника АВС получаем,
180=(3a -180) + (3a-180) + (180 - a)
Откуда 5a=360, значит a=72.
Итак, каждый из углов при основании треугольника ВЕС вдвое больше угла при вершине, равного 36 градусов. Следовательно, чтобы построить правильный пятиугольник, необходимо лишь провести любую окружность с центром в точке Е, пересекающую ЕС в точке Х и сторону ЕВ в точке Y: отрезок XY служит одной из сторон вписанного в окружность правильного пятиугольника; Обойдя вокруг всей окружности, можно найти и все остальные стороны.
Докажем теперь, что АС=АЕ. Предположим, что вершина С соединена отрезком прямой с серединой N отрезка ВЕ. Заметим, что поскольку СВ=СЕ, то угол СNЕ прямой. По теореме Пифагора:
CN2 = а2 – (а/2j) 2= а2 (1-4j 2)
Отсюда имеем (АС/а) 2 = (1+1/2j) 2 + (1-1/4j 2) = 2+1/j = 1 + j =j 2
Итак, АС = jа = jАВ = АЕ, что и требовалось доказать
5.4.Спираль Архимеда.
Последовательно отсекая от золотых прямоугольников квадраты до бесконечности, каждый раз соединяя противоположные точки четвертью окружности, мы получим довольно изящную кривую. Первым внимание на неё обратил древнегреческий ученый Архимед, имя которого она и носит. Он изучал её и вывел уравнение этой спирали.


В настоящее время спираль Архимеда широко используется в технике.
6.Числа Фибоначчи.
С золотым сечением косвенно связано имя итальянского математика Леонардо из Пизы, который известен больше по своему прозвищу Фибоначчи (Fibonacci - сокращенное filius Bonacci, то есть сын Боначчи)
В 1202г. им была написана книга "Liber abacci", то есть "Книга об абаке" . "Liber abacci" представляет собой объемистый труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший заметную роль в развитии математики в Западной Европе в течение нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими ("арабскими") цифрами.
Сообщаемый в книге материал поясняется на большом числе задач, составляющих значительную часть этого трактата.
Рассмотрим одну такую задачу:
"Сколько пар кроликов в один год от одной пары рождается?
Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, дабы узнать, сколько пар кроликов родится в течение этого года, если природа кроликов такова, что через месяц пара кроликов воспроизведет другую, а рождают кролики со второго месяца после своего рождения"
|
Месяцы |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Пары кроликов |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
55 |
89 |
144 |
233 |
377 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перейдем теперь от кроликов к числам и рассмотрим следующую числовую последовательность:
u1, u2 … un
в которой каждый член равен сумме двух предыдущих, т.е. при всяком n>2
un=un-1+un-2.
Данная последовательность асимптотически (приближаясь все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.
Если какой-либо член последовательности Фибоначчи разделить на предшествующий ему (например, 13:8), результатом будет величина, колеблющаяся около иррационального значения 1.61803398875... и через раз то превосходящая, то не достигающая его.
Асимптотическое поведение последовательности, затухающие колебания ее соотношения около иррационального числа Ф могут стать более понятными, если показать отношения нескольких пеpвых членов последовательности. В этом примере приведены отношения второго члена к первому, третьего ко второму, четвертого к третьему, и так далее:
1:1 = 1.0000, что меньше фи на 0.6180
2:1 = 2.0000, что больше фи на 0.3820
3:2 = 1.5000, что меньше фи на 0.1180
5:3 = 1.6667, что больше фи на 0.0486
8:5 = 1.6000, что меньше фи на 0.0180
По мере продвижения по суммационной последовательности Фибоначчи каждый новый член будет делить следующий со все большим и большим приближением к недостижимому Ф.
Человек подсознательно ищет Божественную пропорцию: она нужна для удовлетворения его потребности в комфорте.
Пpи делении любого члена последовательности Фибоначчи на следующий за ним получается просто обратная к 1.618 величина (1 : 1.618=0.618). Hо это тоже весьма необычное, даже замечательное явление. Поскольку пеpвоначальное соотношение – бесконечная дpобь, у этого соотношения также не должно быть конца.
При делении каждого числа на следующее за ним через одно, получаем число 0.382
1:0.382=2.618
Подбирая таким образом соотношения, получаем основной набор коэффициентов Фибоначчи: 4.235 ,2.618 ,1.618,0.618,0.382,0.236.Упомянем также 0.5.Все они играют особую роль в природе и в частности в техническом анализе.
Тут необходимо отметить, что Фибоначчи лишь напомнил свою последовательность человечеству, так как она была известна еще в древнейшие времена под названием Золотое сечение.
Золотое сечение, как мы видели, возникает в связи с правильным пятиугольником, поэтому и числа Фибоначчи играют роль во всем, что имеет отношение к правильным пятиугольникам - выпуклым и звездчатым.
Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления. Ученые продолжали активно развивать теорию чисел Фибоначчи и золотого сечения. Ю. Матиясевич с использованием чисел Фибоначчи решает 10-ю проблему Гильберта (о решении Диофантовых уравнений). Возникают изящные методы решения ряда кибернетических задач (теории поиска, игр, программирования) с использованием чисел Фибоначчи и золотого сечения. В США создается даже Математическая Фибоначчи-ассоциация, которая с 1963 года выпускает специальный журнал.
Одним из достижений в этой области является открытие обобщенных чисел Фибоначчи и обобщенных золотых сечений. Ряд Фибоначчи (1, 1, 2, 3, 5, 8) и открытый им же «двоичный» ряд чисел 1, 2, 4, 8, 16...(то есть ряд чисел до n , где любое натуральное число, меньшее n можно представить суммой некоторых чисел этого ряда) на первый взгляд совершенно разные. Но алгоритмы их построения весьма похожи друг на друга: в первом случае каждое число есть сумма предыдущего числа с самим собой 2 = 1 + 1; 4 = 2 + 2..., во втором – это сумма двух предыдущих чисел 2 =1 + 1, 3 = 2 + 1, 5 = 3 + 2.... Нельзя ли отыскать общую математическую формулу, из которой получаются и «двоичный» ряд, и ряд Фибоначчи?
Действительно, зададимся числовым параметром S, который может принимать любые значения: 0, 1, 2, 3, 4, 5... Рассмотрим числовой ряд, S + 1 первых членов которого – единицы, а каждый из последующих равен сумме двух членов предыдущего и отстоящего от предыдущего на S шагов. Если n-й член этого ряда мы обозначим через S (n), то получим общую формулу S (n) = S (n – 1) + S (n – S – 1).
Очевидно, что при S = 0 из этой формулы мы получим «двоичный» ряд, при S = 1 –ряд Фибоначчи, при S = 2, 3, 4. новые ряды чисел, которые получили название S-чисел Фибоначчи.
В общем виде золотая S-пропорция есть положительный корень уравнения золотого S-сечения xS+1 – xS – 1 = 0.
Нетрудно показать, что при S = 0 получается деление отрезка пополам, а при S = 1 – знакомое классическое золотое сечение.
Отношения соседних S-чисел Фибоначчи с абсолютной математической точностью совпадают в пределе с золотыми S-пропорциями! То есть золотые S-сечения являются числовыми инвариантами S-чисел Фибоначчи.
7.Золотое сечение в искусстве.
7.1. Золотое сечение в живописи.
Переходя к примерам «золотого сечения» в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды».
 Нет сомнений, что Леонардо да Винчи
был великим художником, это признавали уже его современники, но его личность и
деятельность останутся покрытыми тайной, так как он оставил потомкам не связное
изложение своих идей, а лишь многочисленные рукописные наброски, заметки, в
которых говорится «обо всем на свете».
Нет сомнений, что Леонардо да Винчи
был великим художником, это признавали уже его современники, но его личность и
деятельность останутся покрытыми тайной, так как он оставил потомкам не связное
изложение своих идей, а лишь многочисленные рукописные наброски, заметки, в
которых говорится «обо всем на свете».
Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника..
Также пропорция золотого сечения проявляется в картине Шишкина. На этой знаменитой картине И. И. Шишкина с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны - освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали.
В картине Рафаэля "Избиение младенцев" просматривается другой элемент золотой пропорции - золотая спираль. На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции - точки, где пальцы воина сомкнулись вокруг лодыжки ребенка - вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Неизвестно, строил ли Рафаэль золотую спираль или чувствовал её.
Т.Кук использовал при анализе картины Сандро Боттичелли «рождение Венеры» золотое сеченеие .
7.2. Пирамиды золотого сечения.
Широко известны медицинские свойства пирамид, особенно золотого сечения. По некоторым наиболее распространенным мнениям, комната, в которой находится такая пирамида, кажется больше, а воздух - прозрачнее. Сны начинают запоминаться лучше. Также известно, что золотое сечение широко применялась в архитектуре и скульптуре. Примером тому стали: Пантеон и Парфенон в Греции, здания архитекторов Баженова и Малевича
8. Заключение.
 Необходимо сказать, что золотое
сечение имеет большое применение в нашей жизни.
Необходимо сказать, что золотое
сечение имеет большое применение в нашей жизни.
Было доказано, что человеческое тело делится в пропорции золотого сечения линией пояса.
Раковина наутилуса закручена подобно золотой спирали.
Благодаря золотому сечению был открыт пояс астероидов между Марсом и Юпитером – по пропорции там должна находиться ещё одна планета.
Возбуждение струны в точке , делящей её в отношении золотого деления, не вызовет колебаний струны, то есть это точка компенсации.
На летательных аппаратах с электромагнитными источниками энергии создаются прямоугольные ячейки с пропорцией золотого сечения.
Джоконда построена на золотых треугольниках, золотая спираль присутствует на картине Рафаэля «Избиение младенцев».
Пропорция обнаружена в картине Сандро Боттичелли «Рождение Венеры»
Известно много памятников архитектуры, построенных с использованием золотой пропорции, в том числе Пантеон и Парфенон в Афинах, здания архитекторов Баженова и Малевича.
Иоанну Кеплеру, жившему пять веков назад, принадлежит высказывание: "Геометрия обладает двумя великими сокровищами. Первое - это теорема Пифагора, второе - деления отрезка в крайнем и среднем отношении"
Список литературы
1. Д. Пидоу. Геометрия и искусство. – М.: Мир, 1979.
2. Журнал "Наука и техника"
3. Журнал «Квант», 1973, № 8.
4. Журнал «Математика в школе», 1994, № 2; № 3.
5. Ковалев Ф.В. Золотое сечение в живописи. К.: Выща школа, 1989.
6. Стахов А. Коды золотой пропорции.
7.Воробьев Н.Н. "Числа Фибоначчи" - М.: Наука 1964
8. "Математика - Энциклопедия для детей" М.: Аванта +, 1998
9. Информация из интернета.
www.referatmix.ru
Рефератна тему : «Золотое сечение»Образовательная область: математика Предмет: геометрия Выполнила: ученица 8 класса МОУ гимназия №9 Вьюшина ВероникаПреподаватель: Зайкова Татьяна Константиновна Екатеринбург 2002 |
Содержание.
| Содержание ………………………………………………………
Литература……………………………………………………….. | 2 3-4 5-7 8 9 10-12 13-15 16-17 18 19 19 |
1.Введение. Пропорция золотого
сечения. Ф и φ.
"Геометрия обладает двумя великими
сокровищами. Первое - это теорема Пифагора,
второе - деления отрезка в крайнем и среднем
отношении"
Иоганн Кеплер
Правильные многоугольники привлекали внимание древнегреческих учёных ещё задолго да Архимеда. Пифагорейцы, выбравшие эмблемой своего союза пентаграмму - пятиконечную звезду, придавали очень большое значение задаче о делении окружности на равные части, то есть о построении правильного вписанного многоугольника. Альбрехт Дюрер (1471-1527гг), ставший олицетворением Возрождения в Германии приводит теоретически точный способ построения правильного пятиугольника, заимствованный из великого сочинения Птолемея "Альмагест".
Интерес Дюрера к построению правильных многоугольников отражает использование их в Средние века в арабских и готических орнаментах, а после изобретения огнестрельного оружия - в планировке крепостей.
Средневековые способы построения правильных многоугольников носили приближенный характер, но были (или не могли не быть) простыми: предпочтение отдавалось способам построения, не требующим даже изменять раствор циркуля. Леонардо да Винчи также много писал о многоугольниках, но именно Дюрер, а не Леонардо, передал средневековые способы построения потомкам. Дюрер, конечно, был знаком с " Началами" Евклида, но не привел в своем "Руководстве к измерению" (о построениях при помощи циркуля и линейки) предложенный Евклидом способ построения правильного пятиугольника, теоретически точный, как и все евклидовы построения. Евклид не пытается разделить заданную дугу окружности на три равные части, и Дюрер знал, хотя доказательство было найдено лишь в XIX веке, что эта задача неразрешима.
Предложенное Евклидом построение правильного пятиугольника включает в себя деление отрезка прямой в среднем и крайнем отношении, названное впоследствии золотым сечением и привлекавшим к себе внимание художников и архитекторов на протяжении нескольких столетий.
Точка В делит отрезок АВЕ в среднем и крайнем отношении или образует золотое сечение, если отношение большей части отрезка к меньшей равно отношению всего отрезка к большей части.
Записанное в виде равенства отношений золотое сечение имеет вид
АВ/ВЕ= АВ/АЕ
Если положить АВ=а, а ВЕ=а/Ф так, чтобы золотое отношение было равно АВ/ВЕ=Ф, то получается соотношение
Ф = 1+1/Ф
То есть Ф удовлетворяет уравнению
Ф2- Ф-1=0
Это уравнение имеет один положительный корень
Ф=(√5+1)/2=1.618034….
Заметим, что 1/Ф = (√5 -1 )/2, так как (√5-1)(√5+1) =5-1=4. За 1/Ф принято считать φ=0.618034….
Фи φ - прописная и строчная формы греческой буквы "фи".
Такое обозначение принято в честь древнегреческого скульптора Фидия (V век до н. э.) Фидий руководил строительством храма Парфенон в Афинах. В пропорциях этого храма многократно присутствует число φ .
2.История золотого сечения
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамсеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

Рис. 7. Динамические прямоугольники
Греки же были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамическихпрямоугольников.
Платон (427...347 гг. до н.э.) также знал о золотом делении. Его диалог "Тимей" посвящен математическим и эстетическим воззрениям школы Пифагора и, в
 частности, вопросам золотого деления.
частности, вопросам золотого деления.
Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по «золотому сечению», то получим те или иные выступы фасада. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.
Рис.8. Парфенон

Рис. 9. Античный циркуль золотого сечения
В дошедшей до нас античной литературе золотое деление впервые упоминается в "Началах" Евклида. Во 2-й книге "Начал" дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др.. В средневековой Европе с золотым делением познакомились по арабским переводам "Начал" Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.
В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением, как в геометрии, так и в искусстве, особенно в архитектуре. Леонардо да Винчи, художник и ученый, видел, что в итальянских художниках большой эмпирический опыт, но недостаток знаний. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем.
Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли "Божественная пропорция" с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее "божественную суть" как выражение божественного триединства: бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок - бога отца, а весь отрезок - бога духа святого).
Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.
В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет: "Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать".
Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица - ртом и т.д. Известен пропорциональный циркуль Дюрера.
Построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).
Если на прямой произвольной длины, отложить отрезок m(φ), рядом откладываем отрезок M. На основании этих двух отрезков выстраиваем шкалу отрезков золотой пропорции восходящего и нисходящего рядов

Рис. 10. Построение шкалы отрезков золотой пропорции
В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы "вместе с водой выплеснули и ребенка". Вновь "открыто" золотое сечение было в середине XIX в. В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд "Эстетические исследования". С Цейзингом произошло именно то, что и должно было неминуемо произойти с исследователем, который рассматривает явление как таковое, без связи с другими явлениями. Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях "математической эстетикой".
3. Построение пропорции.
З десь приводится построение точки Е, делящий отрезок прямой в пропорции золотое сечение.
десь приводится построение точки Е, делящий отрезок прямой в пропорции золотое сечение.
Рис. 1. Деление отрезка прямой по золотому сечению. BC = 1/2 AB; CD = BC
Из точки В восстанавливается перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.
Именно эти отрезки использовал Евклид при построении правильного пятиугольника, т.к. каждая из сторон пятиугольной звезды делится другими именно в такой пропорции.
Таким образом, звездчатый пятиугольник также обладает «золотым сечением». Интересно, что внутри пятиугольника можно продолжить строить пятиугольники, и это отношение будет сохраняться.
Звездчатый пятиугольник называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком.
В настоящее время существует гипотеза, что пентаграмма – первичное понятие, а «золотое сечение» вторично. Пентаграмму никто не изобретал, ее только скопировали с натуры. Вид пятиконечной звезды имеют пяти-лепестковые цветы плодовых деревьев и кустарников, морские звезды. Те и другие создания природы человек наблюдает уже тысячи лет. Поэтому естественно предположить, что геометрический образ этих объектов – пентаграмма – стала известна раньше, чем «золотая» пропорция.
4.Второе золотое сечение.
Болгарский журнал «Отечество» (№10, 1983 г.) опубликовал статью Цветана Цекова-Карандаша «О втором золотом сечении», которое вытекает из основного сечения и дает другое отношение 44 : 56.
Такая пропорция обнаружена в архитектуре, а также имеет место при построении композиций изображений удлиненного горизонтального формата.<!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN"><!-- saved from url=(0026)http://n-t.ru/tp/iz/zs.htm --><DIV align=center>

Деление осуществляется следующим образом. Отрезок АВ делится в пропорции золотого сечения. Из точки С восставляется перпендикуляр СD. Радиусом АВ находится точка D, которая соединяется линией с точкой А. Прямой угол АСD делится пополам. Из точки С проводится линия до пересечения с линией AD. Точка Е делит отрезок AD в отношении 56 : 44.
Рис. 2. Построение второго золотого сечения
На рисунке показано положение линии второго золотого сечения. Она находится посередине между линией золотого сечения и средней линией прямоугольника.

Рис. 3. Деление прямоугольника линией второго золотого сечения
Таким образом было доказано, что разделить отрезок в крайнем и среднем отношении можно не единственным способом.
5. "Золотые" фигуры.
5.1.Золотой прямоугольник:
Если построить квадрат со стороной АВ=а, найти середину М отрезка АВ и провести дугу окружности радиусом МС с центром в точке М до пересечения с продолжением стороны АВ в точке Е, то точка В разделит отрезок АЕ в крайнем и среднем отношении.
Чтобы убедиться в этом, заметим, что по теореме Пифагора
МС2=а2+(а/2)2=5а2/4
В силу чего
Рис 20 стр74
АЕ=а/2 +МЕ=(√5+1)а/2=φАВПрямоугольник АЕFD со сторонами АЕ=φАD называется золотым прямоугольником. Четырехугольник АВСD - квадрат. Нетрудно видеть, что прямоугольник ВЕFС также золотой, поскольку BC=a=φВЕ. Это обстоятельство сразу наводит на мысль о дальнейшем разбиении прямоугольника ВЕFС.
Можно ли считать, что прямоугольник с отношением сторон, равным φ, выглядит изящнее, чем прямоугольники с отношением сторон, скажем, 2:1, 3:2 или 5:7? Чтобы ответить на этот вопрос, были проведены специальные эксперименты. Результаты их не вполне убедительны, но все же свидетельствуют о некотором предпочтении, отдаваемом золотому сечению. Впрочем, может ли прямоугольник сам по себе быть захватывающе прекрасным или отталкивающе безобразным?
5.2.Золотой треугольник:
Проводим прямую АВ. От точки А
о ткладываем на ней три раза отрезок О
ткладываем на ней три раза отрезок О
произвольной величины, через
полученную точку Р проводим перпендикуляр к линии
АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1
откладываем на линию Ad1, получая точку С. Она разделила линию Ad1 в пропорции золотого сечения. Линиями Ad1 и dd1 пользуются для построения «золотого»
прямоугольника.
5.3. Золотой пятиугольник; построение Евклида.
Замечательный пример «золотого сечения» представляет собой правильный пятиугольник – выпуклый и звездчатый (рис. 5).

Рис.6. Построение правильного пятиугольника и пентаграммы.
Для построения пентаграммы необходимо построить правильный пятиугольник.
Пусть О - центр окружности, А - точка на окружности и Е - середина отрезка ОА. Перпендикуляр к радиусу ОА, восстановленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.
Есть и золотой кубоид- это прямоугольный параллелепипед с ребрами, имеющими длины 1.618, 1 и 0.618.
Теперь рассмотрим доказательство, предложенное Евклидом в «Началах».
П
стр.75)
осмотрим теперь, как Евклид использует золотое сечение для того, чтобы построить угол в 72 градуса – именно под таким углом видна сторона правильного пятиугольникаиз центра описанной окружности. Начнем с
отрезка АВЕ, разделенного в среднем и
крайнем отношении точкой В. Проведем далее дуги окружностей с центрами в точках В и Е и радиусах АВ, пересекающиеся в точке С. Чуть ниже докажем, что АС=АЕ, а пока примем это на веру.
Итак, пусть АС=АЕ. Обозначим через равные углы ЕВС и СЕВ. Так как АС=АЕ, то угол АСЕ также равен . Теорема о том, что сумма углов треугольника равна 180 градусов, позволяет найти угол ВСЕ: он равен 180-2, а угол ЕАС - 3 - 180. Но тогда угол АВС равен 180-. Суммируя углы треугольника АВС получаем,
180=(3 -180) + (3-180) + (180 - )
Откуда 5=360, значит =72.
Итак, каждый из углов при основании треугольника ВЕС вдвое больше угла при вершине, равного 36 градусов. Следовательно, чтобы построить правильный пятиугольник, необходимо лишь провести любую окружность с центром в точке Е, пересекающую ЕС в точке Х и сторону ЕВ в точке Y: отрезок XY служит одной из сторон вписанного в окружность правильного пятиугольника; Обойдя вокруг всей окружности, можно найти и все остальные стороны.
Докажем теперь, что АС=АЕ. Предположим, что вершина С соединена отрезком прямой с серединой N отрезка ВЕ. Заметим, что поскольку СВ=СЕ, то угол СNЕ прямой. По теореме Пифагора:
CN2 = а2 – (а/2) 2= а2 (1-4 2)
Отсюда имеем (АС/а) 2 = (1+1/2) 2 + (1-1/4 2) = 2+1/ = 1 + = 2
Итак, АС = а = АВ = АЕ, что и требовалось доказать
5.4.Спираль Архимеда.
Последовательно отсекая от золотых прямоугольников квадраты до бесконечности, каждый раз соединяя противоположные точки четвертью окружности, мы получим довольно изящную кривую. Первым внимание на неё обратил древнегреческий ученый Архимед, имя которого она и носит. Он изучал её и вывел уравнение этой спирали.

Рис.7.Спираль Архимеда
В настоящее время спираль Архимеда широко используется в технике.
6.Числа Фибоначчи.
С золотым сечением косвенно связано имя итальянского математика Леонардо из Пизы, который известен больше по своему прозвищу Фибоначчи (Fibonacci - сокращенное filius Bonacci, то есть сын Боначчи)
В 1202г. им была написана книга "Liber abacci", то есть "Книга об абаке" . "Liber abacci" представляет собой объемистый труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший заметную роль в развитии математики в Западной Европе в течение нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими ("арабскими") цифрами.
Сообщаемый в книге материал поясняется на большом числе задач, составляющих значительную часть этого трактата.
Рассмотрим одну такую задачу:
"Сколько пар кроликов в один год от одной пары рождается?
Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, дабы узнать, сколько пар кроликов родится в течение этого года, если природа кроликов такова, что через месяц пара кроликов воспроизведет другую, а рождают кролики со второго месяца после своего рождения"
| Месяцы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Пары кроликов | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 |
Табл.1 Ряд Фибоначчи при u1=1
Перейдем теперь от кроликов к числам и рассмотрим следующую числовую последовательность:
u1, u2 … un
в которой каждый член равен сумме двух предыдущих, т.е. при всяком n>2
un=un-1+un-2.
Данная последовательность асимптотически (приближаясь все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.
Если какой-либо член последовательности Фибоначчи разделить на предшествующий ему (например, 13:8), результатом будет величина, колеблющаяся около иррационального значения 1.61803398875... и через раз то превосходящая, то не достигающая его.
Асимптотическое поведение последовательности, затухающие колебания ее соотношения около иррационального числа Ф могут стать
более понятными, если показать отношения нескольких пеpвых членов последовательности. В этом примере приведены отношения второго члена к первому, третьего ко второму, четвертого к третьему, и так далее:
1:1 = 1.0000, что меньше фи на 0.6180
2:1 = 2.0000, что больше фи на 0.3820
3:2 = 1.5000, что меньше фи на 0.1180
5:3 = 1.6667, что больше фи на 0.0486
8:5 = 1.6000, что меньше фи на 0.0180
По мере продвижения по суммационной последовательности Фибоначчи каждый новый член будет делить следующий со все большим и большим приближением к недостижимому Ф.
Человек подсознательно ищет Божественную пропорцию: она нужна для удовлетворения его потребности в комфорте.
Пpи делении любого члена последовательности Фибоначчи на следующий за ним получается просто обратная к 1.618 величина (1 : 1.618=0.618). Hо это тоже весьма необычное, даже замечательное явление. Поскольку пеpвоначальное соотношение – бесконечная дpобь, у этого соотношения также не должно быть конца.
При делении каждого числа на следующее за ним через одно, получаем число 0.382
1:0.382=2.618
Подбирая таким образом соотношения, получаем основной набор коэффициентов Фибоначчи: 4.235 ,2.618 ,1.618,0.618,0.382,0.236.Упомянем также 0.5.Все они играют особую роль в природе и в частности в техническом анализе.
Тут необходимо отметить, что Фибоначчи лишь напомнил свою последовательность человечеству, так как она была известна еще в древнейшие времена под названием Золотое сечение.
Золотое сечение, как мы видели, возникает в связи с правильным пятиугольником, поэтому и числа Фибоначчи играют роль во всем, что имеет отношение к правильным пятиугольникам - выпуклым и звездчатым.
Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления. Ученые продолжали активно развивать теорию чисел Фибоначчи и золотого сечения. Ю. Матиясевич с использованием чисел Фибоначчи решает 10-ю проблемуГильберта (о решении Диофантовых уравнений). Возникают изящные методы решения ряда кибернетических задач (теории поиска, игр, программирования) с использованием чисел Фибоначчи и золотого сечения. В США создается даже Математическая Фибоначчи-ассоциация,которая с 1963 года выпускает специальный журнал.
Одним из достижений в этой области является открытие обобщенных чисел Фибоначчи и обобщенных золотых сечений. Ряд Фибоначчи (1, 1, 2, 3, 5, 8) и открытый им же «двоичный» ряд чисел 1, 2, 4, 8,16...(то есть ряд чисел до n , где любое натуральное число, меньшее n можно представить суммой некоторых чисел этого ряда) на первый взгляд совершенно разные. Но алгоритмы их построения весьмапохожи друг на друга: в первом случае каждое число есть сумма предыдущего числас самим собой 2 = 1 + 1; 4 = 2 + 2..., во втором – это сумма двух предыдущих чисел 2 =1 + 1, 3 = 2 + 1, 5 = 3 + 2.... Нельзя ли отыскать общую математическую формулу, изкоторой получаются и «двоичный» ряд, и ряд Фибоначчи?
Действительно, зададимся числовым параметром S, который может приниматьлюбые значения: 0, 1, 2, 3, 4, 5... Рассмотрим числовой ряд, S + 1 первых членовкоторого – единицы, а каждый из последующих равен сумме двух членовпредыдущего и отстоящего от предыдущего на S шагов. Если n-й член этого ряда мыобозначим через S (n), то получим общую формулу S (n) = S (n – 1) + S (n – S – 1).
Очевидно, что при S = 0 из этой формулы мы получим «двоичный» ряд, при S = 1 –ряд Фибоначчи, при S = 2, 3, 4. новые ряды чисел, которые получили названиеS-чисел Фибоначчи.
В общем виде золотая S-пропорция есть положительный корень уравнения золотогоS-сечения xS+1 – xS – 1 = 0.
Нетрудно показать, что при S = 0 получается деление отрезка пополам, а при S = 1–знакомое классическое золотое сечение.
Отношения соседних S-чисел Фибоначчи с абсолютной математической точностьюсовпадают в пределе с золотыми S-пропорциями! То есть золотые S-сечения являются числовыми инвариантами S-чисел Фибоначчи.
7.Золотое сечение в искусстве.
7.1. Золотое сечение в живописи.
Переходя к примерам «золотого сечения» в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды».

Нет сомнений, что Леонардо да Винчи был великим художником, это признавали уже его современники, но его личность и деятельность останутся покрытыми тайной, так как он оставил потомкам не связное изложение своих идей, а лишь многочисленные рукописные наброски, заметки, в которых говорится «обо всем на свете».
Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника..
Также пропорция золотого сечения проявляется в картине Шишкина. На этой знаменитой картине И. И. Шишкина с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны - освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали.
В картине Рафаэля "Избиение младенцев" просматривается другой элемент золотой пропорции - золотая спираль. На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции - точки, где пальцы воина сомкнулись вокруг лодыжки ребенка - вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Неизвестно, строил ли Рафаэль золотую спираль или чувствовал её.
Т.Кук использовал при анализе картины Сандро Боттичелли «рождение Венеры» золотое сеченеие .
7.2. Пирамиды золотого сечения.
Широко известны медицинские свойства пирамид, особенно золотого сечения. По некоторым наиболее распространенным мнениям, комната, в которой находится такая пирамида, кажется больше, а воздух - прозрачнее. Сны начинают запоминаться лучше. Также известно, что золотое сечение широко применялась в архитектуре и скульптуре. Примером тому стали: Пантеон и Парфенон в Греции, здания архитекторов Баженова и Малевича
8. Заключение.
Н еобходимо сказать, что золотое сечение имеет большое применение в нашей жизни.
еобходимо сказать, что золотое сечение имеет большое применение в нашей жизни.
Было доказано, что человеческое тело делится в пропорции золотого сечения линией пояса.
Раковина наутилуса закручена подобно золотой спирали.
Благодаря золотому сечению был открыт пояс астероидов между Марсом и Юпитером – по пропорции там должна находиться ещё одна планета.
Возбуждение струны в точке , делящей её в отношении золотого деления, не вызовет колебаний струны, то есть это точка компенсации.
На летательных аппаратах с электромагнитными источниками энергии создаются прямоугольные ячейки с пропорцией золотого сечения.
Джоконда построена на золотых треугольниках, золотая спираль присутствует на картине Рафаэля «Избиение младенцев».
Пропорция обнаружена в картине Сандро Боттичелли «Рождение Венеры»
Известно много памятников архитектуры, построенных с использованием золотой пропорции, в том числе Пантеон и Парфенон в Афинах, здания архитекторов Баженова и Малевича.
Иоанну Кеплеру, жившему пять веков назад, принадлежит высказывание: "Геометрия обладает двумя великими сокровищами. Первое - это теорема Пифагора, второе - деления отрезка в крайнем и среднем отношении"
Литература:
1. Д. Пидоу. Геометрия и искусство. – М.: Мир, 1979. 2. Журнал "Наука и техника"
3. Журнал «Квант», 1973, № 8. 4. Журнал «Математика в школе», 1994, № 2; № 3.
5. Ковалев Ф.В. Золотое сечение в живописи. К.: Выща школа, 1989.
6. Стахов А. Коды золотой пропорции.
7.Воробьев Н.Н. "Числа Фибоначчи" - М.: Наука 1964
8. "Математика - Энциклопедия для детей" М.: Аванта +, 1998
9. Информация из интернета.
Курсовая: Геологическое строение, классификация и образование россыпей Курсовая работа представляет попытку обобщения материала некоторых научных робот касающихся "учения о россыпях". Объем этого материала весьма значителен и поэтому в работе приведено описание процессов образования, строения и классификации россыпей лишь в самых общих чертах.
Реферат Дизайн Термин "дизайн" появился в нашей стране недавно. До этого проектирование вещей назвалось "художественным конструированием", а теория создания вещей “технической эстетикой". В переводе с английского "дизайн" означает рисование. Это слово породило и производные понятия: “дизайнер" - художник-конструктор, "дизайн-форма” - внешняя форма предмета и др.
Реферат Кубизм. На примере творчества П. Пикассо Сложившиеся в 1900-е годы художественные тенденции, для которых характерно выраженное в полемической форме противопоставление себя прежним традициям творчества, равно как окружающим социальным стереотипам в целом, получили название авангардизм.
Тезисы, конспект: Пирамиды Чудеса света создавались на протяжении огромного промежутка времени c xxx по III век до нашей эры. Много великих событий случилось за это время. Целые народы исчезли с лица земли, одни цивилизации сменялись другими. Но влияние погибших культур осталось.
Доклад: Золотое сечение в природе и искусстве Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии.
Реферат Правильные и полуправильные многогранники Правильным многогранником называется выпуклый многогранник, грани которого – равные правильные многоугольники, а двугранные углы при всех вершинах равны между собой. Доказано, что в каждой из вершин правильного многогранника сходится одно и то же число граней и одно и то же число ребер. Всего в природе существует пять правильных многогранников.
Курсовая: Благородные металлы на службе у человека История благородных металлов - одна из самых интересных глав истории материальной культуры. По мнению многих ученых, золото было первым металлом, который человечество начало использовать для изготовления украшений, предметов домашнего обихода и религиозного культа. Золотые изделия были найдены в культурных слоях эпохи неолита (V-IV тысячелетия до н.э.).
Билеты: Ответы на билеты по физике за 9 класс МД – изменение тела в пространстве относ других тел. Тело, размерами которого можно пренебречь называется материальной точкой. Положение тела в пространстве можно опред. Спомощью другого тела (это будет тело отсчета). Т.О.+сис.коор.+t - сис.отсч. Характ м
nreferat.ru
ГОУ Гимназия №1505
«Московская городская педагогическая гимназия-лаборатория»
Реферат
Золотое сечение
Выполнила
ученица 9 класса «А» Павлова Анна
Руководитель
Илларионова Т.И.
Москва
2011
Оглавление
Введение. 3
Глава 1 Золотое сечение — симметрия или ассиметрия?.. 4
Золотое сечение. 9
Глава 2 Золотые фигуры… 11
1. Золотой прямоугольник. 11
2. Золотой треугольник. 12
3. Золотой кубоид. 12
4. Пентаграмма. 13
5. *Золотая спираль. 16
Глава 3 Применение золотого сечения и его фигур. 18
Золотое сечение в скульптуре. 21
Золотое сечение в архитектуре. 24
Золотое сечение в изобразительном искусстве. 26
Заключение. 30
Список литературы… 31
Я люблю гулять по центру Москвы, где стоит множество старинных зданий с украшением в виде геометрических фигур содержащих золотое сечение. Они приковывают взгляд человека и заставляют восхищаться своей красотой. Мне стало интересно заглянуть за рамки учебника по геометрии, и посмотреть о роли золотого сечения в культурной сфере жизни.
Золотое сечение (или пропорция Фидия), по мнению многих исследователей, является наиболее приятной для человеческого глаза. Этим можно объяснить ее многогранное применение человеком, например такие сферы как архитектура, живопись, фотография и ландшафтный дизайн широко используют эту пропорцию и связанные с ней свойства. Это пропорция была в почете у умнейших людей, таких как Леонардо Да Винчи и Ле Корьбюзье. Художник и архитектор Леонардо Да Винчи считал, что идеальные пропорции человеческого тела должны быть связаны с золотым сечением. Архитектор Ле Корьбюзье руководствовался им во множестве своих работ. Мне же хотелось получить первоначальные знания по этой теме.
В эпоху Возрождения золотое сечение было очень популярно например было принято брать размеры картины такими, чтобы отношение ширины к высоте было равно числу Фидия. Форму золотого сечения придавали не только картинам, но и книгам, столам, открыткам. Поэтому мне бы хотелось подробнее рассмотреть применение золотого сечения в различные эпохи от древности, эпохи Возрождения до XlX века. Для этого нужно прочитать и изучить литературу, связанную с этой темой, найти наиболее интересные факты и изложить их в своем реферате.
Цель данного реферата заключается в том, чтобы представить информацию наглядно и интересно. Для достижения цели поставлены следующие задачи
1. дать определение понятий симметрии и ассиметрии, золотое сечение.
2. описать золотые фигуры и построить некоторые из них
3. рассказать о применении и использовании божественной пропорции человеком
Для написания своей работы я использую следующую литературу: Азевич А.И. «Двадцать уроков гармонии», Ведов В. «Пирамиды здоровья», Сагателова С. С., Студенецкая В.Н. «Геометрия: красота и гармония. Простейшие задачи аналитической геометрии на плоскости. Золотая симметрия, Пропорция вокруг нас. 8-9 классы: элективные курсы», Н.Я. Виленкин «За страницами учебника математики», статьи из электронной версии библиотеки «Наука и техника», электронная версия энциклопедии для детей по математике. Книга Азевич А.И. «Двадцать уроков гармонии», по моему мнению, хорошо раскрывает тему симметрии и ассиметрии, и дает понятные и подробные начальные сведения о золотом сечении. Сагателова С. С., Студенецкая В.Н. «Геометрия: красота и гармония. Простейшие задачи аналитической геометрии на плоскости. Золотая симметрия, Пропорция вокруг нас. 8-9 классы: элективные курсы» хорошо описывает золотые фигуры и способы их построения. Н.Я. Виленкин «За страницами учебника математики» подробно объясняет выведение формул золотого сечения и их свойства, так же хорошо описывает построения золотого сечения и пентаграммы. Ведов В. «Пирамиды здоровья» доступно и понятно объясняет ряд Фибоначчи и получения числа Фидия. Статьи из электронной версии библиотеки «Наука и техника», электронная версия энциклопедии для детей по математике дают подробное описание применения золотого сечения в древности, эпохи Возрождения и XIX веке.
Важнейшая цель этого реферата – показать красоту как главную категорию эстетики и математики.
Задумывались ли вы когда-нибудь над значением слова «гармония»?
Гармония греческое слово, обозначающее «согласованность, соразмерность, единство частей и целого». Внешне гармония может проявляться в мелодии, ритме, симметрии и пропорциональности. Две последние относятся к математике. Математика уникальное средство познания красоты. Поскольку красота многогранна и многолика, она подтверждает универсальность математических закономерностей.
Во всем царит гармонии закон,
И в мире всё суть ритм, аккорд и тон.
Дж. Драйден[1]
Продолжим рассказ по принципу от большего к меньшему.
Симметрия – основополагающий принцип устройства мира.
Симметрия – в широком или узком смысле, в зависимости от того, как вы определяете значение этого понятия, — является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство.[2]
Г. Вейль
Симметрия – распространенное явление, ее всеобщность служит эффективным методом познания природы. Симметрия в природе нужна, чтобы сохранять устойчивость. Внутри внешней симметрии лежит внутренняя симметрия построения, гарантирующая равновесие. Симметрия – проявление стремления материи к надежности и прочности.
Симметричные формы обеспечивают повторяемость удачных форм, поэтому более устойчивы к различным воздействиям. Симметрия многообразна.
Неизменность тех или иных объектов может наблюдаться по отношению к разным операциям – поворотам, отражениям, переносам.
Существует три главных вида симметрии изучаемых в школе: симметрия относительно точки (центральная симметрия), симметрия относительно прямой (осевая симметрия) и симметрия относительно плоскости.
Центральная симметрия цветка
Центральная симметрия в орнаменте созданном человеком.
Симметрия относительно прямой на примере здания МГУ
Симметрия относительно плоскости в шаре.
Это не единственные виды симметрии, также существует и винтовая симметрия. Если рассматривать расположение листьев на ветке дерева мы заметим, что лист отстоит от другого, но и повернут вокруг оси ствола. Листья располагаются на стволе по винтовой линии, чтобы не заслонять друг от друга солнечный свет.
Винтовая симметрия в природе на примере ракушки .
Использование винтовой симметрии человеком на примере лестницы .
Симметрия многолика. Она обладает свойствами, которые одновременны и просты и сложны, способны проявляться и единожды и бесконечно много раз.
Если человеку мало знакомому предложить несколько фигур, он интуитивно выберет наиболее симметричные. Скорее всего, оказавшись в такой ситуации, мы выберем равносторонний треугольник или квадрат.
Человек инстинктивно стремится к устойчивости, удобству и красоте. Мир настолько хаотичен и непредсказуем, что человеку наиболее приятны для восприятия фигуры и вещи, содержащие в себе порядок, гармонию, симметрию. Работать с фигурами, у которых больше симметрий легче.
По тому, сколько симметрий имеют фигуры, можно проводить их классификацию. Самой совершенной фигурой считается шар, обладающий всеми видами симметрии.
Симметрия трудолюбива. Каждому своему виду она дает могущество порождать все новые и новые фигуры.
Симметрию можно наблюдать во всех сферах нашей жизни: симметрия построения зданий, музыки и симметрия образов в литературе, симметрия танца.
Симметрия является одним из принципов построения мира.
Симметрия – страж покоя,
Асимметрия – двигатель жизни.[3]
Гармоничным может быть и ассиметричное. Симметрия вызывает чувство покоя, неподвижности, то асимметрия вызывает ощущение движения и свободы.
Исследователи, получившие Нобелевскую премию, показали, что наш мир несимметричен, законы симметрии во Вселенной не наблюдаются. Мир асимметричен на всех уровнях: от элементарных частиц до биологических видов.
Золотое сечение
Самым известным примером гармонии ассиметрии является золотое сечение. Есть слова, принадлежащие Иоганну Кеплеру: «Геометрия владеет двумя сокровищами: одно из них – теорема Пифагора, другое – деление отрезка в среднем и крайнем отношении»[4] Великий ученый пол словами «деление отрезка в среднем и крайнем отношении» имеет ввиду известную пропорцию – золотое сечение. Именно эта пропорция является темой моего реферата. В следующих главах я расскажу о применении золотого сечения, а ниже дам определение этого понятия и способы его получения.
Деление отрезка в среднем и крайнем отношении называют золотым сечением. Другое название – «золотая пропорция».[5]
с: b = b: а.
Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему отрезку.
a=c-b
b:c= (c-b): а
В пропорции произведение крайних членов равно произведению средних
b2 + cb – c2 =0
Длина отрезка выражается положительным числом, поэтому после преобразований
b= −(c+√5с2 )∕2 или b=(√5−1)∕2∙с
Число (√5−1)∕2 обозначается буквой в честь древнегреческого скульптора Фидия, в творениях которого это число встречается многократно.
Число — иррациональное. В практике его используют округляя до тысячных 0,618 или сотых 0,62 или десятых 0,6.
Части золотого сечения приблизительно составляют 62% и 38% всего отрезка.
Древние математики обнаружили, что золотое сечение можно получить при помощи геометрии, и потом применять в любом масштабе, даже для строительства пирамид.
Я предлагаю рассмотреть один из многих способов, как это можно сделать.
1. Построим отрезок AB, восстановим в точке B перпендикуляр к AB, на нем отложим точку E таким образом, чтобы BE=0,5AB
2. Далее соединив точки A и E, отложим ED=BE, и AC=AD. Точка С является искомой, она производит «золотое сечение» отрезка AB.
Заметим, что по теореме Пифагора
(AD + DE)2 =AB2 + BD2 ,
а по построению AD=AC, DE=BE=0,5AB
Из этих равенств следует, что AC2 + AC∙AB=AB2, а отсюда можно получить равенство
AC:AB=CB:AC
Свойства [6]
Первое свойство:
1∕ ≈ −1
то есть 1∕1,618≈1,618−1
Второе свойство:
2 ≈ +1
то есть 1,618∙1,618≈2,618=1,618+1
Эти свойства имеют многогранные применения, но об этом в следующей части.
На основе идеи золотого сечения существуют различные фигуры, содержащие эту пропорцию. Аналогично названию пропорции, их называют «золотые фигуры». Каждая такая фигура обязательно содержит пропорцию Фидия.
1. Золотой прямоугольник [7]
Золотой прямоугольник – прямоугольник, у которого отношение смежных сторон дает пропорцию Фидия. А форму «золотого сечения» придавали книгам, столам и т.д. «Золотой прямоугольник» обладает интересным свойством: если от него отрезать квадрат, то останется вновь «золотой прямоугольник». Так можно продолжать до бесконечности. Если провести диагонали первого и второго прямоугольников, то точка О их пересечения принадлежит всем получаемым «золотым прямоугольникам»
Произведения в искусстве значительно улучшены с использованием знания Золотого прямоугольника. Притягательность его ценности и употребления были особенно сильны в древнем Египте и Греции и во времена Ренессанса, т.е. во всех важных периодах цивилизации. Леонардо да Винчи ( Leonardo da Vinci ) придавал огромное значение Золотой пропорции. Он также находил ее приятной в своих соотношениях и говорил: Если предмет не имеет правильного облика, он не работает. Многие из его картин обладают правильным обликом, потому что он использовал Золотое сечение для того, чтобы усилить их привлекательность.
2. Золотой треугольник [8]
Золотой треугольник представляет собой равнобедренный треугольник, у которого отношение длины боковой стороны к длине основания равняется числу Фидия. Одним из его свойств является то что, длины биссектрис его углов при основании равны длине самого основания. Остальные свойства «вытекают» из свойств пентаграммы, которую мы рассмотрим позже.
Стороны золотого треугольника образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.
Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.
Одним из свойств золотого треугольника является то что, длины биссектрис его углов при основании равны длине самого основания. Остальные свойства вытекают из свойств пентаграммы, которую мы рассмотрим позже.
Построение золотого треугольника
Проводим прямую АВ. От точки А откладываем на ней три раза отрезок О произвольной величины, через полученную точку Р проводим перпендикуляр к линии АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1 откладываем на линию Ad1, получая точку С. Точка С разделила линию Ad1 в пропорции золотого сечения.
3. Золотой кубоид
«Золотой кубоид» — это прямоугольный параллелепипед с ребрами. «Золотой кубоид» – это прямоугольный параллелепипед с ребрами длиной Ф, 1 и j. Площадь его поверхности равна 4Ф, а диагональ – 2. Описанная вокруг него сфера имеет радиус «1». Значит, площадь ее поверхности равна 4p. Следовательно, отношение площади поверхности этой сферы к площади поверхности «золотого кубоида» равно p / Ф.
Пятиконечная звезда, пожалуй, является одной из самых известных фигур. Она постоянно привлекала внимание людей своим совершенством. Пифагорейцы – ученики Пифагора выбрали ее в качестве символа своего союза именно эту звезду. Ее же считали амулетом здоровья. Сейчас звезда используются на многих флагах и гербах многих стран. Почему же она так привлекает, притягивает взгляд? Дело в том, что в этой звезде есть удивительное постоянство отношений составляющих ее отрезков.
Нужно построить ее, чтобы в этом убедиться.
Для построения пентаграммы необходимо построить правильный пятиугольник. Способ его построения разработал немецкий живописец и график Альбрехт Дюрер (1471...1528). Пусть O – центр окружности, A – точка на окружности и Е – середина отрезка ОА. Перпендикуляр к радиусу ОА, восставленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения. Описание построения золотого треугольника написано выше.
Линиями Ad1 и dd1 пользуются для построения «золотого» прямоугольника.
Построения золотых пятиугольника и пентаграммы содержатся уже в «Началах» Евклида, написанных за 300 лет до нашей эры. Процесс построения циркулем и линейкой описан еще в первой главе.
Пентаграмма из церкви Святого Петра .
Структура яблока в разрезе.
Если разрезать поперёк яблоко или грушу, то мы увидим вот такую структуру расположения семян. Цветы этих деревьев так же имеют структуру пятиугольника.
Пятиконечная звезда – это вторая пространственная структура вокруг которой гнездятся мистика и в разное время у разных народов пятиконечная звезда означала разное.
У пифагорейцев — символ здоровья и совершенства, опознавательный знак общины.
В христианской символике пентаграмма символизирует пять ран Иисуса или, в числовом толковании, сумму Троицы (Отец, Сын и Дух Святой) и двойственной природы Христа (божественной и человеческой).
На фото приведена деталь отделки северного фасада Амьенского собора. Амьенский собор (фр. Cathédrale Notre-Dame d'Amiens) — самый большой из французских соборов по своему объему (200 000 м³).
Перевёрнутая пентаграмма, пятиконечная звезда с тремя лучами, направленными вниз, в начале истории христианства перевёрнутая пентаграмма трактовалась как символ Преображения Христа.
Различают также “мужскую” и “женскую” пентаграммы (женская в с двумя лучами кверху). Иногда (особенно в Алхимии) упоминается как защитный знак, так как вызванный демон не мог переступить её линий. Например, в “Фаусте” Гёте сам Мефистофель не мог покинуть комнату, пока на выходе была нарисованна пентаграмма. Тамплиеры считали Пентаграмму символом Священного Женского Начала, а в Индии пентаграмма — символ Венеры (богини Кали).[10]
5. *Золотая спираль
Расскажем ещё об одном замечательном применении золотого сечения в геометрии – о золотой спирали. Строго говоря, спираль не является фигурой, скорее кривой, но именно в этой главе уместно описать её.
Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется его именем. Увеличение ее шага всегда равномерно. В настоящее время спираль Архимеда широко применяется в технике.
Еще Гете подчеркивал тенденцию природы к спиральности. Он называл спираль «кривой жизни». Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Совместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке, семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения. Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Молекула ДНК закручена двойной спиралью.
Существует математическая прогрессия, известная как ряд Фибоначчи, и она имеет особое отношение к числу фи и пирамидам в Гизе. Принципы этого ряда впервые изложил средневековый математик Леонардо Фибоначчи. Этот ряд использовали для описания роста растений. Вот эта последовательность: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 и так далее. Для того, чтобы получить каждое следующее число в этом ряду, надо сложить два предыдущих: 1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13 и так далее.
У этой последовательности очень интересное соотношение с числом фи: если разделить каждый член этого ряда на предыдущий, полученные результаты будут стремиться к трансцендентному числу 1,6180339.
1/1=1, 2/1=2, 3/2=1.5, 5/3=1.66, 13/8=1.625, 21/13=1.615, 34/21=1.619, 55/34=1.617, 89/55=1.6181, Чем дальше вы будете продолжать считать, тем ближе будете подходить к числу фи. Конечно, вы никогда не дойдете до него, потому что у него нет арифметического решения, но вы будете бесконечно приближаться к нему. Эту последовательность можно изобразить графически, в виде так называемой спирали Фибоначчи.
Эта спираль почти идентична логарифмической спирали фи, известной как спираль золотого сечения. Разница заключается в том, что спираль Фибоначчи – это интерпретация (при помощи целых чисел) арифметически невозможной спирали золотого сечения, у которой нет ни конца, ни начала. У спирали Фибоначчи есть определенное начало.[11]
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Kорбюзье нашел, что в рельефе из храма фараонa Cети I в Абидосе и в рельефе, изображающем фараона Pамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.
Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Kвадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.
Платон (427...347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления. В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.
В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж.Kампано из Наварры (III в.) сделал к переводу комментарии. Cекреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.
В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре. Леонардо да Винчи, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески, написавшего две книги, одна из которых называлась «О перспективе в живописи». Его считают творцом начертательной геометрии.
Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Kнига была восторженным гимном золотой пропорции. Cреди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок — бога отца, а весь отрезок — бога духа святого).
Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.
В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет. «Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать».Cудя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Pост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица — ртом и т.д. Известен пропорциональный циркуль Дюрера.
Великий астроном XVI в. Иоган Kеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение). Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности».
В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы «вместе с водой выплеснули и ребенка». Вновь «открыто» золотое сечение было в середине XIX в.
В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях «математической эстетикой».[12]
Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа — важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13: 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8: 5 = 1,6. У новорожденного пропорция составляет отношение 1: 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела — длина плеча, предплечья и кисти, кисти и пальцев и т.д.
Справедливость своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского. Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры. Цейзинг дал определение золотому сечению, показал, как оно выражается в отрезках прямой и в цифрах.
Когда цифры, выражающие длины отрезков, были получены, Цейзинг увидел, что они составляют ряд Фибоначчи, который можно продолжать до бесконечности в одну и в другую сторону. Следующая его книга имела название «Золотое деление как основной морфологический закон в природе и искусстве». В 1876 г. в России была издана небольшая книжка, почти брошюра, с изложением этого труда Цейзинга. Автор укрылся под инициалами Ю.Ф.В. В этом издании не упомянуто ни одно произведение живописи.
Золотое сечение в скульптуре
Эти пропорции человеческого тела использовались еще античными скульпторами при создании скульптур. Известна золотая пропорция статуи Аполлона Бельведерского: рост изображенного человека делится пупочной линией в золотом сечении.
Дорифор — это не изображение конкретного спортсмена-победителя, а иллюстрация канонов мужской фигуры.
Иногда эту статую так и называли — «Канон Поликлета», вслед за одноименным теоретическим трактатом его создателя. Поликлет выводил там цифровой закон идеальных пропорций человека. Эти пропорции находятся друг с другом в цифровом соотношении. Вдобавок, в нем воплощаются теоретические идеи о перекрещенном распределении напряжения в руках и ногах. Основы пифагореизма, этой числовой магии, которой придерживался Поликлет, тоже повлияли на пропорции Копьеносца.
Венера Милосская, статуя богини Афродиты и эталон женской красоты, является одним из лучших памятников греческого скульптурного искусства — также построена на пропорциях золотого сечения
Хочется так же подтвердить на примере восхищение этой скульптурой. Многие поэты посвящали ей стихи и строчки, например, такие как Маяковский и Афанасий Фет, Марк Лисянский, Татьяна Бориневич-Эклога, Дроздова.[13] И мне хочется процитировать наиболее удачные из них:
Афанасий Фет «Венера Милосская»
И целомудренно и смело,
До чресл сияя наготой,
Цветет божественное тело
Неувядающей красой.
Под этой сенью прихотливой
Слегка приподнятых волос
Как много неги горделивой
В небесном лике разлилось!
Так, вся дыша пафосской страстью,
Вся млея пеною морской
И все победной вея властью,
Ты смотришь в вечность пред собой.
Марк Лисянский «Венера» [14]
Одной рукой поддерживая тогу,
Не поднимая трепетных ресниц,
Как тайна красоты,
Как вызов богу.
Она стоит. царица всех цариц.
На длинной шее
Ни единой складки,
Две линии намечены едва.
И ямка у ключицы
Дышит сладко,
И ожерелье словно кружева.
Она стоит открыто,
Не таится,
А молодая мраморная грудь
Вздымается, волнуется, теснится,
Высокая и теплая чуть-чуть.
Весенним ранним утром
Земледелец
Её нашел случайно в борозде.
Крестьянский сын,
Тудяга и умелец,
Он ахнул,
Удивился красоте.
Он за неё в тревоге был,
Не зная
Среди своих бесчисленных забот,
Что женщина вот эта неземная
До наших дней
Спокойно доживет.Золотое сечение в архитектуре
Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.). [15]
На рисунках виден целый ряд закономерностей, связанных с золотым сечением. Пропорции здания можно выразить через различные степени числа Ф=0,618...
Золотое соотношение мы можем увидеть и в здании собора Парижской Богоматери (Нотр-дам де Пари), и в пирамиде Хеопса:
Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.
Что касается пирамид, то не только египетские пиpамиды постpоены в соответствии с совеpшенными пpопоpциями золотого сечения, то же самое явление обнаpужено и у Мексикансих пирамид.[16]
Мексиканские пирамиды
Hа попеpечном сечении пиpамиды видна фоpма, подобная лестнице.В пеpвом яpусе 16 ступеней, во втоpом 42 ступени и в тpетьем — 68 ступеней.
Эти числа основаны на соотношении Фибоначчи следующим обpазом:
16 x 1.618 = 26
16 + 26 = 42
26 x 1.618 = 42
42 + 26 = 68
Золотое сечение в изобразительном искусстве
На картине И.И. Шишкина «Сосновая роща» просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины приблизительно в золотом сечении. Справа от сосны — освещенный солнцем пригорок. Он делит в золотом сечении правую часть картины по горизонтали. Слева от главной сосны находится множество сосен — при желании можно с успехом продолжить деление картины в пропорциях золотого сечения.
Наличие в картине ярких вертикалей и горизонталей, делящих ее в отношении золотого сечения, придает ей характер уравновешенности и спокойствия, в соответствии с замыслом художника. Когда художник создает картину с бурно развивающимся действием, подобная геометрическая схема композиции (с преобладанием вертикалей и горизонталей) становится неприемлемой.
Ощущение динамики, волнения проявляется, пожалуй, сильней всего в другой простой геометрической фигуре — спирали. Многофигурная композиция, выполненная в 1509 — 1510 годах Рафаэлем, когда прославленный живописец создавал свои фрески в Ватикане, отличается динамизмом и драматизмом сюжета. Рафаэль так и не довел свой замысел до завершения, однако, его эскиз был гравирован неизвестным итальянским графиком Маркантинио Раймонди, который на основе этого эскиза и создал гравюру«Избиение младенцев».
Если на подготовительном эскизе Рафаэля мысленно провести линии, идущие от смыслового центра композиции — точки, где пальцы воина сомкнулись вокруг лодыжки ребенка, — вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза (на рисунке эти линии проведены красным цветом), а после этого соединить эти куски кривой пунктиром, то с очень большой точностью получается золотая спираль. Это можно проверить, измеряя отношение длин отрезков, высекаемых спиралью на прямых, проходящих через начало кривой.
Неизвестно, рисовал ли на самом деле Рафаэль золотую спираль при создании композиции «Избиение младенцев» или только «чувствовал» ее. Однако с уверенностью можно сказать, что гравер Раймонди эту спираль увидел. Об этом свидетельствуют добавленные им новые элементы композиции, подчеркивающие разворот спирали в тех местах, где она у нас обозначена лишь пунктиром. Эти элементы можно увидеть на окончательной гравюре Раймонди: арка моста, идущая от головы женщины, — в левой части композиции и лежащее тело ребенка — в ее центре.
Переходя к примерам “золотого сечения” в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Посмотрим внимательно на картину «Джоконда». Композиция портрета построена на«золотых треугольниках».
Портрет Моны Лизы (Джоконда) привлекает тем, что композиция рисунка построена на «золотых треугольниках», точнее на треугольниках, являющихся кусками правильного звездчатого пятиугольника. Зрачок левого глаза, через который проходит вертикальная ось полотна, находится на пересечении двух биссектрис верхнего золотого треугольника, которые с одной стороны, делят пополам углы при основании золотого треугольника, а с другой стороны, в точках пересечения с бедрами золотого треугольника делят их в пропорции Золотого сечения. [17]
Таким образом, Леонардо Да Винчи использовал в своей картине не только принцип симметрии, но и Золотое сечение
Картина «Святое семейство» Микеланджело признана одним из шедевров западноевропейского искусства эпохи Возрождения. Гармонический анализ показал, что композиция картины основана на пентакле.
В. И. Суриков «Боярыня Морозова».
Роли ее отведена средняя часть картины. Она окована точкой высшего взлёта и точкой низшего спадания сюжета картины.
1) Это — взлёт руки Морозовой с двуперстным крестным знамением как высшая точка.
2) Это — беспомощно протянутая к той же боярыне рука, но на этот раз — рука старухи — нищей странницы, рука, из-под которой вместе с последней надеждой на спасение выскальзывает конец розвальней.
А как обстоит дело с «высшей точкой»? На первый взгляд имеем кажущееся противоречие: ведь сечение А1В1, отстоящее на 0,618… от правого края картины, проходит не через руку, не даже через голову или глаз боярыни, а оказывается где-то перед ртом боярыни!
Золотое сечение режет здесь действительно по самому главному.
В нём, и именно в нём, — величайшая сила Морозовой.[18]
В ходе работы были раскрыты понятия симметрии и ассиметрии, золотого сечения и золотых фигур. Были описаны произведения изобразительного искусства, зодчества, скульптурного мастерства, созданные с использованием золотой пропорции.
Таким образом, цель реферата я считаю выполненной.
В 13 веке от Рождества Христова известный итальянский математик известный по имени Фиббоначи, наблюдая за различными явлениями живой природы, открыл золотую пропорцию – бесконечную последовательность чисел, где каждое последующее число является сумой двух предыдущих; разделив каждое предыдущее на последующее мы всегда будем получать приблизительно 0,618 (например 987/1597=0,618034). Леонардо Да Винчи, создавая свои картины, использовал особый способ структурного совершенства: он называл его Золотым Сечением, при котором отношение всего отрезка к большей части равно отношению большей части к меньшей и приблизительно равно 0,618. До этого в 6 веке нашей эры греческий философ и математик Пифагор находит это соотношение в геометрии. А в 3 веке нашей эры упоминание о нем можно найти и у древних египтян, которые называли его божественной сутью. Возможно, им было дано знание о существовании особых законов гармонии, которые являются основой всего совершенного в этом мире. Теперь о воде. В обычной воде угол между водородными связями равен 104, а у талой 108 и соотношение длин водородных связей 0,618. Некоторые ученые предполагают, что замерзая и оттаивая, вода неизменно сохраняет одну базовую программу жизни, именно по этой программе и создавалось все совершенное.
Литература
1) Азевич А.И. Двадцать уроков гармонии — Москва, изд-во «Школа-Пресс», 1998 год.
2) Ведов В. Пирамиды здоровья. – Санкт-Петербург, издательство «Весь» — добрые вести, 2000 год.
3)Сагателова С. С., Студенецкая В.Н. Геометрия: красота и гармония. Простейшие задачи аналитической геометрии на плоскости. Золотая симметрия, Пропорция вокруг нас. 8-9 классы: элективные курсы – Волгоград, изд-во «Учитель», 2007 год
4) Виленкин Н.Я. «За страницами учебника математики» — Москва, изд-во «Просвещение», 2007 год.
Интернет- ресурсы
1) сайт электронной библиотеки «Наука и техника»: n-t.ru/tp/iz/zs.htm
Данные соответствуют – 19.04.2011
2) статьи из энциклопедии для детей по математике: netnotes.narod.ru/math/gold6.html Данные соответствуют -20.04.2011
[1] Азевич А.И. Двадцать уроков гармонии — Москва, изд-во «Школа-Пресс», 1998 год.
[2] Там же
[3] Азевич А.И. указанное сочинение
[4] Сагателова С. С., Студенецкая В.Н. Геометрия: красота и гармония. Простейшие задачи аналитической геометрии на плоскости. Золотая симметрия, Пропорция вокруг нас. 8-9 классы: элективные курсы – Волгоград, изд-во «Учитель», 2007 год
[5] n-t.ru/tp/iz/zs.htm Данные соответствуют 10.04.2011. Интернет сайт Библиотеки Мошкова, автор данной статьи Виктор Лаврус.
[6] Азевич А.И. указанное сочинение
[7] n-t.ru/tp/iz/zs.htm электронная библиотека «Наука и техника» — действительно на 11.04.2011
[8] Там же.
[9] Виленкин Н.Я. За страницами учебника математики – Москва, изд-во «Просвещение», 2007 год.
[10] fictionbook.ru/author/litagent_audiokniga/yenciklopediya_simvolov/read_online.html?page=1 действительна на 04.04.2011
[11] n-t.ru/tp/iz/zs.htm указанное сочинение действительна на 19.04.2011
[12] www.abc-people.com/data/leonardov/zolot_sech-txt.htm действительна на 10.04.2011. Электронная версия энциклопедии «энциклопедия замечательных людей и идей»
Часть фактов была взята с world.lib.ru/s/shakirow_d_s/zolotoececxenie.shtml Шакиров Даян Шамилевич «секрет гениальности» Действительна на 10.04.2011
[13] www.liveinternet.ru/community/1726655/post64489082/ Действительна на 24.04.2010
[14] Там же
[15] www.tech-to-life.com/publ/1-1-0-18 Действительна на 19.04.2011
[16] piramidlandia.at.ua/ Действительна на 19.04.2011
[17] www.abc-people.com/idea/zolotsech/golden-section-pic002.htm указанное сочинение
[18] www.tech-to-life.com/publ/1-1-0-18 указанное сочинение
www.ronl.ru