Геометрия Евклида – первая естественно-научная теория. Зарождение геометрии начала евклида реферат

Реферат:

Государственное учреждение высшего профессионального образования

«Национальный исследовательский Томский политехнический университет»

Евклидова и неевклидова геометрия

Выполнил:

студент 1-ого курса

группа 4А21 ИФВТ

Асеев Александр

Томск 2012

Евклидовая и неевклидовая геометрия

Постулаты Евклида

Евклид – автор первого дошедшего до нас строгого логического построения геометрии. В нем изложение настолько безупречно для своего времени, что в течение двух тысяч лет с момента появления его труда “Начал” оно было единственным руководством для изучающих геометрию.

“Начала” состоят из 13 книг, посвященных геометрии и арифметике в геометрическом изложении.

Каждая книга “Начал” начинается определением понятий, которые встречаются впервые. Так, например, первой книге предпосланы 23 определения. В частности,

1. Точка есть то, что не имеет частей.

2. Линия есть длины без ширины

3. Границы линии суть точки.

Вслед за определениями Евклид приводит постулаты и аксиомы, то есть утверждения, принимаемые без доказательства.

Постулаты

1. Требуется, чтобы от каждой точки ко всякой другой точке можно было провести прямую линию.

2. И чтобы каждую прямую можно было неопределенно продолжить.

3. И чтобы из любого центра можно было описать окружность любым радиусом.

4. И чтобы все прямые углы были равны.

5. И чтобы всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними односторонние внутренние углы, сумма которых меньше двух прямых, эти прямые пересекались с той стороны, с которой эта сумма меньше двух прямых.

Аксиомы

1. Равные порознь третьему равны между собой.

2. Если к ним прибавим равные, то получим равные.

3. Если от равных отнимем равные, то получим равные.

4. Если к неравным прибавим равные, то получим неравные.

5. Если удвоим равные, то получим равные.

6. Половины равных равны между собой.

7. Совмещающиеся равны.

8. Целое больше части.

9. Две прямые не могут заключать пространства.

Иногда IV и V постулаты относят к числу аксиом. Поэтому пятый постулат иногда называют XI аксиомой. По какому принципу одни утверждения относятся к постулатам, а другие к аксиомам, неизвестно.

Никто не сомневался в истинности постулатов Евклида, что касается и V постулата. Между тем уже с древности именно постулат о параллельных привлек к себе особое внимание ряда геометров, считавших неестественным помещение его среди постулатов. Вероятно, это было связано с относительно меньшей очевидностью и наглядностью V постулата: в неявном виде он предполагает достижимость любых, как угодно далеких частей плоскости, выражая свойство, которое обнаруживается только при бесконечном продолжении прямых.

Попытки доказательств V постулата Евклида

Возможно, что уже сам Евклид пытался доказать постулат о параллельных. В пользу этого говорит то обстоятельство, что первые 28 предложений “Начал” не опираются на V постулат. Евклид как бы старался отодвинуть применение этого постулата до тех пор, пока использование его не станет настоятельно необходимым.

Одни математики старались доказать постулат о параллельных, применяя только другие постулаты и те теоремы, которые можно вывести из последних, не используя сам V постулат. Все такие попытки оказались неудачными. Их общий недостаток в том, что в доказательстве неявно применялось какое-нибудь предположение, равносильное доказываемому постулату.

Другие предлагали по-новому определить параллельные прямые или же заменить V постулат каким-либо, по их мнению, более очевидным предложением. Так, например, в XI веке Омар Хайям ввел вместо V постулата “принцип”, согласно которому две лежащие в одной плоскости сходящиеся прямые пересекаются и не могут расходиться в направлении схождения. С помощью этого принципа Хайям доказывает, что в четырехугольнике ABCD, в котором углы при основании А и В – прямые и стороны АС, ВD равны, углы С и D так же прямые, а из этого предложения о существовании прямоугольника выводится V постулат. Рассуждения Хайяма получили оригинальное развитие в XIII веке у Насирэдинна ат-Туси, работы которого в свою очередь стимулировали исследования Д. Валлиса. В 1663 году Валлис доказал постулат о параллельных, исходя из явного допущения, что для каждой фигуры существует подобная ей фигура произвольной величины. Это допущение он считал вытекающим из существа пространственных отношений.

С логической точки зрения результаты Хайяма или Валлиса лишь выявляли равносильность V постулата и некоторых других предложений геометрии. Так, Хайям, по существу, установил эквивалентность постулата и предложения о сумме углов треугольника, а Валлис показал, что не только из V постулата можно вывести учение о подобии, но и обратно – их евклидова учения о подобии следует V постулат.

Один из обнадеживающих способов подхода к доказательству пятого постулата, которым пользовались многие геометры XVIII и первой половины XIX веков, состоит в том, что пятый постулат заменяется его отрицанием или каким-либо утверждением, эквивалентным отрицанию. Опираясь на измененную таким образом систему постулатов и аксиом, доказываются всевозможные предложения, логически из нее вытекающие. Если пятый постулат действительно вытекает из остальных постулатов и аксиом, то измененная указанным образом система постулатов и аксиом противоречива. Поэтому рано или поздно мы придем к двум взаимно исключающим выводам. Этим и будет доказан пятый постулат.

Именно таким путем пытались доказать пятый постулат Д. Саккери (1667-1733), И. Г. Ламберт (1728-1777) и А.М. Лежандр (1752-1833).

Исследования Саккери были опубликованы в 1733 году под названием “Евклид, очищенный от всяких пятен, или опыт, устанавливающий самые первые принципы универсальной геометрии”.

Саккери исходил из рассмотрения четырехугольника с двумя прямыми углами при основании и с двумя равными боковыми сторонами, из симметрии фигуры относительно перпендикуляра к середине основания следует, что углы при вершинах равны. Если принять пятый постулат и, следовательно, евклидову теорию параллельных, то можно установить, что углы прямые. Обратно, как доказывает Саккери, если хотя бы в одном четырехугольнике указанного вида углы при верхнем основании окажутся прямыми, то будет иметь место евклидов постулат о параллельных. Желая доказать этот постулат Саккери делает три возможных предположения: либо углы прямые, либо тупые, либо острые (гипотезы прямого, острого и тупого угла). Для доказательства пятого постулата необходимо опровергнуть гипотезы острого и тупого угла. Совершенно точными рассуждениями Саккери приводит к противоречию гипотезу тупого угла. Вслед за тем, приняв гипотезу острого угла, он выводит весьма далеко идущие ее следствия с тем, чтобы и здесь получить противоречие. Развивая эти следствия Саккери строит сложную геометрическую систему, не заключая о противоречии только потому, что полученные им выводы не соответствуют привычным представлениям о расположении прямых. Он “находит” логическое противоречие, но в результате вычислительной ошибки.

Идеи Ламберта, развитые им в сочинении “теория параллельных линий” (1766г.), близко примыкают к соображениям Саккери.

Он рассматривает четырехугольник с тремя прямыми углами. Относительно четвертого угла так же возникают три гипотезы: этот угол прямой, тупой или острый. Доказав эквивалентность пятого постулата гипотезе прямого угла и сведя к противоречию гипотезу тупого угла, Ламберт, подобно Саккери, вынужден заниматься гипотезой острого угла. Она приводит Ламберта к сложной геометрической системе, в которой ему не удалось встретить логического противоречия. Ламберт нигде в своем сочинении не утверждает, что V постулат им доказан, и приходит к твердому заключению, что и все другие попытки в этом направлении не привели к цели.

“Доказательства евклидова постулата, - пишет Ламберт, - могут быть доведены столь далеко, что остается, по-видимому, ничтожная мелочь. Но при тщательном анализе оказывается, что в этой кажущейся мелочи и заключается вся суть вопроса; обыкновенно она содержит либо доказываемое предложение, либо равносильный ему постулат”.

Более того, развивая систему гипотезы острого угла, Ламберт обнаруживает аналогию этой системы со сферической геометрией и в этом усматривает возможность ее существования.

“Я склонен даже думать, что третья гипотеза справедлива на какой-нибудь мнимой сфере. Должна же быть причина, вследствие которой она на плоскости далеко не поддается опровержению, как это легко может быть сделано со второй гипотезой”.

Лежандр в своем доказательстве пятого постулата рассматривает три гипотезы относительно суммы углов треугольника.

1. Сумма углов треугольника равна двум прямым.

2. Сумма углов треугольника больше двух прямых.

3. Сумма углов треугольника меньше двух прямых.

Он доказал, что первая гипотеза эквивалентна пятому постулату, вторая гипотеза невозможна; и приняв третью гипотезу приходит к противоречию, неявно воспользовавшись в доказательстве пятым постулатом через один из его эквивалентов.

В результате проблема параллельных оставалась к началу XIX века неразрешенной и положение казалось безвыходным. Большой знаток вопроса венгерский математик Фаркаш Бояи в 1820 году писал своему сыну Яношу: “Молю тебя, не делай только и ты попыток одолеть теорию параллельных линий: ты затратишь на это все свое время, а предложения этого вы не докажете все вместе. Не пытайся одолеть теорию параллельных линий ни тем способом, который ты сообщаешь мне, ни каким-либо другим. Я изучил все пути до конца: я не встретил ни одной идеи, которой бы я не разрабатывал. Я прошел весь беспросветный мрак этой ночи, и всякий светоч, всякую радость жизни я в ней похоронил… Этот беспросветный мрак… никогда не прояснится на земле, и никогда несчастный род человеческий не будет владеть чем-либо совершенным даже в геометрии. Это большая и вечная рана в моей душе…”. Беспросветный мрак, о котором с горечью писал старший Бойяи, рассеял Лобачевский и, несколько позднее, Бояи.

studfiles.net

Возникновение геометрии. Геометрия Евклида и геометрия Лобачевского

Геометрия зародилась в Древнем Египте как набор правил решения практических задач, возникавших в строительстве, при распределении земельных участков, измерении площадей, объемов и других величин. Свидетельством этому являются египетские пирамиды, построенные около 4800 лет назад. Их строительство требовало достаточно сложных и точных геометрических расчетов. Но особенно важной была задача распределения земельных наделов.

Обширные сведения о свойствах фигур, накопленные египтянами, были заимствованы греками. Произошло это в YIII-Y вв.до н.э. А так как особенно важной задачей было землемерие, то греки назвали науку о фигурах геометрией, так как с греческого «геос» - земля, а «метрио» - измеряю.

К сказанному можно добавить, что многие геометрические понятия возникли в результате многократных наблюдений реальных предметов той или иной формы, т.е. познавая окружающий мир, люди знакомились с простейшими геометрическими формами. Овладению этими знаниями способствовало изготовление орудий, имеющих сравнительно правильную геометрическую форму, строительство жилья, шитье одежды, изготовление посуды, украшений.

Огромное влияние на развитие геометрических представлений оказали систематические астрономические наблюдения. Они способствовали возникновению понятий шара, окружности, угла, угловой меры.

Развитие землемерия, обобщение накопленного опыта наблюдений привело к созданию практических правил измерения земельных участков, нахождения площадей и объемов простейших фигур, правил, необходимых для строительства, и др. Так, формулы для вычисления площадей земельных участков, имеющих форму треугольника, трапеции, встречаются у древних египтян, вавилонян. К XYII-XYI вв.до н.э. были установлены такие факты, как теорема Пифагора, найдено выражение для подсчета объема шара и многие другие. Но выступали они не как логически доказанные утверждения, а как выводы из опыта.

Таким образом, геометрия возникла как прикладная наука для решения практических задач: сравнения фигур, нахождения геометрических величин, простейших геометрических построений.

Практические правила постепенно приводились в систему. Кроме того, одни правила стали выводиться из других и обосновываться посредством рассуждений. Возникло доказательство, правила стали превращаться в теоремы, которые доказывались без прямых ссылок на опыт. Вообще совершенствование геометрических знаний шло по пути их отделения от опыта – в результате предметом геометрии стали не реальные, а идеальные фигуры, т.е. фигуры, являющиеся образами предметов, в которых абстрагируются от всего, кроме формы. Более того, эти фигуры стали дополняться свойствами, которыми реальные предметы не обладали. Например, понятие прямой, возникшее как отражение такого свойства реальных предметов, как протяженность, было дополнено представлением о ее бесконечности.

Получение новых геометрических утверждений при помощи рассуждений относится к YI в.до н.э. и связано с именем древнегреческого математика Фалеса. Считают, что им доказаны свойства равнобедренного треугольника, равенство вертикальных углов и ряд других фактов.

К Ш в.до н.э. геометрия становится дедуктивной наукой, одновременно решая многие практические задачи: дает точно обоснованные правила для построения фигур с заданными свойствами, позволяет различными способами сравнивать фигуры, по одним свойствам фигуры делать выводы о других ее свойствах и т.д.

Основные достижения в области математики были систематизированы около 300 лет до н.э. греческим ученым Евклидом и изложены в его знаменитом труде «Начала», состоящем из тринадцати книг. Это сочинение является первым дошедшим до нас строгим логическим построением геометрии.

Каждая книга «Начал» начинается с определений основных понятий. Так, в книге по геометрии 35 определений. Среди них определения точки, линии, прямой, поверхности.

Точка есть то, что не имеет частей.

Линия есть длина без ширины.

Прямая линия есть та, которая одинаково лежит относительно всех своих точек.

Поверхность есть то, что имеет длину и ширину.

Кроме перечисленных даются определения плоского и прямого углов, перпендикуляра, тупого и острого углов, круга, окружности, треугольника и его видов, четырехугольника и его видов и др.

За определениями следуют постулаты и аксиомы.

За постулатами и аксиомами, которые рассматривались как утверждения, принимаемые без доказательств, формулировались теоремы и задачи на построение. Они располагались в строгой последовательности так, что каждое последующее опирается на предыдущее, а также на постулаты и аксиомы.

Определения, постулаты, аксиомы и дальнейшие выводы в геометрии Евклида имели наглядный, опирающийся на практику смысл, хотя выражали его в идеализированном, абстрактном виде.

Таким образом, геометрия сложилась как наука о пространственных формах и отношениях, рассматриваемых отвлеченно от их математического содержания. В Древней Греции она сформировалась в абстрактную логическую систему, в основе которой лежат первоначальные понятия и аксиомы, новые факты формулируются в виде теорем и выводятся дедуктивным способом, а каждое новое понятие вводится с помощью определения на основе ранее введенных понятий.

«Начала» Евклида оставили глубокий след в истории и в течение многих веков служили образцом научного изложения математики.

После Ш в до н.э. геометрия развивалась медленно – требовались новые идеи и методы, необходимо было развитие понятия числа и алгебры. Первые шаги в этом направлении были сделаны в Греции (работы Диафанта, Ш в.), а затем в Индии, где были открыты десятичная система счисления, отрицательные и иррациональные числа.

В IX в. Благодаря работам Мухаммада аль-Хорезми дальнейшее развитие получила алгебра. Позже таджикский поэт и ученый Омар Хайям (конец XI – начало XII в.) дал определение числа как отношения любых величин. Через 600 лет это же определение было дано Ньютоном во «Всеобщей арифметике». В геометрии новые идеи и методы появились в XYII в. Они были обусловлены развитием алгебры и созданием математического анализа. Принадлежали эти идеи французскому философу и математику Рене Декарту. В своем сочинении «Геометрия» он впервые представил метод координат на плоскости, установив тем самым взаимосвязь геометрии с алгеброй.

Важным направлением в развитии геометрии был поиск логически безупречного построения геометрии. Дело в том, что аксиоматически построенная теория должна удовлетворять определенным требованиям математической строгости. Они не абсолютны и в разные периоды истории были различными. Эти требования заставили обратить особое внимание на пятый постулат геометрии Евклида – его трудно было принять очевидным, как остальные аксиомы и постулаты. Поэтому возникло стремление вывести его из остальных постулатов и аксиом. Однако попытки, которые длились более двух тысяч лет, были безуспешными, хотя и сыграли положительную роль в развитии геометрии, так как были сформулированы и доказаны теоремы, раскрывающие новые свойства геометрических фигур.

Переворот в геометрии произошел в начале XIX в., когда несколько ученых пришли к мысли о существовании геометрии, отличной от евклидовой. Первым, кто построил эту геометрию, был Н.И.Лобачевский, профессор Казанского университета. Его рассуждения сводились к следующему.

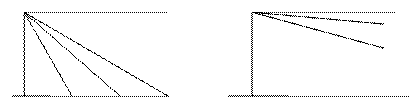
Рассмотрим в плоскости прямую а и проведем из точки А перпендикуляр АС к прямой а и луч АВ, перпендикулярный АС. Возьмем некоторую прямую АМ, пересекающую прямую а в точке М. При неограниченном удалении точки М по прямой а прямая АМ будет приближаться к некоторому предельному положению Логически могут представиться две возможности:

а) луч АМ совпадает с лучом АВ;

б) луч АМ составит с лучом АВ некоторый острый угол.

А В А В

а

С М С

а) б)

Случай а) соответствует аксиоме параллельности: АВ – единственная прямая, проходящая через А и не пересекающая а.

Допуская, что имеет место случай б), Лобачевский начал выводить различные следствия из этого допущения, надеясь, что рано или поздно придет к противоречию, чем и завершится доказательство. Однако, доказав несколько десятков теорем, он так и не обнаружил логических противоречий. И тогда Лобачевский высказал мысль: если заменить пятый постулат его отрицанием (т.е. принять, что через точку вне прямой можно провести более одной прямой, ей параллельной) и сохранить все остальные аксиомы евклидовой геометрии, то получим новую геометрию, которую он назвал «воображаемой», а позднее она была названа его именем – геометрией Лобачевского.

Все теоремы, доказываемые в евклидовой геометрии без использования пятого постулата, сохраняются и в геометрии Лобачевского. Например, вертикальные углы равны; углы при основании равнобедренного треугольника равны; из данной точки можно опустить на данную прямую только один перпендикуляр. Теоремы же, доказываемые в геометрии с помощью пятого постулата, видоизменяются. Например, сумма величин внутренних углов любого треугольника меньше 180º, не существует подобных треугольников: если углы двух треугольников соответственно равны, то эти треугольники равны. Так как в геометрии Лобачевского сумма внутренних углов четырехугольника меньше 360º, то в ней не существует прямоугольников. Позже было доказано, что аксиоматика, предложенная им, независима и непротиворечива.

Открытие, сделанной Н.И.Лобачевским, сыграло огромную роль в развитии математики и физики. В его работах была не только полностью решена проблема независимости аксиомы параллельности от других аксиом евклидовой геометрии, но и было показано, что аксиомы могут подвергаться изменению, что привлекло внимание ученых к вопросам аксиоматики геометрии. Кроме того, было установлено, что геометрия Лобачевского точно описывает взаимосвязь пространства и времени, открытую А.Эйнштейном в теории относительности.

Итог всем исследованиям в этой области подвел крупнейший немецкий математики Д.Гильберт. Произошло это в конце XIX столетия. В своей книге «Основания геометрии» он дает полный список аксиом евклидовой геометрии и доказывает непротиворечивость этой аксиоматики. Сформулированные им аксиомы относятся к точкам, прямым, плоскостям и отношениям между ними, которые выражаются словами «принадлежит», «делать между», «конгруэнтен». Что такое точка, прямая и плоскость и каков конкретный смысл указанных отношений, Гильберт не уточняет. Все, что предполагается известным о них, выражено в аксиомах. Они разбиты на пять групп.

Читайте также:

lektsia.com

Реферат неевклидова геометрия - Реферат

МУНИЦИПАЛЬНООЕ ОБЩЕОБРАЗОВАТЕЛЬНОН УЧРЕЖДЕНИЕ

«Рунгинская средняя общеобразовательная школа Буинского района

Республики Татарстан»

РЕФЕРАТ

Неевклидова геометрия

Работу выполнил учитель

математики Рунгинской

среднй общеобразовательной

школы Буинского

муниципального района РТ

Комисарова Л. И.

Рунга, 2008.

Введение.

Любая теория современной науки считается единственно верной, пока не создана следующая. Это своеобразная аксиома развития науки.

Этот факт многократно подтверждался. Физика Ньютона переросла в релятивистскую физику, а та в квантовую. Теория флогистона стала химией, а самозарождение мышей из грязи обернулось биологией. Такова судьба всех наук, и нельзя сказать, что сегодняшнее открытие через двадцать лет не окажется грандиозной ошибкой. Но это тоже нормально – ещё Ломоносов говорил: «Алхимия – мать химии: дочь не виновата, что её мать глуповата».

Участь эта не обошла и геометрию. Традиционная Евклидова геометрия переросла в неевклидову, геометрию Лобачевского. Именно этому разделу математики, его истории и особенностям и посвящен этот проект.

История геометрии.

Считается, что геометрия началась в так называемой Ионийской школе. Её основателем считается Фалес Милетский (640-540 (546?) гг. до н. э.). Он считался одним из семи мудрецов Греции, первым математиком, астрономом и философом. Он доказал, что углы при основании равнобедренного треугольника равны, что вертикальные углы равны, что диаметр делит окружность пополам и ещё множество теорем. Предсказание затмения солнца в 585 году также приписывается ему.

Огромный импульс развития этой школе дал Пифагор (569-470 гг. до н. э.). В основном о его личных качествах пишут то же самое, что и о Фалесе. Но к этому ещё можно добавить титул чемпиона по боксу на олимпийских играх – звание, среди математиков редкое.

Несмотря на все его достижения, мнение современников хорошо выразил Гераклит: «Многознание без разума». Что ж, это было вполне заслужено: Пифагор засекречивал открытия и приписывал себе работы учеников. Пифагор также заставлял своих воспитанников исполнять целый свод очень странных правил: например, не прикасаться к белому петуху.

Но факт есть факт - и одна из теорем Пифагора теперь известна каждому – это теорема о равенстве квадрата гипотенузы сумме квадратов катетов. Эта теорема настолько популярна в мире математиков, что одних только доказательств накопилось 39 штук. Их можно посмотреть на сайте /pythagoras.

Платон (428-348) знаменит введением принципа дедуктивности в математике, или принципа развития от простого к сложному. Он также знаменит постановкой трех задач на построение. Используя только циркуль и линейку, надо было:

1. Разделить угол на три части (задача о трисекции угла).

2.Построить квадрат, равный по площади данному кругу (задача о квадратуре круга).

3.Построить куб, равный по объему данному (задача об удвоении куба).

Нерешаемость этих задач была доказана только в 19 веке, но перед этим они успели вызвать настоящую бурю: например, задача №2 вызвала появление интегрального исчисления.

Биография Николая Ивановича Лобачевского. (1729 – 1856)

Детство Лобачевского было тяжелым и бедным. В Казанской гимназии он был казеннокоштным студентом, что накладывало определенные обязанности и ограничения. Самым простым было учиться лучше других; но казеннокоштным студентам, например, не разрешалось выходить дальше, чем за пределы парадного двора. Но уже с самого начала жизни Лобачевский интересовался геометрией. Это неудивительно, ведь его отец был землемером. Лобачевский проявил также большую склонность к языкам – например, французский он выучил за три месяца. Он писал стихи – его поэмы о Волге считаются одними из лучших. Но при этом он не забывал учиться – в 1807 году он студент, а в 1811 – магистр. Работая над развитием геометрии, в 1826 году, уже будучи деканом физико-математического факультета, он сделал доклад, содержавший основы неевклидовой геометрии. Однако время было не совсем подходящим: открылись хищения из казны Магницким – ещё одним математиком этой эпохи, Магницкого «записали» в декабристы… Словом, ученому миру было не до новых теорий.

Но он не сдался. С 1829 по 1830 год он публиковал в журнале «Казанский вестник» мемуар «О началах геометрии», и это была первая публикация основ его теории.

Взлеты и падения следовали один за другим. Только были сданы в печать первая и вторая части «Новых начал геометрии», как умер его кумир Пушкин, а потом и дочь Надежда.

Лобачевский пользовался уважением и любовью студентов и коллег. Когда упразднили должность директора университета, то его кандидатуру на пост главного ректора утвердили без возражений. Не высказался даже его главный соперник – Симонов.

В 1842 году, во время большого пожара в Казани он героически спас древние книги, до этого, во время эпидемии холеры, превратил университет в мини-госпиталь – из-за чего умерло гораздо меньше студентов, чем в других ВУЗ’ах.

Когда негде было разместить второй класс Казанской гимназии, он предложил свой дом, обещав потом построить для гимназии дворец. Понятно, что в 1845 году он получил должность управляющего Казанским учебным округом, а после стал член-корреспондентом Гуттенгенского университета.

Но жизнь нанесла ещё один удар: он начал слепнуть. Он начал играть со своей женой в страшную игру, пытаясь убедить её, что ещё хорошо видит. Она закатывала истерики, уговаривала лечиться, но все тщетно – Лобачевский ослеп. Но, тем не менее, он продолжал преподавать и пользоваться безграничной любовью и уважением учеников. Знаменателен случай, когда молодого студента, засмеявшегося над споткнувшимся Лобачевским, однокурсники заставили уйти из университета. Лобачевский об этом даже не узнал.

В 1855 году он был уволен со службы с причислением к министерству. В этом же году опубликовал свою последнюю работу – «Пангеометрия», которую диктовал своим ученикам. Его горячим желанием было создать единую механику – но времени не хватило. Он умер в 1856 году – забытый царем, лишившись орденов и квартиры – ордена украли, а квартиру конфисковали. В его формулярном листе за сорок лет работы в графе отпусков бисерным почерком Лобачевского было написано: «Не был».

Ему поставлен памятник – и поэт В. Фирсов написал о нем:

Высокий лоб, нахмуренные брови,

В холодной бронзе – отраженный луг…

Но даже неподвижный и суровый,

Он, как живой, - спокоен и могуч.

Когда – то здесь, на площади широкой,

Задумчивый, неторопливый, строгий,

Он шел на лекции – великий и живой.

Пусть новых линий не начертят руки,

Он здесь стоит, взнесенный высоко,

Как утверждение бессмертья своего,

Как вечный символ торжества науки.

Другие авторы.

Идея неевклидовой геометрии пришла в голову не только Лобачевскому – просто ему относительно повезло. Одним из «конкурентов» был Гаусс – великий затворник, отказавшийся от услуг почты, чтобы никто не смог обвинить его в плагиате.

В это время сын старого друга Гаусса, Янош Больяи, занялся теорией параллельных линий. В 1832 году он выпустил труд «Аппендикс», содержащий начала неевклидовой геометрии. Но его работа почти совпадала с мемуаром Лобачевского «О началах геометрии» 1829 года; подобных результатов достиг и сам Гаусс.

Тога Гаусс написал Фаркашу Больяи то, что тот сам говорил сыну: время для этих выкладок ещё не пришло. Януш же посчитал, что Гаусс решил присвоить его труд. Но Гаусс не публиковал его – ведь он был королем математики того периода, и боялся, что его сочтут свихнувшимся.

Гаусс в то время хотел уехать – куда-нибудь далеко, где никто не помешает. Он думал о Петербурге или Казани. Но из-за бюрократии российских чиновников поездка расстроилась.

Но если Януш Больяи считал себя гением-одиночкой, то Гаусс узнал о Лобачевском, прочитав «Геометрические исследования по теории параллельных линий Николая Лобачевского». Гаусс говорил, что, читая этот труд, он видел в первую очередь себя. Гаусс закончил затворничество, начал изучать русский язык – и стал бегло читать уже через два месяца. Но – ирония судьбы – Гаусс стеснялся открыто попросить сочинения Лобачевского, а тот не отсылал их в Геттинген, так как не знал, что Гаусс понимает по-русски.

Через шесть лет Гаусс все ещё думает о Лобачевском. Но он понимает, что слишком стар, чтобы защищать новые идеи. А Лобачевский погибал без поддержки.

Больяи же, получив в 1848 году «Геометрические исследования», посчитал, что Гаусс выпустил мемуар под псевдонимом Лобачевский. Целью его жизни было превзойти этот труд. Это была агония разума – а Лобачевский даже не подозревал о существовании талантливого венгра.

За год до этого, зимой 1848 года, к Гауссу пришел студент. Его звали Бернард Риман. Но Гаусс оттолкнул его. Тогда Риман, сжав зубы, уехал в Берлин. Но мир тесен, и, защитив докторскую диссертацию, он решает стать профессором. Удивительно, но тему пробной лекции утверждает и принимает именно Гаусс. Риман создал геометрию, где прямые замкнуты, где нет параллельных прямых, а сумма углов треугольника больше 180о. Она похожа на геометрию сферы Гаусса.

Риман оказался хорошим учеником великого математика, и из нежеланного гостя стал единственным другом. Он умер в Италии, не закончив последний мемуар. На русском языке он появился только в в 1893 году. Его название было: «О гипотезах, лежащих в основе геометрии».

Краткое описание геометрии Лобачевского.

Иногда говорят, что в геометрии Лобачевского параллельные прямые пересекаются в бесконечности. Но это не совсем так. Есть только немного другое свойство параллельности: через одну точку вне прямой можно провести бесконечно много прямых, параллельных данной.

Это видно на рисунке 1. Причем параллельность сохраняется только в сторону уменьшения расстояния между прямыми. Этот, казалось

бы, простой факт, меняет всю геометрию. Как, например, в геометрии Евклида доказывается,

что сумма углов треугольника равна 180о? Классическое доказательство приведено на рисунке 2. Используется свойство углов при накрест лежащих прямых, и выходит, что 1+2+3=180о. Но

так как в геометрии Лобачевского параллельность сохраняется только в одном направлении, то

для нахождения суммы углов треугольника*, то нужно провести

две прямые, параллельные данной в разные стороны. Что получается, видно на рисунке 3. Понятно, что теперь сумма углов треугольника меньше 180о. Эта разница была названа Лобачевским дефектом треугольника.

Одними из важных объектов на плоскости Лобачевского являются пучки прямых. Но чтобы описать эти пучки, сначала надо уяснить, что в плоскости Лобачевского есть три типа расположения прямых: прямые или параллельны, или пересекаются, или являются расходящимися.* Здесь и далее подразумевается геометрия Лобачевского, если нет оговорки на геометрию Евклида.

Так вот, первый вид пучков образован прямыми, имеющими общую точку – центр пучка (рис. 4а). Пучок расходящихся прямых – это перпендикуляры к одной прямой – оси пучка (рис. 4б). Из этого определения выходит интересное и, казалось бы, абсурдное утверждение, что два перпендикуляра к одной прямой непараллельны, и отличие от геометрии Евклида.

И, наконец, пучок, образуемый прямыми, параллельными данной прямой в заданном направлении (рис. 4в).

Следующими объектами геометрии Лобачевского являются кривые. Для их построения Лобачевским было введено понятие соответственных точек. В пучке первого рода это точки на прямых, равноудаленные от центра (рис. 5а). В пучке второго рода это точки прямых, лежащие по одну сторону от оси и отстоящие от нее на одинаковые расстояния (рис. 5б). Наконец, в пучке третьего рода они расположены симметрично относительно биссектрисы полосы между двумя прямыми, на которых лежа эти точки (рис. 5в).

Соединив соответствующие точки первого пучка, мы получим окружность. В случае второго пучка мы получаем линию равных расстояний, а в третьем случае – так называемую предельную линию.

Примеры таких построений – на рисунке 6.

Из определения предельных линий выходит, что она бесконечна. Поэтому в теоремах используется понятие предельной дуги, или дуги предельной линии.

Для концентрических предельных дуг существуют несколько правил: во-первых, равным хордам соответствуют равные дуги, большей хорде – большая дуга; отрезки осей, заключенные между дугами, равны, и отношение двух предельных дуг, заключенных между одинаковыми осями, зависит только от расстояния. Причем это отношение при S1>S2 равно , где х – расстояние, а к – некоторая константа. Сам Лобачевский дает её определение так: к – это расстояние между двумя предельными дугами, заключенными между двумя осями, отношение которых равно е. Физический смысл этой константы заключается в отображении кривизны пространства Лобачевского.

Лобачевским была создана и стереометрия. Прямые в пространстве могут или скрещиваться, или лежать в одной плоскости. Скрещивающиеся прямые имеют смысл двух прямых, имеющих общий перпендикуляр, определяющий кратчайшее расстояние между ними. У параллельных прямых есть два основных свойства: во-первых, если через две параллельные прямые провести две пересекающиеся плоскости, то прямая пересечения плоскостей будет параллельна двум другим; во-вторых, две прямые, параллельные третьей, параллельны одна другой в том же направлении – даже если третья прямая не лежит в плоскости первых двух.

Для анализа расположения прямой и плоскости, на плоскость опускается проекция. Если прямая и плоскость параллельны, то прямая и её проекция на плоскость тоже параллельны, и наоборот. Так же определяется и расположение двух плоскостей – с тем лишь отличием, что, если нельзя провести плоскость, перпендикулярную двум выбранным плоскостям и проходящую через выбранную прямую и её проекцию, то плоскости обязательно пересекутся.

Аналогию пучкам в пространстве составляют связки. Связки также делятся на три рода: первые образуются прямыми и плоскостями, проходящими через одну точку – центр связки; вторые образованны прямыми и плоскостями, перпендикулярными некой плоскости; и, наконец, третьи образованы прямыми и плоскостями, параллельными данной плоскости в одном направлении. Точно так же определяются соответствующие точки. В случае связки первого рода они формируют сферу, второго – поверхность равных расстояний, третьего – предельную поверхность. Предельная поверхность обладает удивительным свойством: на ней справедлива геометрия Евклида. Этот факт свидетельствует о том, что неевклидова геометрия не опровергает евклидову, а включает её в себя как органичную часть.

В процессе нахождения тригонометрических формул, Лобачевский проецировал прямоугольный треугольник с предельной плоскости на плоскость, касательную к ней. Пользуясь формулами и , вывод которых приведен в приложении, он получил тригонометрические формулы своего пространства. Соотношения в прямоугольном треугольнике при этом остаются одинаковыми, но cos, sin и tg определяются по-другому: , , , где с – сторона против прямого угла, а – против , в – против .

Несмотря на все кажущиеся странности, геометрия Лобачевского является настоящей геометрией нашего мира, и Евклидова является только её составной частью. Но в пределах ежедневных измерений Евклидова геометрия дает исчезающие малые ошибки, и мы пользуемся именно ею.

5 постулат.

Итак, мы дошли до пятого постулата. Сам Евклид формулировал его так: «Если прямая пересекает две прямые и образует внутренние односторонние углы в сумме меньше двух прямых, то при неограниченном продолжении этих двух прямых они пересекутся с той стороны, где сумма углов меньше двух прямых». Другие формулировки гораздо проще, например: «через точку вне прямой можно провести одну и только одну прямую, параллельную данной».

Конечно, ещё сам Евклид пытался вывести этот сложный постулат из более простых. После него этой проблемой занимались почти все известные математики, но чаще всего это заканчивалось тем, что постулат выводился только при принятии каких-то дополнительных предположений. У менее удачливых математиков не получалось вообще ничего.

Самую известную попытку доказать пятый постулат методом от противного предпринял итальянский монах Джироламо Саккерти в 1733 году. Но отрицание пятого постулата – это и есть главное отличие геометрии Лобачевского от геометрии Евклида. Он, как и другой математик И. Г. Ламберт в 1766 году, вплотную подошел к неевклидовой геометрии, но не нашел её реальной.

Гаусс, Больяи, Швейкарт, Тауринус – они все рано или поздно убеждались, что доказать пятый постулат невозможно. Сам Лобачевский говорил об этой проблеме: «Напрасные страданья … в продолжение двух тысяч лет». И именно он смог отверг этот постулат, создав новую геометрию.

Гаусс, изучая поверхности, обнаружил, что на поверхностях отрицательной кривизны сумма углов треугольника меньше 180о. Он был в шаге от опровержения пятого постулата.

Попыток было много – и именно недоказуемость этого предположения привела к открытию неевклидовой геометрии.

Геометрия Лобачевского в реальном мире.

Если геометрия Евклида является только частью геометрии Лобачевского, то выходит, что наш мир – не мир Евклида, как принято считать? Почему же мы не замечаем разницы?

Как пример можно привести тот факт, что видимый звездный свод это ни что иное, как предельная плоскость. Астрономам после признания достижений Лобачевского пришлось пересчитывать все расстояния между звездами – и ошибки достигали 1/6.

Но вернемся на землю. Есть такое понятие – гауссова кривизна пространства. Если мы возьмем кривую поверхность, проведем к какой-то точке касательную, проведем в точку касания отрезок, перпендикулярный касательной плоскости, то мы получим нормаль. Проведя через нормаль плоскость, мы можем найти окружность, наиболее плотно прилегающую к поверхности. Так как мы можем провести сколько угодно плоскостей, то мы можем найти окружности с минимальным и максимальным радиусом. Подставив их в выражение , мы получим Гауссову кривизну пространства. Если К>0, то поверхность в этой точке эллиптическая. Если К<0, то гиперболическая. Если К=0, то параболическая.

Как мы уже знаем, на поверхностях

с отрицательной кривизной

работает геометрия Лобачевского.

Но именно такую кривизну имеют

графики интенсивности всех электромагнитных полей! Состояние поверхности плазмы

также описывается геометрией Лобачевского.

Но наглядно геометрию Лобачевского можно устроить и на бумаге. Если нарисовать окружность, то мы можем, не выходя за её пределы, провести сколько угодно прямых, не пересекающих данную (рис. 7). Взяв сферу, можно построить стереометрическую модель. Такая модель называется моделью Клейна.

Все эти модели служат одной цели – полнее представить наш мир, не прибегая к вселенским масштабам.

Заключение.

Когда Евклид формулировал пятый постулат, вряд ли он знал, какую бурю тот вызовет. Когда Лобачевский отказался от пятого постулата, он не знал, что его «воображаемая геометрия» на поверку окажется реальной.

Нельзя сказать, что неевклидова геометрия единственно правильна. На данный момент к ней нет никаких претензий. Но, может быть, через много лет она устареет – или это произойдет быстрее? Так или иначе, но наука никогда не будет стоять на месте, и когда - нибудь и этот проект окажется макулатурой.

Но думаю, что этого времени он успеет исполнить свое предназначение – рассказать и заинтересовать читателя настоящей геометрией нашего мира. Именно из-за популярного характера в нем нет ни строгих доказательств, ни полного описания неевклидовой геометрии. Но для поверхностного ознакомления с ней он вполне годен.

Использованная литература.

1. Смилга В.П. В погоне за красотой./. Н-п издание. – М.: Молодая гвардия, 1968. – 200 стр. с илл.

2. Колесников М. Лобачевский./. Серия «Жизнь замечательных людей». – М.: Молодая гвардия, 1965. – 320 стр. с илл.

3. Широков П.А. Краткий очерк основ геометрии Лобачевского./. – М.: Наука, 1983.–76 стр.

Приложение.

При доказательства используют рисунок 1. Пусть ОХ перпендикулярно ОY.

Через точку А прямой ОY проведем прямую АА’ , параллельную ОХ, и построим предельную линию с осью ОХ, проходящую через точку О. Дугу , заключенную между осями ОХ и АА’, обозначим через s, отрезки ОА и АВ – соответственно через u и v. Проведем прямую ММ’, параллельную ОХ и ОY. Предельную дугу ОС, заключенную между ОХ и ММ’, обозначим через . Нашей задачей является вывод следующих формул: (А) и (В).

Построим прямую NN’, параллельную ОY и перпендикулярную АА’, и через точку N проведем предельную дугу , концентрическую дуге . Так как прямая М’М параллельна NN’ и АА’, то NР = . Далее, так как ОАА’ = П(u)*,  YАN, то АN = u, т.е. NВ = u + v. Применяя формулу к концентрическим дугам =  и =  - s, получаем (3). Отложим теперь отрезок ОА = u и проведем прямую АА’, параллельную ОХ, и прямую ММ’, параллельную ОХ и ОY. Строим прямую NN’, перпендикулярную АА’ и параллельную ОY (рис. 2). Через точку О проведем ортогонально к ОХ предельную дугу = s + , через точку N – концентрическую дугу = . Так как  ОАА’ = П(ОА) = П(АN), то АN = ОА = u, т.е. ВN = u – v. Итак, (4). Складывая отношения (3) и (4), получаем формулу (А). вычитая (3) из (4), имеем . Подставляя сюда из (А) , получаем соотношение (В).

*Имеется ввиду, что отрезок u определяется углом параллельности ОАА’ .

**Гиперболические функции определяются так:

1. Синус: .

2. Косинус: .

3. Тангенс: .

refdb.ru

Геометрия Евклида – первая естественно-научная теория — реферат

Федеральное агентство по образованию 

Саратовский государственный университет  

Реферат

на  тему: 

«Геометрия Евклида – первая естественно-научная  теория». 

Выполнила: студентка 1 курса факультета

ИФиЖ, специальность:

«Журналистика»,

131-я группа, Лаптиёва Д.С. 

                                                                      Проверил:     

Саратов 2008 

Содержание

Введение.

1. История геометрии.
2. «Начала» - главный труд Евклида.

3. Геометрия Евклида – первая естественно-научная  теория.

Заключение.

Список  литературы.                      

Введение.

    Любая цивилизация, достойная так называться, занимается поиском истин. Мыслящие люди не могли не пытаться понять многообразие явлений природы, разгадать тайну появления на Земле человека, постичь смысл жизни и выяснить предназначение человека. Во всех древних цивилизациях, кроме одной, ответы на эти вопросы давались религиозными лидерами и принимались всеми. Единственным исключением была цивилизация, созданная древними греками. Греки совершили открытие, величайшее из когда-либо совершенных человеком: они открыли могущество разума.

    Греки размышляли над политическими системами, этикой, юриспруденцией, рациональными путями воспитания молодежи и многими другими видами человеческой деятельности. Их главный вклад, оказавший решающее влияние на всю последующую культуру, состоял в том, что они взялись за изучение законов природы. Решающим шагом, позволившим рассеять ореол таинственности и мистицизма, окружавший явления природы, и «навести порядок» в их кажущемся хаосе, стало применение математики.

    Геометрия, как раздел математики, возникла из практической потребности изучения окружающего пространства и его свойств. Развитие представлений о пространстве и усложнение проводимых измерений требовали изучения свойств все более сложных геометрических фигур.

  К концу III в. до н.э. греки имели обширные знания геометрических фактов и обладали методами их доказательств, но геометрия как наука еще не существовала. В это время возникла задача собрать этот геометрический материал и расположить его в логическом порядке. Такая задача была решена с появлением «Начал» Евклида, в которых было представлено систематическое изложение начал геометрии, выполненное с таким большим мастерством, что многие века преподавание геометрии велось по этому сочинению.

    «Начала»  Евклида составляют целую эпоху  в элементарной геометрии. В них  учёный излагает геометрию как цепочку  строгих логических выводов, доказательства теорем на основании определений, постулатов и аксиом. Материал, содержащийся в «Началах», по существу охватывает элементарную геометрию, как мы ее понимаем в настоящее время.

  В реферате, на основе рассмотрения исторических предпосылок и фактических положений книги «Начал» сделана попытка показать, что именно классические труды Евклида, посвященные изучению свойств пространства и пространственных фигур, превратили математику из свода неясных, эмпирических, разрозненных фрагментов в блестящую, обширную, систематическую и глубокую науку.                                          

4. История геометрии.

    Геометрия возникла очень давно, это одна из самых древних наук. Геометрия (греческое, от ge - земля и metrein - измерять)- наука о пространстве, точнее - наука о формах, размерах и границах тех частей пространства, которые в нем занимают вещественные тела. Таково классическое определение геометрии, или, вернее, таково действительное значение классической геометрии. Однако современная геометрия во многих своих дисциплинах выходит далеко за пределы этого определения. Развитие геометрии принесло с собой глубоко идущую эволюцию понятия о пространстве.

    За  несколько столетий до нашей эры  в Вавилоне, Китае, Египте и Греции уже существовали начальные геометрические знания, которые добывались в основном опытным путем, но они не были еще систематизированы и передавались от поколения к поколению в виде правил и рецептов. Не было еще доказательств этих правил, и их изложение не представляло собой научной теории.

    Геометрия стала наукой только после того, как в ней начали систематически применять логические доказательства, начали выводить геометрические предложения не только путем непосредственных измерений, но и путем умозаключений, путем вывода одного положения из другого, и устанавливать их в общем виде.

    В трудах Фалеса, Пифагора, Платона, Демокрита, Гиппократа, Динострата, Никомеда, Аристотеля, если назвать только важнейших, с  необычайной быстротой производятся установление и систематизация фактического материала классической геометрии.

    Первый  принцип, которого неуклонно придерживались греки, состоял в том, что математика должна иметь дело с абстракциями. Предпочтение, отдаваемое греками абстракции, имело под собой особую причину. Чтобы обрести мощь, математика должна охватывать в едином абстрактном понятии существенные черты всех физических реализаций этого понятия. Греки вполне отчетливо и явно утверждали, что их математика имеет дело с абстракциями. В «Государстве» Платон говорит о геометрах следующее: Разве ты не знаешь, что, хотя они используют видимые формы и рассуждают о них, мыслят они не о самих формах, а об идеалах, с которыми не имеют сходства; не о фигурах, которые они чертят, а об абсолютном квадрате и абсолютном диаметре... и что в действительности геометры стремятся постичь то, что открыто лишь мысленному взору?

    Итак, геометрия должна заниматься, прежде всего, изучением таких абстрактных понятий, как точка, прямая и целое число. Другие понятия, например треугольник, квадрат и окружность, можно определить через основные понятия, которые, как отметил Аристотель, должны оставаться неопределимыми, ибо в противном случае у нас не было бы отправной точки.

    Свои  рассуждения о математических понятиях греки начинали с аксиом - истин, столь очевидных, что в справедливости их невозможно усомниться. Такие истины грекам были известны. Платон обосновал принятие аксиом своей теорией воспоминаний - анамнезисом. Аристотель подошел к проблеме иначе. Истинность аксиом, утверждал он, мы познаем посредством безошибочной интуиции. Кроме того, аксиомы необходимы нам как основа для рассуждений. Если бы в своих рассуждениях мы использовали факты, истинность которых неизвестна, то для установления их истинности потребовались бы новые рассуждения, и так до бесконечности. В результате мы бесконечно «спускались» бы в наших доказательствах - но нигде не могли бы остановиться. Среди аксиом Аристотель различал общие понятия и постулаты. Общие понятия истинны во всех областях мысли. Постулаты применимы к такой специфической области, как геометрия. Таково, например, утверждение «Две [разные] точки определяют прямую и притом только одну».

    Из  аксиом с помощью рассуждений  выводятся заключения. Существует много типов рассуждений, например рассуждения по индукции, по аналогии и дедукции. Правильность заключения гарантирует лишь один из многих типов рассуждений. Дедуктивное рассуждение, несмотря на множество различных форм, гарантирует истинность заключения. Так, допуская, что все люди смертны и Сократ - человек, следует прийти к заключению, что Сократ смертен. Используемое в этом рассуждении правило логики является одной из форм суждения, которое Аристотель назвал силлогистическим выводом. К правилам дедуктивного рассуждения Аристотель относил также закон противоречия (никакое высказывание не может быть одновременно истинным и ложным) и закон исключенного третьего (любое высказывание должно быть либо истинным, либо ложным).

    Аристотель, а вслед за ним и весь мир  приняли за неоспоримую истину, что  применение правил дедуктивного вывода к любым посылкам гарантирует получение заключений, не уступающих по надежности посылкам. Иначе говоря, если посылки истинны, то истинны и заключения.

    Наиболее  совершенным образцом такой теории на протяжении более 2 тысяч лет служили «Начала» Евклида, написанные около 300 года до нашей эры».

    Однако  все новые проблемы и созданные  в связи с ними теории привели  к тому, что совершенствовались сами способы математических доказательств, возрастала потребность создания стройной логической системы в геометрии.

    Около IV в. до н. э. уже стали появляться сводные сочинения под названием «Начал геометрии», имевшие задачей систематизировать добытый геометрический материал. Такие «Начала» по свидетельству Прокла, составили Гиппократ Хиосский, Феодосии из Магнезии, Гиероним Колофонский и др. Ни одно из этих сочинений до нас не дошло: все они утратили свое значение и были забыты, когда появилось замечательное руководство по геометрии - «Начала» Евклида.

    О жизни Евклида почти ничего не известно. До нас дошли только отдельные легенды о нем. Первый комментатор «Начал» Прокл (V век нашей эры) не мог указать, где и когда родился и умер Евклид. По Проклу, «этот ученый муж» жил в эпоху царствования Птолемея I. Некоторые биографические данные сохранились на страницах арабской рукописи XII века: «Евклид, сын Наукрата, известный под именем «Геометра», ученый старого времени, по своему происхождению грек, по местожительству сириец, родом из Тира».

    Достоверно  установлено, что Евклид жил и  преподавал в Александрии около 300г. до н. э. (сам Евклид скорее всего получил образование в Платоновской Академии в Афинах). Это почти единственная информация, которой мы располагаем о частной жизни Евклида. Свои труды Евклид облекал в форму обширных систематических дедуктивных обзоров отдельных открытий многих греческих авторов классического периода. В главном труде Евклида — «Началах» излагаются основные свойства пространства и пространственных фигур.

2. «Начала» - главный труд Евклида.

    Из  дошедших до нас сочинений Евклида  наиболее знамениты «Начала». «Начала» Евклида состоят из 13 книг (т.е. глав). Первые четыре книги «Начал» посвящены геометрии на плоскости, и в них изучаются основные свойства прямолинейных фигур и окружностей.

    Книге I предпосланы определения понятий, используемых в дальнейшем. Они носят интуитивный характер, поскольку определены в терминах физической реальности.

Так, в  начале книги I даны 23 определения. Приведем первые семь из них.

1.  Точка  есть то, что не имеет частей.

2.  Линия  есть длина без ширины.

3.  Границы  линии суть точки.

4. Прямая  есть такая линия,  которая одинаково расположена по отношению ко всем своим точкам.

5.  Поверхность  есть то, что имеет только длину  и ширину.

6.  Границы  поверхности суть линии.

7. Плоскость  есть поверхность, которая одинаково  расположена по отношению ко  всем прямым, на ней лежащим.

    Затем Евклид приводит предложения, принимаемые  без доказательства, которые он разделяет на постулаты и аксиомы.

    Постулаты

I. Требуется,  чтобы от каждой точки ко  всякой другой точке можно  было провести прямую.

II.   И чтобы каждую прямую можно было неопределенно продолжить.

III. И  чтобы от любого центра можно  было описать окружность любого  радиуса.

IV. И  чтобы все прямые углы были  равны.

V.  И чтобы всякий раз, когда  прямая при пересечении с двумя  другими прямыми образует с ними внутренние односторонние углы, сумма  которых меньше двух прямых, эти  прямые пересекались с той стороны, с которой эта сумма меньше двух прямых.

    Три первых постулата обеспечивают существование  прямой и окружности. Пятый, так называемый постулат о параллельных - самый  знаменитый. Он всегда интриговал математиков, которые пытались вывести его из четырех предыдущих или вообще отбросить, до тех пор, когда в XIX в. обнаружилось, что можно построить другие, неевклидовы геометрии и что пятый постулат имеет право на существование.

freepapers.ru

Реферат Математика История развития неевклидовой геометрии