В предыдущих лекциях при исследовании функционала
предполагалось, что граничные точки 
и 
заданы. Подобное предположение не всегда выполняется для многих интересных и практически важных вариационных задач. Рассмотрим в качестве примера задачу навигации.
Задача навигации
В этой задаче рассматривается река ширины 
с прямыми параллельными берегами. Считая один берег реки совпадающим с осью 
, введем скорость течения реки 
. Лодка с постоянной скоростью
( 
– величина скорости, 
), за кратчайшее время должна пересечь реку, отчалив из точки 
(рис.1).
Обозначим через 
угол, который образует вектор скорости лодки с положительным направлением оси 
. Тогда реальная скорость движения лодки в момент времени 
определяется равенствами
, 
.
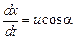Отсюда
,
что позволяет выразить через 
:
,
откуда
.
Для времени пересечения реки находим
.
Последний интеграл должен быть минимизирован за счет выбора функции 
при условии 
.
Как видим, в отличие от предыдущих задач, правый конец искомой кривой заранее не определен: он может оказаться на любой точке вертикальной прямой 
. Мы приходим, таким образом, к задаче со свободной (подвижной) границей. Найдем ее решение в общей постановке.
Вариационная задача с вертикальными границами
Пусть в задаче об отыскании экстремума функционала
фиксирована одна граничная точка 
, условий же на 
нет. Иными словами, второй конец допустимой кривой может перемещаться по вертикальной прямой 
.
Нулевая вариация 
, как и ранее, является необходимым условием экстремальности. Вычисляя вариацию функционала по известной формуле, получаем:
.
Как и ранее,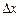 
– произвольная функция, в частности, можно взять 
, что сведет задачу к уже решенной задаче с закрепленными границами. Для нее, как известно, необходимое условие экстремальности означает обращение в тождество уравнения Эйлера. Отсюда следует, что 
, то есть интеграл в формуле для вариации равен нулю.
Теперь выберем функцию 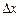так, чтобы 
. Тогда требование равенства нулю вариации сводится к условию
.
Если бы левый конец тоже был свободным, получили бы аналогичное условие
.
Решение задачи навигации
Вернемся к задаче навигации и найдем ее решение, используя полученный выше результат.
Итак, нам следует найти минимум функционала
при условии , а 
может принимать любое значение.
Согласно вышеприведенной схеме, решаем уравнение Эйлера. Так как подынтегральная функция
зависит только от 
и 
, то уравнение Эйлера допускает первый интеграл: 
. С другой стороны, поскольку вторая граница экстремали перемещается по вертикальной прямой, для нее должно выполняться условие 
. Отсюда сразу следует, что вышеприведенный первый интеграл имеет вид: 
. Получаем дифференциальное уравнение первого порядка
,
для которого легко найти решение. Находя явное выражение для , получаем 
. Так как предполагается (см. рис. 1), что переправа осуществляется с левого берега на правый, то перед дробью следует выбрать знак плюс. Учитывая, что , получаем окончательно:
.
В частности, если 
, то искомый маршрут наибыстрейшей переправы реализуется на прямой 
.
cyberpedia.su
Предположим, что одна или более граничных точек может перемещаться.
Если на какой-нибудь кривой 
достигается экстремум в задаче с подвижными граничными точками, то экстремум тем более достигается по отношению к более узкому классу кривых, имеющих общие граничные точки с кривой . Таким образом, должна удовлетворять уравнению Эйлера. 
. Решение этого уравнения содержит произвольные постоянные, которые определялись из граничных условий в задачах с неподвижными границами. В случае подвижных границ они определяются из равенства нулю функционала.
Пусть 
закреплены, тогда найдём вариацию функционала 
. Допустимые кривые будем считать близкими, если модули вариаций 
и 
малы и малы модули приращений 
.
Второе слагаемое по формуле Тейлора.
Так как 
закреплена, то нижняя подстановка обращается в ноль. 
!
Если приращения независимы, то отсюда следует. Что
и 
Но чаще приходится рассматривать случай, когда вариации 
и 
зависимы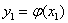 
.
условие транверсальности.
Пример найти условие трансверсальности для функционалов вида
Или
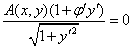
Т. е 
условие ортогональности.
, 
Интегральными кривыми являются окружности 
. Первое граничное условие даёт 
. Так как условие трансверсальности для данного функционала сводится, условию ортогональности 
т. е. 
Если граничная точка 
может перемещаться лишь по вертикальной прямой, то 
и
Вариационные задачи на условный экстремум.
Найти экстремум функционала 
при условии 
, 
. Здесь также можно доказать справедливость метода неопределённых множителей Лагранжа.
Составим функцию Лагранжа 
для неё записываем уравнение Эйлера.
Неизвестные 
находим из условий связи.
Пример. Найти кривую , заданной длины 
, для которой площадь 
Под ней достигает максимума.
, 
При изопериметрическом условии 
не зависит от 
, поэтому уравнение Эйлера имеет первый интеграл 
вводя параметр 
, полагая 
, тогда получим
, откуда 
, 
,
Получим семейство окружностей 
Константы определяются из условия , 
.
Задача о максимальной площади между двумя кривыми.
Найти экстремаль 
, 
и интегральной связи 
уравнение Эйлера 
=
.
| Следующая > |
matica.org.ua
Постановка вариационной задачи с подвижными границами. Количество просмотров публикации Постановка вариационной задачи с подвижными границами. - 58
| Наименование параметра | Значение |
| Тема статьи: | Постановка вариационной задачи с подвижными границами. |
| Рубрика (тематическая категория) | Математика |
Пусть в простейшей вариационной задаче точки A и B находятся на кривых (1)
Функция y допустима, в случае если удовлетворяет условиям допустимости в простейшей вариационной задаче, а граничные точки выбираются произвольно на кривых, определяемых (1). Минимизируемый функционал имеет нефиксированные пределы интегрирования.
Рассмотрим задачу:
Рассмотрим сначала случай удовлетворяет уравнению:
. Функционал обозначим:
- класс допустимых функций в простейшей задаче вариационного расчёта , в которой
Теорема 1. В случае если - решение задачи с подвижным правым концом, то крайне важно
(2)
(3)
Доказательство:
-решение простейшей задачи для
и (2) имеет место. Пусть
Т.к. , то
, что
Пусть
такая, что
- непрерывно дифференцируемое расширение
на
принадлежит
Положим
Т.к. , то
в
достигает локального минимума и
+ (4)
.
Т.к. удовлетворяет дифференциальному уравнению Эйлера-Лагранжа, отвечающему основной функции
, то
(5)
А (6)
Преобразуя (4) с учетом (5) и (6), получаем
Равенство (3) называют условием трансверсальности на правом конце. В случае если правая кривая (граница) имеет уравнение ,
, то оно принимает вид
Аналогично можно рассмотреть случай незакрепленного левого конца или обоих концов.
Постановка вариационной задачи с подвижными границами. - понятие и виды. Классификация и особенности категории "Постановка вариационной задачи с подвижными границами." 2014, 2015.
referatwork.ru
При исследовании функционала 
предполагалось, что граничные точки
заданы. Предположим, что одна или обе точки могут перемещаться. Тогда класс допустимых кривых расширяется. Кроме кривых сравнения, имеющих общие граничные точки, можно уже брать и кривые со смещенными граничными точками. Поэтому, если на какой-либо кривой
достигается экстремум по отношению к более узкому классу кривых, имеющих общие граничные точки с кривой
, и, следовательно, должна быть выполнена основная необходимая для достижения экстремума задача с неподвижными границами.
Функция 
должна быть решением уравнения Эйлера:
Кривые 
, на которых реализуется экстремум, должны быть экстремалями.
Общее решение уравнения Эйлера:
содержит две произвольные постоянные, чтобы их определить, надо иметь два условия.
Для задачи с подвижными границами это условие выполнено в виде: 
- начальные точки фиксированы.
В задачах с подвижными границами одно или оба эти условия отсутствуют, и недостающее условие для определения произвольных постоянных общего решения уравнения Эйлера должны быть получены из основного необходимого условия экстремума:
.
Таким образом, если в задачах с подвижными границами решение достигается на решении уравнения Эйлера:
то в дальнейшем можно рассматривать значение функционала лишь на функциях этого семейства. При этом функционал 
превращается в функцию параметров
и
и пределов интегрирования
и
, а вариация функционала совпадает с дифференциалом этой функции. Для упрощения будем считать, что одна из граничных точек, например
, закреплена, а другая
может перемещаться и переходит в точку
. Или, как принято в вариационном исчислении, в точку
.
Допустимые кривые 
будем считать близкими, если модули вариаций
и
малы, и малы модули приращений
и
. Вариации
и
называются вариациями в точках
и
. Экстремали, проходящие через точку
, образуют пучок экстремалей
. Функционал
на кривых этого пучка превращается в функцию аргументов
и
.
Если кривые пучка 
в окрестности рассматриваемой экстремали не пересекаются, то можно рассматривать как однозначную функцию
и
, так как задание
и
определяет экстремаль пучка и тем самым определяет значение функционала (рис. 1).
Вычислим вариацию функционала 
на экстремалях пучка
. При перемещении граничной точки из положения
в положение
. Так как функционалVна кривых пучка превращается в функцию двух аргументов
и
, то вариация совпадает с дифференциалом этой функции. Выделим из приращения
главную линейную по отношению к
и
часть.
Имеем:
(1)
Первое слагаемое правой части преобразуется, используя теорему о среднем:
;
В силу непрерывности функции 
, будем иметь:
Итак:
Второе слагаемое правой части (1) преобразуем путем разложения подынтегральной функции по теореме Тейлора:
является бесконечно малой величиной большего порядка, чем
и
. В свою очередь линейная часть функционала
может быть преобразована путем интегрирования по частям второго слагаемого подынтегральной функции:
Значения функционала берутся лишь на экстремалях, следовательно, справедливо равенство:
Так как граничная точка 
закреплена, то это значит, что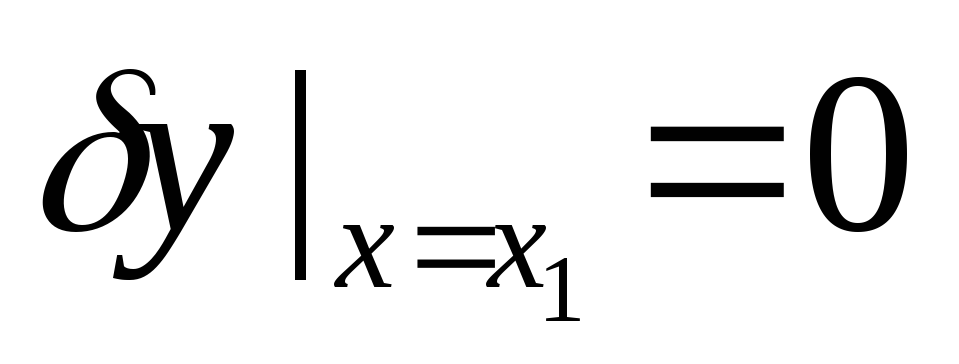
, следовательно:
Здесь важно знать, что 
не равно
, так как
- это приращение
при перемещении граничной точки в точку с координатами
. А
- это приращение ординаты к точке
. При переходе от экстремали, проходящей через две граничные точки
, к экстремали, проходящей через точки
и
(Рис. 2).
Из рисунка видно, что справедливы равенства:
,
,
,
,
При этом приближенное равенство справедливо с точностью до бесконечно малых более высокого порядка.
Итак, окончательно получаем:
Где приближенные равенства справедливы с точностью до бесконечно малых более высокого порядка относительно 
и
.
Следовательно, из уравнения (1) получаем:
Или:
Где функция, в которую превратился функционал 
на экстремалях
.
А 
и
- приращение координат граничной точки.
Основное необходимое условие экстремума 
принимает вид:
(2)
Если вариации 
и
независимы, то отсюда следует справедливость равенств:
Однако часто приходится рассматривать случай, когда эти вариации зависимы. Пусть граничная точка 
может перемещаться по кривой
, тогда условие (2) принимает вид:
Или, так как 
меняется произвольно:
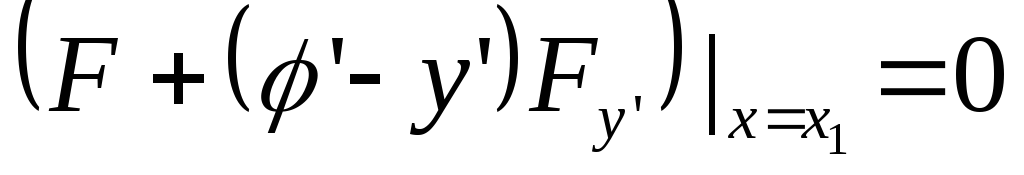
Это условие устанавливает зависимость между 
и
в граничной точке и оно называется условием трансверсальности. Условие трансверсальности совместимо с условием
позволяет определить одну или несколько экстремалей, на которых может достигаться экстремум
.
Если граничная точка
может пересекаться по некоторой кривой, то совершенно также обнаружим, что в точке
должно выполняться условие трансверсальности:
studfiles.net
