Количество просмотров публикации Трение качения - 830
Трением качения принято называть сопротивление, возникающее при качении одного тела по поверхности другого.
Рассмотрим цилиндрический каток радиуса r на горизонтальной плоскости. Под катка и плоскости в месте их соприкосновения могут возникнуть реакции, препятствующие действием активных сил каток может катиться по плоскости. Из-за деформации поверхностей не только скольжению, но и качению.
Активные силы, действующие на катки в виде колес, обычно состоят из силы тяжести , горизонтальной силы
, приложенной к центру катка, и пары сил с моментом
, стремящейся катить колесо. Колесо в данном случае принято называть ведомо-ведущим. В случае если
, а
, то колесо принято называть ведомым.В случае если
, а
, то колесо принято называть ведущим.
Соприкосновение катка с неподвижной плоскостью из-за деформации катка и плоскости происходит не в точке, а по некоторой линии BD. По этой линии на каток действуют распределенные силы реакции. В случае если привести силы реакции к точке А, то в этой точке получим главный вектор этих распределенных сил с составляющими
(нормальная реакция) и
(сила трения скольжения), а также пару сил с моментом
.
(x)
(y)
(MA)
Момент принято называть моментом трения качения. Наибольшее значение М достигается в момент начала качения катка по плоскости.
Установлены следующие приближенные законы для наибольшего момента пары сил, препятствующих качению.
1. Наибольший момент пары сил, препятствующих качению, в довольно широких пределах не зависит от радиуса катка.
2. Предельное значение момента пропорционально нормальной реакции
.
.
Коэффициент пропорциональности k называют коэффициентом трения качения при покое. Размерность k - это размерность длины.
3. Коэффициент трения качения k зависит от материала катка, плоскости и физического состояния их поверхностей. Коэффициент трения качения при качении в первом приближении можно считать не зависящим от угловой скорости качения катка и его скорости скольжения по плоскости.
Для вагонного колеса по рельсу мм.
Рассмотрим движение ведомого колеса. , а
.
Качение колеса начнется, когда выполнится условие или
Скольжение колеса начнется, когда выполнится условие .
Обычно отношение и качение начинается раньше скольжения.
В случае если , то колесо будет скользить по поверхности, без качения.
referatwork.ru
Трение качения - раздел Образование, ТЕМА 2. ПЛОСКАЯ СИСТЕМА СХОДЯЩИХСЯ СИЛ
Трением качения называется трение движения, при котором скорости соприкасающихся тел в точках касания одинаковы по величине и направлению.
Если движение двух соприкасающихся тел происходит при одновременном качении и скольжении, то в этом случае возникает трение качения с проскальзыванием.
Рассмотрим качение со скольжением. Если сила F отсутствует, то под давлением силы Q произойдёт деформация катка и опорной поверхности вместе их соприкосновения (рис.13.3,а ).
Деформацией по высоте катка и опорной поверхности незначительны по сравнению с размерами катка пренебрегаем. Со стороны опорной поверхности на цилиндр будет действовать распределённая по площади контакта система сил.
Рис.13.3
При каком-то критическом значении F катка придёт в движение и будет равномерно перекатываться по опорной плоскости. При действии силы Q интенсивность давления в точке А минимальное, а у края в точке В максимальное (рис.13.3,б). В результате реакция N оказывается смещённой в сторону действия силы F. С увеличением F это смещение растёт до некоторой предельной величины К. Таким образом, в предельном положении на каток будет действовать пара сил (Fтр,F) с моментом Fтр х R и уравновешивающая её пара (N,Q) с моментом N x k.
Из равенства моментов: Fтр х R = N x k.
Линейная величина К называется коэффициентом трения качения. Измеряют величину К обычно в см. Значение коэффициента К зависит от материала тел и определяется опытным путём. Значения этого коэффициента для некоторых материалов:
Мягкая сталь по мягкой стали…0,005
Закалённая сталь по закалённой стали…0,001
Чугун по чугуну…0,005
Дерево по стали…0,03-0,04
Дерево по дереву…0,05-0,08
Резиновая шина по шоссе…0,24
– Конец работы –
Эта тема принадлежит разделу:
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА ВВЕДЕНИЕ ТЕМА...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Трение качения
Аксиомы статики В статике используются некоторые вполне очевидные истины, называемые аксиомами. Аксиома первая. Дв
Сила и её векторное изображение. Меру действия одного тела на другое, в результате которого происходит изменение движение тела, называют с
Сложение сходящихся сил. Равнодействующая плоской системы сходящихся сил Если линии действия всех сил расположены в одной плоскости и пересекаются в одной точке, то они образуют п
Графический метод определения равнодействующей Пример 2.1. Произвести сложение двух векторов ,если они имеют общее начала векторов в точк
Системы сил по правилу параллелограмма и силового многоугольника Пример 4.2. На тело действуют силы линии, действия которых пересекаются в точке О.
Практическая работа 1. Графическое определение равнодействующей сходящихся сил На тело в точке О (рис.9) действуют силы F1 = 50 кН; F2 = 100 кН; F3.= 150 кН. α 1
Графоаналитический метод определения равнодействующей плоской системы сил В точке О приложены силы F1 = 30 Н, F2 = 60 Н. Угол между вект
Практическая работа 2. Графоаналитический метод определения равнодействующей Рис.2.8 1. Определение равнодействующей R12 (рис.2.9):
ТЕМА 3. СВЯЗИ И ИХ РЕАКЦИИ 18 Твёрдое тело называется свободным, если оно может перемещаться в пространстве в любом направлении. Твёрдое
Определение реакции опор двухопорных балках Для определения опорных реакций необходимо составить уравнения равновесия сил и моментов и решить их отно
Определение реакции опор одноопорной (защемлённой) балки Пример 3.3. Определить опорные реакции жёстко защемлённой балки (рис.3.5) при следующих данных: F =
Тема 4. СОЧЛЕНЕННЫЕ СИСТЕМЫ Сочленённой называется система нескольких тел, соединённых друг с другом при помощи внутренних связей: про
Тема 5. ОПРЕДЕЛЕНИЕ УСИЛИЙ В ЭЛЕМЕНТАХ КРОНШТЕЙНА Пример 5.1. К шарниру C перекинутый через блок прикреплён трос (рис.5.1), несущий груз G = 100 H. Положение
Пара сил и момент силы относительно точки Две равные и параллельные силы, направленные в противоположные стороны и не лежащие на одной прямой, назы
Основные свойства пар. Эквивалентность пар сил Свойство пар.Всякую пару, приложенную к твёрдому телу, можно как угодно перемещать в плоскости её
Сложение пар Если в одной плоскости действует несколько пар, то их можно заменить одной парой, момент которой равен суме
Условия равновесия пар сил и моментов Известно, что тело получает вращательное движение, если приложенные силы создают момент относительно возм
Равновесие рычага В задачах механики часто приходится рассматривать равновесие тела, шарнирно закреплённого на некоторой не
Момент сил. Момент сил относительно точки В реальных условиях к телу могут быть приложены силы, линии, действия которых не пересекаются в одной точке
Тема 8. Приведение силы к данной точке Силу можно переносить в любую точку, лежащую на линии её действия. Изменится ли действие силы на тело, если п
Тема 9. Теорема Вариньона для системы сходящихся сил (теорема о моменте равнодействующей) Момент равнодействующей плоской системы сходящихся сил относите
Тема 10. Главный вектор. Главный момент Приведение плоской системы произвольно расположенных сил к данной точке. В реальных условиях к телу м
Момент силы относительно оси Для определения момента от силы F относительно оси ОУ решаем задачу в следующей последовательности
Разложение силы по трём осям координат Система сил, линии, действия которых расположенных в различных плоскостях, называется пространственной с
Равновесие пространственной системы сходящихся сил Пример 11.3. Сила тяжести груза F=80 kH поддерживается кронштейном, показанным на рис.51. Определить уси
Коэффициент устойчивости Пример12.1. Твёрдое тело весом Q=10 кН, находящееся на плоскости и способное опрокидываться вокруг ре
Трение скольжения Трением называется сопротивление, возникающее при перемещении одного тела по поверхности другого.
Трение в направляющих Ползун В равномерно движется по направляющим. Определим связь между силой F и давлением G на ползун. Для подд
Сложение двух параллельных сил направленных в одну сторону Параллельными называют силы, линии, действия которых образуют параллельные прямые. Система сил, ли
Сложение двух неравных параллельных сил, направленных в разные стороны Пример14.2. К телу в точках А и В (рис.14.3) приложены две параллельные и направленные в противополо
Разложение силы на две параллельные составляющие Любая сила может быть разложена на две параллельные составляющие силы или более. Необходимость разложения
Центр параллельных сил. Центр тяжести При сложении, каких угодно параллельных сил на векторе равнодействующей всегда получается точка, обладающ
Определение центра тяжести поперечного сечения Пример 14.4. Для поперечного сечения (Рис.) определить: Статический момент площади поперечного
Параметры геометрических фигур Рис.14.14 Таблица 7 №п.п Осевой момент инерции, см4 Мом
Практическая работа 7. Определение центра тяжести сечения составленных из стандартных профилей Пример 17.5. Определить координаты центра тяжести сечения (рис.60), составленной из прокатных профиле
Вопросы для самопроверки 1. Что такое материальная точка? 2. Абсолютно твёрдое тело? 3. Что называется силой и каковы её едини
Библиографический список 1 Аркуша,А.И.Теоретическая механика и сопротивление материалов[Текст].- М., 1989. 2 Бать,М.И.,Джанелидзе,Г.Ю.,
allrefers.ru
План реферата
Введение
Трение
Трение покоя, скольжения
Трение качения
Сопротивление среды
Заключение
Автор: студент РК-5-12 Павлов В.В.
2001г.
Вступление
Почему звучит скрипичная струна, когда по ней ведут смычком? Ведь смычок движется, а колебания струны периодические. А как разгоняется автомобиль, и какая сила замедляет его при торможении? Почему автомобиль «заносит» на скользкой дороге? Ответы на все эти и многие другие важные вопросы, связанные с движением тел, дают законы трения.
Вы видите, как разнообразно и порой неожиданно проявляется трение в окружающей нас обстановке. Трение принимает участие, и притом весьма существенное, там, где мы о нём даже и не подозреваем. Если бы трение внезапно исчезло из мира, множество обычных явлений протекало бы совершенно иным образом.
Очень красочно пишет о роли трения французский физик Гильом:
«Всем нам случалось выходить в гололедицу; сколько усилий стоило нам удерживаться от падения, сколько смешных движений приходилось нам проделать, чтобы устоять! Это заставляет нас признать, что обычно земля, по которой мы ходим, обладает драгоценным свойством, благодаря которому мы сохраняем равновесие без особых усилий. Та же мысль возникает у нас, когда мы едем на велосипеде по скользкой мостовой или когда лошадь скользит по асфальту и падает. Изучая подобные явления, мы приходим к открытию тех следствий, к которым приводит трение. Инженеры стремятся по возможности устранить его в машинах – и хорошо делают. В прикладной механике о трении говорится как о крайне нежелательном явлении, и это правильно, - однако лишь в узкой специальной области. Во всех прочих случаях мы должны быть благодарны трению: оно даёт нам возможность ходить, сидеть и работать без опасения, что книги и чернильница упадут на пол, что стол будет скользить, пока не упрётся в угол, а перо выскальзывать из пальцев.
Трение представляет настолько распространенное явление, что нам, за редкими исключениями, не приходится призывать его на помощь: оно является к нам само.
Трение способствует устойчивости. Плотники выравнивают пол так, что столы и стулья остаются там, куда их поставили. Блюдца, тарелки, стаканы, поставленные на стол, остаются неподвижными без особых забот с нашей стороны, если только дело не происходит на пароходе во время качки.
Вообразим, что трение может быть устранено совершенно. Тогда никакие тела, будь они величиною с каменную глыбу или малы, как песчинки, никогда не удержатся одно на другом: всё будет скользить и катиться, пока не окажется на одном уровне. Не будь трения, Земля представляла бы шар без неровностей, подобно жидкому».
К этому можно прибавить, что при отсутствии трения гвозди и винты выскальзывали бы из стен, ни одной вещи нельзя было бы удержать в руках, никакой вихрь никогда бы не прекращался, никакой звук не умолкал бы, а звучал бы бесконечным эхом, неослабно отражаясь, например, от стен комнаты.
Наглядный урок, убеждающий нас в огромной важности трения, даёт нам всякий раз гололедица. Застигнутые ею на улице, мы оказываемся беспомощными, и всё время рискуем упасть. Вот поучительная выдержка из газеты (декабрь 1927 г.):
«Лондон, 21. Вследствие сильной гололедицы уличное и трамвайное движение в Лондоне сильно затруднено. Около 1400 человек поступило в больницы с переломами рук, ног и т. д.».
«При столкновении вблизи Гайд-Парка трёх автомобилей и двух трамвайных вагонов машины были уничтожены из-за взрыва бензина…»
«Париж, 21. Гололедица в Париже и его пригородах вызвала многочисленные несчастные случаи…»
Однако Ничтожное трение на льду может быть успешно использовано технически. Уже обыкновенные сани служат тому примером. Ещё лучше свидетельствуют об этом так называемые ледяные дороги, которые устраивали для вывозки леса с места рубки к железной дороге или к пунктам сплава. На такой дороге, имеющей гладкие ледяные рельсы, две лошади тащат сани, нагруженные 70 тоннами брёвен.
Ледяная дорога; А – колея; В – полоз; С – уплотнённый снег; D – земляное основание дороги.
Трение
Трение покоя, скольжения
Прежде думали, что механизм трения не сложен: поверхность покрыта неровностями и трение есть результат подъёма скользящих частей на эти неровности; но это неправильно, ведь тогда не было бы потерь энергии, а на самом деле энергия на трение тратится.
Механизм потерь иной. И здесь крайне неожиданным оказывается, что эмпирически это трение можно приближенно описать простым законом. Сила нужная для того, чтобы преодолевать трение и тащить один предмет по поверхности другого, зависит от силы, направленной по нормали к поверхностям соприкосновения.
Поверхность твёрдого тела обычно обладает неровностями. Например, даже у очень хорошо отшлифованных металлов в электронный микроскоп видны «горы» и «впадины» размером в 100-1000Å. При сжатии тел соприкосновение происходит только в самых высоких местах и площадь реального контакта значительно меньше общей площади соприкасающихся поверхностей. Давление в местах соприкосновения может быть очень большим, и там возникает пластическая деформация. При этом площадь контакта увеличивается, а давление падает. Так продолжается до тех пор, пока давление не достигнет определённого значения, при котором деформация прекращается. Поэтому площадь фактического контакта оказывается пропорциональной сжимающей силе.
В месте контакта действуют силы молекулярного сцепления (известно, например, что очень чистые и гладкие металлические поверхности прилипают друг к другу).
Эта модель сил сухого трения (так называют трение между твёрдыми телами), по-видимому, близка к реальной ситуации в металлах.
Если тело, например, просто лежит на горизонтальной поверхности, то сила трения на него не действует. Трение возникает, если попытаться сдвинуть тело, приложить к нему силу. Пока величина этой силы не превышает определённого значения, тело остаётся в покое и сила трения равна по величине и обратна по направлению приложенной силе. Затем начинается движение.
Может показаться удивительным, но именно сила трения покоя
разгоняет автомобиль. Ведь при движении автомобиля колеса не проскальзывают относительно дороги, и между шинами и поверхностью дороги возникает сила трения покоя. Как легко видеть, она направлена в сторону движения автомобиля. Величина этой силы не может превосходить максимального значения трения покоя. Поэтому если на скользкой дороге резко нажать на газ, то автомобиль начнет буксовать. А вот если нажать на тормоза, то вращение колёс прекратится, и автомобиль будет скользить по дороге. Сила трения изменит своё направление и начнёт тормозить автомобиль.
Сила трения при скольжении твёрдых тел зависит не только от свойств поверхностей и силы давления (это зависимость качественно такая же, как для трения покоя), но и от скорости движения. Часто с увеличением скорости сила трения сначала резко падает, а затем снова начинает возрастать.
Эта важная особенность силы трения скольжения как раз и объясняет, почему звучит скрипичная струна. Вначале между смычком и струной нет проскальзывания, и струна захватывается смычком. Когда сила трения покоя достигнет максимального значения, струна сорвется, и дальше она колеблется почти как свободная, затем снова захватывается смычком и т.д.
Подобные, но уже вредные колебания могут возникнуть при обработке металла на токарном станке вследствие трения между снимаемой стружкой и резцом. И если смычок натирают канифолью, чтобы сделать зависимость силы трения от скорости более резкой, то при обработке металла приходится действовать наоборот (выбирать специальную форму резца, смазку и т.п.). Так что важно знать законы трения и уметь ими пользоваться.
Кроме сухого трения существует ещё так называемое жидкое трение, возникающее при движении твёрдых тел в жидкостях и газах и связанное с их вязкостью. Силы жидкого трения пропорциональны скорости движения и обращаются в нуль, когда тело останавливается. Поэтому в жидкости можно заставить тело двигаться, прикладывая даже очень маленькую силу. Например, тяжелую баржу на воде человек может привести в движение, отталкиваясь то дна шестом, а на земле такой груз ему, конечно, не сдвинуть. Эта важная особенность сил жидкого трения объясняет, например, тот факт, почему автомобиль «заносит» на мокрой дороге. Трение становится жидким, и даже небольшие неровности дороги, создающие боковые силы, приводят к «заносу» автомобиля.
Трение качения
Возьмем деревянный цилиндр и положим его на стол так, чтобы он касался стола по образующей. В центры оснований цилиндра вставим концы проволочной вилки и прикрепим к ней снабженный очень чувствительный динамометр. Если тянуть за динамометр, то цилиндр покатится по столу. По показаниям динамометра увидим, что нужна весьма небольшая сила тяги, чтобы сдвинуть с места цилиндр и катить его равномерно дальше, гораздо меньшая, чем при скольжении того же цилиндра, если бы он не вращался и скользил бы по столу. При той же силе давления на стол сила трения качения много меньше силы трения скольжения. Например, при качении стальных колёс по стальным рельсам трение качения примерно в 100 раз меньше, чем трение скольжения. Поэтому в машинах стремятся заменить трение скольжения трением качения, применяя так называемые шариковые или роликовые подшипники.
Происхождение трения качения можно наглядно представить себе так. Когда шар или цилиндр катится по поверхности другого тела, он немного вдавливается в поверхность этого тела, а сам немного сжимается. Таким образом, катящееся тело всё время как бы вкатывается на горку.
Вместе с тем происходит отрыв участков одной поверхности от другой, а силы сцепления, действующие между этими поверхностями, препятствуют этому. Оба эти явления и вызывают силы трения качения. Чем твёрже поверхности, тем меньше вдавливание и тем меньше трение качения.
Сопротивление среды
Если твёрдое тело находится внутри жидкости или газа, то вся его поверхность всё время соприкасается с частицами жидкости или газа. При движении тела на него со стороны жидкости или газа действуют силы, направленные навстречу движению. Эти силы называют сопротивлением среды. Как силы трения, сопротивление среды всегда направленно против движения. Сопротивление среды можно рассматривать как один из видов трения.
Особенностью сил трения в жидкости или газе является отсутствие трения покоя. Твёрдое тело лежащее на другом твёрдом теле, может быть сдвинуто с места, только если к нему приложена достаточно большая сила, превосходящая наибольшую силу трения покоя. При меньшей силе твёрдое тело с места не сдвинется, сколько бы времени эта сила ни действовала. Картина получается иной, если тело находится в жидкости. В этом случае, чтобы сдвинуть с места тело, достаточно сколь угодно малых сил: хотя и очень медленно, но всё же тело начнёт двигаться. Человек вообще никогда не сдвинет с места голыми руками камень весом в сто тонн. В то же время баржу весом в сто тонн, плавающую на воде, один человек, хотя и очень медленно, но всё же сможет двигать. Однако по мере увеличения скорости сопротивление среды сильно увеличивается, так что, сколько бы времени сила не действовала, она не сможет разогнать тело до большой скорости.
Важной характеристикой жидких и газообразных сред является вязкость. Вязкость – свойство текучих тел (жидкостей и газов) сопротивляться перемещению одной их части относительно другой под действием внешних сил.
Количественно вязкость определяется величиной касательной силы, которая должна быть приложена к единице площади сдвигаемого слоя, чтобы поддерживать в этом слое ламинарное течение с постоянной скоростью относительно сдвига, равной единице.
Вязкость газов и жидкостей, согласно молекулярной кинетической теории, вызвана передачей импульса от молекул более быстро движущегося слоя к молекулам более медленного слоя, которая происходит при перемешивании молекул соседних слоёв вследствие теплового движения.
Силы внутреннего трения гораздо меньше сил трения скольжения. Поэтому для уменьшения трения между движущимися частями машин и механизмов используется смазка – слой вязкой жидкости, заполняющий пространство между трущимися поверхностями и оттесняющий их друг от друга. Это приводит к существенному уменьшению нагрева и износа деталей. Вместе с тем следует избегать попадания жидкости между фрикционными муфтами, ремнём и шкивом в ременной передаче, ведущими колесами локомотива и рельсом и т.п., ибо во всех этих случаях именно сила трения служит для передачи движения.
С увеличением температуры вязкость газов возрастает, а жидкостей (за некоторым исключением) резко падает. Это связано с различиями в характере движения молекул в жидкости и газе. При понижении температуры вязкость некоторых жидкостей настолько возрастает, что они теряют характерную для них способность течь, превращаясь в аморфные твёрдые тела.
Сопротивление воздуха
При движении твёрдого тела в воздухе на тело действует сила сопротивления воздуха, направленная противоположно движению тела. Такая же сила возникает, если на неподвижное тело набегает пучок воздуха; она направлена, конечно, по движению потока.
Сила сопротивления вызывается, во-первых, трением воздуха о поверхность тела и, во-вторых, изменением движения потока, вызванным телом. В воздушном потоке, изменённом присутствием тела, давление на передней стороне тела растёт, а на задней – понижается по сравнению с давлением в невозмущенном потоке.
Таким образом, создаётся разность давлений, тормозящая движущееся тело или увлекающая тело, погруженное в поток. Движение воздуха позади тела принимает беспорядочный вихревой характер.
Сила сопротивления зависит от скорости потока, от размеров и формы тела.
Для всех тел, изображенных на рисунке, сопротивление движению одинаково, несмотря на весьма разные размеры тел.
«Обтекаемое» тело почти не нарушает правильности потока; поэтому давление на заднюю часть тела лишь немного понижено по сравнению с передней частью и сопротивление не велико.
Различные обтекатели, устанавливаемые на выдающихся частях самолёта, как раз имеют своим назначением устранять завихрения потока выступающими частями конструкции. Вообще же конструкторы стремятся оставлять на поверхности возможно меньшее количество выдающихся частей и неровностей, могущих создавать завихрения.
Влияние сопротивления воздуха сильно сказывается и для наземных средств передвижения: с увеличением скорости автомобилей на преодоление сопротивления воздуха затрачивается всё большая часть мощности мотора. Поэтому современным автомобилям также придают по возможности обтекаемую форму.
Для уменьшения трения при сверхзвуковой скорости нужно заострять переднюю часть движущегося тела, в то время как при меньших скоростях наибольшее значение имеет «обтекаемость».
Сопротивление воды
При движении тел в воде также возникаю силы сопротивления, направленные противоположно движению тела. Если тело движется под водой, то сопротивление теми же обстоятельствами, что и при движении в воздухе: трение воды о поверхность тела и изменением потока, создающим дополнительное сопротивление. Быстро плавающие рыбы и китообразные имеют «обтекаемую форму тела, уменьшающую сопротивление воды при их движении. Обтекаемую форму придают и подводным лодкам. Вследствие большой плотности воды по сравнению с плотностью воздуха, сопротивление движению данного тела в воде много больше сопротивления в воздухе при той же скорости движения.
Для обычных судов, идущих на поверхности воды, есть ещё дополнительное волновое сопротивление: от идущего судна на поверхности воды расходятся волны, на создание которых непроизводительно затрачивается часть работы судовой машины.
Для уменьшения волнового сопротивления, которое для быстроходных судов может составлять 3/4 полного сопротивления, корпусу судна придают специальную форму. Нос судна в подводной части иногда делают «бульбообразной» формы; при этом образование волн на поверхности воды уменьшается, а значит, уменьшается и сопротивление.
Заключение
Чем больше мы будем изучать законы трения, тем сложней, а не проще представятся они нам. Иными словами, всё глубже вникая в закон торможения самолёта, мы всё ясней будем понимать его «фальшь». Чем глубже взгляд, чем аккуратней измерения, тем сложнее становится истина; она не предстанет перед нами как итог простых фундаментальных процессов. Тем больше человек понимание того, что, расширяя круг знаний человек расширяет круг своих не знаний.
Список основной литературы:
Р. Фейнман, Р. Лейтон, М. Сендс «ФЕЙНМАНОВСКИЕ ЛЕКЦИИ ПО ФИЗИКЕ» 1976г.
«ЭЛЕМЕНТАРНЫЙ УЧЕБНИК ФИЗИКИ» под ред. Академика Г.С. Ландсберга 1971г.
3. Перельман Я.И. «ЗАНИМАТЕЛЬНАЯ ФИЗИКА» 1999г.
referat.store
Трение качения - раздел Механика, Теоретическая Механика
Если одно тело, например цилиндрический каток, катить или стремиться катить по поверхности другого тела, то кроме силы трения скольжения из-за деформации поверхностей тел дополнительно возникает пара сил, препятствующая качению катка. Явление возникновения пары сил, препятствующей качению, называют трением качения или трением второго рода.
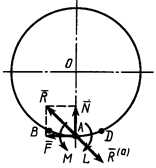
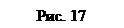
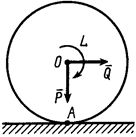Активные силы, действующие на катки в виде колес (рис. 17), кроме силы тяжести 
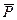обычно состоят из силы 
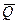, приложенной к центру колеса параллельно общей касательной в точке 
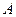, и пары сил с моментом 
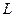, стремящейся катить колесо, называемое в этом случае ведомо-ведущим. Если 
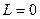, а 
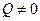, то колесо называют ведомым; если 
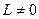, а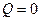 
, то ведущим. Ведомо-ведущими являются колеса локомотива, идущего вторым в составе поезда.
Приведем активные силы в общем случае к точке 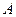. В этой точке получим главный вектор этих сил 
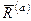и пару сил, момент которой равен главному моменту 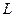(рис. 18).
При равновесии катка, т.е. когда каток не катится и не скользит по плоскости, активные силы уравновешиваются силами реакций связи и, следовательно,
; 
.
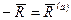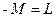Изменив активные силы, приложенные к катку так, чтобы увеличивался момент 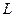пары активных сил, стремящейся катить каток. Пока каток находится в равновесии, увеличивается и равный ему по числовой величине, но противоположный по направлению момент 
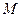пары сил, препятствующий качению катка и возникающий от действия на каток неподвижной плоскости. Наибольшее значение 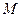достигается в момент начала качения катка по плоскости.
Установлены следующие приближенные законы для наибольшего момента пары сил, препятствующей качению:
1. Наибольший момент пары сил, препятствующей качению, в довольно широких пределах не зависит от радиуса катка.
2. Предельное значение момента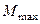 
пропорционально нормальному давлению, а следовательно, и равной ему нормальной реакции 
:
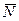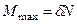. (31)
Коэффициент пропорциональности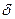 
называют, коэффициентом трения качения при покое или коэффициентом трения второго рода. Из формулы (31) следует, что 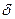имеет размерность длины.
3. Коэффициент трения качения 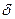зависит от материала катка, плоскости и физического состояния их поверхностей. Коэффициент трения качения при качении в первом приближении можно считать не зависящим от угловой скорости качения катка и его скорости скольжения по плоскости.
Алгебраический момент силы относительно точки Алгебраическим моментом силыотносительно точки называ
Векторный момент силы относительно точки Векторным
Момент силы относительно оси Моментом силы относительно оси называют алгебраический момент проекции этой силы на плоскость, перпенди
Пара сил и алгебраический момент пары сил Парой сил называют систему двух равных по модулю параллел
Аксиомы статики При формулировке аксиом предполагаем, что на твердое тело или материальную точку действуют силы, которые у
Простейшие теоремы статики Теорема о переносе силы вдоль линии действия: Действие силы на твердое тело не изменится от переноса
Приведение системы сил к простейшей системе. Условия равновесия Лемма о параллельном переносе сил: силу можно переносить параллельно самой себе в любую точку твердог
Равновесие пар сил Если на твердое тело действуют пары сил, как угодно расположенные в пространстве, то эти пары сил можно заме
Условия равновесия произвольной системы сил в векторной форме Векторные условия равновесия произвольной системы сил: для равновесия системы сил, приложенных к твердом
Условия равновесия пространственной системы сходящихся сил Для равновесия пространственной системы сходящихся сил, приложенных к твердому телу, необходимо и достат
Условия равновесия плоской системы сил Расположим оси и
Центр параллельных сил Пусть на тело действует система параллельных сил . Такая сис
Способы нахождения центра тяжести Симметричные тела. Если тело имеет плоскость (ось, центр) симметрии, то его центр тяжести находится в
Распределенные силы В статике рассматривают силы, приложенные к твердому телу в какой-либо его точке, и поэтому такие силы назыв
Трение скольжения При движении или стремлении двигать одно тело по поверхности другого в касательной плоскости поверхностей
Решение задач статики Пример 1.На угольник (
Кинематика точки В кинематике точки рассматриваются характеристики движения точки, такие, как скорость, ускорение, и методы
Скорость и ускорение точки Одной из основных характеристик движения точки является ее
Частные случаи движения точки Равномерное движение. При равномерном движении точки по траектории любой формы
Кинематика твердого тела Числом степеней свободы твердого тела называют число независимых параметров, определяющих положение тел
Поступательное движение твердого тела Поступательным движением твердого тела называют такое его движение, при котором любая прямая, жестко с
Вращение твердого тела вокруг неподвижной оси Вращением твердого тела вокруг неподвижной оси (оси вращения) называется такое его движение, при которо
Частные случаи вращения твердого тела Вращение называется равномерным, если . Алгебраическая
Скорости и ускорения точек тела при вращении вокруг неподвижной оси Известно уравнение вращения твердого тела вокруг неподвижной оси
Векторы угловой скорости и углового ускорения Введем понятия векторов угловой скорости и углового ускорения тела. Если
Векторные формулы для скоростей и ускорений точек тела Выразим скорость, касательное, нормальное и полное ускорения точки тела в векторной форме (рис. 32). Скорость
Сложное движение точки Для изучения некоторых, более сложных видов движений твердого тела целесообразно рассмотреть простейшее с
Ускорение Кориолиса Рассмотрим ускорение Кориолиса и его свойства. Оно определяется формулой (81)
Плоское (плоскопараллельное) движение твердого тела Плоским движением твердого тела называют такое его движение, при котором каждая его точка все время движе
Скорости точек плоской фигуры Применяя к плоскому движению теорему о сложении скоростей для какой-либо точки
Мгновенный центр скоростей В каждый м
Ускорения точек плоской фигуры Рассматривая плоское движение плоской фигуры как сложное, состоящее из переносного поступательного вмест
Мгновенный центр ускорений В каждый момент движения плоской фигуры в своей плоскости, если
Решение задач кинематики Пример 3. Даны уравнения движения точки в плоскости
Аксиомы динамики I. Первая аксиома (законом классической механики, закон инерции): материальная точка, на котору
Дифференциальные уравнения движения материальной точки Используя основной закон динамики, можно получить дифференциальные уравнения движения материальной точки
Первая задача Зная массу точки и ее закон движения, можно найти действующую на точку силу. Действительно, если, наприм
Вторая задача По заданной массе и действующей на точку силе необходимо определить движение этой точки. Рассмотрим ре
Дифференциальные уравнения относительного движения материальной точки Имеем инерциальную систему отсчета и материальную точку ма
Центр масс При рассмотрении движения твердых тел и других механических систем важное значение имеет точка, называема
Моменты инерции относительно точки и оси Моментом инерции механической системы, состоящей из
Теорема Штейнера Установим з
Однородный стержень Имеем однородный стержень длиной и массой
Прямоугольная пластина Прямоугольная тонкая пластина имеет размеры и
Сплошной диск Имеем тонкий однородный диск радиусом и массой
Тонкое кольцо (круглое колесо) Имеем тонкое кольцо радиусом и массой
Круглый цилиндр Для круглого однородного цилиндра, масса которого , радиус
Теоремы динамики Внешними силами механической системы называются силы, с которыми действуют на точки системы тела и точ
Теорема о движении центра масс Центр масс системы движется так же, как и материальная точка, масса которой равна массе всей системы, если
Количество движения точки и системы Количеством движения материальной точки называют в
Теорема об изменении количества движения точки Теорема об изменении количества движения точки в дифференциальной форме: первая производная по в
Теорема об изменении количества движения системы Теорема об изменении количества движения системы в дифференциальной форме: производная по времени от
Законы сохранения количества движения Законы сохранения количества движения системы получаются как частные случаи теоремы об изменении количес
Теорема об изменении кинетического момента Для материальной точки массой , движущейся со скоростью
Теорема об изменении кинетического момента точки Первая производная по времени от кинетического момента точки относительно какого-либо центра равна моме
Теорема об изменении кинетического момента системы Первая производная по времени от кинетического момента системы относительно какой-либо точки равна вект
Законы сохранения кинетических моментов 1. Если главный момент внешних сил системы относительно точки
Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси Из теоремы об изменении кинетического момента (172') следует дифференциальное уравнение вращения твердого т
Теорема об изменении кинетического момента системы в относительном движении по отношению к центру масс Пусть механическая система совершает движение относительно основной системы координат
Дифференциальные уравнения плоского движения твердого тела Для твердого тела, совершающего плоское движение и, следовательно, имеющего три степени свободы, соответст
Работа силы Работа силы на каком-либо перемещении является одной из основных характеристик, оценивающих действие силы
Кинетическая энергия Кинетическая энергия точки и системы. Кинетической энергией материальной точки назы
Теорема об изменении кинетической энергии точки Теорема об изменении кинетической энергии точки в дифференциальной форме: дифференциал кинетической
Теорема об изменении кинетической энергии системы Теорема об изменении кинетической энергии системы в дифференциальной форме: дифференциал от кине
Принцип Даламбера для материальной точки Принцип Даламбера для свободной материальной точки эквивалентен основному закону динамики. Для несвободн
Принцип Даламбера для системы материальных точек Рассмотрим систему материальных точек. К каждой точке сист
Силы инерции твердого тела в частных случаях его движения При поступательном движении. Если твердое тело движется поступательно, то ускорения его точек один
Возможные перемещения Для одной точки возможным (виртуальным) перемещением называется такое бесконечно милое (элементарное) мы
Элементарная работа силы на возможном перемещении. Идеальные связи Элементарную работу силы на возможном перемещении ее точки приложения вычисляют по обычным формулам для э
Принцип возможных перемещений Принцип возможных перемещений, или принцип Лагранжа, содержит необходимые и достаточные условия ра
Обобщенные координаты системы Пусть система состоит из точек и, следовательно, ее положен
Обобщенные силы Запишем сумму элементарных работ сил, действующих на точки системы, на возможном перемещении системы:
Вычисление обобщенной силы 1. Обобщенную силу можно вычислить по формуле (227), ее определяющей, т.е.
Общее уравнение динамики Общее уравнение динамики для системы с любыми связями (объединенный принцип Даламбера-Лагранжа или о
Уравнения Лагранжа второго рода Уравнения Лагранжа можно рассматривать как алгоритм получения дифференциальных уравнений движения систе
Решение задач динамики Пример 7. На вертикальном участке
Библиографический список 1. Никитин Н.Н. Курс теоретической механики: учебник для машиностроит. и приборостроит. спец. вузов / Н.Н. Ники
allrefers.ru
