Исследовательский реферат «Гармонические колебания». Сложение гармонических колебаний реферат
Реферат: Сложение колебаний
Реферат
Студента I –го курса гр. 107
Шлыковича Сергея
Минск 2001
Векторная диаграмма
Колебанияминазываются движения или процессы, обладающие той или иной повторяемостью во времени.
Сложение нескольких гармонических колебаний одного направления и одинаковой частоты становится наглядным, если изображать колебания графически в виде векторов на плоскости. Полученная таким способом схема называетсявекторной диаграммой.
 Возьмем ось, вдоль которой будем откладывать колеблющуюся величинуx. Из взятой на оси точкиОотложим вектор длины A, образующий с осью угол б. Если привести этот вектор во вращение с угловой скоростью щ0, то проекция конца вектора будет перемещаться по оси x в пределах от —Адо +A, причем координата этой проекции будет изменяться со временем по закону
Возьмем ось, вдоль которой будем откладывать колеблющуюся величинуx. Из взятой на оси точкиОотложим вектор длины A, образующий с осью угол б. Если привести этот вектор во вращение с угловой скоростью щ0, то проекция конца вектора будет перемещаться по оси x в пределах от —Адо +A, причем координата этой проекции будет изменяться со временем по закону
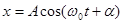
Следовательно, проекция конца вектора на ось будет совершать гармонические колебания с амплитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с начальной фазой, равной углу, образуемому вектором с осью в начальный момент времени.
Таким образом, гармоническое колебание может быть задано с помощью вектора, длина которого равна амплитуде колебания, а направление образует с осьюx угол, равный начальной фазе колебаний.
Рассмотрим сложение двух гармонических колебаний одного направления и одинаковой частоты. Результирующее колебаниебудет суммой колебанийх1иx2,которые определяются функциями
 ,
, (1)
(1)
Представим оба колебания с помощью векторовA1иА2. Построим по правилам сложения векторов результирующий векторА.На рисунке видно, что проекция этого вектора на осьxравна сумме проекций складываемых векторов:

 Поэтому, векторAпредставляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью щ0, как и векторыА1иА2,так что суммаx1их2является гармоническим колебанием с частотой (щ0, амплитудойAи начальной фазой б. Используя теорему косинусов получаем, что
Поэтому, векторAпредставляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью щ0, как и векторыА1иА2,так что суммаx1их2является гармоническим колебанием с частотой (щ0, амплитудойAи начальной фазой б. Используя теорему косинусов получаем, что
 (2)
(2)
Также, из рисунка видно, что
 (3)
(3)
Представление гармонических колебаний с помощью векторов позволяет заменить сложение функций сложением векторов, что значительно проще.
Сложение колебаний во взаимно перпендикулярных направлениях.
Представим две взаимно перпендикулярные векторные величиныxиy,изменяющиеся со временем с одинаковой частотой щ по гармоническому закону, то

 (1)
(1)
Гдеexиeу—орты координатных осейxиy, АиB —амплитуды колебаний. Величинамиxиуможет быть, например, смещения материальной точки (частицы) из положения равновесия.
В случае колеблющейся частицы величины
 ,
, (2)
(2)
определяют координаты частицы на плоскостиxy.Частица будет двигаться по некоторой траектории, вид которой зависит от разности фаз обоих колебаний. Выражения (2) представляют собой заданное в параметрической форме уравнение этой траектории. Чтобы получить уравнение траектории в обычном виде, нужно исключить из уравнений (2) параметрt.Из первого уравнения следует, что
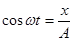 (3) Соответственно
(3) Соответственно (4)
(4)
Развернем косинус во втором из уравнений (2) по формуле для косинуса суммы:

Подставим вместоcos щtи sinщt их значения (3) и (4):
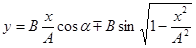

Преобразуем это уравнение



 (5)
(5)
Это уравнение эллипса, оси которого повернуты относительно координатных осейхиу.Ориентация эллипса и его полуоси зависят довольно сложным образом от амплитудAиВи разности фаз б.
Попробуем найти форму траектории для нескольких частных случаев.
1. Разность фаз б равна нулю. В этом случае уравнение (5) упрощается следующим образом:

Отсюда получается уравнение прямой:

Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой щ и амплитудой, равной (рис. 1 а).
(рис. 1 а).
2. Разность фаз б равна ±р. Из уравнение (5)имеет вид

Следовательно, результирующее движение представляет собой гармоническое колебание вдоль прямой
 (рис. 1 б)
(рис. 1 б)

Рис.1
 3. При
3. При уравнение (5) переходит в уравнение эллипса, приведенного к координатным осям:
уравнение (5) переходит в уравнение эллипса, приведенного к координатным осям:

Полуоси эллипса равны соответствующим амплитудам колебаний. При равенстве амплитудАиВэллипс превращается в окружность.
Случаи и
и отличаются направлением движения по эллипсу или окружности.
отличаются направлением движения по эллипсу или окружности.
Следовательно, равномерное движение по окружности радиуса R с угловой скоростью щ может быть представлено как сумма двух взаимно перпендикулярных колебаний:
 ,
,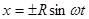
(знак плюс в выражении дляусоответствует движению против часовой стрелки, знак минус — движению по часовой стрелке).
Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектории результирующего движения имеют вид сложных кривых, называемых фигурами Лиссажу.


Фигура Лиссажу для
отношения частот 1:2 и
разности фаз р/2
Фигура Лиссажу для отношения частот 3:4 и разности фаз р/2
superbotanik.net
Исследовательский реферат «Гармонические колебания»
Всероссийский конкурс исследовательских работ учащихся
“ЮНОСТЬ, НАУКА, КУЛЬТУРА”
Направление - математика
Исследовательский реферат
«Гармонические колебания»
Бородич Никита Георгиевич
МБОУ СОШ № 1 ЗАТО Озерный Тверской области
11 класс
Научный руководитель:
Бородич Ирина Сергеевна
учитель математики
МБОУ СОШ № 1 ЗАТО Озерный
Данная работа была разработана в целях освоения и знакомства с математическими методами физических расчетов. Математические методики обсчетов радио и электромагнитных волн, обсчет механических колебаний и прочих физических явлений. Колебания сопровождают и биологические процессы, например, слух, зрение, восприятие ультрафиолета, (используемые многими биологическими видами), передачу возбуждения по нервной ткани, работу сердца и мозга. Записывая работу сердца или мозга, врачи получают электрокардиограммы и энцефалограммы. Как говорил создатель учения о биосфере академик Вернадский: “Кругом нас, в нас самих, всюду и везде, без перерыва, вечно сменяясь, совпадая и сталкиваясь, идут излучения разной длины – от волн, длина которых измеряется десятимиллионными долями миллиметра, до длинных, измеряемых километрами”.
Содержание
Введение, актуальность, цели, задачи……………………………………3
1.Гармонические колебания……………………………………………….4
2.Основные определения…………………………………………………..4
3.Скорость и ускорение при гармонических колебаниях………………..7
4.Представление гармонических колебаний с помощью ………………..8
метода векторных диаграмм
5.Сложение синхронных скалярных колебаний………………………….9
6.Биения …………………………………………………………………….10
7.Сложение колебаний с кратными частотами……………………………11
8.Сложение ортогональных колебаний с равными частотами…………...12
9.Сложение ортогональных колебаний с кратными частотами………….12
Заключение…………………………………………………………………..13
Литература……………………………………………………………………13
В повседневной жизни мы сталкиваемся с различными колебательными процессами.
Механические колебания применяются для скорейшей укладки бетона специальными виброукладчиками, для просеивания материалов на виброситах и даже для почти безболезненного высверливания отверстий в зубах. Акустические колебания нужны для приема и воспроизведения звука, а электромагнитные – для радио, телевидения, связи с космическими ракетами. Электромагнитные колебания доносят до нас вести о сложных процессах, происходящих внутри звезд, о взрывах в отдаленных галактиках, о таких диковинных вещах, как пульсары (нейтронные звезды), черные дыры и т.д. С помощью электромагнитных колебаний учеными были получены снимки обратной стороны Луны и вечно закрытой облаками Венеры.
Но колебания не всегда полезны. Вибрация станка действует на резец и обрабатываемую деталь и может привести к браку; вибрация жидкости в топливных баках ракеты угрожает их целостности, а вибрация самолетных крыльев при неблагоприятных условиях может привести к катастрофе. Даже хорошо затянутая гайка под влиянием вибрации ослабевает и станок разбалтывается. А самое страшное – под действием вибрации меняется внутренняя структура металлов, что приводит к так называемой “усталости” и последующему неожиданному разрушению конструкции. Колебаниями объясняются случаи падения мостов во время ураганов, катастрофы в кузнечных цехах, где несколько механических молотов начинали работать в такт. Колебания, контролируемые человеком, весьма полезны. Однако они могут превратиться в опасного врага. Поэтому надо изучать колебания, знать их свойства. А здесь без математических расчетов не обойтись.
infourok.ru
Реферат - Сложение колебаний - Наука и техника
Реферат
На тему «Сложение колебаний»
Студента I –го курса гр. 107
Шлыковича Сергея
Минск 2001
Векторная диаграмма
Колебаниями называются движения или процессы, обладающие той или иной повторяемостью во времени.
Сложение нескольких гармонических колебаний одного направления и одинаковой частоты становится наглядным, если изображать колебания графически в виде векторов на плоскости. Полученная таким способом схема называется векторной диаграммой .
Возьмем ось, вдоль которой будем откладывать колеблющуюся величину x. Из взятой на оси точки О отложим вектор длины A, образующий с осью угол б. Если привести этот вектор во вращение с угловой скоростью щ0, то проекция конца вектора будет перемещаться по оси x в пределах от —А до +A, причем координата этой проекции будет изменяться со временем по закону
Следовательно, проекция конца вектора на ось будет совершать гармонические колебания с амплитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с начальной фазой, равной углу, образуемому вектором с осью в начальный момент времени.
Таким образом, гармоническое колебание может быть задано с помощью вектора, длина которого равна амплитуде колебания, а направление образует с осью x угол, равный начальной фазе колебаний.
Рассмотрим сложение двух гармонических колебаний одного направления и одинаковой частоты. Результирующее колебаниебудет суммой колебаний х1 и x2, которые определяются функциями
, (1)
Представим оба колебания с помощью векторов A1 и А2 . Построим по правилам сложения векторов результирующий вектор А . На рисунке видно, что проекция этого вектора на ось x равна сумме проекций складываемых векторов:
Поэтому, вектор A представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью щ0, как и векторы А1 и А2 , так что сумма x1 и х2 является гармоническим колебанием с частотой (щ0, амплитудой A и начальной фазой б. Используя теорему косинусов получаем, что
(2)
Также, из рисунка видно, что
(3)
Представление гармонических колебаний с помощью векторов позволяет заменить сложение функций сложением векторов, что значительно проще.
Сложение колебаний во взаимно перпендикулярных направлениях.
Представим две взаимно перпендикулярные векторные величины x и y , изменяющиеся со временем с одинаковой частотой щ по гармоническому закону, то
(1)
Где ex и eу — орты координатных осей x и y, А и B — амплитуды колебаний. Величинами x иу может быть, например, смещения материальной точки (частицы) из положения равновесия.
В случае колеблющейся частицы величины
, (2)
определяют координаты частицы на плоскости xy. Частица будет двигаться по некоторой траектории, вид которой зависит от разности фаз обоих колебаний. Выражения (2) представляют собой заданное в параметрической форме уравнение этой траектории. Чтобы получить уравнение траектории в обычном виде, нужно исключить из уравнений (2) параметр t. Из первого уравнения следует, что
(3) Соответственно (4)
Развернем косинус во втором из уравнений (2) по формуле для косинуса суммы:
Подставим вместо cos щ t и sinщt их значения (3) и (4):
Преобразуем это уравнение
(5)
Это уравнение эллипса, оси которого повернуты относительно координатных осей х и у. Ориентация эллипса и его полуоси зависят довольно сложным образом от амплитуд A и В и разности фаз б.
Попробуем найти форму траектории для нескольких частных случаев.
1. Разность фаз б равна нулю. В этом случае уравнение (5) упрощается следующим образом:
Отсюда получается уравнение прямой:
Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой щ и амплитудой, равной (рис. 1 а).
2. Разность фаз б равна ±р. Из уравнение (5)имеет вид
Следовательно, результирующее движение представляет собой гармоническое колебание вдоль прямой
(рис. 1 б)
Рис.1
3. При уравнение (5) переходит в уравнение эллипса, приведенного к координатным осям:
Полуоси эллипса равны соответствующим амплитудам колебаний. При равенстве амплитуд А и В эллипс превращается в окружность.
Случаи и отличаются направлением движения по эллипсу или окружности.
Следовательно, равномерное движение по окружности радиуса R с угловой скоростью щ может быть представлено как сумма двух взаимно перпендикулярных колебаний:
,
(знак плюс в выражении для у соответствует движению против часовой стрелки, знак минус — движению по часовой стрелке).
Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектории результирующего движения имеют вид сложных кривых, называемых фигурами Лиссажу.
Фигура Лиссажу для
отношения частот 1:2 и
разности фаз р/2
Фигура Лиссажу для отношения частот 3:4 и разности фаз р/2
www.ronl.ru
Реферат - Сложение колебаний - Физика
Реферат
На тему «Сложение колебаний» Студента I –го курса гр. 107
ШлыковичаСергея
Минск 2001
Векторная диаграмма Колебанияминазываются движения или процессы, обладающие той или иной повторяемостью вовремени.
Сложениенескольких гармонических колебаний одного направления и одинаковой частоты становится наглядным, если изображать колебания графическив виде векторов на плоскости. Полученная таким способом схема называется векторнойдиаграммой.
/>Возьмем ось, вдоль которой будем откладывать колеблющуюсявеличину x. Из взятой на оси точки О отложим вектор длины A, образующий сосью угол α. Если привести этот вектор во вращение с угловойскоростью ω0,то проекция конца вектора будет перемещаться по оси x в пределах от —А до+A, причем координата этой проекции будет изменяться современем по закону
/>
Следовательно, проекция конца вектора на ось будет совершать гармонические колебания с амплитудой, равной длине вектора, с круговой частотой, равной угловойскорости вращения вектора, и с начальной фазой, равной углу, образуемомувектором с осью в начальный момент времени.
Таким образом,гармоническое колебание может быть задано с помощью вектора, длина которого равнаамплитуде колебания, а направление образует с осью x угол, равныйначальной фазе колебаний.
Рассмотрим сложение двухгармонических колебаний одного направления и одинаковой частоты.Результирующее колебаниебудет суммой колебаний х1и x2, которые определяются функциями
/>, /> (1)
Представим оба колебания спомощью векторов A1и А2. Построимпо правилам сложения векторов результирующий вектор А. Нарисунке видно, что проекция этого вектора на ось x равна сумме проекций складываемых векторов:
/>
/>Поэтому, вектор Aпредставляет собой результирующее колебание. Этот векторвращается с той же угловой скоростью ω0,как и векторы А1и А2,так что сумма x1и х2является гармоническим колебанием счастотой (ω0, амплитудой A иначальной фазой α. Используя теорему косинусов получаем, что
/> (2)
Также, из рисунка видно, что
/> (3)
Представление гармонических колебаний спомощью векторов позволяет заменить сложение функций сложением векторов, что значительно проще.
Сложение колебаний во взаимноперпендикулярных направлениях.
Представим две взаимноперпендикулярные векторные величины xи y, изменяющиеся современем с одинаковой частотой ω по гармоническому закону, то
/> /> (1)
Где exи eу— орты координатныхосей x и y, А и B — амплитудыколебаний. Величинами x иу можетбыть, например, смещения материальной точки (частицы) из положения равновесия.
В случае колеблющейсячастицы величины
/>, /> (2)
определяют координаты частицы на плоскости xy. Частица будет двигаться по некоторой траектории, видкоторой зависит от разности фаз обоих колебаний. Выражения (2) представляютсобой заданное в параметрической форме уравнение этой траектории. Чтобыполучить уравнение траектории в обычном виде, нужно исключить из уравнений (2)параметр t. Из первого уравненияследует, что
/> (3)Соответственно /> (4)
Развернем косинус во втором из уравнений (2) поформуле для косинуса суммы:
/>
Подставим вместо cos ωt и sinωt их значения (3) и (4):
/>
/>
Преобразуем это уравнение
/>
/>
/>
/> (5)
Это уравнение эллипса, оси которого повернуты относительнокоординатных осей х и у. Ориентация эллипса и его полуосизависят довольно сложным образом от амплитуд A и В и разности фаз α.
Попробуем найти форму траектории для несколькихчастных случаев.
1. Разность фаз α равна нулю.В этом случае уравнение (5) упрощается следующим образом:
/>
Отсюда получается уравнение прямой:
/>
Результирующее движение является гармоническимколебанием вдоль этой прямой с частотой ω и амплитудой, равной /> (рис. 1 а).
2. Разность фаз α равна±π. Из уравнение (5) имеет вид
/>
Следовательно, результирующее движение представляетсобой гармоническое колебание вдоль прямой
/> (рис. 1 б)
/>
Рис.1/>3. При /> уравнение(5) переходит в уравнение эллипса, приведенного к координатным осям:
/>
Полуоси эллипса равны соответствующим амплитудамколебаний. При равенстве амплитуд А и В эллипс превращается вокружность.
Случаи />и /> отличаются направлением движения по эллипсу илиокружности.
Следовательно, равномерноедвижение по окружности радиуса R с угловой скоростью ω может бытьпредставлено как сумма двух взаимно перпендикулярных колебаний:
/>, />
(знак плюс в выражении для у соответствуетдвижению против часовой стрелки, знак минус — движению по часовой стрелке).
Есличастоты взаимно перпендикулярных колебаний не одинаковы, то траекториирезультирующего движения имеют вид сложных кривых, называемых фигурамиЛиссажу.
www.ronl.ru
Реферат - Сложение колебаний - Теоритическая физика
Векторная диаграмма Колебаниями называются движения или процессы, обладающие той или иной повторяемостью во времени. Сложение нескольких гармонических колебаний одного направления и одинаковой частоты становится наглядным, если изображать колебания графически в виде векторов на плоскости. Полученная таким способом схема называется векторной диаграммой. Возьмем ось, вдоль которой будем откладывать колеблющуюся величину x. Из взятой на оси точки О отложим вектор длины A, образующий с осью угол ?. Если привести этот вектор во вращение с угловой скоростью ?0, то проекция конца вектора будет перемещаться по оси x в пределах от —А до +A, причем координата этой проекции будет изменяться со временем по законуСледовательно, проекция конца вектора на ось будет совершать гармонические колебания с амплитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с начальной фазой, равной углу, образуемому вектором с осью в начальный момент времени.
Таким образом, гармоническое колебание может быть задано с помощью вектора, длина которого равна амплитуде колебания, а направление образует с осью x угол, равный начальной фазе колебаний.
Рассмотрим сложение двух гармонических колебаний одного направления и одинаковой частоты. Результирующее колебание будет суммой колебаний х1 и x2, которые определяются функциями
, (1)
Представим оба колебания с помощью векторов A1и А2. Построим по правилам сложения векторов результирующий вектор А. На рисунке видно, что проекция этого вектора на ось x равна сумме проекций складываемых векторов:
Поэтому, вектор A представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью ?0, как и векторы А1 и А2, так что сумма x1 и х2 является гармоническим колебанием с частотой (?0, амплитудой A и начальной фазой ?. Используя теорему косинусов получаем, что
(2)
Также, из рисунка видно, что
(3)
Представление гармонических колебаний с помощью векторов позволяет заменить сложение функций сложением векторов, что значительно проще.
Сложение колебаний во взаимно перпендикулярных направлениях.
Представим две взаимно перпендикулярные векторные величины x и y, изменяющиеся со временем с одинаковой частотой ? по гармоническому закону, то
(1)
Где ex и eу — орты координатных осей x и y, А и B — амплитуды колебаний. Величинами x и у может быть, например, смещения материальной точки (частицы) из положения равновесия.
В случае колеблющейся частицы величины
, (2)
определяют координаты частицы на плоскости xy. Частица будет двигаться по некоторой траектории, вид которой зависит от разности фаз обоих колебаний. Выражения (2) представляют собой заданное в параметрической форме уравнение этой траектории. Чтобы получить уравнение траектории в обычном виде, нужно исключить из уравнений (2) параметр t. Из первого уравнения следует, что
(3) Соответственно (4)
Развернем косинус во втором из уравнений (2) по формуле для косинуса суммы:
Подставим вместо cos ?t и sin?t их значения (3) и (4):
Преобразуем это уравнение
(5)
Это уравнение эллипса, оси которого повернуты относительно координатных осей х и у. Ориентация эллипса и его полуоси зависят довольно сложным образом от амплитуд A и В и разности фаз ?.
Попробуем найти форму траектории для нескольких частных случаев.
1. Разность фаз ? равна нулю. В этом случае уравнение (5) упрощается следующим образом:
Отсюда получается уравнение прямой:
Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой ? и амплитудой, равной (рис. 1 а).
2. Разность фаз ? равна ±?. Из уравнение (5) имеет вид
Следовательно, результирующее движение представляет собой гармоническое колебание вдоль прямой
(рис. 1 б)
Рис.1
3. При уравнение (5) переходит в уравнение эллипса, приведенного к координатным осям:
Полуоси эллипса равны соответствующим амплитудам колебаний. При равенстве амплитуд А и В эллипс превращается в окружность.
Случаи и отличаются направлением движения по эллипсу или окружности.
Следовательно, равномерное движение по окружности радиуса R с угловой скоростью ? может быть представлено как сумма двух взаимно перпендикулярных колебаний:
,
(знак плюс в выражении для у соответствует движению против часовой стрелки, знак минус — движению по часовой стрелке).
Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектории результирующего движения имеют вид сложных кривых, называемых фигурами Лиссажу.
Фигура Лиссажу для
отношения частот 1:2 и
разности фаз ?/2
Фигура Лиссажу для отношения частот 3:4 и разности фаз ?/2
www.ronl.ru
Исследовательский реферат «Гармонические колебания» страница 6
Если сдвиг фаз 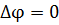 , то будет справедливо следующее выражение:
, то будет справедливо следующее выражение:
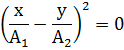
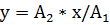
Т.е. фигура Лиссажу представляет из себя прямую линию с углом наклона 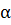 к оси
к оси  (
( ). Если
). Если 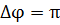 , то
, то 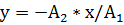 .
.
Если 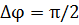 то имеем классическое уравнение эллипса, полуоси которого параллельны осям координат:
то имеем классическое уравнение эллипса, полуоси которого параллельны осям координат:
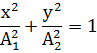
Если 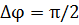 и
и 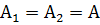 , то эллипс превращается в окружность радиуса
, то эллипс превращается в окружность радиуса 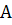 .
.
Рассмотрим случай сложения несинхронных перпендикулярных колебаний. Пусть 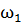 не равняется
не равняется 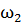 , но частоты исходных колебаний относятся как целые числа:
, но частоты исходных колебаний относятся как целые числа: 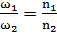 . Рассмотрим следующий пример:
. Рассмотрим следующий пример:
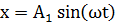
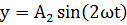
Для нахождения вида фигуры Лиссажу используем метод графического исключения 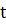 . Изобразим на одном графике зависимости
. Изобразим на одном графике зависимости 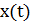 и
и 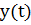 . Отметим на этом графике положение точек в некоторые последовательные моменты времени. Затем перенесем эти точки на плоскость
. Отметим на этом графике положение точек в некоторые последовательные моменты времени. Затем перенесем эти точки на плоскость 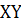 . В результате получим фигуру Лиссажу типа восьмерки:
. В результате получим фигуру Лиссажу типа восьмерки:
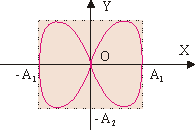
Рисунок 11. Пример фигуры Лиссажу типа восьмерки для 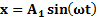 И
И 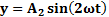
Если взять колебания с разными начальными фазами, то при таком же соотношении частот также получим фигуры Лиссажу типа восьмерки, но не симметричные относительно осей координат. При 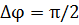 фигура Лиссажу примет вид параболы.
фигура Лиссажу примет вид параболы.
Существует правило частот Лиссажу, по которому можно определить частоты складываемых колебаний. Об их соотношении судят по числу точек пересечения фигуры прямыми, параллельными осям координат:
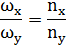
Откуда это следует? Обозначим за 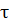 - минимальное время, в течение которого полностью описывается фигура Лиссажу. Очевидно, что
- минимальное время, в течение которого полностью описывается фигура Лиссажу. Очевидно, что 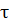 равно наименьшему кратному периодов колебаний
равно наименьшему кратному периодов колебаний 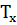 и
и 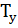 , совершающихся вдоль осей
, совершающихся вдоль осей  и
и 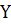 . За один период конец вектора
. За один период конец вектора 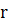 пересечет ось
пересечет ось  2 раза. Следовательно, за время
2 раза. Следовательно, за время 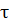 число пересечений этой оси будет равно
число пересечений этой оси будет равно 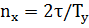 . Аналогично
. Аналогично 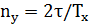 . Следовательно,
. Следовательно, 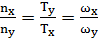 .
.
Метод фигур Лиссажу широко используется для определения соотношения частот и фаз складываемых колебаний (например, в радиотехнике для градуировки генераторов). Чувствительность фигуры Лиссажу к разности фаз используется также для исследования фазовых соотношений в цепях переменного тока.
Заключение
Математика – царица наук. Гармонические колебания – физические явления, но для их изучения не обойтись без математических исследований. Таким образом, для использования колебательных процессов во благо человека, необходимо создавать математические модели реальных ситуаций, изучать их с помощью удивительно красивых тригонометрических функций.
Литература
-
А. М. Афонин. Физические основы механики. — Изд. МГТУ им. Баумана, 2006.
2. А.Г. Мордкович. Учебник. Алгебра и начала анализа 10-11-е класс
3. Физика. В 5 книгах. Книга 4. Колебания и волны. Оптика, А. Н. Леденев
infourok.ru
Исследовательский реферат «Гармонические колебания» страница 2
Важность изучения данного материала определяется необходимостью познания явления гармонических колебаний. Данная тема является и разделом математической физики. Так как я хочу стать инженером, то аознанием данной темы является частью моей довузовской подготовки. Данная тема формирует логику, развивает математическое мышление и тренирует алгоритмы тригонометрических исчислений.
Цель:
Создать представление о гармонических колебаниях, их сложении и основных характеристиках. Показать значимость одной из тем математики и физики «Гармонические колебания»
-
Собрать имеющуюся информацию по вопросу «Гармонические колебания».
-
Проанализировать информацию по данной теме.
-
Показать важность математических обоснований при изучении данной темы.
В технике и в окружающем нас мире часто приходится сталкиваться с периодическими (или почти периодическими) процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать колебательные процессы различной природы с единой точки зрения.
Механическими колебаниями называются периодические (или почти периодические) изменения физической величины, описывающей механическое движение (скорость, перемещение, кинетическая и потенциальная энергия и т. п.).
Особую роль в колебательных процессах имеет простейший вид колебаний – гармонические колебания. Гармонические колебания лежат в основе единого подхода при изучении колебаний различной природы, так как колебания, встречающиеся в природе и технике, часто близки к гармоническим, а периодические процессы иной формы можно представить как наложение гармонических колебаний.
Гармоническими колебаниями называются такие колебания, при которых колеблющаяся величина меняется от времени по закону синуса или косинуса.Уравнение гармонических колебаний имеет вид:
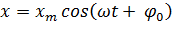
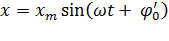
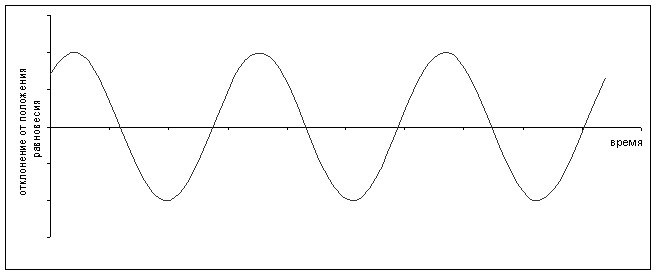
Рисунок 1. Простейший пример гармонических колебаний
Здесь 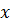 – смещение тела от положения равновесия, А =
– смещение тела от положения равновесия, А = 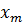 – амплитуда колебаний, т. е. максимальное смещение от положения равновесия,
– амплитуда колебаний, т. е. максимальное смещение от положения равновесия,  –
–
циклическая или круговая частота колебаний, 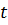 – время. Величина, стоящая под знаком косинуса
– время. Величина, стоящая под знаком косинуса 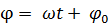 называется фазой гармонического процесса. При
называется фазой гармонического процесса. При 
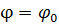 , поэтому
, поэтому  называют начальной фазой. Приведенные формулы отличаются определением начальной фазы и при
называют начальной фазой. Приведенные формулы отличаются определением начальной фазы и при 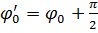 полностью совпадают. Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия. Если выведение происходит толчком (сообщается кинетическая энергия), то при
полностью совпадают. Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия. Если выведение происходит толчком (сообщается кинетическая энергия), то при  смещение
смещение 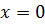 , следовательно, удобнее пользоваться функцией
, следовательно, удобнее пользоваться функцией 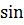 , положив
, положив 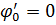 ; при отклонении от положения равновесия (сообщается потенциальная энергия) при
; при отклонении от положения равновесия (сообщается потенциальная энергия) при  смещение
смещение 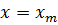 , следовательно, удобнее пользоваться функцией
, следовательно, удобнее пользоваться функцией 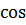 и
и 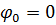 . Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе).
. Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе).
infourok.ru
 Возьмем ось, вдоль которой будем откладывать колеблющуюся величинуx. Из взятой на оси точкиОотложим вектор длины A, образующий с осью угол б. Если привести этот вектор во вращение с угловой скоростью щ0, то проекция конца вектора будет перемещаться по оси x в пределах от —Адо +A, причем координата этой проекции будет изменяться со временем по закону
Возьмем ось, вдоль которой будем откладывать колеблющуюся величинуx. Из взятой на оси точкиОотложим вектор длины A, образующий с осью угол б. Если привести этот вектор во вращение с угловой скоростью щ0, то проекция конца вектора будет перемещаться по оси x в пределах от —Адо +A, причем координата этой проекции будет изменяться со временем по закону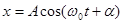
 ,
, (1)
(1)
 Поэтому, векторAпредставляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью щ0, как и векторыА1иА2,так что суммаx1их2является гармоническим колебанием с частотой (щ0, амплитудойAи начальной фазой б. Используя теорему косинусов получаем, что
Поэтому, векторAпредставляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью щ0, как и векторыА1иА2,так что суммаx1их2является гармоническим колебанием с частотой (щ0, амплитудойAи начальной фазой б. Используя теорему косинусов получаем, что (2)
(2) (3)
(3)
 (1)
(1) ,
, (2)
(2)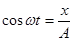 (3) Соответственно
(3) Соответственно (4)
(4)
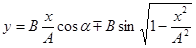




 (5)
(5)

 (рис. 1 а).
(рис. 1 а).

 3. При
3. При уравнение (5) переходит в уравнение эллипса, приведенного к координатным осям:
уравнение (5) переходит в уравнение эллипса, приведенного к координатным осям:
 и
и отличаются направлением движения по эллипсу или окружности.
отличаются направлением движения по эллипсу или окружности. ,
,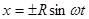


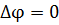 , то будет справедливо следующее выражение:
, то будет справедливо следующее выражение: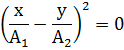
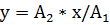
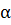 к оси
к оси  (
( ). Если
). Если 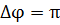 , то
, то 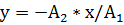 .
.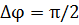 то имеем классическое уравнение эллипса, полуоси которого параллельны осям координат:
то имеем классическое уравнение эллипса, полуоси которого параллельны осям координат: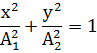
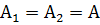 , то эллипс превращается в окружность радиуса
, то эллипс превращается в окружность радиуса 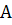 .
.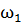 не равняется
не равняется 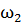 , но частоты исходных колебаний относятся как целые числа:
, но частоты исходных колебаний относятся как целые числа: 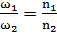 . Рассмотрим следующий пример:
. Рассмотрим следующий пример: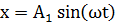
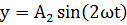
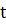 . Изобразим на одном графике зависимости
. Изобразим на одном графике зависимости 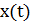 и
и 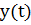 . Отметим на этом графике положение точек в некоторые последовательные моменты времени. Затем перенесем эти точки на плоскость
. Отметим на этом графике положение точек в некоторые последовательные моменты времени. Затем перенесем эти точки на плоскость 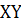 . В результате получим фигуру Лиссажу типа восьмерки:
. В результате получим фигуру Лиссажу типа восьмерки:
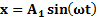 И
И 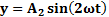
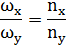
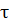 - минимальное время, в течение которого полностью описывается фигура Лиссажу. Очевидно, что
- минимальное время, в течение которого полностью описывается фигура Лиссажу. Очевидно, что 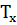 и
и 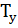 , совершающихся вдоль осей
, совершающихся вдоль осей 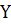 . За один период конец вектора
. За один период конец вектора 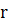 пересечет ось
пересечет ось 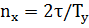 . Аналогично
. Аналогично 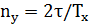 . Следовательно,
. Следовательно, 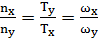 .
.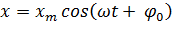
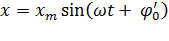

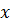 – смещение тела от положения равновесия, А =
– смещение тела от положения равновесия, А = 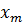 – амплитуда колебаний, т. е. максимальное смещение от положения равновесия,
– амплитуда колебаний, т. е. максимальное смещение от положения равновесия,  –
–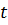 – время. Величина, стоящая под знаком косинуса
– время. Величина, стоящая под знаком косинуса 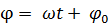 называется фазой гармонического процесса. При
называется фазой гармонического процесса. При 
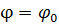 , поэтому
, поэтому  называют начальной фазой. Приведенные формулы отличаются определением начальной фазы и при
называют начальной фазой. Приведенные формулы отличаются определением начальной фазы и при 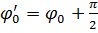 полностью совпадают. Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия. Если выведение происходит толчком (сообщается кинетическая энергия), то при
полностью совпадают. Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия. Если выведение происходит толчком (сообщается кинетическая энергия), то при 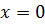 , следовательно, удобнее пользоваться функцией
, следовательно, удобнее пользоваться функцией 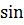 , положив
, положив 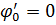 ; при отклонении от положения равновесия (сообщается потенциальная энергия) при
; при отклонении от положения равновесия (сообщается потенциальная энергия) при 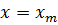 , следовательно, удобнее пользоваться функцией
, следовательно, удобнее пользоваться функцией 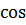 и
и 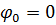 . Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе).
. Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе).