Реферат: Великая теорема Ферма:. Реферат великая теорема ферма

Реферат по математике на тему "Великая теорема Ферма"

«Великая теорема Ферма»

2016

Великая теорема Ферма

Издание 1670 года «Арифметики» Диофанта включает комментарий Ферма, в частности его «последнюю теорему» (Observatio Domini Petri de Fermat)

Великая теорема Ферма (или Последняя теорема Ферма) — одна из самых популярных теорем математики. Её условие формулируется просто, на «школьном» арифметическом уровне, однако доказательство теоремы искали многие математики более трёхсот лет. Доказана в 1994 году Эндрю Уайлсом.

Формулировка

Теорема утверждает, что:

Для любого натурального числа 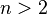 уравнение

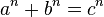
не имеет решений в целых ненулевых числах .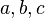

Встречается более узкий вариант формулировки, утверждающий, что это уравнение не имеет натуральных решений. Однако очевидно, что если существует решение для целых чисел, то существует и решение в натуральных числах. В самом деле, пусть 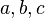 — целые числа, дающие решение уравнения Ферма. Если  чётно, то  тоже будут решением, а если нечётно, то перенесём все степени отрицательных значений в другую часть уравнения, изменив знак. Например, если бы существовало решение уравнения 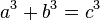 и при этом  отрицательно, а прочие положительны, то , и получаем натуральные решения  Поэтому обе формулировки эквивалентны.

Обобщениями утверждения теоремы Ферма являются опровергнутая гипотеза Эйлера и открытая гипотеза Ландера — Паркина — Селфриджа.

История

Для случая  эту теорему в X веке пытался доказать ал-Ходжанди, но его доказательство не сохранилось.

В общем виде теорема была сформулирована Пьером Ферма в 1637 году на полях «Арифметики» Диофанта. Дело в том, что Ферма делал свои пометки на полях читаемых математических трактатов и там же формулировал пришедшие на ум задачи и теоремы. Теорему, о которой ведётся речь, он записал с припиской, что найденное им остроумное доказательство этой теоремы слишком длинно, чтобы его можно было поместить на полях книги:

«Наоборот, невозможно разложить куб на два куба, биквадрат на два биквадрата и вообще никакую степень, большую квадрата, на две степени с тем же показателем. Я нашёл этому поистине чудесное доказательство, но поля книги слишком узки для него».

Доказательство самого Ферма для случая  в сорок пятом комментарии к «Арифметике» Диофанта

Ферма приводит только доказательство, как решение задачи, сводимой к четвёртой степени теоремы , в сорок пятом комментарии к «Арифметике» Диофанта и в письме к Каркави (август 1659 года). Кроме этого, Ферма включил третью степень теоремы  в список задач, решаемых методом бесконечного спуска.

Эйлер в 1770 году доказал теорему для случая , Дирихле и Лежандр в 1825 — для , Ламе — для 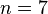. Куммер показал, что теорема верна для всех простых n, меньших 100, за возможным исключением т. н.иррегулярных простых 37, 59, 67.

Над полным доказательством Великой теоремы работало немало выдающихся математиков и множество дилетантов-любителей; считается, что теорема стоит на первом месте по количеству некорректных «доказательств». Тем не менее, эти усилия привели к получению многих важных результатов современной теории чисел. Давид Гильберт в своём докладе «Математические проблемы» на II Международном конгрессе математиков (1900) так отозвался об этой проблеме:

Проблема доказательства этой неразрешимости являет разительный пример того, какое побуждающее влияние на науку может оказать специальная и на первый взгляд малозначительная проблема. Ибо, побуждённый задачей Ферма, Куммер пришёл к введению идеальных чисел и к открытию теоремы об однозначном разложении чисел в круговых полях на идеальные простые множители — теоремы, которая теперь, благодаря обобщениям на любую алгебраическую числовую область, полученным Дедекиндом и Кронекером, является центральной в современной теории чисел и значение которой выходит далеко за пределы теории чисел в область алгебры и теории функций.

В 1908 году немецкий любитель математики Вольфскель завещал 100 000 немецких марок тому, кто докажет теорему Ферма. Однако после войны премия обесценилась.

В 1980-х годах появился новый подход к решению проблемы. Из гипотезы Морделла, доказанной Фальтингсом в 1983 году, следует, что уравнение 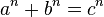 при  может иметь лишь конечное число взаимно простых решений.

Последний, но самый важный, шаг в доказательстве теоремы был сделан Уайлсом в сентябре 1994 года. Его 130-страничное доказательство было опубликовано в журнале «Annals of Mathematics». Доказательство основано на предположении немецкого математика Герхарда Фрая о том, что Великая теорема Ферма является следствием гипотезы Таниямы — Симуры (это предположение было доказано Кеном Рибетом при участии Ж.П. Серра).

Первый вариант своего доказательства Уайлс опубликовал в 1993 году (после 7 лет напряжённой работы), но в нём вскоре был обнаружен серьёзный пробел, который с помощью Ричарда Лоуренса Тейлора удалось достаточно быстро устранить. В 1995 году был опубликован завершающий вариант.

Колин Мак-Ларти отметил, что доказательство Уайлса может быть упрощено, чтобы не предполагать существования так называемых «больших кардиналов».

«Ферматисты»

Авторское свидетельство, выданное Министерством образования и науки Украины на доказательство теоремы Ферма Г. А. Середкину и Л. В. Шаповаловой

Простота формулировки теоремы Ферма (доступная в понимании даже школьнику), а также сложность единственного известного доказательства (или неведение о его существовании), вдохновляют многих на попытки найти другое, более простое, доказательство. Людей, пытающихся доказать теорему Ферма элементарными методами, называют «ферматистами» или «ферматиками». Ферматисты зачастую не владеют основами математической культуры и допускают ошибки в арифметических действиях или логических, хотя некоторые представляют весьма изощрённые «доказательства», в которых трудно найти ошибку.

Доказывать теорему Ферма в среде любителей математики было настолько популярно, что в 1972 году журнал «Квант», публикуя статью о теореме Ферма, сопроводил её следующей припиской:

Редакция «Кванта» со своей стороны считает необходимым известить читателей, что письма с проектами доказательств теоремы Ферма рассматриваться (и возвращаться) не будут.

Немецкому математику Эдмунду Ландау очень докучали «ферматисты». Чтобы не отвлекаться от основной работы, он заказал несколько сот бланков со следующим текстом:

Уважаемый …! Благодарю Вас за присланную Вами рукопись с доказательством Великой теоремы Ферма. Первая ошибка находится на странице … в строке …

Находить ошибку и заполнять пробелы в бланке он поручал своим аспирантам.

Примечательно, что отдельные ферматисты добиваются публикации своих (неверных) «доказательств» в ненаучной прессе, которая раздувает их значение до научной сенсации. Впрочем, иногда такие публикации появляются и в уважаемых научных изданиях, как правило, с последующими опровержениями. Среди других примеров:

• Брошюра В. И. Будкина, изданная в Ярославле под названием «Методика познания „истины“. Доказательство Великой теоремы Ферма» (47 с., 5000 экз., Верхне-Волжское книжное издательство, 1975).

• Книга Л. Ш. Райхеля «Великая теорема», изданная в Ленинграде в 1990 году.

• Свидетельство о регистрации авторских прав на произведение «доказательство теоремы Ферма», выданное Министерством образования и науки Украины Л. В. Шаповаловой и Г. А. Середкину. Следует пояснить, что этот документ не удостоверяет каким-либо образом правильность доказательства, а лишь регистрирует авторские права на поданный в Министерство образования и науки печатный труд; на это министерство возложена обязанность ведения реестра таких свидетельств.

Теорема Ферма в культуре и искусстве

Великая теорема Ферма стала символом труднейшей научной проблемы и в этом качестве часто упоминается в беллетристике. Далее перечислены некоторые произведения, в которых теорема не просто упомянута, но является существенной частью сюжета или идеологии произведения.

• В повести Е. Велтистова «Победитель невозможного» друг Сыроежкина и Электроника Вова Корольков в качестве свободного задания по математике доказал Великую теорему Ферма.

• В телесериале «Звёздный Путь» капитан космического корабля Жан-Люк Пикар был озадачен разгадкой Великой теоремы Ферма во второй половине XXIV века. Таким образом, создатели фильма предполагали, что решения у Великой теоремы Ферма не будет в ближайшие 400 лет. Серия «Рояль» с этим эпизодом была снята в 1989 году, когда Эндрю Уайлс был в самом начале своих работ. В действительности решение было найдено всего спустя 5 лет.

• В рассказе Артура Порджеса «Саймон Флэгг и дьявол» профессор Саймон Флегг обращается за доказательством теоремы к дьяволу. По этому рассказу снят игровой научно-популярный фильм «Математик и чёрт» (СССР, 1972, производство Центрнаучфильм, творческое объединение «Радуга», режиссёр Райтбурт).

• В рассказе Кира Булычева «Мечта заочника» студент-заочник Гаврилов приходит к профессору Минцу и приносит купленную курсовую работу, в которой приводится доказательство теоремы, с просьбой объяснить, что он написал.

• В посвящённой Хэллоуину 1995 года серии «Симпсонов» двумерный Гомер Симпсон случайно попадает в третье измерение. Во время его путешествия в этом странном мире в воздухе парят геометрические тела и математические формулы, включая равенство . Калькулятор с точностью не более 9 значащих цифр подтверждает это равенство:

178212 + 184112 = 2541210258614589176288669958142428526657 ≈ 254121026·1031,

              192212 = 2541210259314801410819278649643651567616 ≈ 254121026·1031.

Тем не менее, даже без вычисления точных значений легко видеть, что равенство неверно: левая часть — нечётное число, а правая часть — чётное.

• В первом издании «Искусства программирования» Дональда Кнута теорема Ферма приведена в качестве упражнения с математическим уклоном в самом начале книги и оценена максимальным числом (50) баллов, как «исследовательская проблема, которая (насколько это было известно автору в момент написания) ещё не получила удовлетворительного решения. Если читатель найдет решение этой задачи, его настоятельно просят опубликовать его; кроме того, автор данной книги будет очень признателен, если ему сообщат решение как можно быстрее (при условии, что оно правильно)». В третьем издании книги это упражнение уже требует знаний высшей математики и оценивается лишь в 45 баллов.

• В книге Стига Ларссона «Девушка, которая играла с огнём» главная героиня Лисбет Саландер, обладающая редкими способностями к аналитике и фотографической памятью, в качестве хобби занята доказательством Великой теоремы Ферма, на которую она наткнулась, читая фундаментальный труд «Измерения в математике», в котором приводится и доказательство Эндрю Уайлса. Лисбет не хочет изучать готовое доказательство, а главным интересом становится поиск собственного решения. Поэтому всё своё свободное время она посвящает самостоятельному поиску «замечательного доказательства» теоремы великого француза, но раз за разом заходит в тупик. В конце книги Лисбет находит доказательство, которое не только совершенно отлично от предложенного Уайлсом, но и является настолько простым, что сам Ферма мог бы его найти. Однако, после ранения в голову она его забывает, и Ларссон не приводит никаких подробностей этого доказательства.

• Мюзикл «Последнее танго Ферма», изданный институтом Клэя, создан в 2000 году Дж. Розенблумом и Дж. С. Лессер по мотивам реальной истории Эндрю Уайлса. Главный герой по имени Дэниел Кин завершает доказательство теоремы, а дух самого Ферма старается ему помешать.

• За несколько дней до своей смерти Артур Кларк успел отрецензировать рукопись романа «Последняя Теорема», над которой он трудился в соавторстве с Фредериком. Книга вышла уже после смерти Кларка.

• В рассказе Натальи Дарьяловой «Великая и загадочная» сюжет строится на теореме Ферма. Рассказывается о том, как молодой человек, будучи студентом, занялся теоремой Ферма, впоследствии стал математиком, получил несколько важных научных результатов, но совершенно загубил свою личную жизнь.

• В романе П. А. Загребельного «Разгон» скромный преподаватель математики из Одессы сумел доказать теорему, через некоторое время стал академиком и возглавил очень серьезное киевское НПО, занимающееся созданием электронно-вычислительных систем.

• А. П. Казанцев в романе «Острее шпаги» в 1983 году предложил оригинальную версию отсутствия доказательства самого Пьера Ферма.

Литература

На русском

На английском

• Donald C. Benson. The Moment of Proof: Mathematical Epophanies. — Oxford University Press, 1999. — ISBN 0-19-513919-4.

• Faltings, Gerd (1995). The Proof of Fermat’s last theorem by R. Taylor and A. Wiles, Notices of the AMS (42) (7), 743—746.

• Daney, Charles (2003). The Mathematics of Fermat’s last theorem. Retrieved Aug. 5, 2004.

• O’Connor, J. J. & and Robertson, E. F. (1996). Fermat’s last theorem. The history of the problem. Retrieved Aug. 5, 2004.

• Shay, David (2003). Fermat’s last theorem. The story, the history and the mystery. Retrieved Aug. 5, 2004.

infourok.ru

Реферат Великая теорема Ферма )

ГОРОДСКОЙ КЛАССИЧЕСКИЙ ЛИЦЕЙ

РЕФЕРАТ

Великая теорема Ферма

Подготовил:

Петров А. А.,

9Б класс (физ-мат)

г. Кемерово - 1998

Содержание

1. Биография Ферма

2. История Большой теоремы Ферма

3. Доказательство леммы 1 (Жермен)

4. Доказательство леммы 2 (вспомогательной)

5. Доказательство теоремы Ферма для показателя 4

6. Примечания к доказательствам

Биография Ферма

Ферма своими работами способствовал развитию новых отраслей в математике: математического анализа, аналитической геометрии (одновременно с Декартом), теории вероятностей.

Главным вкладом Ферма в алгебру явилась развитая им теория соединений или, как её ещё называют, комбинаторика. Отдельные задачи теории соединений были решены уже в древности греками и индийцами, но научная постановка этих вопросов возникла лишь в XVII веке в работах Ферма и его современника, знаменитого французского философа, математика и физика Блеза Паскаля. Исходя из основ комбинаторики, эти два учёных и положили начало новой математической науке, называемой теорией вероятностей, получившей в XVIII веке значительную теоретическую базу, при этом она стала получать всё большее распространение и использоваться в различных областях науки и практической деятельности. Прежде всего, она была применима к вопросам страхования, а в дальнейшем область её применения всё расширялась и расширялась.

Много внимания Ферма также уделял и вопросу о магических квадратах. Эти квадраты сначала стали известны индийцам и арабам, и уже только в эпоху средних веков они появились в Западной Европе. Различные математики заинтересовались исследованиями их свойств, это содействовало развитию некоторых математических теорий. Ещё Мезириак нашёл способы составления магических квадратов с нечётным числом клеток, а уже Ферма распространил идею составления магических квадратов на пространство, т. е. поставил вопрос о составлении кубов, обладающих свойствами, аналогичными свойствам магических квадратов.

Хотя Ферма внёс большой вклад в развитие теории алгебраических чисел, доказательства его доводов почти ни в одном случае найдены не были (доказательство Большой теоремы Ферма для n=4 – исключение, т. к. в рукописях оно было). Некоторые выводы, сделанные Ферма, были и вовсе ошибочными, но теоремы, полные доказательства которых, как утверждал Ферма, у него имелись, все впоследствии были доказаны (основной вклад в доказательство которых внёс Эйлер). Но было и одно исключение – приятное исключение – это Великая теорема Ферма:

История Большой теоремы Ферма

Большой известностью во всём мире пользуется «Великая теорема Ферма» (она же – «Большая» или «Последняя»).

Великой теоремой Ферма называется то заключение, которое было сделано им при чтении изданной Мезириаком «Арифметики» Диофанта. На полях этой книги, против того места, где идёт речь о решении уравнения вида ­­­­­x2 + y2 = z2, Ферма написал: «Между тем, совершенно невозможно разложить полный куб на сумму кубов, четвёртую степень – на сумму четвёртых степеней, вообще какую-нибудь степень – на сумму степеней с тем же показателем. Я нашёл поистине удивительное доказательство этого предположения, но здесь слишком мало места, чтобы его поместить». Это положение Ферма теперь формулируется как теорема в следующем виде: «Уравнение xn + yn = zn не может быть решено в рациональных числах относительно x, y и z при целых значениях показателя n, больших 2» (общеизвестно, что при n=2такие числа существуют, например, 3, 4, 5 – числа, которые, если являются длинами сторон, образуют знаменитый треугольник Пифагора). Справедливость этой теоремы подтверждается для многих частных случаев (при этом ещё не найдено ни одного опровержения), однако до сих пор она не доказана в общем виде, хотя ей интересовались и её пытались доказать многие крупные математики (в «Истории теории чисел» Диксона прореферировано более трёхсот работ на эту тему). В 1907 году в городе Дармштадте в Германии умер математик Вольфскель, который завещал 100000 марок тому, кто даст полное доказательство теоремы. Немедленно сотни и тысячи людей, движимых одним лишь стремлением к наживе, стали бомбардировать научные общества и журналы своими рукописями, якобы содержащими доказательство теоремы Ферма. Только в Гёттингенское математическое общество за первые три года после объявления завещания Вольфскеля пришло более тысячи «решений». Но премия эта до сих пор никому не выдана за отсутствием настоящего доказательства Большой теоремы Ферма.

Элементарного доказательства Великой теоремы Ферма нет ни для одного показателя n  4.

Случай, когда n = 3, был доказан Эйлером ещё в 1768 году.И тот потребовал ещё много лет, чтобы теория, которой необоснованно пользовался Эйлер при своём доказательстве, была доказана Гауссом.

Доказательство теоремы Ферма для случая, когда n = 5, предложили в 1825 году почти одновременно Лежен Дирихле и Лежандр. Своё доказательство Дирихле опубликовал в 1828 году, но оно было очень сложным, и в 1912 году его упростил Племель.

Для следующего простого показателя n = 7 теорема Ферма была доказана лишь в 1839 году Ламе. Доказательство Ламе было почти сразу же усовершенствовано Лебегом.

В 1847 году Ламе объявил, что ему удалось найти доказательство теоремы Ферма для всех простых показателей n  3. Метод Ламе представлял собой весьма далёкое развитие идей Эйлера и основывался на арифметических свойствах чисел. Однако сразу же Лиувилль обнаружил в рассуждениях Ламе серьёзный пробел, чем опровергнул это доказательство. Ламе был вынужден признать свою ошибку.

На ЭВМ, пользуясь идеями Куммера и Вандивера доказали справедливость теоремы Ферма для всех простых показателей n < 100000.

Доказательство леммы 1 (Жермен)

Если произведение двух взаимно простых натуральных чисел является n-ой степенью, то каждый из сомножителей также будет n-ой степенью:

ab = cn; НОД(a; b) = 1; a, b  N

Доказать: a = xn; b = yn

Доказательство: Если разложить cnна простые множители, то: cn = d1 * … * d1 * d2 * … * d2 * … * dm * … * dm, где каждого множителя по n. Если же разложить на простые множители числа aи b, то какие-то из чисел d1 … dmуйдут к a, какие-то – к b, причём одинаковые уйти и туда, и туда не могут в силу того, что НОД(a; b) = 1, т. е. a есть произведение n-х степеней неких простых чисел, и b также – произведение n-х степеней каких-то чисел, следовательно: a = xn; b = yn.

Доказательство леммы 2 (вспомогательной)

x2 + y2 = z2 (1)

Если(x; y; z) – решение, то (y; x; z) также будет решением, потому чтоxи yсимметричны в данном уравнении. Предположим, что z = 2k, тогда z2 = 4k, если же z = 2k – 1, то z2 = (2k – 1)2 = 4k2 – 4k + 1 = 4(k2 – k) + 1, следовательно, хотя бы одно из чисел x и y чётно, т. к. если бы оба они были нечётными, то x2 + y2 = (2k – 1)2 + (2d – 1)2 = 4k2 – 4k + 1 + 4d2 – 4d + 1 = 4(k2 + d2 – k – d) + 2, чего быть не может, т. к. x2 + y2 = z2. Кроме того (x; y; z)также является решением уравнения, т. к. x2 = (-x)2; y2 = (-y)2; z2 = (-z)2.

Из этих замечаний непосредственно следует, что нам достаточно найти лишь состоящие из положительных чисел примитивные решения (x; y; z)уравнения (1), т. е. исключим все следующие решения: (x; y; z), кроме(x; y; z), (y, x, z), для которых x = 2a.

Лемма 2: «Любое состоящее из положительных чисел примитивное решение (x, y, z) уравнения (1), для которого x = 2a, выражается формулами:

x = 2mn; y = m2 – n2; z = m2 + n2,

где n < m, НОД(m; n) = 1, m и n – числа разной чётности».

Доказательство: Пусть (x; y; z) – произвольное, состоящее из положительных чисел примитивное решение уравнения (1), где x = 2a. Из уравнения 4a2 + y2 = z2следует (z – y)(z + y) = 4k2. Чётность чисел z – yи z + y совпадают и произведение их равно 4k2, следовательно, z – yи z + y чётные. Пусть z + y = 2b; z – y = 2c, где bи cположительны, т. к. y < z, исходя из уравнения (1). Каждый общий делитель чисел bи cявляется также общим делителем z = b + c и y = b – c.

НОД(y; z) = 1, т. к. (x; y; z) – примитивное решение уравнения (1), следовательно, НОД(b; c) = 1. С другой стороны 4a2 = x2 = z2 – y2 = (z – y)(z + y) = 4bc, т. е. a2 = bc. Следовательно, согласно лемме 1, применённой к случаю, когда n = 2, существуют такие взаимно простые положительные числа разной чётности mи n, что b = m2; c = n2. Тогда a2 = (mn)2, т. е. a = mnи

x = 2a = 2mn; y = b – c = m2 – n2; z = b + c = m2 + n2.

Для завершения доказательства остаётся лишь добавить, что n < m, т. к. x, y > 0.

Доказательство теоремы Ферма для показателя 4

x4 + y4 = z4

Докажем ещё более общий случай:

«Уравнение

x4 + y4 = z2 (2)

не имеет решений в целых отличных от нуля числах».

Доказательство: Предположим, что существует решение уравнения (2) в целых отличных от нуля числах. Ясно, что, не теряя общности, мы можем считать, что оно состоит из попарно взаимно простых положительных чисел (если (x; y; z)является решением уравнения (2), то, сразу же видно, что (x; y; z)также является его решением). Так как в любом множестве натуральных чисел существует наименьшее из них, то среди всех таких решений найдётся решение (x; y; z)с наименьшим z. Рассмотрим именно это решение:

Так же, как и при доказательстве леммы 2 немедленно доказывается, что одно из чисел xи y должно быть чётным. Предположим, что чётно число x. Это предположение также общности не ограничивает.

Так как числа x2, y2иzположительны и взаимно просты, а число x2 чётно, то, согласно лемме 2, существуют такие взаимно простые числа mи n < mразной чётности, что x2 = 2mn; y2 = m2 – n2; z2 = m2 + n2. Если m = 2kиn = 2f +1, то y = 4(k2 – f2 – f – 1) + 3, что невозможно, ибо, как выше было уже отмечено, любой квадрат должен иметь вид 4k + 1, или 4k. Следовательно, m – нечётно, а n – чётно.

Пусть n = 2q. Тогда x2 = 4mqи потому mq = (x/2)2. Поскольку НОД(m; q) = 1, а x чётно, то, исходя из леммы 1, m = z12; q = t2, где z1 и t – некоторые целые взаимно простые положительные числа. В частности, уравнение y2 = m2 – n2то же самое, что и y2 = (z12)2 – (2t2)2, т. е. (2t2)2 + y2 = (z12)2.

Так как НОД(t; z1) = 1, то к этому неравенству снова применима лемма 2. Следовательно, существуют такие положительные взаимно простые числа aи b < aразличной чётности, что 2t2 = 2ab, т. е. t2 = ab; y2 = a2 – b2; z12 = a2 + b2. Так как НОД(a; b) = 1, из равенства t2 = ab по лемме 1 вытекает, что существу целые числа x1и y1, для которых a = x12; b = y12. Поэтому z12 = a2 + b2то же, что и x14 + y14 = z12. Это означает, что числа x1, y1, z1составляют примитивное решение уравнения (2), состоящее из положительных чисел. Поэтому в силу выбора решения (x; y; z), должно иметь место неравенство z1  z, а потому и неравенство z12  z, т. е., учитывая, что z = m2 + n2, m  m2 + n2, чего быть не может, т. к. m, n > 0.

Таким образом, предположение о существовании у записанного выше уравнения (2) целочисленных решений приводит к противоречию. Следовательно, это уравнение не имеет решений в целых отличных от нуля числах.

Примечания к доказательствам

Доказательство леммы 1 здесь дано не то, которое было известно ещё из средневековья, а то, что придумал я сам, основанное в большей степени на логических выводах. Теорема Ферма для показателя 4 (и все прилагающиеся для её доказательства леммы) – это единственная теорема, доказанная здесь, т. к. доказательство её считается элементарным, т. е. основанным на простых алгебраических преобразованиях чисел, известнымещё индусам. Доказательство же это было здесь необходимо, т. к. ещё даже у Ферма оно было, только в несколько иной форме.

Во Франции не так давно появилась книга, являющаяся, вроде как, полным доказательством Великой теоремы Ферма, но в ней использовано столько новых в математике абстрактных понятий, что проверить эти труды, кроме автора, никто не может.

Список литературы

1. М. М. Постников «Теорема Ферма», М., 1978

2. Б. В. Болгарский «Очерки по истории математики», Минск, 1979

3. М. Я. Выгодский «Справочник по элементарной математике», М., 1974.

4. Сеть Internet

Реферат Пьер де Ферма “Пьер, сын Доминика Ферма, буржуа и второго консулата города Бомона , крещен 20 августа 1601 г. Крестный отец - Пьер Ферма, купец и брат названного Доминика, крестная мать - Жанна Казнюв, и я”. Подпись отсутствует, но предыдущая запись подписана: “Дюма, викарий”. Этот документ искали полтора века и обнаружили лишь в 1846 г. благодаря усилиям адвоката Топиака.

Реферат Александр Флеминг Об Александре Флеминге, открывшем пенициллин, без преувеличения можно сказать: он победил не только болезни, он победил смерть. Немногие учёные-медики удостоились столь великой исторической славы. По словам Бальзака “нужны совершенно исключительные обстоятельства, чтобы имя учёного попало из науки в историю человечества”.

Реферат Древнее Двуречье Материальная культура народов древнего Двуречья находилась на сравнительно высоком уровне. Однако каменные орудия вышли окончательно из употребления лишь в начале 3-го тыс. до н. э. В металлургии в середине 3-го тыс. были известны литье, ковка, чеканка, изготовление золотой и серебряной проволоки, филигрань.

Реферат Евклид и его "Начала" В течение двух тысяч лет геометрию узнавали либо из “Начал” Евклида, либо из учебников, написанных на основе этой книги. Лишь профессиональные математики обращались к трудам других великих греческих геометров: Архимеда, Аполлония и геометров более позднего времени. Классическую геометрию стали называть евклидовой в отличие от появившихся в XIX в “неевклидовой геометрий”.

Реферат История тригонометрии Слово тригонометрия впервые встречается в 1505 году в заглавии книги немецкого математика Питискуса. Тригонометрия – слово греческое и в буквальном переводе означает измерение треугольников ( - треугольник, а - измеряю). В данном случае измерение треугольников следует понимать как решение треугольников, т.е.

Реферат Представление чисел в виде суммы двух квадратов и ... ВВЕДЕНИЕ Быть может, потомство будет признательно мне за то, что я показал ему, что Древние знали не все. Пьер Ферма Лишь один математик удостоился того, что имя его стало нарицательным.

Эссе: Джордж Оруэлл "Ферма животных ("Скотный двор")" Джордж Оруэлл английский писатель середины 20 века. Однако я уверена, что на просторах бывшего Советского Союза мало кто слышал это имя. А если оно где-то и упоминалось, то с непременными комментариями вполне определенного характера: антикоммунист, пасквилянт и т. п. На самом деле, в своих политических взглядах Оруэлл твердо стоял на позициях демократического социализма.

nreferat.ru

Доклад - Великая теорема Ферма 2

Содержание

1. Биография Ферма 3

2. Достижения в математике 4

3. Малая теорема Ферма 6

4. История Великой теоремы Ферма 7

Биография Ферма

“Пьер, сын Доминика Ферма, буржуа и второго консула города Бомона, крещен 20 августа 1601 г. Крестный отец — Пьер Ферма, купец и брат названного Доминика, крестная мать — Жанна Казнюв, и я”. Подпись отсутствует, но предыдущая запись подписана: “Дюма, викарий”. Этот документ искали полтора века и обнаружили лишь в 1846 г. благодаря усилиям адвоката Топиака. До этого считалось, что Ферма родился и умер в Тулузе, где 34 года исправно служил чиновником кассационной палаты Тулузского парламента. Маленький городок Бомон на левом берегу Гаронны вблизи Монтабане-на-Тарне и все его пять тысяч жителей по сей день не в силах осознать значимость находки адвоката. Здесь родился великий Ферма, последний математик-алхимик, замучивший человечество своими загадками, один из четырех титанов математики нового времени.

Пьер провел детство с родителями, а учиться поехал в Тулузу — ближайший университетский город. Изучив право, Пьер Ферма успешно начал карьеру адвоката, но решил перейти на государственную службу. Пьер женился на кузине своей матери Луизе де Лонг, дочери советника парламента. Благодаря тестю он дослужился до звания советника и приобрел вожделенную приставку “де”. В 1631 г. актом от 14 мая Ферма зачисляется на должность советника кассационной палаты Тулузкого парламента.

В семье гениального математика родились три сына и две дочери. Один сын стал юристом, два других священниками, а обе дочери Ферма приняли монашество.

В свой бурный век Ферма прожил основательно и тихо. Он не писал философских трактатов, не был наперсником французских королей, не воевал, не путешествовал, не создавал и не посещал математические кружки, не имел учеников и почти не печатался при жизни. Он изменил себе лишь перед смертью, опубликовав в Тулузе далеко не самые блестящие из своих находок в небольшом трактате “О сравнении кривых линий прямыми”. Всю свою жизнь Ферма провел в Тулузе, в той же должности, и неожиданно скончался в возрасте 64 лет во время поездки по делам службы. Жизнь его бедна внешними событиями, но следы, оставленные им в математике, таковы, что интерес к его личности не ослабевает.

Достижения в математике

Достижения Ферма относятся к разным разделам математики: к аналитической геометрии, теории чисел, анализу, вычислению интегралов и т.д. В теории чисел Ферма разработал способ систематического нахождения всех делителей произвольного числа, сформулировал теорему о возможности представления произвольного числа суммой не более четырех квадратов. С именем Ферма связаны две замечательные теоремы — большая (иногда ее называют последней) и малая. Ферма и Р. Декарт — основоположники аналитической геометрии. Кроме того, Ферма раньше Декарта и более систематизировано ввел прямолинейные координаты, изложил метод координат и применил его к геометрии, выведя уравнения прямой и кривых второго порядка. В работе «Введение к теории плоских и пространственных мест», ставшей известной в 1636 г., Ферма показал, что прямым соответствуют уравнения 1-й степени, а коническим сечениям — уравнения 2-й степени. Ферма исследовал общие виды уравнений 1-й и 2-й степени преобразованием координат. Важное место в истории дифференциального и интегрального исчисления заняла работа Ферма «Метод отыскания наибольших и наименьших значений», опубликованная лишь в 1679 г. В ней Ферма фактически осуществил операцию, называемую теперь дифференцированием, и применил ее для нахождения не только максимумов и минимумов, но и касательных к кривым. Ферма сформулировал общий закон дифференцирования дробных степеней; распространил формулу интегрирования степени на случаи дробных и отрицательных показателей.

Наследие Ферма неисчерпаемо по глубине содержания. Ферма своими работами способствовал развитию новых отраслей в математике: математического анализа, аналитической геометрии (одновременно с Декартом), теории вероятностей. Главным вкладом Ферма в алгебру явилась развитая им теория соединений или, как её ещё называют, комбинаторика. Отдельные задачи теории соединений были решены уже в древности греками и индийцами, но научная постановка этих вопросов возникла лишь в XVII веке в работах Ферма и его современника, знаменитого французского философа, математика и физика Блеза Паскаля. Исходя из основ комбинаторики, эти два учёных и положили начало новой математической науке, называемой теорией вероятностей, получившей в XVIII веке значительную теоретическую базу.

Ферма работал также над некоторыми вопросами физики, например, сформулировал так называемый принцип геометрической оптики, из которого выводятся законы отражения и преломления света (принцип Ферма).

Прижизненная известность Ферма основана на обильной переписке, в которой он донимал друзей и недругов необычными задачами. Его посмертная слава разрослась благодаря скромным пометкам на полях “Арифметики” Диофанта. Обычно человечеству необходимо несколько десятков лет, чтобы разобраться с наследием очередного неуемного гения. На окончательное осмысление загадок Ферма понадобилось без малого четыре века.

Малая теорема Ферма

Один из важнейших результатов Ферма получил специальное название “Малая теорема Ферма”. Это фундаментальный факт теории делимости на простые числа: для любого простого p и любого a ³ 1, которое не делится на p, разность делится наp .

Например, пусть a =5, p =2, 3, 7, 11. Тогда 52-1 -1=2×2, 53-1 -1=3×8, 57-1 -1=7×2232, 511-1 -1=11×887784. Ферма высказал эту теорему в письме Френиклю де Бесси в 1640 г. с обычным для него замечанием: “… я бы Вам прислал доказательство, если бы не опасался быть слишком длинным”.

Первое доказательство “Малой теоремы Ферма” дал Лейбниц. Затем Эйлер, начиная с 1736 г., опубликовал сразу три различных доказательства, которые показывают, что Ферма вполне мог уметь доказывать свою теорему. Потомки часто искали элементарные доказательства утверждений Ферма, пытаясь понять, насколько лукавил великий тулузец. Проблемы Ферма волновали Эйлера на протяжении всей жизни. В 1760 г. он получил существенное обобщение его “Малой теоремы”: пусть j (m ) — число натуральных чисел, не превосходящих m и взаимно простых с m. Тогда для любого m и любого a ³ 1, взаимно простого с m, разностьa j(m )-1 делится наm. Эту терему Эйлер скромно опубликовал в качестве четвертого доказательства “Малой теоремы Ферма”.

История Великой теоремы Ферма

Наконец, мы переходим к изложению самой знаменитой теоремы в истории математики. Эта теорема получила известность как “Великая теорема Ферма” (она же “Большая”, она же “Последняя”). На современном языке это звучит так:

не существует отличных от нуля целых чисел x, y и z, для которых имеет место равенство

(*)

при n>2 .

Разумеется, никакого уравнения у Ферма не было. Он вообще не знал знака равенства, а использовал латинское eq. Приводим утверждение Ферма в оригинальном виде:

“Куб, однако, на два куба или квадроквадрат на два квадроквадрата и вообще никакую до бесконечности сверх квадрата степень в две того же названия невозможно разделить ”. И не поставив точку, Ферма приписал: ”я открыл поистине удивительное доказательство этого предложения. Но оно не умещается на узких полях“.

Она-то, эта запись, и явилась причиной последующей грандиозной суматохи вокруг теоремы.

Этой фразой Ферма прокомментировал задачу из Диофанта: “Заданный квадрат разложить на два квадрата”. Данное замечание является вторым по счету из сделанных им на полях “Арифметики”. Первое касалось житейских тем.

Неопределенные уравнения (т. е. уравнениями с двумя неизвестными) вида x 2 + y 2 = z 2 интересовали древних греков в связи с теоремой Пифагора. Они искали (и находили) тройки целых чисел, образующие стороны прямоугольного треугольника. Это означает, что при n =1, 2 уравнение (*) имеет бесчисленное множество решений. Догадка Ферма заключалась в том, что при всех прочих n таких троек не существует.

В отношении Ферма достоверно известно, что он доказал “Великую теорему” при n =4 на полях все той же “Арифметики”. И это единственное теоретико-числовое доказательство Ферма, дошедшее до наших дней. На протяжении 20 лет Ферма упорно старался привлечь внимание математиков к “Великой теореме”, предлагая частные случаи в качестве задач. Случай n =3 он формулирует в пяти письмах, причем в последнем письме (от августа 1659 г.) пишет, что доказал теорему для n =3 методом спуска. Между тем “Великую теорему” для общего случая n> 2 Ферма сформулировал только один раз в упомянутом замечании на полях “Арифметики”. Он не формулирует ее ни разу ни в одном из писем. Он предлагает только частные случаи (n =3, 4), в отношении которых уверенно говорит, что располагает доказательством. Даже в письме к де Каркави от 1659 г., в котором Ферма перечисляет свои основные достижения, о “Великой теореме” в общем виде нет ни слова. Это может означать только одно: Ферма обнаружил пробелы в своем “поистине удивительном доказательстве”, которые так и не смог устранить.

Разумеется, это не охладило потомков. Начиная с конца XVII в. началась невиданная по своей напряженности гонка за доказательством “Великой теоремы Ферма”. Обманчивая простота формулировки теоремы обрекла тысячи поклонников математики на бесплодные поиски доказательства или опровержения теоремы. Более ста лет никому из ученых не удавалось продвинуться вперед даже при рассмотрении частных случаев конкретных значений показателя n .

Первый серьезный результат был получен Эйлером (1768). Он показал, что случай n =4 уникален. Это единственный частный вариант “Великой теоремы ”, когда доказательство имеет вполне элементарный характер. Уже при n=3 возникают значительные осложнения. Настолько существенные, что появляется повод в очередной раз сомневаться в честности Ферма. Эйлер доказал теорему для случая n =3, рассматривая комплексные числа вида , где a, b — целые числа. Строго говоря, доказательство Эйлера было дефектным, поскольку он необоснованно перенес ряд свойств обычных чисел на числа вида . В частности он предполагал единственность разложения таких чисел на простые множители. Для устранения пробелов в доказательстве Эйлера понадобились принципиально новые алгебраические абстракции: числовые кольца и поля. Реализацию этой программы начал Гаусс, которому принадлежит первое абсолютно строгое доказательство “Великой теоремы Ферма” для n =3.

Доказательство для случая n=5 предложили почти одновременно в атмосфере острого соперничества два француза: Лежен Дирихле и Лежандр (1825). Оба доказательства были очень сложными. В 1839 г. теорема Ферма была доказана для следующего простого показателя n=7. Это удалось благодаря титаническим усилиям Ламе. Он же в 1847 г. объявил, что доказал теорему для всех простых показателей n >3. Однако бдительный Лиувиль сразу же обнаружил в рассуждениях Ламе ошибку, сходную с той, которую допустил Эйлер. Ламе был вынужден признать свое поражение.

Пока во Франции происходили эти события, в Германии молодой математик Куммер упорно занимается теоремой Ферма. Повторив все ошибки Ламе, он пришел к понятию “идеальных чисел”, для которых разложение на простые множители единственно. Обобщение этого понятия привело к созданию головокружительных абстрактных конструкций, которые сегодня изучаются в специальном разделе алгебры под названием “Теория идеалов”. Куммер, посвятивший теореме несколько десятков лет, к концу жизни умел доказывать “Великую теорему Ферма” для всех простых показателей n <100. В 1857 г. ему была вручена премия Французской академии наук в размере 3 тыс. франков. Работы Куммера окончательно похоронили надежды на возможность доказательства теоремы Ферма элементарными средствами. Стало ясно, что Ферма никогда не имел и не мог иметь доказательства теоремы в общем виде.

После Куммера серьезных сдвигов в доказательстве теоремы Ферма не происходило вплоть до 1929 г., когда Вандивер, используя метод Куммера, получил в явном виде некие условия, позволяющие проверять истинность теоремы для любого простого показателя. С этого момента доказательство теоремы для конкретного n свелось к чисто вычислительным проблемам, с которыми легко справляются современные ЭВМ. В результате, к концу семидесятых годов двадцатого века, “Великая теорема Ферма” была доказана для всех n <100000. Это очень большое число, но это еще не все n, а значит “Великая теорема Ферма” не доказана и не опровергнута.

“Великая теорема” обернулась проклятием для десятков, может быть сотен тысяч людей, имевших несчастье вникнуть в ее формулировку и заразиться желанием испытать свои силы. Вступившие на эту стезю уже не внимали никаким доводам рассудка. Иллюстрацией может служить анекдотичная телеграмма, пришедшая в Президиум АН СССР: “Доказал теорему Ферма. Основная идея перенести игрек энной в правую часть. Подробности письмом”.

Ведущие математики всех времен и народов неоднократно объясняли, что элементарное доказательство теоремы Ферма, во-первых, не существует, а во-вторых, не будет иметь никакого значения для науки. Оно всего лишь закроет проблему. Подлинное значение “Великой теоремы” в том, что при попытках ее доказательства были выкованы мощные средства, приведшие к созданию новых обширных разделов математики.

Движение “ферматистов” приняло невероятный размах, после того, как в 1908 г. немецкий любитель математики Вольфскель завещал 100000 марок тому, кто докажет теорему Ферма. Право присуждения премии предоставлялось Гетингенской академии Германии. Немедленно тысячи людей стали бомбардировать научные общества и редакции журналов рукописями, якобы содержащими доказательство “Великой теоремы”. Только в Геттингенское математическое общество за первые три года после объявления завещания Вольфскеля пришло более тысячи “доказательств”. Педантичные немцы даже заготовили бланки: “Ваше доказательство содержит ошибку на стр. ____, которая заключатся в том, что ____________”.

После первой мировой войны во время инфляции премия Вольфскеля обесценилась, но поток доказательств не прекратился.

В то время в кругу математиков появилось полупрезрительное прозвище — ферматист. Так называли всякого самоуверенного выскочку, которому не хватало знаний, но зато с лихвой хватало амбиций для того, чтобы второпях попробовать силы в доказательстве Великой теоремы, а затем, не заметив собственных ошибок, гордо хлопнув себя в грудь, громко заявить: «Я первый доказал теорему Ферма!».

Финал этой истории банален. В 1993 г. все ведущие информационные агентства передали сообщение о том, что двум американским математикам удалось доказать теорему Ферма в общем виде.

В энциклопедии «Британника» (Britannica) за 2002 год обо всем сказанном выше подробно написано в обширной статье: «Fermat, Pierre de». А в еще более обширной статье «Theorem» приводятся истории появления, содержания и решения других подобных Теорем. Но в этом ряду Теорема Ферма по своему содержанию, истории и интересу вне конкуренции. В этой же энциклопедии в заключение зафиксировано: «Используя новейшие методы алгебраической геометрии, английский математик Эндрю Уайлс (Andrew Wiles) при участии своего бывшего ученика Ричарда Тейлора (Richard Taylor) представили решение Последней Теоремы Ферма в общем виде и опубликовали его в 1995 году в журнале „Annals of Mathematics“.

Через полгода в нашей прессе выступил крупнейший алгебраист акад. Фадеев, который подтвердил факт доказательства. XX век покончил с “Великой теоремой Ферма” тихо и буднично. При помощи обычной теории идеалов.

www.ronl.ru

Реферат: Великая теорема Ферма

Великая теорема Ферма

Для целых чисел n больше 2 уравнение xn + yn = zn не имеет ненулевых решений в натуральных числах.

Вы, наверное, помните со школьных времен теорему Пифагора: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Возможно, вы помните и классический прямоугольный треугольник со сторонами, длины которых соотносятся как 3 : 4 : 5. Для него теорема Пифагора выглядит так:

32 + 42 = 52

Это пример решения обобщенного уравнения Пифагора в ненулевых целых числах при n = 2. Великая теорема Ферма (ее также называют «Большой теоремой Ферма» и «Последней теоремой Ферма») состоит в утверждении, что при значениях n > 2 уравнения вида xn + yn = zn не имеют ненулевых решений в натуральных числах.

История Великой теоремы Ферма весьма занимательна и поучительна, и не только для математиков. Пьер де Ферма внес вклад в развитие самых различных областей математики, однако основная часть его научного наследия была опубликована лишь посмертно. Дело в том, что математика для Ферма была чем-то вроде хобби, а не профессиональным занятием. Он переписывался с ведущими математиками своего времени, однако публиковать свои работы не стремился. Научные труды Ферма в основном обнаружены в форме частной переписки и обрывочных записей, часто сделанных на полях различных книг. Именно на полях (второго тома древнегреческой «Арифметики» Диофанта. — Прим. переводчика) вскоре после смерти математика потомки и обнаружили формулировку знаменитой теоремы и приписку:

«Я нашел этому поистине чудесное доказательство, но поля эти для него слишком узки».

Увы, судя по всему, Ферма так и не удосужился записать найденное им «чудесное доказательство», и потомки безуспешно искали его три с лишним века. Из всего разрозненного научного наследия Ферма, содержащего немало удивительных утверждений, именно Великая теорема упорно не поддавалась решению.

Кто только не брался за доказательство Великой теоремы Ферма — всё тщетно! Другой великий французский математик, Рене Декарт (René Descartes, 1596–1650), называл Ферма «хвастуном», а английский математик Джон Уоллис (John Wallis, 1616–1703) — и вовсе «чертовым французом». Сам Ферма, правда, все-таки оставил после себя доказательство своей теоремы для случая n = 4. С доказательством для n = 3 справился великий швейцарско-российский математик XVIII века Леонард Эйлер (1707–83), после чего, не сумев найти доказательств для n > 4, в шутку предложил устроить обыск в доме Ферма, чтобы найти ключ к утерянному доказательству. В XIX веке новые методы теории чисел позволили доказать утверждение для многих целых чисел в пределах 200, однако, опять же, не для всех.

В 1908 году была учреждена премия в размере 100 000 немецких марок за решение этой задачи. Призовой фонд был завещан германским промышленником Паулем Вольфскелем (Paul Wolfskehl), который, согласно преданию, собирался покончить жизнь самоубийством, но так увлекся Великой теоремой Ферма, что передумал умирать. С появлением арифмометров, а затем и компьютеров планка значений n стала подниматься всё выше — до 617 к началу Второй мировой войны, до 4001 в 1954 году, до 125 000 в 1976 году. В конце XX столетия мощнейшие компьютеры военных лабораторий в Лос-Аламосе (Нью-Мексико, США) были запрограммированы на решение задачи Ферма в фоновом режиме (по аналогии с режимом экранной заставки персонального компьютера). Таким образом удалось показать, что теорема верна для невероятно больших значений x, y, z и n, но строгим доказательством это послужить не могло, поскольку любые следующие значения n или тройки натуральных чисел могли опровергнуть теорему в целом.

Наконец в 1994 году английский математик Эндрю Джон Уайлс (Andrew John Wiles, р. 1953), работая в Принстоне, опубликовал доказательство Великой теоремы Ферма, которое, после некоторых доработок, было признано исчерпывающим. Доказательство заняло более ста журнальных страниц и основывалось на использовании современного аппарата высшей математики, который в эпоху Ферма разработан не был. Так что же тогда имел в виду Ферма, оставляя на полях книги сообщение о том, что доказательство им найдено? Большинство математиков, с которыми я беседовал на эту тему, указывали, что за века накопилось более чем достаточно некорректных доказательств Великой теоремы Ферма, и что, скорее всего, сам Ферма нашел подобное доказательство, однако не сумел усмотреть в нем ошибку. Впрочем, не исключено, что все-таки имеется какое-то короткое и изящное доказательство Великой теоремы Ферма, которое никто до сих пор не нашел. С уверенностью можно утверждать лишь одно: сегодня мы точно знаем, что теорема верна. Большинство математиков, я думаю, безоговорочно согласятся с Эндрю Уайлсом, который заметил по поводу своего доказательства: «Теперь наконец мой ум спокоен».

***

Пьер де ФЕРМА

Pierre de Fermat, 1601–65

Французский математик и юрист. Родился в Бомон-де-Ломань (Beaumont-de-Lomagne). Изучал право, работал судьей. В свободное время увлекался математикой и внес значительный вклад в развитие различных отраслей этой науки, за что получил прозвище «король любителей». Помимо теории чисел (так называется область математики, к которой относится Великая теорема Ферма) еще до Ньютона разработал многие основы дифференциального исчисления, а совместно с Блезом Паскалем (Blaise Pascal, 1623–62) основал теорию вероятностей. В оптике сформулировал принцип Ферма, согласно которому преломление света на границе двух сред обусловлено различной скоростью распространения света в различных средах.

www.referatmix.ru

Реферат Великая теорема Ферма

Реферат на тему:

План:

Введение
• 1 Формулировка
• 2 История
• 3 «Ферматисты»
• 4 Теорема Ферма в культуре и искусстве
• 5 Примечания
Литература
• 7.1 На русском
• 7.1.2 На английском

Введение

Вели́кая теоре́ма Ферма́ (или Последняя теорема Ферма) — одна из самых популярных теорем математики; её условие формулируется на понятийном уровне среднего общего образования, а доказательство теоремы искали многие математики более трёхсот лет. Окончательно доказана в 1995 году Эндрю Уайлсом.

1. Формулировка

Теорема утверждает, что:

Для любого натурального числа n > 2 уравнение 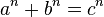не имеет натуральных решений a, b и c.

2. История

Для случая n = 3 эту теорему в X веке пытался доказать ал-Ходжанди, но его доказательство не сохранилось.

В общем виде теорема была сформулирована Пьером Ферма в 1637 году на полях «Арифметики» Диофанта. Дело в том, что Ферма делал свои пометки на полях читаемых математических трактатов и там же формулировал пришедшие на ум задачи и теоремы. Теорему, о которой ведётся речь, он записал с припиской, что найденное им остроумное доказательство этой теоремы слишком длинно, чтобы его можно было поместить на полях книги:

Наоборот, невозможно разложить куб на два куба, биквадрат на два биквадрата и вообще никакую степень, большую квадрата, на две степени с тем же показателем. Я нашел этому поистине чудесное доказательство, но поля книги слишком узки для него.

Оригинальный текст  (лат.)  

Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duas ejusdem nominis fas est dividere; cujus rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.

Несколько позже сам Ферма опубликовал доказательство частного случая для n = 4, что добавляет сомнений в том, что у него было доказательство общего случая.

Эйлер в 1770 году доказал теорему для случая n = 3[1], Дирихле и Лежандр в 1825 — для n = 5, Ламе — для n = 7. Куммер показал, что теорема верна для всех простых n, меньших 100, за возможным исключением т. н. иррегулярных простых (англ.) 37, 59, 67.

Над полным доказательством Великой теоремы работало немало выдающихся математиков и множество дилетантов-любителей; считается, что теорема стоит на первом месте по количеству некорректных «доказательств». Тем не менее эти усилия привели к получению многих важных результатов современной теории чисел. Давид Гильберт в своём докладе «Математические проблемы» на II Международном конгрессе математиков (1900) так отозвался об этой проблеме[2]:

Проблема доказательства этой неразрешимости являет разительный пример того, какое побуждающее влияние на науку может оказать специальная и на первый взгляд малозначительная проблема. Ибо, побуждённый задачей Ферма, Куммер пришёл к введению идеальных чисел и к открытию теоремы об однозначном разложении чисел в круговых полях на идеальные простые множители — теоремы, которая теперь, благодаря обобщениям на любую алгебраическую числовую область, полученным Дедекиндом и Кронекером, является центральной в современной теории чисел и значение которой выходит далеко за пределы теории чисел в область алгебры и теории функций.

В 1908 году немецкий любитель математики Вольфскель завещал 100 000 немецких марок тому, кто докажет теорему Ферма. Однако после Первой мировой войны премия обесценилась.

В 1980-х годах появился новый подход к решению проблемы. Из гипотезы Морделла, доказанной Фальтингсом в 1983 году, следует, что уравнение an + bn = cn при n > 3 может иметь лишь конечное число взаимно простых решений.

Последний, но самый важный, шаг в доказательстве теоремы был сделан Уайлсом в сентябре 1994 года. Его 130-страничное доказательство было опубликовано в журнале «Annals of Mathematics»[3]. Доказательство основано на предположении немецкого математика Герхарда Фрая о том, что Великая теорема Ферма является следствием гипотезы Таниямы — Симуры (это предположение было доказано Кеном Рибетом при участии Ж.‑П.Серра[4]).

Первый вариант своего доказательства Уайлс опубликовал в 1993 году (после 7 лет напряжённой работы), но в нём вскоре обнаружился серьёзный пробел, который с помощью Ричарда Лоуренса Тейлора удалось достаточно быстро устранить[5]. В 1995 году был опубликован завершающий вариант[6].

3. «Ферматисты»

Авторское свидетельство, выданное Министерством образования и науки Украины на доказательство теоремы Ферма Г. А. Середкину и Л. В. Шаповаловой

Простота формулировки теоремы Ферма (доступная в понимании даже школьнику), а также сложность единственного известного доказательства (или неведение о его существовании), вдохновляют многих на попытки найти другое, более простое, доказательство. Людей, вопреки здравому смыслу пытающихся доказать теорему Ферма элементарными методами, называют «ферматистами» или «ферматиками».[7] Ферматисты зачастую не владеют основами математической культуры и допускают ошибки в арифметических действиях или логических выводах, хотя некоторые представляют весьма изощренные «доказательства», в которых трудно найти ошибку.

Доказывать теорему Ферма в среде любителей математики было настолько популярно, что в 1972 году журнал «Квант», публикуя статью о теореме Ферма, сопроводил ее следующей припиской:[7]

Немецкому математику Эдмунду Ландау очень докучали «ферматисты». Чтобы не отвлекаться от основной работы, он заказал несколько сот бланков со следующим текстом:

Находить ошибку и заполнять пробелы в бланке он поручал своим аспирантам.

Примечательно, что отдельные ферматисты добиваются публикации своих (неверных) «доказательств» в ненаучной прессе, которая раздувает их значение до научной сенсации.[8][9] Впрочем, иногда такие публикации появляются и в уважаемых научных изданиях,[10] как правило, с последующими опровержениями.[11] Среди других примеров:

• Брошюра В. И. Будкина, изданная в Ярославле под названием «Методика познания „истины“. Доказательство Великой теоремы Ферма» (47 стр., 5000 экз., Верхне-Волжское книжное издательство, 1975).[12]
• Авторское свидетельство на доказательство теоремы Ферма, выданное Министерством образования и науки Украины Л. В. Шаповаловой и Г. А. Середкину. (Следует пояснить, что этот документ не удостоверяет каким-либо образом правильность доказательства, а лишь регистрирует авторские права на поданный в Министерство образования и науки печатный труд; на это министерство возложена обязанность ведения реестра таких свидетельств. [13])

4. Теорема Ферма в культуре и искусстве

• В детективе Валерия Горбунова «Коллекция» талантливый математик Митя, грезящий о славе и деньгах, пытается доказать теорему Ферма, за решение которой назначена премия.
• В фильме «Каменская. Стечение обстоятельств» гражданский муж Каменской Чистяков планирует доказать теорему Ферма. Позже Каменская использует этот факт.
• В повести Е. Велтистова «Победитель невозможного» друг Сыроежкина и Электроника Вова Корольков в качестве свободного задания по математике решил Великую теорему Ферма.
• В повести М. Анчарова «Самшитовый лес» главный герой Сапожников приводит доказательство Великой теоремы Ферма.
• В телесериале «Звёздный Путь», капитан космического корабля Энтерпрайз NCC-1701-D Жан-Люк Пикар был озадачен разгадкой Великой теоремы Ферма во второй половине XXIV века, о чём он поведал в начале серии своему первому помощнику. Таким образом, создатели фильма предполагали, что решения у Великой теоремы Ферма не будет в ближайшее время. Серия «Рояль» с этим эпизодом была снята в 1989 году, когда Джон Уайлс был в самом начале своих работ. Решение теоремы найдено всего спустя 5 лет, а не более 400 лет, как показали в сериале.
• В рассказе Артура Порджеса «Саймон Флэгг и дьявол»[14] профессор Саймон Флегг просит помощи дьявола в доказательстве теоремы, но и дьявол оказывается бессилен. По этому рассказу был также снят игровой научно-популярный фильм «Математик и чёрт» (СССР, 1972, производство Центрнаучфильм, творческое объединение «Радуга», режиссёр Райтбурт).[15]
• В рассказе Сергея Снегова «Умершие живут» теорема в XXV веке является ещё недоказанной.
• В романе Сергея Лукьяненко «Звезды — холодные игрушки» представитель цивилизации Счётчиков утверждает, что знает контрпример к теореме, но не оглашает его.
• В рассказе Кира Булычева «Мечта заочника» студент-заочник Гаврилов приходит к профессору Минцу и приносит купленную курсовую работу, в которой приводится доказательство теоремы, с просьбой объяснить, что он написал.
• В 15 серии известного аниме Lucky Star на 9—10 минуте присутствует момент, когда семья Цукасы и Кагами смотрят телевикторину. Один из вопросов звучал: «Одна из сложнейших математических теорем, доказанная в 1994 году сэром Уайлсом из Принстона, — это…»
• В посвящённой Хэллоуину 1995 года серии «Симпсонов» двумерный Гомер Симпсон случайно попадает в третье измерение. Во время его путешествия в этом странном мире, в воздухе парят геометрические тела и математические формулы, включая равенство 178212 + 184112 = 192212. Калькулятор с точностью не более 9 значащих цифр подтверждает это равенство: 178212 + 184112 = 2541210258614589176288669958142428526657 ≈ 254121026×1031               192212 = 2541210259314801410819278649643651567616 ≈ 254121026×1031

• В первом издании «Искусства программирования» Дональда Кнута теорема Ферма приведена в качестве упражнения с математическим уклоном в самом начале книги и оценена максимальным числом (50) баллов, как «исследовательская проблема, которая (насколько это было известно автору в момент написания) ещё не получила удовлетворительного решения. Если читатель найдет решение этой задачи, его настоятельно просят опубликовать его; кроме того, автор данной книги будет очень признателен, если ему сообщат решение как можно быстрее (при условии, что оно правильно)». В третьем издании книги это упражнение уже требует знаний высшей математики и оценивается лишь в 45 баллов.
• В пьесе Тома Стоппарда «Аркадия» Септимус Ходж, домашний учитель Томасины Каверли, даёт ей задание найти доказательство теоремы Ферма.
• В фильме «Женщин обижать не рекомендуется» (Россия, 2000) главная героиня — школьная учительница математики Вера пресекает рассуждения ученика, мотивируя это тем, что теорема Ферма недоказуема.
• В триллере «Западня Ферма» (исп. La habitación de Fermat) (Испания, 2007) четверо выдающихся математиков попадают в западню к незнакомцу, именующему себя Ферма.
• В фильме «Доказательство» сюжет крутится вокруг доказательства теоремы Ферма, но это ни разу явно не упоминается в фильме.
• В фильме «Космические дальнобойщики» космический пират Набел, давая время на принятие решения своим пленникам, доказывал в уме теорему Ферма, на что у него уходило несколько секунд.
• В книге Стига Ларссона «Девушка, которая играла с огнём»[16] главная героиня Лисбет Саландер, обладающая редкими способностями к аналитике и фотографической памятью, в качестве хобби занята доказательством Великой теоремы Ферма, на которую она наткнулась, читая фундаментальный труд «Измерения в математике», в котором приводится и доказательство Эндрю Уайлса. Лисбет не хочет изучать готовое доказательство, а главным интересом становится поиск собственного решения. Поэтому всё своё свободное время она посвящает самостоятельному поиску «замечательного доказательства» теоремы великого француза, но раз за разом заходит в тупик. В конце книги Лисбет находит доказательство, которое не только совершенно отлично от предложенного Уайлсом, но и является настолько простым, что сам Ферма мог бы его найти. Однако, Ларссон не приводит своего доказательства.
• Мюзикл «Последнее танго Ферма», изданный институтом Клэя, создан в 2000 году Дж. Розенблумом и Дж. С. Лессер по мотивам реальной истории Эндрю Уайлса. Главный герой по имени Дэниел Кин завершает доказательство теоремы, а дух самого Ферма старается ему помешать[17].
• В фильме «Ослепленный желаниями» школьникам предлагается доказать данную теорему дома.
• За несколько дней до своей смерти Артур Кларк успел отрецензировать рукопись романа «Последняя Теорема», над которой он трудился в соавторстве с Фредериком Полом. Книга вышла уже после смерти Кларка.

5. Примечания

1. Ю. Ю. Мачис О предполагаемом доказательстве Эйлера - mi.mathnet.ru/mz3992 // Математические заметки. — 2007. — Т. 82. — № 3. — С. 395-400. Английский перевод: J. J. Mačys (2007). «On Euler’s hypothetical proof - www.springerlink.com/content/u46jj0nuk3678591/». Mathematical Notes 82 (3-4): 352-356. DOI:10.1134/S0001434607090088 - dx.doi.org/10.1134/S0001434607090088. MR2364600 - www.ams.org/mathscinet-getitem?mr=2364600.
2. Давид Гильберт. МАТЕМАТИЧЕСКИЕ ПРОБЛЕМЫ - vivovoco.rsl.ru/VV/PAPERS/NATURE/GILBERT_R.HTM.
3. Wiles, Andrew (1995). «Modular elliptic curves and Fermat’s last theorem - math.stanford.edu/~lekheng/flt/wiles.pdf». Annals of Mathematics 141 (3): 443—551.  (англ.)
4. Соловьев Ю.П. Гипотеза Таниямы и последняя теорема Ферма - window.edu.ru/window/library?p_rid=20763 // Соросовский образовательный журнал. — ISSEP, 1998. — Т. 4. — № 2. — С. 135–138.
5. Taylor, Richard & Wiles, Andrew (1995). «Ring theoretic properties of certain Hecke algebras - www.math.harvard.edu/~rtaylor/hecke.ps». Annals of Mathematics 141 (3): 553—572. (англ.)
6. Стиллвелл Д. Математика и её история. — Москва — Ижевск: Институт компьютерных исследований, 2004. — С. 199—200.
7. ↑ 12Гастев Ю., Смолянский М. Несколько слов о Великой теореме Ферма - kvant.mccme.ru/1972/08/neskolko_slov_o_velikoj_teorem.htm // Квант. — 1972. — Т. 8. — С. 23-25.
8. Теоремой — по ракетам! - www.ng.ru/printed/205772
9. ЧЕЛОВЕЧЕСТВО МОЖЕТ РАССЛАБИТЬСЯ? - 2005.novayagazeta.ru/nomer/2005/61n/n61n-s00.shtml
10. Человечество может расслабиться - www.ras.ru/news/shownews.aspx?ID=b6179d64-ce47-4aa3-afba-f79e7276cda4. Сайт Российской академии наук.
11. Теорема Ферма доказала, что попытки доказать её не прекратятся никогда - www.ras.ru/digest/showdnews.aspx?id=002e5897-c7b3-494e-8357-ebf4149fe3b3. Сайт Российской академии наук.
12. Пионеры. - cdtolyk.narod.ru/txt/miron.doc
13. Постановление Кабинета министров Украины от 27.12.2001 г. N 1756 "О государственной регистрации авторского права...". - zakon1.rada.gov.ua/cgi-bin/laws/main.cgi?nreg=1756-2001-
14. A. Porges (1954). «Devil and Simon Flagg». The Magazine of Fantasy and Science Fiction.. Русский перевод: А. Порджес Саймон Флэгг и дьявол - kvant.mccme.ru/1972/08/sajmon_flegg_i_dyavol.htm // Квант. — 1972. — Т. 8. — С. 17-22. (альтернативная ссылка - ega-math.narod.ru/Quant/Porges.htm)
15. Игровой научно-популярный фильм «Математик и чёрт» - www.smartvideos.ru/matematik-i-chert (СССР, 1972 режиссёр Райтбурт). (альтернативные ссылки: часть 1 - www.youtube.com/watch?v=fgVLe7CK-CA, часть 2 - www.youtube.com/watch?v=Ga94Sl6pbbE)
16. . В 2010 году вышла на русском языке, издательство «Эксмо», в оригинале название «Flickan som lekte med elden», в английском переводе «The girl who played with fire».
17. Fermat’s Last Tango - www.claymath.org/publications/Fermats_Last_Tango/

Литература

7.1. На русском

• Абраров Дмитрий. Теорема Ферма: феномен доказательств Уайлса - polit.ru/science/2006/12/28/abrarov_print.html.
• Кирсанов Ф. История Великой Теоремы Ферма - www.orator.ru/rass19.html.
• Рибенбойм П. Последняя теорема Ферма для любителей. — М.: Мир, 2003.
• Сингх С. Великая теорема Ферма - ega-math.narod.ru/Singh/FLT.htm. — М.: МЦНМО, 2000.

7.1.2. На английском

• Faltings, Gerd (1995). The Proof of Fermat’s last theorem by R. Taylor and A. Wiles - www.ams.org/notices/199507/faltings.pdf, Notices of the AMS (42) (7), 743—746.
• Daney, Charles (2003). The Mathematics of Fermat’s last theorem - cgd.best.vwh.net/home/flt/flt01.htm. Retrieved Aug. 5, 2004.
• O’Connor, J. J. & and Robertson, E. F. (1996). Fermat’s last theorem. The history of the problem - www-gap.dcs.st-and.ac.uk/~history/HistTopics/Fermat's_last_theorem.html. Retrieved Aug. 5, 2004.
• Shay, David (2003). Fermat’s last theorem. The story, the history and the mystery - fermat.workjoke.com/. Retrieved Aug. 5, 2004.
• Donald C. Benson The Moment of Proof: Mathematical Epophanies. — Oxford University Press, 1999. — ISBN 0-19-513919-4

Категории: Теория чисел, Теоремы, Диофантовы уравнения.

wreferat.baza-referat.ru

Реферат: Великая теорема Ферма

Издание 1670 года «Арифметики» Диофанта включает комментарий Ферма, в частности его «последнюю теорему» (Observatio Domini Petri de Fermat).

Вели?кая теоре?ма Ферма? (или Последняя теорема Ферма) — одна из самых популярных теорем математики. Её условие формулируется на понятийном уровне среднего общего образования, а доказательство теоремы искали многие математики более трёхсот лет. Окончательно доказана в 1995 году Эндрю Уайлсом.

Формулировка

Теорема утверждает, что:

Для любого натурального числа уравнение

не имеет натуральных решений , и .

История

Для случая эту теорему в X веке пытался доказать ал-Ходжанди, но его доказательство не сохранилось.

В общем виде теорема была сформулирована Пьером Ферма в 1637 году на полях «Арифметики» Диофанта. Дело в том, что Ферма делал свои пометки на полях читаемых математических трактатов и там же формулировал пришедшие на ум задачи и теоремы. Теорему, о которой ведётся речь, он записал с припиской, что найденное им остроумное доказательство этой теоремы слишком длинно, чтобы его можно было поместить на полях книги:

Наоборот, невозможно разложить куб на два куба, биквадрат на два биквадрата и вообще никакую степень, большую квадрата, на две степени с тем же показателем. Я нашел этому поистине чудесное доказательство, но поля книги слишком узки для него.

Оригинальный текст  (лат.)  

Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duas ejusdem nominis fas est dividere; cujus rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.

Несколько позже сам Ферма опубликовал доказательство частного случая для , что добавляет сомнений в том, что у него было доказательство общего случая.

Эйлер в 1770 году доказал теорему для случая [1], Дирихле и Лежандр в 1825 — для , Ламе — для . Куммер показал, что теорема верна для всех простых n, меньших 100, за возможным исключением т. н. иррегулярных простых 37, 59, 67.

Над полным доказательством Великой теоремы работало немало выдающихся математиков и множество дилетантов-любителей; считается, что теорема стоит на первом месте по количеству некорректных «доказательств». Тем не менее эти усилия привели к получению многих важных результатов современной теории чисел. Давид Гильберт в своём докладе «Математические проблемы» на II Международном конгрессе математиков (1900) так отозвался об этой проблеме[2]:

Проблема доказательства этой неразрешимости являет разительный пример того, какое побуждающее влияние на науку может оказать специальная и на первый взгляд малозначительная проблема. Ибо, побуждённый задачей Ферма, Куммер пришёл к введению идеальных чисел и к открытию теоремы об однозначном разложении чисел в круговых полях на идеальные простые множители — теоремы, которая теперь, благодаря обобщениям на любую алгебраическую числовую область, полученным Дедекиндом и Кронекером, является центральной в современной теории чисел и значение которой выходит далеко за пределы теории чисел в область алгебры и теории функций.

В 1908 году немецкий любитель математики Вольфскель завещал 100 000 немецких марок тому, кто докажет теорему Ферма. Однако после Первой мировой войны премия обесценилась.

В 1980-х годах появился новый подход к решению проблемы. Из гипотезы Морделла, доказанной Фальтингсом в 1983 году, следует, что уравнение при может иметь лишь конечное число взаимно простых решений.

Последний, но самый важный, шаг в доказательстве теоремы был сделан Уайлсом в сентябре 1994 года. Его 130-страничное доказательство было опубликовано в журнале «Annals of Mathematics»[3]. Доказательство основано на предположении немецкого математика Герхарда Фрая о том, что Великая теорема Ферма является следствием гипотезы Таниямы — Симуры (это предположение было доказано Кеном Рибетом при участии Ж.?П.Серра[4]).

Первый вариант своего доказательства Уайлс опубликовал в 1993 году (после 7 лет напряжённой работы), но в нём вскоре обнаружился серьёзный пробел, который с помощью Ричарда Лоуренса Тейлора удалось достаточно быстро устранить[5]. В 1995 году был опубликован завершающий вариант[6].

«Ферматисты»

Авторское свидетельство, выданное Министерством образования и науки Украины на доказательство теоремы Ферма Г. А. Середкину и Л. В. Шаповаловой

Простота формулировки теоремы Ферма (доступная в понимании даже школьнику), а также сложность единственного известного доказательства (или неведение о его существовании), вдохновляют многих на попытки найти другое, более простое, доказательство. Людей, пытающихся доказать теорему Ферма элементарными методами, называют «ферматистами» или «ферматиками».[7] Ферматисты зачастую не владеют основами математической культуры и допускают ошибки в арифметических действиях или логических выводах, хотя некоторые представляют весьма изощренные «доказательства», в которых трудно найти ошибку.

Доказывать теорему Ферма в среде любителей математики было настолько популярно, что в 1972 году журнал «Квант», публикуя статью о теореме Ферма, сопроводил ее следующей припиской:[7]

Редакция «Кванта» со своей стороны считает необходимым известить читателей, что письма с проектами доказательств теоремы Ферма рассматриваться (и возвращаться) не будут.

Немецкому математику Эдмунду Ландау очень докучали «ферматисты». Чтобы не отвлекаться от основной работы, он заказал несколько сот бланков со следующим текстом:

Уважаемый …! Благодарю Вас за присланную Вами рукопись с доказательством Великой теоремы Ферма. Первая ошибка находится на стр. … в строке …

Находить ошибку и заполнять пробелы в бланке он поручал своим аспирантам.

Примечательно, что отдельные ферматисты добиваются публикации своих (неверных) «доказательств» в ненаучной прессе, которая раздувает их значение до научной сенсации.[8][9] Впрочем, иногда такие публикации появляются и в уважаемых научных изданиях,[10] как правило, с последующими опровержениями.[11] Среди других примеров:

Брошюра В. И. Будкина, изданная в Ярославле под названием «Методика познания „истины“. Доказательство Великой теоремы Ферма» (47 стр., 5000 экз., Верхне-Волжское книжное издательство, 1975).[12]

Авторское свидетельство на доказательство теоремы Ферма, выданное Министерством образования и науки Украины Л. В. Шаповаловой и Г. А. Середкину. (Следует пояснить, что этот документ не удостоверяет каким-либо образом правильность доказательства, а лишь регистрирует авторские права на поданный в Министерство образования и науки печатный труд; на это министерство возложена обязанность ведения реестра таких свидетельств.[13])

Теорема Ферма в культуре и искусстве

Великая теорема Ферма стала символом труднейшей научной проблемы и в этом качестве часто упоминается в беллетристике. Далее перечислены некоторые произведения, в которых теорема не просто упомянута, но является существенной частью сюжета или идеологии произведения.

В повести Е. Велтистова «Победитель невозможного» друг Сыроежкина и Электроника Вова Корольков в качестве свободного задания по математике доказал Великую теорему Ферма.

В телесериале «Звёздный Путь», капитан космического корабля Энтерпрайз NCC-1701-D Жан-Люк Пикар был озадачен разгадкой Великой теоремы Ферма во второй половине XXIV века, о чём он поведал в начале серии своему первому помощнику. Таким образом, создатели фильма предполагали, что решения у Великой теоремы Ферма не будет в ближайшее время. Серия «Рояль» с этим эпизодом была снята в 1989 году, когда Джон Уайлс был в самом начале своих работ. В действительности решение было найдено всего спустя 5 лет.

В рассказе Артура Порджеса «Саймон Флэгг и дьявол»[14] профессор Саймон Флегг просит помощи дьявола в доказательстве теоремы, но и дьявол оказывается бессилен. По этому рассказу был также снят игровой научно-популярный фильм «Математик и чёрт» (СССР, 1972, производство Центрнаучфильм, творческое объединение «Радуга», режиссёр Райтбурт).[15]

В рассказе Кира Булычева «Мечта заочника» студент-заочник Гаврилов приходит к профессору Минцу и приносит купленную курсовую работу, в которой приводится доказательство теоремы, с просьбой объяснить, что он написал.

В посвящённой Хэллоуину 1995 года серии «Симпсонов» двумерный Гомер Симпсон случайно попадает в третье измерение. Во время его путешествия в этом странном мире, в воздухе парят геометрические тела и математические формулы, включая равенство . Калькулятор с точностью не более 9 значащих цифр подтверждает это равенство:

178212 + 184112 = 2541210258614589176288669958142428526657 ≈ 254121026·1031

              192212 = 2541210259314801410819278649643651567616 ≈ 254121026·1031

Тем не менее, даже без вычисления точных значений легко видеть, что равенство неверно: левая часть — нечётное число, а правая часть — чётное.

В первом издании «Искусства программирования» Дональда Кнута теорема Ферма приведена в качестве упражнения с математическим уклоном в самом начале книги и оценена максимальным числом (50) баллов, как «исследовательская проблема, которая (насколько это было известно автору в момент написания) ещё не получила удовлетворительного решения. Если читатель найдет решение этой задачи, его настоятельно просят опубликовать его; кроме того, автор данной книги будет очень признателен, если ему сообщат решение как можно быстрее (при условии, что оно правильно)». В третьем издании книги это упражнение уже требует знаний высшей математики и оценивается лишь в 45 баллов.

В фильме «Доказательство» сюжет крутится вокруг доказательства теоремы Ферма, но это ни разу явно не упоминается в фильме.

В книге Стига Ларссона «Девушка, которая играла с огнём»[16] главная героиня Лисбет Саландер, обладающая редкими способностями к аналитике и фотографической памятью, в качестве хобби занята доказательством Великой теоремы Ферма, на которую она наткнулась, читая фундаментальный труд «Измерения в математике», в котором приводится и доказательство Эндрю Уайлса. Лисбет не хочет изучать готовое доказательство, а главным интересом становится поиск собственного решения. Поэтому всё своё свободное время она посвящает самостоятельному поиску «замечательного доказательства» теоремы великого француза, но раз за разом заходит в тупик. В конце книги Лисбет находит доказательство, которое не только совершенно отлично от предложенного Уайлсом, но и является настолько простым, что сам Ферма мог бы его найти. Однако, после ранения в голову она его забывает, и Ларссон не приводит никаких подробностей этого доказательства.

Мюзикл «Последнее танго Ферма», изданный институтом Клэя, создан в 2000 году Дж. Розенблумом и Дж. С. Лессер по мотивам реальной истории Эндрю Уайлса. Главный герой по имени Дэниел Кин завершает доказательство теоремы, а дух самого Ферма старается ему помешать[17].

За несколько дней до своей смерти Артур Кларк успел отрецензировать рукопись романа «Последняя Теорема», над которой он трудился в соавторстве с Фредериком Полом. Книга вышла уже после смерти Кларка.

В рассказе Натальи Дарьяловой «Великая и загадочная» сюжет строится на теореме Ферма. Рассказывается о том, как молодой человек, будучи студентом, занялся теоремой Ферма, и впоследствии стал математиком, получил несколько важных научных результатов, но совершенно загубил свою личную жизнь.

В романе П. А. Загребельного «Разгон»[18] скромный преподаватель математики из Одессы сумел доказать теорему, через некоторое время он становится академиком и возглавляет очень серьезное киевское НПО, занимающееся созданием электронно-вычислительных систем.

А.П. Казанцев в своем романе "Острее шпаги" в 1983 в стиле Дюма довольно ярко описал Пьера Ферма и предложил оригинальную версию отсутствия доказательства самого Ферма.

www.referatmix.ru

Реферат: Великая теорема Ферма

Издание 1670 года «Арифметики» Диофанта включает комментарий Ферма, в частности его «последнюю теорему» (Observatio Domini Petri de Fermat).

Вели?кая теоре?ма Ферма? (или Последняя теорема Ферма) — одна из самых популярных теорем математики. Её условие формулируется на понятийном уровне среднего общего образования, а доказательство теоремы искали многие математики более трёхсот лет. Окончательно доказана в 1995 году Эндрю Уайлсом.

Формулировка

Теорема утверждает, что:

Для любого натурального числауравнение

не имеет натуральных решений,и.

История

Для случаяэту теорему в X веке пытался доказать ал-Ходжанди, но его доказательство не сохранилось.

В общем виде теорема была сформулирована Пьером Ферма в 1637 году на полях «Арифметики» Диофанта. Дело в том, что Ферма делал свои пометки на полях читаемых математических трактатов и там же формулировал пришедшие на ум задачи и теоремы. Теорему, о которой ведётся речь, он записал с припиской, что найденное им остроумное доказательство этой теоремы слишком длинно, чтобы его можно было поместить на полях книги:

Наоборот, невозможно разложить куб на два куба, биквадрат на два биквадрата и вообще никакую степень, большую квадрата, на две степени с тем же показателем. Я нашел этому поистине чудесное доказательство, но поля книги слишком узки для него.

Оригинальный текст (лат.)

Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duas ejusdem nominis fas est dividere; cujus rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.

Несколько позже сам Ферма опубликовал доказательство частного случая для, что добавляет сомнений в том, что у него было доказательство общего случая.

Эйлер в 1770 году доказал теорему для случая[1], Дирихле и Лежандр в 1825 — для, Ламе — для. Куммер показал, что теорема верна для всех простых n, меньших 100, за возможным исключением т. н. иррегулярных простых 37, 59, 67.

Над полным доказательством Великой теоремы работало немало выдающихся математиков и множество дилетантов-любителей; считается, что теорема стоит на первом месте по количеству некорректных «доказательств». Тем не менее эти усилия привели к получению многих важных результатов современной теории чисел. Давид Гильберт в своём докладе «Математические проблемы» на II Международном конгрессе математиков (1900) так отозвался об этой проблеме[2]:

Проблема доказательства этой неразрешимости являет разительный пример того, какое побуждающее влияние на науку может оказать специальная и на первый взгляд малозначительная проблема. Ибо, побуждённый задачей Ферма, Куммер пришёл к введению идеальных чисел и к открытию теоремы об однозначном разложении чисел в круговых полях на идеальные простые множители — теоремы, которая теперь, благодаря обобщениям на любую алгебраическую числовую область, полученным Дедекиндом и Кронекером, является центральной в современной теории чисел и значение которой выходит далеко за пределы теории чисел в область алгебры и теории функций.

В 1908 году немецкий любитель математики Вольфскель завещал 100 000 немецких марок тому, кто докажет теорему Ферма. Однако после Первой мировой войны премия обесценилась.

В 1980-х годах появился новый подход к решению проблемы. Из гипотезы Морделла, доказанной Фальтингсом в 1983 году, следует, что уравнениеприможет иметь лишь конечное число взаимно простых решений.

Последний, но самый важный, шаг в доказательстве теоремы был сделан Уайлсом в сентябре 1994 года. Его 130-страничное доказательство было опубликовано в журнале «Annals of Mathematics»[3]. Доказательство основано на предположении немецкого математика Герхарда Фрая о том, что Великая теорема Ферма является следствием гипотезы Таниямы — Симуры (это предположение было доказано Кеном Рибетом при участии Ж.?П.Серра[4]).

Первый вариант своего доказательства Уайлс опубликовал в 1993 году (после 7 лет напряжённой работы), но в нём вскоре обнаружился серьёзный пробел, который с помощью Ричарда Лоуренса Тейлора удалось достаточно быстро устранить[5]. В 1995 году был опубликован завершающий вариант[6].

«Ферматисты»

Авторское свидетельство, выданное Министерством образования и науки Украины на доказательство теоремы Ферма Г. А. Середкину и Л. В. Шаповаловой

Простота формулировки теоремы Ферма (доступная в понимании даже школьнику), а также сложность единственного известного доказательства (или неведение о его существовании), вдохновляют многих на попытки найти другое, более простое, доказательство. Людей, пытающихся доказать теорему Ферма элементарными методами, называют «ферматистами» или «ферматиками».[7] Ферматисты зачастую не владеют основами математической культуры и допускают ошибки в арифметических действиях или логических выводах, хотя некоторые представляют весьма изощренные «доказательства», в которых трудно найти ошибку.

Доказывать теорему Ферма в среде любителей математики было настолько популярно, что в 1972 году журнал «Квант», публикуя статью о теореме Ферма, сопроводил ее следующей припиской:[7]

Редакция «Кванта» со своей стороны считает необходимым известить читателей, что письма с проектами доказательств теоремы Ферма рассматриваться (и возвращаться) не будут.

Немецкому математику Эдмунду Ландау очень докучали «ферматисты». Чтобы не отвлекаться от основной работы, он заказал несколько сот бланков со следующим текстом:

Уважаемый …! Благодарю Вас за присланную Вами рукопись с доказательством Великой теоремы Ферма. Первая ошибка находится на стр. … в строке …

Находить ошибку и заполнять пробелы в бланке он поручал своим аспирантам.

Примечательно, что отдельные ферматисты добиваются публикации своих (неверных) «доказательств» в ненаучной прессе, которая раздувает их значение до научной сенсации.[8][9] Впрочем, иногда такие публикации появляются и в уважаемых научных изданиях,[10] как правило, с последующими опровержениями.[11] Среди других примеров:

Брошюра В. И. Будкина, изданная в Ярославле под названием «Методика познания „истины“. Доказательство Великой теоремы Ферма» (47 стр., 5000 экз., Верхне-Волжское книжное издательство, 1975).[12]

Авторское свидетельство на доказательство теоремы Ферма, выданное Министерством образования и науки Украины Л. В. Шаповаловой и Г. А. Середкину. (Следует пояснить, что этот документ не удостоверяет каким-либо образом правильность доказательства, а лишь регистрирует авторские права на поданный в Министерство образования и науки печатный труд; на это министерство возложена обязанность ведения реестра таких свидетельств.[13])

Теорема Ферма в культуре и искусстве

Великая теорема Ферма стала символом труднейшей научной проблемы и в этом качестве часто упоминается в беллетристике. Далее перечислены некоторые произведения, в которых теорема не просто упомянута, но является существенной частью сюжета или идеологии произведения.

В повести Е. Велтистова «Победитель невозможного» друг Сыроежкина и Электроника Вова Корольков в качестве свободного задания по математике доказал Великую теорему Ферма.

В телесериале «Звёздный Путь», капитан космического корабля Энтерпрайз NCC-1701-D Жан-Люк Пикар был озадачен разгадкой Великой теоремы Ферма во второй половине XXIV века, о чём он поведал в начале серии своему первому помощнику. Таким образом, создатели фильма предполагали, что решения у Великой теоремы Ферма не будет в ближайшее время. Серия «Рояль» с этим эпизодом была снята в 1989 году, когда Джон Уайлс был в самом начале своих работ. В действительности решение было найдено всего спустя 5 лет.

В рассказе Артура Порджеса «Саймон Флэгг и дьявол»[14] профессор Саймон Флегг просит помощи дьявола в доказательстве теоремы, но и дьявол оказывается бессилен. По этому рассказу был также снят игровой научно-популярный фильм «Математик и чёрт» (СССР, 1972, производство Центрнаучфильм, творческое объединение «Радуга», режиссёр Райтбурт).[15]

В рассказе Кира Булычева «Мечта заочника» студент-заочник Гаврилов приходит к профессору Минцу и приносит купленную курсовую работу, в которой приводится доказательство теоремы, с просьбой объяснить, что он написал.

В посвящённой Хэллоуину 1995 года серии «Симпсонов» двумерный Гомер Симпсон случайно попадает в третье измерение. Во время его путешествия в этом странном мире, в воздухе парят геометрические тела и математические формулы, включая равенство. Калькулятор с точностью не более 9 значащих цифр подтверждает это равенство:

178212 + 184112 = 2541210258614589176288669958142428526657 ≈ 254121026·1031

192212 = 2541210259314801410819278649643651567616 ≈ 254121026·1031

Тем не менее, даже без вычисления точных значений легко видеть, что равенство неверно: левая часть — нечётное число, а правая часть — чётное.

В первом издании «Искусства программирования» Дональда Кнута теорема Ферма приведена в качестве упражнения с математическим уклоном в самом начале книги и оценена максимальным числом (50) баллов, как «исследовательская проблема, которая (насколько это было известно автору в момент написания) ещё не получила удовлетворительного решения. Если читатель найдет решение этой задачи, его настоятельно просят опубликовать его; кроме того, автор данной книги будет очень признателен, если ему сообщат решение как можно быстрее (при условии, что оно правильно)». В третьем издании книги это упражнение уже требует знаний высшей математики и оценивается лишь в 45 баллов.

В фильме «Доказательство» сюжет крутится вокруг доказательства теоремы Ферма, но это ни разу явно не упоминается в фильме.

В книге Стига Ларссона «Девушка, которая играла с огнём»[16] главная героиня Лисбет Саландер, обладающая редкими способностями к аналитике и фотографической памятью, в качестве хобби занята доказательством Великой теоремы Ферма, на которую она наткнулась, читая фундаментальный труд «Измерения в математике», в котором приводится и доказательство Эндрю Уайлса. Лисбет не хочет изучать готовое доказательство, а главным интересом становится поиск собственного решения. Поэтому всё своё свободное время она посвящает самостоятельному поиску «замечательного доказательства» теоремы великого француза, но раз за разом заходит в тупик. В конце книги Лисбет находит доказательство, которое не только совершенно отлично от предложенного Уайлсом, но и является настолько простым, что сам Ферма мог бы его найти. Однако, после ранения в голову она его забывает, и Ларссон не приводит никаких подробностей этого доказательства.

Мюзикл «Последнее танго Ферма», изданный институтом Клэя, создан в 2000 году Дж. Розенблумом и Дж. С. Лессер по мотивам реальной истории Эндрю Уайлса. Главный герой по имени Дэниел Кин завершает доказательство теоремы, а дух самого Ферма старается ему помешать[17].

За несколько дней до своей смерти Артур Кларк успел отрецензировать рукопись романа «Последняя Теорема», над которой он трудился в соавторстве с Фредериком Полом. Книга вышла уже после смерти Кларка.

В рассказе Натальи Дарьяловой «Великая и загадочная» сюжет строится на теореме Ферма. Рассказывается о том, как молодой человек, будучи студентом, занялся теоремой Ферма, и впоследствии стал математиком, получил несколько важных научных результатов, но совершенно загубил свою личную жизнь.

В романе П. А. Загребельного «Разгон»[18] скромный преподаватель математики из Одессы сумел доказать теорему, через некоторое время он становится академиком и возглавляет очень серьезное киевское НПО, занимающееся созданием электронно-вычислительных систем.

А.П. Казанцев в своем романе "Острее шпаги" в 1983 в стиле Дюма довольно ярко описал Пьера Ферма и предложил оригинальную версию отсутствия доказательства самого Ферма.

superbotanik.net

Смотрите также

• 
  Финансово правовая ответственность реферат
• 
  Титульный лист реферат тгпу
• 
  Современные антисептические средства реферат
• 
  Реферат теория ожиданий врума
• 
  Реферат судебная система германии
• 
  Реферат по физике фотоэлементы
• 
  Реферат на тему обсе
• 
  Реферат китайская традиционная медицина
• 
  Реферат аз фанни экология
• 
  Политика и интернет реферат
• 
  Педагог 21 века реферат