Координаты и векторы. Реферат вектор и координаты

Векторы и координаты — творческая работа

ФГОБУ ВПО «Государственный университет МинФина России» Владикавказский филиал

Презентация

По дисциплине «Математика»

Тема:«Векторы и координаты»

выполнили :

студенты группы1-3Э

Гуссаов Георгий

Петросянц Марсель

проверил преподаватель:

Солонина Г.Ю.

Владикавказ 2012г.

Оглавление

Понятие вектора
Длина вектора
Коллинеарные вектора
Сонаправленные вектора
Противоположно направленные вектора
Сложение векторов
Вычитание векторов
Произведение вектора на число
Вектор и его координаты

Понятие вектора

Многие физические величины характеризуются числовым значением и направлением в пространстве, их называют векторными величинами

Длина вектора

вектор MN или вектор а

вектор КК или нулевой вектор

Длиной вектора или модулем не нулевого вектора называется длина отрезка

|MN| = |a| длина вектора MN

|KK| = 0

Нулевой вектор считается коллинеарным любому вектору

Коллинеарные вектора

Ненулевые вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых

Сонаправленные вектора

Коллинеарные вектора имеющие одинаковое направление, называются сонаправленными векторами

c ↑↑ KL AB ↑↑ b MM ↑↑ c (любому вектору)

Противоположно направленные вектора

Коллинеарные вектора имеющие противоположное направление, называются противоположно направленными векторами

b ↑↓ KL AB ↑↓ c

c↑↓ b KL ↑↓ AB

Сложение векторов Правило треугольника

a + b = c

Дано: a, b

Построить: c = a + b

Построение:

Сумма нескольких векторов

a + b + c + d + m + n

Вычитание векторов

a - b = c

Построение:

Дано: a, b

Построить: c = a - b

Умножение вектора a на число k

k·a = b,

|a| ≠ 0, k – произвольное число

|b| = |k|·|a|,

если k>0, то a ↑↑ b

если k<0, то a ↑↓ b

-2a

Для любых чисел k, l и любых векторов a, b справедливы равенства:

1º. (kl)a= k(la) (сочетательный закон),

2º. (k+l)a= ka+la (первый распределительный закон),

3º. k(a+b) = ka+kb (второй распределительный закон).

Координаты вектора

Отрицательная полуось

Положительная полуось

Отрицательная полуось

Положительная полуось

Отрицательная полуось

Луч, направление которого совпадает с направлением оси, называется положительной полуосью,

а другой луч – отрицательной полуосью

В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел, которые называются координатами точки

M (x; y; z)

x = OM1

абсцисса

y = OM2

ордината

z = OM3

аппликата

O (0; 0; 0)

I I I I I I I I I

N (5; 0; 0)

I I I I I I I I

I I I I I I I I I I I

F (0; -2; 0)

D(0; 0; 4)

R(0; 0; -0,5)

M(0; 3; 0)

S(x; 0; 0)

P(0; y; 0)

T(0; 0; z)

N (5; 4; 0)

C (2;-1; 0)

I I I I I I I I I I I

R (-3; -3; 0)

F(0; 4; 3)

A(0; -3; 4)

M(7; 0; 2)

S(x; y; 0)

P(0; y; z)

T(x; 0; z)

Oxy

Oyz

Oxz

I I I I I I I I I

I I I I I I I I

D(6; 0;-3)

I I I I I I I I

p{ x; y; z} координаты вектора

разложение вектора по координатным векторам

, и – координатные векторы

=1;

F(x; y; z)

Координатные векторы не компланарны. Поэтому любой вектор можно разложить по координатным векторам, т.е. представить в виде

причем коэффициенты разложения определяются единственным образом.

p = xi + yj + zk

Вектор, начало которого совпадает с началом координат – радиус-вектор.

Координаты радиус-вектора совпадают с координатами конца вектора.

I I I I I I I I

p {4; 5; 8}

S(4; 5; 8)

p =4i +5j +8k

I I I I I I I

0 {0;0;0}

O (0; 0; 0)

i {1;0;0}

j {0;1;0}

e {-1;0;0}

r {0;-1;0}

I I I I I I I I

0 =0i + 0j + 0k

k {0;0;1}

f {0;0;-1}

e = – i

r = – j

f = – k

Координаты равных векторов равны.

I I I I I I I I

p {4; 5; 8}

I I I I I I I

c = p

c {4; 5; 8}

Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.

a+b = + =

a +b {x1+x2; y1+y2; z1+z2}

Рассмотрим векторы

a {x1;y1;z1}

b {x2;y2;z2}

= (x1+ x2)i + (y1 +y2 )j + (z1 + z2 )k

a = x1i +y1 j +z1 k

b = x2i +y2 j +z2 k

x1i +y1 j +z1 k

x2i +y2 j +z2 k

a –b = – =

a –b {x1–x2; y1 –y2; z1– z2}

Рассмотрим векторы

a {x1;y1;z1}

b {x2;y2;z2}

= (x1– x2)i + (y1 –y2 ) j + (z1 –z2 )k

a = x1i +y1 j +z1 k

b = x2i +y2 j +z2 k

x1i +y1 j +z1 k

x2i +y2 j +z2 k

Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.

( )

Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.

ka {kx; ky; kz}

a {x; y; z}

Рассмотрим вектор

3a {-6; 3; 0}

a {-2; 1;0}

(-2)

-2a {4; 0;-6}

a {-2; 0; 3}

(-1)

-a {2; -5; 3}

a {-2; 5;-3}

a = xi +y j +z k

ka = kxi +ky j +kz k

Спасибо

за внимание !!!

«Геометрия 7-9» Л.С. Атанасян и др.

referat911.ru

Векторы и координаты

Количество просмотров публикации Векторы и координаты - 73

1) векторы на плоскости:

скалярное произведение:

признак коллинеарности: или

признак перпендикулярности: x1∙x2 + y1∙y2 = 0 ;

2) векторы в пространстве:

скалярное произведение:

признак коллинеарности: или

признак перпендикулярности: x1∙x2 + y1∙y2 + z1∙z2 = 0 ;

признак компланарности трёх векторов:

x1 y1 z1

x2 y2 z2 = 0 ;

x3 y3 z3

векторное произведение двух векторов:

i j k

= x1 y1 z1 ; = Sпараллелограмма = 2∙SΔ;

x2 y2 z2

смешанное произведение трёх векторов:

x1 y1 z1

= = x2 y2 z2 ;

x3 y3 z3

объём параллелепипеда: Vпарал = ││ ;

объём пирамиды: Vпирам = Vпарал = ││ ;

3) аналитическая геометрия на плоскости:

расстояние между двумя точками M1(x1 ; y1) и M2(x2 ; y2)

;

уравнение прямой, проходящей через две точки M1(x1 ; y1) и M2(x2 ; y2)

;

деление отрезка M1M2 в данном отношении λ

координаты середины отрезка (M1M = MM2 , ᴛ.ᴇ. λ = 1)

уравнение прямой, проходящей через точку M0(x0 ; y0) перпендикулярно

вектору ()

A∙(x – x0) + B∙(y – y0) = 0 ;

уравнение прямой с угловым коэффициентом k и проходящей через

точку M0(x0 ; y0)

y – y0 = k∙(x – x0) ;

острый угол между двумя прямыми y = k1∙x + b1 и y = k2∙x + b2

условие параллельности двух прямых: k1 = k2 ;

условие перпендикулярности двух прямых: k1∙k2 = −1 ;

расстояние от точки M0(x0 ; y0) до прямой A∙x + B∙y + C = 0

площадь треугольника с вершинами A(x1 ; y1) , B(x2 ; y2) , C(x3 ; y3)

или в другом виде то же самое

x1 y1 1

S∆ABC = , где D = x2 y2 1 ;

x3 y3 1

уравнение окружности радиуса R

(x – a)2 + (y – b)2 = R2 ; центр в точке A(a ; b)

x2 + y2 = R2 ; центр в точке O(0 ; 0)

4) аналитическая геометрия в пространстве:

расстояние между двумя точками M1(x1 ; y1 ; z1) и M2(x2 ; y2 ; z2)

;

уравнение прямой в каноническом виде, проходящей через две точки

M1(x1 ; y1 ; z1) и M2(x2 ; y2 ; z2)

;

деление отрезка M1M2 в данном отношении λ

координаты середины отрезка (M1M = MM2 , ᴛ.ᴇ. λ = 1)

уравнение плоскости, проходящей через точку M0(x0 ; y0 ; z0)

перпендикулярно вектору

()

A∙(x – x0) + B∙(y – y0) + C∙(z – z0) = 0 ;

расстояние от точки M0(x0 ; y0 ; z0) до плоскости A∙x + B∙y + C∙z + D = 0

уравнение плоскости, проходящей через три заданные точки

M1(x1 ; y1 ; z1) , M2(x2 ; y2 ; z2) , M3(x3 ; y3 ; z3) :

x – x1 y – y1 z – z1

x2 – x1 y2 – y1 z2 – z1 = 0 ;

x3 – x1 y3 – y1 z3 – z1

уравнение сферы радиуса R

(x – a)2 + (y – b)2 + (z – c)2 = R2 ; центр в точке A(a ; b ; c)

x2 + y2 + z2 = R2 ; центр в точке O(0 ; 0 ; 0)

referatwork.ru

Реферат Вектор (геометрия)

скачать

Реферат на тему:

План:

1 Определения
- 1.1 Алгебраический подход
- 1.2 Геометрический подход
  - 1.2.1 Свободные, скользящие и фиксированные векторы
- 1.3 Вектор как последовательность
2 Обозначения
3 Связанные определения
4 Свойства
5 Линейные операции над векторами
- 5.1 Сложение векторов
  - 5.1.1 Сложение коллинеарных скользящих векторов
- 5.2 Произведение вектора на число
- 5.3 Скалярное произведение
- 5.4 Векторное произведение
- 5.5 Смешанное произведение
6 История

Введение

Вектор $\overrightarrow{AB}$

Вектор — понятие, определяемое в разных разделах математики различно.

1. Определения

1.1. Алгебраический подход

В линейной алгебре вектор — это элемент векторного пространства (или иначе: линейного пространства). Векторы можно складывать и умножать на число. Вектор также можно представить в виде линейной комбинации других векторов. Базис — это линейно независимая совокупность векторов, которая порождает всё пространство. В конечномерном пространстве существует конечный базис, и тогда любой вектор пространства может быть единственным образом представлен в виде разложения вида

$\vec{x}=\sum_{i=1}^n x_i \vec{e}_i,$

где $\vec{e}_1,\dots,\vec{e}_n$ — это базис, а $x_1,\dots,x_n$ — координаты вектора $\vec{x}$ в заданном базисе.

1.2. Геометрический подход

Понятие вектор в геометрии отлично от определяемого в алгебре. Различают понятие свободного и связанного (приложенного, закреплённого) вектора.

Связанный вектор или направленный отрезок — упорядоченная пара точек евклидова пространства.
Свободный вектор — класс эквивалентности направленных отрезков.

При этом два направленных отрезка считаются эквивалентными, если они:

коллинеарны
равны по длине
одинаково направлены (сонаправлены)

Существует естественный изоморфизм свободных векторов и параллельных переносов пространства (каждый перенос взаимно однозначно соответствует какому-то свободному вектору). На этом также строят геометрическое определение свободного вектора, просто отождествляя его с соответственным переносом.

Большую роль играют векторы в изучении бесконечно малых трансформаций пространства.

1.2.1. Свободные, скользящие и фиксированные векторы

Иногда вместо того, чтобы рассматривать в качестве векторов множество всех равных направленных отрезков, берут только некоторую модификацию этого множества (фактормножество). Так, говорят о «свободных» (когда отождествляются все равные по длине и направлению направленные отрезки, считаясь полностью равными или одним и тем же вектором), «скользящих» (отождествляются между собой все направленные отрезки, равные в смысле свободных векторов, начала и концы которых расположены на одной прямой) и «фиксированных» векторах (по сути дела, просто о направленных отрезках, когда разное начало означает уже неравенство векторов).

Определение. Говорят, что свободные векторы $\overrightarrow{AB}$ и $\ \overrightarrow{CD}$ равны, если найдутся точки E и F такие, что четырёхугольники ABFE и CDFE — параллелограммы.

Замечание. «Ухищрение» (введение дополнительных точек) в определении равенства касается, прежде всего, случая, когда точки A,B,C,D располагаются на одной прямой. В противном случае определение выглядит проще:

Определение. Говорят, что свободные векторы $\overrightarrow{AB}$ и $\ \overrightarrow{CD}$ , не лежащие на одной прямой, равны, если четырёхугольник ABDC — параллелограмм.

Определение. Говорят, что скользящие векторы $\overrightarrow{AB}$ и $\ \overrightarrow{CD}$ равны, если

точки A,B,C,D располагаются на одной прямой,
векторы $\overrightarrow{AB}$ и $\ \overrightarrow{CD}$ равны между собой как свободные векторы.

Неформально говоря, скользящему вектору разрешено двигаться вдоль его прямой без изменения величины и направления.

Замечание. Скользящие векторы особо употребимы в механике. Простейший пример скользящего вектора в механике — сила. Перенос такого начала вектора вдоль прямой, на которой он лежит, не меняет момента силы ни относительно никакой точки; перенос же его на другую прямую, даже если не менять величины и направления вектора, может вызвать изменение его момента (скорее даже почти всегда вызовет): поэтому нельзя рассматривать силу как свободный вектор.

Определение. Говорят, что фиксированные векторы $\overrightarrow{AB}$ и $\ \overrightarrow{CD}$ равны, если попарно совпадают точки A и C, B и D. Вектором в простейшем случае называется направленный отрезок, а в других случаях различные векторы — это разные классы эквивалентности направленных отрезков, определяемые неким конкретным отношением эквивалентности. Причем отношение эквивалентности может быть разным, определяя тип вектора («свободный», «фиксированный» итд). Проще говоря, внутри класса эквивалентности все входящие в него направленные отрезки рассматриваются как совершенно равные, и каждый может равно представлять весь класс.

1.3. Вектор как последовательность

Вектор — упорядоченная пара чисел (последовательность, кортеж) однородных элементов. Это наиболее общее определение в том смысле, что может быть не задано обычных векторных операций вообще, их может быть меньше, или они могут не удовлетворять обычным аксиомам линейного пространства. Именно в таком виде вектор понимается в программировании, где, как правило, обозначается именем-идентификатором с квадратными скобками (например, object[]). Перечень свойств моделирует принятое в теории систем определение класса и состояния объекта. Так типы элементов вектора определяют класс объекта, а значения элементов — его состояние. Впрочем, вероятно, это употребление термина уже выходит за рамки обычно принятого в алгебре, да и в математике вообще.

Многие математические объекты (например матрицы, тензоры, функции и т. д.), в том числе обладающие структурой более общей, чем счётный или конечный упорядоченный список, удовлетворяют аксиомам векторного пространства, то есть являются с точки зрения алгебры векторами.

2. Обозначения

Вектор, представленный набором n элементов (компонент) $a_1, a_2, \ldots, a_n$ допустимо обозначить следующим способами:

$\langle a_1, a_2, \ldots, a_n\, \rangle,\ \left ( a_1, a_2, \ldots, a_n\, \right )$ .

Для того, чтобы подчеркнуть, что это вектор (а не скаляр), используют черту сверху, стрелочку сверху, жирный или готический шрифт:

$\bar a,\ \vec a, \mathbf a, \mathfrak A,\ \mathfrak a.$

Сложение векторов почти всегда обозначается знаком плюс:

$\mathbf a + \mathbf b$ .

Умножение на число — просто написанием рядом, без специального знака, например:

$k \mathbf a$ ,

причём число при этом обычно пишут слева.

Умножение на матрицу также обозначают написанием рядом, без специального знака, но здесь перестановка сомножителей в общем случае влияет на результат. Действие линейного оператора на вектор также обозначается написанием оператора слева, без специального знака.

Длина (модуль) вектора $\mathbf a$ — скаляр, равный арифметическому квадратному корню из суммы квадратов координат (компонент) вектора. Обозначается $|\mathbf a|$ или просто a.

3. Связанные определения

Вектор, начало которого совпадает с его концом, называют нулевым: $\overrightarrow{AA} = \vec{\mathbf{0}}.$

Вектор $\overrightarrow{BA}$ называют противоположным вектору $\overrightarrow{AB}$ .

Длиной вектора, или модулем вектора, называют длину соответствующего направленного отрезка: $|\overrightarrow{AB}|=|AB|$ .

4. Свойства

Ортогональность Векторы являются ортогональными тогда и только тогда, когда их скалярное произведение равно нулю.

Часто вместо этого термина употребляют термин "перпендикулярность", однако следует учитывать, что нулевой вектор ортогонален любому вектору, но понятие перпендекулярности для него не определено, поскольку не определён угол между нулевым и другим вектором.

Пример:Даны два вектора $\vec a(x_1;y_1)$ и $\vec b(x_2;y_2)$ . Эти векторы будут ортогональными, если выражение x1x2 + y1y2 = 0.

Коллинеарность Векторы являются коллинеарными тогда и только тогда, когда их векторное произведение равно нулю.

Часто вместо этого термина употребляют термин "параллельность", однако следует учитывать, что нулевой вектор коллинеарен любому вектору, но понятие параллельности для него не определено, поскольку не определён угол между нулевым и другим вектором.

Пример:Даны два вектора $\vec a=(x_1;y_1)$ и $\vec b=(x_2;y_2)$ . Эти векторы коллинеарны, если x1 = λx2 и y1 = λy2, где $\lambda \in \mathbb R$

5. Линейные операции над векторами

5.1. Сложение векторов

Два вектора u, v и вектор их суммы

Сложение двух свободных векторов можно осуществлять как по правилу параллелограмма, так и по правилу треугольника.

Правило треугольника. Для сложения двух векторов $\vec{u}$ и $\vec{v}$ по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.

Правило параллелограмма. Для сложения двух векторов $\vec{u}$ и $\vec{v}$ по правилу параллелограмма оба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.

А модуль (длину) вектора суммы $\vec{v+u}=\vec{u} + \vec{v}$ определяют по теореме косинусов $|\vec{u+v}|=\sqrt{|u|^2+|v|^2-2|u|\cdot |v|\cdot \cos \alpha},$ где $\alpha\,$ — угол между векторами, когда начало одного совпадает с концом другого. Так же используется формула $|\vec{u+v}|=\sqrt{|u|^2+|v|^2+2|u|\cdot |v|\cdot \cos \alpha},$ теперь $\alpha\,$ — угол между векторами выходящими из одной точки.

Сложение двух скользящих векторов определено лишь в случае, когда прямые, на которых они расположены, пересекаются. Тогда каждый из векторов переносится вдоль своей прямой в точку пересечения этих прямых, после чего сложение осуществляется по правилу параллелограмма.

Сложение двух фиксированных векторов определено лишь в случае, когда они имеют общее начало. Их сложение в этом случае осуществляется по правилу параллелограмма.

5.1.1. Сложение коллинеарных скользящих векторов

Если скользящие векторы параллельны, то при их сложении главная трудность состоит в определении прямой, на которой будет расположена их сумма. (Величину и направление вектора суммы было бы естественно определить точно так же, как и в случае сложения свободных векторов.) В механике при изучении статики для решения вопроса о сложении параллельных сил, которые, как известно, задаются скользящими векторами, вводится дополнительная гипотеза: к системе векторов можно добавить два вектора, равных по величине, противоположных по направлению и расположенных на одной прямой, пересекающей прямые, на которых расположены данные вектора. Пусть, например, надо сложить скользящие векторы $\vec{a}$ и $\vec{b}$ , расположенные на параллельных прямых. Добавим к ним векторы $\vec{c}$ и $-\vec{c}$ , расположенные на одной прямой. Прямые, на которых расположены векторы $\vec{a}$ и $\vec{c}$ , $\vec{b}$ и $-\vec{c}$ пересекаются. Поэтому определены векторы

$\vec{a}'=\vec{a}+\vec{c}, \quad \vec{b}'=\vec{b}-\vec{c}$

Прямые, на которых расположены векторы $\vec{a}'$ и $\vec{b}'$ , пересекаются всегда, за исключением случая, когда векторы $\vec{a}$ и $\vec{b}$ равны по величине и противоположны по направлению, в котором говорят, что векторы $\vec{a}$ и $-\vec{a}$ образуют пару (векторов).

Таким образом, под суммой векторов $\vec{a}$ и $\vec{b}$ можно понимать сумму векторов $\vec{a}'$ и $\vec{b}'$ , и эта сумма векторов определена корректно во всех случаях, когда векторы $\vec{a}$ и $\vec{b}$ не образуют пару.

5.2. Произведение вектора на число

Произведением вектора $\vec{a}$ и числа λ называется вектор, обозначаемый $\lambda\vec{a}$ (или $\vec{a}\lambda$ ), модуль которого равен $|\lambda|\cdot|\vec{a}|$ , а направление совпадает с направлением вектора $\vec{a}$ , если $\lambda>0 \,$ , и противоположно ему, если $\lambda<0 \,$ . Если же $\lambda=0 \,$ , или вектор $\vec{a}$ нулевой, тогда и только тогда произведение $\lambda\vec{a}$ — нулевой вектор.

Обычно принято в записи произведения числа и вектора число записывать слева, но в принципе допустим и обратный порядок, хотя все же обычное соглашение состоит в том, чтобы его избегать, если нет прямой необходимости. Так или иначе, $\lambda\vec{a} = \vec{a}\lambda$ .

Из определения произведения вектора на число легко вывести следующие свойства:

если $\vec{b} = \vec{a}\lambda$ , то $\vec{b}||\vec{a}$ . Наоборот, если $\vec{b}||\vec{a}\ (\vec{a}\not= 0)$ , то при некотором λ верно равенство $\vec{b}=\vec{a}\lambda$ ;
всегда $\vec{a}=|\vec{a}|\cdot\vec{a}$ °, то есть каждый вектор равен произведению его модуля на орт.

5.3. Скалярное произведение

Скалярным произведением векторов $\vec{a}$ и $\vec{b}$ называют число, равное $|\mathbf{a}|\cdot|\mathbf{b}|\cos \varphi \,$ , где $\varphi \,$ — угол между векторами $\mathbf{a}$ и $\mathbf{b}$ . Обозначения: $(\mathbf{a},\mathbf{b})$ или $\mathbf{a}\cdot\mathbf{b}$ .

Если один из векторов является нулевым, то несмотря на то, что угол $\varphi$ не определён, произведение равно нулю.

Свойства скалярного произведения векторов:

$\mathbf{a}\cdot\mathbf{b}=\mathbf{b}\cdot\mathbf{a}\,$ — коммутативность.
$\mathbf{a}\cdot(\mathbf{b}+\mathbf{c})=\mathbf{a}\cdot\mathbf{b}+\mathbf{a}\cdot\mathbf{c}\,$ — дистрибутивность.
$(k\mathbf{a},\mathbf{b})=k (\mathbf{a},\mathbf{b})$ — линейность по отношению к умножению на число.
$(\mathbf{a},\mathbf{a})=|\mathbf{a}|^2\,$ — норма вектора (Квадрат вектора).

Геометрически скалярное произведение есть произведение длины одного из сомножителей на ортогональную проекцию другого на направление первого (или наоборот). Скалярное произведение какого-то вектора $\vec{a}$ с единичным вектором есть ортогональная проекция вектора $\vec{a}$ на направление единичного вектора.

5.4. Векторное произведение

Векторным произведением вектора a на вектор b называется вектор c, удовлетворяющий следующим требованиям:

длина вектора c равна произведению длин векторов a и b на синус угла φ между ними

вектор c ортогонален каждому из векторов a и b
вектор c направлен так, что тройка векторов abc является правой.

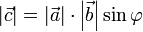
Обозначение: $\vec c = \left[ \vec a \vec b \right] = \left[ \vec a, \vec b \right] = \vec a \times \vec b$

Геометрически векторное произведение $\vec a \times \vec b$ есть ориентированная площадь параллелограмма, построенного на векторах $\vec a, \vec b$ , представленная псевдовектором, ортогональным этому параллелограмму.

Свойства векторного произведения:

При перестановке сомножителей векторное произведение меняет знак (антикоммутативность), т.е $\vec a \times \vec b = -(\vec b \times \vec a)$
Векторное произведение обладает сочетательным свойством относительно скалярного множителя, то есть $\lambda(\vec a \times \vec b) = (\lambda \vec a) \times \vec b = \vec a \times (\lambda \vec b)$
Векторное произведение обладает распределительным свойством: $(\vec a + \vec b) \times \vec c = \vec a \times \vec c + \vec b \times \vec c$

5.5. Смешанное произведение

Сме́шанное произведе́ние $( \vec{a}, \vec{b}, \vec{c} )$ векторов $\vec{a}, \vec{b}, \vec{c}$ — скалярное произведение вектора $\vec{a}$ на векторное произведение векторов $\vec{b}$ и $\vec{c}$ :

$(\vec{a}, \vec{b}, \vec{c}) = \left(\vec{a}, [\vec{b}, \vec{c}]\right) = \vec{a}\cdot\left(\vec{b}\times\vec{c}\right)$

(равенство записано для разных обозначений скалярного и векторного произведения).

Иногда смешанное произведение называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).

Геометрически смешанное произведение $( \vec{a}, \vec{b}, \vec{c} )$ есть (ориентированный) объём параллелепипеда, построенного на векторах $\vec{a}, \vec{b}, \vec{c}$ .

6. История

Интуитивно вектор понимается как объект, имеющий величину, направление и (необязательно) точку приложения. Зачатки векторного исчисления появились вместе с геометрической моделью комплексных чисел (Гаусс, 1831). Развитые операции с векторами опубликовал Гамильтон как часть своего кватернионного исчисления (вектор образовывали мнимые компоненты кватерниона). Гамильтон предложил сам термин вектор (лат. vector, несущий) и описал некоторые операции векторного анализа. Этот формализм использовал Максвелл в своих трудах по электромагнетизму, тем самым обратив внимание учёных на новое исчисление. Вскоре вышли «Элементы векторного анализа» Гиббса (1880-е годы), а затем Хевисайд (1903) придал векторному анализу современный вид.

Литература

Г. С. М. Коксетер (англ.), С. П. Грейтцер. Новые встречи с геометрией. — М.: Наука, 1978. — Т. 14. — (Библиотека математического кружка).

wreferat.baza-referat.ru

Координаты и векторы | Бесплатные курсовые, рефераты и дипломные работы

1. Расстояние между точками A1 (x1;y1) и A2(x2;y2) находится по формуле: 2. Координаты (x;y) середины отрезка с концами A1 (x1;y1) и A2 (x2;y2) находится по формулам: 3. Уравнение прямой с угловым коэффициентом и начальной ординатой имеет вид: y = kx + q. Угловой коэффициент k представляет собой значение тангенса угла, образуемого прямой с положительным направлением оси Ox, а начальная ордината q – значение ординаты точки пересечения прямой с осью Oy.	4. Общее уравнение прямой имеет вид: ax + by + … c = 0. 5. Уравнения прямых, параллельных соответственно осям Oy и Ox, имеют вид: ax + by + c = 0. 6. Условия параллельности и перпендикулярности прямых y1=kx1+q1 и y2=kx2+q2 соответственно имеют вид: 7. Уравнения окружностей с радиусом R и с центром соответственно в точках O(0;0) и C(x0;y0) имеют вид: 8. Уравнение: представляет собой уравнение параболы с вершиной в точке, абсцисса которой
Прямоугольная декартова система координат в пространстве
1. Расстояние между точками A1(x1;y1;z1) и A2(x2;y2;z2) находится по формуле: 2. Координаты (x;y;z) середины отрезка с концами A1(x1;y1;z1) и A2(x2;y2;z2) находятся по формулам: 3. Модуль вектора 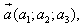заданного своими координатами, находится по формуле: 4. При сложении векторов их соответствующие координаты складываются, а при умножении вектора на число все его координаты умножаются на это число, т.е. справедливы формулы: 5. Единичный вектор сонаправленный с вектором находится по формуле: 6. Скалярным произведением векторов называется число: где — угол между векторами.	7. Скалярное произведение векторов 8. Косинус угла между векторами и находится по формуле: 9. Необходимое и достаточное условие перпендикулярности векторов и имеет вид: 10. Общее уравнение плоскости, перпендикулярной вектору имеет вид: ax + by + cz + d = 0. 11. Уравнение плоскости, перпендикулярной вектору и проходящей через точку (xo;yo;zo), имеет вид: a(x — xo) + b(y — yo) + c(z — zo) = 0. 12. Уравнение сферы с центром O(0;0;0) записывается в виде:

Список литературы:

1. Богомолов Н.В. Сергиенко Л.Ю. Сборник дидактических заданий по математике: Учебное пособие для ссузов Изд. 3-е,стереотип. Дрофа 2010. -Глава 17, § 7, стр. 281, Глава 21,§ 1, стр. 335.

2. Валуцэ И.И. Математика для техникумов на базе средней школы: Учебное пособие. / И.И. Валуцэ, Г.Д. Дилигул.– 2-е изд., перераб. и доп. – М.: Наука, 1989. – 576 с. – Глава 2, § 8-11, стр. 63-77.

refac.ru

Векторы и координаты | Бесплатные курсовые, рефераты и дипломные работы

1) векторы на плоскости:

скалярное произведение:

признак коллинеарности: или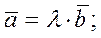

признак перпендикулярности: x1∙x2 + y1∙y2 = 0 ;

2) векторы в пространстве:

скалярное произведение:

признак коллинеарности: или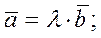

признак перпендикулярности: x1∙x2 + y1∙y2 + z1∙z2 = 0 ;

признак компланарности трёх векторов:

x1 y1 z1

x2 y2 z2 = 0 ;

x3 y3 z3

векторное произведение двух векторов:

i j k

= x1 y1 z1 ; = Sпараллелограмма = 2∙SΔ;

x2 y2 z2

смешанное произведение трёх векторов:

x1 y1 z1

= = x2 y2 z2 ;

x3 y3 z3

объём параллелепипеда: Vпарал = ││ ;

объём пирамиды: Vпирам = Vпарал = ││ ;

3) аналитическая геометрия на плоскости:

расстояние между двумя точками M1(x1 ; y1) и M2(x2 ; y2)

;

уравнение прямой, проходящей через две точки M1(x1 ; y1) и M2(x2 ; y2)

;

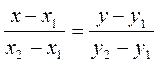деление отрезка M1M2 в данном отношении λ

координаты середины отрезка (M1M = MM2 , т.е. λ = 1)

уравнение прямой, проходящей через точку M0(x0 ; y0) перпендикулярно

вектору ()

A∙(x – x0) + B∙(y – y0) = 0 ;

уравнение прямой с угловым коэффициентом k и проходящей через

точку M0(x0 ; y0)

y – y0 = k∙(x – x0) ;

острый угол между двумя прямыми y = k1∙x + b1 и y = k2∙x + b2

условие параллельности двух прямых: k1 = k2 ;

условие перпендикулярности двух прямых: k1∙k2 = −1 ;

расстояние от точки M0(x0 ; y0) до прямой A∙x + B∙y + C = 0

площадь треугольника с вершинами A(x1 ; y1) , B(x2 ; y2) , C(x3 ; y3)

или в другом виде то же самое

x1 y1 1

S∆ABC = , где D = x2 y2 1 ;

x3 y3 1

уравнение окружности радиуса R

(x – a)2 + (y – b)2 = R2 ; центр в точке A(a ; b)

x2 + y2 = R2 ; центр в точке O(0 ; 0)

4) аналитическая геометрия в пространстве:

расстояние между двумя точками M1(x1 ; y1 ; z1) и M2(x2 ; y2 ; z2)

;

уравнение прямой в каноническом виде, проходящей через две точки

M1(x1 ; y1 ; z1) и M2(x2 ; y2 ; z2)

;

деление отрезка M1M2 в данном отношении λ

координаты середины отрезка (M1M = MM2 , т.е. λ = 1)

уравнение плоскости, проходящей через точку M0(x0 ; y0 ; z0)

перпендикулярно вектору

()

A∙(x – x0) + B∙(y – y0) + C∙(z – z0) = 0 ;

расстояние от точки M0(x0 ; y0 ; z0) до плоскости A∙x + B∙y + C∙z + D = 0

уравнение плоскости, проходящей через три заданные точки

M1(x1 ; y1 ; z1) , M2(x2 ; y2 ; z2) , M3(x3 ; y3 ; z3) :

x – x1 y – y1 z – z1

x2 – x1 y2 – y1 z2 – z1 = 0 ;

x3 – x1 y3 – y1 z3 – z1

уравнение сферы радиуса R

(x – a)2 + (y – b)2 + (z – c)2 = R2 ; центр в точке A(a ; b ; c)

x2 + y2 + z2 = R2 ; центр в точке O(0 ; 0 ; 0)

refac.ru

НОУ ИНТУИТ | Лекция | Координаты и векторы

Аннотация: Решение типовых задач в базовых системах координат (декартова прямоугольная, полярная) с векторными операциями на плоскости, в пространстве, обучение реферированию и Интернет–поиску по этой теме

Задачи

Постройте вектор длины 5 единиц и направления, совпадающего с направлением возрастания чисел числовой прямой. Постройте противоположный ему вектор. Указание: направление первого вектора – луч x >= 0 ; второго – луч x <= 0.
Постройте вектор длины 6 единиц и направления, совпадающего с направлением убывания чисел числовой прямой. Постройте противоположный ему вектор. Указание: направление первого вектора – луч x <= 0.
Постройте вектор длины 7 единиц и направления, совпадающего с направлением биссектрисы первого координатного угла. Постройте противоположный ему вектор. Указание: направление первого вектора – луч y = x, x >= 0.
Постройте проекции векторов задач 1-3 на оси координат. Найдите вектор суммы этих проекций. Указание: изобразите все три вектора на одном чертеже и используйте правило построения суммы векторов.
Постройте и запишите вектора в полярной системе координат для всех задач 1-3. Указание: использовать формулы перехода от декартовой системы координат к полярной.
Выпишите по полярным координатам $(1; \pi /3)$ декартовы координаты вектора. Указание: использовать формулы перехода от полярных координат декартовы координаты.
Постройте два коллинеарных вектора в пространстве. Запишите их координаты и проверьте выполнение условия коллинеарности. Указание: коллинеарные векторы лежат на параллельных или совпадающих прямых.
Постройте два компланарных вектора в пространстве. Запишите их координаты и проверьте выполнение условия компланарности. Указание: компланарные векторы лежат в одной плоскости.
Выяснить, какие вектора равны между собой, если эти вектора заданы следующими координатами: (1,1,0), (0,1,1), (1,1,1), (1,0), (sin90, cos90, cos90). Указание: равенство векторов возможно лишь тогда, когда равны все соответствующие координаты.
Постройте вектор по его проекциям на оси координат x, y, z, соответственно, (1,1), (2.0), (1,3). Указание: использовать разложение вектора по его проекциям.

Темы научных исследований и рефератов (Интернет-листов)

История и предпосылки появления и использования систем координат и их эволюция. Примеры.
Виды и применения различных систем координат с древнейших времен и до наших дней. Примеры.
Скалярные и векторные величины. Общее и различное. Взаимосвязи и взаимообусловленность. Примеры.
Теоремы школьной планиметрии и их векторное изложение.
Теоремы школьной стереометрии и их векторное изложение.
Проекции в природе, науке, технике.
Ортонормированные системы векторов и их использование.
Разложения векторов по системам других векторов. Линейная независимость и зависимость векторов.
Гуманитарные приложения векторов. Примеры.
Социально-экономические приложения векторов. Примеры.

www.intuit.ru

Реферат Длина вектора

скачать

Реферат на тему:

План:

1 Определения
- 1.1 Алгебраический подход
- 1.2 Геометрический подход
  - 1.2.1 Свободные, скользящие и фиксированные векторы
- 1.3 Вектор как последовательность
2 Обозначения
3 Связанные определения
4 Свойства
5 Линейные операции над векторами
- 5.1 Сложение векторов
  - 5.1.1 Сложение коллинеарных скользящих векторов
- 5.2 Произведение вектора на число
- 5.3 Скалярное произведение
- 5.4 Векторное произведение
- 5.5 Смешанное произведение
6 История

Введение

Вектор $\overrightarrow{AB}$

Вектор — понятие, определяемое в разных разделах математики различно.

1. Определения

1.1. Алгебраический подход

$\vec{x}=\sum_{i=1}^n x_i \vec{e}_i,$

где $\vec{e}_1,\dots,\vec{e}_n$ — это базис, а $x_1,\dots,x_n$ — координаты вектора $\vec{x}$ в заданном базисе.

1.2. Геометрический подход

Связанный вектор или направленный отрезок — упорядоченная пара точек евклидова пространства.
Свободный вектор — класс эквивалентности направленных отрезков.

При этом два направленных отрезка считаются эквивалентными, если они:

коллинеарны
равны по длине
одинаково направлены (сонаправлены)

Большую роль играют векторы в изучении бесконечно малых трансформаций пространства.

1.2.1. Свободные, скользящие и фиксированные векторы

Замечание. «Ухищрение» (введение дополнительных точек) в определении равенства касается, прежде всего, случая, когда точки A,B,C,D располагаются на одной прямой. В противном случае определение выглядит проще:

Определение. Говорят, что скользящие векторы $\overrightarrow{AB}$ и $\ \overrightarrow{CD}$ равны, если

точки A,B,C,D располагаются на одной прямой,
векторы $\overrightarrow{AB}$ и $\ \overrightarrow{CD}$ равны между собой как свободные векторы.

Замечание. Скользящие векторы особо употребимы в механике. Простейший пример скользящего вектора в механике — сила. Перенос такого начала вектора вдоль прямой, на которой он лежит, не меняет момента силы ни относительно никакой точки; перенос же его на другую прямую, даже если не менять величины и направления вектора, может вызвать изменение его момента (скорее даже почти всегда вызовет): поэтому нельзя рассматривать силу как свободный вектор.

1.3. Вектор как последовательность

2. Обозначения

$\langle a_1, a_2, \ldots, a_n\, \rangle,\ \left ( a_1, a_2, \ldots, a_n\, \right )$ .

$\bar a,\ \vec a, \mathbf a, \mathfrak A,\ \mathfrak a.$

Сложение векторов почти всегда обозначается знаком плюс:

$\mathbf a + \mathbf b$ .

Умножение на число — просто написанием рядом, без специального знака, например:

$k \mathbf a$ ,

причём число при этом обычно пишут слева.

3. Связанные определения

Вектор, начало которого совпадает с его концом, называют нулевым: $\overrightarrow{AA} = \vec{\mathbf{0}}.$

Вектор $\overrightarrow{BA}$ называют противоположным вектору $\overrightarrow{AB}$ .

Длиной вектора, или модулем вектора, называют длину соответствующего направленного отрезка: $|\overrightarrow{AB}|=|AB|$ .

4. Свойства

Пример:Даны два вектора $\vec a(x_1;y_1)$ и $\vec b(x_2;y_2)$ . Эти векторы будут ортогональными, если выражение x1x2 + y1y2 = 0.

Пример:Даны два вектора $\vec a=(x_1;y_1)$ и $\vec b=(x_2;y_2)$ . Эти векторы коллинеарны, если x1 = λx2 и y1 = λy2, где $\lambda \in \mathbb R$

5. Линейные операции над векторами

5.1. Сложение векторов

Два вектора u, v и вектор их суммы

5.1.1. Сложение коллинеарных скользящих векторов

$\vec{a}'=\vec{a}+\vec{c}, \quad \vec{b}'=\vec{b}-\vec{c}$

5.2. Произведение вектора на число

Обычно принято в записи произведения числа и вектора число записывать слева, но в принципе допустим и обратный порядок, хотя все же обычное соглашение состоит в том, чтобы его избегать, если нет прямой необходимости. Так или иначе, $\lambda\vec{a} = \vec{a}\lambda$ .

Из определения произведения вектора на число легко вывести следующие свойства:

если $\vec{b} = \vec{a}\lambda$ , то $\vec{b}||\vec{a}$ . Наоборот, если $\vec{b}||\vec{a}\ (\vec{a}\not= 0)$ , то при некотором λ верно равенство $\vec{b}=\vec{a}\lambda$ ;
всегда $\vec{a}=|\vec{a}|\cdot\vec{a}$ °, то есть каждый вектор равен произведению его модуля на орт.

5.3. Скалярное произведение

Свойства скалярного произведения векторов:

$\mathbf{a}\cdot\mathbf{b}=\mathbf{b}\cdot\mathbf{a}\,$ — коммутативность.
$\mathbf{a}\cdot(\mathbf{b}+\mathbf{c})=\mathbf{a}\cdot\mathbf{b}+\mathbf{a}\cdot\mathbf{c}\,$ — дистрибутивность.
$(k\mathbf{a},\mathbf{b})=k (\mathbf{a},\mathbf{b})$ — линейность по отношению к умножению на число.
$(\mathbf{a},\mathbf{a})=|\mathbf{a}|^2\,$ — норма вектора (Квадрат вектора).

5.4. Векторное произведение

Векторным произведением вектора a на вектор b называется вектор c, удовлетворяющий следующим требованиям:

длина вектора c равна произведению длин векторов a и b на синус угла φ между ними

вектор c ортогонален каждому из векторов a и b
вектор c направлен так, что тройка векторов abc является правой.

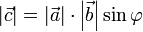
Обозначение: $\vec c = \left[ \vec a \vec b \right] = \left[ \vec a, \vec b \right] = \vec a \times \vec b$

Свойства векторного произведения:

При перестановке сомножителей векторное произведение меняет знак (антикоммутативность), т.е $\vec a \times \vec b = -(\vec b \times \vec a)$
Векторное произведение обладает сочетательным свойством относительно скалярного множителя, то есть $\lambda(\vec a \times \vec b) = (\lambda \vec a) \times \vec b = \vec a \times (\lambda \vec b)$
Векторное произведение обладает распределительным свойством: $(\vec a + \vec b) \times \vec c = \vec a \times \vec c + \vec b \times \vec c$

5.5. Смешанное произведение

$(\vec{a}, \vec{b}, \vec{c}) = \left(\vec{a}, [\vec{b}, \vec{c}]\right) = \vec{a}\cdot\left(\vec{b}\times\vec{c}\right)$

(равенство записано для разных обозначений скалярного и векторного произведения).

6. История

Литература

Г. С. М. Коксетер (англ.), С. П. Грейтцер. Новые встречи с геометрией. — М.: Наука, 1978. — Т. 14. — (Библиотека математического кружка).

wreferat.baza-referat.ru

Координаты и векторы. Реферат вектор и координаты

Векторы и координаты — творческая работа

Векторы и координаты

Реферат Вектор (геометрия)

План:

Введение

1. Определения

1.1. Алгебраический подход

1.2. Геометрический подход

1.2.1. Свободные, скользящие и фиксированные векторы

1.3. Вектор как последовательность

2. Обозначения

3. Связанные определения

4. Свойства

5. Линейные операции над векторами

5.1. Сложение векторов

5.1.1. Сложение коллинеарных скользящих векторов

5.2. Произведение вектора на число

5.3. Скалярное произведение

5.4. Векторное произведение

5.5. Смешанное произведение

6. История

Литература

Координаты и векторы | Бесплатные курсовые, рефераты и дипломные работы

Векторы и координаты | Бесплатные курсовые, рефераты и дипломные работы

НОУ ИНТУИТ | Лекция | Координаты и векторы

Задачи

Темы научных исследований и рефератов (Интернет-листов)

Реферат Длина вектора

План:

Введение

1. Определения

1.1. Алгебраический подход

1.2. Геометрический подход

1.2.1. Свободные, скользящие и фиксированные векторы

1.3. Вектор как последовательность

2. Обозначения

3. Связанные определения

4. Свойства

5. Линейные операции над векторами

5.1. Сложение векторов

5.1.1. Сложение коллинеарных скользящих векторов

5.2. Произведение вектора на число

5.3. Скалярное произведение

5.4. Векторное произведение

5.5. Смешанное произведение

6. История

Литература

Смотрите также