���������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������зультат, известный также как «теорема о невозможности», Эрроу получил, выдвинув в качестве непременных условий выбора абсолютно естественные, даже ключевые признаки демократии. Эти условия сводятся к следующим положениям. Во-первых, выбор должен быть определён в той же системе, в которой сформулирована и сама альтернатива выбора (аксиома гомогенности). То есть если мы выбираем президента, то мы должны отдать предпочтение тому кандидату, который, по нашему мнению, лучше всех будет управлять страной, а не тому, который лучше всех выглядит (что было бы логично на конкурсе красоты).
Во-вторых, выбор должен зависеть от индивидуальных предпочтений голосующих и, кроме того, быть универсальным, то есть давать ответ при любых предпочтениях членов сообщества (аксиома универсальности). Первое предполагает, что если предпочтения части индивидов изменятся, то общественный выбор должен учесть эти изменения, второе помогает избегать замкнутых циклов.
В-третьих, при единогласном предпочтении одного варианта общественный выбор должен указывать на него (аксиома единогласия). То есть если все голосуют за Петрова, то избран должен быть он, а не Сидоров, за которого никто не отдал свой голос. (Как может получиться обратное, описано у Кондорсе)
И наконец, выбор не должен зависеть от посторонних альтернатив, не участвующих в выборе, т. е. избиратели должны определять свои предпочтения между избираемыми альтернативами, исходя только из качеств выбираемых вариантов, а не под давлением тех или иных групп влияния либо других, не имеющих отношения к выбору, факторов (аксиома независимости). Последнее, в частности, предполагает, что если надо выбрать между Петровым и Сидоровым, то голосующий руководствуется тем, какой из них двоих для него предпочтительнее, а не тем, что он, к примеру, голосовал бы за Иванова, если бы он был в числе альтернатив.
Как выяснил Эрроу, всем перечисленным условиям в совокупности отвечает только диктаторски, но не демократический выбор. Иными словами, нужно выбрать какого-нибудь произвольного члена общества и осуществлять общественный выбор в соответствии с предпочтениями этого «эталона». Других рациональных с точки зрения математической науки правил не существует.
Получается, что не существует рациональных правил общественного выбора, учитывающих мнение всех членов общества; другими словами, общественный выбор не может быть последовательно компромиссным.
Невозможность одновременного соблюдения требований разумности и равенства, невозможность эффективного ранжирования социальных приоритетов получила наименование теоремы невозможности, или теоремы Эрроу.
Теорема Эрроу отчасти объясняет, почему общепринятые правила общественного выбора — процедуры голосования — нетранзитивны, то есть если, например, голосующий предпочитает Иванова Петрову, а Петрова Сидорову, то вполне может случиться, что в результате голосования Сидоров займёт место выше Иванова.
studfiles.net
2.3 Теорема Эрроу о невозможности. Теория общественного выбора
Теория общественного выбора
курсовая работа Американский математик Кеннет Джордж Эрроу профессор Стэндфордского, Гарвардского и ряда других университетов, лауреат Нобелевской премии по экономике (1972г.) за пионерские работы в области теории общего экономического равновесия, заложил основы современной теории выбора, а его работа до сих пор определяет развитие этой теории.
В 1951г. Кеннет Эрроу, обобщив парадокс Кондорсе, доказал теорему о невозможности, суть которой состоит в том, что не существует правила коллективного выбора, способного одновременно удовлетворить следующие шесть требований:
Полнота. Правило должно обеспечивать выбор между любыми двумя альтернативами, отдавая предпочтение одной из них либо признавая обе равноценными.
Универсальность. Правило обеспечивает результативный выбор при любом сочетании индивидуальных предпочтений.
Транзитивность. Для любого набора из трех альтернатив x, y и z, если xRy и yRz, то xRz.
Единогласие. Если xRi y выполняется для любого i, т.е. все участники коллективного выбора отдают предпочтение первой из двух альтернатив, то xRy, иначе говоря, коллективный выбор совершается в пользу первой альтернативы (это не что иное, как выполнение требования Парето-оптимизации).
Независимость от посторонних альтернатив. Коллективный выбор между любыми двумя альтернативами x и y зависит от того, как индивиды оценивают эти две альтернативы по отношению друг к другу, но не зависят от отношения индивидов к какой бы то ни было посторонней альтернативе z, (например, будет ли признано xRy, может зависеть, в частности, от того, верно ли, что xRiy, но не от того, справедливо ли, что xRiz или что xRjzRjy).
Отсутствие диктатора. Среди участников коллективного выбора нет такого индивида, любое предпочтение которого xRjy влекло бы за собой xRy независимо от предпочтений всех других индивидов.
Введя понятие рационального выбора, можно сформулировать теорему иным образом: выбор является рациональным, если он отвечает требованиям полноты и транзитивности. Рациональность индивидуального выбора - одна из ключевых аксиом микроэкономики.
Решающая коалиция - совокупность индивидов, входящих в общее число участников коллективного выбора и при единогласии внутри этой коалиции позиция ее членов становится результатом коллективного выбора. Решающей коалиция может быть только для конкретной пары альтернативных вариантов (а против в). Коалиции, которые являются решающими для любой допустимой пары альтернатив, называются решающими без указания конкретной пары.
В своей теореме Эрроу доказал, что, если выполняются перечисленные выше шесть условий, то для произвольной пары альтернатив найдется решающая коалиция, состоящая из одного члена. Так же он доказал, что если коалиция состоящая их одного члена - решающая для некоторой пары х и у, то она является решающей для любой пары альтернатив а и в.
Принципиальное значение теоремы Эрроу заключается в том, она определяет ключевые предпосылки осуществимость или неосуществимости рационального демократического выбора. Условия теоремы допускают выбор между всевозможными Парето-оптимальными состояниями при самых разных профилях предпочтений, что влечет за собой улучшение положения одних индивидов за счет других, создает непримиримые конфликты и провоцирует формирование неустойчивых коалиций.
История демократических институтов достаточно четко говорит о том, их решения далеко не всегда лучше частных решений. Руководствуясь решением ареопага, афиняне осудили на смерть Сократа и едва не казнили Аристотеля. Единогласно принимались решения коллективного руководящего органа НАТО о начале операции в Югославии и политбюро СССР о вводе ограниченного контингента в Афганистан. При этом последствия этих решений и в настоящее время до конца не ясны.
Пытаясь ответить на вопрос о том, как на самом действует правило общественного выбора, Эрроу, введя очевидные и необременительные правила, пришел к поразительному выводу - всем перечисленным требованиям удовлетворяют только диктаторские правила.
Несуществование рационального правила общественного выбора, утверждаемое этой теоремой, означает, что рациональный общественный выбор не может быть достигнут в результате компромисса - так можно интерпретировать результат Эрроу.
Обобщая вышесказанное, можно сделать вывод, что теорема Эрроу позволяет понять, что безупречное демократическое устройство государства, при наличии разнонаправленных интересов практически не возможно. А при условии полного совпадения интересов, государство и его принуждающая сила были бы не востребованными.
polit.bobrodobro.ru
Теория общественного выбора - Курсовой проект стр. 3
одного кандидата другому. Подобным образом можно сравнить любых кандидатов.
В то же время, современник маркиза де Кондорсе шевалье Жан Шарль Борда еще во времена Великой французской революции высказал точку зрения, что никакого универсального способа выявления коллективных предпочтений нет и быть не может. Рассматривая множество разумных правил голосования (правила абсолютного и относительного большинства, правило отсеивания наихудших и т.д.), напрашивается вывод, что результаты могут быть прямо противоположными: победитель по одному из правил может оказаться худшим по другому. Видимо это и является одной из причин постоянного недовольства избирателей результатами любых голосований. Ведь довольно часто случается так, что, проголосовав по одной системе, результаты голосования люди часто оценивают, исходя из других, более выгодных для них принципов.
Таким образом, не следует переоценивать мнение большинства, так как результаты голосования могут быть абсолютно противоположными, что зависит от способа выражения этого мнения.
Любые правила дают возможность благодаря вполне законным манипуляциям, построенным с точным расчетом портфелей голосования, получить необходимый результат.
2.3 Теорема Эрроу о невозможности
Американский математик Кеннет Джордж Эрроу профессор Стэндфордского, Гарвардского и ряда других университетов, лауреат Нобелевской премии по экономике (1972г.) за пионерские работы в области теории общего экономического равновесия, заложил основы современной теории выбора, а его работа до сих пор определяет развитие этой теории.
В 1951г. Кеннет Эрроу, обобщив парадокс Кондорсе, доказал теорему о невозможности, суть которой состоит в том, что не существует правила коллективного выбора, способного одновременно удовлетворить следующие шесть требований:
Полнота. Правило должно обеспечивать выбор между любыми двумя альтернативами, отдавая предпочтение одной из них либо признавая обе равноценными.
Универсальность. Правило обеспечивает результативный выбор при любом сочетании индивидуальных предпочтений.
Транзитивность. Для любого набора из трех альтернатив x, y и z, если xRy и yRz, то xRz.
Единогласие. Если xRi y выполняется для любого i, т.е. все участники коллективного выбора отдают предпочтение первой из двух альтернатив, то xRy, иначе говоря, коллективный выбор совершается в пользу первой альтернативы (это не что иное, как выполнение требования Парето-оптимизации).
Независимость от посторонних альтернатив. Коллективный выбор между любыми двумя альтернативами x и y зависит от того, как индивиды оценивают эти две альтернативы по отношению друг к другу, но не зависят от отношения индивидов к какой бы то ни было посторонней альтернативе z, (например, будет ли признано xRy, может зависеть, в частности, от того, верно ли, что xRiy, но не от того, справедливо ли, что xRiz или что xRjzRjy).
Отсутствие диктатора. Среди участников коллективного выбора нет такого индивида, любое предпочтение которого xRjy влекло бы за собой xRy независимо от предпочтений всех других индивидов.
Введя понятие рационального выбора, можно сформулировать теорему иным образом: выбор является рациональным, если он отвечает требованиям полноты и транзитивности. Рациональность индивидуального выбора - одна из ключевых аксиом микроэкономики.
Решающая коалиция - совокупность индивидов, входящих в общее число участников коллективного выбора и при единогласии внутри этой коалиции позиция ее членов становится результатом коллективного выбора. Решающей коалиция может быть только для конкретной пары альтернативных вариантов (а против в). Коалиции, которые являются решающими для любой допустимой пары альтернатив, называются решающими без указания конкретной пары.
В своей теореме Эрроу доказал, что, если выполняются перечисленные выше шесть условий, то для произвольной пары альтернатив найдется решающая коалиция, состоящая из одного члена. Так же он доказал, что если коалиция состоящая их одного члена - решающая для некоторой пары х и у, то она является решающей для любой пары альтернатив а и в.
Принципиальное значение теоремы Эрроу заключается в том, она определяет ключевые предпосылки осуществимость или неосуществимости рационального демократического выбора. Условия теоремы допускают выбор между всевозможными Парето-оптимальными состояниями при самых разных профилях предпочтений, что влечет за собой улучшение положения одних индивидов за счет других, создает непримиримые конфликты и провоцирует формирование неустойчивых коалиций.
История демократических институтов достаточно четко говорит о том, их решения далеко не всегда лучше частных решений. Руководствуясь решением ареопага, афиняне осудили на смерть Сократа и едва не казнили Аристотеля. Единогласно принимались решения коллективного руководящего органа НАТО о начале операции в Югославии и политбюро СССР о вводе ограниченного контингента в Афганистан. При этом последствия этих решений и в настоящее время до конца не ясны.
Пытаясь ответить на вопрос о том, как на самом действует правило общественного выбора, Эрроу, введя очевидные и необременительные правила, пришел к поразительному выводу - всем перечисленным требованиям удовлетворяют только диктаторские правила.
Несуществование рационального правила общественного выбора, утверждаемое этой теоремой, означает, что рациональный общественный выбор не может быть достигнут в результате компромисса
www.studsell.com
Аксиомы и теорема невозможности Эрроу: VIKENT.RU
Аксиомы и «теорема о невозможности» Кеннета Эрроу
«Суть этой теоремы состоит в том, что любой коллективный выбор, удовлетворяющий вполне разумным аксиомам, может обеспечить наилучшую альтернативу лишь в том случае, если он содержит черты принудительности, или диктаторства. Теорема невозможности Эрроу очень остро поставила вопрос о природе экономической науки, а вместе с ней и экономической этики. Она имеет ограничительный характер, ибо выявляет границы состоятельности экономики».
Канке В.А., Философия науки: краткий энциклопедический словарь, М., «Омега-Л», 2008 г., с. 309.
«Кеннет Эрроу из Стенфордского университета поставил вопрос в наиболее общем виде: можно ли создать такую систему голосования, чтобы она была одновременно рациональной (без противоречий), демократической (один человек - один голос) и решающей (позволяла осуществить выбор)?
Вместо попыток изобретения такой системы Эрроу предложил набор требований, аксиом, которым эта система должна удовлетворять. Эти аксиомы были интуитивно понятны, приемлемы с точки зрения здравого смысла и допускали математическое выражение в виде некоторых условий.
На основе этих аксиом Эрроу попытался в общем виде доказать существование системы голосования, удовлетворяющей одновременно трём перечисленным выше принципам: рациональная, демократическая и решающая.
Первая аксиома Эрроу требует, чтобы система голосования была достаточно общей для того, чтобы учитывать все возможные распределения голосов избирателей. Интуитивно это требование вполне очевидно. Заранее нельзя предсказать распределение голосов. Совершенно необходимо, чтобы система была действенной при любых предпочтениях избирателей. Эта аксиома получила название аксиомы универсальности.
Ещё более очевидной с точки зрения здравого смысла является вторая аксиома Эрроу: аксиома единогласия, в соответствии с ней необходимо, чтобы коллективный выбор повторял в точности единогласное мнение всех голосующих. Если, например, каждый из голосующих считает, что кандидат А лучше кандидата В, то и система голосования должна приводить к этому результату.
Третья аксиома Эрроу получила название независимости от несвязанных альтернатив. Пусть избиратель считает, что из пары кандидатов А и В лучшим является А. Это предпочтение не должно зависеть от отношения избирателя к прочим кандидатам. Третья аксиома достаточно привлекательна, но не столь очевидна с точки зрения каждодневного человеческого поведения. Так, в одной из работ приводится убедительный пример нарушения этой аксиомы. Посетитель ресторана первоначально сравнивает блюдо А и В и хочет заказать А, потому что приготовление блюда В требует высокой квалификации повара, а , по его мнению, такой повар вряд ли есть в данном ресторане. Вдруг он замечает в меню блюдо С - очень дорогое и также требующее высокого искусства приготовления. Тогда он выбирает блюдо В, считая, что повар умеет хорошо готовить.
Часто третья аксиома Эрроу нарушается судьями в фигурном катании. Давая сравнительные оценки двум сильным фигуристам в одиночном катании, они стараются учесть возможность хорошего выступления третьего сильного кандидата, оставляя ему шансы стать победителем. Отличное выступление в произвольном катании фигуриста С, имевшего ранее не очень высокий результат в обязательной программе, может повлиять на оценки фигуристов А и В. Если А имел отличный результат в обязательной программе, судьи иногда ставят его ниже фигуриста В при примерно равном выступлении, чтобы повысить шансы фигуриста С.
Тем не менее, сама возможность предъявления требования независимости к системе голосования в качестве обязательного не вызывает сомнения.
Четвёртая аксиома Эрроу носит название аксиомы полноты: система голосования должна сравнить любую пару кандидатов, определив, кто из них лучше. При этом имеется возможность объявить двух кандидатов равнопривлекательными. Требование полноты не кажется слишком строгим для системы голосования.
Пятая аксиома Эрроу является уже знакомым условием - транзитивности: если в соответствии с мнением избирателей кандидат В не лучше кандидата А (хуже или эквивалентен), кандидат С не лучше кандидата В, то кандидат С не лучше кандидата А. Считается, что система голосования, не допускающая нарушения транзитивности, ведет себя рациональным образом.
Определив пять аксиом - желательных свойств системы голосования, Эрроу доказал, что системы, удовлетворяющие этим аксиомам, обладают недопустимым с точки зрения демократических свобод недостатком: каждая из них является правилом диктатора - личности, навязывающей всем остальным избирателям свои предпочтения.
Результаты, выявленные Эрроу, получили широкую известность. Они развеяли надежды многих экономистов, социологов, математиков найти совершенную систему голосования. Требование исключения диктатора приводит к невозможности создания системы голосования, удовлетворяющей всем аксиомам Эрроу.
Поэтому результат Эрроу называют «теоремой невозможности».
Ларичев О.И., Теория и методы принятия решений, М., «Логос», 2000 г., с.181-183.
vikent.ru
НОУ ИНТУИТ | Лекция | Теоремы Эрроу и Гиббарда-Саттертуэйта
Аннотация: В этой лекции мы будем рассматривать вопрос, который, на первый взгляд, даже не обязательно лежит в области экономики. Мы будем рассматривать голосования, возможные схемы голосований и то, к каким результатам они могут привести.
Голосования и наши главные цели
На самом деле, конечно, это частный, но вместе с тем одновременно и наиболее общий случай тех самых задач, которые мы решаем в этом курсе. Голосование — очень простой и естественный частный случай экономического механизма. У голосования есть множество возможных исходов, из которых участники должны выбрать; например, это кандидаты  ,
,  и
и  , из которых один должен стать президентом. У каждого участника голосования (агента) есть определенный порядок на этих исходах (нам будет достаточно случая, когда этот порядок линейный, то есть каждый исход сравним с каждым), который отражает его предпочтения. Например, кандидат
, из которых один должен стать президентом. У каждого участника голосования (агента) есть определенный порядок на этих исходах (нам будет достаточно случая, когда этот порядок линейный, то есть каждый исход сравним с каждым), который отражает его предпочтения. Например, кандидат  мне нравится больше, чем
мне нравится больше, чем  , а
, а  — больше, чем
— больше, чем  ; мы это будем обозначать через
; мы это будем обозначать через  . Этот порядок можно рассматривать как скрытую функцию предпочтений агента. И, наконец, есть некоторая функция социального выбора, которая определяет, какой кандидат должен бы победить при том или ином соотношении голосов.
. Этот порядок можно рассматривать как скрытую функцию предпочтений агента. И, наконец, есть некоторая функция социального выбора, которая определяет, какой кандидат должен бы победить при том или ином соотношении голосов.
Заметим, что этот частный случай вместе с тем оказывается и наиболее общим. Мы не предполагаем вообще никаких ограничений, никакой структуры на множестве предпочтений каждого из агентов; любой исход может оказаться на любом месте в его внутренней функции предпочтения. Поэтому результаты о невозможности, которые мы получим в этой лекции, окажутся весьма полезными в доказательстве результатов о невозможности в теории экономических механизмов, которыми мы будем заниматься в течение следующих трех лекций. Основным результатом станет теорема Эрроу, которая была доказана Кеннетом Эрроу в 1963 году [3].
Однако прежде всего нужно понять, что бы мы хотели получить от системы голосования. Каковы цели, которых мы будем (безуспешно) пытаться достигнуть?
Для этого рассмотрим достаточно простой и понятный случай голосования: случай, когда в нем участвует ровно один агент. Какими самыми базовыми, самыми естественными свойствами будет обладать множество предпочтений одного агента? Давайте сформулируем три основных свойства, три в высшей степени естественных предположения.
- Транзитивность. Это совершенно естественное свойство порядка: если
 и
и  , то
, то  . В примере, который приводился выше, мы даже не говорили отдельно, что в приведенной там ситуации кандидат
. В примере, который приводился выше, мы даже не говорили отдельно, что в приведенной там ситуации кандидат  нравится мне больше, чем
нравится мне больше, чем  : это было понятно по транзитивности.
: это было понятно по транзитивности. - Попарная независимость предпочтений. Это свойство утверждает, что мой выбор между
 и
и  зависит только от того, как соотносятся друг с другом
зависит только от того, как соотносятся друг с другом  и
и  в моем "персональном рейтинге", и никак не зависит от положения там других альтернатив
в моем "персональном рейтинге", и никак не зависит от положения там других альтернатив 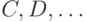 . Довольно естественно, правда ведь: если вам предлагают выбор между персиком и апельсином, ваши предпочтения насчет яблок не должны на этот выбор повлиять1.
. Довольно естественно, правда ведь: если вам предлагают выбор между персиком и апельсином, ваши предпочтения насчет яблок не должны на этот выбор повлиять1. - Положительная ассоциированность. Это значит, что если мои предпочтения изменились к лучшему для какой-либо альтернативы, то в результате голосования шансы этой альтернативы на победу могут только возрасти. Грубо говоря, если у меня раньше был профиль предпочтений
 , а сейчас
, а сейчас 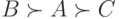 , то шансы
, то шансы  в любом голосовании, даже против
в любом голосовании, даже против  , не должны от этого ухудшиться.
, не должны от этого ухудшиться.
Наконец, четвертое свойство является по сути свойством функции социального выбора, а не свойством одного-единственного агента, как первые три. Мы его уже рассматривали в предыдущих лекциях.
- 4 Единогласие. Если все участники голосования предпочитают возможный исход
 другому возможному исходу
другому возможному исходу  , то в результате голосования не может быть выбран
, то в результате голосования не может быть выбран  . Это свойство нам хорошо знакомо; в более общем экономическом контексте оно называется оптимальностью по Парето (вспомните и проверьте, что это действительно она!).
. Это свойство нам хорошо знакомо; в более общем экономическом контексте оно называется оптимальностью по Парето (вспомните и проверьте, что это действительно она!).
Согласитесь, все эти свойства звучат абсолютно естественно, правда? Было бы очень странно, если бы система голосования не удовлетворяла этим свойствам. Один пример хорошей системы мы уже привели: система, в которой ровно один агент, удовлетворяет всем четырем свойствам.
Можно провести и менее тривиальный пример. Предположим, что возможных исходов всего два, то есть голосование превратилось в референдум. Тогда можно предложить простейшую систему голосования: выбирать нужную альтернативу большинством голосов. Рекомендуем читателю проверить, что выбор простым большинством из двух исходов удовлетворяет всем четырем интересующим нас свойствам.
Однако оказывается, что для трех и более возможных исходов голосования такую систему построить непросто. Подходящих механизмов голосования мало, и вряд ли существующие механизмы смогут удовлетворить поборников демократической процедуры, потому что непременно окажутся диктаторскими: результат голосования будет просто совпадать с предпочтениями какого-то одного его участника. Это и будет теорема Эрроу.
Но начнем мы с того, что продемонстрируем, почему естественные системы голосований оказываются беспомощными перед столь простыми условиями. Наше изложение будет в основном следовать [75].
Парадоксы голосований
В этом параграфе мы будем приводить примеры разного рода странных конструкций, которые, философски говоря, доказывают одну простую вещь: на свете не существует рационального "общего мнения группы людей". Есть мнение каждого конкретного человека. Но общее мнение, если пытаться его как-то более или менее "равномерно" вычислять из множества мнений членов интересующей нас группы, вообще никакими разумными свойствами обладать не будет. Формализуем мы это в теореме Эрроу, а в этом параграфе дадим важную интуицию.
Первый пример восходит аж к XVIII веку. В 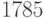 году маркиз де Кондорсе придумал конструкцию парадокса, который под его именем вошел в политическую и экономическую теорию. Идея парадокса Кондорсе проста: рассмотрим три возможных исхода
году маркиз де Кондорсе придумал конструкцию парадокса, который под его именем вошел в политическую и экономическую теорию. Идея парадокса Кондорсе проста: рассмотрим три возможных исхода  ,
,  и
и  и трех участников
и трех участников  ,
,  и
и  . Предположим, что их предпочтения распределены так:
. Предположим, что их предпочтения распределены так:
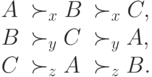
Иначе говоря, предпочтения трех участников получаются циклическим сдвигом одного линейного порядка.
Что будет происходить при голосованиях? Если на выбор предложат  и
и  , то
, то  и
и  проголосуют за
проголосуют за  , и будет избран
, и будет избран  :
:  . Если референдум пройдет между
. Если референдум пройдет между  и
и  , то победа альтернативы
, то победа альтернативы  будет обеспечена голосованием агентов
будет обеспечена голосованием агентов  и
и  :
:  . Но если предложат выбор между
. Но если предложат выбор между  и
и  , то
, то  и
и  проголосуют за
проголосуют за  , и окажется, что
, и окажется, что  ! В парадоксе Кондорсе нарушается транзитивность "мнения большинства".
! В парадоксе Кондорсе нарушается транзитивность "мнения большинства".
Давайте посмотрим на это с точки зрения дизайна механизмов. Как построить механизм голосования, который примет верное решение? Да и что вообще такое в данном случае "верное решение"? Вполне естественным может показаться механизм, который последовательно осуществляет референдумы, голосования с двумя исходами, до тех пор, пока (в предположении транзитивности, разумеется) не получит достаточно информации для выбора оптимального исхода. На парадоксе Кондорсе такой алгоритм может работать бесконечно (или выдавать ошибку): сколько ни ходи по кругу, единого оптимального выбора не сделаешь.
Но этим дело не ограничивается. Здесь пока кажется, что вообще все равно, какой выбор делать: все три варианта абсолютно симметричны, так что какая разница функции социального выбора, какой из них предпочесть. Давайте рассмотрим небольшую модификацию парадокса Кондорсе, на которой результаты алгоритма попарного голосования окажутся еще интереснее. Для примера нам потребуются аж семь альтернатив, поэтому давайте назовем их как-нибудь поинтереснее, не просто буквами латинского алфавита.
Пример 6.1. Семеро великих вождей собираются в поход на семивратные Фивы. Собираются в поход двое изгнанников — Тидей и Полиник, собирается царь Адраст, двое аргивских вождей — Капаней и Гиппомедонт, ясновидец Амфиарай и аркадец Парфенопей2
А в это время на Олимпе Гера, Афина и Артемида решают, кого из семи вождей сделать своим любимцем, кому больше других поспособствовать при осаде Фив. Предпочтения богинь весьма замысловаты. Вот они (в таблице сверху вниз степень предпочтения убывает).
Гера Афина Артемида
| Тидей | Капаней | Гиппомедонт |
| Полиник | Гиппомедонт | Тидей |
| Капаней | Тидей | Парфенопей |
| Гиппомедонт | Амфиарай | Полиник |
| Адраст | Парфенопей | Капаней |
| Амфиарай | Полиник | Адраст |
| Парфенопей | Адраст | Амфиарай |
В лучших традициях древнегреческой демократии богини согласились решить дело голосованием. Они начали устанавливать общий порядок поочередными голосованиями. И вот что у них получилось...
- Тидей против Гиппомедонта: Гера в меньшинстве, Гиппомедонт идет дальше.
- Гиппомедонт против Капанея: Гера и Афина проводят дальше Капанея.
- Капаней против Полиника: Полиник побеждает и проходит в следующий бой.
- Полиник против Парфенопея: несмотря на то, что Гере Парфенопей ну совсем не мил, он побеждает.
- Парфенопей против Амфиарая: выигрывает Амфиарай.
- Амфиарай против Адраста: Адраст побеждает, Афина в меньшинстве.
В результате не просто Афина оказалась в меньшинстве в последнем голосовании, а как будто мудрость в этом голосовании и вовсе не ночевала. Богини медленно, но верно спускались вниз по таблице, хотя на каждом шаге делали выбор большинством (можно сказать, конституционным большинством — две трети набиралось). В результате победил царь Адраст, хотя в изначальных предпочтениях и Тидей, и Полиник, и Капаней, и Гиппомедонт у всех трех богинь стояли выше Адраста.
Таким образом, в этом примере голосование привело к тому, что нарушился принцип единогласия; вполне честным и естественным протоколом мы выбрали вариант, не оптимальный по Парето (причем ну совсем далеко не оптимальный).
Конец примера 6.1.
Но и на этом интересные следствия парадокса Кондорсе не заканчиваются. Давайте подумаем: какие вообще были варианты у наших голосований? Предположим, что мы хотим пока ограничиться выбором между двумя альтернативами. Таким образом, голосование получается двухступенчатым: сначала две альтернативы сражаются друг с другом, потом победитель с третьей. Рассмотрим возможные варианты для классического парадокса Кондорсе (см. рис. 6.1).
 Рис. 6.1. Парадокс Кондорсе: как результат зависит от порядка
Рис. 6.1. Парадокс Кондорсе: как результат зависит от порядка-
 побеждает
побеждает  , затем
, затем  побеждает
побеждает  . Выигрывает
. Выигрывает  (рис. 6.1а).
(рис. 6.1а). -
 побеждает
побеждает  , затем
, затем  побеждает
побеждает  . Выигрывает
. Выигрывает  (рис. 6.1б).
(рис. 6.1б). -
 побеждает
побеждает  , затем
, затем  побеждает
побеждает  . Выигрывает
. Выигрывает  (рис. 6.1в).
(рис. 6.1в).
Получается, что результат при одних и тех же предпочтениях кардинально зависит от формата голосования! А значит, тот, кто контролирует формат голосования (а в реальных ситуациях его обычно кто-то контролирует), имеет существенное преимущество и может победить, даже оказавшись в меньшинстве.
Более того, эта зависимость от формата приводит к тому, что попарная независимость предпочтений в этом случае тоже не выполняется. Давайте рассмотрим простую ситуацию, в которой есть ровно две альтернативы:  и
и  , причем большинство хочет выбрать
, причем большинство хочет выбрать  . Тогда простым большинством, конечно,
. Тогда простым большинством, конечно,  без проблем выберут. Но если у меньшинства получится построить такую третью возможность
без проблем выберут. Но если у меньшинства получится построить такую третью возможность  , что при выборах
, что при выборах  и
и  , то это самое меньшинство сможет, установив правильный порядок выборов (сначала
, то это самое меньшинство сможет, установив правильный порядок выборов (сначала  против
против  , затем
, затем  против победителя), провести
против победителя), провести  , а не
, а не  .
.
Пример 6.2. В политике такие ситуации редко, но действительно возникают на практике. Они называются "поправки-убийцы" (killer amendments). Вот любопытный пример из практики [75].
В США сенаторов поначалу выбирали не прямым всенародным голосованием, а законодательными органами соответствующего штата. В том, чтобы ввести голосования на пост сенатора, заключалась 17-я поправка к Конституции США, которая в конце концов все же была принята в 1913. Но на пути к ее принятию был один любопытный случай.
Проблема заключалась в том, что в те годы в США Юг и Север все еще не слишком любили друг друга, и южные сенаторы беспокоились, что если федеральное ("северное") государство возьмет выборы сенаторов под свой контроль, то северяне-республиканцы сделают что-нибудь ужасное, например допустят на выборы чернокожих — и действительно, некоторые республиканцы так и собирались сделать.
Был достигнут компромисс: билль, который вводил прямые выборы сенаторов, но содержал поправки, ограничивающие контроль федерального правительства над выборами в южных штатах. Его поддерживало большинство (это была возможность  ), и на прямом голосовании между этим биллем и тем, чтобы вообще не вводить прямые выборы (возможность
), и на прямом голосовании между этим биллем и тем, чтобы вообще не вводить прямые выборы (возможность  ), билль бы прошел.
), билль бы прошел.
Однако сенатор Сазерленд, лидер меньшинства, которое было против выборов сенаторов как таковых, сумел придумать поправку-убийцу  . Таковой стало предложение о прямых выборах сенаторов без каких-либо поправок про южные штаты. Сазерленд устроил дело так, что сначала голосование шло между
. Таковой стало предложение о прямых выборах сенаторов без каких-либо поправок про южные штаты. Сазерленд устроил дело так, что сначала голосование шло между  и
и  . Меньшинство Сазерленда проголосовало за
. Меньшинство Сазерленда проголосовало за  , северяне-республиканцы тоже проголосовали за
, северяне-республиканцы тоже проголосовали за  , и
, и  победило
победило  . Но на этом дело не закончилось: затем встал выбор между
. Но на этом дело не закончилось: затем встал выбор между  и
и  . Сазерленд внезапно "изменил свою точку зрения" и стал голосовать не за
. Сазерленд внезапно "изменил свою точку зрения" и стал голосовать не за  , а за
, а за  , то есть против выборов совсем. В результате билль
, то есть против выборов совсем. В результате билль  сначала выполнил свою функцию и выбил поддерживаемый большинством билль
сначала выполнил свою функцию и выбил поддерживаемый большинством билль  , а затем не прошел на следующих выборах. Получилась ситуация, изображенная на рис. 6.2 сплошными линиями, вместо ситуации, изображенной там же пунктиром.
, а затем не прошел на следующих выборах. Получилась ситуация, изображенная на рис. 6.2 сплошными линиями, вместо ситуации, изображенной там же пунктиром.
 Рис. 6.2. Поправка сенатора Сазерленда
Рис. 6.2. Поправка сенатора СазерлендаКонец примера 6.2.
Этот же пример демонстрирует, что правдивости при таких выборах тоже лучше не ждать: меньшинство, стоявшее против выборов вообще, здесь было вынуждено сначала голосовать за них, чтобы затем иметь возможность провалить этот исход на следующих выборах. И он же показывает, что попарная независимость тоже недоступна: ведь по этому свойству выбор между  и
и  не должен зависеть от наличия или отсутствия третьей альтернативы
не должен зависеть от наличия или отсутствия третьей альтернативы  .
.
Но отсутствие попарной независимости, а также еще более интересный эффект, можно проиллюстрировать и более наглядно.
Пример 6.3. В этом примере мы попробуем "повыбирать" президента Российской Федерации. Делать это мы будем так, как это и делается в реальности: в первом туре участвуют все кандидаты, и если никто не набирает больше 50%, то двое лидеров выходят во второй тур. Предположим, что у нас есть три кандидата на высокий пост и 27 избирателей, чьи предпочтения распределены следующим образом. Цифры в таблице показывают, на какое место ставят данного кандидата эти избиратели, а число в первой строке — сколько избирателей так думают.
К-во избирателей 6 6 6 4 2 3
| Барсуков | 1 | 2 | 3 | 2 | 3 | 1 |
| Гризлев | 2 | 3 | 1 | 1 | 2 | 3 |
| Углеводский | 3 | 1 | 2 | 3 | 1 | 2 |
В первом туре Барсуков наберет 9 голосов, Углеводский — 8, а Гризлев — 10. Однако во втором туре ситуация изменится, и победит Барсуков, набрав 15 голосов против 12 у Гризлева. Пока все нормально.
Предположим, однако, что Барсуков, пытаясь победить Гризлева в первом туре, сумел воздействовать на сердца некоторых избирателей, и они изменили свои предпочтения между Гризлевым и Барсуковым в пользу последнего: трое из четырех с распределением 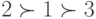 переместили Барсукова на первое место, а двое с распределением
переместили Барсукова на первое место, а двое с распределением 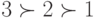 изменили его на
изменили его на 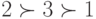 . Итого получается следующая таблица:
. Итого получается следующая таблица:
К-во избирателей 9 8 6 1 3
| Барсуков | 1 | 2 | 3 | 2 | 1 |
| Гризлев | 2 | 3 | 1 | 1 | 3 |
| Углеводский | 3 | 1 | 2 | 3 | 2 |
Согласитесь, что все это, казалось бы, может быть только в пользу Барсукова. Но... В первом туре Барсуков действительно выигрывает с большим отрывом, получив 12 голосов. Однако во второй тур теперь выходит не Гризлев, а Углеводский, который в итоге побеждает Барсукова с счетом  .
.
Иначе говоря, Барсуков сделал распределение строго лучше для себя, но в итоге сменил победу на поражение. И все это во вполне естественной системе голосования, по которой действительно выбирают президента РФ... \
Конец примера 6.3.
Итак, мы показали, что если пытаться сформулировать более или менее естественную систему голосования, совершенно ничего не получается, вообще ни одного естественного и крайне желательного свойства. Конечно, это еще не доказательство: возможно, мы просто не смогли придумать правильную систему голосования?
Доказательство будет в следующем параграфе.
www.intuit.ru
|
|
|
|
|
|
|
|
|
|
.
 ,
,  и
и  , из которых один должен стать президентом. У каждого участника голосования (агента) есть определенный порядок на этих исходах (нам будет достаточно случая, когда этот порядок линейный, то есть каждый исход сравним с каждым), который отражает его предпочтения. Например, кандидат
, из которых один должен стать президентом. У каждого участника голосования (агента) есть определенный порядок на этих исходах (нам будет достаточно случая, когда этот порядок линейный, то есть каждый исход сравним с каждым), который отражает его предпочтения. Например, кандидат  мне нравится больше, чем
мне нравится больше, чем  , а
, а  — больше, чем
— больше, чем  ; мы это будем обозначать через
; мы это будем обозначать через  . Этот порядок можно рассматривать как скрытую функцию предпочтений агента. И, наконец, есть некоторая функция социального выбора, которая определяет, какой кандидат должен бы победить при том или ином соотношении голосов.
. Этот порядок можно рассматривать как скрытую функцию предпочтений агента. И, наконец, есть некоторая функция социального выбора, которая определяет, какой кандидат должен бы победить при том или ином соотношении голосов. и
и  , то
, то  . В примере, который приводился выше, мы даже не говорили отдельно, что в приведенной там ситуации кандидат
. В примере, который приводился выше, мы даже не говорили отдельно, что в приведенной там ситуации кандидат  . Довольно естественно, правда ведь: если вам предлагают выбор между персиком и апельсином, ваши предпочтения насчет яблок не должны на этот выбор повлиять1.
. Довольно естественно, правда ведь: если вам предлагают выбор между персиком и апельсином, ваши предпочтения насчет яблок не должны на этот выбор повлиять1. , то шансы
, то шансы 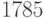 году маркиз де Кондорсе придумал конструкцию парадокса, который под его именем вошел в политическую и экономическую теорию. Идея парадокса Кондорсе проста: рассмотрим три возможных исхода
году маркиз де Кондорсе придумал конструкцию парадокса, который под его именем вошел в политическую и экономическую теорию. Идея парадокса Кондорсе проста: рассмотрим три возможных исхода  ,
,  и
и  . Предположим, что их предпочтения распределены так:
. Предположим, что их предпочтения распределены так: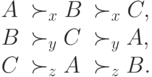
 ! В парадоксе Кондорсе нарушается транзитивность "мнения большинства".
! В парадоксе Кондорсе нарушается транзитивность "мнения большинства". Рис. 6.1. Парадокс Кондорсе: как результат зависит от порядка
Рис. 6.1. Парадокс Кондорсе: как результат зависит от порядка Рис. 6.2. Поправка сенатора Сазерленда
Рис. 6.2. Поправка сенатора Сазерленда переместили Барсукова на первое место, а двое с распределением
переместили Барсукова на первое место, а двое с распределением 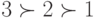 изменили его на
изменили его на 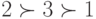 . Итого получается следующая таблица:
. Итого получается следующая таблица: .
.