Методические указания предназначены для студентов дневного и вечернего отделения факультета №14 специальностей 150601, 160301, 230102. Указания выделяют основные понятия темы, определяют последовательность изучения материала. Большое количество рассмотренных примеров помогает в практическом освоении темы. Методические указания служат методической основой для практических занятий и выполнения индивидуальных заданий.

СХЕМА БЕРНУЛЛИ. ФОРМУЛА БЕРНУЛЛИ

Схема Бернулли - схема повторных независимых испытаний, при которой какое-то событие А может многократно повторяться с постоянной вероятностью Р(А)=р.

Примеры испытаний, проводимых по схеме Бернулли: многократное подбрасывание монеты или игральной кости, изготовление партии деталей, стрельба по мишени и т.п.

Теорема. Если вероятность наступления события А в каждом испытании постоянна и равна р, то вероятность того, что событие А наступит m раз в n испытаниях (безразлично в какой последовательности), можно определить по формуле Бернулли:

или

где q = 1 – p.

ПРИМЕР 1. Вероятность того, что расход электроэнергии на протяжении одних суток не превысит установленной нормы, равна р=0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.

РЕШЕНИЕ. Вероятность нормального расхода электроэнергии на протяжении каждых из 6 суток постоянна и равна р = 0,75. Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна q = 1р = 1  0,75 = 0,25.

Искомая вероятность по формуле Бернулли равна:

ПРИМЕР 2. Стрелок производит по мишени три выстрела. Вероятность попадания в мишень при каждом выстреле равна р=0,3. Найти вероятность того, что поражена: а) одна мишень; б) все три мишени; в) ни одной мишени; г) хотя бы одна мишень; д) менее двух мишеней.

РЕШЕНИЕ. Вероятность попадания в мишень при каждом выстреле постоянна и равна р=0,75. Следовательно, вероятность промаха равна q = 1 р = 1  0,3= 0,7. Общее число проведенных опытов n=3.

а) Вероятность поражения одной мишени при трех выстрелах равна:

б) Вероятность поражения всех трех мишеней при трех выстрелах равна:

в) Вероятность трех промахов при трех выстрелах равна:

г) Вероятность поражения хотя бы одной мишени при трех выстрелах равна:

или:

д) Вероятность поражения менее двух мишеней, то есть или одной мишени, или ни одной:

Локальная и интегральная теоремы муавра-лапласа

Если произведено большое число испытаний, то вычисление вероятностей по формуле Бернулли становится технически сложным, так как формула требует действий над огромными числами. Поэтому существуют более простые приближенные формулы для вычисления вероятностей при больших n. Эти формулы называются асимптотическими и определяются теоремой Пуассона, локальной и интегральной теоремой Лапласа.

Локальная теорема Муавра-Лапласа. Если вероятность наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие А произойдет m раз в n испытаниях при достаточно большом числе n (n→∞), приближенно равна:

где функция а аргумент

Чем больше n, тем точнее вычисление вероятностей. Поэтому теорему Муавра-Лапласа целесообразно применять при npq20.

Для нахождения значений функции f(x) составлены специальные таблицы (см. приложение 1). При использовании таблицы необходимо иметь в виду свойства функции f(x):

Функция f(x) является четной f(x)= f(x).
При х∞ функция f(x)0. Практически можно считать, что уже при х>4 функция f(x)≈0.

ПРИМЕР 3. Найти вероятность того, что событие А наступит 80 раз в 400 испытаниях, если вероятность появления события А в каждом испытании равна р=0,2.

РЕШЕНИЕ. По условию n=400, m=80, p=0,2, q=0,8. Следовательно:

По таблице определим значение функции f(0)=0,3989.

Интегральная теорема Муавра-Лапласа. Если вероятность наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие А произойдет от m1 до m2 раз в n испытаниях при достаточно большом числе n (n→∞), приближенно равна:

где  интеграл или функция Лапласа,

Для нахождения значений функции Ф(x) составлены специальные таблицы (например, см. приложение 2). При использовании таблицы необходимо иметь в виду свойства функции Лапласа Ф(x):

Функция Ф(x) является нечетной Ф(x)= Ф(x).
При х∞ функция Ф(x)0,5. Практически можно считать, что уже при х>5 функция Ф(x)≈0,5.
Ф(0)=0.

ПРИМЕР 4. Вероятность того, что деталь не прошла проверку ОТК, равна 0,2. Найти вероятность того, что среди 400 деталей окажется непроверенных от 70 до 100 деталей.

РЕШЕНИЕ. По условию n=400, m1=70, m2=100, p=0,2, q=0,8. Следовательно:

По таблице, в которой приведены значения функции Лапласа, определяем:

Ф(x1)=Ф(1,25)=Ф(1,25)=0,3944; Ф(x2)=Ф(2,5)=0,4938.

Тогда:

studfiles.net

Повторение испытаний. Схема бернулли

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение

высшего профессионального образования

«МАТИ»  РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. К.Э. ЦИОЛКОВСКОГО

Кафедра «Моделирование систем и информационные технологии»

Методические указания к практическим занятиям

по дисциплине «Высшая математика»

Составители: Егорова Ю.Б.

Мамонов И.М.

Москва 2006 введение

СХЕМА БЕРНУЛЛИ. ФОРМУЛА БЕРНУЛЛИ

или

где q = 1 – p.

Искомая вероятность по формуле Бернулли равна:

а) Вероятность поражения одной мишени при трех выстрелах равна:

б) Вероятность поражения всех трех мишеней при трех выстрелах равна:

в) Вероятность трех промахов при трех выстрелах равна:

г) Вероятность поражения хотя бы одной мишени при трех выстрелах равна:

или:

д) Вероятность поражения менее двух мишеней, то есть или одной мишени, или ни одной:

Локальная и интегральная теоремы муавра-лапласа

где функция а аргумент

Функция f(x) является четной f(x)= f(x).
При х∞ функция f(x)0. Практически можно считать, что уже при х>4 функция f(x)≈0.

РЕШЕНИЕ. По условию n=400, m=80, p=0,2, q=0,8. Следовательно:

По таблице определим значение функции f(0)=0,3989.

где  интеграл или функция Лапласа,

Функция Ф(x) является нечетной Ф(x)= Ф(x).
При х∞ функция Ф(x)0,5. Практически можно считать, что уже при х>5 функция Ф(x)≈0,5.
Ф(0)=0.

РЕШЕНИЕ. По условию n=400, m1=70, m2=100, p=0,2, q=0,8. Следовательно:

По таблице, в которой приведены значения функции Лапласа, определяем:

Ф(x1)=Ф(1,25)=Ф(1,25)=0,3944; Ф(x2)=Ф(2,5)=0,4938.

Тогда:

studfiles.net

Повторные независимые испытания. Формула Бернулли

Рассмотрим случай многократного повторения одного и того же испытания или случайного эксперимента. Результат каждого испытания будем считать не зависящим от того, какой результат наступил в предыдущих испытаниях. В качестве результатов или элементарных исходов каждого отдельного испытания будем различать лишь две возможности:

1) появление некоторого события А;

2) появление события , (события, являющегося дополнением А)

Пусть вероятность P(A) появления события А постоянна и равна p (0<.p<1). Вероятность P() события обозначим через q: P() = 1– p=q.

Примерами таких испытаний могут быть:

Возможно вы искали - Реферат: Случайный эксперимент, элементарные исходы, события

1) подбрасывание монеты: А – выпадение герба; – выпадение цифры.

P(A) = P() = 0,5.

2) бросание игральной кости: А – выпадение количества очков, равного пяти, выпадение любого количества очков кроме пяти.

P(A) =1/6, P() =5/6.

3) извлечение наудачу из урны, содержащей 7 белых и 3 черных шара, одного шара (с возвращением): А – извлечение белого шара, – извлечение черного шара

Похожий материал - Реферат: Интуитивное понятие алгоритма и его свойств

P(A) = 0,7; P() = 0,3

Пусть произведено n испытаний, которые мы будем рассматривать как один сложный случайный эксперимент. Составим таблицу из n клеток, расположенных в ряд, пронумеруем клетки, и результат каждого испытания будем отмечать так: если в i-м испытании событие А произошло, то в i-ю клетку ставим цифру 1, если событие А не произошло (произошло событие ), в i-ю клетку ставим 0.

Если, например, проведено 5 испытаний, и событие А произошло лишь во 2-м и 5-м испытаниях, то результат можно записать такой последовательностью нулей и единиц: 0; 1; 0; 0; 1.

Каждому возможному результату n испытаний будет соответствовать последовательность n цифр 1 или 0, чередующихся в том порядке, в котором появляются события A и в n испытаниях, например:

1; 1; 0; 1; 0; 1; 0; 0; ... 0; 1; 1; 0

Очень интересно - Курсовая работа: Поиск и исследование внеземных форм жизни. Планетарный карантин, необходимый при этом

14444442444443

n цифр

Всего таких последовательностей можно составить (это читатель может доказать сам).

Так как испытания независимы, то вероятность P каждого такого результата определяется путем перемножения вероятностей событий A и в соответствующих испытаниях. Так, например, для написанного выше результата найдем

P = p×p×q×p×q×p×q×q×...×q×p×p×q

Вам будет интересно - Статья: О реализации дискретных состояний в ходе флуктуаций в макоскопических процессах

Если в написанной нами последовательности единица встречается х раз (это значит, что нуль встречается n–x раз), то вероятность соответствующего результата будет pn qn-x независимо от того, в каком порядке чередуются эти x единиц и n–x нулей.

Все события, заключающиеся в том, что в n испытаниях событие A произошло x раз, а событие произошло n-x раз, являются несовместными. Поэтому для вычисления вероятности объединения этих событий (или суммы этих событий), нужно сложить вероятности всех этих событий, каждая из которых равна pn qn-x . Всего таких событий можно насчитать столько, сколько можно образовать различных последовательностей длины n, содержащих x цифр "1" и n–x цифр "0". Таких последовательностей получается столько, сколькими способами можно разместить x цифр "1" (или n–x цифр "0") на n местах, то есть число этих последовательностей равно

Отсюда получается формула Бернулли:

Pn (x) =

По формуле Бернулли рассчитывается вероятность появления события A "x" раз в n повторных независимых испытаниях, где p – вероятность появления события A в одном испытании, q - вероятность появления события в одном испытании.

Похожий материал - Реферат: История геометрии

Сформулированные условия проведения испытаний иногда называются "схемой повторных независимых испытаний" или "схемой Бернулли"

Число x появления события A в n повторных независимых испытаниях называется частотой.

Пример. Из урны, содержащей 2 белых и 6 черных шаров, наудачу выбирается с возвращением 5 раз подряд один шар. Подсчитать вероятность того, что 4 раза появится белый шар.

В приведенных выше обозначениях n=8; p=1/4; q=3/4; x=5. Искомую вероятность вычисляем по формуле Бернулли:

К-во Просмотров: 249

Бесплатно скачать Реферат: Повторные независимые испытания. Формула Бернулли

cwetochki.ru

Схемы Бернулли повторных испытаний — Информио

Аннотация: Рассмотрены на примерах Схемы Бернулли повторных испытаний из теории вероятностей, механизмы ее действия и применения в жизни.

Ключевые слова: Теория вероятностей, схемы Бернулли.

Людей всегда интересовало будущее. Человечество во все времена искало способ его предугадать или спланировать: в разное время разными способами. В современном мире есть теория, которую наука признает и пользуется для планирования и прогнозирования будущего. Речь о теории вероятностей.

Теория вероятностей - это математическая наука, изучающая закономерности в случайных явлениях. На сегодняшний день это полноценная наука, имеющая большое практическое значение.

В жизни мы часто сталкиваемся со случайными явлениями. Чем обусловлена их случайность - нашим незнанием истинных причин происходящего или случайность лежит в основе многих явлений? Споры на эту тему не утихают в самых разных областях науки. Случайным ли образом возникают мутации, насколько зависит историческое развитие от отдельной личности, можно ли считать Вселенную случайным отклонением от законов сохранения? Пуанкаре, призывая разграничить случайность, связанную с неустойчивостью, от случайности, связанной с нашим незнанием, приводил следующий вопрос: «Почему люди находят совершенно естественным молиться о дожде, в то время как они сочли бы смешным просить в молитве о затмении?»

У каждого «случайного» события есть четкая вероятность его наступления. В стабильной системе вероятность наступления событий сохраняется из года в год. То есть с точки зрения человека с ним произошло случайное событие, а с точки зрения системы оно было предопределенно.

Разумный человек должен стремиться мыслить, исходя из законов вероятностей (статистики). Но в жизни о вероятности мало кто думает. Решения принимаются эмоционально. Люди боятся летать самолетами. А между тем, самое опасное в полете на самолете - это дорога в аэропорт на автомобиле. Но попробуй кому-то объяснить, что машина опасней самолета. Вероятность того, что пассажир, севший в самолет погибнет в авиакатастрофе составляет примерно 1/8 000 000. Если пассажир будет садиться каждый день на случайный рейс, ему понадобится 21 000 лет чтобы погибнуть.

Согласно исследованиям, в США в первые 3 месяца после терактов 11 сентября 2001 года погибло еще одна тысяч людей косвенно. Они в страхе перестали летать самолетами и начали передвигаться по стране на автомобилях. А так как это опасней, то количество смертей возросло. Миром правит вероятность и нужно помнить об этом. Они помогут вам взглянуть на мир с точки зрения случая.

Существует мнение, что решающее влияние на возникновение теории вероятностей оказали азартные игры. Действительно, карты, рулетка, игральные кости, различные лотереи издавна привлекали внимание определенных кругов общества.

Возникновение теории вероятностей как науки относится к середине XVII столетия, когда усилиями Паскаля, Ферма, Гюйгенса были введены специфические понятия и доказаны простейшие теоремы о вероятностях случайных событий.

Важный этап в развитие теории вероятностей связан с именем Я. Бернулли. Теорема, которая носит ныне его имя, вскрывает следующую важную особенность вероятностных задач: рассмотрению подлежат лишь те опыты со случайными исходами, которые независимо друг от друга могут быть повторены любое число раз в одинаковых условиях. Для определенности будем говорить о подбрасываниях монеты. Каждое отдельное подбрасывание монеты приводит к непредсказуемому исходу: выпадает либо герб, либо решка. Если число гербов, выпадающих при n бросаниях монеты, то непредсказуемой является и частота выпадений герба. Однако с ростом n эта непредсказуемость ослабевает: наблюдаемые значения величины имеют тенденцию группироваться около числа 0,5. Отмеченный принцип устойчивости частот выражает одну из важнейших закономерностей случайных явлений.

Своей знаменитой теоремой Бернулли дал математическое истолкование принципа устойчивости частот и закрепил за теорией вероятностей право называться наукой о математических методах изучения закономерностей случайных явлений.

Вероятность события в жизни не так уж часто считается по формулам, скорее интуитивно. Но проверить, совпадает ли «эмпирический анализ» с математическим, иногда очень полезно. Выбранная мною тема актуальна, т.е. практически полезная и представляет интерес в научном отношении.

Выбирая данную тему, я руководствовался несколькими правилами: тема очень интересна, увлекательна, соответствует моей склонности к изучению «Теории вероятностей», данная тема выполнима, решение ее принесёт реальную пользу (получение новых полезных знаний, умений, навыков, развитие интеллекта, реализация исследовательской потребности). Тема оригинальна, в ней есть элемент неожиданности, необычности, способности нестандартно смотреть на традиционные предметы и явления.

При практическом применении теории вероятностей часто приходится встречаться с задачами, в которых одно и то же испытание повторяется неоднократно. В результате каждого испытания может появиться или не появиться некоторое событие А. Причем нас интересует не результат каждого отдельного испытания, а общее число появлений события А в результате серии опытов. Например, если производится группа выстрелов по одной и той же цели, нас, как правило, не интересует результат каждого выстрела, а лишь общее число попаданий. В подобных задачах требуется уметь определять вероятность любого заданного числа появлений события в результате серии опытов. Такие задачи и будут рассмотрены. Они решаются весьма просто в случае, когда испытания являются независимыми.

Испытания называются независимыми, если вероятность того или иного исхода каждого из испытаний не зависит от того, какие исходы имели другие испытания. Например, несколько бросаний монеты представляют собой независимые испытания.

Актуальность темы «Схемы Бернулли повторных испытаний» рассмотрим на примерах из теории вероятностей, механизмы ее действия и применения в жизни, так как очень много процессов в нынешнее время решаются с помощью схем Бернулли.

Я решил проверить классическое определение вероятности.

Определение: «Пусть множество исходов опыта состоит из n равновероятных исходов. Если m из них благоприятствуют событию A, то вероятностью события A называется число Р(А) = m/n.»

Возьмем, к примеру, игру в монету. При бросании может быть два равновероятных исхода: монета может упасть кверху гербом или решкой. Бросая монету один раз нельзя предугадать, какая сторона окажется сверху. Однако, бросив монету 100 раз, можно сделать выводы. Можно заранее сказать, что герб выпадет не 1 и не 2 раза, а больше, но и не 99 и не 98 раз, а меньше. Число выпадений герба будет близко к 50. На самом деле, и на опыте можно в этом убедиться, что это число будет заключено между 40 и 60. Кто и когда впервые проделал опыт с монетой, неизвестно.

Проведём опыт. Для начала, возьмем в руки монетку, будем ее бросать и записывать результат последовательно в виде строки: О, Р, Р, О, О, Р. Здесь буквами О и Р обозначено выпадение орла или решки. В нашем случае бросание монетки - это испытание, а выпадение орла или решки - событие, то есть возможный исход нашего испытания. В процессе проведения 100 испытаний орел выпал 55 раз, решка - 45. Вероятность выпадения орла в данном случае-0,55; решки – 0,45. Таким образом, я показал, что теория вероятности в данном случае имеет место быть.

Можно ли выиграть в лотерею или рулетку?

Каждый из нас хоть раз в жизни покупал лотерею или играл в азартные игры, но далеко не все использовали заранее спланированную стратегию. Умные игроки давно перестали надеяться на удачу и включили рациональное мышление.

Дело в том, что каждое событие имеет определенное математическое ожидание, как гласят высшая математика и теория вероятности, и, если правильно оценивать ситуацию, то можно обойти неудовлетворительный исход события.

Повторные независимые испытания называются испытаниями Бернулли, если каждое испытание имеет только два возможных исхода и вероятности исходов остаются неизменными для всех испытаний.

Приведу пример практического применения схемы испытаний Бернулли на примере нашего института. На I курс ТИЖТа в 2016г. поступило 295 студентов. Требуется найти наиболее вероятное число первокурсников, родившихся в один день, день знаний 1-го сентября, и вероятность этого события.

Решение. В нашем случае р= 1:365 n=295 Используем соотношение для наивероятнейшего числа: m0

295*(1:365)-(364:365)m0295*(1:365)+(1:365)Учитывая, что m0 целое число, получаем m0= 1.

Найдем теперь P295(1), используя теорему Пуассона и то, ƛ=295*(1:365)

P295(1)е-10,37

Приведу следующий пример практического применения схемы испытаний Бернулли. Колёсные пары, изготовляемые при массовом производстве, могут отличаться по толщине, но при проверке они классифицируются на годные и дефектные - в зависимости от того, находится ли толщина в предписанных границах. И хотя продукция по многим причинам не может вполне соответствовать схеме Бернулли, эта схема задает идеальный стандарт для промышленного контроля качества продукции, несмотря даже на то, что этот стандарт никогда не достигается вполне точно. Вагоны подвержены изменениям, и поэтому вероятности не остаются одними и теми же. В режиме эксплуатации вагонов имеется некоторое постоянство, в результате чего длинные серии одинаковых отклонений оказываются более вероятными, чем это было бы при действительной независимости испытаний. Однако с точки зрения контроля качества продукции желательно, чтобы процесс соответствовал схеме Бернулли, и важно то, что в некоторых пределах этого можно добиться. Целью текущего контроля является обнаружение уже на ранней стадии существенных отступлений от идеальной схемы и использование их как указаний на угрожающее нарушение правильности эксплуатации вагонов.

Можем ли мы предугадать с помощью этой теории, что случится с нами через день, два, тысячу? Конечно, нет. Событий, связанных с нами в каждый момент времени, очень много. Только на одну лишь типизацию этих событий не хватит и жизни. А уж их совмещение и вовсе гиблое дело. С помощью Схемы Бернулли предугадывать можно лишь однотипные события. Например, такое как бросание монеты - это событие из 2 вероятностных результатов. В общем, прикладное применение теории вероятностей связанно с немалым количеством условий и ограничений, а для сложных процессов сопряжено с вычислениями, которые под силу лишь компьютеру.

Но следует помнить, что в жизни есть ещё такое понятие как удача, везение. Это то, что мы говорим - повезло, когда например какой-нибудь человек не учился никогда, никуда не стремился, лежал на диване, играл в компьютер, а теперь, предположим, он выступил в шоу «Минута славы». У него была вероятность 0.001 стать музыкантом, она выпала, ему повезло, такое схождение обстоятельств. То, что мы называем - оказался в нужном месте и в нужное время, когда срабатывают те самые 0.001.

Таким образом, работаем над собой, принимаем решения, которые могут повысить вероятность выполнения наших желаний и стремлений, каждый случай может добавить те заветные 0.00001, которые сыграют решающую роль в итоге.

В заключение хочется отметить то, что распределение Бернулли является достаточно распространенным и важным распределением, имеющим применение как в теории вероятностей и ее приложениях, так и в математической статистике.

Список литературы

Журбенко, Л.Н., Никонова, Г.А., Никонова, Н.В. Дегтярева, О.М. Математика в примерах и задачах: Учеб. пособие / Л.Н. Журбенко, Г.А. Никонова, Н.В. Никонова, О.М. Дегтярева. - М.: ИНФРА-М, 2012. - 372 с.: 60x88 1/16. - (Высшее образование). (обложка) ISBN 978-5-16-003841-4
Павлов, С.В. Теория вероятностей и математическая статистика: Учебное пособие / С.В. Павлов. - М.: ИЦ РИОР: ИНФРА-М, 2013. - 186 с.: 70x100 1/32. - (Карманное учебное пособие). (обложка, карм. формат) ISBN 978-5-369-00679-5
Балдин, К.В., Башлыков, В.Н., Рукосуев, А.В. Основы теории вероятностей и математической статистики: Учебник / К.В. Балдин, В.Н. Башлыков, А.В. Рукосуев. - М.: Флинта: МПСИ, 2013. - 488 с.: 60x88 1/16. (переплет) ISBN 978-5-9765-0314-4

Оригинал работы:

Схемы Бернулли повторных испытаний

www.informio.ru

Схема испытаний Бернулли. Повторные испытания в схеме Бернулли. Рекуррентная формула для подсчета вероятностей в схеме Бернулли

ЛЕКЦИЯ 3

СХЕМА ИСПЫТАНИЙ БЕРНУЛЛИ

3.1. Повторные испытания в схеме Бернулли. 1

3.2. Рекуррентная формула для подсчета вероятностей в схеме Бернулли. 2

3.3.Наивероятнейшее число испытаний события в схеме Бернулли. 3

3.4. Приближенные формулы в схеме испытаний Бернулли. 4

3.5.Локальные теоремы Муавра-Лапласа. 5

3.6. Интегральная теорема Лапласа. 5

3.7. Отклонение относительной частоты от вероятности. 6

3.1. Повторные испытания в схеме Бернулли

Повторные испытания независимы, если вероятность появления любого исхода в каждом испытании не зависит от реализации результатов в предыдущем испытании.

Определение 3.1. Схемой Бернулли – это выполнение следующих 3 условий:

1) производится n повторных испытаний,

2) в каждом испытании возможно только 2 исхода: событие появилось и событие не появилось,

3) вероятность появления события одинакова для каждого испытания и равна :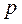

, .

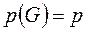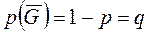Примеры.

· Игральная кость бросается 5 раз:

, ,

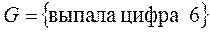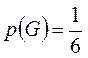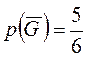
· Найти вероятность того, что при 3-х бросаниях монеты герб выпадет 2 раза:

W= {ГГГ, ГГР, ГРГ, РГГ, РГР, ГРР, РРР}

В = {выпало 2 герба и 1 решка}

Теорема 3.1. Вероятность того, что в 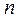испытаниях схемы Бернулли событие произошло 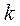раз, вычисляется по формуле

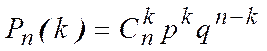►Пусть 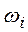– исход 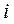-того испытания.

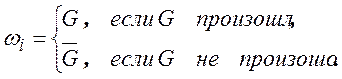
Тогда результатами испытания будут:

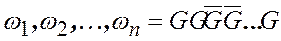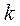где событие произошло раз, 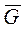произошло 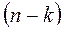раз.

Тогда

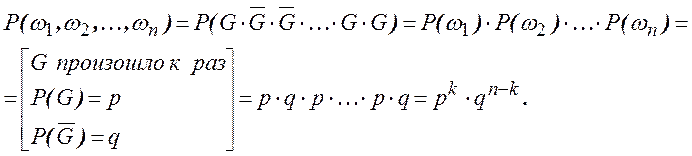
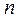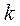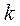Вероятность события в испытаниях (событие произошло раз) есть сумма стольких элементарных событий { – произошло раз, ` 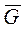произошло 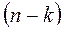) раз}, сколько существует сочетаний из 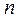элементов по 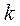, т. е. .

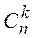Поэтому .◄

Примеры.

· Завод выпускает изделия, среди которых 5% - бракованные. Для проверки взято 5 деталей. Найти вероятности событий: , .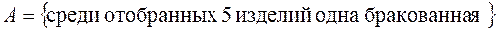

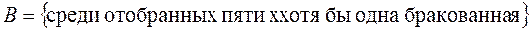Решение.

, .

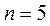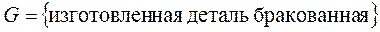Тогда ,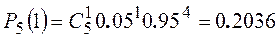

· Завод изготавливает изделия, каждое из которых с вероятностью 0,05 может быть дефектным. Сколько деталей должно быть в партии, чтобы вероятность встретить в них хотя бы 1 дефектную деталь была не меньшей, чем 0,98.

Решение.

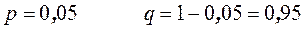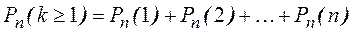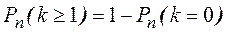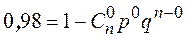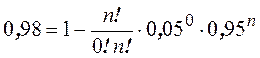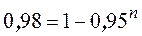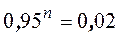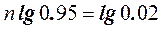3.2. Рекуррентная формула для подсчета вероятностей в схеме Бернулли

Теорема 3.2. , .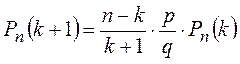

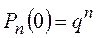Пример. Найти распределение вероятностей числа бракованных деталей среди 5-ти отобранных, если вероятность брака 0,60.

Решение.

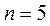, = {деталь бракованная}

р = 0,6, q = 0,4.

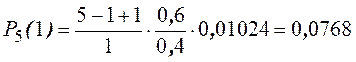
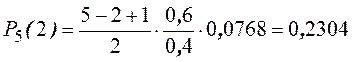
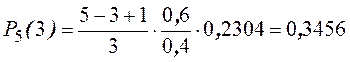
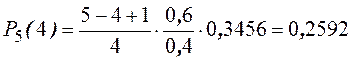
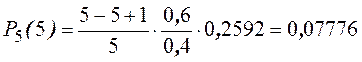
События Рn(0), Рn(1), …, Рn(n) составляют полную группу событий. Поэтому их сумма равна единице, т. е.

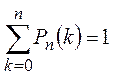Если сравнить полученную формулу с формулой Бинома Ньютона

Поэтому распределение вероятностей Рn(0), Рn(1), …, Рn(n) называется биноминальным распределением.

3.3.Наивероятнейшее число испытаний события в схеме Бернулли

Определение 3.2. Наивероятнейшее числоm0 появления события в n независимых испытаниях – число, для которого вероятность Pn(m0) превышает или не меньше вероятности каждого из возможных остальных исходов испытаний.

Теорема 3.3.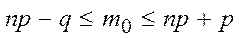

► По теореме 3.2. имеем:

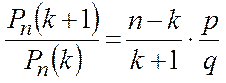Согласно определению числа m0 имеем неравенства:

◄

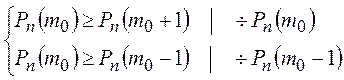
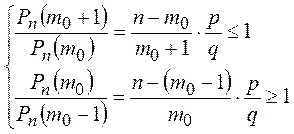
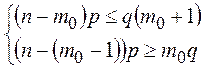
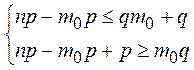
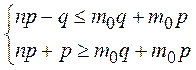
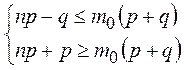
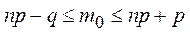Пример. При данном технологическом процессе 85% произведенной продукции высшего качества. Найти наивероятнейшее число изделий высшего сорта в партии из 120 изделий.

Решение.

n = 120, = {изделия высшего сорта}, р = 0,85, q = 0,15

120*0,85 – 0,15≤m0≤120*0,85 + 0,85

101,85≤m0≤102,85

m0 = 102

3.4. Приближенные формулы в схеме испытаний Бернулли.

По определению:

Теорема3.4. (Пуассона) Если в схеме испытаний Бернулли 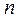– велико, 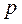– мало, – конечное число, то справедлива формула Пуассона:

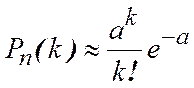► По формуле Бернулли

.◄

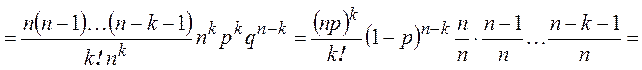
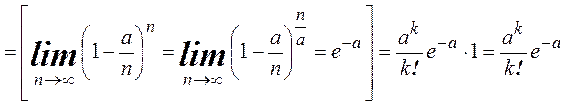Пример. Прибор содержит тысячу элементов. Вероятность выхода из строя каждого элемента 0,002. Найти вероятность того, что из строя вышло не более 7 элементов.

Решение.

n=1000,р = 0,002,к£7

= 1000*0,002 = 2

3.5.Локальные теоремы Муавра-Лапласа.

Теорема 3.5. Если в схеме испытаний Бернулли число испытаний 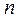велико, 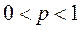, число 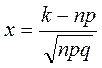ограничено, то вероятность того, что в 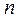испытаниях событие произойдет 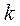раз, находится по формул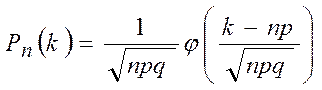е , где - функция Лапласа.

Функция Лапласа вычисляется по специальным таблицам. Для того чтобы уметь пользоваться таблицами, надо знать свойства функции j(х):

1. График функции:

2. Функция 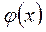является четной, поэтому таблицы составлены только для положительных значений.

3. Ось 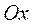является асимптотой графика функции 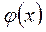и к ней достаточно быстро приближаются ветви графика. Поэтому таблицы составлены для значений х от 0 до 4. Если надо найти значение j(х), х>4, то берут последнее табличное значение.

Пример. По данным ОТК 80% всей продукции, выпускаемой заводом, стандартны. Найти вероятность того, что среди взятых 400 изделий бракованными будут 40.

Решение.

= {1 изделие бракованное}, n = 400, р = 0,2, к = 40

3.6. Интегральная теорема Лапласа

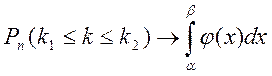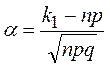Теорема 3.6. Если в схеме испытаний Бернулли n – велико, 0<р<1, то вероятность того, что в n испытаниях событие А произойдет не менее к1 раз и не более к2 раз, удовлетворяет соотношению:, где и .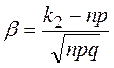

Преобразуем формулу:

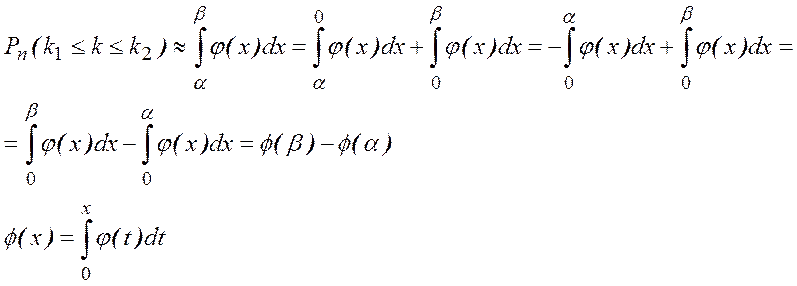
Поэтому интегральную формулу Муавра – Лапласа можно записать в виде

где .

Значения функции f(х) находятся в таблицах.

Свойства функции f(x):

1. График функции:

2. f(х) – функция нечетная, поэтому таблицы приведены только для положительных значений х.

3. График функции имеет 2 асимптоты у1 = 0,5 и у2 = -0,5, к которой быстро приближаются, поэтому таблицы составлены для значений х от 0 до 4. При х>4 берется последнее значение таблицы.

Пример. Промышленная телевизионная установка содержит 2000 транзисторов. Вероятность выхода из строя каждого из транзисторов – 0,0005. Найти вероятность выхода из строя от 50 до 60 транзисторов.

Решение.

50£к£60, n = 2000, р = 0,0005

3.7. Отклонение относительной частоты от вероятности

Относительная частота появления события в 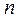испытаниях .

При 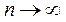относительная частота стремится к вероятности события . Тогда – абсолютное отклонение относительной частоты от вероятности.

Теорема 3.7.

►Пусть дано 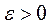. Тогда:

◄

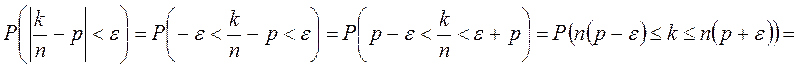
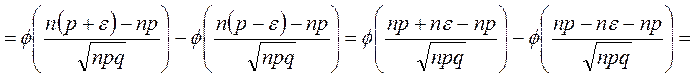
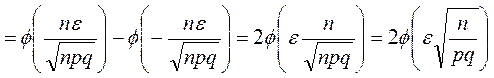vunivere.ru

6. Повторные независимые испытания (схема Бернулли)

Ряд классических распределений связан с экспериментом, в котором проводятся последовательные независимые испытания и наблюдается результат совместного осуществления тех или иных исходов каждого испытания.

Последовательные испытания называются независимыми, если вероятность осуществления любого исхода вn-м по счету испытании не зависит от реализации исходов предыдущих испытаний.

Простейшим классом повторных независимых испытаний является последовательность независимых испытаний с двумя исходами(«успех» и «неуспех») и с неизменными вероятностями «успеха» (р) и «неуспеха» в каждом испытании (схема испытаний Бернулли).

Вероятность получить ровно mуспехов вnнезависимых испытаниях вычисляется по формуле, называемойформулой Бернулли

Пример 6.1.Изделия некоторого производства содержат 5 % брака. Найти вероятность того, что среди пяти взятых наугад изделий: а) нет ни одного испорченного; б) будут два испорченных.

Решение. а) По условию задачи . Так как вероятность наступления событияА(появление бракованной детали) постоянна для каждого испытания, то задача подходит под схему Бернулли. Находим вероятность того, что среди пяти взятых наудачу изделий нет ни одного испорченного. По формуле Бернулли

а) ;

б) ,

Ответ:а); б).

Определение.Число наступлений событияАназываетсянаивероятнейшим, если оно имеет наибольшую вероятность по сравнению с вероятностями наступления событияА любое другое количество раз.

Наивероятнейшее число наступлений события Авnиспытаниях заключено между числамии:. Если— целое число, то наивероятнейших чисел дваи.

Пример 6.2.В помещении четыре лампы. Вероятность работы в течение года для каждой лампы 0,8. Чему равно наивероятнейшее число ламп, которые будут работать в течение года?

Решение. По формуленайдемПо условию

Следовательно, имеются два наивероятнейших числа или.

Ответ:или.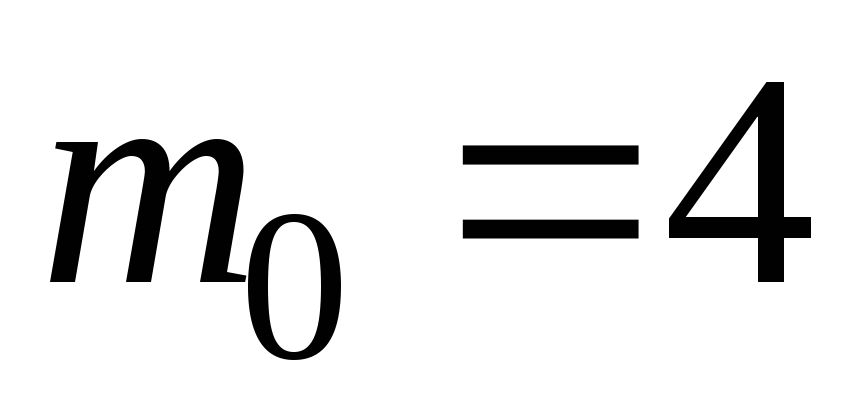

Пример 6.3.Вероятность попадания в кольцо при штрафном броске для баскетболиста равна 0,8. Сколько надо произвести бросков, чтобы наивероятнейшее число попаданий было равно 20?

Решение. Известно, что. Тогдаиnнайдем из системы неравенств

Так как n— целое число, тоили.

Ответ:24 или 25.

Задачи для самостоятельного решения

Наблюдениями установлено, что в некоторой местности в сентябре в среднем бывает 12 дождливых дней. Какова вероятность того, что из случайно взятых в этом месяце 8 дней 3 дня окажутся дождливыми?

Ответ:

6.2.Что вероятнее: выиграть у равносильного противника (ничейный исход партии исключен) три партии из четырех или пять из восьми?

Ответ:

6.3.В банк поступило 6 заявлений от физических лиц на получение кредита. Вероятность получить первый кредит для каждого равна . Найти вероятности следующих событий:

1) будет выдано ровно 3 кредита;

2) будет выдано не менее двух кредитов.

Ответ:.

Вероятность рождения мальчика равна 0,515, девочки 0,485. В некоторой семье шестеро детей. Найти вероятность того, что среди них не больше двух девочек.

Ответ:;.

6.5. Два баскетболиста делают по три броска в корзину. Вероятность попадания мяча при каждом броске равна соответственно 0,6 и 0,7. Найти вероятность того, что у обоих будет равное количество попаданий.

Ответ:

6.6. Игральная кость подбрасывается 5 раз. Найти вероятность того, что два раза появится число очков, кратное трем.

Ответ:

6.7. Экзаменационный билет состоит из пяти вопросов в виде теста с тремя возможными ответами на каждый из пяти вопросов, из которых нужно выбрать один правильный. Какова вероятность сдать экзамен методом простого угадывания, если достаточно ответить хотя бы на 4 вопроса?

Ответ:

6.8. Три охотника одновременно выстрелили по волку. Вероятности попадания каждым из охотников одинаковы и равны 0,4. Определить вероятность того, что волк будет убит, если известно, что при одном попадании охотники убивают волка с вероятностью 0,2, при двух – с вероятностью 0,5 и при трех – с вероятностью 0,8.

Ответ:

На контроль поступила партия деталей из цеха. Известно, что 5 % всех деталей не удовлетворяет стандарту. Сколько нужно испытать деталей, чтобы с вероятностью не менее 0,95 обнаружить хотя бы одну нестандартную деталь?

Ответ:

Для данного баскетболиста вероятность забросить мяч в корзину при броске равна 0,4. Произведено 10 бросков. Найти наивероятнейшее число попаданий и соответствующую вероятность.

Ответ:,.

Найти наивероятнейшие числа отрицательных и положительных ошибок и соответствующую вероятность при четырех измерениях, если при каждом измерении вероятность получения положительной ошибки равна , а отрицательной —.

Ответ:

Вероятность попадания в десятку при одном выстреле р= 0,2. Сколько нужно провести независимых выстрелов, чтобы с вероятностью не менее 0,9 попасть в десятку хотя бы один раз?

Ответ:

Какое наименьшее количество чисел необходимо взять из таблицы случайных чисел, чтобы с наибольшей вероятностью обеспечивалось появление среди них трех чисел, оканчивающихся цифрой 7?

Ответ:

Вероятность появления события в каждом из независимых испытаний равна 0,3. Найти число испытаний n, при котором наивероятнейшее число появлений события в этих испытаниях будет равно 30.

Ответ:

6.15. Доля крупных заказов в строительной фирме составляет 40%. Чему равно наивероятнейшее число крупных заказов, если фирма предполагает заключить 120 договоров на следующий год?

Ответ:.

6.16. Пусть вероятность того, что студент опоздает на лекцию, равна 0,08. Найти наиболее вероятное число опоздавших из 96 студентов.

Ответ: .

Чему равна вероятность рнаступления события в каждом из 49 независимых испытаний, если наивероятнейшее число наступлений события в этих испытаниях равно 30?

Ответ:

Чему равна вероятность рнаступления события в каждом из 39 независимых испытаний, если наивероятнейшее число наступлений события в этих испытаниях равно 25?

Ответ:

studfiles.net

Смотрите также

..:::Новинки:::..

Windows Commander 5.11 Свежая версия.

Новая версия
IrfanView 3.75 (рус)

Обновление текстового редактора TextEd, уже 1.75a

System mechanic 3.7f
Новая версия

Обновление плагинов для WC, смотрим :-)

Весь Winamp
Посетите новый сайт.

WinRaR 3.00
Релиз уже здесь

PowerDesk 4.0 free
Просто - напросто сильный upgrade проводника.

..:::Счетчики:::..

Реферат: Повторные независимые испытания. Формула Бернулли. Реферат схемы повторных испытаний бернулли

Повторение испытаний. Схема бернулли

Москва 2006 введение

Локальная и интегральная теоремы муавра-лапласа

Повторение испытаний. Схема бернулли

Москва 2006 введение

Локальная и интегральная теоремы муавра-лапласа

Повторные независимые испытания. Формула Бернулли

Схемы Бернулли повторных испытаний — Информио

Схема испытаний Бернулли. Повторные испытания в схеме Бернулли. Рекуррентная формула для подсчета вероятностей в схеме Бернулли

3.1. Повторные испытания в схеме Бернулли

3.2. Рекуррентная формула для подсчета вероятностей в схеме Бернулли

3.3.Наивероятнейшее число испытаний события в схеме Бернулли

3.4. Приближенные формулы в схеме испытаний Бернулли.

3.5.Локальные теоремы Муавра-Лапласа.

3.6. Интегральная теорема Лапласа

3.7. Отклонение относительной частоты от вероятности

6. Повторные независимые испытания (схема Бернулли)

Задачи для самостоятельного решения

Смотрите также