Реферат на тему:
Теорети́ческая меха́ника — наука об общих законах механического движения и взаимодействия материальных тел. Будучи по существу одним из разделов физики, теоретическая механика, вобрав в себя фундаментальную основу в виде аксиоматики, выделилась в самостоятельную науку и получила широкое развитие благодаря своим обширным и важным приложениям в естествознании и технике, одной из основ которой она является.
По Ньютону, «Рациональная механика есть учение о движениях, производимых какими бы то ни было силами, и о силах, требуемых для производства каких бы то ни было движений, точно изложенное и доказанное»[1].
В физике под теоретической механикой подразумевается часть теоретической физики, изучающая математические методы классической механики, альтернативные прямому применению законов Ньютона (так называемая аналитическая механика). Сюда входят, в частности, методы, основанные на уравнениях Лагранжа, принципы наименьшего действия, уравнении Гамильтона-Якоби и др.
Следует подчеркнуть, что аналитическая механика может быть как нерелятивистской — тогда она пересекается с классической механикой, так и релятивистской. Принципы аналитической механики являются настолько общими, что её релятивизация не приводит к фундаментальным трудностям.
В технических науках под теоретической механикой подразумевается набор физико-математических методов, облегчающих расчёты механизмов, сооружений, летательных аппаратов и т. п. (так называемая прикладная механика или инженерная механика) . Практически всегда эти методы выводятся из законов классической механики — в основном, из законов Ньютона, хотя в некоторых технических задачах оказываются полезными некоторые из методов аналитической механики.
Теоретическая механика опирается на некоторое число законов, установленных в опытной механике, принимаемых за истины, не требующих доказательств — аксиомы. Эти аксиомы заменяют собой индуктивные истины опытной механики. Теоретическая механика имеет дедуктивный характер. Опираясь на аксиомы как на известный и проверенный практикой и экспериментом фундамент, теоретическая механика возводит свое здание при помощи строгих математических выводов.
Теоретическая механика как часть естествознания, использующая математические методы, имеет дело не с самими реальными материальными объектами, а с их моделями. Такими моделями, изучаемыми в теоретической механике, являются
Обычно в теоретической механике выделяют такие разделы, как
В теоретической механике широко применяются методы
Теоретическая механика явилась основой для создания многих прикладных направлений, получивших большое развитие. Это механика жидкости и газа, механика деформируемого твердого тела, теория колебаний, динамика и прочность машин, гироскопия, теория управления, теория полета, навигация и др.
Теоретическая механика является одной из фундаментальных механических дисциплин на механико-математических факультетах университетов России. По этой дисциплине проводятся ежегодные Всероссийские[2], национальные (например, украинские) и региональные студенческие олимпиады, а также Международная олимпиада[3].
wreferat.baza-referat.ru
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИИ ФГБОУ ВПО ТУЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра теоретической механики
Вариант № 1
Выполнила: студенткагр.Б360811 Пашута А.А.,шифр 120191Научный руководитель:профессорМитяев А.Г
Тула, 2013
1. Аннотация
2. Часть I. Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии системы.
3. Часть II. Определение закона движения системы.
4. Часть III. Определение реакций внешних и внутренних связей.
5. Часть IV. Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа.
6. Часть V. Составление дифференциального уравнения движения механизма с помощью уравнения Лагранжа 2-го рода.
7. Часть VI. Результаты вычислений.
8. Приложение.
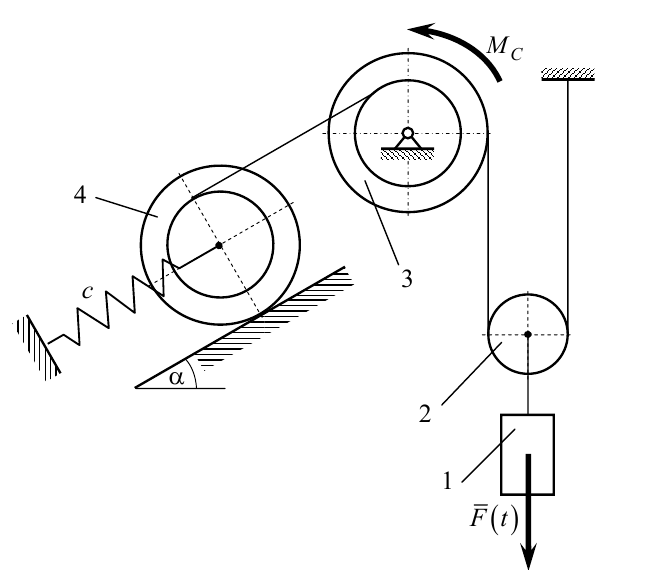
Исследуется движение механической системы с одной степенью свободы, на которую действует момент сопротивления Mc=µ ω и возмущающая гармоническая сила F(t). Трением качения и скольжения пренебрегаем. Качение катков происходит без скольжения. Проскальзывание нитей на блоках отсутствует. Требуется, используя основные теоремы динамики системы и аналитические методы теоретической механики, определить закон движения первого тела и реакции внешних и внутренних связей.
Схема механизма и данные для выполнения задания:

Дано:
m1 = 2 кг
m2 = 1 кг r2 = 0,15 м сплошной цилиндр
m3 = 3 кг r3 = 0,1 м R3 = 0,2 м i3 = 0,2
m4 = 4 кг r4 = 0,2 м R4 = 0,3 м сплошной цилиндр
µ = 1 кг/с α = 450
υ = 0,5 Н м с x0 = 0.05 м
c = 2000 Н/м p = 2π с-1
fсц = 0,25
F0 = 20 Н
Рис.1. Схема механизма и исходные данные
Изобразим расчетную схему (рис. 2)
Рис. 2. Расчетная схема
На рис. 2 обозначено:
Р1,Р2,Р3 ,Р4 – силы тяжести,
N4 – нормальные реакции опорной плоскости,
Fуп – упругая реакция пружины,
Х3, У3 – реакции подшипника блока 3,
R=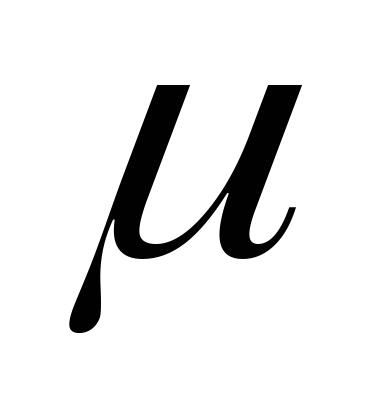 V – сила вязкого сопротивления,
V – сила вязкого сопротивления, 
F(t) – возмущающая сила.
Рассматриваемая механическая система имеет одну степень свободы (нити нерастяжимые, качение катка 3 происходит без скольжения). Будем определять ее положение с помощью координаты S. Начало отсчета координаты совместим с положением статического равновесия центра масс груза 1.
Для построения дифференциального уравнения движения системы используем теорему об изменении кинетической энергии механической системы в форме:
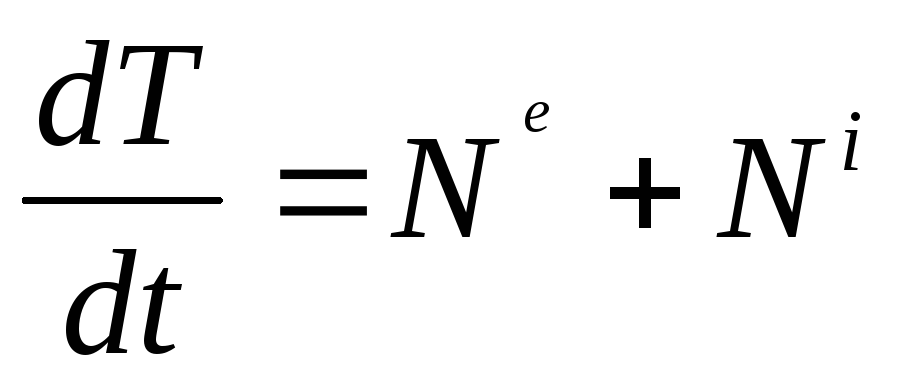 , (1.1)
, (1.1)
где Т - кинетическая энергия системы,
 - сумма мощностей внешних сил,
- сумма мощностей внешних сил,
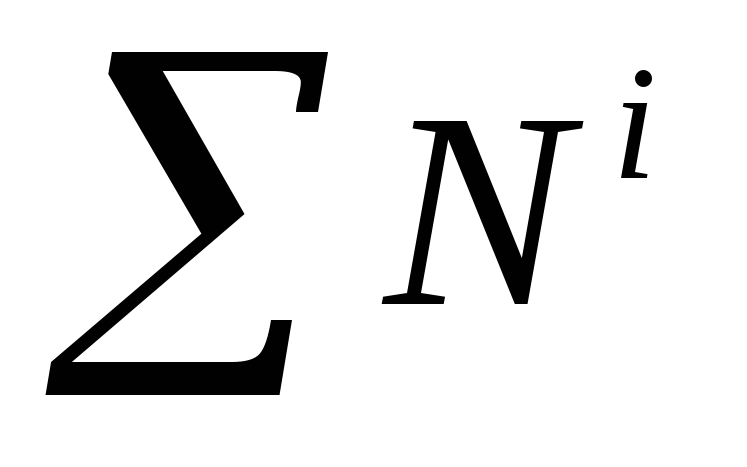 - сумма мощностей внутренних сил.
- сумма мощностей внутренних сил.
Теорема (1.1) формулируется так: "Производная по времени от кинетической энергии механической системы равна алгебраической сумме мощностей внешних и внутренних сил, действующих на точки механической системы".
Вычислим кинетическую энергию системы как сумму кинетических энергий тел 1-3:
Т=Т1+Т2+Т3 +Т4. (1.2)
Груз 1 совершает поступательное движение. Его кинетическая энергия равна:
Т1=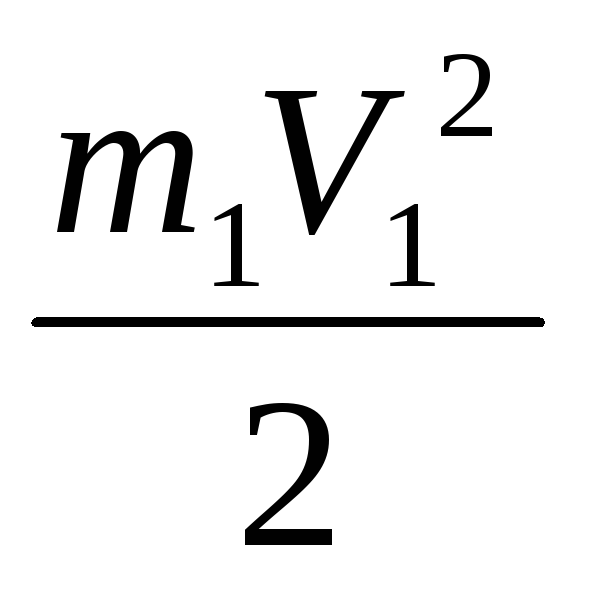 (1.3)
(1.3)
Каток 2 совершает плоскопараллельное движение, поэтому его кинетическая энергия определяется по теореме Кенига
T2=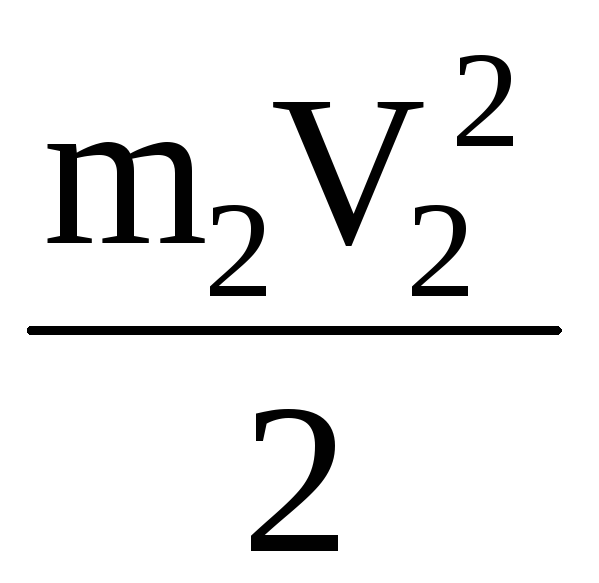 +
+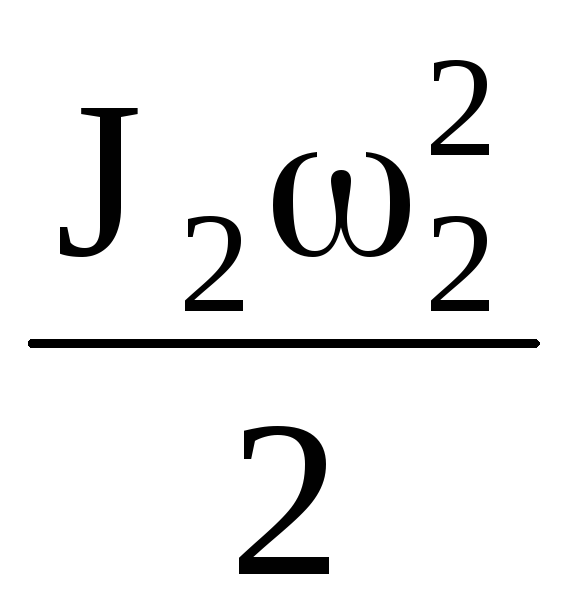 , (1.4)
, (1.4)
где V2 – скорость катка 2
JO2 - момент инерции относительно центральной оси блока;
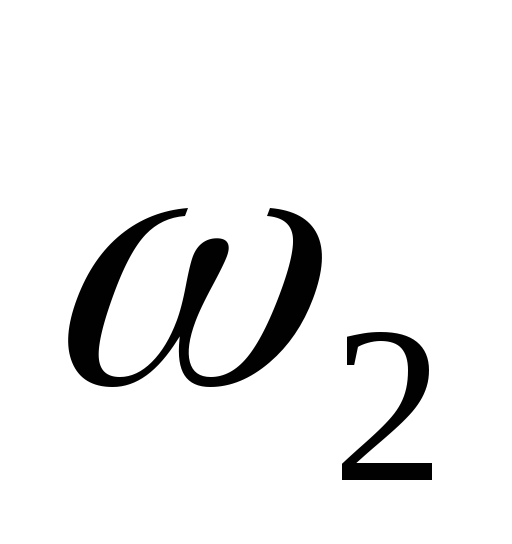 - угловая скорость блока.
- угловая скорость блока.
Блок 3 совершает вращательное движение около неподвижной оси. Его кинетическая энергия
T3=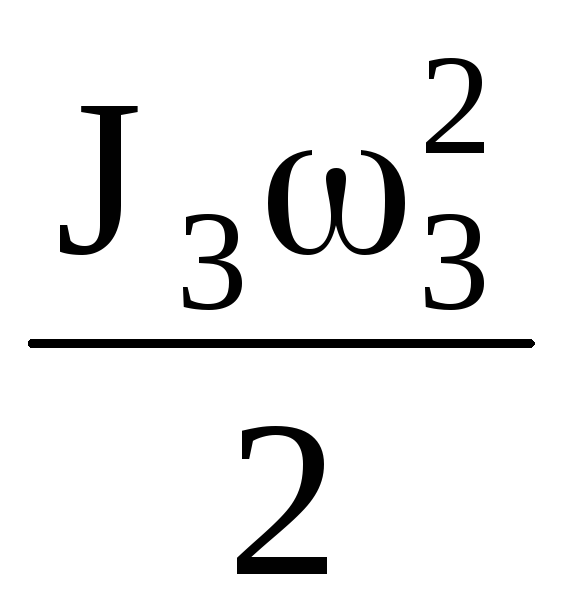 , (1.5)
, (1.5)
где J3 - момент инерции относительно центральной оси катка,
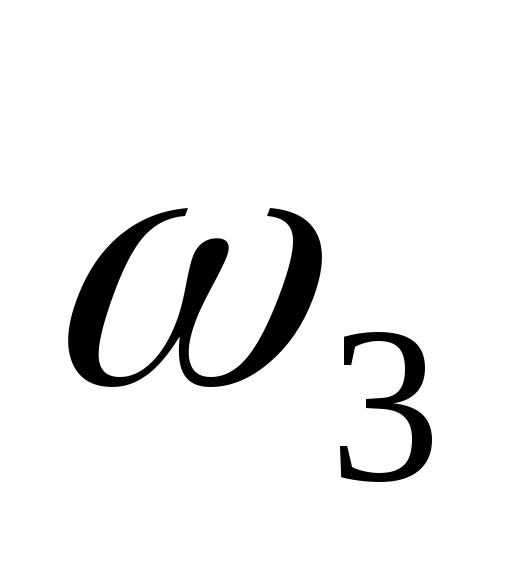 - угловая скорость катка.
- угловая скорость катка.
Блок 4 совершает плоское движение.
T=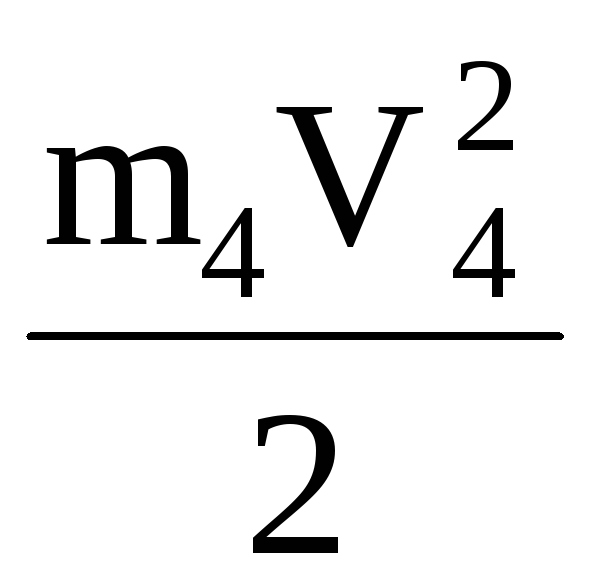 ,
,
где m4 – масса блока 4,
V4 – скорость блока 4
Кинетическая энергия всего механизма будет равна:
T=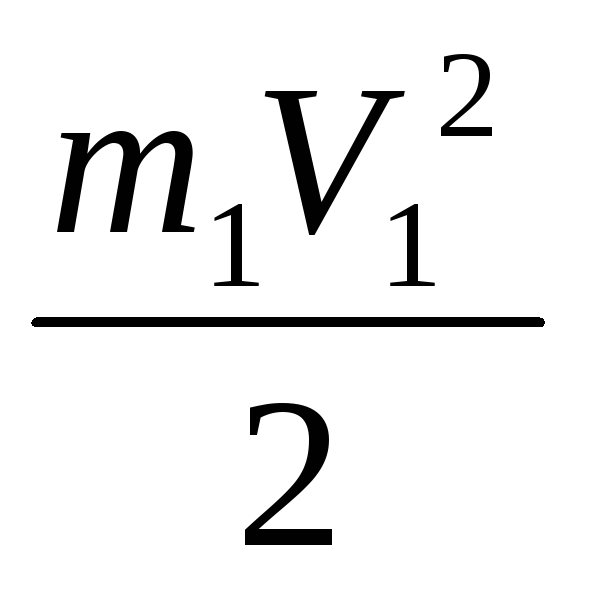 +
+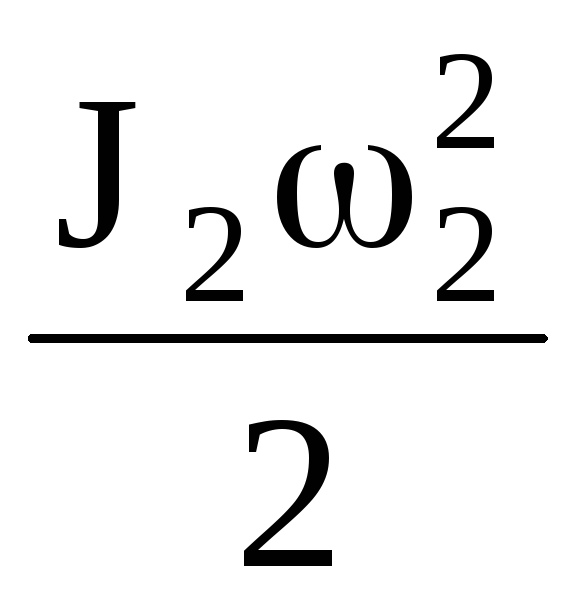 +
+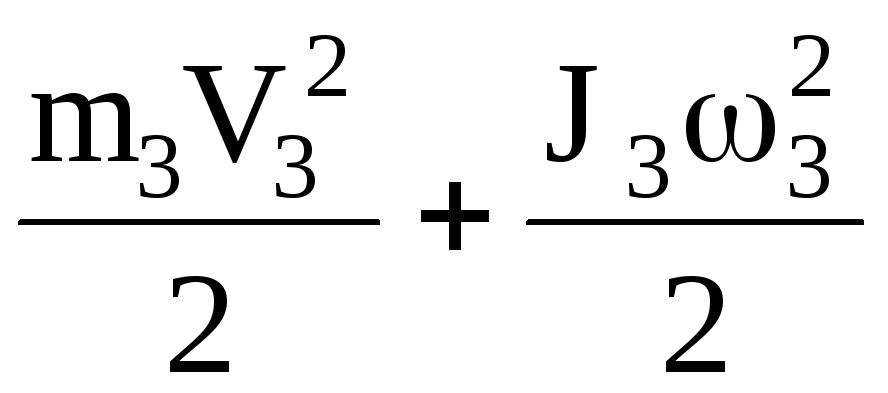 +
+ 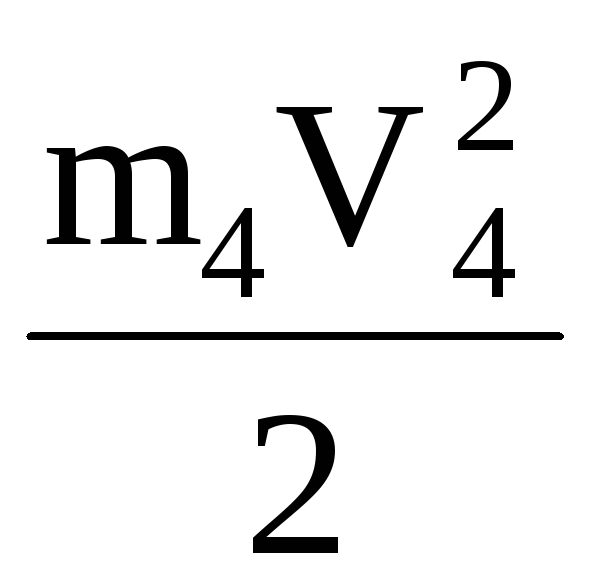 (1.6)
(1.6)
Выразим V3, V4,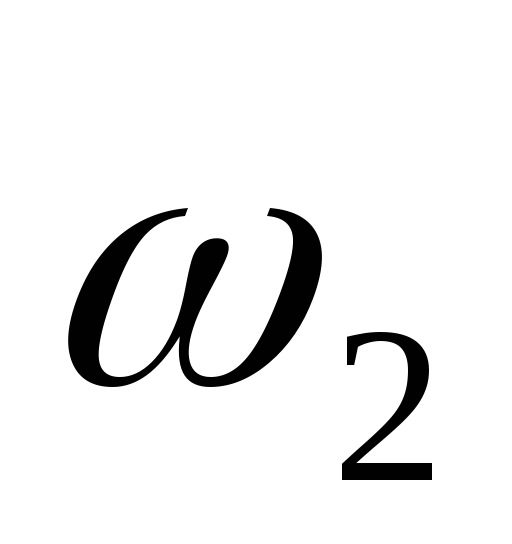 ,
, 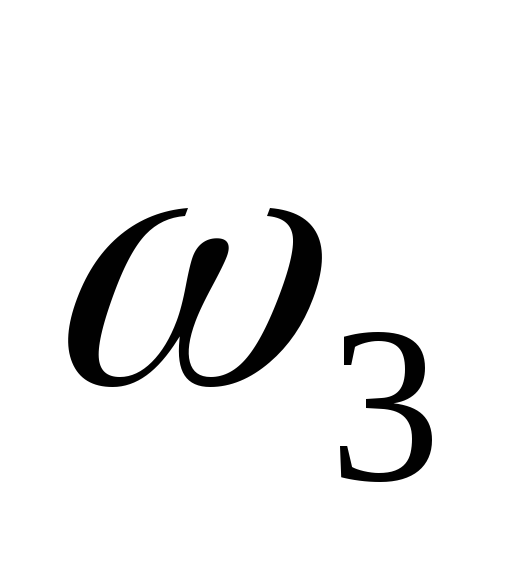 ,J2, J3 через скорость груза 1.
,J2, J3 через скорость груза 1.
Положив V1=V=V2, получим
J3=m3i32, J2=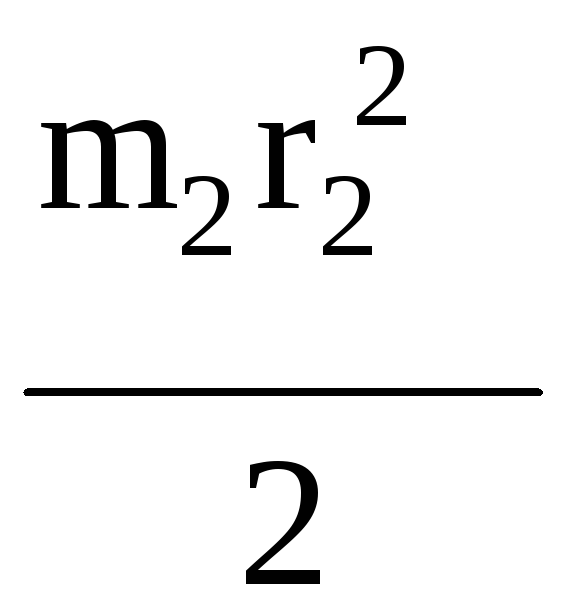 ,
, 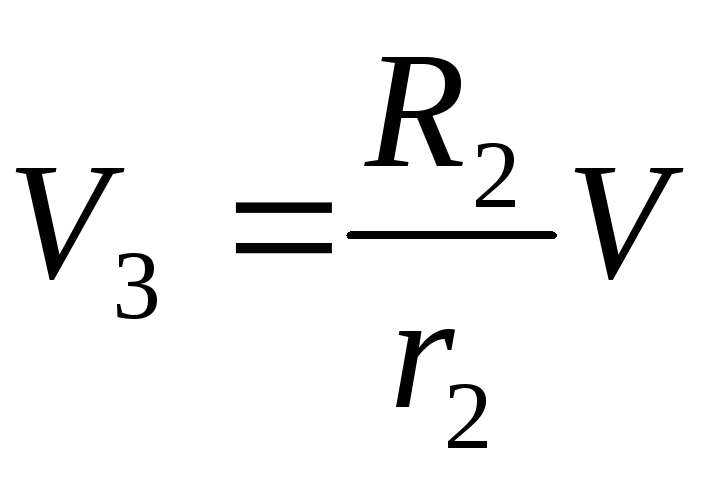 ,V4=
,V4=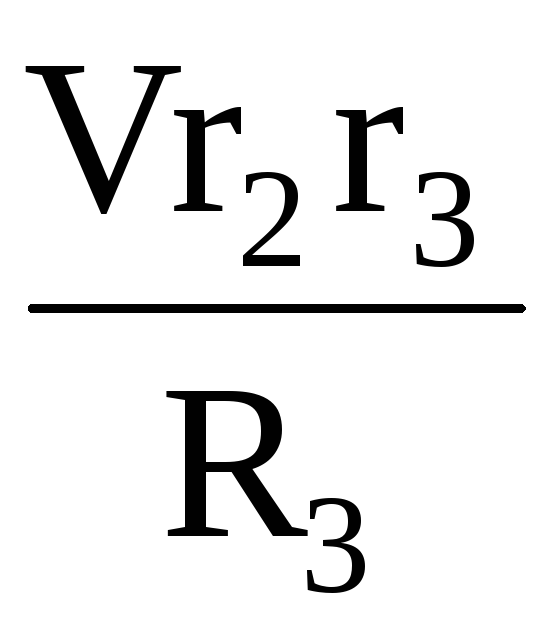

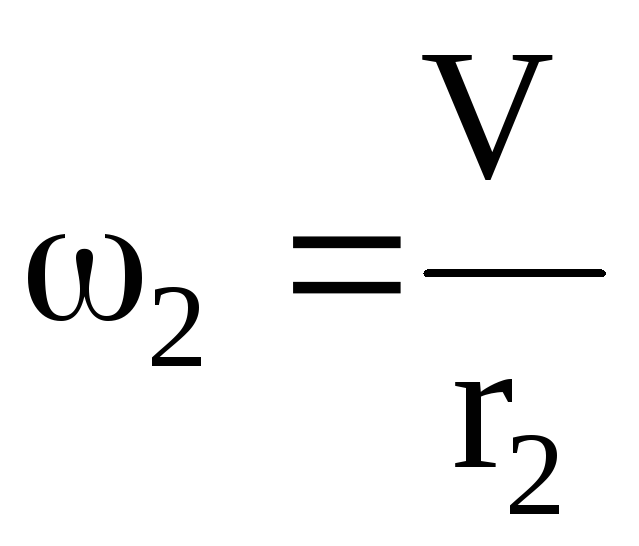 ,
, 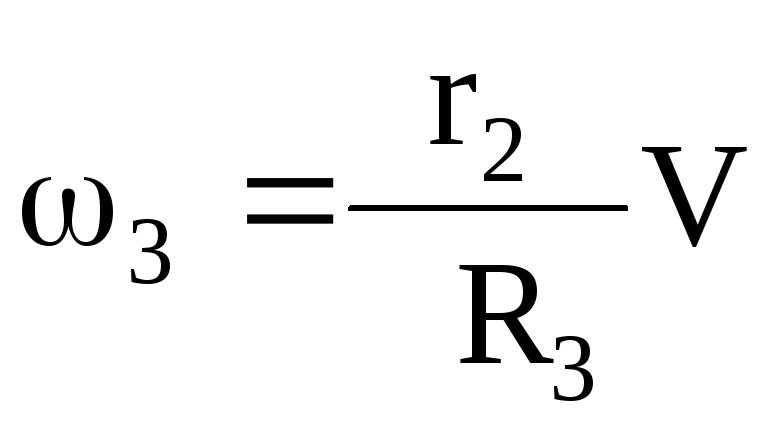 , (1.7)
, (1.7)
Подставляя (1.3), (1.4), (1.5) в (1.6) с учетом (1.7), получаем:
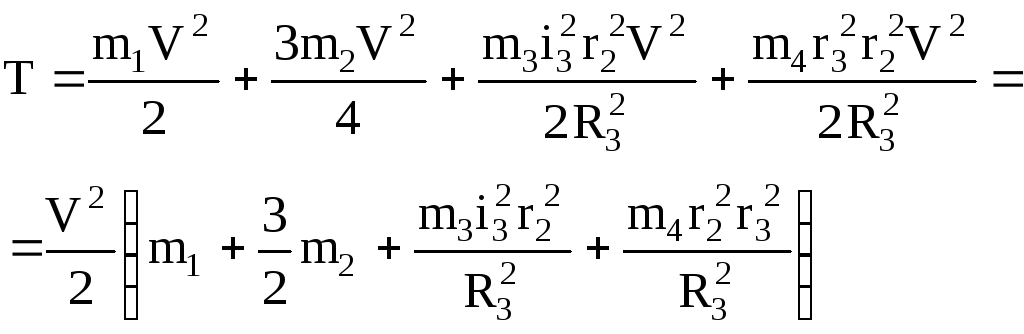 (1.8)
(1.8)
или
T=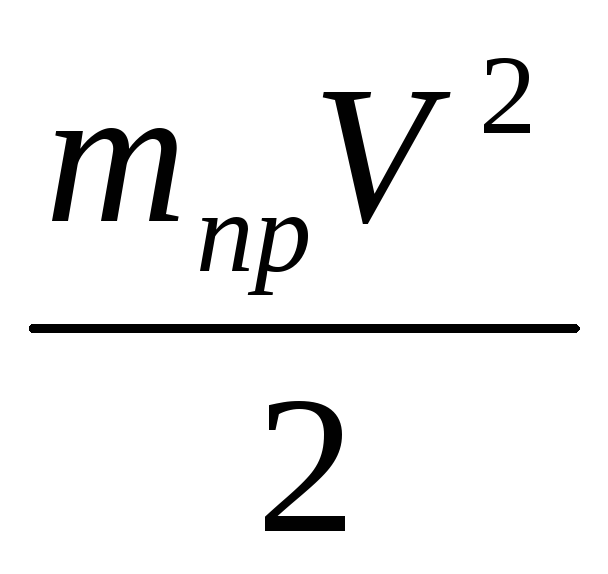 , (1.9)
, (1.9)
где mпр=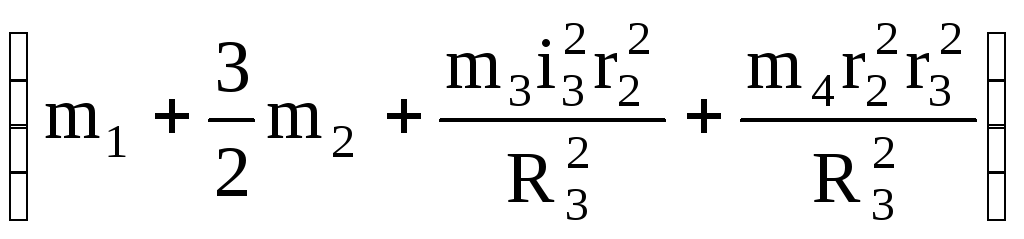 =3,68 кг (1.10)
=3,68 кг (1.10)
Величину mпр=const будем называть приведенной массой. Найдем производную от кинетической энергии по времени
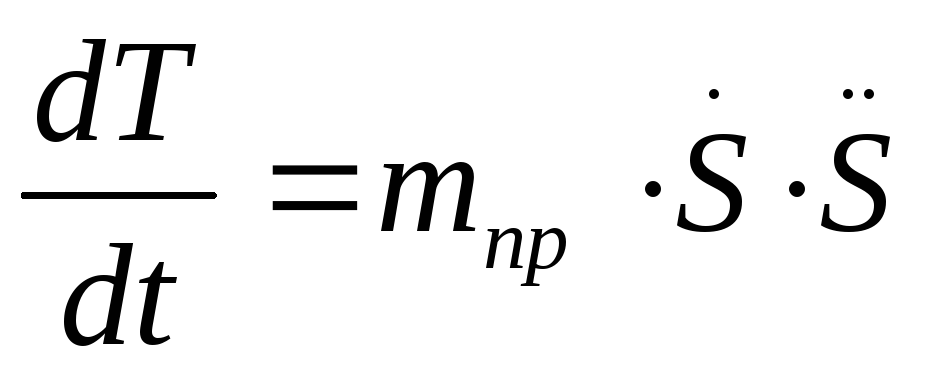 (1.11)
(1.11)
Теперь вычислим правую часть уравнения (1.1) - сумму мощностей внешних и внутренних сил.
Мощность силы равна скалярному произведению вектора силы на скорость точки ее приложения
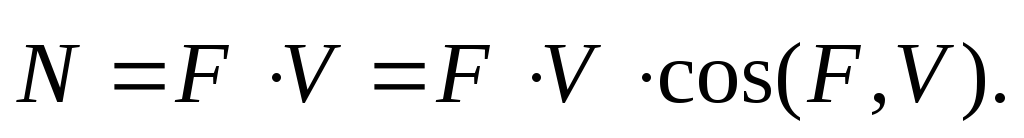 (1.12)
(1.12)
Рассматриваемая нами механическая система является неизменяемой, т. е. тела, входящие в систему, недеформируемы и скорости их точек относительно друг друга равны нулю. Поэтому сумма мощностей всех внутренних сил будет равняться нулю:
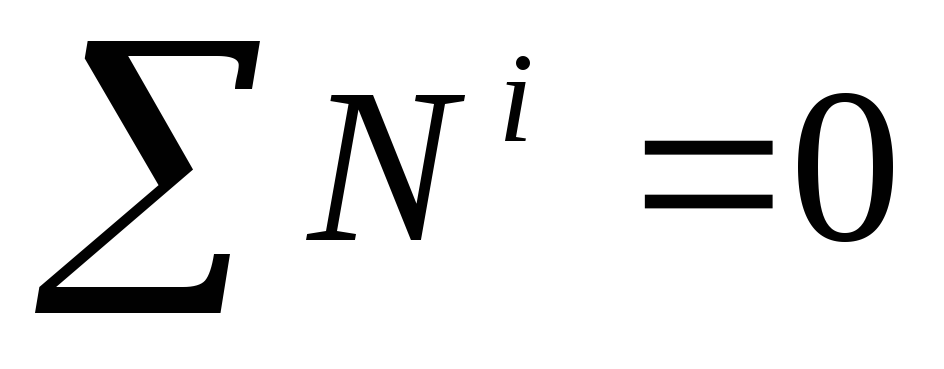 (1.13)
(1.13)
Будут равняться нулю и мощности некоторых внешних сил, приложенных в точках, скорости которых равны нулю. Как видно из расчетной схемы, таковыми являются силы
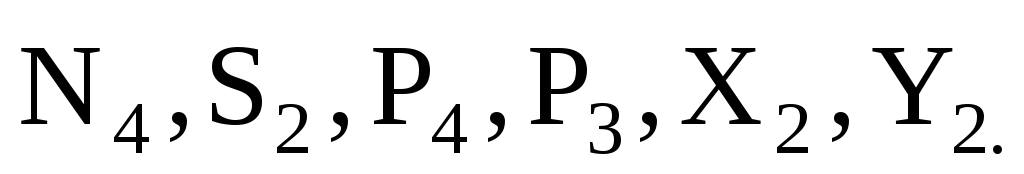

Сумма мощностей остальных сил
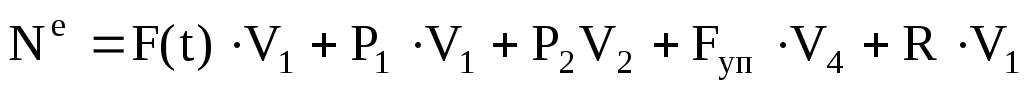 (1.14)
(1.14)
или, раскрывая скалярные произведения,
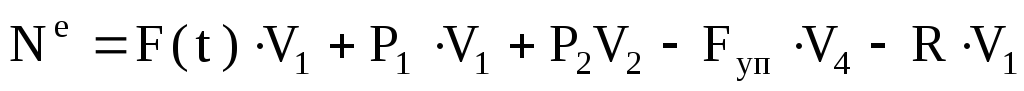 (1.15)
(1.15)
С учетом кинематических соотношений (1.7) сумму мощностей внешних сил преобразуем к виду:
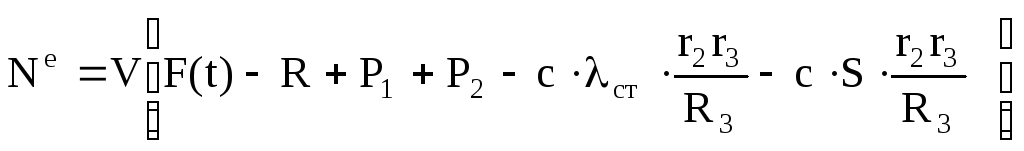
В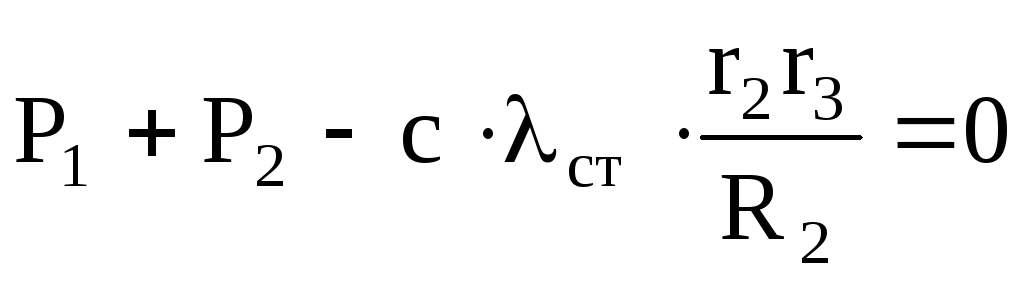 состоянии покоя приведенная сила равна нулю. Полагая
состоянии покоя приведенная сила равна нулю. Полагая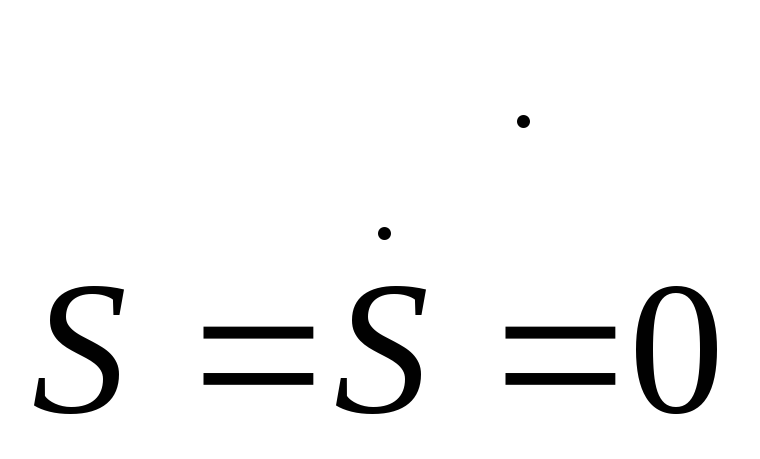 , получаем условие равновесия системы
, получаем условие равновесия системы
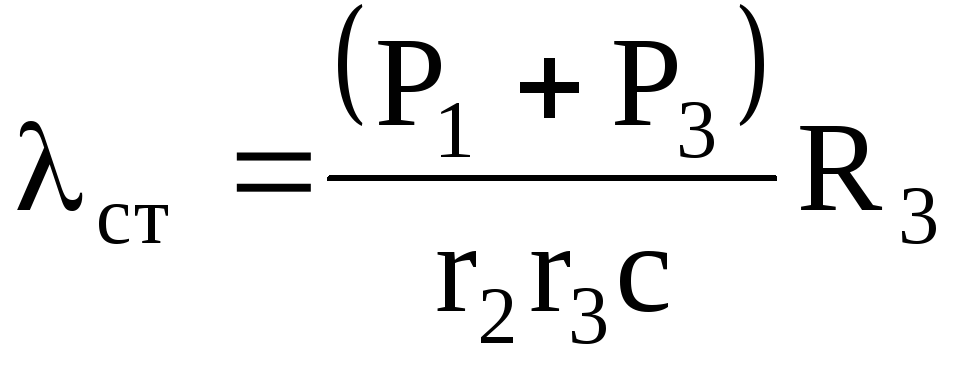
тогда, учитывая, что сила вязкого сопротивления 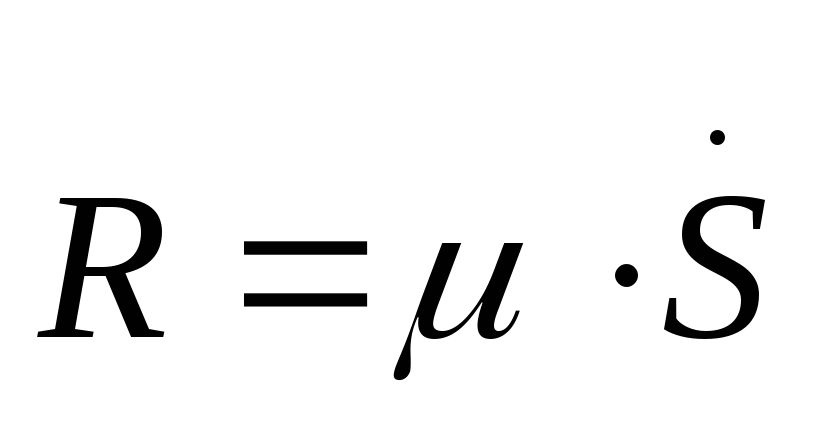
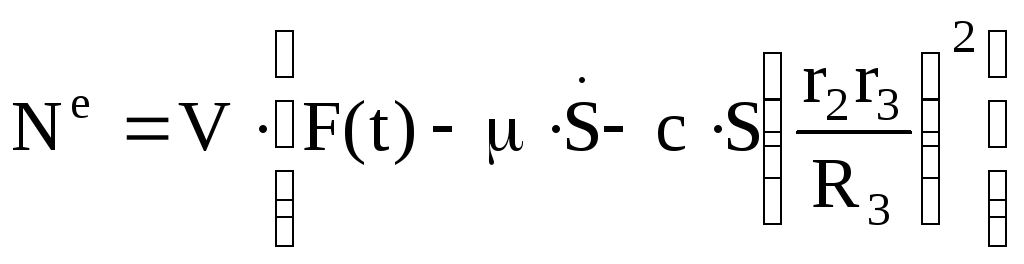 (1.16)
(1.16)
или
Ne=V Fпр , (1.17)
где
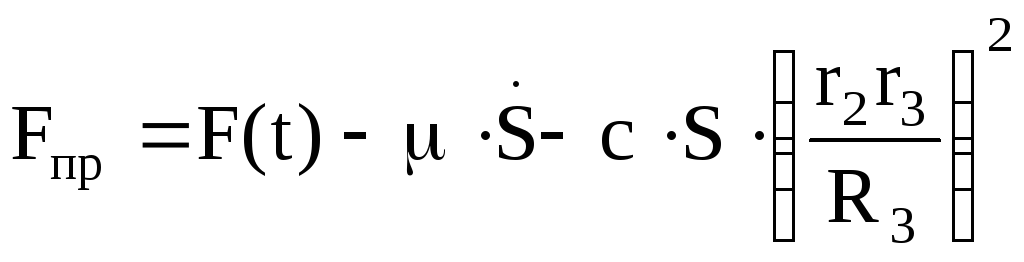 (1.18)
(1.18)
Величину Fпр будем называть приведенной силой.
Подставим выражения для производной от кинетической энергии (1.11) и сумму мощностей всех сил (1.17) с учетом (1.18) в уравнение (1.1). Тогда, получаем дифференциальное уравнение движения системы:
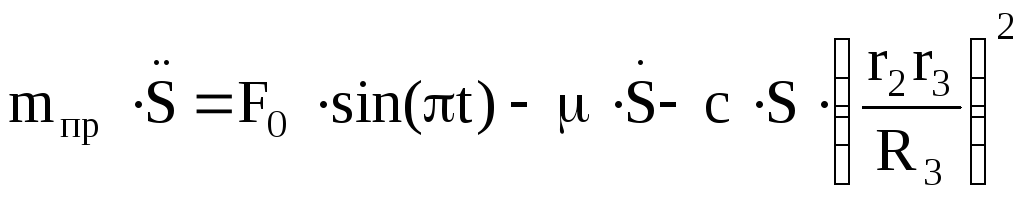 (1.19)
(1.19)
Запишем последнее уравнение в виде:
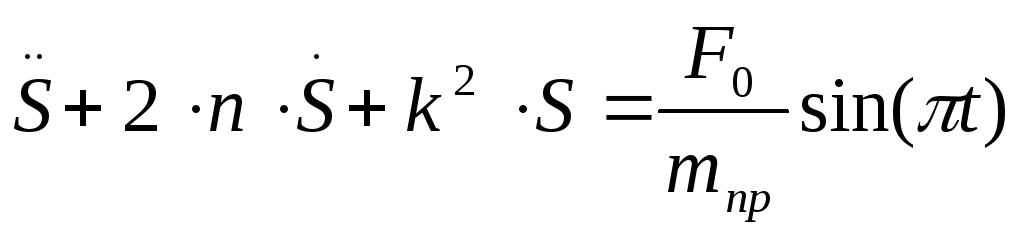 , (1.20)
, (1.20)
где введены коэффициенты, имеющие определенный физический смысл:
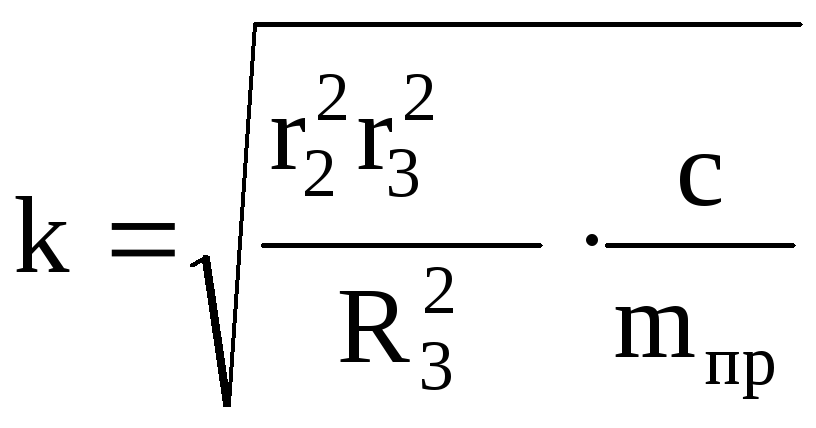 - циклическая частота свободных колебаний,
- циклическая частота свободных колебаний,
k = 3,06 с-1
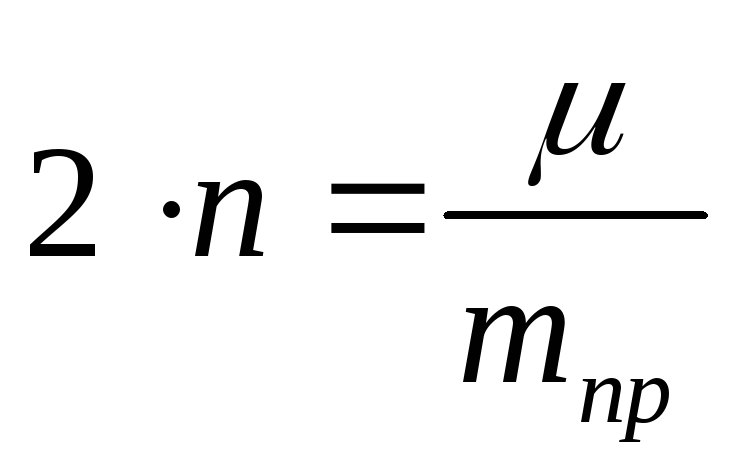 - показатель степени затухания колебаний.
- показатель степени затухания колебаний.
n = 0,14 с-1
Запишем начальные условия движения:
t=0 | 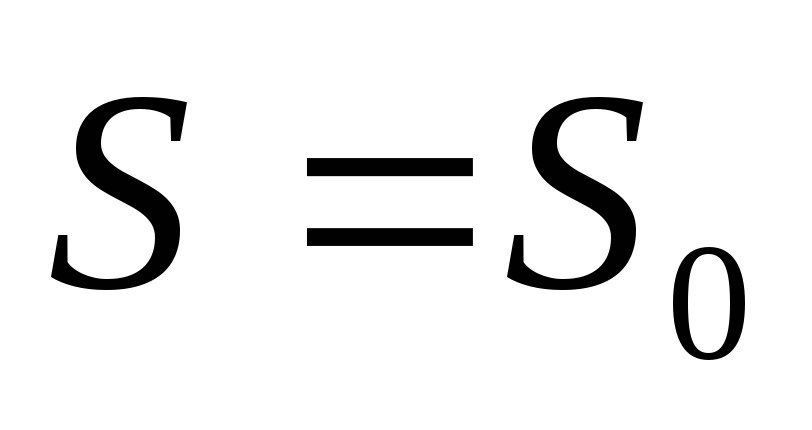
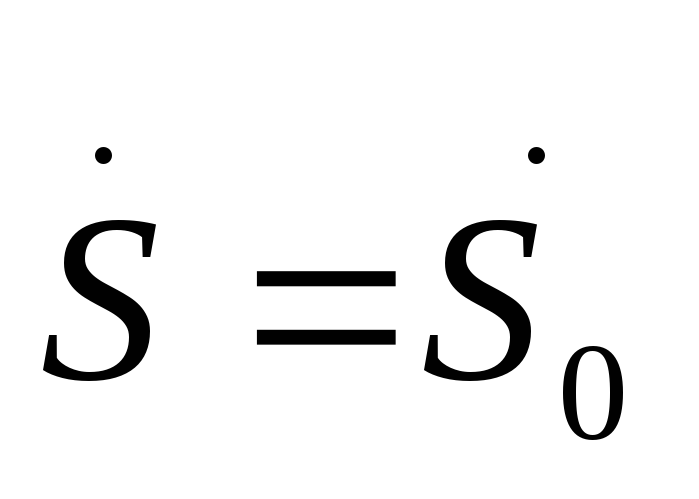 . (1.21)
. (1.21)
Выражения (1.20) и (1.21) совместно представляют математическую модель для решения второй задачи динамики.
studfiles.net
Статика :
Уравновешенные силы:
Система сил, под действием которой свободное твердое тело может находится в покое, называется уравновешенной.
Аксиомы статики:
а) Аксиома о уравновешенных силах (о абсолютном твердом теле) — две одинаковые силы, приложенные к абс. твердому телу и действуют вдоль одной прямой в противоположных направлениях назыв. уравновешенными силами. б) Аксиома о прибавлении или вычитании уравновешенной системы сил — действие системы сил на твердое тело не меняется, если если прибавить к ней уравновешенные силы. в) Аксиома сложения сил — силы, которые действуют на точку, можно складывать как векторы или аналитично. г) Аксиома о опорах (связи) и их реакции — силы могут быть активными и пассивными. Первые стремятся вызвать ускорение матер. точек. Другие — ограничивают движение. Они возникают как реакции системы на движение или на действие активных сил. Движение матер. точек может быть свободным или ограниченным. Во втором случае тело или точка назыв. несвободной. Все, что ограничивает движение тел в пространстве называется опорой (связью). д) Аксиома о освобождении от связи (опоры) — механическое состояние системы материальных точек не изменится, если освободить ее от связей, меняя их силами, действие которых такое же, как и связей (опор). Эти силы назыв. реакциями связей — пассивные силы, которые направлены в противоположную сторону относительно ограничения движения.
Момент силы относительно точки.
Вращательный эффект силы характеризуется ее эффектом. Моментом силы относительно центра О называется величина, равная взятому с соотв. знаком произведению модуля силы на длину плеча.
Момент силы относительно оси.
Моментом силы относительно оси называется скалярная величина, равная моменту проэкции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью.
Пара сил, момент пары. Свойства пар сил.
Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абс. твердое тело. Моментом пары наз. величина, равная взятому с соотв. знаком произведению модуля одной из сил пары на ее плечо (Понятие момента силы связано с точкой, относительно к-рой берется момент. Момент пары определяется только ее моментом и плечом; ни с какой точкой плоскости эта величина не связана). Св-ва: сумма моментов сил пары относительно точки не зависит от выбора точки и всегда равняется моменту пары, Пара сил не имеет равнодействующей — нельзя уравновесить одной силой.
Сложение пар сил.
Система пар, лежащих в одной плоскости, эквивалентна одной паре, лежащей в той же плоскости и имеющей момент, равный алгебраической сумме моментов слагаемых пар.
Теорема Вариньона.
О моменте равнодействующей — момент равнодействующей плоской системы сходящихся сил относительно любого центра равен алгебраической сумме моментов слагаемых сил относительно того же центра.
Виды нагрузок.
а) Сосредоточенная, б) Рассредоточенная равномерная и неравномерная, в) Пара сил — момент.
Параллельный перенос сил. Приведение системы сил к одному центру.
Силу можно переносить в любую точку тела, к-рая называется точкой приведения, если прибавить при этом пару сил (в точку приведения).
Главный вектор и главный момент произвольной системы сил.
Все силы, которые действуют на тело можно привести к одной точке, при этом вместо сил имеем эквивалентную систему сил, которая состоит из главного вектора и главного момента (пара сил).Частные случаи приведения произвольной системы сил к одному центру — а) главный момент равен равнодействующей, если главный момент М=0, б) Fгол =0, Мгол <>0, в) Fгол <>0, Мгол <>0, Мгол перпендик. Fгол — плоская система сил. г) Мгол <>0 Fгол <>0 Мгол || Fгол — силовой винт. е) Fгол =0, Мгол =0 — равновесие тела.
Условия равновесия произвольной пространственной системы сил.
S — сумма, Мгол = S Мi(F) = 0; Fгол = S Fi = 0;
Написать проекции на все оси.
Условия равновесия произвольной плоской системы сил.
а)Одной проекции силы нет, зато есть один момент с индексом этой оси б) есть два момента — нет двух сил в) Все моменты равны нулю.
Формы условий равновесия. ??????
Центр параллельных сил — это точка приложения равнодействующей системы параллельных сил.
Центр тяжести однородного тела.
Центр тяжести плоской фигуры.
Трение скольжения, угол трения.
Закон Кулона-Амонтона — F=fN. Угол трения — это угол, тангенс к-рого равен коэффициенту трения — предельный угол силы к нормали пов-ти, чтобы тело поехало.
Кинематика :
Теоремы о скоростях.
а) Проекции скоростей (абсол. твердого тела) двух точек на прямую, которая проходит через них равны. б) Скорость любой точки складывается из скорости какой-либо другой точки, принятой за полюс, и скорости ее вращения вокруг этой точки.
Мгновенный центр скоростей. Связь скоростей точек с мгновенными радиусами при п.п.д.
МЦС — это точка в плоскости движения, скорость к-рой в данный момент времени равна нулю.
Способы определения мгновенного центра скоростей.
Всего — четыре.
Динамика точки и системы :
Основное уравнение динамики для свободной и несвободной материальной точки в векторной, координатной и естественной формах.
Для несвободной точки – к силе прибавляется вектор N – реакция опоры.Теорема – о независимом действии сил – если на точку действует несколько сил или равнодействующая то точка будет двигаться с ускорением = сумме ускорений, к-рые возникают при действии каждой силы отдельно.
Вывести и сформулировать принцип Даламбера для точки.
ma = F + N; F + N + (-ma) = 0; Ф = -ma; — сила инерции.
Решение второй задачи динамики точки.
Это — зная силы найти закон движения. а) Показываем начальное и конечное положение тела. б) Направляем ось х из начального в конечное положение, ось у – перпендикулярно х с начального положения, в) Показываем тело в свободном положении и действующие на него силы, г) составляем дифур движения точки в проекции на ось х, д) интегрируем это уравнение, е) находим постоянные интегрирования с начальных условий и неизвестные величины. That all.
Две основные меры механического движения точки.
Импульс (кол-во движения) и кинетическая энергия.
Работа упругой силы. — Частный случайРабота силы, когда тело вращается.
Теорема об изменении кинетической энергии точки.
Изменение кинетической энергии точки при некотором ее перемещении равно сумме работ внешних сил, которые действуют на этом перемещении на точку.
Диф. уравнение движения мех системы и св-во внутренних сил.
Теорема об изменении кинетической энергии системы.
Идеальные связи – сумма возможных работ реакций которых равна нулю.
Возможные перемещения, возможная работа силы.
Возможное перемещение – это бесконечно малые перемещения точек мех. системы, которые мы представляем и которые разрешены связями. Возможные работы находятся по таким же правилам как и действительные, но вместо дифференциалов записываются их вариации.
Принцип Лагранжа-Даламбера (Общее уравнение динамики)
Необходимыми и достаточными условиями действительного движения мех. системы на к-рую действуют голономные двусторонние стационарные и идеальные связи есть равенство нулю суммы возможных работ всех активных сил и сил инерции на любых возможных перемещениях системы.Связи, классификация связей.
а) геометрические (без производных), б) кинематические (дифференциальные rj’=V), в) интегрируемые (это кинемат. К-рые можно привести к геометрич. rj=s), г) односторонние, д) двухсторонние, е) нестационарные –f(t).
Принцип возможных перемещений.
Необходимыми и достаточными условиями для равновесия мех. системы, к которой приложены двусторонние, стационарные и идеальные связи, есть равенство нулю суммы возможных работ всех активных сил на любых возможных перемещениях из положения равновесия.
Обобщенные координаты, скорости, силы.
Называются независимые параметры, которые однозначно определяют положение мех. системы (эти параметры – любой размерности).Обобщенная сила – это коэффициент при вариации обобщенной координаты в выражении возможной работы.
Обобщенная сила инерции.
Уравнение Лагранжа второго рода.
www.ronl.ru
Конспект лекций по предмету
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Для студентов специальности:
260501.65 Технология продуктов общественного питания,
форма обучения - очная
Конспект лекций составлен на основе:
Буторин Л.В., Бусыгина Е.Б. Теоретическая механика. Учебно-практическое пособие. – М., МГУ ТУ, 2004
Тарг С.М. Краткий курс теоретической механики. – М.: Высшая школа, 2001г. - с.
Яблонский А.А., Никифорова В.Н. Курс теоретической механики. М. “Лань”, 2000г.
Введение
Современные промышленные производства, в том числе пищевые, являются высокомеханизированными производствами. На технологическое оборудование возлагается решение все более сложных задач, что в свою очередь ведет к усложнению оборудования. Формирование современного инженера немыслимо без знания фундаментальных дисциплин. Одной из таких дисциплин является теоретическая механика.
Теоретическая механика – раздел механики, в котором излагаются основные законы механического движения и механического взаимодействия материальных тел. Механическим движением называется изменение с течением времени взаимного положения в пространстве материальных тел, механическим взаимодействием – такое взаимодействие, в результате которого изменяется механическое движение или изменяется взаимное положение частей тела.
Теоретическую механику принято делить на: статику, кинематику и динамику.
В статике изучаются условия равновесия материальных тел и методы тождественного преобразования системы сил. Равновесие – это состояние, при котором тело при действии сил остается неподвижным или движется равномерно прямолинейно.
В кинематике рассматриваются общие геометрические характеристики движения тел. Действующие на тело силы не рассматриваются. Закон движения задается. Закон движения тела – это зависимость положения тела в пространстве от времени.
В динамике изучают общие законы движения тел под действием сил.
1. Cтатика твердого тела
1.1 Основные понятия статики
Абсолютно твердое тело (твердое тело, тело) – материальное тело, расстояние между любыми точками в котором не изменяется. Следствие размеры и форма тела не изменяются.
Материальная точка – тело, размерами которого по условиям задачи можно пренебречь.
Свободное тело – тело, на перемещение которого не наложено никаких ограничений.
Несвободное (связанное) тело – тело, на перемещение которого наложены ограничения.
Связи – тела, препятствующие перемещению рассматриваемого объекта (тела или системы тел).
Механическая система – совокупность взаимосвязанных между собой тел или материальных точек.
Твердое тело можно рассматривать как механическую систему, положения и расстояние между точками которой не изменяются.
Сила – векторная величина, характеризующая механическое действие одного материального тела на другое.
Сила как вектор характеризуется точкой приложения, направлением действия и абсолютным значением (рис.1.1). Единица измерения модуля силы – Ньютон.
Рис.1.1. Рис.1.2.
Линия действия силы – прямая, вдоль которой направлен вектор силы.
Сосредоточенная сила – сила, приложенная в одной точке.
Распределенные силы (распределенная нагрузка) – силы, действующие на все точки объема, поверхности или длины тела (рис.1.2).
Распределенная нагрузка задается силой, действующей на единицу объема (поверхности, длины).Размерность распределенной нагрузки – Н/м3 (Н/м2, Н/м).
Внешняя сила – сила, действующая со стороны тела, не принадлежащего рассматриваемой механической системе.
Внутренняя сила – сила, действующая на материальную точку механической системы со стороны другой материальной точки, принадлежащей рассматриваемой системе.
Система сил – совокупность сил, действующих на механическую систему.
Плоская система сил – система сил, линии действия которых лежат в одной плоскости.
Пространственная система сил – система сил, линии действия которых не лежат в одной плоскости.
Система сходящихся сил – система сил, линии действия которых пересекаются в одной точке (рис.1.3).
Произвольная система сил – система сил, линии действия которых не пересекаются в одной точке.(рис.1.4)
Рис.1.3 Рис.1.4
Эквивалентные системы сил – такие системы сил, замена которых одна на другую не изменяет механического состояния тела. Принятое обозначение:
Уравновешенная система сил – система сил, которая будучи приложена к свободному твердому телу не изменяет его механического состояния (не выводит из равновесия).
Равнодействующая сила – сила, действие которой на тело эквивалентно действию системы сил.
Момент силы – величина, характеризующая вращающую способность силы.
Пара сил – система двух параллельных равных по модулю противоположно направленных сил. Принятое обозначение – ().Под действием пары сил тело будет совершать вращательное движение.
Проекция силы на ось – отрезок, заключенный между перпендикулярами, проведенными из начала и конца вектора силы к этой оси (рис.1.5 ).
Проекция положительна, если направление отрезка совпадает с положительным направлением оси.
Проекция силы на плоскость – вектор на плоскости, заключенный между перпендикулярами, проведенными из начала и конца вектора силы к этой плоскости (рис.1.6).
Рис.1.5 Рис.1.6
1.2. Аксиомы статики
В основе теоретических положений статики лежит ряд аксиом. Аксиома, это закон, сформулированный в результате обобщения результатов наблюдений.
Аксиома равновесия.
Две силы, действующие на твердое тело, уравновешиваются только в том случае, если они равны по модулю и действуют вдоль одной прямой в противоположные стороны (рис.1.7).
Рис.1.7 Рис.1.8
Аксиома присоединения ( исключения) уравновешенной системы сил.
Действие системы сил на твердое тело не изменится, если к ней присоединить или исключить из нее уравновешенную систему сил (рис 1.8).
Аксиома о параллелограмме сил.
Система двух сил, приложенных в одной точке твердого тела, имеет равнодействующую, приложенную в той же точке. Вектор равнодействующей является диагональю параллелограмма, построенного на этих силах (рис.1.9).
Рис. 1.9 Рис.1.10
4.Аксиома противодействия.
При действии одного твердого тела на другое возникает сила противодействия, равная по модулю, противоположно направленная действующей силе (рис.1.10).
Примечание. Силу, действие которой задано, называют активной силой, силу противодействия называют реакцией.
5.Аксиома связей.
Всякое несвободное тело можно рассматривать как свободное, если его мысленно освободить от связей, заменив их действие соответствующими реакциями.
1.3 Связи и их реакции
Тела, препятствующие перемещению рассматриваемого объекта, будем называть связями. Сила, с которой связь действует на рассматриваемый объект, называется реакцией связи. При определении возможных реакций связи следует исходить из того, что реакция это сила, препятствующая перемещению рассматриваемого тела. Реакция направлена в сторону, противоположную той, куда связь не позволяет перемещаться телу.
Рассмотрим некоторые часто встречающиеся связи .
Гладкая поверхность ограничивает перемещение по нормали к поверхности опоры. Реакция направлена перпендикулярно поверхности (рис.1.11).
Шарнирная подвижная опора ограничивает перемещение тела по нормали к опорной плоскости. Реакция направлена по нормали к поверхности опоры (рис.1.12)
Шарнирная неподвижная опора противодействует любому перемещению в плоскости ,перпендикулярной оси вращения. При расчетах реакцию Fr, как правило, представляют в виде двух составляющих по осям X и Y (рис.1.13).
Шарнирный невесомый стержень противодействует перемещению тела вдоль линии стержня. Реакция будет направлена вдоль линии стержня (рис.1.14).
Глухая заделка противодействует любому перемещению и вращению в плоскости (рис.1.15). Ее действие можно заменить силой, представленной в виде двух составляющих и парой сил с моментом.
www.coolreferat.com