|
|
|
|
 Far Far |
 WinNavigator WinNavigator |
 Frigate Frigate |
 Norton
Commander Norton
Commander |
 WinNC WinNC |
 Dos
Navigator Dos
Navigator |
 Servant
Salamander Servant
Salamander |
 Turbo
Browser Turbo
Browser |
|
|
 Winamp,
Skins, Plugins Winamp,
Skins, Plugins |
 Необходимые
Утилиты Необходимые
Утилиты |
 Текстовые
редакторы Текстовые
редакторы |
 Юмор Юмор |
|
|
|
File managers and best utilites |
Реферат Окружности в треугольниках и четырехугольниках. Реферат окружность
Окружность — реферат
Введение
Я выбрала именно эту тему для своего реферата, потому что многие интересные, красивые, но и трудные теоремы связаны с окружностью. Окружность можно назвать своего рода «колесом геометрии». К тому же одно из свойств колеса – его ось остаётся всё время на неизменном расстоянии от поверхности, по которой оно катится,- в математической формулировке превращается в определение окружности.
Поэтому, целью своей работы считаю:
- обобщить свои знания об окружности;
- существенно расширить кругозор, рассмотрев новые геометрические теоремы и свойства, связанные с окружностью;
- также, предложенные мною некоторые задачи имеют практическое значение (задачи о сечении головки газового вентиля, о поперечном сечении деревянного бруска).
Примечание к работе:
можно использовать при работе математического кружка,
при подготовке тематических геометрических вечеров.
Определения
Окружностью называется множество точек плоскости, равноудалённых от данной точки, называемой центром.
Радиусом окружности называется отрезок, соединяющий центр окружности с любой точкой окружности.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром. Диаметр равен удвоенному радиусу окружности.
Уравнение окружности
Если точка С – центр окружности, R – её радиус, а М – произвольная точка окружности, то по определению окружности | СМ | = R.
Пусть на плоскости задана прямоугольная система координат (рис.2) и точка С (a; b) – центр окружности радиуса R.
Пусть М (x; y) – произвольная точка этой окружности.
Так как | СМ | = √ (x – a)² + (y – b)², то уравнение можно записать так:
√ (x − a)² + (y − b)² = R
или
(x − a)² + (y − b)² = R²
Это уравнение называют общим уравнением окружности или радиуса R с центром в точке (а; b).
Например, уравнение (x – 1)² + (y + 3)² = 25 есть уравнение окружности радиуса R = 5 с центром в точке (1; -3).
Если центр окружности совпадает с началом координат, то уравнение принимает вид: x² + y² = R².
Это уравнение называют каноническим уравнением окружности.
Взаимное положение прямой и окружности
Возможны следующие три случая взаимного положения прямой и окружности: 1) Прямая не имеет с окружностью ни одной общей точки (рис.3).
2) Прямая с окружностью имеет только одну общую точку (рис.4).
Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности.
3) Прямая имеет с окружностью две общие точки (рис.5).
Такая прямая называется секущей.
Теорема о касательной к окружности
Теорема 1: Прямая, перпендикулярная к радиусу в конечной его точке, лежащей на окружности, является касательной к окружности.
Пусть ОМ – радиус окружности, CD _|_ ОM (рис.4).
Требуется доказать, что CD – касательная к окружности.
Доказательство:
Если ОМ _|_ СD, то расстояние от центра О до любой другой точки прямой СD больше радиуса ОМ, следовательно, всякая точка прямой СD, кроме точки М, лежит вне круга. Поэтому точка М – единственная общая точка прямой СD и окружности, а это означает, что СD – касательная к окружности. Теорема доказана.
Градусная мера дуги окружности
Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром окружности. На рис.11, а изображены две полуокружности, одна из которых выделена цветом.
Угол с вершиной в центре окружности называется ее центральным углом. Пусть стороны центрального угла окружности с центром О пересекают ее в точках А и В. Центральному АОВ соответствуют две дуги с концами А и В (рис.11, а, b). Если ﮮАОВ развернутый, то ему соответствуют две полуокружности (рис.11, а).
Если ﮮАОВ неразвернутый, то говорят, что дуга АВ, меньше полуокружности. На рисунке 11, б эта дуга выделена цветом. Про другую дугу с концами А и В говорят, что она больше полуокружности (ںАLВ на рис.11, в).
Дугу окружности можно измерять в градусах. Если дуга АВ окружности с центром в точке О меньше полуокружности или является полуокружностью, то ее градусная мера считается равной градусной мере центрального угла АОВ (см. рис.11, а, б). Если же дуга АВ больше полуокружности, то ее градусная мера считается равной 360˚ – ﮮАОВ (см. рис.11, в).
Отсюда следует, что сумма градусных мер двух дуг окружности с общими концами равна 360˚.
Градусная мера дуги АВ (ںАLВ), как и сама дуга, обозначается символом ںАВ (ںАLВ). На рис.12 градусная мера дуги САВ равна 145˚. Обычно говорят кратко: «ںСАВ равна 145˚» - и пишут: ںСАВ=145˚. На этом же рисунке ںАDВ=360˚-115˚=245˚,
ںСDВ=360˚-145˚=215˚, ںDВ=180˚.
Теорема о вписанном угле
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
На рис.13 ﮮАВС вписанный, дуга АМС расположена внутри этого угла. В таком случае говорят, что вписанный угол опирается на дугу АМС. Докажем теорему о вписанном угле.
Теорема: Вписанный угол измеряется половиной дуги, на которую он опирается.
Доказательство:
Пусть ﮮАВС – вписанный угол окружности с центром О, опирающийся на дугу АС (рис.14). Докажем, что ﮮАВС = ½ ں АС. Рассмотрим один из возможных случаев расположения луча ВО относительно угла АВС.
Луч ВО совпадает с одной из сторон угла АВС, например со стороной ВС (рис.14). В этом случае дуга АС меньше полуокружности, поэтому ﮮАОС= ںАС. Так как угол АОС – внешний угол равнобедренного треугольника АВО – внешний угол равнобедренного треугольника АВО, а углы 1 и 2 при основании равнобедренного треугольника равны, то ﮮАОС = ﮮ1+ﮮ2=2ﮮ1.
Отсюда следует, что 2ﮮ1 = ںАС или ﮮАВС = ﮮ1 = ½ ںАС.
Теорема доказана.
Следствие 1: Вписанные углы, опирающиеся на одну и ту же дугу, равны (рис.15).
Следствие 2: Вписанный угол, опирающийся на полуокружность – прямой (рис.16).
Основные теоремы об описанной и вписанной окружности
Окружность называется описанной около многоугольника, если все вершины многоугольника лежат на этой окружности, а многоугольник
называется вписанным в эту окружность.
Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются этой окружности, а многоугольник называется описанным около этой окружности.
Теорема: В любой треугольник можно вписать окружность.
Доказательство:
Рассмотрим произвольный треугольник АВС и обозначим буквой О точку пересечения его биссектрис. Проведем из точки О перпендикуляры ОК, ОL, и ОМ соответственно к сторонам АВ, ВС и СА (рис.18). Так как точка О равноудалена от сторон треугольника АВС, то ОК = ОL = ОМ. Поэтому окружность с центром О радиуса ОК проходит через точки К, L и М. Стороны треугольника АВС касаются этой окружности в точках К, L и М, так как они перпендикулярны к радиусам ОК, ОL и ОМ. Значит, окружность с центром О радиуса ОК является вписанной в треугольник АВС. Теорема доказана.
Рис.18
Замечание:
1) Отметим, что в треугольник можно вписать только одну окружность.
2) В отличие от треугольника не во всякий четырехугольник можно вписать окружность.
Теорема: Около любого треугольника можно описать окружность.
Доказательство:
Рассмотрим произвольный треугольник АВС. Обозначим буквой О точку пересечения серединных перпендикуляров к его сторонам и проведем отрезки ОА, ОВ и ОС (рис.21). Так как точка О равноудалена от вершин треугольника ABC, то OA = OB = OC. Следовательно, окружность с центром О радиуса ОА проходит через все три вершины треугольника и, значит, является описанной около треугольника АВС. Теорема доказана.
Рис.21
Замечание:
1) Отметим, что около треугольника можно описать только одну окружность.
2) В отличие от треугольника около четырехугольника не всегда можно описать окружность.
Около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:
Если сумма противоположных углов четырехугольника равна 1800, то около него можно описать окружность.
Теорема об окружности, описанной около правильного многоугольника
Теорема: Около любого правильного многоугольника можно описать окружность, и притом только одну.
Теорема об окружности, вписанной в правильный многоугольник
Теорема: В любой правильный многоугольник можно вписать окружность, и притом только одну.
Задача № 1
Сечение головки газового вентиля имеет форму правильного треугольника, сторона которого равна 3см. Каким должен быть минимальный диаметр круглого железного стержня, из которого изготовляют вентиль?
Дано: r АВС - правильный,
а = 3 см,
описанная окружность (О,R).
Найти: D.
Решение:
D = 2R,
a3 = R Þ R = =.
D = 2 · R =.
Ответ: минимальный диаметр круглого железного стержня должен быть равным см.
Задача №2
Поперечное сечение деревянного бруска является квадратом со стороной 6 см. Найдем наибольший диаметр круглого стержня, который можно выточить из этого бруска?
Дано: АВСD – квадрат,
А В а = 6 см,
вписанная окружность (O,r).
D С Найти: d.
Решение:
r = = 3 (см),
d = 2r = 2 ·3 = 6 см.
Ответ: наибольший диаметр круглого стержня равен 6 см.
Длина окружности
Если длину окружности обозначить буквой С, диаметр – буквой D, радиус - буквой r, то получим для вычисления длины окружности такую формулу: С = Dπ, или С = 2πr.
Греческой буквой π (пи) обозначают - число, показывающее отношение окружности к своему диаметру.
Обыкновенно при вычислениях длины окружности ограничиваются сотыми долями и принимают π ≈ 3,14.
Длина дуги в nº
Чтобы найти длину дуги в n˚, надо сначала определить длину дуги в 1˚, для чего длину окружности разделить на 360, а затем полученный результат умножить на n.
Получаем формулу: l = 2πrn = πrn, где l – длина дуги.
360 180
Площадь круга
Площадь круга вычисляется по формуле: S = π r ²,
где S – площадь круга.
Задача:
Дано: ∆АВС – описан около круга (О; r), АВ = ВС = АС = а.
Найти: S круга.
Решение:
АВ = r · 2√3,
r = а = а√3
2√3 6
S = π r ² = π a ² .
12
ИЗ ИСТОРИИ:
0 вписанных углах. Гиппократ Хиосский
Изложенное в современных учебниках доказательство того, что вписанный угол измеряется половиной дуги, на которую он опирается, дано в «Началах» Евклида. На это предложение ссылается, однако, еще Гиппократ Хиосский (V в. до н. э.) в своем труде о «луночках». Труды Гиппократа свидетельствуют о том, что уже во второй половине V в. до н. э. было известно большое число теорем, изложенных в «Началах» Евклида, и геометрия достигла высокого развития.
Тот факт, что опирающийся на диаметр вписанный угол—прямой, был известен вавилонянам еще 4000 лет назад. Первое его доказательство приписывается Памфилией, римской писательницей времен Нерона, Фалесу Милетскому. Некоторые комментаторы Евклида полагают, что доказательство Фалеса, основанное на предложении, что сумма углов трёугольника равна 2d, было следующее: обозначив углы при диаметре через 1, 2, а части угла АВС, на которые он рассекается радиусом ОС, через 3, 4, получаем, с одной стороны:
myunivercity.ru
Реферат Описанная окружность
скачатьРеферат на тему:
План:
- Введение
- 1 Свойства
- 1.1 Для треугольника
- 1.2 Для четырехугольника
- 1.3 Для многоугольника
ЛитератураПримечания
Введение

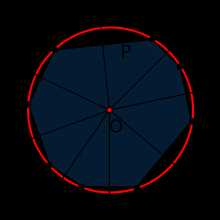
Описанная окру́жность многоугольника — окружность, содержащая все вершины многоугольника. Центром является точка (принято обозначать O) пересечения серединных перпендикуляров к сторонам многоугольника.
1. Свойства
- Центр описанной окружности выпуклого n-угольника лежит в точке пересечения серединных перпендикуляров к его сторонам. Как следствие: если рядом с n-угольником описана окружность, то все серединные перпендикуляры к его сторонам пересекаются в одной точке (центре окружности).
- Вокруг любого правильного многоугольника можно описать окружность.
1.1. Для треугольника

Окружность, описанная вокруг треугольника
- Вокруг любого треугольника можно описать окружность, притом только одну. Её центром будет являться точка пересечения серединных перпендикуляров.
- У остроугольного треугольника центр описанной окружности лежит внутри, у тупоугольного — вне треугольника, у прямоугольного — на середине гипотенузы.
-
Остроугольный
-
Прямоугольный
Обозначаем буквой О точку пересечения серединных перпендикуляров к его сторонам и проведем отрезки ОА, ОВ и ОС. Так как точка О равноудалена от вершин треугольника АВС, то ОА = OB = ОС. Поэтому окружность с центром О радиуса ОА проходит через все три вершины треугольника и, значит, является описанной около треугольника ABC.
- 3 из 4 окружностей, описанных относительно серединных треугольников (образованных средними линиями треугольника), пересекаются в одной точке внутри треугольника. Эта точка и есть центр описанной окружности основного треугольника.
- Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника.
- Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.
- Радиус описанной окружности может быть найден по формулам
- Положение центра описанной окружности.
Пусть радиус-векторы вершин треугольника, — радиус-вектор центра описанной окружности. Тогда
где
- Уравнение описанной окружности.
Пусть координаты вершин треугольника в некоторой декартовой системе координат на плоскости, — координаты центра описанной окружности. Тогда
а уравнение описанной окружности имеет вид
Для точек , лежащих внутри окружности, определитель отрицателен, а для точек вне ее — положителен.
- Теорема о трезубце: Если W — точка пересечения биссектрисы угла A с описанной окружностью, а I — центр вписанной окружности то | WI | = | WB | = | WC | .
- Формула Эйлера: Если d — расстояние между центрами вписанной и описанной окружностей, а их радиусы равны r и R соответственно, то d2 = R2 − 2Rr.
1.2. Для четырехугольника
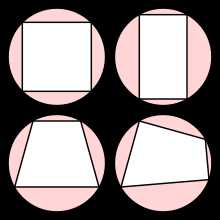
Вписанный простой (без самопересечений) четырёхугольник необходимо является выпуклым.
Вокруг выпуклого четырёхугольника можно описать окружность тогда и только тогда, когда сумма его внутренних противоположных углов равна 180° (π радиан).
Можно описать окружность вокруг:
- любого прямоугольника (частный случай квадрат)
- любой равнобедренной трапеции
У четырёхугольника, вписанного в окружность, произведение длин диагоналей равно сумме произведений длин пар противоположных сторон:[1]
|AC|·|BD| = |AB|·|CD| + |BC|·|AD|1.3. Для многоугольника
- Если из отрезков составить многоугольник, то его площадь будет максимальна, когда он вписанный.
найти уравнение для описаной около треугольника окружности
Литература
- Элементарная геометрия / Киселёв А.П.. — М.: Просвещение, 1980.
- Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — С. 87. — 383 с. — ISBN 5-09-001287-3
- Понарин Я.П. Элементарная геометрия. В 2 тт.. — М.: МЦНМО, 2004. — С. 53-54. — ISBN 5-94057-170-0
Примечания
- Теорема Птолемея - www.mccme.ru/free-books/prasolov/planim/gl6s3.htm
www.wreferat.baza-referat.ru
доклад про окружность лица - Школьные Знания.com
Школьная пора для большинства взрослых людей ассоциируется с беззаботным детством. Конечно, многие неохотно посещают школу, но только там они могут получить базовые знания, которые впоследствии пригодятся им в жизни. Одним из таких является вопрос о том, что такое окружность и круг. Спутать данные понятия достаточно просто, ведь слова являются однокоренными. Но разница между ними не настолько большая, как может показаться неопытному ребенку. Дети данную тему любят по причине ее простоты.
Что такое окружность?Окружность - это замкнутая линия, каждая точка которой равно удалена от центральной. Самым ярким примером окружности является обруч, который представляет собой замкнутое тело. Собственно, и говорить особо об окружности не приходится. В вопросе о том, что такое окружность и круг, значительно интереснее вторая его часть.
Что такое круг?Представьте, что вы решили разукрасить нарисованную выше окружность. Для этого можно выбрать любые краски: синие, желтые или зеленые - кому что ближе по душе. И вот вы начали заполнять пустоту чем-то. После того как это было закончено, у нас получилась фигура, которая называется кругом. По сути, круг - это часть поверхности, очерченная окружностью.
У круга есть несколько важных параметров, часть из которых также характерна и для окружности. Первый - это радиус. Им называется расстояние между центральной точкой круга (ну или окружности) и самой окружностью, что создает границы кругу. Вторая важная характеристика, которая неоднократно используется в школьных задачах - это диаметр (то есть расстояние между противоположными точками окружности).
Ну и наконец, третья характеристика, присущая кругу - это площадь. Данное свойство специфичное только для него, окружность не имеет площади в силу того, что у нее нет ничего внутри, а центр, в отличие от круга, скорее воображаемый, чем настоящий. В самом же круге можно установить четкий центр, через который провести ряд линий, которые делят его на сектора.
Примеры круга в реальной жизниНа самом деле возможных предметов, которые можно назвать разновидностью круга, достаточно. Например, если посмотреть на колесо машины прямо, то вот вам пример готового круга. Да, он необязательно должен быть заполнен однотонно, вполне возможны различные узоры внутри него. Второй пример круга - это солнце. Конечно, на него посмотреть будет тяжело, но оно на небе выглядит, как маленький кружочек.
Да, сама звезда Солнце - это не круг, она имеет еще и объем. Но вот само солнце, которое мы видим над нашей головой в летнее время, является типичным кругом. Правда, площадь у него все равно высчитать не получится. Ведь сравнение его с кругом приводится только для наглядности, чтобы было проще понять, что такое окружность и круг.
Отличия окружности от кругаЗначит, какой вывод мы можем сделать? Чем отличается окружность от круга, так это тем, что у последнего есть площадь, и в большинстве случаев окружность является границей круга. Хотя бывают и исключения на первый взгляд. Может показаться иногда, что нет окружности в круге, но это не так. В любом случае что-то да есть. Просто окружность может быть очень маленькой, и тогда ее не видно невооруженным глазом.
Также окружностью может быть то, что выделяет круг из фона. Например, на приведеном выше изображении синий круг находится на белом фоне. А вот та черта, по которой мы понимаем, что здесь начинается фигура, и называется в данном случае окружностью. Таким образом, окружность - это граница круга. Вот чем отличается окружность от круга.
Что такое сектор?Сектор - это участок круга, который образуется двумя проведенными по нему радиусами. Чтобы понять это определение, нужно просто вспомнить пиццу. Когда ее разрезают на равные кусочки, все они и являются секторами круга, который представлен в виде такого вкусного блюда. При этом совершенно необязательно секторы должны быть равны. Они могут быть разной величины. Например, если отрезать половину пиццы, то она также будет сектором этого круга.
Предмет, отображаемый этим понятием, может иметь только круг. Окружность (радиус тоже можно провести, конечно, но после этого она станет кругом) не имеет площади, поэтому и сектор выделить не получится.
ВыводыДа, тема о круге и окружности (что это такое) очень проста для понимания. Но вообще все то, что касается этих геометрических фигур, является самым сложным для изучения. Школьнику нужно быть готовым к тому, что круг - фигура капризная. Но, как говорится, тяжело в учении - легко в бою. Да, геометрия - наука сложная. Зато успешное ее освоение позволяет сделать маленький шажок в сторону успеха. Потому что старания при обучении позволяют не только пополнять багаж собственных знаний, но и получать необходимые в жизни навыки. Собственно, на это и нацелена школа. А ответ на вопрос о том, что такое окружность и круг, является вторичным, хоть и важным.
znanija.com
Реферат Описанная окружность
скачатьРеферат на тему:
План:
- Введение
- 1 Свойства
- 1.1 Для треугольника
- 1.2 Для четырехугольника
- 1.3 Для многоугольника
ЛитератураПримечания
Введение

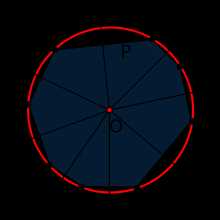
Описанная окру́жность многоугольника — окружность, содержащая все вершины многоугольника. Центром является точка (принято обозначать O) пересечения серединных перпендикуляров к сторонам многоугольника.
1. Свойства
- Центр описанной окружности выпуклого n-угольника лежит в точке пересечения серединных перпендикуляров к его сторонам. Как следствие: если рядом с n-угольником описана окружность, то все серединные перпендикуляры к его сторонам пересекаются в одной точке (центре окружности).
- Вокруг любого правильного многоугольника можно описать окружность.
1.1. Для треугольника

Окружность, описанная вокруг треугольника
- Вокруг любого треугольника можно описать окружность, притом только одну. Её центром будет являться точка пересечения серединных перпендикуляров.
- У остроугольного треугольника центр описанной окружности лежит внутри, у тупоугольного — вне треугольника, у прямоугольного — на середине гипотенузы.
-
Остроугольный
-
Прямоугольный
Обозначаем буквой О точку пересечения серединных перпендикуляров к его сторонам и проведем отрезки ОА, ОВ и ОС. Так как точка О равноудалена от вершин треугольника АВС, то ОА = OB = ОС. Поэтому окружность с центром О радиуса ОА проходит через все три вершины треугольника и, значит, является описанной около треугольника ABC.
- 3 из 4 окружностей, описанных относительно серединных треугольников (образованных средними линиями треугольника), пересекаются в одной точке внутри треугольника. Эта точка и есть центр описанной окружности основного треугольника.
- Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника.
- Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.
- Радиус описанной окружности может быть найден по формулам
- Положение центра описанной окружности.
Пусть радиус-векторы вершин треугольника, — радиус-вектор центра описанной окружности. Тогда
где
- Уравнение описанной окружности.
Пусть координаты вершин треугольника в некоторой декартовой системе координат на плоскости, — координаты центра описанной окружности. Тогда
а уравнение описанной окружности имеет вид
Для точек , лежащих внутри окружности, определитель отрицателен, а для точек вне ее — положителен.
- Теорема о трезубце: Если W — точка пересечения биссектрисы угла A с описанной окружностью, а I — центр вписанной окружности то | WI | = | WB | = | WC | .
- Формула Эйлера: Если d — расстояние между центрами вписанной и описанной окружностей, а их радиусы равны r и R соответственно, то d2 = R2 − 2Rr.
1.2. Для четырехугольника

Вписанный простой (без самопересечений) четырёхугольник необходимо является выпуклым.
Вокруг выпуклого четырёхугольника можно описать окружность тогда и только тогда, когда сумма его внутренних противоположных углов равна 180° (π радиан).
Можно описать окружность вокруг:
- любого прямоугольника (частный случай квадрат)
- любой равнобедренной трапеции
У четырёхугольника, вписанного в окружность, произведение длин диагоналей равно сумме произведений длин пар противоположных сторон:[1]
|AC|·|BD| = |AB|·|CD| + |BC|·|AD|1.3. Для многоугольника
- Если из отрезков составить многоугольник, то его площадь будет максимальна, когда он вписанный.
найти уравнение для описаной около треугольника окружности
Литература
- Элементарная геометрия / Киселёв А.П.. — М.: Просвещение, 1980.
- Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — С. 87. — 383 с. — ISBN 5-09-001287-3
- Понарин Я.П. Элементарная геометрия. В 2 тт.. — М.: МЦНМО, 2004. — С. 53-54. — ISBN 5-94057-170-0
Примечания
- Теорема Птолемея - www.mccme.ru/free-books/prasolov/planim/gl6s3.htm
wreferat.baza-referat.ru
Реферат Вписанная окружность
Реферат на тему:

План:
- Введение
- 1 В многоугольнике
- 2 В треугольнике
- 3 В четырёхугольнике Литература
Введение

Окружность, вписанная в многоугольник ABCDE
Окружность называется вписанной в угол, если она лежит внутри угла и касается его сторон. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
Окружность называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника и касается всех прямых, проходящих через его стороны.
1. В многоугольнике
Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех углов данного многоугольника пересекаются в одной точке, которая является центром вписанной окружности.
- Радиус вписанной в многоугольник окружности равен отношению его площади к полупериметру[1]
- Теорема о трезубце или о трилистнике: Если W — точка пересечения биссектрисы угла A с описанной окружностью, а I — центр вписанной окружности, то | WI | = | WB | = | WC | . Здесь C и B — вершины многоугольника, соседние с вершиной A.
2. В треугольнике
Свойства вписанной окружности:
- В каждый треугольник можно вписать окружность, притом только одну.
- Центр O вписанной окружности называется инцентром, он равноудалён от всех сторон и является точкой пересечения биссектрис треугольника.
- Радиус вписанной в треугольник окружности равен
- Если AB — основание равнобедренного , то окружность, касающаяся сторон в точках A и B, проходит через точку О.
- Формула Эйлера: R2 − 2Rr = | OI | 2, где R — радиус описанной вокруг треугольника окружности, r — радиус вписанной в него окружности, O — центр описанной окружности, I — центр вписанной окружности.
- Если прямая, проходящая через точку О параллельно стороне AB, пересекает стороны BC и CA в точках A1 и B1, то A1B1 = A1B + AB1.
- Точки касания вписанной в треугольник T окружности соединены отрезками — получается треугольник T1
- биссектрисы T являются серединными перпендикулярами T1
- Пусть T2 — ортотреугольник T1. Тогда его стороны параллельны сторонам исходного треугольника T.
- Пусть T3 — серединный треугольник T1. Тогда биссектрисы T являются высотами T3.
- Пусть T4 — ортотреугольник T3, тогда биссектрисы T являются биссектрисами T4.
- Радиус вписанной в прямоугольный треугольник с катетами a, b и гипотенузой c окружности равен .
- Расстояние от вершины С треугольника до точки, в которой вписанная окружность касается стороны равно .
- Расстояние от от вершины C до центра вписаной окружности равно , где r - радиус вписаной окружности, а γ - угол вершины C.
- Расстояние от вершины C до центра вписаной окружности может так же быть найдено по формуле
3. В четырёхугольнике
Описанный четырёхугольник, если у него нет самопересечений («простой»), должен быть выпуклым.
В выпуклый четырёхугольник ABCD можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны: AB + CD = BC + AD.
Во всяком описанном четырёхугольнике середины диагоналей и центр вписанной окружности лежат на одной прямой (теорема Ньютона). На ней же лежит середина отрезка с концами в точках пересечения противоположных сторон четырёхугольника. Эта прямая называется прямой Гаусса.
Литература
- Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — С. 89. — 383 с. — ISBN 5-09-001287-3
- Понарин Я.П. Элементарная геометрия. В 2 тт.. — М.: МЦНМО, 2004. — С. 52-53. — ISBN 5-94057-170-0
Категории: Геометрия треугольника, Кривые.
Текст доступен по лицензии Creative Commons Attribution-ShareAlike.www.wreferat.baza-referat.ru
Окружности в треугольниках и четырехугольниках
Муниципальное общеобразовательное учреждение
средняя общеобразовательная школа № 8
Реферат по геометрии на тему:
Окружности в треугольниках и четырехугольниках
Работу выполнил ученик 9 «А» класса
МОУ СОШ № 8 Петров Игорь
Руководитель: учитель математики МОУ СОШ № 8
Смирнова Надежда Анатольевна
Содержание:
1. Введение
2. Теоретическая часть:
2.1 Вписанная окружность
2.2 Описанная окружность
2.3 Взаимное расположение прямой и окружности
2.4 Площади фигур
2.5 Свойства прямоугольного треугольника
3. Практическая часть:
3.1 Задачи с окружностью, описанной около треугольника
3.2 Задачи с окружностью, вписанной в треугольник
3.3 Задачи с окружностью, описанной около четырехугольника
3.4 Задачи с окружностью, вписанной в четырехугольник
4. Заключение
Список литературы:
1. Введение
Тема «Вписанные и описанные окружности в треугольниках и четырехугольниках» является одной из самых сложных в курсе геометрии. На уроках ей уделяется очень мало времени.
Геометрические задачи этой темы включаются во вторую часть экзаменационной работы ЕГЭ за курс средней школы.
Для успешного выполнения этих заданий необходимы твердые знания основных геометрических фактов и некоторый опыт в решении геометрических задач.
Цель:
- Углубить знания по теме «Вписанная и описанная окружности в треугольниках и четырехугольниках»
Задачи:
- Систематизировать знания по этой теме
- Подготовиться к решению задач повышенной сложности ЕГЭ
2.Теоретическая часть
2.1Вписанная окружность
Определение:если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.
Теорема:в любой треугольник можно вписать окружность, и притом только одну.
Центр окружности, вписанной в треугольник, находится на пересечении биссектрис треугольника.
Свойство:в любом описанном четырехугольнике суммы противоположных сторон равны.
Признак:если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
2.2 Описанная окружность
Определение:если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.
Теорема:около любого треугольника можно описать окружность, и притом только одну.
Центр окружности, описанной около треугольника, находится на пересечении серединных перпендикуляров.
Свойство:в любом вписанном четырехугольнике сумма противоположных углов равна 180˚.
Признак:если сумма противоположных углов четырехугольника равна 180˚, то около него можно описать окружность.
2.3 Взаимное расположение прямой и окружности:
AB – касательная, если OH = r
Свойство касательной:
AB┴OH (OH – радиус, проведенный в точку касания H)
Свойство отрезков касательных, проведенных из одной точки:
AB = AC
ﮮ BAO = ﮮ CAO
Свойство хорд:если две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM ∙ MB = CM ∙ MD.
Медиана
Медиана (от лат. mediana — средняя), отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
Теорема:сумма углов треугольника равна 180°
Основное тригонометрическое тождество:sin2A + cos2A = 1
Теорема косинусов:квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними: a2= b2+ c2– 2bc ∙ cos A
2.4 Площади фигур
Площадь параллелограмма
Площадь параллелограмма равна произведению его основания на высоту:
· Площадь параллелограмма равна произведению двух соседних его сторон на синус угла между ними:
Площадь треугольника
- Площадь треугольника равна половине произведения двух его сторон на синус угла между ними:
- Площадь треугольника равна половине произведения его основания на высоту:
- Площадь прямоугольного треугольника равна половине произведения его катетов:
- Если высоты двух треугольников равны, то их площади относятся как основания.
- Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы:
Площадь трапеции
Площадь трапеции равна произведению полусуммы её оснований на высоту:
Теорема: отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
2.5 Прямоугольный треугольник
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой:
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы:
Теорема Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c2= a2+ b2
3. Практическая часть
3.1 Задачи с окружностью, описанной около треугольника
Задача 1:Около равнобедренного треугольника с основанием AC и углом при основании 75˚ описана окружность с центром O. Найдите ее радиус, если площадь треугольника BOC равна 16.
Дано: ∆ ABC – равнобедренный, AC – основание, ﮮ ACB = 75˚,
площадь ∆ BOC равна 16
Найти: радиус описанной окружности
Решение:
1. Проведем медианы AF, CE, BH
2. ∆ ABC – равнобедренный, BH – медиана, следовательно, BH – высота, а значит ∆ HBC – прямоугольный
3. ﮮ HBC = 90˚ - ﮮ ACB, ﮮ HBC = 90˚ - 75˚ = 15˚
4. BO = OC = R, следовательно, ∆ BOC – равнобедренный, значит ﮮHBC = ﮮECB = 15˚
5. ﮮ COB = 180˚ - (ﮮ HBC + ﮮECB), ﮮ COB = 180˚ - (15˚ + 15˚) = 150˚
6. S =∙ BO ∙ OC ∙ sin ﮮ BOC (теорема о площади треугольника), SBOC=∙ R ∙ R ∙ sin 150˚ =∙ R ∙ R ∙=∙ R2;∙ R2= 16; R2= 16 := 64; R == 8
Ответ: R = 8
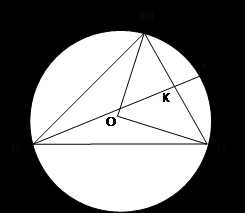
Задача 2:треугольник BMP с углом B, равным 45˚, вписан в окружность радиуса 6. Найдите длину медианы BK, если BK пересекает окружность в точке C и CK = 3.
Решение:
1. ﮮ MOP = 2 ﮮMBP
ﮮ MOP = 2 ∙ 45˚ = 90˚, следовательно, ∆ MOP – прямоугольный
2. MP2= OM2+ OP2
MP2= 62+ 62= 36 + 36 = 36 ∙ 2
MP =
3. MK = KP = 0,5 ∙ MP
MK = KP = 0,5 ∙=
4. MK ∙ KP = BK ∙ KC
= BK ∙ 3
BK ∙ 3 = 9 ∙ 2
BK ∙ 3 = 18
BK = 6
Ответ: BK = 6
Задача 3:остроугольный равнобедренный треугольник BCD с основанием CD, равным 16, вписан в окружность с центром O и радиусом 10. Найдите площадь треугольника BOC.
Решение:
1. ∆ BCD – равнобедренный, CD = 16, следовательно, DH = HC = 8
2. ∆ DOH – прямоугольный
По теореме Пифагора:
Oh3= 102– 82
Oh3= 100 – 64 = 36
OH = 6
3. BH = BO + OH = 10 + 6 =16
4. По теореме Пифагора:
BC2= 162+ 82= 256 + 64 = 320
BC =
5. ∆ KBO ~ ∆ HBC
6. SBHC=
7.
SBOK= 20
8. SBOC= 2 ∙ SBOK= 2 ∙ 20 = 40
Ответ: SBOC= 40
3.2 Задачи с окружностью, вписанной в треугольник
Задача 4:радиус окружности, вписанной в прямоугольный треугольник, равен 2 м, а радиус описанной окружности равен 5 м. Найдите больший катет треугольника.
Решение:
1. AC = 2r = 10 м
2. Пусть AM = AK = x, MC = CL = y
По теореме Пифагора:
x + y = 10
(x + 2)2+ (y + 2)2= (x + y)2
y = 10 – x
(x + 2)2+ (10 – x + 2)2= (x + 10 – x)2
(x + 2)2+ (12 – x)2= 100
x2+ 4x + 4 +144 – 24x + x2= 100
2x2– 20x + 148 = 100
2x2– 20x + 48 = 0
x2– 10x + 24 = 0
x1= 6, x2= 4
y = 10 – x
x = 6 x = 4
y = 4 y = 6
3. Так как нужно найти больший катет, то берем y = 6
BC = 2 + 6 = 8 м
Ответ: BС = 8 м
Задача 5:окружность, вписанная в равнобедренный треугольник, касается его боковых сторон в точках K и A. Точка K делит сторону этого треугольника на отрезки 15 и 10, считая от основания. Найдите длину отрезка KA.
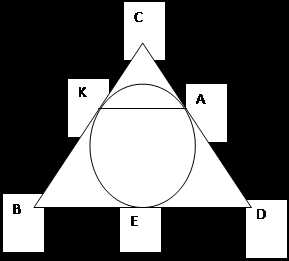 |
Дано: ∆ BCD – равнобедренный, K є BC, A є DC, BK = 15, KC = 10
Найти: KA
Решение:
1. CD = CB = BK + KC, CD = CB = 15 + 10 = 25
2. CK = CA = 10 (отрезки касательных, проведенные из одной точки), CB = CD, следовательно AD = CD – CA, AD = 25 – 10 = 15
3. BE = BK = 15, DE = DA = 15 (отрезки касательных, проведенные из одной точки), следовательно BD = 15 + 15 = 30
4. ∆ CKA ~ ∆ CBD (ﮮC – общий, CK : CB = CA : CD), следовательно KA : BD = CA : CD, KA : 30 = 10 : 25, KA = 10 ∙ 30 : 25 = 12
Ответ: KA = 12
1. BC = x + y
BC = 18 + 12 = 30 (м)
Ответ: 30 м – диаметр описанной окружности
3.3. Задачи с окружностью, описанной около четырехугольника
Задача 6:в равнобедренной трапеции основания 21 и 9 сантиметров, высота – 8 сантиметров. Найти радиус описанной окружности.
Решение:
1. Проведем серединные перпендикуляры к основаниям Н и К, тогда центр окружности О лежит на прямой НК.
2. АО=ОВ=R. Точка О делит отрезок НК на две части: пусть НО = х, тогда ОК = 8 – х.
3. АО2= АК2+ КО2; ОВ2= ВН2+ НО2;
так как ОА2=ОВ2, получим:
АК2+ КО2= ВН2+ НО2
90 + 64 – 16x = 0
16x = 154
ОВ2= ВН2+ НО2
Ответ: OB = 10,625
3.4 Задачи с окружностью, вписанной в четырехугольник
Задача 7:в ромб вписана окружность радиуса R. Найти площадь ромба, если его большая диагональ в 4 раза больше радиуса вписанной окружности.
Дано: ромб, радиус вписанной окружности – R, BDr в 4 раза
Найти:
Решение:
1. Пусть OE = R, BD = 4OE = 4R
2.
3.
4.
Ответ:
Задача 8:найдите площадь равнобедренной трапеции, описанной около окружности с радиусом 4, если известно, что боковая сторона трапеции равна 10.
Дано: ABCD – равнобедренная трапеция, r = 4, AB = 10
Найти:
Решение:
1. AB = CD = 10 по условию
2. AB + CD = AD + BC по свойству вписанной окружности
3. AD + BC = 10 + 10 = 20
4. FE = 2r = 2 · 4 = 8
5.
Ответ:
Задача 9:внутри правильного треугольника со стороной a расположены три равные окружности, каждая из которых касается двух сторон треугольника и двух других окружностей. Найти площадь части треугольника, расположенной вне этих окружностей.
Решение:
1. Пусть AB = BC = AC = a.
2. Обозначим O1E = O1K = ED = r, тогда AD = AE + ED = AE + r =.
3. AO1– биссектриса угла A, следовательно, ﮮ O1AE = 30˚ и в прямоугольном ∆AO1E имеем AO1= 2O1E = 2r и AE ===. Тогда AE + r = ==, откуда.
4.
Ответ:
Задача 10: вся дуга окружности радиуса R разделена на 4 большие и 4 малые части, которые чередуются одна за другой. Большая часть в два раза длиннее малой. Определить площадь восьмиугольника, вершинами которого являются точки деления дуги окружности.
Решение:
1. Пусть ﮮAOB = 2x, ﮮBOC = x, тогда по условию 8x + 4x = 360°, x = 30°, 2x = 60°, ﮮAOB = 60°, ﮮBOC = 30°
2.
3.
4.
Ответ:
Задача 11:стороны треугольника равны 12 м, 16 м и 20 м. Найдите го высоту, проведенную из вершины большего угла.
Решение:
1. 202= 122+ 162
400 = 144 + 256
400 = 400 верно, следовательно, ∆ АВС – прямоугольный (по теореме, обратной теореме Пифагора)
2.
3.
96 = 10 · ВН
ВН = 9,6
Ответ: ВН = 9,6
Задача 12:в прямоугольный треугольник вписан квадрат, имеющий с ним общий угол. Найдите площадь квадрата, если катеты треугольника равны 10 м и 15 м.
Дано: ∆ ABC – прямоугольный, AC = 15, CB = 10
Найти:
Решение:
1. ∆ ADE ~ ∆ ACB (ﮮ A – общий, ﮮ ADE = ﮮ ACB = 90°)
2. Пусть DE = DC = X, тогда AD = 15 – X
3.
15 · X = 10(15 – X)
15 · X = 150 – 10 · X
25 · X = 150
X = 6
DE = DC = 6
4. Sкв.= 6 · 6 = 36
Ответ: Sкв.= 36
Задача 13:основания трапеции равны 10 м и 31 м, а боковые стороны – 20 м и 13 м. Найдите высоту трапеции.
Решение:
1. HK = BC = 10 м
2. Пусть BH = CK = x, AH=y, тогда KD = 21 – y
3. По теореме Пифагора:
x2+ y2= 132
x2+ (21 – y)2= 202
x2+ y2= 169
x2+ 441 – 42y + y2= 400
441 – 42y = 231
42y = 210
y = 5
AH = 5 м
4. По теореме Пифагора:
Bh3= AB2– Ah3
Bh3= 132– 52
Bh3= 169 – 25
Bh3= 144
BH = 12
Ответ: BH = 12
4. Заключение
В процессе работы я расширил знания по теме «Вписанные и описанные окружности в треугольниках и четырехугольниках», научился решать задачи, казавшиеся ранее недоступными, систематизировал знания по этой теме, и закрепил методы решения этих задач на практике.
Так как геометрические задачи этой темы включаются во вторую часть экзаменационной работы ЕГЭ за курс средней школы, то в дальнейшем мне будет намного легче справиться с ними на ЕГЭ.
Список литературы:
1. «Единый государственный экзамен 2006. Математика. Учебно-тренировочные материалы для подготовки учащихся/ Рособрнадзор, ИСОП – М.: Интеллект-Центр, 2006»
2. Мазур К. И. «Решение основных конкурсных задач по математике сборника под редакцией М. И. Сканави»
3. Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина «Геометрия, 7 – 9: учебник для общеобразовательных учреждений»
4. Т. А. Корешкова, Ю. А. Глазков, В. В. Мирошин, Н. В. Шевелева «Математика. Единый государственный экзамен 2006. Типовые тестовые задания»
superbotanik.net
Реферат Окружности в треугольниках и четырехугольниках
Муниципальное общеобразовательное учреждение
средняя общеобразовательная школа № 8
Реферат по геометрии на тему:
Окружности в треугольниках и четырехугольниках
Работу выполнил ученик 9 «А» класса
МОУ СОШ № 8 Петров Игорь
Руководитель: учитель математики МОУ СОШ № 8
Смирнова Надежда Анатольевна
Содержание:
Введение
Теоретическая часть:
2.1 Вписанная окружность
2.2 Описанная окружность
2.3 Взаимное расположение прямой и окружности
2.4 Площади фигур
2.5 Свойства прямоугольного треугольника
Практическая часть:
3.1 Задачи с окружностью, описанной около треугольника
3.2 Задачи с окружностью, вписанной в треугольник
3.3 Задачи с окружностью, описанной около четырехугольника
3.4 Задачи с окружностью, вписанной в четырехугольник
Заключение
Список литературы:
1. Введение
Тема «Вписанные и описанные окружности в треугольниках и четырехугольниках» является одной из самых сложных в курсе геометрии. На уроках ей уделяется очень мало времени.
Геометрические задачи этой темы включаются во вторую часть экзаменационной работы ЕГЭ за курс средней школы.
Для успешного выполнения этих заданий необходимы твердые знания основных геометрических фактов и некоторый опыт в решении геометрических задач.
Цель:
Задачи:
Систематизировать знания по этой теме
Подготовиться к решению задач повышенной сложности ЕГЭ
2.Теоретическая часть
2.1 Вписанная окружность
Определение: если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.
Теорема: в любой треугольник можно вписать окружность, и притом только одну.
Центр окружности, вписанной в треугольник, находится на пересечении биссектрис треугольника.
Свойство: в любом описанном четырехугольнике суммы противоположных сторон равны.
Признак: если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
2.2 Описанная окружность
Определение: если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.
Теорема: около любого треугольника можно описать окружность, и притом только одну.
Центр окружности, описанной около треугольника, находится на пересечении серединных перпендикуляров.
Свойство: в любом вписанном четырехугольнике сумма противоположных углов равна 180˚.
Признак: если сумма противоположных углов четырехугольника равна 180˚, то около него можно описать окружность.
2.3 Взаимное расположение прямой и окружности:
AB – касательная, если OH = r
Свойство касательной:
AB ┴ OH (OH – радиус, проведенный в точку касания H)
Свойство отрезков касательных, проведенных из одной точки:
AB = AC
ﮮ BAO = ﮮ CAO
Свойство хорд: если две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM ∙ MB = CM ∙ MD.
Медиана
Медиана (от лат. mediana — средняя), отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
Теорема: сумма углов треугольника равна 180°
Основное тригонометрическое тождество: sin2A + cos2A = 1
Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними: a2 = b2 + c2 – 2bc ∙ cos A
2.4 Площади фигур
Площадь параллелограмма
Площадь параллелограмма равна произведению его основания на высоту:
Площадь треугольника
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы:
Площадь трапеции
Площадь трапеции равна произведению полусуммы её оснований на высоту:
Теорема: отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
2.5 Прямоугольный треугольник
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой:
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы:
Теорема Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c2 =a2 + b2
3. Практическая часть
3.1 Задачи с окружностью, описанной около треугольника
Задача 1: Около равнобедренного треугольника с основанием AC и углом при основании 75˚ описана окружность с центром O. Найдите ее радиус, если площадь треугольника BOC равна 16.
Дано: ∆ ABC – равнобедренный, AC – основание, ﮮ ACB = 75˚,
площадь ∆ BOC равна 16
Найти: радиус описанной окружности
Решение:
Проведем медианы AF, CE, BH
∆ ABC – равнобедренный, BH – медиана, следовательно, BH – высота, а значит ∆ HBC – прямоугольный
ﮮ HBC = 90˚ - ﮮ ACB, ﮮ HBC = 90˚ - 75˚ = 15˚
BO = OC = R, следовательно, ∆ BOC – равнобедренный, значит ﮮHBC = ﮮECB = 15˚
ﮮ COB = 180˚ - (ﮮ HBC + ﮮECB), ﮮ COB = 180˚ - (15˚ + 15˚) = 150˚
S = ∙ BO ∙ OC ∙ sin ﮮ BOC (теорема о площади треугольника), SBOC = ∙ R ∙ R ∙ sin 150˚ = ∙ R ∙ R ∙ = ∙ R2 ; ∙ R2 = 16; R2 = 16 : = 64; R = = 8
Ответ: R = 8
Задача 2: треугольник BMP с углом B, равным 45˚, вписан в окружность радиуса 6. Найдите длину медианы BK, если BK пересекает окружность в точке C и CK = 3.
Решение:
ﮮ MOP = 2 ﮮMBP
ﮮ MOP = 2 ∙ 45˚ = 90˚, следовательно, ∆ MOP – прямоугольный
MP2 = OM2 + OP2
MP2 = 62 + 62 = 36 + 36 = 36 ∙ 2
MP =
MK = KP = 0,5 ∙ MP
MK = KP = 0,5 ∙ =
MK ∙ KP = BK ∙ KC
= BK ∙ 3
BK ∙ 3 = 9 ∙ 2
BK ∙ 3 = 18
BK = 6
Ответ: BK = 6
Задача 3: остроугольный равнобедренный треугольник BCD с основанием CD, равным 16, вписан в окружность с центром O и радиусом 10. Найдите площадь треугольника BOC.
Решение:
∆ BCD – равнобедренный, CD = 16, следовательно, DH = HC = 8
∆ DOH – прямоугольный
По теореме Пифагора:
Oh3 = 102 – 82
Oh3 = 100 – 64 = 36
OH = 6
BH = BO + OH = 10 + 6 =16
По теореме Пифагора:
BC2 = 162 + 82 = 256 + 64 = 320
BC =
∆ KBO ~ ∆ HBC
SBHC =
SBOK = 20
SBOC = 2 ∙ SBOK = 2 ∙ 20 = 40
Ответ: SBOC = 40
3.2 Задачи с окружностью, вписанной в треугольник
Задача 4: радиус окружности, вписанной в прямоугольный треугольник, равен 2 м, а радиус описанной окружности равен 5 м. Найдите больший катет треугольника.
Решение:
AC = 2r = 10 м
Пусть AM = AK = x, MC = CL = y
По теореме Пифагора:
x + y = 10
(x + 2)2 + (y + 2)2 = (x + y)2
y = 10 – x
(x + 2)2 + (10 – x + 2)2 = (x + 10 – x)2
(x + 2)2 + (12 – x)2 = 100
x2 + 4x + 4 +144 – 24x + x2 = 100
2x2 – 20x + 148 = 100
2x2 – 20x + 48 = 0
x2 – 10x + 24 = 0
x1 = 6, x2 = 4
y = 10 – x
x = 6 x = 4
y = 4 y = 6
3. Так как нужно найти больший катет, то берем y = 6
BC = 2 + 6 = 8 м
Ответ: BС = 8 м
Задача 5: окружность, вписанная в равнобедренный треугольник, касается его боковых сторон в точках K и A. Точка K делит сторону этого треугольника на отрезки 15 и 10, считая от основания. Найдите длину отрезка KA.
Дано: ∆ BCD – равнобедренный, K є BC, A є DC, BK = 15, KC = 10
Найти: KA
Решение:
CD = CB = BK + KC, CD = CB = 15 + 10 = 25
CK = CA = 10 (отрезки касательных, проведенные из одной точки), CB = CD, следовательно AD = CD – CA, AD = 25 – 10 = 15
BE = BK = 15, DE = DA = 15 (отрезки касательных, проведенные из одной точки), следовательно BD = 15 + 15 = 30
∆ CKA ~ ∆ CBD (ﮮC – общий, CK : CB = CA : CD), следовательно KA : BD = CA : CD, KA : 30 = 10 : 25, KA = 10 ∙ 30 : 25 = 12
Ответ: KA = 12
BC = x + y
BC = 18 + 12 = 30 (м)
Ответ: 30 м – диаметр описанной окружности
3.3. Задачи с окружностью, описанной около четырехугольника
Задача 6: в равнобедренной трапеции основания 21 и 9 сантиметров, высота – 8 сантиметров. Найти радиус описанной окружности.
Решение:
Проведем серединные перпендикуляры к основаниям Н и К, тогда центр окружности О лежит на прямой НК.
АО=ОВ=R. Точка О делит отрезок НК на две части: пусть НО = х, тогда ОК = 8 – х.
АО2 = АК2 + КО2; ОВ2 = ВН2 + НО2;
так как ОА2=ОВ2, получим:
АК2 + КО2 = ВН2 + НО2
90 + 64 – 16x = 0
16x = 154
ОВ2 = ВН2 + НО2
Ответ: OB = 10,625
3.4 Задачи с окружностью, вписанной в четырехугольник
Задача 7: в ромб вписана окружность радиуса R. Найти площадь ромба, если его большая диагональ в 4 раза больше радиуса вписанной окружности.
Дано: ромб, радиус вписанной окружности – R, BD r в 4 раза
Найти:
Решение:
Пусть OE = R, BD = 4OE = 4R
Ответ:
Задача 8: найдите площадь равнобедренной трапеции, описанной около окружности с радиусом 4, если известно, что боковая сторона трапеции равна 10.
Дано: ABCD – равнобедренная трапеция, r = 4, AB = 10
Найти:
Решение:
AB = CD = 10 по условию
AB + CD = AD + BC по свойству вписанной окружности
AD + BC = 10 + 10 = 20
FE = 2r = 2 · 4 = 8
Ответ:
Задача 9: внутри правильного треугольника со стороной a расположены три равные окружности, каждая из которых касается двух сторон треугольника и двух других окружностей. Найти площадь части треугольника, расположенной вне этих окружностей.
Решение:
Пусть AB = BC = AC = a.
Обозначим O1E = O1K = ED = r, тогда AD = AE + ED = AE + r = .
AO1 – биссектриса угла A, следовательно, ﮮ O1AE = 30˚ и в прямоугольном ∆AO1E имеем AO1 = 2O1E = 2r и AE ===. Тогда AE + r = == , откуда .
4.
Ответ:
Задача 10: вся дуга окружности радиуса R разделена на 4 большие и 4 малые части, которые чередуются одна за другой. Большая часть в два раза длиннее малой. Определить площадь восьмиугольника, вершинами которого являются точки деления дуги окружности.
Решение:
Пусть ﮮAOB = 2x, ﮮBOC = x, тогда по условию 8x + 4x = 360°, x = 30°, 2x = 60°, ﮮAOB = 60°, ﮮBOC = 30°
Ответ:
Задача 11: стороны треугольника равны 12 м, 16 м и 20 м. Найдите го высоту, проведенную из вершины большего угла.
Решение:
202 = 122 + 162
400 = 144 + 256
400 = 400 верно, следовательно, ∆ АВС – прямоугольный (по теореме, обратной теореме Пифагора)
96 = 10 · ВН
ВН = 9,6
Ответ: ВН = 9,6
Задача 12: в прямоугольный треугольник вписан квадрат, имеющий с ним общий угол. Найдите площадь квадрата, если катеты треугольника равны 10 м и 15 м.
Дано: ∆ ABC – прямоугольный, AC = 15, CB = 10
Найти:
Решение:
∆ ADE ~ ∆ ACB (ﮮ A – общий, ﮮ ADE = ﮮ ACB = 90°)
Пусть DE = DC = X, тогда AD = 15 – X
15 · X = 10(15 – X)
15 · X = 150 – 10 · X
25 · X = 150
X = 6
DE = DC = 6
S кв. = 6 · 6 = 36
Ответ: S кв.= 36
Задача 13: основания трапеции равны 10 м и 31 м, а боковые стороны – 20 м и 13 м. Найдите высоту трапеции.
Решение:
HK = BC = 10 м
Пусть BH = CK = x, AH=y, тогда KD = 21 – y
По теореме Пифагора:
x2 + y2 = 132
x2 + (21 – y)2 = 202
x2 + y2 = 169
x2 + 441 – 42y + y2 = 400
441 – 42y = 231
42y = 210
y = 5
AH = 5 м
По теореме Пифагора:
Bh3 = AB2 – Ah3
Bh3 = 132 – 52
Bh3 = 169 – 25
Bh3 = 144
BH = 12
Ответ: BH = 12
4. Заключение
В процессе работы я расширил знания по теме «Вписанные и описанные окружности в треугольниках и четырехугольниках», научился решать задачи, казавшиеся ранее недоступными, систематизировал знания по этой теме, и закрепил методы решения этих задач на практике.
Так как геометрические задачи этой темы включаются во вторую часть экзаменационной работы ЕГЭ за курс средней школы, то в дальнейшем мне будет намного легче справиться с ними на ЕГЭ.
Список литературы:
«Единый государственный экзамен 2006. Математика. Учебно-тренировочные материалы для подготовки учащихся/ Рособрнадзор, ИСОП – М.: Интеллект-Центр, 2006»
Мазур К. И. «Решение основных конкурсных задач по математике сборника под редакцией М. И. Сканави»
Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина «Геометрия, 7 – 9: учебник для общеобразовательных учреждений»
Т. А. Корешкова, Ю. А. Глазков, В. В. Мирошин, Н. В. Шевелева «Математика. Единый государственный экзамен 2006. Типовые тестовые задания»
bukvasha.ru
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|







