Степенные функции, их свойства и графики. Реферат на тему степенная функция ее свойства и график

Степенные функции, их свойства и графики

Вопросы занятия:

· рассмотреть степенные функции;

· рассмотреть свойства и графики степенных функций, в зависимости от основания.

Материал урока

Определение.

Степенными функциями называют функции вида:

Случаи, когда r – натуральное или целое число мы с вами уже изучали.

Давайте повторим основные моменты.

Сегодня на уроке мы познакомимся с функцией:

Для начала рассмотрим случай, когда показатель степени больше 0. Этот случай можно разбить ещё на два: когда показатель степени находится в (0; 1) и когда показатель степени больше 1.

Первым рассмотрим случай, когда показатель степени находится в промежутке (0; 1).

Рассмотрим частный случай такой степенной функции:

Как выглядит график этой функции, мы знаем.

Точно так же будут выглядеть графики любой степенной функции вида:

По графику мы очень просто можем записать основные свойства таких функций.

Областью определения будет являться луч [0; +∞).

Областью значения является промежуток [0; +∞).

Функция не является ни чётной, ни нечётной.

Функция возрастает на всей области определения.

Она не ограничена сверху, но ограничена снизу.

Наименьшее значение равно 0, а наибольшего значения нет.

Функция непрерывна на всей области определения.

График функции выпуклый вверх на всей области определения.

Теперь рассмотрим степенную функцию, показатель которой – любое рациональное число больше единицы.

Графиком функции будет ветвь параболы, проходящая через точки (0; 0) и (1; 1), причём чем больше показатель, тем круче будет идти график.

Запишем основные свойства функции.

Областью определения является луч [0; +∞).

Область значений – это промежуток (0; +∞).

Функция не является ни чётной, ни нечётной.

Функция возрастает на всей области определения.

Функции не ограничена сверху, но ограничена снизу.

Наименьшим значением будет 0, наибольшего значения нет.

Функция непрерывна на всей области определения.

График функции выпуклый вниз на всей области определения.

Теперь рассмотрим функцию:

Сегодня мы уже с вами вспоминали как выглядит график функции y = x-n, в случае натурального эн. Поскольку степень с рациональным отрицательным показателем рассматривается на интервале (0; +∞), то график функции y = xr, если r – это отрицательное рациональное число будет похож на ветвь гиперболы и проходить через точку (1; 1).

График имеет горизонтальную асимптоту игрек равно нулю и вертикальную асимптоту икс равно нулю.

Запишем основные свойства функции.

Областью определения будет промежуток (0; +∞).

Областью значения будет промежуток (0; +∞).

Функция не является ни чётной, ни нечётной.

Функция убывает на всей области определения.

Функция ограничена снизу, но не ограничена сверху.

Функция не имеет ни наибольшего ни наименьшего значения.

Функция непрерывна на всей области определения.

График функции выпуклый вниз на всей области определения.

Обратите внимание, что при рассмотрении функций мы нигде не проверяли функцию на дифференцируемость. Прежде чем говорить о дифференцируемости давайте посмотрим, как находится производная таких функций.

Производную функции игрек равно x в натуральной степени эн мы знаем, это табличное значение.

Чему равна производная функции x-n, в случае натурального n, найти нетрудно:

Эти две формулы можно объединить в одну:

Ещё одним табличным значением является производная функции:

Эту формулу можно записать следующим образом:

Теорема.

Если x > 0 и r – любое рациональное число, то производная степенной функции y = xrвычисляется по формуле:

Поскольку производные данных функции существуют на всей области определения, то в свойства можно дописать, что функции дифференцируемы на всей области определения.

Рассмотрим несколько примеров.

Пример.

Давайте повторим ещё раз основные свойства и графики функций.

videouroki.net

Степенная функция, ее свойства и график

Вы знакомы с функциями y=x, y=x2, y=x3, y=1/xи т. д. Все эти функции являются частными случаями степенной функции, т. е. функцииy=xp, где p - заданное действительное число. Свойства и график степенной функции существенно зависит от свойств степени с действительным показателем, и в частности от того, при каких значенияхx иp имеет смысл степеньxp. Перейдем к подобному рассмотрению различных случаев в зависимости от показателя степениp.

Показатель p=2n -четное натуральное число.

В этом случае степенная функция y=x2n, гдеn- натуральное число, обладает следующими

свойствами:

область определения - все действительные числа, т. е. множество R;
множество значений - неотрицательные числа, т. е. y больше или равно 0;
функция y=x2n четная, так какx2n=(-x)2n
функция является убывающей на промежутке x<0 и возрастающей на промежутке x>0.

График функции y=x2n имеет такой же вид, как например график функцииy=x4.

2. Показатель p=2n-1- нечетное натуральное число В этом случае степенная функцияy=x2n-1 , где натуральное число, обладает следующими свойствами:

область определения - множество R;
множество значений - множество R;
функция y=x2n-1нечетная, так как (-x)2n-1=x2n-1;
функция является возрастающей на всей действительной оси.

График функции y=x2n-1имеет такой же вид, как, например, график функцииy=x3.

3.Показатель p=-2n, гдеn - натуральное число.

В этом случае степенная функция y=x-2n=1/x2n обладает следующими свойствами:

область определения - множество R, кроме x=0;
множество значений - положительные числа y>0;
функция y=1/x2nчетная, так как1/(-x)2n=1/x2n;
функция является возрастающей на промежутке x<0 и убывающей на промежутке x>0.

График функции y=1/x2nимеет такой же вид, как, например, график функции y=1/x2.

4.Показатель p=-(2n-1), гдеn- натуральное число. В этом случае степенная функцияy=x-(2n-1)обладает следующими свойствами:

область определения - множество R, кроме x=0;
множество значений - множество R, кроме y=0;
функция y=x-(2n-1)нечетная, так как (-x)-(2n-1)=-x-(2n-1);
функция является убывающей на промежутках x<0иx>0.

График функции y=x-(2n-1)имеет такой же вид, как, например, график функцииy=1/x3.

Обратные тригонометрические функции, их свойства и графики.

Обратные тригонометрические функции, их свойства и графики.Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям.

Функция arcsin

График функции .

Арксинусом числа m называется такое значение угла x, для которого

Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго возрастающей.

[Править]Свойства функции arcsin

[Править]Получение функции arcsin

Дана функция На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все значения области значений — . Так как для функции на интервале каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция график которой симметричен графику функции на отрезке относительно прямой

studfiles.net

Степенные функции, их свойства и графики. Степенные функции с рациональным показателем

Дополнительные сочинения

На данном уроке мы продолжим изучение степенных функций с рациональным показателем, рассмотрим функции с отрицательным рациональным показателем.

1. Основные понятия и определения

Напомним свойства и графики степенных функций с целым отрицательным показателем.

При четных n, :

Пример функции:

Все графики таких функций проходят через две фиксированные точки: (1;1), (-1;1). Особенность функций данного вида – их четность, графики симметричны относительно оси ОУ.

Рис. 1. График функции

При нечетных n, :

Пример функции:

Все графики таких функций проходят через две фиксированные точки: (1;1), (-1;-1). Особенность функций данного вида – их нечетность, графики симметричны относительно начала координат.

Рис. 2. График функции

2. Функция с отрицательным рациональным показателем степени, графики, свойства

Напомним основное определение.

Степенью неотрицательного числа а с рациональным положительным показателем называется число .

Степенью положительного числа а с рациональным отрицательным показателем называется число .

Для выполняется равенство:

Например: ; – выражение не существует по определению степени с отрицательным рациональным показателем; существует, т. к. показатель степени целый,

Перейдем к рассмотрению степенных функций с рациональным отрицательным показателем.

Например:

Для построения графика данной функции можно составить таблицу. Мы поступим иначе: сначала построим и изучим график знаменателя – он нам известен (рисунок 3).

Рис. 3. График функции

График функции знаменателя проходит через фиксированную точку (1;1). При построении графика исходной функции данная точка остается, при корень также стремится к нулю, функция стремится к бесконечности. И, наоборот, при стремлении х к бесконечности функция стремится к нулю (рисунок 4).

Рис. 4. График функции

Рассмотрим еще одну функцию из семейства изучаемых функций.

Важно, что по определению

Рассмотрим график функции, стоящей в знаменателе: , график данной функции нам известен, она возрастает на своей области определения и проходит через точку (1;1) (рисунок 5).

Рис. 5. График функции

При построении графика исходной функции точка (1;1) остается, при корень также стремится к нулю, функция стремится к бесконечности. И, наоборот, при стремлении х к бесконечности функция стремится к нулю (рисунок 6).

Рис. 6. График функции

Рассмотренные примеры помогают понять, каким образом проходит график и каковы свойства изучаемой функции – функции с отрицательным рациональным показателем.

Графики функций данного семейства проходят через точку (1;1), функция убывает на всей области определения.

Область определения функции:

Функция не ограничена сверху, но ограничена снизу. Функция не имеет ни наибольшего, ни наименьшего значения.

Функция непрерывна, принимает все положительные значения от нуля до плюс бесконечности.

Функция выпукла вниз (рисунок 15.7)

На кривой взяты точки А и В, через них проведен отрезок, вся кривая находится ниже отрезка, данное условие выполняется для произвольных двух точек на кривой, следовательно функция выпукла вниз. Рис. 7.

Рис. 7. Выпуклость функции

3. Решение типовых задач

Важно понять, что функции данного семейства ограничены снизу нулем, но наименьшего значения не имеют.

Пример 1 – найти максимум и минимум функции на интервале [1;8):

вычислим значения функции в концах заданного промежутка:

Теперь мы можем выписать ответ на основании того, что функция монотонно убывает.

, минимального значения нет, так как правая граница не включена в интервал.

Пример 2 – построить и прочесть график функции:

Преобразуем заданную функцию по определению рациональной степени:

Не забудем указать, что по определению

Строим график функции , для нас это стандартная кривая, она проходит через точку (1;1), убывает. После этого сдвигаем полученный график на одну единицу вверх, точка (1;1) переходит в точку (1;2) (рисунок 8)

Читаем полученный график: если аргумент возрастает от нуля (не включая) до бесконечности, функция убывает от бесконечности до единицы (не включая).

Рис. 8. Построение графика функции

Пример 3 – построить и прочесть график функции:

Преобразуем заданную функцию по определению степени с рациональным показателем:

Нам известен график функции , построим его. Полученная кривая возрастает и проходит через точку (1;1), поскольку показатель степени больше единицы – кривая выпукла вниз. Сдвинем построенную кривую на две единицы вправо (получаем график функции ) и на одну единицу вверх – получаем искомый график (рисунок 9)

Прочтем полученный график:

При возрастании аргумента от двух до бесконечности функция возрастает от единицы до бесконечности.

Пример 4 – построить и прочесть график функции:

В данном случае функция задана кусочно.

Напомним, что такое модуль, раскроем его по определению:

Итак, строим график функции . Имеем две ветки: и . После этого строим стандартную кривую на интервале (Рисунок 10)

Прочтем график построенной функции:

Если аргумент возрастает от минус бесконечности до нуля, функция убывает от бесконечности до нуля. Когда аргумент возрастает от нуля до единицы, функция также возрастает от нуля до единицы. Наконец, когда аргумент возрастает от единицы не включительно до плюс бесконечности, функция убывает от единицы не включительно до нуля не включительно.

Рис. 9. Построение графика функции

Рис. 10. График кусочно заданной функции

Пример 5 – найти значения параметра, при котором уравнение а) имеет хотя бы одно решение; б) имеет только одно решение:

График заданной функции мы уже построили в предыдущем примере. Теперь рассечем его семейством прямых и найдем количество точек пересечения для каждого случая.

Выполним рассечение (рисунок 11).

Рис. 11. Рассечение графика прямыми

При уравнение имеет три решения; при уравнение имеет единственное решение

Ответ: при уравнение имеет хотя бы одно решение, при уравнение имеет единственное решение.

Итак, мы рассмотрели степенные функции, их свойства и графики. На следующем уроке мы перейдем к дифференцированию и интегрированию степенных функций.

Список литературы

Мордкович А. Г. Алгебра и начала математического анализа. – М.: Мнемозина. Муравин Г. К., Муравина О. В. Алгебра и начала математического анализа. – М.: Дрофа. Колмогоров А. Н., Абрамов А. М., Дудницын Ю. П. и др. Алгебра и начала математического анализа. – М.: Просвещение.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Uztest. ru . Edu. glavsprav. ru . Pm298.ru .

Домашнее задание

1. Найдите наибольшее и наименьшее значение функции на интервале:

а) ; б) ; в) ; г)

2. Построить и прочесть график функции:

а) ; б); в); г)

3. Решите уравнение с параметром:

dp-adilet.kz

Степенная функция.

Степенная функция задается формулой вида .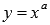

Рассмотрим вид графиков степенной функции и свойства степенной функции в зависимости от значения показателя степени.

Начнем со степенной функции с целым показателем a. В этом случае вид графиков степенных функций и свойства функций зависят от четности или нечетности показателя степени, а также от его знака. Поэтому сначала рассмотрим степенные функции 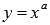при нечетных положительных значениях показателя a, далее - при четных положительных, далее - при нечетных отрицательных показателях степени, и, наконец, при четных отрицательных a.

Свойства степенных функций с дробными и иррациональными показателями (как и вид графиков таких степенных функций) зависят от значения показателя a. Их будем рассматривать, во-первых, при a от нуля до единицы, во-вторых, при a больших единицы, в-третьих, при a от минус единицы до нуля, в-четвертых, при a меньших минус единицы.

В заключении этого пункта для полноты картины опишем степенную функцию с нулевым показателем.

Степенная функция с нечетным положительным показателем.

Рассмотрим степенную функцию 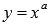при нечетном положительном показателе степени, то есть, при а=1,3,5,….

На рисунке ниже приведены графики степенных фнукций 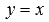– черная линия, – синяя линия, – красная линия, – зеленая линия. При а=1 имеем линейную функцию y=x.

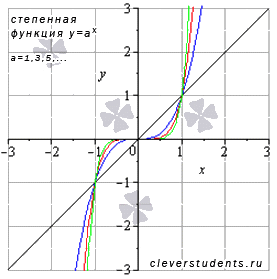
Свойства степенной функции с нечетным положительным показателем.

Область определения: .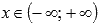
Область значений: .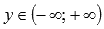
Функция нечетная, так как .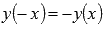
Функция возрастает при .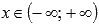
Функция выпуклая при 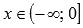и вогнутая при 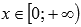(кроме линейной функции).
Точка (0;0) является точкой перегиба (кроме линейной функции).
Асимптот нет.
Функция проходит через точки (-1;-1), (0;0), (1;1).

Степенная функция с четным положительным показателем.

Рассмотрим степенную функцию 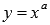с четным положительным показателем степени, то есть, при а=2,4,6,….

В качестве примера приведем графики степенных функций 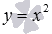– черная линия, 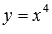– синяя линия, 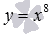– красная линия. При а=2 имеем квадратичную функцию, графиком которой является квадратичная парабола.

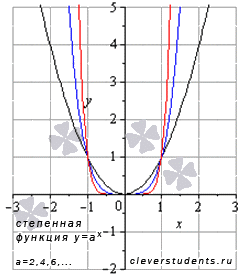
Свойства степенной функции с четным положительным показателем.

Область определения: .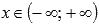
Область значений: .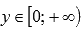
Функция четная, так как .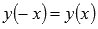
Функция возрастает при 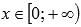, убывает при .
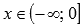Функция вогнутая при .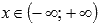
Точек перегиба нет.
Асимптот нет.
Функция проходит через точки (-1;1), (0;0), (1;1).

Степенная функция с нечетным отрицательным показателем.

Посмотрите на графики степенной функции 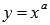при нечетных отрицательных значениях показателя степени, то есть, при а=-1,-3,-5,….

На рисунке в качестве примеров показаны графики степенных функций – черная линия, 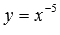– синяя линия, 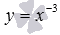– красная линия, 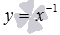– зеленая линия. При а=-1имеем обратную пропорциональность, графиком которой является гипербола.

Свойства степенной функции с нечетным отрицательным показателем.

Область определения: 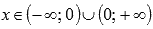. При x=0 имеем разрыв второго рода, так как 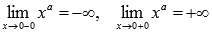приа=-1,-3,-5,…. Следовательно, прямая x=0 является вертикальной асимптотой.
Область значений: .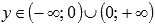
Функция нечетная, так как .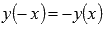
Функция убывает при .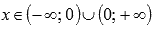
Функция выпуклая при 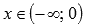и вогнутая при .
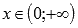Точек перегиба нет.
Горизонтальной асимптотой является прямая y = 0, так как 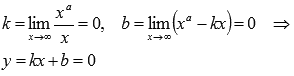при а=-1,-3,-5,….
Функция проходит через точки (-1;-1), (1;1).

studfiles.net

Реферат Показательная функция

скачать

Реферат на тему:

План:

1 Вещественная функция
- 1.1 Определение показательной функции
- 1.2 Свойства
- 1.3 Асимптотика
2 Комплексная функция

Введение

Показательная функция — математическая функция $f(x) = a^x\,\!$ , где a называется «основанием», а x — «показателем» степени.

В вещественном случае основание степени $a\,\!$ — некоторое неотрицательное вещественное (действительное) число, а аргументом функции является вещественный показатель степени.
В теории комплексных функций рассматривается более общий случай, когда аргументом и показателем степени может быть произвольное комплексное число.
В самом общем виде — uv, введена Лейбницем в 1695 г.

Особо выделяется случай, когда в качестве основания степени выступает число e. Такая функция называется экспонентой (вещественной или комплексной).

1. Вещественная функция

1.1. Определение показательной функции

Пусть a — неотрицательное вещественное число, x — рациональное число: $x=\frac{m}{n}$ . Тогда $a^x\,\!$ определяется по следующим правилам.

Если x > 0, то $a^x=\sqrt[n]{a^m}$ .
Если x = 0 и , то .
- Значение 00 не определено (см. Раскрытие неопределённостей).
Если x < 0 и a > 0, то .
- Значение ax при x < 0,a = 0 не определено.

Для произвольного вещественного показателя x значение ax можно определить как предел последовательности $a^{r_n}$ , где rn — рациональные числа, сходящиеся к x. Для экспоненты есть и другие определения через предел, например:

$e^x = \lim_{n \rightarrow \infty} \left(1 + \frac{x}{n}\right)^{n}.$

1.2. Свойства

График экспоненты

Используя функцию натурального логарифма $\ln \, x$ , можно выразить показательную функцию с произвольным положительным основанием через экспоненту:

$a^x = e^{x\cdot \ln a}$

Эта связь позволяет ограничиться изучением свойств экспоненты.

Аналитические свойства:

${d \over dx} a^x = (\ln a) a^x.$

В частности:

$\,{d \over dx} e^x = e^x$

Доказательство

Разложение в ряд:

$e^x = \sum_{n = 0}^{\infty} {x^n \over n!} = 1 + x + {x^2 \over 2!} + {x^3 \over 3!} + {x^4 \over 4!} + \cdots$ .

1.3. Асимптотика

Показательная функция растёт на бесконечности быстрее любой полиномиальной:

$\lim\limits_{x\to \infty}\frac{x^n}{a^x}=0$

Большая скорость роста может быть проиллюстрирована, например, задачей о складывании бумаги.

2. Комплексная функция

Для расширения экспоненты на комплексную плоскость определим её с помощью того же ряда, заменив вещественный аргумент на комплексный:

$e^z = \sum_{n = 0}^{\infty} {z^n \over n!} = 1 + z + {z^2 \over 2!} + {z^3 \over 3!} + {z^4 \over 4!} + \cdots$

Эта функция имеет те же основные алгебраические и аналитические свойства, что и вещественная. Отделив в ряде для eix вещественную часть от мнимой, мы получаем знаменитую формулу Эйлера:

$~e^{ix}=\cos x+i\sin x$

Таким образом, комплексная экспонента периодична вдоль мнимой оси.

Показательная функция с произвольным комплексным основанием и показателем степени легко вычисляется с помощью комплексной экспоненты и комплексного логарифма.

Пример: $i^i=e^{i~\ln(i)}$ ; поскольку $\ln (i) = i \frac{\pi} {2}$ (главное значение логарифма), окончательно получаем: $i^i = e^{i \frac{i \pi} {2}} = e^{- \frac{\pi} {2}}$ .

Литература

Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, тома I, II. — М.: ФИЗМАТЛИТ, 2001. — ISBN 5-9221-0156-0, 5-9221-0155-2

wreferat.baza-referat.ru

График и свойства степенной функции

Разделы: Математика, Конкурс «Презентация к уроку»

Презентация к уроку

Загрузить презентацию (1,5 МБ)

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цели урока: Повторить правила построения графика функции у = х р, при различных значениях р, научиться применять приемы преобразования графиков, демонстрировать применение свойств степенной функции при сравнении значений выражений, а также решение простейших уравнений и неравенств.

Задачи урока:

Образовательная – формирование функциональных представлений на наглядном материале, формирование умений построения графиков функции у=xр при различных преобразованиях, формирование навыков свободного чтения построенных графиков, умение отражать свойства функции на графике.

Развивающая – формирование способности анализировать, обобщать полученные знания. Формирование логического мышления.

Воспитательная – активизировать интерес к получению новых знаний, воспитание графической культуры, формирование точности и аккуратности при выполнении чертежей.

Оснащене: мультимедийный проектор, экран, операционная система Microsoft Windows 98/Me/2000/XP, программа MS Office 2003: Power Point, Microsoft Word, электронная приставка mimio.

Ход урока

№	Этап урока (действия учителя и учащихся)	Демонстрация слайдов	Время
1	Организационный момент. Приветствие		1
2	Проверка домашнего задания.	Слайд №14	2
3	Объявление темы и цели урока.		1
4	Актуализация опорных знаний. Теоретический опрос Выполнение устных упражнений.	Слайды №4, 7, 10,13 Слайд №15, 16	7
5	Изложение нового материала. Задачи на построение графиков путем сдвига вдоль оси ОУ Обсуждение свойств. Задачи на построение графиков путем сдвига вдоль оси ОХ. Сдвиг вдоль осей ОХ и ОУ Обсуждение свойств построенных функций.	Слайд №17–19	9
6	Закрепление первичных знаний. С/р: 1. Найти соответствие графика функции и его уравнения. 2. Построение графиков функции и описание их свойств (задание выполняется в группах, по карточкам)	Проверка решения с помощью слайдов №19-22	12
7	Дополнительное задание. Задачи банка ЕГЭ 2012, построение более сложных графиков.	Демонстрация задания с помощью слайда № 13	8
9	Подведение итогов. Итоги урока Выставление оценок		3
10	Домашнее задание.	§6 №127(1,2) №1069 (1), №1073(1) открытый банк ЕГЭ В 12 №27969	2

Цели урока: Повторить правила построения графика функции у = х р, при различных значениях р научиться применять приемы преобразования графиков, демонстрировать применения свойств степенной функции при сравнении значений выражений, а также решение простейших уравнений и неравенств.

1. Организационный момент. Приветствие.

2. Проверка домашнего задания. Слайд №14

№ 123 (2), № 124(1)

3. Объявление темы и цели урока

4. Актуализация опорных знаний.

Повторение.

Теоретический опрос:

1.Определение степенной функции.

2. Прокомментировать свойства степенной функции по слайдам 4, 7, 10, 13.

3. Какой симметрией обладает четная функция?

4. Какой симметрией обладает нечетная функция?

Слайд 15, 16

5. Изложение нового материала.

Учащимся выдается раздаточный материал “Преобразование графиков функции”. (Приложение 1)

1. Задачи на построение графиков путем сдвига вдоль оси ОУ графика функции №128 (2).

Сопровождается демонстрацией слайда 17.

В ходе беседы обсуждаются свойства этих функций.

2. Задачи на построение графиков путем сдвига вдоль оси ОХ графика функции №128(3).

Сопровождается демонстрацией слайда 18.

3.Сдвиг вдоль осей ОХ и ОУ сопровождается слайдом 19. Обсуждение свойств фунуции.

6. Закрепление первичных знаний

Работа в группах.

При выполнении заданий па построение учащиеся могут пользоваться опорными конспектами и таблицей преобразования графиков. (Приложение 2)

Задание 1: найти соответствие графика функции и его уравнения.

Раздаточный материал: (Приложение 3)

Группа 1. Cлайд 20

Группа 2. Cлайд 21

Группа 3. Cлайд 22

Группа 4. Cлайд 23

Проверка работы каждой группы с помощью слайдов № 19, 20, 21,22.

Задание 2

Раздаточный материал: (Приложение 4)

Группа 1

Уровень 1

а) В одной системе координат построить графики функций:

у=х3 и у=х1/3

б) Найти область определения и множество значений для каждой функции.

в) С помощью графиков решить уравнение х3=х1/3

с) С помощью графиков решить неравенство х3< х1/3

Уровень 2

Изобразить схематически график функции у = хП+1

Найти область определения и множество значений функции.

Определить возрастает или убывает функция.

Уровень 3

Построить график функции и указать область определения, множество значений и промежутки возрастания и убывания функции:

у |х|1/3

Группа 2

Уровень 1

а) В одной системе координат построить графики функций:

у = х2 и у = х -2

б) Найти область определения и множество значений для каждой функции.

в) С помощью графиков решить уравнение х2=х-2

с) С помощью графиков решить неравенство х2 > х -2

Уровень 2

Изобразить схематически график функции

Найти область определения и множество значений функции.

Определить возрастает или убывает функция.

Уровень 3

у =|х|5

Группа 3

Уровень 1

а) В одной системе координат построить графики функций:

у = х4 и у = х 1/4

б) Найти область определения и множество значений для каждой функции.

в) С помощью графиков решить уравнение х4=х1/4

с) С помощью графиков решить неравенство х4 > х 1/4

Уровень 2

Изобразить схематически график функции

Найти область определения и множество значений функции.

Определить возрастает или убывает функция.

Уровень 3

у =|х|3+1

Группа 4

Уровень 1

1 .

а) В одной системе координат построить графики функций:

у = х5 и у = х -5

б) Найти область определения и множество значений для каждой функции.

в) С помощью графиков решить уравнение х5=х-5

с) С помощью графиков решить неравенство х5 < х -5

Уровень 2

Изобразить схематически график функции

Найти область определения и множество значений функции.

Определить возрастает или убывает функция.

Уровень 3

у =¦х+2¦1/3

Дополнительное задание. (Приложение 5)

1. Подготовка к ЕГЭ Открытый банк задач В12 №28193

Для определения эффективной температуры звeзд используют закон Стефана-Больцмана, согласно которому мощность излучения нагретого тела P, измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвeртой степени температуры: , где — постоянная, площадь S измеряется в квадратных метрах, а температура T — в градусах Кельвина. Известно, что некоторая звезда имеет площадь м2, а излучаемая ею мощность P не менее Вт. Определите наименьшую возможную температуру этой звезды. Приведите ответ в градусах Кельвина.

(Ответ: Т=10000 о К)

2. Построить графики с описанием свойств функции:

Проверка:

9. Подведение итогов. Итоги урока. Выставление оценок.

В результате изучения темы “Функция у = хр” учащиеся научились строить степенную функцию, читать по графику ее свойства, применять свойства этой функции при сравнении значений выражений и решать простейшие уравнения и неравенства.

10. Домашнее задание: § 6 №127 (1, 2), №1069 (1), №1073 (1) открытый банк ЕГЭ В 12 №27969.

11. Список литературы.

Ш.А. Алимов “Алгебра и начала анализа 10-11” М., Просвещение, 2005.
Н.Е. Федорова “Изучение алгебры и начал анализа в 10-11 классах”, М., Просвещение, 2004.
Наглядный справочник по алгебре, Москва-Харьков, Илекса, 1997 г.
Открытый банк ЕГЭ 2012 http://mathege.ru/or/ege/ShowProblems.html?posMask=2048

xn--i1abbnckbmcl9fb.xn--p1ai

Степенные функции, их свойства и графики. Реферат на тему степенная функция ее свойства и график