
Разделы: Информатика, Конкурс «Презентация к уроку»
Загрузить презентацию (387,8 кБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Загрузить презентацию (131,3 кБ)
Тип урока: Урок изучения новой темы.
Дидактическая цель: создать условия для актуализации и закрепления учебной информации
Цель урока:
Образовательная:
Развивающая:
Воспитательная:
Методы обучения: наглядный, информационно-развивающий, опрос.
Формы организации познавательной деятельности: индивидуальная.
Средства обучения: учебник Семакина “Информатика и ИКТ. 9 класс. ” учебник для 9 класса общеобразовательных учреждений, рабочие тетради, авторучки, проектор, компьютер, компьютерная презентация по теме урока.
План урока:
Ход урока
1. Организационный момент.
Приветствие, проверка присутствующих. Мы сегодня начинаем изучение новой темы. Данная тема очень важна. Хотелось бы отметить умение решать задачи на систему счисления дает возможность набрать более высокие баллы, что очень важно при сдаче ЕГЭ и поступлении в ВУЗЫ. Открываем тетрадки, записываем сегодняшнее число и тему: СИСТЕМЫ СЧИСЛЕНИЯ.
План темы
2. Объяснение нового материала (по плану, приложение 3)
2.1. Историческая справка
Люди научились считать еще в незапамятные времена. Сначала они просто различали один предмет перед ними или нет. Если предмет был не один, то говорили «много». Постепенно появилось слово для обозначения двух предметов. Счет парами очень удобен.
Наиболее древней и простой «счетной машиной» издавна являются пальцы рук и ног. И даже в наше время еще пользуются этим «счетным прибором», который всегда при нас. На пальцах можно решать примеры не только в пределах десяти. В древние времена люди ходили босиком. Поэтому они могли пользоваться для счета пальцами как рук, так и ног.

Записывали числа поначалу совсем просто: делали зарубки на куске дерева или кости. На этой кости тридцать тысяч лет назад сделаны нарезки, они показывают, что уже тогда наши предки умели не только считать, но и записывать результаты счета!

Когда понадобилось записывать большие числа, то для пятерок и десяток стали придумывать новые знаки. Вот как египтяне записывали число 3 246: 
Запомнить большие числа трудно, поэтому к «счетной машине» рук и ног добавляли механические приспособления. Веревочные счеты с узелками применялись и в России, и во многих странах Европы. Остатками этого способа является практикуемое еще до сих пор завязывание узелков на носовых платках «на память». Так, одни пользовались для запоминания чисел камешками, зернами, веревкой с узелками, другие - палочками с зарубками. Это были первые счетные приборы, которые в конце концов привели к образованию различных систем счисления

2.2. Система счисления - это совокупность правил и приемов записи чисел с помощью набора цифровых знаков.

Непозиционные СС. Единичная система счисления. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков (бирок): зарубок, черточек, точек. Позже значки стали группировать по три или по пять. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Отголоски единичной системы счисления встречаются и сегодня (счетные палочки для обучения счету; полоски, нашитые на рукаве, означают на каком курсе учится курсант военного училища). Неудобства такой системы записи чисел и ограниченность ее применения очевидны: чем большее число надо записать, тем длиннее строка из палочек.
Римская система счисления является непозиционной системой. В ней для записи чисел используются буквы латинского алфавита. При записи чисел в римской системе счисления значением числа является алгебраическая сумма цифр, в него входящих. При этом цифры в записи числа следуют, как правило, в порядке убывания их значений, и не разрешается записывать рядом более трех одинаковых цифр. В том случае, когда за цифрой с большим значением следует цифра с меньшим, ее вклад в значение числа в целом является отрицательным. Типичные примеры, иллюстрирующие общие правила записи чисел в римской система счисления, приведены в таблице.
Таблица 1. Запись чисел в римской системе счисления
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
50 |
100 |
500 |
1000 |
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
IX |
X |
L |
C |
D |
M |
Недостатком римской системы является отсутствие формальных правил записи чисел и, соответственно, арифметических действий с многозначными числами. По причине неудобства и большой сложности в настоящее время римская система счисления используется там, где это действительно удобно: в литературе (нумерация глав), в оформлении документов (серия паспорта, ценных бумаг и др.), в декоративных целях на циферблате часов и в ряде других случаев.
Мы с вами более подробно рассмотрим позиционные системы счисления.
В позиционной системе счисления основными понятиями являются понятие алфавита и основания системы счисления.
Алфавитом системы счисления называется совокупность всех цифр.
Количество цифр, необходимых для записи числа в системе, называют основанием системы счисления. Основание системы записывается в справа числа в нижнем индексе: 7810, 110001012, AF1216 и т. д.
Количество цифр, составляющих алфавит, называется его мощностью.
В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места(разряда), где он расположен. Разряд - номер позиции в числе. Нумеруются справа налево, начиная с нуля.
Пример. Число618410 запишется в форме многочлена следующим образом:
618410 = 6*10 3 +1*10 2 +8*10 1 +4*10 0
2.3. Виды систем счисления.
В компьютерах принято использовать 4 основные системы счисления – двоичную, восьмеричную, десятичную и шестнадцатеричную. Именно их подробно рассмотрим.
Десятичная система счисления – в настоящее время наиболее известная и используемая. Древнее изображение десятичных цифр не случайно: каждая цифра обозначает число по количеству углов в ней. Например, 0 - углов нет, 1 - один угол, 2 - два угла и т.д. Написание десятичных цифр претерпело существенные изменения. Форма, которой мы пользуемся, установилась в XVI веке.
Десятичная система впервые появилась в Индии примерно в VI веке новой эры. Индийская нумерация использовала девять числовых символов и нуль для обозначения пустой позиции
Десятичная система использует десять цифр – 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, а также символы “+” и “–” для обозначения знака числа и запятую или точку для разделения целой и дробной частей числа.
Если взять правило, по которым строятся числа в десятичной системе счисления, заменив основание 10 на натуральное число N, можно построить позиционную систему счисления с основанием N.
В вычислительных машинах используется двоичная система счисления, её основание - число 2. Для записи чисел в этой системе используют только две цифры - 0 и 1. Двоичная система счисления была придумана математиками и философами задолго до появления компьютеров, еще в ХVII - ХIХ веках. Двоичная система удобна для компьютера, но неудобна для человека: числа получаются длинными и их трудно записывать и запоминать. Конечно, можно перевести число в десятичную систему и записывать в таком виде, а потом, когда понадобится перевести обратно, но все эти переводы трудоёмки. Поэтому применяются системы счисления, родственные двоичной - восьмеричная и шестнадцатеричная. Для записи чисел в этих системах требуется соответственно 8 и 16 цифр. В 16-теричной первые 10 цифр общие, а дальше используют заглавные латинские буквы. Шестнадцатеричная цифра A соответствует десятеричному числу 10, шестнадцатеричная B – десятичному числу 11 и т. д. Использование этих систем объясняется тем, что переход к записи числа в любой из этих систем от его двоичной записи очень прост. Ниже приведена таблица соответствия чисел, записанных в разных системах.
Учащиеся заполняют таблицу в тетрадях (приложение 1, таблица 1).
2.4. Правила перевода чисел из одной системы счисления в другую
Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.
1. При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную надо это число представить в виде суммы степеней основания его системы счисления.
Числа 101001102 , 7038 , 23FA116 перевести в десятичную систему счисления.
101001102=1*27+0*26+1*25+0*24+0*23+1*22+1*21+0*20=128+32+4+2=16610
7038=7*82+0*81+3*80=448+3=44710
23FA116=2*164+3*163+15*162+10*161+1*160=131072+12288+3840+160+1=147361
2. Правило перевода из десятичной системы счисления в систему с основанием q:
1. Последовательно выполнять деление исходного числа и получаемых частных на q до тех пор, пока не получим частное, меньшее делителя.
2. Полученные при таком делении остатки – цифры числа в системе счисления q – записать в обратном порядке (снизу вверх).
Пример. Перевести числа из десятичной системы счисления

3. Чтобы перевести число из двоичной системы в восьмеричную (шестнадцатеричную), его нужно разбить на триады (тетрады), начиная с младшего разряда (справа налево), в случае необходимости дополнив старшую триаду (тетраду) нулями, и каждую триаду (тетраду) заменить соответствующей восьмеричной (шестнадцатеричной) цифрой (табл.).
Число 100101101112 перевести в восьмеричную и в шестнадцатеричную системы счисления.

4. Для перевода восьмеричного (шестнадцатеричного) числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой (тетрадой).
Числа 7268 и 74С16 перевести в двоичную систему счисления.
7268= 111 010 1102
74С16 = 0111 0100 11002 (при записи числа первый 0 не пишется)
5. При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.
Число FAE16 перевести в восьмеричную систему счисления.
FAE16=1111101011102
111 110 101 1102=76568
Число 6358 перевести в шестнадцатеричную систему счисления.
6358 =1100111012
1 1001 11012=19D16
3. Физкультминутка (см. презентация 2)
4. Формирование умений и навыков
Работа с вопросником. Отвечают устно на вопросы, используя свой конспект.
5. Домашнее задание (приложение 4)
Подведение итогов урока.
Анализ и оценка успешности достижения цели занятия. Определение перспективы последующей работы.
Приложение 2
xn--i1abbnckbmcl9fb.xn--p1ai
Тема: Системы счисления.
Тип урока: Урок изучения новой темы.
Дидактическая цель: создать условия для актуализации и закрепления учебной информации
Межпредметные связи: математика, история, обществоведение.
Цель: введение понятия двоичной системы счисления. Научить правилам перевода чисел из одной системы счисления в другую и обратно
Задачи:
Образовательная:
знакомство с понятием «система счисления»;
умение различать виды систем счисления и применять их на практическом занятии;
умение правильно записывать числа в системах счисления;
формирование способности для применения правил перевода чисел из одной системы счисления в другие.
Развивающая:
развивать логическое мышление, умение обобщать, конкретизировать;
формирование внимания, умения наблюдать и закреплять знания;
Воспитательная:
воспитывать самостоятельность, уважительное отношение друг к друг;
воспитание информационной культуры учащихся.
План урока:
Организационный момент.
Изучение нового материала.
Физкультминутка.
Формирование умений, навыков.
Домашнее задание
Ход урока
1. Организационный момент.
Приветствие, проверка присутствующих. Мы сегодня начинаем изучение новой темы. Данная тема очень важна. Хотелось бы отметить умение решать задачи на систему счисления дает возможность набрать более высокие баллы при сдаче ГИА(задание № 13) и ЕГЭ (задание А1 и В7) по информатике, что очень важно при поступлении.
Перед тем, как мы приступим к изучению нового материала, обратите ваше внимание на листы самоконтроля по теме «Системы счисления». Через 5 уроков будет зачет по этой теме. В зачет войдут контрольные вопросы и задания, аналогичные заданиям из самоконтроля.
Открываем тетрадки, записываем сегодняшнее число и тему: СИСТЕМЫ СЧИСЛЕНИЯ.
План темы
Историческая справка
Определение системы счисления
Виды системы счисления
Правила перевода чисел из одной системы счисления в другую
2. Объяснение нового материала (по плану, приложение 3)
2.1. Историческая справка
Люди научились считать еще в незапамятные времена. Сначала они просто различали один предмет перед ними или нет. Если предмет был не один, то говорили «много». Постепенно появилось слово для обозначения двух предметов. Счет парами очень удобен.
Наиболее древней и простой «счетной машиной» издавна являются пальцы рук и ног. И даже в наше время еще пользуются этим «счетным прибором», который всегда при нас. На пальцах можно решать примеры не только в пределах десяти. В древние времена люди ходили босиком. Поэтому они могли пользоваться для счета пальцами как рук, так и ног.

Записывали числа поначалу совсем просто: делали зарубки на куске дерева или кости. На этой кости тридцать тысяч лет назад сделаны нарезки, они показывают, что уже тогда наши предки умели не только считать, но и записывать результаты счета!

Когда понадобилось записывать большие числа, то для пятерок и десяток стали придумывать новые знаки. Вот как египтяне записывали число 3 246: 
Запомнить большие числа трудно, поэтому к «счетной машине» рук и ног добавляли механические приспособления. Веревочные счеты с узелками применялись и в России, и во многих странах Европы. Остатками этого способа является практикуемое еще до сих пор завязывание узелков на носовых платках «на память». Так, одни пользовались для запоминания чисел камешками, зернами, веревкой с узелками, другие - палочками с зарубками. Это были первые счетные приборы, которые в конце концов привели к образованию различных систем счисления

2.2. Система счисления - это совокупность правил и приемов записи чисел с помощью набора цифровых знаков.

позиционные, когда значение каждой цифры числа определяется ее позицией в записи числа;
непозиционные, когда значение цифры в числе не зависит от ее места в записи числа.
Непозиционные СС. Единичная система счисления. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков (бирок): зарубок, черточек, точек. Позже значки стали группировать по три или по пять. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Отголоски единичной системы счисления встречаются и сегодня (счетные палочки для обучения счету; полоски, нашитые на рукаве, означают на каком курсе учится курсант военного училища). Неудобства такой системы записи чисел и ограниченность ее применения очевидны: чем большее число надо записать, тем длиннее строка из палочек.
Сообщение Барлит Елены. Римская система счисления является непозиционной системой. В ней для записи чисел используются буквы латинского алфавита. При записи чисел в римской системе счисления значением числа является алгебраическая сумма цифр, в него входящих. При этом цифры в записи числа следуют, как правило, в порядке убывания их значений, и не разрешается записывать рядом более трех одинаковых цифр. В том случае, когда за цифрой с большим значением следует цифра с меньшим, ее вклад в значение числа в целом является отрицательным. Типичные примеры, иллюстрирующие общие правила записи чисел в римской система счисления, приведены в таблице.
Таблица 1. Запись чисел в римской системе счисления
1
2
3
4
5
6
7
8
9
10
50
100
500
1000
I
II
III
IV
V
VI
VII
VIII
IX
X
L
C
D
M
Возможно, знак V означал раскрытую руку, а X – две такие руки. Но есть и иное объяснение. Когда счет шел десятками, то, нарисовав 9 палочек, десятой их перечеркивали. А чтобы не писать слишком много палочек, перечеркивали одну палочку и писали десять так: . отсюда и получилась римская цифра X. А цифра 5 получилась просто разрезанием цифры для числа 10 пополам.
Спорят ученые и о происхождении других римских цифр. Возможно, что обозначения C и M связаны с римскими названиями сотни и тысячи. Тысячу римляне называли "милле" (слово "миля" когда-то обозначало путь в тысячу шагов).
Недостатком римской системы является отсутствие формальных правил записи чисел и, соответственно, арифметических действий с многозначными числами. По причине неудобства и большой сложности в настоящее время римская система счисления используется там, где это действительно удобно: в литературе (нумерация глав), в оформлении документов (серия паспорта, ценных бумаг и др.), в декоративных целях на циферблате часов и в ряде других случаев.
Мы с вами более подробно рассмотрим позиционные системы счисления.
В позиционной системе счисления основными понятиями являются понятие алфавита и основания системы счисления.
Алфавитом системы счисления называется совокупность всех цифр.
Количество цифр, необходимых для записи числа в системе, называют основанием системы счисления. Основание системы записывается в справа числа в нижнем индексе: 7810, 110001012, AF1216 и т. д.
Количество цифр, составляющих алфавит, называется его мощностью.
В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места(разряда), где он расположен. Разряд - номер позиции в числе. Нумеруются справа налево, начиная с нуля.
Пример. Число618410 запишется в форме многочлена следующим образом:
618410 = 6*10 3 +1*10 2 +8*10 1 +4*10 0
2.3. Виды систем счисления.
В компьютерах принято использовать 4 основные системы счисления – двоичную, восьмеричную, десятичную и шестнадцатеричную. Именно их подробно рассмотрим.
У вас на столах лежат ваши опорные конспекты, состоящие из 2-х табличек, которые будут помогать вам на протяжении всего времени изучения темы «Системы счисления». Но нам сейчас необходимо их заполнить.
Если взять правило, по которым строятся числа в десятичной системе счисления, заменив основание 10 на натуральное число N, можно построить позиционную систему счисления с основанием N.
Вызывается ученик к доске и вместе с классом заполняем таблицу на доске и в опорных конспектах на местах(приложение 1, таб.1)
Система счисления
Основание
Алфавит цифр
Десятичная
10
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Двоичная
2
0, 1
Восьмеричная
8
0, 1, 2, 3, 4, 5, 6, 7
Шестнадцатеричная
16
0, 1, 2, 3, 4, 5, 6, 7, 8, 9,
A, B, C, D, E, F
В вычислительных машинах используется двоичная система счисления, её основание - число 2. Для записи чисел в этой системе используют только две цифры - 0 и 1. Двоичная система счисления была придумана математиками и философами задолго до появления компьютеров, еще в ХVII - ХIХ веках. Двоичная система удобна для компьютера, но неудобна для человека: числа получаются длинными и их трудно записывать и запоминать. Конечно, можно перевести число в десятичную систему и записывать в таком виде, а потом, когда понадобится перевести обратно, но все эти переводы трудоёмки. Поэтому применяются системы счисления, родственные двоичной - восьмеричная и шестнадцатеричная. Для записи чисел в этих системах требуется соответственно 8 и 16 цифр. В 16-теричной первые 10 цифр общие, а дальше используют заглавные латинские буквы. Шестнадцатеричная цифра A соответствует десятеричному числу 10, шестнадцатеричная B – десятичному числу 11 и т. д. Использование этих систем объясняется тем, что переход к записи числа в любой из этих систем от его двоичной записи очень прост.
2.4. Правила перевода чисел из одной системы счисления в другую
Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.
1. При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную надо это число представить в виде суммы степеней основания его системы счисления.
Числа 101001102 , 7038 , 23FA116 перевести в десятичную систему счисления.
101001102=1*27+0*26+1*25+0*24+0*23+1*22+1*21+0*20=128+32+4+2=16610
7038=7*82+0*81+3*80=448+3=44710
23FA116=2*164+3*163+15*162+10*161+1*160=131072+12288+3840+160+1=147361
2. Правило перевода из десятичной системы счисления в систему с основанием q:
1. Последовательно выполнять деление исходного числа и получаемых частных на q до тех пор, пока не получим частное, меньшее делителя.
2. Полученные при таком делении остатки – цифры числа в системе счисления q – записать в обратном порядке (снизу вверх).
Пример. Перевести числа из десятичной системы счисления

3. Чтобы перевести число из двоичной системы в восьмеричную (шестнадцатеричную), его нужно разбить на триады (тетрады), начиная с младшего разряда (справа налево), в случае необходимости дополнив старшую триаду (тетраду) нулями, и каждую триаду (тетраду) заменить соответствующей восьмеричной (шестнадцатеричной) цифрой (табл.).
Число 100101101112 перевести в восьмеричную и в шестнадцатеричную системы счисления.

4. Для перевода восьмеричного (шестнадцатеричного) числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой (тетрадой).
Числа 7268 и 74С16 перевести в двоичную систему счисления.
7268= 111 010 1102
74С16 = 0111 0100 11002 (при записи числа первый 0 не пишется)
5. При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.
Число FAE16 перевести в восьмеричную систему счисления.
FAE16=1111101011102
111 110 101 1102=76568
Число 6358 перевести в шестнадцатеричную систему счисления.
6358 =1100111012
1 1001 11012=19D16
3. Физкультминутка
4. Формирование умений и навыков
Выполнение творческого задания.
Работа с вопросником. Отвечают устно на вопросы, используя свой конспект.
5. Домашнее задание
Учить конспект, прочитать §16 по учебнику.
Написать дату своего дня рождения в римской системе счисления.
Подведение итогов урока.
Анализ и оценка успешности достижения цели занятия. Определение перспективы последующей работы
www.metod-kopilka.ru
ppt-online.org
Урок по информатике в 9 классе
Тема урока: «Системы счисления»
Цель урока: Организовать деятельность обучающихся по закреплению, обобщению и систематизации знаний по теме «Системы счисления»- правил перевода чисел из одной системы в другую;
Задачи урока:
Тип урока: урок обобщения и систематизации знаний.
Формы и методы обучения: словесный, наглядный, практический - индивидуальная работа, работа в команде, работа на компьютере.
Технологии, применяемые на уроке:
личностно-ориентированная;
информационно-коммуникационная;
игровая;
здоровьесберегающая
Оснащение урока: компьютерная презентация «Системы счисления», интерактивная доска, персональные компьютеры, мультимедийный проектор, дидактический раздаточный материал.
Сценарный план урока
Оргмомент. Вводное слово – 2мин.
Актуализация знаний – 10мин.
Систематизация теоретических знаний, решение задач – 15 мин.
Физкультминутка – 2 мин.
Практическая работа -7-10 мин.
Итоги урока и дом. задание. -2 мин.
Ход урока
1.Организационный момент.
Учитель проверяет явку учащихся, их внешний вид.
Приветствие.
2. Постановка целей урока.
Учитель. Потребность в записи чисел появилась в очень древние времена, как только люди начали считать. Количество предметов изображалось нанесением черточек или засечек на какой-либо твердой поверхности: камне, глине, дереве (до изобретения бумаги было еще очень и очень далеко). Археологами найдены такие «записи» при раскопках культурных слоев, относящихся к периоду палеолита (10 – 11 тысяч лет до н.э.).
«Всё есть число», – говорили древнегреческие философы, ученики Пифагора, подчёркивая необычайно важную роль чисел в практической деятельности. Известно множество способов представления чисел. (слайды1-3)
3. Актуализация знаний
Учитель. Система счисления — это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами (Слайд 4).
Цифры – это знаки, используемые при записи чисел. Сами знаки составляют алфавит системы счисления.
Все системы счисления делятся на два класса (Слайд 5):
– позиционные – величина, обозначаемая цифрой, зависит от места (позиции) цифры в числе (например, в десятичной системе счисления число 222; первая слева направо цифра 2 – показывает количество сотен, следующая – количество десятков и последняя – количество единиц).
Называет позиционные системы счисления (слайд 6)
Ученики: Делают короткие сообщения о непозиционных системах счисления:
Единичная система счисления(слайд7).
Египетская нумерация(слайд8).
Древнегреческая нумерация(слайд9).
Славянская кириллическая нумерация(Слайд10)
Римская система счисления(Слайд11)
Наэывают позиционные системы счисления и делают сообщения:
Вавилонская система счисления
Десятичная система счисления.(Слайды12-14)
4.Систематизация теоретических знаний, решение задач
Учитель : Выполним задание1 : в таблице данных приведены некоторые позиционные системы счисления, необходимо по образцу первой строки заполнить оставшуюся часть таблицы.
Класс разбивает на две команды.
Ученики: Анализируют данные первой строки и поочерёдно заполняют оставшиеся незаполненные ячейки таблицы, получая за правильный ответ 1 балл.(Слайд15)
Учитель: Предлагает выполнить задание2:
На слайде заданы несколько неверных равенств, нужно получить верные равенства.
Ученики: Строят логическую цепь рассуждений, анализируют неверные равенства
и получают верные равенства(Слайд 16).
Учитель: Предлагает выполнить индивидуальное задание 3 (Слайд 17)
На слайде загадка поэта. Необходимо разгадать загадку, выписав упомянутые в
стихотворении числа с переводом в десятичную систему счисления.
Остальным обучающимся предлагается выполнить задание4 по группам.
На экранах компьютеров образцы заданий и примеры их решения.
На ученических столах опорные коспекты.
Ученики: У доски один обучающийся выполняет индивидуальное задание,
Остальные работают по группам и заносят результаты работы в свои опорные
конспекты.
5.Физкультминутка
Учитель: Включает музыкальный видеоролик на интерактивной доске и даёт команды на выполнение физических упражнений.
Ученики: Выполняют физические упражнения под команды учителя.
6.Практическая работа
Учитель: На интерактивной доске кроссвод. Предлагает разрешить кроссворд.
Ученики: Последовательно отвечают на вопросы кроссворда и получают 1 балл
за правильный ответ.
7.Подведение итогов урока.
Домашнее задание.(Слайды17-20)
Формируемые компетенции:
ценностно-смысловые компетенции:
умение формулировать собственные учебные цели данной темы, принимать решение, брать ответственность на себя (быть лидером в группе, принимать решение в случае нестандартной ситуации, нести ответственность за выбор).
общекультурные компетенции:
понимание места информатики в системе других наук: математики, физики, истории; применение знаний, полученных в данной теме, в другой деятельности, в повседневной жизни;
учебно-познавательные:
знание определений изучаемых понятий системы счисления, видов систем счисления (унарные, позиционные, непозиционные), основание, алфавит, цифра, базис, разряд; умение задавать вопросы к изучаемым фактам, выбирать необходимые алгоритмы для перевода из одной системы счисления в другие: перевод в десятичную систему счисления, из десятичной системы счисления, перевод дробных и смешанных чисел, перевод целых и смешанных чисел из двоичной в восьмеричную, шестнадцатеричную систему счисления и обратно, овладение измерительными навыками;
информационные:
владеть навыками работы со справочной литературой; самостоятельно извлекать, систематизировать, анализировать, отбирать необходимую для решения учебной задачи информацию; владеть навыками использования технических устройств ПК и программного обеспечения.
коммуникативные:
уметь организовываться, представить свою группу; владеть способами деятельности в группе; следовать этическим нормам и правилам ведения диалога; уметь высказать свое суждение и спросить мнение партнера.
компетенции личностного самосовершенствования:
владеть навыками оценки и самооценки
Планируемые результаты:
Обучающиеся владеют умениями работать со справочной литературой, принимать решения в нестандартной ситуации, всеми вышеперечисленными понятиями «Системы счисления, виды систем счисления (унарные, позиционные, непозиционные), основание, алфавит, цифра, базис, разряд» и оперируют ими; знают различие между позиционными и непозиционными системами счисления, знают алгоритмы перевода из одной системы счисления в другие, умеют переводить целые, дробные и смешанные числа из одной системы счисления в другие, используя алгоритмы перевода, выполняют арифметические операции с двоичными числами, решают примеры и задачи в других позиционных системах счисления, занимательные задачи.
Интернет-ресурсы:
http://nsportal.ru
http://pedsovet.su
http://www.videouroki.net
infourok.ru
МАОУ «Средняя общеобразовательная школа № 8» с. Кашино
РАБОЧАЯ ТЕТРАДЬ
по информатике и ИКТ
по теме «Системы счисления»
ученика 9 класса ____________
Разработал: учитель информатики
МАОУ СОШ №8 С. Кашино
В.М.Бугаева
Кашино – 2014
СОДЕРЖАНИЕ
Пояснительная записка
Обращение к учащимся
Урок 1. История счёта и систем счисления
Урок 2. Позиционные системы счисления
Урок 3. Перевод чисел в позиционных системах счисления
Урок 4. Двоичная Арифметика
Урок 5. Заключительный урок
МАТЕРИАЛ ДЛЯ ДОПОЛНИТЕЛЬНОГО ИЗУЧЕНИЯ
Перевод чисел из двоичной СС в восьмеричную
Перевод чисел из двоичной СС в шестнадцатеричную
Занимательные задачи
Самостоятельная работа №1
Самостоятельная работа №2
Контрольная работа
Системы счисления в ГИА и ЕГЭ
ЛИТЕРАТУРА
Представленная ниже рабочая тетрадь содержит теоретический материал и практические задания по теме «Системы счисления», дополняющие и углубляющие сведения, представленные в учебнике Семакина И. Г., Залоговой Л. А., Русакова С. В., Шестаковой Л. В. Информатика и ИКТ. 9 класс (М.: БИНОМ. Лаборатория знаний, 2010). Тетрадь составлена в соответствии с минимумом содержания среднего (полного) общего образования и Рекомендациями Минобразования РФ.
Главный эффект рабочей тетради – расширены горизонты изучения материалов учебника, обучающемуся предоставлена возможность остановиться, подумать, проанализировать и/или проверить понимание тех или иных вопросов, самостоятельное решение наиболее интересных проблем и задач.
Рабочая тетрадь содержит гибкую систему заданий и упражнений, позволяющих преподавателю выбирать требуемое для конкретной группы обучающихся количество упражнений с учетом их индивидуальных способностей. Предназначена для работы, как в аудитории, так и дома.
Рабочая тетрадь используется для отработки изученного материала, тренировки получаемых навыков и умений, развития интеллектуальных способностей обучающегося, для самостоятельной подготовки по теме «Системы счисления».
Данное пособие содержит теоретический материал по теме «Системы счисления», задания, разобраны решения типовых задач, предложены задания для самостоятельного изучения и закрепления новых знаний и умений. Можно использовать для самостоятельного изучения нового материала.
Тема «Системы счисления» вызывают у учащихся затруднения потому, что при изучении мало используется компьютер и приходится выполнять много вычислений. Это не способствует эффективному усвоению материала, и у ребят пропадает интерес к обучению. Для того чтобы этого не произошло, я предлагаю задания творческого характера.
В дополнительном разделе представлены занимательные задачи и две самостоятельных работы обучающего характера. Самостоятельные работы составлены на 10 вариантов, что понижает возможность списывания. Понимая это, учащимся приходится вникать в тему и работать самим, чтобы избежать отрицательной отметки. Этим обуславливается хорошая подготовка к заключительному уроку и твёрдые знания по теме.
В конце тетради предлагаются несколько вариантов итоговой контрольной работы. Представленные варианты дают возможность ученику выбрать задание по своему уровню знаний и получить на уроке положительную оценку.
После изучения темы «Системы счисления» учащиеся должны:
Знать:
Определение понятий; система счисления, позиционная СС, непозиционная СС, алфавит, основание, базис системы счисления
Алгоритм записи числа в развёрнутой форме.
Правила перевода чисел из двоичной системы счисления в десятичную систему счисления и наоборот.
Правила выполнения арифметических операций в двоичной системе счисления.
Уметь:
Представлять числа в развёрнутой форме.
Переводить числа в позиционных системах счисления.
Выполнять арифметические операции в двоичной системе счисления.
Рабочую тетрадь можно использовать как дидактический материал на уроках информатики по данной теме.
Дорогие друзья!
Перед вами рабочая тетрадь, занимаясь по которой вы сможете эффективно подготовиться к урокам информатики по теме «Системы счисления». В тетради представлены творческие задания, которые помогут вам и при подготовке к ЕГЭ по информатике.
Эта рабочая тетрадь позволит вам выявить пробелы в знаниях и отработать навыки перевода чисел из одной системы счисления в другую.
В тетради содержатся теоретические сведения и практические задания. Выполняя задания, вы можете писать ответы прямо в рабочей тетради.
Работая по этой тетради, не забывайте следующее:
во-первых, следует вчитаться в формулировку задания, понять его;
во-вторых, не забывайте, что без теории нет практики, т. е. необходимо знать теоретический материал, изученный на уроках информатики: правила, определения и т. д.
ЦЕЛЬ:
Сформировать понятие о позиционных и непозиционных СС.
Рассмотреть способы представления чисел в различных СС.
У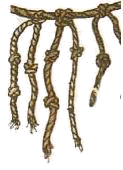
 нарная система счисления
нарная система счисления
КОГДА: ___________________________________
ЦИФРЫ: зарубки, чёрточки, палочки, узелки и т.д.
ПРАВИЛА: Число образуется путем повторения одного знака, символизирующего единицу.
Е гипетская система счисления
гипетская система счисления
КОГДА: ___________________________________
ГДЕ: ______________________________________
ЦИФРЫ:

ПРАВИЛА: Все остальные числа составлялись из этих символов при помощи сложения.
ЗАДАНИЕ: Реши пример
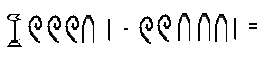
Р имская система счисления
имская система счисления
КОГДА: ___________________________________
ГДЕ: ______________________________________
ЦИФРЫ:
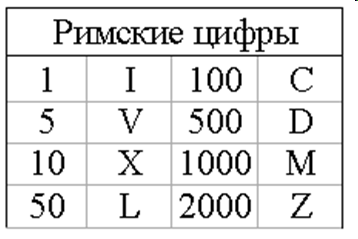

ПРАВИЛА:
Числа записывались слева направо, от больших к меньшим.
Цифры I, X, C, M могут повторяться не более трёх раз.
Каждый меньший знак, поставленный слева от большего, вычитается из него.
Каждый меньший знак, поставленный справа от большего, прибавляется к нему.
ЗАДАНИЕ: В Санкт-Петербурге стоит памятник Петру I. На гранитном постаменте памятника есть римское число: MDCCLXXXII. Переведите его в обычную систему счисления и вы узнаете год открытия памятника.
С лавянская система счисления
лавянская система счисления
КОГДА: ___________________________________
ГДЕ: ______________________________________
ЦИФРЫ:
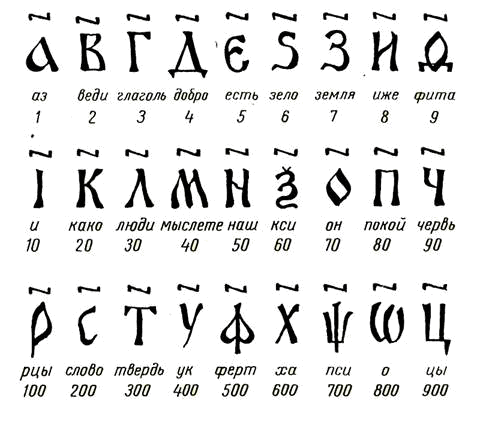
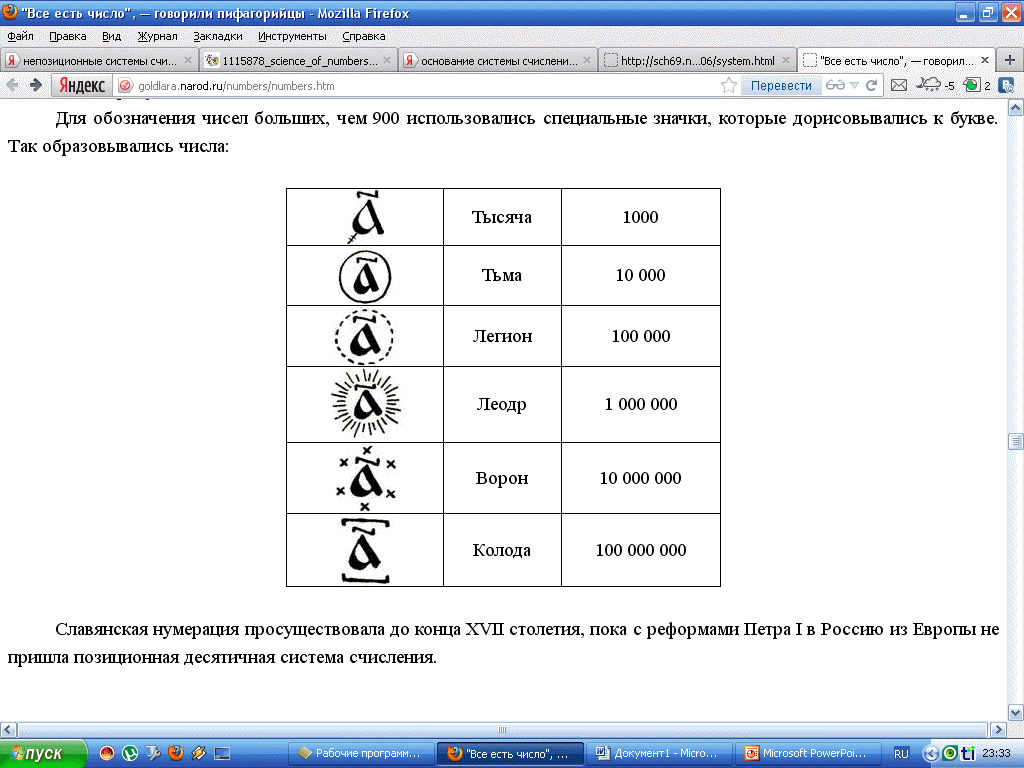
ПРАВИЛА:
Числа записывали из цифр слева направо, от больших к меньшим.
Числа от 11 до 19 записывались двумя цифрами, причем единица шла перед десятком. Читаем дословно «четырнадцать» – «четыре и десять». Как слышим, так и пишем: не 10+4, а 4+10, – четыре и десять. Числа от 21 и выше записывались наоборот, сначала писали знак полных десятков.
ЗАДАНИЕ: Отгадайте число и узнаете, в каком году была построена наша школа ацпв
В авилонская система счисления
авилонская система счисления
КОГДА: ___________________________________
ГДЕ: ______________________________________
Ц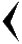 ИФРЫ:
ИФРЫ:
– единица
– десяток
– пропущенный разряд (60), играет роль нуля
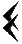

П РАВИЛА:
РАВИЛА:
Для определения значения числа его запись нужно было разбить на разряды справа налево.
Чередование групп одинаковых цифр соответствовало чередованию разрядов.
Значение числа определяли по значениям составляющих его цифр, но с учетом того, что цифры в каждом последующем разряде «весили» в 60 раз больше таких же цифр предыдущего разряда.
ЗАДАНИЕ: В нашем школе учится 345 учеников. А как бы это число записали вавилоняне?
Д есятичная система счисления
есятичная система счисления
КОГДА: ___________________________________
ГДЕ: ______________________________________
Ц ИФРЫ:
ИФРЫ:
ЛИСТ ДОСТИЖЕНИЙ
Задание
Баллы
Египетская СС
Римская СС
Алфавитная СС
Вавилонская СС
Тест «ДаНет»
Выступление с сообщением
ИТОГО
ОЦЕНКА за урок
ЗАПОЛНИТЕ АНКЕТУ (выберите и подчеркните)
На уроке я работал
активно / пассивно
Своей работой на уроке я
доволен / не доволен
Урок для меня показался
коротким / длинным
За урок я
не устал / устал
Мое настроение
стало лучше / стало хуже
Материал урока мне был
понятен / не понятен
Заполни кластер:

















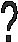
Египетская СС
Допишите самостоятельно ещё несколько непозиционных СС.
Допишите самостоятельно ещё несколько позиционных СС.
Римская СС
Славянская СС
Вавилонская СС
Десятичная СС
ДОМАШНЕЕ ЗАДАНИЕ
Выучить определения, дополнить кластер примерами СС.
Выполнить задания:
Какие числа записаны с помощью римских цифр:
MMIV
LXV
CMLXIIV
Запишите дату своего рождения:
Число
Месяц
Год
в древнеегипетской СС
в римской системе СС
в древнеславянской СС
Выполните действия:
а) MMMD + LX =
б) 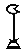 +
+ 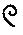
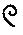
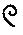
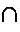
в
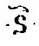 )
)
*Творческое задание: заполните одну из колонок таблицы на https://docs.google.com/document/d/1P6P_hO0vi2Yhg-pnxNluieIQFmQ_dPSHqTZEN_mdSLI/edit?usp=sharing
ЦЕЛЬ:
ЛИСТ ДОСТИЖЕНИЙ
Количество заработанных жетонов
«5» – от 4 и более жетонов
«4» – 3 жетона
«3» – 1-2 жетона
ОЦЕНКА за урок

А лфавит СС – это множество всех символов (знаков), используемых для записи чисел в данной системе счисления.
лфавит СС – это множество всех символов (знаков), используемых для записи чисел в данной системе счисления.
Основание СС – это размер алфавита (число цифр) СС.
ЗАПОЛНИ ТАБЛИЦУ Таблица 1
Название
Основание
Алфавит
Двоичная
10
0, 1, 2, 3, 4
8
Шестнадцатеричная
Б азис СС – это последовательность чисел, каждое из которых задает значение цифры «по месту» или «вес» каждого разряда.
азис СС – это последовательность чисел, каждое из которых задает значение цифры «по месту» или «вес» каждого разряда.
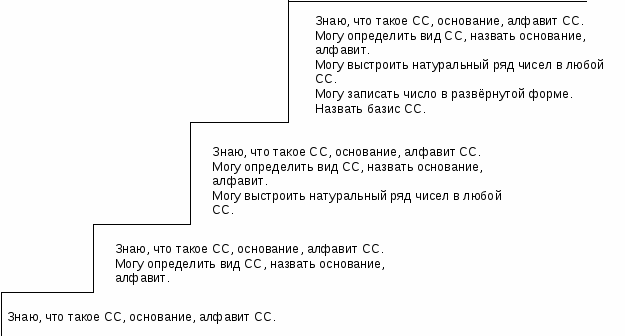
Запишите любое многозначное число в развёрнутой форме:
__________________________________________________________________
Составьте алгоритм записи числа в развёрнутой форме:
1)
2)
ДОМАШНЕЕ ЗАДАНИЕ
Выучить определения. Выполни задания:
1) Подчеркните числа, которые записаны с ошибками.
1567; 3005,234; 185,7948; 11022; 1345,526; 112,0113; В105,А16
2) Запиши в свернутой форме следующее число:
А16 = А*161 + 160 + 7*16-1 + 5*16-2 = ___________________________
3) Запиши в развернутом виде числа:а) А8=143 ______________________________________________________
б) А2=1011 ______________________________________________________
в) А16=153 ______________________________________________________
г) А10=143,5 ______________________________________________________
* Творческое задание: Составьте кроссворд по теме «Системы счисления»
ЦЕЛЬ: Овладеть навыками перевода чисел из разных систем счисления в десятичную систему счисления и обратно
ЛИСТ ДОСТИЖЕНИЙ
Задание
Баллы
Домашнее задание
Работа в группах
ИТОГО
ОЦЕНКА за урок
ВЕРЮ НЕ ВЕРЮ. Если согласен с утверждением поставь 1, нет – 0.

Алгоритм перевода чисел в десятичную систему счисления
Для перевода числа из какой-либо СС в десятичную необходимо:
Пронумеровать разряды целого числа справа налево, начиная с нуля по возрастанию.
Записать число в развернутой форме, заменив все цифры числа, показатели степени и основание СС десятичными числами.
Определить значение полученного выражения, выполнив действия в десятичной СС.
ПРИМЕРЫ:
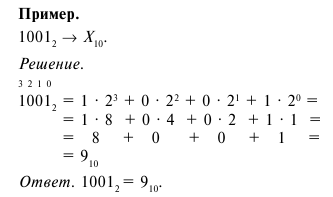
ПРИМЕРЫ:

ТАБЛИЦА СТЕПЕНЕЙ ДВОЙКИ
20
21
22
23
24
25
26
27
28
29
210
0
2
4
8
16
32
64
128
256
512
1024
ДОМАШНЕЕ ЗАДАНИЕ
Выучить алгоритмы перевода чисел в позиционных СС.
Переведи:
5310
Х8
100100112
Х10
1А16
Х10
4810
Х2
12310
Х16
*Творческое задание (по желанию): Придумать задачу, подобную автобиографии чудака-математика.
ЦЕЛЬ:
Составить таблицы сложения и умножения одноразрядных двоичных чисел.
Научиться выполнять арифметические операции в двоичной системе счисления
ЛИСТ ДОСТИЖЕНИЙ
Задание
Баллы
14-15 баллов – «5»
12-13 баллов – «4»
9-12 баллов – «3»
Домашнее задание
Морской бой
Самостоятельная работа
ИТОГО
ОЦЕНКА за урок
ЗАПОЛНИ ТАБЛИЦЫ
Сложение
Вычитание
 ___________________________________________________________
___________________________________________________________
ЗАПОЛНИ ТАБЛИЦУ
Умножение
 ___________________________________________________________
___________________________________________________________
САМОСТОЯТЕЛЬНАЯ РАБОТА
ДОМАШНЕЕ ЗАДАНИЕ
Повторить основные понятия по теме «Системы счисления»
*Задание повышенного уровня: Составьте таблицы сложения, умножения в троичной системе счисления. Выполните действия:
1023*2223 =
1023+2223 =
Перевод из двоичной СС в восьмеричную
Двоичная запись числа разбивается справа налево на триады (каждая по 3 разряда).
Если в самой левой триаде меньше 3 цифр – слева добавляются нули.
Трехразрядное двоичное число каждой триады заменяется на число, равное ему в восьмеричной СС.
СС2
000
001
010
011
100
101
110
111
СС8
0
1
2
3
4
5
6
7
П РИМЕР: Переведите 1010010102 х8
РИМЕР: Переведите 1010010102 х8
101001010
ß
(101 ) (001) (010 )
ß
(5) (1) (2)
ß
512 Ответ:1010010102=5128
СС2
СС16
0000
0
0001
1
0010
2
0011
3
0100
4
0101
5
0110
6
0111
7
1000
8
1001
9
1010
A
1011
B
1100
C
1101
D
1110
E
1111
F
Перевод из двоичной СС в шестнадцатеричную
Двоичная запись числа разбивается справа налево на тетрады (каждая по 4 разряда).
Если в самой левой тетраде меньше 4 цифр – слева добавляются нули.
Четырёхразрядное двоичное число каждой тетрады заменяется на число, равное ему в шестнадцатеричной СС.
Если старшие разряды полученного числа равны 0, то они отбрасываются
П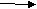 РИМЕР: 1010010102 х16
РИМЕР: 1010010102 х16
101001010
ß
(0001) (0100) (1010)
ß
(1) (4) (A)
ß
14A
Ответ: 1010010102 = 14А16
Задание 1. Мартышка висит на хвосте и жует бананы. В каждой руке по 101 банану, а в каждой ноге – на 1 банан больше, чем в руке. Сколько бананов у мартышки? Ответ дайте в 2-й СС.
Задача 2. Заполните пропуски в предложении:
Первый портативный электронный калькулятор был выпущен американским филиалом японской фирмы __________________ в ______году. Он весил около килограмма и “знал” только четыре действия арифметики.
Для этого выполните:
Переведите числа в восьмеричную систему счисления:
1710
3710
1910
3610
Переведите числа в десятичную систему счисления:
1012
10102
1108
738
Зачеркните в таблицах те столбики, где не стоят числа, которые вы получили, выполняя задание, и прочитайте текст.
Ш
Т
А
Р
О
К
М
П
218
228
458
238
278
328
548
448
1
8
9
9
6
7
4
9
510
6410
5710
1010
7210
7410
6310
5910
Задача 3. Когда был впервые выпущен гибкий магнитный диск, вы узнаете, решив следующие цепочки:


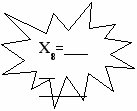
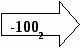
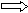
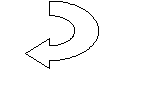
+ 36008 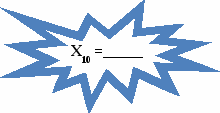
ОТВЕТ: в _________году.
Задача 4. Мартышка-мама связала 111 своим непослушным детишкам по перчатке на каждую руку и ногу. Но они порвали все свои перчатки, кроме младшего, который порвал только 11. Сколько перчаток попадет маме в починку? Ответ дайте в 8-й системе счисления.
Задача 5. Переведите координаты точек в 10-ую СС и постройте рисунок в координатной плоскости:
(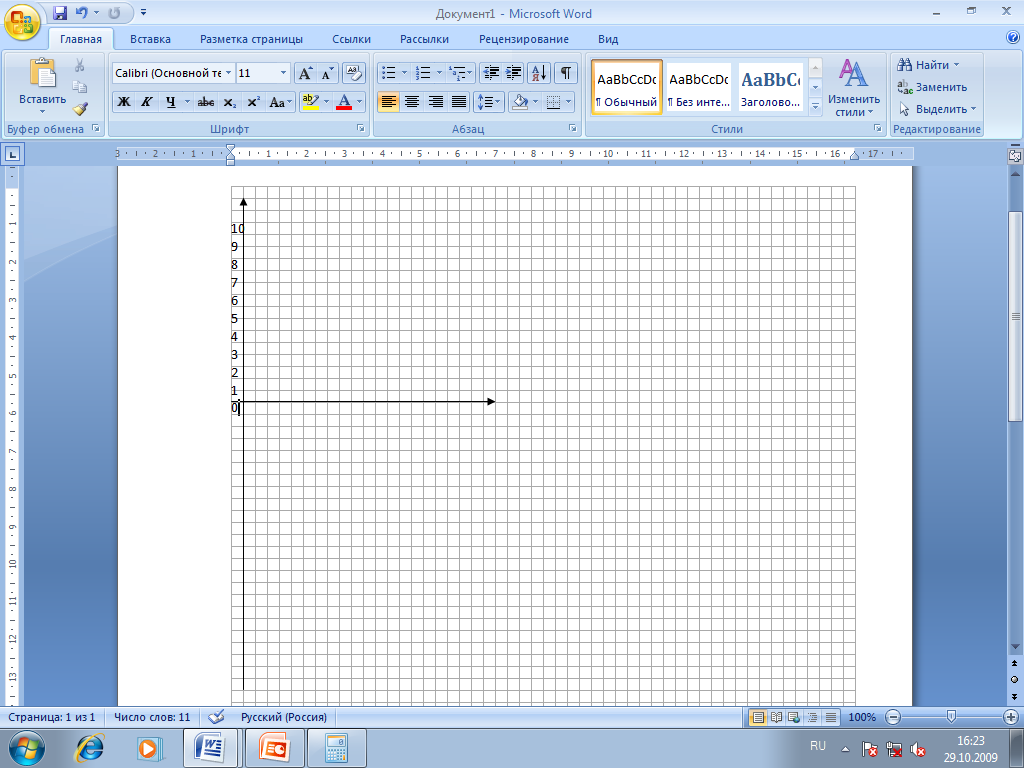 1; 11)
1; 11)
(101; 11)
(101;1001)
(1000; 110)
(101; 11)
(1010; 110)
(1001; 1)
(11;1)
(1;11)
(101; 1001)
(101; 1010)
(1000; 1010)
(1000; 1001)
(101; 1001)
Задача 6. Расшифруй слово.
Самый популярный из искусственных языков – ____________________________________
12010 = …8 4510 = …8 3110 = …8 ГОРОД
Белосток
1010
Варшава
1410
Торунь
910
Гданьск
1110
5010 = …8 3310 = …8 2210 = …81110 = …8 910 = …8 810 = …8
Н
П
С
Р
Э
Е
А
О
И
Т
138
378
558
418
1708
628
268
108
178
118
Изобретен в 238 ____________ веке жителем польского города 128 _______________________
Людвигом Заменгофом, который в 35378 _____________году опубликовал брошюру, описывающую новый язык, и подписал ее “доктор …” (надеющийся).
Задача 7. Переведите координаты точек из 8-ой системы счисления в десятичную и постройте рисунок в координатной плоскости
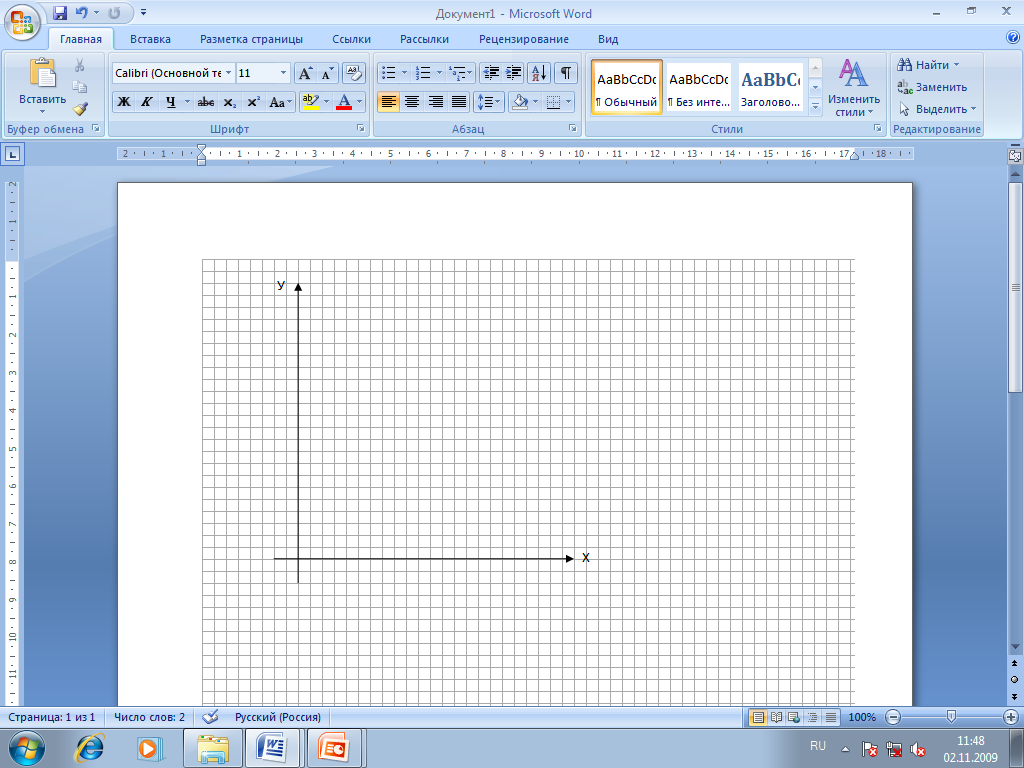
№
Х
У
1
1
4
2
4
7
3
6
13
4
12
13
5
14
7
6
14
4
7
15
3
8
14
2
9
14
3
10
13
6
11
10
3
12
10
1
13
6
1
14
6
3
15
4
3
16
4
1
17
2
1
18
2
5
ПОПРОБУЙ РЕШИТЬ!
Выпишите целые десятичные числа, принадлежащие следующим числовым промежуткам: а)[1011012;1100002]; б) [148; 208]; в) [2816; 3016].
В классе 11112 девочек и 11002 мальчиков. Сколько учеников в классе?
В классе 36q учеников, из них 21q девочек и 15q мальчиков. В какой системе счисления велся счет учеников?
В саду 100q фруктовых деревьев, из них 33q яблони, 22q груши, 16q слив и 5q вишен. В какой системе счисления посчитаны деревья?
У меня 100 братьев. Младшему 1000 лет, а старшему 1111 лет. Старший учится в 1001 классе. Может ли такое быть?
Некогда был пруд, в центре которого рос один лист водяной лилии. Каждый день число таких листьев удваивалось, и на десятый день вся поверхность пруда уже была заполнена листьями лилий. Сколько дней понадобилось, чтобы заполнить листьями половину пруда? Сколько листьев было после девятого дня?
Путем подбора степеней числа 2, в сумме дающих заданное число, переведите в двоичную систему счисления следующие числа: а) 5; б) 7; в) 12; г) 25; д) 32; е) 33.
Перевод чисел в десятичную систему счисления
№ вар.
Задание 1
Задание 2
Переведите числа из восьмеричной СС в десятичную
Определите десятичный эквивалент шестнадцатеричных чисел
250, 2022, 2757, 123
113, 2ACF, 691, D306F
247, 2021, 2756, 122
112, 2ACE, 690, D306E
246, 2020, 2755, 121
111, 2ACD, 68F, D306D
244, 2016, 2753, 117
10F, 2ACB, 68D, D306B
243, 2015, 2752, 116
10E, 2ACA, 68C, D306A
242, 2014, 2751, 115
10D, 2AC9, 68B, D3069
241, 2013, 2750, 114
10C, 2AC8, 68A, D3068
240, 2012, 2747, 113
10B, 2AC7, 688, D3067
237, 2011, 2746, 112
10A, 2AC6, 688, D3066
236, 2010, 2745, 111
109, 2AC5, 687, D3065
Перевод чисел из десятичной СС в любую другую
Задание 1. Используя таблицу кодировки букв и правила перевода чисел из двоичной системы в десятичную, расшифруйте приведенное слово.
Буква
А
В
Д
Е
Ж
И
К
Л
М
Н
О
П
Р
Ь
Ш
10-ый код
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
№ вар.
Заданное слово
11012 01002 10102 10112
10112 11002 01002 10002 11112
11002 01002 01012 10112
00102 10112 10002 11112 00102 10112
00112 01102 10112 11012
10002 10112 11012 00012 10102
11102 00012 10102 01002 10002 11112
01112 10002 00012 00112
11102 00012 11012 01012
11002 10112 11012 11102 01002 10102 11112
Задание 2 (для всех вариантов). Из таблицы составьте свое слово (3-4 буквы) и получите его двоичный код.
I вариант
1) Переведите из 10-ой системы счисления:
 38910 х2
38910 х2
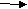 21510 х8
21510 х8
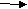 78610 х16
78610 х16
4) Запишите число римскими цифрами:
427
353
2618
2) Переведите в десятичную систему счисления:
11100010112
1000101012
10010010012
5) Переведите из римской системы счисления:
LXXVI
XLIX
CMXCIV
3) Переведите из 10-ой системы счисления в двоичную систему счисления:
48910
1382
5122
6) Сравните:
1102 и 1103
5506 и 5058
Е316 и 278
II вариант
1) Переведите из 10-ой системы счисления:
 27210 х2
27210 х2
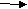 36910 х8
36910 х8
 18610 х16
18610 х16
4) Запишите число римскими цифрами:
145
473
2048
2) Переведите в десятичную систему счисления:
11010010112
1010101012
1010010012
5) Переведите из римской системы счисления:
LXVI
XLIII
MCMXCIV
3) Переведите из 10-ой системы счисления в двоичную систему счисления:
52810
1922
10242
6) Сравните:
1002 и 1003
5508 и 5056
3А16 и 378
III вариант
1) Переведите из 10-ой системы счисления:
 14810 х2
14810 х2
 56810 х8
56810 х8
 40410 х16
40410 х16
4) Запишите число римскими цифрами:
421
765
1648
2) Переведите в десятичную систему счисления:
1111111112
1000000002
1001001002
5) Переведите из римской системы счисления:
LXXXVIII
XLIX
MCXV
3) Переведите из 10-ой системы счисления в двоичную систему счисления:
48910
1382
5122
6) Сравните:
1112 и 1003
4506 и 5408
3F16 и 338
IV вариант
1) Переведите из 10-ой системы счисления:
 17410 х2
17410 х2
 14710 х8
14710 х8
 73610 х16
73610 х16
4) Запишите число римскими цифрами:
154
347
1997
2) Переведите в десятичную систему счисления:
10101010102
1001001002
1111111111112
5) Переведите из римской системы счисления:
MDLXVI
DXLI
MDXCIV
3) Переведите из 10-ой системы счисления в двоичную систему счисления:
58310
1282
13192
6) Сравните:
1542 и 1533
2356 и 2538
2D16 и 478
Системы счисления в ГИА и ЕГЭ
ЕГЭ: A1 – кодирование чисел в разных системах счисления
B7 – позиционные системы счисления
ГИА: А13 – перевод чисел в СС.
Примеры задач:
Сколько единиц в двоичной записи десятичного числа 194,5?
1) 5 2) 6 3) 3 4) 4
Чему равно х, если выполнено равенство 25х + 183х = 126х? Если таких значений х несколько, перечислите их через запятую в порядке возрастания.
Укажите основание системы счисления, в которой 16*16=304. Если таких оснований несколько, перечислите их через запятую в порядке возрастания.
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием четыре оканчивается на 11.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.
В системе счисления с некоторым основанием число 12 записывается в виде 110. Укажите это основание.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 29 оканчивается на 5.
Укажите через запятую в порядке возрастания все десятичные натуральные числа, не превосходящие 17, запись которых в троичной системе счисления оканчивается на две одинаковые цифры?
Десятичное число, переведенное в восьмеричную и в девятеричную систему, в обоих случаях заканчивается на цифру 0. Какое минимальное десятичное число удовлетворяет этому условию?
Запись числа 3010 в системе счисления с основанием N оканчивается на 0 и содержит 4 цифры. Чему равно основание этой системы счисления N?
В каком отношении находятся числа 10010012 и 1118?
их невозможно сравнить, потому что они записаны в разных СС;
первое число меньше второго;
первое число больше второго;
они равны.
Дано А = 2478, B = A916. Какое из чисел C, записанных в двоичной системе, отвечает условию A < C < B ?
1) С = 101010002 2) С = 101010102 3) С = 101010112 4) С = 101011002
Чему равна сумма чисел 348 и 4616?
1) 1028 2) 1428 3) 17A16 4) 10100102
Чему равна разность чисел 1018 и 1001112?
1) 1A16 2) 548 3) 428 4) 6816
Для кодирования букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11, соответственно). Если таким способом закодировать последовательность символов БАВГ и записать результат шестнадцатеричным кодом, то получится
1) 4B 2) 411 3) BACD 4) 1023
ЛИТЕРАТУРА:
Босова Л.Л. Занимательные задачи по информатике: задачник/ Л.Л. Босова, А.Ю. Босова, Ю.Г. Коломенская. – 3-е изд. – М.: БИНОМ. Лаборатория знаний, 2007. – 119 с.
Информатика и ИКТ. 9 класс: учебник / И.Г. Семакин, Л.А. Залогова, С.В. Русаков, Л.В. Шестакова. – М.: БИНОМ. Лаборатория знаний, 2010. – 371 с.
Молодик Т.А. Рабочая тетрадь по информатике / Т.А. Молодик // Информатика в школе. – 2013. – №2(85). – с. 31-38.
ЕГЭ по информатике / Сайт К. Полякова «Преподавание, наука и жизнь»
URL: http://kpolyakov.narod.ru/school/ege.htm
infourok.ru