 – это масса единицы объёма жидкости (кг/м3):
– это масса единицы объёма жидкости (кг/м3):Введение
Гидростатика – это раздел гидравлики (механики жидкости), изучающий покоящиеся жидкости. Она изучает законы равновесия жидкости и распределения в ней давления. Основные величины, используемые в гидростатике, – это давление p и напор H .
В гидравлике при изучении законов равновесия и движения широко пользуются различными физическими характеристиками жидкости (например, плотность, вязкость, удельный вес, удельный объём). Студенту нужно уметь определять основные физические характеристики жидкости, знать единицы этих характеристик. Следует также рассмотреть основные физические свойства капельных жидкостей: сжимаемость, тепловое расширение и др.
1. Физические свойства жидкости
Существуют следующие физические свойства жидкости:
1) Плотность – это масса единицы объёма жидкости (кг/м3 ):
r= m / V ,
где m – масса, кг;
V – объём, м3 .
Плотность воды при температуре +4°С равна 1000кг/м3. Легко заметить, что плотность воды зависит от температуры незначительно. В большинстве гидравлических расчётов свойствами сжимаемости и температурного расширения жидкостей пренебрегают, например, для воды считают плотность постоянной и равной 1000 кг/м3 .
2) Удельный вес – это вес единицы объёма жидкости (Н/м3 ):
g= G / V ,
где G – вес (сила тяжести), Н ;
V – объём, м3 .
Связаны удельный вес и плотность через ускорение свободного падения (g = 9,81 » 10 м/с2 ) так:
g= rg .
3) Коэффициент объёмного сжатияw (Па-1 )– это относительное изменение объёма жидкости при изменении давления на единицу:
,
где D W – изменение объёма W ;
Dr– изменение плотности r, соответствующее изменению давления на величину Dp .
Величина, обратная коэффициенту объёмного сжатия, называется модулем упругости жидкостейE ж (Па):
Е ж= 1/ W .
Значение модуля упругости жидкостей зависит от давления и температуры. Если принять, что приращение давления D p = p – p 0, а изменение объёма D W = W - W 0, то:
W =W 0 ·(1-W ·Dp ),
r =r0 ·(1-W ·Dp ).
4) Коэффициент температурного расширения t (0С)-1 выражает относительное изменение объёма жидкости при изменении температуры на один градус:
,
где DW – изменение объёма W, соответствующее изменению температуры на величину Dt .
Коэффициент температурного расширения воды увеличивается с возрастанием температуры и давления; для большинства других капельных жидкостей bt с увеличением давления уменьшается. Если принять, что приращение температуры D t = t – t0, а изменение объёма D W = W – W 0, то:
W = W 0 (1+ t -Dt ),
r= r0(1+ t ·Dt ).
5) Вязкость– это свойство жидкости проявлять внутреннее трение при её движении, обусловленное сопротивлением взаимному сдвигу её частиц. В покоящейся жидкости вязкость не проявляется. Количественно вязкость может быть выражена в виде динамической или кинематической вязкости, которые легко переводятся одна в другую.
Вязкость динамическая m, Па· с = Н· с/м2. Динамический коэффициент вязкости µ не зависит от давления и от характера движения, а определяется лишь физическими свойствами жидкости и её температурой.
В практике для характеристики вязкости жидкости чаще применяют не коэффициент динамической вязкости, а коэффициент кинематической вязкости (м2 /с). Коэффициентом кинематической вязкости называется отношение коэффициента динамической вязкости к плотности жидкости:
Вязкость кинематическая , м2 /с.
Вязкость проявляется в том, что при движении жидкости возникает сила внутреннего трения Т между перемещающимися один относительно другого слоями с площадью соприкосновения S . определяется законом Ньютона:
,
где S – площадь соприкасающихся слоёв, м2 ;
du – скорость смещения слоя «b » относительно слоя «a », м/с;
dy – расстояние, на котором скорость движения слоёв изменилась на du, м;
du / dy – градиент скорости, изменение скорости по нормали к направлению движения (с -1 ).
Если силу трения T отнести к единице площади соприкасающихся слоёв, то получим величину касательного напряжения , которую можно определить по формуле:
.
Вязкость жидкости определяют при помощи вискозиметра Энглера и выражают в градусах Энглера (0Е). Градус Энглера (0Е) есть отношение времени истечения испытуемой жидкости ко времени истечения дистиллированной воды. Для перехода от вязкости в градусах Энглера к коэффициенту кинематической вязкости применяется формула Убеллоде:
.
Вязкость также определяют капиллярным вискозиметром Оствальда. Коэффициент кинематической вязкости определяют по формуле:
n= c · T ж· 10-4 ,
где с – постоянная прибора;
T ж – время истечения жидкости, с.
2. Гидростатическое давление
Гидростатическое давлениеp – это скалярная величина, характеризующая напряжённое состояние жидкости. Давление равно модулю нормального напряжения в точке: p = /s /.
Давление в системе СИ измеряется в паскалях: Па = Н/м2 .
Связь единиц давления в различных системах измерения такая:
100 000 Па = 0,1 МПа = 1 кгс/см2 = 1 ат = 10 м вод. ст.
Два свойства гидростатического давления:
1. Давление в покоящейся жидкости на контакте с твёрдым телом вызывает напряжения, направленные перпендикулярно к поверхности раздела.
2. Давление в любой точке жидкости действует одинаково по всем направлениям. Это свойство отражает скалярность давления.
2.1 Гидростатический парадокс
Суммарное давление на горизонтальное дно зависит только от глубины погружения дна h 0 и величины площади последнего и не зависит от формы сосуда, а следовательно, и от веса налитой в эти сосуды жидкости. На рис. 1 показано несколько сосудов личных форм с плоским дном площадью глубиной жидкости в них h, одинаковыми для всех сосудов.
Рис. 1. Гидростатический парадокс
Различные формы стенок сосудов и различные веса жидкости в этих сосудах не оказывают никакого влияния на величину суммарного давления на их дно, равного для всех сосудов согласно:
p = h .
Это кажущееся противоречие известно под названием гидростатического парадокса. Объясняется это явление тем, что разность между силой давления на горизонтальное дно.
2.2 Основное уравнение гидростатики
Основное уравнение гидростатики гласит, что полное давление в жидкости p равно сумме внешнего давления на жидкость p 0и давления веса столба жидкости p ж, то есть
p = p 0+ p ж= p 0+ gh ,
где h – высота столба жидкости над точкой (глубина её погружения), в которой определяется давление (рис. 2).
Из уравнения следует, что давление в жидкости увеличивается с глубиной и зависимость является линейной.
Рис. 2. Схема к основному уравнению гидростатики
Рис. 3. Изменение давления: 1 – открытый резервуар; 2 – пьезометр
В частном случае для открытых резервуаров, сообщающихся с атмосферой (рис. 3), внешнее давление на жидкость равно атмосферному давлению p o = p атм = 101 325 Па1 ат. Тогда основное уравнение гидростатики принимает вид:
p = p атм+ gh .
Открытые резервуары– это не только баки, ёмкости, сообщающиеся с атмосферой, но также любые канавы с водой, озёра, водоёмы и т.д.
Избыточное давление (манометрическое) есть разность между полным и атмосферным давлением. Из последнего уравнения получаем, что для открытых резервуаров избыточное давление равно давлению столба жидкости:
p изб= p ман= p — p атм= gh .
3. Вакуум
Рассмотрим два сосуда I и II (риc. 4), соединённые между собой. Сосуд II заполнен жидкостью и имеет давление на свободной поверхности, равное атмосферному P A. Из сосуда I, постепенно откачивая воздух, создадим разрежение с давлением Р РАЗР меньше атмосферного. Тогда жидкость из сосуда II начнёт подниматься (всасываться) по трубке.
Рис. 4. Определение величины вакуума
Пусть при каком-то Р разр уровень в трубке поднялся на величину hV . Рассмотрим равновесие частиц жидкости в трубке на уровне а – а. Так как частицы жидкости в трубке на уровне а – а находятся в равновесии, то это значит, что давление со стороны сосуда I, равное Р разр + г hV, и давление состороны сосуда II, равное PA, между собой равны.
В этом случае можно написать, что Р разр + г hV = PA . отсюда:
PA – Р разр = г hV = PV .
Разность между атмосферным PA и абсолютным давлением Р разр, когда оно меньше атмосферного, называется вакуумметрическим давлением, или вакуумом. Иначе, вакуум – это недостаток давления до атмосферного.
Вакуум измеряется в тех же единицах, что и гидростатическое давление. Вакуум можно измерить и высотой столба жидкости. Вакуум встречается в насосах и иных гидравлических аппаратах и сооружениях, например в сифонах, и т.п.
Теоретически наибольшая величина вакуума может быть равна 1 кгc/см2, или 10,33 м вод. ст., или 101,3 кН/м2. Практически такой величины вакуума добиться нельзя, так как абсолютное разрежение над жидкостью создать невозможно, потому что в пространстве над жидкостью неизбежно будут пары жидкости и выделяющийся из жидкости растворённый воздух. Поэтому при перекачке холодной воды величина вакуума практически в насосах бывает не более 7 м вод. ст., при перекачке горячей воды и лёгких жидкостей – значительно меньше.
4. Приборы для измерения давления
Давление в жидкости измеряется приборами:
– пьезометрами;
– манометрами;
– вакуумметрами.
Пьезометры и манометры измеряют избыточное (манометрическое) давление, то есть они работают, если полное давление в жидкости превышает величину, равную одной атмосфере p = 1кгс/см2= 0,1МПа. Эти приборы показывают долю давления сверх атмосферного. Для измерения в жидкости полного давления p необходимо к манометрическому давлению p ман прибавить атмосферное давление p атм, снятое с барометра. Практически же в гидравлике атмосферное давление считается величиной постоянной p атм= 101325» 100000Па.
Пьезометр обычно представляет собой вертикальную стеклянную трубку, нижняя часть которой сообщается с исследуемой точкой в жидкости, где нужно измерить давление (например, точка А на рис. 3), а верхняя её часть открыта в атмосферу. Высота столба жидкости в пьезометре hp является показанием этого прибора и позволяет измерять избыточное (манометрическое) давление в точке по соотношению:
жидкость гидростатический вакуум давление
p изб= ghp .
где hp – пьезометрический напор (высота), м.
Упомянутые пьезометры применяются главным образом для лабораторных исследований. Их верхний предел измерения ограничен высотой до 5 м, однако их преимущество перед манометрами состоит в непосредственном измерении давления с помощью пьезометрической высоты столба жидкости без промежуточных передаточных механизмов.
В качестве пьезометра может быть использован любой колодец, котлован, скважина с водой или даже любое измерение глубины воды в открытом резервуаре, так как оно даёт нам величину hp .
Манометрычаще всего применяются механические, реже – жидкостные. Все манометры измеряют не полное давление, а избыточное:
p ман= p изб= p — p атм.
Преимуществами их перед пьезометрами являются более широкие пределы измерения, однако есть и недостаток: они требуют контроля их показаний. Манометры, выпускаемые в последнее время, градуируются в единицах СИ: МПа или кПа. Однако ещё продолжают применяться и старые манометры со шкалой в кгс/см2, они удобны тем, что эта единица равна одной атмосфере. Нулевое показание любого манометра соответствует полному давлению p, равному одной атмосфере.
Вакуумметр по своему внешнему виду напоминает манометр, а показывает он ту долю давления, которая дополняет полное давление в жидкости до величины одной атмосферы. Вакуум в жидкости – это не пустота, а такое состояние жидкости, когда полное давление в ней меньше атмосферного на величину p в, которая измеряется вакуумметром. Вакуумметрическое давлениеp в, показываемое прибором, связано с полным и атмосферным так:
p в= p атм– p .
Величина вакуума p в не может быть больше 1 атм, то есть предельное значение p в 100000Па, так как полное давление не может быть меньше абсолютного нуля.
Приведём примеры снятия показаний с приборов:
– пьезометр, показывающий hp = 160см вод. ст., соответствует в единицах СИ давлениям p изб= 16000Па и p= 100000+ 16000= =116000 Па;
– манометр с показаниями p ман= 2,5кгс/см2 соответствует водяному столбу hp = 25 м и полному давлению в СИ p = 0,35МПа;
– вакуумметр, показывающий p в= 0,04МПа, соответствует полному давлению p= 100 000–40 000=60 000Па, что составляет 60% от атмосферного.
5. Эпюры давления жидкости
Эпюра давления жидкости – это графическое изображение распределения давления жидкости по твёрдой поверхности, соприкасающейся с ней. Примеры эпюр для плоских и криволинейных поверхностей приведены на рис. 5 и 6. Стрелками на эпюре показывают направление действия давления (вернее, направление нормальных напряжений, возникающих от действия давления, так как по 2-му свойству давление скалярно). Величина стрелки (ордината) откладывается в масштабе и количественно показывает величину давления.
Рис. 5. Эпюры давления жидкости на плоские поверхности
Рис. 6. Эпюры давления жидкости на криволинейную поверхность
Эпюры давления жидкости на плоские поверхности служат исходными данными для проведения расчётов на прочность и устойчивость конструкций, взаимодействующих с жидкостями: стенок плавательных бассейнов, баков, резервуаров, цистерн. Расчёты ведутся методами сопротивления материалов и строительной механики.
В большинстве случаев строят эпюры избыточного давления вместо полного, а атмосферное не учитывают из-за его взаимного погашения с той и другой стороны ограждающей конструкции. При построении таких эпюр для плоских и криволинейных поверхностей (см. рис. 5 и 6) используют линейную зависимость давления от глубины p изб= gh и 1-е свойство гидростатического давления.
Библиографический список
1. Тимченко, В.И. Гидравлика: практикум для студентов / В.И. Тимченко; Южно-Рос. гос. ун-т экономики и сервиса. – Шахты: ЮРГУЭС, 2010. – 41 с.
2. Гидравлика. Гидравлические и пневматические системы: практикум / В.И. Тимченко. – Шахты: Изд-во ЮРГУЭС, 2008. – 53 с.
3. Гидравлика. Гидравлические и пневматические системы в автомобилях и гаражном оборудовании: практикум / В.И. Тимченко, И.К. Гугуев, А.И. Шилин, А.Г. Илиев. – Шахты: Изд-во ЮРГУЭС, 2008. – 53 с.
4. Гидравлика, гидромашины и гидропневмопривод: учеб. пособие для вузов / Т.В. Артемьева [и др.]; под ред. С.П. Стесина. – М.: Академия, 2009. – 336 с.
5. Сологаев, В.И. Механика жидкости и газа: конспекты лекций / В.И. Сологаев; СибАДИ. – Омск, 2010. – 56 с.
6. Механика жидкости и газа: пособие / К.Г. Донец; Южно-Рос. гос. ин-т экономики и сервиса (филиал). – Шахты: ЮРГУЭС, 2008. – 48 с.
7. Башта, Т.М. Гидравлика, гидромашины и гидроприводы: учебник для вузов / Т.М. Башта, С.С. Руднев, Б.Б. Некрасов [и др.]. – 2-е изд., перераб. – М.: Машиностроение, 2010. – 423 с.
8. Сапронов, А.Г. Энергосбережение на предприятиях бытового обслуживания: учеб. пособие / А.Г. Сапронов, В.А. Шаповалов; под ред. А.Г. Сапронова. – Шахты: Изд-во ЮРГУЭС, 2009. – 115 с.
9. Гидравлика, гидромашины и гидропневмопривод: учеб. пособие для вузов / Т.В. Артемьева [и др.]; под ред. С.П. Стесина. – 3-е изд., стер. – М.: Академия, 2008. – 336 с.
www.ronl.ru
Введение
Гидростатика – это раздел гидравлики (механики жидкости), изучающий покоящиеся жидкости. Она изучает законы равновесия жидкости и распределения в ней давления. Основные величины, используемые в гидростатике, – это давлениеpи напорH.
В гидравлике при изучении законов равновесия и движения широко пользуются различными физическими характеристиками жидкости (например, плотность, вязкость, удельный вес, удельный объём). Студенту нужно уметь определять основные физические характеристики жидкости, знать единицы этих характеристик. Следует также рассмотреть основные физические свойства капельных жидкостей: сжимаемость, тепловое расширение и др.
1. Физические свойства жидкости
Существуют следующие физические свойства жидкости:
1) Плотность – это масса единицы объёма жидкости (кг/м3):
– это масса единицы объёма жидкости (кг/м3):
r=m/V,
гдеm– масса, кг;
V –объём, м3.
Плотность воды при температуре +4°С равна 1000кг/м3. Легко заметить, что плотность воды зависит от температуры незначительно. В большинстве гидравлических расчётов свойствами сжимаемости и температурного расширения жидкостей пренебрегают, например, для воды считают плотность постоянной и равной 1000 кг/м3.
2) Удельный вес – это вес единицы объёма жидкости (Н/м3):
g=G/V,
гдеG– вес (сила тяжести),Н;
V –объём, м3.
Связаны удельный вес и плотность через ускорение свободного падения (g =9,81 » 10 м/с2) так:
g=rg.
3) Коэффициент объёмного сжатия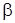 w(Па-1)–это относительное изменение объёма жидкости при изменении давления на единицу:
w(Па-1)–это относительное изменение объёма жидкости при изменении давления на единицу:
 ,
,
гдеDW– изменение объёмаW;
Dr– изменение плотности r, соответствующее изменению давления на величину Dp.
Величина, обратная коэффициенту объёмного сжатия, называется модулем упругости жидкостейEж(Па):
Еж=1/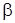 W.
W.
Значение модуля упругости жидкостей зависит от давления и температуры. Если принять, что приращение давленияDp=p–p0, а изменение объёмаDW=W-W0, то:
W=W0·(1-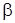 W·Dp),
W·Dp),
r =r0·(1-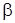 W·Dp).
W·Dp).
4) Коэффициент температурного расширения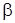 t(0С)-1выражает относительное изменение объёма жидкости при изменении температуры на один градус:
t(0С)-1выражает относительное изменение объёма жидкости при изменении температуры на один градус:
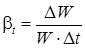 ,
,
где DW– изменение объёмаW, соответствующее изменению температуры на величину Dt.
Коэффициент температурного расширения воды увеличивается с возрастанием температуры и давления; для большинства других капельных жидкостей btс увеличением давления уменьшается. Если принять, что приращение температурыDt = t – t0, а изменение объёмаDW = W – W0, то:
W=W0(1+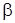 t-Dt),
t-Dt),
r=r0(1+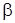 t·Dt).
t·Dt).
5) Вязкость–это свойство жидкости проявлять внутреннее трение при её движении, обусловленное сопротивлением взаимному сдвигу её частиц. В покоящейся жидкости вязкость не проявляется. Количественно вязкость может быть выражена в виде динамической или кинематической вязкости, которые легко переводятся одна в другую.
Вязкость динамическая m, Па·с =Н·с/м2. Динамический коэффициент вязкости µ не зависит от давления и от характера движения, а определяется лишь физическими свойствами жидкости и её температурой.
В практике для характеристики вязкости жидкости чаще применяют не коэффициент динамической вязкости, а коэффициент кинематической вязкости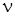 (м2/с). Коэффициентом кинематической вязкости называется отношение коэффициента динамической вязкости к плотности жидкости:
(м2/с). Коэффициентом кинематической вязкости называется отношение коэффициента динамической вязкости к плотности жидкости:
Вязкость кинематическая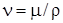 , м2/с.
, м2/с.
Вязкость проявляется в том, что при движении жидкости возникает сила внутреннего тренияТмежду перемещающимися один относительно другого слоями с площадью соприкосновенияS.определяется законом Ньютона:
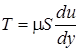 ,
,
гдеS –площадь соприкасающихся слоёв, м2;
du –скорость смещения слоя «b» относительно слоя «a», м/с;
dy –расстояние, на котором скорость движения слоёв изменилась наdu, м;
du/dy–градиент скорости, изменение скорости по нормали к направлению движения (с-1).
Если силу тренияTотнести к единице площади соприкасающихся слоёв, то получим величину касательного напряжения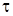 , которую можно определить по формуле:
, которую можно определить по формуле:
 .
.
Вязкость жидкости определяют при помощи вискозиметра Энглера и выражают в градусах Энглера (0Е). Градус Энглера (0Е) есть отношение времени истечения испытуемой жидкости ко времени истечения дистиллированной воды. Для перехода от вязкости в градусах Энглера к коэффициенту кинематической вязкостиприменяется формула Убеллоде:
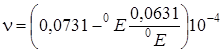 .
.
Вязкость также определяют капиллярным вискозиметром Оствальда. Коэффициент кинематической вязкости определяют по формуле:
n=c·Tж·10-4,
гдес– постоянная прибора;
Tж– время истечения жидкости, с.
2. Гидростатическое давление
Гидростатическое давлениеp –это скалярная величина, характеризующая напряжённое состояние жидкости. Давление равно модулю нормального напряжения в точке:p =/s /.
Давление в системе СИ измеряется в паскалях: Па = Н/м2.
Связь единиц давления в различных системах измерения такая:
100 000 Па = 0,1 МПа = 1 кгс/см2= 1 ат = 10 м вод. ст.
Два свойства гидростатического давления:
1. Давление в покоящейся жидкости на контакте с твёрдым телом вызывает напряжения, направленные перпендикулярно к поверхности раздела.
2. Давление в любой точке жидкости действует одинаково по всем направлениям. Это свойство отражает скалярность давления.
2.1 Гидростатический парадокс
Суммарное давление на горизонтальное дно зависит только от глубины погружения днаh0и величины площади последнего и не зависит от формы сосуда, а следовательно, и от веса налитой в эти сосуды жидкости. На рис. 1 показано несколько сосудов личных форм с плоским дном площадью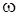 глубиной жидкости в нихh,одинаковыми для всех сосудов.
глубиной жидкости в нихh,одинаковыми для всех сосудов.
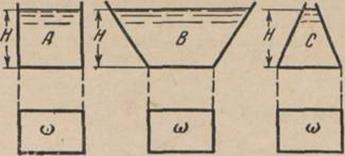
Рис. 1. Гидростатический парадокс
Различные формы стенок сосудов и различные веса жидкости в этих сосудах не оказывают никакого влияния на величину суммарного давления на их дно, равного для всех сосудов согласно:
p= h
h .
.
Это кажущееся противоречие известно под названием гидростатического парадокса. Объясняется это явление тем, что разность между силой давления на горизонтальное дно.
2.2 Основное уравнение гидростатики
Основное уравнение гидростатики гласит, что полное давление в жидкостиpравно сумме внешнего давления на жидкостьp0и давления веса столба жидкостиpж, то есть
p=p0+pж=p0+gh,
гдеh– высота столба жидкости над точкой (глубина её погружения), в которой определяется давление (рис. 2).
Из уравнения следует, что давление в жидкости увеличивается с глубиной и зависимость является линейной.

Рис. 2. Схема к основному уравнению гидростатики

Рис. 3. Изменение давления: 1 – открытый резервуар; 2 – пьезометр
В частном случае для открытых резервуаров, сообщающихся с атмосферой (рис. 3), внешнее давление на жидкость равно атмосферному давлениюpo=pатм= 101 325 Па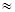 1 ат. Тогда основное уравнение гидростатики принимает вид:
1 ат. Тогда основное уравнение гидростатики принимает вид:
p=pатм+gh.
Открытые резервуары–это не только баки, ёмкости, сообщающиеся с атмосферой, но также любые канавы с водой, озёра, водоёмы и т.д.
Избыточное давление (манометрическое) есть разность между полным и атмосферным давлением. Из последнего уравнения получаем, что для открытых резервуаров избыточное давление равно давлению столба жидкости:
pизб=pман=p-pатм=gh.
3. Вакуум
Рассмотрим два сосуда I и II (риc. 4), соединённые между собой. Сосуд II заполнен жидкостью и имеет давление на свободной поверхности, равное атмосферномуPA. Из сосуда I, постепенно откачивая воздух, создадим разрежение с давлениемРРАЗРменьше атмосферного. Тогда жидкость из сосуда II начнёт подниматься (всасываться) по трубке.
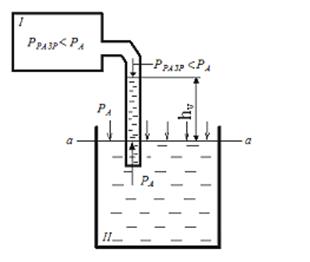
Рис. 4. Определение величины вакуума
Пусть при каком-тоРразруровень в трубке поднялся на величинуhV.Рассмотрим равновесие частиц жидкости в трубке на уровнеа – а. Так как частицы жидкости в трубке на уровнеа – анаходятся в равновесии, то это значит, что давление со стороны сосудаI, равноеРразр+ гhV, и давление состороны сосудаII, равноеPA,между собой равны.
В этом случае можно написать, чтоРразр+ гhV=PA.отсюда:
PA– Рразр= гhV=PV.
Разность между атмосфернымPAи абсолютным давлениемРразр, когда оно меньше атмосферного, называетсявакуумметрическим давлением,иливакуумом.Иначе, вакуум – это недостаток давления до атмосферного.
Вакуум измеряется в тех же единицах, что и гидростатическое давление. Вакуум можно измерить и высотой столба жидкости. Вакуум встречается в насосах и иных гидравлических аппаратах и сооружениях, например в сифонах, и т.п.
Теоретически наибольшая величина вакуума может быть равна 1 кгc/см2, или 10,33 м вод. ст., или 101,3 кН/м2. Практически такой величины вакуума добиться нельзя, так как абсолютное разрежение над жидкостью создать невозможно, потому что в пространстве над жидкостью неизбежно будут пары жидкости и выделяющийся из жидкости растворённый воздух. Поэтому при перекачке холодной воды величина вакуума практически в насосах бывает не более 7 м вод. ст., при перекачке горячей воды и лёгких жидкостей – значительно меньше.
4. Приборы для измерения давления
Давление в жидкости измеряется приборами:
– пьезометрами;
– манометрами;
– вакуумметрами.
Пьезометры и манометры измеряют избыточное (манометрическое) давление, то есть они работают, если полное давление в жидкости превышает величину, равную одной атмосфереp =1кгс/см2=0,1МПа. Эти приборы показывают долю давления сверх атмосферного. Для измерения в жидкости полного давленияpнеобходимо к манометрическому давлениюpманприбавить атмосферное давлениеpатм, снятое с барометра. Практически же в гидравлике атмосферное давление считается величиной постояннойpатм=101325»100000Па.
Пьезометр обычно представляет собой вертикальную стеклянную трубку, нижняя часть которой сообщается с исследуемой точкой в жидкости, где нужно измерить давление (например, точка А на рис. 3), а верхняя её часть открыта в атмосферу. Высота столба жидкости в пьезометреhpявляется показанием этого прибора и позволяет измерять избыточное (манометрическое) давление в точке по соотношению:
жидкость гидростатический вакуум давление
pизб=ghp.
гдеhp– пьезометрический напор (высота), м.
Упомянутые пьезометры применяются главным образом для лабораторных исследований. Их верхний предел измерения ограничен высотой до 5 м, однако их преимущество перед манометрами состоит в непосредственном измерении давления с помощью пьезометрической высоты столба жидкости без промежуточных передаточных механизмов.
В качестве пьезометра может быть использован любой колодец, котлован, скважина с водой или даже любое измерение глубины воды в открытом резервуаре, так как оно даёт нам величинуhp.
Манометрычаще всего применяются механические, реже – жидкостные. Все манометры измеряют не полное давление, а избыточное:
pман=pизб=p-pатм.
Преимуществами их перед пьезометрами являются более широкие пределы измерения, однако есть и недостаток: они требуют контроля их показаний. Манометры, выпускаемые в последнее время, градуируются в единицах СИ: МПа или кПа. Однако ещё продолжают применяться и старые манометры со шкалой в кгс/см2, они удобны тем, что эта единица равна одной атмосфере. Нулевое показание любого манометра соответствует полному давлениюp, равному одной атмосфере.
Вакуумметр по своему внешнему виду напоминает манометр, а показывает он ту долю давления, которая дополняет полное давление в жидкости до величины одной атмосферы. Вакуум в жидкости – это не пустота, а такое состояние жидкости, когда полное давление в ней меньше атмосферного на величинуpв, которая измеряется вакуумметром. Вакуумметрическое давлениеpв, показываемое прибором, связано с полным и атмосферным так:
pв=pатм–p.
Величина вакуумаpвне может быть больше 1 атм, то есть предельное значениеpв 100000Па, так как полное давление не может быть меньше абсолютного нуля.
100000Па, так как полное давление не может быть меньше абсолютного нуля.
Приведём примеры снятия показаний с приборов:
– пьезометр, показывающийhp=160см вод. ст., соответствует в единицах СИ давлениямpизб=16000Па иp=100000+ 16000= =116000 Па;
– манометр с показаниямиpман=2,5кгс/см2соответствует водяному столбуhp=25 м и полному давлению в СИp =0,35МПа;
– вакуумметр, показывающийpв=0,04МПа, соответствует полному давлениюp=100 000–40 000=60 000Па, что составляет 60% от атмосферного.
5. Эпюры давления жидкости
Эпюра давления жидкости – это графическое изображение распределения давления жидкости по твёрдой поверхности, соприкасающейся с ней. Примеры эпюр для плоских и криволинейных поверхностей приведены на рис. 5 и 6. Стрелками на эпюре показывают направление действия давления (вернее, направление нормальных напряжений, возникающих от действия давления, так как по 2-му свойству давление скалярно). Величина стрелки (ордината) откладывается в масштабе и количественно показывает величину давления.
Рис. 5. Эпюры давления жидкости на плоские поверхности
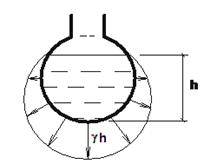
Рис. 6. Эпюры давления жидкости на криволинейную поверхность
Эпюры давления жидкости на плоские поверхности служат исходными данными для проведения расчётов на прочность и устойчивость конструкций, взаимодействующих с жидкостями: стенок плавательных бассейнов, баков, резервуаров, цистерн. Расчёты ведутся методами сопротивления материалов и строительной механики.
В большинстве случаев строят эпюры избыточного давления вместо полного, а атмосферное не учитывают из-за его взаимного погашения с той и другой стороны ограждающей конструкции. При построении таких эпюр для плоских и криволинейных поверхностей (см. рис. 5 и 6) используют линейную зависимость давления от глубиныpизб= ghи 1-е свойство гидростатического давления.
Библиографический список
1. Тимченко, В.И. Гидравлика: практикум для студентов / В.И. Тимченко; Южно-Рос. гос. ун-т экономики и сервиса. – Шахты: ЮРГУЭС, 2010. – 41 с.
2. Гидравлика. Гидравлические и пневматические системы: практикум / В.И. Тимченко. – Шахты: Изд-во ЮРГУЭС, 2008. – 53 с.
3. Гидравлика. Гидравлические и пневматические системы в автомобилях и гаражном оборудовании: практикум / В.И. Тимченко, И.К. Гугуев, А.И. Шилин, А.Г. Илиев. – Шахты: Изд-во ЮРГУЭС, 2008. – 53 с.
4. Гидравлика, гидромашины и гидропневмопривод: учеб. пособие для вузов / Т.В. Артемьева [и др.]; под ред. С.П. Стесина. – М.: Академия, 2009. – 336 с.
5. Сологаев, В.И. Механика жидкости и газа: конспекты лекций / В.И. Сологаев; СибАДИ. – Омск, 2010. – 56 с.
6. Механика жидкости и газа: пособие / К.Г. Донец; Южно-Рос. гос. ин-т экономики и сервиса (филиал). – Шахты: ЮРГУЭС, 2008. – 48 с.
7. Башта, Т.М. Гидравлика, гидромашины и гидроприводы: учебник для вузов / Т.М. Башта, С.С. Руднев, Б.Б. Некрасов [и др.]. – 2-е изд., перераб. – М.: Машиностроение, 2010. – 423 с.
8. Сапронов, А.Г. Энергосбережение на предприятиях бытового обслуживания: учеб. пособие / А.Г. Сапронов, В.А. Шаповалов; под ред. А.Г. Сапронова. – Шахты: Изд-во ЮРГУЭС, 2009. – 115 с.
9. Гидравлика, гидромашины и гидропневмопривод: учеб. пособие для вузов / Т.В. Артемьева [и др.]; под ред. С.П. Стесина. – 3-е изд., стер. – М.: Академия, 2008. – 336 с.
superbotanik.net
Введение
Гидростатика – это раздел гидравлики (механики жидкости), изучающий покоящиеся жидкости. Она изучает законы равновесия жидкости и распределения в ней давления. Основные величины, используемые в гидростатике, – это давление p и напор H.
В гидравлике при изучении законов равновесия и движения широко пользуются различными физическими характеристиками жидкости (например, плотность, вязкость, удельный вес, удельный объём). Студенту нужно уметь определять основные физические характеристики жидкости, знать единицы этих характеристик. Следует также рассмотреть основные физические свойства капельных жидкостей: сжимаемость, тепловое расширение и др.
1. Физические свойства жидкости
Существуют следующие физические свойства жидкости:
1) Плотность  – это масса единицы объёма
жидкости (кг/м3):
– это масса единицы объёма
жидкости (кг/м3):
r = m/V,
где m – масса, кг;
V – объём, м3.
Плотность воды при температуре +4°С равна 1000 кг/м3. Легко заметить, что плотность воды зависит от температуры незначительно. В большинстве гидравлических расчётов свойствами сжимаемости и температурного расширения жидкостей пренебрегают, например, для воды считают плотность постоянной и равной 1000 кг/м3.
2) Удельный вес – это вес единицы объёма жидкости (Н/м3):
g = G/V,
где G – вес (сила тяжести), Н;
V – объём, м3.
Связаны удельный вес и плотность через ускорение свободного падения (g = 9,81 » 10 м/с2) так:
g = r g.
3) Коэффициент объёмного сжатия  w (Па-1) – это
относительное изменение объёма жидкости при изменении давления на единицу:
w (Па-1) – это
относительное изменение объёма жидкости при изменении давления на единицу:
 ,
,
где DW – изменение объёма W;
Dr – изменение плотности r, соответствующее изменению давления на величину Dp.
Величина, обратная коэффициенту объёмного сжатия, называется модулем упругости жидкостей Eж (Па):
Еж = 1/  W.
W.
Значение модуля упругости жидкостей зависит от давления и температуры. Если принять, что приращение давления Dp = p – p0, а изменение объёма DW=W-W0, то:
W=W0 ·(1- W·Dp),
W·Dp),
r =r0 ·(1- W·Dp).
W·Dp).
4)
Коэффициент температурного расширения  t
(0С)-1 выражает относительное изменение объёма жидкости
при изменении температуры на один градус:
t
(0С)-1 выражает относительное изменение объёма жидкости
при изменении температуры на один градус:
 ,
,
где DW – изменение объёма W, соответствующее изменению температуры на величину D t.
Коэффициент температурного расширения воды увеличивается с возрастанием температуры и давления; для большинства других капельных жидкостей bt с увеличением давления уменьшается. Если принять, что приращение температуры D t = t – t0, а изменение объёма DW = W – W0, то:
W=W0 (1+ t-Dt),
t-Dt),
r =r0 (1+  t·Dt).
t·Dt).
5) Вязкость – это свойство жидкости проявлять внутреннее трение при её движении, обусловленное сопротивлением взаимному сдвигу её частиц. В покоящейся жидкости вязкость не проявляется. Количественно вязкость может быть выражена в виде динамической или кинематической вязкости, которые легко переводятся одна в другую.
Вязкость динамическая m, Па· с = Н· с/м2. Динамический коэффициент вязкости µ не зависит от давления и от характера движения, а определяется лишь физическими свойствами жидкости и её температурой.
В практике
для характеристики вязкости жидкости чаще применяют не коэффициент динамической
вязкости, а коэффициент кинематической вязкости  (м2/с).
Коэффициентом кинематической вязкости называется отношение коэффициента
динамической вязкости к плотности жидкости:
(м2/с).
Коэффициентом кинематической вязкости называется отношение коэффициента
динамической вязкости к плотности жидкости:
Вязкость
кинематическая  , м2/с.
, м2/с.
Вязкость проявляется в том, что при движении жидкости возникает сила внутреннего трения Т между перемещающимися один относительно другого слоями с площадью соприкосновения S. определяется законом Ньютона:
 ,
,
где S – площадь соприкасающихся слоёв, м2;
du – скорость смещения слоя «b» относительно слоя «a», м/с;
dy – расстояние, на котором скорость движения слоёв изменилась на du, м;
du/dy – градиент скорости, изменение скорости по нормали к направлению движения (с-1).
Если
силу трения T отнести к единице площади соприкасающихся слоёв,
то получим величину касательного напряжения  ,
которую можно определить по формуле:
,
которую можно определить по формуле:
 .
.
Вязкость жидкости определяют при помощи вискозиметра Энглера и выражают в градусах Энглера (0Е). Градус Энглера (0Е) есть отношение времени истечения испытуемой жидкости ко времени истечения дистиллированной воды. Для перехода от вязкости в градусах Энглера к коэффициенту кинематической вязкости применяется формула Убеллоде:
 .
.
Вязкость также определяют капиллярным вискозиметром Оствальда. Коэффициент кинематической вязкости определяют по формуле:
n = c ·Tж ·10-4,
где с – постоянная прибора;
Tж – время истечения жидкости, с.
2. Гидростатическое давление
Гидростатическое давление p – это скалярная величина, характеризующая напряжённое состояние жидкости. Давление равно модулю нормального напряжения в точке: p = /s /.
Давление в системе СИ измеряется в паскалях: Па = Н/м2.
Связь единиц давления в различных системах измерения такая:
100 000 Па = 0,1 МПа = 1 кгс/см2 = 1 ат = 10 м вод. ст.
Два свойства гидростатического давления:
1. Давление в покоящейся жидкости на контакте с твёрдым телом вызывает напряжения, направленные перпендикулярно к поверхности раздела.
2. Давление в любой точке жидкости действует одинаково по всем направлениям. Это свойство отражает скалярность давления.
2.1 Гидростатический парадокс
Суммарное давление на горизонтальное дно зависит только от глубины
погружения дна h0 и величины площади последнего и не зависит от формы сосуда, а
следовательно, и от веса налитой в эти сосуды жидкости. На рис. 1 показано
несколько сосудов личных форм с плоским дном площадью  глубиной жидкости в
них h, одинаковыми для всех сосудов.
глубиной жидкости в
них h, одинаковыми для всех сосудов.

Рис. 1. Гидростатический парадокс
Различные формы стенок сосудов и различные веса жидкости в этих сосудах не оказывают никакого влияния на величину суммарного давления на их дно, равного для всех сосудов согласно:
p =  h
h .
.
Это кажущееся противоречие известно под названием гидростатического парадокса. Объясняется это явление тем, что разность между силой давления на горизонтальное дно.
2.2 Основное уравнение гидростатики
Основное уравнение гидростатики гласит, что полное давление в жидкости p равно сумме внешнего давления на жидкость p0 и давления веса столба жидкости pж, то есть
p=p0+ pж= p0+gh,
где h – высота столба жидкости над точкой (глубина её погружения), в которой определяется давление (рис. 2).
Из уравнения следует, что давление в жидкости увеличивается с глубиной и зависимость является линейной.

Рис. 2. Схема к основному уравнению гидростатики

Рис. 3. Изменение давления: 1 – открытый резервуар; 2 – пьезометр
В частном
случае для открытых резервуаров, сообщающихся с атмосферой (рис. 3),
внешнее давление на жидкость равно атмосферному давлению po =
pатм = 101 325 Па 1
ат. Тогда основное уравнение гидростатики принимает вид:
1
ат. Тогда основное уравнение гидростатики принимает вид:
p = pатм+gh.
Открытые резервуары – это не только баки, ёмкости, сообщающиеся с атмосферой, но также любые канавы с водой, озёра, водоёмы и т.д.
Избыточное давление (манометрическое) есть разность между полным и атмосферным давлением. Из последнего уравнения получаем, что для открытых резервуаров избыточное давление равно давлению столба жидкости:
pизб=pман= p- pатм = gh.
3. Вакуум
Рассмотрим два сосуда I и II (риc. 4), соединённые между собой. Сосуд II заполнен жидкостью и имеет давление на свободной поверхности, равное атмосферному PA. Из сосуда I, постепенно откачивая воздух, создадим разрежение с давлением РРАЗР меньше атмосферного. Тогда жидкость из сосуда II начнёт подниматься (всасываться) по трубке.

Рис. 4. Определение величины вакуума
Пусть при каком-то Рразр уровень в трубке поднялся на величину hV. Рассмотрим равновесие частиц жидкости в трубке на уровне а – а. Так как частицы жидкости в трубке на уровне а – а находятся в равновесии, то это значит, что давление со стороны сосуда I, равное Рразр + г hV, и давление со стороны сосуда II, равное PA, между собой равны.
В этом случае можно написать, что Рразр + г hV = PA. отсюда:
PA – Рразр = г hV = PV.
Разность между атмосферным PA и абсолютным давлением Рразр, когда оно меньше атмосферного, называется вакуумметрическим давлением, или вакуумом. Иначе, вакуум – это недостаток давления до атмосферного.
Вакуум измеряется в тех же единицах, что и гидростатическое давление. Вакуум можно измерить и высотой столба жидкости. Вакуум встречается в насосах и иных гидравлических аппаратах и сооружениях, например в сифонах, и т.п.
Теоретически наибольшая величина вакуума может быть равна 1 кгc/см2, или 10,33 м вод. ст., или 101,3 кН/м2. Практически такой величины вакуума добиться нельзя, так как абсолютное разрежение над жидкостью создать невозможно, потому что в пространстве над жидкостью неизбежно будут пары жидкости и выделяющийся из жидкости растворённый воздух. Поэтому при перекачке холодной воды величина вакуума практически в насосах бывает не более 7 м вод. ст., при перекачке горячей воды и лёгких жидкостей – значительно меньше.
4. Приборы для измерения давления
Давление в жидкости измеряется приборами:
– пьезометрами;
– манометрами;
– вакуумметрами.
Пьезометры и манометры измеряют избыточное (манометрическое) давление, то есть они работают, если полное давление в жидкости превышает величину, равную одной атмосфере p = 1 кгс/см2 = 0,1 МПа. Эти приборы показывают долю давления сверх атмосферного. Для измерения в жидкости полного давления p необходимо к манометрическому давлению pман прибавить атмосферное давление pатм, снятое с барометра. Практически же в гидравлике атмосферное давление считается величиной постоянной pатм=101325 » 100000 Па.
Пьезометр обычно представляет собой вертикальную стеклянную трубку, нижняя часть которой сообщается с исследуемой точкой в жидкости, где нужно измерить давление (например, точка А на рис. 3), а верхняя её часть открыта в атмосферу. Высота столба жидкости в пьезометре hp является показанием этого прибора и позволяет измерять избыточное (манометрическое) давление в точке по соотношению:
жидкость гидростатический вакуум давление
pизб = g hp.
где hp – пьезометрический напор (высота), м.
Упомянутые пьезометры применяются главным образом для лабораторных исследований. Их верхний предел измерения ограничен высотой до 5 м, однако их преимущество перед манометрами состоит в непосредственном измерении давления с помощью пьезометрической высоты столба жидкости без промежуточных передаточных механизмов.
В качестве пьезометра может быть использован любой колодец, котлован, скважина с водой или даже любое измерение глубины воды в открытом резервуаре, так как оно даёт нам величину hp.
Манометры чаще всего применяются механические, реже – жидкостные. Все манометры измеряют не полное давление, а избыточное:
pман=pизб= p- pатм.
Преимуществами их перед пьезометрами являются более широкие пределы измерения, однако есть и недостаток: они требуют контроля их показаний. Манометры, выпускаемые в последнее время, градуируются в единицах СИ: МПа или кПа. Однако ещё продолжают применяться и старые манометры со шкалой в кгс/см2, они удобны тем, что эта единица равна одной атмосфере. Нулевое показание любого манометра соответствует полному давлению p, равному одной атмосфере.
Вакуумметр по своему внешнему виду напоминает манометр, а показывает он ту долю давления, которая дополняет полное давление в жидкости до величины одной атмосферы. Вакуум в жидкости – это не пустота, а такое состояние жидкости, когда полное давление в ней меньше атмосферного на величину pв, которая измеряется вакуумметром. Вакуумметрическое давление pв, показываемое прибором, связано с полным и атмосферным так:
pв=pатм – p.
Величина
вакуума pв не может быть больше 1 атм, то есть предельное значение pв  100000
Па, так как полное давление не может быть меньше абсолютного нуля.
100000
Па, так как полное давление не может быть меньше абсолютного нуля.
Приведём примеры снятия показаний с приборов:
– пьезометр, показывающий hp=160 см вод. ст., соответствует в единицах СИ давлениям pизб=16000 Па и p= 100000+ 16000= =116000 Па;
– манометр с показаниями pман = 2,5 кгс/см2 соответствует водяному столбу hp=25 м и полному давлению в СИ p = 0,35 МПа;
– вакуумметр, показывающий pв=0,04 МПа, соответствует полному давлению p=100 000–40 000=60 000 Па, что составляет 60% от атмосферного.
5. Эпюры давления жидкости
Эпюра давления жидкости – это графическое изображение распределения давления жидкости по твёрдой поверхности, соприкасающейся с ней. Примеры эпюр для плоских и криволинейных поверхностей приведены на рис. 5 и 6. Стрелками на эпюре показывают направление действия давления (вернее, направление нормальных напряжений, возникающих от действия давления, так как по 2-му свойству давление скалярно). Величина стрелки (ордината) откладывается в масштабе и количественно показывает величину давления.

Рис. 5. Эпюры давления жидкости на плоские поверхности

Рис. 6. Эпюры давления жидкости на криволинейную поверхность
Эпюры давления жидкости на плоские поверхности служат исходными данными для проведения расчётов на прочность и устойчивость конструкций, взаимодействующих с жидкостями: стенок плавательных бассейнов, баков, резервуаров, цистерн. Расчёты ведутся методами сопротивления материалов и строительной механики.
В большинстве случаев строят эпюры избыточного давления вместо полного, а атмосферное не учитывают из-за его взаимного погашения с той и другой стороны ограждающей конструкции. При построении таких эпюр для плоских и криволинейных поверхностей (см. рис. 5 и 6) используют линейную зависимость давления от глубины pизб = gh и 1-е свойство гидростатического давления.
Библиографический список
1. Тимченко, В.И. Гидравлика: практикум для студентов / В.И. Тимченко; Южно-Рос. гос. ун-т экономики и сервиса. – Шахты: ЮРГУЭС, 2010. – 41 с.
2. Гидравлика. Гидравлические и пневматические системы: практикум / В.И. Тимченко. – Шахты: Изд-во ЮРГУЭС, 2008. – 53 с.
3. Гидравлика. Гидравлические и пневматические системы в автомобилях и гаражном оборудовании: практикум / В.И. Тимченко, И.К. Гугуев, А.И. Шилин, А.Г. Илиев. – Шахты: Изд-во ЮРГУЭС, 2008. – 53 с.
4. Гидравлика, гидромашины и гидропневмопривод: учеб. пособие для вузов / Т.В. Артемьева [и др.]; под ред. С.П. Стесина. – М.: Академия, 2009. – 336 с.
5. Сологаев, В.И. Механика жидкости и газа: конспекты лекций / В.И. Сологаев; СибАДИ. – Омск, 2010. – 56 с.
6. Механика жидкости и газа: пособие / К.Г. Донец; Южно-Рос. гос. ин-т экономики и сервиса (филиал). – Шахты: ЮРГУЭС, 2008. – 48 с.
7. Башта, Т.М. Гидравлика, гидромашины и гидроприводы: учебник для вузов / Т.М. Башта, С.С. Руднев, Б.Б. Некрасов [и др.]. – 2-е изд., перераб. – М.: Машиностроение, 2010. – 423 с.
8. Сапронов, А.Г. Энергосбережение на предприятиях бытового обслуживания: учеб. пособие / А.Г. Сапронов, В.А. Шаповалов; под ред. А.Г. Сапронова. – Шахты: Изд-во ЮРГУЭС, 2009. – 115 с.
9. Гидравлика, гидромашины и гидропневмопривод: учеб. пособие для вузов / Т.В. Артемьева [и др.]; под ред. С.П. Стесина. – 3-е изд., стер. – М.: Академия, 2008. – 336 с.
www.neuch.ru
· во-вторых, выталкивающая (архимедова) сила:
· в-третьих, сила Стокса, порождаемая вязким трением на поверхности шарика: .В определенных выражениях примяты следующие выражения:·
– плотность материала шарика;
· – плотность жидкости;
· W – объём шарика;
· V- скорость опускания шарика;
· g – ускорение свободного падения;
· d – диаметр шарика;
· μ – динамический коэффициент вязкости.
Так как скорость тела постоянная, то по второму закону Ньютона можно записать:Объём шарика: .Подставляя полученные выражения в уравнение сил, действующих на шарик, получим:
Выразив из последней формулы μ, будем иметь выражение для определения динамического коэффициента вязкости:
Если изменить время пропускания шарика, заранее измерить глубину, то не трудно определить вязкость любой жидкость.22. Что такое абсолютное, манометрической и вакуумметрическое давление? Как они связаны между собой?Абсолютным называется давление, определенное с учётом атмосферного давления. Избыточное давление – это давление сверх атмосферного, определенное без учёта атмосферного.
.Абсолютное давление может быть отрицательным, т.к. жидкость не воспринимает растягивающих напряжений:
Избыточное давление может быть и больше и меньше нуля:
Для удобства, отрицательное избыточное давление, взятое со знаком «+», называют вакуумметрическим давлением.
Очень часто избыточное давление называют манометрическим, т.к. оно изменяется с помощью манометров, или пьезометрическим т.к. оно измеряется с помощью пьезометров. 32. Что такое кавитация?Если при входе в рабочее колесо насоса абсолютное давление окажется меньшим или равным упругости паров перекачиваемой жидкости при данной температуре, то жидкость начинает вскипать, происходит разрыв потока и подача прекращается. При длительной работе насоса в таких условиях разрушается рабочее колесо. Явления, происходящие в насосе при вскипании жидкости, называются кавитацией. При этом из жидкости выделяются пары и растворенные газы в том месте, где давление равно или меньше давления насыщенных паров. Пузырьки пара и газов, увеличенные потоком в область повышенного давления, резко конденсируются с уменьшением объема в микроскопических зонах; это явление, подобное взрывам мельчайших бомб, приводит к механическим повреждениям лопаток колеса и их разрушению. Происходит и химическое разрушение металла в зоне кавитации выделившимся кислородом воздуха (коррозия). Кавитация может происходить не только в рабочем колесе, но и в направляющем аппарате, и в спиральном корпусе. Эти явления сопровождаются потрескиванием, шумом и вибрацией насоса. При кавитации резко падает к. п. Д. насоса, производительность и напор. Особенно сильно при кавитации разрушаются чугун и углеродистая сталь, наиболее устойчивы бронза и нержавеющая сталь. Поэтому в последнее время для изготовления насосов применяют высококачественные материалы и защитные покрытия (наплавка твердых сплавов, поверхностная закалка, металлизация в холодном состоянии), что повышает надежность работы насосов. Во избежание явления кавитации насос следует располагать как можно ниже. Кавитационный запас уровня определяют по уравнению:
42. Как определяется сила гидростатического давления на криволинейную поверхность? Давление - напряжение, возникающее в жидкости под действием сжимающих сил. В общем случае поверхностная сила
, действующая на площадке
под некоторым углом к ней, может быть разложена на нормальную
и тангенциальную составляющие.
Первая, направленная внутрь объема, называется силой давления, вторая - силой трения. Нормальная составляющая вызывает в жидкости нормальные напряжения или гидромеханическое давление, которое в покоящейся жидкости называется гидростатическим. Если сила
равномерно распределена по площадке
, то
или переходя к пределу:
В любом случае причиной возникновения давления является внешняя сила, приложенная к жидкости. Часто в гидроприводе такой силой является нагрузка
, приложенная к исполнительному органу. Эта нагрузка воздействует на жидкость через какую-то жёсткую поверхность и, следовательно, распределена равномерно, например площадь поршня гидроцилиндра
. В таком случае давление
определяется по формуле. 52. В чем заключаются особые состояния воды? Под особыми состояниями жидкости обычно понимают случаи двухфазного состояния. Это может быть движение газожидкостной смеси или транспорт жидкостью твердых частиц. Аэрация потока – насыщение жидкости газами (воздухом) не поглощаемых жидкостью. Чаще всего это проникновение в жидкость пузырьков воздуха и их движение с большими скоростями, препятствующими их разделению. Транспорт твердых частиц (наносов) – обычно это насыщение потока со дна канала или русла. (Например - размыв русла реки). Образование в жидкости разрывов, заполненных парами жидкости (КАВИТАЦИЯ) – при снижении давления и повышении температуры жидкости повышается вероятность вскипания жидкости. Это явление может наблюдаться при движении тел в жидкости (например: лопасти гребного винта, подводное крыло) или при распространении в жидкости звуковой волны высокой интенсивности (обычно, это явление наблюдается при распространении ультразвуковой волны). Это явление в технике в абсолютном большинстве случаев нежелательно, т.к. захлопывание паровых пузырьков приводит к локальному повышению давления в жидкости и разрушению деталей и конструкций. Подробнее о механизме повышения давления можно узнать в разделе, посвященном гидроудару. Образование в воде кристаллов льда – это явление возникает при снижении температуры воды или при повышении давления. При этом получается двухфазная система. Чаще всего это наблюдается при интенсивном перемешивании воды. В обычных условиях лед образуется на поверхности, т.к. вода, в отличие от других жидкостей, имеет наибольшую плотность при температуре около Благодаря этому, вода, находящаяся при температуре замерзания, всплывает на поверхность. 62. Какими свойствами обладает эпюра гидростатического давления?
Эпюра гидростатического давления характеризуется следующими двумя свойствами:
1. каждая ордината эпюры давления, измеренная перпендикулярно к щиту ОА, выражает заглубление соответствующей точки щита, а, следовательно, и гидростатическое давление в этой точке;
2. площадь эпюры давления выражает силу гидростатического давления (суммарное гидростатическое давление). ЧАСТЬ 2: ГИДРОДИНАМИКА.
2. Каково взаимосвязь между средней скорости потока и площадью его поперечного сечения?Живым сечением потока называется поверхность (поперечное сечение), нормальная ко всем линиям тока, его пересекающим, и лежащая внутри потока жидкости. Площадь живого сечения обозначается буквой Для элементарной струйки жидкости используют понятие живого сечения элементарной струйки (сечение струйки, перпендикулярное линиям тока), площадь которого обозначают через
. Средняя скорость потока жидкости в данном сечении это не существующая в действительности скорость потока, одинаковая для всех точек данного живого сечения, с которой должна была бы двигаться жидкость, что бы её расход был равен фактическому. 12. Каков геометрический смысл уравнения Бернулли? Положение любой частицы жидкости. относительно некоторой произвольной линии нулевого уровня
определяется вертикальной координатой
для реальных гидравлических систем, это может быть уровень, ниже которого жидкость из данной гидросистемы вытечь не может. Например, уровень пола цеха для станка или уровень подвала дома для домашнего водопровода. ü Как и в гидростатике, величину
называют нивелирной высотой;
ü Второе слагаемое носит название пьезометрическая высота. Эта величина соответствует высоте, на которую поднимается жидкость в пьезометре, если его установить в рассматриваемом сечении, под действием давления
;
ü Сумма первых двух членов уравнения – гидростатический напор;
ü Третье слагаемое в уравнении Бернулли называется скоростной высотой или скоростным напором. Данную величину можно представить как высоту, на которую поднимется жидкость, начавшая двигаться вертикально со скорость и при отсутствии сопротивления движению;
ü Сумму всех трёх членов (высот) называют гидродинамическим полным напором и, как уже было сказано, обозначают буквой . Все слагаемые уравнения Бернулли имеют размерность длины и их можно изобразить графически.
Значение
,
– нивелирную, пьезометрическую и скоростную высоты можно определить для каждого сечения элементарной струйки жидкости. Геометрическое тело точек, высоты которых равны
называется пьезометрической линией. Если к этим высотам добавить скоростные высоты, равные , то получится другая линия, которая называется гидродинамической или напорной линией.Из уравнения Бернулли, для струйки невязкой жидкости (и графика) следует, что гидродинамический напор по длине струйки постоянен.22. Каков физический смысл критерия Рейнольдса? Что такое критическое число Рейнольдса? Где этот критерий применяется?Посмотрим, какому условию должны удовлетворять те же геометрически и кинематически подобные потоки для того, чтобы было обеспечено их гидродинамическое подобие при наличии сил вязкости, а, следовательно, и потерь энергии, т.е. при каком условии числа
будут одинаковы для этих потоков. Уравнение Бернулли для этого случая применит вид:
Или по аналогии с предыдущими рассуждениями, учтя, что
, можно написать:
Как видно из последнего уравнения, числа
будут иметь одинаковые значения для рассматриваемых потоков, а сами потоки будут подобны друг другу гидродинамически при условии равенства коэффициентов сопротивления (равенство коэффициентов
для сходственных сечений двух потоков следует из их кинематического подобия). Таким образом, коэффициенты сопротивлений
в подобных потоках должны быть одинаковыми, а это значит, что потери напора для сходственных участков пропорциональны скоростным напорам.
Рассмотрим очень важный в гидравлике случай движения жидкости движение с трением в цилиндрической трубе, для которого коэффициент трения можно описать формулой:
Для геометрически подобных потоков отношение
одинаково, следовательно, условием гидродинамического подобия в данном случае является одинаковое значение для этих потоков коэффициента
. Он выражается через напряжение трения
на стенке и динамическое давление, как было установлено ранее, следующим образом:
Следовательно, для двух подобных потоков I и II можно записать
т. е. напряжения трения пропорциональны динамическим давлениям. Учитывая закон трения Ньютона и тот факт, что в последних уравнениях , предыдущие отношения, равные
, можно выразить:где индекс
означает, что производная взята при
, т. е. у стенки трубы. При этом заметим, что закон трения Ньютона применим лишь при ламинарном течении. Однако, как было показано выше, при турбулентном течении в трубах вблизи стенок образуется тонкий ламинарный слой, внутри которого справедлив закон трения Ньютона. Поэтому напряжение трения
на стенке может определяться по этому закону также и при турбулентном течении. После умножения и деления на диаметр трубы
и перегруппировки множителей получим: Здесь буквой
обозначено выражение в квадратных скобках, представляющее собой безразмерный градиент скорости вблизи стенки. Для кинематически способных потоков величина
одинакова, поэтому после сокращения на
, условие динамического подобия потоков примет вид:
Или переходя к выбранным величинам: В этом заключается критерий подобия Рейнольдса, который можно сформулировать следующим образом: для гидродинамического подобия геометрически и кинематически подобных потоков с учетом сил вязкости требуется равенство чисел Рейнольдса, подсчитанных для любой пары сходственных сечений этих потоков.32. Каков физический смысл коэффициента Кориолиса? Может ли он быть меньше единицы, равен единице?
- коэффициент Кориолиса, учитывающий неравномерность распределения скоростей по сечению потока (или корректив кинетической энергии). Безразмерный коэффициент
представляет собой отношение действительной кинетической энергии потока к кинетической энергии, вычисленной по средней скорости. При равномерном распределении скоростей его значение равно единице, а при неравномерном - всегда больше единицы и для любого потока его значение находится в пределах от 1 до 2 и более. На основе обработки многочисленных данных, полученных на реках и каналах, установлено, что для больших открытых потоков
. При равномерном движении в трубах и каналах практически
Величины относительно малы, менее
Вторая область – зона неустойчивого режима или переходная зона зона, внутри которой происходит переход ламинарного режима в турбулентный и наоборот - турбулентного режима в ламинарный. Числа Рейнольдса лежат в пределах от
до
Третья область – область турбулентного режима. Данная область в свою очередь разбивается на три области: 1. область гладких русел:
;
2. область доквадратичного сопротивления шероховатых труб: ;
3. область квадратичного сопротивления шероховатых русел: .72. Что такое автомодельность в отношении числа Рейнольдса? В случае моделирования безнапорных турбулентных потоков, отвечающих квадратичной области сопротивления, исходят из числа Фруда, считая, что такого рода движение обуславливается только силами тяжести. Эта область параметров потока, когда движение жидкости не зависит от числа Рейнольдса, называется автомодельной в отношении чисел Рейнольдса. 82. В чем состоит отличие формулы Блазиуса от формулы Шифринсона? Блазиус в 1913 г. на основании обработки многочисленных опытов по исследованию движения жидкости в круглых гладких трубах при числах Рейнольдса от 4000 до 100000 установил эмпирическую зависимость:
Формула Шифринсона для квадратичной области сопротивления:
При
92. Что учитывает коэффициент расхода при истечении из отверстия? где
.
коэффициент расхода отверстия. Этот коэффициент учитывает, и потери напора
и степень сжатия струи выходящей из отверстия.102. Безнапорное и напорное движение грунтовых вод. Напорным движением называется такое движение, при котором поток со всех боковых сторон ограничен твердыми стенками. Безнапорным движением называется движение, характеризуемое наличием свободной поверхности.
112. Чем отличаются, друг от друга простой и сложный трубопроводы? Учитывая гидравлическую схему работы длинных трубопроводов, их можно разделить также на простые и сложные.
Простыми называются последовательно соединенные трубопроводы одного или различных сечений, не имеющих никаких ответвлений.
К сложным трубопроводам относятся системы труб с одним или несколькими ответвлениями, параллельными ветвями и т.д. К сложным относятся и так называемые кольцевые трубопроводы.
bukvasha.ru
ГИДРОСТАТИКА
Гидростатическое давление и его свойства
Гидростатика — раздел гидравлики, в котором изучаются законы жидкости в состоянии равновесия и распределение давления покоящейся жидкости на различные поверхности.
Рассмотрим основное понятие гидростатики — гидростатическое давление. На рис. 2.1 представлен некоторый произвольный объем покоящейся жидкости. Разделим этот объем плоскостью ВС на две части — I и II. В плоскости ВС выделим площадь ω с центром в точке А. Давление со стороны части I объема будет передаваться на поверхность ВС с силой Р.
Гидростатическим давлением Р называется сила давления жидкости на единицу площади ω, и его можно представить формулой
| | (2.1) |
рис. 2.1
Гидростатическое давление имеет размерность в системе СИ Паскаль (Па). Оно обладает тремя свойствами.
Первое свойство. Гидростатическое давление направлено по внутренней нормали к поверхности, на которую оно действует.
Второе свойство. Гидростатическое давление в точке действует одинаково по всем направлениям и может быть выражено соотношением
Третье свойство. Гидростатическое давление в точке зависит от ее координат в пространстве и может быть записано следующим образом:Уравнения гидростатики
При изучении законов покоящейся жидкости рассмотрим три уравнения: а) основные дифференциальные уравнения равновесия; б) уравнения гидростатического давления; в) уравнение гидростатического давления жидкости, находящейся под воздействием сил тяжести.
а. Основные дифференциальные уравнения равновесия Л. Эйлера выведены в Российской Академии наук в 1755 г. Уравнения выражают связь между массовыми (объемными) силами, давлением и координатами любой точки жидкости в состоянии равновесия.
Не приводя вывода уравнений, поясним ход рассуждений.
В покоящейся жидкости выделяется какой-либо объем. В данном примере на рис. 2.2 рассматривается параллелепипед с гранями abсd и a'b'c'd'. На выделенный объем действуют силы поверхностного суммарного гидростатического давления и массовые (объемные) силы. Жидкость находится в равновесии, следовательно поверхностные и массовые силы должны уравновешиваться, т. е. сумма этих сил должна быть равна нулю.
рис. 2.2
ПОВЕРХНОСТНЫЕ СИЛЫ. Силы суммарного гидростатического давления по оси х с учетом приращения дРхбудут равны
| | (2.4) |
МАССОВЫЕ (ОБЪЕМНЫЕ) СИЛЫ. Объемной силой называется сила, приложенная к массе жидкости в объеме параллелепипеда. Такой силой может быть сила тяжести p = mg. При постоянной плотности масса жидкости выделенного объема равна m = rdxdydz. В гидравлике проекции ускорения объемных сил, отнесенных к единице массы, обозначаются X, Y, Z. Таким образом, по оси x можно записать
Сумма поверхностных и массовых сил по оси x будет равна| Pxdydz – Pxdydz - dxdydz + Xrdxdydz = 0 |
| | (2.7) |
| |
б. Уравнение гидростатического давления можно получить из уравнений Л. Эйлера. Если умножить каждый его член на rdx, rdy и rdz и сложить их, то получим
| | (2.8) |
В случае, если имеется поверхность равного давления, Р=const и dP=0, поскольку r не равно 0, то уравнение в случае равного давления имеет вид
в. Уравнение гидростатического давления жидкости, находящейся под действием силы тяжести. Основное уравнение гидростатического давления в дифференциальной форме следующее:Интегрируя данное уравнение, можно его использовать для различных случаев покоя жидкости. Рассмотрим частный случай, когда жидкость находится в покое под действием силы тяжести. На рис. 2.3 на поверхности жидкости наметим точку в, в которой давление Р0. Начало координат совместим с точкой в, а ось z направим вниз. Выделим точку а, в которой жидкость находится под действием силы тяжести, равной весу р=mg. Примем массу m=1, тогда p=g, т. е. единичная массовая сила будет равна ускорению. Проекции этой силы на ось x и y будут равны 0: X=0; Y=0. Проекция силы тяжести на ось z = g, т. к. направление оси совпадает с направлением силы тяжести вниз, к центру Земли.рис. 2.3
Согласно уравнению гидростатического давления dP будет равно
Интегрируем это уравнение в пределах от Р0 до Р и от z0 до z| |
Если свободная поверхность жидкости соприкасается с атмосферой, то Р0=Ра и полное гидростатическое давление будет иметь вид
Из уравнения гидростатического давления следует закон Паскаля: давление, воспринимаемое жидкостью, передается во все точки жидкости с одинаковой силой.Избыточным, или манометрическим, давлением называется превышение давления над атмосферным
Некоторые понятия в гидростатикеа. Пьезометрическая высота давления. На рис. 2.4 в состоянии равновесия представлен закрытый сосуд, наполненный жидкостью, на поверхности которой давление Р>Ра. К стекам сосуда подведены две открытые трубки, называемые пьезометрами («пьезо» - греческое слово – давление, «метр» - измерение). Трубки А и В расположены на разных уровнях zА и zВ от плоскости сравнения 0-0. Жидкость в точках А и В, которая находится под давлением Р, поднимется по пьезометрам и, испытывая атмосферное давление Ра, остановится на одной плоскости 0’-0’, называемой напорной плоскостью.
bukvasha.ru