Реферат на тему:
Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.
В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.
В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.
В географии координаты — широта, долгота и высота над известным общим уровнем (например, океана). Смотри географические координаты.
В астрономии координаты — величины, при помощи которых определяется положение звезды, например, прямое восхождение и склонение.
Небесные координаты — числа, с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой систему полярных координат на сфере с соответствующим образом выбранным полюсом. Систему небесных координат задают большим кругом небесной сферы (или его полюсом, отстоящим на 90° от любой точки этого круга) с указанием на нём начальной точки отсчёта одной из координат. В зависимости от выбора этого круга системы небесных координат называлась горизонтальной, экваториальной, эклиптической и галактической.
Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат).
Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Известным обобщением системы координат являются системы отсчёта и системы референции.
В этом разделе даются разъяснения к наиболее употребляемым системам координат в элементарной математике.
Расположение точки P на плоскости определяется декартовыми координатами с помощью пары чисел (x,y):
В пространстве же необходимо уже 3 координаты (x,y,z):
Полярные координаты.
В полярной системе координат положение точки определяется расстояние до центра координат и углом радиус-вектора с осью Ox.
Термин «полярные координаты» используется только на плоскости, в пространстве применяются цилиндрические и сферические системы координат.
Цилиндрические координаты.
Цилиндрические координаты — трехмерный аналог полярных, в котором точка P представляется трехкомпонентным кортежем (r,θ,h). В терминах декартовой системы координат,
Полярные координаты имеют один недостаток: значение θ теряет смысл, если r = 0.
Цилиндрические координаты полезны для изучения систем, симметричных вокруг некой оси. Например, длинный цилиндр в декартовых координатах имеет уравнение 2x + 2y = 2c, тогда как в цилиндрических оно выглядит как r = c
Сферические координаты.
Сферические координаты — трехмерный аналог полярных
В сферической системе координат, расположение точки P определяется тремя компонентами: (ρ,φ,θ). В терминах декартовой системы координат,
Сферическая система координат также имеет недостаток: φ теряет смысл если ρ = 0, также и θ теряет смысл, если ρ = 0 или φ = 0 или φ = 180°.
Для построения точки по её сферическими координатами, нужно: от полюса отложить отрезок, равный ρ вдоль положительной z-оси, вернуть его на угол φ вокруг оси y в направлении положительной x-оси, и вернуть на угол θ вокруг z-оси в направлении положительной y-оси.
Сферические координаты полезны при изучении систем, симметричных вокруг точки. Так, уравнение сферы в декартовых координатах выглядит как x2 + y2 + z2 = c2, тогда как в сферических становится намного проще: ρ = c.
В Европе принято использовать другие обозначения. Положение точки задаётся числами: , Где r — расстояние от точки до начала координат, θ — полярный угол, который изменяется в пределах от 0 до π,
— Азимутальный угол, который изменяется в пределах от 0 до 2π. То есть, в европейской системе, которая применяется также и в России, обозначения для углов переставлены по сравнению с американской.

где u0 — функция Хевисайда с u0(0) = 0, а sgn — функция signum . Здесь функции u0 и sgn используются как «логические» переключатели, аналогичные по значению операторам «если .. то» (if…else) в языках программирования. Некоторые языки программирования имеют специальную функцию atan2 (y, x), которая находит правильный θ в необходимом квадранте, определённом x и y.


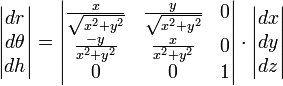


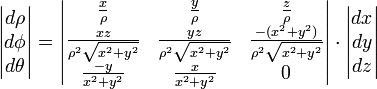
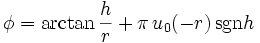
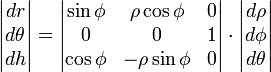

wreferat.baza-referat.ru
Реферат на тему:
Прямоугольная, или Декартова система координат — наиболее простая и поэтому часто используемая система координат на плоскости и в пространстве.
Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X'X и Y'Y. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление. В правосторонней системе координат положительное направление осей выбирают так, чтобы при направлении оси Y'Y вверх, ось X'X смотрела направо.
Четыре угла (I, II, III, IV), образованные осями координат X'X и Y'Y, называются координатными углами или квадрантами (см. рис. 1).
Рис. 1
Положение точки A на плоскости определяется двумя координатами x и y. Координата x равна длине отрезка OB, координата y — длине отрезка OC в выбранных единицах измерения. Отрезки OB и OC определяются линиями, проведёнными из точки A параллельно осям Y'Y и X'X соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A. Записывают так: .
Если точка A лежит в координатном углу I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном углу II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном углу III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном углу IV, то точка A имеет положительную абсциссу и отрицательную ординату.
Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно одинаковы для всех осей (что не является обязательным). OX — ось абсцисс, OY — ось ординат, OZ — ось аппликат.
Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Иначе говоря, положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY, если этот поворот наблюдать со стороны положительного направления оси OZ. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси (см. рис. 2).
Рис. 2
Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x равна длине отрезка OB, координата y — длине отрезка OC, координата z — длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки A параллельно плоскостям YOZ, XOZ и XOY соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A. Записывают так: .
Прямоугольная система координат (любой размерности) также описывается набором ортов, сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу.
В трёхмерном случае такие орты обычно обозначаются ,
и
или
,
и
.
При этом в случае правой системы координат действительны следующие формулы с векторным произведением векторов:
Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости.
Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.
wreferat.baza-referat.ru
Реферат на тему:
Прямоугольная, или Декартова система координат — наиболее простая и поэтому часто используемая система координат на плоскости и в пространстве.
Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X'X и Y'Y. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление. В правосторонней системе координат положительное направление осей выбирают так, чтобы при направлении оси Y'Y вверх, ось X'X смотрела направо.
Четыре угла (I, II, III, IV), образованные осями координат X'X и Y'Y, называются координатными углами или квадрантами (см. рис. 1).
Рис. 1
Положение точки A на плоскости определяется двумя координатами x и y. Координата x равна длине отрезка OB, координата y — длине отрезка OC в выбранных единицах измерения. Отрезки OB и OC определяются линиями, проведёнными из точки A параллельно осям Y'Y и X'X соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A. Записывают так: .
Если точка A лежит в координатном углу I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном углу II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном углу III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном углу IV, то точка A имеет положительную абсциссу и отрицательную ординату.
Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно одинаковы для всех осей (что не является обязательным). OX — ось абсцисс, OY — ось ординат, OZ — ось аппликат.
Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Иначе говоря, положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY, если этот поворот наблюдать со стороны положительного направления оси OZ. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси (см. рис. 2).
Рис. 2
Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x равна длине отрезка OB, координата y — длине отрезка OC, координата z — длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки A параллельно плоскостям YOZ, XOZ и XOY соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A. Записывают так: .
Прямоугольная система координат (любой размерности) также описывается набором ортов, сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу.
В трёхмерном случае такие орты обычно обозначаются ,
и
или
,
и
.
При этом в случае правой системы координат действительны следующие формулы с векторным произведением векторов:
Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости.
Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.
wreferat.baza-referat.ru
Реферат на тему:
Прямоугольная, или Декартова система координат — наиболее простая и поэтому часто используемая система координат на плоскости и в пространстве.
Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X'X и Y'Y. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление. В правосторонней системе координат положительное направление осей выбирают так, чтобы при направлении оси Y'Y вверх, ось X'X смотрела направо.
Четыре угла (I, II, III, IV), образованные осями координат X'X и Y'Y, называются координатными углами или квадрантами (см. рис. 1).
Рис. 1
Положение точки A на плоскости определяется двумя координатами x и y. Координата x равна длине отрезка OB, координата y — длине отрезка OC в выбранных единицах измерения. Отрезки OB и OC определяются линиями, проведёнными из точки A параллельно осям Y'Y и X'X соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A. Записывают так: .
Если точка A лежит в координатном углу I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном углу II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном углу III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном углу IV, то точка A имеет положительную абсциссу и отрицательную ординату.
Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно одинаковы для всех осей (что не является обязательным). OX — ось абсцисс, OY — ось ординат, OZ — ось аппликат.
Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Иначе говоря, положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY, если этот поворот наблюдать со стороны положительного направления оси OZ. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси (см. рис. 2).
Рис. 2
Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x равна длине отрезка OB, координата y — длине отрезка OC, координата z — длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки A параллельно плоскостям YOZ, XOZ и XOY соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A. Записывают так: .
Прямоугольная система координат (любой размерности) также описывается набором ортов, сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу.
В трёхмерном случае такие орты обычно обозначаются ,
и
или
,
и
.
При этом в случае правой системы координат действительны следующие формулы с векторным произведением векторов:
Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости.
Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.
www.wreferat.baza-referat.ru
Реферат на тему:
Прямоугольная, или Декартова система координат — наиболее простая и поэтому часто используемая система координат на плоскости и в пространстве.
Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X'X и Y'Y. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление. В правосторонней системе координат положительное направление осей выбирают так, чтобы при направлении оси Y'Y вверх, ось X'X смотрела направо.
Четыре угла (I, II, III, IV), образованные осями координат X'X и Y'Y, называются координатными углами или квадрантами (см. рис. 1).
Рис. 1
Положение точки A на плоскости определяется двумя координатами x и y. Координата x равна длине отрезка OB, координата y — длине отрезка OC в выбранных единицах измерения. Отрезки OB и OC определяются линиями, проведёнными из точки A параллельно осям Y'Y и X'X соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A. Записывают так: .
Если точка A лежит в координатном углу I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном углу II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном углу III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном углу IV, то точка A имеет положительную абсциссу и отрицательную ординату.
Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно одинаковы для всех осей (что не является обязательным). OX — ось абсцисс, OY — ось ординат, OZ — ось аппликат.
Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Иначе говоря, положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY, если этот поворот наблюдать со стороны положительного направления оси OZ. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси (см. рис. 2).
Рис. 2
Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x равна длине отрезка OB, координата y — длине отрезка OC, координата z — длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки A параллельно плоскостям YOZ, XOZ и XOY соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A. Записывают так: .
Прямоугольная система координат (любой размерности) также описывается набором ортов, сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу.
В трёхмерном случае такие орты обычно обозначаются ,
и
или
,
и
.
При этом в случае правой системы координат действительны следующие формулы с векторным произведением векторов:
Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости.
Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.
wreferat.baza-referat.ru
Слайд 2
История возникновения систем координат Во II веке до н.э. греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами, покрыв его как бы условной сеткой, и ввести географические координаты - широту и долготу. Правда, еще до этого астрономы использовали данный прием, изучая небесный свод.
Слайд 3
История возникновения систем координат Во II веке н.э. знаменитый древнегреческий астроном и математик Клавдий Птолемей активно пользовался долготой и широтой в качестве географических координат. Но систематизировал эти понятия в 17 веке Рене Декарт.
Слайд 4
Рене Декарт Рене́ Дека́рт (1596 — 1650) — французский математик, философ, физик и физиолог. Именно он придумал в 1637 году систему координат, которая используется во всем мире и известна каждому человеку. Ее называют также « Декартова система координат» .
Слайд 5
Биография Декарта Декарт происходил из дворянского рода и был младшим (третьим) сыном в семье. Он родился в 1596 году во Франции. Его мать умерла, когда ему был 1 год. Рене получил прекрасное начальное образование в престижном коллеже Ла Флеш. Здесь он обучался у священников-иезуитов.
Слайд 6
Биография Декарта За десять лет, проведенных в колледже, Декарт приобрел писательские навыки, изучил музыкальное и драматическое искусства и даже овладел такими благородными занятиями, как верховая езда и фехтование. Проведя еще два года в Университете Пуатье, он получил ученую степень в области юриспруденции, но отказался от карьеры юриста. Рене поступил на военную службу и стал много путешествовать по Европе.
Слайд 7
Биография Декарта Затем Декарт около двадцати лет жил в Нидерландах. Терпимые голландцы в XVII веке спокойно обходились без таких вещей, как инквизиция, ересь, дыба и сожжение на костре, которые грозили всем европейским оригинальным мыслителям. Здесь, в отличие от других стран, не требовалось расплачиваться за свои идеи. Декарт ведёт обширную переписку с лучшими учёными Европы, изучает самые различные науки, пишет книги. Он занимался астрономией и медициной.
Слайд 8
Достижения в философии Декарт – автор метода радикального сомнения в философии . Ему принадлежит знаменитая фраза: «Cogito, ergo sum» , что в переводе с латинского означает: «Мыслю, следовательно, существую».
Слайд 9
Жертва королевской прихоти Декарт стал знаменитым, его труды читали даже короли. Молодая королева Швеции Христина пригласила его обучать ее философии. В октябре 1649 года он поплыл в Стокгольм. Наступила суровая шведская зима. Королева решила, что занятия философией должны начинаться в 5 утра. И в колледже, и в армии Декарт вставал не раньше 11 ч.. Вскоре Декарт простудился и слёг: у него началось воспаление лёгких. На девятый день болезни, Декарта не стало. Ему было всего 53 года.
Слайд 10
Трехмерное пространство Трёхмерное пространство — геометрическая модель материального мира, в котором мы находимся. Это пространство называется трёхмерным, так оно имеет три измерения — высоту, ширину и длину.
Слайд 11
Декартова система координат Чтобы задать декартову прямоугольную систему координат на плоскости выбирают взаимно перпендикулярные прямые, называемые осями. Точка пересечения осей – «O» называется началом координат. На каждой оси (О X и О Y ) задается положительное направление и выбирается единица масштаба (единичный отрезок).
Слайд 12
Координатная плоскость Положение точки A на плоскости определяется двумя координатами x и y. Координата x равна длине отрезка OB, координата y — длине отрезка OC в выбранных единицах измерения. Координата x называется абсциссой точки A, координата y — ординатой точки A. Каждой точке на координатной плоскости соответствует пара чисел: ее абсцисса и ордината: (х; у). И обратно: каждой паре чисел соответствует единственная точка на координатной плоскости.
Слайд 13
Практическая работа Рисунок на координатной плоскости Задание: на координатной плоскости построить точки по заданным координатам и последовательно соединить их отрезками.
Слайд 14
Рисунок на координатной плоскости «Рыбка» «Рыбка»
Слайд 15
Мальчики 6 «г», спасибо за внимание!
nsportal.ru
1.3.1. Введём три взаимно перпендикулярные прямые, пересекающиеся в одной точке, и введём на каждой из них системы координат, взяв за начало на каждой из них их общую точку пересечения О и взяв на каждой из них один и тот же масштаб. Как правило, одна ось берётся вертикальной с направлением снизу вверх, а другие две — на горизонтальной плоскости с направлениями так, как это показано на рис. 1.7.

Горизонтальные оси обозначим через Ox, Оу (так, как это изображено на рис. 1.8) и назовём их соответственно осями абсциис и ординат, а вертикальную — через Oz и назовём её осью аппликат. Плоскости, содержащие пары координатных осей, называются координатными плоскостями. Они обозначаются … в соответствии с тем, какие оси содержат: xOy, xOz, yOz. Тройка (Ox, Oу, Oz) называется прямоугольной декартовой системой координат в пространстве.

Возьмём в пространстве произвольную точку А и проведём через неё плоскости, перпендикулярные к осям Ox, Oy и Oz. Эти плоскости пересекают оси в некоторых точках. Обозначим их соответственно через Ax, Ay и Az. Они имеют на осях какие-то координаты, скажем, xA, yAи zA. Таким образом, Ax(xA), Ay(yA) и Az(zA) — основания перпендикулярных к осям плоскостей, проведённых из точки А (рис. 1.9).
Тройка чисел (xA, yA, zA) называется координатами точки А, при этом xA — абсцисса точки А, yA — ордината точки А, zA — аппликата точки А. Тот факт, что точка А имеет координаты (xA, yA, zA), обозначается через А(xA, yA, zA).

 При изображении положения точки А(xA, yA, zA) относительно своих координат проводят проекцию A¢ точки A на координатную плоскость xOy, затем проводят отрезки A¢Ax, A¢Ay, параллельные соответственно осям Oy, Ox, и отрезок AAz, параллельный отрезку A¢O (рис.1.10, здесь точки Ax, Ay, Az обозначены их координатами, соответственно через xA, yA, zA).
При изображении положения точки А(xA, yA, zA) относительно своих координат проводят проекцию A¢ точки A на координатную плоскость xOy, затем проводят отрезки A¢Ax, A¢Ay, параллельные соответственно осям Oy, Ox, и отрезок AAz, параллельный отрезку A¢O (рис.1.10, здесь точки Ax, Ay, Az обозначены их координатами, соответственно через xA, yA, zA).
1.3.2. Теорема. Если точки A(xA, yA, zA) и B(xB, yB, zB) заданы своими координатами, то расстояние между ними равно
|АВ|=  ,
,
и если точка C(xC, yC, zC) делит отрезок АВ в отношении l, то xC=  , yC=
, yC=  , zC=
, zC=  .
.
1.3.3. Упражнение.Даны точки A и B своими координатами. Известно, что точка C делит отрезок AB в отношении l. Найти длину отрезка AB и координаты точки C. В системе координат изобразить отрезок AB:
а) A(-2; 3; 4), B(4; 2; -3), l=  ;
;
б) A(3; -2; 1), B(-4; 2; 0), l=  ;
;
в) A(2; -4; 3), B(4; -2; 2), l=3.
Решение. а) По теореме 1.3.2 имеем
|АВ|=  =
=  =
=  ,
,
По той же теореме
xC=  =
=  =
=  , yC=
, yC=  =
=  =
=  , zC=
, zC=  =
=  = —
= — 
то есть  — координаты точки С.
— координаты точки С.
В системе координат изобразим отрезок AB:

Ответ: |АВ|=  ,
,  — координаты точки С.
— координаты точки С.
refac.ru