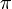Исследовательская работа "Математический бильярд". Реферат математический бильярд

Исследовательская работа "Математический бильярд"

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕСРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №20

Школьный конкурс исследовательских работ

обучающихся средней ступени

Математический бильярд

Исследовательская работа

Выполнил:

обучающийся 6 б класса

Кузнецов Дмитрий

Руководитель:

учитель математики II КК

Чупошева Татьяна

Александровна

Тулун

2012

Содержание

Введение…………………………………………………………………………….

1. История бильярда…………………………………………………………………

2.Русский бильярд…………………………………………………………………..

3. Траектория движения…………………………………………………………….

4. Метод математического бильярда……………………………………………….

Заключение……………………………………………………………………………

Список литературы……………………………………………………………… Приложение………………………………………………………………………….

Введение

В век скоростей и нехватки времени люди начинают искать возможности для совмещения нескольких видов деятельности. Игра в бильярд позволяет совместить занятия спортом, общение и отдых.

Играть в бильярд рекомендуется для поддержания отличной физической формы, правильной осанки. При этом игра в бильярд доступна людям со слабым сердцем и лёгкими; более того, игра в бильярд организм человека закаляет. У людей, играющих в бильярд, развивается глазомер, движения становятся координированными и чёткими. Человек приобретает быструю реакцию, становится находчивым.

Игрок в бильярд обычно хладнокровен и терпелив.

Лучший отдых - это игра в бильярд. Он даёт возможность расслабиться, отвлечься от повседневности, от стрессовых ситуаций. К тому же игрок вовлекается в соревнование.

Игрок в бильярд становится эмоционально уравновешенным, волевым. Игра в бильярд помогает сохранять присутствие духа при проигрыше, способствует сохранению веры в себя, учит не впадать в отчаяние и в панику.

Бильярд - редкостная игра, дозволяющая усовершенствовать физические и умственные способности человека, помогает научиться быть хозяином своих эмоций, добиваться назначенных целей, с честью вести поединок.

Впервые о математическом базисе бильярдной игры заговорил известный физик Гаспар Густав Кориолис в своей книге "Математическая теория явлений бильярдной игры" 1835-го года. Прошло более полутораста лет и математический бильярд по сути превратился в огромное дерево с тьмой отростков и гигантских ветвей. "Теория биллиардов" сегодня имеет важнейшее применение в физике.

Поэтому целью данной работы является исследование теории математического бильярда и его применении при решении задач на переливание

Задачи:

1. Рассмотреть историю возникновения бильярда

2. Изучить русский бильярд

3.Выяснить принципы метода математического бильярда

4. Изучить алгоритм решения задач на переливание.

Методы исследования: сравнение, анализ, синтез и методик сбора и обработки материала.

Структура работы:

Работа состоит из введения, четырех параграфов, заключения и списка литературы.

1.История возникновения бильярда.

Игра в шары – одна из первых игр, о которых имеются исторические сведения. Многие исследователи считают, что именно игры в шары, родиной которых стала Азия, стали основой для появления бильярда. Считается, что китайские купцы завезли простенькую игру в шары в Англию, в период средних веков. И уже англичане, усовершенствовав ее – стали родоначальниками бильярда. В тот период англичане играли в Pall-Mall, суть которой была в перемещении нескольких шаров по утрамбованной земляной площадке. Так же, в пользу того, что игрой в бильярд мир обязан Англии говорит происхождение слова бильярд от английского ball (мяч) и yeard (палка). И даже великий Шекспир, в одной из своих пьес упоминает о том, что Клеопатра играла в бильярд со своим евнухом Мардьяном. Однако, другие специалисты опровергают эти теории.

Возникновение бильярда правильно бы было отнести к тому историческому периоду, когда шары стали перемещать при помощи приспособлений, похожих на кий, на плоской поверхности, приподнятой над полом или землей. Поэтому, другая версия говорит о том, что бильярд зародился во Франции, так как первое упоминание о бильярдном столе было найдено в инвентарной описи короля Людовика XI, и относится к 1470 году.

Первыми игроками в бильярд стали коронованные особы и знатные вельможи Западной Европы. Именно им был доступен дорогой бильярдный стол и большой зал для него. Есть исторические свидетельства о том, что в 1588 году, пребывающая в заточении королева Шотландии Мария Стюарт, много времени проводила за игрой в бильярд.

Важный этап в развитии бильярда – это его распространение среди других социальных слоев населения. Такое развитие бильярд получил в период царствования французских кролей Людовика XIII и Людовика XIV. Игрой в бильярд заинтересовались деловые люди той эпохи, и стали обустраивать общественные залы для этой игры. Государство так же было заинтересовано в том, чтобы бильярдные столы устанавливались в общественных местах, потому что это приносило доход в казну, благодаря налогам. Так бильярд зашагал по Европе уверенным шагом.

Чрезвычайно любил играть в бильярд Людовик XIV. Он гордился тем, как хорошо он управляется с шарами, и насколько он грациозен при этом. Король считался очень хорошим игроком в бильярд, а его постоянным партнером был Шамильяр, у которого была слава очень сильного игрока. Он нарочно проигрывал королю, но иногда выигрывал. Говорят, именно благодаря бильярду Шамильяр сделал блестящую карьеру - от писаря до военного министра.

Из Западной Европы игра в бильярд постепенно распространилась на страны более восточные, в том числе и в Россию. А с началом времен колонизации, бильярд широко распространялся и в колонии. Однако, не так быстро, как в Европе. Например, Америка была открыта Колумбом в 1492 году, а распространение бильярда в Америке относят ко времени более двухсот лет со дня легендарного открытия.

Кто же на самом деле и в какой стране первым придумал бильярд, может так и останется неизвестным. Да, наверное, это и не слишком важно. Важно то, что эта замечательная, умная и азартная игра так любима многими сегодня.

2. Русский бильярд

Доступность бильярдного спорта делает его одинаково ценным для самых различных возрастных категорий, для мужчин и женщин, для физически развитых людей и для людей, которым болезнь или инвалидность не позволяет заниматься другими видами спорта.Следует особо отметить, что именно в России, где бильярд развивался автономно, в конце концов, выработался свой, отечественный тип лузного бильярда. Еще в 30-40-х годах прошлого века инвентарь отличался большим разнообразием и непропорциональностью деталей. Попадались шары намного меньшего по сравнению с шириной луз диаметра; борта были или очень низки, или слишком высоки, на многих столах лузы имели длинное устье, в результате чего не идеально точно пущенные шары не отталкивались от луз, а часто застревали в них. При состязании на таких столах шансы плохих и хороших игроков уравнивались, и борьба между ними теряла интерес.Только в 1850 году хороший игрок и управляющий бильярдной фабрикой в Петербурге А. Фрейберг создал образец русского шестилузного бильярда, который удовлетворял необходимым требованиям: -для определенного усложнения игры все шары должны класться только при точных ударах, а значит, ширина луз должна лишь на несколько миллиметров превышать диаметр шаров; - в среднюю лузу шар по борту не должен падать; - все лузы должны иметь короткие устья, чтобы шары меньше в них застревали, и была возможность сыгрывать бортовые шары в угловые лузы.Вместе с формой стола, конструкцией луз совершенствовалась, и форма выступа бортов в той их части, которая обтягивается резиной. На первых лузных бильярдах этот выступ по всей высоте представлял собой как бы сплошную вертикальную стенку. Шар при этом имел много точек соприкосновения с резиной, из-за чего отражался в непредсказуемом направлении, да и технически изготовить совершенный борт было трудно.В "дальнейшем усилиями многих бильярдных специалистов, а особенно А.Фрейберга, был выработан так называемый "нормальный борт". Ему соответствует умеренное закругление резины и высота, обеспечивающая прикосновение шара в точке, расположенной чуть выше его центра. Такая форма бортов сохраняется и до настоящего времени.Вплоть до конца 20-х годов XIX столетия действия кием не отличались замысловатостью. "Диапазон" их ограничивался простым ударом в центр шapa, посредством которого невозможно было дать шару-битку произвольное направление. Причиной тому было залитое гипсом углубление в тонком конце кия. При попытке ударить такой нашлепкой в любую точку шара, кроме центра, происходил сбой или, как его называют, "кикс". Кроме того, каждый игрок имел около себя несколько киев, которые регулярно макал в жидкий гипс. Столы пачкались и имели неопрятный вид. Гипсовые кии часто рвали сукно.Изобретателем такого, неплохого все же для своего времени гипсового кия считается французский офицер майор Дуга. За бильярдным столом он много лет был непобедим. Но невозможность хорошо владеть "своим" шаром из-за несовершенства кия побудила игроков искать способы улучшения этого орудия игры.В 1827 году французский виртуоз бильярда Менго изобрел круглую кожаную наклейку для кия. Это на первый взгляд простое новшество произвело своего рода революцию. При игре гипсовым кием требовался лишь механический кавык - после удара в центр шар катился строго по прямой. Теперь, с помощью кожаной наклейки, ее изобретатель стал демонстрировать несравненно более сложные удары: шар вращался и двигался по искривленной траектории, вдруг сам собой останавливался и откатывался назад, перескакивал через другие шары и т. д. Такая игра вызывала у всех окружающих удивление и восхищение.Вскоре Менго написал книгу. Она называлась "Теория бильярдной игры. Руководство для желающих сделаться первоклассными игроками". Перевод ее на русский язык был издан в Санкт-Петербурге в 1847 году. В этой книге автор привел описание бильярда, его принадлежностей, рассмотрел движение шара при горизонтальном и наклонном ударах кием, особенности отражения шаров при столкновении их с бортами и друг с другом.Очередным поворотным пунктом в развитии бильярда стало появление американских резиновых бортов, благодаря которым игра усложнилась, а интерес к ней повысился. Шары хорошо отражались бортами, что незамедлительно сказалось на занимательности и зрелищности игры.В 1912 году в Париже было создано "Международное объединение федераций любителей бильярда". Эта ведущая организация всех европейских спортсменов-бильярдистов намечала мировые соревнования, разрабатывала правила их проведения, вела работу по их организации, готовила бильярдных судей, назначала ставки (призовые фонды). К этому времени главными европейскими бильярдными странами стали: Франция, Англия, Германия, Бельгия, Голландия, Швеция, Австрия и за океаном - США.Как уже отмечалось, а России бильярд появился в начале XVIII столетия при Петре I. Будучи за границей, в Голландии, он самолично привез оттуда шары и стол, приказав его установить в своей приемной, строго наказав: посетители должны не сидеть и не бить баклуши в ожидании, когда примет их царь, а тренироваться на заморской диковинке. И посмел бы кто ослушаться! Впрочем, аппетит всегда приходит во время еды. Царское окружение с увлечением принялось заколачивать шары в лузы. Но особенно в этом отличался офицерский люд - самый азартный и охочий до всего нового народ. Буквально в несколько лет игра утвердилась в гостиницах, постоялых дворах, в клубах, в Офицерских собраниях. Карты были почти заброшены. Более того, в XIX веке русские офицеры завезли русский бильярд в Финляндию, где он любим и по сей день. Кстати, русский бильярд постепенно завоевывает популярность и на Западе - в Швеции, Греции, Германии. Не хотят его менять ни на какой другой и в Монголии. И, несмотря на то, что стоил тогда один бильярдный стол громадные деньги - 250-300 золотыми (их меняли даже один к одному на кровных арабских скакунов), очереди на приобретение этих столов были немалые. Новая игра стала любимой всеми. Уж на что была обременена государственными заботами Екатерина II, но и та время для бильярда находила всегда. И это именно в ее век с чьей-то легкой руки родилось название первой нашей игры - "русская пирамида". Позже в России появляется еще одна "пирамида" - "московская".Еще большее распространение бильярд получил при императрице Анне Иоанновне, которая играла на нем почти ежедневно. С началом XIX столетия игра из дворцов и поместий переместилась в общественные места: гостиницы, трактиры, клубы. Например, уже к 40-м годам прошлого века в русской армии не было ни одного полка, в офицерском собрании которого не стоял бы бильярд.На 20-30-е годы прошлого века приходится начало увлечения французской трехшаровой карамбольной партией в России. Этому способствовала довольно распространенная в то время мода среди состоятельных русских дворян путешествовать по Европе, причем особое значение придавалось пребыванию в Париже. Находясь во Франции, некоторые из таких путешественников становились заядлыми игроками, приобретали там столы, кии, шары. Возвратившись на родину, новоиспеченные поклонники бильярда не только сами с удовольствием играли в карамболь, но и приобщали к нему своих знакомых.С распространением "французской" игры у нас даже произошла переориентация бильярдного производства. Талантливые деловые люди из числа игроков, знатоков и любителей бильярда наладили изготовление новых столов и принадлежностей. Наиболее известными фабрикантами такого рода были А. Фрейберг и М, Ерыкалов в Петербуре, В. Щульц, К. Щульц и братья Богомоловы в Москве, Я. Гоц в Ростове-на-Дону, В. Галушкин в Одессе. Наиболее предприимчивые из них, не оставив изготовление лузных столов, быстро освоили и производство французских бильярдов. Так, самая первая построенная в России петербургская фабрика А. Фрейберга славилась большими масштабами производства и высоким качеством продукции. В середине XIX столетия здесь наряду с десятью типами лузных столов начался выпуск двух видов французского карамбольного бильярда. Пятая часть из 200 ежегодно выпускаемых фабрикой Я. Гоца столов также были карамбольными. В игры на традиционном русском бильярде были включены и карамбольные удары. Так появилась интересная и любимая многими отечественными игроками прошлого века партия "Пять шаров с карамболями", в которой французский карамболь удачно сочетается с покладкой шаров в лузы. И хотя "колыбелью" бильярда были Франция и Англия, в дальнейшем именно в нашей стране игра была доведена до совершенства.В России с самого начала освоение бильярда шло автономно. Именно в Москве и Петербурге появились не только строгие столы, на которых шары могли быть положены лишь точными ударами, но и новые интересные игры, В 30-х годах XIX века в России придумали "Малую русскую пирамиду", которая сразу приобрела большую популярность. Эта игра до сих пор остается классикой бильярда. Наглядность борьбы и разнообразие ударов никого не могут оставить равнодушными. Выдающимися бильярдными игроками были академик М. В. Ломоносов, граф Г. Г. Орлов, герои войны 1812 года генералы И. Н. Скобелев (дед знаменитого генерала М. Н. Скобелева), Д. Г. Бибиков, граф А. Н. Остерман-Толстой, маркеры Английского клуба в Петербурге Андрей Часовщик, московского купеческого клуба Роман Бакастов, московский игрок Роженков и др. В середине XVIII столетия в петербургских трактирах собиралась "золотая" молодежь того времени. Судя по некоторым источникам, в жарких схватках за бильярдным столом сходились такие известные исторические личности, как великий русский ученый Михаил Васильевич Ломоносов и гвардейский офицер Григорий Григорьевич Орлов.Особого упоминания заслуживают колоритные фигуры трех генералов русской армии: Ивана Никитича Скобелева, Дмитрия Гавриловича Бибикова и Александра Ивановича Остермана-Толстого. Все они в сражениях потеряли по руке, но, несмотря на это, систематическими упражнениями и тренировками достигли больших успехов в бильярде.

Порой бильярд относили к проявлению буржуазного образа жизни, хотя на деле многие такие теоретики сами не прочь были покатать шары на столах, установленных на личных и правительственных дачах и в резиденциях для руководящей номенклатуры. Выше уже отмечалось, что со времен Петра I бильярдные столы в России были непременной принадлежностью царского обихода. Эта традиция в своеобразном преломлении нашла свое продолжение и в послереволюционное время среди советского руководства. Например, бильярд был установлен в резиденциях Сталина, на его "дальней" и "ближней" дачах под Москвой.

Настоящая игра должна доставлять как партнерам, так и зрителям зрелищное удовольствие. Это достигается умением сыграть красиво, так, чтобы "свой" шар вышел на новую позицию по желанию спортсмена, выполняющего удар. Следовательно, в игре присутствует и эстетический элемент.В то же время бильярд - прекрасное средство отдыха. Он снимает накопившееся нервное напряжение в первые же минуты. Играющий почти полностью отвлекается от повседневных мелочей и отдается увлекательному состязанию.Бильярд уравновешивает эмоции и вырабатывает ряд качеств, необходимых человеку в жизни. Он учит выигрывать, напрягая всю силу воли, и преодолевать сопротивление соперника, причем настоящий профессионал воспринимает выигрыш без какого-либо злорадства и неприличного ликования. Бильярд учит и проигрывать - не впадая в панику или отчаяние и не теряя веры в себя. Настоящий игрок не падает духом и сохраняет хладнокровие в трудные моменты, а если и переживает неудачу, то делает это с достоинством и с юмором. Настоящий игрок скорее проиграет, чем нарушит правила, а в обычной жизни это и называется честностью и принципиальностью. Бильярд доступен всем возрастам и потому особенно привлекателен для пожилых. И, наконец, следует отметить доступность бильярда в любое время года. Занятия им не зависят от погодных условий.В нашей стране и без посторонней помощи тысячи поклонников стремятся приобщиться к этой оригинальной и полезной игре. Но необходимы и организационные мероприятия: надо воспользоваться положительным опытом развития бильярда в других странах, создать хорошую материальную базу (качественный инвентарь, просторные и удобные бильярдные залы), развернуть широкую сеть бильярдных клубов, а также наладить подготовку высококлассных мастеров, тренеров-инструкторов, разработать и издать достаточными тиражами специальную литературу.Все это вселяет надежду на то, что в недалеком будущем наряду с другими видами спортивных игр достойное место займет и бильярд.

Бильярд в науке

Впервые о математическом базисе бильярдной игры заговорил Гаспар Густав Кориолис в своей книге «Théorie mathématique du jeu de billard» (Русск. перевод: «Математическая теория явлений бильярдной игры») в 1835 году. Он использовал в своей работе элементы теории вероятностей, теории пределов и общего анализа. Однако особого интереса у современников (по мнению Лемана) книга не вызвала: ни у математиков, ни у бильярдистов.

Прошло более полутораста лет, и математический бильярд развился в свою теорию, породив несколько побочных. «Теория бильярдов» сегодня неотъемлемая часть эргодической теории и теории динамических систем, имеет важнейшее применение в физике. Математиком Гальпериным создан способ определения числа 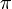с помощью бильярда. Намного ближе общеобразованному читателю результаты исследований математиков Штейнгауза, Альхазена и Гарднера.

Определение из словаря Даля

БИЛЬЯРД, м. — род стола с закраинами (бортами) и шестью подвесными к углам и посреди длинных краев кошелями (лузами), для известной игры, и сама игра, посредством кия и костяных шаров. Бильярд составлен из двух круглых четырехугольников (квадратов), устанавливается и укрепляется по уровню и обтягивается сукном, без шва. Китайский бильярд, биксовый, малый, наклонный; шарик, сбегая обратно, после удара, определяет выигрыш. Бильярдный, относящийся до бильярда. Билия или биль ж. бильярдный шар, сделанный, положенный ударом кия в лузу; также взаимное расположение шаров на бильярде; он на билии, расстановка шаров для него выгодна. Бильярдчик м. бильярдный мастер, столяр.

Основные разновидности

3.Траектория движения

Словарь живого великорусского языка Владимира Даля определял понятие «стратегия», как «ученье о лучшем расположении и употреблении всех военных сил и средств». Замените «военных» на «игровых» - и получите краткое определение стратегии игры на бильярде

Заглянем в Экономико-математический словарь. «СТРАТЕГИЯ [strategy] (в исследовании операций) — способ использования средств и ресурсов, направленный на достижение цели операции. Стратегия определяется принимаемыми значениями управляемых переменных. Для выбора этих значений важно знать также условия “внешней среды”, т.е. значения неуправляемых переменных. В многошаговых процессах сам способ может меняться, в этом случае С. определяет правила принятия дальнейших решений (т.е. выбора траектории) на основе получаемой на каждом этапе информации о ходе процесса и изменениях среды. Задача исследования операций, как правило, состоит именно в выборе оптимальной из числа альтернативных. Стратегий (альтернатив) на основе того или иного критерия.

Не правда ли, очень похоже на описание игры на бильярде. Здесь и «использование средств и ресурсов» - умений и знаний игрока, и «цель операции», то бишь игры – выигрыш партии, и «управляемые переменные» - прямое указание на бильярдные шары, «условия внешней среды» - действия соперника. Многошаговость и альтернативность бильярдных комбинаций и стратегий очевидна для любого игрока в бильярд, как и то, что от положения шаров на столе (информации о ходе процесса и изменениях среды) зависит принятие дальнейшего решения, то есть выбор «траектории».

Впрочем, слово «траектория» можно и нужно употреблять уже без кавычек, поскольку явственное сходство этого определения с реальностью бильярдной игры уже более, чем очевидно.

Понятие стратегии и позиционной игры нередко употребляют в отношении спортивных игр и во внеигровых беседах, стремясь подчеркнуть интеллектуальную составляющую данной игры. Самым, пожалуй, устоявшимся является понятие «шахматная стратегия». И, видимо, не стоит удивляться, что Чемпион мира по шахматам Анатолий Карпов выразил свое отношение к интеллектуальной, стратегической сложности бильярда, назвав в свое время бильярд шахматами в движении.

Реализация же стратегических замыслов в позиционной игре требует от игрока высокого технического мастерства и наработанных навыков игры, включая владение кием, умения управлять шаром и иных, нарабатываемых со временем и тренировками преимуществ. Лузный бильярд в отношении стратегической и технической составляющих весьма требователен.

Крайне важна для бильярдиста техника нанесения удара. Не менее значимо и мастерство позиционной игры. Нередко приходится сталкиваться с тем, что, фиксируя внимание на технике нанесения удара, игрок не придает значения позиционной составляющей. Почти так же часто встречается и противоположная ошибка: крайне внимательно относясь к расположению шаров после удара, технике игрок не уделяет должного внимания. Чтобы достичь мастерства в этой интереснейшей многофакторной игре, стоит найти свою «золотую середину» и действовать, исходя из сложившейся игровой ситуации

Давайте же попытаемся раскрыть понятие позиционной игры. Профессионалы скажут вам, что позиционная игра – это совокупность тактических приемов (позиционных ударов), призванных облегчить игру себе и затруднить игру сопернику. Но для более простого понимания достаточно упомянуть, что каждый игрок в бильярд визуально, графически представляет в уме каждый из последующей серии ударов, которые должны привести к планируемым промежуточным и конечному результату. Сказать об игроке «он видит стол на несколько шагов вперед» - сделать профессиональный комплимент, признать профессионализм игрока. Число предугадываемых «шагов» - это определенный показатель для опытного игрока.

Однако помимо просчитывания положения задействованных играющих шаров следует иметь в виду, не упускать и положение других шаров на игровом столе, анализ ситуации в целом. Следует чувствовать игровое пространство, видеть и понимать развитие игры.

Необходимо заранее решить, где и когда должен оказаться шар, какой техникой, под каким углом и с какой силой наносить удар. Затем, до удара, следует определить, какие из шаров являются проблемными и/или сложными, и лишь затем грамотно совершить удар.

Подобное бильярдное мастерство приходит, конечно, не сразу. Проведя не одну тысячу часов в тренировках и сыграв не одну сотню партий опытный игрок в бильярд уже умеет дать верную оценку расположению шаров и примет оптимальное решение. Однако начинающие игроки, особенно в предчувствии близкой победы, нередко излишне зацикливаются на технике исполнения удара, упуская из виду позиционный фактор. Игрок думающий, опытный зафиксирует в уме положение на столе каждого шара. Такой игрок видит траекторию движения шара еще до удара. Он знает, как и куда нанести удар, чтобы шар пошел по требуемой траектории. Он умеет сконцентрироваться в момент нанесения удара. Он делает этот удар. И это приводит к победе.

Мастерство, в том числе тактическое и стратегическое, и навыки игры приходят с опытом. Даже любительская игра в бильярд станет интереснее за счет своей красоты и стратегической составляющей, как для самих игроков, так и для зрителей. С повышением класса игры увеличивается и удовольствие от применения полученных знаний и навыков и успешного достижения поставленных целей. Это уже не только единичный красиво закатанный в лузу шар. Это не неожиданный «дурак», стремительно влетевший в лузу от противоположного борта. Это уже искусство партии, искусство игры, искусство бильярда.

4.Метод математического бильярда

В этом разделе мы приведем одно изящное применение математического бильярда к решению задач на переливание.

Задачи на переливание жидкостей можно очень легко решать, вычерчивая бильярдную траекторию шара, отражающегося от бортов стола, имеющего форму параллелограмма. Рассмотрим туже задачу, что и в предыдущем разделе (Метод блок-схем).

Задача. Имеются два сосуда — трехлитровый и пятилитровый. Нужно, пользуясь этими сосудами, получить 1, 2, 3, 4, 5, 6, 7 и 8 литров воды. В нашем распоряжении водопроводный кран и раковина, куда можно выливать воду.

Решение. В рассматриваемой задаче стороны параллелограмма должны иметь длины 3 и 5 единиц. По горизонтали будем откладывать количество воды в литрах в 5-литровом сосуде, а по вертикали – в 3-литровом сосуде. На всем параллелограмме нанесена сетка из одинаковых равносторонних треугольников.

Бильярдный шар может перемещаться только вдоль прямых, образующих сетку на параллелограмме. После удара о стороны параллелограмма шар отражается и продолжает движение вдоль выходящего из точки борта, где произошло соударение. При этом каждая точка параллелограмма, в которой происходит соударение, полностью характеризует, сколько воды находится в каждом из сосудов.

Пусть шар находится в левом нижнем углу и после удара начнет перемещаться вверх вдоль левой боковой стороны параллелограмма до тех пор, пока не достигнет верхней стороны в точке А. Это означает, что мы полностью наполнили водой малый сосуд. Отразившись упруго, шар покатится вправо вниз и ударится о нижний борт в точке В, координаты которой 3 по горизонтали и 0 по вертикали. Это означает, что в большом сосуде 3 литра воды, а в малом сосуде воды нет, то есть мы перелили воду из малого сосуда в большой сосуд.

Прослеживая дальнейший путь шара и записывая все этапы его движения в виде отдельной таблицы (табл.1), в конце концов, мы попадаем в точку Н, которая соответствует состоянию, когда малый сосуд пуст, а в большом сосуде 4 литра воды. Таким образом, получен ответ и указана последовательность переливаний, позволяющих отмерить 4 литра воды. Все 8 переливаний изображены схематически в таблице.

Является ли это решение самым коротким? Нет, существует второй путь, когда воду сначала наливают в пятилитровый сосуд. Если на диаграмме шар из точки О покатится вправо по нижней стороне параллелограмма и затем, отразившись от правой боковой стороны, в точку 2 на верхней стороне параллелограмма и т.д., то получим более короткое решение задачи. Можно показать, что полученное решение с 6 переливаниями уже является самым коротким.

Требуется немного сообразительности, чтобы применить метод бильярда к любой задаче о переливании жидкости с помощью не более чем трех сосудов. Остановимся отдельно на случае задачи с тремя сосудами.

Рассмотрим следующую интерпретацию предыдущей задачи. Восьмилитровый сосуд до краев наполнен водой. С помощью двух пустых сосудов емкостью 3 и 5 литров надо поровну разделить в два больших сосуда. Диаграмма для этой задачи точно такая же – параллелограмм со сторонами 5 и 3 единицы. Чтобы фиксировать количество воды в третьем, восьмилитровом сосуде, дополнительно проводим главную диагональ параллелограмма (рис.2). Она делится наклонными прямыми на 8 частей. Отметив точку деления, начиная с верхней правой вершины параллелограмма, получаем возможность фиксировать количество воды в третьем, восьмилитровом, сосуде.

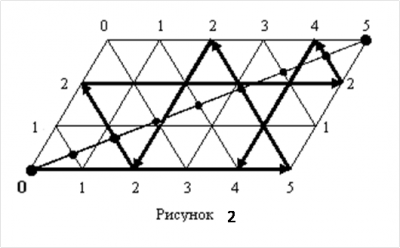
Первые две координаты любой точки параллелограмма, куда может попасть бильярдный шар, определяются, как и выше, а третья координата равна величине отрезка, отсекаемого на главной диагонали соответствующей наклонной. Как и раньше, шар начинает движение от точки О. Совсем несложно нарисовать его траекторию. С ее помощью получим решение с числом переливаний, равным 7. (таб. 2)

Если объемы двух меньших сосудов не имеют общего делителя (т.е. взаимно просты), а объем третьего сосуда больше или равен сумме объемов двух меньших, то с помощью этих трех сосудов можно отмерить любое целое число литров, начиная с 1 литра и кончая объемом среднего сосуда. Имея, например, сосуды вместимостью 15, 16 и 31 литр, вы сумеете отмерить любое количество воды от 1 до 16 литров. Такая процедура невозможна, если объемы двух меньших сосудов имеют общий делитель. Когда объем большего сосуда меньше суммы объемов двух других, возникают новые ограничения. Если, например, объемы сосудов равны 7, 9 и 12 литров, то у параллелограмма надо отсечь верхний правый угол (рис. 3). Это происходит потому, что на диагонали должно быть отложено не более 12 единиц. В этом случае главную диагональ, на которой будет фиксироваться количество воды в самом большом сосуде, полезно вынести за пределы "усеченного параллелограмма", чтобы не загромождать рисунок. В остальном правила игры в бильярд остаются прежними.

Отметим, что бильярдный шар может попасть в любую точку от 1 до 9, за исключением точки 6. Легко видеть, что точки с цифрой 6 образуют на диаграмме правильный треугольник, и мы не можем никак попасть на этот треугольник из любой другой точки, лежащей вне него (рис. 3). Таким образом, несмотря на то, что 7 и 9 взаимно просты, отмерить 6 литров воды оказывается невозможным из-за того, что самый большой сосуд имеет слишком маленький объем. Отметим также, что обобщение метода математического бильярда на случай четырех сосудов сводится к движению шара в пространственной области (параллелепипеде). Но возникающие при этом трудности изображения траекторий делают метод неудобным.

В задачах на переливания требуется указать последовательность действий, при которой осуществляется требуемое переливание и выполнены все условия задачи. Если не сказано ничего другого, считается, что:

все сосуды без делений
нельзя переливать жидкости "на глаз"
невозможно ниоткуда добавлять жидкости и никуда сливать.

Мы можем точно сказать, сколько жидкости в сосуде, только в следующих случаях.

знаем, что сосуд пуст,
знаем, что сосуд полон, а в задаче дана его вместимость,
в задаче дано, сколько жидкости в сосуде, а переливания с использованием этого сосуда не проводились
в переливании участвовали два сосуда, в каждом из которых известно, сколько было жидкости, и после переливания вся жидкость поместилась в один из них
в переливании участвовали два сосуда, в каждом из которых известно, сколько было жидкости, известна вместимость того сосуда, в который переливали, и известно, что вся жидкость в него не поместилась: мы можем найти, сколько ее осталось в другом сосуде

Приведем типичные задачи на переливание.

Задача 1. Имеются три сосуда вместимостью 8, 5 и 3 литра. Наибольший сосуд полон молока. Как разделить это молоко на две равные части, используя остальные сосуды?

Решение.

В таблице указан объем молока в литрах после каждого переливания.

8-литровый сосуд 5-литровый сосуд 3-литровый сосуд

8 0 0

3 5 0

3 2 3

6 2 0

6 0 2

1 5 2

1 4 3

4 4 0

После переливания оказалось по 4 л молока в 8-литровом и 5-литровом сосудах, а это и требовалось.

Задача 2. В бочке не менее 10 л бензина. Как отлить из неё 6 л с помощью девятилитрового ведра и пятилитрового бидона?

Решение.

В таблице указан объем бензина в литрах после каждого переливания.

бочка ведро бидон

не менее 10 0 0

не менее 5 0 5

не менее 5 5 0

не менее 0 5 5

не менее 0 9 1

не менее 9 0 1

не менее 9 1 0

не менее 4 1 5

не менее 4 6 0

Задача 3. Имеется три сосуда без делений объемами 4 л, 5 л, 6 л, кран с водой, раковина и 4 л сиропа в самом маленьком сосуде. Можно ли с помощью переливаний получить 8 л смеси воды с сиропом, так чтобы в каждом сосуде воды и сиропа было поровну?

Решение

4-литровый сосуд 5-литровый сосуд 6-литровый сосуд

4 л сиропа 0 0

0 4 л сиропа 0

4 л воды 4 л сиропа 0

0 4 л сиропа 4 л воды

4 л воды 4 л сиропа 4 л воды

2 л воды 4 л сиропа 6 л воды

2 л воды 4 л сиропа 0

2 л воды, 2 л сиропа 2 л сиропа 0

2 л воды, 2 л сиропа 0 2 л сиропа

0 2 л воды, 2 л сиропа 2 л сиропа

2 л сиропа 2 л воды, 2 л сиропа 0

2 л воды, 2 л сиропа 2 л воды, 2 л сиропа 0

По сути, в данных задачах реализуются два алгоритма.

Первый: последовательно из большего сосуда наполняется меньший сосуд, из него жидкость сливается в сосуд промежуточного объема, эти два действия повторяются до полного наполнения сосуда промежуточного объема, после чего жидкость из него сливается в самый большой. Процедура повторяется несколько раз до тех пор, пока два меньших сосуда будут пустыми, а вся жидкость окажется в большом сосуде. Таким образом, будут реализованы все возможные варианты наполнения сосудов.

Второй алгоритм соответствует действиям первого, записанным в обратном порядке, т.е. с конца. Сначала из большего сосуда наполняется сосуд промежуточного объема. Из него жидкость переливается в самый маленький, а из наименьшего - в наибольший. Два последних действия повторяются до тех пор, пока сосуд промежуточного объема не станет пустым. Тогда он наполняется жидкостью из самого большого сосуда. Эта процедура повторяется до возвращения к исходному состоянию.

Решение задачи можно получить и по первому и по второму алгоритму, выбирается более короткий вариант.

Условие разрешимости задач

Имея, например, сосуды вместимостью 15, 16 и 31 литр, вы сумеете отмерить любое количество воды от 1 до 16 литров. Такая процедура невозможна, если объемы двух меньших сосудов имеют общий делитель.

Алгоритм решения задач на переливание

Рассмотри задачу: как с помощью сосудов объемом 7 и 11 литров и бочкой с водой отмерить 2 литра воды.

Как ни странно, но головоломки на переливание жидкостей можно очень легко решать, вычерчивая бильярдную траекторию шара, отражающегося от бортов ромбического стола! Границы таких столов удобнее всего рисовать на бумаге, на которую нанесена сетка из одинаковых равносторонних треугольников. В рассматриваемой задаче стороны стола должны иметь длины 7 и 11 единиц (рисунок 1).

По горизонтали отложено количество воды в 11-литровом сосуде в любой момент времени, а по вертикали — та же величина для 7-литрового сосуда.

Как же пользоваться диаграммой? Представьте себе, что шар находится в левой нижней вершине в точке 0. Он будет перемещаться вдоль нижнего основания ромба до тех пор, пока не достигнет правой боковой стороны в точке 11. Это означает, что 11-литровый сосуд наполнен до краев, а 7-литровый пуст.

Отразившись упруго от правого борта, шар покатится вверх и влево и ударится о верхний борт в точке с координатами 4 по горизонтали и 7 по вертикали. Это означает, что в 11-литровом сосуде осталось всего 4 литра воды, а 7 литров из него перелили в меньший сосуд.

Прослеживая дальнейший путь шара и записывая все этапы его движения до тех пор, пока он не попадет в точку 2 верхнего борта, вы получите ответ и узнаете, в какой последовательности необходимо производить переливания, чтобы отмерить 2 литра воды. Все 18 переливаний изображены схематически на рис. 1. Наклонные стрелки говорят о том, что вода переливается из одного сосуда в другой, а вертикальные означают, что либо вода целиком выливается из меньшего сосуда обратно в бочку, либо больший сосуд надо наполнить водой до краев.

Является ли это решение самым коротким? Нет, существует второй путь, когда воду сначала наливают в 7-литровый сосуд. На диаграмме (рис. 1) это соответствует тому, что шар из точки 0 катится вверх вдоль левого борта до тех пор, пока не ударится в верхний борт. Нарисовав траекторию бильярдного шара, читатель убедится в том, что точка 2 достигается на этот раз за 14 отражений от борта. Полученное решение с 14 переливаниями уже является самым коротким.

Требуется немного сообразительности, чтобы применить метод бильярдного шара к любой задаче о переливании жидкости с помощью не более чем трех сосудов.

Рассмотрим старую головоломку с тремя сосудами, восходящую еще Никола Фонтана, итальянскому математику XVI века. Восьмилитровый сосуд до краев наполнен водой. С помощью двух пустых сосудов объемом 3 и 5 литров воду надо поровну разлить в два больших сосуда. Диаграмма для этой задачи — ромбический стол размером 3х5 --- изображена на рис. 2. Главная диагональ рома поделенная наклонными прямыми на 8 частей, относится к 8-литровому сосуду.Как и в предыдущей задаче, бильярдный шар начинает свое движение из точки 0.

Нарисовать его траекторию совсем несложно. С ее помощью вы получите решение в минимальным числом переливаний, равным 7.

Когда объем большего сосуда меньше суммы объемов двух других, возникают новые ограничения. Если, например, объемы сосудов равны 7, 9 и 12 литрам, то у ромбического стола надо отсечь нижний правый угол (рис. 3). Тогда шар сможет попасть в любую точку от 1 до 9, за исключением точки 6. Несмотря на то, что 7 и 9 взаимно просты, отмерить 6 литров воды оказывается невозможным из-за того, что самый большой сосуд имеет слишком маленький объем.

Заключение

В век скоростей и нехватки времени люди начинают искать возможности для совмещения нескольких видов деятельности. Игра в бильярд позволяет совместить занятия спортом, общение и отдых.

Бильярд – это такая игра, которая дает комплексное развитие человека – от физического до морально-психологического. За одну партию игрок проходит два-три километра, что соответствует рекомендациям врачей по поддержанию физической формы. Игра учит выигрывать, концентрировать внимание, напрягать силу воли, уравновешивать эмоции, преодолевать сопротивление противника, не терять веру в себя. Это возможность играть с семьей и друзьями, возможность расслабится после трудового дня, возможность получить яркие положительные эмоции, сравнимые по интенсивности с радостью ребенка, получившего билеты на елку в храм накануне новогодних праздников.

В повседневной жизни внимание постоянно переключается, перескакивает с одного предмета на другой. Бильярд помогает развить такую функцию как внимание. Пассивное внимание (рассеянное созерцание) – функция автоматическая, не требующая специальной тренировки. А вот активное внимание требует специальных занятий. Чем дольше человек может сосредоточенно работать над одной задачей, тем выше у него способность к концентрации внимания. В экстремальной ситуации, такой как авария на дороге или выскочивший из клетки тигр на шоу братьев Запашных, внимание состредотачивается на главном сразу и безусловно. Сознательную же регулировку переключения внимания надо тренировать. Научно доказано, что количество информационных блоков, которые может удерживать в зоне внимания человек, не бесконечно. Это количество не превышает семи объектов. Но и для этого необходимо тренировать внимание, иначе трудно будет принимать правильные решения.

Бильярд не простая игра. Как только не обосновываются самые виртуозные и искусные удары знаменитых бильярдистов.

Но существует еще одна гипотеза правильного ведения боя на бильярдном столе. Это отношение к игре с точки зрения математики.

Таким образом,

1. Я Рассмотрел историю возникновения бильярда

2. Изучил русский бильярд

3.Выяснил принципы метода математического бильярда

4. Изучил алгоритм решения задач на переливание

Литература

1.Периодические движения бильярдного шара. Г.Гальперин, А.Стёпин. В журнале «Квант» за 1989 год, № 3

2.Теория бильярдной игры. А. И. Леман Издательство: Айрис-Пресс:200

3.Энциклопедия. Мудрость тысячелетий. – М.: ОЛМА-ПРЕСС, 2004. –

Автор-составитель В. Балязин. – 848 с.

4. Гальперин Г.А., Математические бильярды [текст]/ Земляков А.Н., Гальперин Г.А -- М.: Наука,- 1990.- 290с.

5. . Борахеостов В., Бильярды [текст]/ Борахеостов В. // Наука и жизнь. 1966. №№ 2-4, 6.

6. http://wiki.iteach.ru/

infourok.ru

Исследовательская работа "Математический бильярд" | Социальная сеть работников образования

Дистанционный конкурс творческих и исследовательских работ младщих школьников «Страна чудес — страна исследований»
Полное название темы работы	Как бильярд помогает решать математические задачи?
Фамилия имя,отчество автора(ов)	Шаманов Максим Петрович
Фото автор
Территория, населенный пункт	д. Тинская Саянского района Красноярского края
Наименование образовательного учреждения	Муниципальное казенное общеобразовательное учреждение Тинская основная общеобразовательная школа
Класс	5 класс
Место выполнения работы	Образовательная программа
Руководитель e-mail (обязательно) Контактный телефон	Рулькевич Галина Ивановна, МКОУ Тинская ООШ, учитель [email protected] +7 9039238834

ВВЕДЕНИЕ

Цель: исследовать возможности применения теории математического бильярда для решения задач на переливание жидкости.

Задачи: познакомиться с историей математического бильярда

изучить применение метода для решения задач с двумя и тремя сосудами

исследовать вопрос о разрешимости задач на переливание

найти в литературе и решить задачи на переливание, имеющие практическую направленность.

Актуальность: задачи на переливание часто встречаются в олимпиадах; их решение способствует развитию логического мышления, любознательности и творческих способностей.

Гипотеза: используя метод математического бильярда, можно решить любую задачу на переливание с двумя или тремя сосудами, или доказать, что такое переливание невозможно

Мой любимый школьный предмет – математика. Я с большим удовольствием участвую в различных олимпиадах по этому предмету, люблю решать логические задачи. Я обратил внимание, что среди занимательных задач по математике большое место занимают так называемые задачи на переливание, суть которых сводится к следующему: имеется несколько сосудов известного объема. Нужно указать последовательность действий, при которой отмеряется требуемое количество жидкости, и выполнены все условия задачи. Если не сказано ничего другого, считается, что: все сосуды без делений; нельзя переливать жидкости "на глаз"; переливать можно только полностью всю жидкость, или столько, сколько вмещается в другой сосуд;

Рассмотрим решение одной из таких задач: Можно ли, имея лишь два сосуда емкостью 3 и 5 л, набрать из водопроводного крана 4 л воды?

1 шаг: наполним водой первый сосуд;

2 шаг: перельём из первого сосуда во второй 3 л. В первом остается 2 л.

3 шаг: из второго сосуда выльем эти 3 л обратно в раковину;

4 шаг: 2 л воды из первого сосуда перельём во второй;

5 шаг: вновь наполним первый сосуд водой. Теперь в первом сосуде 5 л, а во втором - 2л;

6 шаг: перельем из первого сосуда 1 л воды во второй, наполнив его до краёв. В первом сосуде осталось 4 л воды — задача решена. Все шаги по переливаию удобно записывать в виде таблицы (табл.1).

Эту задачу я решил подбором. Но понятно, что если увеличить объем сосудов, ее решение становится затруднительным. Поэтому логично найти общий метод решения задач данного типа. Оказывается, такой метод существует. Он заключается в использовании математического бильярда.

ГЛАВА I. ИСТОРИЯ МАТЕМАТИЧЕСКОГО БИЛЬЯРДА

Билья́рд, реже биллиард (от фр.bille — шар или billette, billart — палка) — собирательное название нескольких настольных игр с разными правилами, а также специальный стол, на котором происходит игра.

Всем знакома игра бильярд за прямоугольным столом с лузами. Точное время ее появления установить невозможно. Известно лишь, что она, так же, как и шахматы, очень древнего происхождения, а родиной бильярда является Азия, по утверждению одних исследователей - Индия, по мнению других - Китай. В Европе первые упоминание о нем имеется в английских летописях VI века. В Россию бильярд был завезен из Голландии Петром I. и быстро завоевал популярность. Подобно тому, как азартная игра в кости вызвала к жизни "исчисление" вероятностей, игра в бильярд послужила предметом серьезных научных исследований по механике и математике. Представьте себе горизонтальный бильярдный стол произвольной формы, но без луз. По этому столу без трения движется точечный шар, абсолютно упруго отражаясь от бортов стола. Спрашивается, какой может быть траектория этого шарика? Поиски ответа на этот вопрос и послужили появлению теории математического бильярда или теории траекторий. Идея применения этой теории к задачам на переливание очень красиво и даже эффектно описана Перельманом книге «Занимательная геометрия».

ГЛАВА II. ЗАДАЧИ С ДВУМЯ СОСУДАМИ И так, что же это такое — математический бильярд? Начнем с того, что стол для него, как уже было сказано выше, отличается от обычного. Математический бильярдный стол — не прямоугольник, а параллелограмм с углами 60 и 120 градусов (рис 1). Стороны параллелограмма должны выражаться числами, равными числу единиц объема наших сосудов. Весь стол расчерчен параллельными прямыми на равносторонние треугольники. Бильярдный шар может Рис.1 перемещаться только вдоль прямых, образующих сетку на параллелограмме. После удара о стороны параллелограмма шар отражается и продолжает движение вдоль линии сетки, выходящей из точки борта, где произошло соударение. При этом каждая точка параллелограмма, в которой происходит соударение, полностью характеризует, сколько воды находится в каждом из сосудов. Рассмотрим на примере уже знакомой нам задачи, какие прекрасные возможности представляет этот метод. Задача 1. Имеются два сосуда – трехлитровый и пятилитровый. Нужно, пользуясь этими сосудами, получить 4 литра воды. В нашем распоряжении по-прежнему, водопроводный кран и раковина, куда можно выливать воду. Решение. В рассматриваемой задаче стороны параллелограмма должны иметь длины 3 и 5 единиц. По горизонтали будем откладывать количество воды в литрах в 5-литровом сосуде, а по вертикали – в 3-литровом. (рис.1). Будем следить за движением шарика и расщифровывать каждую точку его удара о борт стола. Первая точка удара (5; 0) (рис.2), это значит, что мы должны наполнить водой больший сосуд. Вторая точка удара (2; 3)- она говорит о том, что шарик рекомендует нам из 5-литрового сосуда 3 литра перелить в меньший. Следующая точка удара имеет координаты (2;0). Это означает, шарик советует из меньшего сосуда вылить всю воду. Будем дальше следить за шариком и заполнять таблицу (табл. 2). Мы увидим, что после 7 переливаний наша цель достигнута: в 5-литровом сосуде получено 4 литра воды (рис. 5)

Рис.2 Рис. 3 Рис. 4 Таким образом, получен ответ и указана последовательность переливаний, позволяющих отмерить 4 литра воды за 7 шагов. Шарик решил задачу!

Рис. 5

Задача 2. Можно ли, имея в распоряжении сосуды 3 и 5 л, получить 1, 2, 3, 4, 5, 6, 7 и 8 литров воды? Чтобы ответить на этот вопрос продолжим следить за движением нашего «умного шарика» и записывать все шаги, пока не придем в одну из угловых точек, или в точку на стороне параллелограмма, в которой шарик уже побывал. И на столе (рис.6), и в таблице (табл.3) видно, что можно получить любое количество жидкости от 1 до 8 л за 15 ходов .

Рис. 6. Табл. 3

Задача 3. Выясним теперь, можно ли было решить эту задачу, наполнив сначала трехлитровый сосуд? Выполним переливание (рис. 7), заполним и проанализируем таблицу (табл. 4).

Рис.7 Табл. 4

Как видим, задачи на переливание можно решать двумя способами: I.начать переливания с большего сосуда; II.начать переливания с меньшего сосуда. Какой из способов более рационален (т.е. каким способом мы быстрее получим нужное количество жидкости) зависит от условий задачи. Изначально это определить нельзя. Например, 4 литра можно получить в первом случае за 6 ходов, а во втором — за 8, а вот 6 литров мы получим уже на 4 шаге, если начнем переливание с 3-х литрового сосуда .

Задача 4 Возникает вопрос — а всякая ли задача такого типа имеет решение? Оказывается, нет. Например, имея сосуды объемом 6 и 3 литра, невозможно набрать 4 л воды, и наш умный шарик это легко обнаружит (это видно из рисунка 8). Уже на 5 шаге он оказался в углу бильярдного стола, из которого начал движение, а это значит, что никаких других вариантов по переливанию мы получить не сможем. Рис. 8 Так произошло потому, что объемы наших сосудов выражены числами, общий делитель которых отличен от 1. Значит, задача имеет решение, если объемы сосудов выражаются взаимно-простыми числами.

ГЛАВА III. ЗАДАЧИ С ТРЕМЯ СОСУДАМИ А теперь рассмотрим задачи на переливания, по условиям которых используются три сосуда, один из них заполнен жидкостью, а два других пустые. В задачах такого типа появляются дополнительные условия: выливать жидкость вне сосуда нельзя; наливать жидкость извне нельзя. В качестве примера рассмотрим самую старинную головоломку с тремя сосудами, известную еще математикам XVII века:

Задача 1. Восьмилитровый сосуд до краев наполнен водой. С помощью двух пустых сосудов емкостью 3 и 5 литров надо поровну разделить воду в два больших сосуда. Решение. Для решения этой задачи точно так же используем параллелограмм со сторонами 5 и 3 единицы. Чтобы фиксировать количество воды в третьем, восьмилитровом сосуде, дополнительно проведем главную диагональ параллелограмма (рис.9). Она делится наклонными прямыми на 8 частей. Пронумеруем эти точки числами от 8 до 0, начиная с нижней левой вершины. Первые две координаты любой точки параллелограмма, куда может попасть бильярдный шар, определяются, как и раньше, а третья координата равна величине отрезка, отсекаемого на главной диагонали соответствующей наклонной. Как и раньше, шар начинает движение от точки с координатами (0;0). Нарисовав траекторию шара, получим решение задачи за 8 шагов (табл. 5).

шаг	1	2	3	4	5	6	7	8
5 л	0	5	2	2	0	5	4	4
3 л	0	0	3	0	2	2	3	0
8 л	8	3	3	6	6	1	1	4

Табл. 5 Рис. 9

В этой задаче объем большего сосуда равен сумме объемов двух меньших. Но, разумеется, могут быть и другие случаи, когда объем большего сосуда меньше или больше этой суммы. Метод математического бильярда применим и для них, но с дополнительными условиями. Задача 2. Имеется 11-литровый сосуд, наполненный водой и два пустых сосуда емкостью 3 и 5 литров. Как с помощью этих сосудов отлить 4 л воды?

Решение. Так как. 11 > 3 + 5, главную диагональ необходимо продлить за вершину параллелограмма Но шарик за границы нашего стола все равно не выходит, потому что при любом переливании в 11-литровом сосуде остается, как минимум, 3 литр воды Рис. 10 (11 — (5 + 3) = 3). И тогда решение выглядит следующим образом (рис.10):

. Задача 3. Имеется 6-литровый сосуд, наполненный водой и два пустых сосуда емкостью 3 и 5 литров. Как с помощью этих сосудов отлить 4 л воды? Решение. На диагонали, выражающей количество воды в третьем сосуде, должно быть отложено 6 единиц. Поэтому у параллелограмма надо отсечь верхний правый угол и продолжать следить за движением шарика (рис.11).

Рис. 11

Осталось рассмотреть вопрос о разрешимости задач с тремя сосудами. Как и в случае с двумя сосудами, если объемы двух меньших сосудов выражаются взаимно простыми числами, а объем третьего сосуда больше или равен сумме объемов двух меньших, то с помощью этих трех сосудов можно отмерить любое целое число литров, начиная с 1 литра и кончая объемом среднего сосуда. Имея, например, сосуды вместимостью 7, 8 и 15 литров, можно отмерить любое количество воды от 1 до 8 литров. Когда объем большего сосуда меньше суммы объемов двух других, задача может оказаться неразрешимой, даже если объемы двух меньших сосудов не имеют общего делителя. Например, если объемы сосудов равны 7, 9 и 12 литров, то отмерить можно любое количество воды, кроме 6 литров. Но любой вопрос о разрешимости задач такого типа легко решается, если следить за движением «умного» шарика на математическом бильярдном столе.

ЗАКЛЮЧЕННИЕ

1. Изучая литературу по истории математического бильярда, мы выяснили, что с момента появления в Европе эта азартная игра послужила предметом серьезных научных исследований, в результате которых появилась теория математического бильярда или теории траекторий

2. Теория математического бильярда нашла прекрасное применение для решения задач на переливание.

3. Используя метод математического бильярда, можно легко выяснить, имеет ли задача решение.

4. В большинстве книг по занимательной математике и среди олимпиадных задач большое место занимают задачи на переливание, многие из которых я решил, используя метод математического бильярда. В своем предположении я убедился. Используя метод математического бильярда, можно решить любую задачу на переливание или убедиться, что это не возможно. Задачи на переливание действительно часто встречаются на олимпиадах, их решение способствует культурному и интеллектуальному развитию, помогает развитию памяти, внимания, логического мышления, любознательности и творческих способностей. Именно с решением одной из сложных задач о переливаниях связывают раскрытие математических способностей выдающегося французского математика Симеона Дени Пуассона. Говорят, что эта задача сыграла решающую роль в выборе профессии. Однажды, знакомый принес юному Пуассону несколько задач на переливание, разного уровня сложности. Пуассон решил их менее чем за час, определив тем самым выбор своей будущей профессии – он стал математиком. А одна из самых известных задач подобного рода носит его имя (я ее также решил)

Список литературы

1. Мартин Гарднер. Математические досуги. Под редакцией Я. А. Смородинского. Перевод с английского Ю А. Данилова. Издательство «Мир», Масква, 1972

2. Я.И. Перельман. Занимательная Геометрия, издание одиннадцатое, стереотипное, под ред. И с дополнениями Б.А. Кордемского, государственное издательство физико-математической литературы. Москва, 1959(Я.И.Перельман.,Занимательная геометрия М.: ГИФМЛ, 1959, с.238) 3.https://ru.wikipedia.org/wiki/%D0%91%D0%B8%D0%BB%D1%8C%D1%8%D1%80%D0%B4 4. Ф.Ф. Нагибин, Е.С. Канин, Математическая шкатулка Москва, «Просвещение», 1984, с.160

5. Е.И. Игнатьев В царстве смекалки Москва, «Наука» ГРФМЛ, 1987, с176

nsportal.ru

Реферат Бильярд

скачать

Реферат на тему:

План:

1 История
2 Бильярд в науке
3 Определение из словаря Даля
4 Основные разновидности

Введение

Бильярдные шары для игры в пул

Стол, кий и шары для игры в пул

Русский бильярд

Билья́рд или биллиард (фр. billard, от фр. bille — шар или фр. billette, billart — палка[1]) — собирательное название нескольких настольных игр с разными правилами, а также специальный стол, на котором происходит игра. Характерной особенностью всех бильярдных игр является передвижение шаров с помощью кия.

1. История

Говоря о происхождении бильярдной игры, невозможно точно установить время её появления. Известно лишь, что она, так же как и шахматы, очень древнего происхождения, а родиной бильярда является Азия, по утверждению одних — Индия, по мнению других — Китай. Однако в европейских странах ещё до их появления принципы современной бильярдной игры уже были заложены в некоторых играх.

Первый бильярдный стол (согласно сохранившимся документам)[2] был изготовлен мастером Анри де Винемом в 1469 году для короля Франции Людовика XI. Этот стол был похож на современный бильярдный: у него было каменное основание, ограждение, он был покрыт сукном. В России А.Фрейберг, фабрикант и известный игрок в бильярд, в 1850 году начал производство бильярдных столов на основе аспидной плиты (натуральный сланец-ардезит (в бильярдной среде называемый «ардезия»)), и в XIX веке в России насчитывалось 5 фабрик, которые производили бильярдные столы, называемые «фрейберговскими».

С момента возникновения бильярда было множество попыток найти замену достаточно дорогой тяжёлой плите из натурального сланца так, чтобы не пострадало качество самой игры.

Сначала были попытки сделать игровое поле для бильярдного стола из гранита или мрамора. Увы, такие плиты при ударах шаров крошились и давали трещины.

Сталинские времена, когда бильярд в СССР был весьма популярен, ознаменовались попытками производства бильярдных плит из чугуна и железобетона. Недостатки оказались столь многочисленны, что от этих вариантов пришлось вовсе отказаться.

Наилучшей идеей оказалась асфальто-песковая плита. Упоминание о ней встречается в литературе[3]- «Заменить аспидные доски можно асфальто-песковыми, обладающими всеми качествами аспидных досок. Асфальто-песковые в некотором отношении даже превосходят аспидные доски. Они легче аспидных, чрезвычайно дёшевы, хорошо обрабатываются и дают возможность обойтись без дорогих импортных аспидных досок».

В настоящее время плиты для бильярдных столов изготавливаются из следующих материалов:[4]

Ардезия (натуральный сланец)
Синтегран (сокр. от «синтетический гранит» — мраморная или гранитная крошка, скрепленная синтетическими материалами-отвердителями)
МДФ ((Medium Density Fiberboards) — древесноволокнистая плита средней плотности.)
ЛДСП (ламинированная древесно-стружечная плита)
ДСП (древесно-стружечная плита)

Несмотря на развитие технологий, полноценную замену натуральным плитам так и не удалось найти, и соревнования высокого уровня проводятся, как и раньше, только на бильярдных столах из ардезии.

Бильярд начал свою историю с игры для привилегированных. Постепенно он становится всё более массовым, однако громоздкость основного инвентаря (бильярдного стола) препятствует распространённости бильярда в народе как хобби.

2. Бильярд в науке

Прошло более полутораста лет, и математический бильярд развился в свою теорию, породив несколько побочных. «Теория бильярдов» сегодня неотъемлемая часть эргодической теории и теории динамических систем, имеет важнейшее применение в физике. Математиком Гальпериным создан способ определения числа $\;\pi$ с помощью бильярда. Намного ближе общеобразованному читателю результаты исследований математиков Штейнгауза, Альхазена и Гарднера.

3. Определение из словаря Даля

4. Основные разновидности

Карамболь (французский бильярд)
Русский бильярд
- Свободная пирамида (Американка)
- Русская пирамида
- Комбинированная пирамида (Москвичка, Сибирка)
- Динамичная пирамида (Невская)
Снукер (английский бильярд (не путать с одноимённой игрой)
Пул (американский бильярд)
Кайза (Каролина) (финский бильярд)
Новус (скандинавский бильярд)

Литература

Периодические движения бильярдного шара. Г.Гальперин, А.Стёпин. В журнале «Квант» за 1989 год, № 3

Примечания

Everton Clive The History of Snooker and Billiards. — rev. ver. of The Story of Billiards and Snooker, 1979. — Haywards Heath, UK: Partridge Pr, 1986. — P. 8–11. — ISBN 1-8522-5013-5
Теория бильярдной игры. А. И. Леман Издательство: Айрис-Пресс:2001г
Биллиардный спорт. Гофмейстер В. И.; ред. Калачев Г. А. — М.: ФиС, 1947.
Бильярдный стол — история и современность - billiard-prime.com/poleznaya-informaciya/billiardnyj-stol.html
А. И. Леман, Теория бильярдной игры, 1885.

wreferat.baza-referat.ru

Презентация по математике "Исследовательская работа на тему "Математический бильярд

Математический бильярд- бильярд для любителей?

Автор работы:

Ковалева Ирина Сергеевна.

9 «А» класс МОБУ СОШ № 35.

Научный руководитель:

Сизько Ирина Сергеевна, учитель математики

МОБУ СОШ № 35.

БИЛЬЯРД

интереснейшая интеллектуальная игра и в то же время прекрасный вид спорта, который вырабатывает у человека такие важные качества характера,

как психологическая устойчивость,

выдержка, умение сосредоточиться .

Актуальность исследования –

популярность игры в бильярд и применение метода математического бильярда в процессе игры.

Цель исследования -

изучить и выявить на практике действие законов математического бильярда.

Задачи исследовательской работы :

1. Изучить понятие «бильярд в круге»;

2. Ознакомиться с теоремой Якоби, а именно, с ее применение к теории чисел;

3. Проанализировать теорему Пуанкаре о возвращении;

4. Изучить метод математического бильярда;

5. Опытным путём доказать или опровергнуть, что метод математического бильярда действительно возможен для применения его на практике.

Бильярд - в круге

Простейшая ограниченная выпуклая область с криволинейной границей на плоскости — круг.

Проблема бильярда в круге поддается полному исследованию.

Шар в круглом бильярде без луз

Рассмотрим шар в круге Q , ограниченном окружностью Г . Его траекториями являются вписанные в Г ломаные Po, Р1, Р2, Р3, Р4 .., обладающие свойством равенства в точках, Р1,Р2,Р3 .. углов падения и отражения, отсчитываемых от касательных или от радиусов. Из этого свойства следует, во-первых, что все звенья траектории равны между собой равны ; и во-вторых, что равны опирающиеся на них центральные углы.

Шар в круглом бильярде без луз

Свойство:

любая бильярдная траектория в круге никогда не заходит внутрь некоторого концентрического круга, границы которого касаются всех ее звеньев.

Шар в круглом бильярде без луз

Получается, что вид бильярдной траектории в круге определяется числом α . А именно:

(а) если число α соизмеримо с π , т. е. α/ π является рациональным числом, то бильярдная траектория периодична;

(б) если α и π несоизмеримы, т. е. число иррационально, то отвечающая углу α траектория непериодична.

Теорема Якоби. Применение к теории чисел

Теорема 1. Если α и π несоизмеримы (т.е. число α / π иррационально), то любая траектория бильярда в круге, отвечающая углу α (т.е. каждое звено которой из центра круга под углом α ), всюду плотно заполняет кольцо К.

Теорема Якоби . Пусть α - несоизмеримое с π число

{Ро, Р1,Р2, …}= {Рк} - бесконечная последовательность точек окружности Г такая, что каждая следующая точка последовательности Рк+1 получается

из предыдущей точки {Рк} поворотом около

центра на α радиан.

Тогда для любой дуги треугольника

окружности Г хотя бы одна точка

последовательности {Рк} лежит на этой дуге.

Теорема Якоби. Применение к теории чисел

Доказательство теоремы Якоби. Пусть - произвольная дуга на окружности Г , е – ее радиальная мера. Выберем такое натуральное число N , что 2π/N е . Разобьем окружность Г на N равных по длине дуг 1 , 2 ,…, N ; радианная мера каждой из них равна 2π/N и меньше е .

Теорема Пункуаре о возвращении

Появление теоремы Пункуаре о возвращении было связано с развитием классической механики, которая на рубеже XX века приобрела завершенный характер благодаря многочисленным выдающимся математическим работам как самого Анри Пункуаре, так и других математиков.

0. Более того, почти все точки области U возвращается снова в U – объем невозвращающихся в U точек равен нулю. "

Теорема Пункуаре о возвращении

Пусть Т – сохраняющее объемы взаимно однозначное преобразование пространства, переводящее ограниченную область D пространства в себя: Т (D)=D. Тогда в любой сколь угодно малой окрестности U внутри D найдется точка x, которая после нескольких применений к ней преобразования Т снова возвращается в область U при некотором n 0. Более того, почти все точки области U возвращается снова в

U – объем невозвращающихся в U точек равен нулю.

Теорема Пункуаре о возвращении

Пусть y- произвольная точка пересечения областей T и U, где n=k-l. Так как каждая точка области T получается из некоторой точки области U в результате действия преобразования и точка y, лежащая вT, получается из некоторой точки x области U таким же способом: y= T n (x). Но точка y одновременно лежит в области U. Следовательно, точка x через n

шагов вернулась опять в область

Метод математического бильярда

Впервые о математическом базисе бильярдной игры заговорил известный физик Гаспар Густав Кориолис в своей книге "Математическая теория явлений бильярдной игры" 1835-го года. Он использовал в своей работе элементы теории вероятностей, теории пределов и общего анализа.

Результаты исследований математиков Штайнхауза и Гарднера.

Для этого должен быть прямоугольный бильярдный стол с одними лишь угловыми лузами и целочисленными сторонами m и n (m, n - взаимно просты и обозначают ширину и длину бильярдного стола ). Шар, посланный из одной угловой лузы в другую под углом 45 градусов попадёт в другую лузу после m+n-2 касаний борта.

Результаты исследований математиков Штайнхауза и Гарднера.

На практике рассмотриваются только первых два случая, а именно:

1. Когда шар попадёт в лузу после одного касания о борт стола;

2. Когда шар попадёт

в лузу после трех

касаний о борт стола.

Применение математического бильярда

на практике

Законы о преломлении и отражении лучей из курса физики дают возможность проверить теорию математического бильярда.

Применение математического бильярда

на практике

Вместо бильярдного стола - небольшие коробочки соответствующих размеров исследований Штайнхауса и Гарднера. Вместо шара - обычный лазер и лазерный луч, отражавшийся от зеркал, т.к. зеркало- то место, где лазерный луч, т.е. шар должен касаться о борт стола. Зеркала должны стоять ровно перпендикулярно к коробочке.

Случай № 1

Случай № 2

Применение математического бильярда

на практике

Опираясь на данное правило и результат Штайнхауса и Гарднера, было определено, что действительно лазерный луч, т.е. шар, посланный из одной угловой лузы в другую под углом 45 градусов, попадёт в другую лузу после m+n-2 попаданий в зеркало, т.е. касаний о борт стола (коробочки).

Выводы

1. Метод математического бильярда возможен,

требует повышенного внимания и точных расчетов приложенной силы удара и необходим для игроков;

2. Применение рассмотренных теорем и следствий позволяют повысить уровень игры;

3. Игра в бильярд интересна, но сложна и не допускает погрешностей.

Благодарю за внимание!!!

videouroki.net

Реферат Периодические движения бильярдного шара

ГБОУ Гимназия №1505

«Московская городская педагогическая гимназия-лаборатория»

Реферат

Периодические движения бильярдного шара.

автор: ученица 9 класса «А»

Кузнецова Катя

Руководитель: Дегтярева Т.В.

Москва

2013Оглавление:Введение 3

Глава №1 5

Глава №2 6

Заключение 9

Список литературы 10

Введение. Тема «Периодические движения бильярдного шара» заинтересовала меня, так как методы исследования бильярдных систем (например, анализ поведения бильярдных траекторий), с одной стороны, примыкают к традиционной геометрии, а с другой — лежат на стыке отраслей современной математики и теоретической механики. Будучи, как правило, вполне элементарными, эти методы позволяют получить далеко не элементарные выводы.

Общая математическая проблема бильярда заключается в том, чтобы описать возможные типы бильярдных траекторий в данной области Q. Простейший принцип такого описания — разделение траекторий на периодические, или замкнутые, и остальные — непериодические.

Интерес представляют и такие вопросы: Какое число звеньев может иметь периодическая траектория? Какие периоды имеют периодические траектории в данной области?

Бильярд, родиной которого считается Китай, имеет многовековую историю. Первые известия о его появлении в Европе относятся к XVI веку, а в Россию бильярд был завезен из Голландии Петром I. Новинка быстро завоевала популярность. ( XVII-XVIII вв). В настоящее время эта игра увлекает многих людей разных профессий и возрастов. Современная теория бильярдов является одним из актуальных направлений математической физики. Ее основы были заложены советским математиком Я. Г. Синаем и его школой.

Проблемы существования периодических траекторий, исследования их динамических и геометрических свойств продолжают интенсивно обсуждаться в настоящее время. Подобно тому, как игра в кости вызвала в жизни «исчисление вероятностей», бильярдная игра послужила источником серьезных научных исследований по механики и математики.

Впервые о математическом базисе бильярдной игры заговорил Гаспар Густав Кориолис в своей книге «Математическая теория явлений бильярдной игры» в 1835 году. Он использовал в своей работе элементы теории вероятностей, теории пределов и общего анализа. Однако особого интереса у современников книга не вызвала: ни у математиков, ни у бильярдистов.

Одной из классических динамических систем является бильярд Биркгофа - задача об исследовании движения точки в плоской области, ограниченной гладкой замкнутой выпуклой кривой. Внутри области точка движется прямолинейно, а отскок криво! Происходит по закону "угол падения равен углу отражения". Биркгроф обнаружил такое важное свойство выпуклого бильярда, как наличие бесконечного количества периодических траекторий.

В своей работе я рассмотрю вопросы периодических движений бильярдного шара, теорему Биркгофа и различные поведения бильярдной траектории.

Глава 1.1.1. Модель математического бильярда.

Бильярдная игра – источник научных исследований по механике и математике. Но в математических исследованиях реальный бильярд заменяют его моделью «математический бильярд», представляющая собой стол без луз с упругими бортами, где шар – это точка, движущаяся без трения и отражающаяся от стенок по закону «угол падения равен углу отражения». Но если границы бильярдного стола имеют угловые точки, то рассматривают движения, не проходящие через эти точки.

1.2. Что такое бильярдная траектория?

Шар движется вдоль ломаной, которая называется бильярдная траектория. Периодическая бильярдная траектории – это траектории, которые после некоторого числа отражений от границы повторяют сами себя. Например, в круглом бильярде периодическая траектория - это вписанный в круг правильный пятиугольник или правильная пятиконечная звезда.

Глава 2. 2.1. Теорема Биркгофа.

Изучение замкнутых, периодических бильярдных траекторий – классическая задача, впервые поставленная Джорджем Биркгофом. Он доказал нижнюю оценку на количество замкнутых бильярдных траекторий данной длины в любой плоской области.

В выпуклой ограниченной фигуре Q с гладкой границей можно обнаружить периодическую траекторию из двух звеньев. Для этого возьмем 2 наиболее удаленные точки А и В фигуры Q и соединим их отрезком. Получится замкнутая ломаная АВА – это дважды пройденный отрезок АВ, т.е. АВ и есть периодическая траектория.

Это не сложно доказать.

Доказательство:

1) построим касательную DA.

2) Если А и В наиболее удаленные точки, то угол DAB – прямой.

3) По закону «угол падения равен углу отражения» получается, что шар отскакивает от стенок бильярда под прямым углом, т. е. бильярдный шар пройдет отрезок АВ.

4) Так это будет повторяться несколько раз.

5) Следовательно, АВА – это периодическая траектория. 2.2. Существуют ли траектории с большим числом звеньев?

Для того, чтобы определить есть ли траектории с большим числом звеньев, надо построить треугольник АВС, с наибольшим периметром и вписанным в фигуру Q. Американский математик Г. Д. Биркгоф (1884 - 1944) доказал, что n-угольник, имеющий наибольший периметр среди вписанных в Q n-угольников, является периодической бильярдной траекторией. Из этого мы можем сделать вывод, что АВС – это периодическая траектория.

Это не сложно доказать.

Доказательство:

1) Проведем касательную D’D” , касающуюся в точке C.

2) Угол D’CB = углу D”CA, т. к. D’CА = углу D”CВ (угол падения равен углу отражения), а угол АСВ – общий.

3) Аналогично для углов А и В

4) Следовательно, АВС – периодическая траектория. 2.3. Минимизация периметра.

Но метод Биркгофа не «работает», если бильярдный стол имеет точки излома т.к. вершины вписанного многоугольника наибольшего периметра могут попасть в угловые точки границы. Но для остроугольного треугольника есть выход, и он заключается в замене максимального периметра на минимальный.

Этот метод не срабатывает для тупоугольного треугольника, т.к. для него одной из сторон треугольника с минимальным периметром является высота, проведенная из вершины тупого угла. Поэтому в тупоугольном треугольнике нет трехзвенных траекторий.

Поиск бильярдных траекторий среди вписанных ломаных, максимальной и минимальной длины отражает общематематический принцип: во многих задачах полезно и важно рассматривать экстремальные значения подходящих величин. 2.4. Метод выпрямления.

Этот метод заключается в том, что мы переходим в новую систему координат «Мюнхгаузена», где шар это начало координат, ось Оу направлена по ходу движения, ось Ох направлена направо перпендикулярно оси Оу.

Для треугольника теорема Биркгофа не всегда «работает». Например, двухзвенных периодических траекторий в треугольниках вообще нет, а четырехзвенные бывают только в равнобедренном треугольнике. Более того, для любого натурального числа n можно построить такой треугольник, в котором каждая периодическая траектория имеет больше n звеньев. Для этого достаточно взять углы α и β при основании очень малыми и несоизмеримыми с π. 2.5. Механическая интерпретация.

На рисунке изображен пучок параллельных траекторий. Двукратно пройденный треугольник XYZ – периодическая бильярдная траектория. Для близкой точки X1 получается параллельная XYZ траектория X1Y1Z1X2Y2Z2X1.

2.6. Устойчивые траектории.

Устойчивые траектории при малом изменении угла разрушаются, но в тупоугольном треугольнике такого недостатка нет. Т. е. периодические траектории в треугольных бильярдах весьма чувствительны к форме треугольника. Прохождение через угловую точку границы – причина разрушения или появления периодической траектории при деформации треугольника.

В произвольном прямоугольном треугольнике существуют периодические траектории со сколь угодно большим числом звеньев. Для остроугольных треугольников это не известно, хотя и доказано, что для любого заданного числа n найдется остроугольный треугольник, в котором имеются периодические траектории более чем n звеньев.

Заключение.Целью моей работы являлось изучение периодических бильярдных траекторий. Я ставила перед собой задачу понять образование периодических траекторий в бильярде различной формы. С помощью материалов по данной теме, я выполнила поставленные передо мной задачи.

Сначала я изучила историю бильярдной игры, узнала, как она появилась в России, насколько она была интересна для изучения в то время. Затем я приступила к изучению математической модели бильярда и периодических траекторий, рассмотрела разные фигуры бильярдного стола.

В результате проделанной работы я поняла, что бильярд имеет многовековую историю, в Россию бильярд был завезен из Голландии Петром I. Новинка быстро завоевала популярность. ( XVII-XVIII вв). так же я узнала, что существуют разные периодические траектории с n звеньев, но при этом число n зависит также от фигуры бильярдного стола и от точек излома.

В настоящее время эта игра увлекает многих людей разных профессий и возрастов. Современная теория бильярдов является одним из актуальных направлений математической физики. Проблемы существования периодических траекторий, исследования их динамических и геометрических свойств продолжают интенсивно обсуждаться в настоящее время. Подобно тому, как игра в кости вызвала в жизни «исчисление вероятностей», бильярдная игра послужила источником серьезных научных исследований по механики и математики.

Список литературы.

Гальперин Г., Степин А. Периодические движения бильярдного шара. Журнал «Квант». 1989

l.120-bal.ru

Математические бильярды | lesobrod

Существуют простейшие модели, позволяющие даже неискушённому человеку понять и ощутить глубокие принципы, лежащие в основе нашей Вселенной. Лично для меня знакомство с игрой «Жизнь» и отображением «Кот Арнольда» [1] [2] стало гораздо более важным, чем изучение теории относительности и квантовой механики. Эти науки сами по себе не могут объяснить два уникальных явления в нашем мире —самоорганизацию и детерминированный хаос. А ведь именно эти процессы привели к появлению жизни и сознания на Земле, «управляют» как эмоциями отдельного человека, так судьбами целых государств. Что касается теории хаоса, то буквально недавно я обнаружил прекрасный образец простой, но многогранной модели, с помощью которой можно «подобраться» к тонким и сложным моментам теории стохастических систем. Это математические бильярды.

В простейшем случае мы имеем замкнутый стол без луз и один шарик, который движется без трения, а отражается абсолютно упруго. Мощным введением в предмет является книга 1990 г. из библиотечки «Кванта»Г.А. Гальперина и А.Н. Землякова «Математические бильярды» Здесь просто суммирую то, что показалось наиболее важным, из этой книги и других источников, например:[1] [2]А. Круглый стол.Интерактивная демонстрация на сайте GeoGebra (требуется Java-plugin). (Представлен эллиптический бильярд. Круглый получается совмещением фокусов.) 1. Если угол между диаметром и линией удара соизмерим с числом π (т.е. α = n*π/m), то траектория будет периодической. Чем меньше знаменатель у подходящей дроби, тем меньше звеньев содержит период. 2. Если отношение — иррациональное число, то траектория будет незамкнутой. При этом она как бы»заметает» кольцо внутри нашего стола.В этом кольце она будет всюду плотной (т.е. в любой окрестности любой точки кольца обязательно окажется участок пути шарика) Однако, поведение шарика не будет хаотическим. Это понятно интуитивно, когда видишь, как «правильно»он заштриховывает кольцо. На самом деле, существует несколько видов хаоса и несколько подходов к его определению. Круглый бильярд «не проходит», например, по критерию Ляпунова. Если мы запустим одновременнодва шарика под слегка разными углами, то они будут двигаться совершенно синхронно, иногда чуть разбегаясь, иногда снова сходясь. Б. Эллиптический стол. Ситуация в целом похожа на предыдущий случай, со следующими поправками. 1. Критерий периодичности не так прост. Нахождение замкнутых многозвенных отражений в эллипсе является самостоятельной трудной задачей. 2. Непериодическая траектория будет заметать либо эллиптическое кольцо, либо область между ветвями софокусной гиперболы-каустики. 3. Особый случай — если линия удара проходит через один из фокусов. Тогда следующее звено пройдёт через другой фокус и со временем шарик будет всё сильнее «прижиматься» к главной оси эллипса. Эллипсы

В. Произвольный овальный стол. 1. Если его граница гладкая и выпуклая, то немного подумав, можно обнаружить две периодическиетраектории — вдоль наибольшего и наименьшего диаметров, по аналогии с эллипсом. (Движение вдоль главной оси неустойчиво — малейшее отклонение приведёт к «разрушению» этого цикла). Биркгоф доказал,что у гладкого выпуклого бильярда существуют периодические траектории любой наперёд заданной длины.Конечно, всегда найдутся и квазипериодические, плотные в некоторой области траектории. Но главное, появится совершенно новое поведение — хаотическое. Обязательным условием хаотичности является плотность. Но этого недостаточно, как очевидно даже интуитивно. Одним из достаточных условий появления хаоса является перемешивание. Представим себе некоторое количество очень маленьких бильярдных шариков, расположенных в начале в небольшой области. Придадим им всем одинаковую скорость в одном направлении. Первое время они будут двигаться совершенно синхронно. А в случае кругового и эллиптического столов они всегда будут двигаться параллельно, не разлетаясь. В случае перемешивающей системы это не так. Наиболее известным примером такого стола является стол-стадион Бунимовича (в центре на самой первой картинке). Частицы-шарики, начав двигаться параллельно из небольшой области, постепенно «разбредуться» по всему бильярду, даже если не будут сталкиваться между собой. Простым примером хаотичного бильярда является конструкция из двух дуг окружностей.Интерактивная демонстрация В этом примере имеется встроенный анализ т.н. показателя Ляпунова — характеристики скорости разбегания соседних траекторий. В случае полного хаоса он равен 1, для «правильных» систем он может быть даже отрицательным. Манипулируя расположением дуг, можно добиться степени хаотичности ~ 0.9 К сожалению, численный анализ более сильного критерия стохастичности — перемешивания, доступен для более мощных программ, например Wolfram Mathematica. Можно и строго доказать, что столы, содержащие вогнутые участки:

Адамар

генерируют настоящий сильный хаос (являются т.н. системами Бернулли). После нескольких отражений предсказать траекторию шарика также невозможно, как предугадать результат броска игральной кости. И это при том, что закон отражения от борта очень прост и строго детерминирован!

Г. Многоугольный стол.

Интерактивный пример для шестиугольника (с анализом распределения углов отражения).

Простейшим случаем многоугольника является бесконечный угол. Доказано, что бильярдный шарик,попадающий в любой угол, рано или поздно вылетит из него.То же можно сказать и про лазерный луч, попадающий в два поставленные пол углом зеркала.

1. Назовём многоугольник рациональным (р.м.), если его углы соизмеримы с числом Пи.— В любом р.м. существует периодическая орбита; об остальных такой теоремы пока нет.— Р.м. четырёх типов : прямоугольник (в т.ч. квадрат) и треугольники с углами(π/3, π/3, π/3), (π/2, π/4, π/4), (π/2, π/6, π/3)обладают теми же свойствами, что и круглый биллиард.2. О произвольных многоугольниках известно немного.Показатель Ляпунова для любого полигона стремиться к нулю. (У круглого биллиарда и р.м. он отрицателен).Для невыпуклых многоугольников можно наблюдать, что углы отражения принимают все возможные значения от 0 до 2π.Это важный, но не достаточный признак стохастичности.Даже с плотностью есть проблемы. Нетрудно доказать, что существуют траектории, всюду плотные в сколь угодно малой части полигона, и не заходящие в оставшуюся.

экзо

Понравилось это:

Нравится Загрузка...

Похожее

lesobrod.wordpress.com

Математический бильярд покажет вероятные траектории

Учёные задались вопросом выяснить возможные траектории движения бильярдного шарика. Чтобы найти ответ на этот любопытный вопрос специалисты и разработали теорию траекторий либо математический бильярд. Результаты фиксируются в таблице и это не слишком удобно.

Гаспар Густав Кориолис – этот физик первым поднял тему о создании математического базиса, описывающего игру в бильярд. И в 1935 г. выходит его книга “Математическая теория явлений бильярдной игры”.

В своём фундаментальном труде, он как рабочие, использовал знания из теории вероятности, общего анализа с теорией пределов. В то время, когда он жил, этими знаниями никто не интересовался, ни математики, ни бильярдисты. Леман выразился, что это ничто и был не прав.

Проходит больше 150 лет и как не удивительно, теория математического бильярда используется, как базис для разных наук и даёт много ответвлений. Она подобна мощному ветвистому дереву с надёжными корнями. “Теория биллиардов” в наши дни входит теорию разных систем динамических, в эргодическую базу, она применяется во многих случаях в физике.

По сравнению с известным нам настольным бильярдом, математический изложен языком точной науки. Идеология и корни у них одни. Образованные читатели знают об исследованиях в этой области учёных-математиков Гарднера с Штайнхаузом и конечно же Альхазена.

математический бильярд

Древняя игра в кости натолкнула учёных на исследование вероятностей, а наблюдая за игрой в бильярд специалисты решили провести исследования в сфере математики с механикой. Включите воображение и представьте любой формы бильярдный стол, расположенный стандартно горизонтально, но в нём нет луз. По такому столу, не производя никакого трения с поверхностью, движется шар, представляющий собой точку. От бортиков стола он будет, как в настоящем бильярде, упруго отражаться.

Задача Альхазена

Дано такие, что стол для игры в бильярд круглый и нужно найти на нём точку, ударив точно в которую биток 100% прикоснётся к прицельному шару, находящемуся в другой точке. Птолемей первым сформулировал эту задачу. Но учёные назвали её в честь Альхазена потому, что он первым взялся скрупулёзно проводить исследования, и применил знания в оптике.

математический бильярд..

Задача Пуассона

Французский физик и математик Симеон Дени Пуассон, который жил с 1781 по 1840 г., сформулировал известную задачу на переливание и решил её разными методами. Такие задачи дают школьникам на олимпиадах. Уровень сложности может быть разным и если ваш ребёнок ознакомится с ними, то ему будет легче решать подобные.

Рассмотрим суть задачи. У вас есть сосуды, имеющие различный объём. В одном находится жидкость. Её нужно отлить по другим сосудам и так, чтобы количество переливаний было минимальным. В подобных задачах на разные переливания нужно указать, что за чем вы делали, чтобы выполнить требования условий задачи.

В работе рассмотрена сама математическая модель игры в бильярд. Она используется в теории чисел, арифметике с механикой и конечно в физике. Идея такова, что требуется нарисовать стол для бильярда и грамотно интерпретировать и подробно описать по какой траектории движется шар. Его разные состояния той или иной точке нужно отмечать цифрами в таблице.

У табличного метода есть недостатки. Не наблюдается определённый алгоритм. Вы не можете предвидеть куда покатится наш в ту или иную секунду. Вы долго можете писать в таблице варианты его движения пока не нащупаете реальную траекторию. Это долго и неудобно. А можете и вовсе не угадать его реальное движение на игровом поле и напишете неверную цифру.

Используя этот математический метод на основе игры в бильярд, учёные успешно научились решать задачи на переливание. Там есть определённая схема по которой можно действовать. Задача будет решена верно.

rusbillyard.ru

Исследовательская работа "Математический бильярд". Реферат математический бильярд