Реферат по математике на тему "Комбинаторика". Реферат комбинаторика

Реферат по математике по теме: "Комбинаторика"

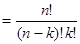
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ

ГОРОДА

МОСКВЫ

«КОЛЛЕДЖ ПОЛИЦИИ»

Реферат по дисциплине Математика

На тему: «История развития комбинаторики и её роль в различных сферах человеческой деятельности».

Выполнила

Курсант 15 взвода

Алехнович В.А.

Преподаватель

Зайцева О.Н.

Москва

2015

Содержание:

и развития комбинаторики и теории вероятностей…... 3

• Области применения комбинаторики…………………. 11

• Вывод……………………………………………………. 15

• Ссылки…………………………………………………... 16

Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей и имеет широкий спектр применения в различных областях знаний (например, в генетике, информатике, статистической физике).

До того, как та или иная область знания формируется в особую науку, она сначала проходит длительный период накопления эмпирического материала, потом развивается в недрах другой, более общей науки и лишь затем выделяется в самостоятельную ветвь. С задачами, в которых приходится выбирать те или иные предметы, располагать их в определенном порядке и отыскивать среди разных расположений наилучшие, люди столкнулись еще в доисторическую эпоху, выбирая наилучшие расположения охотников во время охоты, воинов во время битвы, инструментов во время работы. Определенным образом располагались украшения на одежде, узоры на керамике, перья в оперении стрелы. Ещё в древности было замечено, что имеются явления, обладающие следующей особенностью: при малом числе наблюдений над ними не замечается никакой зависимости, но по мере увеличения числа наблюдений всё яснее проявляется определенная закономерность. Наши предки понимали, что у десятка охотников вероятность поразить животное на охоте больше, чем у одного; вероятность благополучно переправиться на противоположный берег реки через брод выше, чем в глубоководном ее месте и т.д. Позднее, на основе наблюдения и опыта, человек стал оценивать случайные события, классифицировать их исходы как невозможные, возможные и достоверные. Он заметил, что случайностями не так уж редко управляют объективные закономерности.

По мере усложнения производственных и общественных отношений все чаще приходилось пользоваться понятиями о порядке, иерархии, группировании.

В пирамиде, где был похоронен египетский фараон Тутанхамон, нашли разграфленную доску с тремя горизонталями и 10 вертикалями и фигурки для древней игры ''сенет'', правило которой мы, вероятно, никогда не узнаем. Позже появились нарды, шашки и шахматы, а также их различные варианты (китайские и японские шахматы, японские облавные шашки ''го'' и т. д.). В каждой из этих игр приходилось рассматривать различные сочетания передвигаемых фигур, и выигрывал тот, кто их лучше заучил.

В китайских рукописях, относящихся к XII-XIII вв. до н.э. встречаются упоминания о вопросах, близких к комбинаторным (точно датировать эти рукописи невозможно, поскольку в 213 г. до н.э. император Цинн Ши-Хуан приказал сжечь все книги, так что до нас дошли сделанные позднее копии). В этих книгах писалось, что все в мире является сочетанием двух начал – мужского и женского, которое авторы обозначали символами -- и ----. В рукописи ''Же Ким'' (''Книга перестановок'') показаны различные соединения этих знаков по два и по три.

Восемь рисунков из трех рядов символов изображали землю, горы, воду, ветер, грозу, огонь, облака и небо (некоторые рисунки имели и иные значения). Неудивительно поэтому, что сумма первых 8 натуральных чисел (т. е. число 36) воплощала в представлениях древних китайцев весь мир.

Понадобилось выразить по мере углубления знаний и другие элементы мироздания с помощью тех же знаков -- и -- --. Были составлены 64 фигуры, содержавшие уже пять рядов черточек. Надо полагать, что автор рукописи ''Же Ким'' заметил удвоенные числа рисунков при добавлении одного ряда символов. Это можно рассматривать как первый общий результат комбинаторики.

В 391 г. н. э. толпа монахов разрушила центр языческой науки александрийский Музеум – и сожгла большую часть хранившейся в нем библиотеки, насчитывавшей многие тысячи томов. Остатки библиотеки разрушались в течение еще трех веков, а в 638 г. н.э. она окончательно погибла при взятии Александрии войсками арабского халифа Омара, и поэтому большинство научных книг безвозвратно погибло, и мы можем лишь догадываться об их содержании по кратким пересказам и намекам в сохранившихся рукописях. По этим намекам можно все же судить, что определенные представления о комбинаторике у греческих ученых были. Философ Ксенократ, живший в IV в. до н.э., подсчитывал число слогов. В III в. до н.э. историк Хрисии полагал, что число утверждений, получаемых из 10 аксиом, превышает миллион. По мнению же Гиппарха, из утверждающих аксиом можно составить 103 049 сочетаний, а добавив к ним отрицающие, 310 952. Мы не знаем, какой именно смысл придавали эти философы своим утверждениям и как они получали свои результаты – приводимые Гиппархом результаты слишком точны, чтобы считать их результатом грубой оценки, и в то же время не поддаются разумному истолкованию. По-видимому, у греческих ученых были какие-то, не дошедшие до нас правила комбинаторных расчетов – скорее всего ложные.

Конкретные комбинаторные задачи, касавшиеся перечисления небольших групп предметов, греки решали без ошибок. Аристотель описал без пропусков все виды правильных трехчленных силлогизмов, а его ученик Арисксен из Тарента перечислил различные комбинации длинных и коротких слогов в стихотворных размерах. Живший в IV в. н.э. математик Папп рассматривал число пар и троек, которые можно получить из трех элементов, допуская их повторения.

Греческие ученые уделяли большое внимание вопросам, пограничным между комбинаторикой и теорией чисел. Еще в VI в. до н.э. в школе философа-идеалиста математика Пифагора возникло убеждение, что миром правят числа, а вещи только отражение чисел. Пифагорейцы начали изучать свойства натуральных чисел. Их исследования о четных и нечетных числах, делимости чисел, простых и составных числах положили основу теории чисел. Как и китайцы, пифагорейцы придавали особое внимание числу 36 – оно было для них не только суммой первых 4 четных и первых 4 нечетных чисел, но и суммой первых трех кубов: 36 = . Символом совершенства пифагорейцы считали совершенные числа, равные сумме своих делителей, например, 6 = 1 + 2 + 3, 28 = 1 + 2 + 4 + 7 + 14, а символом дружбы – дружественные числа, каждое из которых равно сумме делителей другого (например, 220 и 284). Отыскание таких чисел требовало комбинаторного искусства.

Доказательство известной теоремы о сторонах прямоугольного треугольника вызвало интерес к представлению чисел в виде суммы двух квадратов, к квадратным числам 1, 4, 0, 10 и т. д. Квадраты натуральных чисел изображались при этом геометрически. Пифагорейцы рассматривали и иные конфигурации точек, такие, как изображены на рисунке (рисунок). Каждый треугольник на рисунке получается из предыдущего увеличением длины его стороны на 1. Подсчитывая число точек в каждом треугольнике, получаем последовательность треугольных чисел: 1, 3, 6, 10 …. Эти числа можно получить, последовательно складывая натуральные числа. Точно так же шестиугольники приводят к последовательности шестиугольных чисел 1, 0, 15… получаемой при последовательном суммировании арифметической прогрессии 1+ 5+ 9+ … В дальнейшем такие суммы удалось выразить с помощью биноминальных коэффициентов, играющих важную роль в комбинаторике.

Магические тайны учения и обряды возникли среди фанатичных иудаистов - сторонников колдовства и магии, проповедовавших культ единого бога. Библия была провозглашена собранием божественных откровений, где каждому слову и числу придавалось особое мистическое значение. В каббалистических вычислениях евреев распространено изучение священных текстов и отдельных слов заменой букв числами. Для латинской азбуки: a = 1, b = 2 c = 3, d = 4… В имени богослова Johanes Huss (Иоганн Гусс)после такой замены букв числами получалась общая сумма «очков», равная 145. На эту сумму надо было подобрать другие слова, отражающие внутреннюю духовную сущность человека. Это магическое действие в каббалистике называется гематрией. Задача не из простых, на поиск таких бесплодных решений нередко тратились годы, а то и жизнь. В нашем примере имени Иоганн Гусс соответствуют слова: sermo domini dei и суммы цифр: 18+ 5+ 17+ 12+ 14 = 66; 4+ 14+ 12+ 9+ 13+ 9 = 61; 4+ 5+ 9 = 18, что в целом равно 145 и в точности соответствует исходной сумме очков. В переводе три латинских слова означают: ''Слово Господа Бога''. Итак, получилось: ''Иоганн Гусс = слово Господа Бога'' – смысл найден.

Упадок науки в эллинистических странах, отражавший общий кризис рабовладельческого общества, начинается со II в. до н.э. Многие работы того времени были посвящены мистическим толкованиям чисел в духе пифагорейцев (например, ''Арифметическая теология'' неопифагорейца Никомаха, жившего в I-II вв. н.э.). Большое развитие получили различные числовые суеверия и толкования, связанные с заменой букв соответствующими числами (греки обозначали числа с помощью букв – первые 9 букв алфавита обозначали числа от 1 до 9, следующие за ними – от 10 до 90, а последние 9 букв – от 100 до 900). Были ''ученые'', называвшиеся каббалистами, которые подвергали такому ''анализу'' слова Библии и других священных книг и делали на основе своих изысканий пророчества о будущем мира.

Не чуждался каббалистических вычислений и известный немецкий математик, монах ордена св. Августина Михаэль Штифель (1468 – 1567). Он применил каббалистику к имени тогдашнего папы римского Льва X, спекулировавшего индульгенциями, и сделал поразительное открытие: католический папа и есть апокалипсический зверь, ведь его имени соответствует число 666. Поисками смысла, заключенного в числе 666, занимался и Исаак Ньютон (1643 – 1727), в конце своей жизни написавший сочинение о пророке Данииле. Мания числа 666 веками использовалась не только для идеологической борьбы с неугодными людьми, но и в борьбе целых религиозных течений.

В Россию числовая мистика проникла из Византии. Православное духовенство неоднократно запрещало сочинения по астрономии и геометрии, не делая строгого различия между действительными и ложными знаниями. Тем не менее тайные науки продолжали существовать, о чем можно судить по широко распространенному в народе взгляду на Петра I как на Антихриста – его число тоже 666.

Астрологи также занимались комбинаторикой. Их интересовал вопрос о движении планет и их влиянии на судьбы людей. Особое значение придавали они сочетаниям планет – встречам различных планет в одном знаке зодиака. Астролог Бен Эзра в 1140 г. рассчитал количество сочетаний семи планет по две, по три и т. д. Он знал, что число сочетаний планет по три равно числу сочетаний по четыре. В окончательном виде формулу для числа сочетаний получил живший в XIV веке Л. Гершон, доказавший, что

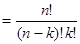
Эту формулу в начале XVII в. вывел французский математик П. Эригон.

Комбинаторные проблемы лишь затрагивались в общих трудах по астрологии, логике и математике, а большей частью относились к области математических развлечений, то уже в 1666 г. Г. В. Лейбниц публикует ''Диссертацию о комбинаторном искусстве'', в которой впервые появляется сам термин ''комбинаторный''. Титульный лист книги двадцатилетнего автора, имевшего уже ученую степень бакалавра… юриспруденции, обещал приложения ко всем областям науки и новый подход к логике изобретения, а тематика введения могла соперничать по своей широте с программой, которую, как свидетельствует Льюис Кэрролл, наметил Плотник для бесед с устрицами. Там провозглашалось приложение теории к замкам, органам, силлогизмам, смешению цветов и стихосложению, к логике, геометрии, военному искусству, грамматике, юриспруденции, медицине и теологии.

Диссертация Г.В.Лейбница должна была стать лишь началом большой работы, о которой он часто упоминал в своих письмах и печатных трудах и для которой делал в своих записных книжках многочисленные заметки. Из них видно, что Лейбниц планировал для комбинаторики все новые и новые приложения: к кодированию и декодированию, играм, статистике, теории наблюдений. Он считал, что комбинаторика должна заниматься одинаковым и различным, похожим и непохожим, абсолютным и относительным расположением, в то время как обычная математика занимается большим и малым, единицей и многим, целым и частью. Иными словами, под комбинаторикой Лейбниц понимал примерно то, что мы теперь называем дискретной математикой. К области комбинаторики Г.В.Лейбниц относил и ''универсальную характеристику'' – математику суждений, т. е. прообраз нынешней математической логики.

Проекты Г.В.Лейбница казались несбыточными здравомыслящим математикам его времени, но сейчас, после создания быстродействующих вычислительных устройств, многие планы Г.В.Лейбница стали претворяться в жизнь, а дискретная математика выросла в своем значении настолько, что начала соперничать с классическим математическим анализом.

В 1713 г. была опубликована книга ''Искусство предположений'' Якоба Бернулли, в которой указывались формулы для числа размещений из n элементов по k, выводились выражения для степенных сумм и т. д.

Таким образом, как наука теория вероятностей зародилась в XVII в. «Математика случая» − так назвал теорию вероятностей один из ее основателей французский ученый Б.Паскаль. Возникновение понятия «вероятности» было связано как с потребностями страхования, получившего значительное распространение в ту эпоху, когда заметно росли торговые связи и морские путешествия, так и в связи с развитием азартных игр, популярных в ту пору среди знати, феодалов и дворян. Слово «азарт», под которым обычно понимается сильное увлечение, горячность, является транскрипцией французского слова «hazard», означающего «случай», «риск». Азартными называют те игры, в которых выигрыш зависит не только и не столько от умения игрока, но и от случайности. Особенно распространенной была игра в кости. Было замечено, что при многократном бросании однородного кубика (все шесть граней которого отмечены соответственно числами 1, 2, 3, 4, 5, 6) число очков от 1 до 6 выпадают в среднем одинаково часто, иными словами, выражаясь языком математики, выпадение определённого числа очков имеет вероятность, равную 1/6. Аналогично вероятность появления на верхней грани кости чётного числа очков равна 3/6, так как из шести равновозможных случаев чётное число появляется только в трёх.

Схема азартных игр была очень проста и могла быть подвергнута всестороннему логическому анализу. Первые попытки этого рода связаны с именами известных учёных - алгебраиста Д. Кардана (1501 − 1576) и Г. Галилея (1564 − 1642). Однако открытие этой теории, которая не только даёт возможность сравнивать случайные величины, но и производить определенные математические операции с ними, принадлежит двум выдающимися ученым − Блезу Паскалю (1623 − 1662) и Пьеру Ферма(1601 − 1665).

Один из представителей французской знати того времени, страстный игрок де Мере написал Б.Паскалю письмо, в котором просил ответить на ряд вопросов. Денежный выигрыш при игре в кости обычно зависит от комбинации выпавших чисел, на которую делаются ставки. Одна из таких комбинаций − выпадение хотя бы одной шестёрки при четырёх бросаниях игральной кости. Де Мере смог подсчитать число шансов этой комбинации. Более сложные комбинации возникали, если бросали сразу две кости. Де Мере пытался определить, сколько раз надо бросить пару костей, чтобы вероятность хотя бы одного появления двух шестёрок была больше 1/2. Он подсчитал, что достаточно 24 бросаний. Однако опыт игрока заставил де Мере сомневаться в правильности своих вычислений. Тогда он и обратился с этой задачей к математику Б.Паскалю, который предложил правильное решение. Эта задача кавалера де Мере заставила Б.Паскаля заняться изучением случайных событий. А в переписке Б.Паскаля и П.Ферма впервые стали упоминаться понятия теории вероятностей.

Подсчёт всех возможных и благоприятствующих данному событию случаев нередко представляет большие трудности. Вот почему для решения таких задач некоторые игроки обращались к крупным учёным. Х.Гюйгенсу был задан такой вопрос: «Если бросить одновременно три игральных кости, то какая сумма очков будет выпадать чаще − 11 или 12?» Подсчёт всех различных случаев здесь прост: N=63=216, но сумма 11 может получиться следующими шестью различными способами: 1+4+6, 1+5+5, 2+3+6, 2+4+5, 3+3+5, 3+4+4. Также шестью различными способами образуется сумма 12: 1+5+6, 2+4+6, 2+5+5, 3+3+6, 3+4+5, 4+4+4. Это обстоятельство наводит на мысль, что обе суммы должны появляться одинаково часто. Однако это не так. Было замечено, что сумма 11 появляется чаще суммы 12. Дело в том, что вышеуказанные суммы по три числа сами по себе неодинаково часто выпадают. Так, если каждую из трех костей окрасить по-разному, скажем, в белый, красный и зелёный цвет, то становится ясным, что сочетание, в котором имеются три различных слагаемых, например (1+4+6), может получаться шестью различными способами:

1) 1 бел. + 4 красн. + 6 зел.; 2) 1 бел. + 6 красн. + 4 зел.;

3) 4 бел. + 1 красн. + 6 зел.; 4) 4 бел. + 6 красн. + 1 зел.;

5) 6 бел. + 1 красн. + 4 зел.; 6) 6 бел. + 4 красн. + 1 зел.

Аналогично сочетание с двумя одинаковыми слагаемыми, например (2+5+5), может получиться тремя различными способами, в то время как сочетания с одинаковыми слагаемыми, вроде (4+4+4), получается единственным способом. И вот для 11 очков мы получим, таким образом, не шесть различных способов, а 1×6 + 1×3 + 1×6 + 1×6 + 1×3 + 1×3 = 27. Аналогично, для суммы же 12 число различных способов будет равно 25.

Решение порой довольно сложных задач, с которыми обращались заинтересованные лица к Б.Паскалю, П.Ферма, Х.Гюйгенсу, способствовало разработке основных понятий и общих принципов теории вероятностей. Азартные игры стали для ученых удобной моделью для решения задач и анализа понятий данной теории. Об этом говорил ещё Х.Гюйгенс в своей книге «De ratiociniis ludo alleae» («О расчётах в азартной игре», 1657), которая была первой книгой в мире по теории вероятностей. Он писал: «При внимательном изучении предмета читатель заметит, что он занимается не только игрой, а что здесь даются основы глубокой и весьма интересной науки». Х.Гюйгенс впервые ввёл важное для теории вероятностей понятие математического ожидания, которое получило дальнейшее развитие в трудах Д. Бернулли, Даламбера и др. На развитие теории вероятностей оказали серьёзное влияние потребности науки и запросы практики, в первую очередь страховое дело, начатое в некоторых странах ещё в XVI в.

Таким образом, в 60-е годы XVII в. были выработаны первые понятия и некоторые элементы теории вероятностей.

Следующий этап истории теории вероятностей (XVIII − начало XIX вв.) связан, главным образом, с именами французских математиков А.Муавром (1667 − 1754), П.Лапласом (1749 − 1827), С.Пуассоном (1781 − 1840) и А.Лежандром (1752 − 1833) и немецкого математика К.Гаусса (1777 − 1855). «Аналитическая теория вероятностей» П.Лапласа считается классическим трудом по данному разделу математики. В это время в теории вероятностей, кроме понятия случайного события, рассматривается и понятие случайной величины. Теория вероятностей начала применяться в теории ошибок измерений, теории стрельбы и т.п.

В конце XVIII в. немецкий ученый Гинденбург и его ученики сделали даже попытку построить общую теорию комбинаторного анализа. Однако она не увенчалась успехом – в то время еще не было накоплено достаточного количества важных и интересных задач, которые могли бы дать необходимый фундамент для такой теории.

В середине XIX в. преподаватель Высшей реальной школы города Брюнн Г.И.Мендель производил опыты с горохом, в результате которых были открыты законы наследственности. Ученый скрестил два сорта гороха с жёлтыми и зелёными семенами, после чего растения дали только желтые семена (первое поколение гибридов). После самоопыления растений, выращенных из этих семян (второе поколение гибридов), появился горох и с жёлтыми, и с зелёными семенами. Мендель подсчитал, что отношение числа растений с жёлтыми семенами к числу растений с зелеными семенами равно 3,01. Механизм наследования так же случаен, как и исход бросания монеты или игральной кости.

В ХХ веке произошло строгое логическое обоснование теории вероятностей советским математиком А.Н.Колмогоровым.

Современный период истории теории вероятностей характеризуется возникновением и развитием многих новых областей и направлений. Наряду с понятием случайного события и случайной величины рассматриваются и играют наиболее существенную роль понятия случайной функции и случайного процесса. Круг применения теории вероятностей в различных областях науки и техники расширился настолько, что сейчас ее по праву можно считать одной из наиболее прикладных частей математики. Методы теории вероятностей широко применяются в различных отраслях техники и естествознания: в теории надёжности, теории массового обслуживания, в теоретической физике, геодезии, астрономии, теории стрельбы, теории ошибок наблюдений, теории автоматического управления, общей теории связи и во многих других теоретических и прикладных науках.

Теория вероятностей служит также для обоснования математической и прикладной статистики, которая используется при планировании и организации производства, при анализе технологических процессов, предупредительном и приёмочном контроле качества продукции и для многого другого.

Комбинаторика это большой и важный раздел математики, изучающий множества целых чисел и перестановки внутри этих множеств. Комбинаторика имеет огромное значение для многих сфер человеческой деятельности.

Многие специалисты в области математики и физики считают, что именно комбинаторная задача может стать толчком в развитии всех технических наук. Достаточно лишь нестандартно подойти к решению тех или иных проблем, и тогда можно будет ответить на вопросы, которые уже несколько веков не дают покоя ученым. Некоторые из них всерьез утверждают, что комбинаторика является подспорьем для всех современных наук, особенно космонавтики. Намного проще будет высчитывать траектории полета кораблей с помощью комбинаторных задач, также они позволят определить точное нахождение тех или иных небесных светил. Реализация нестандартного подхода уже давно началась в азиатских странах, там ученики даже элементарные задачи по умножению, вычитанию, сложению и делению решают, используя комбинаторные методы. На удивление многих европейских ученых, методика действительно работает. Школы Европы пока что только начали перенимать опыт своих коллег. Когда именно комбинаторика станет одним из основных разделов математики, предположить сложно. Сейчас наука изучается ведущими учеными планеты, которые стремятся популяризировать ее.

Ссылки:

http://www.edubrilliant.ru/brigens-345-1.html

http://e-science.ru/node/106887

http://yandex.ru/clck

http://fb.ru/article/149409/kombinatornaya-zadacha-prosteyshie-kombinatornyie-zadachi-kombinatornyie-zadachi-primeryi

infourok.ru

Реферат по математике на тему "Комбинаторика"

Реферат

По дисциплине: Математика

„ Комбинаторика “

Комбинаторика

Комбинаторика (Комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка). Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей и имеет широкий спектр применения в различных областях знаний (например, в генетике, информатике, статистической физике).

Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».

Иногда под комбинаторикой понимают более обширный раздел дискретной математики, включающий, в частности, теорию графов.

Примеры комбинаторных конфигураций и задач

Для формулировки и решения комбинаторных задач используют различные модели комбинаторных конфигураций. Примерами комбинаторных конфигураций являются:

• Размещением из n элементов по k называется упорядоченный набор из k различных элементов некоторого n-элементного множества.

• Перестановкой из n элементов (например, чисел 1,2,…,n) называется всякий упорядоченный набор из этих элементов. Перестановка также является размещением из n элементов по n.

• Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.

• Композицией числа n называется всякое представление n в виде упорядоченной суммы целых положительных чисел.

• Разбиением числа n называется всякое представление n в виде неупорядоченной суммы целых положительных чисел.

Примеры комбинаторных задач:

1. Сколькими способами можно разместить n предметов по m ящикам, чтобы выполнялись заданные ограничения?

2. Сколько существует функций 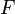из m-элементного множества в n-элементное, удовлетворяющих заданным ограничениям?

3. Сколько существует различных перестановок из 52 игральных карт?

Ответ: 52! (52 факториал), то есть, 80658175170943878571660636856403766975289505440883277824000000000000 или примерно 8,0658 × 1067.

4. При игре в кости бросаются две кости, и выпавшие очки складываются; сколько существует комбинаций, в которых сумма очков на верхних гранях равна двенадцати?

Решение: Каждый возможный исход соответствует функции 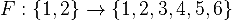(аргумент функции — это номер кости, значение — очки на верхней грани). Очевидно, что лишь 6+6 даёт нам нужный результат 12. Таким образом, существует лишь одна функция, ставящая в соответствие 1 число 6, и 2 число 6. Или, другими словами, существует всего одна комбинация, при которой сумма очков на верхних гранях равна двенадцати.

Разделы комбинаторики

Перечислительная комбинаторика

Перечислительная комбинаторика (или исчисляющая комбинаторика) рассматривает задачи о перечислении или подсчёте количества различных конфигураций (например, перестановок) образуемых элементами конечных множеств, на которые могут накладываться определённые ограничения, такие как: различимость или неразличимость элементов, возможность повторения одинаковых элементов и т. п.

Количество конфигураций, образованных несколькими манипуляциями над множеством, подсчитывается согласно правилам сложения и умножения.

Типичным примером задач данного раздела является подсчёт количества перестановок. Другой пример — известная Задача о письмах.

Структурная комбинаторика

К данному разделу относятся некоторые вопросы теории графов, а также теории матроидов.

Экстремальная комбинаторика

Примером этого раздела может служить следующая задача: какова наибольшая размерность графа, удовлетворяющего определённым свойствам.

Теория Рамсея

Теория Рамсея изучает наличие регулярных структур в случайных конфигурациях элементов. Примером утверждения из теории Рамсея может служить следующее:

в группе из 6 человек всегда можно найти трёх человек, которые либо попарно знакомы друг с другом, либо попарно незнакомы.

В терминах структурной комбинаторики это же утверждение формулируется так:

в любом графе с 6 вершинами найдётся либо клика, либо независимое множество размера 3.

Вероятностная комбинаторика

Этот раздел отвечает на вопросы вида: какова вероятность присутствия определённого свойства у заданного множества.

Топологическая комбинаторика

Топологическая комбинаторика (англ.) применяет идеи и методы комбинаторики в топологии, при изучении дерева принятия решений, частично упорядоченных множеств, раскрасок графа и др.

Инфинитарная комбинаторика

Инфинитарная комбинаторика (англ.) — применение идей и методов комбинаторики к бесконечным (в том числе, несчётным) множествам.

Открытые проблемы

Комбинаторика, и в частности, теория Рамсея, содержит много известных открытых проблем, подчас с весьма несложной формулировкой. Например, неизвестно, при каком наименьшем N в любой группе из N человек найдутся 5 человек, либо попарно знакомых друг с другом, либо попарно незнакомых (хотя известно, что 49 человек достаточно).[1]

Исторический очерк

Джероламо Кардано написал математическое исследование игры в кости, опубликованное посмертно. Теорией этой игры занимались также Тарталья и Галилей. В историю зарождавшейся теории вероятностей вошла переписка заядлого игрока шевалье де Мерэ с Пьером Ферма и Блезом Паскалем, где были затронуты несколько тонких комбинаторных вопросов. Помимо азартных игр, комбинаторные методы использовались (и продолжают использоваться) в криптографии — как для разработки шифров, так и для их взлома.

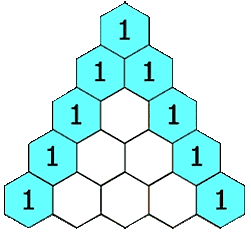
Треугольник Паскаля

Блёз Паскаль много занимался биномиальными коэффициентами и открыл простой способ их вычисления: «треугольник Паскаля». Хотя этот способ был уже известен на Востоке (примерно с X века), Паскаль, в отличие от предшественников, строго изложил и доказал свойства этого треугольника. Наряду с Лейбницем, он считается основоположником современной комбинаторики. Сам термин «комбинаторика» придумал Лейбниц, который в 1666 году (ему было тогда 20 лет) опубликовал книгу «Рассуждения о комбинаторном искусстве». Правда, термин «комбинаторика» Лейбниц понимал чрезмерно широко, включая в него всю конечную математику и даже логику. Ученик Лейбница Якоб Бернулли, один из основателей теории вероятностей, изложил в своей книге «Искусство предположений» (1713) множество сведений по комбинаторике.

В этот же период формируется терминология новой науки. Термин «сочетание» (combination) впервые встречается у Паскаля (1653, опубликован в 1665 году). Термин «перестановка» (permutation) употребил в указанной книге Якоб Бернулли (хотя эпизодически он встречался и раньше). Бернулли использовал и термин «размещение» (arrangement).

После появления математического анализа обнаружилась тесная связь комбинаторных и ряда аналитических задач. Абрахам де Муавр и Джеймс Стирлинг нашли формулы для аппроксимации факториала.

Окончательно комбинаторика как самостоятельный раздел математики оформилась в трудах Эйлера. Он детально рассмотрел, например, следующие проблемы:

Кроме перестановок и сочетаний, Эйлер изучал разбиения, а также сочетания и размещения с условиями.

Комбинаторика в языкознании

Комбинаторика (языкознание) — это свойство единиц языка и соответствующих им единиц речи вступать в синтагматические отношения, то есть в отношения сочетаемости.

Литература

• Андерсон Джеймс. Дискретная математика и комбинаторика = Discrete Mathematics with Combinatorics. — М.: «Вильямс», 2006. — С. 960. — ISBN 0-13-086998-8.

• Виленкин Н.Я. Популярная комбинаторика. — М.: Наука, 1975.

• Ерош И. Л. Дискретная математика. Комбинаторика — СПб.: СПбГУАП, 2001. — 37 c.

• Липский В. Комбинаторика для программиста. — М.: Мир, 1988. — 213 с.

• Раизер Г. Дж. Комбинаторная математика. — пер. с англ. — М., 1966.

• Райгородский А. М. Линейно-алгебраические и вероятностные методы в комбинаторике. — Летняя школа «Современная математика». — Дубна, 2006.

• Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы. Теория и практика. — М.: Мир, 1980. — 476 с.

• Риордан Дж. Введение в комбинаторный анализ — пер. с англ. — М., 1963.

• Р. Стенли. Перечислительная комбинаторика = Enumerative Combinatorics. — М.: «Мир», 1990. — С. 440. — ISBN 5-03-001348-2.

• Р. Стенли. Перечислительная комбинаторика. Деревья, производящие функции и симметрические функции = Enumerative Combinatorics. Volume 2. — М.: «Мир», 2009. — С. 767. — ISBN 978-5-03-003476-8.

infourok.ru

Реферат - Комбинаторика - Математика

/>Реферат на тему:

/>

Выполнилученик 10 класса «В»

среднейшколы №53

ГлуховМихаил Александрович

г. Набережные Челны

2002 г. Содержание

Из истории комбинаторики

Комбинаторика занимается различного вида соединениями,которые можно образовать из элементов конечного множества. Некоторые элементыкомбинаторики были известны в Индии еще во II в. до н. э. Нидийцы умеливычислять числа, которые сейчас называют «сочетания». В XII в.Бхаскара вычислял некоторые виды сочетаний и перестановок. Предполагают, чтоиндийские ученые изучали соединения в связи с применением их в поэтике, науке оструктуре стиха и поэтических произведениях. Например, в связи с подсчетомвозможных сочетаний ударных (долгих) и безударных (кратких) слогов стопы из nслогов. Как научная дисциплина, комбинаторика сформировалась в XVII в. В книге«Теория и практика арифметики» (1656 г.) французский автор А. Такжепосвящает сочетаниям и перестановкам целую главу. Б. Паскаль в «Трактате об арифметическом треугольнике» и в«Трактате о числовых порядках» (1665 г.) изложил учение обиномиальных коэффициентах. П. Ферма знал о связях математических квадратов и фигурныхчисел с теорией соединений. Термин "комбинаторика"стал употребляться после опубликования Лейбницем в 1665 г. работы«Рассуждение о комбинаторном искусстве», в которой впервые данонаучное обоснование теории сочетаний и перестановок. Изучением размещенийвпервые занимался Я. Бернулли во второй части своей книги «Arsconjectandi» (искусство предугадывания) в 1713 г. Современная символикасочетаний была предложена разными авторами учебных руководств только в XIX в.

Все разнообразие комбинаторных формул может бытьвыведено из двух основных утверждений, касающихся конечных множеств – правилосуммы и правило произведения.

Правило суммы

Если конечные множества не пересекаются, то число элементов X U Y{или} равно сумме числа элементов множества X и числа элементов множества Y.

То есть, если на первойполке стоит X книг, а на второй Y, то выбрать книгу из первой или второй полки,можно X+Y способами.

Ученик должен выполнить практическую работу по математике. Емупредложили на выбор 17 тем по алгебре и 13 тем по геометрии. Сколькимиспособами он может выбрать одну тему для практической работы?

Решение: X=17, Y=13

По правилу суммы X U Y=17+13=30 тем.

Имеется 5 билетов денежно-вещевой лотереи, 6 билетов спортлото и 10билетов автомотолотереи. Сколькими способами можно выбрать один билет изспортлото или автомотолотереи?

Решение: Так как денежно-вещевая лотерея в выборе не участвует, товсего 6+10=16 вариантов.

Если элемент X можно выбрать k способами, а элемент Y-m способамито пару (X,Y) можно выбрать k*m способами.

То есть, если на первой полке стоит 5 книг, а на второй 10, то выбратьодну книгу с первой полки и одну со второй можно 5*10=50 способами.

Решение: Имеется 12 книг и 3 цвета, значит по правилу произведениявозможно 12*3=36 вариантов переплета.

Сколько существует пятизначных чисел, которые одинаково читаются слеванаправо и справа налево?

Решение: В таких числах последняя цифра будет такая же, как и первая, апредпоследняя — как и вторая. Третья цифра будет любой. Это можно представить ввиде XYZYX, где Y и Z -любые цифры, а X — не ноль. Значит по правилупроизведения количество цифр одинаково читающихся как слева направо, так исправа налево равно 9*10*10=900 вариантов.

Пересекающиеся множества

Но бывает, что множества X и Yпересекаются, тогда пользуются формулой/>,где X и Y — множества, а /> - область пересечения.

/>Примеры задач

20 человек знают английский и 10 — немецкий,из них 5 знают и английский,и немецкий. Сколько Человек всего?

Ответ: 10+20-5=25 человек.

Также часто для наглядного решения задачи применяются круги Эйлера.Например:

/>Из100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют30 человек, английским — 28, французским — 42. Английским и немецким одновременновладеют 8 человек, английским и французским — 10, немецким и французским — 5,всеми тремя языками — 3. Сколько туристов не владеют ни одним языком?

 Решение: Выразим условие этой задачи графически. Обозначимкругом тех, кто знает английский, другим кругом — тех, кто знает французский, итретьим кругом — тех, кто знают немецкий.

/>Всеми тремя языками владеют три туриста, значит, в общейчасти кругов вписываем число 3. Английским и французским языком владеют 10человек, а 3 из них владеют еще и немецким. Следовательно, только английским ифранцузским владеют 10-3=7 человек.

Аналогично получаем, что только английским и немецким владеют 8-3=5 человек, а немецким и французским 5-3=2 туриста. Вносим этиданные в соответствующие части.

/>Определим теперь, сколько человек владеют только одним изперечисленных языков. Немецкий знают 30 человек, но 5+3+2=10 из них владеют идругими языками, следовательно, только немецкий знают 20 человек. Аналогичнополучаем, что одним английским владеют 13 человек, а одним французским — 30 человек.

По условию задачи всего 100 туристов. 20+13+30+5+7+2+3=80 туристовзнают хотя бы один язык, следовательно, 20 человек не владеют ни одним изданных языков.

Размещениябез повторений.

Сколько можносоставить телефонных номеров из 6 цифр каждый, так чтобы все цифры былиразличны?

Это пример задачи на размещениебез повторений. Размещаются здесь 10 цифр по 6. А варианты, при которыходинаковые цифры стоят в разном порядке считаются разными.

Если X-множество, состоящие из nэлементов, m≤n, то размещением без повторений из n элементов множества Xпо m называется упорядоченное множество X, содержащее m элементов называетсяупорядоченное множество X, содержащее m элементов.

Количество всех размещений из n элементов по mобозначают

/>

n! — n-факториал (factorial анг. сомножитель) произведениечисел натурального ряда от 1 до какого либо числа n

n!=1*2*3*...*n       0!=1

Значит, ответ на вышепоставленную задачу будет

/>

Задача

Сколькими способами 4 юноши могут пригласить четырех изшести девушек на танец?

Решение: два юноши не могут одновременно пригласить одну и туже девушку. И варианты, при которых одни и те же девушки танцуют с разнымиюношами считаются, разными, поэтому:

/> 

Возможно 360 вариантов.

Перестановки без повторений

В случаеn=m (см. размещения без повторений) из n элементов по m  называется перестановкоймножества x.

Количествовсех перестановок из n элементов обозначают Pn.

Pn=n!

Действительно при n=m:

/>

Примеры задач

Сколькоразличных шестизначных чисел можно составить из цифр 0, 1, 2, 3, 4,5, еслицифры в числе не повторяются?

Решение:

1)      Найдемколичество всех перестановок из этих цифр: P6=6!=720

2)      0 не можетстоять впереди числа, поэтому от этого числа необходимо отнять количествоперестановок, при котором 0 стоит впереди. А это P5=5!=120.

P6-P5=720-120=600

Квартет

ПроказницаМартышка

Осел,

Козел,

Дакосолапый Мишка

Затеялииграть квартет

…

Стой,братцы стой! –

КричитМартышка, — погодите!

Какмузыке идти?

Ведь выне так сидите…

И так, и этакпересаживались – опять музыка на лад не идет.

Тут пущепрежнего пошли у низ раздоры

И споры,

Кому икак сидеть…

Вероятно,крыловские музыканты так и не перепробовали всех возможных мест. Однако способовне так уж и много. Сколько?

Здесь идетперестановка из четырех, значит, возможно

P4=4!=24варианта перестановок.

Сочетаниябез повторений

Сочетанием безповторений называется такое размещение, при котором порядок следования элементовне имеет значения.

Всякоеподмножество X состоящее из m элементов, называется сочетанием из n элементовпо m.

Таким образом,количество вариантов при сочетании будет меньше количества размещений.

Число сочетанийиз n элементов по m обозначается />.

/>.

Примеры задач

/>Сколькотрехкнопочных комбинаций существует на кодовом замке (все три кнопки нажимаютсяодновременно), если на нем всего 10 цифр.

Решение:

Так как кнопкинажимаются одновременно, то выбор этих трех кнопок – сочетание. Отсюда возможно/>вариантов.

У одногочеловека 7 книг по математике, а у второго – 9. Сколькими способами они могутобменять друг у друга две книги на две книги.

Решение:

Так как надо порядок следования книг не имеет значения, то выбор 2ух книг — сочетание. Первый человек может выбрать 2 книги />/> способами. Второй человек можетвыбрать 2 книги />. Значит всего поправилу произведения возможно 21*36=756 вариантов.

При игре вдомино 4 игрока делят поровну 28 костей. Сколькими способами они могут это сделать?

Первый игрокделает выбор из 28 костей. Второй из 28-7=21 костей, третий 14, а четвертыйигрок забирает оставшиеся кости. Следовательно, возможно />.Размещения и сочетания с повторениями

Часто взадачах по комбинаторике встречаются множества, в которых какие-либо компонентыповторяются. Например: в задачах на числа – цифры. Для таких задач приразмещениях используется формула />, а длясочетаний />.

Примеры задач

Сколькотрехзначных чисел можно составить из цифр 1, 2, 3, 4, 5?

Решение.Так как порядок цифр в числе существенен, цифры могут повторяться, то это будутразмещения с повторениями из пяти элементов по три, а их число равно />.

Вкондитерском магазине продавались 4 сорта пироженных: эклеры, песочные,наполеоны и слоеные. Сколькими способами можно купить 7 пироженных.

Решение:Покупка не зависит от того, в каком порядке укладывают купленные пироженные в коробку.Покупки будут различными, если они отличаются количеством купленных пирожныххотя бы одного сорта. Следовательно, количество различных покупок равно числусочетаний четырех видов пироженных по семь — />.

Обезьянупосадили за пишущую машинку с 45 клавишами, определить число попыток, необходимыхдля того, чтобы она наверняка напечатала первую строку романа Л.Н. Толстого«Анна Каренина», если строка содержит 52 знака и повторений не будет?

Решение:порядок букв имеет значение. Буквы могут повторяться. Значит, всего есть /> вариантов.

Перестановки сповторениями

/>/>,где n-количество всех элементов, n1,n2,…,nr-количествоодинаковых элементов.

Примеры задач

Сколькимиспособами можно переставить буквы слова «ананас»?

Решение:всего букв 6. Из них одинаковы n1«а»=3, n2«н»=2, n3«с»=1.Следовательно, число различных перестановок равно />.

/>Задачи для самостоятельного решения

Сколько перестановок можно сделать из букв слова«Миссисипи».

Ответ: 2520

  Имеется пять различных стульев и семь рулонов обивочнойткани различных цветов. Сколькими способами можно осуществить обивку стульев.

Ответ: 16807

На памятныесувениры в «Поле Чудес» спонсоры предлагают кофеварки, утюги, телефонныеаппараты, духи. Сколькими способами 9 участников игры могут получить эти сувениры?Сколькими способами могут быть выбраны 9 предметов для участников игры?

Ответ: 49, 220

Сколькимиспособами можно расставить на шахматной доске 8 ладей так, чтобы на одна из нихне могла бить другую?

Ответ: 40320

Сколько можетбыть случая выбора 2 карандашей и 3 ручек из пяти различных карандашей и шестиразличных ручек?

Ответ:200

Сколькоспособов раздачи карт на 4 человека существует в игре                 «Верю ‑ не верю»(карты раздаются полностью, 36 карт).

Ответ: />.

В течении 30дней сентября было 12 дождливых дней, 8 ветреных, 4 холодных, 5 дождливых иветреных, 3 дождливых и холодных, а один день был и дождливым, и ветреным, ихолодным. В течение скольких дней в сентябре стояла хорошая погода.

Ответ: 15

На ферме есть20 овец и 24 свиньи. Сколькими способами можно выбрать одну овцу и одну свинью?Если такой выбор уже сделан, сколькими способами можно сделать его еще раз?

Ответ: 480, 437

Сколькимиспособами можно выбрать гласную и согласную буквы из слова «здание»?

Ответ: 9

Сколькосуществует четных пятизначных чисел, начинающихся нечетной цифрой?

Ответ: 25000

В книжныймагазин  поступили романы Ф. Купера «Прерия», «Зверобой», «Шпион», «Пионеры»,«Следопыт» по одинаковой цене. Сколькими способами библиотека может закупить 17книг на выбранный чек?

Ответ:: 2985Список используемой литературы

Савина Л.Н.,Попырев А.В. «КОМБИНАТОРИКА» издательство Елабужский государственный педагогическийинститут 1999г

Халамайзер А.Я. «Математика? – Забавно!» издание автора 1989г

Интернет

http:\www.mathclub.zala.ru/0921.html

www.ronl.ru

Реферат Комбинаторика

Реферат на тему:

План:

Введение
• 1 Примеры комбинаторных конфигураций и задач
• 2 Разделы комбинаторики
  • 2.1 Перечислительная комбинаторика
  • 2.2 Структурная комбинаторика
  • 2.3 Экстремальная комбинаторика
  • 2.4 Теория Рамсея
  • 2.5 Вероятностная комбинаторика
  • 2.6 Топологическая комбинаторика
• 3 Открытые проблемы
• 4 Исторический очерк
ПримечанияЛитература

Введение

Комбинато́рика (Комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка). Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей, и имеет широкий спектр применения в различных областях знаний (например в генетике, информатике, статистической физике).

Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».

Иногда под комбинаторикой понимают более обширный раздел дискретной математики, включающий, в частности, теорию графов.

1. Примеры комбинаторных конфигураций и задач

Для формулировки и решения комбинаторных задач используют различные модели комбинаторных конфигураций. Примерами комбинаторных конфигураций являются:

• Размещением из n элементов по k называется упорядоченный набор из k различных элементов некоторого n-элементного множества.
• Перестановкой из n элементов (например чисел 1,2,…,n) называется всякий упорядоченный набор из этих элементов. Перестановка также является размещением из n элементов по n.
• Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
• Композицией числа n называется всякое представление n в виде упорядоченной суммы целых положительных чисел.
• Разбиением числа n называется всякое представление n в виде неупорядоченной суммы целых положительных чисел.

Примерами комбинаторных задач являются:

1. Сколькими способами можно разместить n предметов по m ящикам так, чтобы выполнялись заданные ограничения?
2. Сколько существует функций F из m-элементного множества в n-элементное, удовлетворяющих заданным ограничениям?
3. Сколько существует различных перестановок из 52 игральных карт? Ответ: 52! (52 факториал) то есть 80658175170943878571660636856403766975289505440883277824000000000000 или примерно 8.0658 × 1067.
4. При игре в кости бросаются две кости и выпавшие очки складываются, сколько существует комбинаций, таких, что сумма очков на верхних гранях равна двенадцати? Решение: Каждый возможный исход соответствует функции (аргумент функции — это номер кости, значение — очки на верхней грани). Очевидно, что лишь 6+6 даёт нам нужный результат 12. Таким образом существует лишь одна функция, ставящая в соответствие 1 число 6, и 2 число 6. Или, другими словами, существует всего одна комбинация, такая, что сумма очков на верхних гранях равна двенадцати.

2. Разделы комбинаторики

2.1. Перечислительная комбинаторика

Перечислительная комбинаторика (или исчисляющая комбинаторика) рассматривает задачи о перечислении или подсчёте количества различных конфигураций (например, перестановок) образуемых элементами конечных множеств, на которые могут накладываться определённые ограничения, такие как: различимость или неразличимость элементов, возможность повторения одинаковых элементов и т. п.

Количество конфигураций, образованных несколькими манипуляциями над множеством, подсчитывается согласно правилам сложения и умножения.

Типичным примером задач данного раздела является подсчёт количества перестановок. Другой пример — известная Задача о письмах.

2.2. Структурная комбинаторика

К данному разделу относятся некоторые вопросы теории графов, а также теории матроидов.

2.3. Экстремальная комбинаторика

Примером этого раздела может служить следующая задача: какова наибольшая размерность графа, удовлетворяющего определённым свойствам.

2.4. Теория Рамсея

Теория Рамсея изучает наличие регулярных структур в случайных конфигурациях элементов. Примером утверждения из теории Рамсея может служить следующее:

В терминах структурной комбинаторики это же утверждение формулируется так:

2.5. Вероятностная комбинаторика

Этот раздел отвечает на вопросы вида: какова вероятность присутствия определённого свойства у заданного множества.

2.6. Топологическая комбинаторика

Аналоги комбинаторных концепций и методов используются и в топологии, при изучении дерева принятия решений, частично упорядоченных множеств, раскрасок графа и др.

3. Открытые проблемы

Комбинаторика, и в частности, теория Рамсея, содержит много известных открытых проблем, подчас с весьма несложной формулировкой. Например, неизвестно, при каком наименьшем N в любой группе из N человек найдутся 5 человек, либо попарно знакомых друг с другом, либо попарно незнакомых (хотя известно, что 49 человек достаточно).[1]

4. Исторический очерк

Примечания

1. Weisstein, Eric W. Числа Рамсея - mathworld.wolfram.com/RamseyNumber.html (англ.) на сайте Wolfram MathWorld.

wreferat.baza-referat.ru

Доклад - Комбинаторика - Математика

/>Реферат на тему:

/>

Выполнилученик 10 класса «В»

среднейшколы №53

ГлуховМихаил Александрович

г. Набережные Челны

2002 г. Содержание

Из истории комбинаторики

Комбинаторика занимается различного вида соединениями,которые можно образовать из элементов конечного множества. Некоторые элементыкомбинаторики были известны в Индии еще во II в. до н. э. Нидийцы умеливычислять числа, которые сейчас называют «сочетания». В XII в.Бхаскара вычислял некоторые виды сочетаний и перестановок. Предполагают, чтоиндийские ученые изучали соединения в связи с применением их в поэтике, науке оструктуре стиха и поэтических произведениях. Например, в связи с подсчетомвозможных сочетаний ударных (долгих) и безударных (кратких) слогов стопы из nслогов. Как научная дисциплина, комбинаторика сформировалась в XVII в. В книге«Теория и практика арифметики» (1656 г.) французский автор А. Такжепосвящает сочетаниям и перестановкам целую главу. Б. Паскаль в «Трактате об арифметическом треугольнике» и в«Трактате о числовых порядках» (1665 г.) изложил учение обиномиальных коэффициентах. П. Ферма знал о связях математических квадратов и фигурныхчисел с теорией соединений. Термин "комбинаторика"стал употребляться после опубликования Лейбницем в 1665 г. работы«Рассуждение о комбинаторном искусстве», в которой впервые данонаучное обоснование теории сочетаний и перестановок. Изучением размещенийвпервые занимался Я. Бернулли во второй части своей книги «Arsconjectandi» (искусство предугадывания) в 1713 г. Современная символикасочетаний была предложена разными авторами учебных руководств только в XIX в.

Все разнообразие комбинаторных формул может бытьвыведено из двух основных утверждений, касающихся конечных множеств – правилосуммы и правило произведения.

Правило суммы

Если конечные множества не пересекаются, то число элементов X U Y{или} равно сумме числа элементов множества X и числа элементов множества Y.

То есть, если на первойполке стоит X книг, а на второй Y, то выбрать книгу из первой или второй полки,можно X+Y способами.

Ученик должен выполнить практическую работу по математике. Емупредложили на выбор 17 тем по алгебре и 13 тем по геометрии. Сколькимиспособами он может выбрать одну тему для практической работы?

Решение: X=17, Y=13

По правилу суммы X U Y=17+13=30 тем.

Имеется 5 билетов денежно-вещевой лотереи, 6 билетов спортлото и 10билетов автомотолотереи. Сколькими способами можно выбрать один билет изспортлото или автомотолотереи?

Решение: Так как денежно-вещевая лотерея в выборе не участвует, товсего 6+10=16 вариантов.

Если элемент X можно выбрать k способами, а элемент Y-m способамито пару (X,Y) можно выбрать k*m способами.

То есть, если на первой полке стоит 5 книг, а на второй 10, то выбратьодну книгу с первой полки и одну со второй можно 5*10=50 способами.

Решение: Имеется 12 книг и 3 цвета, значит по правилу произведениявозможно 12*3=36 вариантов переплета.

Сколько существует пятизначных чисел, которые одинаково читаются слеванаправо и справа налево?

Решение: В таких числах последняя цифра будет такая же, как и первая, апредпоследняя — как и вторая. Третья цифра будет любой. Это можно представить ввиде XYZYX, где Y и Z -любые цифры, а X — не ноль. Значит по правилупроизведения количество цифр одинаково читающихся как слева направо, так исправа налево равно 9*10*10=900 вариантов.

Пересекающиеся множества

Но бывает, что множества X и Yпересекаются, тогда пользуются формулой/>,где X и Y — множества, а /> - область пересечения.

/>Примеры задач

20 человек знают английский и 10 — немецкий,из них 5 знают и английский,и немецкий. Сколько Человек всего?

Ответ: 10+20-5=25 человек.

Также часто для наглядного решения задачи применяются круги Эйлера.Например:

/>Из100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют30 человек, английским — 28, французским — 42. Английским и немецким одновременновладеют 8 человек, английским и французским — 10, немецким и французским — 5,всеми тремя языками — 3. Сколько туристов не владеют ни одним языком?

 Решение: Выразим условие этой задачи графически. Обозначимкругом тех, кто знает английский, другим кругом — тех, кто знает французский, итретьим кругом — тех, кто знают немецкий.

/>Всеми тремя языками владеют три туриста, значит, в общейчасти кругов вписываем число 3. Английским и французским языком владеют 10человек, а 3 из них владеют еще и немецким. Следовательно, только английским ифранцузским владеют 10-3=7 человек.

Аналогично получаем, что только английским и немецким владеют 8-3=5 человек, а немецким и французским 5-3=2 туриста. Вносим этиданные в соответствующие части.

/>Определим теперь, сколько человек владеют только одним изперечисленных языков. Немецкий знают 30 человек, но 5+3+2=10 из них владеют идругими языками, следовательно, только немецкий знают 20 человек. Аналогичнополучаем, что одним английским владеют 13 человек, а одним французским — 30 человек.

По условию задачи всего 100 туристов. 20+13+30+5+7+2+3=80 туристовзнают хотя бы один язык, следовательно, 20 человек не владеют ни одним изданных языков.

Размещениябез повторений.

Сколько можносоставить телефонных номеров из 6 цифр каждый, так чтобы все цифры былиразличны?

Это пример задачи на размещениебез повторений. Размещаются здесь 10 цифр по 6. А варианты, при которыходинаковые цифры стоят в разном порядке считаются разными.

Если X-множество, состоящие из nэлементов, m≤n, то размещением без повторений из n элементов множества Xпо m называется упорядоченное множество X, содержащее m элементов называетсяупорядоченное множество X, содержащее m элементов.

Количество всех размещений из n элементов по mобозначают

/>

n! — n-факториал (factorial анг. сомножитель) произведениечисел натурального ряда от 1 до какого либо числа n

n!=1*2*3*...*n       0!=1

Значит, ответ на вышепоставленную задачу будет

/>

Задача

Сколькими способами 4 юноши могут пригласить четырех изшести девушек на танец?

Решение: два юноши не могут одновременно пригласить одну и туже девушку. И варианты, при которых одни и те же девушки танцуют с разнымиюношами считаются, разными, поэтому:

/> 

Возможно 360 вариантов.

Перестановки без повторений

В случаеn=m (см. размещения без повторений) из n элементов по m  называется перестановкоймножества x.

Количествовсех перестановок из n элементов обозначают Pn.

Pn=n!

Действительно при n=m:

/>

Примеры задач

Сколькоразличных шестизначных чисел можно составить из цифр 0, 1, 2, 3, 4,5, еслицифры в числе не повторяются?

Решение:

1)      Найдемколичество всех перестановок из этих цифр: P6=6!=720

2)      0 не можетстоять впереди числа, поэтому от этого числа необходимо отнять количествоперестановок, при котором 0 стоит впереди. А это P5=5!=120.

P6-P5=720-120=600

Квартет

ПроказницаМартышка

Осел,

Козел,

Дакосолапый Мишка

Затеялииграть квартет

…

Стой,братцы стой! –

КричитМартышка, — погодите!

Какмузыке идти?

Ведь выне так сидите…

И так, и этакпересаживались – опять музыка на лад не идет.

Тут пущепрежнего пошли у низ раздоры

И споры,

Кому икак сидеть…

Вероятно,крыловские музыканты так и не перепробовали всех возможных мест. Однако способовне так уж и много. Сколько?

Здесь идетперестановка из четырех, значит, возможно

P4=4!=24варианта перестановок.

Сочетаниябез повторений

Сочетанием безповторений называется такое размещение, при котором порядок следования элементовне имеет значения.

Всякоеподмножество X состоящее из m элементов, называется сочетанием из n элементовпо m.

Таким образом,количество вариантов при сочетании будет меньше количества размещений.

Число сочетанийиз n элементов по m обозначается />.

/>.

Примеры задач

/>Сколькотрехкнопочных комбинаций существует на кодовом замке (все три кнопки нажимаютсяодновременно), если на нем всего 10 цифр.

Решение:

Так как кнопкинажимаются одновременно, то выбор этих трех кнопок – сочетание. Отсюда возможно/>вариантов.

У одногочеловека 7 книг по математике, а у второго – 9. Сколькими способами они могутобменять друг у друга две книги на две книги.

Решение:

Так как надо порядок следования книг не имеет значения, то выбор 2ух книг — сочетание. Первый человек может выбрать 2 книги />/> способами. Второй человек можетвыбрать 2 книги />. Значит всего поправилу произведения возможно 21*36=756 вариантов.

При игре вдомино 4 игрока делят поровну 28 костей. Сколькими способами они могут это сделать?

Первый игрокделает выбор из 28 костей. Второй из 28-7=21 костей, третий 14, а четвертыйигрок забирает оставшиеся кости. Следовательно, возможно />.Размещения и сочетания с повторениями

Часто взадачах по комбинаторике встречаются множества, в которых какие-либо компонентыповторяются. Например: в задачах на числа – цифры. Для таких задач приразмещениях используется формула />, а длясочетаний />.

Примеры задач

Сколькотрехзначных чисел можно составить из цифр 1, 2, 3, 4, 5?

Решение.Так как порядок цифр в числе существенен, цифры могут повторяться, то это будутразмещения с повторениями из пяти элементов по три, а их число равно />.

Вкондитерском магазине продавались 4 сорта пироженных: эклеры, песочные,наполеоны и слоеные. Сколькими способами можно купить 7 пироженных.

Решение:Покупка не зависит от того, в каком порядке укладывают купленные пироженные в коробку.Покупки будут различными, если они отличаются количеством купленных пирожныххотя бы одного сорта. Следовательно, количество различных покупок равно числусочетаний четырех видов пироженных по семь — />.

Обезьянупосадили за пишущую машинку с 45 клавишами, определить число попыток, необходимыхдля того, чтобы она наверняка напечатала первую строку романа Л.Н. Толстого«Анна Каренина», если строка содержит 52 знака и повторений не будет?

Решение:порядок букв имеет значение. Буквы могут повторяться. Значит, всего есть /> вариантов.

Перестановки сповторениями

/>/>,где n-количество всех элементов, n1,n2,…,nr-количествоодинаковых элементов.

Примеры задач

Сколькимиспособами можно переставить буквы слова «ананас»?

Решение:всего букв 6. Из них одинаковы n1«а»=3, n2«н»=2, n3«с»=1.Следовательно, число различных перестановок равно />.

/>Задачи для самостоятельного решения

Сколько перестановок можно сделать из букв слова«Миссисипи».

Ответ: 2520

  Имеется пять различных стульев и семь рулонов обивочнойткани различных цветов. Сколькими способами можно осуществить обивку стульев.

Ответ: 16807

На памятныесувениры в «Поле Чудес» спонсоры предлагают кофеварки, утюги, телефонныеаппараты, духи. Сколькими способами 9 участников игры могут получить эти сувениры?Сколькими способами могут быть выбраны 9 предметов для участников игры?

Ответ: 49, 220

Сколькимиспособами можно расставить на шахматной доске 8 ладей так, чтобы на одна из нихне могла бить другую?

Ответ: 40320

Сколько можетбыть случая выбора 2 карандашей и 3 ручек из пяти различных карандашей и шестиразличных ручек?

Ответ:200

Сколькоспособов раздачи карт на 4 человека существует в игре                 «Верю ‑ не верю»(карты раздаются полностью, 36 карт).

Ответ: />.

В течении 30дней сентября было 12 дождливых дней, 8 ветреных, 4 холодных, 5 дождливых иветреных, 3 дождливых и холодных, а один день был и дождливым, и ветреным, ихолодным. В течение скольких дней в сентябре стояла хорошая погода.

Ответ: 15

На ферме есть20 овец и 24 свиньи. Сколькими способами можно выбрать одну овцу и одну свинью?Если такой выбор уже сделан, сколькими способами можно сделать его еще раз?

Ответ: 480, 437

Сколькимиспособами можно выбрать гласную и согласную буквы из слова «здание»?

Ответ: 9

Сколькосуществует четных пятизначных чисел, начинающихся нечетной цифрой?

Ответ: 25000

В книжныймагазин  поступили романы Ф. Купера «Прерия», «Зверобой», «Шпион», «Пионеры»,«Следопыт» по одинаковой цене. Сколькими способами библиотека может закупить 17книг на выбранный чек?

Ответ:: 2985Список используемой литературы

Савина Л.Н.,Попырев А.В. «КОМБИНАТОРИКА» издательство Елабужский государственный педагогическийинститут 1999г

Халамайзер А.Я. «Математика? – Забавно!» издание автора 1989г

Интернет

http:\www.mathclub.zala.ru/0921.html

www.ronl.ru

Реферат: Комбинаторика

Реферат на тему:

Выполнил ученик 10 класса «В»

средней школы №53

Глухов Михаил Александрович

г. Набережные Челны

2002 г.Содержание

Из истории комбинаторики

Комбинаторика занимается различного вида соединениями, которые можно образовать из элементов конечного множества. Некоторые элементы комбинаторики были известны в Индии еще во II в. до н. э. Нидийцы умели вычислять числа, которые сейчас называют "сочетания". В XII в. Бхаскара вычислял некоторые виды сочетаний и перестановок. Предполагают, что индийские ученые изучали соединения в связи с применением их в поэтике, науке о структуре стиха и поэтических произведениях. Например, в связи с подсчетом возможных сочетаний ударных (долгих) и безударных (кратких) слогов стопы из n слогов. Как научная дисциплина, комбинаторика сформировалась в XVII в. В книге "Теория и практика арифметики" (1656 г.) французский автор А. Также посвящает сочетаниям и перестановкам целую главу. Б. Паскаль в "Трактате об арифметическом треугольнике" и в "Трактате о числовых порядках" (1665 г.) изложил учение о биномиальных коэффициентах. П. Ферма знал о связях математических квадратов и фигурных чисел с теорией соединений. Термин "комбинаторика" стал употребляться после опубликования Лейбницем в 1665 г. работы "Рассуждение о комбинаторном искусстве", в которой впервые дано научное обоснование теории сочетаний и перестановок. Изучением размещений впервые занимался Я. Бернулли во второй части своей книги "Ars conjectandi" (искусство предугадывания) в 1713 г. Современная символика сочетаний была предложена разными авторами учебных руководств только в XIX в.

Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств – правило суммы и правило произведения.

Правило суммы

Если конечные множества не пересекаются, то число элементов X U Y {или} равно сумме числа элементов множества X и числа элементов множества Y.

То есть, если на первой полке стоит X книг, а на второй Y, то выбрать книгу из первой или второй полки, можно X+Y способами.

Ученик должен выполнить практическую работу по математике. Ему предложили на выбор 17 тем по алгебре и 13 тем по геометрии. Сколькими способами он может выбрать одну тему для практической работы?

Решение: X=17, Y=13

По правилу суммы X U Y=17+13=30 тем.

Имеется 5 билетов денежно-вещевой лотереи, 6 билетов спортлото и 10 билетов автомотолотереи. Сколькими способами можно выбрать один билет из спортлото или автомотолотереи?

Решение: Так как денежно-вещевая лотерея в выборе не участвует, то всего 6+10=16 вариантов.

Если элемент X можно выбрать k способами, а элемент Y-m способами то пару (X,Y) можно выбрать k*m способами.

То есть, если на первой полке стоит 5 книг, а на второй 10, то выбрать одну книгу с первой полки и одну со второй можно 5*10=50 способами.

Переплетчик должен переплести 12 различных книг в красный, зеленый и коричневые переплеты. Сколькими способами он может это сделать?

Решение: Имеется 12 книг и 3 цвета, значит по правилу произведения возможно 12*3=36 вариантов переплета.

Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?

Решение: В таких числах последняя цифра будет такая же, как и первая, а предпоследняя - как и вторая. Третья цифра будет любой. Это можно представить в виде XYZYX, где Y и Z -любые цифры, а X - не ноль. Значит по правилу произведения количество цифр одинаково читающихся как слева направо, так и справа налево равно 9*10*10=900 вариантов.

Пересекающиеся множества

Но бывает, что множества X и Y пересекаются, тогда пользуются формулой, где X и Y - множества, а  - область пересечения.

Примеры задач

20 человек знают английский и 10 - немецкий, из них 5 знают и английский, и немецкий. Сколько Человек всего?

Ответ: 10+20-5=25 человек.

Также часто для наглядного решения задачи применяются круги Эйлера. Например:

Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским - 28, французским - 42. Английским и немецким одновременно владеют 8 человек, английским и французским - 10, немецким и французским - 5, всеми тремя языками - 3. Сколько туристов не владеют ни одним языком?

 Решение: Выразим условие этой задачи графически. Обозначим кругом тех, кто знает английский, другим кругом - тех, кто знает французский, и третьим кругом - тех, кто знают немецкий.

Всеми тремя языками владеют три туриста, значит, в общей части кругов вписываем число 3. Английским и французским языком владеют 10 человек, а 3 из них владеют еще и немецким. Следовательно, только английским и французским владеют 10-3=7 человек.

Аналогично получаем, что только английским и немецким  владеют 8-3=5 человек, а немецким и французским 5-3=2 туриста. Вносим эти данные в соответствующие части.

Определим теперь, сколько человек владеют только одним из перечисленных языков. Немецкий знают 30 человек, но 5+3+2=10 из них владеют и другими языками, следовательно, только немецкий знают 20 человек. Аналогично получаем, что одним английским владеют 13 человек, а одним французским - 30 человек.

По условию задачи всего 100 туристов. 20+13+30+5+7+2+3=80 туристов знают хотя бы один язык, следовательно, 20 человек не владеют ни одним из данных языков.

Размещения без повторений.

Сколько можно составить телефонных номеров из 6 цифр каждый, так чтобы все цифры были различны?

Это пример задачи на размещение без повторений. Размещаются здесь 10 цифр по 6. А варианты, при которых одинаковые цифры стоят в разном порядке считаются разными.

Если X-множество, состоящие из n элементов, m≤n, то размещением без повторений из n элементов множества X по m называется упорядоченное множество X, содержащее m элементов называется упорядоченное множество X, содержащее m элементов.

Количество всех размещений из n элементов по m обозначают

n! - n-факториал (factorial анг. сомножитель) произведение чисел натурального ряда от 1 до какого либо числа n

n!=1*2*3*...*n       0!=1

Значит, ответ на вышепоставленную задачу будет

Задача

Сколькими способами 4 юноши могут пригласить четырех из шести девушек на танец?

Решение: два юноши не могут одновременно пригласить одну и ту же девушку. И варианты, при которых одни и те же девушки танцуют с разными юношами считаются, разными, поэтому:

Возможно 360 вариантов.

Перестановки без повторений

В случае n=m (см. размещения без повторений) из n элементов по m  называется перестановкой множества x.

Количество всех перестановок из n элементов обозначают Pn.

Pn=n!

Действительно при n=m:

Примеры задач

Сколько различных шестизначных чисел можно составить из цифр 0, 1, 2, 3, 4,5, если цифры в числе не повторяются?

Решение:

1)             Найдем количество всех перестановок из этих цифр: P6=6!=720

2)             0 не может стоять впереди числа, поэтому от этого числа необходимо отнять количество перестановок, при котором 0 стоит впереди. А это P5=5!=120.

P6-P5=720-120=600

Квартет

Проказница Мартышка

Осел,

Козел,

Да косолапый Мишка

Затеяли играть квартет

…

Стой, братцы стой! –

Кричит Мартышка, - погодите!

Как музыке идти?

Ведь вы не так сидите…

И так, и этак пересаживались – опять музыка на лад не идет.

Тут пуще прежнего пошли у низ раздоры

И споры,

Кому и как сидеть…

Вероятно, крыловские музыканты так и не перепробовали всех возможных мест. Однако способов не так уж и много. Сколько?

Здесь идет перестановка из четырех, значит, возможно

P4=4!=24 варианта перестановок.

Сочетания без повторений

Сочетанием без повторений называется такое размещение, при котором порядок следования элементов не имеет значения.

Всякое подмножество X состоящее из m элементов, называется сочетанием из n элементов по m.

Таким образом, количество вариантов при сочетании будет меньше количества размещений.

Число сочетаний из n элементов по m обозначается .

.

Примеры задач

Сколько трехкнопочных комбинаций существует на кодовом замке (все три кнопки нажимаются одновременно), если на нем всего 10 цифр.

Решение:

Так как кнопки нажимаются одновременно, то выбор этих трех кнопок – сочетание. Отсюда возможно вариантов.

У одного человека 7 книг по математике, а у второго – 9. Сколькими способами они могут обменять друг у друга две книги на две книги.

Решение:

Так как надо  порядок следования книг не имеет значения, то выбор 2ух книг - сочетание. Первый человек может выбрать 2 книги  способами. Второй человек может выбрать 2 книги . Значит всего по правилу произведения возможно 21*36=756 вариантов.

При игре в домино 4 игрока делят поровну 28 костей. Сколькими способами они могут это сделать?

Первый игрок делает выбор из 28 костей. Второй из 28-7=21 костей, третий 14, а четвертый игрок забирает оставшиеся кости. Следовательно, возможно .Размещения и сочетания с повторениями

Часто в задачах по комбинаторике встречаются множества, в которых какие-либо компоненты повторяются. Например: в задачах на числа – цифры. Для таких задач при размещениях используется формула , а для сочетаний .

Примеры задач

Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5?

Решение. Так как порядок цифр в числе существенен, цифры могут повторяться, то это будут размещения с повторениями из пяти элементов по три, а их число равно .

В кондитерском магазине продавались 4 сорта пироженных: эклеры, песочные, наполеоны и слоеные. Сколькими способами можно купить 7 пироженных.

Решение: Покупка не зависит от того, в каком порядке укладывают купленные пироженные в коробку. Покупки будут различными, если они отличаются количеством купленных пирожных хотя бы одного сорта. Следовательно, количество различных покупок равно числу сочетаний четырех видов пироженных по семь - .

Обезьяну посадили за пишущую машинку с 45 клавишами, определить число попыток, необходимых для того, чтобы она наверняка напечатала первую строку романа Л.Н. Толстого «Анна Каренина», если строка содержит 52 знака и повторений не будет?

Решение: порядок букв имеет значение. Буквы могут повторяться. Значит, всего есть  вариантов.

Перестановки с повторениями

, где n-количество всех элементов, n1,n2,…,nr-количество одинаковых элементов.

Примеры задач

Сколькими способами можно переставить буквы слова «ананас»?

Решение: всего букв 6. Из них одинаковы n1«а»=3, n2«н»=2, n3«с»=1. Следовательно, число различных перестановок равно .

Задачи для самостоятельного решения

Сколько перестановок можно сделать из букв слова «Миссисипи».

Ответ: 2520

  Имеется пять различных стульев и семь рулонов обивочной ткани различных цветов. Сколькими способами можно осуществить обивку стульев.

Ответ: 16807

На памятные сувениры в «Поле Чудес» спонсоры предлагают кофеварки, утюги, телефонные аппараты, духи. Сколькими способами 9 участников игры могут получить эти сувениры? Сколькими способами могут быть выбраны 9 предметов для участников игры?

Ответ: 49, 220

Сколькими способами можно расставить на шахматной доске 8 ладей так, чтобы на одна из них не могла бить другую?

Ответ: 40320

Сколько может быть случая выбора 2 карандашей и 3 ручек из пяти различных карандашей и шести различных ручек?

Ответ:200

Сколько способов раздачи карт на 4 человека существует в игре                 «Верю ‑ не верю» (карты раздаются полностью, 36 карт).

Ответ: .

В течении 30 дней сентября было 12 дождливых дней, 8 ветреных, 4 холодных, 5 дождливых и ветреных, 3 дождливых и холодных, а один день был и дождливым, и ветреным, и холодным. В течение скольких дней в сентябре стояла хорошая погода.

Ответ: 15

На ферме есть 20 овец и 24 свиньи. Сколькими способами можно выбрать одну овцу и одну свинью? Если такой выбор уже сделан, сколькими способами можно сделать его еще раз?

Ответ: 480, 437

Сколькими способами можно выбрать гласную и согласную буквы из слова «здание»?

Ответ: 9

Сколько существует четных пятизначных чисел, начинающихся нечетной цифрой?

Ответ: 25000

В книжный магазин  поступили романы Ф. Купера «Прерия», «Зверобой», «Шпион», «Пионеры», «Следопыт» по одинаковой цене. Сколькими способами библиотека может закупить 17 книг на выбранный чек?

Ответ:: 2985Список используемой литературы

Савина Л.Н., Попырев А.В. «КОМБИНАТОРИКА» издательство Елабужский государственный педагогический институт 1999г

Халамайзер А. Я. «Математика? – Забавно!» издание автора 1989г

Интернет

http:\www.mathclub.zala.ru/0921.html

www.referatmix.ru

Реферат Комбинаторика

Р еферат на тему:

Выполнил ученик 10 класса «В»

средней школы №53

Глухов Михаил Александрович

г. Набережные Челны

2002 г.

Содержание

Из истории комбинаторики

Комбинаторика занимается различного вида соединениями, которые можно образовать из элементов конечного множества. Некоторые элементы комбинаторики были известны в Индии еще во II в. до н. э. Нидийцы умели вычислять числа, которые сейчас называют "сочетания". В XII в. Бхаскара вычислял некоторые виды сочетаний и перестановок. Предполагают, что индийские ученые изучали соединения в связи с применением их в поэтике, науке о структуре стиха и поэтических произведениях. Например, в связи с подсчетом возможных сочетаний ударных (долгих) и безударных (кратких) слогов стопы из n слогов. Как научная дисциплина, комбинаторика сформировалась в XVII в. В книге "Теория и практика арифметики" (1656 г.) французский автор А. Также посвящает сочетаниям и перестановкам целую главу. Б. Паскаль в "Трактате об арифметическом треугольнике" и в "Трактате о числовых порядках" (1665 г.) изложил учение о биномиальных коэффициентах. П. Ферма знал о связях математических квадратов и фигурных чисел с теорией соединений. Термин "комбинаторика" стал употребляться после опубликования Лейбницем в 1665 г. работы "Рассуждение о комбинаторном искусстве", в которой впервые дано научное обоснование теории сочетаний и перестановок. Изучением размещений впервые занимался Я. Бернулли во второй части своей книги "Ars conjectandi" (искусство предугадывания) в 1713 г. Современная символика сочетаний была предложена разными авторами учебных руководств только в XIX в.

Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств – правило суммы и правило произведения.

Правило суммы

Если конечные множества не пересекаются, то число элементов X U Y {или} равно сумме числа элементов множества X и числа элементов множества Y.

То есть, если на первой полке стоит X книг, а на второй Y, то выбрать книгу из первой или второй полки, можно X+Y способами.

Примеры задач

Ученик должен выполнить практическую работу по математике. Ему предложили на выбор 17 тем по алгебре и 13 тем по геометрии. Сколькими способами он может выбрать одну тему для практической работы?

Решение: X=17, Y=13

По правилу суммы X U Y=17+13=30 тем.

Имеется 5 билетов денежно-вещевой лотереи, 6 билетов спортлото и 10 билетов автомотолотереи. Сколькими способами можно выбрать один билет из спортлото или автомотолотереи?

Решение: Так как денежно-вещевая лотерея в выборе не участвует, то всего 6+10=16 вариантов.

Правило произведения

Если элемент X можно выбрать k способами, а элемент Y-m способами то пару (X,Y) можно выбрать k*m способами.

То есть, если на первой полке стоит 5 книг, а на второй 10, то выбрать одну книгу с первой полки и одну со второй можно 5*10=50 способами.

Примеры задач

Переплетчик должен переплести 12 различных книг в красный, зеленый и коричневые переплеты. Сколькими способами он может это сделать?

Решение: Имеется 12 книг и 3 цвета, значит по правилу произведения возможно 12*3=36 вариантов переплета.

Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?

Решение: В таких числах последняя цифра будет такая же, как и первая, а предпоследняя - как и вторая. Третья цифра будет любой. Это можно представить в виде XYZYX, где Y и Z -любые цифры, а X - не ноль. Значит по правилу произведения количество цифр одинаково читающихся как слева направо, так и справа налево равно 9*10*10=900 вариантов.

Пересекающиеся множества

Но бывает, что множества X и Y пересекаются, тогда пользуются формулой , где X и Y - множества, а - область пересечения.

П

Если множеств больше, например 5 языков, то также складывается количество человек знающих английский, немецкий, французский и т.д., отнимается количество человек, знающих 2 языка одновременно, прибавляется по 3, отнимаются по 4 и т.д.

20 человек знают английский и 10 - немецкий, из них 5 знают и английский, и немецкий. Сколько Человек всего?

Ответ: 10+20-5=25 человек.

Также часто для наглядного решения задачи применяются круги Эйлера. Например:

И з 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским - 28, французским - 42. Английским и немецким одновременно владеют 8 человек, английским и французским - 10, немецким и французским - 5, всеми тремя языками - 3. Сколько туристов не владеют ни одним языком?

Решение: Выразим условие этой задачи графически. Обозначим кругом тех, кто знает английский, другим кругом - тех, кто знает французский, и третьим кругом - тех, кто знают немецкий.

В семи тремя языками владеют три туриста, значит, в общей части кругов вписываем число 3. Английским и французским языком владеют 10 человек, а 3 из них владеют еще и немецким. Следовательно, только английским и французским владеют 10-3=7 человек.

Аналогично получаем, что только английским и немецким владеют 8-3=5 человек, а немецким и французским 5-3=2 туриста. Вносим эти данные в соответствующие части.

О пределим теперь, сколько человек владеют только одним из перечисленных языков. Немецкий знают 30 человек, но 5+3+2=10 из них владеют и другими языками, следовательно, только немецкий знают 20 человек. Аналогично получаем, что одним английским владеют 13 человек, а одним французским - 30 человек.

По условию задачи всего 100 туристов. 20+13+30+5+7+2+3=80 туристов знают хотя бы один язык, следовательно, 20 человек не владеют ни одним из данных языков.

Размещения без повторений.

Сколько можно составить телефонных номеров из 6 цифр каждый, так чтобы все цифры были различны?

Это пример задачи на размещение без повторений. Размещаются здесь 10 цифр по 6. А варианты, при которых одинаковые цифры стоят в разном порядке считаются разными.

Если X-множество, состоящие из n элементов, m≤n, то размещением без повторений из n элементов множества X по m называется упорядоченное множество X, содержащее m элементов называется упорядоченное множество X, содержащее m элементов.

Количество всех размещений из n элементов по m обозначают

n! - n-факториал (factorial анг. сомножитель) произведение чисел натурального ряда от 1 до какого либо числа n

n!=1*2*3*...*n 0!=1

Значит, ответ на вышепоставленную задачу будет

Задача

Сколькими способами 4 юноши могут пригласить четырех из шести девушек на танец?

Решение: два юноши не могут одновременно пригласить одну и ту же девушку. И варианты, при которых одни и те же девушки танцуют с разными юношами считаются, разными, поэтому:

Возможно 360 вариантов.

Перестановки без повторений

В случае n=m (см. размещения без повторений) из n элементов по m называется перестановкой множества x.

Количество всех перестановок из n элементов обозначают Pn.

Pn=n!

Действительно при n=m:

Примеры задач

Сколько различных шестизначных чисел можно составить из цифр 0, 1, 2, 3, 4,5, если цифры в числе не повторяются?

Решение:

1. Найдем количество всех перестановок из этих цифр: P6=6!=720

2. 0 не может стоять впереди числа, поэтому от этого числа необходимо отнять количество перестановок, при котором 0 стоит впереди. А это P5=5!=120.

P6-P5=720-120=600

Квартет

Проказница Мартышка

Осел,

Козел,

Да косолапый Мишка

Затеяли играть квартет

…

Стой, братцы стой! –

Кричит Мартышка, - погодите!

Как музыке идти?

Ведь вы не так сидите…

И так, и этак пересаживались – опять музыка на лад не идет.

Тут пуще прежнего пошли у низ раздоры

И споры,

Кому и как сидеть…

Вероятно, крыловские музыканты так и не перепробовали всех возможных мест. Однако способов не так уж и много. Сколько?

Здесь идет перестановка из четырех, значит, возможно

P4=4!=24 варианта перестановок.

Сочетания без повторений

Сочетанием без повторений называется такое размещение, при котором порядок следования элементов не имеет значения.

Всякое подмножество X состоящее из m элементов, называется сочетанием из n элементов по m.

Таким образом, количество вариантов при сочетании будет меньше количества размещений.

Число сочетаний из n элементов по m обозначается .

.

Примеры задач

С колько трехкнопочных комбинаций существует на кодовом замке (все три кнопки нажимаются одновременно), если на нем всего 10 цифр.

Решение:

Так как кнопки нажимаются одновременно, то выбор этих трех кнопок – сочетание. Отсюда возможно вариантов.

У одного человека 7 книг по математике, а у второго – 9. Сколькими способами они могут обменять друг у друга две книги на две книги.

Решение:

Так как надо порядок следования книг не имеет значения, то выбор 2ух книг - сочетание. Первый человек может выбрать 2 книги способами. Второй человек может выбрать 2 книги . Значит всего по правилу произведения возможно 21*36=756 вариантов.

При игре в домино 4 игрока делят поровну 28 костей. Сколькими способами они могут это сделать?

Первый игрок делает выбор из 28 костей. Второй из 28-7=21 костей, третий 14, а четвертый игрок забирает оставшиеся кости. Следовательно, возможно .

Размещения и сочетания с повторениями

Часто в задачах по комбинаторике встречаются множества, в которых какие-либо компоненты повторяются. Например: в задачах на числа – цифры. Для таких задач при размещениях используется формула , а для сочетаний .

Примеры задач

Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5?

Решение. Так как порядок цифр в числе существенен, цифры могут повторяться, то это будут размещения с повторениями из пяти элементов по три, а их число равно .

В кондитерском магазине продавались 4 сорта пироженных: эклеры, песочные, наполеоны и слоеные. Сколькими способами можно купить 7 пироженных.

Решение: Покупка не зависит от того, в каком порядке укладывают купленные пироженные в коробку. Покупки будут различными, если они отличаются количеством купленных пирожных хотя бы одного сорта. Следовательно, количество различных покупок равно числу сочетаний четырех видов пироженных по семь - .

Обезьяну посадили за пишущую машинку с 45 клавишами, определить число попыток, необходимых для того, чтобы она наверняка напечатала первую строку романа Л.Н. Толстого «Анна Каренина», если строка содержит 52 знака и повторений не будет?

Решение: порядок букв имеет значение. Буквы могут повторяться. Значит, всего есть вариантов.

Перестановки с повторениями

, где n-количество всех элементов, n1,n2,…,nr-количество одинаковых элементов.

Примеры задач

Сколькими способами можно переставить буквы слова «ананас»?

Решение: всего букв 6. Из них одинаковы n1«а»=3, n2«н»=2, n3«с»=1. Следовательно, число различных перестановок равно .

З адачи для самостоятельного решения

Сколько перестановок можно сделать из букв слова «Миссисипи».

Ответ: 2520

Имеется пять различных стульев и семь рулонов обивочной ткани различных цветов. Сколькими способами можно осуществить обивку стульев.

Ответ: 16807

На памятные сувениры в «Поле Чудес» спонсоры предлагают кофеварки, утюги, телефонные аппараты, духи. Сколькими способами 9 участников игры могут получить эти сувениры? Сколькими способами могут быть выбраны 9 предметов для участников игры?

Ответ: 49, 220

Сколькими способами можно расставить на шахматной доске 8 ладей так, чтобы на одна из них не могла бить другую?

Ответ: 40320

Сколько может быть случая выбора 2 карандашей и 3 ручек из пяти различных карандашей и шести различных ручек?

Ответ:200

Сколько способов раздачи карт на 4 человека существует в игре «Верю ‑ не верю» (карты раздаются полностью, 36 карт).

Ответ: .

В течении 30 дней сентября было 12 дождливых дней, 8 ветреных, 4 холодных, 5 дождливых и ветреных, 3 дождливых и холодных, а один день был и дождливым, и ветреным, и холодным. В течение скольких дней в сентябре стояла хорошая погода.

Ответ: 15

На ферме есть 20 овец и 24 свиньи. Сколькими способами можно выбрать одну овцу и одну свинью? Если такой выбор уже сделан, сколькими способами можно сделать его еще раз?

Ответ: 480, 437

Сколькими способами можно выбрать гласную и согласную буквы из слова «здание»?

Ответ: 9

Сколько существует четных пятизначных чисел, начинающихся нечетной цифрой?

Ответ: 25000

В книжный магазин поступили романы Ф. Купера «Прерия», «Зверобой», «Шпион», «Пионеры», «Следопыт» по одинаковой цене. Сколькими способами библиотека может закупить 17 книг на выбранный чек?

Ответ:: 2985

Список используемой литературы

Савина Л.Н., Попырев А.В. «КОМБИНАТОРИКА» издательство Елабужский государственный педагогический институт 1999г

Халамайзер А. Я. «Математика? – Забавно!» издание автора 1989г

Интернет

http:\www.mathclub.zala.ru/0921.html

Реферат Имя - средство закрепления и систематизации фактов культуры Имя - средство закрепления и систематизации фактов культуры.                                     1        Свойство языка служить посредником между всеми семиотическими систе- мами  объясняется  тем, что язык, частью которого являются имена, позволяет самым  экономичным способом передавать мысли и чувства.

Реферат Программа Mathematics Едва исчезли со страниц журналов восторженные от­зывы на новую версию математического пакета Maple V 4.0 компании Maple Waterloo, как компания Wolfram Research представила не менее интересный продукт — Mathematica 3.0. Она разработана компанией Wolfram Research Inc , ос­нованной известным математиком и физиком Стефаном Вольфрамом, одним из создателей теории сложных систем.

Реферат Великая теорема Ферма ) Биография Ферма Пьер Ферма жил с 1601 по 1665 год. Был он сыном одного из многочисленных торговцев во Франции, получил юридическое образование и работал сначала адвокатом, а впоследствии стал даже советником парламента. Служебные его обязанности, далёкие по содержанию от математических наук, оставляли ему достаточно досуга, который Ферма и посвящал занятиям математическими исследованиями.

nreferat.ru

Смотрите также

• 
  Реферат анимация
• 
  Реферат бородин
• 
  Реферат оркестр
• 
  Реферат панда
• 
  Сновидение реферат
• 
  Реферат самбо
• 
  Реферат микроскопия
• 
  Реферат гераклит
• 
  Вавилов реферат
• 
  Реферат ортопедия
• 
  Клапан реферат