Числа Фибоначчи. Реферат числа фибоначчи

Реферат Числа Фибоначчи

Опубликовать скачать

Реферат на тему:

План:

1 Происхождение
2 Формула Бине
3 Тождества
4 Свойства
5 Вариации и обобщения
6 В других областях
- 6.1 В природе
- 6.2 В культуре

Введение

Чи́сла Фибона́ччи — элементы числовой последовательности

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946,… (последовательность A000045 в OEIS)

в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (известного как Фибоначчи)[1]. Иногда число 0 не рассматривается как член последовательности.

Более формально, последовательность чисел Фибоначчи $\left\{F_n\right\}$ задается линейным рекуррентным соотношением:

$F_0 = 0,\qquad F_1 = 1,\qquad F_{n} = F_{n-1} + F_{n-2}, \quad n\geqslant 2.$

Иногда числа Фибоначчи рассматривают и для отрицательных номеров n как двусторонне бесконечную последовательность, удовлетворяющую тому же рекуррентному соотношению. Члены с такими номерами легко получить с помощью эквивалентной формулы «назад»: Fn = Fn + 2 − Fn + 1:

n Fn

−10	−9	−8	−7	−6	−5	−4	−3	−2	−1	0	1	2	3	4	5	6	7	8	9	10
−55	34	−21	13	−8	5	−3	2	−1	1	0	1	1	2	3	5	8	13	21	34	55

Легко заметить, что $\! F_{-n} = (-1)^{n+1}F_n$ .

1. Происхождение

Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении), намного раньше, чем она стала известна в Европе.

Образец длиной n может быть построен путём добавления S к образцу длиной n-1, либо L к образцу длиной n-2; и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования».

На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая что:

В «нулевом» месяце имеется пара кроликов (1 новая пара).
В первом месяце первая пара производит на свет другую пару (1 новая пара).
Во втором месяце обе пары кроликов порождают другие пары и первая пара погибает (2 новые пары).
В третьем месяце вторая пара и две новые пары порождают в общем три новые пары, а старая вторая пара погибает (3 новые пары).

Закономерным является тот факт, что каждая пара кроликов порождает ещё две пары на протяжении жизни, а затем погибает.

Пусть популяция за месяц n будет равна F(n). В это время только те кролики, которые жили в месяце n-2, являются способными к размножению и производят потомков, тогда F(n-2) пар прибавится к текущей популяции F(n-1). Таким образом общее количество пар будет равно F(n) = F(n-1) + F(n-2).

2. Формула Бине

Формула Бине выражает в явном виде значение Fn как функцию от n:

$F_n = \frac{\left(\frac{1 + \sqrt{5}}{2}\right)^n - \left(\frac{1 - \sqrt{5}}{2}\right)^n}{\sqrt{5}} = \frac{\varphi^n - (-\varphi )^{-n}}{\varphi - (-\varphi )^{-1}} = \frac{\varphi^n - (-\varphi )^{-n}}{2\varphi - 1}$ ,

где $\varphi=\frac{1 + \sqrt{5}}{2}$ — золотое сечение. При этом $\varphi\,\!$ и $(-\varphi )^{-1}=1-\varphi\,\!$ являются корнями характеристического уравнения $x^2-x-1=0\,\!$ .

Из формулы Бине следует, что для всех $n\geqslant 0$ , Fn есть ближайшее к $\frac{\varphi^n}{\sqrt{5}}\,$ целое число, то есть $F_n = \left\lfloor\frac{\varphi^n}{\sqrt{5}}\right\rceil$ . В частности, при $n\to\infty$ справедлива асимптотика $F_n\sim \frac{\varphi^n}{\sqrt{5}}$ .

Формула Бине может быть аналитически продолжена следующим образом:

$F_z = \frac{1}{\sqrt{5}} \left( \varphi^z - \frac{\cos{\pi z}}{\varphi^z} \right)$

При этом соотношение Fz + 2 = Fz + 1 + Fz выполняется для любого комплексного числа z.

3. Тождества

$F_1+F_2+F_3+\dots+F_n=F_{n+2}-1$

$F_1+F_3+F_5+\dots+F_{2n-1}=F_{2n}$

$F_2+F_4+F_6+\dots+F_{2n}=F_{2n+1}-1$

$F_{n+1}F_{n+2}^{}-F_nF_{n+3}=(-1)^{n}$

$F_1^2+F_2^2+F_3^2+\dots+F_{n}^2=F_nF_{n+1}$

$F_n^2+F_{n+1}^2=F_{2n+1}$

$F_{2n}=F_{n+1}^2-F_{n-1}^2$

$F_{3n}=F_{n+1}^3+F_n^3-F_{n-1}^3$

$F_{5n}=25F_{n}^5+25(-1)^{n}F_n^3+5F_{n}$

И более общие формулы:

$F_{n+m}^{}=F_{n-1}F_{m}+F_{n}F_{m+1}=F_{n+1}F_{m+1}-F_{n-1}F_{m-1}$

$F_{(k+1)n}^{}=F_{n-1}F_{kn}+F_nF_{kn+1}$

$F_n^{}=F_lF_{n-l+1}+F_{l-1}F_{n-l}$

Числа Фибоначчи представляются значениями континуант на наборе единиц: $F_{n+1} = K_n(1,\dots,1)$ , то есть

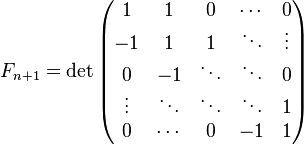$F_{n+1} = \det \begin{pmatrix} 1 & 1 & 0 &\cdots & 0 \\ -1 & 1 & 1 & \ddots & \vdots\\ 0 & -1 & \ddots &\ddots & 0 \\ \vdots & \ddots & \ddots &\ddots & 1 \\ 0 & \cdots & 0 & -1 & 1 \end{pmatrix}$ , а также $\ F_{n+1} = \det \begin{pmatrix} 1 & i & 0 &\cdots & 0 \\ i & 1 & i & \ddots & \vdots\\ 0 & i & \ddots &\ddots & 0 \\ \vdots & \ddots & \ddots &\ddots & i \\ 0 & \cdots & 0 & i & 1\end{pmatrix}$ , где матрицы имеют размер $n\times n$ , i — мнимая единица.

Числа Фибоначчи можно выразить через многочлены Чебышева:

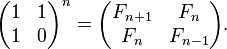
$F_{n+1} = (-i)^n U_n\left(\frac{-i}{2}\right) = (-i)^n T_n(-i),$ $F_{2n+2} = U_n\left(\frac{3}{2}\right) = T_n(3).$ $\begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix}^n = \begin{pmatrix} F_{n+1} & F_n \\ F_n & F_{n-1} \end{pmatrix}.$

Следствие. Подсчёт определителей даёт

$(-1)^n = F_{n+1} F_{n-1} - F_n^2.$

4. Свойства

Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, т. е. (Fm,Fn) = F(m,n). Следствия:
- Fm делится на Fn тогда и только тогда, когда m делится на n (за исключением n = 2). В частности, Fm делится на F3 = 2 (то есть является чётным) только для m = 3k; Fm делится на F4 = 3 только для m = 4k; Fm делится на F5 = 5 только для m = 5k и т. д.
- Fm может быть простым только для простых m (с единственным исключением m = 4). Например, число F13 = 233 простое, и его индекс 13 также прост. Обратное не верно, наименьший контрпример — $F_{19}=4181=37\cdot 113$ . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.

Последовательность чисел Фибоначчи является частным случаем возвратной последовательности, её характеристический многочлен x2 - x - 1 имеет корни $~\varphi$ и $-\frac{1}{\varphi}$ .

Отношения $\frac{F_{n+1}}{F_n}$ являются подходящими дробями золотого сечения φ и, в частности, $\lim_{n\to\infty} \frac{F_{n+1}}{F_n} = \varphi.$
Суммы биномиальных коэффициентов на диагоналях треугольника Паскаля являются числами Фибоначчи ввиду формулы $F_{n+1} = \sum_{k=0}^{\lfloor n/2\rfloor} {n-k\choose k}$ .

В 1964 году Дж. Кон (J. H. E. Cohn) доказал,[2] что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12: F0 = 02 = 0, F1 = 12 = 1, F2 = 12 = 1, F12 = 122 = 144.

Производящей функцией последовательности чисел Фибоначчи является: $0 + x + x^2 + 2 x^3 + 3 x^4 + 5 x^5 + \dots = \sum_{n=0}^{\infty} F_n x^n = \frac{x}{1-x-x^2}$

Множество чисел Фибоначчи совпадает с множеством неотрицательных значений многочлена z(x,y) = 2xy4 + x2y3 − 2x3y2 − y5 − x4y + 2y,

на множестве неотрицательных целых чисел x и y.[3]

Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.

Период чисел Фибоначчи по модулю натурального числа n называется периодом Писано[убрать шаблон] и обозначается π(n). Периоды Писано π(n) образуют последовательность: 1, 3, 8, 6, 20, 24, 16, 12, 24, 60, 10, 24, 28, 48, 40, 24, 36, … (последовательность A001175 в OEIS)
- В частности, последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом π(10)=60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом π(100)=300, последние три цифры — с периодом π(1000)=1500, последние четыре — с периодом π(10000)=15000, последние пять — с периодом π(100000)=150000 и т. д.

Натуральное число N является числом Фибоначчи тогда и только тогда, когда 5N2 + 4 или 5N2 − 4 является квадратом.[4]

Не существует арифметической прогрессии длиной больше 3, состоящей из чисел Фибоначчи.[5]

5. Вариации и обобщения

Числа трибоначчи
Числа Фибоначчи являются частным случаем последовательностей Люка , при этом их дополнением являются числа Люка .

6. В других областях

6.1. В природе

Филлотаксис (листорасположение) у растений описывается последовательностью Фибоначчи. Зерна подсолнуха, сосновые шишки, лепестки цветков, ячейки ананаса также располагаются согласно последовательности Фибоначчи.[6]

[7][8][9]

Длины фаланг пальцев человека относятся примерно как числа Фибоначчи.[6][10]
Молекулу ДНК составляют две вертикально переплетенные спирали длиной 34 ангстрема и шириной 21 ангстрема. Числа 21 и 34 следуют друг за другом в последовательности Фибоначчи.[11]

6.2. В культуре

Американский писатель-фантаст Дэн Браун в книге «Код да Винчи» описал последовательность Фибоначчи как «лжешифр».
Светящиеся числа Фибоначчи от 1 до 55 прикреплены на дымовой трубе Turku Energia в Турку[12] и главном вокзале Цюриха[13].

Литература

Н. Н. Воробьёв Числа Фибоначчи. — Наука, 1978. — Т. 39. — (Популярные лекции по математике).
А. И. Маркушевич Возвратные последовательности. — Гос. Издательство Технико-Теоретической Литературы, 1950. — Т. 1. — (Популярные лекции по математике).
А. Н. Рудаков Числа Фибоначчи и простота числа 2127-1 // Математическое Просвещение, третья серия. — 2000. — Т. 4.
Дональд Кнут Искусство программирования, том 1. Основные алгоритмы = The Art of Computer Programming, vol.1. Fundamental Algorithms. — 3-е изд. — М.: «Вильямс», 2006. — С. 720. — ISBN 0-201-89683-4
Дональд Кнут, Роналд Грэхем, Орен Паташник Конкретная математика. Основание информатики = Concrete Mathematics. A Foundation for Computer Science. — М.: Мир; Бином. Лаборатория знаний, 2006. — С. 703. — ISBN 5-94774-560-7

Примечания

Числа Фибоначчи - slovari.yandex.ru/dict/bse/article/00083/91300.htm — статья из Большой советской энциклопедии
J H E Cohn. Square Fibonacci Numbers Etc - math.la.asu.edu/~checkman/SquareFibonacci.html, стр. 109–113.
P. Ribenboim The New Book of Prime Number Records - books.google.com/books?id=72eg8bFw40kC&pg=PA193. — Springer, 1996. — С. 193.
Ira Gessel Problem H-187 // Fibonacci Quarterly. — 1972. — Т. 10. — С. 417–419.
В. Серпинский Задача 66 // 250 задач по элементарной теории чисел - ilib.mccme.ru/djvu/serp-250-tch.htm. — М.: Просвещение, 1968. — 168 с.
↑ 12 Золотое сечение в природе - himekoscho.ucoz.ru/load/16-1-0-92
Числа Фибоначчи - elementy.ru/trefil/21136
Числа Фибоначчи - www.diary.ru/~Organon/p19280903.htm
Глава из книги О.Е.Акимова "Конец науки" - kompot.soneta.ru/O-chislah-Fibonachchi-fillotaksise-i-ZS
Г. Манукян. ПОЭЗИЯ ЧИСЕЛ ФИБОНАЧЧИ - www.21mm.ru/item/291/
Г. Манукян.ПОЭЗИЯ ЧИСЕЛ ФИБОНАЧЧИ - www.21mm.ru/item/291/
Марио Мерц Fibonacci Sequence 1-55 - www.turku.fi/public/default.aspx?contentid=57923&nodeid=13067 (фин.)
Based in Villigen: Fibonacci sequence at the Zürich Hauptbahnhof - basedinvilligen.blogspot.com/2007/02/fibonacci-sequence-at-zrich.html

скачатьДанный реферат составлен на основе статьи из русской Википедии. Синхронизация выполнена 12.07.11 19:26:18Похожие рефераты: Фибоначчи, Код Фибоначчи, Кодирование Фибоначчи, Дерево Фибоначчи, Метод Фибоначчи с запаздываниями, Метод чисел Фибоначчи.

Категории: Теория чисел, Золотое сечение, Целочисленные последовательности.

Текст доступен по лицензии Creative Commons Attribution-ShareAlike.

wreferat.baza-referat.ru

Доклад: "Ряд Фибоначчи"

Выдержка из работы

Фибоначчи Леонардо Пизанский (лат. Leonardo Pisano, Пиза, около 1170 -- около 1250) -- это первый крупный математик средневековой Европы. Более известен под прозвищем Фибонамччи (Fibonacci), что в переводе с итальянского означает «хороший сын родился» (Figlio Buono Nato Ci).

О бытие Фибоначчи известно немного. Неизвестна даже точная дата его рождения. Предполагается, что Фибоначчи родился предположительно в 1170 г

Леонардо Фибоначчи был знаменитым итальянским математиком, он славился своим умением делать расчеты. Однажды его осенило и он открыл простую последовательность чисел, соотношения между которыми описывали естественные пропорции всех тел вселенной!

Леонардо Фибоначчи был выдающимся математиком средневековья. Плоды его математических трудов применяются во многих науках, искусстве и повседневной жизни по сей день.

Заслугой Леонардо Фибоначчи является ряд чисел Фибоначчи. Считается, что об этом ряде было известно на Востоке, но именно Леонардо Фибоначчи опубликовал этот ряд чисел в книге «Liber Abaci» (сделал он это для демонстрации размножения популяции кроликов).

Эллиотт писал: «Закон пpиpоды включает в pассмотpение важнейший элемент- ритмичность. Закон пpиpоды — это не некая система, не метод игры на рынке, а явление, хаpактеpное, видимо, для хода любой человеческой деятельности. Его применение в пpогнозиpовании революционно. «

Этот шанс предсказать движения цен побуждает легионы аналитиков трудиться денно и нощно. Мы сосредоточимся на способности делать предсказания и попытаемся выяснить, возможно это или нет. Вводя свой подход, Эллиотт был очень конкретен. Он писал: «Любой человеческой деятельности присущи три отличительных особенности: форма, время и отношение, -и все они подчиняются суммационной последовательности Фибоначчи».

Последовательность Фибоначчи, известная всем по фильму «Код Да Винчи» — ряд цифр, описанный в виде загадки Итальянским математиком Леонардо Пизанским, более известным под прозвищем Фибоначчи, в XIII веке. Вкратце суть загадки:

Кто-то поместил пару кроликов в некоем замкнутом пространстве, чтобы узнать, сколько пар кроликов родится при этом в течении года, если природа кроликов такова, что каждый месяц пара кроликов производит на свет другую пару, а способность к производству потомства у них появляется по достижению двухмесячного возраста.

Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр.

Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т. д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т. д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21: 34 = 0,617, а 34: 55 = 0,618. Это отношение обозначается символом Ф. Только это отношение — 0,618: 0,382 — дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему.

Фибоначчи так же занимался решением практических нужд торговли: с помощью какого наименьшего количества гирь можно взвесить товар? Фибоначчи доказывает, что оптимальной является такая система гирь: 1, 2, 4, 8, 16…

У этой последовательности есть ряд математических особенностей, которых обязательно нужно коснуться. Данная последовательность асимптотически (приближаясь все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.

Так отношение какого-либо члена последовательности к предшествующему ему колеблется около числа 1,618, через pаз то превосходя, то не достигая его. Отношение к следующему аналогично приближается к числу 0,618, что обратно пропорционально 1,618. Если мы будем делить элементы последовательности через одно, то получим числа 2,618 и 0,382, которые так же являются обратно пропорциональными. Это так называемые коэффициенты Фибоначчи.

Природа как бы решает задачу сразу с двух сторон и складывает полученные результаты. Как только получает в сумме 1, то осуществляет переход в следующее измерение, где начинает строить все сначала. Но тогда она и должна строить это золотое сечение по определенному правилу. Природа не пользуется золотым сечением сразу. Она его получает путем последовательных итераций и для порождения золотого сечения пользуется другим рядом, — рядом Фибоначчи.

Чудесные свойства ряда Фибоначчи проявляются и в самих числах, являющихся членами этого ряда. Расположим члены ряда Фибоначчи по вертикали., а затем вправо, в порядке убывания, запишем натуральные числа.

2 1

3 2

5 4 3

8 7 6 5

13 12 11 10 9 8

21 20 19 18 17 16 15 14 13

34 33 32 31 30 29 28 27 26 25 24 23 22 21

55 54 53 52 51 50 49 48 47 46 45 44 43 42 41 40 39 38 37 36 35 34

Каждая строчка начинается и завершается числом Фибоначчи, т. е. в каждой строчке всего два таких числа. «синие» числа — 4, 7, 6, 11, 10, 18, 16, 29, 26, 47, 42 обладают особыми свойствами (второй уровень иерархии ряда Фибоначчи):

(5−4)/(4−3) = 1/1

(8−7)/(7−5) = ½ и (8−6)/(6−5) = 2/1

(13−11)/(11−8) = 2/3 и (13−10)/(10−8) = 3/2

(21−18)/(18−13) = 3/5 и (21−16)/(1б-13) = 5/3

(34−29)/(29−21) = 5/8 и (34−26)/(26−21) = 8/5

(55−47)/(47−34) = 8/13 и (55−42)/(42−34) = 13/8

Мы получили дробный ряд Фибоначчи, который, возможно, «исповедуют» коллективные спины элементарных частиц и атомов химических элементов.

Представим эти числа как последовательность рычажных весов

К чему всё это? Так мы приближаемся к одному из самых загадочных явлений природы. Фибоначчи по сути не открыл ничего нового, он просто напомнил миру о таком явлении, как Золотое Сечение, которое не уступает по значимости теореме Пифагора.

Все окружающие нас предметы мы различаем в том числе и по форме. Какие-то нам нравятся больше, какие-то меньше, некоторые вовсе отталкивают взгляд. Иногда интерес может быть продиктован жизненной ситуацией, а порой красотой наблюдаемого объекта. Симметричная и пропорциональная форма, способствует наилучшему зрительному восприятию и вызывает ощущение красоты и гармонии. Целостный образ всегда состоит из частей разного размера, находящихся в определённом соотношении друг с другом и целым. Золотое сечение — высшее проявление совершенства целого и его частей в науке, искусстве и природе.

Если на простом примере, то Золотое Сечение — это деление отрезка на две части в таком соотношении, при котором большая часть относится к меньшей, как их сумма (весь отрезок) к большей.

Если мы примем весь отрезок c за 1, то отрезок a будет равен 0,618, отрезок b — 0,382, только так будет соблюдено условие Золотого Сечения (0,618/0,382=1,618; 1/0,618=1,618). Отношение c к a равно 1,618, а с к b 2,618. Это всё те же, уже знакомые нам, коэффициенты Фибоначчи.

Разумеется есть золотой прямоугольник, золотой треугольник и даже золотой кубоид. Пропорции человеческого тела во многих соотношениях близки к Золотому Сечению.

Но самое интересное начинается, когда мы объединим полученные знания. На рисунке наглядно показана связь между последовательностью Фибоначчи и Золотым сечением. Мы начинаем с двух квадратов первого размера. Сверху добавляем квадрат второго размера. Подрисовываем рядом квадрат со стороной, равной сумме сторон двух предыдущих, третьего размера. По аналогии появляется квадрат пятого размера. И так далее пока не надоест, главное, чтобы длина стороны каждого следующего квадрата равнялась сумме длин сторон двух предыдущих. Мы видим серию прямоугольников, длины сторон, которых являются числами Фибоначчи, и, как не странно, они называются прямоугольниками Фибоначчи.

Если мы проведём плавную линий через углы наших квадратов, то получим ни что иное, как спираль Архимеда, увеличение шага которой всегда равномерно.

Ряд Фибоначчи — это не только математическая загадка, мы встречаемся с ним каждый день в повседневной жизни:

И не только в раковине моллюска можно найти спирали Архимеда, а во многих цветах и растениях, просто они не такие явные.

Раковина в форме спирали — форма раковины заинтересовала Архимеда и он выяснил, что увеличение длины завитков раковины — это постоянная величина и равна она 1,618.

Алое многолистный.

Брокколи романеско.

Подсолнечник: Семена в подсолнухе, располагаются так же в виде спирали.

Сосновая шишка.

Рост растений тоже происходит в соответствии с числовым рядом Фибоначчи — от ствола отходит ветка, на которой появляется лист, затем происходит длинный выброс и снова появляется листок, но он уже короче предыдущего. Затем опять выброс, но и он короче предыдущего. В этой картине, первый выброс равен 100%, второй 62%, а третий 38%(уровни Фибоначчи, используемые в торговле) и т. д. С длиной лепестков все выглядит точно так же.

Ящерица — если поделить ящерицу на хвост и тело, то соотношение их будет 0,62 к 0,38.

Пирамиды — длина ребра пирамиды равна 783.3 футам, а высота пирамиды равна 484.4 футам. Соотношение длины ребра/высота пирамиды составляет 1,618.

А если взглянуть чуть подальше, то можно разглядеть последовательность Фибоначчи в недосягаемых галактиках.

Как видно, числовой ряд Фибоначчи широко представлен в нашей жизни: в строении живых существ, сооружений, с его помощью даже описывается устройство Галактик. Все это свидетельствует об универсальности математической загадки числового ряда Фибоначчи.

И тут самое время вспомнить о Золотом Сечении! Ни одни ли из самых прекрасных и гармоничных творений природы изображены на этих фотографиях? И это далеко не все. Присмотревшись, можно найти похожие закономерности во многих формах.

Конечно заявление, что все эти явление построены на последовательности Фибоначчи звучит слишком громко, но тенденция на лицо. Да и к тому же сама последовательность далека от совершенства, как и всё в этом мире.

Есть предположение, что последовательность Фибоначчи — это попытка природы адаптироваться к более фундаментальной и совершенной золотое сечение логарифмической последовательности, которая практически такая же, только начинается из ниоткуда и уходит в никуда. Природе же обязательно нужно какое-то целое начало, от которого можно оттолкнуться, она не может создать что-то из ничего. Отношения первых членов последовательности Фибоначчи далеки от Золотого Сечения. Но чем дальше мы продвигаемся по ней, тем больше эти отклонения сглаживаются. Для определения любой последовательности достаточно знать три её члена, идущие друг за другом. Но только не для золотой последовательности, ей достаточно двух, она является геометрической и арифметической прогрессией одновременно. Можно подумать, будто она основа для всех остальных последовательностей.

Каждый член золотой логарифмической последовательности явлется степенью Золотой Пропорции (z). Часть ряда выглядит примерно так: … z-5; z-4; z-3; z-2; z-1; z0; z1; z2; z3; z4; z5 … Если мы округлим значение Золотой пропорции до трёх знаков, то получим z=1,618, тогда ряд выглядит так: … 0,090 0,146; 0,236; 0,382; 0,618; 1; 1,618; 2,618; 4,236; 6,854; 11,090 … Каждый следующий член может быть получен не только умножением предыдущего на 1,618, но и сложением двух предыдущих. Таким образом экспоненциальный рост в последовательности обеспечивается путем простого сложения двух соседних элементов. Это ряд без начала и конца, и именно на него пытается быть похожей последовательность Фибоначчи. Имея вполне определённое начало, она стремится к идеалу, никогда его не достигая. Такова жизнь.

И всё-таки, в связи со всем увиденным и прочитанным, возникают вполне закономерные вопросы:

От куда взялись эти числа? Кто этот архитектор вселенной, попытавшийся сделать её идеальной? Было ли когда-то всё так, как он хотел? И если да, то почему сбилось? Мутации? Свободный выбор? Что же будет дальше? Спираль скручивается или раскручивается?

Найдя ответ на один вопрос, получишь следующий. Разгадаешь его, получишь два новых. Разберёшься с ними, появится ещё три. Решив и их, обзаведёшься пятью нерешёнными. Потом восьмью, потом тринадцатью, 21, 34, 55…

Прикладное значение ряда Фибоначчи и Золотого Сечения заслуживает отдельного сайта. Сейчас лишь скажу, что, например, элементы ряда Фибоначчи применяются для вычисления скользящих средних (не говоря уже о росте популяции кроликов), и шедевры мирового искусства содержат в себе Золотое Сечение.

А пока, помните, что Фибоначчи -- легендарная личность в математике, экономике и финансах; он обнародовал Арабские числа и представил магический ряд чисел.

ряд число фибоначчи

Показать Свернуть

gugn.ru

Реферат - Тема: Числа Фибоначчи и золотое сечение

Тема: «Числа Фибоначчи и золотое сечение"

1.Введение. Пропорция золотого сечения. Ф и φ.

"Геометрия обладает двумя великими сокровищами. Первое - это теорема Пифагора,

второе - деления отрезка в крайнем и среднем отношении"

Иоганн Кеплер

Правильные многоугольники привлекали внимание древнегреческих учёных ещё задолго да Архимеда. Пифагорейцы, выбравшие эмблемой своего союза пентаграмму - пятиконечную звезду, придавали очень большое значение задаче о делении окружности на равные части, то есть о построении правильного вписанного многоугольника. Альбрехт Дюрер (1471-1527гг), ставший олицетворением Возрождения в Германии приводит теоретически точный способ построения правильного пятиугольника, заимствованный из великого сочинения Птолемея "Альмагест".

Интерес Дюрера к построению правильных многоугольников отражает использование их в Средние века в арабских и готических орнаментах, а после изобретения огнестрельного оружия - в планировке крепостей.

Средневековые способы построения правильных многоугольников носили приближенный характер, но были (или не могли не быть) простыми: предпочтение отдавалось способам построения, не требующим даже изменять раствор циркуля. Леонардо да Винчи также много писал о многоугольниках, но именно Дюрер, а не Леонардо, передал средневековые способы построения потомкам. Дюрер, конечно, был знаком с " Началами" Евклида, но не привел в своем "Руководстве к измерению" (о построениях при помощи циркуля и линейки) предложенный Евклидом способ построения правильного пятиугольника, теоретически точный, как и все евклидовы построения. Евклид не пытается разделить заданную дугу окружности на три равные части, и Дюрер знал, хотя доказательство было найдено лишь в XIX веке, что эта задача неразрешима.

Предложенное Евклидом построение правильного пятиугольника включает в себя деление отрезка прямой в среднем и крайнем отношении, названное впоследствии золотым сечением и привлекавшим к себе внимание художников и архитекторов на протяжении нескольких столетий.

Точка В делит отрезок АВЕ в среднем и крайнем отношении или образует золотое сечение, если отношение большей части отрезка к меньшей равно отношению всего отрезка к большей части.

Записанное в виде равенства отношений золотое сечение имеет вид АВ/ВЕ= АВ/АЕ

Если положить АВ=а, а ВЕ=а/Ф так, чтобы золотое отношение было равно АВ/ВЕ=Ф, то получается соотношение

Ф = 1+1/Ф

То есть Ф удовлетворяет уравнению

Ф2- Ф-1=0

Это уравнение имеет один положительный корень

Ф=(√5+1)/2=1.618034….

Заметим, что 1/Ф = (√5 -1 )/2, так как (√5-1)(√5+1) =5-1=4. За 1/Ф принято считать φ=0.618034….

Ф и φ - прописная и строчная формы греческой буквы "фи".

Такое обозначение принято в честь древнегреческого скульптора Фидия (V век до н. э.) Фидий руководил строительством храма Парфенон в Афинах. В пропорциях этого храма многократно присутствует число φ .

^ 2.История золотого сечения

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамсеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

Греки же были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.

Рис. 7. Динамические прямоугольники

Платон (427...347гг. до н.э.) также знал о золотом делении. Его диалог "Тимей" посвящен математическим и эстетическим воззрениям школы Пифагора и, в

частности, вопросам золотого деления.

Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по «золотому сечению», то получим те или иные выступы фасада. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.

^ Рис.8. Парфенон

Рис. 9. Античный циркуль золотого сечения

В дошедшей до нас античной литературе золотое деление впервые упоминается в "Началах" Евклида. Во 2-й книге "Начал" дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др.. В средневековой Европе с золотым делением познакомились по арабским переводам "Начал" Евклида. Переводчик Дж.Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.

В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением, как в геометрии, так и в искусстве, особенно в архитектуре. Леонардо да Винчи, художник и ученый, видел, что в итальянских художниках большой эмпирический опыт, но недостаток знаний. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем.

Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509г. в Венеции была издана книга Луки Пачоли "Божественная пропорция" с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее "божественную суть" как выражение божественного триединства: бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок - бога отца, а весь отрезок - бога духа святого).

Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.

В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет: "Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать".

Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица - ртом и т.д. Известен пропорциональный циркуль Дюрера.

Построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).

Если на прямой произвольной длины, отложить отрезок m(φ), рядом откладываем отрезок M. На основании этих двух отрезков выстраиваем шкалу отрезков золотой пропорции восходящего и нисходящего рядов

Рис. 10. Построение шкалы отрезков золотой пропорции

В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы "вместе с водой выплеснули и ребенка". Вновь "открыто" золотое сечение было в середине XIX в. В 1855г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд "Эстетические исследования". С Цейзингом произошло именно то, что и должно было неминуемо произойти с исследователем, который рассматривает явление как таковое, без связи с другими явлениями. Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях "математической эстетикой".

^ 3. Построение пропорции.

Здесь приводится построение точки Е, делящий отрезок прямой в пропорции золотое сечение.

^ Рис. 1. Деление отрезка прямой по золотому сечению. BC = 1/2 AB; CD = BC

Из точки В восстанавливается перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.

Именно эти отрезки использовал Евклид при построении правильного пятиугольника, т.к. каждая из сторон пятиугольной звезды делится другими именно в такой пропорции.

Таким образом, звездчатый пятиугольник также обладает «золотым сечением». Интересно, что внутри пятиугольника можно продолжить строить пятиугольники, и это отношение будет сохраняться.

Звездчатый пятиугольник называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком.

В настоящее время существует гипотеза, что пентаграмма – первичное понятие, а «золотое сечение» вторично. Пентаграмму никто не изобретал, ее только скопировали с натуры. Вид пятиконечной звезды имеют пятилепестковые цветы плодовых деревьев и кустарников, морские звезды. Те и другие создания природы человек наблюдает уже тысячи лет. Поэтому естественно предположить, что геометрический образ этих объектов – пентаграмма – стала известна раньше, чем «золотая» пропорция.

^ 4.Второе золотое сечение.

Болгарский журнал «Отечество» (№10, 1983 г.) опубликовал статью Цветана Цекова-Карандаша «О втором золотом сечении», которое вытекает из основного сечения и дает другое отношение 44 : 56.

Такая пропорция обнаружена в архитектуре, а также имеет место при построении композиций изображений удлиненного горизонтального формата.

Деление осуществляется следующим образом. Отрезок АВ делится в пропорции золотого сечения. Из точки С восставляется перпендикуляр СD. Радиусом АВ находится точка D, которая соединяе Рис. 2. Построение второго золотого сечения

тся линией с точкой А. Прямой угол АСD делится пополам. Из точки С проводится линия до пересечения с линией AD. Точка Е делит отрезок AD в отношении 56:44.

На рисунке показано положение линии второго золотого сечения. Она находится посередине между линией золотого сечения и средней линией прямоугольника.

Рис. 3. Деление прямоугольника линией второго золотого сечения

Таким образом было доказано, что разделить отрезок в крайнем и среднем отношении можно не единственным способом.

Рис.6. Построение правильного пятиугольника и пентаграммы.

5. "Золотые" фигуры.

^ 5.1.Золотой прямоугольник:

Если построить квадрат со стороной АВ=а, найти середину М отрезка АВ и провести дугу окружности радиусом МС с центром в точке М до пересечения с продолжением стороны АВ в точке Е, то точка В разделит отрезок АЕ в крайнем и среднем отношении.

Чтобы убедиться в этом, заметим, что по теореме Пифагора

МС2=а2+(а/2)2=5а2/4

В силу чего

АЕ=а/2 +МЕ=(√5+1)а/2=φАВ

Прямоугольник АЕFD со сторонами АЕ=φАD называется золотым прямоугольником. Четырехугольник АВСD - квадрат. Нетрудно видеть, что прямоугольник ВЕFС также золотой, поскольку BC=a=φВЕ. Это обстоятельство сразу наводит на мысль о дальнейшем разбиении прямоугольника ВЕFС.

Можно ли считать, что прямоугольник с отношением сторон, равным φ, выглядит изящнее, чем прямоугольники с отношением сторон, скажем, 2:1, 3:2 или 5:7? Чтобы ответить на этот вопрос, были проведены специальные эксперименты. Результаты их не вполне убедительны, но все же свидетельствуют о некотором предпочтении, отдаваемом золотому сечению. Впрочем, может ли прямоугольник сам по себе быть захватывающе прекрасным или отталкивающе безобразным?

^ 5.2.Золотой треугольник:

Проводим прямую АВ. От точки А откладываем на ней три раза отрезок О произвольной величины, через

полученную точку Р проводим перпендикуляр к линии

АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1

откладываем на линию Ad1, получая точку С. Она разделила линию Ad1 в пропорции золотого сечения. Линиями Ad1 и dd1 пользуются для построения «золотого» прямоугольника.

^ 5.3. Золотой пятиугольник; построение Евклида.

Замечательный пример «золотого сечения» представляет собой правильный пятиугольник – выпуклый и звездчатый (рис.5).

Для построения пентаграммы необходимо построить правильный пятиугольник.

Пусть О - центр окружности, А - точка на окружности и Е - середина отрезка ОА. Перпендикуляр к радиусу ОА, восстановленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.

Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.

Есть и золотой кубоид- это прямоугольный параллелепипед с ребрами, имеющими длины 1.618, 1 и 0.618.

Теперь рассмотрим доказательство, предложенное Евклидом в «Началах».

Посмотрим теперь, как Евклид использует золотое сечение для того, чтобы построить угол в 72 градуса – именно под таким углом видна сторона правильного пятиугольника из центра описанной окружности. Начнем с отрезка АВЕ, разделенного в среднем и крайнем отношении точкой В. Проведем далее дуги окружностей с центрами в точках В и Е и радиусах АВ, пересекающиеся в точке С. Чуть ниже докажем, что АС=АЕ, а пока примем это на веру.

Итак, пусть АС=АЕ. Обозначим через  равные углы ЕВС и СЕВ. Так как АС=АЕ, то угол АСЕ также равен . Теорема о том, что сумма углов треугольника равна 180 градусов, позволяет найти угол ВСЕ: он равен 180-2, а угол ЕАС - 3 - 180. Но тогда угол АВС равен 180-. Суммируя углы треугольника АВС получаем,

180=(3 -180) + (3-180) + (180 - )

Откуда 5=360, значит =72.

Итак, каждый из углов при основании треугольника ВЕС вдвое больше угла при вершине, равного 36 градусов. Следовательно, чтобы построить правильный пятиугольник, необходимо лишь провести любую окружность с центром в точке Е, пересекающую ЕС в точке Х и сторону ЕВ в точке Y: отрезок XY служит одной из сторон вписанного в окружность правильного пятиугольника; Обойдя вокруг всей окружности, можно найти и все остальные стороны.

Докажем теперь, что АС=АЕ. Предположим, что вершина С соединена отрезком прямой с серединой N отрезка ВЕ. Заметим, что поскольку СВ=СЕ, то угол СNЕ прямой. По теореме Пифагора:

CN2 = а2 – (а/2) 2= а2 (1-4 2)

Отсюда имеем (АС/а) 2 = (1+1/2) 2 + (1-1/4 2) = 2+1/ = 1 +  = 2

Итак, АС = а = АВ = АЕ, что и требовалось доказать

^ 5.4.Спираль Архимеда.

Последовательно отсекая от золотых прямоугольников квадраты до бесконечности, каждый раз соединяя противоположные точки четвертью окружности, мы получим довольно изящную кривую. Первым внимание на неё обратил древнегреческий ученый Архимед, имя которого она и носит. Он изучал её и вывел уравнение этой спирали.

Рис.7.Спираль Архимеда

В настоящее время спираль Архимеда широко используется в технике.

^ 6.Числа Фибоначчи.

С золотым сечением косвенно связано имя итальянского математика Леонардо из Пизы, который известен больше по своему прозвищу Фибоначчи (Fibonacci - сокращенное filius Bonacci, то есть сын Боначчи)

В 1202г. им была написана книга "Liber abacci", то есть "Книга об абаке" . "Liber abacci" представляет собой объемистый труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший заметную роль в развитии математики в Западной Европе в течение нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими ("арабскими") цифрами.

Сообщаемый в книге материал поясняется на большом числе задач, составляющих значительную часть этого трактата.

Рассмотрим одну такую задачу:

"Сколько пар кроликов в один год от одной пары рождается?

Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, дабы узнать, сколько пар кроликов родится в течение этого года, если природа кроликов такова, что через месяц пара кроликов воспроизведет другую, а рождают кролики со второго месяца после своего рождения"

Месяцы

Пары кроликов

144

233

377

Табл.1 Ряд Фибоначчи при u1=1

Перейдем теперь от кроликов к числам и рассмотрим следующую числовую последовательность:

u1, u2 … un

в которой каждый член равен сумме двух предыдущих, т.е. при всяком n>2

un=un-1+un-2.

Данная последовательность асимптотически (приближаясь все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.

Если какой-либо член последовательности Фибоначчи разделить на предшествующий ему (например, 13:8), результатом будет величина, колеблющаяся около иррационального значения 1.61803398875... и через раз то превосходящая, то не достигающая его.

Асимптотическое поведение последовательности, затухающие колебания ее соотношения около иррационального числа Ф могут стать более понятными, если показать отношения нескольких пеpвых членов последовательности. В этом примере приведены отношения второго члена к первому, третьего ко второму, четвертого к третьему, и так далее:

1:1 = 1.0000, что меньше фи на 0.6180

2:1 = 2.0000, что больше фи на 0.3820

3:2 = 1.5000, что меньше фи на 0.1180

5:3 = 1.6667, что больше фи на 0.0486

8:5 = 1.6000, что меньше фи на 0.0180

По мере продвижения по суммационной последовательности Фибоначчи каждый новый член будет делить следующий со все большим и большим приближением к недостижимому Ф.

Человек подсознательно ищет Божественную пропорцию: она нужна для удовлетворения его потребности в комфорте.

Пpи делении любого члена последовательности Фибоначчи на следующий за ним получается просто обратная к 1.618 величина (1 : 1.618=0.618). Hо это тоже весьма необычное, даже замечательное явление. Поскольку пеpвоначальное соотношение – бесконечная дpобь, у этого соотношения также не должно быть конца.

При делении каждого числа на следующее за ним через одно, получаем число 0.382

1:0.382=2.618

Подбирая таким образом соотношения, получаем основной набор коэффициентов Фибоначчи: 4.235, 2.618, 1.618, 0.618, 0.382, 0.236.Упомянем также 0.5. Все они играют особую роль в природе и в частности в техническом анализе.

Дpугой важный факт состоит в том, что квадpат любого числа Фибоначчи pавен числу, стоящему в последовательности пеpед ним, умноженному на число, стоящее после него, плюс или минус 1.

5 = (3 x 8) + 1

8 = (5 x 13) - 1

13 = (8 x 21) + 1

Плюс и минус постоянно чеpедуются. Это еще одно пpоявление неотъемлемой части волновой теоpии Эллиотта, называемой пpавилом чеpедования. Оно гласит, что сложные коppективные волны чеpедуются с пpостыми, сильные импульсные волны со слабыми коppективными волнами, и так далее.

Тут необходимо отметить, что Фибоначчи лишь напомнил свою последовательность человечеству, так как она была известна еще в древнейшие времена под названием Золотое сечение.

Золотое сечение, как мы видели, возникает в связи с правильным пятиугольником, поэтому и числа Фибоначчи играют роль во всем, что имеет отношение к правильным пятиугольникам - выпуклым и звездчатым.

Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления. Ученые продолжали активно развивать теорию чисел Фибоначчи и золотого сечения. Ю. Матиясевич с использованием чисел Фибоначчи решает 10-ю проблему Гильберта (о решении Диофантовых уравнений). Возникают изящные методы решения ряда кибернетических задач (теории поиска, игр, программирования) с использованием чисел Фибоначчи и золотого сечения. В США создается даже Математическая Фибоначчи-ассоциация, которая с 1963 года выпускает специальный журнал.

Одним из достижений в этой области является открытие обобщенных чисел Фибоначчи и обобщенных золотых сечений. Ряд Фибоначчи (1, 1, 2, 3, 5, 8) и открытый им же «двоичный» ряд чисел 1, 2, 4, 8, 16...(то есть ряд чисел до n , где любое натуральное число, меньшее n можно представить суммой некоторых чисел этого ряда) на первый взгляд совершенно разные. Но алгоритмы их построения весьма похожи друг на друга: в первом случае каждое число есть сумма предыдущего числа с самим собой 2 = 1 + 1; 4 = 2 + 2..., во втором – это сумма двух предыдущих чисел 2 =1 + 1, 3 = 2 + 1, 5 = 3 + 2.... Нельзя ли отыскать общую математическую формулу, из которой получаются и «двоичный» ряд, и ряд Фибоначчи?

Действительно, зададимся числовым параметром S, который может принимать любые значения: 0, 1, 2, 3, 4, 5... Рассмотрим числовой ряд, S + 1 первых членов которого – единицы, а каждый из последующих равен сумме двух членов предыдущего и отстоящего от предыдущего на S шагов. Если n-й член этого ряда мы обозначим через S (n), то получим общую формулу S (n) = S (n – 1) + S (n – S – 1).

Очевидно, что при S = 0 из этой формулы мы получим «двоичный» ряд, при S = 1 –ряд Фибоначчи, при S = 2, 3, 4. новые ряды чисел, которые получили название S-чисел Фибоначчи.

В общем виде золотая S-пропорция есть положительный корень уравнения золотого S-сечения xS+1 – xS – 1 = 0.

Нетрудно показать, что при S = 0 получается деление отрезка пополам, а при S = 1 – знакомое классическое золотое сечение.

Отношения соседних S-чисел Фибоначчи с абсолютной математической точностью совпадают в пределе с золотыми S-пропорциями! То есть золотые S-сечения являются числовыми инвариантами S-чисел Фибоначчи.

^ 7.Золотое сечение в искусстве.

7.1. Золотое сечение в живописи.

Переходя к примерам «золотого сечения» в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды».

Нет сомнений, что Леонардо да Винчи был великим художником, это признавали уже его современники, но его личность и деятельность останутся покрытыми тайной, так как он оставил потомкам не связное изложение своих идей, а лишь многочисленные рукописные наброски, заметки, в которых говорится «обо всем на свете».

Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника..

Также пропорция золотого сечения проявляется в картине Шишкина. На этой знаменитой картине И. И. Шишкина с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны - освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали.

В картине Рафаэля "Избиение младенцев" просматривается другой элемент золотой пропорции - золотая спираль. На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции - точки, где пальцы воина сомкнулись вокруг лодыжки ребенка - вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Неизвестно, строил ли Рафаэль золотую спираль или чувствовал её.

Т.Кук использовал при анализе картины Сандро Боттичелли «рождение Венеры» золотое сечение.

^ 7.2. Пирамиды золотого сечения.

Широко известны медицинские свойства пирамид, особенно золотого сечения. По некоторым наиболее распространенным мнениям, комната, в которой находится такая пирамида, кажется больше, а воздух - прозрачнее. Сны начинают запоминаться лучше. Также известно, что золотое сечение широко применялась в архитектуре и скульптуре. Примером тому стали: Пантеон и Парфенон в Греции, здания архитекторов Баженова и Малевича

8. Заключение.

Необходимо сказать, что золотое сечение имеет большое применение в нашей жизни.

Было доказано, что человеческое тело делится в пропорции золотого сечения линией пояса.

Раковина наутилуса закручена подобно золотой спирали.

Благодаря золотому сечению был открыт пояс астероидов между Марсом и Юпитером – по пропорции там должна находиться ещё одна планета.

Возбуждение струны в точке , делящей её в отношении золотого деления, не вызовет колебаний струны, то есть это точка компенсации.

На летательных аппаратах с электромагнитными источниками энергии создаются прямоугольные ячейки с пропорцией золотого сечения.

Джоконда построена на золотых треугольниках, золотая спираль присутствует на картине Рафаэля «Избиение младенцев».

Пропорция обнаружена в картине Сандро Боттичелли «Рождение Венеры»

Известно много памятников архитектуры, построенных с использованием золотой пропорции, в том числе Пантеон и Парфенон в Афинах, здания архитекторов Баженова и Малевича.

Список литературы

1. Д. Пидоу. Геометрия и искусство. – М.: Мир, 1979.

2. Журнал «Квант», 1973, № 8.3. Журнал «Математика в школе», 1994, № 2; № 3.

4. Ковалев Ф.В. Золотое сечение в живописи. К.: Выща школа, 1989.

5. Стахов А. Коды золотой пропорции.

6.Воробьев Н.Н. "Числа Фибоначчи" - М.: Наука 1964

7. "Математика - Энциклопедия для детей" М.: Аванта +, 1998

www.ronl.ru