
Министерство образования и науки Российской Федерации
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ им. А.И. ГЕРЦЕНА»
Санкт-Петербург
РЕФЕРАТ
По дисциплине: Математика
Тема: Дифференциал
Выполнила:
Студентка 1 курса
дневного отделения
факультета управления
направления «Туризм»
Сахарова Анна Ильинична
Санкт-Петербург
2012
Дифференциа́л (от лат. differentia — разность, различие)
в математике, главная линейная часть приращения функции. Если функция y = f (x) одного переменного х имеет при х = х0производную, то приращение
Δy = f (x0 + Δx) - f (x0)
функции f (x) можно представить в виде
Δy = f' (x0) Δx + R,
где член R бесконечно мал по сравнению с Δх. Первый член
dy = f' (x0) Δх
в этом разложении и называется дифференциалом функции f (x) в точке x0. Из этой формулы видно, что дифференциал dy линейно зависит от приращения независимого переменного Δx, а равенство
Δy = dy + R
показывает, в каком смысле Д. dy является главной частью приращения Δy.
Обобщение понятия дифференциала. Обобщение понятия Д. на вектор-функции, начало которому положили в начале 20 в. французские математики Р. Гато и М. Фреше, позволяет лучше выяснить смысл понятия «дифференциал» для функций нескольких переменных, а в применении к Функционалам приводит к понятию вариации, лежащему в основе вариационного исчисления (См.Вариационное исчисление).Важную роль в этом обобщении играет понятие линейной функции (линейного отображения). Функция L (x) векторного аргумента хназывается линейной, если она непрерывна и удовлетворяет равенству
L (x' + х ") = L (x') + L (x ")
для любых х' и х " из области определения. Линейная функция n-мерного аргумента х = {x1,..., xn} всегда имеет вид
L (x) = a1x1 +... + anxn,
где a1,..., an — постоянные. Приращение
ΔL = L (x + h) - L (x)
линейной функции L (x) имеет вид
ΔL = L (h),
т. е. зависит только от векторного приращения h, и притом линейно. Функция f (x) называется дифференцируемой при значении аргумента х, если её приращение Δf = f (x + h) - f (x), рассматриваемое как функция от h, имеет главную линейную часть L (h), т. е. выражается в виде
Δf = L (h) + R (h),
где остаток R (h) при h → 0 бесконечно мал по сравнению с h. Главная линейная часть L (h) приращения Δf и называется дифференциалом df функции f в точке x. При этом в зависимости от того, в каком смысле понимается бесконечная малость R (h) по сравнению с h, различают слабый дифференциал, или дифференциал Гато, и сильный дифференциал, или дифференциал Фреше. Если существует сильный Д., то существует и слабый Д., равный сильному Д. Слабый Д. может существовать и тогда, когда сильный не существует.
В случае f (x) ≡ x из общего определения следует, что df = h, т. е. можно приращение h считать Д. аргумента x и обозначать dx.
Если сделать теперь переменной точку x, в которой определяется Д. df, то он будет функцией двух переменных:
df (x; h).
Далее, считая h = h2 постоянным, можно найти Д. от дифференциала df (x; h2) как главную часть приращения
df (x + h3; h2) — df (x; h2),
где h3 — некоторое второе, не связанное с h2 приращение x. Получаемый таким образом второй дифференциал d2f = d2f (x; h2, h3) является функцией трёх векторных аргументов x, h2 и h3, линейной по каждому из двух последних аргументов. Если d2f непрерывно зависит от x, то он симметричен относительно h2 и h3:
d2f (x; h2, h3) = d2f (x; h3, h2).
Аналогично определяется дифференциал dnf = dnf (x; h2,..., hn) любого порядка n.
В вариационном исчислении сам векторный аргумент x является функцией x (t), а дифференциалы df и d2f функционала f [x (t)] называются его первой и второй вариациями и обозначаются δf и δ2f.
Всюду выше речь шла об обобщении понятия Д. на числовые функции векторного аргумента. Существует обобщение понятия Д. и на случай вектор-функций, принимающих значения в банаховых пространствах.
Лит.: Ильин В. А., Позняк Э. Г., Основы математического анализа, 2 изд., М., 1967; Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 2 изд., М., 1968; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 1, М., 1969; Кудрявцев Л. Д., Математический анализ, т. 1, М., 1970; Рудин У., Основы математического анализа, пер. с англ., М., 1966; Дьедонне Ж., Основы современного анализа, пер. с англ., М., 1964.
А. Н. Колмогоров.
II Дифференциа́л Дифференциальный механизм в приводе ведущих колёс автомобиля, трактора или др. транспортных машин. Д. обеспечивает вращение ведущих колёс с разными относительными скоростями при прохождении кривых участков пути.annettesa.livejournal.com

 |
 Репетитор: Васильев Алексей Александрович Репетитор: Васильев Алексей Александрович
Стоимость: 2000 руб / 90 мин. |
 |
 Репетитор: Крюков Илья Хассанович Репетитор: Крюков Илья Хассанович
Стоимость: 1600 руб / 60 мин. |
 |
 Репетитор: Скрипаленко Михаил Михайлович Репетитор: Скрипаленко Михаил Михайлович
Стоимость: 1200 руб / 60 мин. |
 |
 Репетитор: Матвеева Милада Андреевна Репетитор: Матвеева Милада Андреевна
Стоимость: 1200 руб / 60 мин. |
 |
 Репетитор: Тверской Василий Борисович Репетитор: Тверской Василий Борисович
Стоимость: 3500 руб / 90 мин. |
 |
 Репетитор: Поздняков Андрей Александрович Репетитор: Поздняков Андрей Александрович
Стоимость: 2000 руб / 60 мин. |
 |
 Репетитор: Ершикова Марина Львовна Репетитор: Ершикова Марина Львовна
Стоимость: 1500 руб / 60 мин. |

Допустим функция y=f(x) определена на промежутке Х и дифференцируема в некоторой окресности точки xϵX, т.е. существует производная y'. Согласно теореме о связи бесконечно малых величин с пределами функции запишем:

из рисунка 1 видно, что угол β равен сумме двух углов: ϕ и γ. tg ϕ = f'(x) в точке М, tg β - tg ϕ = а(∆x) представляет собой бесконечно малую величину, зависящую от ∆x.
∆y/∆x = f'(x) + а(∆x)
где а(∆x) - бесконечно малая величина при ∆х →0, откуда
∆y = f'(x)∆x + а(∆x)∆x
из формулы можно увидеть, что приращение функции ∆y состоит из двух слагаемых: линейного относительно ∆x и нелинейного. Таким образом, дифференциалом функции называется главная, линейная часть приращения функции относительно ∆x, равная произведению производной на приращение независимой переменной. dy =f'(x) ∆x или dy = f'(x) dxДопустим задана функция y = f(x). Возьмем произвольную точку М(x,y). Дадим переменной x приращение ∆x. Тогда функция получит приращение ∆y = f(x+∆x) - f(x). (см.рис. 1). Проведем касательную к кривой y = f(x) в точке М, которая образует угол ϕ с положительным направлением оси Ох, т.е f'(x) = tg ϕ. Из прямоугольного треугольника МAB AB = MB · tg ϕ = ∆x tg ϕ = f' (x)∆x т.е. dy = AB. Можно сказать что, дифференциал функции есть приращение ординаты касательной, проведенной к графику функции y = f(x) в данной точке, когда х получает приращение ∆x.

Рис 1. Геометрический смысл дифференциала.
Дифференциал имеет следующие свойства.
1. dc=0 2. d(cu)= c du 3. d(u+v)=du+dv 4. d(uv)=v du + u dv 5. d(u/v) = (v du - u dv) / v²
Дифференциал функции dy = f'(x) dx. Рассмотрим функцию y = f(u), где f(u) является сложной функцией, т.е. y = f(g(x)). Если функции y = f(u) и u = g(x) - дифференцируемые функции от своих аргументов, то производная сложной функции равна:
dy = f'(x) dx = f'(u) · u'dx = f'(u) du. т.е. dy = f'(u) du
Из формулы ∆y = f'(x)∆x + а(∆x)∆x можно увидеть, что приращение функции приблизительно равно ее дифференциалу, т.к. величина а(∆x)∆x бесконечно малая. Именно поэтому, при достаточно малых значениях ∆x можно считать, что ∆y≈ dy т.е. f(x+∆x)≈f(x)+f '(x)∆x. Данная формула тем точнее, чем меньше значение ∆x. Это приближенное равенство можно применить в приближенных вычислениях.


www.mathtask.ru
Определение. Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.
Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента).
Это записывается так:

или
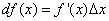
или же
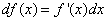
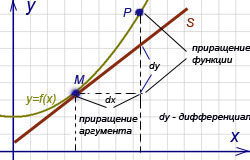
Геометрический смысл дифференциала. Дифференциал функции y = f(x) равен приращению ординаты касательной S, проведённой к графику этой функции в точке M(x; y), при изменении x (аргумента) на величину 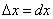 (см. рисунок).
(см. рисунок).
Дифференциал функции в точке x и обозначают
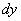
или

Следовательно,
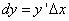 (1)
(1)
или
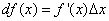 , (2)
, (2)
поскольку дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной.
Замечание. Нужно помнить, что если x – исходное значение аргумента,
а 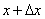 - наращенное значение, то производная в выражении дифференциала берётся в исходной точке x ; в формуле (1) этого не видно из записи.
- наращенное значение, то производная в выражении дифференциала берётся в исходной точке x ; в формуле (1) этого не видно из записи.
Дифференциал функции можно записать в другой форме:
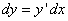 (3)
(3)
или
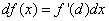 (4)
(4)
Пример 1. Найти дифференциалы функций:
1) 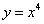 ;
;
2) 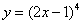 ;
;
3) 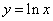 ;
;
4) 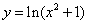 .
.
Решение. Применяя формулы дифференцироивания степенной и логарифмической функций из таблицы производных, а также формулу (4), находим:
1) 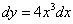 ;
;
2) 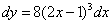 ;
;
3) 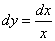 ;
;
4) 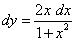 .
.
Пример 2. Найти дифференциал функции
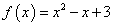
в точке x = 2,
1) выделив линейную часть;
2) по формуле.
Пример 3. Найти дифференциал функции
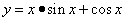
в точке x.
В основном же задачи на дифференциалы - это более сложные, чем рассмотренные выше для разминки, поэтому стоит посетить страницу с решением задач на дифференциалы сложных функций. Скорее всего, вызывающие у вас трудности задачи именно к таким и относятся.
В этом и следующем параграфах каждую из функций будем считать дифференцируемой при всех рассматриваемых значениях её аргументов.
Дифференциал обладает свойствами, аналогичными свойствам производной:
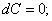 (С – постоянная величина) (5)
(С – постоянная величина) (5)
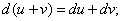 (6)
(6)
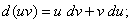 (7)
(7)
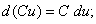 (8)
(8)
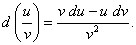 (9)
(9)
Формулы (5) – (9) получаются из соответствующих формул для производной умножением обеих частей каждого равенства на 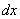 .
.
Одно из особеннейших свойств дифференциала - инвариантность формы дифференциала в случае сложных функций.
Установленное во втором параграфе приближенное равенство
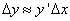
или
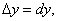 (10)
(10)
позволяет использовать дифференциал для приближенных вычислений значений функции.
Запишем приближенное равенство более подробно. Так как
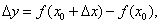
а
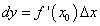
то
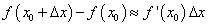
или
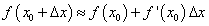 (11)
(11)
Пример 5. Пользуясь понятием дифференциала, вычислить приближенно ln 1,01.
Решение. Число ln 1,01 является одним из значений функции y = ln x . Формула (11) в данном случае примет вид
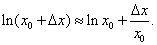
Положим
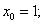
тогда
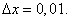
Следовательно,
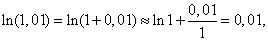
что является очень хорошим приближением: табличное значение ln 1,01 = 0,0100.
Пример 6. Пользуясь понятием дифференциала, вычислить приближенно

Решение. Число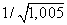 является одним из значений функции
является одним из значений функции
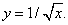
Так как производная этой функции
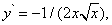
то формула (11) примет вид
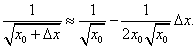
Полагая

и
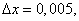
получаем
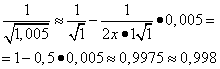
(табличное значение
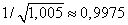 ).
).
Пользуясь приближенным значением числа, нужно иметь возможность судить о степени его точности. С этой целью вычисляют его абсолютную и относительную погрешности.
Абсолютная погрешность  приближенного числа
приближенного числа 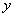 равна абсолютной величине разности между точным числом
равна абсолютной величине разности между точным числом 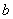 и его приближенным значением:
и его приближенным значением:
 (12)
(12)
Относительной погрешностью 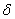 приближенного числа
приближенного числа 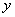 называется отношение абсолютной погрешности этого числа к абсолютной величине соответствующего точного числа:
называется отношение абсолютной погрешности этого числа к абсолютной величине соответствующего точного числа:
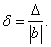 (13)
(13)
Если точное число неизвестно, то
 (14)
(14)
Иногда, прежде чем применить формулу (11), требуется предварительно преобразовать исходную величину. Как правило, это делается в двух целях. Во-первых, надо добиться, чтобы величина 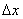 была достаточно малой по сравнению с
была достаточно малой по сравнению с 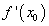 , так как чем меньше
, так как чем меньше 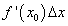 , тем точнее результат приближенного вычисления. Во-вторых, желательно, чтобы величина
, тем точнее результат приближенного вычисления. Во-вторых, желательно, чтобы величина 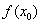 вычислялась просто.
вычислялась просто.
Пример 8. Пользуясь понятием дифференциала, вычислить приближенно 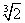 . Оценить точность полученного результата.
. Оценить точность полученного результата.
Решение. Рассмотрим функцию
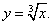
Её производная равна

а формула (11) примет вид
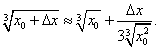
В данном случае было бы нерационально вычислять приближенно 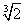 следующим образом:
следующим образом:

так как значение
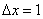
не является малым по сравнению со значением производной в точке
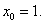
Здесь удобно предварительно вынести из под корня некоторое число, например 4/3. Тогда
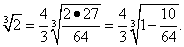
Теперь, полагая
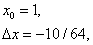
получим
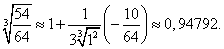
Умножая на 4/3, находим
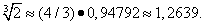
Принимая табличное значение корня
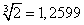
за точное число, оценим по формулам (12) и (13) абсолютную и относительную погрешности приближенного значения:
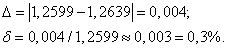

Весь блок "Производная"
Поделиться с друзьями
function-x.ru
Пусть функция  в точке
в точке  имеет отличную от нуля производную
имеет отличную от нуля производную
![Rendered by QuickLaTeX.com \[ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f'(x) \ne 0 \]](/800/600/http/ru.solverbook.com//wp-content/ql-cache/quicklatex.com-573065d544c2277bddbe109a45a4c49d_l3.png)
Тогда в некоторой окрестности этой точки отношение
![Rendered by QuickLaTeX.com \[ \frac{\Delta y}{\Delta x} = f'(x) + \alpha \]](/800/600/http/ru.solverbook.com//wp-content/ql-cache/quicklatex.com-9076e328de817569b89b4736b6a12268_l3.png)
где  при
при  Тому приращение функции можно представить в виде:
Тому приращение функции можно представить в виде:
![Rendered by QuickLaTeX.com \[ \Delta y = f'(x) \cdot \Delta x + \alpha \cdot \Delta x \]](/800/600/http/ru.solverbook.com//wp-content/ql-cache/quicklatex.com-e19d6a6a5f87f11cd68bfeb1c92e6348_l3.png)
При этом величина  является бесконечно малой более высокого порядка, чем
является бесконечно малой более высокого порядка, чем  и бесконечно малая
и бесконечно малая  поэтому величину
поэтому величину  называют главной частью приращения функции
называют главной частью приращения функции  .
.
Замечание. Дифференциал  называют также дифференциалом первого порядка.
называют также дифференциалом первого порядка.
Найдем дифференциал независимой переменной  то есть дифференциал функции
то есть дифференциал функции  Так как получаем, что
Так как получаем, что
![Rendered by QuickLaTeX.com \[ y' = 1 \]](/800/600/http/ru.solverbook.com//wp-content/ql-cache/quicklatex.com-04f2254ff0702fe57b2b6389e90d47d3_l3.png)
то
![Rendered by QuickLaTeX.com \[ dy = dx = 1 \cdot \Delta x = \Delta x \]](/800/600/http/ru.solverbook.com//wp-content/ql-cache/quicklatex.com-8e410ef44b491a1458699456dbb10ded_l3.png)
То есть дифференциал независимой переменной равен ее приращению:
![Rendered by QuickLaTeX.com \[ dx = \Delta x \]](/800/600/http/ru.solverbook.com//wp-content/ql-cache/quicklatex.com-f0e0ab2192c84f1457fab753be31162c_l3.png)
Тогда формула для дифференциала перепишется в виде:
![Rendered by QuickLaTeX.com \[ dy = f'(x)dx \]](/800/600/http/ru.solverbook.com//wp-content/ql-cache/quicklatex.com-0b8055e1b422389bc83b8b7522483778_l3.png)
Таким образом, дифференциал функции равен произведению производной указанной функции на дифференциал независимой переменной.
Геометрически дифференциал функции  в точке
в точке  равен приращению ординаты касательной к графику функции в рассматриваемой точке, когда переменная
равен приращению ординаты касательной к графику функции в рассматриваемой точке, когда переменная  получает приращение
получает приращение  .
.
Механический смысл дифференциала. Пусть материальная точка двигается по закону  Дифференциал функции
Дифференциал функции  равен:
равен:
![Rendered by QuickLaTeX.com \[ ds = s'(t) \Delta t \]](/800/600/http/ru.solverbook.com//wp-content/ql-cache/quicklatex.com-661a43512f1726b479fd73929be05154_l3.png)
Для фиксированных значений  и
и  – это тот путь, который бы прошла материальная точка за время
– это тот путь, который бы прошла материальная точка за время  в случае, если она будет двигаться равномерно и прямолинейно с постоянною скоростью
в случае, если она будет двигаться равномерно и прямолинейно с постоянною скоростью 
Стоит отметить, что фактический путь  в случае неравномерного движения материальной точки, в отличии от дифференциала
в случае неравномерного движения материальной точки, в отличии от дифференциала  не является линейной функцией времени
не является линейной функцией времени  а поэтому отличается от пути
а поэтому отличается от пути  Но все же, если время
Но все же, если время  является достаточно малым, то скорость движения существенно не изменяется и поэтому движение точки на промежутке времени от
является достаточно малым, то скорость движения существенно не изменяется и поэтому движение точки на промежутке времени от  до
до  есть практически равномерным.
есть практически равномерным.
Основные формулы, которые связаны с дифференциалами, можно получить, используя связь между дифференциалом функции и ее производной, то есть тот факт, что  а также соответствующие формулы для производных.
а также соответствующие формулы для производных.
Рассмотрим две дифференцируемые функции  и
и  Тогда имеют место следующие равенства:
Тогда имеют место следующие равенства:




ru.solverbook.com
Министерство образования и науки Российской Федерации
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ им. А.И. ГЕРЦЕНА»
Санкт-Петербург
РЕФЕРАТ
По дисциплине: Математика
Тема: Дифференциал
Выполнила:
Студентка 1 курса
дневного отделения
факультета управления
направления «Туризм»
Сахарова Анна Ильинична
Санкт-Петербург
2012
Дифференциа́л (от лат. differentia — разность, различие)
в математике, главная линейная часть приращения функции. Если функция y = f (x) одного переменного х имеет при х = х0производную, то приращение
Δy = f (x0 + Δx) - f (x0)
функции f (x) можно представить в виде
Δy = f' (x0) Δx + R,
где член R бесконечно мал по сравнению с Δх. Первый член
dy = f' (x0) Δх
в этом разложении и называется дифференциалом функции f (x) в точке x0. Из этой формулы видно, что дифференциал dy линейно зависит от приращения независимого переменного Δx, а равенство
Δy = dy + R
показывает, в каком смысле Д. dy является главной частью приращения Δy.
Обобщение понятия дифференциала. Обобщение понятия Д. на вектор-функции, начало которому положили в начале 20 в. французские математики Р. Гато и М. Фреше, позволяет лучше выяснить смысл понятия «дифференциал» для функций нескольких переменных, а в применении к Функционалам приводит к понятию вариации, лежащему в основе вариационного исчисления (См.Вариационное исчисление).Важную роль в этом обобщении играет понятие линейной функции (линейного отображения). Функция L (x) векторного аргумента хназывается линейной, если она непрерывна и удовлетворяет равенству
L (x' + х ") = L (x') + L (x ")
для любых х' и х " из области определения. Линейная функция n-мерного аргумента х = {x1,..., xn} всегда имеет вид
L (x) = a1x1 +... + anxn,
где a1,..., an — постоянные. Приращение
ΔL = L (x + h) - L (x)
линейной функции L (x) имеет вид
ΔL = L (h),
т. е. зависит только от векторного приращения h, и притом линейно. Функция f (x) называется дифференцируемой при значении аргумента х, если её приращение Δf = f (x + h) - f (x), рассматриваемое как функция от h, имеет главную линейную часть L (h), т. е. выражается в виде
Δf = L (h) + R (h),
где остаток R (h) при h → 0 бесконечно мал по сравнению с h. Главная линейная часть L (h) приращения Δf и называется дифференциалом df функции f в точке x. При этом в зависимости от того, в каком смысле понимается бесконечная малость R (h) по сравнению с h, различают слабый дифференциал, или дифференциал Гато, и сильный дифференциал, или дифференциал Фреше. Если существует сильный Д., то существует и слабый Д., равный сильному Д. Слабый Д. может существовать и тогда, когда сильный не существует.
В случае f (x) ≡ x из общего определения следует, что df = h, т. е. можно приращение h считать Д. аргумента x и обозначать dx.
Если сделать теперь переменной точку x, в которой определяется Д. df, то он будет функцией двух переменных:
df (x; h).
Далее, считая h = h2 постоянным, можно найти Д. от дифференциала df (x; h2) как главную часть приращения
df (x + h3; h2) — df (x; h2),
где h3 — некоторое второе, не связанное с h2 приращение x. Получаемый таким образом второй дифференциал d2f = d2f (x; h2, h3) является функцией трёх векторных аргументов x, h2 и h3, линейной по каждому из двух последних аргументов. Если d2f непрерывно зависит от x, то он симметричен относительно h2 и h3:
d2f (x; h2, h3) = d2f (x; h3, h2).
Аналогично определяется дифференциал dnf = dnf (x; h2,..., hn) любого порядка n.
В вариационном исчислении сам векторный аргумент x является функцией x (t), а дифференциалы df и d2f функционала f [x (t)] называются его первой и второй вариациями и обозначаются δf и δ2f.
Всюду выше речь шла об обобщении понятия Д. на числовые функции векторного аргумента. Существует обобщение понятия Д. и на случай вектор-функций, принимающих значения в банаховых пространствах.
Лит.: Ильин В. А., Позняк Э. Г., Основы математического анализа, 2 изд., М., 1967; Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 2 изд., М., 1968; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 1, М., 1969; Кудрявцев Л. Д., Математический анализ, т. 1, М., 1970; Рудин У., Основы математического анализа, пер. с англ., М., 1966; Дьедонне Ж., Основы современного анализа, пер. с англ., М., 1964.
А. Н. Колмогоров.
II Дифференциа́л Дифференциальный механизм в приводе ведущих колёс автомобиля, трактора или др. транспортных машин. Д. обеспечивает вращение ведущих колёс с разными относительными скоростями при прохождении кривых участков пути.annettesa.livejournal.com
Министерство образования и молодежной политики Ставропольского края
Государственное бюджетное профессиональное образовательное учреждение
« Георгиевский региональный колледж «Интеграл»
ИНДИВИДУАЛЬНЫЙ ПРОЕКТ
По дисциплине « Математика: алгебра, начала математического анализа, геометрия»
на тему: «Дифференциалы и их приложения»
Выполнила студентка группы ЭКП-61,обучающаяся по специальности
«Экономика и бухгалтерский учет (по отраслям)»
Вирабян Оксана Тимуровна
Руководитель:
Дата сдачи: «____» ______________ 2017г.
Дата защиты: «____» ______________ 2017г.
Георгиевск
2017
СОДЕРЖАНИЕ
Введение
Пояснительная записка
Возникновение понятия дифференциала
Понятие дифференциала функции. Свойства. Применение дифференциала в приближенных вычислениях
Современное определение
Механическое истолкование
Геометрическая интерпретация
Производная и дифференциал
Что более универсально: приращение аргумента или его дифференциал?
Замена приращений дифференциалами
Дифференциал функции: примеры
Приближенные вычисления с применением дифференциала
Приближенные вычисления с помощью дифференциала функции одной переменной
Абсолютная и относительная погрешность вычислений
Оценка погрешности формул при помощи применения дифференциала
Почему дифференциал можно использовать в приближенных вычислениях?
О разных формах записи дифференциала
Заключение
Список используемых источников
Введение
В проекте рассматриваются понятия дифференциалов и их применение в различных областях науки.В практической части проекта представлены задачи различного содержания (экономического, химического и т.д.). Наряду с производными функций их дифференциалы – это одни из базовых понятий дифференциального исчисления, основного раздела математического анализа. Являясь неразрывно связанными между собой, оба они уже несколько столетий активно используются при решении практически всех задач, которые возникали в процессе научно-технической деятельности человека. В современном научном сообществе принято однозначно разделять науку на античный период и период нового времени. Но в чём же состоит отличие этих периодов? Чем принципиально отличался научный подход Платона, Аристотеля и прочих известных учёных античности от подхода крупных деятелей науки нового времени? В реальности, у разделения на два периода существует множество оснований. В рамках данной статьи мы рассмотрим одно, наиболее фундаментальное и показательное основание – возникновение дифференциального исчисления. Через предпосылки к появлению этого известнейшего метода в современной науке в трудах философов и математиков мы сможем проследить чёткую границу между античным и современным взглядом на науку, однозначно ответив на поставленные в начале статьи вопросы. Рубеж XVI-XVII вв. в истории науки действительно был переломным моментом, когда европейская наука совершила качественный скачок. В это время был совершен переход от античной науки к науке нового времени. Ни для кого не секрет, что «локомотивами» прогресса в рассматриваемый период были такие великие учёные как Рене Декарт, Галилео Галилей, Иоганн Кеплер, Бонавентура Кавальери, Исаак Ньютон. Каждый из них сказал свое новое слово в механике, математике, астрономии и прочих дисциплинах. Но не столько важны их заслуги в отдельных науках, сколько важен вклад в формирование методологии науки нового времени. Плоды трудов этих известных ученых в области методологии науки имели широкое распространение, и многие из них по сей день остаются основополагающими принципами современной науки. Легче всего связь методологических достижений самых крупных деятелей науки XVI-XVII вв. можно проследить именно через историю возникновения дифференциального исчисления и «принцип непрерывности», так или иначе встречающийся в трудах Кеплера, Кавальери, Декарта, а позднее Ньютона.
infourok.ru