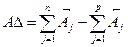
определяться статистически для того, чтобы регулировать долю дефектных деталей при незначительном и приемлемом уровне. В сущности, статистическое определение допусков будет указывать величину, на которую можно увеличить допуск, основываясь на приемлемой степени риска получения незначительной доли дефектных деталей. Вычисление статистических допусков звеньев размерной цепи основано на использовании выводов теорем теории вероятности. В соответствии с выводами теорем решают четыре вида суммирования:
суммирование независимых скалярных случайных величин;
суммирование независимых векторных случайных величин;
суммирование коррелятивно зависимых величин;
суммирование функциональнозависимых величин, связанных
линейной зависимостью.
Первый ряд суммирования излагается ниже, последние три вида используются в точностных расчетах методик нормирования.
Моделирование точности угловой размерной цепи фланцевых соединений.
При сборке составные части изделия часто соединяются между собой с помощью круглых фланцевых соединений. Отверстия располагаются по окружности, причем взаимное их расположение координируется одновременно угловыми размерами, проставленными на чертеже цепочкой или лесенкой в радиальном направлении и межосевом расстоянии. Собираемость фланцевых соединений зависит от допуска на межосевое расстояние t, погрешностей угловой и радиуса окружности r центров крепежных деталей, которые между собой находятся в функциональной зависимости (см. рис.3, б-З). Для одной пары отверстий при угловой координации лесенкой проведем расчет независимого допуска на межосевое расстояние, т.е. без учета посадки болтов с отверстием, в вероятностной постановке. Эта задача может быть также решена для всех пар отверстий с координацией по цепочке на основе правила умножения вероятностей, при условии полной независимости погрешностей.
Случайная величина для одного фланца имеет вид
Последние три случайные величины имеют нормальное распределение с математическим ожиданием 0 (нуль) и среднеквадратическими отклонениями
Следовательно, сумма этих величин также нормально
распределена с математическим ожиданием 0 и среднеквадратическим
отклонением
3. Моделирование электронных цепей
Моделирование электронных цепей состоит в определении функции цепи и отклонения функции цепи. Функция цепи зависит от параметров цепи в билинейной и биквадратной форме, на биквадратный случай распространяют метод корневого годографа. В определении отклонения функции цепи используются методы максимума и минимума, теоретико-вероятностный, Монте-Карло, методика смешанного расчета. Функция цепи. Функция цепи весьма просто зависит от
параметров цепи — комплексной частоты Р, и элементов цепи х. Зависимость функции цепи (полный импеданс) от пассивных элементов — сопротивление R, индуктивность L, емкость С — приводится к соотношению
Данное соотношение описывает конформное отображение, трансформирующее окружности в окружности. Математические свойства конформного отображения известны и широко используются для построения диаграммы импедансов. Если отдельные переменные коррелированы, то дисперсия
результирующего распределения задается с введением коэффициента
корреляции.
Методика смешанного расчета. В случае смешанного расчета элементы цепи разбиваются на три группы: а) элементы, не влияющие на работу цепи; б) элементы, изменяющиеся детерминированно; в) элементы, изменяющиеся стохастически. Отсюда следует порядок смешанного расчета: во-первых, выбираются допуски функции цепи для групп б) и в) и затем выполняются вычисления по методам максимума — минимума и теоретико-вероятностному. Метод Монте-Карло. Для вычисления отклонения функции цепи можно также применять методы статического моделирования, использующие вычислительную машину. В этом случае определяются псевдослучайные значения элементов цепи, и с помощью вычислительной машины выполняется анализ цепи. Статистические свойства функции цепи оцениваются путем многократного построения этого процесса. В противоположность методам, описанным выше, этот метод допускает произвольное распределение значений элементов цепи; кроме того, на свойства отдельных элементов цепи могут быть наложены дополнительные ограничения. Метод Монте-Карло может быть легко запрограммирован, но это потребует длительного времени.
stud24.ru
Размерной цепью называется совокупность размеров, непосредственно участвующих в решении поставленной задачи и образующей замкнутый контур (ГОСТ 16319-80).
По виду задач, в решении которых цепи участвуют, они делятся на конструкторские, технологические и измерительные.
Конструкторские размерные цепи решают задачу по обеспечению точности при конструировании. Они устанавливают связь размеров детали в изделии.
Технологические размерные цепи решают задачу по обеспечению точности при
изготовлении машин. Они устанавливают связь размеров деталей на разных этапах
технологического процесса.
Измерительные размерные цепи решают задачу обеспечения точности при измерении. Они устанавливают связь между звеньями, которые влияют на точность измерения.
Замыкающее звено ( А∆, Б∆, В∆ и т.д.) – то звено, которое непосредственно не выдерживается, а получается в результате выполнения размеров составляющих звеньев. Размерная цепь всегда замкнута. На основании этого свойства существует зависимость, которая связывает номинальные размеры звеньев. Для плоских размерных цепей с номинальными звеньями она имеет следующий вид:
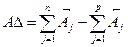
где n и p - число соответственно увеличивающих и уменьшающих звеньев в размерной цепи.
Для определения зависимости, которая связывает допуски звеньев в размерной цепи, найдем вначале наибольшее значение замыкающего звена:
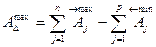
Наименьшее значение допуска: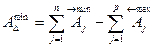 
Вычтем AΔmin из AΔmax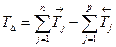
Верхнее отклонение: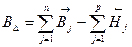 
Нижнее отклонение: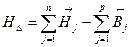 
Координата середины поля допуска: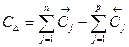 
Допуск замыкающего звена: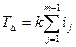 
Значение k характеризует точность, с какой следует получать все составляющие звенья размерной цепи. Рассчитанное по формуле значение k в общем случае не будет соответствовать строго определенному квалитету, поэтому для назначения допусков на соответствующие звенья выбирают ближайшие квалитеты по табл. 4.1.
Метод полной взаимозаменяемости
Метод, при котором требуется точность замыкающего звена размерной цепи, получается при любом сочетании размеров составляющих звеньев. При этом предполагают, что в размерной цепи одновременно могут оказаться все звенья с предельными значениями, причем в любом из двух наиболее неблагоприятных сочетаний (все увеличивающие звенья с верхними предельными размерами, а уменьшающие с нижними, или наоборот). Такой метод расчета, который учитывает эти неблагоприятные сочетания, называется методом расчета на максимум - минимум.
Обратная задача.
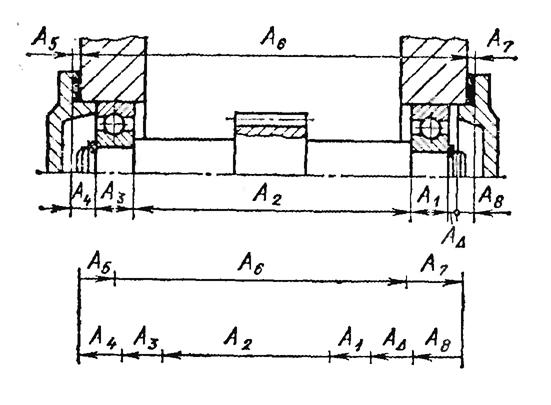
Расчет размерной цепи по методу полной взаимозаменяемости..
А1=А3=19-0,12, А2=150-0,08-0,24, А4=А8=10-0,06, А5=А7=1-0,015, А6=206+0,35+0,05
Номинальное значение AD:
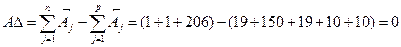
Допуск замыкающего звена:
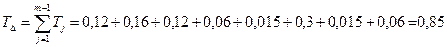
Координаты середины поля допуска:
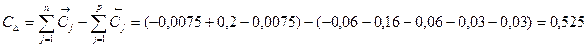
Верхнее отклонение:
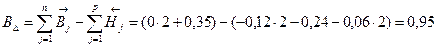
Нижнее отклонение:
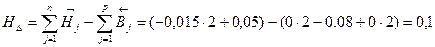
Проверка правильности решения:
Наибольшее значение замыкающего звена:
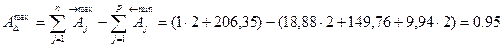
Наименьшее значение допуска:
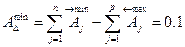
Прямая задача.
1. Определение номинальных размеров составляющих звеньев.
Номинальные размеры стандартных деталей, например, подшипников качения, находят по соответствующим стандартам. Остальные размеры составляющих звеньев, кроме звена А9→, определяют непосредственно по чертежу узла.
Для нахождения номинального размера А9→ воспользуемся зависимостью:
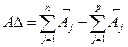
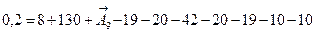
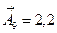
2. Определение средней точности размерной цепи.
По формуле найдем значение k :
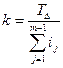
k=19,9
Найденное число единиц допуска лежит в пределах стандартных значений k =16 (7-й квалитет) и k = 25 (8-й квалитет). Отсюда следует, что часть звеньев должна изготавливаться по 7-му квалитету, часть – по 8-му. При этом следует назначать допуски таким образом, чтобы допуск звена A9→ лежал в пределах между 7-м и 8-м квалитетами либо соответствовал одному из этих квалитетов.
Предельные отклонения на составляющие звенья, кроме A9→, рекомендуется назначать на размеры, относящиеся к валам – по h, относящиеся к отверстиям – по H; на остальные ±IT/2, т.е. симметричные предельные отклонения.
Результаты поэтапных расчетов внесены в табл.
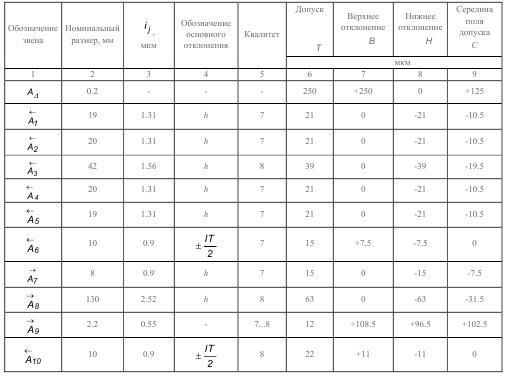
3. Определение допуска звена A9→ .
Воспользуемся формулой:
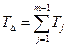
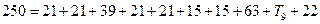
T9=12мкм.
4.Определение предельных отклонений звена А9→.
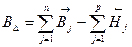
В9=+108,5
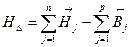
Н9=+96,5мкм.
5. Проверка. Чтобы убедиться в правильности проведенных расчетов, воспользуемся зависимостью для координат середины полей допусков :
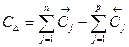
+125=+125
Метод неполной взаимозаменяемости
Это метод, при котором требуемая точность замыкающего звена размерной цепи получается не при любых сочетаниях, а при ранее обусловленной части сочетаний размеров составляющих звеньев.
Сборка осуществляется без пригонки, регулировки и подбора звеньев.
Метод исходит из предположения, что сочетание действительных размеров составляющих звеньев в изделии носит случайный характер, и вероятность того, что все звенья с самыми неблагоприятными сочетаниями окажутся в одном изделии, весьма мала.
Такой метод расчета, который учитывает рассеяние размеров и вероятность их различных сочетаний, называется вероятностным методом расчета. Другими словами, метод допускает малый процент изделий, у которых замыкающее звено выйдет за рамки поля допусков. При этом расширяются допуски составляющих цепь размеров, и тем самым снижается себестоимость изготовления деталей.
Задачей расчета является назначение допусков на составляющие звенья, соответствующих одинаковой степени точности.
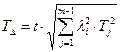
Формула устанавливает связь между допуском на замыкающий размер и допусками на составляющие звенья.
Для того чтобы добиться одинаковой точности составляющих звеньев размерной цепи, воспользуемся известной формулой Tj = k j ⋅i j и подставим ее в выражение. Потребуем, чтобы k у всех звеньев были одинаковыми, тогда :
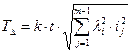
Окончательно:
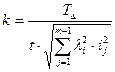
Значение k характеризует точность, с которой следует изготовить все составляющие звенья размерной цепи при заданных условиях.
При обработке деталей разброс размеров у них может распределяться и не по закону Гаусса. В этом случае можно также воспользоваться формулой, только при этом следует поставить другие значения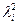 
.
Если предполагается, что рассеяние размеров близко, например, к закону Симпсона, то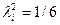 
.
При неизвестном характере рассеяния размеров рекомендуется принимать закон равной вероятности с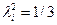 
.
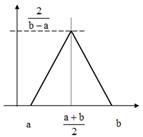
Распределение Симпсона. Распределение равной вероятности.
В зависимости от принятого процента риска P, значения t выбирают из ряда, приведенного в табл.
P – процент риска; t – коэффициент риска.
Пример
Вероятностный метод расчета рассмотрим на том же узле. По техническим
требованиям необходимо обеспечить осевой зазор ∆=+ A0 ,20,25. Требуется назначить допуски и отклонения на составляющие звенья при P = 0.27% и нормальном законе распределения рассеяния размеров составляющих звеньев (процент брака и закон распределения студент выбирает сам).
Решение
1. Определение номинальных размеров составляющих звеньев.
Этот пункт решения задачи полностью соответствует первому пункту при расчете на максимум - минимум.
2. Определение средней точности размерной цепи.
Воспользуемся зависимостью:
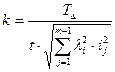
k=58,3
Найденное число единиц допуска k лежит ближе к стандартному значению k = 64 , что соответствует 10-му квалитету. Допуски на все звенья назначаются по 10-му квалитету.
3. Определение истинного процента брака.
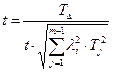
t=2,7
что соответствует 0.693% брака. Полагаем, что такой процент брака нас устраивает. Если же количество брака мы сочли бы чрезмерным, тогда необходимо было допуски на ряд звеньев назначить по 9-му квалитету. Результаты поэтапных расчетов внесены в табл.
4. Определение предельных отклонений звена A9→.
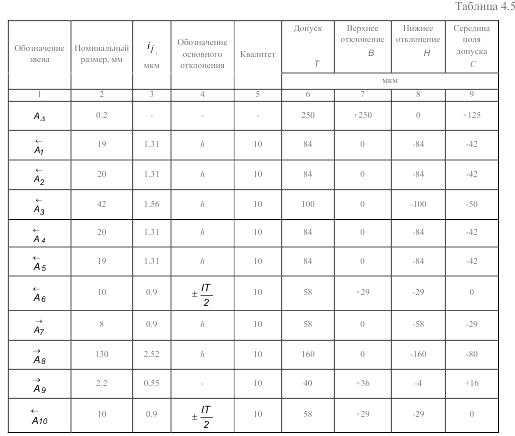
Вначале определим координату середины поля допуска звена A9→ по формуле:
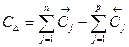
C9=+16
Верхнее отклонение:
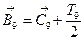В9=36
Нижнее отклонение:
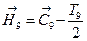Н9=-4
Метод пригонки
Это метод, при котором требуемая точность замыкающего звена размерной цепи достигается изменением размера компенсирующего звена путем снятия с компенсатора слоя металла. Его суть состоит в том, что допуски на составляющие звенья назначаются по экономически приемлемым квалитетам, например, по 12-14-му квалитетам. Получающийся после этого у замыкающего звена избыток поля рассеяния при сборке устраняют за счет компенсатора. Смысл расчета заключается в определении припуска на пригонку, достаточного для компенсации величины превышения предельных значений замыкающего звена и вместе с тем наименьшего для
сокращения объема пригоночных работ.
Роль компенсатора обычно выполняет деталь, наиболее доступная при разборке механизма, несложная по конструкции и неточная, например, прокладки, шайбы, проставочные кольца и т.п.
ПРИМЕР
Определить размеры заготовки компенсатора А9 для размерной цепи. Замыкающее звено должно быть А∆=0,2+0,25
Решение
1. Определение номинальных размеров составляющих звеньев.
Этот пункт решения задачи полностью соответствует первому пункту при расчете на максимум - минимум.
2. Выбор и назначение допусков на составляющие звенья.
Считаем, что для размеров звеньев экономически приемлемым является 12-й квалитет. Назначаем по этому квалитету допуски на все размеры, кроме допусков на монтажную высоту шариковых радиальных подшипников, и на звено A9→, которое выбрали в качестве компенсатора.
3. Определение наибольшей величины компенсации.
По формуле:
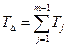
Нетрудно заметить, что сумма допусков составляющих звеньев значительно превосходит допуск Т∆ , т.е. колебание размера замыкающего звена от изделия к изделию значительно увеличится.
Наибольшая расчетная компенсация избыточного колебания размера замыкающего звена :
Т9’=-1510
Следовательно, при самом неблагоприятном сочетании размеров надо с компенсатора снять слой материала толщиной 1.51 мм, чтобы замыкающее звено попало в предписанные пределы.
Результаты расчетов представлены в табл.
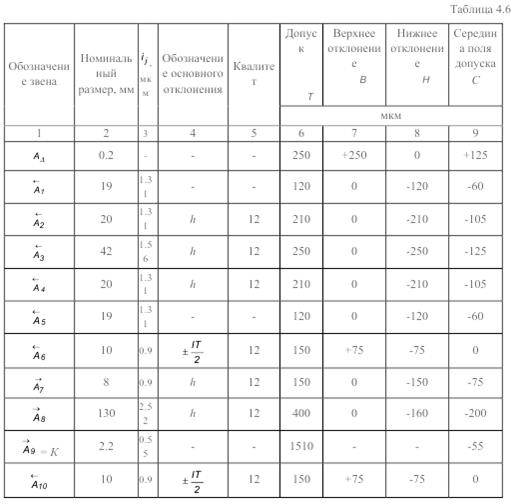
4. Определение предельных размеров компенсатора звена A9→.
Вначале определим координату середины поля допуска звена A9→:
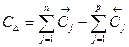
С9=-55
Минимальный размер компенсатора:
, 
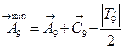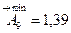
Максимальный размер:
, 
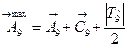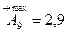
5. Определение размера заготовки компенсатора.
Исполнительный размер заготовки компенсатора определяется его наибольшей величиной, так как в прочих случаях он будет подгоняться.
Для изготовления компенсатора на него надо назначить приемлемый допуск, например, по тому же 12-му квалитету (IT12 = 0.1 мм), но так, чтобы его наименьший размер был не менее 2.9 мм :
; 
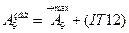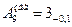
Метод регулирования с применением неподвижного компенсатора
Это метод, при котором требуемая точность замыкающего звена размерной цепи достигается изменением компенсирующего звена без снятия слоя металла.
Его суть состоит в том, что избыток поля рассеивания замыкающего звена устраняют путем подбора компенсатора из некоторого количества компенсаторов, заранее изготовленных с различными размерами.
Смысл расчета заключается в определении наименьшего количества компенсаторов в комплекте.
Пример
Определить размеры компенсационных прокладок в комплекте для размерной цепи. Замыкающее звено должно быть А∆=0,2+0,25
Решение
Прежним порядком (cм. метод пригонки) устанавливаем номинальные размеры и назначаем допуски на составляющие звенья размерной цепи. Рассчитываем величину компенсации Т9’=-1,51мм. и наименьший размер компенсатора в комплекте .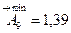
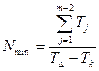
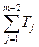- сумма допусков всех составляющих звеньев без допуска на компенсатор; Тк – допуск на отдельный компенсатор в комплекте.
Допуск на отдельный компенсатор выбирается в пределах : Tk = (0,1…0,3)⋅T∆; мкм.
Тк=0,15.250=37,5мкм. Принимаем Тк=40 (10-й квалитет).
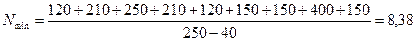
Число ступеней компенсации следует всегда округлять в большую сторону, так как по формуле (4.10) определяется наименьшее число ступеней. Принимаем: N=9.
2. Величина ступени компенсации.
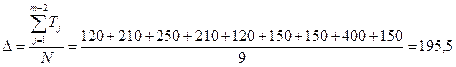мкм.
3. Размеры компенсаторов в комплекте.
Количество компенсаторов в комплекте соответствует числу ступеней компенсации.
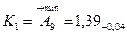
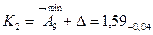
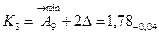
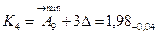
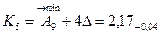
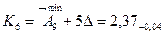
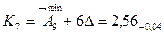
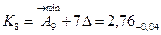
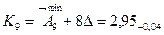
poznayka.org
90
Рассмотрим фрагмент конструкции (рис. 4.1).
А∆
Рис. 4.1
Для свободного вращения зубчатого колеса на оси необходим зазор А∆ . ВеличинаА∆ получает-
ся автоматически при сопряжении деталей, контуры которых выделены. Если размеры их выполнены неверно (см. рис. 4.1 б,в) либо зазора не будет вовсе, либо он будет слишком большой, что сделает невозможным нормальное функционирование узла.
Установим те размеры деталей, которые при сборке автоматически создадут необходимый зазор А∆ (рис. 4.2). Обозначив размеры деталей, которые влияют на зазорА∆ , мы тем самым построим
размерную цепь. |
|
|
|
|
|
|
|
|
| Размерной цепью называется совокупность размеров, непо- | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| средственно участвующих в решении поставленной задачи и об- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| разующей замкнутый контур (ГОСТ 16319-80). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| По виду задач, в решении которых цепи участвуют, они делят- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ся на конструкторские, технологические и измерительные. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Конструкторские размерные цепи решают задачу по обес- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| печению точности при конструировании. Они устанавливают связь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| размеров детали в изделии. На рис. 4.3 приведены примеры сбо- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| рочных размерных цепей. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
| А2 |
|
|
| А1 |
|
|
|
|
|
|
| А∆ | На рис. 4.3, а приведена элементарная сборочная размерная | |||||||
|
|
|
|
|
|
|
|
| А3 |
|
|
|
|
|
|
|
|
| цепь, решающая задачу обеспечения точности сопряжения двух | |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| деталей. На рис 4.3, б тоже показана сборочная цепь, которая | ||||
|
| А∆ =А3 -А1 |
|
|
|
|
|
|
|
|
| решает задачу обеспечения перпендикулярности поверхности 2 к | ||||||||||
|
| - А2 | оси 1, необходимой для базирования подшипника качения. | |||||||||||||||||||
|
| Технологические размерные цепи решают задачу по обес- | ||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| печению точности при изготовлении машин. Они устанавливают |
|
|
|
|
|
|
|
| Рис. 4.2 |
|
|
|
|
|
|
|
|
| связь размеров деталей на разных этапах технологического про- | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| цесса. На рис. 4.4, а изображена деталь с размерами, которые |
следует выдержать при изготовлении. Последовательность получения размеров приведена на рис. 4.4, б, в,г. На основании предложенного маршрута обработки построена технологическая размерная
91 | Допуски и посадки. В.И. Анухин |
цепь (см. рис 4.4, д). При обработке детали выдерживаются размерыС1 , С2 , С3 , а размерС∆ получается автоматически.
|
|
|
| β 1 |
|
|
|
|
| β∆ |
| β | 2 |
|
|
|
|
|
| |
|
|
| 1 |
|
|
|
| Б1 | Б∆ | 2 |
|
|
|
|
|
|
|
|
| |
| Б2 |
|
|
|
|
|
| а) |
|
| б) |
|
|
|
|
| Рис. 4.3 |
|
|
|
Готовая | 1-яоперация |
| 2-яоперация | 3-яоперация | Размерная | |
деталь |
|
|
|
| цепь | |
С∆ |
|
|
| С∆ |
| С3 |
С3 | С1 | С2 | С3 | С∆ |
|
|
|
| С2 |
|
|
|
| С1 |
Рис. 4.4
Измерительные размерные цепи решают задачу обеспечения точности при измерении. Они устанавливают связь между звеньями, которые влияют на точность измерения.
Размеры, образующие размерную цепь, называются звеньями. В зависимости от расположения звеньев, цепи делятся на плоские (звенья расположены в одной или параллельных плоскостях) и пространственные. В зависимости от вида звеньев различают линейные размерные цепи (звеньями являются линейные размеры, см. рис. 4.2, 4.3,а) и угловые (см. рис. 4.3,б). Звенья линейной размерной цепи обозначаюткакой-либоодной прописной буквой русского алфавита с соответствующим числовым индексом, звенья угловых цепей – строчной буквой греческого алфавита.
Любая размерная цепь состоит из составляющих звеньев и одного замыкающего.
Замыкающее звено (А∆ , Б∆ , В∆ и т.д.) – то звено, которое непосредственно не выдерживается,
а получается в результате выполнения размеров составляющих звеньев.
Составляющие звенья делятся на увеличивающие и уменьшающие. Увеличивающие звенья
( A j , Бj ) - те, с увеличением которых замыкающее звено увеличивается, ауменьшающие (Аj , Б j )
-
92
те, с увеличением которых замыкающее звено уменьшается. При правильном определении увеличивающих и уменьшающих звеньев стрелки над буквами должны указывать движение в одном направлении по замкнутому контуру размерной цепи.
Перед тем как построить размерную цепь, следует выявить замыкающее звено, которое, допустим, определяет нормальное функционирование механизма. Размер или предельное отклонение замыкающего звена назначают или рассчитывают исходя из условий работы и (или) требуемой точности.
Например, размер и предельные отклонения А∆ (см. рис. 4.2) принимаются такими, которые обес-
печивали бы свободное вращение зубчатого колеса при минимальном возможном смещении его вдоль оси. Несовпадение вершины делительного конуса конической шестерни с осью вращения конического колеса (рис. 4.7, а,б) определяется степенью точности зубчатых колес, а его предельные значения находятся по соответствующему стандарту.
В курсовом проекте замыкающее звено и допуск на него уже заданы. Надо только установить, между какими деталями стоит размер замыкающего звена, а затем связать эти детали цепью размеров.
Например, на рис.4.5, б размер замыкающего звенаБ∆ стоит между осью и торцом зубчатого колеса; на рис. 4.7,а А∆ стоит между осью отверстия в корпусе и вершиной делительного конуса кони-
ческого колеса и т.д.
Рассмотрим наиболее типичные варианты сборочных размерных цепей *. Первый вид размерных цепей приведен на рис. 4.5, второй – на рис. 4.6, третий – на рис. 4.7.
При построении размерных цепей следует руководствоваться их основными свойствами :
•цепь должна быть замкнута;
•размер любого звена сборочной цепи должен относиться к элементам одной и той же детали; исключением является замыкающее звено, которое всегда соединяет элементы разных деталей;
•цепь должна быть проведена наикратчайшим способом, т.е. деталь своими элементами должна входить в размерную цепь только один раз.
Размерная цепь всегда замкнута. На основании этого свойства существует зависимость, которая связывает номинальные размеры звеньев. Для плоских размерных цепей с номинальными звеньями она имеет следующий вид:
n | → | p | ← |
|
А∆ = ∑ Aj − ∑ Aj , | (4.1) | |||
j =1 |
| j =1 |
|
|
где n иp – число соответственно увеличивающих и уменьшающих звеньев в размерной цепи. Для определения зависимости, которая связывает допуски звеньев в размерной цепи, найдем
вначале наибольшее значение замыкающего звена:
n | → max | p | ← min |
A∆max= ∑ A j | − ∑ A j , | ||
j =1 |
| j =1 |
|
* Размерные цепи на рис. 4.5,в; 4.6,в; 4.7,в попытайтесь построить самостоятельно. Ответ дан в приложении, рис.П.8.1.
studfiles.net
