superbotanik.net

Реферат Число пи

скачать

Реферат на тему:

План:

1 Свойства
- 1.1 Трансцендентность и иррациональность
- 1.2 Соотношения
2 История
- 2.1 Геометрический период
- 2.2 Классический период
- 2.3 Эра компьютерных вычислений
3 Рациональные приближения
4 Нерешённые проблемы
5 Метод иглы Бюффона
6 Дополнительные факты
7 В культуре

Введение

Если принять диаметр окружности за единицу, то длина окружности — это число «пи»

Winamp, Skins, Plugins

Необходимые Утилиты

Текстовые редакторы

Юмор

File managers and best utilites

История возникновения числа Пи. Пи реферат число

Реферат о числе Пи

Исследовательская работа на тему:

Выполнила: Тиранова Юлия, 6 «б» класс

Руководитель: Миненкова М.Л. – учитель математики.

ПЛАН:

Актуальность проблемы:

Раскрытие проблемы:
Применение.
Способы запоминания цифр в числе Пи.

Заключение.

Памятники числа Пи.
Праздники числа Пи.
Сайт.
Список литературы.

Жизненная необходимость числа «пи»

Число «пи» это отношение длины окружности к её диаметру. С древности людям приходилось, и приходиться иметь дело с различными измерениями. Особенно при строительстве и архитектуре. Хорошо, если это измерение длин отрезков или площадей прямоугольной формы. Но как быть, если это круглые тела? Измерение площадей круглых тел люди производили путём сравнения или с помощью палетки. Например считали, что

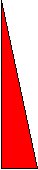
всякий круг равновелик прямоугольному треугольнику, катеты которого соответственно равны длине окружности и её радиусу

Но результаты оказывались с большой погрешностью (неточностью).

И вот на помощь к нам из далёкого прошлого пришло известное уже сейчас, и знакомое число П.

История числа "пи"

История числа П, началась в Древнем Египте. Число, выражающее это отношение, принято обозначать греческой буквой П – первой буквой слова «периферия», что в переводе с греческого обозначает «окружность». Впервые это обозначение использовал в 1706 году английский математик У.Джонс, но общепринятым оно стало после того, как его с 1736 года стал систематически употреблять Леонард Эйлер.

В глубокой древности считалось, что окружность ровно в 3 раза длиннее диаметра. Эти сведения содержатся в клинописных табличках Древнего Междуречья. Итак, первым приближением числа П было 3. В папирусе Райнда, который датируется приблизительно 1650 г. до н. э., для числа П приводится значение (16\9)2 , в десятичном приближении это 3,16. В священной книге джайнизма одной из древнейших религий, существовавших в Индии и возникшей в седьмом в. до н.э. имеется указание, из которого следует, что число П в то время принимали равным 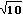, что даёт дробь 3,162...

С шестого в. до н. э. математическая наука стремительно развивалась в Древней Греции. Именно древнегреческие геометры строго доказали, что длина окружности пропорциональна её диаметру, а площадь круга равна половине произведения длины окружности и радиуса. Эти доказательства приписывают Архимеду. Таким образом он установил, что число «Пи» заключено в пределах от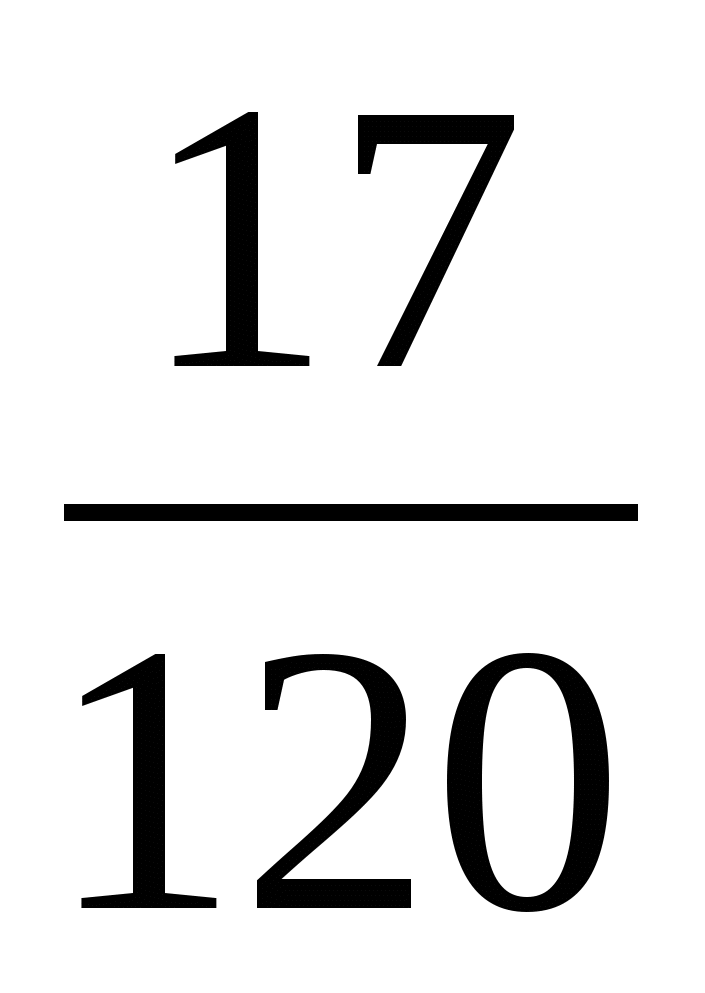 3 до 3,т. е. 3,1408<П< 3,1428. Значение 3 до сих пор считается вполне хорошим приближением числа П для прикладных задач.

В конце V в. китайский математик Цзу Чун Чжи получил приближение 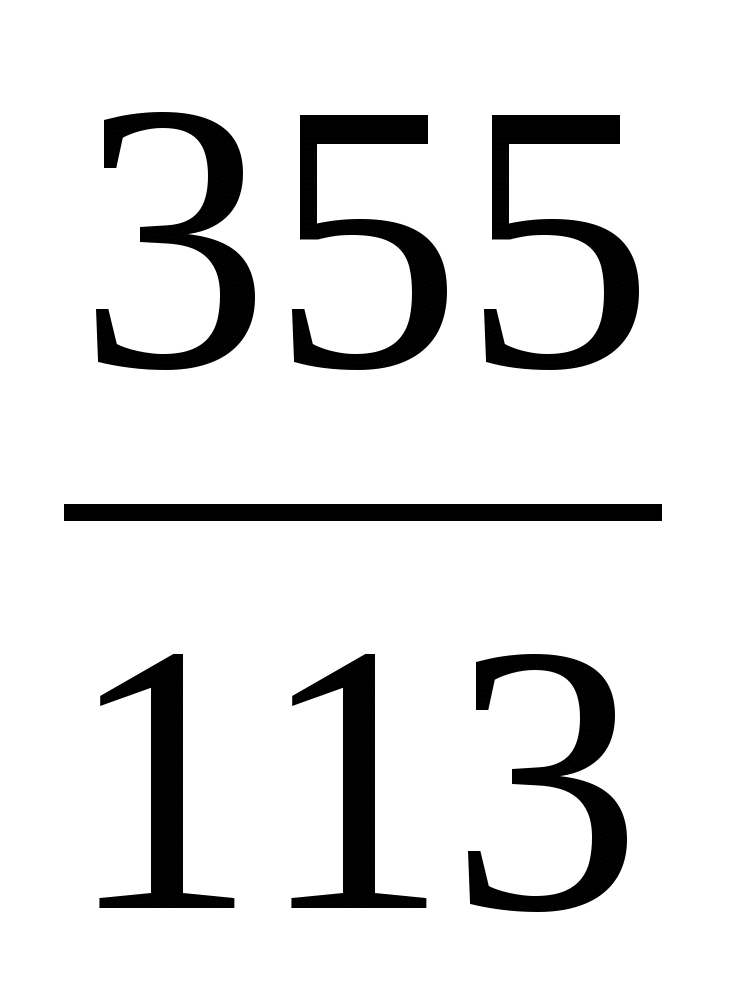. Было найдено много формул, которые содержат число П. Некоторые из этих формул позволяют вычислить П приёмами, отличными от метода Архимеда и более рациональными. Например, к числу П можно прийти, отыскивая пределы некоторых рядов.

Так, Готфрид Вильгельм Лейбниц (1646-1716) получил в 1674 г., ряд который дал возможность вычислить П более коротким путём, нежели Архимед :

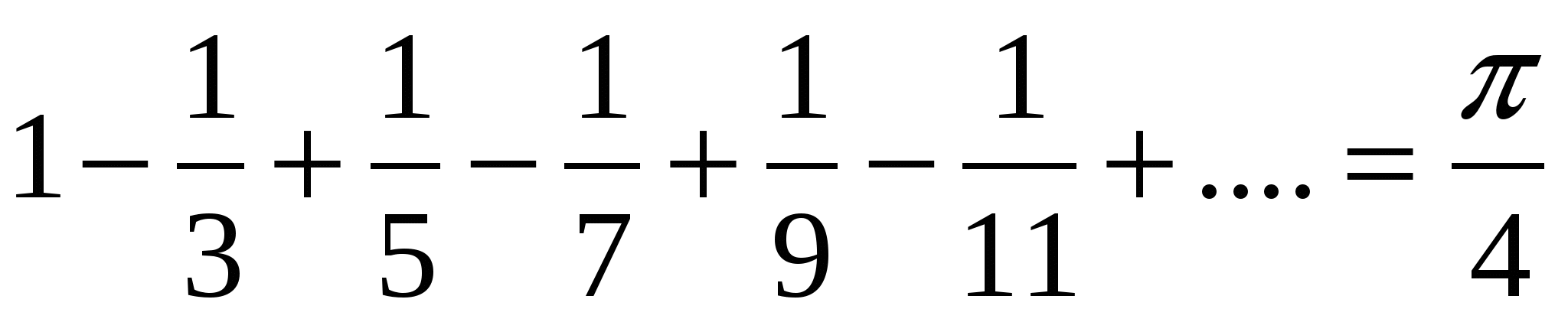
Однако этот ряд сходится очень медленно. Чтобы вычислить П с точностью до десяти знаков, потребовалось бы, как сказал Исаак Ньютон, найти сумму 5 миллиардов слагаемых и затратить на это около тысячи лет непрерывной работы.

В1706г. лондонский математик Джон Мэчин нашёл формулу которая до сих пор считается одной из лучших для приближённого вычисления П. Сам Джон Мэчин вычислил П со 100 верными знаками по формуле:

Эта и другие взаимозависимости позволили математикам ещё глубже выяснить природу числа Пи.

На протяжении всего существования числа Пи вплоть до наших дней, велась своеобразная "погоня" за десятичными знаками числа Пи. Вот некоторая информация о ней:

1949 год- 2.037 десятичных знаков (Джон фон Нейман). 1958 год- 10.000 десятичных знаков (Ф.Женюи). 1961 год- 100.000 десятичных знаков (Д.Шенкс). 1973 год- 10.000.000 десятичных знаков (Ж.Гийу, М.Буйе). 1986 год- 29.360.000 десятичных знаков (Д.Бейли). 1987 год- 134.217.000 десятичных знаков (Т.Канада). 1989 год- 1.011.196.691 десятичных знаков (Д.Чудновски и Г.Чудновски). Они же добились в 1991 году 2.260.000.000 знаков, а в 1994 году – 4.044.000.000 знаков. Дальнейшие рекорды принадлежат японцу Тамуре Канада: в 1995 году 4.294.967.286 знаков, в 1997 – 51.539.600.000.

И, последний на сегодня рекорд -206.158.430.000 знаков.

В наше время с помощью ЭВМ число вычислено с миллионами правильных знаков после запятой. Но такая точность не нужна ни в каких вычислениях и представляет скорее технический, чем научный интерес. Вот посмотрите 100.000 знаков после запятой числа П. Ведь за ними стоят история нашей цивилизации, жизни сотен лучших умов человечества и тайна устройства мироздания. Есть гипотезы, предполагающие, что в числе Пи скрыта любая информация, которая когда - либо была или будет доступна людям.

3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 93751957781857780532 1712268066 13001927876 611195909 2164201989 3809525720 1065485863 2788659361 5338182796 8230301952 0353018529 6899577362 2599413891 2497217752 8347913151 5574857242 4541506959 5082953311 6861727855 8890750983 8175463746 4939319255 0604009277 0167113900 9848824012 8583616035 6370766010 4710181942 9555961989 4676783744 9448255379 7747268471 0404753464 6208046684 2590694912 9331367702 8989152104 7521620569 6602405803 8150193511 2533824300 3558764024 7496473263 9141992726 0426992279 6782354781 6360093417 2164121992 4586315030 2861829745 5570674983 8505494588 5869269956 9092721079 7509302955 3211653449 8720275596 0236480665 4991198818 3479775356 6369807426 5425278625 5181841757 4672890977 7727938000 8164706001 6145249192 1732172147 7235014144 1973568548 1613611573 5255213347 5741849468 4385233239 0739414333 4547762416 8625189835 6948556209 9219222184 2725502542 5688767179 0494601653 466804988606611863 0674427862 2039194945 0471237137 86 96095636 4371917287 4677646575 7396241389 0865832645 9958133904 7802759009 94 65764078 9512694683 9835259570 9825822620 5224894077 2671947826 8482601476 99 09026401 3639443745 5305068203 4962524517 4939965143 1429809190 6592509372 21 69646151 5709858387 4105978859 5977297549 8930161753 9284681382 6868386894 2774155991 8559252459 5395943104 9972524680 8459872736 4469584865 3836736222 6260991246 0805124388 4390451244 1365497627 8079771569 1435997700 1296160894 4169486855 5848406353 4220722258 2848864815 8456028506 0168427394 5226746767 8895252138 5225499546 6672782398 6456596116 3548862305 7745649803 5593634568 1743241125 1507606947 9451096596 0940252288 7971089314 5669136867 2287489405 6010150330 8617928680 9208747609 1782493858 9009714909 6759852613 6554978189 3129784821 6829989487 2265880485 7564014270 4775551323 7964145152 3746234364 5428584447 9526586782 1051141354 7357395231 1342716610 2135969536 2314429524 8493718711 0145765403 5902799344 0374200731 0578539062 1983874478 0847848968 3321445713 8687519435 0643021845 3191048481 0053706146 8067491927 8191197939 9520614196 6342875444 0643745123 7181921799 9839101591 956181467514269123974 894090718 6494231961 5679452080 9514655022 5231603881 9301420937 6213785595 6638937787 0830390697 9207734672 2182562599 6615014215 0306803844 7734549202 6054146659 2520149744 2850732518 6660021324 3408819071 0486331734 6496514539 0579626856 1005508106 6587969981 6357473638 4052571459 1028970641 4011097120 6280439039 7595156771 5770042033 7869936007 2305587631 7635942187 3125147120 5329281918 2618612586 7321579198 4148488291 6447060957 5270695722 0917567116 7229109816 9091528017 3506712748 5832228718 3520935396 5725121083 5791513698 8209144421 0067510334 6711031412 6711136990 8658516398 3150197016 5151168517 1437657618 3515565088 4909989859 9823873455 2833163550 7647918535 8932261854 8963213293 3089857064 2046752590 7091548141 6549859461 6371802709 8199430992 4488957571 2828905923 2332609729 9712084433 5732654893 8239119325 9746366730 5836041428 1388303203 8249037589 8524374417 0291327656 1809377344 4030707469 2112019130 2033038019 7621101100 4492932151 6084244485 9637669838 9522868478 3123552658 2131449576 8572624334 4189303968 6426243410 7732269780 2807318915 4411010446 8232527162 0105265227 2111660396 6655730925 4711055785 3763466820 6531098965 2691862056 4769312570 5863566201 85 58100729 3606598764 8611791045 3348850346 1136576867 5324944166 8039626579 7877185560 8455296541 2665408530 6143444318 5867697514 5661406800 7002378776 5913440171 2749470420 5622305389 9456131407 1127000407 8547332699 3908145466 4645880797 2708266830 6343285878 5698305235 8089330657 5740679545 7163775254 2021149557 6158140025 0126228594 1302164715 5097925923 0990796547 3761255176 5675135751 7829666454 7791745011 2996148903 0463994713 2962107340 4375189573 5961458901 9389713111 7904297828 5647503203 1986915140 2870808599 0480109412 1472213179 4764777262 2414254854 5403321571 8530614228 8137585043 0633217518 2979866223 7172159160 7716692547 4873898665 4949450114 6540628433 6639379003 9769265672 1463853067 3609657120 9180763832 7166416274 8888007869 2560290228 4721040317 2118608204 1900042296 6171196377 9213375751 1495950156 6049631862 9472654736 4252308177 0367515906 7350235072 8354056704 0386743513 6222247715 8915049530 9844489333 0963408780 7693259939 7805419341 4473774418 4263129860 8099888687 4132604721 5695162396 5864573021 6315981931 9516735381 2974167729 4786724229 2465436680 0980676928 2382806899 6400482435 4037014163 1496589794 0924323789 6907069779 4223625082 2168895738 37 98623001 5937764716 5122893578 6015881617 5578297352 3344604281 5126272037 3431465319 7777416031 9906655418 7639792933 4419521541 3418994854 4473456738 3162499341 9131814809 2777710386 3877343177 2075456545 3220777092 1201905166 0962804909 2636019759 8828161332 3166636528 6193266863 3606273567 6303544776 2803504507 7723554710 5859548702 7908143562 4014517180 6246436267 9456127531 8134078330 3362542327 8394497538 2437205835 3114771199 2606381334 6776879695 9703098339 1307710987 0408591337 4641442822 7726346594 7047458784 7787201927 7152807317 6790770715 7213444730 6057007334 9243693113 8350493163 1284042512 1925651798 0694113528 0131470130 4781643788 5185290928 5452011658 3934196562 1349143415 9562586586 5570552690 4965209858 0338507224 2648293972 8584783163 0577775606 8887644624 8246857926 0395352773 4803048029 0058760758 2510474709 1643961362 6760449256 2742042083 2085661190 6254543372 1315359584 5068772460 2901618766 7952406163 4252257719 5429162991 9306455377 9914037340 4328752628 8896399587 9475729174 6426357455 2540790914 5135711136 9410911939 3251910760 2082520261 8798531887 7058429725 9167781314 9699009019 2116971737 2784768472 6860849003 3770242429 1651300500 5168323364 3503895170 2989392233 4517220138 1280696501 1784408745 1960121228 5993716231 3017114448 4640903890 6449544400 6198690754 8516026327 5052983491 8740786680 8818338510 2283345085 0486082503 9302133219 7155184306 3545500766 8282949304 1377655279 3975175461 3953984683 3936383047 4611996653 8581538420 5685338621 8672523340 2830871123 2827892125 0771262946 3229563989 8989358211 6745627010 2183564622 0134967151 8819097303 8119800497 3407239610 3685406643 1939509790 1906996395 5245300545 0580685501 9567302292 1913933918 5680344903 9820595510 0226353536 1920419947 4553859381 0234395544 9597783779 0237421617 2711172364 3435439478 2218185286 2408514006 6604433258 8856986705 4315470696 5747458550 3323233421 0730154594 0516553790 6866273337 9958511562 5784322988 2737231989 8757141595 7811196358 3300594087 3068121602 8764962867 4460477464 9159950549 7374256269 0104903778 1986835938 1465741268 0492564879 8556145372 3478673303 9046883834 3634655379 4986419270 5638729317 4872332083 7601123029 9113679386 2708943879 9362016295 1541337142 4892830722 0126901475 4668476535 7616477379 4675200490 7571555278 1965362132 3926406160 1363581559 0742202020 3187277605 2772190055 6148425551 8792530343 5139844253 2234157623 361 0642506 3904975008 6562710953 5919465897 5141310348 2276930624 7435363256 9160781547 8181152843 6679570611086153315 4452127473 9245449454 2368288606 1340841486 3776700961 2071512491 4043027253 8607648236 3414334623 5189757664 5216413767 9690314950 1910857598 4423919862 9164219399 4907236234 6468441173 9403265918 4044378051 3338945257 4239950829 6591228508 5558215725 0310712570 1266830240 2929525220 1187267675 6220415420 5161841634 8475651699 9811614101 0029960783 8690929160 3028840026 9104140792 8862150784 2451670908 7000699282 1206604183 7180653556 7252532567 5328612910 4248776182 5829765157 9598470356 2226293486 0034158722 9805349896 5022629174 8788202734 2092222453 3985626476 6914905562 8425039127 5771028402 7998066365 8254889264 8802545661 0172967026 6407655904 2909945681 5065265305 3718294127 0336931378 5178609040 7086671149 6558343434 7693385781 7113864558 7367812301 4587687126 6034891390 9562009939 3610310291 6161528813 8437909904 2317473363 9480457593 1493140529 7634757481 1935670911 0137751721 0080315590 2485309066 9203767192 2033229094 3346768514 2214477379 3937517034 4366199104 0337511173 5471918550 4644902636 5512816228 8244625759 1633303910 7225383742 1821408835 0865739177 1509682887 4782656995 9957449066 1758344137 5223970968 3408005355 9849175417 3818839994 4697486762 6551658276 5848358845 3142775687 9002909517 0283529716 3445621296 4043523117 6006651012 4120065975 5851276178 5838292041 9748442360 8007193045 7618932349 2292796501 9875187212 7267507981 2554709589 0455635792 1221033346 6974992356 3025494780 2490114195 2123828153 0911407907 3860251522 7429958180 7247162591 6685451333 1239480494 7079119153 2673430282 4418604142 6363954800 0448002670 4962482017 9289647669 7583183271 3142517029 6923488962 7668440323 2609275249 6035799646 9256504936 8183609003 2380929345 9588970695 3653494060 3402166544 3755890045 6328822505 4525564056 4482465151 8754711962 1844396582 5337543885 6909411303 1509526179 3780029741 2076651479 3942590298 9695946995 5657612186 5619673378 6236256125 2163208628 6922210327 4889218654 3648022967 8070576561 5144632046 9279068212 0738837781 4233562823 6089632080 6822246801 2248261177 1858963814 0918390367 3672220888 3215137556 0037279839 4004152970 0287830766 7094447456 0134556417 2543709069 7939612257 1429894671 5435784687 8861444581 2314593571 9849225284 7160504922 1242470141 2147805734 5510500801 9086996033 0276347870 8108175450 1193071412 2339086639 3833952942 5786905076 4310063835 1983438934 1596131854 3475464955 6978103829 3097164651 4384070070 7360411237 3599843452 2516105070 2705623526 6012764848 3084076118 3013052793 2054274628 6540360367 4532865105 7065874882 2569815793 6789766974 2205750596 8344086973 5020141020 6723585020 0724522563 2651341055 9240190274 2162484391 4035998953 5394590944 0704691209 1409387001 2645600162 3742880210 9276457931 0657922955 2498872758 4610126483 6999892256 9596881592 0560010165 5256375678…

Спиральный рисунок числа Пи.

Применение числа «Пи» в школьной программе.

В школьной программе число П используется для вычисления длины окружности и её частей, и для вычисления площади круга, сектора и сегмента.

Длину окружности можно найти с помощью формулы: С=r . а длину дуги можно вычислить с помощью формулы: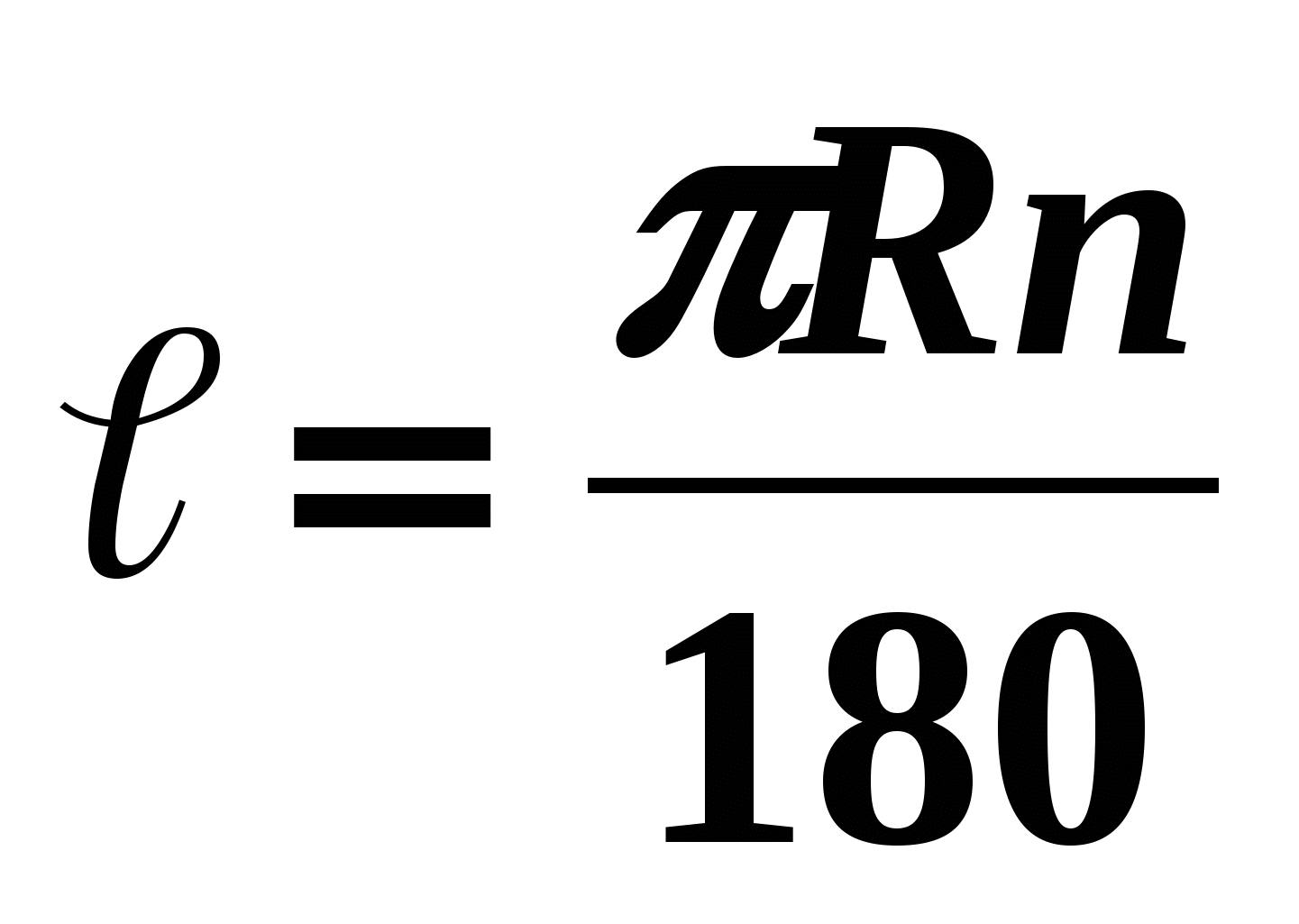 где n –величина дуги в градусах.

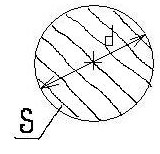
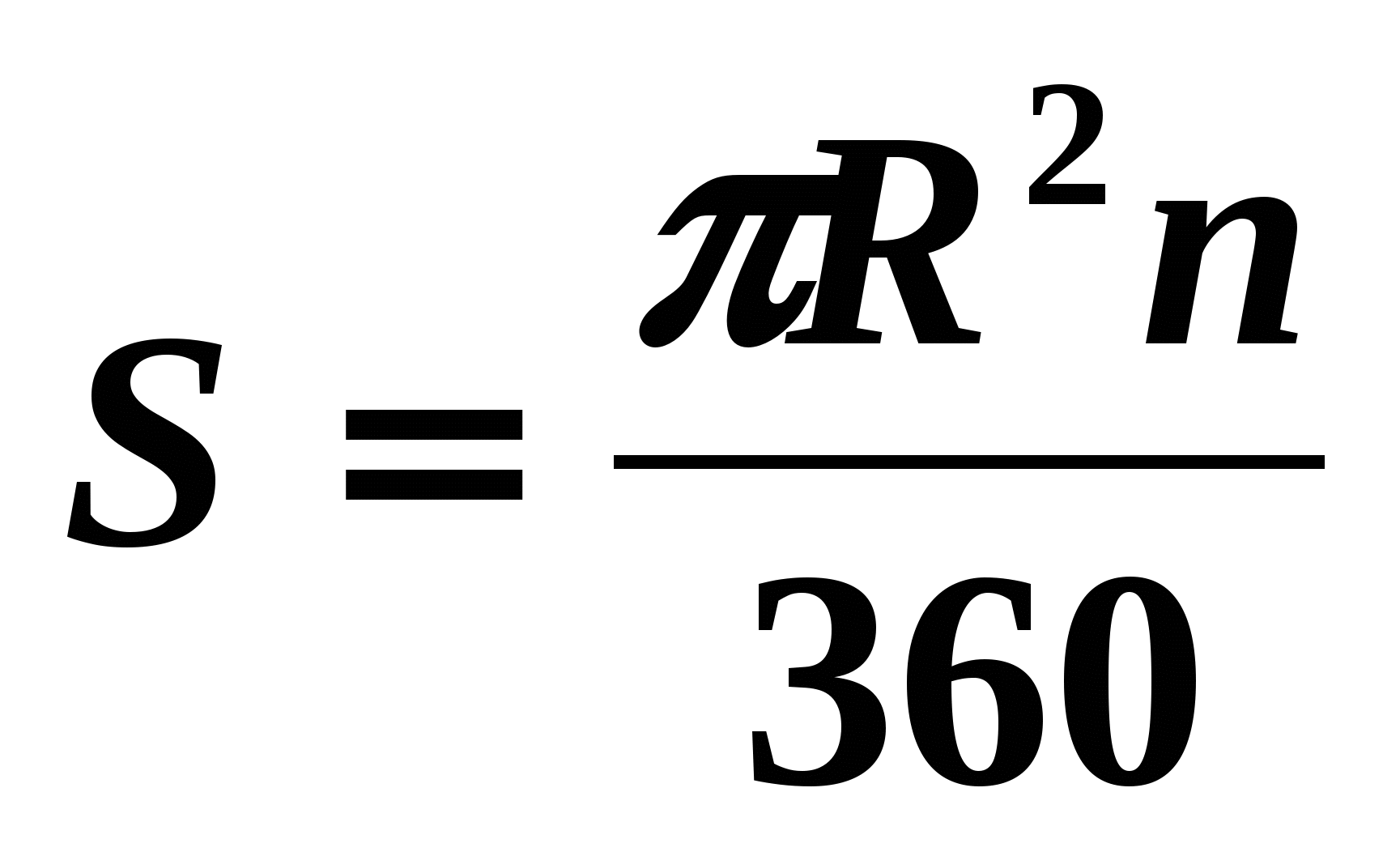Площадь круга можно вычислить по формуле: S=R2 ,площадь сектора -, площадь сегмента – S= Sсектора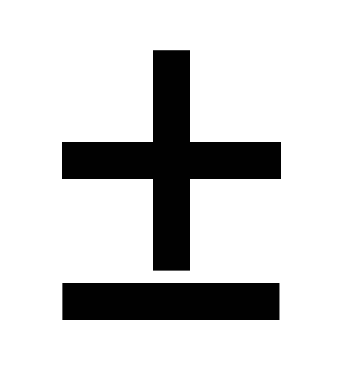Sтреугольника. «Плюс» в том случае, если сегмент больше полукруга, и «минус»- если сегмент меньше полукруга

В обиходе нам достаточно знать три знака 3,14. Однако в некоторых расчетах нужна большая точность.

Число П = 3,1415926…..

Вот некоторые стихотворения, которые помогают запомнить ряд цифр в числе П :

Поэзия и математика

Гордый Рим трубил победуНад твердыней Сиракуз;Но трудами АрхимедаМного больше я горжусь.Надо нынче нам заняться,Оказать старинке честь,Чтобы нам не ошибаться,Чтоб окружность верно счесть,Надо только постаратьсяИ запомнить все как естьТри, четырнадцать,пятнадцать, девяносто два и шесть. С.Бобров

Вот и Маша, и Анюта прибежали Пи узнать число они желали

( число букв в слове, означает соответствующую цифру числе пи)

П = 3,1415926536…

У наших предков не было компьютеров, калькуляторов и справочников, но со времен Петра I они занимались геометрическими расчетами в астрономии, в машиностроении, в корабельном деле. Впоследствии сюда добавилась электротехника – там есть понятие «круговой частоты переменного тока». Для запоминания числа «Пи» было придумано двустишие (к сожалению, мы не знаем автора и места первой публикации его; но еще в конце 40-х годов двадцатого века московские школьники занимались по учебнику геометрии Киселева, где оно приводилось).

Кто и шутя, и скоро пожелаетъ

«Пи» узнать число - ужъ знаетъ

П=3,1415926536

Это двустишие написано по правилам старой русской орфографии, по которой после согласной в конце слова обязательно ставился мягкий или твёрдый знак.

Чтобы нам не ошибаться,

Надо правильно прочесть:

Три, четырнадцать, пятнадцать,

Девяносто два и шесть.

Ну и дальше надо знать,

Если мы вас спросим –

Это будет пять, три, пять,

Восемь, девять, восемь.

П = 3,1415926535898…

Заключение.

Число Пи применяется во многих формулах математики, физики, биологии, экономики и др. Интерес к числу Пи оказался так велик, что ему воздвигнуты памятники в различных частях света:

Стоунхендж. Великобритания.

Здесь в кругу закодированное изображение первых десяти знаков числа .

Мало того, числу П объявлены праздники:

Сиэтл (Австралия)

Южное побережье Крымского полуострова.

Неофициальный праздник «День числа Пи» отмечается 14 марта, которое в американском формате дат (месяц/день) записывается как 3.14, что соответствует приближённому значению числа π.
Е
Если вас заинтересовало это загадочное ,то вы можете посетить его специальный сайт…
щё одной датой, связанной с числом π, является 22 июля, которое называется «Днём приближённого числа Пи», так как в европейском формате дат этот день записывается как 22/7, а значение этой дроби 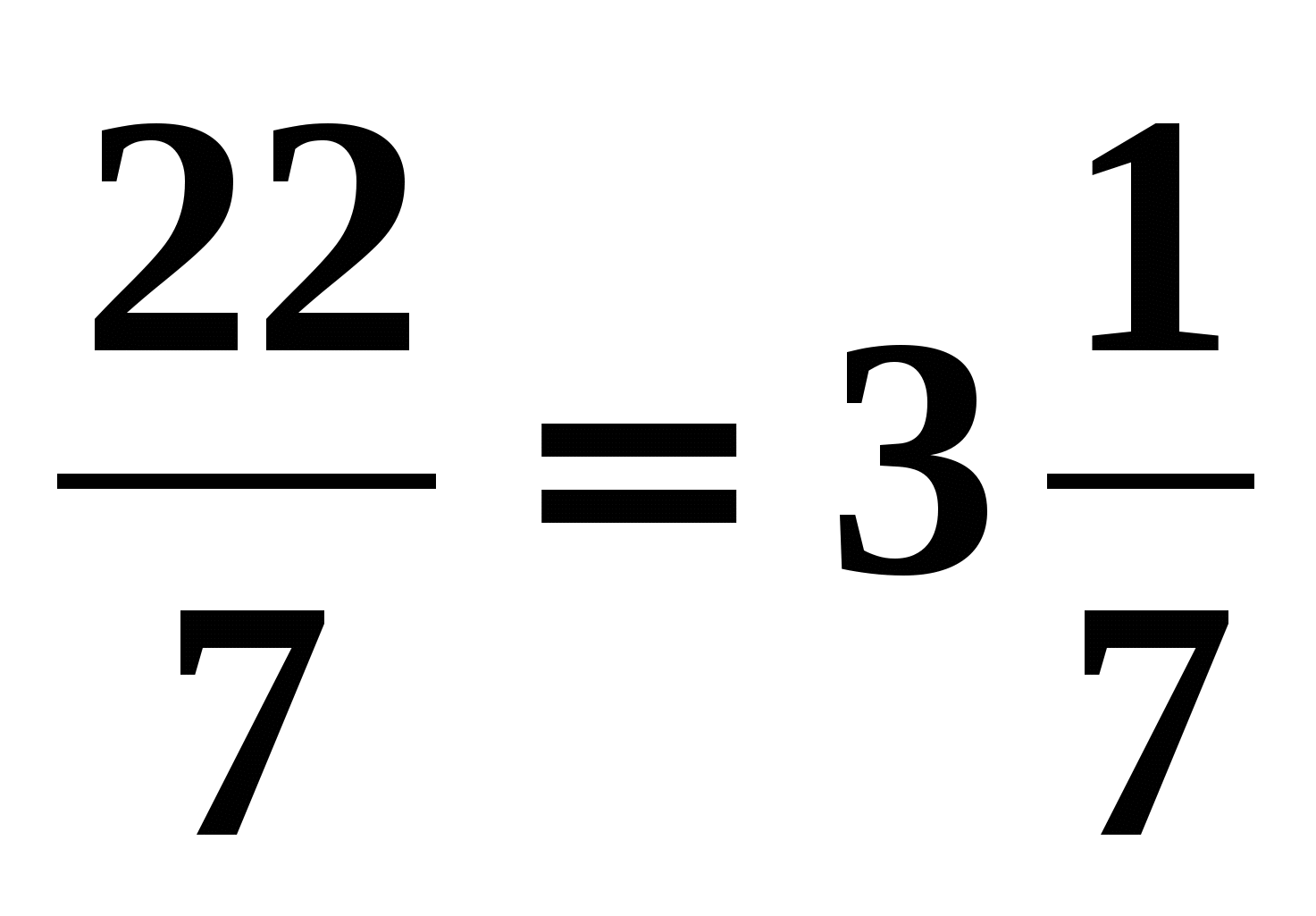,является приближённым значением числа π.

Список литературы.

Энциклопедия для детей. Т. 11. Математика/Глав. редактор - М.Д. Аксёнова; Авита+,2003г. 688с. (195с.)
Энциклопедический словарь юного математика/Сост. А.П.Савлин.-М.:Педагогика, 1989г.-352с.(29,136,225,248,306,333).
Детская энциклопедия для среднего и старшего возраста. Изд. 3,т. 2, 480 с.(438,440,464,466)
http://slovo67.ucoz.ru/forum/10-43-1

infourok.ru

Реферат на тему "Число Пи"

МБУ СОШ№48

г.Нижнеудинск

Реферат

«Число p»

Автор Юрченко Татьяна

ученица 9 класса

МБУ СОШ№48

г.Нижнеудинск

руководитель

Шаповалова Римма Ивановна

учитель математики

2014год

Содержание:

-Цель работы

-Задачи работы

-Первое знакомство с числом p

-Возникновение числа p

-Примеры возникновения числа p (пример №1, пример №2, пример №3)

-Запись числа p

-Мнемоническое правило

-Забавные факты (2 части)

Математика пронизывает все науки без исключения, и каждый из нас должен быть в ней более или менее компетентен. В математике есть удивительное и загадочное число. Это число p

Цель работы:

Исследование числа p и выявление его роли в окружающей среде

Задачи работы

Повысить математическую культуру

Уметь обрабатывать информацию

Развить умение анализировать и делать выводы

Научиться кратко излагать свои мысли

Первое знакомство с числом p

В школьном курсе математики с числом p мы впервые встречаемся в 6 классе в теме: «Длина окружности и площадь круга». В учебнике мы сталкиваемся со следующим объяснением: «Длина окружности прямо пропорциональна длине её диаметра. Поэтому для всех окружностей отношение длины окружности к длине её диаметра является одним и тем же числом. Его обозначают греческой буквой p («читается «пи»»). Длина окружности: C=2pr; площадь круга S=pr2 ».

Потом, только в старших классах мы опять встречаемся с числом p, но уже в курсе геометрии пытаются доказать длину окружности следующим образом. «Периметр любого правильного вписанного в окружность многоугольника является приближённым значением длины окружности. Чем больше число сторон такого многоугольника, тем точнее это приближённое значение, так как многоугольник при увеличении числа сторон всё ближе и ближе «прилегает» к окружности

Возникновение числа p

Более двух тысячелетий назад было подмечено, что все окружности длиннее своих диаметров в одно и то же число раз. Впоследствии это было доказано.

Отношение длины окружности к её диаметру лет 250 назад стали обозначать кратко одной буквой p. Эта греческая буква – первая буква греческого слова «периферия», что означает «окружность». В древнем Вавилоне считали, что окружность длиннее её диаметра в три раза (т.е. p приблизительно равно трём). Но древнегреческие геометры уже знали, что p не равно трём. Об этом мы знаем из школьного курса геометрии. Почему же тогда Бертран Рассел в своей книге «Кошмары выдающихся личностей» писал: «лицо p было скрыто маской. Все понимали, что сорвать её, оставшись при этом в живых, не сможет никто. Сквозь прорези маски пронзительно, безжалостно, холодно и загадочно смотрели глаза …».

Английский математик Август де Морган назвал как-то p «…загадочным числом 3,14159…, которое лезет в дверь, в окно и через крышу».

Число p связывают с окружностью. Однако это число появляется в различных математических результатах, в которых ни о какой окружности речи не идёт.

Примеры возникновения числа p

Пример №1

Рассмотрим множество положительных чисел. Если у них случайным образом выбрать два числа, то какова вероятность того, что выбранные числа не будут иметь общего делителя? Ответ неожидан: искомая вероятность равна 6/ p в квадрате.

Пример №2

Когда-то немецкий математик Лейбниц (1646-1716) заинтересовался, сколько получится в пределе, если последовательно будем складывать такие числа:1-1/3+1/5-1/7+1/9-1/11+... Оказалось, что в пределе мы получим p /4. (Для доказательства Лейбниц пользовался приёмами высшей математики).

Пример №3

Было найдено и много других формул, где неожиданно появляется число p. Вот формула английского математика Джона Валлиса:

Записи числа p

2 знака после запятой:

p =3,14

510 знаков после запятой:

p =3,141 592 653 589 793 238 462 643 383 279 502 884 192 169 399 375 105 280 974 944 592 307 816 406 286 208 998 628 034 825 342 117 067 982 148 086 513 282 306 647 093 844 609 550 582 231 725 359 408 128 481 117 450 284 102 701 938 521 105 559 644 622 948 954 930 381 964 428 810 975 665 933 446 128 475 648 233….

Мнемоническое правило

Чтобы нам не ошибаться,
Надо правило прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Надо только постараться
И запомнить все как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Три, четырнадцать, пятнадцать,
Девять, два, шесть, пять, три, пять.
Чтоб наукой заниматься
Это каждый должен знать.

Если подсчитать количество букв в каждом слове в нижеприведенных фраза

х ( без учета знаков препинания) и записать эти цифры подряд, не забывая про десятичную запятую после первой цифры «3». Получится приближенное число p

Забавные факты

Международный день числа p

14 марта человечество отмечает Международный день числа p. Почему 14 марта? Если быть точнее, то поздравлять окружающих с днем «пи» нужно в марте 14-го в 1:59:26, в соответствии с цифрами числа p – 3,1415926…

Интересно, что праздник числа p, отмечающийся 14 марта, совпадает с днем рождения одного из наиболее выдающихся физиков современности Альбертом Эйнштейном.

Еще одной датой, связанной с числом p, является 22 июля, которою называют «Днем приближенного числа p», так как в европейском формате дат этот день записывается как 22/7. а значение этой дроби является приближенным значением числа p

Мировой рекорд по запоминанию знаков числа пи принадлежит японцу Акира Харагути. Он запомнил число p до 100- тысячного знака после запятой. Ему понадобилось почти 16 часов, чтобы назвать всё число целиком.

В штате Индиана ( США) в 1897 был выпушен билль, законодательно устанавливающий значение числа p равным 3,2. Данный билль не стал законом благодаря своевременному вмешательству профессора Университета Пердью,присутствовавшем во время рассмотрения принятого данного закона.

Список литературы

1 Стройк Д.Я. Краткий очерк истории математики. Перевод с немецкого и дополнения И.Б. Погребысского - М.: «Наука» Главная редакция физико-математической литературы 2012г

2. Глейзер. Г.И. история математики в средней школе / Г.И. Глейзер. – М.: Просвещение, 2011г.

3. Виленкин Н.Я. Математика: Учеб. Для 6 кл. общеобразоват. Учреждений / Н.Я Виленкин, В.И. Жохов, А.С Чесноков, С.И Шварцбурд.- 15-е изд. Перераб. – М.:

Мнемозина, 2012.

4. Атанасян Л.С. Геометрии: Учеб. Для 7-9 кл. общеобразоват. Учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 13-е изд. – М.: росвещение, 2014.

5. Математика в школе, журнал, 2010г год.

6. Мантуров О.В. Толковый словарь математических терминов: Пособие для учителей / О.В.Мантуров, Ю.К.Солнцев, Ю.И.Соркин, Н.Г.Федин. – М.: Просвещение, 2013г

kopilkaurokov.ru

Реферат: Краткая история числа пи

С тех пор, как у людей появилась возможность считать и они начали исследовать свойства абстрактных объектов, называемых числами, поколения пытливых умов совершали завораживающие открытия. По мере того как наши знания о числах увеличивались, некоторые из них привлекали особое внимание, а некоторым даже придавали мистические значения. Был, который обозначает ничего, и который при умножении на любое число дает себя. Была, начало всего, также обладающая редкостными свойствами, простые числа. Затем обнаружили, что существуют числа, которые не являются целыми, а иногда получаются в результате деления двух целых чисел, — числа рациональные. Иррациональные числа, которые не могут быть получены как отношение целых чисел, и т.д. Но Если и есть число, которое очаровало и вызвало написание массы трудов, то это(пи). Число, которое, несмотря на долгую историю, не называли так, как мы называем его сегодня, до восемнадцатого века.

Начало

Число пи получается делением длины окружности на ее диаметр. При этом размер окружности не важен. Большая или маленькая, отношение длины к диаметру одно и то же. Хотя вполне вероятно, что это свойство было известно ранее, самые первые свидетельства об этом знании — Московский математический папирус 1850 г. до н.э. и папирус Ахмеcа 1650 г. до н.э. (хотя это копия более старого документа). В нем имеется большое количество математических задач, в некоторых из которыхприближается как, что чуть более чем на 0,6% отличается от точного значения. Примерно в это же время вавилоняне считалиравным. В Ветхом Завете, написанном более десяти столетий спустя, Яхве не усложняет жизнь и божественным указом устанавливает, чтов точности равно.

Однако великими исследователями этого числа были древние греки, такие как Анаксагор, Гиппократ из Хиоса и Антифон из Афин. Ранее значениеопределялось, почти наверняка, с помощью экспериментальных измерений. Архимед был первым, кто понял, как теоретически оценить его значение. Использование описанного и вписанного многоугольников (больший описан около окружности, в которую вписан меньший) позволило определить, чтобольшеи меньше. С помощью метода Архимеда другие математики получили лучшие приближения, и уже в 480 г. Цзу Чунчжи определил, что значениянаходится междуи. Тем не менее метод многоугольников требует много вычислений (напомним, что все делалось вручную и не в современной системе счисления), так что у него не было будущего.

Представления

Нужно было дождаться XVII века, когда с открытием бесконечного ряда свершилась революция в вычислении, хотя первый результат не был рядом, это было произведение. Бесконечные ряды — это суммы бесконечного числа членов, образующих некоторую последовательность (например, все числа вида, гдепринимает значения отдо бесконечности). Во многих случаях сумма конечна и может быть найдена различными методами. Оказывается, что некоторые из этих рядов сходятся кили некоторой величине, имеющей отношение к. Для того чтобы ряд сходился, необходимо (но не достаточно), чтобы с ростомсуммируемые величины стремились к нулю. Таким образом, чем больше чисел мы складываем, тем точнее мы получаем значение. Теперь у нас есть две возможности получения более точного значения. Или сложить больше чисел, или найти другой ряд, сходящийся быстрее, так чтобы складывать меньшее количество чисел.

Благодаря этому новому подходу точность вычислениярезко возросла, и в 1873 году Уильям Шенкс опубликовал результат многолетней работы, приведя значениес 707 десятичными знаками. К счастью, он не дожил до 1945 года, когда было обнаружено, что он сделал ошибку и все цифры, начиная с 528, были неправильными. Тем не менее, его подход был наиболее точным до появления компьютеров. Это была предпоследняя революция в вычислении. Математические операции, которые при выполнении их вручную занимают несколько минут, в настоящее время выполняются в доли секунды, причем ошибки практически исключены. Джону Ренчу и Л. Р. Смиту удалось вычислить 2000 цифр за 70 часов на первом электронном компьютере. Барьер в миллион цифр был достигнут в 1973 году.

Последнее (на данный момент) достижение в вычислении— открытие итерационных алгоритмов, которые сходятся кбыстрее, чем бесконечные ряды, так что можно достичь намного более высокой точности при той же вычислительной мощности. Текущий рекорд составляет чуть более 10 триллионов верных цифр. Зачем же так точно вычислять? Учитывая, что, зная 39 цифр этого числа, можно вычислить объем известной Вселенной с точностью до атома, не за чем… пока.

Некоторые интересные факты

Однако вычисление значенияявляется лишь малой частью его истории. Это число обладает свойствами, благодаря которым эта константа столь любопытна.

Возможно, самой большой проблемой, связанной с, является известная задача о квадратуре круга, задача о построении с помощью циркуля и линейки квадрата, площадь которого равна площади данного круга. Квадратура круга мучила поколения математиков в течение двадцати четырех столетий, пока фон Линдеман не доказал, что— трансцендентное число (оно не является решением никакого полиномиального уравнения с рациональными коэффициентами) и, следовательно, невозможно объять необъятное. До 1761 г. не было доказано, что числоиррациональное, то есть что не существует двух натуральных чиселитаких, что. Трансцендентностьне была доказана до 1882 года, однако пока неизвестно, являются ли числаили(— это еще одно иррациональное трансцендентное число) иррациональными. Появляется много соотношений, которые не связаны с окружностями. Это часть коэффициента нормализации нормальной функции, видимо, наиболее широко используемой в статистике. Как уже упоминалось ранее, числопоявляется как сумма многих рядов и равно бесконечным произведениям, оно важно и при изучении комплексных чисел. В физике его можно найти (в зависимости от применяемой системы единиц) в космологической постоянной (самая большая ошибка Альберта Эйнштейна) или константе постоянного магнитного поля. В системе счисления с любым основанием (в десятичной, двоичной…), цифрыпроходят все тесты на случайность, не наблюдается никакого порядка или последовательности. Дзета-функция Римана тесно связывает числос простыми числами. Это чило имеет долгую историю и наверняка до сих пор хранит множество сюрпризов.

Список литературы

http://lacienciaysusdemonios.com/2013/02/14/breve-historia-de-pi/

3.1415926535 8979323846 2643383279 5028841971 6939937510

5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989...

Первые 1000 знаков после запятой числа π.[1]

$\pi~$ (произносится «пи») — математическая константа, выражающая отношение длины окружности к длине её диаметра.[2] Обозначается буквой греческого алфавита «пи». Старое название — лудольфово число.

1. Свойства

1.1. Трансцендентность и иррациональность

π — иррациональное число, то есть его значение не может быть точно выражено в виде дроби m/n, где m и n — целые числа. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. Иррациональность числа π была впервые доказана Иоганном Ламбертом в 1761[3] году путём разложения числа $\frac{e-1}{2^n}$ в непрерывную дробь. В 1794 году Лежандр привёл более строгое доказательство иррациональности чисел π и π2.
π — трансцендентное число, это означает, что оно не может быть корнем какого-либо многочлена с целыми коэффициентами. Транcцендентность числа π была доказана в 1882 году профессором Кёнигсбергского, а позже Мюнхенского университета Линдеманом. Доказательство упростил Феликс Клейн в 1894 году.[4]
- Поскольку в евклидовой геометрии площадь круга и длина окружности являются функциями числа π, то доказательство трансцендентности π положило конец спору о квадратуре круга, длившемуся более 2,5 тысяч лет.
В 1934 году Гельфонд доказал трансцендентность числа eπ.[5] В 1996 году Юрий Нестеренко доказал, что для любого натурального n числа π и $e^{\pi\sqrt n}$ алгебраически независимы, откуда, в частности, следует трансцендентность чисел π + eπ,πeπ и $e^{\pi\sqrt n}$ .[6][7]

1.2. Соотношения

Известно много формул числа π:

$\frac2\pi= \frac{\sqrt{2}}2\cdot \frac{\sqrt{2+\sqrt2}}2\cdot \frac{\sqrt{2+\sqrt{2+\sqrt2}}}2 \cdot \ldots$

Формула Валлиса:

$\frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdots = \frac{\pi}{2}$ $\frac{1}{1} - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \cdots = \frac{\pi}{4}$

Тождество Эйлера:

$e^{i \pi} + 1 = 0\;$

Т. н. «интеграл Пуассона» или «интеграл Гаусса»

$\int\limits_{-\infty}^{+\infty}\ e^{-x^2}{dx} = \sqrt{\pi}$

Интегральный синус:

$\int\limits_{-\infty }^{+\infty }{\frac{\sin x}{x}dx}=\pi$

Выражение через полилогарифм:[8]

$\pi=\sqrt{6\ln^2 2+12\ \operatorname{Li}_2\left(\frac{1}{2}\right)}$

2. История

Символ константы

Впервые обозначением этого числа греческой буквой $\pi~$ воспользовался британский математик Джонс в 1706 году, а общепринятым оно стало после работ Леонарда Эйлера в 1737 году.

Это обозначение происходит от начальной буквы греческих слов περιφέρεια — окружность, периферия и περίμετρος — периметр.

История числа π шла параллельно с развитием всей математики. Некоторые авторы разделяют весь процесс на 3 периода: древний период, в течение которого π изучалось с позиции геометрии, классическая эра, последовавшая за развитием математического анализа в Европе в XVII веке, и эра цифровых компьютеров.

2.1. Геометрический период

То, что отношение длины окружности к диаметру одинаково для любой окружности, и то, что это отношение немногим более 3, было известно ещё древнеегипетским, вавилонским, древнеиндийским и древнегреческим геометрам. Самое раннее из известных приближений датируется 1900 годом до н. э.; это 25/8 (Вавилон) и 256/81 (Египет), оба значения отличаются от истинного не более, чем на 1 %. Ведический текст «Шатапатха-брахмана» даёт π как 339/108 ≈ 3,139. По-видимому, в Танахе, в третьей книге Царств, предполагается, что π = 3, что является гораздо более худшей оценкой, чем имевшиеся на момент написания (600 год до н. э.).

Алгоритм Лю Хуэя для вычисления π

Архимед, возможно, первым предложил математический способ вычисления π. Для этого он вписывал в окружность и описывал около неё правильные многоугольники. Принимая диаметр окружности за единицу, Архимед рассматривал периметр вписанного многоугольника как нижнюю оценку длины окружности, а периметр описанного многоугольника как верхнюю оценку. Рассматривая правильный 96-угольник, Архимед получил оценку $3+\frac{10}{71} < \pi <3+\frac{1}{7}$ .

Чжан Хэн во 2 веке уточнил значение числа π, предложив два его эквивалента: 1) 92/29 ≈ 3,1724…; 2) $\sqrt{10}$ ≈ 3,1622

В Индии Ариабхата и Бхаскара использовали приближение 3,1416. Брахмагупта в 7 веке предложил в качестве приближения $\sqrt{10}$ .

Около 265 года н. э. математик Лю Хуэй из царства Вэй предоставил простой и точный итеративный алгоритм (англ. Liu Hui's π algorithm) для вычисления π с любой степенью точности. Он самостоятельно провёл вычисление для 3072-угольника и получил приближённое значение для π по следующему принципу:

$\pi\approx A_{3072} = {3 \cdot 2^8\cdot \sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+1}}}}}}}}}} \approx 3,14159.$

Позднее Лю Хуэй придумал быстрый метод вычисления π и получил приближённое значение 3,1416 только лишь с 96-угольником, используя преимущества того факта, что разница в площади следующих друг за другом многоугольников формирует геометрическую прогрессию со знаменателем 4.

В 480-х годах китайский математик Цзу Чунчжи продемонстрировал, что π ≈ 355/113, и показал, что 3,1415926 < π < 3,1415927, используя алгоритм Лю Хуэя применительно к 12288-угольнику. Это значение оставалось самым точным приближением числа π в течение последующих 900 лет.

2.2. Классический период

До II тысячелетия было известно не более 10 цифр π. Дальнейшие крупные достижения в изучении π связаны с развитием математического анализа, в особенности с открытием рядов, позволяющих вычислить π с любой точностью, суммируя подходящее количество членов ряда. В 1400-х годах Мадхава из Сангамаграма (англ. Madhava of Sangamagrama) нашёл первый из таких рядов:

${\pi} = \frac{4}{1} - \frac{4}{3} + \frac{4}{5} - \frac{4}{7} + \cdots$

Этот результат известен как ряд Мадхавы — Лейбница, или ряд Грегори — Лейбница (после того как он был заново обнаружен Джеймсом Грегори и Готфридом Лейбницем в XVII веке). Однако этот ряд сходится к π очень медленно, что приводит к сложности вычисления многих цифр числа на практике — необходимо сложить около 4000 членов ряда, чтобы улучшить оценку Архимеда. Однако преобразованием этого ряда в

$\pi = \sqrt{12} \, \left(1-\frac{1}{3 \cdot 3} + \frac{1}{5 \cdot 3^2} - \frac{1}{7 \cdot 3^3} + \cdots\right)$

Мадхава смог вычислить π как 3,14159265359, верно определив 11 цифр в записи числа. Этот рекорд был побит в 1424 году персидским математиком Джамшидом ал-Каши, который в своём труде под названием «Трактат об окружности» привёл 17 цифр числа π, из которых 16 верные.

Первым крупным европейским вкладом со времён Архимеда был вклад голландского математика Людольфа ван Цейлена, затратившего десять лет на вычисление числа π с 20-ю десятичными цифрами (этот результат был опубликован в 1596 году). Применив метод Архимеда, он довёл удвоение до n-угольника, где n = 60·229. Изложив свои результаты в сочинении «Об окружности» («Van den Circkel»), Лудольф закончил его словами: «У кого есть охота, пусть идёт дальше». После смерти в его рукописях были обнаружены ещё 15 точных цифр числа π. Лудольф завещал, чтобы найденные им знаки были высечены на его надгробном камне. В честь него число π иногда называли «лудольфовым числом», или «константой Лудольфа».

Примерно в это же время в Европе начали развиваться методы анализа и определения бесконечных рядов. Первым таким представлением была формула Виета (англ. Viète's formula)

$\frac2\pi = \frac{\sqrt2}2 \cdot \frac{\sqrt{2+\sqrt2}}2 \cdot \frac{\sqrt{2+\sqrt{2+\sqrt2}}}2 \cdot \cdots$ ,

найденная Франсуа Виетом в 1593 году. Другим известным результатом стала формула Валлиса:

$\frac{\pi}{2} = \frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdots$ ,

выведенная Джоном Валлисом в 1655 году.

В Новое время для вычисления π используются аналитические методы, основанные на тождествах. Перечисленные выше формулы малопригодны для вычислительных целей, поскольку либо используют медленно сходящиеся ряды, либо требуют сложной операции извлечения квадратного корня.

Первую эффективную формулу нашёл в 1706 году Джон Мэчин (англ. John Machin)

$\frac{\pi}{4} = 4\,\mathrm{arctg}\frac{1}{5} - \mathrm{arctg}\frac{1}{239}$

Разложив арктангенс в ряд Тейлора

$\mathrm{arctg}\ x = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \cdots$ ,

можно получить быстро сходящийся ряд, пригодный для вычисления числа π с большой точностью. Эйлер, автор обозначения π, получил 153 верных знака.

Формулы такого типа, в настоящее время известные как формулы Мэчина (англ. Machin-like formula), использовались для установки нескольких последовательных рекордов и остались наилучшими из известных методов для быстрого вычисления π в эпоху компьютеров. Выдающийся рекорд был поставлен феноменальным счетчиком Иоганном Дазе (англ. Johann Dase), который в 1844 году по распоряжению Гаусса применил формулу Мэчина для вычисления 200 цифр π в уме. Наилучший результат к концу XIX века был получен англичанином Вильямом Шенксом (англ. William Shanks), у которого ушло 15 лет для того, чтобы вычислить 707 цифр, хотя из-за ошибки только первые 527 были верными. Чтобы избежать подобных ошибок, современные вычисления подобного рода проводятся дважды. Если результаты совпадают, то они с высокой вероятностью верные. Ошибку Шенкса обнаружил один из первых компьютеров в 1948 году; он же за несколько часов подсчитал 808 знаков π.

Теоретические достижения в XVIII веке привели к постижению природы числа π, чего нельзя было достичь лишь только с помощью одного численного вычисления. Иоганн Генрих Ламберт доказал иррациональность π в 1761 году, а Адриен Мари Лежандр в 1774 году доказал иррациональность π2. В 1735 году была установлена связь между простыми числами и π, когда Леонард Эйлер решил знаменитую Базельскую проблему (англ. Basel problem) — проблему нахождения точного значения

$\frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots$ ,

которое составляет $\frac{\pi^2}{6}$ . И Лежандр, и Эйлер предполагали, что π может быть трансцендентным, что было в конечном итоге доказано в 1882 году Фердинандом фон Линдеманом.

Считается, что книга Уильяма Джонса «Новое введение в математику» c 1706 года первая ввела в использование греческую букву π для обозначения этой константы, но эта запись стала особенно популярной после того, как Леонард Эйлер принял её в 1737 году. Он писал:

Существует множество других способов отыскания длин или площадей соответствующей кривой или плоской фигуры, что может существенно облегчить практику; например, в круге диаметр относится к длине окружности как 1 к $\left(\frac{16}{5}-\frac{4}{239}\right)-\frac{1}{3} \cdot \left(\frac{16}{5^3}-\frac{4}{239^3}\right)+\cdots = 3{,}14159 \cdots = \pi$

2.3. Эра компьютерных вычислений

Эпоха цифровой техники в XX веке привела к увеличению скорости появления вычислительных рекордов. Джон фон Нейман и другие использовали в 1949 году ЭНИАК для вычисления 2037 цифр π, которое заняло 70 часов. Ещё одна тысяча цифр была получена в последующие десятилетия, а отметка в миллион была пройдена в 1973 году. Такой прогресс имел место не только благодаря более быстрому аппаратному обеспечению, но и благодаря алгоритмам. Одним из самых значительных результатов было открытие в 1960 году быстрого преобразования Фурье, что позволило быстро осуществлять арифметические операции над очень большими числами.

В начале XX века индийский математик Сриниваса Рамануджан обнаружил множество новых формул для π, некоторые из которых стали знаменитыми из-за своей элегантности и математической глубины. Одна из этих формул — это ряд:

$\frac{1}{\pi} = \frac{2 \sqrt 2}{9801} \sum_{k=0}^\infty \frac{(4k)!(1103+26390k)}{(k!)^4 396^{4k}}$ ,

братьями Чудновскими (англ. Chudnovsky brothers) в 1987 году, найдена похожая на неё:

$\frac{426880 \sqrt{10005}}{\pi} = \sum_{k=0}^\infty \frac{(6k)! (13591409 + 545140134k)}{(3k)!(k!)^3 (-640320)^{3k}}$ ,

который вычисляет по 14 цифр за ход. Чудновские использовали эту формулу для того, чтобы установить несколько рекордов в вычислении π в конце 1980-х, включая то, в результате которого в 1989 году было получено 1 011 196 691 цифр десятичного разложения. Эта формула используется в программах, вычисляющих π на персональных компьютерах, в отличие от суперкомпьютеров, которые устанавливают современные рекорды.

В то время как последовательность обычно повышает точность на фиксированную величину с каждым следующим членом, существуют итеративные алгоритмы, которые на каждом шагу умножают количество правильных цифр, требуя, правда, высоких вычислительных затрат на каждом из таких шагов. Прорыв в этом отношении был сделан в 1975 году, когда Ричард Брент (англ. Richard P. Brent) и Юджин Саламин (англ. Eugene Salamin (mathematician)) независимо друг от друга открыли алгоритм Брента — Саламина (англ. Gauss–Legendre algorithm), который, используя лишь арифметику, на каждом шагу удваивает количество известных знаков.[9] Алгоритм состоит из установки начальных значений

$a_0 = 1 \quad \quad \quad b_0 = \frac{1}{\sqrt 2} \quad \quad \quad t_0 = \frac{1}{4} \quad \quad \quad p_0 = 1$

и итераций:

$a_{n+1} = \frac{a_n+b_n}{2} \quad \quad \quad b_{n+1} = \sqrt{a_n b_n}$ $t_{n+1} = t_n - p_n (a_n-a_{n+1})^2 \quad \quad \quad p_{n+1} = 2 p_n$

пока an и bn не станут достаточно близки. Тогда оценка π даётся формулой

$\pi \approx \frac{(a_n + b_n)^2}{4 t_n}.$

При использовании этой схемы 25 итераций достаточно для получения 45 миллионов десятичных знаков. Похожий алгоритм, увеличивающий на каждом шаге точность в четыре раза, был найден Джонатаном Боруэйном (англ. Jonathan Borwein) Питером Боруэйном (англ. Peter Borwein).[10] При помощи этих методов Ясумаса Канада и его группа, начиная с 1980 года, установили большинство рекордов вычисления π вплоть до 206 158 430 000 знаков в 1999 году. В 2002 году Канада и его группа установили новый рекорд — 1 241 100 000 000 десятичных знаков. Хотя большинство предыдущих рекордов Канады были установлены при помощи алгоритма Брента — Саламина, вычисление 2002 года использовало две формулы типа мэчиновских, которые работали медленнее, но радикально снижали использование памяти. Вычисление было выполнено на суперкомпьютере Hitachi из 64 узлов с 1 терабайтом оперативной памяти, способном выполнять 2 триллиона операций в секунду.

Важным развитием недавнего времени стала формула Бэйли — Боруэйна — Плаффа (англ. Bailey–Borwein–Plouffe formula), открытая в 1997 году Саймоном Плаффом (англ. Simon Plouffe) и названная по авторам статьи, в которой она впервые была опубликована[11]. Эта формула,

$\pi = \sum_{k=0}^\infty \frac{1}{16^k} \left( \frac{4}{8k + 1} - \frac{2}{8k + 4} - \frac{1}{8k + 5} - \frac{1}{8k + 6}\right),$

примечательна тем, что она позволяет извлечь любую конкретную шестнадцатеричную или двоичную цифру числа π без вычисления предыдущих.[11] С 1998 до 2000 года распределённый проект PiHex использовал видоизменённую формулу ББП Фабриса Беллара для вычисления квадриллионного бита числа π, который оказался нулём.[12]

В 2006 году Саймон Плафф, используя PSLQ, нашёл ряд красивых формул.[13] Пусть q = eπ, тогда

$\frac{\pi}{24} = \sum_{n=1}^\infty \frac{1}{n} \left(\frac{3}{q^n-1} - \frac{4}{q^{2n}-1} + \frac{1}{q^{4n}-1}\right)$ $\frac{\pi^3}{180} = \sum_{n=1}^\infty \frac{1}{n^3} \left(\frac{4}{q^n-1} - \frac{5}{q^{2n}-1} + \frac{1}{q^{4n}-1}\right)$

и другие вида

$\pi^k = \sum_{n=1}^\infty \frac{1}{n^k} \left(\frac{a}{q^n-1} + \frac{b}{q^{2n}-1} + \frac{c}{q^{4n}-1}\right)$

где q = eπ, k — нечётное число, и a, b, c — рациональные числа. Если k — вида 4m + 3, то эта формула имеет особенно простой вид:

$p\pi^k = \sum_{n=1}^\infty \frac{1}{n^k} \left(\frac{2^{k-1}}{q^n-1} - \frac{2^{k-1}+1}{q^{2n}-1} + \frac{1}{q^{4n}-1}\right)$

для рационального p у которого знаменатель — число, хорошо разложимое на множители, хотя строгое доказательство ещё не предоставлено.

В августе 2009 года учёные из японского университета Цукубо рассчитали последовательность из 2 576 980 377 524 десятичных разрядов.[14]

31 декабря 2009 года французский программист Фабрис Беллар на персональном компьютере рассчитал последовательность из 2 699 999 990 000 десятичных разрядов.[15]

2 августа 2010 года американский студент Александр Йи и японский исследователь Сигэру Кондо рассчитали последовательность с точностью в 5 триллионов цифр после запятой.[16][17]

3. Рациональные приближения

$\frac{22}{7}$ — Архимед,

$\frac{377}{120}$ — дана в книге индийского мыслителя и астронома Ариабхаты в V веке н. э.,

$\frac{355}{113}$ — приписывается современнику Ариабхаты китайскому астроному Цзу Чунчжи.

4. Нерешённые проблемы

Неизвестно, являются ли числа π и e алгебраически независимыми.
Неизвестно, являются ли числа $\pi + e, \pi - e, \pi \cdot e, \pi / e, \pi ^ e, \pi ^{\sqrt 2}, \ln \pi, \pi ^ \pi, e^{\pi^2}$ рациональными, алгебраическими иррациональными или трансцендентными.[6][18][19][20][21][22]
До сих пор ничего не известно о нормальности числа π; неизвестно даже, какие из цифр 0—9 встречаются в десятичном представлении числа π бесконечное количество раз.

5. Метод иглы Бюффона

На разлинованную равноудалёнными прямыми плоскость произвольно бросается игла, длина которой равна расстоянию между соседними прямыми, так что при каждом бросании игла либо не пересекает прямые, либо пересекает ровно одну. Можно доказать, что отношение числа пересечений иглы с какой-нибудь линией к общему числу бросков стремится к $\frac2\pi$ при увеличении числа бросков до бесконечности.[23] Данный метод иглы базируется на теории вероятностей и лежит в основе метода Монте-Карло.[24]

6. Дополнительные факты

Памятник числу «пи» на ступенях перед зданием Музея искусств в Сиэтле

Неофициальный праздник «День числа пи» отмечается 14 марта, которое в американском формате дат (месяц/день) записывается как 3.14, что соответствует приближённому значению числа π. Считается[25], что праздник придумал в 1987 году физик из Сан-Франциско Ларри Шоу, обративший внимание на то, что 14 марта ровно в 01:59 дата и время совпадают с первыми разрядами числа Пи = 3,14159.
Ещё одной датой, связанной с числом π, является 22 июля, которое называется «Днём приближённого числа Пи» (англ. Pi Approximation Day), так как в европейском формате дат этот день записывается как 22/7, а значение этой дроби является приближённым значением числа π.
Мировой рекорд по запоминанию знаков числа π после запятой принадлежит китайцу Лю Чао, который в 2006 году в течение 24 часов и 4 минут воспроизвёл 67 890 знаков после запятой без ошибки.[26][27] В том же 2006 году японец Акира Харагути заявил, что запомнил число π до 100-тысячного знака после запятой,[28] однако проверить это официально не удалось.[29]
В штате Индиана (США) в 1897 году был выпущен билль (см.: en:Indiana Pi Bill), законодательно устанавливающий значение числа Пи равным 3,2.[30] Данный билль не стал законом благодаря своевременному вмешательству профессора университета Пердью, присутствовавшего в законодательном собрании штата во время рассмотрения данного закона.
«Число Пи для гренландских китов равно трем» написано в «Справочнике китобоя» 1960-х годов выпуска.[31]

В настоящее время вычислено 5 триллионов знаков после запятой.[17]

7. В культуре

Существует художественный фильм, названный в честь числа Пи.
В произведения Сергея Лукьяненко Спектр упоминаются миры где Пи равно 4.

Примечания

PI - www.math.com/tables/constants/pi.htm
Это определение пригодно только для евклидовой геометрии. В других геометриях отношение длины окружности к длине её диаметра может быть произвольным. Например, в геометрии Лобачевского это отношение меньше, чем $\pi~$ .
Lambert, Johann Heinrich. Mémoire sur quelques propriétés remarquables des quantités transcendentes circulaires et logarithmiques, стр. 265–322.
Доказательство Клейна приложено к работе «Вопросы элементарной и высшей математики», ч. 1, вышедшей в Гёттингене в 1908 году.
Weisstein, Eric W. Постоянная Гельфонда - mathworld.wolfram.com/GelfondsConstant.html (англ.) на сайте Wolfram MathWorld.
↑ 12Weisstein, Eric W. Иррациональное число - mathworld.wolfram.com/IrrationalNumber.html (англ.) на сайте Wolfram MathWorld.
Модулярные функции и вопросы трансцендентности - www.mathnet.ru/php/getFT.phtml?jrnid=sm&paperid=158&volume=187&year=1996&issue=9&fpage=65&what=fullt&option_lang=eng
Weisstein, Eric W. Pi Squared - mathworld.wolfram.com/PiSquared.html (англ.) на сайте Wolfram MathWorld.
Brent, Richard (1975), Traub, J F, ed., "Multiple-precision zero-finding methods and the complexity of elementary function evaluation - wwwmaths.anu.edu.au/~brent/pub/pub028.html", Analytic Computational Complexity (New York: Academic Press): 151–176, <http://wwwmaths.anu.edu.au/~brent/pub/pub028.html - wwwmaths.anu.edu.au/~brent/pub/pub028.html> (англ.)
Jonathan M Borwein. Pi: A Source Book. — Springer, 2004. — ISBN 0387205713 (англ.)
↑ 12David H. Bailey, Peter B. Borwein, Simon Plouffe. On the Rapid Computation of Various Polylogarithmic Constants - crd.lbl.gov/~dhbailey/dhbpapers/digits.pdf // Mathematics of Computation. — 1997. — В. 218. — Т. 66. — С. 903—913. (англ.)
Fabrice Bellard. A new formula to compute the nth binary digit of pi - bellard.org/pi/pi_bin/pi_bin.html (англ.).
Simon Plouffe. Indentities inspired by Ramanujan’s Notebooks (part 2) - www.lacim.uqam.ca/~plouffe/inspired2.pdf (англ.).
Установлен новый рекорд точности вычисления числа π - science.compulenta.ru/451031/
Pi Computation Record - bellard.org/pi/pi2700e9/
Число «Пи» рассчитано с рекордной точностью - science.compulenta.ru/552828/
↑ 12 5 Trillion Digits of Pi - New World Record - www.numberworld.org/misc_runs/pi-5t/announce_en.html (англ.)
Weisstein, Eric W. Pi - mathworld.wolfram.com/Pi.html (англ.) на сайте Wolfram MathWorld.
en:Irrational number#Open questions
Some unsolved problems in number theory - www.math.ou.edu/~jalbert/courses/openprob2.pdf
Weisstein, Eric W. Трансцендентное число - mathworld.wolfram.com/TranscendentalNumber.html (англ.) на сайте Wolfram MathWorld.
An introduction to irrationality and transcendence methods - www.math.jussieu.fr/~miw/articles/pdf/AWSLecture5.pdf
Обман или заблуждение? - kvant.mirror1.mccme.ru/1983/05/obman_ili_zabluzhdenie.htm Квант №5 1983 год
Г. А. Гальперин. Биллиардная динамическая система для числа пи - nature.web.ru/db/msg.html?mid=1161679&uri=node2.html.
Статья в Los Angeles Times «Желаете кусочек π»? (название обыгрывает сходство в написании числа π и слова pie (англ. пирог)) - latimesblogs.latimes.com/thehomeroom/2008/03/a-slice-of-pi-p.html (англ.).
Chinese student breaks Guiness record by reciting 67,890 digits of pi - www.newsgd.com/culture/peopleandlife/200611280032.htm
Interview with Mr. Chao Lu - www.pi-world-ranking-list.com/lists/details/luchaointerview.html
How can anyone remember 100,000 numbers? - search.japantimes.co.jp/print/fl20061217x1.html — The Japan Times, 17.12.2006.
Pi World Ranking List - www.pi-world-ranking-list.com/news/index.html
The Indiana Pi Bill, 1897 - www.agecon.purdue.edu/crd/Localgov/Second Level pages/indiana_pi_bill.htm (англ.)
В. И. Арнольд любит приводить этот факт, см. например книгу Что такое математика - www.mccme.ru/edu/viarn/whatis.ps (ps), стр. 9.

Литература

Жуков А. В. О числе π - www.mccme.ru/mmmf-lectures/books/books/book.18.pdf М.: МЦМНО, 2002. 32 с. ISBN 5-94057-030-5
Перельман Я. И. Квадратура круга. Л.: Дом занимательной науки, 1941. Текст в формате djv/zip - publ.lib.ru/ARCHIVES/P/PEREL'MAN_Yakov_Isidorovich/Kvadratura_kruga.(1941).[djv].zip.

wreferat.baza-referat.ru

Краткая история числа пи | Рефераты KM.RU

С тех пор, как у людей появилась возможность считать и они начали исследовать свойства абстрактных объектов, называемых числами, поколения пытливых умов совершали завораживающие открытия. По мере того как наши знания о числах увеличивались, некоторые из них привлекали особое внимание, а некоторым даже придавали мистические значения. Был , который обозначает ничего, и который при умножении на любое число дает себя. Была , начало всего, также обладающая редкостными свойствами, простые числа. Затем обнаружили, что существуют числа, которые не являются целыми, а иногда получаются в результате деления двух целых чисел, — числа рациональные. Иррациональные числа, которые не могут быть получены как отношение целых чисел, и т.д. Но Если и есть число, которое очаровало и вызвало написание массы трудов, то это (пи). Число, которое, несмотря на долгую историю, не называли так, как мы называем его сегодня, до восемнадцатого века.

Начало

Число пи получается делением длины окружности на ее диаметр. При этом размер окружности не важен. Большая или маленькая, отношение длины к диаметру одно и то же. Хотя вполне вероятно, что это свойство было известно ранее, самые первые свидетельства об этом знании — Московский математический папирус 1850 г. до н.э. и папирус Ахмеcа 1650 г. до н.э. (хотя это копия более старого документа). В нем имеется большое количество математических задач, в некоторых из которых приближается как , что чуть более чем на 0,6% отличается от точного значения. Примерно в это же время вавилоняне считали равным . В Ветхом Завете, написанном более десяти столетий спустя, Яхве не усложняет жизнь и божественным указом устанавливает, что в точности равно .

Однако великими исследователями этого числа были древние греки, такие как Анаксагор, Гиппократ из Хиоса и Антифон из Афин. Ранее значение определялось, почти наверняка, с помощью экспериментальных измерений. Архимед был первым, кто понял, как теоретически оценить его значение. Использование описанного и вписанного многоугольников (больший описан около окружности, в которую вписан меньший) позволило определить, что больше и меньше . С помощью метода Архимеда другие математики получили лучшие приближения, и уже в 480 г. 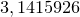Цзу Чунчжи определил, что значения находится между и . Тем не менее метод многоугольников требует много вычислений (напомним, что все делалось вручную и не в современной системе счисления), так что у него не было будущего.

Представления

Нужно было дождаться XVII века, когда с открытием бесконечного ряда свершилась революция в вычислении , хотя первый результат не был рядом, это было произведение. Бесконечные ряды — это суммы бесконечного числа членов, образующих некоторую последовательность (например, все числа вида , где принимает значения от до бесконечности). Во многих случаях сумма конечна и может быть найдена различными методами. Оказывается, что некоторые из этих рядов сходятся к или некоторой величине, имеющей отношение к . Для того чтобы ряд сходился, необходимо (но не достаточно), чтобы с ростом суммируемые величины стремились к нулю. Таким образом, чем больше чисел мы складываем, тем точнее мы получаем значение . Теперь у нас есть две возможности получения более точного значения . Или сложить больше чисел, или найти другой ряд, сходящийся быстрее, так чтобы складывать меньшее количество чисел.

Благодаря этому новому подходу точность вычисления резко возросла, и в 1873 году Уильям Шенкс опубликовал результат многолетней работы, приведя значение с 707 десятичными знаками. К счастью, он не дожил до 1945 года, когда было обнаружено, что он сделал ошибку и все цифры, начиная с 528, были неправильными. Тем не менее, его подход был наиболее точным до появления компьютеров. Это была предпоследняя революция в вычислении . Математические операции, которые при выполнении их вручную занимают несколько минут, в настоящее время выполняются в доли секунды, причем ошибки практически исключены. Джону Ренчу и Л. Р. Смиту удалось вычислить 2000 цифр за 70 часов на первом электронном компьютере. Барьер в миллион цифр был достигнут в 1973 году.

Последнее (на данный момент) достижение в вычислении — открытие итерационных алгоритмов, которые сходятся к быстрее, чем бесконечные ряды, так что можно достичь намного более высокой точности при той же вычислительной мощности. Текущий рекорд составляет чуть более 10 триллионов верных цифр. Зачем же так точно вычислять ? Учитывая, что, зная 39 цифр этого числа, можно вычислить объем известной Вселенной с точностью до атома, не за чем… пока.

Некоторые интересные факты

Однако вычисление значения 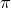является лишь малой частью его истории. Это число обладает свойствами, благодаря которым эта константа столь любопытна.

Возможно, самой большой проблемой, связанной с , является известная задача о квадратуре круга, задача о построении с помощью циркуля и линейки квадрата, площадь которого равна площади данного круга. Квадратура круга мучила поколения математиков в течение двадцати четырех столетий, пока фон Линдеман не доказал, что — трансцендентное число (оно не является решением никакого полиномиального уравнения с рациональными коэффициентами) и, следовательно, невозможно объять необъятное. До 1761 г. не было доказано, что число иррациональное, то есть что не существует двух натуральных чисел и таких, что . Трансцендентность не была доказана до 1882 года, однако пока неизвестно, являются ли числа или (— это еще одно иррациональное трансцендентное число) иррациональными. Появляется много соотношений, которые не связаны с окружностями. Это часть коэффициента нормализации нормальной функции, видимо, наиболее широко используемой в статистике. Как уже упоминалось ранее, число появляется как сумма многих рядов и равно бесконечным произведениям, оно важно и при изучении комплексных чисел. В физике его можно найти (в зависимости от применяемой системы единиц) в космологической постоянной (самая большая ошибка Альберта Эйнштейна) или константе постоянного магнитного поля. В системе счисления с любым основанием (в десятичной, двоичной…), цифры проходят все тесты на случайность, не наблюдается никакого порядка или последовательности. Дзета-функция Римана тесно связывает число с простыми числами. Это чило имеет долгую историю и наверняка до сих пор хранит множество сюрпризов.

Список литературы

http://lacienciaysusdemonios.com/2013/02/14/breve-historia-de-pi/

Для подготовки данной работы были использованы материалы с сайта http://hijos.ru

Дата добавления: 09.09.2013

www.km.ru

История возникновения числа Пи. | Социальная сеть работников образования

li{counter-increment:lst-ctn-kix_list_3-8}#doc6344709 .lst-kix_list_1-1>li:before{content:"\0025cf "}#doc6344709 .lst-kix_list_3-2>li:before{content:"" counter(lst-ctn-kix_list_3-2,lower-roman) ". "}#doc6344709 .lst-kix_list_1-2>li:before{content:"\0025cf "}#doc6344709 ol.lst-kix_list_5-8.start{counter-reset:lst-ctn-kix_list_5-8 0}#doc6344709 .lst-kix_list_1-5>li:before{content:"\0025cf "}#doc6344709 ol.lst-kix_list_5-3.start{counter-reset:lst-ctn-kix_list_5-3 0}#doc6344709 .lst-kix_list_5-3>li{counter-increment:lst-ctn-kix_list_5-3}#doc6344709 .lst-kix_list_2-3>li:before{content:"\0025cf "}#doc6344709 .lst-kix_list_1-4>li:before{content:"\0025cf "}#doc6344709 .lst-kix_list_5-1>li{counter-increment:lst-ctn-kix_list_5-1}#doc6344709 .lst-kix_list_3-3>li{counter-increment:lst-ctn-kix_list_3-3}#doc6344709 .lst-kix_list_5-7>li:before{content:"" counter(lst-ctn-kix_list_5-7,lower-latin) ". "}#doc6344709 ol.lst-kix_list_3-7.start{counter-reset:lst-ctn-kix_list_3-7 0}#doc6344709 .lst-kix_list_4-3>li:before{content:"\0025cf "}#doc6344709 .lst-kix_list_2-7>li:before{content:"\0025cf "}#doc6344709 .lst-kix_list_3-7>li{counter-increment:lst-ctn-kix_list_3-7}#doc6344709 .lst-kix_list_1-8>li:before{content:"\0025cf "}#doc6344709 ol.lst-kix_list_3-6.start{counter-reset:lst-ctn-kix_list_3-6 0}#doc6344709 ol.lst-kix_list_3-0.start{counter-reset:lst-ctn-kix_list_3-0 0}#doc6344709 ol.lst-kix_list_5-0.start{counter-reset:lst-ctn-kix_list_5-0 0}#doc6344709 .lst-kix_list_3-3>li:before{content:"" counter(lst-ctn-kix_list_3-3,decimal) ". "}#doc6344709 .lst-kix_list_3-6>li:before{content:"" counter(lst-ctn-kix_list_3-6,decimal) ". "}#doc6344709 .lst-kix_list_5-2>li:before{content:"" counter(lst-ctn-kix_list_5-2,lower-roman) ". "}#doc6344709 ol.lst-kix_list_3-2.start{counter-reset:lst-ctn-kix_list_3-2 0}#doc6344709 .lst-kix_list_3-2>li{counter-increment:lst-ctn-kix_list_3-2}#doc6344709 ol.lst-kix_list_5-7.start{counter-reset:lst-ctn-kix_list_5-7 0}#doc6344709 .lst-kix_list_4-7>li:before{content:"\0025cf "}#doc6344709 .lst-kix_list_5-0>li{counter-increment:lst-ctn-kix_list_5-0}#doc6344709 .lst-kix_list_5-4>li{counter-increment:lst-ctn-kix_list_5-4}#doc6344709 .lst-kix_list_1-6>li:before{content:"\0025cf "}#doc6344709 .lst-kix_list_2-6>li:before{content:"\0025cf "}#doc6344709 .lst-kix_list_3-6>li{counter-increment:lst-ctn-kix_list_3-6}#doc6344709 ul.lst-kix_list_1-0{list-style-type:none}#doc6344709 ul.lst-kix_list_1-2{list-style-type:none}#doc6344709 ul.lst-kix_list_1-1{list-style-type:none}#doc6344709 .lst-kix_list_2-2>li:before{content:"\0025cf "}#doc6344709 ol.lst-kix_list_3-3.start{counter-reset:lst-ctn-kix_list_3-3 0}#doc6344709 ul.lst-kix_list_1-4{list-style-type:none}#doc6344709 ul.lst-kix_list_1-3{list-style-type:none}#doc6344709 ul.lst-kix_list_1-6{list-style-type:none}#doc6344709 ul.lst-kix_list_1-5{list-style-type:none}#doc6344709 ul.lst-kix_list_1-8{list-style-type:none}#doc6344709 ul.lst-kix_list_1-7{list-style-type:none}#doc6344709 .lst-kix_list_2-1>li:before{content:"\0025cf "}#doc6344709 .lst-kix_list_4-8>li:before{content:"\0025cf "}#doc6344709 .lst-kix_list_5-5>li:before{content:"" counter(lst-ctn-kix_list_5-5,lower-roman) ". "}#doc6344709 .lst-kix_list_3-0>li{counter-increment:lst-ctn-kix_list_3-0}#doc6344709 .lst-kix_list_2-8>li:before{content:"\0025cf "}#doc6344709 .lst-kix_list_3-7>li:before{content:"" counter(lst-ctn-kix_list_3-7,lower-latin) ". "}#doc6344709 .lst-kix_list_3-4>li{counter-increment:lst-ctn-kix_list_3-4}#doc6344709 .lst-kix_list_2-0>li:before{content:"\0025cf "}#doc6344709 ol.lst-kix_list_3-1{list-style-type:none}#doc6344709 ol.lst-kix_list_3-2{list-style-type:none}#doc6344709 ol.lst-kix_list_3-3{list-style-type:none}#doc6344709 ol.lst-kix_list_3-4{list-style-type:none}#doc6344709 ol.lst-kix_list_3-0{list-style-type:none}#doc6344709 ol.lst-kix_list_3-6{list-style-type:none}#doc6344709 ol.lst-kix_list_3-5{list-style-type:none}#doc6344709 ol.lst-kix_list_3-8{list-style-type:none}#doc6344709 ol.lst-kix_list_3-7{list-style-type:none}#doc6344709 .lst-kix_list_5-7>li{counter-increment:lst-ctn-kix_list_5-7}#doc6344709 .lst-kix_list_2-4>li:before{content:"\0025cf "}#doc6344709 .lst-kix_list_3-5>li:before{content:"" counter(lst-ctn-kix_list_3-5,lower-roman) ". "}#doc6344709 .lst-kix_list_3-5>li{counter-increment:lst-ctn-kix_list_3-5}#doc6344709 ol.lst-kix_list_5-5.start{counter-reset:lst-ctn-kix_list_5-5 0}#doc6344709 .lst-kix_list_4-2>li:before{content:"\0025cf "}#doc6344709 .lst-kix_list_4-6>li:before{content:"\0025cf "}#doc6344709 ol.lst-kix_list_5-8{list-style-type:none}#doc6344709 ol.lst-kix_list_5-7{list-style-type:none}#doc6344709 .lst-kix_list_5-3>li:before{content:"" counter(lst-ctn-kix_list_5-3,decimal) ". "}#doc6344709 .lst-kix_list_4-1>li:before{content:"\0025cf "}#doc6344709 .lst-kix_list_4-5>li:before{content:"\0025cf "}#doc6344709 ol.lst-kix_list_5-4{list-style-type:none}#doc6344709 ol.lst-kix_list_5-3{list-style-type:none}#doc6344709 ol.lst-kix_list_5-6{list-style-type:none}#doc6344709 ol.lst-kix_list_5-5{list-style-type:none}#doc6344709 .lst-kix_list_5-2>li{counter-increment:lst-ctn-kix_list_5-2}#doc6344709 .lst-kix_list_3-0>li:before{content:"" counter(lst-ctn-kix_list_3-0,decimal) ") "}#doc6344709 ol.lst-kix_list_5-0{list-style-type:none}#doc6344709 ol.lst-kix_list_5-1{list-style-type:none}#doc6344709 ol.lst-kix_list_5-2{list-style-type:none}#doc6344709 .lst-kix_list_2-5>li:before{content:"\0025cf "}#doc6344709 .lst-kix_list_1-0>li:before{content:"\0025cf "}#doc6344709 .lst-kix_list_5-8>li:before{content:"" counter(lst-ctn-kix_list_5-8,lower-roman) ". "}#doc6344709 .lst-kix_list_5-4>li:before{content:"" counter(lst-ctn-kix_list_5-4,lower-latin) ". "}#doc6344709 .lst-kix_list_4-4>li:before{content:"\0025cf "}#doc6344709 .lst-kix_list_3-4>li:before{content:"" counter(lst-ctn-kix_list_3-4,lower-latin) ". "}#doc6344709 .lst-kix_list_1-3>li:before{content:"\0025cf "}#doc6344709 .lst-kix_list_5-8>li{counter-increment:lst-ctn-kix_list_5-8}#doc6344709 .lst-kix_list_5-0>li:before{content:"" counter(lst-ctn-kix_list_5-0,upper-roman) ". "}#doc6344709 ul.lst-kix_list_4-8{list-style-type:none}#doc6344709 ul.lst-kix_list_4-7{list-style-type:none}#doc6344709 ul.lst-kix_list_4-6{list-style-type:none}#doc6344709 ul.lst-kix_list_4-1{list-style-type:none}#doc6344709 ul.lst-kix_list_4-0{list-style-type:none}#doc6344709 ol.lst-kix_list_5-6.start{counter-reset:lst-ctn-kix_list_5-6 0}#doc6344709 ol.lst-kix_list_3-5.start{counter-reset:lst-ctn-kix_list_3-5 0}#doc6344709 ul.lst-kix_list_4-5{list-style-type:none}#doc6344709 ul.lst-kix_list_4-4{list-style-type:none}#doc6344709 .lst-kix_list_3-8>li:before{content:"" counter(lst-ctn-kix_list_3-8,lower-roman) ". "}#doc6344709 .lst-kix_list_4-0>li:before{content:"\0025cf "}#doc6344709 ul.lst-kix_list_4-3{list-style-type:none}#doc6344709 ul.lst-kix_list_4-2{list-style-type:none}#doc6344709 ol.lst-kix_list_3-4.start{counter-reset:lst-ctn-kix_list_3-4 0}#doc6344709 .lst-kix_list_5-6>li{counter-increment:lst-ctn-kix_list_5-6}#doc6344709 ol.lst-kix_list_5-4.start{counter-reset:lst-ctn-kix_list_5-4 0}#doc6344709 .lst-kix_list_5-6>li:before{content:"" counter(lst-ctn-kix_list_5-6,decimal) ". "}#doc6344709 .lst-kix_list_3-1>li:before{content:"" counter(lst-ctn-kix_list_3-1,lower-latin) ". "}#doc6344709 ol.lst-kix_list_5-1.start{counter-reset:lst-ctn-kix_list_5-1 0}#doc6344709 ul.lst-kix_list_2-4{list-style-type:none}#doc6344709 ol.lst-kix_list_3-8.start{counter-reset:lst-ctn-kix_list_3-8 0}#doc6344709 ul.lst-kix_list_2-5{list-style-type:none}#doc6344709 ul.lst-kix_list_2-6{list-style-type:none}#doc6344709 .lst-kix_list_5-5>li{counter-increment:lst-ctn-kix_list_5-5}#doc6344709 ul.lst-kix_list_2-7{list-style-type:none}#doc6344709 .lst-kix_list_1-7>li:before{content:"\0025cf "}#doc6344709 ul.lst-kix_list_2-0{list-style-type:none}#doc6344709 ol.lst-kix_list_5-2.start{counter-reset:lst-ctn-kix_list_5-2 0}#doc6344709 ol.lst-kix_list_3-1.start{counter-reset:lst-ctn-kix_list_3-1 0}#doc6344709 ul.lst-kix_list_2-1{list-style-type:none}#doc6344709 .lst-kix_list_3-1>li{counter-increment:lst-ctn-kix_list_3-1}#doc6344709 ul.lst-kix_list_2-2{list-style-type:none}#doc6344709 ul.lst-kix_list_2-3{list-style-type:none}#doc6344709 .lst-kix_list_5-1>li:before{content:"" counter(lst-ctn-kix_list_5-1,lower-latin) ". "}#doc6344709 ul.lst-kix_list_2-8{list-style-type:none}#doc6344709 ol{margin:0;padding:0}#doc6344709 .c1{line-height:1.0;padding-top:0pt;widows:2;orphans:2;height:11pt;text-align:center;direction:ltr;padding-bottom:0pt;page-break-after:avoid}#doc6344709 .c3{padding-left:0pt;line-height:1.1500000000000001;padding-top:0pt;widows:2;orphans:2;direction:ltr;margin-left:36pt;padding-bottom:0pt}#doc6344709 .c0{line-height:1.0;padding-top:0pt;widows:2;orphans:2;text-indent:35.4pt;text-align:justify;direction:ltr;padding-bottom:0pt}#doc6344709 .c2{line-height:1.0;padding-top:0pt;widows:2;orphans:2;height:11pt;direction:ltr;padding-bottom:0pt}#doc6344709 .c4{line-height:1.0;padding-top:0pt;widows:2;orphans:2;direction:ltr;margin-left:279pt;padding-bottom:0pt}#doc6344709 .c6{line-height:1.0;padding-top:0pt;widows:2;orphans:2;text-align:center;direction:ltr;padding-bottom:0pt}#doc6344709 .c16{line-height:1.0;padding-top:0pt;widows:2;orphans:2;direction:ltr;padding-bottom:0pt}#doc6344709 .c10{line-height:1.1500000000000001;padding-top:0pt;widows:2;orphans:2;direction:ltr;padding-bottom:0pt}#doc6344709 .c19{line-height:1.15;padding-top:0pt;height:11pt;text-align:left;direction:ltr;padding-bottom:0pt}#doc6344709 .c7{line-height:1.5;padding-top:0pt;widows:2;orphans:2;direction:ltr;padding-bottom:0pt}#doc6344709 .c9{line-height:1.1500000000000001;padding-top:0pt;widows:2;orphans:2;direction:ltr;padding-bottom:10pt}#doc6344709 .c20{vertical-align:baseline;color:#ff0000;font-size:26pt;font-family:"Times New Roman";font-weight:bold}#doc6344709 .c8{vertical-align:baseline;color:#0070c0;font-size:14pt;font-family:"Times New Roman";font-weight:normal}#doc6344709 .c17{vertical-align:baseline;color:#ff0000;font-size:48pt;font-family:"Times New Roman";font-weight:bold}#doc6344709 .c15{vertical-align:baseline;font-size:16pt;font-family:"Times New Roman";font-weight:normal}#doc6344709 .c23{vertical-align:baseline;font-size:14pt;font-family:"Times New Roman";font-weight:bold}#doc6344709 .c12{vertical-align:baseline;font-size:14pt;font-family:"Times New Roman";font-weight:normal}#doc6344709 .c25{max-width:467.7pt;background-color:#ffffff;padding:56.7pt 42.5pt 56.7pt 85pt}#doc6344709 .c18{margin:0;padding:0}#doc6344709 .c22{padding-left:18pt;margin-left:36pt}#doc6344709 .c21{height:11pt}#doc6344709 .c14{margin-left:279pt}#doc6344709 .c24{color:#0070c0}#doc6344709 .c11{page-break-after:avoid}#doc6344709 .c13{text-align:center}#doc6344709 .c5{text-align:justify}#doc6344709 .title{widows:2;padding-top:24pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:36pt;font-family:"Arial";font-weight:bold;padding-bottom:6pt;page-break-after:avoid}#doc6344709 .subtitle{widows:2;padding-top:18pt;line-height:1.15;orphans:2;text-align:left;color:#666666;font-style:italic;font-size:24pt;font-family:"Georgia";padding-bottom:4pt;page-break-after:avoid}#doc6344709 li{color:#000000;font-size:11pt;font-family:"Arial"}#doc6344709 p{color:#000000;font-size:11pt;margin:0;font-family:"Arial"}#doc6344709 h2{widows:2;padding-top:24pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:24pt;font-family:"Arial";font-weight:bold;padding-bottom:6pt;page-break-after:avoid}#doc6344709 h3{widows:2;padding-top:18pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:18pt;font-family:"Arial";font-weight:bold;padding-bottom:4pt;page-break-after:avoid}#doc6344709 h4{widows:2;padding-top:14pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:14pt;font-family:"Arial";font-weight:bold;padding-bottom:4pt;page-break-after:avoid}#doc6344709 h5{widows:2;padding-top:12pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:12pt;font-family:"Arial";font-weight:bold;padding-bottom:2pt;page-break-after:avoid}#doc6344709 h5{widows:2;padding-top:11pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:11pt;font-family:"Arial";font-weight:bold;padding-bottom:2pt;page-break-after:avoid}#doc6344709 h6{widows:2;padding-top:10pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:10pt;font-family:"Arial";font-weight:bold;padding-bottom:2pt;page-break-after:avoid}#doc6344709 ]]>

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «НОВОАГАНСКАЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ CРЕДНЯЯ ШКОЛА №2»

История возникновения

числа Пи.

Выполнила Шевченко Надежда,

ученица 6 «Б» класса

Руководитель: Чекина Ольга Александровна, учитель математики

пгт. Новоаганск

2014

План.

Ведение.

Цели.

II. Основная часть.

1)Первый шаг к числу пи.

2)Не разгаданная загадка.

3)Интересные факты.

III. Заключение

Использованная литература.

Введение

Цели моей работы

1)Найти историю происхождения пи.

2)Рассказать интересные факты числа пи

3)Сделать презентацию и оформить доклад.

4) Подготовить выступление на конференцию.

Основная часть.

Пи (π) - буква греческого алфавита, применяемая в математике для обозначения отношения длины окружности к диаметру. Это обозначение происходит от начальной буквы греческих слов περιφέρεια — окружность, периферия и περίμετρος — периметр. Оно стало общепринятым после работы Л. Эйлера, относящейся к 1736г., однако впервые оно было употреблено английским математиком У. Джонсом (1706г.). Как и всякое иррациональное число, π представляется бесконечной непериодической десятичной дробью:

π = 3,141592653589793238462643.

Первый шаг в изучении свойств числа π сделал Архимед. В сочинении «Измерение круга» он вывел знаменитое неравенство: [формула]Это означает, что π лежит в интервале длиной 1/497. В десятичной системе счисления получаются три правильных значащих цифры: π = 3,14…. Зная периметр правильного шестиугольника и последовательно удваивая число его сторон, Архимед вычислил периметр правильного 96-угольника, откуда и следует неравенство. 96-угольник визуально мало отличается от окружности и является хорошим приближением к ней.В том же сочинении, последовательно удваивая число сторон квадрата, Архимед нашел формулу площади круга S = π R2. Позднее он дополнил ее также формулами площади сферы S = 4 π R2 и объема шара V = 4/3 π R3.

В древнекитайских трудах попадаются самые разные оценки, из которых самая точная — это известное китайское число 355/113. Цзу Чунчжи (V век) даже считал это значение точным.Лудольф ван Цейлен (1536—1610) затратил десять лет на вычисление числа π с 20-ю десятичными цифрами (этот результат был опубликован в 1596 году). Применив метод Архимеда, он довёл удвоение до n-угольника, где n=60·229. Изложив свои результаты в сочинении «Об окружности», Лудольф закончил его словами: «У кого есть охота, пусть идёт дальше». После смерти в его рукописях были обнаружены ещё 15 точных цифр числа π. Лудольф завещал, чтобы найденные им знаки были высечены на его надгробном камне. В честь него число π иногда называли «лудольфовым числом».

Но загадка таинственного числа не разрешена вплоть до сегодняшнего дня, хотя по-прежнему волнует ученых. Попытки математиков полностью вычислить всю числовую последовательность часто приводят к курьезным ситуациям. Например, математики братья Чудновские в Политехническом Университете Бруклина специально с этой целью сконструировали суперскоростной компьютер. Однако установить рекорд им не удалось – пока рекорд принадлежит японскому математику Ясумаса Канада, который смог вычислить 1,2 биллиона чисел бесконечной последовательности.

Интересные фактыНеофициальный праздник «День числа Пи» отмечается 14 марта, которое в американском формате дат (месяц/день) записывается как 3/14, что соответствует приближённому значению числа Пи.Ещё одной датой, связанной с числом π, является 22 июля, которое называется «Днём приближённого числа Пи», так как в европейском формате дат этот день записывается как 22/7, а значение этой дроби является приближённым значением числа π.Мировой рекорд по запоминанию знаков числа π принадлежит японцу Акира Харагути (Akira Haraguchi). Он запомнил число π до 100-тысячного знака после запятой. Ему понадобилось почти 16 часов, чтобы назвать всё число целиком.Германский король Фридрих Второй был настолько очарован этим числом, что посвятил ему… целый дворец Кастель дель Монте, в пропорциях которого можно вычислить Пи. Сейчас волшебный дворец находится под охраной ЮНЕСКО.

ЗаключениеВ настоящее время с числом π связано труднообозримое множество формул, математических и физических фактов. Их количество продолжает стремительно расти. Всё это говорит о возрастающем интересе к важнейшей математической константе, изучение которой насчитывает уже более двадцати двух веков.

Мою работу можно использовать на уроках математики.

Итоги моей работы:

Нашла историю происхождения числа пи.
Рассказала о интересных фактах числа пи.
Узнала много нового о числе пи.
Оформила работу и Выступила на конференции.

nsportal.ru

Защита реферата "Число Пи" | Социальная сеть работников образования

Гимназическая конференция Ступени

Защита реферата «Число Пи»

МБОУ гимназия №1, город Липецк

Глинкина Дарья 8 Б

Публичное выступление

Тема моего реферата: «Число Пи». Число Пи обратило на себя внимание людей ещё в доисторические времена, когда они не умели записывать ни своих знаний, ни своих переживаний, ни своих воспоминаний. Но, как писала бессмертная Тэффи, «все, что касается древнейших времен, и о чем мы ровно ничего не знаем, называется периодом доисторическим. Ученые ровно ничего об этом периоде не знают (потому что если бы знали, то его пришлось бы уже назвать историческим)». Однако уже тогда люди заинтересовались соотношением длины окружности и ее диаметра, которое и выражает число пи.

История числа Пи началась в Древнем Египте. В священной книге джайнизма (одной из древнейших религий, существовавших в Индии и возникшей в VI в. до н.э.) имеется указание, из которого следует, что число Пи в то время принимали равным квадратному корню из 10, что даёт дробь 3,162.

Следует заметить, что на протяжении многих столетий математики разных стран и народов пытались выразить отношение длины окружности к диаметру рациональным числом.

По расчётам Архимеда Пи = 3,1419...

В V в. до н.э. китайским математиком Цзу Чунчжи было найдено более точное значение этого числа, с семью знаками после запятой.

В первой половине XV в. обсерватории Улугбека, возле Самарканда, астроном и математик Ал-Каши вычислил Пи с 16 десятичными знаками.

Спустя полтора столетия в Европе Франсуа Виет нашёл число Пи только с 9 правильными десятичными знаками. Но при этом Ф.Виет первым заметил, что это число можно отыскать, используя пределы некоторых рядов. Это открытие имело большое значение, так как позволило вычислить Пи с какой угодно точностью. Только через 250 лет после Ал-Каши его результат был превзойдён. На протяжении всего существования числа Пи, вплоть до наших дней, велась своеобразная "погоня" за десятичными знаками числа Пи. На данный момент известно 500.000.000.000 знаков!

Первым ввёл обозначение отношения длины окружности к диаметру современным символом английский математик У. Джонсон в 1706 г. В качестве символа он взял первую букву греческого слова "periferia", что в переводе означает "окружность". Введённое У. Джонсоном обозначение стало общепринятым после опубликования работ Л. Эйлера, который воспользовался введённым символом впервые в 1736 г.

Работая над рефератом, я выяснила, что есть праздник числа Пи. Когда же празднуют день числа Пи? Неофициальный праздник «День числа пи» отмечается 14 марта, которое в американском формате дат (месяц/день) записывается как 3.14, что соответствует приближённому значению числа.

Считается, что праздник придумал в 1987 году физик из Сан-Франциско Ларри Шоу, обративший внимание на то, что 14 марта ровно в 01:59 дата и время совпадают с первыми разрядами числа Пи = 3,14159. Ещё одной датой, связанной с числом Пи, является 22 июля, которое называется «Днём приближённого числа Пи» (англ. Pi Approximation Day), так как в европейском формате дат этот день записывается как 22/7, а значение этой дроби является приближённым значением числа Пи.

Полюбуйтесь на него. Рассмотрите внимательно, первые тысячи знаков этого числа, проникнитесь поэзией этих цифр, ведь за ними стоят история нашей цивилизации, жизни сотен лучших умов человечества и тайна устройства мироздания. Есть гипотезы, предполагающие, что в числе Пи скрыта любая информация, которая когда либо была или будет доступна людям.

1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989 3809525720 1065485863 2788659361 5338182796 8230301952 0353018529 6899577362 2599413891 2497217752 8347913151 5574857242 4541506959 5082953311 6861727855 8890750983 8175463746 4939319255 0604009277 0167113900 9848824012

Зачем вообще вычисляют знаки числа Пи? Может и без них можно обойтись? В Древней Греции точные науки процвели просто-таки необычайно, а также появилась архитектура. А где архитектура - там и расчеты. И всем известный Архимед еще уточнил значение числа Пи.

Для простого бытового использования этих знаков уже достаточно. Но неутомимые ученые продолжали и продолжали вычислять десятичные знаки числа пи, что является на самом деле нетривиальной задачей, потому что просто так в столбик его не вычислить: число это не только иррациональное, но и трансцендентное (это вот как раз такие числа, которые не вычисляются путем простых уравнений). Ученые Токийского университета сумели поставить мировой рекорд в вычислениях числа Пи до 12411-триллионного знака. Для этого группе программистов и математиков, которую возглавлял профессор Ясумаса Канада, понадобилась специальная программа, суперкомпьютер и 400 часов машинного времени. ( Книга рекордов Гиннеса ). Зачем они это делают? Ну, во-первых, для очень точных вычислений какой-нибудь орбиты спутника желательно иметь этих знаков по - больше, а то можно и в Луну не попасть. Да и для строительства плотин и гигантских мостов тоже нужна точность. А во-вторых, и в главных, это число имеет и собственную научную ценность. В процессе вычислений этих самых знаков было открыто множество разных научных методов и целых наук. Но самое главное - в десятичной части числа Пи нет повторений, как в обычной периодической дроби, а число знаков после запятой у него - бесконечно. На сегодняшний день проверено, что в 500 млрд. знаков числа Пи повторений действительно нет. Есть основания полагать, что их нет вообще. Это архи важно! Поскольку в последовательности знаков числа Пи нет повторений - это значит, что последовательность знаков Пи подчиняется теории хаоса, точнее, число Пи - это и есть хаос, записанный цифрами. Более того, при желании, можно этот хаос представить графически, и есть предположение, что этот Хаос разумен. В 1965-м году американский математик М. Улэм, сидя на одном скучном собрании, от нечего делать начал писать на клетчатой бумаге цифры, входящие в число Пи. Поставив в центре 3 и двигаясь по спирали против часовой стрелки, он выписывал 1, 4, 1, 5, 9, 2, 6, 5 и прочие цифры после запятой. Попутно он обводил все простые числа кружками. Каково же было его удивление и ужас, когда кружки стали выстраиваться вдоль прямых линий! Позже он сгенерировал на основе этого рисунка цветовую картину с помощью специального алгоритма. Что изображено на этой картине - засекречено.

А нам-то что с того? А следует из этого то, что в десятичном хвосте числа Пи можно отыскать любую задуманную последовательность цифр. Ваш телефон? Пожалуйста, и не раз! Слово: любая последовательность цифр в десятичных знаках числа Пи рано или поздно найдется. Любая!

Приведу другой пример: если зашифровать все буквы цифрами, то в десятичном разложении числа Пи можно найти всю мировую литературу и науку, и все священные книги всех религий. Это строгий научный факт. Ведь последовательность бесконечна и сочетания не повторяются,следовательно, она содержит все сочетания цифр, и это уже доказано. А развсе, то все. В том числе и такие, которые соответствуют любой выбранной книге. А это опять-таки означает, что там содержится не только вся мировая литература, которая уже написана, но и все книги, которые еще будут написаны. Получается, что число Пи управляет нашим миром.

Но каким образом происходит это управление? Как правило, с помощью познанных, так и еще не познанных и не написанных законов физики, химии, физиологии, астрономии, которые в нем содержатся!

nsportal.ru

Смотрите также

..:::Новинки:::..

Windows Commander 5.11 Свежая версия.

Новая версия
IrfanView 3.75 (рус)

Обновление текстового редактора TextEd, уже 1.75a

System mechanic 3.7f
Новая версия

Обновление плагинов для WC, смотрим :-)

Весь Winamp
Посетите новый сайт.

WinRaR 3.00
Релиз уже здесь

PowerDesk 4.0 free
Просто - напросто сильный upgrade проводника.

..:::Счетчики:::..