annettesa. Параллельность прямой и плоскости реферат

Паралельность прямой и плоскости - реферат

Реферат по теме Параллельность прямой и плоскости . Ученика10 класса АШколы1127ЛеонтьеваИвана Москва 2004 05 учебный год. Оглавление 1. Вступление Появление Математики. 3- 42. Теоретическая часть Признак параллельности прямой иплоскости. а Теорема. 5б Примеры задач. 5в Чертежи к теореме изадачам.

63. Заключение Мо отношениек теме реферата. 21. ПоявлениеМатематики. Нашипервоначальные представления о числе и форме относятся к очень отдаленной эпохедревнего каменного века палеолита. В течение сотен тысячелетий этого периодалюди жили в пещерах, в условиях, мало отличавшихся от жизни животных, и ихэнергия уходила преимущественно на добывание пищи простейшим способом собиранием ее, где только это было возможно.

Люди изготовляли орудия для охотыи рыболовства, вырабатывали язык для общения друг с другом, а в эпоху позднегопалеолита украшали свое существование, создавая произведения искусства,статуэтки и рисунки.Пока не произошел переход от простого собиранияпищи к активному ее производству, от охоты и рыболовства к земледелию,люди мало продвинулись в понимании числовых величин и пространственныхотношений. Лишь с наступлением этого фундаментального перелома, переворота,когда пассивное отношение человека

к природе сменилось активным, мы вступаем вновый каменный век неолит.Постепенно прекращались кочевые странствия в поискахпищи. Рыболовы и охотники все больше вытеснялись первобытными земледельцами.Такие земледельцы, оставаясь на одном месте, пока почва сохраняла плодородие,строили жилища, рассчитанные на долгие сроки.Деревнивели между собой значительную торговлю, которая настолько развилась, что можно

проследить наличие торговыхсвязей между областями, удаленными на сотни километров друг от друга. Этукоммерческую деятельность сильно стимулировали открытие техники выплавки меди ибронзы и изготовление сначала медных, а затем бронзовых орудий и оружия. Это всвою очередь содействовало дальнейшему формированию языков. Слова этих языковвыражали вполне конкретные вещи и весьма немногочисленные абстрактные понятия,но языки

уже имели известный запас слов для простых числовых терминов и длянекоторых пространственных образов.Числовыетермины, выражающие некоторые из наиболее абстрактных понятий, какие всостоянии создать человеческий ум , как сказал Адам Смит, медленно входили вупотребление. Впервые они появляются скорее как качественные, чемколичественные термины, выражая различие лишь между одним или вернее, каким-то какой-то скорее, чем один человек и двумя и многими.

С понятия числа большие числа сначалаобразовывались с помощью сложения 3 путем сложения 2 и 1, 4 путем сложения 2 и2, 5 путем сложения 2 и 3.3Развитиеремесла и торговли содействовало кристаллизации понятия числа. Числагруппировали и объединяли в большие единицы, обычно пользуясь пальцами однойруки или обеих рук обычный в торговле прием.Пальцевойсчет, то есть счет пятками и десятками, возник только на известной ступениобщественного развития. Но раз до этого дошли, появилась возможность выражатьчисла в системе

счисления, что позволяло образовывать большие числа. Так возниклапримитивная разновидность арифметики. Четырнадцать выражали как 10 4, иногдакак 15 - 1. Умножение зародилось тогда, когда 20 выразили не как 10 10, а как10. Подобные двоичные действия выполнялись в течение тысячелетий,представляя собой нечто среднее между сложением и умножением.Возникла и необходимость измерять длину и емкостьпредметов.

Единицы измерения были грубы, и при этом часто исходили из размеровчеловеческого тела. Об этом нам напоминают такие единицы, как палец, фут тоесть ступня , локоть. Когда начали строить дома такие, как уземледельцев Индии или обитателей свайных построек Центральной Европы, сталивырабатываться правила, как строить по прямым линиям и под прямым углом.Человек неолита обладал так же острым чувством геометрическойформы.

Обжиг и раскраска глиняных сосудов, изготовление камышовых циновок,корзин и тканей, позже обработка металлов вырабатывали представление оплоскостных и пространственных соотношениях. 42.Прямая и плоскость называются параллельными, если онине пересекаются.а Теорема Если прямая, не принадлежащая плоскости, параллельнакакой-либо прямой в этой плоскости, то она параллельна и самой плоскости.Доказательство от противного

Пусть а пересекает плоскость вточке А. Через точку А можно провести прямую с параллельную b, с принадлежит , тогда с параллельна b, но b параллельнаа по признаку параллельных прямых , значит должно быть с параллельнаа, но у с и а есть общая точка А, следовательнопредположение, что прямая а пересекает плоскость неверно и а параллельна .б Примеры задач 1. Докажите, что плоскость, пересекающая одну из двухпараллельных прямых, пересекает и

другую.Доказательство Пусть a и b две параллельные прямые и плоскость,пересекающая прямую aв точке A. Провед м через прямые a иb плоскость.Она пересекает плоскость по некоторойпрямой с. Прямая с пересекает прямую a вточке A , а значит, пересекает параллельную ей прямую b. Так какпрямая с лежит в плоскости ,то плоскость пересекает прямую b.2. Докажите,что через любую из двух скрещивающихся прямых можно провести плоскость,параллельную другой

прямой.Доказательство Пусть a и b скрещивающиесяпрямые. Через любую точку на прямой a провед мпрямую c параллельную прямой b. Тогдапрямые a и с образуют плоскость . По выше изложенной теореме онабудет параллельна прямой b.лоскость. резэтипрямыерямую 5в Чертежи К теореме К задаче 1 К задаче 2 6Мо отношение к теме реферата.Я считаю тему своего реферата одной из многих темстереометрии,

не пройдя которую нельзя двигаться дальше в изучении раздела, ккоторому она принадлежит, но в тоже время эта тема не является одной изважнейших тем стереометрии. 7

2dip.su

Реферат по Математике на тему " Условие параллельности плоскостей"

Министерство образования и науки Российской Федерации

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ им. А.И. ГЕРЦЕНА»

Санкт-Петербург

РЕФЕРАТ

По дисциплине: Математика

Тема: Условие параллельности плоскостей

Выполнила:

Студентка 1 курса

дневного отделения

факультета управления

направления «Туризм»

Сахарова Анна Ильинична

Санкт-Петербург

2012

ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПЛОСКОСТЕЙ

Две плоскости называются параллельными, если они не пересекаются.

Теорема

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Параллельные плоскости

Доказательство

Пусть α и β - данные плоскости, a1 и a2 – прямые в плоскости α, пересекающиеся в точке A, b1 и b2 – соответственно параллельные им прямые в плоскости β. Предположим, что плоскости α и β не параллельны, а значит пересекаются по некоторой прямой с. По теореме о признаке параллельности прямой и плоскости прямые a1 и a2, как параллельные прямые b1 и b2, параллельны плоскости β, и поэтому они не пересекают лежащую в этой плоскости прямую с. Таким образом, в плоскости α через точку A проходят прямые a1 и a2, параллельные прямой с. Это невозможно по аксиоме параллельных. Что противоречит предположению. Теорема доказана.

АНАЛИТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ

Если плоскости

$~A_{1}x+B_{1}y+C_1z+D_1 = 0$ и $~A_{2}x+B_{2}y+C_2z+D_2 = 0$

параллельны, то нормальные векторы ~N_1(A_1,B_1,C_1) и ~N_2(A_2,B_2,C_2) коллинеарны (и обратно). Поэтому условие

$\frac{A_2}{A_1} = \frac{B_2}{B_1} = \frac{C_2}{C_1}$ [1] есть необходимое и достаточное условие параллельности или совпадения

ПРИМЕР 1 :Плоскости ~2x-3y-4z+11 = 0 и ~-4x+6y+8z+36=0 параллельны, так как $\frac{-4}{2} = \frac{6}{-3} = \frac{8}{-4}$ ПРИМЕР 2 Плоскости ~2x-3z-12 = 0 (A_1 = 2, B_1 = 0, C_1 = -3) и ~4x+4y-6z+7=0 (A_2 = 4, B_2 = 4, C_2 = -6) непараллельны так как B_1 = 0 , а $B_2 \ne 0$ Замечание. Если не только коэффициенты при координатах, но и свободные члены пропорциональны, то есть если $\frac{A_2}{A_1} = \frac{B_2}{B_1} = \frac{C_2}{C_1} = \frac{D_2}{D_1},$ [2] то плоскости совпадают. Так уравнения ~3x+7y+5z+4=0 и ~6x+14y+10z+8=0 представляют одну и ту же плоскость.

annettesa.livejournal.com

Параллельность плоскостей.

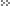Образование Параллельность плоскостей.

Количество просмотров публикации Параллельность плоскостей. - 134

Наименование параметра	Значение
Тема статьи:	Параллельность плоскостей.
Рубрика (тематическая категория)	Образование

Главные линии плоскости (горизонталь и фронталь)

Горизонталью плоскостипринято называть всякая прямая линия, лежащая в любой плоскости и расположенная параллельно плоскости П1

5. Перпендикулярность прямой и плоскости

Плоскости параллельны, в случае если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Параллельность плоскостей. - понятие и виды. Классификация и особенности категории "Параллельность плоскостей." 2014, 2015.

Параллельность прямой и плоскости.

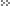Образование Параллельность прямой и плоскости.

Количество просмотров публикации Параллельность прямой и плоскости. - 38

Наименование параметра	Значение
Тема статьи:	Параллельность прямой и плоскости.
Рубрика (тематическая категория)	Образование

Взаимное положение прямой и плоскости.

Прямая и плоскость в пространстве могут иметь одну собственную или несобственную общую точку или множество общих точек, следовательно, прямая может пересекаться с плоскостью, быть ей параллельна либо совпадать с плоскостью.

Из элементарной геометрии известно, что прямая параллельна плоскости, в случае если в плоскости можно провести прямую, параллельную заданной прямой.

(mn)(n) m

Через точку, не принадлежащую плоскости, можно провести бесконечное количество прямых, параллельных плоскости. Для получения единственного решения нужно наложить дополнительное условие, к примеру, построить прямую, параллельную сразу двум плоскостям.

Пример 1: Через точку А провести прямую l, параллельную заданной плоскости .

Пример 2: Через точку А провести прямую, параллельную заданной плоскости и плоскости проекций V.

Параллельность прямой и плоскости. - понятие и виды. Классификация и особенности категории "Параллельность прямой и плоскости." 2014, 2015.