Смоленский промышненно-экономический колледж
Доклад на тему: «Сведения из истории логарифмов»
Смоленск
2011 г
Логарифмы
На всем протяжении XVI века быстро возрастало количество приближенных вычислений, прежде всего в астрономии. Исследование планетных движений требовало колоссальных расчетов. Астрономы просто могли утонуть в невыполнимых расчетах. Очевидные трудности возникали и в других областях, таких как финансовое и страховое дело. Основную трудность представляли умножение и деление многозначных чисел, особенно же тригонометрических величин.
Иногда для приведения умножения к более легкому сложению и вычитанию пользовались таблицами синусов и косинусов. Была также составлена таблица квадратов до 100 000, с помощью которой умножение можно было производить по определенному правилу. Однако эти приемы не давали удовлетворительного решения вопроса. Его принесли с собой таблицы логарифмов. «Открытие логарифмов опиралось на хорошо известные к концу XVI века свойства прогрессий, — пишут М. В. Чириков и А. П. Юшкевич. — Связь между членами геометрической прогрессии и арифметической прогрессией не раз отмечалась математиками, о ней говорилось еще в „Псаммите“ Архимеда. Другой предпосылкой было распространение понятия степени на отрицательные и дробные показатели, позволившее перенести только что упомянутую связь на более общий случай. Многие авторы указывали, что умножению, делению, возведению в степень и извлечению корня в геометрической прогрессии соответствуют в арифметической — в том же порядке — сложение, вычитание, умножение и деление. Здесь уже скрывалась идея логарифма числа как показателя степени, в которую нужно возвести данное основание, чтобы получить это число. Оставалось перенести знакомые свойства прогрессии с общим членом на любые действительные показатели. Это дало бы непрерывную показательную функцию, принимающую любые положительные значения, а также обратную ей логарифмическую. Но эту идею глубокого принципиального значения удалось развить через несколько десятков лет». Логарифмы изобрели независимо друг от друга Непером и Бюрги лет на десять позднее. Их цель была одна — желание дать новое удобное средство арифметических вычислений. Подход же оказался разный. Непер кинематически выразил логарифмическую функцию, что позволило ему по существу вступить в почти неизведанную область теории функций. Бюрги остался на почве рассмотрения дискретных прогрессий. Надо заметить, что у обоих определение логарифма не походило на современное. Первый изобретатель логарифмов — шотландский барон Джон Непер (1550−1617) получил образование на родине в Эдинбурге. Затем после путешествия по Германии, Франции и Испании, в возрасте двадцати одного года, он навсегда поселился в семейном поместье близ Эдинбурга. Непер занялся главным образом богословием и математикой, которую изучал по сочинениям Евклида, Архимеда, Региомонтана, Коперника. «К открытию логарифмов, — отмечают Чириков и Юшкевич, — Непер пришел не позднее 1594 года, но лишь двадцать лет спустя опубликовал свое „Описание удивительной таблицы логарифмов“ (1614), содержавшее определение Неперовых логарифмов, их свойства и таблицы логарифмов синусов и косинусов от 0 до 90 градусов с интервалом в 1 минуту, а также разности этих логарифмов, дающие логарифмы тангенсов. Теоретические выводы и объяснения способа вычисления таблицы он изложил в другом труде, подготовленном, вероятно, до „Описания“, но изданном посмертно, в „Построении удивительной таблицы логарифмов“ (1619). Упомянем, что в обоих сочинениях Непер рассматривает и некоторые вопросы тригонометрии. Особенно известны удобные для логарифмирования „аналогии“, т. е. пропорции Непера, применяемые при решении сферических треугольников по двум сторонам и углу между ними, а также по двум углам и прилежащей к ним стороне. Непер с самого начала вводил понятие логарифма для всех значений непрерывно меняющихся тригонометрических величин — синуса и косинуса. При тогдашнем состоянии математики, когда еще не было аналитического аппарата исчисления бесконечно малых, естественным и единственным средством для этого являлось кинематическое определение логарифма. Быть может, здесь не остались без влияния и традиции, восходившие к оксфордской школе XIV века». В основе определения логарифма у Непера лежит кинематическая идея, обобщающая на непрерывные величины связь между геометрической прогрессией и арифметической прогрессией показателей ее членов. Теорию логарифмов Непер изложил в сочинении «Построение удивительных таблиц логарифмов», посмертно опубликованном в 1619 году и переизданном в 1620 году его сыном Робертом Непером. Вот выдержки из нее: «Таблица логарифмов — небольшая таблица, с помощью которой можно узнать посредством весьма легких вычислений все геометрические размеры и движения. Она по справедливости названа небольшой, ибо по объему превосходит таблицы синусов, весьма легкой, потому что с ее помощью избегают всех сложных умножений, делений и извлечений корня, и все вообще фигуры и движения измеряются посредством выполнения более легких сложения, вычитания и деления на два. Она составлена из чисел, следующих в непрерывной пропорции. Если из полного синуса с добавленными семью нулями ты вычтешь его 10 000 000-ую часть, а из полученного таким образом числа — его 10 000 000-ую часть и так далее, то этот ряд можно легко продолжить до ста чисел в геометрическом отношении, существующем между полным синусом и синусом, меньшим его на единицу, а именно между 10 000 000 и 9 999 999, и этот ряд пропорциональных мы назовем Первой таблицей. Вторая таблица следует от полного синуса с шестью добавленными нулями через пятьдесят других чисел, пропорционально убывающих в отношении, которое является простейшим и возможно более близким к отношению между первым и последним числами Первой таблицы. Поскольку первое и последнее числа Первой таблицы суть 10 000 000. 0 и 9 999 900. 4 950, то в этом отношении трудно образовать пятьдесят пропорциональных чисел. Близким и в то же время простым отношением является 100 000 к 99 999, которое можно с достаточной точностью продолжить, добавив к полному синусу шесть нулей и последовательно вычитая из предшествующего его 100 000-ую часть. Эта таблица содержит, кроме полного синуса, являющегося первым числом, еще пятьдесят пропорциональных чисел, последнее из которых будет 9 995 001. 222 927.
Третья таблица состоит из шестидесяти девяти столбцов и в каждом столбце расположено двадцать одно число, следующее в отношении, которое является простейшим и возможно более близким к отношению, существующему между первым и последним членами Второй таблицы. Поэтому ее первый столбец может быть очень легко получен из полного синуса с пятью добавленными нулями и из последующих чисел вычитанием из них 2000-ой части. Первые числа всех столбцов следуют от полного синуса с добавленными четырьмя нулями в отношении, которое является простейшим и близким к отношению, существующему между первым и последним числами первого столбца… В том же отношении должна быть образована прогрессия со второго числа первого столбца для вторых чисел всех столбцов, и с третьего для третьих, и с четвертого для четвертых, и соответственно с остальных для остальных. Таким образом, из любого числа предыдущего столбца вычитанием его сотой части получается число того же порядка следующего столбца, этих трех таблиц (после их составления) достаточно для вычисления таблицы логарифмов". В 1620 году швейцарец Иост Бюрги (1552−1632) — высококвалифицированный механик и часовых дел — мастер опубликовал книгу «Таблицы арифметической и геометрической прогрессий, вместе с основательным наставлением, как их нужно понимать и с пользой применять во всяческих вычислениях» (1620). Как писал сам Бюрги, он исходил из соображений о соответствии между умножением в геометрической прогрессии и сложением в арифметической. Задача состояла в выборе прогрессии со знаменателем, достаточно близким к единице, с тем, чтобы ее члены следовали друг за другом с интервалами, достаточно малыми для практических вычислений. Однако таблицы Бюрги не получили значительного распространения. Они не могли конкурировать с таблицами Непера, более удобными и к тому времени уже широко известными. Ни у Непера, ни у Бюрги не было, строго говоря, основания логарифмов, поскольку логарифм единицы отличается от нуля. И значительно позднее, когда уже перешли к десятичным и натуральным логарифмам, еще не было сформулировано определение логарифма, как показателя степени данного основания. В руководствах оно появляется впервые, вероятно, у В. Гардинера (1742). Впрочем, сам Гардинер использовал при этом бумаги преподавателя математики В. Джонса. Широкому распространению современного определения логарифма более других содействовал Эйлер, который применил в этой связи и термин «основание». Термин «логарифм» принадлежит Неперу, он возник из сочетания греческих слов «отношение» и «число», и означает «число отношения». Хотя первоначально Непер пользовался другим термином — «искусственные числа». Таблицы Непера, приспособленные к тригонометрическим вычислениям, были неудобны для действий с данными числами. Чтобы устранить эти недостатки, Непер предложил составить таблицы логарифмов, приняв за логарифм единицы нуль, а за логарифм десяти просто единицу. Это предложение он сделал в ходе обсуждения с посетившим его в 1615 году профессором математики Грешем-колледжа в Лондоне Генри Бригсом (1561−1631), который и сам задумывался, как усовершенствовать таблицы логарифмов. Заняться осуществлением своего плана Непер не мог из-за пошатнувшегося здоровья, но указал идею двух вычислительных приемов, развитых далее Бригсом. Бригc опубликовал первые результаты своих кропотливых вычислений — «Первую тысячу логарифмов» (1617) в год смерти Непера. Здесь даны были десятичные логарифмы чисел от 1 до 1000 с четырнадцатью знаками. Большинство десятичных логарифмов простых чисел Бригc нашел с помощью извлечения квадратных корней. Позднее, уже став профессором в Оксфорде, он выпустил «Логарифмическую арифметику» (1624). В книге содержались четырнадцатизначные логарифмы чисел от 1 до 20 000 и от 90 000 до 100 000. Оставшийся пробел был восполнен голландским книготорговцем и любителем математики Андрианом Флакком (1600−1667). Несколько ранее семизначные десятичные таблицы логарифмов синусов и тангенсов вычислил коллега Бригса по Грешем-колледжу, воспитанник Оксфордского университета Эдмунд Гунтер (1581−1626), опубликовавший их в «Своде треугольников» (1620). Открытие Непера в первые же годы приобрело исключительно широкую известность. Составлением логарифмических таблиц и совершенствованием их занялись очень многие математики. Так, Кеплер в Марбурге в 1624—1625 годах применил логарифмы к построению новых таблиц движений планет. В приложении ко второму изданию «Описания» Непера (1618) было вычислено и несколько натуральных логарифмов. Здесь можно усмотреть подход к введению предела. Вероятнее всего, это дополнение принадлежит В. Отреду. Вскоре лондонский учитель математики Джон Спейделл издал таблицы натуральных логарифмов чисел от 1 до 1000. Термин «натуральные логарифмы» ввели П. Менголи (1659), а несколько позднее — Н. Меркатор (1668). Практическое значение вычисленных таблиц было очень велико. Но открытие логарифмов имело также глубочайшее теоретическое значение. Оно вызвало к жизни исследования, о которых не могли и мечтать первые изобретатели, преследовавшие цель только облегчить и ускорить арифметические и тригонометрические выкладки с большими числами. Открытие Непера, в частности, открыло путь в область новых трансцендентных функций и сообщило мощные стимулы в развитии анализа.
Принцип, лежащий в основе любой системы логарифмов, известен очень давно и может быть прослежен в глубь истории вплоть до древневавилонской математики (около 2000 до н.э.). В те времена интерполяция между табличными значениями целых положительных степеней целых чисел использовалась для вычисления сложных процентов. Гораздо позже Архимед (287−212 до н.э.) воспользовался степенями числа 108 для нахождения верхнего предела числа песчинок, необходимого для того, чтобы целиком заполнить известную в те времена Вселенную. Архимед обратил внимание на свойство показателей степеней, лежащее в основе эффективности логарифмов: произведение степеней соответствует сумме показателей степеней. В конце Средних веков и начале Нового времени математики все чаще стали обращаться к соотношению между геометрической и арифметической прогрессиями. М. Штифель в своем сочинении Арифметика целых чисел (1544) привел таблицу положительных и отрицательных степеней числа 2:
< ="" div="""div=""style="border-top-style: none; border-right-style: none; border-bottom-style: none; border-left-style: none; «> поэтому таблицы Непера состояли главным образом из логарифмов тригонометрических функций. Хотя понятие основания не входило в явном виде в предложенное Непером определение, роль, эквивалентную основанию системы логарифмов, в его системе играло число (1 — 10−7)ґ107, приближенно равное 1/e. Независимо от Непера и почти одновременно с ним система логарифмов, довольно близкая по типу, была изобретена и опубликована Й. Бюрги в Праге, издавшем в 1620 Таблицы арифметической и геометрической прогрессий. Это были таблицы антилогарифмов по основанию (1 + 10−4)*10 4, достаточно хорошему приближению числа e. В системе Непера логарифм числа 107 был принят за нуль, и по мере уменьшения чисел логарифмы возрастали. Когда Г. Бриггс (1561−1631) навестил Непера, оба согласились, что было бы удобнее использовать в качестве основания число 10 и считать логарифм единицы равным нулю. Тогда с увеличением чисел их логарифмы возрастали бы. Таким образом мы получили современную систему десятичных логарифмов, таблицу которых Бриггс опубликовал в своем сочинении Логарифмическая арифметика (1620). Логарифмы по основанию e, хотя и не совсем те, которые были введены Непером, часто называют неперовыми. Термины «характеристика» и «мантисса» были предложены Бриггсом. Первые логарифмы в силу исторических причин использовали приближения к числам 1/e и e. Несколько позднее идею натуральных логарифмов стали связывать с изучением площадей под гиперболой xy = 1 (рис. 1). В 17 в. было показано, что площадь, ограниченная этой кривой, осью x и ординатами x = 1 и x = a (на рис. 1 эта область покрыта более жирными и редкими точками) возрастает в арифметической прогрессии, когда a возрастает в геометрической прогрессии. Именно такая зависимость возникает в правилах действий над экспонентами и логарифмами. Это дало основание называть неперовы логарифмы «гиперболическими логарифмами».
Рис. 1 — График ветви гиперболы xy = 4
Площади под гиперболой на отрезках от x =1 до x = 2, от x = 2 до x = 4 и от x = 4 до x = 8 равны; общая площадь заштрихованной фигуры возрастает в арифметической прогрессии (1, 2, 3, 4), тогда как длина отрезков на оси x возрастает в геометрической прогрессии (1, 2, 4, 8).
Логарифмическая функция. Было время, когда логарифмы рассматривались исключительно как средство вычислений, однако в 18 в., главным образом благодаря трудам Эйлера, сформировалась концепция логарифмической функции. График такой функции y = lnx, ординаты которого возрастают в арифметической прогрессии, тогда как абсциссы — в геометрической, представлен на рис. 2, а. График обратной, или показательной (экспоненциальной), функции y = ex, ординаты которого возрастают в геометрической прогрессии, а абсциссы — в арифметической, представлен, соответственно, на рис. 2, б. (Кривые y = logx и y = 10x по форме аналогичны кривым y = lnx и y = ex.) Были предложены также альтернативные определения логарифмической функции, например,
логарифм пропорция непер гиперболический
Рис. 2 — Логарифмическая и экспоненциальная кривые: а — Логарифмическая кривая y = lnx. Ординаты возрастают в арифметической прогрессии, абсциссы — в геометрической прогрессии
Рис. 3 — Логарифмическая и экспоненциальная кривые: б — Экспоненциальная кривая y = ex. Ординаты возрастают в геометрической прогрессии, абсциссы — в арифметической прогрессии
< ="" div="" style="border-top-style:none;border-right-style:none;border-bottom-style:none;border-left-style:none;«>Благодаря работам Эйлера стали известны соотношения между логарифмами и тригонометрическими функциями в комплексной плоскости. Исходя из тождества eix=cos x + i sin x(где угол x измеряется в радианах),Эйлер заключил,что каждое отличное от нуля действительное число имеет бесконечно много натуральных логарифмов;все они являются комплексными в случае отрицательных чисел и все,кроме одного, —в случае положительных чисел. Поскольку eix=1 не только при x=0,но и при x=±2kp,где k —любое положительное целое число,за натуральный логарифм числа 1 можно принять любое из чисел 0 ±2kpi;и,аналогично,натуральные логарифмы числа -1 являются комплексными числами вида(2k + 1) pi,где k —целое число. Аналогичные утверждения справедливы и относительно общих логарифмов или других систем логарифмов. Кроме того,определение логарифмов можно обобщить,пользуясь тождествами Эйлера так,чтобы оно включало комплексные логарифмы комплексных чисел. Альтернативное определение логарифмической функции дает функциональный анализ. Если f(x) —непрерывная функция действительного числа x,обладающая следующими тремя свойствами:f(1)=0,f(b)=1,f(uv)=f(u)+ f(v),то f(x)определяется как логарифм числа x по основанию b. Это определение обладает рядом преимуществ перед определением,приведенным в начале этой статьи. Логарифмы первоначально использовались исключительно для упрощения вычислений,и это их приложение до сих пор остается одним из самых главных. Вычисление произведений,частных,степеней и корней облегчается не только благодаря широкой доступности опубликованных таблиц логарифмов,но и благодаря использованию т.н. логарифмической линейки —вычислительного инструмента,принцип работы которого основан на свойствах логарифмов. Линейка снабжена логарифмическими шкалами,т. е. расстояние от числа 1 до любого числа x выбрано равным log x;сдвигая одну шкалу относительно другой,можно откладывать суммы или разности логарифмов,что дает возможность считывать непосредственно со шкалы произведения или частные соответствующих чисел. Воспользоваться преимуществами представления чисел в логарифмическом виде позволяет и т.н. логарифмическая бумага для построения графиков(бумага с нанесенными на нее по обеим осям координат логарифмическими шкалами). Если функция удовлетворяет степенному закону вида y=kxn,то ее логарифмический график имеет вид прямой,т.к. log y=log k + n log x —уравнение,линейное относительно log y и log x. Наоборот,если логарифмический график какой-нибудь функциональной зависимости имеет вид прямой,то эта зависимость —степенная. Полулогарифмическая бумага(у которой ось ординат имеет логарифмическую шкалу,а ось абсцисс —равномерную шкалу)удобна в тех случаях,когда требуется идентифицировать экспоненциальные функции. Уравнения вида y=kbrx возникают всякий раз,когда некая величина,такая как численность населения,количество радиоактивного материала или банковский баланс,убывает или возрастает со скоростью,пропорциональной имеющемуся в данный момент количеству жителей,радиоактивного вещества или денег. Если такую зависимость нанести на полулогарифмическую бумагу,то график будет иметь вид прямой. Логарифмическая функция возникает в связи с самыми разными природными формами. По логарифмическим спиралям выстраиваются цветки в соцветиях подсолнечника,закручиваются раковины моллюска Nautilus,рога горного барана и клювы попугаев. Все эти природные формы могут служить примерами кривой,известной под названием логарифмической спирали,потому что в полярной системе координат ее уравнение имеет вид r=aebq,или lnr=lna + bq. Такую кривую описывает движущаяся точка,расстояние от полюса которой растет в геометрической прогрессии,а угол,описываемый ее радиусом-вектором —в арифметической. Повсеместность такой кривой,а следовательно и логарифмической функции,хорошо иллюстрируется тем,что она возникает в столь далеких и совершенно различных областях,как контур кулачка-эксцентрика и траектория некоторых насекомых,летящих на свет.
Показать Свернутьgugn.ru
Н.Меркатор
.В течение 16 века резко возрос объем работы,связанный с проведением приближенных вычислений в ходе решения задач,и в первую очередь задач астрономии,имеющий непосредственное практическое применение( в частности , при определении положения сосудов по звездам и по Солнцу). Наибольшие проблемы возникали при выполнении операций умножения и деления. Попытки частично упрощения этих операций путем сведения их к сложению большого успеха не приносили. Поэтому открытие логарифмов, сводящее умножение, деление чисел к сложению,вычитанию их логарифмов,удлинило, по выражению Лапласа, жизнь вычислителей.
Логарифмы необычайно быстро вошли в практику. Изобретатели логарифмов не ограничились разработкой новой теории.Было создано практическое средство-таблица логарифмов, - резко повысившее производительность труда вычислителей. Добавим, что уже всего через 9 лет после издания первых таблиц, английским математиком Д. Гантером была изобретена первая логарифмическая линейка, ставшая рабочим инструментом для многих поколений.(Вплоть до самого последнего времен, когда на наших глазах повсеместное распространение получает электронная вычислительная техника и роль логарифмов, как средство вычисления резко снижается.) Первые таблицы логарифмов составлены независимо друг от друга шотландским математиком Непером (1550-1617) и швейцарцем И. Бюрги.
Джон Непер
И.Бюрги
В таблицы Непера, изданные под названиями "Описание удивительной таблицы логарифмов"(1614 г.) и "Устройство удивительной таблицы логарифмов"(1619) вошли значения логарифмов синусов, косинусов и тангенсов для углов от 0 до 90 градусов с шагом в одну минуту. Бюрги подготовил свои таблицы логарифмов чисел, по-видимому, к 1610 г. но вышли в свет они в 1620 году, уже после издания таблиц Непера , и поэтому остались незамеченными.
Одна из важных идей,лежащих в основе изобретения логарифмов,была уже известна. Штифель и ряд других математиков обратили внимание на то,что умножение и деление геометрической прогрессии
Соответствуют сложению и вычитанию показателей,образующих арифметическую прогрессию ...,-3,-2,-1,0,1,2,3,....Но одной этой идеи недостаточно.Например,"сеть" целых степеней числа 2 слишком редка; многие числа "остаются без логарифмов",поэтому была еще одна идея: возводить в степень числа очень близкие к единице.Заметив,что степени
при больших значениях n близки , Непер и Бюрги приняли аналогичное решение : Непер брал в качестве основания число 
,а Бюрги-число 
. Дальнейший ход их рассуждения и описания схем вычисления перессказать довольно трудно,как потому,что имеется много непростых деталей,так и потому,что тексты 16 века довольно туманны.Заметим только,что фактически Непер переходит к основанию 
,а Бюрги- к основанию 
.Это не изменило существа дела,но позволило несколько упростить вычисления и сами таблицы. Таким образом , по существу оба изобретателя логарифма пришли к выводу о целесообразности рассмотрения степеней вида
где М очень большое число.Рассмотрение чисел такого вида приводит к известному вам числу e , которое определялось как
.Осталось уже немного до идеи принятия в качестве основания логарифмов числа е (основания таблицы логарифмов Бюрги совпадает с точностью третьего знака с е , основания таблицы логарифмов Непера близко к числу 1/е). Первые таблицы десятичных логарифмов (1617 г) были составлены по совету Непера английским математиком Г.Бриггсом. 
Многие из них были найдены с помощью выведенной Бриггсом приближенной формулы достаточно точной при больших значениях m и n в виде степеней двойки:это давало ему возможность свести вычисления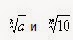 
к последовательному извлечению квадратных корней.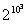 
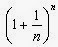Другая идея Бриггса позволяет находить значения десятичных логарифмов некоторых чисел самостоятельно,без помощи таблиц.Целая часть логарифма целого числа на единицу меньше количество цифр в самом числе.Поэтому,например, для нахождения lg2 с точностью до трех знаков достаточно найти число цифр .Это не очень трудно. При составлении таблиц логарифмов важную роль сыграло найденное Непером и Бюрги соотношение между приращениями x и y в произвольной точке x для функции y=logx.Отвлекаясь от деталей их системы изложения,основной результат можно выразить так: 
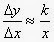, где k-некоторое постоянная.Если основание логарифмов -степень где n- достаточно большое число,то 
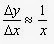Устремляя к нулю,приходим к дифференциальному уравнению y'=1/x,решением которого,как вы знаете,является функция lnx+C.Существует система изложения при которой 
с самого начала определяется как 
,т.е.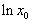 
-площадь криволинейной трапеции, ограниченной гиперболой,осью абсцисс и прямыми x =1 и x=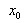
Из определения следует, что нахождение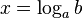 
равносильно решению уравнения 
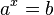. Например, 
потому что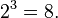 
gtchulkova.blogspot.ru
Графики логарифмических функций
Логарифм числа b по основанию a (от греч. λόγος — «слово», «отношение» и ἀριθμός — «число»[1]) определяется как показатель степени, в которую надо возвести число a, чтобы получить число b. Обозначение: . Из определения следует, что записи и равносильны.
Пример: , потому что .
Наиболее широкое применение нашли следующие виды логарифмов.
Докажем, что .
(так как по условию bc > 0).
Ч. т. д.
Доказательство [показать]Докажем, что
(так как по условию
Ч. т. д.
Доказательство [показать]Докажем, что .
(так как bp > 0 по условию).
Ч. т. д.
Доказательство [показать]Докажем, что Ч. т. д.
Используем для доказательства тождество . Логарифмируем обе части тождества по основанию c. Получаем:Ч. т. д.
Доказательство [показать]Логарифмируем левую и правую части по основанию c:
Левая часть:
Правая часть:
Равенство выражений очевидно. Т. к. логарифмы равны, то в силу монотонности логарифмической функции равны и сами выражения.
Ч. т. д.
При справедливо равенство
В частности,Формула (1) не имеет большой практической ценности из-за того, что ряд очень медленно сходится и значение x ограничено весьма узким диапазоном. Однако нетрудно получить из неё более удобную формулу:Этот ряд сходится быстрее, а кроме того, левая часть формулы теперь может выразить логарифм любого положительного числа.Связь с десятичным логарифмом: .
Рис. 2. Логарифмическая шкала
Логарифмы по основанию 10 (обозначение: lg a) до изобретения калькуляторов широко применялись для вычислений. Неравномерная шкала десятичных логарифмов обычно наносится и на логарифмические линейки. Подобная шкала широко используется в различных областях науки, например:
Область значения:
График любой логарифмической функции проходит через точку (1;0)
Производная логарифмической функции равна:
Доказательство [2] [показать]I. Докажем, что
Запишем тождество elnx = x и продифференцируем его левую и правую части
Получаем, что , откуда следует, что
II. Докажем, что Ч. т. д.
Функция являются строго возрастающей при a > 1 и строго убывающей при 0 < a < 1
Прямая x = 0 является левой вертикальной асимптотой, поскольку при a > 1 и при 0 < a < 1
,
то логарифм находится по формуле:Здесь — вещественный логарифм, r = | w | , k — произвольное целое число. Значение, получаемое при k = 0, называется главным значением комплексного натурального логарифма; принято брать в нём значение аргумента в интервале ( − π,π]. Соответствующая (уже однозначная) функция называется главной ветвью логарифма и обозначается . Иногда через также обозначают значение логарифма, лежащее не на главной ветви.
Из формулы следует:
Примеры (приведено главное значение логарифма):
Аналогично рассматриваются комплексные логарифмы с другим основанием. Следует, однако, быть осторожным при преобразованиях комплексных логарифмов, принимая во внимание, что они многозначны, и поэтому из равенства логарифмов каких-либо выражений не следует равенство этих выражений. Пример ошибочного рассуждения:iπ = ln( − 1) = ln(( − i)2) = 2ln( − i) = 2( − iπ / 2) = − iπ — явная нелепость.
Отметим, что слева стоит главное значение логарифма, а справа — значение из нижележащей ветви (k = − 1). Причина ошибки — неосторожное использования свойства , которое, вообще говоря, подразумевает в комплексном случае весь бесконечный набор значений логарифма, а не только главное значение.
Риманова поверхность логарифма является универсальной накрывающей для комплексной плоскости без точки 0.
В 1614 году шотландский математик-любитель Джон Непер опубликовал на латинском языке сочинение под названием «Описание удивительной таблицы логарифмов». В нём было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1'. Термин логарифм, предложенный Непером, утвердился в науке.
Понятия функции тогда ещё не было, и Непер определил логарифм кинематически, сопоставив равномерное и логарифмически-замедленное движение. В современной записи модель Непера можно изобразить дифференциальным уравнением: dx/x = -dy/M, где M — масштабный множитель, введённый для того, чтобы значение получилось целым числом с нужным количеством знаков (десятичные дроби тогда ещё не нашли широкого применения). Непер взял M = 10000000.
Строго говоря, Непер табулировал не ту функцию, которая сейчас называется логарифмом. Если обозначить его функцию LogNap(x), то она связана с натуральным логарифмом следующим образом:Очевидно, LogNap(M) = 0, то есть логарифм «полного синуса» есть нуль — этого и добивался Непер своим определением. LogNap(0) = ∞.
Основное свойство логарифма Непера: если величины образуют геометрическую прогрессию, то их логарифмы образуют прогрессию арифметическую. Однако правила логарифмирования для неперовой функции отличались от правил для современного логарифма.
Например, LogNap(ab) = LogNap(a) + LogNap(b) — LogNap(1).
К сожалению, все значения таблицы Непера содержали вычислительную ошибку после шестого знака. Однако это не помешало новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялись многие европейские математики, включая Кеплера.
В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов — незаменимый инструмент инженера.
Близкое к современному понимание логарифмирования — как операции, обратной возведению в степень — впервые появилось у Валлиса и Иоганна Бернулли, а окончательно было узаконено Эйлером в XVIII веке. В книге «Введение в анализ бесконечных» (1748) Эйлер дал современные определения как показательной, так и логарифмической функций, привёл разложение их в степенные ряды, особо отметил роль натурального логарифма.
Эйлеру принадлежит и заслуга распространения логарифмической функции на комплексную область.
Хотя спор продолжался (Даламбер отстаивал свою точку зрения и подробно аргументировал её в статье своей «Энциклопедии» и в других трудах), однако точка зрения Эйлера быстро получила всеобщее признание.
Логарифмические таблицы
Из свойств логарифма следует, что вместо трудоёмкого умножения многозначных чисел достаточно найти (по таблицам) и сложить их логарифмы, а потом по тем же таблицам выполнить потенцирование, то есть найти значение результата по его логарифму. Выполнение деления отличается только тем, что логарифмы вычитаются. Лаплас говорил, что изобретение логарифмов «продлило жизнь астрономов», многократно ускорив процесс вычислений.
При переносе десятичной запятой в числе на n разрядов значение десятичного логарифма этого числа изменяется на n. Например, lg8314,63 = lg8,31463 + 3. Отсюда следует, что достаточно составить таблицу десятичных логарифмов для чисел в диапазоне от 1 до 10.
Первые таблицы логарифмов опубликовал Джон Непер (1614), и они содержали только логарифмы тригонометрических функций, причём с ошибками. Независимо от него свои таблицы опубликовал Иост Бюрги, друг Кеплера (1620). В 1617 году оксфордский профессор математики Генри Бригс опубликовал таблицы, которые уже включали десятичные логарифмы самих чисел, от 1 до 1000, с 8 (позже — с 14) знаками. Но и в таблицах Бригса обнаружились ошибки. Первое безошибочное издание на основе таблиц Вега (1783) появилось только в 1857 году в Берлине (таблицы Бремивера).
В России первые таблицы логарифмов были изданы в 1703 году при участии Л. Ф. Магницкого. В СССР выпускались несколько сборников таблиц логарифмов.
· Том 2 Математика XVII столетия. (1970)
bukvasha.ru
