|
|
|
|
 Far Far |
 WinNavigator WinNavigator |
 Frigate Frigate |
 Norton
Commander Norton
Commander |
 WinNC WinNC |
 Dos
Navigator Dos
Navigator |
 Servant
Salamander Servant
Salamander |
 Turbo
Browser Turbo
Browser |
|
|
 Winamp,
Skins, Plugins Winamp,
Skins, Plugins |
 Необходимые
Утилиты Необходимые
Утилиты |
 Текстовые
редакторы Текстовые
редакторы |
 Юмор Юмор |
|
|
|
File managers and best utilites |
Однофазные электрические цепи переменного тока. Однофазные электрические цепи переменного тока реферат
Однофазные электрические цепи переменного тока
Основные понятия и определения
Широкое применение в электрических цепях находят периодические ЭДС, напряжения и токи.
Периодические величины изменяются во времени по значению и направлению, причем эти изменения повторяются через некоторые промежутки времени Т, называемые периодом.
На практике подавляющее большинство промышленных источников переменного тока (генераторы электростанций) создают ЭДС, изменяющуюся по синусоидальному закону.
Преимущества такого закона:
а) простота получения;
б) напряжение легко трансформируется;
в) синусоидальная функция является единственной, которая в процессе интегрирования и дифференцирования не меняет своей формы и в процессе передачи и преобразования (в процессе трансформации) напряжения временная зависимость остается неизменной, т.е. синусоидальной.
Любая периодическая величина, изменяющаяся по синусоидальному закону, имеет ряд характерных параметров:
период - Т [c];
2) частота - f [Гц] .
Величина обратная периоду называется частотой:
 .
.
Частота для всех электроустановок строго нормируется:
- для наземных систем - 50 (60)Гц;
- в авиации - 400Гц;
- космические летательные аппараты - 1000Гц.
Увеличение частоты позволяет уменьшить габариты электроустановок.
3) Циклическая частота - ω=2πf.
Для частоты 50Гц циклическая частота ω=2*3,14*50=314рад/с или 1/с.
4) Мгновенное значение - значение периодически изменяющейся величины в рассматриваемый момент времени.
Мгновенные значения обозначают - e, i, u.
5) Амплитудное значение
Максимальное значение или амплитуду ЭДС, напряжения и тока обозначают - Em, Um, Im.
6) Действующее значение
Действующее значение ЭДС, напряжения и тока обозначают - E, U, I.
Для количественной оценки синусоидального тока, который в течение времени непрерывно, периодически изменяется, используют значение постоянного тока, эквивалентное значению переменного тока по совершаемой работе. Такое значение будет действующим для синусоидального тока.
Действующим (или эффективным)значением синусоидального тока называют такое значение постоянного тока, при протекании которого в одном и том же резисторе с сопротивлением R за время одного периода Т выделятся столько же тепла, сколько при прохождении синусоидальнего тока.
При синусоидальном токе:
i=Imsinωt
количество теплоты, выделяемое в резисторе R за время Т равно:
 ,
,
а при постоянном токе
 .
.
Согласно определению Q≈=Q- , тогда
 ,
,  .
.
Таким образом действующее значение синусоидального тока I является его среднеквадратичным значением за период Т

Действующее значение переменного тока обозначается как постоянный ток и в  раз меньше чем его амплитуда.
раз меньше чем его амплитуда.
Аналогично

 .
.
Большинство электроизмерительных приборов работают на тепловом или электродинамическом эффекте, поэтому они всегда показывают действующее значение. Основные расчеты электроцепей синусоидального тока проводятся по действующим значениям. Для несинусоидальных величин эти соотношения будут другими.
7) Среднее значение
Среднее значение синусоидальной величины это ее среднеарифметическое значение. Однако, если определять среднее значение синусоидальной величины за период Т, то оно будет равно нулю, так как положительная и отрицательная полуволны синусоидальной кривой совпадают по форме. Поэтому среднее значение определяют за полпериода.
За среднее значение синусоидального тока принимают такое значение постоянного тока, при котором за полпериода переносится такой же электрический заряд, что и при синусоидальном токе:
 ,
,
 ,
,
 /
/
Таким образом, среднее значение меньше действующего.
Изображение синусоидальных величин в прямоугольных координатах
В общем случае синусоидальные величины (рис.1), могут быть записаны:
e=Emsin(ωt+ψe)
u=Umsin(ωt+ψu),
i=Imsin(ωt+ψi),
где e,u,i - мгновенные значения ЭДС, напряжения и тока;
Em,Um,Im - амплитуды ЭДС, напряжения и тока.
(ωt+ψe) - фазовый угол;
ψe, ψu, ψi - начальные фазы ЭДС, тока и напряжения.

На практике чаще имеют место случаи, когда электрические величины не совпадают по фазе.
Из рис. 1 видно, что напряжение опережает ток на угол ψu-ψi . Разность фазовых углов называется разностью или сдвигом фаз.
φ=ψu-ψi - разность фаз между напряжением и током.
При этом пользуются правилом: начальные фазы расположенные по левую сторону от начала координат имеют положительные значения, а по правую отрицательные.
Если угол φ >0, то ток отстает от напряжения по фазе. Если φ<0, то ток опережает напряжение по фазе.
При сложении двух синусоидальных величин (одинаковой частоты), изображенных в прямоугольных координатах, необходимо сложить ординаты для ряда значений угла ωt и по точкам построить суммарную синусоиду. Получается новая амплитуда, новый фазовый сдвиг, причем:
Im ≠ Im1 + Im2;
φi≠ φi1+ φi2.
Такой расчет является трудоемким и имеет недостаточную точность.
В екторное изображение синусоидальных величин
екторное изображение синусоидальных величин
Рис.2
Наиболее просто складывать синусоидальные величины, представив их вращающимися векторами (рис.3).

Рис.3
В плоскости с осями ОX и ОY рассмотрим вращающийся с постоянной скоростью, равной угловой частоте ω, вектор ОА, длина которого равна амплитуде синусоидальной ЭДС, т.е.  .
.
Мгновенное значение ЭДС описывается известным соотношением:
e=Emsin(ωt+ψe).
За положительное направление вращения принимают направление против часовой стрелки, а угол поворота отсчитывают от оси ОX. В начальном положении (при t=0) вектор ОА повернут по отношению к оси OX на угол ψe
Построим проекцию вектора ОА на ось OY, которые изменяются по мере поворота вектора на угол ωt по отношению к начальному положению. В начальном положении (при t=0) проекция ОА0= Emsinψe=e0, т.е. равна мгновенному значению ЭДС при t=0.
Через некоторое время (t=t1) вектор ОА будет повернут на угол ωt1 и составлять с осью ОX угол (ωt1+ψe). Проекция его на ось OY :
ОА1= Emsin(ωt1+ψe)=e1, т.е. равна мгновенному значению ЭДС при t=t1.
При t=t2 вектор ОА совпадает с осью OY и его проекция ОА2= Em= e2. При дальнейшем вращении вектора АО его проекции на ось YO начнут уменьшаться, затем станут отрицательными и т.д.
Таким образом, проекции на ось OY вектора, вращающегося с постоянной скоростью ω и имеющего длину, равную амплитуде ЭДС, изменяются по синусоидальному закону, т.е. представляют собой мгновенные значения синусоидальной ЭДС. Следовательно, справедливо и обратное: если имеем синусоидальную величину. то ее можно представить вращающимся вектором.
Правила построения векторных диаграмм
Любую синусоидально изменяющуюся во времени величину (ЭДС, напряжение, ток) можно представить в виде вращающегося вектора, длина которого равна амплитуде, а угловая скорость угловой частоте этой синусоидальной величины.
Начальное положение вращающегося вектора определяется углом, равным начальной фазе синусоидальной величины и откладываем от положительного направления оси O в сторону, противоположную вращению часовой стрелки.
В одних и тех же осях можно представить векторы всех ЭДС, действующих в данной цепи, напряжений на всех участках данной цепи и токов во всех ее ветвях (в заданных масштабах).
Так как синусоидальные величины имеют одинаковую частоту, то изображающие их векторы вращаются с одинаковой скоростью. Их взаимное положение на плоскости, относительно друг друга, остается неизменным. Поэтому на практике векторы не вращают, а строят их, соблюдая углы между векторами (углы сдвига фаз).
Отказавшись от вращения вектора можно строить векторы не только максимальных, но и действующих значений.
Вектора можно складывать, по правилу параллелограмма, получив при этом суммарный вектор (рис. 4).

Рис.4
В связи с отсутствием необходимости вращения нас интересует только взаимное расположение векторов, один из которых можно строить по направления оси OX, остальные вектора направляются относительно этого вектора (рис.5).
Например, если к элементам электрической цепи подается переменное напряжение u=Umsin(ωt+ψu), то возникнет переменный ток i=Imsin(ωt-ψi). В этом случае ток отстает от напряжения по фазе на угол φ=ψu-ψi. Начальные фазы ψu и ψi на векторной диаграмме не изображают, так как взаимное положение векторов определяется полностью разностью фаз - φ. Принимаем начальную фазу тока равную нолю (ψi=0), тогда начальная фаза напряжения ψu равна сдвигу фаз - φ.
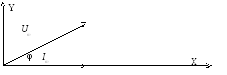
Рис.5
Графический метод расчета является грубым неточным. На практике переходят к точным математическим методам расчета на основе теории комплексных чисел.
Понятия о комплексных числах
Комплексная плоскость - прямоугольная системе координат, на которой по одной оси откладываются вещественные числа +1, на другой (перпедикулярной) - мнимые числа +j.

Здесь j= - мнимая единица.
- мнимая единица.
Действия с мнимой единицей:
1) j2=-1; 2) 
Любую точку на комплексной плоскости можно охарактеризовать комплексным числом. Известно, что комплексное число С имеет вещественную Re и мнимую Im составляющие.
Алгебраическая форма записи комплексного числа:
С=а+jв,
где а= Аcosα – реальная часть комплексного числа,
в= Аsinα – мнимая часть, γ=arctg - фаза,
- фаза,
с= - модуль комплексного числа.
- модуль комплексного числа.
Тригонометрическая форма записи комплексного числа:
С=с(cosγ+jsinγ).
Показательная форма записи комплексного числа:
 , где
, где  - оператор поворота (поворотный множитель).
- оператор поворота (поворотный множитель).
cosγ + jsinγ =  - формула Эйлера.
- формула Эйлера.
Частные случаи:
Для γ= π/2  ;
;
γ= -π/2  ;
;
γ= π  .
.
Тригонометрическая форма записи служит для перехода из алгебраической формы в показательную и наоборот.
studfiles.net
Однофазные электрические цепи переменного тока
Количество просмотров публикации Однофазные электрические цепи переменного тока - 822
§ 4.1. Переменный ток, получение, параметры.
Переменным принято называть периодический ток, значения которого повторяются через определенные промежутки времени, называемые периодом. Период (Т, секунды) одного полного колебания.
Рис.4-1. Модель генератора переменного тока.
Рис.4-2. График синусоидального тока.
Источником силовых линий магнитного поля является постоянный магнит NS, между полюсами которого расположен цилиндрический ротор (вращающаяся часть). Ротор, с целью уменьшения потерь на вихревые токи набран из отдельных тонких листов электротехнической стали, изолированных лаковой пленкой друг от друга. Полюсам придается такая форма, что в воздушном зазоре между ними и ротором магнитная индукция изменяется по закону синуса
,
где a - угол между плоскостью катушки, расположенной на роторе, и нейтральной плоскостью ОО’. При вращении ротора с угловой скоростью ω в каждой активной стороне витка катушки (число витков W), согласно явлению электромагнитной индукции, наводится ЭДС. Тогда, ЭДС индуктируемая на концах этой катушки, будет равна
, (1)
ei – ЭДС, индуктируемая в одной активной стороне витка катушки; 2 – число активных сторон в одном витке; W – число витков; ωt=a. Здесь .
Из выражения (1) вытекает, что при создании такой модели генератора ЭДС, возникающая в обмотке, закрепленной на роторе, изменяется по закону синуса. Для подключения к такому генератору нагрузки нужно:
1. концы обмотки подключаются к контактным кольцам;
2. к контактным кольцам приложить щетки, с помощью которых снимаем ЭДС, и подключаем нагрузку.
Параметры переменного тока.
1.Период.
2.Циклическая частота – число полных колебаний в секунду.
.
Единицей измерения служит Гц=1/с.
3.Мгновенной значение тока i, напряжения u, ЭДС e – значение этих величин в произвольный момент времени, к примеру, времени t, мгновенное значение тока i (см. график).
4.Амплитудное или максимальное значение тока Imax, напряжения Umax, ЭДС Emax - наибольшее из мгновенных.
5.Действующее значение - ϶ᴛᴏ величина тока, которая определяется в цепях переменного тока с помощью измерительных приборов.
.
Здесь U, E и I – действующие значения.
6.Среднее значение величины за период. Т.к., в течении одной половины периода ток течет в одном направлении, а в течении другой то же количество электричества протекает в обратном направлении, то среднее значение тока за период равно 0.
§ 4.2. Фаза переменного тока. Сдвиг фаз.
Пусть на якоре генератора укреплены два одинаковых витка 1 и 2, сдвинутых в просранстве на угол φ, как показано на рис.4-3. При вращении якоря в витках будет наводиться ЭДС индукции одинаковой частоты ω и амплитуды Emax рис.4-4, т.к, витки вращаются с одинаковой угловой скоростью в одном и том же магнитном поле.
Рис.4-3.
Рис.4-4.
Положение витков задано углами ψ1 и ψ2 для произвольного момента времени, ĸᴏᴛᴏᴩᴏᴇ можно положить t=0. Плоскости витков не совпадают с нейтральной плоскостью ОО’. Мгновенные значения ЭДС как функции времени будут определяться выражениями:
;
.
Следовательно, в момент времени t=0 ЭДС отличны от нуля:
;
.
Электрически углы ψ1 и ψ2 определяют значения ЭДС в начальный момент времени и называются начальными фазовыми углами или начальными фазами.
Временной сдвиг определяется разностью начальных фаз и принято называть углом сдвига фаз или сдвигом фаз φ. (рис.4-4).
§ 4.3. Векторные диаграммы.
Сложить, вычесть токи, напряжения двух синусоидальных величин, имеющих разные начальные фазы, является трудоемкой операцией. По этой причине, возникла крайне важно сть заменить синусоидальные величины вектором, длина которого равна действующему значению данной величины, а его положение по отношению к нейтральной плоскости будет определяться начальным углом. Такая замена принято называть векторной диаграммой. Совокупность нескольких векторов, соответствующих нулевому моменту времени, принято называть векторной диаграммой.
§ 4.4. Особенности электрических цепей переменного тока.
При изучении электрических цепей крайне важно помнить, что электрический ток неразрывно связан с магнитным полем. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, при возникновении тока в электрической цепи и в окружающей среде имеются магнитные и электрические поля. Вместе с тем, в электрической цепи происходит преобразование электромагнитной энергии в тепловую.
В реальных цепях электрическое и магнитное поля распределены вдоль всей оси. Но такое равномерное распределение полей встречается редко, к примеру, в линиях передачи энергии. Как правило, магнитное и электрическое поля распределяются вдоль цепи неравномерно, причем, на одних участках резко выражены магнитные поля (индуктивные катушки), на других – электрические (конденсаторы). Имеются также участки цепей, где происходит в основном преобразование электромагнитной энергии в тепловую (резисторы). Указанные цепи, называемые цепями с сосредоточенными параметрами, позволяют изучить свойства отдельных участков, а затем рассмотреть работу цепи в целом.
§ 4.5. Цепь переменного тока с активным сопротивлением.
Рис.4-5.
u-мгновенное напряжение.
Ток в цеп определяем по закону Ома:
,
где U – действующее; R – активное сопротивление. Пример – лампа накаливания.
Такая цепь потребляет мощность, называемою активной
[Вт],
I – действующее значение тока.
Под активной мощностью можно приблизительно считать ту полезную мощность, которая участвует в преобразовании электрической энергии в другие виды энергии.
Векторная диаграмма.
Рис.4-6.
При составлении диаграммы следует помнить, что вектора вращаются против часовой стрелки с угловой скоростью ω или же говорят с угловой частотой ω, равной
.
Здесь, UR – напряжение на активном сопротивлении, равное
.
Как видно из векторной диаграммы в активном сопротивлении вектор тока и вектор напряжения совпадают по направлению.
§ 4.6. Цепь переменного тока с емкостью.
Рис.4-7.
Ток в цепи
,
где XC – емкостное сопротивление цепи, равное
,
здесь с – емкость в Фарадах, и т.к. эта величина очень большая, а сети имеют значения емкости в мкФ, то чаще пользуются формулой
,
здесь с в мкФ.
В такой цепи, независимо от направления тока, на участках 0 – 1, 2 – 3 (см. график переменного тока) идет потребление электрической энергии, конденсатор накапливает ее на пластинах и она присутствует в этой цепи в виде энергии электрического поля. В эти промежутки времени цепь работает как потребитель и значения мощности берут со знаком ʼʼ+ʼʼ.
Когда напряжение на входе в цепи характеризуется участком 1 – 2, 3 – 4, то запасенная электрическая энергия в цепи с емкостью возвращается в сеть, цепь ведет себя как генератор, а значение мощности берут со знаком ʼʼ-ʼʼ. По этой причине, активная мощность, потребляемая такой цепью, равна 0.Наибольшее значение мощности, потребляемой цепь, принято называть реактивной мощностью и определяется
[вар] – вольт ампер реактивная.
Векторная диаграмма.
Рис.4-8.
Здесь UС – напряжение на емкостном сопротивлении
.
Как видно из векторной диаграммы вектор тока опережает вектор напряжения на угол φ=90°. При этом, говорят так, φ=90° - опережающий, ᴛ.ᴇ. вектор тока опережает вектор напряжения на угол 90°.
§ 4.7. Цепь переменного тока с индуктивностью.
Рис.4-9.
Ток в цепи
,
где XL – индуктивное сопротивление цепи, равное
,
где L – индуктивность (Гн) – параметр, характеризующий свойства обмоток катушек электрических аппаратов и машин.
В такой цепи, также в соответствии с формой напряжения приложенной к цепи и в различное время (участки 0 – 1, 1 – 2), идет вначале потребление электрической энергии, которая накапливается в виде энергии магнитного поля, после чего она возвращается в сеть. По этой причине, Р=0. При этом, наибольшее значение мощности принято называть реактивной мощностью индуктивности.
.
Векторная диаграмма.
Рис.4-10.
Здесь, напряжение на индуктивном сопротивлении равно
.
Как видно из векторной диаграммы вектор тока отстает от вектора напряжения на угол φ=90°. Теперь, под записью φ=90° - отстающий – нужно понимать то, что вектор тока отстает от вектора напряжения на угол φ=90°.
§ 4.8. Неразветвленная цепь переменного тока с R, XL, XC.
Рис.4-11.
Ток в цепи
,
где Z – полное сопротивление цепи, равное
.
Связь между этими сопротивлениями можно графически изобразить в виде прямоугольного треугольника сопротивления.
Рис.4-12.
Здесь X – реактивное сопротивление цепи. ,
.
В такой цепи присутствует:
активная мощность
.
реактивная мощность
.
полная мощность
[ВА] – вольт ампер.
Треугольник мощностей (прямоугольный).
Рис.4-13.
Из треугольника мощностей следует, что коэффициент мощности – число, показывающее отношение активной мощности к полной мощности. Цепь потребляет мощность, которая принято называть полной. И только часть этой мощности идет на выполнение активной и полезной работы. По этой причине, cosφ (коэффициент мощности) называют КПД электрической цепи. .
Векторная диаграмма. Порядок построения.
1. Находим напряжение на элементах цепи
.
2. Выбираем масштаб по току и по напряжению.
МI=
МU=
При выборе масштаба следует учитывать:
§ длина вектора тока должна быть чуть больше или равна длине вектора общего напряжения;
§ масштаб по напряжению должен быть таким, чтобы длины векторов напряжения на элементах цепи получились целыми числами или дробными 5 (с дробью 0,5, к примеру 2,5).
3. По горизонтали откладываем вектор тока. Длина вектора тока равняется числовому значению тока деленного на масштаб.
4. С учетом углов сдвига фаз в активном, индуктивном и емкостном сопротивлениях откладываем вектора напряжений на элементах цепи. Чтобы правильно отложить вектора напряжений делают так:
§ обходят цепь по часовой стрелке, но можно и по-другому;
§ для получения вектора напряжения на зажимах цепи нужно все вектора сложить поочередно друг к другу, ᴛ.ᴇ. начало второго должно идти с конца первого, а начало первого будет совпадать с началом вектора тока. Стоит сказать, что для нашей цепи вектор напряжения на зажимах цепи равен
;
§ не забывать, что вектора вращаются против часовой стрелки.
Рис.4-14.
Угол φ отмечается стрелкой, направление стрелки от вектора тока к вектору напряжения. Диаграмма построена для случая XL>XC/
Важно заметить, что для случая XL<XC диаграмма будет иметь следующий вид
Рис.4-15.
Важно заметить, что для случая XL=XC
Рис.4-16.
Такая векторная диаграмма показывает, что в цепи наступает резонанс напряжений. при резонансе напряжения такая цепь ведет себя как цепь с чисто активной нагрузкой, ᴛ.ᴇ. Z=R, cosφ=1, т.к. φ=0, то Q=0, P=S, а напряжение на зажимах цепи равно напряжению на активном сопротивлении. Добиться резонанса напряжения можно подбором индуктивности, емкости, реактивных сопротивлений или питать такую цепь резонансной частотой
.
§ 4.9. Разветвленная цепь переменного тока.
Цепь рис.4-17 состоит из параллельно соединенных катушки и конденсатора, находящихся под общим напряжением U.
Рис.4-17. Схема разветвленной цепи.
Ток в катушке
.
Этот ток отстает по фазе от напряжения на угол φ1, тангенс которого
.
Ток катушки можно разложить на две слагающие, активную , совпадающую по фазе с напряжением, и реактивную
, отстающую по фазе от напряжения на угол π/2.
Ток конденсатора
.
Он опережает по фазе напряжение на угол π/2.
Общий ток найдем из прямоугольного треугольника токов (рис.4-18), одним катетом которого является активная слагающая тока , а другим реактивная слагающая общего тока, равная разности реактивной слагающей тока катушки и тока конденсатора
.
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, общий ток
.
Угол сдвига общего тока от напряжения определяется через его тангенс (рис.4-18):
.
Рис.4-18. Векторная диаграмма для разветвленной цепи.
Рис.4-19. Векторная диаграмма при резонансе токов.
Ток в неразветвленной части цепи может отставать от напряжения на угол φ при IL>IC, или опережать его при IL<IC, или, наконец, совпадать по фазе с напряжением (рис.2) при IC=IL. В последнем случае в цепи наступает резонанс токов, при котором , а мощность
, т.к. φ=0, а cosφ=1.
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, общий ток равен активной составляющей тока катушки. При этом общий ток всегда меньше тока в катушке, т.к. активная составляющая тока катушки всегда меньше тока катушки (Ia1<I1).
Отношение тока в контуре или в катушке (I1≈I2) к общему току при резонансе (Iрез)
,
представляющее собой добротность контура, показывает, во сколько раз ток в параллельном контуре при резонансе больше общего тока в подводящих проводах.
В этом случае максимальная мощность, затрачиваемая на получение магнитного поля (U/IL), равна максимальной мощности, затрачиваемой на получение электрического поля (UIC), а следовательно, равны и максимальные значения энергии в магнитном и электрическом полях цепи WLм=WCм. Как и в рассмотренном выше колебательном контуре, в течении одной четверти периода энергия, запасаемая в электрическом поле, целиком получается от магнитного поля, а в течении второй четверти периода энергия, запасаемая в магнитном поле, целиком получается от электрического поля. От генератора в цепь поступает только энергия, расходуемая в активном сопротивлении. Т.к. реактивные слагающие тока компенсируют друг друга, то в цепи генератора проходит только активный ток, обусловленный потерями энергии в активном сопротивлении.
§ 4.10. Коэффициент мощности.
Для полного использования генератора он должен работать при номинальном напряжении Uн с номинальным током Iн и cosφ=1. В этом случае генератор развивает наибольшую активную мощность, равную его полной номинальной мощности,
.
Уменьшение cosφ вызывает пропорциональное уменьшение активной мощности, ᴛ.ᴇ. неполное использование номинальной мощности генератора.
У приемника энергии, работающего при неизменном номинальном напряжении Uн и с постоянной активной мощностью Р, ток изменяется обратно пропорционально cosφ, т.к.
.
Следовательно, уменьшение cosφ вызывает увеличение тока и увеличение мощности потерь на нагревание проводов I2r.
По указанным соображениям стремятся повышать cosφ каждой установки до значения, близкого к единице.
Контрольные вопросы:
1. Что принято называть переменным электрическим током?
2. Как можно изобразить переменный электрический ток?
3. Период, частота͵ амплитуда переменного тока.
4. Мгновенные и действующие значения тока, напряжения и ЭДС.
5. Фаза переменного тока. Сдвиг фаз.
6. Векторные диаграммы цепи переменного тока.
7. Что представляют из себяособенности электрических цепей переменного тока?
8. Как рассчитать цепь переменного тока с активным сопротивлением?
9. Как рассчитать цепь переменного тока с емкостью?
10. Как рассчитать цепь переменного тока с индуктивностью?
11. Что представляет собой неразветвленная цепь переменного тока с активным сопротивлением, емкостью и индуктивностью?
12. Как построить векторную диаграмму неразветвленной цепи переменного тока?
13. Что представляет собой разветвленная цепь переменного тока?
14. Коэффициент мощности.
ГЛАВА 5
referatwork.ru
Тема 6.5.Однофазные электрические цепи переменного тока.
Студент должен знать:
особенности переменного тока;
характеристики синусоидальных величин.
Уметь:
рассчитывать простейшие электрические цепи;
строить векторные диаграммы для цепей переменного тока
Переменный ток: определение, получение синусоидальных э.д.с и тока, их уравнения и графики. Характеристики синусоидальных величин: амплитуда, фаза, начальная фаза, угловая частота, период, частота, мгновенные величины.
Действующая и средняя величина переменного тока.
Векторная диаграмма и ее обоснование. Элементы и параметры электрических цепей переменного тока. Цепь с активным сопротивлением, цепь с индуктивностью, цепь с емкостью; уравнения и графики тока и напряжения, векторные диаграммы; определение тока по заданному напряжению; мощности активная и реактивная, их определение для каждой цепи.
Цепь с активными и реактивными элементами: индуктивная катушка и конденсатор с потерями энергии, их схемы замещения; уравнения, графики, векторные диаграммы; определение тока по заданному напряжению и напряжения по заданному току; активные и реактивные сопротивления; активные и реактивные мощности; треугольники сопротивлений и мощностей. Неразветвленная цепь переменного тока: векторная диаграмма, расчетные формулы; резонанс напряжений. Разветвленная цепь переменного тока: векторная диаграмма, расчетные формулы, резонанс токов.
Методические указания
Переменный ток имеет громадное практическое значение, что объясняется в первую очередь возможностью его трансформирования.
При изучении данной темы необходимо обратить внимание на способы получения переменного тока, его основные характеристики и понятия, параметры. Кроме того следует учесть, что при расчетах электрических цепей переменного тока вводятся такие понятия как активные, реактивные элементы, их составляющие.
При изучении разветвленных и неразветвленных электрических цепей переменного тока следует обратить внимание на условия возникновения явлений резонанса напряжения и токов, их промышленного применения.
Тема 6. 6. Трехфазные электрические цепи переменного тока
Студент должен знать:
принцип получения электроснабжения по трехфазной системе;
соотношение между фазными и линейными токами и напряжениями.
Уметь:
рассчитывать трехфазные цепи при соединении приемников электрической энергии звездой и треугольником.
Трехфазная система электрических цепей, трехфазная цепь. Соединения обмоток трехфазных генераторов электрической энергии: трехфазная симметричная система э.д.с., прямая и обратная последовательность фаз;
соединение обмоток генератора и потребителей звездой; соединение обмоток генератора треугольником; фазные и линейные напряжения, соотношения между ними.
Трехфазные симметричные цепи: соединения обмоток генератора и приемника энергии звездой, четырехпроводная трехфазная цепь, роль нулевого провода; краткие сведения об аварийных режимах в трехфазных цепях.
Методические указания
Трехфазная система переменного тока получила широкое распространение как система, обеспечивающая более выгодную передачу энергии и позволяющая создать надежные в работе и простые по устройству электрические машины и аппараты.
Трехфазной системой электрических цепей называется система, состоящая из трех электрических цепей переменного тока одной частоты, с системой трех э.д.с., которые сдвинуты по фазе на 1/3 периода.
Каждая из обмоток трехфазного генератора может быть самостоятельным источником электрической энергии и может замыкаться на свой приемник энергии. В этом случае получается несвязная трехфазная система. На практике такие системы не применяются. Обычно обмотки трехфазного генератора соединяются звездой или треугольником. В зависимости от способа соединения генератора и приемников энергии трехфазная система может быть четырех- или трехпроводной.
В данной теме необходимо обратить внимание на особенности и взаимосвязи между параметрами при соединениях обмоток генераторов и приемников энергии звездой и треугольником.
studfiles.net
Однофазные электрические цепи переменного тока — реферат
ЖЕЗКАЗГАНСКИЙ КОЛЛЕДЖ БИЗНЕСА И ТРАНСПОРТА
На тему: «Однофазные электрические цепи переменного тока»
Выполнила: Дутбаева Г.Т
Проверила: Мусина Г.Г
Жезказган 2010
Содержание
1.Введение………………………………………….
2.Основные определения………………………….
3.Переменный однофазный ток…………………...
4.Список использованной литературы…………...
Введение
Большинство потребителей электрической энергии работает на переменном токе. В настоящее время почти вся электрическая энергия вырабатывается в виде энергии переменного тока. Это объясняется преимуществом производства и распределения этой энергии. Переменный ток получают на электростанциях, преобразуя с помощью генераторов механическую энергию в электрическую. Основное преимущество переменного тока по сравнению с постоянным заключается в возможности с помощью трансформаторов повышать или понижать напряжение, с минимальными потерями передавать электрическую энергию на большие расстояния, в трехфазных источниках питания получать сразу два напряжения: линейное и фазное. Кроме того, генераторы и двигатели переменного тока более просты по устройству, надежней в работе и проще в эксплуатации по сравнению с машинами постоянного тока.
В электрических цепях переменного тока наиболее часто используют синусоидальную форму, характеризующуюся тем, что все токи и напряжения являются синусоидальными функциями времени. В генераторах переменного тока получают ЭДС, изменяющуюся во времени по закону синуса, и тем самым обеспечивают наиболее выгодный эксплуатационный режим работы электрических установок. Кроме того, синусоидальная форма тока и напряжения позволяет производить точный расчет электрических цепей с использованием метода комплексных чисел и приближенный расчет на основе метода векторных диаграмм. При этом для расчета используются законы Ома и Кирхгофа, но записанные в векторной или комплексной форме
Основные определения
Переменным называется электрический ток, величина и направление которого изменяются во времени.
Область применения переменного тока намного шире, чем постоянного. Это объясняется тем, что напряжение переменного тока можно легко понижать или повышать с помощью трансформатора, практически в любых пределах. Переменный ток легче транспортировать на большие расстояния. Но физические процессы, происходящие в цепях переменного тока, сложнее, чем в цепях постоянного тока из-за наличия переменных магнитных и электрических полей.
Значение переменного тока в рассматриваемый момент времени называют мгновенным значением и обозначают строчной буквой i.
Мгновенный ток называется периодическим, если значения его повторяются через одинаковые промежутки времени
Наименьший промежуток времени, через который значения переменного тока повторяются, называется периодом.
Период T измеряется в секундах. Периодические токи, изменяющиеся по синусоидальному закону, называются синусоидальными.
Мгновенное значение синусоидального тока определяется по формуле
где Im - максимальное, или амплитудное, значение тока.
Аргумент синусоидальной функции называют фазой; величину φ, равную фазе в момент времени t = 0, называют начальной фазой. Фаза измеряется в радианах или градусах. Величину, обратную периоду, называют частотой. Частота f измеряется в герцах.
В Западном полушарии и в Японии используется переменный ток частотой 60 Гц, в Восточном полушарии - частотой 50 Гц.
Величину называют круговой, или угловой, частотой. Угловая частота измеряется в рад/c.
Если у синусоидальных токов начальные фазы при одинаковых частотах одинаковы, говорят, что эти токи совпадают по фазе. Если неодинаковы по фазе, говорят, что токи сдвинуты по фазе. Сдвиг фаз двух синусоидальных токов измеряется разностью начальных фаз
С помощью осциллографа можно измерить амплитудное значение синусоидального тока или напряжения.
Амперметры и вольтметры электромагнитной системы измеряют действующие значения переменного тока и напряжения.
Действующим значением переменного тока называется среднеквадратичное значение тока за период. Действующее значение тока (для синусоиды) .
Аналогично определяются действующие значения ЭДС и напряжений
Действующие значения переменного тока, напряжения, ЭДС меньше максимальных в √2 раз.
Законы Ома и Кирхгофа справедливы для мгновенных значений токов и напряжений.
Закон Ома для мгновенных значений:
Законы Кирхгофа для мгновенных значений:
Переменный однофазный ток
Ток, изменяющийся во времени по значению и направлению, называется переменным. В практике применяют периодически изменяющийся по синусоидальному закону переменный ток (рис. 1).
Синусоидальные величины характеризуются следующими основными параметрами: периодом, частотой, амплитудой, начальной фазой или сдвигом фаз.
Рис. 1 График синусоидальной величины
Период (T) - время (с), в течение которого переменная величина совершает полное колебание.
Частота — число периодов в секунду. Единица измерения частоты - Герц (сокращенно Гц), 1 Гц равен одному колебанию в секунду. Период и частота связаны зависимостью
T = 1 / f
В странах бывшего СССР промышленный переменный ток имеет частоту 50 Гц. Можно представить, что полярность зажимов источника переменного тока с частотой 50 Гц меняется 100 раз в секунду.
Изменяясь с течением времени, синусоидальная величина (напряжение, ток, ЭДС) принимает различные значения. Значение величины в данный момент времени называют мгновенным.
Амплитуда — наибольшее значение синусоидальной величины.
Амплитуды тока, напряжения и ЭДС обозначают прописными буквами с индексом: Im, Um, Em, а их мгновенные значения - строчными буквами i, u, e.
Мгновенное значение синусоидальной величины, например тока, определяют по формуле
i = Imsin(ωt + ψ)
, где ωt + ψ — фаза-угол, определяющий значение синусоидальной величины в данный момент времени; ψ - начальная фаза, т. е. угол, определяющий значение величины в начальный момент времени.
Синусоидальные величины, имеющие одинаковую частоту, но разные начальные фазы, называются сдвинутыми по фазе.
Разница начальных фаз φ = ψi − ψu определяет угол сдвига фаз. На рис. 2 приведены графики синусоидальных величин (тока, напряжения), сдвинутых по фазе. Когда же начальные фазы двух величин равны ψi = ψu, то разница ψi − ψu = 0 и, значит, сдвига фаз нет φ = 0 (рис. 3).
Эффективность механического и теплового действия переменного тока оценивается действующим его значением. Действующее значение переменного тока равно такому значению постоянного тока, который за время, равное одному периоду переменного тока, выделит в том же сопротивлении такое же количество тепла, что и переменный ток. Действующее значение обозначают прописными буквами без индекса: I, U, E.
Рис. 2 Графики синусоидальных тока и напряжения, сдвинутых по фазе
Рис. 3 Графики синусоидальных тока и напряжения, совпадающих по фазе
Для синусоидальных величин действующие и амплитудные значения связаны соотношениями:
I = IM / √2; U = UM / √2; E = EM√2.
Действующие значения тока и напряжения измеряют амперметрами и вольтметрами переменного тока, а среднее значение мощности - ваттметрами.
В цепи переменного тока, состоящей из резистора R, напряжение и ток совпадают по фазе. На рис. 4 приведена векторная диаграмма тока и напряжения для цепи с резистором.
Рис. 4 Электрическая цепь с резистором:
а - схема, б - векторная диаграмма
Средняя за период мощность цепи резистором называется активной мощностью; она равна произведению действующих значений напряжения и тока:
P = U·I.
Изменение тока в цепи с индуктивностью L вызывает ЭДС самоиндукции, которая по закону Ленца противодействует изменению тока. При увеличении тока ЭДС самоиндукции действует навстречу току, а при убывании — в направлении тока, противодействуя его уменьшению. Вследствие этого ток в цепи с катушкой индуктивности отстает от напряжения на угол π/2 радиан — четверть периода (рис. 5).
Закон Ома для цепи переменного тока, содержащей индуктивность, будет иметь вид
I = UL / xL.
Величина xL называется индуктивным сопротивлением цепи или реактивным сопротивлением индуктивности; измеряется в Омах.
Индуктивное сопротивление рассчитывают по формуле
xL = ωL
, где ω = 2πF - круговая частота (ω = 2·3,14·50), L - индуктивность катушки, Г.
При включении в цепь переменного тока конденсатора (рис. 6, а) происходит непрерывное перемещение электрических зарядов. При увеличении напряжения ток в цепи конденсатора будет зарядным, а при уменьшении - разрядным. Поэтому ток в цепи, содержащей конденсатор, опережает напряжение на угол π/2 радиан (рис. 6, б).
На векторной диаграмме (рис. 6, в) вектор тока Ic опережает вектор приложенного напряжения Uc.
Выражение закона Ома для цепи переменного тока, содержащей емкость, имеет вид
I = Uc / xc.
Величина xc называется емкостным сопротивлением или реактивным сопротивлением емкости, которую определяют по формуле
xc = 1 / 2πfc = 1 / ωc.
При последовательном соединении катушки индуктивности и конденсатора их реактивные сопротивления вычитаются, т. е.
x = xL − xC.
Эта величина называется реактивным сопротивлением цепи.
Геометрическая сумма активного и реактивного сопротивлений равна полному сопротивлению электрической цепи, т. е.
R2 + x2 = R2 + (xL − xC)2 = z2
Эта зависимость показывает, что используя значение R, x, z можно построить треугольник сопротивлений (рис. 7). Умножая значения сторон этого треугольника на силу тока в цепи, получим треугольник напряжений. Умножив сопротивления на квадрат тока, получим треугольник мощностей.
Рис. 5 Электрическая цепь с катушкой индуктивности:
а - схема, б - графики тока, напряжения, ЭДС самоиндукции, в - векторная диаграмма
Рис. 6 Электрическая цепь с конденсатором:
а - схема, б - линейная диаграмма тока, напряжения, в - векторная диаграмма
Работающие электрические установки потребляют активную и реактивную мощности и энергию. Лампы накаливания и электрические нагревательные приборы потребляют практически только активную мощность. Такие же электроприемники, как асинхронные электродвигатели, трансформаторы, дроссели, линии электропередачи и другие потребляют и активную и реактивную мощности.
Рис. 7 Треугольник сопротивлений электрической цепи переменного тока
Потребность электроустановок в активной и реактивной мощностях покрывается энергией, вырабатываемой генераторами электростанций. Активная энергия преобразуется потребителями в другие виды энергии: тепловую, световую, механическую и др. Потребляемая предприятиями реактивная мощность есть мощность, идущая на создание переменного магнитного потока (магнитного поля). Магнитный поток, сцепляющийся с контуром электрической цепи, пропорционален току в этой цепи. Мерой пропорциональности служит так называемая индуктивность цепи, предопределяющая в каждом конкретном случае числовую связь между током и магнитным потоком. Следовательно, с любой цепью переменного тока, в которой и напряжение и ток изменяются по периодической кривой, создается переменный (периодически изменяющийся) магнитный поток, который имеет инерцию. Поэтому при всяком приращении (или уменьшении) магнитного потока, вызванном увеличением (или уменьшением) силы тока, неизбежно должно проявляться своего рода инерциальное сопротивление магнитного потока. Это сопротивление проявляется в форме ЭДС самоиндукции, представляющей собой электромагнитную реакцию всегда обратного знака по отношению к изменению магнитного потока.
Это означает, что ЭДС самоиндукции всегда стремится изменить силу тока таким образом, чтобы ослабить или замедлить изменение магнитного потока, сцепляющегося с контуром. Отсюда следует, что переменное напряжение источника электрической энергии должно содержать кроме составляющей, расходуемой на тепловые процессы, обусловленные наличием активного сопротивления, еще и такую составляющую, которая в каждый момент времени компенсировала бы ЭДС самоиндукции. Следовательно, мгновенное значение мощности в цепи переменного тока также должно в любой момент времени представлять собой сумму двух слагаемых: активной мощности, расходуемой в активных сопротивлениях, и реактивной мощности, вызванной действием ЭДС самоиндукции. В течение первой четверти каждого периода, когда ток увеличивается от нуля до наибольшего значения, соответственно растет (в результате преодоления ЭДС (самоиндукции) и магнитный поток. При этом в магнитном поле накапливается энергия за счет реактивной мощности, поступающей из генератора в цепь потребителя. В течение второй четверти каждого периода, когда ток и магнитный поток уменьшаются (от наибольшего значения до нуля), энергия магнитного поля также уменьшается до нуля. Это уменьшение энергии магнитного поля сопровождается возвращением реактивной мощности из цепи потребителя в генератор (под действием обратно направленной ЭДС самоиндукции).
Таким образом, мощность, идущая на создание магнитного поля, четыре раза в течение каждого периода меняет свое направление, причем среднее значение этой мощности за каждый полупериод (или целое число периодов) равно нулю, так что процесс обмена мощностью между генератором и цепью потребителя происходит в форме колебательного процесса.
turboreferat.ru
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|


