WinNavigator

Frigate

Norton Commander

WinNC

Dos Navigator

Servant Salamander

Turbo Browser

Winamp, Skins, Plugins

Необходимые Утилиты

Текстовые редакторы

Юмор

File managers and best utilites

Объем тела вращения. Объем тела вращения реферат

Объем тела вращения | Бесплатные курсовые, рефераты и дипломные работы

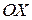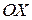Рассмотрим тело, образованное вращением вокруг оси фигуры, ограниченной непрерывной кривой , осью и прямыми (рис. 7). Разобьем отрезок на частей точками Проведем через точки деления плоскости, перпендикулярные оси 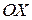. Сечение тела вращения плоскостью есть круг радиусом с площадью . Проведенные плоскости разобьют тело на слои. Каждый -й слой

приближенно заменим прямым цилиндром (рис. 7) с радиусом , высотой и объемом

Сумма … объемов всех цилиндров равна .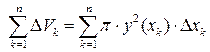

Объем тела вращения определяется как предел этой суммы

при стремлении к нулю величины 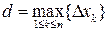. Мы получили предел интегральной суммы непрерывной функции по отрезку , который существует и равен интегралу

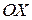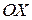Итак, объем тела, полученного при вращении вокруг оси фигуры, ограниченной кривой , осью и прямыми , вычисляется по формуле

или .

Аналогично вычисляется объем тела, полученного при вращении вокруг оси фигуры, ограниченной линией , осью , прямыми (рис. 8):

или .

Пример 1. Вычислить объем тела, образованного вращением фигуры, ограниченной линиями ,

а) вокруг оси 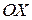, б) вокруг оси .

Решение. Построим параболу прямые и заштрихуем фигуру, ограниченную этими линями (рис. 31).

а). Объем тела, полученного при вращении этой фигуры вокруг оси 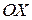, вычислим по формуле:

Подынтегральная функция − четная, поэтому используем следствие 2 к теореме.

б). Для вычисления объема тела вращения фигуры вокруг оси нельзя непосредственно воспользоваться формулой, так как фигура сверху ограничена не прямой, а параболой. Поэтому сначала рассмотрим фигуру, ограниченную прямой , осью , прямыми . При ее вращении вокруг оси получим цилиндр, объем которого можно вычислить по формуле или по формуле

Теперь рассмотрим фигуру, ограниченную линиями осью и прямой . При ее вращении вокруг оси получим тело, объем которого вычислим по формуле:

Тогда искомый объем будет равен

7. Лекционное занятие. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ ПЕРВОГО РОДА

Случай 1. Пусть на плоскости дуга задана уравнением Будем предполагать, что функция непрерывна вместе со своей производной на .

Рассмотрим на кривой точки с абсциссами Проведем хорды длины которых обозначим (рис. 1).

Вычислим длину -й хорды

Для вычисления приращения воспользуемся формулой конечных приращений Лагранжа

где − некоторая точка из промежутка Тогда длина й хорды

Учтем это и возьмем в определении криволинейного интеграла в качестве промежуточных точек на дугах 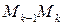точки :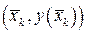

Мы получили предел интегральной суммы функции по отрезку , который равен интегралу Следовательно,

Итак, для вычисления криволинейного интеграла по дуге АВ с уравнением нужно:

1) заменить в подынтегральной функции на его значение на дуге;

2) заменить на ;

3) вычислить получившийся определенный интеграл по отрезку .

Иногда удобнее использовать уравнение кривой в виде . Тогда

Пример 1. Вычислить длину дуги кривой .

Решение. Уравнение кривой разрешено относительно , поэтому воспользуемся формулой (7.16), учитывая, что ,

Тогда

Случай 2. Пусть на плоскости дуга задана параметрическими уравнениями

причем функции непрерывны на вместе со своими производными и .

Для определенности, пусть . Уравнения определяют функцию , которая имеет непрерывную производную . Учитывая, что , получим .

Итак, справедливы следующие формулы и

Аналогично, для пространственной кривой, заданной параметрическими уравнениями , имеем

Пример 2. Найти массу верхней полуокружности радиуса , если плотность в каждой ее точке равна ординате этой точки.

Решение. Масса кривой вычисляется с помощью криволинейного интеграла:

Для вычисления интеграла запишем параметрические уравнения окружности: .

Параметр есть угол между радиус-вектором точки окружности и осью 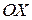(рис. 2). Для верхней полуокружности параметр меняется от 0 до . Теперь вычислим :

Подставим в искомый интеграл выражения для расставим пределы изменения и вычислим получившийся определенный интеграл:

refac.ru

Реферат : Тела вращения

Тела вращения

Цилиндр

Цилиндром называется тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.

Круги называются основаниями цилиндра, а отрезки, соединяющими цилиндра.

{1}

Так как параллельный перенос есть движение, то основания цилиндра равны.

Так как при параллельном переносе плоскость переходит в параллельную плоскость ( или в себя), то у цилиндра основания лежат в параллельных плоскостях. Так как при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние, то у цилиндра образующие параллельны и равны.

Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих.

Цилиндр называется прямым, если его образующие перпендикулярны плоскостям основания.

Радиусом цилиндра называется радиус его основания. Высотой цилиндра называется расстояние между плоскостями его оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим.

Конус

Конусом называется тело, которое состоит из круга - основания конуса, точки, не лежащей в плоскости этого круга, - вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания.

Отрезки, соединяющие вершину конуса с точьками окружности основания, называются образующими конуса. Поверхность конуса состоит из основания и боковой поверхности. {2}

Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания.

Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания. Осью прямого кругового конуса называется прямая, содержащая его высоту

Шар

Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки. Эта точка называется центром шара, а данное расстояние радиусом шара.

Граница шара называется шаровой поверхностью, или сферой.

{3}

Таким образом, точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Любой отрезок, соединяющий центр шара с точкой шаровой поверхности, также называется радиусом.

Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром. Концы любого диаметра называются диаметрально противоположными точками шара.

Шар, так же как цилиндр и конус, является телом вращения. Он получается при вращении полукруга вокруг его диаметра как оси.

Пирамида

Пирамидой называется многогранник, который состоит из плоского многоугольника - основания пирамиды, точки, не лежащей в плоскости основания, - вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания.

Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами. Поверхность пирамиды состоит из основания и боковых граней. Каждая боковая грань - треугольник.

Одной из его вершин является вершина пирамиды, а противолежащей стороной - сторона основания пирамиды.

Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды, на плоскость основания. Треугольная пирамида называется также тетрайдером.

Правильная пирамида

Пирамида называется правильной , если ее основанием является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника. Осью правильной пирамиды называется прямая, содержащая ее высоту. Очевидно, у правильной пирамиды боковые ребра равны; следовательно, боковые грани - равные равнобедренные треугольники. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой. Боковой поверхностью пирамиды называется сумма площадей ее боковых граней.

Многогранники

Призма

Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки эти многоугольников. Многоугольники называются основаниями призмы, а отрезки, соединяющие соответствующие вершины, - боковыми ребрами призмы. Так как параллельный перенос есть движение, то основания призмы равны. Так как при параллельном переносе плоскость переходит в параллельную плоскость, то у призмы основания лежат в параллельных плоскостях. Так как при параллельном переносе точки смещаются по параллельным прямым на одно и то же расстояние, то у призмы боковые ребра параллельны и равны. Поверхность призмы состоит из оснований и боковой поверхности. Боковая поверхность состоит из параллелограммов. У каждого из этих параллелограммов две стороны являются соответствующими сторонами оснований, а две другие - соседними боковыми ребрами. Высотой призмы называется расстояние между плоскостями ее основания. Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани, называется диагональю призмы.

topref.ru

Реферат Тела вращения

Формат: doc

Дата создания: 07.12.1998

Размер: 6.46 KB

Скачать реферат

Тела вращения

Цилиндр

Круги называются основаниями цилиндра, а отрезки, соединяющими цилиндра.

Так как параллельный перенос есть движение, то основания цилиндра равны.

Цилиндр называется прямым, если его образующие перпендикулярны плоскостям основания.

Конус

Отрезки, соединяющие вершину конуса с точьками окружности основания, называются образующими конуса. Поверхность конуса состоит из основания и боковой поверхности.

Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания.

Шар

Граница шара называется шаровой поверхностью, или сферой.

Пирамида

Одной из его вершин является вершина пирамиды, а противолежащей стороной - сторона основания пирамиды.

Правильная пирамида

Многогранники

Призма

Подобные документы:

Реферат Развитие авиации .

Реферат Пьер де Ферма “Пьер, сын Доминика Ферма, буржуа и второго консулата города Бомона , крещен 20 августа 1601 г. Крестный отец - Пьер Ферма, купец и брат названного Доминика, крестная мать - Жанна Казнюв, и я”. Подпись отсутствует, но предыдущая запись подписана: “Дюма, викарий”. Этот документ искали полтора века и обнаружили лишь в 1846 г. благодаря усилиям адвоката Топиака.

Реферат Программа Mathematics Едва исчезли со страниц журналов восторженные отзывы на новую версию математического пакета Maple V 4.0 компании Maple Waterloo, как компания Wolfram Research представила не менее интересный продукт — Mathematica 3.0. Она разработана компанией Wolfram Research Inc , основанной известным математиком и физиком Стефаном Вольфрамом, одним из создателей теории сложных систем.

Реферат Движение 2.Определение движения с 1 3. Общие свойства движения с 1 4. Параллельный перенос с 2 5. Центральная симметрия с 2 6. Зеркальная симметрия (отражение в плоскости) с 3 7. Поворот вокруг прямой с 3 8. Неподвижные точки движений пространства с 4 8.1. Основные теоремы о задании движений пространства с 4 9.1. Базисы и их ориентация с 4 9.2. Два рода движения с 5 10.

Реферат Архимед. Его достижения в области математики Архимед родился в 287 году до н.э. в Сиракузах на острове Сицилия. Отец Архимеда - астроном и математик Фидий. Фидий дал сыну хорошее образование. Затем Архимед продолжил своё обучение в Александрии, где познакомился со знаменитым астрономом Кононом, астрономом и математиком Эратосфеном, с которыми он поддерживал в дальнейшем научную переписку.

Диплом и связанное с ним: Обобщающее повторение по геометрии (на примере темы "Четырехугольник") §3. Содержание и методика обобщающего повторения на примере темы: «Четырехугольники». 24 В процессе обучения математике важное место отводится организации повторения изученного материала. Необходимость повторения обусловлена задачами обучения, требующими прочного и сознательного овладения ими.

Доклад: Прокатка Прокатка. Прокатку производят на металлургических и машиностроительных заводах, при этом получают прокат — готовые изделия или заготовки для последующей обработки ковкой, штамповкой, прессованием (выдавливанием), волочением или резанием. В прокат перерабатывают около 80 % всей выплавляемой стали и большую часть цветных металлов и сплавов.

Реферат Специальные виды литья 1.1 Сущность метода и область применения. Сущность состоит в том, что по неразъемной легкоплавкой модели изготавливают неразъемную разовую форму. Модели из этой формы выплавляют, а образовавшуюся полость заливают жидким металлом. При этом способе получаемые отливки настолько точны, что объем механической обработки, уменьшается на 80... 100% ив 1,5...2 раза сокращается расход жидкого металла.

Реферат Волоконно-оптические гироскопы Гироскоп выполняет функции детектора угловой скорости в инерциальном пространстве и по праву может называться абсолютным тахометром, являясь структурным элементом инерциальной навигационной системы, обрабатывающей информацию о местонахождении самолета или судна с целью выведения его на курс.

Курсовая: Основы автоматизации производственных процессов .

Диплом и связанное с ним: Проектирование технологического процесса изготовления детали - Стабилизатор Мне дано задание спроектировать технологический процесс изготовления детали “Стабилизатор”, программа выпуска 500000 единиц в год. Данная программа выпуска указывает на массовое производство. Обработка металлов резанием является основным видом обработки, с помощью которой можно получить детали с высокой точностью и чистотой обработанных поверхностей.

Реферат История токарного станка История относит изобретение токарного станка к 650 гг. до н. э. Станок представлял собой два установленных центра, между которыми зажималась заготовка из дерева, кости или рога. Раб или подмастерье вращал заготовку (один или несколько оборотов в одну сторону, затем в другую). Мастер держал резец в руках и, прижимая его в нужном месте к заготовке, снимал стружку, придавая заготовке требуемую форму.

Курсовая: Технология изготовления листоштамповочной детали Рассчитать технологию изготовления листоштамповочной детали типа «фланец» по следующим данным: Отбортовка отверстий представляет собой образование бортов вокруг предварительно пробитого отверстия или по краю полых деталей.

Курсовая: Разработка технологического процесса восстановления шатуна двигателя автомобиля ГАЗ-53А

Шпаргалки: Кинематика точки, сложное движение точки, движение точки вокруг неподвижной оси (Шпаргалка) 6. Определить абсолютное ускорение точки, записать выражение абсолютного ускорения точки в развернутой форме 1. Для определения ур-ния траектории точки из ур-ний движения точки исключить время t.

Реферат Архимед Архимед (≈287-212 гг. до н. э.) родился в городе Сиракузы на острове Сицилия. Его отец, Фидий, был математиком и астрономом. Видимо, он и оказал влияние на научные интересы Архимеда еще в детстве. Легенды рассказывают, что Архимед забывал о пище, подолг

nreferat.ru

Объем тела вращения

Количество просмотров публикации Объем тела вращения - 159

приближенно заменим прямым цилиндром (рис. 7) с радиусом , высотой и объёмом

Сумма объёмов всех цилиндров равна .

Объем тела вращения определяется как предел этой суммы

Итак, объём тела, полученного при вращении вокруг оси фигуры, ограниченной кривой , осью и прямыми , вычисляется по формуле

или .

Аналогично вычисляется объём тела, полученного при вращении вокруг оси фигуры, ограниченной линией , осью , прямыми (рис. 8):

или .

Пример 1. Вычислить объём тела, образованного вращением фигуры, ограниченной линиями ,

а) вокруг оси , б) вокруг оси .

Решение. Построим параболу прямые и заштрихуем фигуру, ограниченную этими линями (рис. 31).

а). Объем тела, полученного при вращении этой фигуры вокруг оси , вычислим по формуле:

Подынтегральная функция − четная, в связи с этим используем следствие 2 к теореме.

б). Для вычисления объёма тела вращения фигуры вокруг оси нельзя непосредственно воспользоваться формулой, так как фигура сверху ограничена не прямой, а параболой. По этой причине сначала рассмотрим фигуру, ограниченную прямой , осью , прямыми . При ее вращении вокруг оси получим цилиндр, объём которого можно вычислить по формуле или по формуле

Теперь рассмотрим фигуру, ограниченную линиями осью и прямой . При ее вращении вокруг оси получим тело, объём которого вычислим по формуле:

Тогда искомый объём будет равен

7. Лекционное занятие. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ ПЕРВОГО РОДА

Рассмотрим на кривой точки с абсциссами Проведем хорды длины которых обозначим (рис. 1).

Вычислим длину -й хорды

Для вычисления приращения воспользуемся формулой конечных приращений Лагранжа

где − некоторая точка из промежутка Тогда длина й хорды

Учтем это и возьмем в определении криволинейного интеграла в качестве промежуточных точек на дугах точки :

Мы получили предел интегральной суммы функции по отрезку , который равен интегралу Следовательно,

Итак, для вычисления криволинейного интеграла по дуге АВ с уравнением нужно:

1) заменить в подынтегральной функции на его значение на дуге;

2) заменить на ;

3) вычислить получившийся определенный интеграл по отрезку .

Иногда удобнее использовать уравнение кривой в виде . Тогда

Пример 1. Вычислить длину дуги кривой .

Решение. Уравнение кривой разрешено относительно , в связи с этим воспользуемся формулой (7.16), учитывая, что ,

Тогда

Случай 2. Пусть на плоскости дуга задана параметрическими уравнениями

причем функции непрерывны на вместе со своими производными и .

Итак, справедливы следующие формулы и

Аналогично, для пространственной кривой, заданной параметрическими уравнениями , имеем

Пример 2. Найти массу верхней полуокружности радиуса , в случае если плотность в каждой ее точке равна ординате этой точки.

Решение. Масса кривой вычисляется с помощью криволинейного интеграла:

Для вычисления интеграла запишем параметрические уравнения окружности: .

Параметр

есть угол между радиус-вектором точки окружности и осью

(рис. 2). Для верхней полуокружности параметр

меняется от 0 до

. Теперь вычислим

referatwork.ru

Объем тела вращения | Бесплатные курсовые, рефераты и дипломные работы

Пусть функция непрерывна на отрезке . Тогда объём тела, полученного вращением вокруг оси криволинейной трапеции, ограниченной сверху графиком функции , снизу (Рис. 10), определяется формулой:

. (11)

Рис. 10

Пример 15. Вычислить объем тела, полученного вращением вокруг оси криволинейной трапеции, ограниченной гиперболой , прямыми , и осью .

Решение: Сделаем чертеж (Рис. 11, 12).

Из условия задачи следует, что , . По формуле (9) получаем

…

Рис. 11

Объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной прямыми и , осью Оу и графиком непрерывной на отрезке функции .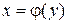

Если криволинейная трапеция ограниченна графиком непрерывной функции и прямыми , , , то объём тела, образованного вращением этой трапеции вокруг оси , равен:

. (12)

Рис. 12

Пример 16. Вычислить объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной линиями , , (Рис. 13).

Решение: В соответствии с условием задачи находим пределы интегрирования: 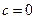, . По формуле (10) получаем:

Рис. 13

refac.ru

Реферат - ТЕЛА ВРАЩЕНИЯ - Математика

При построении линии взаимного пересечения многогранника с телом вращения образуется замкнутая пространственная линия, которая может состоять из прямых и различных кривых линий (рис. 305 и 306). Если боковая поверхность одного из пересекающихся тел полностью проходит через поверхность второго тела, то получатся две замкнутые линии пересечения (рис. 306). Если боковая поверхность одного из пересекающихся тел частично проходит через поверхность второго тела, то получится одна замкнутая линия пересечения (рис. 305).

При построении линии взаимного пересечения сначала строят характерные точки: точки, в которых ребра многогранника (как прямые) пересекаются с поверхностью тела вращения, и точки, в которых крайние образующие тела вращения пересекаются с поверхностью многогранника. Затем (при необходимости) строят промежуточные точки линии взаимного пересечения.

Построение линии взаимного пересечения поверхности прямого кругового цилиндра с поверхностью прямой призмы. На рис. 305 показано самое простое пересечение этих тел, так как их боковые поверхности в данном случае проецирующие.

Так же как и при решении задач на взаимное пересечение поверхностей двух многогранников, в этой задаче сначала определяют проекцию, на которой нужно строить линию взаимного пересечения.

Поскольку линия взаимного пересечения принадлежит одновременно поверхностям двух тели поверхность одного из геометрических телпроецируется на одну из плоскостей проекций в линию, совпадающую с проекцией основания, то линия пересечения на этой проекции совпадет с проекцией боковой поверхности данного тела. На рис. 305 боковая поверхность четырехугольной призмы является проецирующей по отношению к плоскости W и совпадает с проекцией основания (четырехугольником). Поэтому линия пересечения, лежащая на гранях боковой поверхности призмы, совпадет с проекцией боковой поверхности призмы, т. е. со сторонами четырехугольника.

Боковая поверхность цилиндра является проецирующей относительно плоскости проекций Н и проецируется в окружность, совпадающую с проекцией контура основания. Так как линия пересечения принадлежит боковой поверхности цилиндра, ее горизонтальная проекция совпадет с проекцией окружности основания. На фронтальной плоскости проекций, где боковые грани призмы и боковая поверхность цилиндра проецируются в прямоугольники, линия взаимного пересечения будет замкнутой линией, состоящей из отдельных участков эллипсов и отрезков прямых линий. Боковые грани призмы, пересекающие ось цилиндра, пересекут его по эллипсам, а грань, параллельная оси,— по образующим.

Для построения фронтальной проекции линии пересечения сначала строят точки, в которых ребра четырехугольной призмы пересекаются с боковой поверхностью цилиндра. Эти точки пересечения хорошо видны на горизонтальной проекции. Верхние и нижние ребра призмы пересекаются здесь с поверхностью цилиндра в точках 1, 2, 13 и 14. С помощью линий проекционной связи точки 1 и2 строят на фронтальной проекции нижнего ребра (1' и 2'), а точки 13 и 14 — на фронтальной проекции верхнего ребра (13' и 14'). Два других ребра призмы в пересечении не участвуют.

Для построения точки пересечения крайней образующей цилиндра с боковой поверхностью призмы используют профильную проекцию. Здесь проекция правой крайней образующей пересекла проекцию верхней грани призмы в точке 8", а нижней — в точке 7". Фронтальная проекция этой образующей совпадает с проекцией оси цилиндра. С помощью линий проекционной связи строят точки 7' и 8' на фронтальной проекции.

С осью цилиндра на профильной проекции совпадают две крайние образующие фронтальной проекции, сливаясь в одну линию, которая пересекает проекцию боковой поверхности призмы в точках 11", 12", 3" и 4". С помощью линий проекционной связи на фронтальной проекции строят точки 3' и 11' на левой крайней образующей, а точки 4', 12' на правой крайней образующей. Задняя грань призмы является горизонтально-проецирующей плоскостью, с которой цилиндр пересекается по двум отрезкам 1 13 и2 14. Между точками 11', 8'; 8', 12'; 3', 7׳ и 7', 4' большой интервал. Необходимо построить дополнительные точки. Для этого на боковой поверхности цилиндра через произвольно взятые на верхнем основании точки Е и F проводят две образующие. На профильной проекции они совпадают, и точки пересечения этих образующих с поверхностью призмы попарно сливаются (5" и 6";9" и 10"). С помощью линий проекционной связи эти образующие строят на горизонтальной проекции, где они проецируются в точки. Затем строят их фронтальные проекции, и на них с помощью линий проекционной связи, проведенных с профильной проекции, строят проекции точек 5', 6', 9', 10'. Построенные точки соединяют. Отрезки 1 13 и2 14 будут невидимыми, так как на фронтальной проекции они лежат на невидимой части цилиндра и невидимой грани призмы. В пересечении нижней и верхней граней призмы с боковой поверхностью цилиндра получатся части эллипсов, поэтому точки 13', 11', 9', 8', 10', 12' и 14' в верхней части геометрических тел и точки 1', 3', 5', 7', 6', 4' и 12' в нижней части соединяют плавной кривой линией. Точки 11', 12', 3' и 4' лежат на крайних образующих и являются границей видимости. Кривые линии, проходящие в верхней части через точки 11', 9', 8', 10' и 12', а в нижней части через точки 3', 5', 7', 6', 4', будут видимыми. Линии 11'13', 12', 14', 3'1' и 2'4' будут невидимыми, так как лежат на невидимой части цилиндра.

Построение линии взаимного пересечения в изометрии.Точки 13, 14, 1 и 2 лежат не только на цилиндре, но и на ребрах призмы. Так как на ребрах, как на отрезках, строить точки проще, чем на поверхности цилиндра, то, измерив расстояние на фронтальной проекции от левого и правого отрезка, в которые проецируются основания призмы, до точек 13', 14', 1׳ и 2', отмечают их на верхнем и нижнем ребре призмы в изометрии. Остальные точки строят с помощью образующих, расположенных на поверхности цилиндра. Расстояние от нижнего основания цилиндра до соответствующих точек измеряют на фронтальной проекции и соответственно переносят в прямоугольную изометрию. Часть линии пересечения, расположенная на верхней грани призмы, будет видимой, а остальная часть невидимой.

Построение линии взаимного пересечения поверхности прямого кругового цилиндра с поверхностью пирамиды.Сначала определяют, на каких проекциях нужно строить линию взаимного пересечения. Затем отмечают и строят характерные точки. Дополнительные точки строят с помощью вспомогательных горизонтальных плоскостей.

На рис. 306 боковая поверхность прямого кругового цилиндра на профильной плоскости проекций проецируется в окружность, совпадающую с проекцией контура основания, так как его поверхность проецирующая. Следовательно, линия взаимного пересечения, принадлежащая и боковой поверхности цилиндра, проецируется в ту же окружность. Боковые поверхности пирамиды и цилиндра не являются относительно фронтальной и горизонтальной плоскостей проекций проецирующими, значит, линии пересечения изобразятся здесь в виде кривых линий, которые нужно строить.

Поскольку боковая поверхность цилиндра полностью проходит через боковую поверхность пирамиды, то получатся две линии взаимного пересечения.

На фронтальной проекции можно сразу отметить точки 1', 3', 2' и 4', в которых проекции s'b' и s'e' ребер пирамиды SB и SE пересекаются с проекциями верхней и нижней образующих цилиндра. Проекции точек 1, 2, 3, 4 строят на плоскости Н с помощью линий проекционной связи. Все остальные точки находят с помощью вспомогательных горизонтальных секущих плоскостей: Р, N и R, профильные следы которых обозначены на профильной проекции. Для этого строят горизонтальные проекции линий пересечения пирамиды с этими плоскостями (шестиугольники) и горизонтальные проекции образующих, по которым пересекается боковая поверхность цилиндра с указанными плоскостями. Здесь определяют точки пересечения проекций образующих цилиндра с проекциями шестиугольников, лежащих в каждой секущей плоскости. Фронтальные проекции полученных точек 5'… 16' строят с помощью линий проекционной связи. Построенные точки соединяют от руки и обводят по лекалу, так как линии взаимного пересечения представляют собой части эллипсов, получившиеся от пересечения поверхности цилиндра с плоскостями — гранями боковой поверхности пирамиды. При обводке линий взаимного пересечения необходимо определить границу их видимости.

Поскольку линия взаимного пересечения принадлежит поверхности пирамиды и цилиндра одновременно, то в прямоугольной изометрии на рис. 306 она строится на поверхности цилиндра, как более простой поверхности. На видимом основании цилиндра от его центра по центровой линии, параллельной оси Оz, вверх и вниз откладывают расстояния между плоскостями Р и R, взятые с профильной проекции. Через отметки проводят линии, по которым плоскости пересекают поверхность цилиндра, и на образующих от видимого основания (эллипса) откладывают расстояния до соответствующих точек, взятых с фронтальной проекции (можно и с горизонтальной). Точки 1, 2, 3, 4, 5, 6, 7 и 8 строят на образующих, идущих от концов диаметров, параллельных осям Оz и Оу. Расстояния до этих точек от основания берут с фронтальной проекции.

www.ronl.ru

Смотрите также

..:::Новинки:::..

Windows Commander 5.11 Свежая версия.

Новая версия
IrfanView 3.75 (рус)

Обновление текстового редактора TextEd, уже 1.75a

System mechanic 3.7f
Новая версия

Обновление плагинов для WC, смотрим :-)

Весь Winamp
Посетите новый сайт.

WinRaR 3.00
Релиз уже здесь

PowerDesk 4.0 free
Просто - напросто сильный upgrade проводника.

..:::Счетчики:::..