Презентация "Математика и искусство. Метапредметные связи". Математика в искусстве реферат

Математика в искусстве - презентация онлайн

1. Математика в искусстве

2. Вступление

3. Вступление

4. Выдающиеся люди с истории математического изобразительного искусства

5. Платон

6. Архимед

7. М. К. Эшер

8. Сальвадор Дали

9. Леонардо да Винчи

10. Пит Мондриан

11. Общие темы в математическом искусстве

12. 1. Мауриц Эшер «Рептилии»(многогранники) 2. Холлистер Дэвид «Семь птиц» (тесселяции)

13. 1.Искаженные перспективы. 2.Фракталы

14. Лента Мебиуса

15. Невозможные фигуры

16. Золотые сечения

17. В искусстве это…

18. Значение золотого сечения

19. Архитектура

20. Вступление

21. Вступление

22. Как математика помогает добиться прочности сооружений.

ppt-online.org

Исследовательская работа "Математика в искусстве"

МБОУ «Средняя общеобразовательная школа №1» город Курск

Исследовательская работа

«Математика в искусстве»

Работу выполнили: уч-ся 11 А класса

Винниченко Оксана

Петрухина Александра

Руководитель Миргородова Т.Г.

Курск - 2016

Математика и искусство

Математика соблюдает пристрастие к строгому дисциплинарному мышлению и точности. Но ещё в начале XIX века ее считали самой гуманитарной наукой, и до сих пор её называют искусством. Исторически, математика играла важную роль в изобразительном искусстве, в частности при изображении перспективы, подразумевающем реалистичное изображение трехмерной сцены на плоском холсте или листе бумаги. Математика не играет очевидной роли в большинстве работ современного искусства, и, фактически, многие художники редко или вообще никогда не используют даже использование перспективы. 

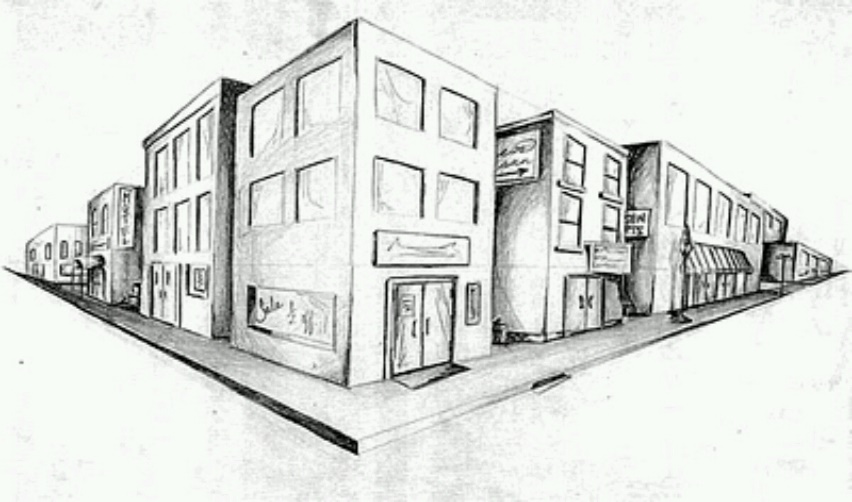
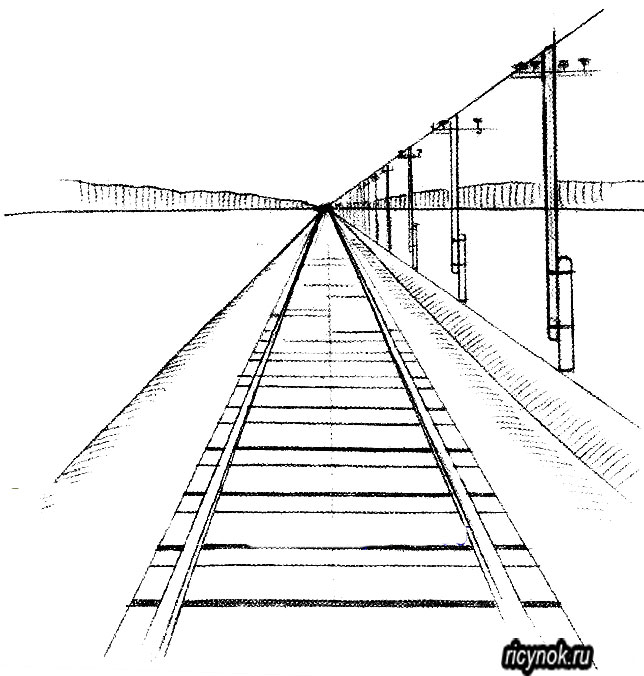
В эпоху Возрождения художники открыли, что любая картина имеет точки, невольно приковывающие наше внимание, так называемые зрительные центры.

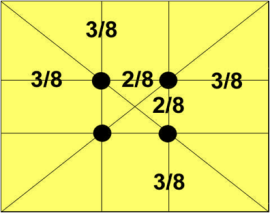
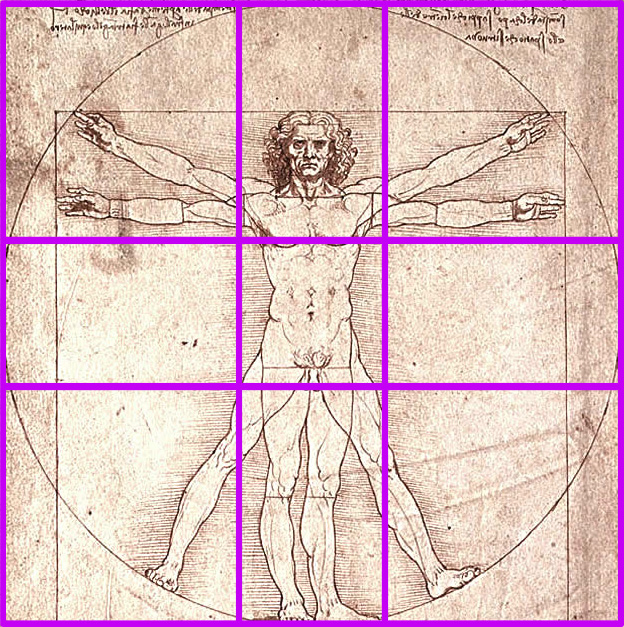
Данное открытие у художников получило название «золотое сечение».

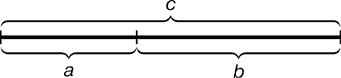
Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей

a : b = b : c

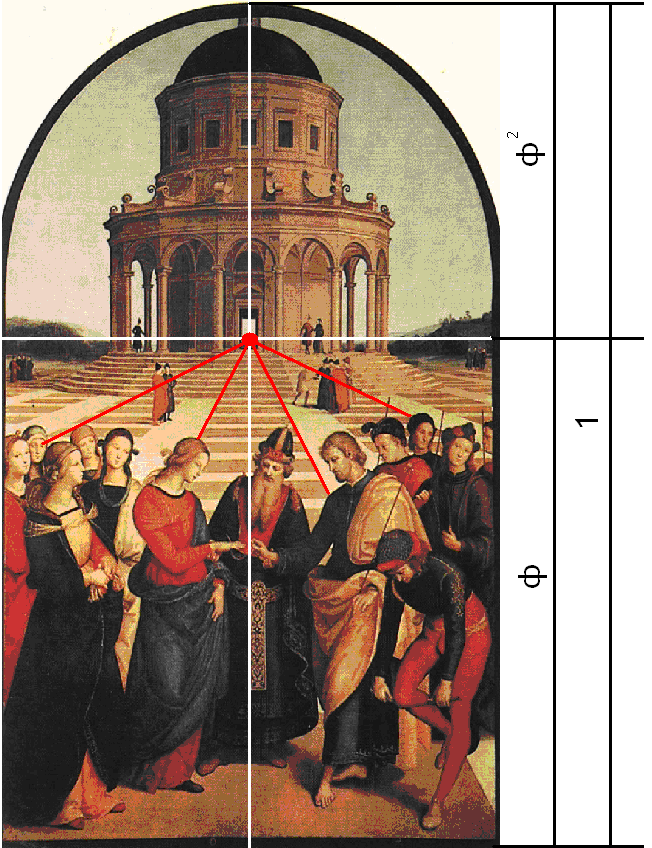
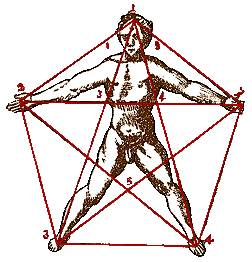
Замечательный пример «золотого сечения» представляет собой правильный пятиугольник – выпуклый и звездчатый. Звездчатый пятиугольник называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком.

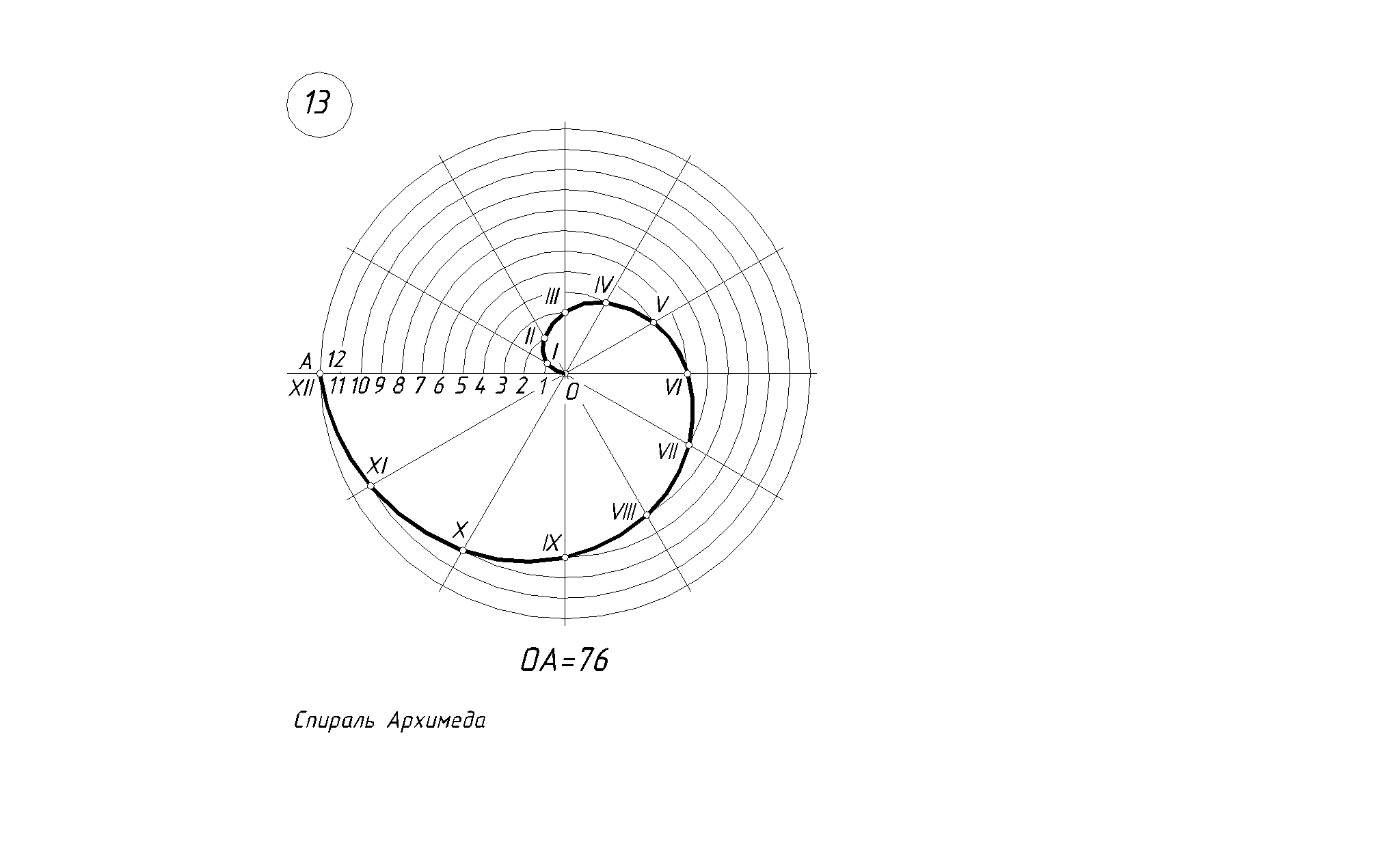
Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется его именем. Увеличение ее шага всегда равномерно.

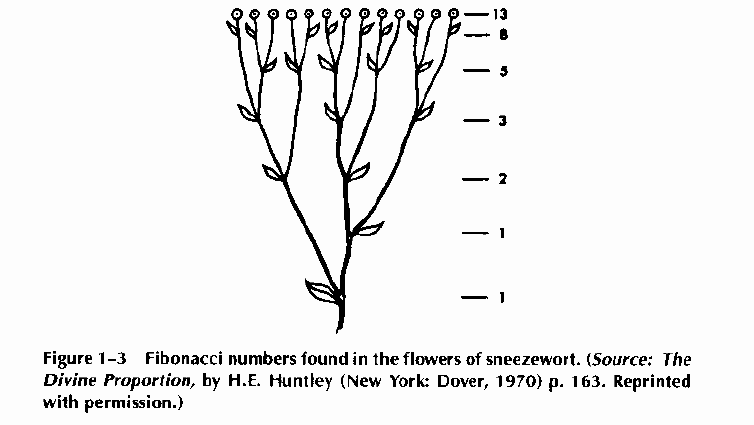
Числовой ряд Фибоначчи: 0,1,1,2,3,5,8,13,21,34,55,89... в котором каждое последующее число равно сумме двух предыдущих чисел.

Платон описал пять правильных многогранников. Он соотносил эти тела с четырьмя элементами: огонь - тетраэдр, воздух - октаэдр, вода - икосаэдр, земля - куб. Далее, он писал, что существует пятая комбинация, которой Бог ограничил Мир, это додекаэдр.

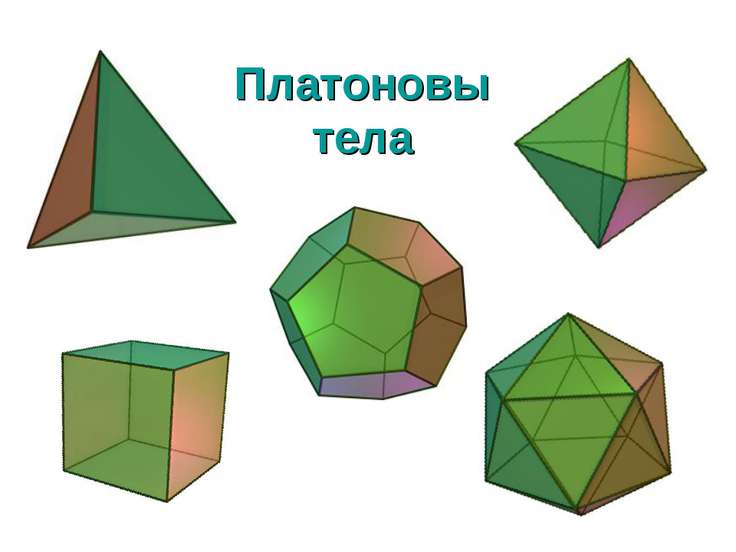
Тетраэдр-Огонь

«Посвящается всем великим завоевателям, прошедшим, настоящим и будущим»

Октаэрд-Воздух

Куб-Земля

Додекаэдр-Вселенная

Балкон.

Трехмерность этих домов — абсолютная имитация. Невозможно нарушить двухмерную природу листа бумаги, на которой они изображены. Однако в центре наблюдается некое вздутие, этакий протуберанец, который также не более чем иллюзия лист остается плоским

Вверх и вниз.

В этой литографии использована одна из удивительных «невозможных фигур»Прямоугольник внутреннего двора замкнут стенами здания, у которого вместо крыши - бесконечная лестница.

Бесконечное единение.Две соединенные спирали создают женскую голову слева и мужскую справа. Лбы обоих перевиваются в бесконечной ленте, создавая единство.

Фантазии Эшера и реклама BBDO «Almap» Brazil придумало оригинальную творческую концепцию для внедорожника Quattro. Вы не увидите бездорожья или атрибутов надежности.На постере показан Audi Quattro стоящий во дворе дома. Но благодаря оптическому эффекту, можно с той же уверенностью сказать, что он висит на потолке дома.Постер выполнен в черно белом цвете, что еще больше подчеркивает его сюрреалистичность и близость к работам Эшера. 

infourok.ru

Математика и искусство

КОНФЕРЕНЦИЯ

«МАТЕМАТИКА И ИСКУССТВО»

                     ЧТО ЕСТЬ КРАСОТА

                     И ПОЧЕМУ ЕЕ ОБОЖЕСТВЛЯЮТ ЛЮДИ?

                     СОСУД ОНА, В КОТОРОМ ПУСТОТА,

                     ИЛИ ОГОНЬ, МЕРЦАЮЩИЙ В СОСУДЕ?

                                       Н.ЗАБОЛОЦКИЙ

Любая наука могла бы гордиться такой историей, как история математики, так как она - меньше всех история ошибок.

Учитель: Человек многогранен. У каждого из вас есть какой-то дар от природы. Кто-то сочиняет стихи, кто-то поет, кто-то рисует, кто-то умеет делать это все сразу. А помогает ли вам в этом математика? Вы даже и не задумывались над этим.

Математика и скульптура, математика и музыка, математика и живопись. Что в них общего? На первый взгляд ничего. А если посмотреть внимательней! Науку и искусство объединяет стремление к познанию и творчеству. Они часть людской цивилизации, поэтому обогащают друг друга.

«Математика и искусство» - так звучит тема нашей конференции.

Выступления учащихся.

Можно к предложенным темам добавить свои или заменить полностью.

                   МАТЕМАТИКА И СКУЛЬПТУРА

Мы в необычной портретной галерее. Здесь можно увидеть древнейших предков человека. Вот воины государства Урарту, Киевский князь Ярослав Мудрый, Иван Грозный, флотоводец Ушаков Ф.Ф.   

Все эти портреты созданы М.М. Герасимовым, скульптором-антропологом.

Можно ли создать документальный портрет человека, который жил очень давно?» Можно, если посмотреть на портрет»,- ответите вы. Но не всем портретам нужно доверять. Художники часто приукрашали или стилизовали портреты. В начале 20 в. у ученых возникла мысль: а можно ли использовать череп для восстановления лица? При этом нужно знать, как связаны мышцы и кости, как зависит внешний вид человека от его скелета. Работы ученых- антропологов говорят нам о такой зависимости. Они брали достоверный портрет и вписывали в него с помощью рентгеновского изображения контуры черепа в соответственном ракурсе и масштабе. Так было решено то, какой из двух черепов принадлежит Рафаэлю.

Герасимов начинал с изучения анатомии. Многолетний труд, тысячи измерений, систематизация связей между формой отдельных частей лица и рельефов черепа. Мужские, женские, детские черепа. Составление таблиц, фотографий, рентгеновские снимки, сравнение, составление графических уравнений - «черновая работа в науке», о которой говорил академик Павлов и без которой невозможно открытие, короче говоря, сплошная математика.

Ключ найден. Только нужен контрольный опыт. Как проверить себя? Нужно восстановить лицо человека, который жил недавно, и сопоставить с фотографиями.

В 1937 году Герасимов получил для контрольного опыта череп, найденный в склепе на кладбище г. Москвы. Ему сказали, что этот человек жил более 100 лет тому назад. Череп сильно пострадал – потрескались зубы, отсутствовали некоторые кости. Герасимов сначала восстановил череп, а потом и лицо с помощью воска, сделал прическу, которую носили в прошлом столетии. Это была женщина с высоким лбом, широким овалом лица, большими красивыми глазами. Закончив работу, Герасимов узнал, что восстановил голову Марии Достоевской – матери известного писателя. Сохраненная фотография и скульптурное изображение показали, что это один и тот же человек. Это была настоящая победа в науке.

МАТЕМАТИКА И АРХИТЕКТУРА

К архитектуре во все времена было три требования – целесообразность, крепость и красота.

Никто не обустроит   себе спальню в высоком зале, а для танцевального вечера не выберет комнатку. Стадион, театр, библиотека отличаются один от другого и внешним видом, и внутренним обустройством. Целесообразность – обязательное соответствие строения своему предназначению.

О крепости архитектурных сооружений хорошо сказано в сказке про трех поросят. Красота, гармония в разные века была разной. В Египте строили колоннами (зал в Корнаке).

Колонны стоят близко, огромные, высокие. В таком «лесу» хорошо пугать. Так же строили греки. Балка, балка, а сверху перекрытие. Такие строения могли расти в длину и ширину.

 Шли года. Цивилизация продвигалась на север. Росли города и стала возникать потребность в высоких домах. Эту функцию взяла на себя арка-дуга.

Поставим руки локтями на стол и переплетем пальцы рук,- выйдет арка. Место переплетения рук – замок арки. Надавите подбородком на него- и почувствуете легкую боль в локтях. Давление по арке распределяется во все стороны и позволяет строить второй этаж. Более того, ряды полукруглых арок позволяют строить полукруглый свод(Колизей).

В начале такие сооружения не имели потолка, т.к. не была решена главная математическая задача: как покрыть круглый дом? И вот в конце 50-х годов прошлого века профессор Московского архитектурного института М.С.Туполев разработал конструкцию кристаллических куполов, которые состоят из равносторонних многоугольных пластин.

Отрасль использования куполов разнообразная.

Их можно использовать и как выставочные павильоны, торговые залы, кафе, рестораны и т.д. Размеры помещений не ограничены. Так, в г. Истра под Москвой построен купол с пролетом в 237 метров. В таком сооружении можно разместить целый микрорайон. Идея использования кристаллических куполов позволяет строить гигантские 60-метровые круглые дома. Пример – выставочный Центр во Флориде. 

Архитектура сегодня движется в двух направлениях:1) конструирование необходимых форм на основе математических методов;2) заимствование этих форм у живой природы. Справедливо высказывание:» Живые прототипы - ключ к новой архитектуре бионики».

Архитектура второго направления теряет поэзию прямого угла, принимая легкие округлые очертания. Но их нужно вычислить. На помощь приходит геометрия. Она - посредник между природой и архитектурой. В чем же секрет гармонии природных форм? Мы знаем, что прямая – кратчайшее расстояние между двумя точками, а шар – компактнейшая геометрическая форма. Почему же в живой природе они не встречаются? Зато они встречаются в своих производных. Наполните шарик водой и положите на стол - он станет похож, но морского ежа. Возьмите несколько одинаковых шариков, положите на ровную поверхность так, чтобы они касались друг друга, а сверху положите прозрачное стекло. Придавите. Видите? Шарики похожи на пчелиные соты.

Архитектурная бионика рассматривает все: паутину паука, крыло Кажана -и возникают тенты на гнущемся контуре; симметрию цветов, морских звезд – возникает, например, дом оперного театра в Сиднее; раскроют раковины моллюсков – и получают купол выставочного зала в Эйндховене (Голландия).

Форма крыльев бабочки вдохновляют архитекторов на создание аэропорта в Нью-Йорке.

Архитектурная бионика имеет древние корни. Р. Декарт на основании метода координат изучал кривую, которая получила название 

    «Лепесток жасмина», ее уравнение х + у = 3аху. В 18 столетии итальянский геометр Г. Гранди описал уравнениями семейство цветов.

Немецкий математик Б. Хабенихт получил уравнение листьев, плодов, жуков.

Архитектурная бионика еще только начинает свой путь. Но уже сейчас понятно, что это перспективное направление в архитектуре.

                  МАТЕМАТИКА И ЖИВОПИСЬ

 Геометрические мотивы нередко присутствуют в картинах известных художников. Хотя художник часто действует интуитивно, а искусствовед – сводит весь художественный арсенал картины к упрощенной геометрической схеме. Чаще всего художественные полотна создаются на основе двух геометрических конструкций – «золотого сечения» и спирали Архимеда.

«Золотое сечение» часто связывают с именем Пифагора. В его школе изучались свойства геометрических фигур. Из наблюдений была выведена математическая зависимость гармонии – AB: CB = CB: AC. (см. выше)  

Архитекторы древности знали, что от домов, построенных по такому правилу, веет теплом и покоем. Наоборот, ощущение динамики проявляется сильнее в спирали. Спиралью называют плоскую линию, образованную точкой, которая движется от начала координат (по заданному закону) и равномерно вращается вокруг своего начала. (См. выше)

Золотое сечение – это такое деление отрезка, при котором длина всего отрезка относится к длине его большей части, как длина его большей части к меньшей (прибл. 0,618).

Золотой прямоугольник обладает многими свойствами. Если от него отрезать квадрат (см. выше), то следует снова золотой прямоугольник и так до бесконечности. Если соединить вершины квадратов плавной линией, то получится золотая спираль.

Перед нами две картины – «Корабельный лес» И.И.Шишкина и «Избиение младенцев» Рафаэля Санти: одна дышит покоем и гармонией, другая вызывает тревогу, желание куда-то спрятаться.

Видите, сосну, которая стоит на переднем плане? Она визуально делит картину на два фрагмента – яркую залитую солнцем поляну и полутень. Если измерять картину, то выйдет, что длина картины к сосне так относится к длине всей картины, как меньшее расстояние до сосны к большему. Каждый из фрагментов картины построен по тому же принципу. Вот откуда этот уравновешенный характер.

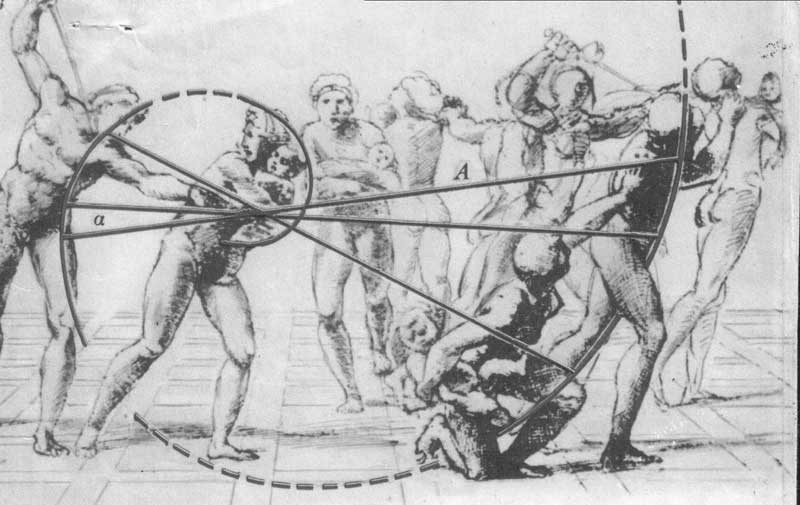
Обратимся к картине Рафаэля и найдем ее центр, т.е. наиболее драматический эпизод. Это женщина с левой стороны, которая закрывает ребенка своим телом от удара. Проведем мысленно линию: руки, голова ребенка, голова женщины, голова злодея, нога женщины, еще одна женщина, которая закрывает ребенка, и еще одна, поднятая для удара рука.

Полученная линия является золотой спиралью Архимеда.

Каждое столетие, каждая эпоха владеет каким-то своим полем деятельности для высокоталантливого человека. Пифагор был математиком, врачом, музыкантом, моралистом, мм политиком.  От Пифагора до Канта почти все философы были математиками. Р. Декарт занимался философией, музыкой, фехтованием, астрономией, физикой, математикой.

Гаусс был в поисках между математикой и филологией. Леонардо да Винчи казалось, что тайны и глубины мира могут быть воплощены только в живописи, в 18ст. считали, что только в музыке, в 19ст. – только в литературе, в 20ст. – только в науке. Однако есть универсальные люди, способные проявить свой талант сразу в нескольких сферах.

МАТЕМАТИКА И МУЗЫКА

Английский математик Д. Сильвестр писал:» Музыка-математика чувств, а математика-музыка разума». Впервые математически описал звук Пифагор. Его целиком можно назвать прадедом акустики.

Пифагор мыслил приблизительно так: целая струна звучит как» до», половина- «ре», треть- «ми», четверть- «фа». Конечно на современную гамму это не похоже, Пифагор пошел далее. Его октава стала выражаться так:

          1     1/2      1/3      1/4     1/5    1/6     1/8     1/16

        До     ре       ми       фа   соль    ля       си       до

Потом он ввел еще несколько дополнительных звуков (бемоли, диезы в современном понимании). Прослушав интервалы, выявилось, что лучше всех звучит квинта (ее соотношение 2:3), и вывел формулу ряда звуков.

Математика помогает мастеру создавать музыкальные инструменты.

Простейшая сопилка делается так: на половине длины сверлят дырочку = «до», на трети – «ре», на четверти – «ми».

А колокольчики. Возраст старейших валдайских колокольчиков неизменных спутников Пушкина в дороге,200 лет. Когда они появились впервые, неизвестно. Но их изображения есть уже на картинах 16ст.

Сначала они качались всем корпусом, а потом стали тяжелеть: мастера сделали их неподвижными, а раскачивался только язычок. Как можно достичь того чтобы звон имел красивый звук и тот же тон, независимо от того, маленькие они или большие? В конце70-х годов в Москве раскрыли секрет красивого звука. Колокол должен содержать 81,94% меди,17,21% олова,0,035% серы. Также вычислили, что в основе формы колокола лежит равнобедренный треугольник со сторонами, которые составляют золотую пропорцию. Есть даже целая наука о колоколах, и называется она компанология.

В понимании Пифагора каждая планета звучит в космосе, как какая-то нота. Например, Солнце – «до», Луна – «фа». Его взгляды разделял                 И. Кеплер, который видел в мироздании оркестр Солнечной системы, которое неслышно для человека исполняет вселенскую симфонию. Можно сказать, что сейчас фантазия Кеплера реализовалась в пульсарах

(космические источники радио-,оптического, рентгеновского,

гамма-излучений, приходящих на Землю в виде периодически повторяющихся всплесков) – пять из них неожиданно звучат аккордом.

Пульсары – нейтронные звезды, которые быстро вращаются и блеск которых периодически меняется. В 1987 году открыли миллисекундные пульсары. Их частота соответствует музыкальным звукам в пределах клавиатуры рояля.

Пульсар 1937+21 поет ми-бемоль второй октавы, а пульсар 1953+29 – ми малой октавы.

                         ИТОГИ КОНФЕРЕНЦИИ

Учитель. Подбивая итоги нашей конференции, хочется сказать словами Льва Болеславского:

                     Спеша из дома лесом любоваться,

                     Дыша цветами, думаю одно,

                     Что в каждом есть незримое богатство,

                     Но нами не измерено оно.

                     Я слышал песнь турбины и ракеты,

                     И грай грачей, и соло соловья,

                     И, раз в моей душе осталось это,

                    Каким богатством обладаю я!

Так пусть все то, что вы услышали сегодня, останется в вашей памяти, чтобы в нужный момент помочь осознать, составить, проанализировать и сделать нужный вывод.

Будьте всесторонне образованы, и пусть языком истины для каждого из вас будет математика. Ведь математика учит честности, формирует умение отличать доказанное от догадки, способствует пониманию различных фактов и понятий. Ее интересует не цель, а способы.

Поэтому польза от математики – награда за честность.

Презентация.

/uploads/33500/33412/section/668439/MATEMATIKA_I_ISKUSSTVO.ppt?1514921081074

Автор: Глушакова М.И.

glushakova-school29.edusev.ru

Презентация "Математика и искусство" | Социальная сеть работников образования

Слайд 1

Слайд 2

Цель работы Исследование связи математики и различных видов искусства, привлечение учащихся к математике, к ее свойствам и законам. Задачи Для достижения заданной цели необходимо решить следующие задачи : 1) Изучить методическую, научно-популярную и тематическую литературу. 2) Используя литературу выбрать комплекс наиболее интересных и увлекательных примеров связи математики и искусства. Краткое содержание : В работе на примерах показана связь математики с различными видами искусства.

Слайд 3

Актуальность проблемы Проведя опрос среди учащихся I-II курсов под руководством учителя было выявлено следующее: 80% учащихся,получающих профессию «художник» считают математику далекой от искусства, никак не связанной с ним и поэтому не достойной для серьезного увлечения ею. Исходя из этого автор пришел к выводу, что большая часть людей просто не хочет замечать связи математики и искусства ,и не считает ее значимой в силу сложившихся на протяжении жизни стереотипов. Поэтому было принято решение продемонстрировать на примерах ошибочность мнения о скучности математики и ее законов, о малой практической применимости в искусстве законов математики и ее свойств. Показать,что без математики не обойтись ни в одном деле, что она окружает нас везде в школе, дома, на работе, в офисе. Показать ,что очень многим мы обязаны математике.

Слайд 4

Практическая значимость Практическая значимость этого исследования заключается в следующем: - В результате привлечения внимания учащихся к математике должна возрасти их заинтересованность в данном предмете, что несомненно может способствовать повышению успеваемость учащихся.

Слайд 5

«Математика и искусство.»

Слайд 6

Великая книга природы написана математическими символами. Галилей

Слайд 7

Математика – царица всех наук, символ мудрости. Красота математики среди наук недосягаема, а красота является одним из связующих звеньев науки и искусства. Это не только стройная система законов, теорем и задач, но и уникальное средство познания красоты.

Слайд 8

Искусство – -творческое отражение, воспроизведение действительности в художественных образах. Искусство существует и развивается как система взаимосвязанных между собой видов, многообразие которых обусловлено многогранностью самого реального мира, отображаемого в процессе художественного творчества.

Слайд 9

Конечно же, все законы красоты невозможно вместить в несколько формул. Но, изучая математику мы открываем всё новые и новые слагаемые прекрасного, приближаясь к пониманию, а в дальнейшем и к созданию красоты и гармонии. Искусство, наука, красота… эти великие сферы человеческой деятельности, внешне столь разные и далекие друг от друга, тесно переплетены между собой незримыми узами! И разорвать эти узы нельзя, не повредив и тому и другому. Красота является самым крепким связующим звеном между наукой и искусством!

Слайд 10

Виды искусств Наиболее распространенной схемой является деление искусства на три группы. пространственные или пластические виды искусств: Изобразительное искусство, Декоративно-прикладное искусство, Архитектура, Фотография. временные или динамические виды искусств: Музыка , Литература пространственно-временные виды, которые называются также синтетическими или зрелищными искусствами: Хореография , Литература, Театральное искусство, Киноискусство.

Слайд 11

Существование различных видов искусств вызвано тем, что ни одно из них своими собственными средствами не может дать художественную всеобъемлющую картину мира. Такую картину может создать только вся художественная культура человечества в целом, состоящая из отдельных видов искусства.

Слайд 12

«Потребность красоты и творчества, воплощающего ее, - неразлучна с человеком, и без нее человек, быть может, не захотел бы жить на свете». Ф. М. Достоевский

Слайд 13

Красота скульптуры, храма, картины, симфонии, поэмы... Что между ними общего? Разве можно сравнивать красоту храма с красотой музыки? Оказывается можно, если будут найдены единые критерии прекрасного, если будут открыты общие формулы красоты, объединяющие понятие прекрасного самых различных объектов - от цветка ромашки до красоты обнаженного человеческого тела.

Слайд 14

Существуют ли объективные законы прекрасного? Нельзя отрицать заглавную роль симметрии в природе, которая обязана своим существованием вечному закону природы - закону тяготения. В основе основ музыки и архитектуры- гамме и пропорции – лежит математика, в частности ряд золотого сечения и модулор Ле Корбюзье. В изобразительном искусстве используется общая теория перспективы .

Слайд 15

“ Симметрия, как бы широко или узко мы не понимали это слово, есть идея, с помощью которой человек пытался объяснить и создать порядок, красоту и совершенство" Герман Вейль

Слайд 16

К фундаментальным понятиям симметрии относятся плоскость симметрии, ось симметрии, центр симметрии. Плоскостью симметрии называется такая плоскость, которая делит фигуру на две зеркально равные части, расположенные друг относительно друга так, как предмет и его зеркальное отражение. Принцип "симметрии" широко используется в искусстве. Бордюры в архитектурных и скульптурных произведениях, орнаменты в прикладном искусстве, - все это примеры использования симметрии. Принцип симметрии очень часто используется совместно с принципом "золотого сечения". Таким примером может служить картина Рафаэля "Обручение Марии"

Слайд 17

Геометрия орнаментов, бордюров, паркетов. Орнаментальное искусство одно из самых древних. С орнаментами мы встречаемся повсюду: в декоративно-прикладном искусстве, в росписях архитектурных сооружений, в чугунных решётках, окаймляющих сады, парки, дворцы. Орнамент – это узор, состоящий из повторяющихся, ритмически упорядоченных элементов. Орнамент, как правило, подчёркивает своим построением и формой архитектурные и конструктивные особенности предмета, природную красоту материала. В построении орнамента используют главным образом принцип симметрии.

Слайд 19

Симметрия в архитектуре. Симметрия…является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство. Г.Вейль

Слайд 20

Театральная площадь, Большой театр О.Бове, А.Михайлов 1821-1853

Слайд 21

Триумфальная арка Ж.Ф.Т.Шальгрен 1806-1836 Франция, Париж

Слайд 22

Золотое сечение - ( золотая пропорция , деление в крайнем и среднем отношении ) — деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине. Отношение большей части к меньшей в этой пропорции выражается квадратичной иррациональностью φ =( √5+1)/2≈1,6180339887… и, наоборот, отношение меньшей части к большей 1/ φ = =( √5-1)/2≈0,6180339887…

Слайд 23

Золотое сечение в искусстве «Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением и если первое можно сравнить с мерой золота, то второе – с драгоценным камнем». Иоганн Кеплер

Слайд 24

Известно, что Сергей Эйзенштейн искусственно построил фильм «Броненосец Потёмкин» по правилам золотого сечения. Он разбил ленту на пять частей. В первых трёх действие развивается на корабле. В двух последних — в Одессе, где разворачивается восстание. Этот переход в город происходит точно в точке золотого сечения. Да и в каждой части есть свой перелом, происходящий по закону золотого сечения. В кадре, сцене, эпизоде происходит некий скачок в развитии темы: сюжета, настроения. Эйзенштейн считал, что, так как такой переход близок к точке золотого сечения, он воспринимается как наиболее закономерный и естественный.

Слайд 25

Математика и музыка. Изучая высоту звука с помощью монохорда – простейшего инструмента Древних греков, Пифагор обнаружил поразительные вещи. Выяснилось, что приятные слуху созвучия – консонансы получаются лишь в том случае, когда длины струн, издающих эти звуки, соотносятся как целые числа первой четвёрки, т.е. 1:2, 2:3, 3:4. Это открытие потрясло Пифагора: оказалось, что звук и созвучие могут быть представлены простыми числами

Слайд 26

Великий немецкий композитор XVII века Иоганн Себастьян Бах писал церковную музыку. Позднее уже после его смерти музыканты-исследователи выяснили, что многие мелодии композитора имеют цифровые коды - символы, а произведения точно математически просчитаны.

Слайд 27

Французский композитор и музыкальный теоретик Жан Филипп Рамо в своём «Трактате о гармонии», написанном в 1722 году, говорил о том, что «музыка подчинена арифметике», уделял много внимания физико-математическим исследованиям.

Слайд 28

Игорь Стравинский , хорошо знавший музыку мастеров эпохи Ренессанса, также находил много общего между математикой и музыкой. «Способ композиторского мышления – способ, которым я мыслю, - мне кажется, не очень отличается от математического», «музыкальная форма математична хотя бы потому, что она идеальна» - эти высказывания Стравинского ярко выражают его убеждения

Слайд 29

Математика и литература "Математик, который не есть отчасти поэт, не будет никогда подлинным математиком" К. Вейерштрасс

Слайд 30

Некоторые ошибочно думают - говорила великий русский математик-женщина С. Ковалевская , что математика - это сухая наука. Они смешивают математику с арифметикой, в которой проводятся вычисления, порой трудные и скучные, с числами. Но для того чтобы быть настоящим математиком, добавила С.Ковалевская, нужно быть поэтом в душе.

Слайд 31

Поэтами были многие восточные ученые-энциклопедисты средневековья. Достаточно упомянуть лишь таких крупных мусульманских ученых, как Ибн Сина (Авиценна) (X-XI в.), аль-Хайям (XI в.), аль-Беруни (XII в.), Ибн аль-Ясмин (XII в.), Ибн аль-Хаим (XV в.) и Ибн Гази (XV в.). Они сделали много в науке вообще и в математике особенно. Ибн Сина (Авиценна) Омар Хайям Аль-Беруни

Слайд 32

Число 12 олицетворяет, в первую очередь, время: 12 часов (ноль часов) - начало новой эпохи, когда из бури и хаоса возникает новый мир. Так же 12 - это число солдат революции, и, невольно напрашивается ассоциация с двенадцатью апостолами новой, еще непонятной веры. Раскрытию авторской идеи способствует и структура поэмы. Она состоит из 12 глав, а число строк в поэме кратно 12...

Слайд 33

Льюис Кэрролл (настоящее имя – Чарлз Латуидж Доджсон). Научные работы Кэрролла предвосхитили некоторые идеи математической логики. Но больше он известен как автор популярных повестей для детей. Так в 1865 году он издал сказку «Алиса в стране чудес». Королева Англии, прочитав книгу, пришла в восторг от сказки и приказала срочно приобрести остальные сочинения Кэрролла. И очень удивилась, когда выяснилось, что все остальные произведения Кэрролла - сочинения по высшей математике, сравнительной анатомии, палеонтологии и систематике животных.

Слайд 34

Никто не замечал, что в самом заглавии романа – «Война и мир» - закодирован закон золотого сечения. В самом деле, название романа построено на первых четырех членах ряда Фибоначчи 1, 2, 3, 5.Один союз, два существительных, три слова. Пять букв в первом ключевом. Отношение ключевых слов 5:3=1,666… есть первое рациональное приближение коэффициента золотого сечения.

Слайд 35

Математика и живопись « И, поистине, живопись – это наука и законная дочь природы, ибо она порождена природой…» Леонардо да Винчи

Слайд 36

Переходя к примерам “золотого сечения” в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: “Пусть никто, не будучи математиком, не дерзнет читать мои труды”. Он снискал славу непревзойденного художника, великого ученого, гения, предвосхитившего многие изобретения, которые не были осуществлены вплоть до XX в.

Слайд 37

Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника. Вся фигура и картина в целом опутана здесь двумя золотыми треугольниками и сетью больших, средних и малых золотых прямоугольников, ориентированных по ширине или высоте полотна.

Слайд 38

Наука и искусство, словно нити холста, переплетались в полотнах мастеров Возрождения. Живопись переходила в начертательную геометрию, а геометрия – в искусство.

Слайд 39

Фракталы. Люди придумали цифры и действия с ними, а потом в них же открыли множество законов, правил и теорем. Кроме того, оказалось, что в жизни цифр, линий, углов и бесконечно малых величин можно увидеть много красивого – изящные теоремы, тела, поверхности, даже условия задач. Числа живут своей жизнью, и мы, соприкоснувшись с ней, удивляемся, а иногда и любуемся ею. Компьютер дает нам возможность видеть на экране те или иные процессы, которые мы программируем.

Слайд 40

Фракталы получают с помощью некоторой ломаной. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется по некоторому правилу на некоторую ломаную в соответствующем масштабе. В результате бесконечного повторения этой процедуры, получается геометрический фрактал.

Слайд 41

Очень часто описанным способом пользуются при рисовании орнаментов, облаков, деревьев и т. д.

Слайд 42

Заключение: Примеры взаимопроникновения математики в различные сферы искусства и наоборот можно приводить бесконечно…И чем дальше этим занимаешься, тем увлекательнее становится такая работа. Но даже приведенных примеров, я думаю, достаточно для того, чтобы согласиться со словами Бертрана Рассела: «Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства».

Слайд 43

Список литературы: 1. сайт: http://actual-art.ru 2. сайт: http://www.goldenmuseum.com/index_rus.html 3. А.И.Азевич «Двадцать уроков гармонии» библиотека журнала «Математика в школе», выпуск 7. Москва «Школа-Пресс», 1998год 4. А.В. Волошинов «Математика и искусство», Москва, «Просвещение», 1992 ГОД 5. Соколов А. Тайны золотого сечения. Техника – молодежи, 1978, № 5, с. 40 6. И.Ф.Шарыгин , Л.Н. Ерганжиева «Наглядная геометрия 5-6 классы» Москва, Издательский дом «Дрофа», 1998 год. . 7. Юшкевич А.П.Математика в ее истории. М. Янус. ИИЕТ РАН.1996

Слайд 44

Спасибо за внимание!

nsportal.ru

Исследовательский проект "Математика и искусство"

Слайд 1

Слайд 2

Цели исследования: сформировать представление о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики; понять значимость математики для научно-технического прогресса, отношение к математике как к части общечеловеческой культуры Задачи: Изучить направления взаимосвязи науки и искусства (на примере пропорции, симметрии) Проанализировать произведения искусства (репродукции картин, произведения архитектуры, скульптуры с точки зрения соответствия законам математики)

Слайд 3

Основополагающие вопросы : Что общего между представлениями ученых о том, какой должна быть научная теория и аналогичным воззрениями представителей искусства? Что общего между красотой природы, красотой искусства, красотой математики? В каких явлениях и объектах реального мира можно найти проявление математических законов? Действуют ли эти законы в природе, архитектуре, живописи и т.д.? Можно ли, отыскивая новые законы математики, продвигаться к пониманию мира и постигать законы красоты?

Слайд 4

Гипотеза: Математические законы имеют значение в понимании мира и постижении законов красоты природы, явлений и объектов реального мира? Математические законы имеют значение в понимании…

Слайд 5

Ход исследования: Изучить литературу по теме исследования Рассмотреть на примере пропорции, в каких явлениях и объектах реального мира можно найти проявление математических законов (в природе, архитектуре, живописи и т.д.) Рассмотреть на примере симметрии, в каких явлениях и объектах реального мира проявляются законы математики Сделать выводы о роли математических законов в понимании мира и постижении законов красоты

Слайд 6

Искусство, наука, красота… Искусство и наука - эти две великие сферы человеческой деятельности, внешне столь разные и далекие друг от друга, тесно переплетены между собой незримыми узами! И разорвать эти узы нельзя не повредив и тому и другому. Красота является самым крепким связующим звеном между наукой и искусством! Васильев. Мокрый луг Шишкин. Рожь

Слайд 7

Все законы красоты невозможно вместить в несколько формул. Но, изучая математику, мы открываем всё новые и новые слагаемые прекрасного, приближаясь к пониманию, а в дальнейшем и к созданию красоты и гармонии. Большой Сфинкс Рим. Колизей

Слайд 8

Очень важно найти математические закономерности в прекрасном - «законы красоты». Попытки хотя бы приблизиться к ним предпринимались с древнейших времён: это и математические законы Пифагора в музыке, и геометрическая модель Вселенной Кеплера, это и система пропорций в скульптуре и архитектуре, и геометрические законы живописи. И сегодня энтузиазм исследователей не убывает. «Математика есть прообраз красоты мира». В.Гейзенберг Венера Милосская

Слайд 9

Поликлет КАНОН В скульптурах Поликлета с большой точностью выдержаны законы ряда золотого сечения 1,  ,  2,  3 ,  4 ,  5 ,  6 . Открытие золотой пропорции в строении человека, которое принадлежит Поликлету, можно считать вслед за открытием закона целочисленных отношений в музыке, вторым важнейшим событием в математической теории искусств. Искусство Древней Греции

Слайд 10

В пропорциях статуи воплощен закон золотого сечения. Поликлет Дорифор

Слайд 11

Каноны Древнего Египта Древнеегипетские художники применяли жёстко систему математических правил, которая на века определила стиль древнеегипетского искусства. Эта математика, ставшая каноном, на века сковала искусство Древнего Египта Вельможа Канефер с супругой и сыном Фрагмент статуи Аменхотепа VI Статуя царевича Рахотепа и его супруги Нофрет

Слайд 12

Легко отыскать примеры прекрасного, но как трудно объяснить, почему они прекрасны . Платон Успенский собор. Владимир. Лондон. Тауэрский мост Буддийский храм Удзи. Япония Кариатиды храма Эрехтейнов. Греция .

Слайд 13

Издревле в пропорции художники видели объективную основу красоты, по крайней мере формы прекрасного. Не все художники желали рассматривать искусство лишь как плод безудержной фантазии и чистой интуиции. И те из них, кто пытался постигнуть объективные законы прекрасного, находили их прежде всего в пропорции. Закон природы – закон красоты

Слайд 14

Золотые пропорции в частях тела человека Золотая пропорция естественным образом входит в пропорции человеческого тела, она пронизывает его от малых размеров до самых больших. Эти закономерности есть в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга и зрительного восприятия.

Слайд 15

Согласно канонам, человеческое тело не только симметрично, но и пропорционально. Леонардо открыл, что тело вписывается в круг и в квадрат. Дюрер занимался поисками единой меры, которая находилась бы в определенном соотношении с длиной туловища или ноги (такой мерой он считал длину руки до локтя). В современных школах живописи в качестве единой меры чаще всего принимается размер головы по вертикали. С известным допущением можно считать, что длина туловища превосходит размер головы в восемь раз. Так, большинство высоких людей отличаются удлиненным черепом и, наоборот, редко можно встретить низкорослого толстяка с головой удлиненной формы. Размеру головы пропорциональна не только длина туловища, но и размеры других частей тела. По этому принципу построены все люди. Однако наши пропорции согласуются лишь приблизительно, а потому люди лишь похожи, но не одинаковы. Во всяком случае, все мы симметричны! К тому же некоторые художники в своих произведениях особенно подчеркивают эту симметрию.

Слайд 16

В отличие от истины красота понятна человеку даже тогда, когда её внутренние закономерности остаются непознанными. Каждый ясно видит разницу между правильными и неправильными чертами человеческого лица, но до сих пор никто не может точно сформулировать закон, которому подчинена форма красивого лица . Струи бьющих фонтанов привлекают правильностью и красотою своих линий, хотя не каждый знает, что это параболы, и тем более не в состоянии написать их уравнения . Мирон Дискобол Артемида

Слайд 17

Аполлон Зевс Олимпийский Скульптура Древней Греции Артемида

Слайд 18

СИММЕТРИЯ В ЖИВОЙ ПРИРОДЕ Симметрией обладают объекты и явления живой природы. Симметрия не только радует глаз и вдохновляет поэтов всех времен и народов, но и позволяет живым организмам лучше приспособиться к среде обитания и просто выжить. В живой природе огромное большинство живых организмов обнаруживает различные виды симметрий

Слайд 19

Математик, так же как и художник или поэт, создает узоры, и если его узоры более устойчивы, то лишь потому, что они составлены из идей . Саврасов Грачи прилетели

Слайд 20

Не стоит наводить «математический » порядок в искусстве. Искусство живёт своей жизнью, оно соткано из диалектически противоположных начал – материального и духовного, рационального и иррационального, сконструированного и сотворённого, рассчитанного и угаданного. В первом случае искусство доступно точному математическому анализу, во второй не подвластно математике, да и не нужно разрушать эту волшебную часть искусства логикой. Врубель. Принцесса Греза

Слайд 21

Заключение: С проявлениями математических законов (на примере пропорции, симметрии) мы встречаемся в технике, искусстве, науке. Математические наблюдения проходят через всю многовековую историю человеческого творчества. Принципы пропорции, симметрии играют важную роль в искусстве: архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы, в свою очередь, также подчиняются законам математики. И этот факт еще раз подчеркивает гармоничность нашего мира

Слайд 22

Единство науки и искусства – важнейший залог последующего развития культуры

nsportal.ru

Исследовательский реферат по теме "Математика в архитектуре"

Исследовательский реферат по теме «Математика в архитектуре»

Цель исследовательского реферата: проанализировать проявление математики в архитектуре и выяснить, как она проявляется в постройках разных культур и в частности в зданиях города Боготола. Методы проведенных исследований: анализ и синтез, методы аналогии и моделирования. Основные результаты научного исследования: выявлено проявление математики в архитектуре разных культур, и в частности в постройках г. Боготола; доказано, что во всех древних постройках, сохранившихся до наших дней, обязательно имеется проявления различных пропорций.

Введение: В современном мире большинство архитектурных построек являются однотипными: они представляют собой здания в форме прямоугольного параллепипеда. Но встречаются и такие постройки, в которых применяются разнообразные геометрические формы, математические отношения и симметрия. При этом если мы посмотрим на памятники древней архитектуры, то обязательно увидим, что в них вся структура здания построена на основе сложных математических расчетов, которые, как мне кажется, придают им не только красоту, но и устойчивость, ведь не зря до нас доходят очень старые архитектурные шедевры древности, которые достаточно сильно сопротивляются вредным воздействиям окружающей среды. В современном обществе архитекторы уже начали понимать вышесказанное и ведутся разработки в данном направление. В моей работе будет затронута проблема, которая заключается в выявление того, как и в каких зданиях проявляются геометрические формы, математические отношения, симметрия. Стоит заметить, что данная проблема рассматривается исследователями уже сравнительно давно. К работам на данную тему можно отнести следующие издательства: А.В. Волошинов «Математика и искусство»; И.М. Шевелев, М.А. Марутаев, И.П. Шмелев «Золотое сечение»; Васютинский Н. А. «Золотая пропорция»; Бартенев И. А. «Конструкция и форма в архитектуре»; Смолина Н.И. « Традиции симметрии в архитектуре» и т.д. Моя же работа отличается от всех выше перечисленных тем, что в ней весь материал по данной теме собран и обобщен в один небольшой по размерам реферат. Кроме того, у меня рассматривается еще и проявление математики в архитектуре моего родного города Боготола.

Основное содержание: Для решения данной проблемы, я поставил перед собой следующую цель: проанализировать проявление математики в архитектуре и выяснить, как она проявляется в постройках разных культур и в частности в зданиях города Боготола. Чтобы достичь ее мне пришлось решить следующие задачи: 1) Просмотреть материал по данной теме; 2) Выбрать главное из него; 3) Обобщить все наработки по этому материалу; 4) Посмотреть, как математика проявляется в архитектуре г. Боготола 5) Написать работу и сделать выводы.

Разнообразие геометрических форм египетских пирамид: самыми известными представителями египетской архитектуры являются их пирамиды. В этих зданиях формы и размеры были выбраны не случайно. Каждая их деталь, каждый элемент формы выбирались тщательно и должны были продемонстрировать высокий уровень знаний создателей пирамид. Правильная четырехгранная пирамида является одной из хорошо изученных геометрических тел, символизирующих простоту и гармонию формы, олицетворяющую устойчивость, надежность, устремление вверх. Среди египетских пирамид самой большой является пирамида Хеопса. (Рис.2, Приложение 1)[2]

Разнообразие геометрических форм в Древнегреческом зодчестве: Великолепные памятники архитектуры оставили нам зодчие Древней Греции. И среди них первое место по праву принадлежит Парфеному (Рис.1, Приложение 1). Геометрия архитектуры храма очень не простая – в ней почти нет прямых линий, поэтому определение его размеров очень затруднено. Кроме того его поверхности не прямые, а слегка изогнутые. Зодчие Греции знали, что строго горизонтальные линии и плоскости наблюдателю издалека представляются изогнувшимися в середине. Чтобы компенсировать этот «оптический обман», они намеренно деформировали геометрические формы. Так, например, поверхность ступней Парфенома постепенно, незаметно для глаза, повышается от краев к середине. Колонны Парфенона тоже не строго вертикальные, а слегка наклонены внутрь здания, так что оси угловых колонн должны пересекаться на большой высоте. Кроме того, они не все одинаковой величины, несколько различаются и расстояния между ними. Угловые колонны сделаны более толстыми, чем остальные, но на светлом фоне они кажутся несколько тоньше. Колоны второго ряда - портики Парфенона - меньше, чем колонны внешнего, вследствие чего они кажутся стоящими глубже. Все эти отклонения от правильных геометрических форм и соотношений незаметны и представляются незначительными. Но именно они придают сооружению цельность, пластичность, предельную гармоничность и ни с чем несравнимую красоту. Колоны разделены вертикальными желобками, которые подчеркивают вертикальность, стройность колонн, а желобки увеличивают светоносность мрамора, «вводят пространство в объём колонн». Оказывается колонна Парфенона идеально равнопрочная. В каждом ее сечение напряжения обеспечивают одинаковый запас прочности. Наверху колонна тоньше, к низу расширяется ровно на столько, чтобы компенсировать увеличение нагрузки за счет веса колонны. Причем это утолщение происходит неравномерно – к середине высоты образуется как бы некоторая «припухлость», плавное утолщение. В результате этого при взгляде на колонны, кажется, что они словно пружинят под нагрузкой: зритель наглядно чувствует то напряжённое состояние, в котором находится колонна, «работающая на сжатие».[2]

Разнообразие геометрических форм в Старославянской архитектуре: Шедеврами архитектуры являются многие русские храмы, которые строились на протяжении многих веков. К таким произведениям можно отнести церковь Покрова на Нерли (Рис.3, Приложение 1), которая считается наиболее совершенным творением владимирских зодчих. Для храма Покрова характерно спокойное равновесие, основанное на симметрии и в то же время – удивительная легкость, устремленность ввысь. Создается впечатление невесомости храма, парящего над поймой реки. В основание композиции лежит крестовокупольная схема. Вертикальное членение храма преобладает над горизонтальным. Узкие окна подчеркивают устремленность храма ввысь. Строение завершено стройной, слегка приподнятой на прямоугольном постаменте главой со шлемовидным покрытием. Также к шедеврам русской архитектуры относится и собор Покрова в Казани (Рис. 4, Приложение 1). Для композиции построек собора характерно содержания большого количества различных геометрических «неправильностей». Так, центральный объем шара смещен на 3 метра к западу от геометрического центра всей композиции. Однако эта неточность делает композицию более живописной.[4]

Разнообразие геометрических форм в Европейской архитектуре: К шедеврам Европейской архитектуры, относительно их геометрических форм, можно отнести большинство современных зданий. Например, центральный офис корпорации «Херст» (Рис. 5, Приложение 2) в Нью-Йорке. Это здание состоит из стеклянных блоков, которые представляют собой правильные треугольники. А они, в свою очередь, составляют правильные шестиугольники. Другим представителем Европейской архитектуры является центральный офис «Свисс Ре» в Лондоне (Рис. 6 Приложение 2). Он состоит из ромбовидных стеклянных панелей разных оттенков, которые, в свою очередь, состоят из меньших по площади ромбов. Все ромбы образуют спирали. Следующим шедевром архитектуры Европы является центральная башня в Токио (Рис.7, Приложение 2). Это двадцатиэтажное здание, хорошо вписывающееся в архитектурную среду города, но при этом имеющее собственный характер. В структуре дома хорошо просматриваются, некоторые геометрические фигуры: трапеции, треугольники и прямоугольники. Это здание состоит из двух башен. Из-за того что здание построено из стекла, минимального количества бетона и железных перекрытий, в самое сердце попадает свет. Таким образом, создается контраст глухой поверхности стен и мягких лучей света, что очень любят японцы. Банк в Гонконге - это тоже шедевр архитектуры (Рис. 8, Приложение 2). В этом здании присутствует симметрия и равнобедренные треугольники. Центр Микроэлектроники (Рис 9, Приложение 3) это тоже шедевр Европейского зодчества. Он имеет цилиндрическую форму. Так же здание симметрично. И последним нами рассмотренным зданием является пожарная часть компании-производителя дизайнерской мебели Vitra (Рис. 10, Приложение 3). Это здание состоит из прямоугольных трапеций.[7]

Золотое сечение — деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине. Оно выражается в виде иррационального числа 1, 618033…, которое называют золотым числом.[3]

Золотое сечение в архитектуре древнего Египта: золотое сечение мы можем наблюдать в самой большой Египетской пирамиде - пирамиде Хеопса (Рис.11, Приложение 3). Отношение сторон в треугольнике OMN пирамиды равно: OM/ON = 1,618 = Ф, OM/MN = ON/OM = 1.272. Как видно, отношение длины апофемы боковой грани к половине стороны ее основания отвечает золотой пропорции. Два других отношения равны корню квадратному из золотой пропорции. Можно предполагать, что основным исходным элементом геометрии пирамиды Хеопса является треугольник в ее вертикальном сечение, в котором отношение катетов равно отношению гипотенузы к большему катету и равно 1,272, а отношение гипотенузы к малому катету равно золотой пропорции 1,618. Существует только один треугольник с таким отношением сторон, которое отвечает геометрической прогрессии. Если обозначить стороны такого треугольника буквами x, y, z, то получим следующее равенство: (z/x)2=1 + z/x, а так как отношение сторон z/x в этом треугольнике равно Ф, то есть золотой пропорции, то получим в итоге простую по-своему красивую зависимость Ф2=Ф+1. Есть основание утверждать, что египетские архитекторы заложили в форму пирамиды Хеопса именно этот замечательный треугольник, основанный на золотой пропорции.[2]

Золотые пропорции в Древнегреческом зодчестве: Золотые пропорции также лежат и основе древнегреческого храма Парфенома (Рис. 12, 13; Приложение 4).Фасад Парфенома вписан в прямоугольник со сторонами 1:2, а план образует прямоугольник со сторонами 1 и корень из 5. Известно, что диагональ прямоугольника 1:2 имеет размер корень из 5, следовательно, прямоугольник фасада и является исходным в построении геометрии Парфенона. Ширина Парфенона оценена в 100 греческие футов (3089 см), а размер высоты несколько варьируется у различных авторов. Так, по данным Н. И. Бруно, высота Парфенона 61.8, высота трех ступеней основания и колонны 38.2, высота перекрытия и фронтона 23.6 футов. Указанные размеры образуют ряд золотой пропорции: 100:61.8 = 61.8:38.2 = 38.2:23.6 = Ф. Многие исследователи, стремившиеся раскрыть секрет гармонии Парфенона, искали и находили в соотношении его частей золотую пропорцию. В работе В. Смоляка, посвященной изучению пропорций Парфенома, установлен закономерный ряд золотых пропорций. Приняв за единицу ширину торцового фасада храма, Б. Смоляков поучил прогрессию состоящую из 8 членов ряда: 1:ф:ф2:ф3:ф4:ф5:ф6:ф7, где ф=0,618. Указанным членам ряда отвечают основные пропорции фасада Парфенона, приведенные Н. И. Бруно. Приведенная Б. Смоляком схема пропорций Парфенона подкупает своей простотой, цельностью, связью с золотой пропорцией. Но не менее интересен и подход И. Шевелева, который увидел реализацию в Парфеноне двух эталонов длинны 1 и корень из 5. Пропорции 1 и корень из 5 отвечают прямоугольнику со сторонами 1:2 и являются основным соотношением частей Парфенона. Следует отметить, что в пропорциях храма, указанных И. Шевелевым, также содержится золотая пропорция, например, в соотношение высоты фасада со ступенями (1557,4 см) и высоты колон (957,4 см): 1557,4/957,4=1,627. Не следует забывать, что величина корень из 5 лежит в основе золотой пропорции, является его сердцевиной, следовательно, связь пропорции ф и корень из 5 вполне естественна.[2]

Золотое сечение в Старославянской архитектуре: Расчет размеров Успенской Елецкой церкви в Чернигове (Рис. 14, 15; Приложение 4) позволил выявить, что композиционный замысел целиком связан с золотым сечением. Длина храма относится к ширине, также как и ширина храма к длине ядра, в отношении золотого сечения. В данной пропорции находятся и многие другие конструктивные размеры элементов и частей церкви (Рис. 16, Приложение 5). [1]Знаменитый русский архитектор М.Ф.Казаков тоже широко использовал в своем творчестве золотое сечение. Например, его можно встретить в архитектуре здания бывшего сената в Кремле, Дворца в Петровском Алабине и Голицынской больницы в Москве, которая в настоящее время называется Первой Клинической больницей имени Н.И.Пирогова. Еще один архитектурный шедевр Москвы - дом Пашкова (Рис. 17, Приложение 5) - является одним из наиболее совершенных произведений архитектора В. Баженова. О своем любимом искусстве он говорил: "Архитектура - главнейшие имеет три предмета: красоту, спокойствие и прочность здания. К достижению сего служит руководством знание пропорции, перспективы, механики или вообще физики, а всем им общим вождем является рассудок".[6] Интересна история реконструкции Великой Печорской церкви. Построенная в 1073 году, эта церковь была разрушена фашистами в годы войны. Однако, используя сохранившееся свидетельство и сопоставляя основные размеры Печерской церкви с Елецкой церковью в Чернигове, все древние части которой сохранились, удалось осуществить реконструкцию объёмов Печерской церкви. Установлено, что основой пропорционального строя Печерской церкви является отношение 2/√5, которое хорошо видно на фасаде и разрезе реконструкции размерной структуры церкви (Рис. 18, приложение 6). Отношение 2/√5 также можно выразить через золотую пропорцию, что свидетельствует о её связи с основными размерами церкви. Храм Василия Блаженного в Москве - это еще один пример, показывающий, насколько органично золотое сечение входит в архитектурные пропорции (Рис. 19, приложение 7) За «целое» а=1 принята высота храма. Пропорции храма определяются восемью членами ряда золотого сечения:1, ф, ф2 ,ф3 ,ф4 ,ф5 ,ф6 ,ф7. Многие из членов ряда неоднократно повторяются в пропорциях этого затейливого архитектурного сооружения, но всегда благодаря свойству золотого сечения, части сойдутся в целое, т.е. ф +ф2=1,ф2+ф3=ф и т.д. Таким образом, свойство золотого сечения делает эту геометрическую пропорцию единственной и неповторимой. В селе Коломенском, на крутом берегу Москвы – реки, в 1532 году, было завершено строительство церкви, поставленной в памяти об рождение здесь Ивана Грозного. Зодчие будто предвидели рождение небывало грозного царя: церковь тоже была небывалой. В ней все: и высота (почти 62 м), и каменный шатер, и устремленная ввысь форма – была невиданными. Новый храм словно символизировал прорыв России в свободное от татарского ига будущее. Весь пропорциональный строй церкви, все ее безудержное стремление ввысь как нельзя более соответствовали названию – храм Вознесения (Рис 20, Приложение 7). Но для нас храм Вознесения интересен еще и тем, что он является не только гимном расправляющей крылья России, но и архитектурным гимном геометрии. Ни один из рассмотренных архитектурных шедевров, в том числе и Парфенон, не пронизан настолько геометрией, как храм Вознесения в селе Коломенском. Соразмерность храма с предельной ясностью определены двумя парными мерами: горизонтальной – малой саженью Ст и косой новгородской саженью Ки (Ст :Ки=1: корень из 2), вертикальные – малой саженью Ст и мерной саженью См, дающее золотое сечение.[2]

Зеркальная симметрия: Простейший вид симметрии - зеркальная симметрия, симметрия левого и правого. В этом случае одна половина формы является как бы зеркальным отражением другой. Воображаемая плоскость, делящая форму на две равные части, называется плоскостью симметрии. Плоскость симметрии в произведениях архитектуры, как правило, вертикальна, так же как вертикальна плоскость симметрии тела человека. В горизонтальной проекции строго дисциплинируется расположение частей здания и его деталей, по вертикали развивается свободное и разнообразное чередование элементов и их частей. На ортогональных чертежах - фасаде, плане, разрезе - плоскость симметрии изображается линией - ее часто называют осью симметрии. Однако собственно центрально-осевая симметрия - это симметрия относительно вертикальной оси, линии пересечения двух (или большего числа) вертикальных плоскостей симметрии. Сооружение при этом состоит из равных частей, которые могут совмещаться при повороте вокруг оси симметрии. Зеркальной симметрии подчинены постройки Древнего Египта и храмы античной Греции, амфитеатры, термы, базилики и триумфальные арки римлян, дворцы и церкви Ренессанса, равно как и многочисленные сооружения современной архитектуры. Симметрия объединяет композицию. Расположение главного элемента на оси подчеркивает его значимость, усиливая соподчиненность частей. Каждая деталь в симметричной системе существует как двойник своей обязательной паре, расположенной по другую сторону оси, и благодаря этому она может рассматриваться лишь как часть целого. Значение общего здесь снижает действенность отдельных элементов. Главной оси, объединяющей всю композицию, могут сопутствовать подчиненные оси, определяющие симметрию частей. Характерный пример много осевой симметрии - здание Главного адмиралтейства в Санкт-Петербурге (Рис. 21,Приложение 8). Башня и арка главного въезда здесь отвечают оси всей композиции; оси второго порядка, объединяющие крылья, выделены большими портиками; осям крыльев подчинены оси малых портиков. Симметричны и части, связывающие крылья с центром, и ризалиты крыльев. Своей вертикальной оси подчинена, и форма наименьшей самостоятельной части композиции - фрагмента стены, включающего оконные проемы трех этажей. Равные элементы здесь или сливаются в единство ряда, или подчинены господству главного элемента. Благодаря этому равенство частей ни в чем не нарушает целостности. Заметим, что на осях симметрии располагаются именно проемы, а не колонны или простенки (т.е. количество колонн в портиках является четным, а количество проемов - нечетным). В противном случае входы пришлось бы расположить по сторонам простенка, занимающего ось симметрии; возникла бы «двойственность» системы, ослабляющая единство целого. Стремление избежать этого определяет неизменность четного числа опор в колоннадах и портиках классической архитектуры. Нечетное число их делали только там, где хотели ослабить центральный акцент, создаваемый симметрией, например, в боковых колоннадах Пропилеи, обрамляющих проход на Акрополь (Рис. 22, приложение 8) в Афинах. Подчеркнутый центр этих колоннад нарушал бы плавкость непрерывного движения, которое они должны были обрамлять. Центрально-осевая симметрия реже использовалась в истории архитектуры. Ей подчинены античные круглые храмы и построенные в подражание им парковые павильоны классицизма. Темпьетто во дворе церкви Сан-Пьетро в Риме (Рис. 23, Приложение 8) отвечает законам центрально-осевой симметрии. Центрально-осевая симметрия определяет также форму некоторых архитектурных деталей - например, колонн и их капителей. Необычно использовал законы симметрии смог Мельников в конкурсном проекте Дворца Советов в Москве (Рис. 24, Приложение 9). Форма его плана - круг. Равные части симметричного чашеобразного объема рассечены по диаметру вертикальной плоскостью и повернуты в этой плоскости на 180° по отношению одна к другой. Подобными экспериментами К. Мельников опроверг представление о симметрии как элементарной закономерности, возможности которой общеизвестны. К редко используемым зодчеством видам симметрии относится и винтообразная. Она издавна применялась для элементов здания - винтовых лестниц и пандусов, витых стволов колонн. Попытку использовать ее для организации крупной части здания сделал американский архитектор Ф.Л. Райт. Экспозиционный корпус построенного по его проекту музея Гуггенхайма (Рис.25, Приложение 9) сформирован несколькими витками железобетонной пологой спирали, образующей своеобразную галерею - пандус. Винтообразная симметрия использована при создании освещения залов Государственной Думы.[8]

Диссимметрия: Абсолютная симметрия в крупных и сложных сооружениях, строго говоря, невозможна. Сложность функциональных систем вызывает частичные отклонения от основной, определяющей характер композиции симметричной схемы. Нарушенную, частично расстроенную симметрию мы называем диссимметрией. Обычно отклонения от точной симметрии в архитектуре вызываются практической необходимостью, тем, что многообразие функций не укладывается в пределы жестких закономерностей симметрии. Иногда такие отклонения дают основу острого эмоционального эффекта. Уничтожение даже мелкой детали в симметричной композиции немедленно нарушает равновесие и порождает напряжение во всей системе. Любое отклонение становится привлекающим внимание и беспокоящим акцентом. Такое воздействие нарушенной симметрии может быть использовано как художественное средство. Размещение восьмигранной часовни в одном из углов здания сломало строгую симметричность дворца Карла V в Гранаде (Рис.26,Приложение 9), одного из первых сооружений архитектуры Возрождения в Испании. Рассудочная холодность композиции преодолена этой «вольностью». Диссимметрию в композицию Санта-Мария-дель-Фьоре (Рис.27 ,Приложение 10) во Флоренции внесла колокольня. Свободное расположение деталей в пределах симметричной схемы обычно для русского народного зодчества и придает особенную привлекательность и индивидуальность его произведениям. Частично нарушенная симметрия, отвечающая сложности жизненных процессов и в то же время служащая художественным средством выражения этой сложности, часто встречается и в современной зарубежной архитектуре. Равенство частей, лежащих по сторонам плоскости симметрии, заменяется подобием их общих очертаний.[8]

Асимметрия: С точки зрения математических понятий асимметрия - лишь отсутствие симметрии. Однако обширная категория приемов композиции отнюдь не покрывается этим негативным определением. В архитектуре - симметрия и асимметрия - два противоположных метода закономерной организации пространственной формы. Подчиненная собственным внутренним законам, асимметрия отнюдь не исчерпывается разрушением симметрии. Единство является целью построения асимметричной системы так же, как и симметричной, однако достигается оно иным путем. Тождество частей и их расположения заменяется зрительным равновесием. Асимметричные композиции в процессе развития архитектуры возникли как воплощение сложных сочетаний жизненных процессов и условий окружающей среды. Конкретные формы таких композиций вырастают как результат неповторимого сочетания факторов. Асимметрия поэтому индивидуальна, в то время как в самом принципе симметрии заложена общность, признак, связывающий все сооружения, имеющие симметрию данного типа. Соподчиненность частей - основное средство объединения асимметричной композиции. Соподчинение проявляется не только в соотношении размеров, расстановке силуэтных и пластических акцентов, но в направленности системы пространств и объемов к главным частям здания или ансамбля, расположение которых не совпадает с геометрическим центром. Асимметричная композиция может складываться из симметричных частей, связи между которыми не подчиняются закономерностям симметрии. Эрехтейон (Рис.28 ,Приложение 10) на Акрополе в Афинах относятся к числу наиболее гармоничных зданий с асимметричной композицией. Особенности его объемно-пространственного построения были вызваны и сложностью назначения - храм посвящен сразу двум божествам - Афине н Посейдону, и необходимостью поставить сооружение на точно определенном месте со сложным рельефом. Основной объем здания вытянут с востока на запад и завершен с восточной стороны шестиколонным портиком. К этому объему по сторонам западного фасада примыкают обращенный на юг портик Кариатида - вертикальная опора, которой придана форма женской фигуры, и глубокий четырехколонный портик, обращенный к северу, вместе формирующие ось, перпендикулярную оси симметрии главного объема. Соотношения сливающихся, взаимосвязанных пространств и объемов, формирующих эти пространства, определяют композицию системы площадей исторического центра Санкт-Петербурга. Асимметрия и здесь возникает из сочетания симметричных частей. Среднее звено этого гигантского ансамбля - Адмиралтейская площадь. Оси Дворцовой и Сенатской площадей, образующих крайние звенья системы, направлены к Неве, перпендикулярно оси связующей части. Главенство Дворцовой площади выявляется сложной формой ее пространства, часть которого обрамляет дугообразное в плане здание Главного штаба. Кульминационная точка ансамбля, пересечение главных его осей, закреплена вертикалью Александровской колонны. Осевые направления, которым подчинены пространства, закреплены ориентирами, намеченными в объемных формах. Ось, параллельную Неве, отмечают Александровская колонна и портик Конногвардейского манежа; ось Дворцовой площади закреплена аркой Главного штаба, колонной и центральным ризалитом Зимнего дворца; ось Сенатской площади, широко открытой к Неве, находит опору в мощном объеме Исаакиевского собора. Эти оси имеют значение главных линий ориентации, диктующих направление движения. Ось не является обязательным признаком симметрии или следствием симметричности построения. Оси - направления, соединяющие главные элементы композиции, - могут быть не только воображаемыми линиями, но и линиями движения. В плане исторического центра Санкт-Петербурга основными осями, имеющими значение линий ориентации, линий зрения и основных функциональных направлений, являются три магистрали, сходящиеся к башне Адмиралтейства. Они служили основой формирования обширной городской структуры, однако не предопределили ее полной симметричности. Ось, подчиняющая себе пространственную структуру, может быть и непрямолинейной. Такова ось композиции Акрополя в Афинах, имевшая два перелома - при выходе из Пропилеи и в геометрическом центре ансамбля. Ось, диктующая направление движения, должна иметь достаточно сильное зрительное завершение - как это сделано в композиции центра Санкт-Петербурга. Заметим, что мощность завершений определяется здесь не физической протяженностью осей, а их смысловой значимостью. Особенно решительно подчеркнута ось Дворцовой площади.[8]

Боготольский вокзал (Рис.29 ,Приложение 11) относится к тем зданиям, в основу которых положено такое математическое явление, как симметрия. Если провести вертикальную ось посередине здания, то мы можем заметить, что обе половины полностью идентичны.

Часовня Татьяны Мученицы (Рис. 30,Приложение 11). В основе этой часовни также лежит горизонтальная симметрия. Кроме того нашему вниманию бросаются в глаза чрезвычайно обычные геометрические формы. В основание этой часовни лежит прямоугольник. Основная часть часовни состоит из куба. Кроме того основная часть этой часовни построена на основе «золотого сечения»: высоту сруба с фундаментом будем считать за «X», а высоту крыши без креста за «Y». Отношение X к Y= отношению X+Y к X и примерно равно 1.6.

Церковь Николая Чудотворца (Рис. 31,Приложение 12). В этом здание проявляется вертикальная симметрия. Кроме того если мы рассмотрим высоты данного здания, то мы можем заметить, что в основу данного здания положено «золотое сечение». Отношение N к M примерно равно отношению M +N к N и примерно равно 1.6, то есть золотому числу.

Дом культуры железнодорожников: (Рис32 ,Приложение 12). На первый взгляд фасад этого здание симметричен. Но, обратив внимание на статуи, находящиеся в верхней части композиции, можно заметить, что они не идентичны, а, следовательно, этот шедевр архитектуры ассиметричен.

Заключение: в заключение мне бы хотелось сказать, что архитектура и математика взаимосвязаны между собой. Нельзя представить не одного здания, в котором не применялись бы геометрические формы, пропорции, различные виды симметрии. Архитектура без математики невозможна. Кроме того стоит заметить, что не одно великое сооружение древних времен, сохранившееся до наших дней, не обходится без применение различных пропорций, таких как «золотое сечение», которые предают сооружениям не только красоту, но и устойчивость, и прочность. Выше сказанное можно подтвердить следующим: все исторически дошедшие до нас шедевры древнего зодчества, достаточно сильно сопротивляются отрицательным воздействиям окружающей среды.

Список используемой литературы:

1) А. В. Волошинов «Математика и искусство»

2) Н. Васютинский «Золотая пропорция»

3) Интернет энциклопедия Википедия

4) Застывшая музыка русских храмов http://vptk.narod.ru/seminar6/musika.html

5) геометрия в архитектуре древнерусского зодчества http://t2012.ru/blog/geometrija_v_arkhitekture_drevnerusskogo_zodchestva/2010-05-26-3323

6) Золотое сечение http://pages.marsu.ru/iac/resurs/gorelysheva/8.html

7) Геометрия в современной архитектуре http://lib.znate.ru/docs/index-231089.html

8) Симметрия в архитектуре http://otherreferats.allbest.ru/construction/00098382_0.html

Приложение 1

Рисунок 2 Пирамида Хеопса

Рисунок 1 Парфенон

Рисунок 4 Собор Покрова в Казани

Рисунок 3 Церковь Покрова на Нерли

Приложение 2

Рисунок 5 Центральный офис корпорации "Херст"

Рисунок 6 Центральный офис "Свисс Ре"

Рисунок 8 Банк в Гонконге

Рисунок 7 Центральная башня в Токио

Приложение 3

Рисунок 10 Пожарная часть

Рисунок 9 Центр Микроэлектроники

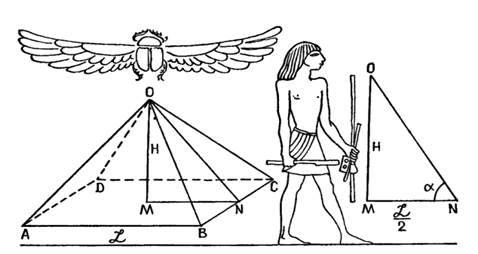
Рисунок 11 Отношения в пирамиде Хеопса

Приложение 4

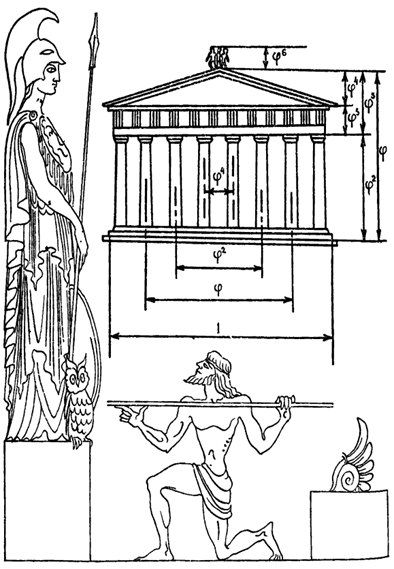
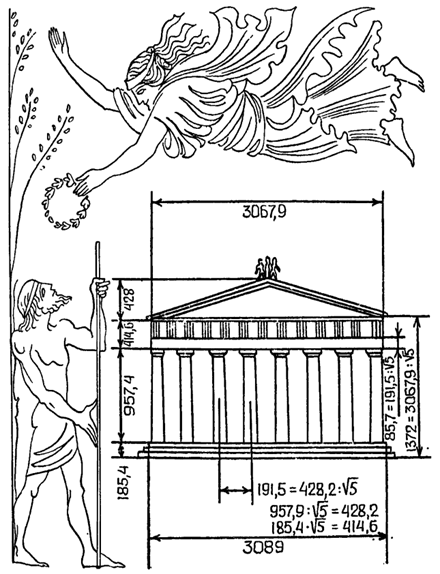
Рисунок 12 Отношение в Парфеноне Рисунок 13 Размеры Парфенона

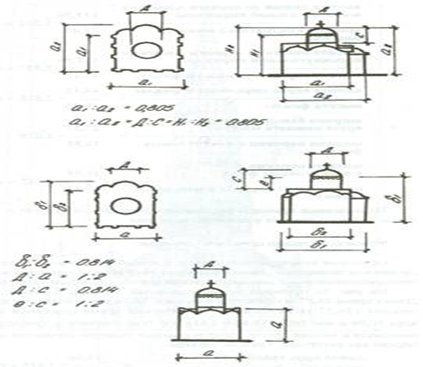
Рисунок 14 Проявление отношений в Елецкой церкви Рисунок 15 Елецкая церковь (внешне)

Приложение 5

Рисунок 16 Пропорции в размерах Елецкой церкви

Рисунок 17 Дом Пашкова

Рисунок 18 Размеры и отношения их в Печорской церкви

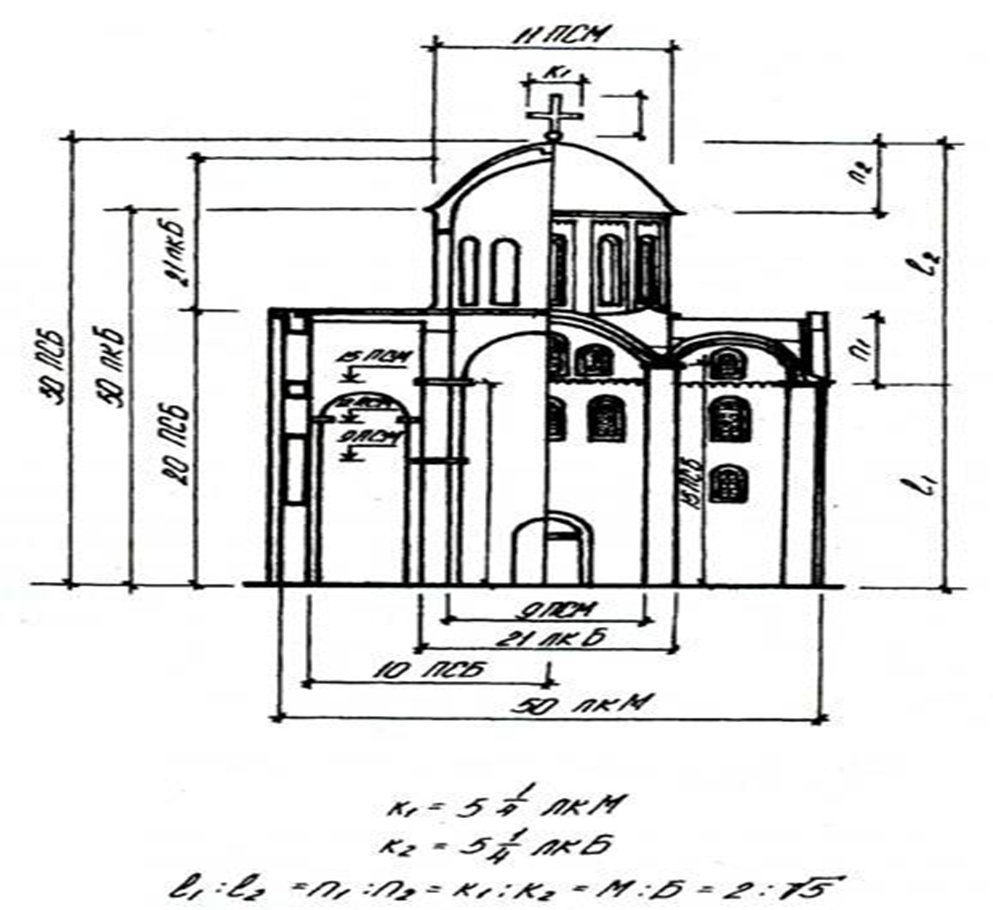
Рисунок 19 храм Василия Блаженного

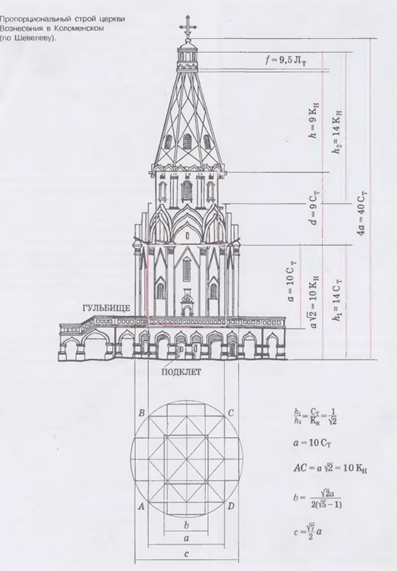
Рисунок 20 Храм Вознесения

Приложение 8

Рисунок 21 здание Главного Адмиралтейства в Санкт-Петербурге

Рисунок 22 Акрополь Рисунок 23 Темпьетто во дворе церкви Сан-Пьетро

Приложение 9

Рисунок 24 проект Дворца Советов Рисунок 25 музея Гуггенхайма

Рисунок 26 дворец Карла V в Гранаде

Приложение 10

Рисунок 27 Санта-Мария-дель-Фьоре

Рисунок 28 Эрехтейон

Приложение 11

Рисунок 29 Боготольский вокзал

Рисунок 30 Часовня Татьяны мученицы

Приложение 12

Рисунок 31 Церковь Николая Чудотворца

Рисунок 32 Дом культуры железнодорожников

infourok.ru

Презентация "Математика и искусство. Метапредметные связи"

Метапредметные связи решают проблему разобщенности, расколотости, оторванности  друг  от  друга  разных дисциплин и, как следствие, учебных предметов, и приводят к целостному образному восприятию мира

Существование различных видов искусств вызвано тем, что ни одно из них своими собственными средствами не может дать художественную всеобъемлющую картину мира. Такую картину может создать только вся художественная культура человечества в целом, состоящая из отдельных видов искусств.

СЛАЙД3ВЕЛИКИЕ СФЕРЫ ЧЕЛОВЕЧЕСКОЙ ДЕЯТЕЛЬНОСТИ

Искусство, наука, красота…  эти великие сферы человеческой деятельности, внешне столь разные и далекие друг от друга, тесно переплетены между собой незримыми узами! И разорвать эти узы нельзя, не повредив и тому, и другому.

Красота является самым крепким связующим звеном между наукой и искусством!

   СЛАЙД4 Красота скульптуры,  храма,  картины, симфонии, поэмы... Что между ними общего? Разве можно сравнивать красоту храма с красотой музыки? Оказывается можно, если будут найдены единые критерии прекрасного, если будут открыты общие формулы красоты, объединяющие понятие прекрасного самых различных объектов - от цветка ромашки до красоты обнаженного человеческого тела.

      Существуют ли объективные законы  прекрасного?

•      Нельзя отрицать заглавную роль симметрии в природе, которая обязана своим существованием вечному закону природы - закону тяготения.

•       В основе основ музыки и архитектуры - гамме и пропорции – лежит математика, в частности ряд золотого сечения и модулор (система пропорций)  Ле Корбюзье.

•       В изобразительном искусстве используется общая теория перспективы.

СЛАЙД5         «Симметрия, как бы широко или узко мы не понимали это слово, - есть идея, с помощью которой человек пытался объяснить и создать порядок, красоту и совершенство»

                                                                                    Герман Вейль

•      К фундаментальным понятиям симметрии относятся плоскость симметрии, ось симметрии, центр симметрии. Плоскостью симметрии называется такая плоскость, которая делит фигуру на две зеркально равные части, расположенные друг относительно друга так, как предмет и его зеркальное отражение.

•      Принцип "симметрии" широко используется в искусстве. Бордюры в архитектурных и скульптурных произведениях, орнаменты в прикладном искусстве, - все это примеры использования симметрии.

•      Принцип симметрии очень часто используется совместно с принципом "золотого сечения". Таким примером может служить картина Рафаэля "Обручение Марии"

СЛАЙД6 Геометрия орнаментов, бордюров, паркетов.

     Орнаментальное искусство одно из самых древних. С орнаментами мы встречаемся повсюду: в декоративно-прикладном искусстве, в росписях архитектурных сооружений, в чугунных решётках, окаймляющих сады, парки, дворцы.  Орнамент – это узор, состоящий из повторяющихся, ритмически упорядоченных элементов.  Орнамент,  как правило, подчёркивает своим построением и формой архитектурные и конструктивные особенности предмета, природную красоту материала. В построении орнамента используют главным образом принцип симметрии.

СЛАЙД7 Симметрия в архитектуре.

Театральная площадь,БольшойтеатрО.Бове, А.Михайлов1821-1853

Триумфальная аркаЖ.Ф.Т.Шальгрен1806-1836Франция, Париж

СЛАЙД8     Симметрия и асимметрия - это две формы проявления одной и той же закономерности - закономерности двойственности.

Симметрия воспринимается нами как покой, скованность, закономерность, тогда как асимметрия означает движение, свободу, случайность.

Это композиция из 10 храмов, каждый из которых обладает центральной симметрией, в целом асимметрична. Симметричные архитектурные детали собора как бы кружатся в асимметричном беспорядочном танце вокруг центрального шатра.

СЛАЙД9 ЗОЛОТОЕ СЕЧЕНИЕ

- (золотая пропорция, деление в крайнем и среднем отношении) — деление непрерывной величины на две части в таком отношении, при котором, меньшая часть так относится к большей, как большая ко всей величине.

Отношение большей части к меньшей в этой пропорции выражается квадратичной иррациональностью

φ=( √5+1)/2≈1,6180339887…

и, наоборот, отношение меньшей части к большей 

1/ φ = =( √5-1)/2≈0,6180339887…

СЛАЙД10   Золотое сечение в искусстве

«Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением и если первое можно сравнить с мерой золота, то второе – с драгоценным камнем

               Иоганн Кеплер    

§       Известно, что Сергей Эйзенштейн искусственно построил фильм «Броненосец Потёмкин» по правилам золотого сечения. Он разбил ленту на пять частей. В первых трёх действие развивается на корабле. В двух последних — в Одессе, где разворачивается восстание. Этот переход в город происходит точно в точке золотого сечения.В каждой части есть свой перелом, происходящий по закону золотого сечения. В кадре, сцене, эпизоде происходит некий скачок в развитии темы: сюжета, настроения.

§  Эйзенштейн считал, что, так как такой переход близок к точке золотого сечения, он воспринимается как наиболее закономерный и естественный.

СЛАЙД11   Математика и музыка.

Изучая высоту звука с помощью монохорда – простейшего инструмента Древних греков,  Пифагор обнаружил поразительные вещи. Выяснилось, что приятные слуху созвучия – консонансы получаются лишь в том случае, когда длины струн, издающих эти звуки, соотносятся как целые числа первой четвёрки, т.е. 1:2, 2:3, 3:4;

звук и созвучия могут быть представлены простыми числами

       Великий немецкий композитор XVII века Иоганн Себастьян Бах писал церковную музыку.  Позднее уже после его смерти музыканты-исследователи выяснили, что многие мелодии композитора имеют цифровые коды - символы, а произведения точно математически просчитаны.

   Французский композитор и музыкальный теоретик Жан Филипп Рамо в своём «Трактате о гармонии», написанном в 1722 году, говорил о том, что «музыка подчинена арифметике», уделял много внимания физико-математическим исследованиям.

   СЛАЙД12   Игорь Стравинский, хорошо знавший музыку мастеров эпохи Ренессанса, также находил много общего между математикой и музыкой. «Способ композиторского мышления – способ, которым я мыслю, - мне кажется, не очень отличается от математического», «музыкальная форма математична хотя бы потому, что она идеальна» - эти высказывания Стравинского ярко выражают его убеждения

СЛАЙД13   Они сделали много в науке

                  "Математик, который не есть отчасти поэт, 

     не будет никогда подлинным  математиком"

                       К. Вейерштрасс

    Поэтами были многие восточные ученые-энциклопедисты средневековья. Достаточно упомянуть лишь таких крупных мусульманских ученых, как Ибн Сина (Авиценна) (X-XI в.), аль-Хайям (XI в.), аль-Беруни (XII в.), Ибн аль-Ясмин (XII в.), Ибн аль-Хаим (XV в.) и Ибн Гази (XV в.). Они сделали много в науке вообще и в математике особенно.

СЛАЙД14    Математика и литература

    Некоторые ошибочно думают - говорила великий русский математик-женщина С. Ковалевская, что математика - это сухая наука. Они смешивают математику с арифметикой, в которой проводятся вычисления, порой трудные и скучные, с числами. Но для того чтобы быть настоящим математиком, добавила С.Ковалевская, нужно быть поэтом в душе.

Александр Блок. Поэма «Двенадцать»

  Число 12 олицетворяет, в первую очередь, время: 12 часов (ноль часов) - начало новой эпохи, когда из бури и хаоса возникает новый мир. Так же 12 - это число солдат революции, и, невольно напрашивается ассоциация с двенадцатью апостолами новой, еще непонятной веры. Раскрытию авторской идеи способствует и структура поэмы. Она состоит из 12 глав, а число строк в поэме кратно 12...

СЛАЙД15 Лев Толстой и Льюис Кэрролл

Льюис Кэрролл (настоящее имя – Чарлз Латуидж Доджсон).

    Научные работы Кэрролла предвосхитили некоторые идеи математической логики. Но больше он известен как автор популярных повестей для детей. Так  в 1865 году он издал сказку «Алиса в стране чудес». Королева Англии, прочитав книгу, пришла в восторг от сказки и приказала срочно приобрести остальные сочинения Кэрролла. И очень удивилась, когда выяснилось, что все остальные произведения Кэрролла - сочинения по высшей математике, сравнительной анатомии, палеонтологии и систематике животных.

    Никто не замечал, что в самом  заглавии романа – «Война и мир» - закодирован закон золотого сечения. В самом деле, название романа построено на  первых четырех членах ряда Фибоначчи 1, 2, 3, 5.Один союз, два существительных, три слова. Пять букв в первом ключевом. Отношение ключевых слов 5:3=1,666… есть первое рациональное приближение коэффициента золотого сечения.  

СЛАЙД16  Математика и живопись

«И, поистине, живопись – это наука и законная дочь природы, ибо она порождена природой…»

                          Леонардо да Винчи

    Переходя к примерам “золотого сечения” в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: “Пусть никто, не будучи математиком, не дерзнет читать мои труды”.Он снискал славу непревзойденного художника, великого ученого, гения, предвосхитившего многие изобретения, которые не были осуществлены вплоть до XX в.

•      Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника. Вся

•      фигура и картина в целом опутана здесь двумя золотыми треугольниками и сетью больших, средних и малых

•      золотых прямоугольников, ориентированных по ширине или высоте полотна.

  СЛАЙД17   Геометрический фрактал

                Наука и искусство, словно нити холста, переплетались в полотнах мастеров Возрождения. Живопись переходила в начертательную геометрию, а геометрия – в искусство.

    Люди придумали цифры и действия с ними, а потом в них же открыли множество законов, правил и теорем. Кроме того, оказалось, что в жизни цифр, линий, углов и бесконечно малых величин можно увидеть много красивого – изящные теоремы, тела, поверхности, даже условия задач.  Числа живут своей жизнью, и мы, соприкоснувшись с ней, удивляемся, а иногда и любуемся ею. Компьютер дает нам возможность видеть на экране те или иные процессы, которые мы программируем.

   Фракталы получают с помощью некоторой ломаной. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется по некоторому правилу на некоторую ломаную в соответствующем масштабе. В результате бесконечного повторения этой процедуры, получается геометрический фрактал.

 СЛАЙД18  Заключение

Примеры взаимопроникновения математики в различные сферы искусства и наоборот можно приводить бесконечно…И чем дальше этим занимаешься, тем  увлекательнее становится такая работа. Но даже приведенных примеров, я думаю, достаточно для того, чтобы согласиться со словами Бертрана Рассела:

                      «Математика владеет не   только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусств

Спасибо за внимание!

infourok.ru

Смотрите также

• 
  Кроль на спине реферат
• 
  Чесотка и педикулез реферат
• 
  Реферат кроль на спине
• 
  Реферат на тему linux
• 
  Язычество древней руси реферат
• 
  Цивилизация древнего китая реферат
• 
  Реферат источники научной информации
• 
  Вторая чеченская война реферат
• 
  История открытия вирусов реферат
• 
  Жизненный цикл товара реферат
• 
  Реферат татаро монгольское иго