Главная » Реферат » Коды хемминга реферат

Код Хэмминга. Коды хемминга реферат


Реферат Код Хемминга

скачать

Реферат на тему:

Question book-4.svg

План:

Введение

Question book-4.svg В этой статье не хватает информации.

Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена.Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники.

Коды Хэмминга — наиболее известные и, вероятно, первые из самоконтролирующихся и самокорректирующихся кодов. Построены они применительно к двоичной системе счисления.

1. История

В середине 1940-х годов Ричард Хэмминг работал в знаменитых Лабораториях Белла на счётной машине Bell Model V. Это была электромеханическая машина, использующая релейные блоки, скорость которых была очень низка: один оборот за несколько секунд. Данные вводились в машину с помощью перфокарт, и поэтому в процессе чтения часто происходили ошибки. В рабочие дни использовались специальные коды, чтобы обнаруживать и исправлять найденные ошибки, при этом оператор узнавал об ошибке по свечению лампочек, исправлял и запускал машину. В выходные дни, когда не было операторов, при возникновении ошибки машина автоматически выходила из программы и запускала другую.

Хэмминг часто работал в выходные дни, и все больше и больше раздражался, потому что часто был должен перезагружать свою программу из-за ненадежности перфокарт. На протяжении нескольких лет он проводил много времени над построением эффективных алгоритмов исправления ошибок. В 1950 году он опубликовал способ, который на сегодняшний день известен как код Хэмминга.

2. Систематические коды

Систематические коды образуют большую группу среди блочных, разделимых кодов (в которых все символы можно разделить на проверочные и информационные). Особенностью систематических кодов является то, что проверочные символы образуются в результате линейных операций над информационными символами. Кроме того, любая разрешенная кодовая комбинация может быть получена в результате линейных операций над набором линейно независимых кодовых комбинаций.

3. Самоконтролирующиеся коды

Коды Хэмминга являются самоконтролирующимися кодами, то есть кодами, позволяющими автоматически обнаруживать ошибки при передаче данных. Для их построения достаточно приписать к каждому слову один добавочный (контрольный) двоичный разряд и выбрать цифру этого разряда так, чтобы общее количество единиц в изображении любого числа было, например, четным. Одиночная ошибка в каком-либо разряде передаваемого слова (в том числе, может быть, и в контрольном разряде) изменит четность общего количества единиц. Счетчики по модулю 2, подсчитывающие количество единиц, которые содержатся среди двоичных цифр числа, могут давать сигнал о наличии ошибок.

При этом невозможно узнать, в каком именно разряде произошла ошибка, и, следовательно, нет возможности исправить её. Остаются незамеченными также ошибки, возникающие одновременно в двух, в четырёх или вообще в четном количестве разрядов. Впрочем, двойные, а тем более четырёхкратные ошибки полагаются маловероятными.

4. Самокорректирующиеся коды

Коды, в которых возможно автоматическое исправление ошибок, называются самокорректирующимися. Для построения самокорректирующегося кода, рассчитанного на исправление одиночных ошибок, одного контрольного разряда недостаточно. Как видно из дальнейшего, количество контрольных разрядов k должно быть выбрано так, чтобы удовлетворялось неравенство 2^k \geq k+m+1или k \geq \log_2(k+m+1), где m — количество основных двоичных разрядов кодового слова. Минимальные значения k при заданных значениях m, найденные в соответствии с этим неравенством, приведены в таблице.

Диапазон m kmin
1 2
2-4 3
5-11 4
12-26 5
27-57 6

В настоящее время наибольший интерес представляют двоичные блочные корректирующие коды. При использовании таких кодов информация передаётся в виде блоков одинаковой длины и каждый блок кодируется и декодируется независимо друг от друга. Почти во всех блочных кодах символы можно разделить на информационные и проверочные. Таким образом, все комбинации кодов разделяются на разрешенные (для которых соотношение информационных и проверочных символов возможно) и запрещенные.

Основными характеристиками самокорректирующихся кодов являются:

  1. Число разрешенных и запрещенных комбинаций. Если n - число символов в блоке, r - число проверочных символов в блоке, k - число информационных символов, то ~2^n - число возможных кодовых комбинаций, ~2^k - число разрешенных кодовых комбинаций, ~2^n - 2^k - число запрещенных комбинаций.
  2. Избыточность кода. Величину ~\tfrac{r}{n} называют избыточностью корректирующего кода.
  3. Минимальное кодовое расстояние. Минимальным кодовым расстоянием d называется минимальное число искаженных символов, необходимое для перехода одной разрешенной комбинации в другую.
  4. Число обнаруживаемых и исправляемых ошибок. Если g - количество ошибок, которое код способен исправить, то необходимо и достаточно, чтобы ~d \geq 2g+1
  5. Корректирующие возможности кодов.

Граница Плоткина даёт верхнюю границу кодового расстояния ~d\leqslant \tfrac{n * 2^{k-1}}{2^k-1} или ~r \geq 2*(d-1)-\log_2 d при ~n \geq 2*d-1

Граница Хемминга устанавливает максимально возможное число разрешенных кодовых комбинаций ~2^k \leq {2^n} / \sum_{i=0}^{\tfrac{d-1}{2}} C_n^i где C_n^i - число сочетаний из n элементов по i элементам. Отсюда можно получить выражение для оценки числа проверочных символов: ~r \geq log_2( \sum_{i=0}^{\tfrac{d-1}{2}} C_n^i) Для значений (d/n) \leq 0.3 разница между границей Хемминга и границей Плоткина невелика.

Граница Варшамова-Гильберта для больших n определяет нижнюю границу числа проверочных символов ~r \geq log_2(\sum_{i=0}^{d-2} C_{n-1}^i) Все вышеперечисленные оценки дают представление о верхней границе d при фиксированных n и k или оценку снизу числа проверочных символов

5. Литература

6. Код Хемминга

Построение кодов Хемминга основано на принципе проверки на четность числа единичных символов: к последовательности добавляется элемент такой, чтобы число единичных символов в получившейся последовательности было четным. ~r_1 = i_1 \oplus i_2 \oplus ... \oplus i_k. знак ~ \oplus здесь означает сложение по модулю 2

~ S = i_1 \oplus i_2 \oplus ... \oplus i_n \oplus r_1 . ~ S = 0 - ошибки нет, ~ s = 1 однократная ошибка. Такой код называется ~ (k+1,k) или ~ (n,n-1) . Первое число - количество элементов последовательности, второе - количество проверочных символов. Для каждого числа проверочных символов ~ r = 3,4,5.. существует классический код Хемминга с маркировкой ~(n,k)=(2^r-1,2^r-1-r) т.е. - ~(7,4),(15,11),(31,26) . При иных значениях k получается так называемый усеченных код, например международный телеграфный код МТК-2, у которого ~ k = 5 . Для него необходим код Хемминга ~ (9,5) , который является усеченным от классического ~ (15,11) . Для Примера рассмотрим классический код Хемминга ~ (7,4) . Сгруппируем проверочные символы следующим образом:

~r_1 = i_1 \oplus i_2 \oplus i_3 ~r_2 = i_2 \oplus i_3 \oplus i_4 ~r_3 = i_1 \oplus i_2 \oplus i_4

знак \oplus здесь означает сложение по модулю 2.

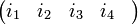
Получение кодового слова выглядит следующим образом: \begin{pmatrix} i_1 & i_2 & i_3 & i_4 & \\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 & 1 & 0 & 1 \\ 0 & 1 & 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 1 & 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 & 1 \\ \end{pmatrix} = \begin{pmatrix} i_1 & i_2 & i_3 & i_4 & r_1 & r_2 & r_3 \\ \end{pmatrix}

На вход декодера поступает кодовое слово ~V = (i_1',i_2',i_3',i_4',r_1',r_2',r_3') где штрихом помечены символы, которые могут исказиться в результате помехи. В декодере в режиме исправления ошибок строится последовательность синдромов:

~S_1 = r_1 \oplus i_1 \oplus i_2 \oplus i_3 ~S_2 = r_2 \oplus i_2 \oplus i_3 \oplus i_4 ~S_3 = r_3 \oplus i_1 \oplus i_2 \oplus i_4

~S = (s_1, s_2, s_3) называется синдромом последовательности.

Получение синдрома выглядит следующим образом:

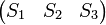
\begin{pmatrix} i_1 & i_2 & i_3 & i_4 & r_1 & r_2 & r_3 \\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} = \begin{pmatrix} S_1 & S_2 & S_3 \\ \end{pmatrix}

Кодовые слова ~ (7,4) кода Хемминга

i1 i2 i3 i4 r1 r2 r3
0 0 0 0 0 0 0
0 0 0 1 0 1 1
0 0 1 0 1 1 0
0 0 1 1 1 0 1
0 1 0 0 1 1 1
0 1 0 1 1 0 0
0 1 1 0 0 0 1
0 1 1 1 0 1 0
1 0 0 0 1 0 1
1 0 0 1 1 1 0
1 0 1 0 0 1 1
1 0 1 1 0 0 0
1 1 0 0 0 1 0
1 1 0 1 0 0 1
1 1 1 0 1 0 0
1 1 1 1 1 1 1

Синдром ~ (0,0,0) указывает на то, что в последовательности нет искажений. Каждому ненулевому синдрому соответствует определенная конфигурация ошибок, которая исправляется на этапе декодирования. Для кода ~ (7,4) в таблице указаны ненулевые синдромы и соответствующие им конфигурации ошибок.

Синдром 001 010 011 100 101 110 111
Конфигурация ошибок 0000001 0000010 0001000 0000100 1000000 0010000 0100000
Ошибка в символе r3 r2 i4 r1 i1 i3 i2

My hemcode.pngHemDecode.PNG

Литература

8. Применение

Код Хэмминга используется в некоторых прикладных программах в области хранения данных, особенно в RAID 2; кроме того, метод Хэмминга давно применяется в памяти типа ECC и позволяет «на лету» исправлять однократные и обнаруживать двукратные ошибки.

wreferat.baza-referat.ru

Коды Хемминга

Количество просмотров публикации Коды Хемминга - 192

Классификация помехоустойчивых кодов

Рис. 4.6

Малые точки означают запрещённые КК. Переход от одной точки к другой соответствует искажению одного разряда.

Обозначим - кратность гарантированно обнаруживаемых ошибок, а

- кратность гарантированно исправляемых ошибок.

Ошибка не обнаруживается, в случае если одна разрешённая КК переходит в другую разрешённую КК. Следовательно, для обнаружения всœех ошибок кратности до включительно крайне важно , чтобы кодовое расстояние определялось неравенством:

или , (4.18)

Это видно из рис. 4.6.

Для обеспечения возможности исправления всœех ошибок кратности до включительно крайне важно , как мы уже рассматривали. Чтобы принятая КК осталась в подмножестве запрещённых КК, ĸᴏᴛᴏᴩᴏᴇ ей принадлежит – на рис. 2.6. Эти подмножества отделœены пунктирными линиями. Для этого случая:

или (4.19)

Чтобы код обнаруживал и исправлял ошибки, требуется:

(4.20)

Рассмотренные формулы (4.18), (4.19), (4.20) указывают на минимальное количество обнаруживаемых и исправляемых ошибок. На практике будут обнаруживаться и исправляться ошибки и большей кратности, поскольку расстояние между отдельными КК должна быть больше, чем . При этом процент таких ошибок невелик.

Другой важной характеристикой кодов выступает вес КК. Под весом КК двоичного кода принято понимать количество 1 в данной КК - .

Стоит сказать, что для наименьшего веса КК справедливы соотношения:

(4.21)

Необходимое кодовое расстояние , а значит, и корректирующие свойства кода, определяются его относительной избыточностью, под которой принято понимать:

(4.22)

где n – общее число разрядов;

K – число информационных разрядов;

R – скорость кода;

R – число проверочных разрядов в КК.

Задача построения избыточного кода сводится к выбору из КК таких n-разрядных КК, для которых обеспечивается максимально возможное расстояние d. Для этого прежде всœего крайне важно определить требуемое число проверочных разрядов r. В общем виде эта задача до настоящего времени не решена. Точная формула, связывающая и r, известна только для

(4.23)

Для остальных случаев известны только верхние и нижние оценки числа избыточных элементов. Так граница Варшамова-Гильберта определяет нижнюю границу для числа проверочных разрядов:

(4.24)

- число сочетаний из n-1 элементов по i элементам.

Граница Плоткина даёт верхнюю границу кодового расстояния при заданном числе информационных (K) и общем (n) числе разрядов в КК:

(4.25)

Использование пропускной способности дискретного канала связи для корректирующих кодов определяется избыточностью данного кода. Используя выражение (4.22) и границы для определœения r можно построить следующий качественный график (рис 4.7)

рис 4.7

Из (4.22) следует, что увеличение избыточности приводит к уменьшению скорости кода и худшему использованию пропускной способности канала связи. При этом, увеличение длины ʼʼnʼʼ КК уменьшает относительную избыточность и улучшает использование дискретного канала. По этой причине при использовании корректирующих кодов стремятся применять, возможно, более длинные КК.

Как мы уже отмечали в настоящее время разработано огромное количество разнообразных кодов. Рассмотрим классификацию помехоустойчивых кодов

(рис. 4.8).

Помехоустойчивые коды делятся на блочные и непрерывные.Непрерывные коды представляют из себянепрерывные последовательности единичных элементов,не разделœенных на блоки. В таких кодах избыточные разряды помещаются в определœенном порядке между информационными. Типичным представителœем непрерывных кодов являются рекуррентные или сверхточные коды.

Рис 4.8

К блочным относятся коды, в которых каждому сообщению и знаку сообщения соответствует блок (КК) из ʼʼnʼʼ единичных элементов или блоки с разным числом разрядов. В этой связи блочные коды делятся на равномерные и неравномерные.

К неравномерным кодам относятся, к примеру, код Морзе, у которого КК имеют разную длину (число разрядов). На практике наибольшее применение нашли равномерные коды, как наиболее просто технически реализуемые.

Равномерные блочные коды делятся на разделимые и неразделимые.

В разделимых кодах КК состоит из информационных проверочных разрядов, причем эти разряды стоят на определœенных местах.

В неразделимых кодах делœение на информационные и проверочные разряды отсутствует.

К таким кодам относятся коды с постоянным весом, к примеру, код МТК-3 –семиразрядный код с весом КК равным 3. Сложность реализации.

Разделимые коды в свою очередь делятся на систематические (линœейные) и несистематические (нелинœейные).

Систематическими называются такие блочные разделимые (n,k) –коды, в которых k –разрядов (обычно первые) представляют из себякомбинацию простого кода, а последующие (n-k) разрядов являются проверочными. Проверочные разряды образуются с помощью линœейных операций над информационными разрядами.

Нелинœейные коды указанным свойством не обладают. Примером несистематического кода является код с контрольным суммированием ( проверка на четность или нечетность). В этом коде проверочные разряды записываются в виде суммы по модулю 2 () единиц в КК. Так в коде МТК-5 8-й разряд есть результат проверки на четность (нечетность) предыдущих семи разрядов.

К несистематическим кодам относятся. как уже отмечалось, коды с постоянным весом - это неразделимые коды. При этом они сложны в технической реализации. Хорош для ассиметричных каналов. Другим представителœем несимметричных кодов являются коды Бергера. Οʜᴎ разделимые. Минимальное кодовое расстояние . Существует ряд вариантов построения этих кодов:

- подсчитывается число единиц в информационной части КК и это число в двоичном коде записывается в качестве проверочных разрядов;

- проверка на четность (нечетность) – добавляется один разряд, который дополняет КК до четной (нечетной).

1. Сумма по модулю 2 двух или нескольких разрешенных кодовых комбинаций

также является разрешенной кодовой комбинацией.

2. Минимальное кодовое расстояние равно минимальному весу его разрешенных КК.

3. При заданном минимальном кодовом расстоянии всœе КК имеют одинаковую длину – равномерность.

На практике широкое распространение получили именно систематические коды.

Различают два метода формирования проверочных разрядов:

- поэлементный

- в целом

Поэлементный способ -формирования проверочных разрядов применяется в кодах Хемминга. Обработка КК целиком для получения проверочной группы разрядов используется в полиномиальных кодах. Циклические коды являются разновидностью этого класса кодов.

Коды Хемминга относятся к линœейным, групповым, систематическим кодам с и

, в которых проверочные разряды формируются линœейным преобразованием информационных разрядов поэлементным способом.

Правило нахождения проверочных разрядов является основной задачей построения корректирующих кодов. Рассмотрим данный процесс для кода Хемминга. Сначала познакомимся с понятием синдром кода.

Обнаружение и исправление ошибок избыточными кодами сводится к определœению и последующему анализу синдрома.

Под синдромом понимают совокупность элементов, сформированных суммированием по модулю 2 принятых проверочных элементов и вычисленных проверочных элементов и вычисленных проверочных элементов по принятым информационным элементам с использованием одного и того же правила на передаче и приеме.

В случае если синдром нулевой, то ошибок в принятой КК нет. либо они не обнаружены. Наличие единиц в синдроме указывает на ошибку в принятой КК. Код Хемминга с может исправить одну ошибку, в связи с этим синдром должен указать номер позиции в КК, где произошла ошибка. Этого достаточно для исправления ошибки в двоичных кодах.

Постараемся таким образом сформировать проверочные разряды, чтобы синдром в двоичном коде указывал номер искаженного разряда в КК.

Рассмотрим пример построения кода с К=5, способным исправлять 1 кратную ошибку.

Пример: Дано К=5; .

1. Определяем при , с .

2. Определяем крайне важно е число проверочных разрядов, поскольку , то

Это неравенство решается методом подбора:

------ не выполняется.

------ выполняется.

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, и код имеет вид (9.5).

Обозначим КК в виде:

(1)

Составим таблицу возможных синдромов, определяющих номер разряда , где произошла ошибка. Т.к. разрядов 4 , то синдром будет состоять из 4-х разрядов.

В алгоритме первой проверки введем те элементы, двоичные номера которых содержат в младшем разряде единицу. Из таблицы следует, что это элементы , , , , .

Аналогично, в алгоритм второй проверки включили те элементы, двоичные коды номеров которых содержат во 2-ом разряде единицу.

Аналогично для 3-ей и 4-ой проверок.

Обозначим результат каждой проверки как П1.В случае если П1=1. то это означает, что один из элементов КК, охватываемых первой проверкой, искажен. Наличие 1 в младшем разряде синдрома С1 указывает, что искомой искаженный элемент является нечетным, т.к. единицу в первом разряде имеют всœе нечетные числа. Следовательно, они и должны охватываться первой проверкой:

; =; (4.26)

Результат второй проверки П2 определяет второй разряд синдрома, ᴛ.ᴇ.

 
 

(4.27)

Далее:

(4.28)

(4.29)

Теперь определим, какие позиции в КК занимают проверочные разряды , а какие информационные. Признаком проверочного элемента является то, что он входит только в один алгоритм проверки. При этом крайне важно учесть. что в каждую проверку проверочный элемент должен входить только один раз.

Анализируя уравнения проверок видим, что элемент , входит только в первую проверку;

элемент входит только во вторую проверку;

элемент входит только в третью проверку;

элемент входит только в четвертую проверку.

По этой причине уравнения проверок можно переписать в виде:

(4.30)

В дискретный канал передается следующая КК:

на приеме производится аналогичные проверки (4.31)

;

;

;

; (4.31)

Крышечки у символов означают оценки единичных элементов в месте приема. По виду синдрома определяют номер разряда, где произошла ошибка.

В классическом коде Хемминга проверочные элементы располагаются на позициях, где i- номер проверочного разряда. При такой структуре КК усложняется аппаратура кодера и декодера. По этой причине на практике пользуются модифицированным кодом Хемминга, в котором изменяют, порядок передачи элементов КК в канал. Сначала передают информационные элементы, а затем проверочные.

Классический код Хемминга

1 2 3 4 5 6 7 8 9

1 2 3 4 5 6 7 8 9

Модифицированный код

Проверка:

вместо

вместо

вместо

вместо

а на передаче проверки запишутся в виде:

Модифицированный код: Классический код:

referatwork.ru

Реферат Код Хэмминга

скачать

Реферат на тему:

Question book-4.svg

План:

Введение

Question book-4.svg В этой статье не хватает информации.

Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена.Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники.

Коды Хэмминга — наиболее известные и, вероятно, первые из самоконтролирующихся и самокорректирующихся кодов. Построены они применительно к двоичной системе счисления.

1. История

В середине 1940-х годов Ричард Хэмминг работал в знаменитых Лабораториях Белла на счётной машине Bell Model V. Это была электромеханическая машина, использующая релейные блоки, скорость которых была очень низка: один оборот за несколько секунд. Данные вводились в машину с помощью перфокарт, и поэтому в процессе чтения часто происходили ошибки. В рабочие дни использовались специальные коды, чтобы обнаруживать и исправлять найденные ошибки, при этом оператор узнавал об ошибке по свечению лампочек, исправлял и запускал машину. В выходные дни, когда не было операторов, при возникновении ошибки машина автоматически выходила из программы и запускала другую.

Хэмминг часто работал в выходные дни, и все больше и больше раздражался, потому что часто был должен перезагружать свою программу из-за ненадежности перфокарт. На протяжении нескольких лет он проводил много времени над построением эффективных алгоритмов исправления ошибок. В 1950 году он опубликовал способ, который на сегодняшний день известен как код Хэмминга.

2. Систематические коды

Систематические коды образуют большую группу среди блочных, разделимых кодов (в которых все символы можно разделить на проверочные и информационные). Особенностью систематических кодов является то, что проверочные символы образуются в результате линейных операций над информационными символами. Кроме того, любая разрешенная кодовая комбинация может быть получена в результате линейных операций над набором линейно независимых кодовых комбинаций.

3. Самоконтролирующиеся коды

Коды Хэмминга являются самоконтролирующимися кодами, то есть кодами, позволяющими автоматически обнаруживать ошибки при передаче данных. Для их построения достаточно приписать к каждому слову один добавочный (контрольный) двоичный разряд и выбрать цифру этого разряда так, чтобы общее количество единиц в изображении любого числа было, например, четным. Одиночная ошибка в каком-либо разряде передаваемого слова (в том числе, может быть, и в контрольном разряде) изменит четность общего количества единиц. Счетчики по модулю 2, подсчитывающие количество единиц, которые содержатся среди двоичных цифр числа, могут давать сигнал о наличии ошибок.

При этом невозможно узнать, в каком именно разряде произошла ошибка, и, следовательно, нет возможности исправить её. Остаются незамеченными также ошибки, возникающие одновременно в двух, в четырёх или вообще в четном количестве разрядов. Впрочем, двойные, а тем более четырёхкратные ошибки полагаются маловероятными.

4. Самокорректирующиеся коды

Коды, в которых возможно автоматическое исправление ошибок, называются самокорректирующимися. Для построения самокорректирующегося кода, рассчитанного на исправление одиночных ошибок, одного контрольного разряда недостаточно. Как видно из дальнейшего, количество контрольных разрядов k должно быть выбрано так, чтобы удовлетворялось неравенство 2^k \geq k+m+1или k \geq \log_2(k+m+1), где m — количество основных двоичных разрядов кодового слова. Минимальные значения k при заданных значениях m, найденные в соответствии с этим неравенством, приведены в таблице.

Диапазон m kmin
1 2
2-4 3
5-11 4
12-26 5
27-57 6

В настоящее время наибольший интерес представляют двоичные блочные корректирующие коды. При использовании таких кодов информация передаётся в виде блоков одинаковой длины и каждый блок кодируется и декодируется независимо друг от друга. Почти во всех блочных кодах символы можно разделить на информационные и проверочные. Таким образом, все комбинации кодов разделяются на разрешенные (для которых соотношение информационных и проверочных символов возможно) и запрещенные.

Основными характеристиками самокорректирующихся кодов являются:

  1. Число разрешенных и запрещенных комбинаций. Если n - число символов в блоке, r - число проверочных символов в блоке, k - число информационных символов, то ~2^n - число возможных кодовых комбинаций, ~2^k - число разрешенных кодовых комбинаций, ~2^n - 2^k - число запрещенных комбинаций.
  2. Избыточность кода. Величину ~\tfrac{r}{n} называют избыточностью корректирующего кода.
  3. Минимальное кодовое расстояние. Минимальным кодовым расстоянием d называется минимальное число искаженных символов, необходимое для перехода одной разрешенной комбинации в другую.
  4. Число обнаруживаемых и исправляемых ошибок. Если g - количество ошибок, которое код способен исправить, то необходимо и достаточно, чтобы ~d \geq 2g+1
  5. Корректирующие возможности кодов.

Граница Плоткина даёт верхнюю границу кодового расстояния ~d\leqslant \tfrac{n * 2^{k-1}}{2^k-1} или ~r \geq 2*(d-1)-\log_2 d при ~n \geq 2*d-1

Граница Хемминга устанавливает максимально возможное число разрешенных кодовых комбинаций ~2^k \leq {2^n} / \sum_{i=0}^{\tfrac{d-1}{2}} C_n^i где C_n^i - число сочетаний из n элементов по i элементам. Отсюда можно получить выражение для оценки числа проверочных символов: ~r \geq log_2( \sum_{i=0}^{\tfrac{d-1}{2}} C_n^i) Для значений (d/n) \leq 0.3 разница между границей Хемминга и границей Плоткина невелика.

Граница Варшамова-Гильберта для больших n определяет нижнюю границу числа проверочных символов ~r \geq log_2(\sum_{i=0}^{d-2} C_{n-1}^i) Все вышеперечисленные оценки дают представление о верхней границе d при фиксированных n и k или оценку снизу числа проверочных символов

5. Литература

6. Код Хемминга

Построение кодов Хемминга основано на принципе проверки на четность числа единичных символов: к последовательности добавляется элемент такой, чтобы число единичных символов в получившейся последовательности было четным. ~r_1 = i_1 \oplus i_2 \oplus ... \oplus i_k. знак ~ \oplus здесь означает сложение по модулю 2

~ S = i_1 \oplus i_2 \oplus ... \oplus i_n \oplus r_1 . ~ S = 0 - ошибки нет, ~ s = 1 однократная ошибка. Такой код называется ~ (k+1,k) или ~ (n,n-1) . Первое число - количество элементов последовательности, второе - количество проверочных символов. Для каждого числа проверочных символов ~ r = 3,4,5.. существует классический код Хемминга с маркировкой ~(n,k)=(2^r-1,2^r-1-r) т.е. - ~(7,4),(15,11),(31,26) . При иных значениях k получается так называемый усеченных код, например международный телеграфный код МТК-2, у которого ~ k = 5 . Для него необходим код Хемминга ~ (9,5) , который является усеченным от классического ~ (15,11) . Для Примера рассмотрим классический код Хемминга ~ (7,4) . Сгруппируем проверочные символы следующим образом:

~r_1 = i_1 \oplus i_2 \oplus i_3 ~r_2 = i_2 \oplus i_3 \oplus i_4 ~r_3 = i_1 \oplus i_2 \oplus i_4

знак \oplus здесь означает сложение по модулю 2.

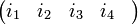
Получение кодового слова выглядит следующим образом: \begin{pmatrix} i_1 & i_2 & i_3 & i_4 & \\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 & 1 & 0 & 1 \\ 0 & 1 & 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 1 & 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 & 1 \\ \end{pmatrix} = \begin{pmatrix} i_1 & i_2 & i_3 & i_4 & r_1 & r_2 & r_3 \\ \end{pmatrix}

На вход декодера поступает кодовое слово ~V = (i_1',i_2',i_3',i_4',r_1',r_2',r_3') где штрихом помечены символы, которые могут исказиться в результате помехи. В декодере в режиме исправления ошибок строится последовательность синдромов:

~S_1 = r_1 \oplus i_1 \oplus i_2 \oplus i_3 ~S_2 = r_2 \oplus i_2 \oplus i_3 \oplus i_4 ~S_3 = r_3 \oplus i_1 \oplus i_2 \oplus i_4

~S = (s_1, s_2, s_3) называется синдромом последовательности.

Получение синдрома выглядит следующим образом:

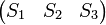
\begin{pmatrix} i_1 & i_2 & i_3 & i_4 & r_1 & r_2 & r_3 \\ \end{pmatrix} \begin{pmatrix} 1 & 0 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} = \begin{pmatrix} S_1 & S_2 & S_3 \\ \end{pmatrix}

Кодовые слова ~ (7,4) кода Хемминга

i1 i2 i3 i4 r1 r2 r3
0 0 0 0 0 0 0
0 0 0 1 0 1 1
0 0 1 0 1 1 0
0 0 1 1 1 0 1
0 1 0 0 1 1 1
0 1 0 1 1 0 0
0 1 1 0 0 0 1
0 1 1 1 0 1 0
1 0 0 0 1 0 1
1 0 0 1 1 1 0
1 0 1 0 0 1 1
1 0 1 1 0 0 0
1 1 0 0 0 1 0
1 1 0 1 0 0 1
1 1 1 0 1 0 0
1 1 1 1 1 1 1

Синдром ~ (0,0,0) указывает на то, что в последовательности нет искажений. Каждому ненулевому синдрому соответствует определенная конфигурация ошибок, которая исправляется на этапе декодирования. Для кода ~ (7,4) в таблице указаны ненулевые синдромы и соответствующие им конфигурации ошибок.

Синдром 001 010 011 100 101 110 111
Конфигурация ошибок 0000001 0000010 0001000 0000100 1000000 0010000 0100000
Ошибка в символе r3 r2 i4 r1 i1 i3 i2

My hemcode.pngHemDecode.PNG

Литература

8. Применение

Код Хэмминга используется в некоторых прикладных программах в области хранения данных, особенно в RAID 2; кроме того, метод Хэмминга давно применяется в памяти типа ECC и позволяет «на лету» исправлять однократные и обнаруживать двукратные ошибки.

wreferat.baza-referat.ru

Значение кода Хемминга — реферат

 

Содержание.

 

1. Значение кода Хемминга.

2. Код Хемминга.

3. Принцип построения кодов Хемминга.

4. Применение.

5.Литература.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1. Значение кода Хемминга

Код Хэмминга – систематический  код, то есть состоящий из информационных и корректирующих символов, расположенных  по строго определенной системе, имеющих  одинаковую длину и всегда занимающих строго определенные места в кодовых  комбинациях.

Предложенные Хэммингом  регулярные методы построения кодов, корректирующих ошибки, имеют фундаментальное значение. Они демонстрируют инженерам  практическую возможность достижения пределов, на которую указывали законы теории информации. Эти коды нашли  практическое применение при создании компьютерных систем. Работа Хэмминга привела к решению проблемы более  плотной упаковки для конечных полей. Он ввел в научный обиход важнейшие  понятия теории кодирования –  расстояние Хэмминга между кодовыми комбинациями в векторном пространстве, определяемом для двоичных кодов  как количество позиций этих комбинаций с различными символами, и границы  Хэмминга для исправляющей способности  блочных корректирующих кодов. Граница  Хэмминга для двоичных кодов рассчитывается по следующей формуле:

В этом выражении число  ошибок e может быть исправлено корректирующим блочным кодом длиной N, имеющим М кодовых комбинаций (CjN – биномиальный коэффициент).

Работа Хэмминга сыграла  ключевую роль в последующем развитии теории кодирования и стимулировала  обширные исследования, выполненные  в последующие годы.

Коды Хэмминга позволяют  не только обнаружить наличие ошибки, но и место ее нахождения и, следовательно, дают возможность ее исправить.

 

2. Коды Хемминга.

 

Коды  Хемминга являются самоконтролирующимися  кодами, т.е кодами, позволяющими автоматически  обнаруживать наиболее вероятные ошибки при передаче данных. Для их построения достаточно приписать к каждому  слову один добавочный (контрольный) двоичный разряд и выбрать цифру  этого разряда так, чтобы общее  количество единиц в изображении  любого числа было, например, четным. Одиночная ошибка в каком-либо разряде  передаваемого слова (в том числе, может быть, и в контрольном  разряде) изменит четность общего количества единиц. Счетчики по модулю 2, подсчитывающие количество единиц, которые содержатся среди двоичных цифр числа, могут  давать сигнал о наличии ошибок.

При этом, разумеется, мы не получаем никаких  указаний о том, в каком именно разряде произошла ошибка, и, следовательно, не имеем возможности исправить  её. Остаются незамеченными также  ошибки, возникающие одновременно в  двух, в четырёх или вообще в  четном количестве разрядов. Впрочем, двойные, а тем более четырёхкратные ошибки полагаются маловероятными.

Коды, в которых возможно автоматическое исправление ошибок, называются самокорректирующимися. Для  построения самокорректирующегося  кода, рассчитанного на исправление  одиночных ошибок, одного контрольного разряда недостаточно.Как видно  из дальнейшего, количество контрольных  разрядов k должно быть выбрано так, чтобы удовлетворялось неравенству  или , где m - количество основных двоичных разрядов кодового слова. Минимальные  значения k при заданных значениях m, найденные в соответствии с этим неравенством, приведены в таблице  № 1

 

Диапазон m

kmin

1

2

2-4

3

5-11

4

12-26

5

27-57

6

 

Имея m+k разрядов, самокорректирующийся код можно построить следующим  образом.

Присвоим каждому из разрядов свой номер - от 1 до m+k; запишем эти номера в двоичной системе счисления. Поскольку  2k > m + k ,каждый номер можно представить, очевидно, k-разрядным двоичным числом.

Предположим далее, что все m+k разрядов кода разбиты на контрольные группы, которые частично перекрываются, причем так, что единицы в двоичном представлении  номера разряда указывают на его  принадлежность к определённым контрольным  группам. Например: разряд № 5 принадлежит  к 1-й и 3-й контрольным группам, потому что в двоичном представлении  его номера 510 = …0001012 - 1-й и 3-й разряды содержат единицы.

Среди m+k разрядов кода при этом имеется k разрядов, каждый из которых принадлежит  только к одной контрольной группе:

Разряд № 1: 110 = …0000012 принадлежит только к 1-й контрольной группе.

Разряд № 2: 210 = …0000102 принадлежит только к 2-й контрольной группе.

Разряд № 4: 410 = …0001002 принадлежит только к 3-й контрольной группе.

…

Разряд № 2k−1 принадлежит только к k-й контрольной группе.

Эти k разрядов мы и будем считать  контрольными. Остальные m разрядов, каждый из которых принадлежит, по меньшей  мере, к двум контрольным группам, будут информационными разрядами.

В каждой из k контрольных групп  будем иметь по одному контрольному разряду. В каждый из контрольных  разрядов поместим такую цифру (0 или 1), чтобы общее количество единиц в его контрольной группе было четным.

Например, довольно распространен  код Хеминга с m=7 и k=4.

Пусть исходное слово (кодовое слово  без контрольных разрядов) - 01101012.

Обозначим Pi - контрольный разряд №i; а Di - информационный разряд №i, где i = 1,2,3,

4…

 

 

 

1

2

3

4

5

6

7

8

9

10

11

№ разряда:

0001

0010

0011

0100

0101

0110

0111

1000

1001

1010

1011

Распределение контрольных  и информационных разрядов

p1

p2

d1

p3

d2

d3

d4

p4

d5

d6

d7

Информационное  кодовое слово :

    

0

  

1

1

0

  

1

0

1

p1

1

  

0

  

1

  

0

  

1

  

1

p2

  

0

0

    

1

0

    

0

1

p3

      

0

1

1

0

        

p4

              

0

1

0

1

Кодовое слово  с контрольными разрядами:

1

0

0

0

1

1

0

0

1

0

1

 

Интересно посмотреть, как перекрываются  контрольные группы в данном случае (Рис №1). Первая группа контролирует разряды № 3,5,7,9,11 исходного кода, вторая — 3,6,7,10,11 (№ группы = № контрольного разряда). Очевидно, что они частично перекрываются.

Рис.№1 Первая группа контролирует разряды  № 3,7,5 исходного кода, вторая — 3,7,6…  Очевидно что они частично перекрываются

Предположим теперь, для примера, что  при передаче данного кодового слова 10001100101 произошла ошибка в 11–м разряде, так, что было принято новое кодовое  слово 10001100100. Произведя в принятом коде проверку четности внутри контрольных групп, мы обнаружили бы, что количество единиц нечетно в 1-й,2-й и 4-й контрольных группах, и четно в 3-й контрольной группе. Это указывает, во-первых, на наличие ошибки, во-вторых, означает, что номер ошибочно принятого разряда в двоичном представлении содержит единицы на первом, втором и четвёртом местах и нуль - на третьем месте, т.к ошибка только одна, и 3-я контрольная сумма оказалась верной.

№ разряда:

0001

0010

0011

0100

0101

0110

0111

1000

1001

1010

1011

    

Распределение контрольных  и информационных разрядов

p1

p2

d1

p3

d2

d3

d4

p4

d5

d6

d7

Контроль по четности в группе

Контрольный бит

Переданное кодовое  слово:

1

0

0

0

1

1

0

0

1

0

1

    

Принятое кодовое  слово:

1

0

0

0

1

1

0

0

1

0

0

    

p1

1

  

0

  

1

  

0

  

1

  

0

Fail

1

p2

  

0

0

    

1

0

    

0

0

Fail

1

p3

      

0

1

1

0

        

Pass

0

p4

              

0

1

0

0

Fail

1

 

 

 

p4

p3

p2

p1

  

В двоичном представлении

1

0

1

1

  

В десятичном представлении

8

  

2

1

Σ = 11

 

Из таблицы следует, что  ошибка произошла в 11-м разряде  и её можно исправить. Построенный  код, разумеется, не рассчитан на возможность  одновременной ошибки в двух разрядах.

Например (Рис №2), когда ошибки одновременно прошли в 3-м и 7-м разрядах исходного кода, первый и второй контрольные биты даже не замечают подмены.

Рис.№2 Когда ошибки прошли в 3-м и 7-м разрядах исходного кода, первый и второй контрольные биты даже не замечают ошибки

Когда в принятом коде производится проверка четности внутри контрольных  групп, случай двойной ошибки ничем  внешне не отличается от случая одиночной  ошибки.

Например, предположим теперь, что  при передаче данного кодового слова 10001100101 произошли ошибки в 3-м и 6-м  разрядах, так, что принято кодовое  слово 10101000101.

№ разряда:

0001

0010

0011

0100

0101

0110

0111

1000

1001

1010

1011

    

Распределение контрольных  и информационных разрядов

p1

p2

d1

p3

d2

d3

d4

p4

d5

d6

d7

Контроль по четности в группе

Контрольный бит

Переданное кодовое  слово:

1

0

0

0

1

1

0

0

1

0

1

    

Принятое кодовое  слово:

1

0

1

0

1

0

0

0

1

0

1

    

p1

1

  

1

  

1

  

0

  

1

  

1

Fail

1

p2

  

0

1

    

0

0

    

0

1

Pass

0

p3

      

0

1

0

0

        

Fail

1

p4

              

0

1

0

1

Pass

0

 

 

 

 

p4

p3

p2

p1

  

В двоичном представлении

0

1

0

1

  

В десятичном представлении

  

4

  

1

Σ = 5

Вывод: ошибка произошла в 5-м разряде Истинное кодовое слово  : 1 0 0 0 1 1 0 0 1 0 1 Ошибочное кодовое слово  : 1 0 1 0 1 0 0 0 1 0 1 Исправленное кодовое слово : 1 0 1 0 0 0 0 0 1 0 1 Результат получается ещё более отдаленным от правильного, чем принятый код. Исправление кода по общему правилу не только не улучшило, но даже ухудшило бы дело.

Можно построить и такой  код, который обнаруживал бы двойные  ошибки и исправлял одиночные. Для  этого к самокорректирующемуся  коду, рассчитанному на исправление  одиночных ошибок, нужно приписать  ещё один контрольный разряд (разряд двойного контроля). Полное количество разрядов кода при этом будет m+k+1. Цифра  в разряде двойного контроля устанавливается  такой, чтобы общее количество единиц во всех m + k + 1 разрядах кода было четным. Этот разряд не включается в общую нумерацию и не входит ни в одну контрольную группу.

Например, код Хеминга с m=7 и k=4 Пусть  информационное кодовое слово - 0110101

№ разряда:

0001

0010

0011

0100

0101

0110

0111

1000

1001

1010

1011

Second Parity

Распределение контрольных  и информационных разрядов

p1

p2

d1

p3

d2

d3

d4

p4

d5

d6

d7

  

Информационное  кодовое слово:

    

0

  

1

1

0

  

1

0

1

  

p1

1

  

0

  

1

  

0

  

1

  

1

  

p2

  

0

0

    

1

0

    

0

1

  

p3

      

0

1

1

0

          

p4

              

0

1

0

1

  

Кодовое слово  с контрольными разрядами:

1

0

0

0

1

1

0

0

1

0

1

1

 

 

При этом могут быть следующие  случаи.

  1. В принятом коде в целом и по всем контрольным группам количество единиц четно. Если тройные ошибки и ошибки в большем количестве разрядов исключаются, то первый случай соответствует безошибочному приему кода. Например

yaneuch.ru

Смотрите также