Статья: Графен и его свойства:. Графен реферат

Графен — самый тонкий и самый прочный материал во Вселенной. Представьте себе углеродную пластину толщиной всего в один атом, но более прочную, чем алмаз, и пропускающую электричество в 100 раз лучше, чем кремний компьютерных чипов. Его уже сейчас сравнивают с появлением самых революционных изобретений, изменивших человечество. Крайне сложно предсказать сейчас практические области применения графена, но он однозначно изменит нашу жизнь. Его появление революционно. Он сравним с появлением танков, которые уничтожили конницу, мобильных телефонов, которые скоро уничтожат стационарные аппараты. Такое открытие не укладывается в стандартную схему, в которой можно было бы предположить пути развития и дальнейшего применения. Графен изменит все, что нас сейчас окружает. Ведь открыто новое материальное вещество с уникальными физическими свойствами. С одной стороны, оно очень тонкое, с другой - очень большое. Оно поменяет наше представление о природе веществ и вещей.

История открытия

Все началось в 2004 году, когда Андрею Гейму и Константину Новоселову впервые удалось получить графен в свободном состоянии. Это стало крупным открытием, несмотря на то что графен - вещество простое по определению: это чистый углерод. Но каждый атом углерода в нем жестко связан с тремя соседними атомами и является двумерной сеткой (рис.1).

Рисунок 1: Атомная сетка графена

К примеру, по предположению ученых, сенсоры на основе графена смогут предсказывать землетрясения, анализировать состояние и прочность узлов самолета. Однако только через лет 10 будет понятно, в каком направлении будет развиваться практическое применение данного вещества.

Новейший материал с потрясающими свойствами скоро покинет стены научных лабораторий. Уже сейчас физики, химики и инженеры-электронщики много говорят о его уникальных возможностях. Количества материала весом всего несколько граммов достаточно для того, чтобы покрыть футбольное поле. Графит, используемый в карандашах, есть ни что иное, как множество слоев графена. Хотя каждый из слоев прочный, связи между ними слабые, так что слои легко распадаются, оставляя след, когда вы пишете карандашом.

Возможные сферы использования графена — сенсорные экраны, солнечные батареи, накопители энергии, сотовые телефоны, и, наконец, — супербыстрые компьютерные чипы. Но в ближней и среднесрочной перспективе, графену будет сложно занять место кремния как основного материала для производства компьютерной «начинки. Производства кремния — это индустрия с 40-летней историей, стоимость производства кремния в мире оценивается в миллиарды долларов. Сейчас над решением сложных проблем, связанных с производством самого графена и изделий из него, трудятся государственные лаборатории и университеты, мега-гиганты — такие, как IBM — и предприятия малого бизнеса.

Новым высокотехнологичным материалом заинтересовался даже Пентагон. Агентство передовых оборонных исследовательских проектов ( Defense Advanced Research Projects Agency) занимается исследованиями, направленными на создание компьютерных чипов и транзисторов на основе графена, общая стоимость исследования составляет 22 миллиона долларов.

На последнем ежегодном заседании Американского физического Общества — организации, объединяющей лучших физиков страны, — проходившего в апреле этого года в Питсбурге, графен стал главной темой для обсуждения. Ученые провели 23 заседания, высказывая мнения и взгляды в отношении нового материала. Только в течение 2008 года в различных источниках было опубликовано 1 500 научных работ, посвященных графену.

studfiles.net

Графен — курсовая работа

Содержание:

1. Введение……………………………………………………………………...3

2. Получение……………………………………………………………………5

3. Возможные применения………………………………………………….…7

4. Физика………………………………………………………………………..9

4.1. Теория……………………………………………………………………9

4.1.1. Кристаллическая структура………………………………………...9

4.1.2. Зонная структура……………………………………………………10

4.1.3. Линейный закон дисперсии…………………………………………12

4.1.4. Эффективная масса…………………………………………………..14

4.1.5. Парадокс Клейна…………………………………………………….15

4.2. Эксперимент……………………………………………………………...16

4.2.1 Проводимость………………………………………………………….16

4.2.2. Квантовый эффект Холла……………………………………………18

5. Факты о графене……………………………………………………………....21

6. Заключение…………………………………………………………………...23

7. Список литературы……………………………………………………….....23

1. Введение.

Идеальная кристаллическая структура графена представляет собой гексагональную кристаллическую решётку. Графен является двумерным кристаллом, состоящим из одиночного слоя атомов углерода, собранных в гексагональную решётку. Его теоретическое исследование началось задолго до получения реальных образцов материала, поскольку из графена можно собрать трёхмерный кристалл графита. Графен является базой для построения теории этого кристалла. Графит является полуметаллом, и как было показано в 1947 году П. Воллесом, в зонной структуре графена также отсутствует запрещённая зона, причём в точках соприкосновения валентной зоны и зоны проводимости энергетический спектр электронов и дырок линеен как функция волнового вектора. Такого рода спектром обладают безмассовые фотоны и ультрарелятивистские частицы, а также нейтрино. Поэтому говорят, что эффективная масса электронов и дырок в графене вблизи точки соприкосновения зон равна нулю. Но здесь стоит заметить, что, несмотря на сходство фотонов и безмассовых носителей, в графене существует несколько существенных различий, делающих носители в графене уникальными по своей физической природе, а именно: электроны и дырки являются фермионами, и они заряжены. В настоящее время аналогов для этих безмассовых заряженных фермионов среди известных элементарных частиц нет.

Специфические особенности — экспериментального подтверждения эти выводы не получили до 2005 года, поскольку не удавалось создать графен. Кроме того, ещё раньше было доказано теоретически, что свободную идеальную двумерную плёнку получить невозможно из-за нестабильности относительно сворачивания или скручивания. Тепловые флуктуации приводят к плавлению двумерного кристалла при любой конечной температуре.

Интерес к графену появился снова после открытия углеродных нанотрубок, поскольку вся первоначальная теория строилась на простой модели нанотрубки как развёртки цилиндра. Поэтому теория для графена в приложении к нанотрубкам хорошо проработана.

Попытки получения графена, прикреплённого к другому материалу, начались с экспериментов, использующих простой карандаш, и продолжились с использованием атомно-силового микроскопа для механического удаления слоёв графита, но не достигли успеха. Использование графита с внедрёнными (интеркалированный графит) в межплоскостное пространство чужеродными атомами (используется для увеличения расстояния между соседними слоями и их расщепления) также не привело к результату.

В 2004 году российскими и британскими учёными была опубликована работа в журнале Science, где сообщалось о получении графена на подложке окисленного кремния. Таким образом, стабилизация двумерной плёнки достигалась благодаря наличию связи с тонким слоем диэлектрика SiO2. Впервые были измерены проводимость, эффект Шубникова — де Гааза, эффект Холла для образцов, состоящих из плёнок углерода с атомарной толщиной.

2. Получение графена

Кусочки графена получают при механическом воздействии на высокоориентированный пиролитический графит или киш-графит. Сначала плоские куски графита помещают между липкими лентами (скотч) и расщепляют раз за разом, создавая достаточно тонкие слои (среди многих плёнок могут попадаться однослойные и двуслойные, которые и представляют интерес). После отшелушивания скотч с тонкими плёнками графита прижимают к подложке окисленного кремния. При этом трудно получить плёнку определённого размера и формы в фиксированных частях подложки (горизонтальные размеры плёнок составляют обычно около 10 мкм). Найденные с помощью оптического микроскопа, (они слабо видны при толщине диэлектрика 300 нм) плёнки подготавливают для измерений. Толщину можно определить с помощью атомно-силового микроскопа (она может варьироваться в пределах 1 нм для графена) или, используя комбинационное рассеяние. Используя стандартную электронную литографию иреактивное плазменное травление, задают форму плёнки для электрофизических измерений.

Кусочки графена также можно приготовить из графита, используя химические методы. Сначала микрокристаллы графита подвергаются действию смеси серной и соляной кислот. Графит окисляется и на краях образца появляются карбоксильные группы графена. Их превращают в хлориды при помощи тионилхлорида. Затем под действием октадециламина в растворах тетрагидрофурана, тетрахлорметана и дихлорэтана они переходят в графеновые слои толщиной 0,54 нм. Этот химический метод не единственный, и, меняя органические растворители и химикаты, можно получить нанометровые слои графита.

В статьях описан ещё один химический метод получения графена, встроенного в полимерную матрицу. Следует упомянуть ещё два метода: радиочастотное плазмохимическое осаждение из газовой фазы (англ. PECVD), рост при высоком давлении и температуре (англ. HPHT) . Из этих методов только последний можно использовать для получения плёнок большой площади.

Если кристалл пиролитического графита и подложку поместить между электродами, то, можно добиться того, что кусочки графита с поверхности, среди которых могут оказаться плёнки атомарной толщины, под действием электрического поля могут перемещаться на подложку окисленного кремния. Для предотвращения пробоя (между электродами прикладывали напряжение от 1 до 13 кВ) между электродами также помещали тонкую пластину слюды.

Существует также несколько сообщений, посвящённых получению графена, выращенного на подложках карбида кремния SiC(0001). Графитовая плёнка формируется при термическом разложении поверхности подложки SiC (этот метод получения графена гораздо ближе к промышленному производству), причём качество выращенной плёнки зависит от того, какая стабилизация у кристалла: C- стабилизированная или Si- стабилизированная поверхность — в первом случае качество плёнок выше. В работах та же группа исследователей показала, что, несмотря на то, что толщина слоя графита составляет больше одного монослоя, в проводимости участвует только один слой в непосредственной близости от подложки, поскольку на границе SiC- C из-за разности работ выхода двух материалов образуется нескомпенсированный заряд. Свойства такой плёнки оказались эквивалентны свойствам графена.

Идеальный графен состоит исключительно из шестиугольных ячеек. Присутствие пяти- и семиугольных ячеек будет приводить к различного рода дефектам.

Наличие пятиугольных ячеек приводит к сворачиванию атомной плоскости в конус. Присутствие одновременно 12 таких дефектов приведёт к образованию фуллерена. Присутствие семиугольных ячеек приводит к образованию седловидных искривлений атомной плоскости. Комбинация этих дефектов и нормальных ячеек может приводить к образованию различных форм поверхностей.

3. Возможные применения

Считается, что на основе графена можно сконструировать баллистический транзистор. В марте 2006 года группа исследователей из технологического института штата Джорджии заявила, что ими был получен полевой транзистор на графене, а также квантово-интерференционный прибор. Исследователи полагают, что благодаря их достижениям в скором времени появится новый класс графеновой наноэлектроники с базовой толщиной транзисторов до 10 нм. Данный транзистор обладает большим током утечки, то есть нельзя разделить два состояния с закрытым и открытым каналом.

Использовать напрямую графен при создании полевого транзистора без токов утечки не представляется возможным благодаря отсутствию запрещённой зоны в этом материале, поскольку нельзя добиться существенной разности в сопротивлении при любых приложенных напряжениях к затвору, то есть, не получается задать два состояния пригодных для двоичной логики: проводящее и непроводящее. Сначала нужно создать каким-нибудь образом запрещённую зону достаточной ширины при рабочей температуре (чтобы термически возбуждённые носители давали малый вклад в проводимость). Один из возможных способов предложен в работе. В этой статье предлагается создать тонкие полоски графена с такой шириной, чтобы благодаря квантово-размерному эффекту ширина запрещённой зоны была достаточной для перехода в диэлектрическое состояние (закрытое состояние) прибора при комнатной температуре (28 мэВ соответствует ширине полоски 20 нм). Благодаря высокой подвижности (имеется в виду, что подвижность выше чем в кремнии, используемом в микроэлектронике) 104 см²·В−1·с−1 быстродействие такого транзистора будет заметно выше. Несмотря на то, что это устройство уже способно работать как транзистор, затвор к нему ещё не создан.

Другая область применения заключается в использовании графена в качестве очень чувствительного сенсора для обнаружения отдельных молекул химических веществ, присоединённых к поверхности плёнки. Сенсор размером 1 мкм × 1 мкм использовался для детектирования присоединения отдельных молекул NO2 к графену. Принцип действия этого сенсора заключается в том, что разные молекулы могут выступать как доноры и акцепторы, что в свою очередь ведёт к изменению сопротивления графена. В работе теоретически исследуется влияние различных примесей (использованных в отмеченном выше эксперименте) на проводимость графена. В работе было показано, что NO2 молекула является хорошим акцептором из-за своих парамагнитных свойств, а диамагнитная молекула N2O4 создаёт уровень близко к точке электронейтральности. В общем случае примеси, молекулы которых имеют магнитный момент (неспаренный электрон), обладают более сильными легирующими свойствами.

Ещё одна перспективная область применения графена — его использование для изготовления электродов в ионисторах (суперконденсаторах) для использования их в качестве перезаряжаемых источников тока. Опытные образцы ионисторов на графене имеют удельную энергоёмкость 32 Вт·ч/кг, сравнимую с таковой для свинцово-кислотных аккумуляторов (30−40 Вт·ч/кг)

Недавно был создан новый тип светодиодов на основе графена (LEC). Процесс утилизации новых материалов экологичен при достаточно низкой цене.

4. Физика

Физические свойства нового материала можно изучать по аналогии с другими подобными материалами. В настоящее время экспериментальное и теоретическое исследование графена сосредоточено на стандартных свойствах двумерных систем: проводимости, квантовом эффекте Холла, слабой локализации и других эффектах, исследованных ранее в двумерном электронном газе.

4.1 Теория. В этом параграфе кратко описываются основные положения теории, некоторые из которых получили экспериментальное подтверждение, а некоторые ещё ждут верификации.

4.1.1 Кристаллическая структура

Кристаллическая решётка графена представляет собой плоскость, состоящую из шестиугольных ячеек, то есть является двумерной гексагональной кристаллической решёткой. Для такой решётки известно, что её обратная решётка тоже будет гексагональной. В элементарной ячейке кристалла находятся два атома, обозначенные A и B. Каждый из этих атомов при сдвиге на вектора трансляций (любой вектор вида , где m и n — любые целые числа) образует подрешётку из эквивалентных ему атомов, то есть свойства кристалла независимы от точек наблюдения, расположенных в эквивалентных узлах кристалла. На рисунке 3 представлены две подрешётки атомов, закрашенные разными цветами: зелёным и красным.

Расстояние между ближайшими атомами углерода в шестиугольниках, обозначенное a0, составляет 0,142 нм. Постоянную решётки (a) можно получить из простых геометрических соображений. Она равна , то есть 0,246 нм. Если определить за начало координат точку, соответствующую узлу кристаллической решётки (подрешётка A), из которой начинаются векторы трансляций: с длиной векторов, равной a, и ввести двумерную декартову систему координат в плоскости графена с осью ординат, направленной вверх, и осью абсцисс, направленной по отрезку, соединяющему соседние узлы A и B, то тогда координаты концов векторов трансляций, начинающихся из начала координат, запишутся в виде:

а соответствующие им вектора обратной решётки:

myunivercity.ru

Реферат - Графеновая электроника - Наука и техника

Слушая глубокомысленные рассуждения государственных чинов о необходимости развивать нанотехнологии, невольно удивляешься нелогичности их поступков: на оборону выделяются средства, несравнимые с бюджетом науки. Притом, что сейчас деньги, вложенные в научные исследования, позволят не только радикально изменить жизнь людей, но и вплотную подойти к решению проблемы бессмертия человека.

Говоря о нанотехнологиях, в первую очередь приходят на ум открытие графена и углеродных нанотрубок. Именно с ними связывают ученые прорыв в области электроники и фармакологии в 21 веке. Создание квантовых компьютеров, систем считывания сигналов на клеточном уровне, нанороботов для лечения организма – это только малый перечень открывающихся возможностей. Сейчас эти возможности перешли из области фантастики в область лабораторных разработок.

Особая тема – это микроэлектроника. Современные микропроцессоры и чипы памяти уже преодолевают значение технологических норм в 10 нанометров. Впереди рубеж 4-6 нм. Но чем дальше двигаются разработчики по пути миниатюризации, тем сложнее задачи приходится решать. Инженера вплотную приблизились к физическим пределам кремниевых чипов. Те, кто интересуются современными микропроцессорами, знают, что их быстродействие затормозилось на тактовой частоте около 4 ГГц и дальше не увеличивается.

Кремний является прекрасным материалом для микроэлектроники, но обладает существенным недостатком – плохой теплопроводностью. И с ростом тактовой частоты и плотности элементов этот недостаток становится барьером на пути дальнейшего развития микроэлектроники.

К счастью, сегодня появилась реальная возможность использовать альтернативные материалы. Это графен, двухмерная форма углерода и углеродные нанотрубки, которые являются трехмерной кристаллической формой того же углерода. Уже первые результаты исследований привели к созданию графеновых транзисторов, работающих на частоте до 300 ГГц. Причем, опытные образцы сохраняли свои характеристики при температурах 125 градусов по Цельсию.

История открытия графенового чуда

Самозабвенно разрисовывая в раннем детстве стены комнат простым карандашом, мы не подозревали, что занимаемся серьезной наукой – производим опыты по получению графена. Взбучка от родителей, не оценивших научную ценность экспериментов, многих отвратила от науки, но не всех. В 2010 году двоим россиянам, сотруднику Манчестерского университета (Великобритания) Андрею Гейму и ученому из Черноголовки (Россия) Константину Новосельцеву присудили Нобелевскую премию за открытие графена – новой кристаллической модификации углерода, толщиной в один атомный слой.

Так в чем же состояла заслуга ученых и значение открытия? Для начала разберемся с самим предметом открытия. Графен – это кристаллическая двумерная поверхность (не пленка!) толщиной в один или два атомных слоя. Самое интересное состоит в том, что теоретически графен был «создан» физиками-теоретиками более 60 лет назад для описания трехмерных структур углерода. Математическая модель двумерной решетки прекрасно описывала теплофизические свойства графита и иных трехмерных модификаций углерода.

Но многочисленные попытки создать двумерные кристаллы углерода заканчивались неудачами. «Медвежью» услугу в этих поисках оказали теоретики, которые математически обосновали невозможность существования кристаллических поверхностей. Не верить им было трудно: ведь это были Лев Ландау и Пайерлс – крупнейшие физики- теоретики 20 века.

Они привели неоспоримые математические доводы, что правильные плоские кристаллические структуры неустойчивы, т.к. за счет тепловых колебаний атомы покинут узлы таких кристаллов и порядок нарушится. Ситуацию усугубило то, что в реальных экспериментах теоретические выкладки ученых получали полное подтверждение. Идею синтеза графена надолго забросили.

И только в 2004 году ученым удалось получить, а главное, доказать, что графен – это реальность. Для получения графена использовалась специальная методика химического скалывания графитовых кристаллических плоскостей. Похожие процессы происходят при рисовании карандашом по шершавым поверхностям, но требования к условиям отслоения образцов неизмеримо жестче.

Второй трудностью было доказательство существования графеновой структуры. Как можно наблюдать поверхность толщиной в один атомный слой? Авторы открытия говорят, что если бы не удалось найти способа наблюдения графена, то его не открыли бы до наших дней.

Остроумная методика наблюдения графена заключалась в формировании двумерной кристаллической поверхности на подложке из окиси кремния. А затем графен наблюдали в обычный оптический микроскоп. Правильная кристаллическая решетка графена создавала интерференционную картину, которая и наблюдалась исследователями.

Перспективы практического применения графена

Открытие графена вызвало реакцию, подобную разорвавшейся бомбы. После десятилетий полной уверенности, что двухмерной модификации углерода не существует, вдруг оказалось, что с помощью достаточно простых процессов его можно получать в неограниченном количестве. Только зачем?

Дело в том, что подобная модификация углерода обладает свойствами, которые, обычно сдержанные ученые, наделяют эпитетами фантастические, чудесные, уникальные. И им можно поверить. Сотни применений этого материала предложены уже сегодня, и каждую неделю появляется информация о новых возможностях графена.

Даже короткий перечень впечатляет: микрочипы с плотностью более 10 миллиардов полевых транзисторов на квадратный сантиметр, квантовые компьютеры, датчики размером несколько нанометров – это только в электронике. А еще аккумуляторные батареи фантастической емкости, фильтры для воды, которые задерживают любые примеси и многое другое.

Особые свойства графена позволяют не только эффективно отводить тепло, но и преобразовывать его обратно в электрическую энергию. Учитывая, что графеновая решетка (плоскость) имеет толщину в один атомный слой, несложно предсказать, что плотность элементом на чипе резко возрастет и может достигнуть 10 миллиардов транзистором на квадратный сантиметр. Уже сегодня реализованы графеновые транзисторы и микросхемы, смесители частоты, модуляторы, работающие на частотах выше 10 ГГц.

Не менее оптимистично относятся разработчики и к применению углеродных нанотрубок в микроэлектронике. На их основе уже реализованы транзисторные структуры, а недавно специалисты IBM продемонстрировали микросхему, на которой было сформировано 10 тысяч нанотрубок.

Конечно, сразу углеродные материалы не смогут заменить кремний в микроэлектронике. Но создание гибридных микросхем, в которых используются преимущества обоих материалов, уже выходит на коммерческий уровень. Не за горами тот день, когда в обычном мобильном устройстве появятся микропроцессоры, вычислительная мощь которых будет превышать производительность современных суперкомпьютеров.

Не стоит думать, что все эти применения – дело отдаленного будущего. В гонку практической реализации научного открытия включились гиганты электронной индустрии — корпорация IBM, Samsung и множество коммерческих исследовательских лабораторий. По мнению специалистов, в ближайшее десятилетие графен станет привычным материалом. А некоторые шутят, что Силиконовую долину в Калифорнии придется переименовывать на Графитовую.

www.ronl.ru

Статья: Графен и его свойства

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

Славянский Педагогический Государственный университет

КАФЕДРА ФИЗИКИ

КУРСОВАЯ РАБОТА

По теме: Графен и его свойства. Нобелевская премия 2010 года по физике

Выполнила

студентка 3-го курса,

физико-математического факультета , группа 3

Щербина И.Л.

Преподаватель

Костиков А.П

Славянск 2011г.

Содержание

1. История открытия

2. Получение

3. Дефекты

4. Возможные применения

5. Физика

5.1 Теория

5.1.1 Кристаллическая структура

5.1.2 Зонная структура

5.1.3 Линейный закон дисперсии

5.1.4 Эффективная масса

5.1.5 Хиральность и парадокс Клейна

5.2 Эксперимент

5.2.1 Проводимость

5.2.2 Квантовый эффект Холла

6. Интересные факты

Литература

1. История открытия

Графен является двумерным кристаллом, состоящим из одиночного слоя атомов углерода, собранных в гексагональную решётку. Его теоретическое исследование началось задолго до получения реальных образцов материала, поскольку из графена можно собрать трёхмерный кристаллграфита.

Графен является базой для построения теории этого кристалла. Графит являетсяполуметаллом. Как было показано в1947 годуП. Воллесом, взонной структуреграфена также отсутствуетзапрещённая зона, причём в точках соприкосновения валентной зоны, изоны проводимостиэнергетический спектрэлектронов идыроклинеен, как функцияволнового вектора. Такого рода спектром, обладают безмассовыефотоныи ультрарелятивистские частицы, а такженейтрино. Поэтому говорят, что эффективная массаэлектронов и дырок в графене вблизи точки соприкосновения зон равна нулю. Но здесь стоит заметить, что несмотря на сходство фотонов и безмассовых носителей, в графене существует несколько существенных различий, делающих носители в графене уникальными по своей физической природе, а именно: электроны и дырки являютсяфермионами, и они заряжены. В настоящее время аналогов для этих безмассовых заряженных фермионов среди известных элементарных частиц нет.

Несмотря на такие специфические особенности, экспериментального подтверждения эти выводы не получили до2005 года, поскольку не удавалось создать графен. Кроме того, ещё раньше было доказано теоретически, что свободную идеальную двумерную плёнку получить невозможно из-за нестабильности относительно сворачивания или скручивания. Тепловые флуктуации приводят к плавлению двумерного кристалла при любой конечной температуре.

Интерес к графену появился снова после открытияуглеродных нанотрубок, поскольку вся первоначальная теория строилась на простой модели нанотрубки как развёртки цилиндра. Поэтому теория для графена в приложении к нанотрубкам хорошо проработана.

Попытки получения графена, прикреплённого к другому материалу, начались с экспериментов, использующих простойкарандаш, и продолжились с использованием атомно-силового микроскопа для механического удаления слоёв графита, но не достигли успеха. Использование графита с внедрёнными (интеркалированный графит)в межплоскостное пространство чужеродными атомами (используется для увеличения расстояния между соседними слоями и их расщепления) также не привело к результату.

В 2004 году российскими и британскими учёными была опубликована работа в журнале Science , где сообщалось о получении графена на подложке окисленного кремния. Таким образом, стабилизация двумерной плёнки достигалась благодаря наличию связи с тонким слоем диэлектрикаSiO2по аналогии с тонкими плёнками, выращенными с помощьюМПЭ. Впервые были измереныпроводимость,эффект Шубникова— де Гааза,эффект Холла для образцов, состоящих из плёнок углерода с атомарной толщиной.

Метод отшелушивания является довольно простым и гибким, поскольку позволяет работать со всеми слоистыми кристаллами, то есть теми материалами, которые представляются как слабо (по сравнению с силами в плоскости) связанные слои двумерных кристаллов. В последующей работе авторы показали, что его можно использовать для получения других двумерных кристаллов:BN,MoS2,NbSe2, Bi2Sr2CaCu2Ox.

2. Получение

Кусочки графена получают при механическом воздействии на высокоориентированный пиролитический графитиликиш-графит. Сначала плоские куски графита помещают между липкими лентами (скотч) и расщепляют раз за разом, создавая достаточно тонкие слои (среди многих плёнок могут попадаться однослойные и двуслойные, которые и представляют интерес). После отшелушивания скотч с тонкими плёнками графита прижимают к подложке окисленного кремния. При этом трудно получить плёнку определённого размера и формы в фиксированных частях подложки (горизонтальные размеры плёнок составляют обычно около 10 мкм).Найденныес помощью оптического микроскопа, (они слабо видны при толщине диэлектрика 300 нм) плёнки подготавливают для измерений. Толщину можно определить с помощью атомно-силового микроскопа (она может варьироваться в пределах 1 нм для графена) или, используякомбинационное рассеяние. Используя стандартнуюэлектронную литографиюиреактивное плазменное травление, задают форму плёнки для электрофизических измерений.

Кусочки графена также можно приготовить из графита, используя химические методы. Сначала микрокристаллы графита подвергаются действию смесисернойисолянойкислот. Графит окисляется и на краях образца появляютсякарбоксильные группыграфена. Их превращают в хлориды при помощитионилхлорида. Затем под действиемоктадециламинав растворахтетрагидрофурана,тетрахлорметанаидихлорэтанаони переходят в графеновые слои толщиной 0,54нм. Этот химический метод не единственный, и, меняя органические растворители и химикаты, можно получить нанометровые слои графита.

В статьях описан ещё один химический метод получения графена, встроенного вполимернуюматрицу. Следует упомянуть ещё два метода: радиочастотное плазмохимическое осаждение из газовой фазы (англ.PECVD), рост при высоком давлении и температуре (англ.HPHT) . Из этих методов только последний можно использовать для получения плёнок большой площади.

Существует также несколько сообщений, посвящённых получению графена, выращенного на подложкахкарбида кремнияSiC(0001). Графитовая плёнка формируется при термическом разложении поверхности подложки SiC (этот метод получения графена гораздо ближе к промышленному производству), причём качество выращенной плёнки зависит от того, какая стабилизация у кристалла:C- стабилизированная илиSi- стабилизированная поверхность — в первом случае качество плёнок выше. В работах та же группа исследователей показала, что, несмотря на то, что толщина слоя графита составляет больше одного монослоя, в проводимости участвует только один слой в непосредственной близости от подложки, поскольку на границе SiC- C из-за разностиработ выходадвух материалов образуется нескомпенсированный заряд. Свойства такой плёнки оказались эквивалентны свойствам графена.

3. Дефекты

Наличие пятиугольных ячеек приводит к сворачиванию атомной плоскости в конус. Структура с 12 такими дефектами одновременно известна под названиемфуллерен. Присутствие семиугольных ячеек приводит к образованию седловидных искривлений атомной плоскости. Комбинация этих дефектов и нормальных ячеек может приводить к образованию различных форм поверхности.

4. Возможные применения

Считается, что на основе графена можно сконструировать баллистический транзистор. В марте 2006 года группа исследователей из технологического института штата Джорджии заявила, что ими был полученполевой транзисторна графене, а такжеквантово-интерференционныйприбор. Исследователи полагают, что благодаря их достижениям в скором времени появится новый класс графеновой наноэлектроники с базовой толщинойтранзисторовдо 10 нм. Данный транзистор обладает большим током утечки, то есть нельзя разделить два состояния с закрытым и открытым каналом.

Использовать напрямую графен при созданииполевого транзисторабез токов утечки не представляется возможным благодаря отсутствию запрещённой зоны в этом материале, поскольку нельзя добиться существенной разности в сопротивлении при любых приложенных напряжениях к затвору, то есть, не получается задать два состояния пригодных для двоичной логики: проводящее и непроводящее. Сначала нужно создать каким-нибудь образом запрещённую зону достаточной ширины при рабочей температуре (чтобы термически возбуждённые носители давали малый вклад в проводимость). Один из возможных способов предложен в работе. В этой статье предлагается создать тонкие полоски графена с такой шириной, чтобы благодаря квантово-размерномуэффекту ширина запрещённой зоны была достаточной для перехода в диэлектрическое состояние (закрытое состояние) прибора при комнатной температуре (28 мэВ соответствует ширине полоски 20 нм). Благодаря высокой подвижности (имеется в виду, что подвижность выше чем вкремнии, используемом вмикроэлектронике) 104см²·В−1·с−1 быстродействие такого транзистора будет заметно выше. Несмотря на то, что это устройство уже способно работать как транзистор, затвор к нему ещё не создан.

Другая область применения предложена в статьеи заключается в использовании графена в качестве очень чувствительногосенсорадля обнаружения отдельных молекул химических веществ, присоединённых к поверхности плёнки. В этой работе исследовались такие вещества, какNh4,CO,h3O,NO2. Сенсор размером 1 мкм × 1 мкм использовался для детектирования присоединения отдельных молекул NO2к графену. Принцип действия этого сенсора заключается в том, что разные молекулы могут выступать какдонорыиакцепторы, что в свою очередь ведёт к изменению сопротивления графена. В работетеоретически исследуется влияние различных примесей (использованных в отмеченном выше эксперименте) на проводимость графена. В работебыло показано, что NO2молекула является хорошим акцептором из-за своихпарамагнитныхсвойств, адиамагнитнаямолекула N2O4создаёт уровень близко к точке электронейтральности. В общем случае примеси, молекулы которых имеютмагнитный момент(неспаренный электрон), обладают более сильными легирующими свойствами.

Ещё одна перспективная область применения графена — его использование для изготовления электродов вионисторах(суперконденсаторах) для использования их в качестве перезаряжаемых источников тока. Опытные образцы ионисторов на графене имеют удельную энергоёмкость 32 Вт·ч/кг, сравнимую с таковой длясвинцово-кислотныхаккумуляторов(30−40 Вт·ч/кг)

5. Физика

Физические свойства нового материала можно изучать по аналогии с другими подобными материалами. В настоящее время экспериментальное и теоретическое исследование графена сосредоточено на стандартных свойствах двумерных систем: проводимости, квантовом эффекте Холла,слабой локализациии других эффектах, исследованных ранее вдвумерном электронном газе.

5.1 Теория

В этом параграфе кратко описываются основные положения теории, некоторые из которых получили экспериментальное подтверждение, а некоторые ещё ждут верификации.

5.1.1 Кристаллическая структура

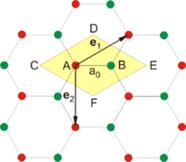
Кристаллическая решёткаграфена представляет собой плоскость, состоящую из шестиугольных ячеек, то есть является двумерной гексагональной кристаллической решёткой. Для такой решётки известно, что еёобратная решёткатоже будет гексагональной. Вэлементарной ячейке кристалла находятся два атома, обозначенные A и B. Каждый из этих атомов при сдвиге навектора трансляций(любой вектор вида, гдеmиn— любые целые числа) образует подрешётку из эквивалентных ему атомов, то есть свойства кристалла независимы от точек наблюдения, расположенных в эквивалентных узлах кристалла. На рисунке 3 представлены две подрешётки атомов, закрашенные разными цветами: зелёным и красным.

Расстояние между ближайшими атомами углерода в шестиугольниках, обозначенноеa0, составляет 0,142 нм.Постоянную решётки(a) можно получить из простых геометрических соображений. Она равна, то есть 0,246 нм. Если определить за начало координат точку, соответствующую узлу кристаллической решётки (подрешётка A), из которой начинаютсявекторы трансляций:с длиной векторов, равнойa,и ввести двумернуюдекартову систему координатв плоскости графена с осью ординат, направленной вверх, и осью абсцисс, направленной по отрезку, соединяющему соседние узлы A и B, то тогда координаты концов векторов трансляций, начинающихся из начала координат, запишутся в виде:

а соответствующие им вектора обратной решётки:

(без множителя2π). В декартовых координатах положение ближайших к узлу подрешётки A (все атомы которой на рисунке 3 показаны красным) в начале координат, атомов из подрешётки B (показаны соответственно зелёным цветом) задаётся в виде:

5.1.2 Зонная структура

Кристаллическая структура материала находит отражение во всех его физических свойствах. В особенности сильно от порядка, в котором расположены атомы в кристаллической решётке, зависит зонная структура кристалла.

Зонная структура графена рассчитана в статье[1]в приближении сильно связанных электронов. На внешней оболочке атома углерода находится 4 электрона, три из которых образуют связи с соседними атомами в решётки при перекрыванииsp²-гибридизированныхорбиталей, а оставшийся электрон находится в 2pz-состоянии (именно это состояние отвечает вграфитеза образование межплоскостных связей, а в графене — за образование энергетических зон). Вприближении сильно связанных электроновполнаяволновая функциявсех электронов кристалла записывается в виде суммы волновых функций электронов из разных подрешёток

где коэффициент λ — некий неизвестный (вариационный) параметр, который определяется из минимума энергии. Входящие в уравнение волновые функцииφ1иφ2записываются в виде суммы волновых функций отдельных электронов в различных подрешётках кристалла

Здесьи—радиус-векторы, направленные на узлы кристаллической решётки, аи— волновые функции электронов, локализованных вблизи этих узлов.

В приближении сильно связанных электронов интеграл перекрытия (γ0), то есть сила взаимодействия, быстро спадает на межатомных расстояниях. Другими словами — взаимодействие волновой функции центрального атома с волновыми функциями атомов, расположенных на зелёной окружности (см. Рис. 4), вносит основной вклад в формирование зонной структуры графена.

Энергетический спектр электронов в графене имеет вид (здесь учтены только ближайшие соседи, координаты которых задаются по формуле (1.3))

где знак «+» соответствует электронам, а «-» — дыркам.

5.1.3Линейный закон дисперсии

Из уравнения (2.4) следует, что вблизи точек соприкосновения валентной зоны и зоны проводимости (K и K')закон дисперсиидля носителей (электронов) в графене представляется в виде:

ГдеvF—скорость Ферми(экспериментальное значениеvF=106м/с) ,k— модуль волнового вектора в двумерном пространстве с компонентамиотсчитанного от K или K ' точек Дирака,— постоянная Планка. Здесь следует отметить, что такого рода спектром обладаетфотон, поэтому говорят, чтоквазичастицы(электроны и дырки, энергия для которых выражается формулой) в графене обладаютнулевойэффективной массой. Скорость ФермиvFиграет роль «эффективной» скорости света. Так как электроны и дырки — фермионы, то они должны описываться уравнением Дирака, но с нулевой массой частиц и античастиц (аналогично уравнениям для безмассовых нейтрино). Кроме того, так как графен — двухдолинный полуметалл, то уравнение Дирака должно быть модифицировано для учёта электронов и дырок из разных долин (K, K'). В итоге мы получим восемь дифференциальных уравнений первого порядка, которые включают такие характеристики носителей, как принадлежность к определённой подрешётке (A, B) кристалла, нахождение в долине (K, K') и проекцию спина. Решения этих уравнений описывают частицы с положительной энергией (электроны) и античастицы с отрицательной энергией (дырки). Обычно спин электрона не принимают во внимание (когда отсутствуют сильные магнитные поля) и гамильтониан уравнения Дирака записывается в виде:

где— вектор-строка, состоящая изматриц Паули.

Линейный закон дисперсии приводит к линейной зависимости плотности состояний от энергии, в отличие от обычных двумерных систем с параболическим законом дисперсии, гдеплотность состоянийне зависитот энергии. Плотность состояний в графене задаётся стандартным способом

где выражение под интегралом и есть искомая плотность состояний (на единицу площади):

Гдеgsиgv— спиновое и долинное вырождение соответственно, а модуль энергии появляется, чтобы описать электроны и дырки одной формулой. Отсюда видно, что при нулевой энергии плотность состояний равна нулю, то есть отсутствуют носители (при нулевой температуре).

Концентрация электронов задаётся интегралом по энергии

ГдеEF—уровень Ферми. Если температура мала по сравнению с уровнем Ферми, то можно ограничиться случаем вырожденного электронного газа

Концентрацией носителей управляют с помощью затворного напряжения. Они связаны простым соотношением(при толщине диэлектрика 300 нм).

Здесь также следует обратить внимание на тот факт, что появление линейного закона дисперсии при рассмотрении гексагональной решётки не является уникальной особенностью для данного типа кристаллической структуры, а может появляться и при существенном искажении решётки вплоть доквадратной решётки.

5.1.4 Эффективная масса

Благодаря линейному закону дисперсии эффективная масса электронов и дырок в графене равна нулю. Но в магнитном поле возникает другая масса, связанная с движением электрона по замкнутым орбитам и называемаяциклотронной массой. Связь между циклотронной массой и энергетическим спектром для носителей в графене получается из следующего рассмотрения. Энергияуровней Ландаудляуравнения Дираказадаётся в виде

где «±» соответствует спиновому расщеплению.Плотность состоянийв графене осциллирует как функция обратного магнитного поля, и её частота равна

ГдеS(E) = πk2 — площадь орбиты в пространстве волновых векторов на уровне Ферми. Осциллирующий характер плотности состояний приводит к осцилляциям магнетосопротивления, что эквивалентноэффекту Шубникова — де Гаазав обычных двумерных системах. Исследуя температурную зависимость амплитуды осцилляций, находят циклотронную массу носителей.

Из периода осцилляций также можно определить концентрацию носителей

Циклотронная массасвязана с площадью орбиты следующим соотношением

Если принять во внимание линейный закон дисперсии для носителей в графене (3.1), то зависимость эффективной массы от концентрации задаётся формулой

Согласие этой корневой зависимости с экспериментальными результатами стало доказательством линейности закона дисперсии в графене

5.1.5 Хиральность ипарадокс Клейна

Рассмотрим часть гамильтониана для долиныK(см. формулу (3.2)):

Матрицы Паули здесь не имеют отношения к спину электрона, а отражают вклад двух подрешёток в формирование двухкомпонентной волновой функции частицы. Матрицы Паули являются операторамипсевдоспинапо аналогии со спином электрона. Данный гамильтониан полностью эквивалентен гамильтониану длянейтрино, и, как и для нейтрино, существует сохраняющаяся величина проекции спина (псевдоспина для частиц в графене) на направление движения — величина, называемаяспиральностью(хиральностью). Для электронов хиральность положительна, а для дырок — отрицательна. Сохранение хиральности в графене приводит к такому явлению, какпарадокс Клейна. В квантовой механике с этим явлением связано нетривиальное поведениекоэффициента прохождениярелятивистской частицейпотенциальных барьеров, высота которых больше, чем удвоенная энергия покоя частицы. Частица более легко преодолевает более высокий барьер. Для частиц в графене можно построить аналог парадокса Клейна с той разницей, что не существует массы покоя. Можно показать, что электрон преодолевает с вероятностью, равной единице, любые потенциальные барьеры при нормальном падении на границу раздела. Если падение происходит под углом, то существует некоторая вероятность отражения. Например, обычный p-n переход в графене является таким преодолимым барьером. В целом парадокс Клейна приводит к тому, что частицы в графене трудно локализовать, что в свою очередь приводит, например, к высокой подвижности носителей в графене. Недавно были предложены несколько моделей, позволяющих локализовать электроны в графене. В работевпервые продемонстрирована квантовая точка из графена и измеренакулоновская блокадапри 0,3 К.

5.2 Эксперимент

Подавляющее большинство экспериментальных работ посвящено графену, полученному отшелушиванием объёмного кристалла пиролитического графита.

5.2.1 Проводимость

Теоретически показано, что основное ограничение наподвижностьэлектронов и дырок в графене (на Si подложке) возникает из-за заряженных примесей в диэлектрике (SiO2), поэтому сейчас ведутся работы по получению свободновисящих плёнок графена, что должно увеличить подвижность до 2×106 см²·В−1·c−1. В настоящее время максимальная достигнутая подвижность составляет 2×105см²·В−1·c−1; она была получена в образце, подвешенном над слоем диэлектрика на высоте 150 нм (часть диэлектрика была удалена с помощьюжидкостного травителя). Образец с толщиной в один атом поддерживался при помощи широких контактов. Для улучшения подвижности образец подвергался очистке от примесей на поверхности посредством пропускания тока[41], который нагревал весь образец до 900 К в высокомвакууме.

Идеальную двумерную плёнку в свободном состоянии нельзя получить из-за её термодинамической нестабильности. Но если в плёнке будут дефекты или она будет деформирована в пространстве (в третьем измерении), то такая «неидеальная» плёнка может существовать без контакта с подложкой[42]. В эксперименте[43]с использованиемпросвечивающего электронного микроскопабыло показано, что свободные плёнки графена существуют и образуют поверхность сложной волнистой формы, с латеральными размерами пространственных неоднородностей около 5—10 нм и высотой 1 нм. В статье[44]было показано, что можно создать свободную от контакта с подложкой плёнку, закреплённую с двух краёв, образуя, таким образом, наноэлектромеханическую систему. В данном случае подвешенный графен можно рассматривать как мембрану, изменение частоты механических колебаний которой предлагается использовать для детектирования массы, силы и заряда, то есть использовать в качестве высокочувствительного сенсора.

Подложка кремния с диэлектриком, на котором покоится[2]графен, должна быть сильно легирована, чтобы её можно было использовать в качествеобратного затвора, при помощи которого можно управлять концентрацией и даже изменятьтип проводимости. Поскольку графен является полуметаллом, то приложение положительного напряжения к затвору приводит к электронной проводимости графена, и напротив — если приложить отрицательное напряжение, то основными носителями станут дырки, поэтому в принципе нельзя обеднить полностью графен от носителей. Заметим, что если графит состоит из нескольких десятков слоёв, то электрическое поле достаточно хорошо экранировано, как и в металлах, огромным количеством носителей в полуметалле[15].

В идеальном случае, когда отсутствует легирование и затворное напряжение равно нулю, не должно быть носителей тока (см.плотность состояний), что, если следовать наивным представлениям, должно приводить к отсутствиюпроводимости. Но как показывают эксперименты и теоретические работы[45][46][47], вблизи дираковской точки или точки электронейтральности для дираковских фермионов существует конечное значение проводимости, хотя величина минимальной проводимости зависит от метода расчёта. Эта идеальная область не изучена просто потому, что нет достаточно чистых образцов. В действительности все плёнки графена соединены с подложкой, и это приводит к неоднородностям, флуктуациям потенциала, что ведёт к пространственной неоднородности типа проводимости по образцу, поэтому даже в точке электронейтральности концентрация носителей теоретически не меньше чем 1012см−2. Здесь проявляются отличие от обычных систем с двумерным электронным или дырочным газом, а именно отсутствуетпереход металл-диэлектрик.

5.2.2Квантовый эффект Холла

Впервые необычный (англ.unconventional) квантовый эффект Холла наблюдали в работах, где было показано, что носители в графене действительно обладают нулевой эффективной массой, поскольку положения плато на зависимости недиагональной компоненты тензора проводимости соответствовали полуцелым значениям холловской проводимостив единицах4e2/h(множитель 4 появляется из-за четырёхкратного вырождения энергии), то естьЭто квантование согласуется с теорией квантового эффекта Холла для дираковских безмассовыхфермионов. Сравнение целочисленного квантового эффекта Холла в обычной двумерной системе и графене см. на рисунке 6. Здесь показаны уширенные уровни Ландау для электронов (выделение красным цветом) и для дырок (синий цвет). Еслиуровень Ферминаходится между уровнями Ландау, то на зависимости холловской проводимостиσxyнаблюдается ряд плато. Эта зависимость отличается от обычных двумерных систем (аналогом может служить двумерный электронный газ в кремнии, который является двухдолинным полупроводником в плоскостях, эквивалентных {100}, то есть тоже обладает четырёхкратным вырождением уровней Ландау, и холловские плато наблюдаются приν = 4 |n|).

Квантовый эффект Холла(КЭХ) может использоваться как эталон сопротивления, потому что численное значение наблюдаемого в графене плато, равноеh/ 2e2,воспроизводится с хорошей точностью, хотя качество образцов уступает высокоподвижномуДЭГвGaAs, и, соответственно, точности квантования. Преимущество КЭХ в графене в том, что он наблюдается при комнатной температуре(в магнитных полях свыше 20Т). Основное ограничение на наблюдение КЭХ при комнатной температуре накладывает не само размытие распределения Ферми-Дирака, а рассеяние носителей на примесях, что приводит к уширению уровней Ландау.

графен хиральность кристаллический дисперсия

Рис. 6. a) Квантовый эффект Холла в обычной двумерной системе. b) Квантовый эффект Холла в графене.G=gsgv= 4 — вырождение спектра

В современных образцах графена (лежащих на подложке) вплоть до 45 Т невозможно наблюдатьдробный квантовый эффект Холла, но наблюдается целочисленный квантовый эффект Холла, который не совпадает с обычным квантовым эффектом Холла. В работе наблюдается спиновое расщеплениерелятивистских уровней Ландауи снятие четырёхкратного вырождения для наинизшего уровня Ландау вблизиточки электронейтральности. Для объяснения этого эффекта предложено несколько теорий, но недостаточное количество экспериментального материала не позволяет выбрать среди них правильную.

Из-за отсутствия запрещённой зоны в графене в структурах с верхним затвором можно сформировать непрерывныйp-n переход, когда напряжение на верхнем затворе позволяет инвертировать знак носителей, задаваемыйобратным затворомв графене, где концентрация носителей никогда не обращается в ноль (кроме точки электронейтральности). В таких структурах тоже можно наблюдать квантовый эффект Холла, но из-за неоднородности знака носителей значения холловских плато отличаются он приведённых выше. Для структуры с одним p-n переходом значения квантования холловской проводимости описываются формулой

Гдеνиν' —факторы заполненияв n- и p- области соответственно (p-область находится под верхним затвором), которые могут принимать значенияи т. д. Тогда плато в структурах с одним p-n переходом наблюдаются при значениях 1, 3/2, 2, и т. д.

Для структуры с двумя p-n переходами соответствующие значения холловской проводимости равны

6. Интересные факты

Со. 7. Для получения нанотрубки (n, m), графитовую плоскость надо разрезать по направлениям пунктирных линий и свернуть вдоль направления вектораR

В статье, опубликованной 10 ноября 2005 года в журнале Nature,Константин НовосёловиАндрей Геймутверждают, чтоэлектрические зарядыв графене ведут себя какрелятивистские частицыс нулевой эффективной массой. Эти частицы, известные как безмассовыефермионыДирака, описываются уравнением Дирака, хотя вэффекте Шубникова-де Гааза(осцилляции магнетосопротивления) наблюдаемые осцилляции соответствуют конечной циклотронной массе.

Так как закон дисперсии для носителей идентичен закону для безмассовых частиц, графен может выступать в качестве экспериментальной лаборатории дляквантовой электродинамики.

Квантовый эффект Холла в графене может наблюдаться даже при комнатной температуреиз-за большой циклотронной энергии, при которой температурное размытие функции распределения Ферми-Дирака меньше этой энергии(это расстояниемежду первым и нулевым уровнями Ландау равно 1200 K при магнитном поле 9 Т).

При сворачивании графена в цилиндр (см. Рис. 7) получается одностенная нанотрубка. В зависимости от конкретной схемы сворачивания графитовой плоскости, нанотрубки могут обладать или металлическими, или полупроводниковыми свойствами.

В графене отсутствует вигнеровская кристаллизация.

В графене нарушается приближение Борна-Оппенгеймера(адиабатическое приближение), гласящее, что в силу медленного движения ионных остовов решётки их можно включить в рассмотрение как возмущение, известное как фононы решётки, — основное приближение, на котором строится зонная теория твёрдых тел.

За получение и исследование свойств графена, Нобелевская премия 2010 года по физике присужденаАндрею ГеймуиКонстантину Новосёлову.

Литература

1. Novoselov K.S. et al. «Electric Field Effect in Atomically Thin Carbon Films», Science 306, 666 (2004)

2. Bunch J.S. et. al. Electromechanical Resonators from Graphene Sheets Science 315, 490 (2007)

3. Chen Zh. et. al. Graphene Nano-Ribbon Electronics Physica E 40, 228 (2007)

4. Novoselov, K. S. et al. «Two-dimensional atomic crystals», PNAS 102, 10451 (2005)

5. Rollings E. et. al. Synthesis and characterization of atomically thin graphite films on a silicon carbide substrate J. Phys. Chem. Solids 67, 2172 (2006)

6. Hass J. et. al. Highly ordered graphene for two dimensional electronics Appl. Phys. Lett. 89, 143106 (2006)

7. Novoselov K.S. et al. «Two-dimensional gas of massless Dirac fermions in graphene», Nature 438, 197 (2005)

8. Shioyama H. Cleavage of graphite to graphene J. Mat. Sci. Lett. 20, 499—500 (2001)

9. Ландау Л.Д., Лифшиц Е.М. Статистическая физика. — 2001.

10. Zhang Y. et al. Fabrication and electric-field-dependent transport measurements of mesoscopic graphite devices Appl. Phys. Lett. 86, 073104 (2005)

11. Parvizi F., et. al. Graphene Synthesis via the High Pressure — High Temperature Growth Process Micro Nano Lett., 3, 29 (2008)

12. Sidorov A.N. et al.,Electrostatic deposition of graphene Nanotechnology 18, 135301 (2007)

13. J. Hass et. al. Why Multilayer Graphene on 4H-SiC(000-1) Behaves Like a Single Sheet of Graphene Phys. Rev. Lett. 100, 125504 (2008).

14. S.R.C. Vivekchand; Chandra Sekhar Rout, K.S. Subrahmanyam, A. Govindaraj and C.N.R. Rao (2008). "Graphene-based electrochemical supercapacitors". J. Chem. Sci., Indian Academy of Sciences 120, January 2008: 9−13.

15. Статья ГрафенизВикипедии, свободной энциклопедии. ДоступноподлицензиейCreative Commons Attribution-Share Alike

superbotanik.net

Реферат Графен и его свойства

МИНИСТЕРСТВООБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

СлавянскийПедагогический Государственный университет

КАФЕДРАФИЗИКИ

КУРСОВАЯРАБОТА

Потеме: Графен и его свойства. Нобелевская премия 2010 года по физике

Выполнила

студентка 3-го курса,

физико-математического факультета, группа 3

Щербина И.Л.

Преподаватель

Костиков А.П

Славянск2011г.

Содержание

1. История открытия

2. Получение

3. Дефекты

4. Возможные применения

5. Физика

5.1 Теория

5.1.1 Кристаллическаяструктура

5.1.2 Зонная структура

5.1.3 Линейный закон дисперсии

5.1.4 Эффективная масса

5.1.5 Хиральность ипарадокс Клейна

5.2 Эксперимент

5.2.1 Проводимость

5.2.2 Квантовый эффектХолла

6. Интересные факты

Литература

1. Историяоткрытия

Графенявляется двумерным кристаллом,состоящим из одиночного слоя атомов углерода, собранных в гексагональную решётку.Его теоретическое исследование началось задолго до получения реальных образцовматериала, поскольку из графена можно собрать трёхмерный кристалл графита.

Графенявляется базой для построения теории этого кристалла. Графит является полуметаллом. Как было показано в 1947 году П. Воллесом, в зонной структуре графена также отсутствует запрещённая зона, причём в точкахсоприкосновения валентной зоны, и зоны проводимости энергетический спектр электронов и дырок линеен,как функция волнового вектора. Такогорода спектром, обладают безмассовые фотоны и ультрарелятивистские частицы, а также нейтрино. Поэтому говорят, что эффективная масса электронов и дырок в графене вблизи точкисоприкосновения зон равна нулю. Но здесь стоит заметить, что несмотря насходство фотонов и безмассовых носителей, в графене существует несколькосущественных различий, делающих носители в графене уникальными по своейфизической природе, а именно: электроны и дырки являются фермионами, и они заряжены. В настоящеевремя аналогов для этих безмассовых заряженных фермионов среди известныхэлементарных частиц нет.

Несмотряна такие специфические особенности, экспериментального подтверждения эти выводыне получили до2005 года, поскольку не удавалось создатьграфен. Кроме того, ещё раньше было доказано теоретически, что свободнуюидеальную двумерную плёнку получить невозможно из-за нестабильностиотносительно сворачивания или скручивания. Тепловые флуктуации приводят кплавлению двумерного кристалла при любой конечной температуре.

Интереск графену появился снова после открытия углеродныхнанотрубок, поскольку вся первоначальная теория строилась на простой моделинанотрубки как развёртки цилиндра. Поэтому теория для графена в приложении кнанотрубкам хорошо проработана.

Попыткиполучения графена, прикреплённого к другому материалу, начались с экспериментов,использующих простой карандаш, и продолжились с использованием атомно-силового микроскопа длямеханического удаления слоёв графита, но не достигли успеха. Использование графитас внедрёнными (интеркалированный графит) в межплоскостное пространство чужероднымиатомами (используется для увеличения расстояния между соседними слоями и ихрасщепления) также не привело к результату.

В2004 году российскими и британскими учёными была опубликована работа в журналеScience, где сообщалось о получении графена на подложке окисленного кремния.Таким образом, стабилизация двумерной плёнки достигалась благодаря наличиюсвязи с тонким слоем диэлектрика SiO2 по аналогии с тонкими плёнками, выращеннымис помощью МПЭ. Впервые были измерены проводимость, эффект Шубникова— де Гааза, эффект Холла для образцов, состоящих из плёнокуглерода с атомарной толщиной.

Методотшелушивания является довольно простым и гибким, поскольку позволяет работатьсо всеми слоистыми кристаллами, то есть теми материалами, которыепредставляются как слабо (по сравнению с силами в плоскости) связанные слоидвумерных кристаллов. В последующей работе авторы показали, что его можноиспользовать для получения других двумерных кристаллов: BN, MoS2, NbSe2,Bi2Sr2CaCu2Ox.

2.Получение

Кусочкиграфена получают при механическом воздействии на высокоориентированный пиролитическийграфит или киш-графит. Сначала плоскиекуски графита помещают между липкими лентами (скотч) и расщепляют раз за разом,создавая достаточно тонкие слои (среди многих плёнок могут попадатьсяоднослойные и двуслойные, которые и представляют интерес). После отшелушиванияскотч с тонкими плёнками графита прижимают к подложке окисленного кремния. Приэтом трудно получить плёнку определённого размера и формы в фиксированныхчастях подложки (горизонтальные размеры плёнок составляют обычно около 10 мкм). Найденныес помощью оптического микроскопа, (они слабо видны при толщинедиэлектрика 300 нм) плёнки подготавливают для измерений. Толщину можноопределить с помощью атомно-силового микроскопа (она может варьироваться впределах 1 нм для графена) или, используя комбинационное рассеяние. Используястандартную электронную литографию иреактивное плазменное травление, задают формуплёнки для электрофизических измерений.

Кусочкиграфена также можно приготовить из графита, используя химические методы.Сначала микрокристаллы графита подвергаются действию смеси серной и солянойкислот. Графит окисляется и на краях образца появляются карбоксильные группы графена. Их превращают в хлориды при помощи тионилхлорида. Затем под действием октадециламина в растворах тетрагидрофурана, тетрахлорметана и дихлорэтана они переходят в графеновые слои толщиной0,54 нм. Этот химический метод неединственный, и, меняя органические растворители и химикаты, можно получитьнанометровые слои графита.

Встатьях описан ещё один химический метод получения графена, встроенного в полимерную матрицу. Следует упомянуть ещё два метода:радиочастотное плазмохимическое осаждение из газовой фазы (англ. PECVD), рост при высокомдавлении и температуре (англ. HPHT). Из этих методовтолько последний можно использовать для получения плёнок большой площади.

Есликристалл пиролитического графита и подложку поместить между электродами, то, можнодобиться того, что кусочки графита с поверхности, среди которых могут оказатьсяплёнки атомарной толщины, под действием электрического поля могут перемещатьсяна подложку окисленного кремния. Для предотвращения пробоя (между электродамиприкладывали напряжение от 1 до 13 кВ) между электродами также помещали тонкуюпластину слюды.

Существуеттакже несколько сообщений, посвящённых получению графена, выращенного наподложках карбида кремния SiC(0001). Графитовая плёнка формируетсяпри термическом разложении поверхности подложки SiC (этот метод полученияграфена гораздо ближе к промышленному производству), причём качество выращеннойплёнки зависит от того, какая стабилизация у кристалла:C — стабилизированнаяили Si — стабилизированнаяповерхность — в первом случае качество плёнок выше. В работах та же группаисследователей показала, что, несмотря на то, что толщина слоя графитасоставляет больше одного монослоя, в проводимости участвует только один слой внепосредственной близости от подложки, поскольку на границе SiC- C из-заразности работ выхода двух материалов образуетсянескомпенсированный заряд. Свойства такой плёнки оказались эквивалентнысвойствам графена.

3.Дефекты

Идеальныйграфен состоит исключительно из шестиугольных ячеек. Присутствие пяти- исемиугольных ячеек будет приводить к различного рода дефектам.

Наличиепятиугольных ячеек приводит к сворачиванию атомной плоскости в конус. Структурас 12 такими дефектами одновременно известна под названием фуллерен. Присутствие семиугольных ячеекприводит к образованию седловидных искривлений атомной плоскости. Комбинацияэтих дефектов и нормальных ячеек может приводить к образованию различных формповерхности.

4.Возможные применения

Считается,что на основе графена можно сконструировать баллистический транзистор. В марте2006 года группа исследователей из технологического института штата Джорджиизаявила, что ими был получен полевой транзистор на графене, а также квантово-интерференционный прибор. Исследователи полагают, чтоблагодаря их достижениям в скором времени появится новый класс графеновойнаноэлектроники с базовой толщиной транзисторов до 10 нм. Данный транзистор обладаетбольшим током утечки, то есть нельзя разделить два состояния с закрытым иоткрытым каналом.

Использоватьнапрямую графен при создании полевоготранзистора без токов утечки непредставляется возможным благодаря отсутствию запрещённой зоны в этомматериале, поскольку нельзя добиться существенной разности в сопротивлении прилюбых приложенных напряжениях к затвору, то есть, не получается задать двасостояния пригодных для двоичной логики: проводящее и непроводящее. Сначаланужно создать каким-нибудь образом запрещённую зону достаточной ширины прирабочей температуре (чтобы термически возбуждённые носители давали малый вкладв проводимость). Один из возможных способов предложен в работе. В этой статьепредлагается создать тонкие полоски графена с такой шириной, чтобы благодаря квантово-размерному эффекту ширина запрещённой зоны быладостаточной для перехода в диэлектрическое состояние (закрытое состояние)прибора при комнатной температуре (28 мэВ соответствует ширине полоски 20 нм).Благодаря высокой подвижности (имеется в виду, что подвижность выше чем в кремнии, используемом в микроэлектронике) 104 см²·В−1·с−1 быстродействиетакого транзистора будет заметно выше. Несмотря на то, что это устройство ужеспособно работать как транзистор, затвор к нему ещё не создан.

Другаяобласть применения предложена в статье изаключается в использовании графена в качестве очень чувствительного сенсора дляобнаружения отдельных молекул химических веществ, присоединённых к поверхностиплёнки. В этой работе исследовались такие вещества, как Nh4, CO, h3O, NO2. Сенсор размером 1 мкм × 1 мкмиспользовался для детектирования присоединения отдельных молекул NO2 к графену. Принцип действия этого сенсоразаключается в том, что разные молекулы могут выступать как доноры и акцепторы, что в свою очередь ведёт кизменению сопротивления графена. В работе теоретическиисследуется влияние различных примесей (использованных в отмеченном вышеэксперименте) на проводимость графена. В работе было показано, что NO2 молекула является хорошим акцептором из-засвоих парамагнитных свойств, а диамагнитная молекула N2O4 создаёт уровень близко к точкеэлектронейтральности. В общем случае примеси, молекулы которых имеют магнитный момент (неспаренный электрон), обладают болеесильными легирующими свойствами.

Ещёодна перспективная область применения графена — его использование дляизготовления электродов в ионисторах (суперконденсаторах) для использования их вкачестве перезаряжаемых источников тока. Опытные образцы ионисторов на графенеимеют удельную энергоёмкость 32 Вт·ч/кг, сравнимую с таковой для свинцово-кислотных аккумуляторов (30−40 Вт·ч/кг)

Недавнобыл создан новый тип светодиодов на основе графена (LEC). Процесс утилизацииновых материалов экологичен при достаточно низкой цене.

5.Физика

Физическиесвойства нового материала можно изучать по аналогии с другими подобнымиматериалами. В настоящее время экспериментальное и теоретическое исследованиеграфена сосредоточено на стандартных свойствах двумерных систем: проводимости,квантовом эффекте Холла, слабой локализации и других эффектах, исследованных ранее в двумерном электронном газе.

5.1Теория

Вэтом параграфе кратко описываются основные положения теории, некоторые изкоторых получили экспериментальное подтверждение, а некоторые ещё ждут верификации.

5.1.1Кристаллическая структура

Кристаллическаярешётка графена представляет собойплоскость, состоящую из шестиугольных ячеек, то есть является двумернойгексагональной кристаллической решёткой. Для такой решётки известно, что её обратная решётка тоже будет гексагональной. В элементарной ячейке кристалла находятся дваатома, обозначенные A и B. Каждый из этих атомов при сдвиге на вектора трансляций (любой вектор вида />, где m и n — любые целые числа) образуетподрешётку из эквивалентных ему атомов, то есть свойства кристалла независимыот точек наблюдения, расположенных в эквивалентных узлах кристалла. На рисунке3 представлены две подрешётки атомов, закрашенные разными цветами: зелёным икрасным.

Расстояниемежду ближайшими атомами углерода в шестиугольниках, обозначенное a0,составляет 0,142 нм. Постоянную решётки (a) можнополучить из простых геометрических соображений. Она равна />, то есть0,246 нм. Если определить за начало координат точку, соответствующую узлукристаллической решётки (подрешётка A), из которой начинаются векторы трансляций: /> с длиной векторов, равной a, и ввести двумернуюдекартову систему координат в плоскости графена с осью ординат,направленной вверх, и осью абсцисс, направленной по отрезку, соединяющемусоседние узлы A и B, то тогда координаты концов векторов трансляций,начинающихся из начала координат, запишутся в виде:

асоответствующие им вектора обратной решётки:

(безмножителя 2π).В декартовых координатах положение ближайших к узлу подрешётки A (все атомыкоторой на рисунке 3 показаны красным) в начале координат, атомов из подрешёткиB (показаны соответственно зелёным цветом) задаётся в виде:

5.1.2Зонная структура

Кристаллическаяструктура материала находит отражение во всех его физических свойствах. Вособенности сильно от порядка, в котором расположены атомы в кристаллическойрешётке, зависит зонная структура кристалла.

Зонная структура графена рассчитана в статье[1] в приближении сильно связанных электронов.На внешней оболочке атома углерода находится 4 электрона, три из которыхобразуют связи с соседними атомами в решётки при перекрывании sp²-гибридизированных орбиталей, а оставшийся электрон находитсяв 2pz-состоянии (именно это состояние отвечает в графите заобразование межплоскостных связей, а в графене — за образование энергетическихзон). В приближении сильно связанныхэлектронов полная волновая функция всех электронов кристалла записывается ввиде суммы волновых функций электронов из разных подрешёток

гдекоэффициент λ — некий неизвестный (вариационный) параметр, которыйопределяется из минимума энергии. Входящие в уравнение волновые функции φ1 и φ2 записываютсяв виде суммы волновых функций отдельных электронов в различных подрешёткахкристалла

Здесь />и />— радиус-векторы,направленные на узлы кристаллической решётки, а /> и />— волновые функции электронов, локализованныхвблизи этих узлов.

Вприближении сильно связанных электронов интеграл перекрытия (γ0), то есть сила взаимодействия, быстро спадает намежатомных расстояниях. Другими словами — взаимодействие волновой функциицентрального атома с волновыми функциями атомов, расположенных на зелёнойокружности (см. Рис. 4), вносит основной вклад в формирование зонной структурыграфена.

Энергетическийспектр электронов в графене имеет вид (здесь учтены только ближайшие соседи,координаты которых задаются по формуле (1.3))

гдезнак «+» соответствует электронам, а «-» — дыркам.

5.1.3 Линейный закон дисперсии

Изуравнения (2.4) следует, что вблизи точек соприкосновения валентной зоны и зоныпроводимости (K и K') закон дисперсии для носителей (электронов) в графенепредставляется в виде:

Где vF — скорость Ферми (экспериментальное значение vF =106 м/с), k — модуль волнового вектора в двумерномпространстве с компонентами />отсчитанного от K или K ' точек Дирака, /> — постояннаяПланка. Здесь следует отметить, что такого рода спектром обладает фотон,поэтому говорят, что квазичастицы (электроны и дырки, энергия для которыхвыражается формулой />) в графене обладают нулевой эффективной массой. Скорость Ферми vF играет роль «эффективной» скорости света.Так как электроны и дырки — фермионы, то они должны описываться уравнениемДирака, но с нулевой массой частиц и античастиц (аналогично уравнениям длябезмассовых нейтрино). Кроме того, так как графен — двухдолинный полуметалл, тоуравнение Дирака должно быть модифицировано для учёта электронов и дырок изразных долин (K, K'). В итоге мы получим восемь дифференциальных уравненийпервого порядка, которые включают такие характеристики носителей, какпринадлежность к определённой подрешётке (A, B) кристалла, нахождение в долине(K, K') и проекцию спина. Решения этих уравнений описывают частицы сположительной энергией (электроны) и античастицы с отрицательной энергией(дырки). Обычно спин электрона не принимают во внимание (когда отсутствуютсильные магнитные поля) и гамильтониан уравнения Дирака записывается в виде:

где />— вектор-строка,состоящая из матриц Паули.

Линейныйзакон дисперсии приводит к линейной зависимости плотности состояний от энергии,в отличие от обычных двумерных систем с параболическим законом дисперсии, где плотность состояний не зависит от энергии. Плотность состояний в графенезадаётся стандартным способом

гдевыражение под интегралом и есть искомая плотность состояний (на единицуплощади):

Где gs и gv — спиновое и долинное вырождение соответственно,а модуль энергии появляется, чтобы описать электроны и дырки одной формулой.Отсюда видно, что при нулевой энергии плотность состояний равна нулю, то естьотсутствуют носители (при нулевой температуре).

Концентрацияэлектронов задаётся интегралом по энергии

Где EF — уровень Ферми. Если температура мала посравнению с уровнем Ферми, то можно ограничиться случаем вырожденногоэлектронного газа

Концентрациейносителей управляют с помощью затворного напряжения. Они связаны простымсоотношением /> (притолщине диэлектрика 300 нм).

Здесь такжеследует обратить внимание на тот факт, что появление линейного закона дисперсиипри рассмотрении гексагональной решётки не является уникальной особенностью дляданного типа кристаллической структуры, а может появляться и при существенномискажении решётки вплоть до квадратной решётки.

5.1.4Эффективная масса

Благодарялинейному закону дисперсии эффективная масса электронов и дырок в графене равнанулю. Но в магнитном поле возникает другая масса, связанная с движениемэлектрона по замкнутым орбитам и называемая циклотронноймассой. Связь между циклотронной массой и энергетическим спектром дляносителей в графене получается из следующего рассмотрения. Энергия уровней Ландау для уравнения Дирака задаётся в виде

где«±» соответствует спиновому расщеплению. Плотностьсостояний в графене осциллирует какфункция обратного магнитного поля, и её частота равна

Где S(E) =πk2 — площадь орбиты в пространстве волновых векторов науровне Ферми. Осциллирующий характер плотности состояний приводит к осцилляцияммагнетосопротивления, что эквивалентно эффекту Шубникова — де Гааза в обычных двумерных системах. Исследуятемпературную зависимость амплитуды осцилляций, находят циклотронную массуносителей.

Изпериода осцилляций также можно определить концентрацию носителей

Циклотроннаямасса связана с площадью орбитыследующим соотношением

Еслипринять во внимание линейный закон дисперсии для носителей в графене (3.1), тозависимость эффективной массы от концентрации задаётся формулой

Согласиеэтой корневой зависимости с экспериментальными результатами сталодоказательством линейности закона дисперсии в графене

5.1.5Хиральность и парадокс Клейна

Рассмотримчасть гамильтониана для долины K (см. формулу (3.2)):

МатрицыПаули здесь не имеют отношения к спину электрона, а отражают вклад двухподрешёток в формирование двухкомпонентной волновой функции частицы. МатрицыПаули являются операторами псевдоспина по аналогии со спином электрона. Данныйгамильтониан полностью эквивалентен гамильтониану для нейтрино, и, как и для нейтрино,существует сохраняющаяся величина проекции спина (псевдоспина для частиц в графене)на направление движения — величина, называемая спиральностью (хиральностью). Для электронов хиральностьположительна, а для дырок — отрицательна. Сохранение хиральности в графенеприводит к такому явлению, как парадоксКлейна. В квантовой механике с этим явлением связано нетривиальное поведение коэффициента прохождения релятивистской частицей потенциальных барьеров, высота которыхбольше, чем удвоенная энергия покоя частицы. Частица более легко преодолеваетболее высокий барьер. Для частиц в графене можно построить аналог парадоксаКлейна с той разницей, что не существует массы покоя. Можно показать, чтоэлектрон преодолевает с вероятностью, равной единице, любые потенциальныебарьеры при нормальном падении на границу раздела. Если падение происходит подуглом, то существует некоторая вероятность отражения. Например, обычный p-nпереход в графене является таким преодолимым барьером. В целом парадокс Клейнаприводит к тому, что частицы в графене трудно локализовать, что в свою очередьприводит, например, к высокой подвижности носителей в графене. Недавно былипредложены несколько моделей, позволяющих локализовать электроны в графене. Вработе впервые продемонстрированаквантовая точка из графена и измерена кулоновская блокада при 0,3 К.

5.2Эксперимент

Подавляющеебольшинство экспериментальных работ посвящено графену, полученномуотшелушиванием объёмного кристалла пиролитического графита.

5.2.1Проводимость

Теоретическипоказано, что основное ограничение на подвижность электронов и дырок в графене (на Siподложке) возникает из-за заряженных примесей в диэлектрике (SiO2), поэтомусейчас ведутся работы по получению свободновисящих плёнок графена, что должноувеличить подвижность до 2×106 см²·В−1·c−1.В настоящее время максимальная достигнутая подвижность составляет 2×105 см²·В−1·c−1; она былаполучена в образце, подвешенном над слоем диэлектрика на высоте 150 нм (частьдиэлектрика была удалена с помощью жидкостного травителя). Образец столщиной в один атом поддерживался при помощи широких контактов. Для улучшенияподвижности образец подвергался очистке от примесей на поверхности посредствомпропускания тока[41], который нагревал весь образец до 900 К в высоком вакууме.

Идеальнуюдвумерную плёнку в свободном состоянии нельзя получить из-за еётермодинамической нестабильности. Но если в плёнке будут дефекты или она будетдеформирована в пространстве (в третьем измерении), то такая «неидеальная»плёнка может существовать без контакта с подложкой[42]. В эксперименте[43] с использованием просвечивающего электронного микроскопа было показано, что свободные плёнки графенасуществуют и образуют поверхность сложной волнистой формы, с латеральнымиразмерами пространственных неоднородностей около 5—10 нм и высотой 1 нм. Встатье[44] было показано, что можно создать свободнуюот контакта с подложкой плёнку, закреплённую с двух краёв, образуя, такимобразом, наноэлектромеханическую систему. В данном случае подвешенный графенможно рассматривать как мембрану, изменение частоты механических колебанийкоторой предлагается использовать для детектирования массы, силы и заряда, тоесть использовать в качестве высокочувствительного сенсора.

Подложкакремния с диэлектриком, на котором покоится[2] графен, должна быть сильно легирована,чтобы её можно было использовать в качестве обратного затвора, при помощикоторого можно управлять концентрацией и даже изменять тип проводимости. Поскольку графен являетсяполуметаллом, то приложение положительного напряжения к затвору приводит кэлектронной проводимости графена, и напротив — если приложить отрицательноенапряжение, то основными носителями станут дырки, поэтому в принципе нельзяобеднить полностью графен от носителей. Заметим, что если графит состоит изнескольких десятков слоёв, то электрическое поле достаточно хорошоэкранировано, как и в металлах, огромным количеством носителей в полуметалле[15].

Видеальном случае, когда отсутствует легирование и затворное напряжение равнонулю, не должно быть носителей тока (см. плотностьсостояний), что, если следовать наивным представлениям, должно приводить котсутствию проводимости.Но как показывают эксперименты и теоретические работы[45][46][47],вблизи дираковской точки или точки электронейтральности для дираковскихфермионов существует конечное значение проводимости, хотя величина минимальнойпроводимости зависит от метода расчёта. Эта идеальная область не изучена простопотому, что нет достаточно чистых образцов. В действительности все плёнкиграфена соединены с подложкой, и это приводит к неоднородностям, флуктуациямпотенциала, что ведёт к пространственной неоднородности типа проводимости пообразцу, поэтому даже в точке электронейтральности концентрация носителейтеоретически не меньше чем 1012 см−2.Здесь проявляются отличие от обычных систем с двумерным электронным илидырочным газом, а именно отсутствует переход металл-диэлектрик.

5.2.2 Квантовый эффект Холла

Впервыенеобычный (англ. unconventional) квантовый эффект Холла наблюдали в работах, гдебыло показано, что носители в графене действительно обладают нулевойэффективной массой, поскольку положения плато на зависимости недиагональнойкомпоненты тензора проводимости соответствовали полуцелым значениям холловскойпроводимости /> в единицах 4e2 / h (множитель 4 появляется из-зачетырёхкратного вырождения энергии), то есть />Это квантование согласуется с теориейквантового эффекта Холла для дираковских безмассовых фермионов. Сравнение целочисленногоквантового эффекта Холла в обычной двумерной системе и графене см. на рисунке6. Здесь показаны уширенные уровни Ландау для электронов (выделение краснымцветом) и для дырок (синий цвет). Если уровеньФерми находится между уровнями Ландау,то на зависимости холловской проводимости σxy наблюдаетсяряд плато. Эта зависимость отличается от обычных двумерных систем (аналогомможет служить двумерный электронный газ в кремнии, который являетсядвухдолинным полупроводником в плоскостях, эквивалентных {100}, то есть тожеобладает четырёхкратным вырождением уровней Ландау, и холловские платонаблюдаются при ν= 4 | n | ).

Квантовый эффект Холла (КЭХ) может использоваться как эталонсопротивления, потому что численное значение наблюдаемого в графене плато,равное h / 2e2, воспроизводится с хорошей точностью, хотякачество образцов уступает высокоподвижному ДЭГ в GaAs, и,соответственно, точности квантования. Преимущество КЭХ в графене в том, что оннаблюдается при комнатной температуре (вмагнитных полях свыше 20 Т). Основноеограничение на наблюдение КЭХ при комнатной температуре накладывает не саморазмытие распределения Ферми-Дирака, а рассеяние носителей на примесях, чтоприводит к уширению уровней Ландау.

графенхиральность кристаллический дисперсия

Рис. 6. a) Квантовый эффект Холла в обычной двумерной системе. b)Квантовый эффект Холла в графене. G = gsgv = 4 — вырождение спектра

Всовременных образцах графена (лежащих на подложке) вплоть до 45 Т невозможнонаблюдать дробный квантовый эффект Холла,но наблюдается целочисленный квантовый эффект Холла, который не совпадает собычным квантовым эффектом Холла. В работе наблюдается спиновое расщепление релятивистских уровней Ландау и снятие четырёхкратного вырождения длянаинизшего уровня Ландау вблизи точки электронейтральности.Для объяснения этого эффекта предложено несколько теорий, но недостаточноеколичество экспериментального материала не позволяет выбрать среди нихправильную.

Из-заотсутствия запрещённой зоны в графене в структурах с верхним затвором можносформировать непрерывный p-n переход,когда напряжение на верхнем затворе позволяет инвертировать знак носителей,задаваемый обратным затвором в графене, где концентрация носителейникогда не обращается в ноль (кроме точки электронейтральности). В такихструктурах тоже можно наблюдать квантовый эффект Холла, но из-за неоднородностизнака носителей значения холловских плато отличаются он приведённых выше. Дляструктуры с одним p-n переходом значения квантования холловской проводимостиописываются формулой

Где ν и ν' — факторызаполнения в n- и p- областисоответственно (p-область находится под верхним затвором), которые могутпринимать значения /> и т. д. Тогдаплато в структурах с одним p-n переходом наблюдаются при значениях 1, 3/2, 2, ит. д.

Дляструктуры с двумя p-n переходами соответствующие значения холловскойпроводимости равны

6.Интересные факты

Со. 7. Для получения нанотрубки (n, m), графитовую плоскость надоразрезать по направлениям пунктирных линий и свернуть вдоль направления вектора R

В статье,опубликованной 10 ноября 2005 года в журнале Nature, Константин Новосёлов и Андрей Гейм утверждают, что электрические заряды в графене ведут себя как релятивистские частицы с нулевой эффективной массой. Эти частицы,известные как безмассовые фермионы Дирака,описываются уравнением Дирака,хотя в эффекте Шубникова-де Гааза (осцилляции магнетосопротивления)наблюдаемые осцилляции соответствуют конечной циклотронной массе.

Так как закондисперсии для носителей идентичен закону для безмассовых частиц, графен можетвыступать в качестве экспериментальной лаборатории для квантовой электродинамики.

Квантовыйэффект Холла в графене может наблюдаться даже при комнатной температуре из-за большой циклотронной энергии, прикоторой температурное размытие функции распределения Ферми-Дирака меньше этойэнергии (это расстояние />между первым и нулевым уровнямиЛандау равно 1200 K при магнитном поле 9 Т).

Присворачивании графена в цилиндр (см. Рис. 7) получается одностенная нанотрубка.В зависимости от конкретной схемы сворачивания графитовой плоскости, нанотрубкимогут обладать или металлическими, или полупроводниковыми свойствами.

В графенеотсутствует вигнеровская кристаллизация.

В графененарушается приближениеБорна-Оппенгеймера (адиабатическоеприближение), гласящее, что в силу медленного движения ионных остовов решёткиих можно включить в рассмотрение как возмущение, известное как фононы решётки, —основное приближение, на котором строится зонная теория твёрдых тел.

За получениеи исследование свойств графена, Нобелевская премия 2010 года по физикеприсуждена Андрею Гейму и КонстантинуНовосёлову.

Литература

1. Novoselov K.S. et al. «Electric Field Effect in Atomically ThinCarbon Films», Science 306, 666 (2004)

2. Bunch J.S. et. al. Electromechanical Resonators from GrapheneSheets Science 315, 490 (2007)

3. Chen Zh. et. al. Graphene Nano-Ribbon Electronics Physica E 40,228 (2007)

4. Novoselov, K. S. et al. «Two-dimensional atomic crystals», PNAS102, 10451 (2005)

5. Rollings E. et. al. Synthesis and characterization of atomicallythin graphite films on a silicon carbide substrate J. Phys. Chem. Solids 67, 2172(2006)

6. Hass J. et. al. Highly ordered graphene for two dimensionalelectronics Appl. Phys. Lett. 89, 143106 (2006)

7. Novoselov K.S. et al. «Two-dimensional gas of massless Diracfermions in graphene», Nature 438, 197 (2005)

8. Shioyama H. Cleavage of graphite to graphene J. Mat. Sci. Lett. 20, 499—500 (2001)

9. ЛандауЛ.Д., Лифшиц Е.М. Статистическая физика. — 2001.

10. Zhang Y. et al. Fabrication and electric-field-dependent transportmeasurements of mesoscopic graphite devices Appl. Phys. Lett. 86, 073104(2005)

11. Parvizi F., et. al. Graphene Synthesis via the High Pressure —High Temperature Growth Process Micro Nano Lett., 3, 29 (2008)

12. Sidorov A.N. et al.,Electrostatic deposition of grapheneNanotechnology 18, 135301 (2007)

13. J. Hass et. al. Why Multilayer Graphene on 4H-SiC(000-1) BehavesLike a Single Sheet of Graphene Phys. Rev. Lett. 100, 125504 (2008).

14. S.R.C. Vivekchand; Chandra Sekhar Rout, K.S. Subrahmanyam, A. Govindarajand C.N.R. Rao (2008). «Graphene-based electrochemicalsupercapacitors». J. Chem. Sci., Indian Academy of Sciences 120, January2008: 9−13.

15. СтатьяГрафен из Википедии, свободной энциклопедии. Доступно под лицензией Creative Commons Attribution-Share Alike

edportal.net

Реферат Получение графена

Опубликовать скачать

Реферат на тему:

План:

1 Механические методы
2 Химические методы
3 Эпитаксия и разложение
4 Другие методы

Введение

Существует несколько способов для получения графена, которые можно разделить на три большие группы. К первой группе относятся механические методы получения графена, основной из которых механическое отшелушивание, который на настоящий момент (2011) является наиболее распространённым методом для производства больших образцов с размером ~10 мкм пригодных для транспортных и оптических измерений. Ко второй группе методов относят химические методы, которые отличаются большим процентом выхода материала, но малыми размерами плёнок ~10-100 нм. К последней группе относятся эпитаксиальные методы и метод термического разложения SiC подложки благодаря которым можно вырастить плёнки графена.

1. Механические методы

Рис. 1. Кусочки тонких слоёв графита, полученные в процессе отшелушивания, на поверхности липкой ленты.

При механическом воздействии на высокоориентированный пиролитический графит или киш-графит[1] можно получить плёнки графена вплоть до ~100 мкм.[2] Сначала тонкие слои графита помещают между липкими лентами и отщепляют раз за разом тонкие плёнки графита, пока не будет получен достаточно тонкий слой (среди многих плёнок могут попадаться и однослойные, которые и представляют интерес). После отшелушивания скотч с тонкими плёнками графита и графена прижимают к подложке окисленного кремния. При этом трудно получить плёнку определённого размера и формы в фиксированных частях подложки (горизонтальные размеры плёнок составляют обычно около 10 мкм).[3] Найденные с помощью оптического микроскопа (они слабо видны при толщине диэлектрика 300 нм) плёнки подготавливают для измерений. С помощью атомно-силового микроскопа определяют реальную толщину плёнки графита (она может варьироваться в пределах 1 нм для графена). Графен можно также определить при помощи рамановского рассеяния света[4] или измерением квантового эффекта Холла[5][1]. Используя электронную литографию и реактивное плазменное травление, задают форму плёнки для электрофизических измерений (холловский мост для магнитотранспортных измерений).

Альтернативный метод предложен в работе[6]. Метод заключается в том, что окисленную подложку кремния покрывают эпоксидным клеем (в работе использовался слой толщиной ~10 мкм) и тонкую пластинку графита прижимают к клею при помощи пресса. После удаления графитовой пластинки с помощью липкой ленты на поверхности клея остаются области с графеном и графитом. Толщину графита определяли с помощью комбинационного рассеяния света и атомно-силовым микроскопом измеряли шероховатость графена, которая оказалась равной всего 0.16 нм (в два раза меньше шероховатости графена на подложке кремния[7]).

В статье[8] предложен метод печати графеновых электрических схем (ранее этот метод использовался для печати тонкоплёночных транзисторов на основе нанотрубок и для органической электроники.[9][10]). Сам процесс печати состоит из последовательного переноса с подложки Si/SiO2 золотых контактов, графена и наконец диэлектрика (PMMA) с металлическим затвором на прозрачную подложку из полиэтилентерефталата (ПЭТФ) предварительно нагретую выше температуры размягчения до 170 °C, благодаря чему контакты, вдавливались в ПЭТФ, а графен приобретает хороший контакт с материалом подложки. При таком методе нанесения графена подвижность не становится меньше, хотя и появляется заметная асимметрия между электронной (μe=10000 см2В−1с−1) и дырочной (μh=4000 см2В−1с−1) областями проводимости. Этот метод пригоден для нанесения графена на любую подложку пригодную, в частности, для оптических измерений.

2. Химические методы

Рис. 2. Слои интеркалированного графита можно легко отделить друг от друга[11]

Кусочки графена также можно приготовить из графита, используя химические методы[12]. Для начала микрокристаллы графита подвергаются действию смеси серной и соляной кислот. Графит окисляется, и на краях образца появляются карбоксильные группы графена. Их превращают в хлориды при помощи тионилхлорида. Затем под действием октадециламина в растворах тетрагидрофурана, тетрахлорметана и дихлорэтана они переходят в графеновые слои толщиной 0,54 нм. Этот химический метод не единственный, и, меняя органические растворители и химикаты, можно получить нанометровые слои графита[13][14][15]

В статьях[16][17] описан ещё один химический метод получения графена, встроенного в полимерную матрицу.

3. Эпитаксия и разложение

Следует упомянуть ещё два метода: радиочастотное плазмохимическое осаждение из газовой фазы (англ. PECVD)[18], рост при высоком давлении и температуре (англ. HPHT)[19]. Из этих методов только последний можно использовать для получения плёнок большой площади.

Работы[20][21] посвящёны получению графена, выращенного на подложках карбида кремния SiC(0001). Графитовая плёнка формируется при термическом разложении поверхности подложки SiC (этот метод получения графена гораздо ближе к промышленному производству), причём качество выращенной плёнки зависит от того, какая стабилизация у кристалла: C-стабилизированная или Si-стабилизированная поверхность — в первом случае качество плёнок выше. В работах[22][23] та же группа исследователей показала, что, несмотря на то, что толщина слоя графита составляет больше одного монослоя, в проводимости участвует только один слой в непосредственной близости от подложки, поскольку на границе SiC-C из-за разности работ выхода двух материалов образуется нескомпенсированный заряд. Свойства такой плёнки оказались эквивалентны свойствам графена.

Графен можно вырастить на металлических подложках рутения[24] и иридия[25].

4. Другие методы

Если кристалл пиролитического графита и подложку поместить между электродами, то, как показано в работе[26], можно добиться того, что кусочки графита с поверхности, среди которых могут оказаться плёнки атомарной толщины, под действием электрического поля могут перемещаться на подложку окисленного кремния. Для предотвращения пробоя (между электродами прикладывали напряжение от 1 до 13 кВ) между электродами также помещали тонкую пластину слюды.

Некоторая комбинация механического метода (графитовым стержнем пишут по поверхности подложки кремния, оставляя плёнки при разрушении) и последующего высокотемпературного отжига (~1100 K) использована для получения тонких слоёв графита вплоть до однослойных плёнок[27].

Примечания

↑ 12 Zhang Y.et. al. «Experimental observation of the quantum Hall effect and Berry’s phase in graphene» Nature 438, 201 (2005) DOI:10.1038/nature04235 - dx.doi.org/10.1038/nature04235
Kuzmenko A. B. cond-mat/0810.2400 - arxiv.org/abs/0810.2400
Novoselov, K. S. et al. «Two-dimensional atomic crystals», PNAS 102, 10451 (2005) DOI:10.1073/pnas.0502848102 - dx.doi.org/10.1073/pnas.0502848102
Ferrari A. C. et. al. Raman Spectrum of Graphene and Graphene Layers Phys. Rev. Lett. 97, 187401 (2006) DOI:10.1103/PhysRevLett.97.187401 - dx.doi.org/10.1103/PhysRevLett.97.187401
Novoselov K. S. et al. «Two-dimensional gas of massless Dirac fermions in graphene», Nature 438, 197 (2005) DOI:10.1038/nature04233 - dx.doi.org/10.1038/nature04233
Huc V., et. al. Large and flat graphene flakes produced by epoxy bonding and reverse exfoliation of highly oriented pyrolytic graphite Nanotechnology 19, 455601 (2008) DOI:10.1088/0957-4484/19/45/455601 - dx.doi.org/10.1088/0957-4484/19/45/455601 Препринт - arxiv.org/abs/0810.1777v1
Ishigami M. et. al. Atomic Structure of Graphene on SiO2 Nano Lett., 7, 1643, (2007) DOI:10.1021/nl070613a - dx.doi.org/10.1021/nl070613a
Chen J.-H. et. al. Printed Graphene Circuits Adv. Mater. 19, 3623 (2007) DOI:10.1002/adma.200701059 - dx.doi.org/10.1002/adma.200701059 Препринт - arxiv.org/abs/0809.1634
Hines D. R. et. al. Nanotransfer printing of organic and carbon nanotube thin-film transistors on plastic substrates Appl. Phys. Lett. 86, 163101 (2005) DOI:10.1063/1.1901809 - dx.doi.org/10.1063/1.1901809
Hines D. R. et. al. Transfer printing methods for the fabrication of flexible organic electronics Appl. Phys. 101, 024503 (2007) DOI:10.1063/1.2403836 - dx.doi.org/10.1063/1.2403836
Shioyama H. Cleavage of graphite to graphene J. Mat. Sci. Lett. 20, 499—500 (2001)
Solution Properties of Graphite and Graphene Sandip Niyogi, Elena Bekyarova, Mikhail E. Itkis, Jared L. McWilliams, Mark A. Hamon, and Robert C. Haddon J. Am. Chem. Soc.; 2006; 128(24) pp 7720 — 7721; (Communication) DOI:10.1021/ja060680r - dx.doi.org/10.1021/ja060680r
Bunch J. S. et al. Coulomb Oscillations and Hall Effect in Quasi-2D Graphite Quantum Dots Nano Lett. 5, 287 (2005) DOI:10.1021/nl048111+ - dx.doi.org/10.1021/nl048111+
Li X. et. al. Highly conducting graphene sheets and Langmuir-Blodgett films Nature Nanotechnology 3, 538 (2008) DOI:10.1038/nnano.2008.210 - dx.doi.org/10.1038/nnano.2008.210
Hernandez Y. et. al. High-yield production of graphene by liquid-phase exfoliation of graphite Nature Nanotech. 3, 563 (2008) DOI:10.1038/nnano.2008.215 - dx.doi.org/10.1038/nnano.2008.215
Stankovich S. et al. «Stable aqueous dispersions of graphitic nanoplatelets via the reduction of exfoliated graphite oxide in the presence of poly(sodium 4-styrenesulfonate)», J. Mater. Chem. 16, 155 (2006) DOI:10.1039/b512799h - dx.doi.org/10.1039/b512799h
Stankovich S. et al. «Graphene-based composite materials», Nature 442, 282 (2006) DOI:10.1038/nature04969 - dx.doi.org/10.1038/nature04969
Wang J. J. et. al. Free-standing subnanometer graphite sheets Appl. Phys. Lett. 85, 1265 (2004) DOI:10.1063/1.1782253 - dx.doi.org/10.1063/1.1782253
Parvizi F., et. al. Graphene Synthesis via the High Pressure — High Temperature Growth Process Micro Nano Lett., 3, 29 (2008) DOI:10.1049/mnl:20070074 - dx.doi.org/10.1049/mnl:20070074 Препринт - arxiv.org/abs/0802.4058
Rollings E. et. al. Synthesis and characterization of atomically thin graphite films on a silicon carbide substrate J. Phys. Chem. Solids 67, 2172 (2006) DOI:10.1016/j.jpcs.2006.05.010 - dx.doi.org/10.1016/j.jpcs.2006.05.010
Hass J. et. al. Highly ordered graphene for two dimensional electronics Appl. Phys. Lett. 89, 143106 (2006) DOI:10.1063/1.2358299 - dx.doi.org/10.1063/1.2358299
Berger, C. et al. «Electronic Confinement and Coherence in Patterned Epitaxial Graphene», Science 312, 1191 (2006) DOI:10.1126/science.1125925 - dx.doi.org/10.1126/science.1125925
J. Hass et. al. Why Multilayer Graphene on 4H-SiC(000-1) Behaves Like a Single Sheet of Graphene Phys. Rev. Lett. 100, 125504 (2008).
Sutter P. W. et. al. Epitaxial graphene on ruthenium Nature Mat. 7, 406 (2008) DOI:10.1038/nmat2166 - dx.doi.org/10.1038/nmat2166
N’Diaye A. T. et. al. Structure of epitaxial graphene on Ir(111) New J. Phys. 10, 043033 (2008) DOI:10.1088/1367-2630/10/4/043033 - dx.doi.org/10.1088/1367-2630/10/4/043033
Sidorov A. N. et al.,Electrostatic deposition of graphene Nanotechnology 18, 135301 (2007) DOI:10.1088/0957-4484/18/13/135301 - dx.doi.org/10.1088/0957-4484/18/13/135301
Banerjee A. and Grebel H. Depositing graphene films on solid and perforated substrates Nanotechnology 19, 365303 (2008) DOI:10.1088/0957-4484/19/36/365303 - dx.doi.org/10.1088/0957-4484/19/36/365303

скачатьДанный реферат составлен на основе статьи из русской Википедии. Синхронизация выполнена 14.07.11 14:20:36Похожие рефераты: Видимость графена, Уравнение Дирака для графена, Зонная структура графена, Получение взятки, Получение скрытой информации, Биотехнологическое получение водорода, Незаконное получение кредита, Получение ресурса есть инициализация.

Категории: Нанотехнология, Графен.

Текст доступен по лицензии Creative Commons Attribution-ShareAlike.

wreferat.baza-referat.ru

Статья: Графен и его свойства:. Графен реферат

Оглавление

Введение

История открытия

Графен — курсовая работа

Реферат - Графеновая электроника - Наука и техника

Статья: Графен и его свойства

Содержание

5.1.5 Хиральность ипарадокс Клейна

5.2.2Квантовый эффект Холла

Литература

Реферат Графен и его свойства

Реферат Получение графена

План:

Введение

1. Механические методы

2. Химические методы

3. Эпитаксия и разложение

4. Другие методы

Примечания

Смотрите также