superbotanik.net

Реферат Геометрия Лобачевского

скачать

Реферат на тему:

Euclidian and non euclidian geometry.png

План:

Введение

Euclidian and non euclidian geometry.png

Геометрия Лобачевского (гиперболическая геометрия) — одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского.

Евклидова аксиома о параллельных (точнее, одно из эквивалентных ей утверждений) гласит:

Через точку, не лежащую на данной прямой, проходит не более одной прямой, лежащей с данной прямой в одной плоскости и не пересекающей её.

В геометрии Лобачевского, вместо неё принимается следующая аксиома:

Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.

Широко распространено заблуждение, что в геометрии Лобачевского параллельные прямые пересекаются[1]. Геометрия Лобачевского имеет обширные применения как в математике, так и в физике. Историческое её значение состоит в том, что её построением Лобачевский показал возможность геометрии, отличной от евклидовой, что знаменовало новую эпоху в развитии геометрии, математики и науки вообще.

1. История

1.1. Попытки доказательства пятого постулата

Отправным пунктом геометрии Лобачевского послужил V постулат Евклида — аксиома, эквивалентная аксиоме о параллельных. Он входил в список постулатов в «Началах» Евклида. Относительная сложность и неинтуитивность его формулировки вызывала ощущение его вторичности и порождала попытки вывести его как теорему из остальных постулатов Евклида.

Среди многих пытавшихся доказать пятый постулат были, в частности, следующие крупные учёные.

При этих попытках доказательства пятого постулата математики вводили (явно или неявно) некоторое новое утверждение, казавшееся им более очевидным.

Были предприняты попытки использовать доказательство от противного:

Наконец, стало возникать понимание о том, что возможно построение теории, основанной на противоположном постулате:

1.2. Создание неевклидовой геометрии

Лобачевский в работе «О началах геометрии» (1829), первой его печатной работе по неевклидовой геометрии, ясно заявил, что V постулат не может быть доказан на основе других посылок евклидовой геометрии, и что допущение постулата, противоположного постулату Евклида, позволяет построить геометрию столь же содержательную, как и евклидова, и свободную от противоречий.

Одновременно и независимо к аналогичным выводам пришёл Янош Бойяи, а Карл Фридрих Гаусс пришёл к таким выводам ещё раньше. Однако труды Бойяи не привлекли внимания, и он вскоре оставил эту тему, а Гаусс вообще воздерживался от публикаций, и о его взглядах можно судить лишь по нескольким письмам и дневниковым записям. Например, в письме 1846 года астроному Г. Х. Шумахеру Гаусс так отозвался о работе Лобачевского:

Это сочинение содержит в себе основания той геометрии, которая должна была бы иметь место и притом составляла бы строго последовательное целое, если бы евклидова геометрия не была бы истинной… Лобачевский называет ее «воображаемой геометрией»; Вы знаете, что уже 54 года (с 1792 г.) я разделяю те же взгляды с некоторым развитием их, о котором не хочу здесь упоминать; таким образом, я не нашёл для себя в сочинении Лобачевского ничего фактически нового. Но в развитии предмета автор следовал не по тому пути, по которому шёл я сам; оно выполнено Лобачевским мастерски в истинно геометрическом духе. Я считаю себя обязанным обратить Ваше внимание на это сочинение, которое, наверное, доставит Вам совершенно исключительное наслаждение.[3]

В итоге Лобачевский выступил как первый наиболее яркий и последовательный пропагандист этой теории.

Хотя геометрия Лобачевского развивалась как умозрительная теория, и сам Лобачевский называл её «воображаемой геометрией», тем не менее именно Лобачевский рассматривал её не как игру ума, а как возможную теорию пространственных отношений. Однако доказательство её непротиворечивости было дано позже, когда были указаны её интерпретации и тем полностью решён вопрос о её реальном смысле, логической непротиворечивости.

1.3. Утверждение геометрии Лобачевского

Лобачевский умер в 1856 году. Спустя несколько лет была опубликована переписка Гаусса, в том числе несколько восторженных отзывов о геометрии Лобачевского, и это привлекло внимание к трудам Лобачевского. Появляются переводы их на французский и итальянский языки, комментарии видных геометров. Публикуется и труд Бойяи.

В 1868 году выходит статья Э. Бельтрами об интерпретациях геометрии Лобачевского. Бельтрами определил метрику плоскости Лобачевского и доказал, что она имеет всюду постоянную отрицательную кривизну. Такая поверхность тогда уже была известна — это псевдосфера Миндинга. Бельтрами сделал вывод, что локально плоскость Лобачевского изометрична участку псевдосферы (см. ниже). Окончательно непротиворечивость геометрии Лобачевского была доказана в 1871 году, после появления модели Клейна.

Вейерштрасс посвящает геометрии Лобачевского специальный семинар в Берлинском университете (1870). Казанское физико-математическое общество организует издание полного собрания сочинений Лобачевского, а в 1893 году столетие русского математика отмечается в международном масштабе.

2. Модели

Модели геометрии Лобачевского дали доказательство её непротиворечивости, точнее показали, что геометрия Лобачевского столь же непротиворечива, как геометрия Евклида.

Сам Лобачевский дал основы своей аналитической геометрии, и тем самым он уже фактически наметил такую модель. Он также заметил что орисфера в пространстве Лобачевского изометрична евклидовой плоскости, тем самым фактически предложил обратную модель. Тем не менее, само понятие о модели прояснилось в работах Клейна и других.

2.1. Псевдосфера

Псевдосфера

Итальянский математик Э. Бельтрами в 1868 году заметил, что геометрия на куске плоскости Лобачевского совпадает с геометрией на поверхностях постоянной отрицательной кривизны, простейший пример которых представляет псевдосфера. Если точкам и прямым на конечном куске плоскости Лобачевского сопоставлять точки и кратчайшие линии (геодезические) на псевдосфере и движению в плоскости Лобачевского сопоставлять перемещение фигуры по псевдосфере с изгибанием, то есть деформацией, сохраняющей длины, то всякой теореме геометрии Лобачевского будет отвечать факт, имеющий место на псевдосфере. При этом длины, углы, площади понимаются в смысле естественного измерения их на псевдосфере.

Однако здесь даётся только локальная интерпретация геометрии, то есть на ограниченном участке, а не на всей плоскости Лобачевского.

2.2. Модель Клейна

Через точку Р проходит бесконечно много «прямых», не пересекающих «прямой» а

В 1871 году Клейн предложил первую полноценную модель плоскости Лобачевского.

Плоскостью служит внутренность круга, прямой — хорда круга без концов, а точкой — точка внутри круга. «Движением» назовём любое преобразование круга в самого себя, которое переводит хорды в хорды. Соответственно, равными называются фигуры внутри круга, переводящиеся одна в другую такими преобразованиями. Тогда оказывается, что любой геометрический факт, описанный на таком языке, представляет теорему или аксиому геометрии Лобачевского. Иными словами, всякое утверждение геометрии Лобачевского на плоскости есть не что иное, как утверждение евклидовой геометрии, относящееся к фигурам внутри круга, лишь пересказанное в указанных терминах. Евклидова аксиома о параллельных здесь явно не выполняется, так как через точку P, не лежащую на данной хорде а (то есть «прямой»), проходит сколько угодно не пересекающих её хорд («прямых») (например, b, b').

В этой модели расстояние между точками A и B на хорде NM определяется через двойное отношение

\ln\left(\frac{AN}{AM}\frac{BM}{BN}\right)

2.3. Модель Пуанкаре

Модель Пуанкаре

Позже Пуанкаре, в связи с задачами теории функций комплексного переменного дал другую модель. За плоскость Лобачевского принимается внутренность круга, прямыми считаются дуги окружностей, перпендикулярных окружности данного круга, и его диаметры, движениями — преобразования, получаемые комбинациями инверсий относительно окружностей, дуги которых служат прямыми.

Модель Пуанкаре замечательна тем, что в ней углы изображаются обычными углами.

2.4. Поверхность постоянной отрицательной кривизны

Другое аналитическое определение геометрии Лобачевского состоит в том, что геометрия Лобачевского определяется как геометрия риманова пространства постоянной отрицательной кривизны. Это определение было фактически дано ещё в 1854 году Риманом и включало модель геометрии Лобачевского как геометрии на поверхностях постоянной кривизны. Однако Риман не связал прямо своих построений с геометрией Лобачевского, а его доклад, в котором он о них сообщил, не был понят и был опубликован лишь после его смерти (в 1868 году).

3. Содержание геометрии Лобачевского

Угол параллельности

Лобачевский строил свою геометрию, отправляясь от основных геометрических понятий и своей аксиомы, и доказывал теоремы геометрическим методом, подобно тому, как это делается в геометрии Евклида. Основой служила теория параллельных линий, так как именно здесь начинается отличие геометрии Лобачевского от геометрии Евклида. Все теоремы, не зависящие от аксиомы о параллельных, являются общими для обеих геометрий; они образуют так называемую абсолютную геометрию, к которой относятся, например, теоремы о равенстве треугольников. Вслед за теорией параллельных строились другие разделы, включая тригонометрию и начала аналитической и дифференциальной геометрии.

Приведём (в современных обозначениях) несколько фактов геометрии Лобачевского, отличающих её от геометрии Евклида и установленных самим Лобачевским.

Через точку P, не лежащую на данной прямой R (см. рисунок), проходит бесконечно много прямых, не пересекающих R и находящихся с ней в одной плоскости; среди них есть две крайние x, y, которые и называются параллельными прямой R в смысле Лобачевского. В моделях Клейна (Пуанкаре) они изображаются хордами (дугами окружностей), имеющими с хордой (дугой) R общий конец (который по определению модели исключается, так что эти прямые не имеют общих точек).

Угол θ между перпендикуляром PB из P на R и каждой из параллельных (называемый углом параллельности) по мере удаления точки P от прямой убывает от 90° до 0° (в модели Пуанкаре углы в обычном смысле совпадают с углами в смысле Лобачевского, и потому на ней этот факт можно видеть непосредственно). Параллель x с одной стороны (а y с противоположной) асимптотически приближается к а, а с другой — бесконечно от неё удаляется (в моделях расстояния определяются сложно, и потому этот факт непосредственно не виден).

Для точки, находящейся от заданной прямой на расстоянии PB = a (см. рисунок), Лобачевский дал формулу для угла параллельности П(a)[4]:

\theta = \Pi(a) = 2 \operatorname{arctg}~e^{-\frac{a}{q}}

Здесь q — некоторая постоянная, связанная с кривизной пространства Лобачевского. Она может служить абсолютной единицей длины аналогично тому, как в сферической геометрии особое положение занимает радиус сферы.

Если прямые имеют общий перпендикуляр, то они бесконечно расходятся в обе стороны от него. К любой из них можно восстановить перпендикуляры, которые не достигают другой прямой.

В геометрии Лобачевского не существует подобных, но неравных треугольников; треугольники равны, если их углы равны.

Сумма углов всякого треугольника меньше π и может быть сколь угодно близкой к нулю. Это непосредственно видно на модели Пуанкаре. Разность δ = π − (α + β + γ), где α, β, γ — углы треугольника, пропорциональна его площади:

S = q^2 \cdot \delta

Из формулы видно, что существует максимальная площадь треугольника, и это конечное число: πq2.

Линия равных расстояний от прямой не есть прямая, а особая кривая, называемая эквидистантой, или гиперциклом.

Предел окружностей бесконечно увеличивающегося радиуса не есть прямая, а особая кривая, называемая предельной окружностью, или орициклом.

Предел сфер бесконечно увеличивающегося радиуса не есть плоскость, а особая поверхность — предельная сфера, или орисфера; замечательно, что на ней имеет место евклидова геометрия. Это служило Лобачевскому основой для вывода формул тригонометрии.

Длина окружности не пропорциональна радиусу, а растёт быстрее. В частности, в геометрии Лобачевского число π не может быть определено как отношение длины окружности к её диаметру.

Чем меньше область в пространстве или на плоскости Лобачевского, тем меньше геометрические соотношения в этой области отличаются от соотношений евклидовой геометрии. Можно сказать, что в бесконечно малой области имеет место евклидова геометрия. Например, чем меньше треугольник, тем меньше сумма его углов отличается от π; чем меньше окружность, тем меньше отношение её длины к радиусу отличается от 2π, и т. п. Уменьшение области формально равносильно увеличению единицы длины, поэтому при безграничном увеличении единицы длины формулы геометрии Лобачевского переходят в формулы евклидовой геометрии. Евклидова геометрия есть в этом смысле «предельный» случай геометрии Лобачевского.

3.1. Заполнение плоскости и пространства правильными политопами

Замощение плоскости Лобачевского правильными треугольниками ({3;7})

Плоскость Лобачевского может быть замощена не только правильными треугольниками, квадратами и шестиугольниками, но и любыми другими правильными многоугольниками. При этом в одной вершине паркета должно сходиться не менее 7 треугольников, 5 квадратов, 4 пяти- и шестиугольников и 3 многоугольников с числом сторон более 6. Каждое замощение \left\{ N;M \right\} (в одной вершине сходится M N-угольников) требует строго определённого размера единичного N-угольника, в частности, его площадь должна равняться:

S_{ \left\{ N;M \right\} } = q^2 \pi \left( N - 2 - 2\frac{N}{M} \right)

Заполнение пространства Лобачевского правильными додекаэдрами ({5,3,4})

В отличие от обычного пространства, которе можно заполнить правильными многогранниками только одним способом (по 8 кубов в вершине), трёхмерное пространство Лобачевского можно заполнить правильными многогранниками четырьмя способами:

Кроме этого, существует 11 способов заполнить пространство Лобаческого правильными мозаичными орисферами.

4. Приложения

~x^2 + y^2 + z^2 = c^2t^2 при делении на t2, то есть для скорости света, даёт ~v_x^2 + v_y^2 + v_z^2 = c^2  — уравнение сферы в пространстве с координатами vx, vy, vz — составляющими скорости по осям х, у, z (в «пространстве скоростей»). Преобразования Лоренца сохраняют эту сферу и, так как они линейны, переводят прямые пространства скоростей в прямые. Следовательно, согласно модели Клейна, в пространстве скоростей внутри сферы радиуса с, то есть для скоростей, меньших скорости света, имеет место геометрия Лобачевского.

Примечания

  1. Параллельные прямые — в мифологии, реальности и математике - elementy.ru/lib/430915 Успенский В. А. Апология математики, глава 8
  2. Розенфельд Б. А. Доказательства пятого постулата Евклида средневековых математиков Хасана ибн ал-Хайсама и Льва Герсонида. — М.: ИМИ, 1958. — Т. XI. — С. 733—742.
  3. Об основаниях геометрии. Сборник классических работ по геометрии Лобачевского и развитию ее идей. М.: Гостехиздат, 1956, С.119-120.
  4. Колмогоров А. Н., Юшкевич А. П. (ред.) Математика XIX века. М.: Наука, том II, с. 62.

6. Труды основоположников

Литература

wreferat.baza-referat.ru

Реферат Геометрия Лобачевского

скачать

Реферат на тему:

Euclidian and non euclidian geometry.png

План:

Введение

Euclidian and non euclidian geometry.png

Геометрия Лобачевского (гиперболическая геометрия) — одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского.

Евклидова аксиома о параллельных (точнее, одно из эквивалентных ей утверждений) гласит:

Через точку, не лежащую на данной прямой, проходит не более одной прямой, лежащей с данной прямой в одной плоскости и не пересекающей её.

В геометрии Лобачевского, вместо неё принимается следующая аксиома:

Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.

Широко распространено заблуждение, что в геометрии Лобачевского параллельные прямые пересекаются[1]. Геометрия Лобачевского имеет обширные применения как в математике, так и в физике. Историческое её значение состоит в том, что её построением Лобачевский показал возможность геометрии, отличной от евклидовой, что знаменовало новую эпоху в развитии геометрии, математики и науки вообще.

1. История

1.1. Попытки доказательства пятого постулата

Отправным пунктом геометрии Лобачевского послужил V постулат Евклида — аксиома, эквивалентная аксиоме о параллельных. Он входил в список постулатов в «Началах» Евклида. Относительная сложность и неинтуитивность его формулировки вызывала ощущение его вторичности и порождала попытки вывести его как теорему из остальных постулатов Евклида.

Среди многих пытавшихся доказать пятый постулат были, в частности, следующие крупные учёные.

При этих попытках доказательства пятого постулата математики вводили (явно или неявно) некоторое новое утверждение, казавшееся им более очевидным.

Были предприняты попытки использовать доказательство от противного:

Наконец, стало возникать понимание о том, что возможно построение теории, основанной на противоположном постулате:

1.2. Создание неевклидовой геометрии

Лобачевский в работе «О началах геометрии» (1829), первой его печатной работе по неевклидовой геометрии, ясно заявил, что V постулат не может быть доказан на основе других посылок евклидовой геометрии, и что допущение постулата, противоположного постулату Евклида, позволяет построить геометрию столь же содержательную, как и евклидова, и свободную от противоречий.

Одновременно и независимо к аналогичным выводам пришёл Янош Бойяи, а Карл Фридрих Гаусс пришёл к таким выводам ещё раньше. Однако труды Бойяи не привлекли внимания, и он вскоре оставил эту тему, а Гаусс вообще воздерживался от публикаций, и о его взглядах можно судить лишь по нескольким письмам и дневниковым записям. Например, в письме 1846 года астроному Г. Х. Шумахеру Гаусс так отозвался о работе Лобачевского:

Это сочинение содержит в себе основания той геометрии, которая должна была бы иметь место и притом составляла бы строго последовательное целое, если бы евклидова геометрия не была бы истинной… Лобачевский называет ее «воображаемой геометрией»; Вы знаете, что уже 54 года (с 1792 г.) я разделяю те же взгляды с некоторым развитием их, о котором не хочу здесь упоминать; таким образом, я не нашёл для себя в сочинении Лобачевского ничего фактически нового. Но в развитии предмета автор следовал не по тому пути, по которому шёл я сам; оно выполнено Лобачевским мастерски в истинно геометрическом духе. Я считаю себя обязанным обратить Ваше внимание на это сочинение, которое, наверное, доставит Вам совершенно исключительное наслаждение.[3]

В итоге Лобачевский выступил как первый наиболее яркий и последовательный пропагандист этой теории.

Хотя геометрия Лобачевского развивалась как умозрительная теория, и сам Лобачевский называл её «воображаемой геометрией», тем не менее именно Лобачевский рассматривал её не как игру ума, а как возможную теорию пространственных отношений. Однако доказательство её непротиворечивости было дано позже, когда были указаны её интерпретации и тем полностью решён вопрос о её реальном смысле, логической непротиворечивости.

1.3. Утверждение геометрии Лобачевского

Лобачевский умер в 1856 году. Спустя несколько лет была опубликована переписка Гаусса, в том числе несколько восторженных отзывов о геометрии Лобачевского, и это привлекло внимание к трудам Лобачевского. Появляются переводы их на французский и итальянский языки, комментарии видных геометров. Публикуется и труд Бойяи.

В 1868 году выходит статья Э. Бельтрами об интерпретациях геометрии Лобачевского. Бельтрами определил метрику плоскости Лобачевского и доказал, что она имеет всюду постоянную отрицательную кривизну. Такая поверхность тогда уже была известна — это псевдосфера Миндинга. Бельтрами сделал вывод, что локально плоскость Лобачевского изометрична участку псевдосферы (см. ниже). Окончательно непротиворечивость геометрии Лобачевского была доказана в 1871 году, после появления модели Клейна.

Вейерштрасс посвящает геометрии Лобачевского специальный семинар в Берлинском университете (1870). Казанское физико-математическое общество организует издание полного собрания сочинений Лобачевского, а в 1893 году столетие русского математика отмечается в международном масштабе.

2. Модели

Модели геометрии Лобачевского дали доказательство её непротиворечивости, точнее показали, что геометрия Лобачевского столь же непротиворечива, как геометрия Евклида.

Сам Лобачевский дал основы своей аналитической геометрии, и тем самым он уже фактически наметил такую модель. Он также заметил что орисфера в пространстве Лобачевского изометрична евклидовой плоскости, тем самым фактически предложил обратную модель. Тем не менее, само понятие о модели прояснилось в работах Клейна и других.

2.1. Псевдосфера

Псевдосфера

Итальянский математик Э. Бельтрами в 1868 году заметил, что геометрия на куске плоскости Лобачевского совпадает с геометрией на поверхностях постоянной отрицательной кривизны, простейший пример которых представляет псевдосфера. Если точкам и прямым на конечном куске плоскости Лобачевского сопоставлять точки и кратчайшие линии (геодезические) на псевдосфере и движению в плоскости Лобачевского сопоставлять перемещение фигуры по псевдосфере с изгибанием, то есть деформацией, сохраняющей длины, то всякой теореме геометрии Лобачевского будет отвечать факт, имеющий место на псевдосфере. При этом длины, углы, площади понимаются в смысле естественного измерения их на псевдосфере.

Однако здесь даётся только локальная интерпретация геометрии, то есть на ограниченном участке, а не на всей плоскости Лобачевского.

2.2. Модель Клейна

Через точку Р проходит бесконечно много «прямых», не пересекающих «прямой» а

В 1871 году Клейн предложил первую полноценную модель плоскости Лобачевского.

Плоскостью служит внутренность круга, прямой — хорда круга без концов, а точкой — точка внутри круга. «Движением» назовём любое преобразование круга в самого себя, которое переводит хорды в хорды. Соответственно, равными называются фигуры внутри круга, переводящиеся одна в другую такими преобразованиями. Тогда оказывается, что любой геометрический факт, описанный на таком языке, представляет теорему или аксиому геометрии Лобачевского. Иными словами, всякое утверждение геометрии Лобачевского на плоскости есть не что иное, как утверждение евклидовой геометрии, относящееся к фигурам внутри круга, лишь пересказанное в указанных терминах. Евклидова аксиома о параллельных здесь явно не выполняется, так как через точку P, не лежащую на данной хорде а (то есть «прямой»), проходит сколько угодно не пересекающих её хорд («прямых») (например, b, b').

В этой модели расстояние между точками A и B на хорде NM определяется через двойное отношение

\ln\left(\frac{AN}{AM}\frac{BM}{BN}\right)

2.3. Модель Пуанкаре

Модель Пуанкаре

Позже Пуанкаре, в связи с задачами теории функций комплексного переменного дал другую модель. За плоскость Лобачевского принимается внутренность круга, прямыми считаются дуги окружностей, перпендикулярных окружности данного круга, и его диаметры, движениями — преобразования, получаемые комбинациями инверсий относительно окружностей, дуги которых служат прямыми.

Модель Пуанкаре замечательна тем, что в ней углы изображаются обычными углами.

2.4. Поверхность постоянной отрицательной кривизны

Другое аналитическое определение геометрии Лобачевского состоит в том, что геометрия Лобачевского определяется как геометрия риманова пространства постоянной отрицательной кривизны. Это определение было фактически дано ещё в 1854 году Риманом и включало модель геометрии Лобачевского как геометрии на поверхностях постоянной кривизны. Однако Риман не связал прямо своих построений с геометрией Лобачевского, а его доклад, в котором он о них сообщил, не был понят и был опубликован лишь после его смерти (в 1868 году).

3. Содержание геометрии Лобачевского

Угол параллельности

Лобачевский строил свою геометрию, отправляясь от основных геометрических понятий и своей аксиомы, и доказывал теоремы геометрическим методом, подобно тому, как это делается в геометрии Евклида. Основой служила теория параллельных линий, так как именно здесь начинается отличие геометрии Лобачевского от геометрии Евклида. Все теоремы, не зависящие от аксиомы о параллельных, являются общими для обеих геометрий; они образуют так называемую абсолютную геометрию, к которой относятся, например, теоремы о равенстве треугольников. Вслед за теорией параллельных строились другие разделы, включая тригонометрию и начала аналитической и дифференциальной геометрии.

Приведём (в современных обозначениях) несколько фактов геометрии Лобачевского, отличающих её от геометрии Евклида и установленных самим Лобачевским.

Через точку P, не лежащую на данной прямой R (см. рисунок), проходит бесконечно много прямых, не пересекающих R и находящихся с ней в одной плоскости; среди них есть две крайние x, y, которые и называются параллельными прямой R в смысле Лобачевского. В моделях Клейна (Пуанкаре) они изображаются хордами (дугами окружностей), имеющими с хордой (дугой) R общий конец (который по определению модели исключается, так что эти прямые не имеют общих точек).

Угол θ между перпендикуляром PB из P на R и каждой из параллельных (называемый углом параллельности) по мере удаления точки P от прямой убывает от 90° до 0° (в модели Пуанкаре углы в обычном смысле совпадают с углами в смысле Лобачевского, и потому на ней этот факт можно видеть непосредственно). Параллель x с одной стороны (а y с противоположной) асимптотически приближается к а, а с другой — бесконечно от неё удаляется (в моделях расстояния определяются сложно, и потому этот факт непосредственно не виден).

Для точки, находящейся от заданной прямой на расстоянии PB = a (см. рисунок), Лобачевский дал формулу для угла параллельности П(a)[4]:

\theta = \Pi(a) = 2 \operatorname{arctg}~e^{-\frac{a}{q}}

Здесь q — некоторая постоянная, связанная с кривизной пространства Лобачевского. Она может служить абсолютной единицей длины аналогично тому, как в сферической геометрии особое положение занимает радиус сферы.

Если прямые имеют общий перпендикуляр, то они бесконечно расходятся в обе стороны от него. К любой из них можно восстановить перпендикуляры, которые не достигают другой прямой.

В геометрии Лобачевского не существует подобных, но неравных треугольников; треугольники равны, если их углы равны.

Сумма углов всякого треугольника меньше π и может быть сколь угодно близкой к нулю. Это непосредственно видно на модели Пуанкаре. Разность δ = π − (α + β + γ), где α, β, γ — углы треугольника, пропорциональна его площади:

S = q^2 \cdot \delta

Из формулы видно, что существует максимальная площадь треугольника, и это конечное число: πq2.

Линия равных расстояний от прямой не есть прямая, а особая кривая, называемая эквидистантой, или гиперциклом.

Предел окружностей бесконечно увеличивающегося радиуса не есть прямая, а особая кривая, называемая предельной окружностью, или орициклом.

Предел сфер бесконечно увеличивающегося радиуса не есть плоскость, а особая поверхность — предельная сфера, или орисфера; замечательно, что на ней имеет место евклидова геометрия. Это служило Лобачевскому основой для вывода формул тригонометрии.

Длина окружности не пропорциональна радиусу, а растёт быстрее. В частности, в геометрии Лобачевского число π не может быть определено как отношение длины окружности к её диаметру.

Чем меньше область в пространстве или на плоскости Лобачевского, тем меньше геометрические соотношения в этой области отличаются от соотношений евклидовой геометрии. Можно сказать, что в бесконечно малой области имеет место евклидова геометрия. Например, чем меньше треугольник, тем меньше сумма его углов отличается от π; чем меньше окружность, тем меньше отношение её длины к радиусу отличается от 2π, и т. п. Уменьшение области формально равносильно увеличению единицы длины, поэтому при безграничном увеличении единицы длины формулы геометрии Лобачевского переходят в формулы евклидовой геометрии. Евклидова геометрия есть в этом смысле «предельный» случай геометрии Лобачевского.

3.1. Заполнение плоскости и пространства правильными политопами

Замощение плоскости Лобачевского правильными треугольниками ({3;7})

Плоскость Лобачевского может быть замощена не только правильными треугольниками, квадратами и шестиугольниками, но и любыми другими правильными многоугольниками. При этом в одной вершине паркета должно сходиться не менее 7 треугольников, 5 квадратов, 4 пяти- и шестиугольников и 3 многоугольников с числом сторон более 6. Каждое замощение \left\{ N;M \right\} (в одной вершине сходится M N-угольников) требует строго определённого размера единичного N-угольника, в частности, его площадь должна равняться:

S_{ \left\{ N;M \right\} } = q^2 \pi \left( N - 2 - 2\frac{N}{M} \right)

Заполнение пространства Лобачевского правильными додекаэдрами ({5,3,4})

В отличие от обычного пространства, которе можно заполнить правильными многогранниками только одним способом (по 8 кубов в вершине), трёхмерное пространство Лобачевского можно заполнить правильными многогранниками четырьмя способами:

Кроме этого, существует 11 способов заполнить пространство Лобаческого правильными мозаичными орисферами.

4. Приложения

~x^2 + y^2 + z^2 = c^2t^2 при делении на t2, то есть для скорости света, даёт ~v_x^2 + v_y^2 + v_z^2 = c^2  — уравнение сферы в пространстве с координатами vx, vy, vz — составляющими скорости по осям х, у, z (в «пространстве скоростей»). Преобразования Лоренца сохраняют эту сферу и, так как они линейны, переводят прямые пространства скоростей в прямые. Следовательно, согласно модели Клейна, в пространстве скоростей внутри сферы радиуса с, то есть для скоростей, меньших скорости света, имеет место геометрия Лобачевского.

Примечания

  1. Параллельные прямые — в мифологии, реальности и математике - elementy.ru/lib/430915 Успенский В. А. Апология математики, глава 8
  2. Розенфельд Б. А. Доказательства пятого постулата Евклида средневековых математиков Хасана ибн ал-Хайсама и Льва Герсонида. — М.: ИМИ, 1958. — Т. XI. — С. 733—742.
  3. Об основаниях геометрии. Сборник классических работ по геометрии Лобачевского и развитию ее идей. М.: Гостехиздат, 1956, С.119-120.
  4. Колмогоров А. Н., Юшкевич А. П. (ред.) Математика XIX века. М.: Наука, том II, с. 62.

6. Труды основоположников

Литература

www.wreferat.baza-referat.ru

Реферат: Геометрия Лобачевского

ing-grafika.ru

Реферат: Геометрия Лобачевского

superbotanik.net

Реферат - Геометрия Лобачевского - Математика

ГеометрияЛобачевского.

<span Book Antiqua",«serif»; color:black">Исаев Андрей.

Гурьев Дмитрий.

«Начала» — величайший памятник деятельности Евклида, в котором он собрал воедино всё то,что сделали его предшественники в области геометрии и «словесной алгебры». Ноне только в этом его заслуга. Он также внёс много своего, нового,оригинального. Вплоть до XXв. геометрию вшколах преподавали по учебникам, в которые были включены евклидовы «Начала»,переведённые и литературно обработанные.

Однако не всёнаписанное Евклидом удовлетворяло живших после него математиков. Великолепнойбыла его попытка дать аксиоматическое изложение геометрии, т.е. сформулироватьнебольшое количество аксиом, из которых логически выводятся все теоремыгеометрии. Список аксиом сразу же подвергся критике, некоторые из них оказалисьсовсем не нужными, например, что «все прямые углы равны между собой».

Так называемый пятыйпостулат Евклида вызвал особые нарекания математиков. Именно эта аксиома,как показала историческое развитие науки, содержала в себе зародыш другой,неевклидовой геометрии.

Вот о чёмговорится в пятом постулате: Если две прямые aи bобразуют припересечении с третьей прямой внутренние односторонние углы α и β,сумма величин которых меньше двух прямых углов (т.е. меньше 180˚; рис 1),то эти две прямые обязательно пересекаются, причём именно стой стороны оттретьей прямой, по которую расположены углы α и β(составляющие вместе не менее 180˚).

Данноеутверждение заметно сложнее остальных аксиом. Потому-то пятый постулат   часто замеряют на равносильную аксиомупараллельности: к данной прямой через данную вне её точку можно провести неболее одной параллельной прямой.

Вообразим. Чтомы взяли две точки А и В на расстоянии 1 м друг от друга и провели через нихдве прямые aи b, причём так что aобразует спрямой АВ равен 89˚59′59″ (рис. 2). <img src="/cache/referats/16327/image002.jpg" v:shapes="_x0000_i1025"><img src="/cache/referats/16327/image004.jpg" v:shapes="_x0000_i1026"> Иначе говоря, сумма двухвнутренних односторонних углов α и β всего на однуугловую секунду меньше 180˚. Продолжим прямые α и β,пока они не пересекутся в точке С. В результате получится прямоугольныйтреугольник АВС, у которого угол А прямой, угол при вершине С равен γ исоставляет 1 угловую секунду. Катет АС этого треугольника имеет длину с/tgγ, где с = 1 м. С помощью калькулятора нетрудно подсчитать, что 1/tgγ≈ 2,06 • 105. Следовательно, длина катета АСсоставляем приблизительно 2,06 • 105 = 206 км.

Угол в 1 угловуюсекунду достаточно ощутим (например при астрономических расчётах). Но проверитьдве указанные выше прямые α и β пересекаются на расстоянии206 км отпрямой АВ,  совсем не просто. Ведьизготовить плоский лист бумаги и линейку длиной более 200 км не предоставляетсявозможным. Использовать оптические приборы? Но тогда надо будет добавить ещёодин постулат: свет распространяется по прямой (а это уже физика). А если суммауглов α и β отличается менее чем на 1 угловую секунду?Как видит, пятый постулат Евклида не так уж прост и убедителен.

<img src="/cache/referats/16327/image006.jpg" align=«left» hspace=«12» v:shapes="_x0000_s1045">Сложностьформулировки пятого постулата и его неубедительность привели к тому, что оченьмногие математики, жившие после Евклида, старались исключить этот постулат изсписка аксиом, т.е. доказать его как теорему с помощью остальных аксиомЕвклида. В «сражениях» с пятым постулатом особенно далеко продвинулись Ламберт,Саккери и Лежандр.

ИтальянецСаккери рассматривал четырёхугольник с тремя прямыми углами (рис. 3). Четвёртыйугол (обозначим его φ) мог быть прямым, тупым или острым. Саккериустановил, что гипотеза прямого угла, т.е. утверждение о том, что четвёртыйугол φ всегда равен 90º, позволяет доказать пятый постулат.Иначе говоря, гипотеза прямого угла представляет собой новую аксиому, пятомупостулату.

Гипотезу тупогоугла, допускающую существование четырёхугольника, у которого четвёртый уголφ тупой, Саккери отверг при помощи строгого рассуждения. Однако доказать,что гипотеза острого угла неверна не смог ни Саккери, ни его последователи.Неприступная «крепость»  пятого постулататак и осталась неприступной.     

    Очень интересны исследования французскогоматематика Адриена Мари Лежандра. Но ни одна из них не привела к успеху.

Вот краткоеописание одной из попыток Лежандра. Пусть aи b– две прямые, перпендикулярныодной и той же третьей прямой и пересекающие её в точках А и В. Эти две прямые aи bнепересекаются. Допустим, что пятый постулат Евклида неверен и через А можнопровести ещё одну прямую a′, так жене пересекающую b(рис 4.) <img src="/cache/referats/16327/image008.jpg" align=«left» hspace=«12» v:shapes="_x0000_s1046">  Симметричная ей ( относительно АВ) прямая а″также не пересекает прямую b. Рассматриваядва получающихся острых угла α′ и α″ (симметричных другдругу), Лежандр строго доказывает, что прямая aкак при продолжении её вправо, так и при продолжении её влево всёболее удаляются от прямой b. Но прямыеaи bне могут вести себя подобным образом: если они непересекаются, то должны находится на ограниченном расстоянии друг от друга насвоём протяжении. Не правда ли убедительно? Однако на самом деле это простодругая аксиома: она следует из пятого постулата, и, в свою очередь, из неёвытекает справедливость пятого постулата.       

В начале XIXв. в «сражение» вступил русский математик профессорКазанского университета Николай Иванович Лобачевский. Он был исключительноталантлив и настойчив. Первое время Лобачевский шёл тем же путём что и егопредшественники, т.е. пытался рассуждать от противного. Допустив, что пятыйпостулат неверен, а остальные аксиомы справедливы, мы рано или поздно придем кпротиворечию. Этим противоречием он и будет доказан.

Итак, допустим, что пятый постулатневерен: через точку А, не принадлежащую прямой b(рис. 5, а), можно провести более чем одну прямую, котораяне пересекается с b. Пусть прямые a′ и a″ непересекаются с b. При  их расположение, как на рисунке, будемповорачивать прямую a′ почасовой стрелке. Тогда найдётся прямая c′, которая «в последний раз» не пересекается с b. Значит, прямые, получившиеся из с′ приповороте по часовой стрелке (на сколь угодно малый угол), будут пересекатьпрямую b, а прямые, получающиеся из спри малом повороте в обратном направлении, не будут пересекать b. Иначе говоря, среди всех прямых, проходящих через точкуА, прямая с′ отделяет пересекающие bпрямые от не пересекающих её. Сама прямая с′не пересекает b. Такая жекартина наблюдается и для прямой с″, симметричной с′  относительно перпендикуляра АР, опущенного наb. Она отделяет пересекающие bот не пересекающих. <img src="/cache/referats/16327/image010.jpg" align=«left» hspace=«12» v:shapes="_x0000_s1047">

Лобачевский называетпрямые с′ и с″ параллельными прямой b, причём с′ параллельна bвправо, а с″ параллельна bвлево. Остальные прямые, проходящие через точку А и непересекающая  прямую b( такие, как a′ и a″ ), именуются расходящимися с прямой b.

Далее,обозначим длину отрезка АР через x, а острый угол, образуемый прямой с′ или с″с прямой АР, — через П(х) (рис. 5, б). Лобачевский вводит эти определенияи обозначения, стремясь, со свойственной ему настойчивостью, узнать, что можетполучиться из его предположения о неверности пятого постулата, и быстрееобнаружить желанное противоречие.

На нашихчертежах линии изогнуты. Но вы должны понять, что Лобачевский рассуждает именноо прямых линиях. Если отрезок АР мал, то острый угол П(х) близок к90˚. Когда отрезок совсем мал, то, мы увидим, что прямые с′ и с″практически сливаются, поскольку угол П(х) очень близок к 90˚(рис.6). <img src="/cache/referats/16327/image012.jpg" align=«left» hspace=«12» v:shapes="_x0000_s1035"> В целом же, в силу предположения о неверностипятого постулата, приходится изображать линии изогнутыми. И если в дальнейшембудут появляться всё более и более странные вещи, то это только хорошо – мыскорее наткнемся на долгожданное противоречие.

Лобачевскийдоказывает (всё в том же предложении о неверности пятого постулата), что двепараллельные прямые неограниченно сближаются друг с другом в сторонупараллельности, но в обратном направлении они неограниченно удаляются друг отдруга (рис.7, а). <img src="/cache/referats/16327/image014.jpg" align=«left» hspace=«12» v:shapes="_x0000_s1036"> А две расходящиеся прямые имеют единственныйобщий перпендикуляр, по обе стороны от которого они неограниченно удаляютсядруг от друга (рис. 7, б). Это очень похоже на то, о чём писал Лежандр, но мыуже знаем, что здесь пока ещё нет никакого противоречия.

ЗатемЛобачевский рассматривает две параллельные прямые bи cи берёт на прямой bдвижущуюся точку М, удаляющуюся в сторону обратнуюпараллельности (рис. 8).  В каждом положенииточки М он восставляет перпендикуляр pк прямой bдо егопересечения с прямой с. длина перпендикуляра непрерывно возрастает придвижении точки М, и, когда она попадает в положение Q, длина перпендикуляра становится бесконечной. Точнее говоря,перпендикуляр р, восставленный к прямой bв точке Q, параллеленпрямой с (рис. 9, а). Построив прямую с′  симметричную относительно перпендикуляра р,получим три прямые – b, cи c′, которыепопарно параллельны друг другу (рис. 9, б). Возникает своеобразный «бесконечныйтреугольник»: у него каждые две стороны параллельны друг другу, а вершин совсемнет (они как бы находятся в бесконечности; рис. 10). Это уже никак несогласуется с привычными представлениями о расположении прямых линий! Нопротиворечия и здесь нет.

<img src="/cache/referats/16327/image016.jpg" align=«left» hspace=«12» v:shapes="_x0000_s1042"><img src="/cache/referats/16327/image018.jpg" align=«left» hspace=«12» v:shapes="_x0000_s1041">ТогдаЛобачевский предпринимает попытку использовать могущество формул. Применяявыведенную им функцию П(х), он получает зависимости, позволяющие посторонам треугольника вычислять его углы. И оказывается что в любомтреугольнике сумма углов меньше 180˚. Значит в четырёхугольнике Саккери(если его разбить диагональю на два треугольника; рис. 11)  сумма углов меньше 360˚. Это означает,что мы находимся в условиях гипотезы острого угла – когда в четырёхугольникеСаккери четвёртый угол φ<90º. Как будто ничего нового нет:Саккери и его последователи долго ломали голову над гипотезой острого угла, нопротиворечий так и не нашли.

ОднакоЛобачевский оказался теперь намного богаче: он имел формулы, выражающиезависимости между сторонами и углами любого треугольника. Пользуясь своимиформулами, Лобачевский доказал: если известны углы треугольника, можнооднозначно вычислить его стороны. Совсем странно! Ведь существуют подобныетреугольники, в которых углы соответственно равны, а стороны неодинаковы, такчто углы треугольника не позволяют вычислить длины всех его сторон (рис.12).

Что это — желанное противоречие? Увы, опять нет! Наличие подобных, но неравныхтреугольников доказывается с помощью аксиомы о параллельных прямых. А потомусам факт, что такие треугольники существуют, может рассматриваться как ещё однановая аксиома, эквивалентная пятому постулату.

И Лобачевскогоосенила гениальная догадка: противоречия никогда не будет! Иначе говоря, еслимы добавляем ко всем прочим аксиомам ещё и пятый постулат, то получаетсянепротиворечивая геометрическая система – та евклидова геометрия, к которой мытак привыкли. Если же ко всем прочим аксиомам вместо пятого постулата мыдобавим отрицание аксиомы параллельности, т.е. аксиому о том, что через точкувне прямой можно провести более одной прямой, параллельной данной, то получимдругую геометрическую систему (Лобачевский назвал её «воображаемой»геометрией), которая, однако, тоже непротиворечива.

В результатедальнейших исследований при помощи материала своей «воображаемой» геометрииЛобачевский построил модель геометрии Евклида. Какая злая ирония судьбы! Еслибы всё было бы наоборот! Гениальный учёный понимал: создай он из материалаевклидовой геометрии (в непротиворечивости которой никто не сомневался) модель собственной«воображаемой» геометрии – и законность его геометрической системы установлена.Это сделали математики уже следующего поколения.

Лобачевский выступил с докладом об открытиинеевклидовой геометрии в1824 г. но поддержки не нашёл. Математики его времениещё не были подготовлены к мысли о возможности существования иной, неевклидовойгеометрии. Учёный умер, так и не добившись признания своих идей.

Впрочем, одинчеловек понимал и поддерживал его работы. Гениальный Гаусс, «корольматематиков» (судя по архиву, разобранному уже после смерти), ещё в 1815 г., задевять лет до сообщения Лобачевского, размышлял над аналогичными идеями. И темне менее Гаусс, к мнению которого прислушивались все, не решился опубликоватьсвои работы. Однако Гаусс добился того, что Лобачевского избрали иностраннымчленом – корреспондентом Гёттингенского учёного общества. Это единственнаяпочесть, возданная Лобачевскому при жизни.

Кроме Гаусса былещё один человек, который вместе с Лобачевским делит заслугу открытиянеевклидовой геометрии. Венгерский математик Янош Больяй очень интересовалсяпроблемой пятого постулата.

<img src="/cache/referats/16327/image020.jpg" align=«left» hspace=«12» v:shapes="_x0000_s1043">Янош не послушалсовета отца, который сказал, что эта проблема выше человеческих сил. И вскореон добился успеха. Он сумел построить неевклидову геометрию, такую же, как и уЛобачевского, хотя и менее глубокую и последовательную. В своём произведении «Appendix» Янош Больяй изложил новую систему. Каки Лобачевский не добился признания. Однако ему сообщили, что за три года донего книгу такого же содержания. Не поверив в это, он изучал русский язык,чтобы прочесть труды Лобачевского в подлиннике. Непризнание и огорчение, из-затого что его опередили, сломили душевные силы Яноша.

Заметим, что уЯноша Больяя были некоторые интересные построения, которых не было у Лобачевского.Например, он определяет орициклы с помощью хорд равного наклона (а не какортогональные траектории, хотя эти два определения эквивалентны; рис. 16).                         

    

   Математики следующего поколения (Клейн,Кэли, Пуанкаре и др.) сумели построить модель геометрии Лобачевского изматериала геометрии Евклида, тем самым установив непротиворечивость изаконность новой геометрии. И математики поняли, что могут быть разныегеометрии и разные пространства.

    

      

www.ronl.ru

 

Начальная

Windows Commander
Far
WinNavigator
Frigate
Norton Commander
WinNC
Dos Navigator
Servant Salamander
Turbo Browser

Winamp, Skins, Plugins
Необходимые Утилиты
Текстовые редакторы
Юмор

File managers and best utilites
Главная » Реферат » Геометрия лобачевского реферат

Реферат: Геометрия Лобачевского:. Геометрия лобачевского реферат


Реферат по теме «Геометрия Лобачевского»

li{counter-increment:lst-ctn-kix_list_3-8}#doc5994803 .lst-kix_list_2-6>li{counter-increment:lst-ctn-kix_list_2-6}#doc5994803 ol.lst-kix_list_2-0.start{counter-reset:lst-ctn-kix_list_2-0 0}#doc5994803 ol.lst-kix_list_6-2.start{counter-reset:lst-ctn-kix_list_6-2 0}#doc5994803 ol.lst-kix_list_5-8.start{counter-reset:lst-ctn-kix_list_5-8 0}#doc5994803 ol.lst-kix_list_5-3.start{counter-reset:lst-ctn-kix_list_5-3 0}#doc5994803 .lst-kix_list_6-6>li{counter-increment:lst-ctn-kix_list_6-6}#doc5994803 .lst-kix_list_6-3>li:before{content:"" counter(lst-ctn-kix_list_6-3,decimal) ". "}#doc5994803 .lst-kix_list_6-7>li:before{content:"" counter(lst-ctn-kix_list_6-7,lower-latin) ". "}#doc5994803 ol.lst-kix_list_1-5.start{counter-reset:lst-ctn-kix_list_1-5 0}#doc5994803 .lst-kix_list_6-2>li:before{content:"" counter(lst-ctn-kix_list_6-2,lower-roman) ". "}#doc5994803 .lst-kix_list_5-1>li{counter-increment:lst-ctn-kix_list_5-1}#doc5994803 .lst-kix_list_6-3>li{counter-increment:lst-ctn-kix_list_6-3}#doc5994803 .lst-kix_list_3-3>li{counter-increment:lst-ctn-kix_list_3-3}#doc5994803 ol.lst-kix_list_4-2.start{counter-reset:lst-ctn-kix_list_4-2 0}#doc5994803 ul.lst-kix_list_7-8{list-style-type:none}#doc5994803 ul.lst-kix_list_7-7{list-style-type:none}#doc5994803 ol.lst-kix_list_2-3.start{counter-reset:lst-ctn-kix_list_2-3 0}#doc5994803 .lst-kix_list_1-5>li{counter-increment:lst-ctn-kix_list_1-5}#doc5994803 ol.lst-kix_list_6-4.start{counter-reset:lst-ctn-kix_list_6-4 0}#doc5994803 .lst-kix_list_4-3>li:before{content:"" counter(lst-ctn-kix_list_4-3,decimal) ". "}#doc5994803 ul.lst-kix_list_7-4{list-style-type:none}#doc5994803 ul.lst-kix_list_7-3{list-style-type:none}#doc5994803 ul.lst-kix_list_7-6{list-style-type:none}#doc5994803 ol.lst-kix_list_3-6.start{counter-reset:lst-ctn-kix_list_3-6 0}#doc5994803 ul.lst-kix_list_7-5{list-style-type:none}#doc5994803 ol.lst-kix_list_3-0.start{counter-reset:lst-ctn-kix_list_3-0 0}#doc5994803 ul.lst-kix_list_7-0{list-style-type:none}#doc5994803 ul.lst-kix_list_7-2{list-style-type:none}#doc5994803 ul.lst-kix_list_7-1{list-style-type:none}#doc5994803 ol.lst-kix_list_5-0.start{counter-reset:lst-ctn-kix_list_5-0 0}#doc5994803 .lst-kix_list_1-0>li{counter-increment:lst-ctn-kix_list_1-0}#doc5994803 .lst-kix_list_4-4>li{counter-increment:lst-ctn-kix_list_4-4}#doc5994803 ol.lst-kix_list_2-1.start{counter-reset:lst-ctn-kix_list_2-1 0}#doc5994803 .lst-kix_list_3-6>li:before{content:"" counter(lst-ctn-kix_list_3-6,decimal) ". "}#doc5994803 .lst-kix_list_4-7>li{counter-increment:lst-ctn-kix_list_4-7}#doc5994803 .lst-kix_list_4-5>li{counter-increment:lst-ctn-kix_list_4-5}#doc5994803 .lst-kix_list_5-2>li:before{content:"" counter(lst-ctn-kix_list_5-2,lower-roman) ". "}#doc5994803 ol.lst-kix_list_2-6.start{counter-reset:lst-ctn-kix_list_2-6 0}#doc5994803 .lst-kix_list_6-8>li:before{content:"" counter(lst-ctn-kix_list_6-8,lower-roman) ". "}#doc5994803 .lst-kix_list_3-2>li{counter-increment:lst-ctn-kix_list_3-2}#doc5994803 .lst-kix_list_7-2>li:before{content:"\002022 "}#doc5994803 ol.lst-kix_list_2-5.start{counter-reset:lst-ctn-kix_list_2-5 0}#doc5994803 ol.lst-kix_list_1-7{list-style-type:none}#doc5994803 ol.lst-kix_list_1-8{list-style-type:none}#doc5994803 .lst-kix_list_1-6>li:before{content:"" counter(lst-ctn-kix_list_1-6,decimal) ". "}#doc5994803 .lst-kix_list_5-4>li{counter-increment:lst-ctn-kix_list_5-4}#doc5994803 .lst-kix_list_4-2>li{counter-increment:lst-ctn-kix_list_4-2}#doc5994803 .lst-kix_list_6-8>li{counter-increment:lst-ctn-kix_list_6-8}#doc5994803 .lst-kix_list_4-1>li{counter-increment:lst-ctn-kix_list_4-1}#doc5994803 ol.lst-kix_list_1-8.start{counter-reset:lst-ctn-kix_list_1-8 0}#doc5994803 ol.lst-kix_list_4-3.start{counter-reset:lst-ctn-kix_list_4-3 0}#doc5994803 ol.lst-kix_list_1-4.start{counter-reset:lst-ctn-kix_list_1-4 0}#doc5994803 ol.lst-kix_list_1-2{list-style-type:none}#doc5994803 ol.lst-kix_list_4-5.start{counter-reset:lst-ctn-kix_list_4-5 0}#doc5994803 ol.lst-kix_list_1-1{list-style-type:none}#doc5994803 .lst-kix_list_2-1>li:before{content:"" counter(lst-ctn-kix_list_2-1,lower-latin) ". "}#doc5994803 ol.lst-kix_list_1-0{list-style-type:none}#doc5994803 .lst-kix_list_4-8>li:before{content:"" counter(lst-ctn-kix_list_4-8,lower-roman) ". "}#doc5994803 ol.lst-kix_list_1-6{list-style-type:none}#doc5994803 .lst-kix_list_3-0>li{counter-increment:lst-ctn-kix_list_3-0}#doc5994803 ol.lst-kix_list_1-5{list-style-type:none}#doc5994803 .lst-kix_list_5-5>li:before{content:"" counter(lst-ctn-kix_list_5-5,lower-roman) ". "}#doc5994803 ol.lst-kix_list_1-4{list-style-type:none}#doc5994803 ol.lst-kix_list_1-3{list-style-type:none}#doc5994803 .lst-kix_list_1-1>li{counter-increment:lst-ctn-kix_list_1-1}#doc5994803 .lst-kix_list_6-0>li{counter-increment:lst-ctn-kix_list_6-0}#doc5994803 .lst-kix_list_2-0>li:before{content:"" counter(lst-ctn-kix_list_2-0,decimal) ". "}#doc5994803 ol.lst-kix_list_1-2.start{counter-reset:lst-ctn-kix_list_1-2 0}#doc5994803 .lst-kix_list_5-7>li{counter-increment:lst-ctn-kix_list_5-7}#doc5994803 .lst-kix_list_4-6>li{counter-increment:lst-ctn-kix_list_4-6}#doc5994803 .lst-kix_list_2-4>li:before{content:"" counter(lst-ctn-kix_list_2-4,lower-latin) ". "}#doc5994803 ol.lst-kix_list_4-5{list-style-type:none}#doc5994803 ol.lst-kix_list_4-4{list-style-type:none}#doc5994803 .lst-kix_list_4-2>li:before{content:"" counter(lst-ctn-kix_list_4-2,lower-roman) ". "}#doc5994803 ol.lst-kix_list_4-7{list-style-type:none}#doc5994803 ol.lst-kix_list_4-6{list-style-type:none}#doc5994803 ol.lst-kix_list_4-8{list-style-type:none}#doc5994803 ol.lst-kix_list_2-4.start{counter-reset:lst-ctn-kix_list_2-4 0}#doc5994803 ol.lst-kix_list_1-1.start{counter-reset:lst-ctn-kix_list_1-1 0}#doc5994803 ol.lst-kix_list_5-8{list-style-type:none}#doc5994803 ol.lst-kix_list_5-7{list-style-type:none}#doc5994803 .lst-kix_list_2-1>li{counter-increment:lst-ctn-kix_list_2-1}#doc5994803 .lst-kix_list_4-1>li:before{content:"" counter(lst-ctn-kix_list_4-1,lower-latin) ". "}#doc5994803 ol.lst-kix_list_5-4{list-style-type:none}#doc5994803 ol.lst-kix_list_5-3{list-style-type:none}#doc5994803 ol.lst-kix_list_5-6{list-style-type:none}#doc5994803 .lst-kix_list_5-2>li{counter-increment:lst-ctn-kix_list_5-2}#doc5994803 ol.lst-kix_list_5-5{list-style-type:none}#doc5994803 ol.lst-kix_list_1-0.start{counter-reset:lst-ctn-kix_list_1-0 0}#doc5994803 ol.lst-kix_list_5-0{list-style-type:none}#doc5994803 ol.lst-kix_list_5-1{list-style-type:none}#doc5994803 .lst-kix_list_1-0>li:before{content:"" counter(lst-ctn-kix_list_1-0,decimal) ". "}#doc5994803 ol.lst-kix_list_5-2{list-style-type:none}#doc5994803 .lst-kix_list_2-4>li{counter-increment:lst-ctn-kix_list_2-4}#doc5994803 .lst-kix_list_5-8>li:before{content:"" counter(lst-ctn-kix_list_5-8,lower-roman) ". "}#doc5994803 ol.lst-kix_list_1-6.start{counter-reset:lst-ctn-kix_list_1-6 0}#doc5994803 ol.lst-kix_list_4-0{list-style-type:none}#doc5994803 ol.lst-kix_list_4-1{list-style-type:none}#doc5994803 ol.lst-kix_list_4-2{list-style-type:none}#doc5994803 ol.lst-kix_list_4-3{list-style-type:none}#doc5994803 .lst-kix_list_3-4>li:before{content:"" counter(lst-ctn-kix_list_3-4,lower-latin) ". "}#doc5994803 .lst-kix_list_1-3>li:before{content:"" counter(lst-ctn-kix_list_1-3,decimal) ". "}#doc5994803 .lst-kix_list_5-8>li{counter-increment:lst-ctn-kix_list_5-8}#doc5994803 ol.lst-kix_list_2-7.start{counter-reset:lst-ctn-kix_list_2-7 0}#doc5994803 ol.lst-kix_list_6-5.start{counter-reset:lst-ctn-kix_list_6-5 0}#doc5994803 .lst-kix_list_6-0>li:before{content:"" counter(lst-ctn-kix_list_6-0,decimal) ". "}#doc5994803 .lst-kix_list_1-2>li{counter-increment:lst-ctn-kix_list_1-2}#doc5994803 .lst-kix_list_4-0>li{counter-increment:lst-ctn-kix_list_4-0}#doc5994803 .lst-kix_list_4-0>li:before{content:"" counter(lst-ctn-kix_list_4-0,decimal) ". "}#doc5994803 .lst-kix_list_4-8>li{counter-increment:lst-ctn-kix_list_4-8}#doc5994803 .lst-kix_list_7-8>li:before{content:"\002022 "}#doc5994803 .lst-kix_list_5-6>li{counter-increment:lst-ctn-kix_list_5-6}#doc5994803 .lst-kix_list_3-1>li:before{content:"" counter(lst-ctn-kix_list_3-1,lower-latin) ". "}#doc5994803 .lst-kix_list_1-7>li:before{content:"" counter(lst-ctn-kix_list_1-7,lower-latin) ". "}#doc5994803 .lst-kix_list_5-5>li{counter-increment:lst-ctn-kix_list_5-5}#doc5994803 .lst-kix_list_3-1>li{counter-increment:lst-ctn-kix_list_3-1}#doc5994803 .lst-kix_list_2-2>li{counter-increment:lst-ctn-kix_list_2-2}#doc5994803 .lst-kix_list_5-1>li:before{content:"" counter(lst-ctn-kix_list_5-1,lower-latin) ". "}#doc5994803 .lst-kix_list_7-3>li:before{content:"\002022 "}#doc5994803 .lst-kix_list_1-1>li:before{content:"" counter(lst-ctn-kix_list_1-1,lower-latin) ". "}#doc5994803 .lst-kix_list_3-2>li:before{content:"" counter(lst-ctn-kix_list_3-2,lower-roman) ". "}#doc5994803 ol.lst-kix_list_6-3.start{counter-reset:lst-ctn-kix_list_6-3 0}#doc5994803 ol.lst-kix_list_4-0.start{counter-reset:lst-ctn-kix_list_4-0 0}#doc5994803 ol.lst-kix_list_4-8.start{counter-reset:lst-ctn-kix_list_4-8 0}#doc5994803 .lst-kix_list_1-2>li:before{content:"" counter(lst-ctn-kix_list_1-2,lower-roman) ". "}#doc5994803 .lst-kix_list_2-8>li{counter-increment:lst-ctn-kix_list_2-8}#doc5994803 .lst-kix_list_1-5>li:before{content:"" counter(lst-ctn-kix_list_1-5,lower-roman) ". "}#doc5994803 .lst-kix_list_2-3>li{counter-increment:lst-ctn-kix_list_2-3}#doc5994803 .lst-kix_list_5-3>li{counter-increment:lst-ctn-kix_list_5-3}#doc5994803 ol.lst-kix_list_6-0.start{counter-reset:lst-ctn-kix_list_6-0 0}#doc5994803 ol.lst-kix_list_1-7.start{counter-reset:lst-ctn-kix_list_1-7 0}#doc5994803 .lst-kix_list_2-3>li:before{content:"" counter(lst-ctn-kix_list_2-3,decimal) ". "}#doc5994803 .lst-kix_list_1-4>li:before{content:"" counter(lst-ctn-kix_list_1-4,lower-latin) ". "}#doc5994803 .lst-kix_list_5-7>li:before{content:"" counter(lst-ctn-kix_list_5-7,lower-latin) ". "}#doc5994803 .lst-kix_list_2-0>li{counter-increment:lst-ctn-kix_list_2-0}#doc5994803 ol.lst-kix_list_3-7.start{counter-reset:lst-ctn-kix_list_3-7 0}#doc5994803 ol.lst-kix_list_6-7.start{counter-reset:lst-ctn-kix_list_6-7 0}#doc5994803 .lst-kix_list_2-7>li:before{content:"" counter(lst-ctn-kix_list_2-7,lower-latin) ". "}#doc5994803 .lst-kix_list_3-7>li{counter-increment:lst-ctn-kix_list_3-7}#doc5994803 .lst-kix_list_1-8>li:before{content:"" counter(lst-ctn-kix_list_1-8,lower-roman) ". "}#doc5994803 .lst-kix_list_1-6>li{counter-increment:lst-ctn-kix_list_1-6}#doc5994803 .lst-kix_list_2-5>li{counter-increment:lst-ctn-kix_list_2-5}#doc5994803 .lst-kix_list_3-3>li:before{content:"" counter(lst-ctn-kix_list_3-3,decimal) ". "}#doc5994803 ol.lst-kix_list_6-1.start{counter-reset:lst-ctn-kix_list_6-1 0}#doc5994803 ol.lst-kix_list_3-2.start{counter-reset:lst-ctn-kix_list_3-2 0}#doc5994803 ol.lst-kix_list_1-3.start{counter-reset:lst-ctn-kix_list_1-3 0}#doc5994803 .lst-kix_list_1-3>li{counter-increment:lst-ctn-kix_list_1-3}#doc5994803 .lst-kix_list_6-4>li:before{content:"" counter(lst-ctn-kix_list_6-4,lower-latin) ". "}#doc5994803 .lst-kix_list_2-7>li{counter-increment:lst-ctn-kix_list_2-7}#doc5994803 .lst-kix_list_6-1>li:before{content:"" counter(lst-ctn-kix_list_6-1,lower-latin) ". "}#doc5994803 .lst-kix_list_6-1>li{counter-increment:lst-ctn-kix_list_6-1}#doc5994803 ol.lst-kix_list_6-8.start{counter-reset:lst-ctn-kix_list_6-8 0}#doc5994803 .lst-kix_list_6-4>li{counter-increment:lst-ctn-kix_list_6-4}#doc5994803 .lst-kix_list_4-7>li:before{content:"" counter(lst-ctn-kix_list_4-7,lower-latin) ". "}#doc5994803 ol.lst-kix_list_5-7.start{counter-reset:lst-ctn-kix_list_5-7 0}#doc5994803 .lst-kix_list_5-0>li{counter-increment:lst-ctn-kix_list_5-0}#doc5994803 .lst-kix_list_6-5>li:before{content:"" counter(lst-ctn-kix_list_6-5,lower-roman) ". "}#doc5994803 .lst-kix_list_2-6>li:before{content:"" counter(lst-ctn-kix_list_2-6,decimal) ". "}#doc5994803 .lst-kix_list_3-6>li{counter-increment:lst-ctn-kix_list_3-6}#doc5994803 ol.lst-kix_list_3-3.start{counter-reset:lst-ctn-kix_list_3-3 0}#doc5994803 .lst-kix_list_2-2>li:before{content:"" counter(lst-ctn-kix_list_2-2,lower-roman) ". "}#doc5994803 .lst-kix_list_7-7>li:before{content:"\002022 "}#doc5994803 .lst-kix_list_7-1>li:before{content:"\002022 "}#doc5994803 .lst-kix_list_1-7>li{counter-increment:lst-ctn-kix_list_1-7}#doc5994803 ol.lst-kix_list_2-8.start{counter-reset:lst-ctn-kix_list_2-8 0}#doc5994803 .lst-kix_list_2-8>li:before{content:"" counter(lst-ctn-kix_list_2-8,lower-roman) ". "}#doc5994803 ol.lst-kix_list_2-0{list-style-type:none}#doc5994803 ol.lst-kix_list_2-1{list-style-type:none}#doc5994803 ol.lst-kix_list_2-2{list-style-type:none}#doc5994803 .lst-kix_list_3-7>li:before{content:"" counter(lst-ctn-kix_list_3-7,lower-latin) ". "}#doc5994803 ol.lst-kix_list_2-3{list-style-type:none}#doc5994803 .lst-kix_list_3-4>li{counter-increment:lst-ctn-kix_list_3-4}#doc5994803 ol.lst-kix_list_2-4{list-style-type:none}#doc5994803 ol.lst-kix_list_2-5{list-style-type:none}#doc5994803 ol.lst-kix_list_3-1{list-style-type:none}#doc5994803 .lst-kix_list_6-6>li:before{content:"" counter(lst-ctn-kix_list_6-6,decimal) ". "}#doc5994803 ol.lst-kix_list_3-2{list-style-type:none}#doc5994803 ol.lst-kix_list_3-3{list-style-type:none}#doc5994803 ol.lst-kix_list_3-4{list-style-type:none}#doc5994803 ol.lst-kix_list_3-0{list-style-type:none}#doc5994803 .lst-kix_list_1-8>li{counter-increment:lst-ctn-kix_list_1-8}#doc5994803 ol.lst-kix_list_3-6{list-style-type:none}#doc5994803 .lst-kix_list_7-0>li:before{content:"\002022 "}#doc5994803 ol.lst-kix_list_3-5{list-style-type:none}#doc5994803 ol.lst-kix_list_3-8{list-style-type:none}#doc5994803 ol.lst-kix_list_3-7{list-style-type:none}#doc5994803 ol.lst-kix_list_2-7{list-style-type:none}#doc5994803 ol.lst-kix_list_2-6{list-style-type:none}#doc5994803 .lst-kix_list_3-5>li:before{content:"" counter(lst-ctn-kix_list_3-5,lower-roman) ". "}#doc5994803 ol.lst-kix_list_2-8{list-style-type:none}#doc5994803 .lst-kix_list_3-5>li{counter-increment:lst-ctn-kix_list_3-5}#doc5994803 ol.lst-kix_list_5-5.start{counter-reset:lst-ctn-kix_list_5-5 0}#doc5994803 .lst-kix_list_4-6>li:before{content:"" counter(lst-ctn-kix_list_4-6,decimal) ". "}#doc5994803 ol.lst-kix_list_6-4{list-style-type:none}#doc5994803 ol.lst-kix_list_6-5{list-style-type:none}#doc5994803 .lst-kix_list_5-3>li:before{content:"" counter(lst-ctn-kix_list_5-3,decimal) ". "}#doc5994803 ol.lst-kix_list_6-2{list-style-type:none}#doc5994803 ol.lst-kix_list_6-3{list-style-type:none}#doc5994803 .lst-kix_list_4-5>li:before{content:"" counter(lst-ctn-kix_list_4-5,lower-roman) ". "}#doc5994803 ol.lst-kix_list_6-8{list-style-type:none}#doc5994803 ol.lst-kix_list_6-6{list-style-type:none}#doc5994803 ol.lst-kix_list_6-7{list-style-type:none}#doc5994803 .lst-kix_list_3-0>li:before{content:"" counter(lst-ctn-kix_list_3-0,decimal) ". "}#doc5994803 .lst-kix_list_7-6>li:before{content:"\002022 "}#doc5994803 .lst-kix_list_2-5>li:before{content:"" counter(lst-ctn-kix_list_2-5,lower-roman) ". "}#doc5994803 ol.lst-kix_list_6-1{list-style-type:none}#doc5994803 ol.lst-kix_list_6-0{list-style-type:none}#doc5994803 .lst-kix_list_5-4>li:before{content:"" counter(lst-ctn-kix_list_5-4,lower-latin) ". "}#doc5994803 ol.lst-kix_list_2-2.start{counter-reset:lst-ctn-kix_list_2-2 0}#doc5994803 .lst-kix_list_4-4>li:before{content:"" counter(lst-ctn-kix_list_4-4,lower-latin) ". "}#doc5994803 ol.lst-kix_list_4-7.start{counter-reset:lst-ctn-kix_list_4-7 0}#doc5994803 ol.lst-kix_list_6-6.start{counter-reset:lst-ctn-kix_list_6-6 0}#doc5994803 .lst-kix_list_7-4>li:before{content:"\002022 "}#doc5994803 ol.lst-kix_list_4-4.start{counter-reset:lst-ctn-kix_list_4-4 0}#doc5994803 .lst-kix_list_4-3>li{counter-increment:lst-ctn-kix_list_4-3}#doc5994803 .lst-kix_list_5-0>li:before{content:"" counter(lst-ctn-kix_list_5-0,decimal) ". "}#doc5994803 .lst-kix_list_6-5>li{counter-increment:lst-ctn-kix_list_6-5}#doc5994803 ol.lst-kix_list_4-1.start{counter-reset:lst-ctn-kix_list_4-1 0}#doc5994803 .lst-kix_list_7-5>li:before{content:"\002022 "}#doc5994803 ol.lst-kix_list_3-5.start{counter-reset:lst-ctn-kix_list_3-5 0}#doc5994803 ol.lst-kix_list_5-6.start{counter-reset:lst-ctn-kix_list_5-6 0}#doc5994803 .lst-kix_list_3-8>li:before{content:"" counter(lst-ctn-kix_list_3-8,lower-roman) ". "}#doc5994803 ol.lst-kix_list_3-4.start{counter-reset:lst-ctn-kix_list_3-4 0}#doc5994803 .lst-kix_list_6-2>li{counter-increment:lst-ctn-kix_list_6-2}#doc5994803 ol.lst-kix_list_4-6.start{counter-reset:lst-ctn-kix_list_4-6 0}#doc5994803 ol.lst-kix_list_5-4.start{counter-reset:lst-ctn-kix_list_5-4 0}#doc5994803 .lst-kix_list_1-4>li{counter-increment:lst-ctn-kix_list_1-4}#doc5994803 .lst-kix_list_5-6>li:before{content:"" counter(lst-ctn-kix_list_5-6,decimal) ". "}#doc5994803 ol.lst-kix_list_3-8.start{counter-reset:lst-ctn-kix_list_3-8 0}#doc5994803 ol.lst-kix_list_5-1.start{counter-reset:lst-ctn-kix_list_5-1 0}#doc5994803 ol.lst-kix_list_3-1.start{counter-reset:lst-ctn-kix_list_3-1 0}#doc5994803 ol.lst-kix_list_5-2.start{counter-reset:lst-ctn-kix_list_5-2 0}#doc5994803 .lst-kix_list_6-7>li{counter-increment:lst-ctn-kix_list_6-7}#doc5994803 ol{margin:0;padding:0}#doc5994803 .c1{line-height:1.5;padding-top:0pt;widows:2;orphans:2;text-indent:35.4pt;text-align:justify;direction:ltr;margin-left:-27pt;padding-bottom:0pt}#doc5994803 .c6{line-height:1.0;padding-top:0pt;widows:2;margin-right:-18.2pt;orphans:2;height:11pt;text-align:center;direction:ltr;padding-bottom:0pt}#doc5994803 .c4{line-height:1.5;padding-top:0pt;text-indent:35.4pt;height:11pt;text-align:center;direction:ltr;margin-left:-27pt;padding-bottom:0pt}#doc5994803 .c11{line-height:1.0;padding-top:0pt;widows:2;margin-right:-0.2pt;orphans:2;text-align:center;direction:ltr;padding-bottom:0pt}#doc5994803 .c31{padding-left:8.4pt;line-height:1.5;padding-top:0pt;text-align:justify;direction:ltr;margin-left:27.6pt;padding-bottom:0pt}#doc5994803 .c7{line-height:1.0;padding-top:0pt;widows:2;orphans:2;height:11pt;direction:ltr;padding-bottom:0pt}#doc5994803 .c13{line-height:1.5;padding-top:0pt;text-indent:36pt;text-align:justify;direction:ltr;margin-left:-27pt;padding-bottom:0pt}#doc5994803 .c2{line-height:1.0;padding-top:0pt;text-indent:35.4pt;text-align:right;direction:ltr;margin-left:-27pt;padding-bottom:0pt}#doc5994803 .c25{line-height:1.5;padding-top:0pt;text-indent:36pt;text-align:center;direction:ltr;margin-left:-27pt;padding-bottom:0pt}#doc5994803 .c15{line-height:1.5;padding-top:0pt;text-indent:35.4pt;text-align:justify;direction:ltr;margin-left:-27pt;padding-bottom:0pt}#doc5994803 .c32{line-height:1.5;padding-top:0pt;height:11pt;text-align:justify;direction:ltr;margin-left:44.4pt;padding-bottom:0pt}#doc5994803 .c24{line-height:1.0;padding-top:0pt;widows:2;orphans:2;text-indent:27pt;direction:ltr;padding-bottom:0pt}#doc5994803 .c14{line-height:1.5;padding-top:0pt;text-indent:35.4pt;text-align:center;direction:ltr;margin-left:-27pt;padding-bottom:0pt}#doc5994803 .c26{line-height:1.5;padding-top:0pt;text-indent:35.4pt;height:11pt;direction:ltr;margin-left:-27pt;padding-bottom:0pt}#doc5994803 .c16{padding-left:0pt;line-height:1.5;padding-top:0pt;direction:ltr;margin-left:18pt;padding-bottom:0pt}#doc5994803 .c30{line-height:1.0;padding-top:0pt;text-indent:-99pt;direction:ltr;margin-left:-207pt;padding-bottom:0pt}#doc5994803 .c28{line-height:1.5;padding-top:0pt;text-indent:35.4pt;direction:ltr;margin-left:-27pt;padding-bottom:0pt}#doc5994803 .c19{padding-left:0pt;line-height:1.5;padding-top:0pt;direction:ltr;margin-left:44.4pt;padding-bottom:0pt}#doc5994803 .c40{line-height:1.5;padding-top:0pt;height:11pt;direction:ltr;padding-bottom:0pt}#doc5994803 .c0{vertical-align:baseline;font-size:14pt;font-style:italic;font-family:"Times New Roman";font-weight:normal}#doc5994803 .c39{line-height:1.5;padding-top:0pt;text-align:center;direction:ltr;padding-bottom:0pt}#doc5994803 .c3{vertical-align:baseline;font-size:14pt;font-family:"Times New Roman";font-weight:normal}#doc5994803 .c33{line-height:1.0;padding-top:0pt;direction:ltr;padding-bottom:0pt}#doc5994803 .c20{vertical-align:baseline;font-size:28pt;font-family:"Times New Roman";font-weight:bold}#doc5994803 .c36{vertical-align:super;font-size:14pt;font-family:"Times New Roman";font-weight:normal}#doc5994803 .c5{vertical-align:baseline;font-size:16pt;font-family:"Times New Roman";font-weight:bold}#doc5994803 .c29{vertical-align:baseline;font-size:12pt;font-family:"Times New Roman";font-weight:normal}#doc5994803 .c21{vertical-align:baseline;font-size:14pt;font-family:"Times New Roman";font-weight:bold}#doc5994803 .c12{max-width:453.5pt;background-color:#ffffff;padding:56.7pt 56.7pt 56.7pt 85pt}#doc5994803 .c10{margin:0;padding:0}#doc5994803 .c35{margin-right:-18.2pt;text-align:center}#doc5994803 .c27{widows:2;orphans:2}#doc5994803 .c23{text-indent:-54pt;text-align:center}#doc5994803 .c9{color:inherit;text-decoration:inherit}#doc5994803 .c17{list-style-position:inside}#doc5994803 .c22{text-align:right}#doc5994803 .c18{text-decoration:none}#doc5994803 .c34{font-style:italic}#doc5994803 .c37{text-decoration:underline}#doc5994803 .c38{margin-right:18pt}#doc5994803 .c8{color:#000000}#doc5994803 .title{widows:2;padding-top:24pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:36pt;font-family:"Arial";font-weight:bold;padding-bottom:6pt;page-break-after:avoid}#doc5994803 .subtitle{widows:2;padding-top:18pt;line-height:1.15;orphans:2;text-align:left;color:#666666;font-style:italic;font-size:24pt;font-family:"Georgia";padding-bottom:4pt;page-break-after:avoid}#doc5994803 li{color:#000000;font-size:11pt;font-family:"Arial"}#doc5994803 p{color:#000000;font-size:11pt;margin:0;font-family:"Arial"}#doc5994803 h2{widows:2;padding-top:24pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:24pt;font-family:"Arial";font-weight:bold;padding-bottom:6pt;page-break-after:avoid}#doc5994803 h3{widows:2;padding-top:18pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:18pt;font-family:"Arial";font-weight:bold;padding-bottom:4pt;page-break-after:avoid}#doc5994803 h4{widows:2;padding-top:14pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:14pt;font-family:"Arial";font-weight:bold;padding-bottom:4pt;page-break-after:avoid}#doc5994803 h5{widows:2;padding-top:12pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:12pt;font-family:"Arial";font-weight:bold;padding-bottom:2pt;page-break-after:avoid}#doc5994803 h5{widows:2;padding-top:11pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:11pt;font-family:"Arial";font-weight:bold;padding-bottom:2pt;page-break-after:avoid}#doc5994803 h6{widows:2;padding-top:10pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:10pt;font-family:"Arial";font-weight:bold;padding-bottom:2pt;page-break-after:avoid}#doc5994803 ]]>

Министерство общего образования 

Муниципальная средняя общеобразовательная школа №12                                  

Реферат по теме

«Геометрия Лобачевского»

        

Выполнила: Чунова Александра, 11 «Б»

                                 

Руководитель: Быкова Елена Анатольевна

Оглавление

  1. Введение…………………………………………… 2
  2. Геометрия Лобачевского………………………….. 3
  3. Заключение………………………………………… 9
  4. Список литературы………………………………. 10

Введение

Геометрия Лобачевского (гиперболическая геометрия) — одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского.

В конце прошлого века в работах Пуанкаре и Клейна была установлена прямая связь геометрии Лобачевского с теорией функций комплексной переменной и с теорией чисел (точнее, арифметикой неопределенных квадратичных форм). С тех пор аппарат геометрии Лобачевского стал неотъемлемым компонентом этих разделов математики. В последние 15 лет значение геометрии Лобачевского еще более возросло благодаря работам американского математика Тёрстона (лауреата Филдсовской медали 1983 г.), установившего ее связь с топологией трехмерных многообразий. Десятки работ ежегодно публикуются в этой области. Современные исследования все больше требуют делового владения геометрией Лобачевского.

Я выбрала данную тему по нескольким причинам:

  1. Теория геометрии Лобачевского помогает взглянуть по-другому на окружающий нас мир.
  2. Это интересный, необычный и прогрессивный раздел современной геометрии.
  3. Она дает материал для размышлений – в ней не все просто, не все ясно с первого взгляда, чтобы ее понять, нужно обладать фантазией и пространственным воображением.

Я поставила перед собой такие задачи, как рассмотреть историю возникновения неевклидовой геометрии, познакомиться с личностью Лобачевского и его работой и определить значение геометрии Лобачевского в современной науке.

Геометрия Лобачевского

Был мудрым Евклид,

Но его параллели,

Как будто бы вечные сваи легли.

И мысли его, что как стрелы летели,

Всегда оставались в пределах Земли.

А там, во вселенной, другие законы,

Там точками служат иные тела.

И там параллельных лучей миллионы

Природа сквозь Марс, может быть, провела.

Геометрия, как наука, впервые сформировалась в Древней Греции, когда геометрические закономерности и зависимости, найденные ранее опытным путем, были приведены в надлежащую систему и доказаны.

«Начала» - величайший памятник деятельности Евклида, в котором он собрал воедино всё то, что сделали его предшественники в области геометрии и «словесной алгебры». Но не только в этом его заслуга. Он также внёс много своего, нового, оригинального. Вплоть до XX века геометрию в школах преподавали по учебникам, в которые были включены евклидовы «Начала», переведённые и литературно обработанные.

Однако не всё написанное Евклидом удовлетворяло живших после него математиков. Он сделал попытку дать аксиоматическое изложение геометрии, т.е. сформулировать небольшое количество аксиом, из которых логически выводятся все теоремы геометрии. Список аксиом сразу же подвергся критике, некоторые из них оказались совсем не нужными, например, что «все прямые углы равны между собой».

Так называемый пятый постулат Евклида вызвал особые нарекания математиков. Именно эта аксиома, как показала историческое развитие науки, содержала в себе зародыш другой, неевклидовой геометрии.

Вот о чём говорится в пятом постулате: если две прямые a и b образуют при пересечении с третьей прямой односторонние внутренние углы α и β, сумма величин которых меньше двух прямых углов (т.е. меньше 180˚), то эти две прямые обязательно пересекаются, причём именно стой стороны от третьей прямой, по которую расположены углы α и β (составляющие вместе не менее 180˚).

Данное утверждение заметно сложнее остальных аксиом, поэтому пятый постулат часто заменяют равносильной аксиомой параллельности: через точку, лежащую вне данной прямой, можно провести не более одной прямой, лежащей с данной в одной плоскости и не пересекающей ее.

Попытки доказательства пятого постулата предпринимались в течение более чем двух тысячелетий сначала в Древней Греции, затем на средневековом Востоке, а позже в Западной Европе. Но неудачные попытки прямого доказательства направили ход мыслей ученных в иное русло. Пятый постулат  решили заменить противоположным утверждением. Двери в новую геометрию приоткрыли такие ученые, как Джованни Саккери и Иоганн Ламберт, а их работу продолжили уже другие ученые, среди которых был выдающийся русский математик Николай Иванович Лобачевский.

Н. И. Лобачевский родился 20 ноября (1 декабря) 1792 года в Нижнем Новгороде. Окончил Казанскую гимназию в конце 1806 года, показав хорошие знания, особенно по математике и языкам — латинскому, немецкому, французскому. В проявившемся уже тогда его интересе к математике — большая заслуга преподавателя гимназии Г. И. Карташевского. В 15 лет поступил на физико-математический факультет Казанского университета. В это время там читал лекции по математике профессор И. Бартельс (1769-1836). Он обратил внимание на одаренного мальчика и начал заниматься с Лобачевским. В 19 лет Николай Иванович получил степень магистра, а в 23 года стал профессором. В течение 40 лет преподавал в Казанском университете, в том числе 19 лет руководил им в должности ректора; его активность и умелое руководство вывели университет в число передовых российских учебных заведений.

Еще до открытия неевклидовой геометрии Лобачевский написал в 1823г. учебное руководство, озаглавленное «Геометрия». В нем впервые со всей четкостью отражена так называемая теперь фузионистская точка зрения, согласно которой планиметрию не следует по евклидовой манере отрывать от стереометрии; наоборот, обе эти части геометрии нужно по возможности объединить, т.е. аналогичные начала планиметрии и стереометрии следует преподавать параллельно. Так рядом с кругом Лобачевский рассматривал шар и сферу; взаимное расположение прямых на плоскости он рассматривает совместно с взаимным расположением плоскостей в пространстве, почти одновременно трактует многоугольники и многогранники. Лишь в конце позапрошлого столетия итальянский математик Г. Веронезе также стал проводить в своих учебных руководствах по элементарной геометрии идею фузионизма.

Хотя Лобачевский занимался различными вопросами математики, мировую известность он получил как создатель новой геометрии. Лобачевский был с юношеских лет заинтересован аксиомой параллельных прямых. Сначала он пытался доказать пятый постулат, но постепенно пришел к выводу, что этого сделать нельзя, исходя из остальных аксиом. Тогда он заменил его на противоположное утверждение, которое сейчас называют аксиомой Лобачевского: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.

В разработанной Лобачевским новой геометрии  многие утверждения звучат неожиданно. Вот некоторые из них:

  1. Через точку А, не лежащую на прямой а, проходит бесконечное множество прямых, не пересекающих  прямую а и лежащих  с ней в одной плоскости.
  2. Геометрическое место точек, равноудаленных от данной прямой, есть кривая линия.
  3. Сумма углов треугольника – величина переменная. Она зависит от размера треугольника, но всегда меньше π. 
  4. Площадь треугольника вычисляется по формуле S = r2(π – A – B –C), где r – радиус кривизны пространства, а A, B, C – величины углов треугольника, выраженные в радианах

Остальные аксиомы Лобачевский оставил без изменения и на основе новой системы построил новую геометрию, отличную от евклидовой.

Можно считать, что неевклидова геометрия родилась в феврале 1826 года. Лобачевский выступил с докладом о своем открытии, но поддержки не нашёл. Математики его времени ещё не были подготовлены к мысли о возможности существования иной, неевклидовой геометрии. Учёный умер, так и не добившись признания своих идей. Впрочем, один человек понимал и поддерживал его работы.

Гениальный Гаусс, «король математиков» (судя по архиву, разобранному уже после смерти), ещё в 1815 г., за девять лет до сообщения Лобачевского, размышлял над аналогичными идеями. И тем не менее Гаусс, к мнению которого прислушивались все, не решился опубликовать свои работы. Однако Гаусс добился того, что Лобачевского избрали иностранным членом – корреспондентом Геттингенского учёного общества. Это единственная почесть, возданная Лобачевскому при жизни.

Кроме Гаусса был ещё один человек, который вместе с Лобачевским делит заслугу открытия неевклидовой геометрии. Венгерский математик Янош Бойяи очень интересовался проблемой пятого постулата. Янош не послушал совета отца, который сказал, что эта проблема выше человеческих сил. И вскоре он добился успеха. Он сумел построить неевклидову геометрию, такую же, как и у Лобачевского, хотя и менее глубокую и последовательную.

Позже для планиметрии Лобачевского была найдена реальная модель. Итальянский математик, профессор римского университета Эудженио Бельтрами (1835-1900) нашел модель для неевклидовой геометрии, показав в своей работе «Опыт интерпретации неевклидовой геометрии»(1868г.), что наряду с плоскостями, на которых осуществляется евклидова геометрия, и сферическими поверхностями, на которые действуют формулы сферической геометрии, существуют и такие реальные поверхности, названные им псевдосферами, на которых частично осуществляется планиметрия Лобачевского.

Псевдосфера

В 1871 году Клейн предложил первую полноценную модель плоскости Лобачевского. Плоскостью служит внутренность круга, прямой — хорда круга без концов, а точкой — точка внутри круга. «Движением» назовём любое преобразование круга в самого себя, которое переводит хорды в хорды. Соответственно, равными называются фигуры внутри круга, переводящиеся одна в другую такими преобразованиями. Тогда оказывается, что любой геометрический факт, описанный на таком языке, представляет теорему или аксиому геометрии Лобачевского.

Модель Клейна

Другую модель геометрии Лобачевского построил в 1882г. французский математик Анри Пуанкаре (1854-1912), применивший ее к решению некоторых важных задач теории функций комплексного переменного.  За плоскость Лобачевского принимается внутренность круга, прямыми считаются дуги окружностей, перпендикулярных окружности данного круга, и его диаметры, движениями — преобразования, получаемые комбинациями инверсий относительно окружностей, дуги которых служат прямыми.

Модель Пуанкаре

Заключение

Любая теория современной науки считается единственно верной, пока  не создана следующая. Это своеобразная аксиома развития науки.

Заслуга Лобачевского состоит в том, что он не только высказал идею, но действительно построил и всесторонне развил новую геометрию, логически столь же совершенную и богатую выводами, как евклидова, несмотря на её несоответствие обычным наглядным представлениям. Лобачевский рассматривал свою геометрию как возможную теорию пространственных отношений

Создание геометрии Лобачевского оказало огромное влияние на все науки. Ее результаты используются внутри математики – в теории чисел, в математическом анализе. В частности сам Лобачевский с помощью своей  геометрии вычислили около 200 интегралов. Но наиболее широкое применение она нашла в современной физике – общей и специальной теории относительности, в квантовой механике и других областях.

Одним из важнейших результатов открытия геометрии Лобачевского было развитие новых неевклидовых геометрий, в первую очередь, геометрии Римана, называемой так же эллиптической геометрией.

Непреходящее значение открытия геометрии Лобачевского для науки состоит в том, что оно разрушило приобретенные веками традиционные взгляды на окружающий мир, вывело ученых из узких рамок созданных ими стереотипов мышления. Они стали более восприимчивы к новым неожиданным научным открытиям.

Все! Перечеркнуты “Начала”.

Довольно мысль на них скучала,

Хоть прав почти во всем Евклид,

Но быть не вечно постоянству:

И плоскость свернута в пространство,

И мир

Иной имеет вид...  

Список литературы

  1. За страницами учебниками математики: Н.Я. Виленкин, Л.П Шибасов. – М.: Просвещение: 1996 – 320с.
  2. История математики в школе: Г.И. Глейзер. – М.: Просвещение, 1983. – 351с.

Интернет ресурсы

  1. ru.wikipedia.org
  2. pereplet.ru
  3. referatbank.ru

nsportal.ru

Реферат: Геометрия Лобачевского

Выполнили Исаев Андрей, Гурьев Дмитрий

«Начала» - величайший памятник деятельности Евклида, в котором он собрал воедино всё то, что сделали его предшественники в области геометрии и «словесной алгебры». Но не только в этом его заслуга. Он также внёс много своего, нового, оригинального. Вплоть до XX в. геометрию в школах преподавали по учебникам, в которые были включены евклидовы «Начала», переведённые и литературно обработанные.

Однако не всё написанное Евклидом удовлетворяло живших после него математиков. Великолепной была его попытка дать аксиоматическое изложение геометрии, т.е. сформулировать небольшое количество аксиом, из которых логически выводятся все теоремы геометрии. Список аксиом сразу же подвергся критике, некоторые из них оказались совсем не нужными, например, что «все прямые углы равны между собой».

Так называемый пятый постулат Евклида вызвал особые нарекания математиков. Именно эта аксиома, как показала историческое развитие науки, содержала в себе зародыш другой, неевклидовой геометрии.

Вот о чём говорится в пятом постулате: Если две прямые a и b образуют при пересечении с третьей прямой внутренние односторонние углы α и β, сумма величин которых меньше двух прямых углов (т.е. меньше 180˚; рис 1), то эти две прямые обязательно пересекаются, причём именно стой стороны от третьей прямой, по которую расположены углы α и β (составляющие вместе не менее 180˚).

Данное утверждение заметно сложнее остальных аксиом. Потому-то пятый постулат часто замеряют на равносильную аксиому параллельности: к данной прямой через данную вне её точку можно провести не более одной параллельной прямой.

Вообразим. Что мы взяли две точки А и В на расстоянии 1 м друг от друга и провели через них две прямые a и b, причём так что a образует с прямой АВ равен 89˚59′59″ (рис. 2).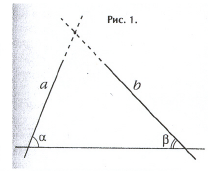

Иначе говоря, сумма двух внутренних односторонних углов α и β всего на одну угловую секунду меньше 180˚. Продолжим прямые α и β, пока они не пересекутся в точке С. В результате получится прямоугольный треугольник АВС, у которого угол А прямой, угол при вершине С равен γ и составляет 1 угловую секунду. Катет АС этого треугольника имеет длину с/tgγ, где с = 1 м. С помощью калькулятора нетрудно подсчитать, что 1/tgγ ≈ 2,06 • 105. Следовательно, длина катета АС составляем приблизительно 2,06 • 105= 206 км.

Угол в 1 угловую секунду достаточно ощутим (например при астрономических расчётах). Но проверить две указанные выше прямые α и β пересекаются на расстоянии206 км от прямой АВ, совсем не просто. Ведь изготовить плоский лист бумаги и линейку длиной более 200 км не предоставляется возможным. Использовать оптические приборы? Но тогда надо будет добавить ещё один постулат: свет распространяется по прямой (а это уже физика). А если сумма углов α и β отличается менее чем на 1 угловую секунду? Как видит, пятый постулат Евклида не так уж прост и убедителен.

Сложность формулировки пятого постулата и его неубедительность привели к тому, что очень многие математики, жившие после Евклида, старались исключить этот постулат из списка аксиом, т.е. доказать его как теорему с помощью остальных аксиом Евклида. В «сражениях» с пятым постулатом особенно далеко продвинулись Ламберт, Саккери и Лежандр.

Итальянец Саккери рассматривал четырёхугольник с тремя прямыми углами (рис. 3). Четвёртый угол (обозначим его φ) мог быть прямым, тупым или острым. Саккери установил, что гипотеза прямого угла, т.е. утверждение о том, что четвёртый угол φ всегда равен 90º, позволяет доказать пятый постулат. Иначе говоря, гипотеза прямого угла представляет собой новую аксиому, пятому постулату.

Гипотезу тупого угла, допускающую существование четырёхугольника, у которого четвёртый угол φ тупой, Саккери отверг при помощи строгого рассуждения. Однако доказать, что гипотеза острого угла неверна не смог ни Саккери, ни его последователи. Неприступная «крепость» пятого постулата так и осталась неприступной.

Очень интересны исследования французского математика Адриена Мари Лежандра. Но ни одна из них не привела к успеху.

Вот краткое описание одной из попыток Лежандра. Пусть a и b – две прямые, перпендикулярны одной и той же третьей прямой и пересекающие её в точках А и В. Эти две прямые a и b не пересекаются. Допустим, что пятый постулат Евклида неверен и через А можно провести ещё одну прямую a′, так же не пересекающую b (рис 4.)Симметричная ей ( относительно АВ) прямая а″ также не пересекает прямую b. Рассматривая два получающихся острых угла α′ и α″ (симметричных друг другу), Лежандр строго доказывает, что прямая a как при продолжении её вправо, так и при продолжении её влево всё более удаляются от прямой b. Но прямые a и b не могут вести себя подобным образом: если они не пересекаются, то должны находится на ограниченном расстоянии друг от друга на своём протяжении. Не правда ли убедительно? Однако на самом деле это просто другая аксиома: она следует из пятого постулата, и, в свою очередь, из неё вытекает справедливость пятого постулата.

В начале XIX в. в «сражение» вступил русский математик профессор Казанского университета Николай Иванович Лобачевский. Он был исключительно талантлив и настойчив. Первое время Лобачевский шёл тем же путём что и его предшественники, т.е. пытался рассуждать от противного. Допустив, что пятый постулат неверен, а остальные аксиомы справедливы, мы рано или поздно придем к противоречию. Этим противоречием он и будет доказан.

Итак, допустим, что пятый постулат неверен: через точку А, не принадлежащую прямой b (рис. 5, а), можно провести более чем одну прямую, которая не пересекается с b. Пусть прямые a′ и a″ не пересекаются с b. При их расположение, как на рисунке, будем поворачивать прямую a′ по часовой стрелке. Тогда найдётся прямая c′, которая «в последний раз» не пересекается с b. Значит, прямые, получившиеся из с′ при повороте по часовой стрелке (на сколь угодно малый угол),будут пересекать прямую b, а прямые, получающиеся из с при малом повороте в обратном направлении, не будут пересекать b. Иначе говоря, среди всех прямых, проходящих через точку А, прямая с′ отделяет пересекающие b прямые от не пересекающих её. Сама прямая с′ не пересекает b. Такая же картина наблюдается и для прямой с″, симметричной с′ относительно перпендикуляра АР, опущенного на b. Она отделяет пересекающие b от не пересекающих.

Лобачевский называет прямые с′ и с″ параллельными прямой b, причём с′ параллельна b вправо, а с″ параллельна b влево. Остальные прямые, проходящие через точку А и не пересекающая прямую b ( такие, как a′ и a″ ), именуются расходящимися с прямой b.

Далее, обозначим длину отрезка АР через x, а острый угол, образуемый прямой с′ или с″ с прямой АР, - через П(х) (рис. 5,б). Лобачевский вводит эти определения и обозначения, стремясь, со свойственной ему настойчивостью, узнать, что может получиться из его предположения о неверности пятого постулата, и быстрее обнаружить желанное противоречие.

На наших чертежах линии изогнуты. Но вы должны понять, что Лобачевский рассуждает именно о прямых линиях. Если отрезок АР мал, то острый угол П(х) близок к 90˚. Когда отрезок совсем мал, то, мы увидим, что прямые с′ и с″ практически сливаются, поскольку угол П(х) очень близок к 90˚(рис. 6).В целом же, в силу предположения о неверности пятого постулата, приходится изображать линии изогнутыми. И если в дальнейшем будут появляться всё более и более странные вещи, то это только хорошо – мы скорее наткнемся на долгожданное противоречие.

Лобачевский доказывает (всё в том же предложении о неверности пятого постулата), что две параллельные прямые неограниченно сближаются друг с другом в сторону параллельности, но в обратном направлении они неограниченно удаляются друг от друга (рис.7,а).А две расходящиеся прямые имеют единственный общий перпендикуляр, по обе стороны от которого они неограниченно удаляются друг от друга (рис. 7,б). Это очень похоже на то, о чём писал Лежандр, но мы уже знаем, что здесь пока ещё нет никакого противоречия.

Затем Лобачевский рассматривает две параллельные прямые b и c и берёт на прямой b движущуюся точку М, удаляющуюся в сторону обратную параллельности (рис. 8).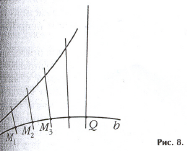В каждом положении точки М он восставляет перпендикуляр p к прямой b до его пересечения с прямой с. длина перпендикуляра непрерывно возрастает при движении точки М, и ,когда она попадает в положение Q, длина перпендикуляра становится бесконечной. Точнее говоря, перпендикуляр р, восставленный к прямой b в точке Q, параллелен прямой с (рис. 9,а). Построив прямую с′ симметричную относительно перпендикуляра р, получим три прямые – b, c и c′, которые попарно параллельны друг другу (рис. 9, б). Возникает своеобразный «бесконечный треугольник»: у него каждые две стороны параллельны друг другу, а вершин совсем нет (они как бы находятся в бесконечности; рис. 10). Это уже никак не согласуется с привычными представлениями о расположении прямых линий! Но противоречия и здесь нет.

Тогда Лобачевский предпринимает попытку использовать могущество формул. Применяя выведенную им функцию П(х), он получает зависимости, позволяющие по сторонам треугольника вычислять его углы. И оказывается что в любом треугольнике сумма углов меньше 180˚. Значит в четырёхугольнике Саккери (если его разбить диагональю на два треугольника; рис. 11) сумма углов меньше 360˚. Это означает, что мы находимся в условиях гипотезы острого угла – когда в четырёхугольнике Саккери четвёртый угол φ<90º. Как будто ничего нового нет: Саккери и его последователи долго ломали голову над гипотезой острого угла, но противоречий так и не нашли.

Однако Лобачевский оказался теперь намного богаче: он имел формулы, выражающие зависимости между сторонами и углами любого треугольника. Пользуясь своими формулами, Лобачевский доказал: если известны углы треугольника, можно однозначно вычислить его стороны. Совсем странно! Ведь существуют подобные треугольники, в которых углы соответственно равны, а стороны неодинаковы, так что углы треугольника не позволяют вычислить длины всех его сторон (рис.12).

Что это - желанное противоречие? Увы, опять нет! Наличие подобных, но неравных треугольников доказывается с помощью аксиомы о параллельных прямых. А потому сам факт, что такие треугольники существуют, может рассматриваться как ещё одна новая аксиома, эквивалентная пятому постулату.

И Лобачевского осенила гениальная догадка: противоречия никогда не будет! Иначе говоря, если мы добавляем ко всем прочим аксиомам ещё и пятый постулат, то получается непротиворечивая геометрическая система – та евклидова геометрия, к которой мы так привыкли. Если же ко всем прочим аксиомам вместо пятого постулата мы добавим отрицание аксиомы параллельности, т.е. аксиому о том, что через точку вне прямой можно провести более одной прямой, параллельной данной, то получим другую геометрическую систему (Лобачевский назвал её «воображаемой» геометрией), которая, однако, тоже непротиворечива.

В результате дальнейших исследований при помощи материала своей «воображаемой» геометрии Лобачевский построил модель геометрии Евклида. Какая злая ирония судьбы! Если бы всё было бы наоборот! Гениальный учёный понимал: создай он из материала евклидовой геометрии (в непротиворечивости которой никто не сомневался) модель собственной «воображаемой» геометрии – и законность его геометрической системы установлена. Это сделали математики уже следующего поколения.

Лобачевский выступил с докладом об открытии неевклидовой геометрии в1824 г. но поддержки не нашёл. Математики его времени ещё не были подготовлены к мысли о возможности существования иной, неевклидовой геометрии. Учёный умер, так и не добившись признания своих идей.

Впрочем, один человек понимал и поддерживал его работы. Гениальный Гаусс, «король математиков» (судя по архиву, разобранному уже после смерти), ещё в 1815 г., за девять лет до сообщения Лобачевского, размышлял над аналогичными идеями. И тем не менее Гаусс, к мнению которого прислушивались все, не решился опубликовать свои работы. Однако Гаусс добился того, что Лобачевского избрали иностранным членом – корреспондентом Гёттингенского учёного общества. Это единственная почесть, возданная Лобачевскому при жизни.

Кроме Гаусса был ещё один человек, который вместе с Лобачевским делит заслугу открытия неевклидовой геометрии. Венгерский математик Янош Больяй очень интересовался проблемой пятого постулата.

Янош не послушал совета отца, который сказал, что эта проблема выше человеческих сил. И вскоре он добился успеха. Он сумел построить неевклидову геометрию, такую же, как и у Лобачевского, хотя и менее глубокую и последовательную. В своём произведении «Appendix» Янош Больяй изложил новую систему. Как и Лобачевский не добился признания. Однако ему сообщили, что за три года до него книгу такого же содержания. Не поверив в это, он изучал русский язык, чтобы прочесть труды Лобачевского в подлиннике. Непризнание и огорчение, из-за того что его опередили, сломили душевные силы Яноша.

Заметим, что у Яноша Больяя были некоторые интересные построения, которых не было у Лобачевского. Например, он определяет орициклы с помощью хорд равного наклона (а не как ортогональные траектории, хотя эти два определения эквивалентны; рис. 16).

Математики следующего поколения (Клейн, Кэли, Пуанкаре и др.) сумели построить модель геометрии Лобачевского из материала геометрии Евклида, тем самым установив непротиворечивость и законность новой геометрии. И математики поняли, что могут быть разные геометрии и разные пространства.

ВОРОНЕЖ 2002г.    Выполнила: Ученица 10 класса «Д» Коробкина Анна.

Муниципальная средняя школа № 1 г. Воронежа.

Доклад по математике. на тему: «Геометрия Лобачевского. Геометрия кривых поверхностей»

Геометрия Лобачевского.

Н.И.Лобачевскийв 1826г. впервые построил и развил одну из возможных геометрий, где аксиома (А) не имеет места. Геометрия Лобачевского основывается на тех же аксиомах , что и евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется противоположным утверждением- аксиомой Лобачевского: Через точку вне прямой в данной плоскости можно провести хотя бы 2 прямые, не пересекающие данную прямую.

Мы видели, что вопрос о том, какая геометрия –Евклида или Лобачевского- точнее описывает мир световых лучей, решается не так уж просто, хотя аксиома Лобачевского и не кажется такой парадоксальной на первый взгляд. Огромной заслугой Лобачевского было то, что он поставил этот вопрос. Но его идеи были столь необычны, что современники их не понимали. Геометрия кривых поверхностей. Многое в геометрии Лобачевского стало яснее, когда учёные хорошо знакомились с геометрией кривых поверхностей. Чтобы пояснить в чем тут дело надо рассмотреть геометрию на шаре. Было время когда люди думали, что земля плоская. Позже, наблюдая за кораблями, уходящими за горизонт, они пришли к выводу о шарообразности земли. Но для этого им пришлось рассматривать предметы (корабли), имеющие определённую высоту, поднимающиеся над поверхностью Земли. Возникает вопрос, нельзя ли убедиться в шарообразности Земли, проводя измерения непосредственно над земной поверхностью и не рассматривая предметов , расположенных над поверхностью Земли. Конечно, это легко сделать- ведь если двигаться по Земле в одном и том же направлении, то в конце концов мы вернёмся на то же место, откуда вышли. Но для такой проверки нужно сделать целое кругосветное путешествие. А нельзя ли убедиться в шарообразности Земли, оставаясь на время на небольшом участке , скажем на острове ? оказывается, возможно. Для этого надо измерять геометрические фигуры на поверхности Земли. Возьмем на этой поверхности 2 точки-А и В. эти точки можно соединить самыми различными линиями. Не покидая нашего острова. Среди всех линий, соединяющих точки А и В, будет одна, имеющая самую маленькую длину. Мы, знающие, что Земля шарообразная, можем сказать , что эта линия – это дуга большого круга, соединяющая точки А и В. А вот человек , живущий на острове и не знающий о шарообразности Земли, назовет эту линию прямой , соединяющей точки А и В. после этого он возьмёт 3 точки А, В, С и измерит углы треугольника АВС . Если остров очень маленький и точность его инструментов тоже мала, то он получит, что сумма углов этого треугольника равна 180. Совсем другой результат получится, если остов велик или инструменты у жителя этого острова очень точны. Чтобы понять в чём дело, рассмотрим такие три точки: за точку А выберем Северный полис, за точку В пересечение экватора с нулевым меридианом и за точку С- пересечение экватора с меридианом, имеющим долготу 90.если вы возьмёте эти 3 точки на глобусе, то сразу увидите, что все 3 угла треугольника АВС равны 90. Но ведь тогда сумма всех углов этого треугольника равна 270. Можно доказать, что у любого треугольника на поверхности шара сумма углов больше, чем 180, и этот избыток тем больше, чем больше площадь треугольника ( потому-то для маленьких треугольников сумма углов равна почти 180). Таким образом, точно измеряя углы большого треугольника, можно убедиться, что мы живём не на плоскости, а на искривлённой поверхности. С помощью ещё более точных измерений можно получить представление и о форме поверхности. Измерения , проведённые на шаре, можно проводить на любой другой поверхности. На любой поверхности есть линии, соединяющие 2 точки и имеющие меньшую длину, чем все остальные линии, соединяющие эти точки. Такие линии называют геодезическими. Измеряя углы треугольников, образованных геодезическими линиями, можно судить о степени искривлённости поверхности. У некоторых кривых поверхностях ( таких, как шар, эллипсиод) эта сумма получается больше 180. У других, например у седла,- больше 180. А есть поверхности, у которых в некоторых местах получается больше 180, а в других- меньше 180, тем сильнее искривлён измеряемые треугольник. Есть такая поверхность( её называют псевдосферой), на которой геодезические линии ведут себя так же, как прямые на плоскости Лобачевского. Известный немецкий ученый Б.РИМАН ввёл очень важное понятие, показав, что можно рассматривать не только искривлённые поверхности, но и искривлённые пространства. Искривлённое пространство очень трудно себе представить- ведь когда мы говорим о кривой поверхности, то представляем себе эту поверхность лежащей на каком-то пространстве. А где же лежит кривое пространство? Дело в том, что в искривленности поверхности можно убедиться, не выходя за её пределы, а измеряя углы в треугольниках на этой поверхности. Точно так же пространство следует считать искривлённым , если сумма углов треугольника, взятом в этом пространстве, отличается от 180.

Чаще всего  для оформления классов , в школе, используют портреты русских писателей 19 века.  Это позволяет школьникам запомнить на подсознательном уровне  имена и  портреты  известных людей прошлого столетия. Заказать портреты для оформления классов можно на www.classno.ru

 

 

 

 

 

Выполнили Исаев Андрей, Гурьев Дмитрий

«Начала» - величайший памятник деятельности Евклида, в котором он собрал воедино всё то, что сделали его предшественники в области геометрии и «словесной алгебры». Но не только в этом его заслуга. Он также внёс много своего, нового, оригинального. Вплоть до XX в. геометрию в школах преподавали по учебникам, в которые были включены евклидовы «Начала», переведённые и литературно обработанные.

Однако не всё написанное Евклидом удовлетворяло живших после него математиков. Великолепной была его попытка дать аксиоматическое изложение геометрии, т.е. сформулировать небольшое количество аксиом, из которых логически выводятся все теоремы геометрии. Список аксиом сразу же подвергся критике, некоторые из них оказались совсем не нужными, например, что «все прямые углы равны между собой».

Так называемый пятый постулат Евклида вызвал особые нарекания математиков. Именно эта аксиома, как показала историческое развитие науки, содержала в себе зародыш другой, неевклидовой геометрии.

Вот о чём говорится в пятом постулате: Если две прямые a и b образуют при пересечении с третьей прямой внутренние односторонние углы α и β, сумма величин которых меньше двух прямых углов (т.е. меньше 180˚; рис 1), то эти две прямые обязательно пересекаются, причём именно стой стороны от третьей прямой, по которую расположены углы α и β (составляющие вместе не менее 180˚).

Данное утверждение заметно сложнее остальных аксиом. Потому-то пятый постулат часто замеряют на равносильную аксиому параллельности: к данной прямой через данную вне её точку можно провести не более одной параллельной прямой.

Вообразим. Что мы взяли две точки А и В на расстоянии 1 м друг от друга и провели через них две прямые a и b, причём так что a образует с прямой АВ равен 89˚59′59″ (рис. 2).

Иначе говоря, сумма двух внутренних односторонних углов α и β всего на одну угловую секунду меньше 180˚. Продолжим прямые α и β, пока они не пересекутся в точке С. В результате получится прямоугольный треугольник АВС, у которого угол А прямой, угол при вершине С равен γ и составляет 1 угловую секунду. Катет АС этого треугольника имеет длину с/tgγ, где с = 1 м. С помощью калькулятора нетрудно подсчитать, что 1/tgγ ≈ 2,06 • 105. Следовательно, длина катета АС составляем приблизительно 2,06 • 105= 206 км.

Угол в 1 угловую секунду достаточно ощутим (например при астрономических расчётах). Но проверить две указанные выше прямые α и β пересекаются на расстоянии206 км от прямой АВ, совсем не просто. Ведь изготовить плоский лист бумаги и линейку длиной более 200 км не предоставляется возможным. Использовать оптические приборы? Но тогда надо будет добавить ещё один постулат: свет распространяется по прямой (а это уже физика). А если сумма углов α и β отличается менее чем на 1 угловую секунду? Как видит, пятый постулат Евклида не так уж прост и убедителен.

Сложность формулировки пятого постулата и его неубедительность привели к тому, что очень многие математики, жившие после Евклида, старались исключить этот постулат из списка аксиом, т.е. доказать его как теорему с помощью остальных аксиом Евклида. В «сражениях» с пятым постулатом особенно далеко продвинулись Ламберт, Саккери и Лежандр.

Итальянец Саккери рассматривал четырёхугольник с тремя прямыми углами (рис. 3). Четвёртый угол (обозначим его φ) мог быть прямым, тупым или острым. Саккери установил, что гипотеза прямого угла, т.е. утверждение о том, что четвёртый угол φ всегда равен 90º, позволяет доказать пятый постулат. Иначе говоря, гипотеза прямого угла представляет собой новую аксиому, пятому постулату.

Гипотезу тупого угла, допускающую существование четырёхугольника, у которого четвёртый угол φ тупой, Саккери отверг при помощи строгого рассуждения. Однако доказать, что гипотеза острого угла неверна не смог ни Саккери, ни его последователи. Неприступная «крепость» пятого постулата так и осталась неприступной.

Очень интересны исследования французского математика Адриена Мари Лежандра. Но ни одна из них не привела к успеху.

Вот краткое описание одной из попыток Лежандра. Пусть a и b – две прямые, перпендикулярны одной и той же третьей прямой и пересекающие её в точках А и В. Эти две прямые a и b не пересекаются. Допустим, что пятый постулат Евклида неверен и через А можно провести ещё одну прямую a′, так же не пересекающую b (рис 4.)Симметричная ей ( относительно АВ) прямая а″ также не пересекает прямую b. Рассматривая два получающихся острых угла α′ и α″ (симметричных друг другу), Лежандр строго доказывает, что прямая a как при продолжении её вправо, так и при продолжении её влево всё более удаляются от прямой b. Но прямые a и b не могут вести себя подобным образом: если они не пересекаются, то должны находится на ограниченном расстоянии друг от друга на своём протяжении. Не правда ли убедительно? Однако на самом деле это просто другая аксиома: она следует из пятого постулата, и, в свою очередь, из неё вытекает справедливость пятого постулата.

В начале XIX в. в «сражение» вступил русский математик профессор Казанского университета Николай Иванович Лобачевский. Он был исключительно талантлив и настойчив. Первое время Лобачевский шёл тем же путём что и его предшественники, т.е. пытался рассуждать от противного. Допустив, что пятый постулат неверен, а остальные аксиомы справедливы, мы рано или поздно придем к противоречию. Этим противоречием он и будет доказан.

Итак, допустим, что пятый постулат неверен: через точку А, не принадлежащую прямой b (рис. 5, а), можно провести более чем одну прямую, которая не пересекается с b. Пусть прямые a′ и a″ не пересекаются с b. При их расположение, как на рисунке, будем поворачивать прямую a′ по часовой стрелке. Тогда найдётся прямая c′, которая «в последний раз» не пересекается с b. Значит, прямые, получившиеся из с′ при повороте по часовой стрелке (на сколь угодно малый угол),будут пересекать прямую b, а прямые, получающиеся из с при малом повороте в обратном направлении, не будут пересекать b. Иначе говоря, среди всех прямых, проходящих через точку А, прямая с′ отделяет пересекающие b прямые от не пересекающих её. Сама прямая с′ не пересекает b. Такая же картина наблюдается и для прямой с″, симметричной с′ относительно перпендикуляра АР, опущенного на b. Она отделяет пересекающие b от не пересекающих.

Лобачевский называет прямые с′ и с″ параллельными прямой b, причём с′ параллельна b вправо, а с″ параллельна b влево. Остальные прямые, проходящие через точку А и не пересекающая прямую b ( такие, как a′ и a″ ), именуются расходящимися с прямой b.

Далее, обозначим длину отрезка АР через x, а острый угол, образуемый прямой с′ или с″ с прямой АР, - через П(х) (рис. 5,б). Лобачевский вводит эти определения и обозначения, стремясь, со свойственной ему настойчивостью, узнать, что может получиться из его предположения о неверности пятого постулата, и быстрее обнаружить желанное противоречие.

На наших чертежах линии изогнуты. Но вы должны понять, что Лобачевский рассуждает именно о прямых линиях. Если отрезок АР мал, то острый угол П(х) близок к 90˚. Когда отрезок совсем мал, то, мы увидим, что прямые с′ и с″ практически сливаются, поскольку угол П(х) очень близок к 90˚(рис. 6).В целом же, в силу предположения о неверности пятого постулата, приходится изображать линии изогнутыми. И если в дальнейшем будут появляться всё более и более странные вещи, то это только хорошо – мы скорее наткнемся на долгожданное противоречие.

Лобачевский доказывает (всё в том же предложении о неверности пятого постулата), что две параллельные прямые неограниченно сближаются друг с другом в сторону параллельности, но в обратном направлении они неограниченно удаляются друг от друга (рис.7,а).А две расходящиеся прямые имеют единственный общий перпендикуляр, по обе стороны от которого они неограниченно удаляются друг от друга (рис. 7,б). Это очень похоже на то, о чём писал Лежандр, но мы уже знаем, что здесь пока ещё нет никакого противоречия.

Затем Лобачевский рассматривает две параллельные прямые b и c и берёт на прямой b движущуюся точку М, удаляющуюся в сторону обратную параллельности (рис. 8).В каждом положении точки М он восставляет перпендикуляр p к прямой b до его пересечения с прямой с. длина перпендикуляра непрерывно возрастает при движении точки М, и ,когда она попадает в положение Q, длина перпендикуляра становится бесконечной. Точнее говоря, перпендикуляр р, восставленный к прямой b в точке Q, параллелен прямой с (рис. 9,а). Построив прямую с′ симметричную относительно перпендикуляра р, получим три прямые – b, c и c′, которые попарно параллельны друг другу (рис. 9, б). Возникает своеобразный «бесконечный треугольник»: у него каждые две стороны параллельны друг другу, а вершин совсем нет (они как бы находятся в бесконечности; рис. 10). Это уже никак не согласуется с привычными представлениями о расположении прямых линий! Но противоречия и здесь нет.

Тогда Лобачевский предпринимает попытку использовать могущество формул. Применяя выведенную им функцию П(х), он получает зависимости, позволяющие по сторонам треугольника вычислять его углы. И оказывается что в любом треугольнике сумма углов меньше 180˚. Значит в четырёхугольнике Саккери (если его разбить диагональю на два треугольника; рис. 11) сумма углов меньше 360˚. Это означает, что мы находимся в условиях гипотезы острого угла – когда в четырёхугольнике Саккери четвёртый угол φ<90º. Как будто ничего нового нет: Саккери и его последователи долго ломали голову над гипотезой острого угла, но противоречий так и не нашли.

Однако Лобачевский оказался теперь намного богаче: он имел формулы, выражающие зависимости между сторонами и углами любого треугольника. Пользуясь своими формулами, Лобачевский доказал: если известны углы треугольника, можно однозначно вычислить его стороны. Совсем странно! Ведь существуют подобные треугольники, в которых углы соответственно равны, а стороны неодинаковы, так что углы треугольника не позволяют вычислить длины всех его сторон (рис.12).

Что это - желанное противоречие? Увы, опять нет! Наличие подобных, но неравных треугольников доказывается с помощью аксиомы о параллельных прямых. А потому сам факт, что такие треугольники существуют, может рассматриваться как ещё одна новая аксиома, эквивалентная пятому постулату.

И Лобачевского осенила гениальная догадка: противоречия никогда не будет! Иначе говоря, если мы добавляем ко всем прочим аксиомам ещё и пятый постулат, то получается непротиворечивая геометрическая система – та евклидова геометрия, к которой мы так привыкли. Если же ко всем прочим аксиомам вместо пятого постулата мы добавим отрицание аксиомы параллельности, т.е. аксиому о том, что через точку вне прямой можно провести более одной прямой, параллельной данной, то получим другую геометрическую систему (Лобачевский назвал её «воображаемой» геометрией), которая, однако, тоже непротиворечива.

В результате дальнейших исследований при помощи материала своей «воображаемой» геометрии Лобачевский построил модель геометрии Евклида. Какая злая ирония судьбы! Если бы всё было бы наоборот! Гениальный учёный понимал: создай он из материала евклидовой геометрии (в непротиворечивости которой никто не сомневался) модель собственной «воображаемой» геометрии – и законность его геометрической системы установлена. Это сделали математики уже следующего поколения.

Лобачевский выступил с докладом об открытии неевклидовой геометрии в1824 г. но поддержки не нашёл. Математики его времени ещё не были подготовлены к мысли о возможности существования иной, неевклидовой геометрии. Учёный умер, так и не добившись признания своих идей.

Впрочем, один человек понимал и поддерживал его работы. Гениальный Гаусс, «король математиков» (судя по архиву, разобранному уже после смерти), ещё в 1815 г., за девять лет до сообщения Лобачевского, размышлял над аналогичными идеями. И тем не менее Гаусс, к мнению которого прислушивались все, не решился опубликовать свои работы. Однако Гаусс добился того, что Лобачевского избрали иностранным членом – корреспондентом Гёттингенского учёного общества. Это единственная почесть, возданная Лобачевскому при жизни.

Кроме Гаусса был ещё один человек, который вместе с Лобачевским делит заслугу открытия неевклидовой геометрии. Венгерский математик Янош Больяй очень интересовался проблемой пятого постулата.

Янош не послушал совета отца, который сказал, что эта проблема выше человеческих сил. И вскоре он добился успеха. Он сумел построить неевклидову геометрию, такую же, как и у Лобачевского, хотя и менее глубокую и последовательную. В своём произведении «Appendix» Янош Больяй изложил новую систему. Как и Лобачевский не добился признания. Однако ему сообщили, что за три года до него книгу такого же содержания. Не поверив в это, он изучал русский язык, чтобы прочесть труды Лобачевского в подлиннике. Непризнание и огорчение, из-за того что его опередили, сломили душевные силы Яноша.

Заметим, что у Яноша Больяя были некоторые интересные построения, которых не было у Лобачевского. Например, он определяет орициклы с помощью хорд равного наклона (а не как ортогональные траектории, хотя эти два определения эквивалентны; рис. 16).

Математики следующего поколения (Клейн, Кэли, Пуанкаре и др.) сумели построить модель геометрии Лобачевского из материала геометрии Евклида, тем самым установив непротиворечивость и законность новой геометрии. И математики поняли, что могут быть разные геометрии и разные пространства.

Смотрите также

 

..:::Новинки:::..

Windows Commander 5.11 Свежая версия.

Новая версия
IrfanView 3.75 (рус)

Обновление текстового редактора TextEd, уже 1.75a

System mechanic 3.7f
Новая версия

Обновление плагинов для WC, смотрим :-)

Весь Winamp
Посетите новый сайт.

WinRaR 3.00
Релиз уже здесь

PowerDesk 4.0 free
Просто - напросто сильный upgrade проводника.

..:::Счетчики:::..

 

     

 

 

Webdistr | Все права защищены © 2018 | Карта сайта

.