|
|
|
|
 Far Far |
 WinNavigator WinNavigator |
 Frigate Frigate |
 Norton
Commander Norton
Commander |
 WinNC WinNC |
 Dos
Navigator Dos
Navigator |
 Servant
Salamander Servant
Salamander |
 Turbo
Browser Turbo
Browser |
|
|
 Winamp,
Skins, Plugins Winamp,
Skins, Plugins |
 Необходимые
Утилиты Необходимые
Утилиты |
 Текстовые
редакторы Текстовые
редакторы |
 Юмор Юмор |
|
|
|
File managers and best utilites |
Двоичная система счисления. Двоичная система счисления реферат
Реферат Двоичная система счисления
скачатьРеферат на тему:
План:
- Введение
- 1 История
- 2 Запись двоичных чисел
- 3 Сложение и умножение двоичных чисел
- 4 Преобразование чисел
- 4.1 Преобразование двоичных чисел в десятичные
- 4.2 Преобразование методом Горнера
- 4.3 Преобразование десятичных чисел в двоичные
- 4.4 Преобразование дробных двоичных чисел в десятичные
- 4.5 Преобразование дробных десятичных чисел в двоичные
- 5 Применения
- 5.1 В цифровых устройствах
- 5.2 В английской системе мер
- 6 Примеры чисел-степеней двойки Примечания
Введение
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления числа записываются с помощью двух символов (0 и 1).
1. История
- Полный набор из 8 триграмм и 64 гексаграмм, аналог 3-битных и 6-битных цифр, был известен в древнем Китае в классических текстах книги Перемен. Порядок гексаграмм в книге Перемен, расположенных в соответствии со значениями соответствующих двоичных цифр (от 0 до 63), и метод их получения был разработан китайским учёным и философом Шао Юн в XI веке. Однако нет доказательств, свидетельствующих о том, что Шао Юн понимал правила двоичной арифметики, располагая двухсимвольные кортежи в лексикографическом порядке.
- Индийский математик Пингала (200 год до н. э.) разработал математические основы для описания поэзии с использованием первого известного применения двоичной системы счисления.[1][2]
- Прообразом баз данных, широко использовавшихся в Центральных Андах (Перу, Боливия) в государственных и общественных целях в I—II тысячелетии н. э., была узелковая письменность Инков — кипу, состоявшая как из числовых записей десятичной системы[3], так и не числовых записей в двоичной системе кодирования[4]. В кипу применялись первичные и дополнительные ключи, позиционные числа, кодирование цветом и образование серий повторяющихся данных[5]. Кипу впервые в истории человечества использовалось для применения такого способа ведения бухгалтерского учёта как двойная запись[6].
- Наборы, представляющие собой комбинации двоичных цифр, использовались африканцами в традиционных гаданиях (таких как Ифа) наряду со средневековой геомантией.
- В 1605 году Френсис Бэкон описал систему, буквы алфавита которой могут быть сведены к последовательностям двоичных цифр, которые в свою очередь могут быть закодированы как едва заметные изменения шрифта в любых случайных текстах. Важным шагом в становлении общей теории двоичного кодирования является замечание о том, что указанный метод может быть использован применительно к любым объектам.[7] (См. Шифр Бэкона)
- Современная двоичная система была полностью описана Лейбницем в XVII веке в работе Explication de l’Arithmétique Binaire[8]. В системе счисления Лейбница были использованы цифры 0 и 1, как и в современной двоичной системе. Как человек, увлекающийся китайской культурой, Лейбниц знал о книге Перемен и заметил, что гексаграммы соответствуют двоичным числам от 0 до 111111. Он восхищался тем, что это отображение является свидетельством крупных китайских достижений в философской математике того времени.[9]
- В 1854 году английский математик Джордж Буль опубликовал знаковую работу, описывающую алгебраические системы применительно к логике, которая в настоящее время известна как Булева алгебра или алгебра логики. Его логическому исчислению было суждено сыграть важную роль в разработке современных цифровых электронных схем.
- В 1937 году Клод Шеннон предствил к защите кандидатскую диссертацию Символический анализ релейных и переключательных схем в MIT, в которой булева алгебра и двоичная арифметика были использованы применительно к электронным реле и переключателям. На диссертации Шеннона по существу основана вся современная цифровая техника.
- В ноябре 1937 года Джордж Штибиц, впоследствии работавший в Bell Labs, создал на базе реле компьютер «Model K» (от англ. «Kitchen», кухня, где производилась сборка), который выполнял двоичное сложение. В конце 1938 года Bell Labs развернула исследовательскую программу во главе со Штибицом. Созданный под его руководством компьютер, завершённый 8 января 1940 года, умел выполнять операции с комплексными числами. Во время демонстрации на конференции American Mathematical Society в Дармутском колледже 11 сентября 1940 года Штибиц продемонстрировал возможность посылки команд удалённому калькулятору комплексных чисел по телефонной линии с использованием телетайпа. Это была первая попытка использования удалённой вычислительной машины посредством телефонной линии. Среди участников конференции, бывших свидетелями демонстрации, были Джон фон Нейман, Джон Мокли и Норберт Винер, впоследствии писавшие об этом в своих мемуарах.
2. Запись двоичных чисел
Двоичная система счисления является частным случаем сдвоенных двоичных показательных позиционных систем счисления с обоими основаниями (a и b) равными 2. Целые числа записываются в виде:
где:
— представляемое число,
— запись числа, строка цифр и знаков,
— число цифр (знаков) в числе x2,2,
— порядковый номер цифры,
— цифры числа x2,2 из множества a={0,1}, весовые коэффициенты, в двоичной системе счисления основание внутриразрядной системы счисления равно 2,
— основание показательной весовой функции, основание межразрядной системы счисления.
Целые числа являются частными суммами степенного ряда:
в котором коэффициенты an берутся из кольца R=a{0,1}, X=2, n=k, а верхний предел в частных суммах ограничен с до — n-1.
Основание показательной функции — b определяет только диапазон представляемых числами x2,b величин.Число записываемых кодов от основания показательной функции - b не зависит.Число записываемых кодов зависит от основания внутриразрядной системы счисления - a, определяется в комбинаторике и равно числу размещений с повторениями:
где a=2 — 2-х элементное множество a={0,1} из которого берутся цифры ak, n — число элементов (цифр) в числе x2,b.
Дробные числа записываются в виде:
где:
— число цифр дробной части числа,
— весовые коэффициенты из множества
, основание внутриразрядной системы счисления равно 2,
— основание показательной весовой функции, основание межразрядной системы счисления.
Следует отметить, что число может быть записано в двоичном виде, а система счисления при этом может быть не двоичной, с другим основанием. Пример: двоично-десятичное кодирование, в котором десятичные цифры записываются в двоичном виде, а система счисления — десятичная.
3. Сложение и умножение двоичных чисел
Таблица сложения
Пример сложения «столбиком» (14 + 5 = 19):
| 1 | ↖ | ||||
| + | 1 | 1 | 1 | 0 | |
| 1 | 0 | 1 | |||
| 1 | 0 | 0 | 1 | 1 | |
Таблица умножения
Пример умножения «столбиком» (14 × 5 = 70):
| × | 1 | 1 | 1 | 0 | |||
| 1 | 0 | 1 | |||||
| + | 1 | 1 | 1 | 0 | |||
| 1 | 1 | 1 | 0 | ||||
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | |
4. Преобразование чисел
Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Начиная с цифры 1 все цифры умножаются на два. Точка, которая стоит после 1, называется двоичной точкой.
4.1. Преобразование двоичных чисел в десятичные
Допустим, вам дано двоичное число 110001. Для перевода в десятичное просто запишите его справа налево как сумму по разрядам следующим образом:
Можно записать это в виде таблицы следующим образом:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | ||||
| +32 | +16 | +1 |
Точно так же, начиная с двоичной точки, двигайтесь справа налево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа.Таким образом, двоичное число 110001 равнозначно десятичному 49.
4.2. Преобразование методом Горнера
Для того, чтобы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47.
4.3. Преобразование десятичных чисел в двоичные
Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :
19 /2 = 9 с остатком 1 9 /2 = 4 c остатком 1 4 /2 = 2 без остатка 0 2 /2 = 1 без остатка 0 1 /2 = 0 с остатком 1Итак, мы делим каждое частное на 2 и записываем остаток в конец двоичной записи. Продолжаем деление до тех пор, пока в частном не будет 0. Результат записываем справо налево. Т.е. нижнее число будет самым левым и.т.д. В результате получаем число 19 в двоичной записи: 10011.
4.4. Преобразование дробных двоичных чисел в десятичные
Нужно перевести число 1011010.101 в десятичную систему. Запишем это число следующим образом:
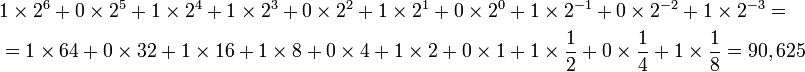
4.5. Преобразование дробных десятичных чисел в двоичные
Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:
- Вначале переводится целая часть десятичной дроби в двоичную систему счисления;
- Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;
- В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;
- Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.
Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.
Перевод целой части дает 20610=110011102 по ранее описанным алгоритмам; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:
.116 • 2 = 0.232.232 • 2 = 0.464.464 • 2 = 0.928.928 • 2 = 1.856.856 • 2 = 1.712.712 • 2 = 1.424.424 • 2 = 0.848.848 • 2 = 1.696.696 • 2 = 1.392.392 • 2 = 0.784и т. д.Получим: 206,11610=11001110,00011101102
5. Применения
5.1. В цифровых устройствах
Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:
- Чем меньше значений существует в системе, тем проще изготовить отдельные элементы, оперирующие этими значениями. В частности, две цифры двоичной системы счисления могут быть легко представлены многими физическими явлениями: есть ток (ток больше пороговой величины) — нет тока (ток меньше пороговой величины), индукция магнитного поля больше пороговой величины или нет (индукция магнитного поля меньше пороговой величины) и т. д.
- Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать. Например, чтобы закодировать три состояния через величину напряжения, тока или индукции магнитного поля, потребуется ввести два пороговых значения и два компаратора, что не будет способствовать помехоустойчивости и надёжности хранения информации.
- Двоичная арифметика является довольно простой. Простыми являются таблицы сложения и умножения — основных действий над числами.
В цифровой электронике одному двоичному разряду в двоичной системе счисления соответствует (очевидно) один двоичный разряд двоичного регистра, то есть двоичный триггер с двумя состояниями (0,1).
5.2. В английской системе мер
При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 715/16″, 311/32″ и т. д.
6. Примеры чисел-степеней двойки
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
| 6 | 64 |
| 7 | 128 |
| 8 | 256 |
| 9 | 512 |
| 10 | 1024 |
| 11 | 2048 |
| 12 | 4096 |
| 13 | 8192 |
| 14 | 16384 |
| 15 | 32768 |
| 16 | 65536 |
| 17 | 131072 |
| 18 | 262144 |
| 19 | 524288 |
| 20 | 1048576 |
| 21 | 2097152 |
| 22 | 4194304 |
| 23 | 8388608 |
| 24 | 16777216 |
| 25 | 33554432 |
| 26 | 67108864 |
| 27 | 134217728 |
| 28 | 268435456 |
| 29 | 536870912 |
| 30 | 1073741824 |
| 31 | 2147483648 |
| 32 | 4294967296 |
| 33 | 8589934592 |
| 34 | 17179869184 |
| 35 | 34359738368 |
| 36 | 68719476736 |
| 37 | 137438953472 |
| 38 | 274877906944 |
| 39 | 549755813888 |
| 40 | 1099511627776 |
| 41 | 2199023255552 |
| 42 | 4398046511104 |
| 43 | 8796093022208 |
| 44 | 17592186044416 |
| 45 | 35184372088832 |
| 46 | 70368744177664 |
| 47 | 140737488355328 |
| 48 | 281474976710656 |
| 49 | 562949953421312 |
| 50 | 1125899906842624 |
Примечания
- Sanchez, Julio & Canton, Maria P. (2007), Microcontroller programming: the microchip PIC, Boca Raton, Florida: CRC Press, p. 37, ISBN 0-8493-7189-9
- W. S. Anglin and J. Lambek, The Heritage of Thales, Springer, 1995, ISBN 0-387-94544-X
- Ordish George, Hyams, Edward. The last of the Incas: the rise and fall of an American empire. — New York: Barnes & Noble, 1996. — С. 80. — ISBN 0-88029-595-3
- Experts 'decipher' Inca strings - news.bbc.co.uk/2/hi/americas/4143968.stm.
- Estudios sobre los quipus - books.google.com/books?id=TmbajGgliYYC&printsec=frontcover. — P. 49.
- Dale Buckmaster (1974). «The Incan Quipu and the Jacobsen Hypothesis - www.jstor.org/stable/2490534». Journal of Accounting Research 12 (1): 178-181. Проверено 2009-12-24.
- Bacon, Francis, The Advancement of Learning - home.hiwaay.net/~paul/bacon/advancement/book6ch2.html, vol. 6, London, pp. Chapter 1, <http://home.hiwaay.net/~paul/bacon/advancement/book6ch2.html - home.hiwaay.net/~paul/bacon/advancement/book6ch2.html>
- http://www.leibniz-translations.com/binary.htm - www.leibniz-translations.com/binary.htm Leibniz Translation.com EXPLANATION OF BINARY ARITHMETIC
- Aiton, Eric J. (1985), Leibniz: A Biography, Taylor & Francis, pp. 245–8, ISBN 0-85274-470-6
wreferat.baza-referat.ru
Реферат: Двоичная система счисления
Федеральное государственное
автономное образовательное учреждение высшего профессионального образования
Новосибирский Государственный Педагогический Университет
Факультет Технологии и Предпринимательства
Кафедра информационных систем и технологий
Р Е Ф Е Р А Т
на тему:
Двоичная система счисления
Кожемякин Владимир Николаевич
Новосибирск, 2014 г.
Введение
Тема «Системы счисления» имеет прямое отношение к математической теории чисел. Необходимость изучения этой темы в курсе информатики связана с тем фактом, что числа в памяти компьютера представлены в двоичной системе счисления, а для внешнего представления содержимого памяти, адресов памяти используют шестнадцатеричную или восьмеричную систему счисления.
Различные системы счисления используются всегда, когда появляется потребность в числовых расчётах, начиная с вычислений младшеклассника, выполняемых карандашом на бумаге, кончая вычислениями, выполняемыми на компьютерах. В работе изложена и занимательно описана одна из наиболее популярных систем счисления - двоичная, а также ее применения, как старые, так и новые, как забавные, так и серьёзные.
Главное достоинство двоичной системы - простота алгоритмов сложения, вычитания умножения и деления. Изучение двоичной системы счисления, которая используется в компьютерах, важно для понимания того, каким образом производится обработка числовых данных в ЭВМ. Поэтому данная тема является актуальной.
Понятие систем счисления
система двоичный счисление кодирование
Понятие «число» является ключевым как для математики, так и для информатики. Люди всегда считали и записывали числа, даже 5 тысяч лет назад. Но записывали их по другим правилам, хотя в любом случае число изображалось с помощью любого или нескольких символов, которые назывались цифрами.
Язык чисел, как и любой другой, имеет свой алфавит. В том языке чисел, которым мы обычно пользуемся, алфавитом служат десять цифр - от 0 до 9. Это десятичная система счисления.
Системой счисления - это способ представления числа символами некоторого алфавита, которые называют цифрами.
Системы счисления делятся на различные группы:
Анатомического происхождения: десятеричная, пятеричная, двенадцатеричная, двадцатеричная.
Алфавитные: древнеармянская, древнегрузинская, древнегреческая, ионическая, славянская.
Машинные: двоичная, восьмеричная, шестнадцатеричная.
Прочие: Римская, Вавилонская, Египетская нумерация, Китайская нумерация и другие.
Также различают позиционные и непозиционные системы счисления.
Непозиционные системы счисления. В непозиционных системах счисления значение числа определяется как сумма или разность цифр в числе. В непозиционных системах счисления считать трудно. Древние греки построили геометрию, которую сегодня изучают в школе, доказали важные теоремы теории чисел, но считать они не умели.
Примеры непозиционных систем счисления:
. У многих народов использовалась система, алфавит которой состоял из одного символа - палочки. Для изображения какого-то числа в этой системе нужно записать определенное множество палочек, равное данному числу: ||||| - число пять.
. Египтяне применяли для записи чисел иероглифы. Единицу обозначали одной вертикальной чертой, а для обозначения чисел, меньших 10, нужно было поставить соответствующее число вертикальных штрихов. Если штрихов нужно изобразить несколько, то их объединяли в группы из трех или четырех черт и изображали в несколько рядов, причем в нижнем должно быть столько же штрихов сколько и в верхнем, или на одну больше.
Для обозначения числа 10, основания системы, египтяне вместо десяти вертикальных черт ввели новый коллективный символ, напоминающий по своим очертаниям подкову или крокетную дужку.
Если нужно изобразить несколько десятков, то иероглиф повторяли нужное количество раз. Тоже самое относится и к остальным иероглифам.
Множество из десяти подковообразных символов, т.е. число 100, они заменили другим новым символом, напоминающим силки; десять силков, т.е. число 1 000, египтяне обозначили стилизованным изображением лотоса. Продолжая в том же духе, египтяне обозначили десять лотосов согнутым пальцем, десять согнутых пальцев - волнистой линией и десять волнистых линий - фигуркой удивленного человека. В итоге древние египтяне могли представлять числа до миллиона.
101001 00010 000100 0001 000 00010 000 000Рис 3. Египетская система счисления
Самым распространенным примером непозиционной системы счисления является римская система счисления
Рис 4. Римская система счисления
Позиционные системы счисления. Позиционной называется такая система счисления, в которой величина, обозначаемая цифрой в записи числа, зависит от ее позиции.
Французский математик Пьер Симон Лаплас (1749- 1827) такими словами оценил "открытие" позиционной системы счисления: "Мысль выражать все числа немногими знаками, придавая им, кроме значения но форме, еще значение по месту, настолько проста, что именно из-за этой простоты трудно оценить, насколько она удивительна".
Первая известная нам система, основанная на позиционном принципе - шестидесятeричная вавилонская. Например, число 59 в данной системе записывается следующим образом:
, т.е. 59 = 5 · 10 + 9.
Запись чисел в позиционных системах счисления осуществляется следующим образом: множество цифр, используемых для записи чисел в позиционных системах счисления, образует алфавит. Количество используемых цифр называется основанием системы счисления. Место каждой цифры в числе - позиция. Сущность позиционного представления чисел отражается в развернутой форме записи числа.
Основание (n)НазваниеАлфавитn=2двоичная0, 1n=3троичная0, 1, 2n=5пятеричная0, 1, 2, 3, 4n=8восьмеричная0, 1, 2, 3, 4, 5, 6, 7n=10десятичная0, 1, 2, 3, 4, 5, 6, 7, 8, 9n=16шестнадцатеричная0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Основные достоинства любой позиционной системы счисления - простота выполнения арифметических операций и ограниченное количество символов, необходимых для записи любого числа.
Двоичная система счисления
Двоичная система счисления - система счисления, построенная на позиционном принципе записи чисел, с использованием только двух знаков - цифр 0 и 1. Главное достоинство двоичной системы - простота алгоритмов сложения, вычитания умножения и деления. Таблица умножения в ней совсем не требует ничего запоминать: ведь любое число, умноженное на нуль равно нулю, а умноженное на единицу равно самому себе. И при этом никаких переносов в следующие разряды, а они есть даже в троичной системе. Таблица деления сводится к двум равенствам 0/1 = 0, 1/1 = 1, благодаря чему деление столбиком многозначных двоичных чисел делается гораздо проще, чем в десятичной системе, и по существу сводится к многократному вычитанию.
Таблица сложения, как ни странно, чуть сложнее, потому что 1+1 = 10 и возникает перенос в следующий разряд. В общем виде операцию сложения однобитовых чисел можно записать в виде x+y = 2w+v, где w, v - биты результата. Внимательно посмотрев на таблицу сложения, можно заметить, что бит переноса w - это просто произведение xy, потому что он равен единице лишь когда x и y равны единице. А вот бит v равен x+y, за исключением случая x = y = 1, когда он равен не 2, а 0. Операцию, с помощью которой по битам x, y вычисляют бит v, называют по-разному. Мы будем использовать для неё название «сложение по модулю 2» и символ . Таким образом, сложение битов выполняется фактически не одной, а двумя операциями.
Если отвлечься от технических деталей, то именно с помощью этих операций и выполняются все операции в компьютере.
Для выполнения сложения однобитовых чисел делают обычно даже специальный логический элемент с двумя входами x, y и двумя выходами w, v, как бы составленный из элемента умножения (его часто называют конъюнкцией, чтобы не путать с умножением многозначных чисел) и элемента сложения по модулю 2. Этот элемент часто называют полусумматором.
Применения двоичной системы счисления
. «Книга перемен»
Двоичная система по существу была известна в Древнем Китае. В классической книге «И цзин» («Книга перемен») приведены так называемые «гексаграммы Фу-си», первая из которых имеет вид , а последняя (64-я) - вид , причем они расположены по кругу и занумерованы в точном соответствии с двоичной системой (нулями и единицами соответствуют сплошные и прерывистые линии). Китайцы не поленились придумать для этих диаграмм специальные иероглифы и названия (например, первая из них называлась «кунь», а последняя - «цянь», сплошной линии сопоставляется мужское начало янь, а прерывистой линии - женское начало инь).
Каждая гексаграмма состоит из двух триграмм (верхней и нижней), им тоже соответствуют определенные иероглифы и названия. Например, триграмме из трех сплошных линий сопоставлен образ-атрибут «небо, творчество», а триграмме из трех прерывистых линий сопоставлен образ-атрибут «земля, податливость, восприимчивость».
. Азбука Морзе
Сэмюель Морзе - изобретатель азбуки, но его самое главное достижение - изобретение телеграфа (а азбука Морзе понадобилась ему для использования телеграфа). Точка и тире оказались самыми элементарными символами, которые мог передавать его телеграф. Они соответствовали коротким и длинным импульсам электрического тока, передаваемым по телеграфным проводам. Длина импульса определялась нажатием руки телеграфиста на ключ телеграфа. Прием сигнала осуществляло реле, которое после появления в нем импульса тока включало электромагнит, который либо заставлял стучать молоточек, либо прижимал колесико с красящей лентой к бумажной ленте, на которой отпечатывались либо точка, либо тире в зависимости от длины импульса.
Азбука Морзе сопоставляет каждой букве алфавита последовательность из точек и тире. Естественней всего использовать такие последовательности длины 6, их всего 64 и хватит даже на русский алфавит. Но Морзе понимал, что длину сообщения желательно уменьшить, насколько возможно, поэтому он решил использовать последовательности длины не более 4, их всего 2 + 4 + 8 + 16 = 30. в русском алфавите пришлось не использовать буквы «э» и «ё» и отождествить мягкий и твердый знаки. Кроме того, наиболее часто используемых буквами он предложил давать самые короткие коды, чтобы уменьшить среднюю длину передаваемого сообщения.
. Штрих-коды
Примером применения двоичного кодирования в современной технике служат штрих-коды. В супермаркетах на упаковках товаров можно увидеть штрих-код. Для чего он нужен, и как его прочитать?
Нужен он только для автоматического занесения информации в кассовый аппарат. Сам штрих-код состоит из тридцати черных полос переменой толщины, разделенной промежутками тоже переменой толщины. Толщина полос может принимать четыре значения - от самой тонкой до самой толстой. Такую же толщину могут иметь и промежутки. Когда по сканеру проводят штрих-кодом, он воспринимает каждую черную полоску как последовательность единиц длины от одной до четырех и также воспринимает промежутки между полосами, но при этом вместо единиц сканер видит нули. Полностью весь штрих-код сканер воспринимает как последовательность из 95 цифр 0 или 1 (их давно уже принято называть битами). Что же содержит этот код? Он кодирует 13-разрядное десятичное число, совершенно открыто написанное под самим штрих-кодом. Если сканер не смог распознать штрих-код, то это число кассир вводит в аппарат вручную. Штрих-код нужен лишь для облегчения распознавания сканером изображения. Распознавать цифры, к тому же повернутые боком, может только сложная программа распознавания на универсальном компьютере, да и то не очень надежно, а не кассовый аппарат.
Рис 5. Расшифровка штрих-кода
Какую же информацию содержит это 13-значное число? Этот вопрос к математике никакого отношения не имеет. Первые две цифры задают страну - производителя товара. Следующие пять цифр - это код производитель, а следующие пять цифр - код самого продукта в принятой этим производителем кодировке. Последняя цифра - это код проверки. Он однозначно вычисляется по предыдущим 12 цифрам, следующим образом. Нужно сложить все цифры с нечетными номерами, утроить сумму, к ней прибавить сумму оставшихся цифр, а полученный результат вычесть из ближайшего кратного 10 числа.
. Компьютерная техника и информационные технологии
Столь привычная для нас десятичная система оказалась неудобной для ЭВМ. Если в механических вычислительных устройствах, использующих десятичную систему, достаточно просто применить элемент с множеством состояний (колесо с девятью зубьями), то в электронных машинах надо было бы иметь 10 различных потенциалов в цепях. Наиболее просто реализуется элементы с двумя состояниями - триггеры. Поэтому естественным был переход на двоичную систему. В этой системе всего две цифры - 0 и 1 . Каждая цифра называется двоичной (от английского binary digit - двоичная цифра). Сокращение от этого выражения привело к появлению термина бит, ставшего названием разряда двоичного числа.
Бит - это минимальная единица измерения информации (0 mini). За битом следует байт, состоящий из восьми бит, затем килобайт (кбайт) - 1024 байта, мегабайт (мбайт) - 1024 кбайта, гигобайт (гбайт) - 1024мбайт.
В компьютере для представления информации используется двоичное кодирование, так как удалось создать надежные работающие технические устройства, которые могут со стопроцентной надежностью сохранять и распознавать не более двух различных состояний (цифр). Все виды информации в компьютере кодируются на машинном языке, в виде логических последовательностей нулей и единиц.
Целые числа в компьютере хранятся в ячейках памяти, в этом случае каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа.
Для хранения целых неотрицательных чисел отводится одна ячейка памяти, состоящая из восьми бит.
Например, число 1910 будет выглядеть:
00010011
Для хранения целых чисел со знаком (отрицательных) отводиться две ячейки памяти (16 битов), причем старший (левый) разряд отводиться под знак числа (если число положительное, то в знаковый разряд записывается 0, если отрицательное - 1).
Например, число -9810 будет выглядеть:
1000000001100010
Начиная с конца 60-х годов, компьютеры все больше использовать для обработки текстовой информации и в настоящее время большая часть компьютеров в мире занято именно обработкой текстовой информации.
Традиционно для кодирования одного символа используется количество информации равное 1 байту, то есть 8 бит. Если рассматривать символы как возможные события, то получаем, что количество различных символов, которые можно закодировать, будет равно 256. Такое количество символов вполне достаточно для представления текстовой информации, включая прописные и строчные буквы русского и латинского алфавитов, а так же цифры, знаки препинания и математических операций, графические символы и так далее. Но способов построения таких кодов очень много, рассмотрим один из них:
Алфавитное неравномерное двоичное кодирование
При алфавитном способе двоичного кодирования символы некоторого первичного алфавита (например, русского) кодируются комбинациями символов двоичного алфавита (т.е. 0 и 1), причем, длина кодов и, соответственно, длительность передачи отдельного кода, могут различаться. Оптимизировать кодирование можно за счет суммарной длительности сообщения. Суммарная длительность сообщения будет меньше, если применить следующий подход: чем буква первичного алфавита, встречается чаще, то присваиваем ей более короткой по длине код. Следовательно, коды букв, вероятность появления которых в сообщении выше, следует строить из возможно меньшего числа элементарных сигналов.
Возможны различные варианты двоичного кодирования, при этом важно, чтобы закодированное сообщение могло быть однозначно декодировано, т.е. чтобы в последовательности 0 и 1, которая представляет собой многобуквенное кодированное сообщение, всегда можно было бы различить обозначения отдельных букв.
Рассмотрим пример построения двоичного кода для символов русского алфавита:
Заключение
В данной работе мы
)рассмотрели понятие систем счисления, выделили их виды,
)рассмотрели двоичную систему счисления;
)выделили применения двоичной системы счисления в жизни человека.
Двоичная система счисления удобна в использовании, что доказывают разнообразные сферы ее применения. В данной работе рассмотрены не все сферы применения двоичной системы счисления и работа в данной области может быть продолжена.
Список используемой литературы
. Занимательные материалы по математике. 7 - 8 классы. / Составитель Галаева Е.А. - Волгоград: Издательско-торговый дом «Корифей», 2006. - 80 с.
. Системы счисления и их применение. (Серия: «Библиотека «Математическое просвещение»») / Гашков С.Б. - Москва: Издательство Московского центра непрерывного математического образования, 2004. - 52 с., ил.
. Раздел информатика, 2001 - 2007. Теле - школа. Интернет - школа «Просвещение.ru»
. Биографический словарь деятелей в области математики. / Бородин А.И., Бугай А.С. - Киев: «Радянська школа», 1979.
. Системы счисления. - 5-е издание. / Фомин С.В. - Москва: «Наука». Главная редакция физико-математической литературы, 1987. - 48 с. - (Популярные лекции по математике).
6. Сайт <http://numeration.ru/bin.html>
Теги: Двоичная система счисления Реферат Математикаdodiplom.ru
Реферат Двоичная система счисления
скачатьРеферат на тему:
План:
- Введение
- 1 История
- 2 Запись двоичных чисел
- 3 Сложение и умножение двоичных чисел
- 4 Преобразование чисел
- 4.1 Преобразование двоичных чисел в десятичные
- 4.2 Преобразование методом Горнера
- 4.3 Преобразование десятичных чисел в двоичные
- 4.4 Преобразование дробных двоичных чисел в десятичные
- 4.5 Преобразование дробных десятичных чисел в двоичные
- 5 Применения
- 5.1 В цифровых устройствах
- 5.2 В английской системе мер
- 6 Примеры чисел-степеней двойки Примечания
Введение
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления числа записываются с помощью двух символов (0 и 1).
1. История
- Полный набор из 8 триграмм и 64 гексаграмм, аналог 3-битных и 6-битных цифр, был известен в древнем Китае в классических текстах книги Перемен. Порядок гексаграмм в книге Перемен, расположенных в соответствии со значениями соответствующих двоичных цифр (от 0 до 63), и метод их получения был разработан китайским учёным и философом Шао Юн в XI веке. Однако нет доказательств, свидетельствующих о том, что Шао Юн понимал правила двоичной арифметики, располагая двухсимвольные кортежи в лексикографическом порядке.
- Индийский математик Пингала (200 год до н. э.) разработал математические основы для описания поэзии с использованием первого известного применения двоичной системы счисления.[1][2]
- Прообразом баз данных, широко использовавшихся в Центральных Андах (Перу, Боливия) в государственных и общественных целях в I—II тысячелетии н. э., была узелковая письменность Инков — кипу, состоявшая как из числовых записей десятичной системы[3], так и не числовых записей в двоичной системе кодирования[4]. В кипу применялись первичные и дополнительные ключи, позиционные числа, кодирование цветом и образование серий повторяющихся данных[5]. Кипу впервые в истории человечества использовалось для применения такого способа ведения бухгалтерского учёта как двойная запись[6].
- Наборы, представляющие собой комбинации двоичных цифр, использовались африканцами в традиционных гаданиях (таких как Ифа) наряду со средневековой геомантией.
- В 1605 году Френсис Бэкон описал систему, буквы алфавита которой могут быть сведены к последовательностям двоичных цифр, которые в свою очередь могут быть закодированы как едва заметные изменения шрифта в любых случайных текстах. Важным шагом в становлении общей теории двоичного кодирования является замечание о том, что указанный метод может быть использован применительно к любым объектам.[7] (См. Шифр Бэкона)
- Современная двоичная система была полностью описана Лейбницем в XVII веке в работе Explication de l’Arithmétique Binaire[8]. В системе счисления Лейбница были использованы цифры 0 и 1, как и в современной двоичной системе. Как человек, увлекающийся китайской культурой, Лейбниц знал о книге Перемен и заметил, что гексаграммы соответствуют двоичным числам от 0 до 111111. Он восхищался тем, что это отображение является свидетельством крупных китайских достижений в философской математике того времени.[9]
- В 1854 году английский математик Джордж Буль опубликовал знаковую работу, описывающую алгебраические системы применительно к логике, которая в настоящее время известна как Булева алгебра или алгебра логики. Его логическому исчислению было суждено сыграть важную роль в разработке современных цифровых электронных схем.
- В 1937 году Клод Шеннон предствил к защите кандидатскую диссертацию Символический анализ релейных и переключательных схем в MIT, в которой булева алгебра и двоичная арифметика были использованы применительно к электронным реле и переключателям. На диссертации Шеннона по существу основана вся современная цифровая техника.
- В ноябре 1937 года Джордж Штибиц, впоследствии работавший в Bell Labs, создал на базе реле компьютер «Model K» (от англ. «Kitchen», кухня, где производилась сборка), который выполнял двоичное сложение. В конце 1938 года Bell Labs развернула исследовательскую программу во главе со Штибицом. Созданный под его руководством компьютер, завершённый 8 января 1940 года, умел выполнять операции с комплексными числами. Во время демонстрации на конференции American Mathematical Society в Дармутском колледже 11 сентября 1940 года Штибиц продемонстрировал возможность посылки команд удалённому калькулятору комплексных чисел по телефонной линии с использованием телетайпа. Это была первая попытка использования удалённой вычислительной машины посредством телефонной линии. Среди участников конференции, бывших свидетелями демонстрации, были Джон фон Нейман, Джон Мокли и Норберт Винер, впоследствии писавшие об этом в своих мемуарах.
2. Запись двоичных чисел
Двоичная система счисления является частным случаем сдвоенных двоичных показательных позиционных систем счисления с обоими основаниями (a и b) равными 2. Целые числа записываются в виде:
где:
— представляемое число,
— запись числа, строка цифр и знаков,
— число цифр (знаков) в числе x2,2,
— порядковый номер цифры,
— цифры числа x2,2 из множества a={0,1}, весовые коэффициенты, в двоичной системе счисления основание внутриразрядной системы счисления равно 2,
— основание показательной весовой функции, основание межразрядной системы счисления.
Целые числа являются частными суммами степенного ряда:
в котором коэффициенты an берутся из кольца R=a{0,1}, X=2, n=k, а верхний предел в частных суммах ограничен с до — n-1.
Основание показательной функции — b определяет только диапазон представляемых числами x2,b величин.Число записываемых кодов от основания показательной функции - b не зависит.Число записываемых кодов зависит от основания внутриразрядной системы счисления - a, определяется в комбинаторике и равно числу размещений с повторениями:
где a=2 — 2-х элементное множество a={0,1} из которого берутся цифры ak, n — число элементов (цифр) в числе x2,b.
Дробные числа записываются в виде:
где:
— число цифр дробной части числа,
— весовые коэффициенты из множества
, основание внутриразрядной системы счисления равно 2,
— основание показательной весовой функции, основание межразрядной системы счисления.
Следует отметить, что число может быть записано в двоичном виде, а система счисления при этом может быть не двоичной, с другим основанием. Пример: двоично-десятичное кодирование, в котором десятичные цифры записываются в двоичном виде, а система счисления — десятичная.
3. Сложение и умножение двоичных чисел
Таблица сложения
Пример сложения «столбиком» (14 + 5 = 19):
| 1 | ↖ | ||||
| + | 1 | 1 | 1 | 0 | |
| 1 | 0 | 1 | |||
| 1 | 0 | 0 | 1 | 1 | |
Таблица умножения
Пример умножения «столбиком» (14 × 5 = 70):
| × | 1 | 1 | 1 | 0 | |||
| 1 | 0 | 1 | |||||
| + | 1 | 1 | 1 | 0 | |||
| 1 | 1 | 1 | 0 | ||||
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | |
4. Преобразование чисел
Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Начиная с цифры 1 все цифры умножаются на два. Точка, которая стоит после 1, называется двоичной точкой.
4.1. Преобразование двоичных чисел в десятичные
Допустим, вам дано двоичное число 110001. Для перевода в десятичное просто запишите его справа налево как сумму по разрядам следующим образом:
Можно записать это в виде таблицы следующим образом:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | ||||
| +32 | +16 | +1 |
Точно так же, начиная с двоичной точки, двигайтесь справа налево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа.Таким образом, двоичное число 110001 равнозначно десятичному 49.
4.2. Преобразование методом Горнера
Для того, чтобы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47.
4.3. Преобразование десятичных чисел в двоичные
Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :
19 /2 = 9 с остатком 1 9 /2 = 4 c остатком 1 4 /2 = 2 без остатка 0 2 /2 = 1 без остатка 0 1 /2 = 0 с остатком 1Итак, мы делим каждое частное на 2 и записываем остаток в конец двоичной записи. Продолжаем деление до тех пор, пока в частном не будет 0. Результат записываем справо налево. Т.е. нижнее число будет самым левым и.т.д. В результате получаем число 19 в двоичной записи: 10011.
4.4. Преобразование дробных двоичных чисел в десятичные
Нужно перевести число 1011010.101 в десятичную систему. Запишем это число следующим образом:
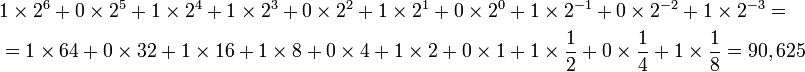
4.5. Преобразование дробных десятичных чисел в двоичные
Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:
- Вначале переводится целая часть десятичной дроби в двоичную систему счисления;
- Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;
- В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;
- Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.
Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.
Перевод целой части дает 20610=110011102 по ранее описанным алгоритмам; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:
.116 • 2 = 0.232.232 • 2 = 0.464.464 • 2 = 0.928.928 • 2 = 1.856.856 • 2 = 1.712.712 • 2 = 1.424.424 • 2 = 0.848.848 • 2 = 1.696.696 • 2 = 1.392.392 • 2 = 0.784и т. д.Получим: 206,11610=11001110,00011101102
5. Применения
5.1. В цифровых устройствах
Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:
- Чем меньше значений существует в системе, тем проще изготовить отдельные элементы, оперирующие этими значениями. В частности, две цифры двоичной системы счисления могут быть легко представлены многими физическими явлениями: есть ток (ток больше пороговой величины) — нет тока (ток меньше пороговой величины), индукция магнитного поля больше пороговой величины или нет (индукция магнитного поля меньше пороговой величины) и т. д.
- Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать. Например, чтобы закодировать три состояния через величину напряжения, тока или индукции магнитного поля, потребуется ввести два пороговых значения и два компаратора, что не будет способствовать помехоустойчивости и надёжности хранения информации.
- Двоичная арифметика является довольно простой. Простыми являются таблицы сложения и умножения — основных действий над числами.
В цифровой электронике одному двоичному разряду в двоичной системе счисления соответствует (очевидно) один двоичный разряд двоичного регистра, то есть двоичный триггер с двумя состояниями (0,1).
5.2. В английской системе мер
При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 715/16″, 311/32″ и т. д.
6. Примеры чисел-степеней двойки
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
| 6 | 64 |
| 7 | 128 |
| 8 | 256 |
| 9 | 512 |
| 10 | 1024 |
| 11 | 2048 |
| 12 | 4096 |
| 13 | 8192 |
| 14 | 16384 |
| 15 | 32768 |
| 16 | 65536 |
| 17 | 131072 |
| 18 | 262144 |
| 19 | 524288 |
| 20 | 1048576 |
| 21 | 2097152 |
| 22 | 4194304 |
| 23 | 8388608 |
| 24 | 16777216 |
| 25 | 33554432 |
| 26 | 67108864 |
| 27 | 134217728 |
| 28 | 268435456 |
| 29 | 536870912 |
| 30 | 1073741824 |
| 31 | 2147483648 |
| 32 | 4294967296 |
| 33 | 8589934592 |
| 34 | 17179869184 |
| 35 | 34359738368 |
| 36 | 68719476736 |
| 37 | 137438953472 |
| 38 | 274877906944 |
| 39 | 549755813888 |
| 40 | 1099511627776 |
| 41 | 2199023255552 |
| 42 | 4398046511104 |
| 43 | 8796093022208 |
| 44 | 17592186044416 |
| 45 | 35184372088832 |
| 46 | 70368744177664 |
| 47 | 140737488355328 |
| 48 | 281474976710656 |
| 49 | 562949953421312 |
| 50 | 1125899906842624 |
Примечания
- Sanchez, Julio & Canton, Maria P. (2007), Microcontroller programming: the microchip PIC, Boca Raton, Florida: CRC Press, p. 37, ISBN 0-8493-7189-9
- W. S. Anglin and J. Lambek, The Heritage of Thales, Springer, 1995, ISBN 0-387-94544-X
- Ordish George, Hyams, Edward. The last of the Incas: the rise and fall of an American empire. — New York: Barnes & Noble, 1996. — С. 80. — ISBN 0-88029-595-3
- Experts 'decipher' Inca strings - news.bbc.co.uk/2/hi/americas/4143968.stm.
- Estudios sobre los quipus - books.google.com/books?id=TmbajGgliYYC&printsec=frontcover. — P. 49.
- Dale Buckmaster (1974). «The Incan Quipu and the Jacobsen Hypothesis - www.jstor.org/stable/2490534». Journal of Accounting Research 12 (1): 178-181. Проверено 2009-12-24.
- Bacon, Francis, The Advancement of Learning - home.hiwaay.net/~paul/bacon/advancement/book6ch2.html, vol. 6, London, pp. Chapter 1, <http://home.hiwaay.net/~paul/bacon/advancement/book6ch2.html - home.hiwaay.net/~paul/bacon/advancement/book6ch2.html>
- http://www.leibniz-translations.com/binary.htm - www.leibniz-translations.com/binary.htm Leibniz Translation.com EXPLANATION OF BINARY ARITHMETIC
- Aiton, Eric J. (1985), Leibniz: A Biography, Taylor & Francis, pp. 245–8, ISBN 0-85274-470-6
www.wreferat.baza-referat.ru
Реферат: "Двоичная система счисления"
Выдержка из работы
Федеральное государственное
автономное образовательное учреждение высшего профессионального образования
Новосибирский Государственный Педагогический Университет
Факультет Технологии и Предпринимательства
Кафедра информационных систем и технологий
Р Е Ф Е Р, А Т
на тему:
Двоичная система счисления
Кожемякин Владимир Николаевич
Новосибирск, 2014 г.
Введение
Тема «Системы счисления» имеет прямое отношение к математической теории чисел. Необходимость изучения этой темы в курсе информатики связана с тем фактом, что числа в памяти компьютера представлены в двоичной системе счисления, а для внешнего представления содержимого памяти, адресов памяти используют шестнадцатеричную или восьмеричную систему счисления.
Различные системы счисления используются всегда, когда появляется потребность в числовых расчётах, начиная с вычислений младшеклассника, выполняемых карандашом на бумаге, кончая вычислениями, выполняемыми на компьютерах. В работе изложена и занимательно описана одна из наиболее популярных систем счисления — двоичная, а также ее применения, как старые, так и новые, как забавные, так и серьёзные.
Главное достоинство двоичной системы -- простота алгоритмов сложения, вычитания умножения и деления. Изучение двоичной системы счисления, которая используется в компьютерах, важно для понимания того, каким образом производится обработка числовых данных в ЭВМ. Поэтому данная тема является актуальной.
Понятие систем счисления
система двоичный счисление кодирование
Понятие «число» является ключевым как для математики, так и для информатики. Люди всегда считали и записывали числа, даже 5 тысяч лет назад. Но записывали их по другим правилам, хотя в любом случае число изображалось с помощью любого или нескольких символов, которые назывались цифрами.
Язык чисел, как и любой другой, имеет свой алфавит. В том языке чисел, которым мы обычно пользуемся, алфавитом служат десять цифр — от 0 до 9. Это десятичная система счисления.
Системой счисления — это способ представления числа символами некоторого алфавита, которые называют цифрами.
Системы счисления делятся на различные группы:
— Анатомического происхождения: десятеричная, пятеричная, двенадцатеричная, двадцатеричная.
— Алфавитные: древнеармянская, древнегрузинская, древнегреческая, ионическая, славянская.
— Машинные: двоичная, восьмеричная, шестнадцатеричная.
— Прочие: Римская, Вавилонская, Египетская нумерация, Китайская нумерация и другие.
Также различают позиционные и непозиционные системы счисления.
Непозиционные системы счисления. В непозиционных системах счисления значение числа определяется как сумма или разность цифр в числе. В непозиционных системах счисления считать трудно. Древние греки построили геометрию, которую сегодня изучают в школе, доказали важные теоремы теории чисел, но считать они не умели.
Примеры непозиционных систем счисления:
1. У многих народов использовалась система, алфавит которой состоял из одного символа — палочки. Для изображения какого-то числа в этой системе нужно записать определенное множество палочек, равное данному числу: ||||| - число пять.
2. Египтяне применяли для записи чисел иероглифы. Единицу обозначали одной вертикальной чертой, а для обозначения чисел, меньших 10, нужно было поставить соответствующее число вертикальных штрихов. Если штрихов нужно изобразить несколько, то их объединяли в группы из трех или четырех черт и изображали в несколько рядов, причем в нижнем должно быть столько же штрихов сколько и в верхнем, или на одну больше.
Для обозначения числа 10, основания системы, египтяне вместо десяти вертикальных черт ввели новый коллективный символ, напоминающий по своим очертаниям подкову или крокетную дужку.
Если нужно изобразить несколько десятков, то иероглиф повторяли нужное количество раз. Тоже самое относится и к остальным иероглифам.
Множество из десяти подковообразных символов, т. е. число 100, они заменили другим новым символом, напоминающим силки; десять силков, т. е. число 1 000, египтяне обозначили стилизованным изображением лотоса. Продолжая в том же духе, египтяне обозначили десять лотосов согнутым пальцем, десять согнутых пальцев — волнистой линией и десять волнистых линий — фигуркой удивленного человека. В итоге древние египтяне могли представлять числа до миллиона.
10 | 100 | 1 000 | 10 000 | 100 000 | 1 000 000 | 10 000 000 | |
Рис 3. Египетская система счисления
Самым распространенным примером непозиционной системы счисления является римская система счисления
Рис 4. Римская система счисления
Позиционные системы счисления. Позиционной называется такая система счисления, в которой величина, обозначаемая цифрой в записи числа, зависит от ее позиции.
Французский математик Пьер Симон Лаплас (1749-- 1827) такими словами оценил «открытие» позиционной системы счисления: «Мысль выражать все числа немногими знаками, придавая им, кроме значения, но форме, еще значение по месту, настолько проста, что именно из-за этой простоты трудно оценить, насколько она удивительна».
Первая известная нам система, основанная на позиционном принципе — шестидесятeричная вавилонская. Например, число 59 в данной системе записывается следующим образом:
, т. е. 59 = 5 · 10 + 9.
Запись чисел в позиционных системах счисления осуществляется следующим образом: множество цифр, используемых для записи чисел в позиционных системах счисления, образует алфавит. Количество используемых цифр называется основанием системы счисления. Место каждой цифры в числе — позиция. Сущность позиционного представления чисел отражается в развернутой форме записи числа.
Основание (n) | Название | Алфавит | |
n=2 | двоичная | 0, 1 | |
n=3 | троичная | 0, 1, 2 | |
n=5 | пятеричная | 0, 1, 2, 3, 4 | |
n=8 | восьмеричная | 0, 1, 2, 3, 4, 5, 6, 7 | |
n=10 | десятичная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 | |
n=16 | шестнадцатеричная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F | |
Основные достоинства любой позиционной системы счисления — простота выполнения арифметических операций и ограниченное количество символов, необходимых для записи любого числа.
Двоичная система счисления
Двоичная система счисления — система счисления, построенная на позиционном принципе записи чисел, с использованием только двух знаков -- цифр 0 и 1. Главное достоинство двоичной системы -- простота алгоритмов сложения, вычитания умножения и деления. Таблица умножения в ней совсем не требует ничего запоминать: ведь любое число, умноженное на нуль равно нулю, а умноженное на единицу равно самому себе. И при этом никаких переносов в следующие разряды, а они есть даже в троичной системе. Таблица деления сводится к двум равенствам 0/1 = 0, 1/1 = 1, благодаря чему деление столбиком многозначных двоичных чисел делается гораздо проще, чем в десятичной системе, и по существу сводится к многократному вычитанию.
Таблица сложения, как ни странно, чуть сложнее, потому что 1+1 = 10 и возникает перенос в следующий разряд. В общем виде операцию сложения однобитовых чисел можно записать в виде x+y = 2w+v, где w, v -- биты результата. Внимательно посмотрев на таблицу сложения, можно заметить, что бит переноса w -- это просто произведение xy, потому что он равен единице лишь когда x и y равны единице. А вот бит v равен x+y, за исключением случая x = y = 1, когда он равен не 2, а 0. Операцию, с помощью которой по битам x, y вычисляют бит v, называют по-разному. Мы будем использовать для неё название «сложение по модулю 2» и символ /
. Таким образом, сложение битов выполняется фактически не одной, а двумя операциями.
Если отвлечься от технических деталей, то именно с помощью этих операций и выполняются все операции в компьютере.
Для выполнения сложения однобитовых чисел делают обычно даже специальный логический элемент с двумя входами x, y и двумя выходами w, v, как бы составленный из элемента умножения (его часто называют конъюнкцией, чтобы не путать с умножением многозначных чисел) и элемента сложения по модулю 2. Этот элемент часто называют полусумматором.
Применения двоичной системы счисления
1. «Книга перемен»
Двоичная система по существу была известна в Древнем Китае. В классической книге «И цзин» («Книга перемен») приведены так называемые «гексаграммы Фу-си», первая из которых имеет вид, а последняя (64-я) — вид, причем они расположены по кругу и занумерованы в точном соответствии с двоичной системой (нулями и единицами соответствуют сплошные и прерывистые линии). Китайцы не поленились придумать для этих диаграмм специальные иероглифы и названия (например, первая из них называлась «кунь», а последняя — «цянь», сплошной линии сопоставляется мужское начало янь, а прерывистой линии — женское начало инь).
Каждая гексаграмма состоит из двух триграмм (верхней и нижней), им тоже соответствуют определенные иероглифы и названия. Например, триграмме из трех сплошных линий сопоставлен образ-атрибут «небо, творчество», а триграмме из трех прерывистых линий сопоставлен образ-атрибут «земля, податливость, восприимчивость».
2. Азбука Морзе
Сэмюель Морзе — изобретатель азбуки, но его самое главное достижение — изобретение телеграфа (а азбука Морзе понадобилась ему для использования телеграфа). Точка и тире оказались самыми элементарными символами, которые мог передавать его телеграф. Они соответствовали коротким и длинным импульсам электрического тока, передаваемым по телеграфным проводам. Длина импульса определялась нажатием руки телеграфиста на ключ телеграфа. Прием сигнала осуществляло реле, которое после появления в нем импульса тока включало электромагнит, который либо заставлял стучать молоточек, либо прижимал колесико с красящей лентой к бумажной ленте, на которой отпечатывались либо точка, либо тире в зависимости от длины импульса.
Азбука Морзе сопоставляет каждой букве алфавита последовательность из точек и тире. Естественней всего использовать такие последовательности длины 6, их всего 64 и хватит даже на русский алфавит. Но Морзе понимал, что длину сообщения желательно уменьшить, насколько возможно, поэтому он решил использовать последовательности длины не более 4, их всего 2 + 4 + 8 + 16 = 30. в русском алфавите пришлось не использовать буквы «э» и «ё» и отождествить мягкий и твердый знаки. Кроме того, наиболее часто используемых буквами он предложил давать самые короткие коды, чтобы уменьшить среднюю длину передаваемого сообщения.
3. Штрих-коды
Примером применения двоичного кодирования в современной технике служат штрих-коды. В супермаркетах на упаковках товаров можно увидеть штрих-код. Для чего он нужен, и как его прочитать?
Нужен он только для автоматического занесения информации в кассовый аппарат. Сам штрих-код состоит из тридцати черных полос переменой толщины, разделенной промежутками тоже переменой толщины. Толщина полос может принимать четыре значения — от самой тонкой до самой толстой. Такую же толщину могут иметь и промежутки. Когда по сканеру проводят штрих-кодом, он воспринимает каждую черную полоску как последовательность единиц длины от одной до четырех и также воспринимает промежутки между полосами, но при этом вместо единиц сканер видит нули. Полностью весь штрих-код сканер воспринимает как последовательность из 95 цифр 0 или 1 (их давно уже принято называть битами). Что же содержит этот код? Он кодирует 13-разрядное десятичное число, совершенно открыто написанное под самим штрих-кодом. Если сканер не смог распознать штрих-код, то это число кассир вводит в аппарат вручную. Штрих-код нужен лишь для облегчения распознавания сканером изображения. Распознавать цифры, к тому же повернутые боком, может только сложная программа распознавания на универсальном компьютере, да и то не очень надежно, а не кассовый аппарат.
Рис 5. Расшифровка штрих-кода
Какую же информацию содержит это 13-значное число? Этот вопрос к математике никакого отношения не имеет. Первые две цифры задают страну — производителя товара. Следующие пять цифр — это код производитель, а следующие пять цифр — код самого продукта в принятой этим производителем кодировке. Последняя цифра — это код проверки. Он однозначно вычисляется по предыдущим 12 цифрам, следующим образом. Нужно сложить все цифры с нечетными номерами, утроить сумму, к ней прибавить сумму оставшихся цифр, а полученный результат вычесть из ближайшего кратного 10 числа.
4. Компьютерная техника и информационные технологии
Столь привычная для нас десятичная система оказалась неудобной для ЭВМ. Если в механических вычислительных устройствах, использующих десятичную систему, достаточно просто применить элемент с множеством состояний (колесо с девятью зубьями), то в электронных машинах надо было бы иметь 10 различных потенциалов в цепях. Наиболее просто реализуется элементы с двумя состояниями — триггеры. Поэтому естественным был переход на двоичную систему. В этой системе всего две цифры — 0 и 1. Каждая цифра называется двоичной (от английского binary digit — двоичная цифра). Сокращение от этого выражения привело к появлению термина бит, ставшего названием разряда двоичного числа.
Бит — это минимальная единица измерения информации (0 mini). За битом следует байт, состоящий из восьми бит, затем килобайт (кбайт) — 1024 байта, мегабайт (мбайт) — 1024 кбайта, гигобайт (гбайт) — 1024мбайт.
В компьютере для представления информации используется двоичное кодирование, так как удалось создать надежные работающие технические устройства, которые могут со стопроцентной надежностью сохранять и распознавать не более двух различных состояний (цифр). Все виды информации в компьютере кодируются на машинном языке, в виде логических последовательностей нулей и единиц.
Целые числа в компьютере хранятся в ячейках памяти, в этом случае каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа.
Для хранения целых неотрицательных чисел отводится одна ячейка памяти, состоящая из восьми бит.
Например, число 1910 будет выглядеть:
Для хранения целых чисел со знаком (отрицательных) отводиться две ячейки памяти (16 битов), причем старший (левый) разряд отводиться под знак числа (если число положительное, то в знаковый разряд записывается 0, если отрицательное — 1).
Например, число -9810 будет выглядеть:
Начиная с конца 60-х годов, компьютеры все больше использовать для обработки текстовой информации и в настоящее время большая часть компьютеров в мире занято именно обработкой текстовой информации.
Традиционно для кодирования одного символа используется количество информации равное 1 байту, то есть 8 бит. Если рассматривать символы как возможные события, то получаем, что количество различных символов, которые можно закодировать, будет равно 256. Такое количество символов вполне достаточно для представления текстовой информации, включая прописные и строчные буквы русского и латинского алфавитов, а так же цифры, знаки препинания и математических операций, графические символы и так далее. Но способов построения таких кодов очень много, рассмотрим один из них:
Алфавитное неравномерное двоичное кодирование
При алфавитном способе двоичного кодирования символы некоторого первичного алфавита (например, русского) кодируются комбинациями символов двоичного алфавита (т.е. 0 и 1), причем, длина кодов и, соответственно, длительность передачи отдельного кода, могут различаться. Оптимизировать кодирование можно за счет суммарной длительности сообщения. Суммарная длительность сообщения будет меньше, если применить следующий подход: чем буква первичного алфавита, встречается чаще, то присваиваем ей более короткой по длине код. Следовательно, коды букв, вероятность появления которых в сообщении выше, следует строить из возможно меньшего числа элементарных сигналов.
Возможны различные варианты двоичного кодирования, при этом важно, чтобы закодированное сообщение могло быть однозначно декодировано, т. е. чтобы в последовательности 0 и 1, которая представляет собой многобуквенное кодированное сообщение, всегда можно было бы различить обозначения отдельных букв.
Рассмотрим пример построения двоичного кода для символов русского алфавита:
Заключение
В данной работе мы
1) рассмотрели понятие систем счисления, выделили их виды,
2) рассмотрели двоичную систему счисления;
3) выделили применения двоичной системы счисления в жизни человека.
Двоичная система счисления удобна в использовании, что доказывают разнообразные сферы ее применения. В данной работе рассмотрены не все сферы применения двоичной системы счисления и работа в данной области может быть продолжена.
Список используемой литературы
1. Занимательные материалы по математике. 7 — 8 классы. / Составитель Галаева Е. А. — Волгоград: Издательско-торговый дом «Корифей», 2006. — 80 с.
2. Системы счисления и их применение. (Серия: «Библиотека „Математическое просвещение“») / Гашков С. Б. — Москва: Издательство Московского центра непрерывного математического образования, 2004. — 52 с., ил.
3. Раздел информатика, 2001 — 2007. Теле — школа. Интернет — школа «Просвещение. ru»
4. Биографический словарь деятелей в области математики. / Бородин А. И., Бугай А. С. — Киев: «Радянська школа», 1979.
5. Системы счисления. — 5-е издание. / Фомин С. В. — Москва: «Наука». Главная редакция физико-математической литературы, 1987. — 48 с. — (Популярные лекции по математике).
6. Сайт http: //numeration. ru/bin. html
Показать Свернутьreferat.bookap.info
Реферат Двоичная система
скачатьРеферат на тему:
План:
- Введение
- 1 История
- 2 Запись двоичных чисел
- 3 Сложение и умножение двоичных чисел
- 4 Преобразование чисел
- 4.1 Преобразование двоичных чисел в десятичные
- 4.2 Преобразование методом Горнера
- 4.3 Преобразование десятичных чисел в двоичные
- 4.4 Преобразование дробных двоичных чисел в десятичные
- 4.5 Преобразование дробных десятичных чисел в двоичные
- 5 Применения
- 5.1 В цифровых устройствах
- 5.2 В английской системе мер
- 6 Примеры чисел-степеней двойки Примечания
Введение
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления числа записываются с помощью двух символов (0 и 1).
1. История
- Полный набор из 8 триграмм и 64 гексаграмм, аналог 3-битных и 6-битных цифр, был известен в древнем Китае в классических текстах книги Перемен. Порядок гексаграмм в книге Перемен, расположенных в соответствии со значениями соответствующих двоичных цифр (от 0 до 63), и метод их получения был разработан китайским учёным и философом Шао Юн в XI веке. Однако нет доказательств, свидетельствующих о том, что Шао Юн понимал правила двоичной арифметики, располагая двухсимвольные кортежи в лексикографическом порядке.
- Индийский математик Пингала (200 год до н. э.) разработал математические основы для описания поэзии с использованием первого известного применения двоичной системы счисления.[1][2]
- Прообразом баз данных, широко использовавшихся в Центральных Андах (Перу, Боливия) в государственных и общественных целях в I—II тысячелетии н. э., была узелковая письменность Инков — кипу, состоявшая как из числовых записей десятичной системы[3], так и не числовых записей в двоичной системе кодирования[4]. В кипу применялись первичные и дополнительные ключи, позиционные числа, кодирование цветом и образование серий повторяющихся данных[5]. Кипу впервые в истории человечества использовалось для применения такого способа ведения бухгалтерского учёта как двойная запись[6].
- Наборы, представляющие собой комбинации двоичных цифр, использовались африканцами в традиционных гаданиях (таких как Ифа) наряду со средневековой геомантией.
- В 1605 году Френсис Бэкон описал систему, буквы алфавита которой могут быть сведены к последовательностям двоичных цифр, которые в свою очередь могут быть закодированы как едва заметные изменения шрифта в любых случайных текстах. Важным шагом в становлении общей теории двоичного кодирования является замечание о том, что указанный метод может быть использован применительно к любым объектам.[7] (См. Шифр Бэкона)
- Современная двоичная система была полностью описана Лейбницем в XVII веке в работе Explication de l’Arithmétique Binaire[8]. В системе счисления Лейбница были использованы цифры 0 и 1, как и в современной двоичной системе. Как человек, увлекающийся китайской культурой, Лейбниц знал о книге Перемен и заметил, что гексаграммы соответствуют двоичным числам от 0 до 111111. Он восхищался тем, что это отображение является свидетельством крупных китайских достижений в философской математике того времени.[9]
- В 1854 году английский математик Джордж Буль опубликовал знаковую работу, описывающую алгебраические системы применительно к логике, которая в настоящее время известна как Булева алгебра или алгебра логики. Его логическому исчислению было суждено сыграть важную роль в разработке современных цифровых электронных схем.
- В 1937 году Клод Шеннон предствил к защите кандидатскую диссертацию Символический анализ релейных и переключательных схем в MIT, в которой булева алгебра и двоичная арифметика были использованы применительно к электронным реле и переключателям. На диссертации Шеннона по существу основана вся современная цифровая техника.
- В ноябре 1937 года Джордж Штибиц, впоследствии работавший в Bell Labs, создал на базе реле компьютер «Model K» (от англ. «Kitchen», кухня, где производилась сборка), который выполнял двоичное сложение. В конце 1938 года Bell Labs развернула исследовательскую программу во главе со Штибицом. Созданный под его руководством компьютер, завершённый 8 января 1940 года, умел выполнять операции с комплексными числами. Во время демонстрации на конференции American Mathematical Society в Дармутском колледже 11 сентября 1940 года Штибиц продемонстрировал возможность посылки команд удалённому калькулятору комплексных чисел по телефонной линии с использованием телетайпа. Это была первая попытка использования удалённой вычислительной машины посредством телефонной линии. Среди участников конференции, бывших свидетелями демонстрации, были Джон фон Нейман, Джон Мокли и Норберт Винер, впоследствии писавшие об этом в своих мемуарах.
2. Запись двоичных чисел
Двоичная система счисления является частным случаем сдвоенных двоичных показательных позиционных систем счисления с обоими основаниями (a и b) равными 2. Целые числа записываются в виде:
где:
— представляемое число,
— запись числа, строка цифр и знаков,
— число цифр (знаков) в числе x2,2,
— порядковый номер цифры,
— цифры числа x2,2 из множества a={0,1}, весовые коэффициенты, в двоичной системе счисления основание внутриразрядной системы счисления равно 2,
— основание показательной весовой функции, основание межразрядной системы счисления.
Целые числа являются частными суммами степенного ряда:
в котором коэффициенты an берутся из кольца R=a{0,1}, X=2, n=k, а верхний предел в частных суммах ограничен с до — n-1.
Основание показательной функции — b определяет только диапазон представляемых числами x2,b величин.Число записываемых кодов от основания показательной функции - b не зависит.Число записываемых кодов зависит от основания внутриразрядной системы счисления - a, определяется в комбинаторике и равно числу размещений с повторениями:
где a=2 — 2-х элементное множество a={0,1} из которого берутся цифры ak, n — число элементов (цифр) в числе x2,b.
Дробные числа записываются в виде:
где:
— число цифр дробной части числа,
— весовые коэффициенты из множества
, основание внутриразрядной системы счисления равно 2,
— основание показательной весовой функции, основание межразрядной системы счисления.
Следует отметить, что число может быть записано в двоичном виде, а система счисления при этом может быть не двоичной, с другим основанием. Пример: двоично-десятичное кодирование, в котором десятичные цифры записываются в двоичном виде, а система счисления — десятичная.
3. Сложение и умножение двоичных чисел
Таблица сложения
Пример сложения «столбиком» (14 + 5 = 19):
| 1 | ↖ | ||||
| + | 1 | 1 | 1 | 0 | |
| 1 | 0 | 1 | |||
| 1 | 0 | 0 | 1 | 1 | |
Таблица умножения
Пример умножения «столбиком» (14 × 5 = 70):
| × | 1 | 1 | 1 | 0 | |||
| 1 | 0 | 1 | |||||
| + | 1 | 1 | 1 | 0 | |||
| 1 | 1 | 1 | 0 | ||||
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | |
4. Преобразование чисел
Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Начиная с цифры 1 все цифры умножаются на два. Точка, которая стоит после 1, называется двоичной точкой.
4.1. Преобразование двоичных чисел в десятичные
Допустим, вам дано двоичное число 110001. Для перевода в десятичное просто запишите его справа налево как сумму по разрядам следующим образом:
Можно записать это в виде таблицы следующим образом:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | ||||
| +32 | +16 | +1 |
Точно так же, начиная с двоичной точки, двигайтесь справа налево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа.Таким образом, двоичное число 110001 равнозначно десятичному 49.
4.2. Преобразование методом Горнера
Для того, чтобы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47.
4.3. Преобразование десятичных чисел в двоичные
Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :
19 /2 = 9 с остатком 1 9 /2 = 4 c остатком 1 4 /2 = 2 без остатка 0 2 /2 = 1 без остатка 0 1 /2 = 0 с остатком 1Итак, мы делим каждое частное на 2 и записываем остаток в конец двоичной записи. Продолжаем деление до тех пор, пока в частном не будет 0. Результат записываем справо налево. Т.е. нижнее число будет самым левым и.т.д. В результате получаем число 19 в двоичной записи: 10011.
4.4. Преобразование дробных двоичных чисел в десятичные
Нужно перевести число 1011010.101 в десятичную систему. Запишем это число следующим образом:
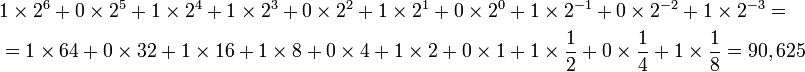
4.5. Преобразование дробных десятичных чисел в двоичные
Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:
- Вначале переводится целая часть десятичной дроби в двоичную систему счисления;
- Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;
- В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;
- Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.
Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.
Перевод целой части дает 20610=110011102 по ранее описанным алгоритмам; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:
.116 • 2 = 0.232.232 • 2 = 0.464.464 • 2 = 0.928.928 • 2 = 1.856.856 • 2 = 1.712.712 • 2 = 1.424.424 • 2 = 0.848.848 • 2 = 1.696.696 • 2 = 1.392.392 • 2 = 0.784и т. д.Получим: 206,11610=11001110,00011101102
5. Применения
5.1. В цифровых устройствах
Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:
- Чем меньше значений существует в системе, тем проще изготовить отдельные элементы, оперирующие этими значениями. В частности, две цифры двоичной системы счисления могут быть легко представлены многими физическими явлениями: есть ток (ток больше пороговой величины) — нет тока (ток меньше пороговой величины), индукция магнитного поля больше пороговой величины или нет (индукция магнитного поля меньше пороговой величины) и т. д.
- Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать. Например, чтобы закодировать три состояния через величину напряжения, тока или индукции магнитного поля, потребуется ввести два пороговых значения и два компаратора, что не будет способствовать помехоустойчивости и надёжности хранения информации.
- Двоичная арифметика является довольно простой. Простыми являются таблицы сложения и умножения — основных действий над числами.
В цифровой электронике одному двоичному разряду в двоичной системе счисления соответствует (очевидно) один двоичный разряд двоичного регистра, то есть двоичный триггер с двумя состояниями (0,1).
5.2. В английской системе мер
При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 715/16″, 311/32″ и т. д.
6. Примеры чисел-степеней двойки
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
| 6 | 64 |
| 7 | 128 |
| 8 | 256 |
| 9 | 512 |
| 10 | 1024 |
| 11 | 2048 |
| 12 | 4096 |
| 13 | 8192 |
| 14 | 16384 |
| 15 | 32768 |
| 16 | 65536 |
| 17 | 131072 |
| 18 | 262144 |
| 19 | 524288 |
| 20 | 1048576 |
| 21 | 2097152 |
| 22 | 4194304 |
| 23 | 8388608 |
| 24 | 16777216 |
| 25 | 33554432 |
| 26 | 67108864 |
| 27 | 134217728 |
| 28 | 268435456 |
| 29 | 536870912 |
| 30 | 1073741824 |
| 31 | 2147483648 |
| 32 | 4294967296 |
| 33 | 8589934592 |
| 34 | 17179869184 |
| 35 | 34359738368 |
| 36 | 68719476736 |
| 37 | 137438953472 |
| 38 | 274877906944 |
| 39 | 549755813888 |
| 40 | 1099511627776 |
| 41 | 2199023255552 |
| 42 | 4398046511104 |
| 43 | 8796093022208 |
| 44 | 17592186044416 |
| 45 | 35184372088832 |
| 46 | 70368744177664 |
| 47 | 140737488355328 |
| 48 | 281474976710656 |
| 49 | 562949953421312 |
| 50 | 1125899906842624 |
Примечания
- Sanchez, Julio & Canton, Maria P. (2007), Microcontroller programming: the microchip PIC, Boca Raton, Florida: CRC Press, p. 37, ISBN 0-8493-7189-9
- W. S. Anglin and J. Lambek, The Heritage of Thales, Springer, 1995, ISBN 0-387-94544-X
- Ordish George, Hyams, Edward. The last of the Incas: the rise and fall of an American empire. — New York: Barnes & Noble, 1996. — С. 80. — ISBN 0-88029-595-3
- Experts 'decipher' Inca strings - news.bbc.co.uk/2/hi/americas/4143968.stm.
- Estudios sobre los quipus - books.google.com/books?id=TmbajGgliYYC&printsec=frontcover. — P. 49.
- Dale Buckmaster (1974). «The Incan Quipu and the Jacobsen Hypothesis - www.jstor.org/stable/2490534». Journal of Accounting Research 12 (1): 178-181. Проверено 2009-12-24.
- Bacon, Francis, The Advancement of Learning - home.hiwaay.net/~paul/bacon/advancement/book6ch2.html, vol. 6, London, pp. Chapter 1, <http://home.hiwaay.net/~paul/bacon/advancement/book6ch2.html - home.hiwaay.net/~paul/bacon/advancement/book6ch2.html>
- http://www.leibniz-translations.com/binary.htm - www.leibniz-translations.com/binary.htm Leibniz Translation.com EXPLANATION OF BINARY ARITHMETIC
- Aiton, Eric J. (1985), Leibniz: A Biography, Taylor & Francis, pp. 245–8, ISBN 0-85274-470-6
wreferat.baza-referat.ru
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|


