|
|
|
|
 Far Far |
 WinNavigator WinNavigator |
 Frigate Frigate |
 Norton
Commander Norton
Commander |
 WinNC WinNC |
 Dos
Navigator Dos
Navigator |
 Servant
Salamander Servant
Salamander |
 Turbo
Browser Turbo
Browser |
|
|
 Winamp,
Skins, Plugins Winamp,
Skins, Plugins |
 Необходимые
Утилиты Необходимые
Утилиты |
 Текстовые
редакторы Текстовые
редакторы |
 Юмор Юмор |
|
|
|
File managers and best utilites |
Кто открыл число Пи? История вычислений. Число пи реферат для 6 класса понятно
Число Пи - значение, история, кто придумал

Все окружности похожи
Если сравнить окружности отличных друг от друга размеров, то можно заметить следующее: размеры разных окружностей пропорциональны. А это значит, что при увеличении диаметра окружности в некоторое количество раз, увеличивается и длина этой окружности в такое же количество раз. Математически это записать можно так:
| C1 | C2 | ||
| = | |||
| d1 | d2 | (1) |
где C1 и С2 – длины двух разных окружностей, а d1 и d2 – их диаметры. Это соотношение работает при наличии коэффициента пропорциональности – уже знакомой нам константы π. Из отношения (1) можно сделать вывод: длина окружности C равна произведению диаметра этой окружности на независящий от окружности коэффициент пропорциональности π:
C = πd.
Также эту формулу можно записать в ином виде, выразив диаметр d через радиус R данной окружности:
С = 2πR.
Как раз эта формула и является проводником в мир окружностей для семиклассников.
Еще с древности люди пытались установить значение этой константы. Так, например, жители Месопотамии вычисляли площадь круга по формуле:
| C2 | |||
| S | = | , | |
| 12 |
где S – площадь круга, C – длина окружности (круга). Если в эту формулу подставить уже знакомые школьнику выражения площади круга S = πr2 и длины окружности С = 2 πR, то мы получим:
| (2πR)2 | ||
| πR2 | = | |
| 12 |
, откуда π = 3.
В древнем Египте значение для π было точнее. В 2000-1700 годах до нашей эры писец, именуемый Ахмесом, составил папирус, в котором мы находим рецепты разрешения различных практических задач. Так, например, для нахождения площади круга он использует формулу:
| 8 | 2 | |||||
| S | = | ( | d | ) | ||
| 9 |
Из каких соображений он получил эту формулу? – Неизвестно. Вероятно, на основе своих наблюдений, впрочем, как это делали и другие древние философы.
По стопам Архимеда
- Какое из двух числе больше 22/7 или 3.14 ?- Они равны.- Почему ?- Каждое из них равно π.А. А. Власов. Из Экзаменационного билета.
Некоторы полагают, что дробь 22/7 и чисо π тождественно равны. Но это является заблуждением. Помимо вышеприведенного неверного ответа на экзамене (см. эпиграф) к этой группе можно также добавить одну весьма занимательную головоломку. Задание гласит: "переложите одну спичку так, чтобы равенство стало верным".
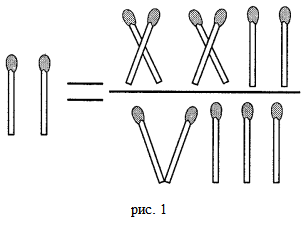
Решение будет таковым: нужно образовать "крышу" для двух вертикальных спичек слева, используя одну из вертикальных спичек в знаменателе справа. Получится визуальное изображение буквы π.
Многие знают, что приближение π = 22/7 определил древнегреческий математик Архимед. В честь этого часто такое приближение называют "Архимедовым" числом. Архимеду удалось не только установить приближенное значение для π, но также найти точность этого приближения, а именно – найти узкий числовой промежуток, которому принадлежит значение π. В одной из своих работ Архимед доказывает цепь неравенств, которая на современный лад выглядела бы так:
| 10 | 6336 | 14688 | 1 | |||||||||
| 3 | < | < | π | < | < | 3 | ||||||
| 71 | 1 | 1 | 7 | |||||||||
| 2017 | 4673 | |||||||||||
| 4 | 2 | |||||||||||
можно записать проще: 3,140 909 < π < 3,1 428 265...
Как видим из неравенств, Архимед нашел довольно-таки точное значение с точностью до 0,002. Самое удивительно то, что он нашел два первых знака после запятой: 3,14... Именно такое значение чаще всего мы используем в несложных расчетах.
Практическое применение
Едут двое в поезде:− Вот смотри, рельсы прямые, колеса круглые. Откуда же стук?− Как откуда? Колеса-то круглые, а площадь круга пи эр квадрат, вот квадрат-то и стучит!
Как правило, знакомятся с этим удивительным числом в 6-7 классе, но более основательно им занимаются к концу 8-го класса. В этой части статьи мы приведем основные и самые важные формулы, которые пригодятся вам в решении геометрических задач, только для начала условимся принимать π за 3,14 для удобства подсчета.
Пожалуй, самая известная формула среди школьников, в которой используется π, это – формула длины и площади окружности. Первая – формула площади круга – записывается так:
где S – площадь окружности, R – ее радиус, D – диаметр окружности.
Длина окружности, или, как ее иногда называют, периметр окружности, вычисляют по формуле:
С = 2 πR = πd,
где C – длина окружности, R – радиус, d – диаметр окружности.
Понятно, что диаметр d равен двум радиусам R.
Из формулы длины окружности можно легко найти радиус окружности:
| C | C | ||
| R= | = | ||
| 2π | d |
Обозначения для этих формул остаются те же.
Диаметр окружности можно найти по формуле:
где D – диаметр, С – длина окружности, R – радиус окружности.
Это базовые формулы, знать которые должен каждый ученик. Также иногда приходится вычислять площадь не всей окружности, а только ее части – сектора. Поэтому представляем вам её – формулу для вычисления площади сектора окружности. Выглядит она так:
| α | |||
| S | = | πR2 | |
| 360˚ |
где S – площадь сектора, R – радиус окружности, α – центральный угол в градусах.
Такое загадочное 3,14
И правда, оно загадочно. Потому что в честь этих магических цифр устраивают праздники, снимают фильмы, проводят общественные акции, пишут стихи и многое другое.
Например, в 1998 году вышел фильм американского режиссера Даррена Аронофски под названием "Пи". Фильм получил множество наград.
Каждый год 14 марта в 1:59:26 люди, интересующиеся математикой, празднуют "День числа Пи". К празднику люди подготавливают круглый торт, усаживаются за круглый стол и обсуждают число Пи, решают задачи и головоломки, связанные с Пи.
Вниманием это удивительное число не обошли и поэты, неизвестный написал: Надо только постараться и запомнить всё как есть – три, четырнадцать, пятнадцать, девяносто два и шесть.
Давайте развлечемся!
Вашему вниманию предлагаются интересные ребусы с числом Пи. Разгадайте слова, какие зашифрованы ниже.
1. π р
2. π L
3. π k
Ответы: 1. Пир; 2. Надпил; 3. Писк.
Число Пи - справочные материалы
Чему равно число Пи
Как запомнить число Пи
Число Пи в Excel
Число Пи на клавиатуре и в Word
Фотографии числа Пи
www.calculator888.ru
Кто открыл число Пи? История вычислений
Уже много веков и даже, как ни странно, тысячелетий люди понимают важность и ценность для науки математической постоянной, равной отношению длины окружности к ее же диаметру. Кто открыл число Пи, до сих пор неизвестно, но к нему имели отношение самые лучшие математики на протяжении всей нашей истории. Большинство из них хотели выразить его рациональным числом.
Интересные сведения о числе Пи
1. Исследователи и истинные поклонники числа Пи организовали клуб, для вступления в который требуется знать наизусть достаточно большое количество его знаков.
2. С 1988 года празднуется «День числа Пи», который приходится на 14 марта. Готовят салаты, торты, печенья, пирожные с его изображением.
3. Число Пи уже переложили на музыку, при этом оно весьма неплохо звучит. Ему даже воздвигли памятник в американском Сиэтле перед зданием городского Музея искусств.


Древний период
В то далекое время число Пи старались вычислить при помощи геометрии. То, что это число постоянно для самых разных окружностей, знали еще геометры в Древнем Египте, Вавилоне, Индии и Древней Греции, утверждавшие в своих работах, что оно всего лишь немного больше трех.
В одной из священных книг джайнизма (древняя индийская религия, которая возникла в VI в. до н. э.) упоминается, что тогда число Пи считалось равным корню квадратному из десяти, что в итоге дает 3,162... .
Древнегреческие математики проводили измерение окружности методом построения отрезка, а вот для того, чтобы измерить круг, им приходилось строить равновеликий квадрат, то есть фигуру, равную ему по площади.
Когда еще не знали десятичных дробей, великий Архимед нашел значение числа Пи с точностью 99,9%. Он открыл способ, который стал основой многих последующих вычислений, вписывал в окружность и описывал вокруг нее правильные многоугольники. В результате Архимед рассчитал значение числа Пи как отношение 22 / 7 ≈ 3,142857142857143.
В Китае, математик и придворный астроном, Цзу Чунчжи в V веке до н. э. обозначил более точное значение числа Пи, рассчитав его до семи цифр после запятой и определил его значение между числами 3, 1415926 и 3,1415927. Более 900 лет понадобилось ученым, чтобы продолжить дальше этот цифровой ряд.


Средние века
Известный индийский ученый Мадхава, который жил на рубеже XIV - XV веков, ставший основателем Керальской школы астрономии и математики, впервые в истории стал работать над разложением тригонометрических функций в ряды. Правда, сохранились всего лишь два его труда, а на другие известны лишь ссылки и цитаты его учеников. В научном трактате «Махаджьянаяна», который приписывают Мадхаве, указано, что число Пи равно 3,14159265359. А в трактате «Садратнамала» приведено число с еще большим количеством точных знаков после запятой: 3,14159265358979324. В указанных числах последние цифры не соответствуют правильному значению.
В XV веке самаркандский математик и астроном Ал-Каши вычислил число Пи с шестнадцатью знаками после запятой. Его результат считался наиболее точным в течение последующих 250 лет.
У. Джонсон, математик из Англии, одним из первых смог обозначить отношение длины окружности к ее диаметру буквой π. Пи — это первая буква греческого слова «περιφέρεια» — окружность. Но этому обозначению удалось стать общепринятым лишь после того, как им воспользовался в 1736 году более известный ученый Л. Эйлер.


Заключение
Современные ученые продолжают работать над дальнейшими вычислениями значений числа Пи. Для этого уже используют суперкомпьютеры. В 2011 г. ученый из Японии Сигэру Кондо, сотрудничая с американским студентом Александром Йи, произвели правильный расчет последовательности из 10 триллионов цифр. Но до сих пор так и неясно, кто открыл число Пи, кто впервые задумался над этой проблемой и произвел первые расчеты этого, по-настоящему мистического числа.
Читайте также:
Кто первым создал азбуку для русского языка?
Кто открыл закон инерции: Галилей или Ньютон?
vseonauke.com
История числа пи — доклад
История числа π, выражающего отношение длины окружности к её диаметру, началась в Древнем Египте. Площадь круга диаметром d египетские математики определяли как (d-d/9)2 (эта запись дана здесь в современных символах). Из приведенного выражения можно заключить, что в то время число p считали равным дроби (16/9)2, или 256/81, т.е. p = 3,160...
В священной книге джайнизма (одной из древнейших религий, существовавших в Индии и возникшей в VI в. до н.э.) имеется указание, из которого следует, что число p в то время принимали равным , что даёт дробь 3,162...
Древние греки Евдокс, Гиппократ и другие измерение окружности сводили к построению отрезка, а измерение круга - к построению равновеликого квадрата. Следует заметить, что на протяжении многих столетий математики разных стран и народов пытались выразить отношение длины окружности к диаметру рациональным числом.
Архимед в III в. до н.э. обосновал в своей небольшой работе "Измерение круга" три положения:
1 Всякий круг равновелик прямоугольному треугольнику, катеты которого соответственно равны длине окружности и её радиусу;
2 Площади круга относятся к квадрату, построенному на диаметре, как 11 к 14;
3 Отношение любой окружности к её диаметру меньше 3 1/7 и больше 3 10/71.
Последнее предложение Архимед обосновал последовательным вычислением периметров правильных вписанных и описанных многоугольников при удвоении числа их сторон. Сначала он удвоил число сторон правильных описанного и вписанного шестиугольников, затем двенадцатиугольников и т.д., доведя вычисления до периметров правильного вписанного и описанного многоугольников с 96 сторонами. По точным расчётам Архимеда отношение окружности к диаметру заключено между числами 3*10/71 и 3*1/7, а это означает, что π = 3,1419... Истинное значение этого отношения 3,1415922653...
В V в. до н.э. китайским математиком Цзу Чунчжи было найдено более точное значение этого числа: 3,1415927...
Впервой половине XV в. обсерватории Улугбека, возле Самарканда, астроном и математик ал-Каши вычислил p с 16 десятичными знаками. Он сделал 27 удвоений числа сторон многоугольников и дошёл до многоугольника, имеющего 3*228 углов. Ал-Каши произвёл уникальные расчёты, которые были нужны для составления таблицы синусов с шагом в 1'. Эти таблицы сыграли важную роль в астрономии.
Спустя полтора столетия в Европе Ф.Виет нашёл число π только с 9 правильными десятичными знаками, сделав 16 удвоений числа сторон многоугольников. Но при этом Ф.Виет первым заметил, что π можно отыскать, используя пределы некоторых рядов. Это открытие имело большое значение, так как позволило вычислить π с какой угодно точностью. Только через 250 лет после ал-Каши его результат был превзойдён.
Первым ввёл обозначение отношения длины окружности к диаметру современным символом π английский математик У.Джонсон в 1706 г. В качестве символа он взял первую букву греческого слова "periferia", что в переводе означает "окружность". Введённое У.Джонсоном обозначение стало обшеупотребительным после опубликования работ Л.Эйлера, который воспользовался введённым символом впервые в 1736 г.
Поиски точного выражения π продолжались и после работ Ф.Виета. В начале XVII в. голландский математик из Кёльна Лудольф ван Цейлен (1540-1610) (некоторое историки его называют Л.ван Кейлен) нашёл 32 правильных знака. С тех пор (год публикации 1615) значение числа π с 32 десятичными знаками получило название числа Лудольфа.
К концу XIX в., после 20 лет упорного труда, англичанин Вильям Шенкс нашёл 707 знаков числа π. Однако в 1945 г. обнаружено с помощью ЭВМ, что Шенкс в своих вычислениях допустил ошибку в 520-м знаке и дальнейшие его вычисления оказались неверными.
Ещё более удобную формулу для вычисления π получил Дж.Мачин. Пользуясь этой формулой, он вычислил π (в 1706 г.) с точностью до 100 верных знаков.
Однако следует помнить, что это равенство надо рассматривать как приближённое, т.к. правая часть его - число алгебраическое, а левая - трансцендентное, следовательно, эти числа равными быть не могут.
В наше время труд вычислителей заменили ЭВМ. С их помощью число "пи" вычислено с точностью более миллиона знаков после запятой, причём эти вычисления продолжались только несколько часов.
В современной математике число π - это не только отношение длины окружности к диаметру, оно входит в большое число различных формул.
Эта и другие взаимозависимости позволили математикам ещё глубже выяснить природу числа π.
Р Е Ф Е Р А Т
на тему
«История
числа π»
Выполнила: ученица 6 «А» класса
школы № 175
Шабанова Екатерина
Ташкент
student.zoomru.ru
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|


