Письменный контролирующий материал
Вариант 1
Разложите данные числа на разрядные единицы и запишите разряд, в котором находится число 7.
2 703 400; 4 372
Запишите решение задачи в виде числового выражения и найдите его значение.
Оля собрала 14 ромашек, а Катя в 2 раза меньше. Сколько всего ромашек собрали девочки?
отметьте на координатном луче точки:
А(2), В(4), С(7), если единичный отрезок равен двум клеткам.
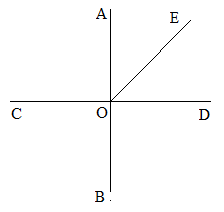
3. Выполните рисунок по описанию: луч AB пересекает прямую CD в точке O, отрезок KN пересекает луч AB, но не пересекает прямую CD.
5О. 1 кг свеклы стоит a р., а 1 кг моркови – b р. Запишите в виде выражения:
а) сколько стоит 5 кг свеклы;
б) сколько стоит 1 кг свеклы и 3 кг моркови;
в) на сколько 4 кг моркови дороже 2 кг свеклы.
Вариант 2
Разложите данные числа на разрядные единицы и запишите разряд, в котором находится число 7.
12 507; 74 000 805
Запишите решение задачи в виде числового выражения и найдите его значение.
Костя съел 8 конфет, а Борис на 3 конфеты больше. Сколько всего конфет съели мальчики?
отметьте на координатном луче точки:
К(3), N(7), M(10), если единичный отрезок равен одной клетке.
3. Выполните рисунок по описанию: отрезок KL пересекает прямую b в точке M, луч NP пересекает отрезок но не пересекает данную прямую.
5О. 1 кг свеклы стоит a р., а 1 кг моркови – b р. Запишите в виде выражения:
а) сколько стоит 4 кг свеклы;
б) сколько стоит 3 кг свеклы и 2 кг моркови;
в) на сколько 2кг моркови дешевле, чем 6 кг свеклы.
Вариант 1
1. Округлите до тысяч: а) 75 860; б) 124 320.
2. Не выполняя вычислений, определите старший разряд суммы, разности, произведения и частного чисел 644 и 28.
3. Вычислите: (12 148 + 305 ∙ 12) : 52.
4О. За какое время при движении против течения реки теплоход пройдет 180 км, если его собственная скорость 16 км/ч, а скорость течения – 1 км/ч?
5О. Один маляр за 6 ч может побелить потолки общей площадью 72 м2 , а второму для этого требуется на 2 ч больше. Какую площадь потолков они смогут побелить за 5 ч совместной работы?
Вариант 2
1. Округлите до сотен тысяч: а) 1 599 300; б) 853 000.
2. Не выполняя вычислений, определите старший разряд суммы, разности, произведения и частного чисел 182 и 26.
3. Вычислите: (1860 – 1010 : 5) ∙ 12.
4О. Двигаясь по течению реки, за 4 ч самоходная баржа прошла 48 км. Определите собственную скорость баржи, если скорость течения – 2 км/ч.
5О. За 8 ч токарь может выточить 24 детали, а его ученик в три раза меньше. Какое количество деталей они могут выточить за 5 ч, работая одновременно?
Вариант 1
1. Упростите выражение и найдите его значение при х = 2: 3х + 15х – 8.
2. Решите уравнение 7y – 2y = 35.
3. Площадь прямоугольника 72 см2, а одна из его сторон равна 9 см. Найдите вторую сторону и периметр прямоугольника.
4О. Для приготовления смеси взяли чай двух сортов: 3 кг чая первого сорта по 220 р. за 1 кг и 7 кг чая второго сорта. Найдите цену чая второго сорта, если цена получившейся смеси – 171 р. за 1 кг.
5О. По течению катер двигается со скоростью y км/ч, а против течения на 2 км/ч медленнее. Запишите на математическом языке:
а) скорость катера при движении против течения;
б) расстояние, пройденное катером за 6 ч движения по течению, больше расстояния, пройденного им за 3 ч против течения на 78 км.
Вариант 2
1. Упростите выражение и найдите его значение при у = 5: 25у + 2у – 7.
2. Решите уравнение 8х + 4х = 24.
3. Площадь прямоугольника 48 см2, а одна из его сторон равна 6 см. Найдите вторую сторону и периметр прямоугольника.
4О. Для составления смеси взяли 6 кг карамели по 70 р. за 1 кг и 4 кг шоколадных конфет. Найдите цену шоколадных конфет, если цена получившейся смеси – 78 р. за 1 кг.
5О. По проселочной дороге велосипедист едет со скоростью x км/ч, а по шоссе в 3 раза быстрее. Запишите на математическом языке:
а) скорость велосипедиста при движении по шоссе;
б) за 3 ч езды по шоссе велосипедист проехал на 35 км больше, чем за 2 ч по проселочной дороге.
Вариант 1
1. Представьте данную дробь в виде дроби со знаменателем 6: а) ; б) .
2. Девочка прочитала 25 страниц, что составило книги. Сколько страниц в книге?.
3. Площадь тепличного хозяйства, которой занята под огурцы, составляет 140 а. Найдите площадь, занятую огурцами
4О. Сколько километров пройдет катер за 5 ч, двигаясь по течению реки, если известно, что скорость течения реки 1200 м/ч и это составляет собственной скорости катера?
5О. Две окружности имеют общий центр. Радиус одной окружности – 4 см, а радиус второй окружности составляет диаметра первой. Начертите эти окружности.
Вариант 2
1. Представьте данную дробь в виде дроби со знаменателем 8: а) ; б) .
2. В книге 352 страницы. Мальчик прочитал книги. Сколько страниц прочитал мальчик?
3. Капустой занято 30 м2, что составляет площади всего огорода. Найдите площадь огорода.
4О. Сколько километров пройдет моторная лодка за 4 ч, двигаясь против течения реки, если ее собственная скорость 22 км/ч, а скорость течения составляет собственной скорости катера?
5О. Две окружности имеют общий центр. Радиус одной окружности – 4 см, и его длина составляет диаметра второй окружности. Начертите эти окружности
Вариант 1
1. Вычислите:а) ; б) 2 + 7 – 8.
2. Выполните действия: а) 5; б) : 3.
3О. Партия обуви, приобретенная предпринимателем, была продана за 3 дня. В первый день было продано , а во второй числа всех пар обуви. Какая часть обуви была продана в третий день?
4О. За 3 ч из бассейна через одну трубу выливается , а через другую – всей воды, находящейся в бассейне. Какая часть воды выльется из бассейна за 1 час, если открыть обе трубы одновременно?
1. Вычислите: а) ; б) 3 – 1 + 5.
2. Выполните действия: а) : 7; б) 3.
3О. За первую неделю бригада выполнила , а за вторую всей работы по строительству дома. Какую часть работы осталось выполнить бригаде?
4О. Один экскаватор за день работы выкапывает , а второй часть котлована. Какую часть котлована выкопают экскаваторы за 4 дня, работая одновременно?
Вариант 1
1. Начертите угол ABC, равный 160°. Проведите биссектрису этого угла, отметьте на ней точку О и проведите через нее прямую, перпендикулярную стороне BC.
2. В треугольнике ABC А составляет 54, а C на 15 меньше. Найдите B треугольника ABC.
3О. Вычислите: 201 15 – 7042 : 14.
4О. В двух мешках было 75 кг крупы. После того как из первого мешка продали 12 кг, а из второго 18 кг, в первом мешке крупы оказалось в 2 раза больше, чем во втором. Сколько килограммов крупы было в каждом мешке первоначально?
Вариант 2
1. Начертите угол MNK, равный 150°. Проведите биссектрису этого угла, отметьте на ней точку О и проведите через нее прямую, перпендикулярную стороне NM.
2. В треугольнике ABC А составляет 35, а B на 17 больше. Найдите C треугольника ABC.
3О. Вычислите: 24 032 : 8 + 108 23.
4О. В двух цистернах было 30 т бензина. После того как из каждой цистерны продали по 6 т, в первой цистерне оказалось в два раза больше бензина, чем во второй. Сколько тонн бензина было в каждой цистерне первоначально?
Вариант 1
1. Вычислите: а) 5,7 + 2,34; б) 1,2 – 0,83.
2. а) Выразите в метрах: 15 дм; 3,4 см; 7 мм.
б) Выразите в килограммах: 940 г; 7,2 т.
3. Длины сторон прямоугольника 1,2 дм и 25 см. Выразите их в метрах и найдите периметр прямоугольника.
4О. Мальчик поймал трех рыб. Масса первой рыбы 0,375 кг, масса второй на 20 г меньше, а масса третьей на 0,11 кг больше массы первой рыбы. Найдите массу трех рыб.
5О. Составьте выражение для длины незамкнутой ломаной ABCD, если AB = a см, BC на 8,45 см меньше AB, а CD на 1,27 дм больше AB, и упростите его.
Вариант 2
1. Вычислите: а) 6,83 + 15,3; б) 8,9 – 5,42.
2. а) Выразите в метрах: 3,2 дм; 543 см; 5 мм.
б) Выразите в килограммах: 56 г; 2,7 т.
3. Длины сторон прямоугольника 3,8 дм и 54 см. Выразите их в метрах и найдите периметр прямоугольника.
4О. Яблоко, груша и апельсин вместе имеют массу 0,85 кг. Масса апельсина 360 г, а груша на 0,158 кг легче. Найдите массу яблока.
5О. Составьте выражение для длины незамкнутой ломаной ABCD, если AB = х дм, BC на 12,71 см меньше AB, а CD на 2,85 дм больше AB, и упростите его.
Вариант 1
1. Вычислите: а) 8,3 ∙ 6; б) 2,06 ∙ 1,5; в) 9,76 : 3,2.
2. Найдите среднее арифметическое чисел 4,2; 4,1; 4,1; 4,3; 3,9.
3О. За 400 г сыра и 1,2 кг колбасы заплатили 126 р. 80 к. Какова цена1 кг колбасы, если 1 кг сыра стоит 95 р.?
4О. На двух складах было 210,2 т картофеля. После того как с первого склада было продано 24,5 т, а со второго 10,8 т, на первом складе картофеля оказалось в 2 раза больше, чем на втором. Сколько тонн картофеля было на каждом складе первоначально?
Вариант 2
1. Вычислите: а) 3,4 ∙ 5; б) 3,08 ∙ 6,7; в) 7,8 : 1,2.
2. Найдите среднее арифметическое чисел 3,2; 4,5; 2,9; 3,1; 4,2.
3О. За 80 см шелка и 2,5 м шерсти заплатили 336 р. 40 к. Какова цена 1 м шерсти, если 1 м шелка стоит 58 р.?
4О. В двух бидонах было 51 л молока. После того как из первого бидона отлили 16,2 л, а из второго 7,2 л, во втором бидоне молока оказалось в 4 раза больше, чем в первом. Сколько литров молока было в каждом бидоне первоначально?
Вариант 1
1. Сметана содержит 20% жира. Сколько жира в 500 г сметаны?
2. В лесопарке посажено 15 кленов, что составляет 1% всех деревьев. Сколько деревьев в лесопарке?
3. Объем комнаты 45,36 м3, а площадь 16,8 м2. Найдите высоту потолка комнаты.
4О. С поля, засаженного капустой, в первый день было вывезено 58% урожая, а во второй – остальные 33,6 тонны. Сколько тонн капусты было вывезено с поля?
5О. Найдите массу 1 м3 сплава, если слиток этого сплава, имеющий форму прямоугольного параллелепипеда с измерениями 2,9 дм, 15 см и 0,8 м, имеет массу 281,88 кг.
Вариант 2
1. Сыр содержит 35% жира. Сколько жира в 400 г сыра?
2. Петрушкой засеяно 3 м2, что составляет 1% площади огорода. Найдите площадь огорода.
3. Найдите высоту потолка спортивного зала, если его объем равен 5465,6 м3, а площадь пола – 854 м2.
4О. За первую неделю тротуарной плиткой было выложено 47% площади тротуара, а за вторую – остальные 561,8 м2. Какова площадь тротуара?
5О. Найдите массу 1 м3 кирпича, если один кирпич с измерениями 2 дм, 15 см и 0,1 м имеет массу 2,7 кг.
Контрольная работа № 10 «Итоговая контрольная работа за курс 5 класса»Вариант 1
1. Вычислите: (8,3 + 4,72) ∙ (5,5 – 3,45).
2. Решите уравнение 3,5x = 7,21.
3. В первом овощехранилище на 5,6 т картофеля больше, чем во втором, а в двух овощехранилищах вместе 80 т картофеля. Сколько тонн картофеля во втором овощехранилище?
4. Постройте с помощью транспортира угол BAC, равный 35, и отложите на луче AB отрезок AM длиной 6 см. Используя угольник, проведите через точку M прямую, перпендикулярную AC и пересекающую луч АВ. Найдите площадь образовавшегося треугольника (в м2). Ответ округлите до сотых.
5. После того как была продана четверть конфет, вес ящика с конфетами уменьшился на 24%. Определите массу пустого ящика, если ящик с конфетами имеет массу 60 кг.
Вариант 2
1. Вычислите: (7,6 + 5,85) ∙ (10,9 – 4,86).
2. Решите уравнение 6,5x = 26,52.
3. На первом складе на 7,6 т угля меньше, чем на втором, а на двух складах вместе 100 т угля. Сколько тонн угля на втором складе?
4. Постройте прямоугольник ABCD со сторонами AB = 5 см, AD = 8 см. Проведите луч AM, пересекающий BС в точке M так, чтобы угол BAM оказался равным 40. Выполните необходимые измерения и найдите площадь образовавшегося треугольника BAM (в м2). Ответ округлите до сотых.
5. После того как была продана половина конфет, вес ящика с конфетами уменьшился на 45 %. Определите массу пустого ящика, если ящик с конфетами имеет массу 50 кг.
infourok.ru
Входная контрольная работа
1 вариант
№1. Выполните действия: а) (1272 – 768)∙7+472 б) (599+289):24 - 16
№2. Решите уравнение: а) х - 807 = 900 б) 59 + х = 219
№3. Длина прямоугольника в два раза больше ширины.
Найдите периметр прямоугольника, если его длина равна 36 см.
№4. Лыжник прошёл за 6 часов расстояние в 90 км. Сколько времени ему
потребуется, чтобы пройти расстояние в 60 км?
№5. Подставьте вместо звёздочек цифры:
_**1200
2*9**
71*28
2 вариант
№1. Выполните действия: а)(1027+ 987): 53 - 13 б) 7∙(3231 - 2573) + 294
№2. Решите уравнение: а)603 – х = 83 б) х + 74 =444
№3. Ширина прямоугольника на 12 дм меньше его длины.
Найдите периметр прямоугольника, если его ширина равна 16 дм.
№4. Туристы в первый день ехали на велосипедах 6 ч со скоростью 12 км/ч.
С какой скоростью они должны ехать во второй день, чтобы такой же
путь проехать за 4 ч?
№5. Подставьте вместо звёздочек цифры:
_** *35
28*
29 8*6
| Контрольная работа № 1 Вариант 1 1. Для числа 12 738 026 запишите: а) старший разряд; б) какая цифра стоит в разряде десятков тысяч; в) в каком разряде стоит цифра 8. 2. Запишите решение задачи в виде числового выражения и найдите его значение: Данила купил 29 гвоздик, а Маша на 8 меньше. Сколько всего гвоздик они купили? 3. Выполните рисунок по описанию: Луч MN пересекает прямую AB в точке K. 4О. 1 кг яблок стоит a р., а 1 кг груш – b р. Запишите в виде выражения стоимость двух килограммов яблок и четырех килограммов груш. 5О. Скорость всадника х км/ч, а поезда – у км/ч. Запишите в виде выражения: а) скорость сближения всадника и поезда при движении навстречу; б) скорость удаления при движении в противоположные стороны; в) скорость сближения, при условии, что поезд догоняет всадника; г) скорость удаления, при условии, что поезд обогнал всадника. | Контрольная работа № 1 Вариант 2 1. Для числа 203 574 320 запишите: а) старший разряд; б) какая цифра стоит в разряде десятков тысяч; в) в каком разряде стоит цифра 5. 2. Запишите решение задачи в виде числового выражения и найдите его значение: В одной коробке было 12 кг конфет, во второй – в 3 раза меньше. Сколько конфет было в двух коробках? 3. Выполните рисунок по описанию: Лучи MN и CDпересекаются в точке K. 4О. 1 кг картофеля стоит x р., а 1 кг моркови – y р. Запишите в виде выражения: на столько 2 кг картофеля дешевле, чем 5 кг моркови. 5О. Скорость движения мотоцикла a км/ч, а велосипеда – b км/ч. Запишите: а) скорость сближения мотоцикла и велосипеда при движении навстречу; б) скорость удаления при движении в противоположные стороны; в) скорость сближения, при условии, что мотоциклдогоняет велосипед; г) скорость удаления, при условии, что мотоциклобогнал велосипед. |
| Контрольная работа № 2 Вариант 1 1. Округлите до тысяч: а) 75 860; б) 124 320. 2. Не выполняя вычислений, определите старший разряд суммы, разности произведения и частного чисел: 644 и 28. 3. Вычислите: (12 148 + 305 12) : 52. 4О. За какое время при движении против течения реки теплоход пройдет 180 км, если его собственная скорость 16 км/ч, а скорость течения – 1 км/ч? 5О. Один маляр за 6 часов окрашивает 72 м2, а второму для этого требуется на 2 часа больше. Какую площадь они могут окрасить за 5 часов, при совместной работе? | Контрольная работа № 2 Вариант 2 1. Округлите до сотен тысяч: а) 1 599 300; б) 853 000. 2. Не выполняя вычислений определите старший разряд суммы, разности, произведения и частного чисел: 182 и 26. 3. Вычислите: (1860 – 1010 : 5) 12. 4О. Двигаясь по течению реки, за 4 часа самоходная баржа прошла 48 км. Определите собственную скорость баржи, если скорость течения – 2 км/ч. 5О. За 8 часов токарь может выточить 24 детали, а его ученик в три раза меньше. Какое количество деталей они могут выточить за 5 часов, работая одновременно? |
| Контрольная работа № 3 Вариант 1 1. Упростите выражение и найдите его значение при х = 2 3х + 15х – 8. 2. Решите уравнение: 7y – 2y = 35. 3. Площадь прямоугольника 72 см2, а одна из его сторон равна 9 см. Найдите вторую сторону и периметр прямоугольника. 4О. Для приготовления смеси взяли чай двух сортов: 3 кг чая первого сорта по 220 р. за 1 кг и 7 кг чая второго сорта. Найдите цену чая второго сорта, если цена получившейся смеси – 171 р. за 1 кг. 5О. По течению катер двигается со скоростью y км/ч, а против течения на 2 км/ч медленнее. Запишите на математическом языке: а) скорость катера при движении против течения; б) расстояние, пройденное катером за 6 ч движения по течению, больше расстояния, пройденного им за 3 часа против течения на 78 км. | Контрольная работа № 3 Вариант 2 1. Упростите выражение и найдите его значение при у = 5 25у + 2у – 7. 2. Решите уравнение: 8х + 4х = 24. 3. Площадь прямоугольника 48 см2, а одна из его сторон равна 6 см. Найдите вторую сторону и периметр прямоугольника. 4О. Для составления смеси взяли 6 кг карамели по 70 р. за 1 кг и 4 кг шоколадных конфет. Найдите цену шоколадных конфет, если цена получившейся смеси – 78 р. за 1 кг. 5О. По проселочной дороге велосипедист едет со скоростью x км/ч, а по шоссе в 3 раза быстрее. Запишите на математическом языке: а) скорость велосипедиста на шоссе; б) за 3 ч езды по шоссе велосипедист проехал на 35 км больше, чем за 2 ч по проселочной дороге. |
| Контрольная работа № 4 Вариант 1 1. Представьте данную дробь в виде дроби со знаменателем 6: а) ; б) . 2. Девочка прочитала 25 страниц, что составило книги. Сколько страниц в книге?. 3. Площадь тепличного хозяйства, которой занята под огурцы, составляет 140 а. Найдите площадь, занятую огурцами 4О. Сколько километров пройдет катер за 5 часов, двигаясь по течению реки, скорость течения которой 1200 м/ч и это составляет собственной скорости катера? 5О. Две окружности имеют общий центр. Радиус одной окружности – 4 см, а радиус второй окружности составляет диаметра первой. Начертите эти окружности. | Контрольная работа № 4 Вариант 2 1. Представьте данную дробь в виде дроби со знаменателем 8: а) ; б) . 2. В книге 352 страницы. Мальчик прочитал книги. Сколько страниц прочитал мальчик? 3. Капустой занято 30 м2, что составляет площади всего огорода. Найдите площадь огорода. 4О. Сколько километров пройдет моторная лодка за 4 часа, двигаясь против течения реки, если ее собственная скорость 22 км/ч, а скорость течения составляет собственной скорости катера? 5О. Две окружности имеют общий центр. Радиус одной окружности – 4 см, и это составляет диаметра второй окружности. Начертите эти окружности. |
| Контрольная работа №5 Вариант 1 1. Вычислите: а) ; б) + – . 2. Выполните действия: а) 5; б) : 3. 3О. Партия обуви, приобретенная предпринимателем, была продана за 3 дня. В первый день было продано числа всех пар обуви, во второй – . Какая часть обуви была продана в третий день? 4О. За 3 часа из бассейна через одну трубу выливается , а через другую – всей воды. Какая часть воды выльется из бассейна за 1 час, если открыть обе трубы одновременно? | Контрольная работа № 5 Вариант 2 1. Вычислите: а) ; б) 3 – 1 + 5. 2. Выполните действия: а) : 7; б) 3. 3О. За первую неделю бригада выполнила всей работы по строительству дома, а за вторую – всей работы. Какую часть работы осталось выполнить бригаде? 4О. Один экскаватор за день работы выкапывает часть котлована, а второй – . Какую часть котлована выкопают экскаваторы за 4 дня, работая одновременно? |
| Контрольная работа № 6 Вариант 1 1. Начертите угол ABC равный 75. Отметьте внутри угла точку О и проведите через нее прямую, перпендикулярную стороне BC. 2. В треугольнике ABC А составляет 54, а C на 15 меньше. Найдите B треугольника ABC. 3О. Вычислите: 201 15 – 7042 : 14. 4О. В двух мешках было 75 кг крупы. После того как из первого мешка продали 12 кг, а из второго 18 кг, в первом мешке крупы оказалось в 2 раза больше, чем во втором. Сколько килограммов крупы было в каждом мешке первоначально? | Контрольная работа № 6 Вариант 2 1. Начертите угол MNK равный 54. Отметьте внутри угла точку О и проведите через нее прямую, перпендикулярную стороне NM. 2. В треугольнике ABC А составляет 35, а B на 17 больше. Найдите C треугольника ABC. 3О. Вычислите: 24 032 : 8 + 108 23. 4О. В двух цистернах было 30 т бензина. После того как из каждой цистерны продали по 6 т, в первой цистерне оказалось в два раза больше бензина, чем во второй. Сколько тонн бензина было в каждой цистерне первоначально |
| Контрольная работа № 7 Вариант 1 1. Вычислите: а) 5,7 + 2,34; б) 1,2 – 0,83. 2. а) Выразите в метрах: 15 дм; 3,4 см; 7 мм. б) Выразите в килограммах: 940 г; 7,2 т. 3. Длины сторон прямоугольника: 1,2 дм и 25 см. Выразите их в метрах и найдите периметр прямоугольника. 4О. Мальчик поймал трех рыб. Масса первой рыбы – 0,375 кг, масса второй на 20 г меньше, а масса третьей на 0,11 кг больше массы первой рыбы. Найдите массу трех рыб. 5О. Составьте выражение для длины ломаной ABCD, если AB = a, BC на 8,45 см меньше AB, а CD на 1,27 дм больше AB и упростите его. | Контрольная работа № 7 Вариант 2 1. Вычислите: а) 6,83 + 15,3; б) 8,9 – 5,42. 2. а) Выразите в метрах: 3,2 дм; 543 см; 5 мм. б) Выразите в килограммах: 56 г; 2,7 т. 3. Длины сторон прямоугольника: 3,8 дм и 54 см. Выразите их в метрах и найдите периметр прямоугольника. 4О. Яблоко, груша и апельсин имеют массу 0,85 кг. Масса апельсина – 360 г, а груша на 0,158 кг легче. Найдите массу яблока. 5О. Составьте выражение для длины ломаной ABCD, если AB = х, BC на 12,71 см меньше AB, а CD на 2,85 дм больше AB и упростите его |
| Контрольная работа № 8 Вариант 1 1. Вычислите: а) 8,3 6; б) 2,06 1,5; в) 9,76 : 3,2. 2. Найдите среднее арифметическое чисел: 4,2; 4,1; 4,1; 4,3; 3,9. 3О. За 400 г сыра и 1,2 кг колбасы заплатили 126 р. 80 к. Какова цена1 кг колбасы, если 1 кг сыра стоит 95 р? 4О. На двух складах было 210,2 т картофеля. После того, как с первого склада было продано 24,5 т, а со второго 10,8 т, на первом складе картофеля оказалось в 2 раза больше, чем на втором. Сколько тонн картофеля было на каждом складе первоначально? | Контрольная работа № 8 Вариант 2 1. Вычислите: а) 3,4 5; б) 3,08 6,7; в) 7,8 : 1,2. 2. Найдите среднее арифметическое чисел: 3,2; 4,5; 2,9; 3,1; 4,2. 3О. За 80 см шелка и 2,5 м шерсти заплатили 336 р. 40 к. Какова цена 1 м шерсти, если 1 м шелка стоит 58 р. 4О. В двух бидонах было 51 л молока. Когда из первого бидона отлили 16,2, а из второго 7,2 литра, то во втором бидоне молока оказалось в 4 раза больше, чем в первом. Сколько литров молока было в каждом бидоне первоначально?. |
| Контрольная работа № 9 Вариант 1 1. Сметана содержит 20% жира. Сколько жира в 500 г сметаны? 2. В лесопарке посажено 15 кленов, что составляет 1% всех деревьев. Сколько деревьев в лесопарке? 3. Объем комнаты 45,36 м3. Найдите высоту потолка комнаты, если её площадь – 16,8 м2. 4О. С поля, засаженного капустой, в первый день было вывезено 58% урожая, а во второй – остальные 33,6 тонны. Сколько тонн капусты было вывезено с поля? 5О. Найдите массу 1 м3 сплава, если слиток этого сплава, имеющий форму прямоугольного параллелепипеда с измерениями 2,9 дм, 15 см и 0,8 м имеет массу 281,88 кг. | Контрольная работа № 9 Вариант 2 1. Сыр содержит 35% жира. Сколько жира в 400 г сыра? 2. Петрушкой засеяно 3 м2, что составляет 1% площади огорода. Найдите площадь огорода. 3. Найдите высоту потолка спортивного зала, если его объем равен 5465,6 м3, а площадь пола – 854 м2. 4О. За первую неделю работы тротуарной плиткой было выложено 47% площади тротуара, а за вторую – остальные 561,8 м2. Какова площадь тротуара? 5О. Найдите массу 1 м3 кирпича, если один кирпич с измерениями 2 дм, 15 см и 0,1 м имеет массу 2,7 кг. |
| Контрольная работа № 10 Вариант 1 1. Вычислите: (8,3 + 4,72) (5,5 – 3,45). 2. Решите уравнение: 3,5x = 7,21. 3. В первом овощехранилище на 5,6 т картофеля больше, чем во втором, а в двух овощехранилищах вместе 80 т картофеля. Сколько тонн картофеля во втором овощехранилище? 4. Постройте с помощью транспортира угол BAC, равный 35, и отложите на луче AB отрезок AMдлиной 6 см. Используя угольник, проведите через точку M прямую перпендикулярную ACи найдите площадь образовавшегося треугольника (в м2). Ответ округлите до сотых. 5. После того, как была продана четверть конфет, вес ящика с конфетами уменьшился на 24%. Определите массу пустого ящика, если масса ящика с конфетами – 60 кг. | Контрольная работа № 10 Вариант 2 1. Вычислите: (7,6 + 5,85) (10,9 – 4,86). 2. Решите уравнение: 6,5x = 26,52. 3. На первом складе на 7,6 т угля меньше, чем на втором, а на двух складах вместе 100 т угля. Сколько тонн угля на втором складе? 4. Постройте прямоугольник ABCD со сторонами AB = 5 см, AD = 8 см. Проведите луч AM, пересекающий BС в точке M так, чтобы угол BAM оказался равным 40. Выполните необходимые измерения и найдите площадь образовавшегося треугольника BAM (в м2). Ответ округлите до сотых. 5. После того, как была продана половина конфет, вес ящика с конфетами уменьшился на 45 %. Определите массу пустого ящика, если масса ящика с конфетами – 50 кг. |
Итоговая контрольная работа
Вариант 1
Выберите правильный ответ:
А1. Найдите весь путь, если 8% пути составляет 48 км.
А2. Укажите формулу, по которой находится площадь прямоугольника:
А3. Назовите вид угла, изображенного на рисунке:
А4. Выразите в километрах 19 м.
А5. Умножьте 5.67 на 1000
А6. Найдите объем прямоугольного параллелепипеда, если длина равна 5 см, ширина – 23 см, высота - 4 см.
Запишите краткий ответ:
В1. В первой корзине 5,68 кг яблок, во второй – в два раза меньше. Сколько яблок в двух корзинах вместе.
В2. Длина комнаты 5 ,3 м , а ширина 3, 88 м. Вычислите площадь комнаты.
Запишите полное решение:
С1. Поезд должен проехать расстояние 1200 км за 16 часов. Оказалось, что первые 35% пути он преодолел за 6 часов. С какой скоростью ему надо двигаться дальше, чтобы прибыть в пункт назначения вовремя?
С2. В двух кувшинах 11, 7 л оливкового масла. Сколько масла в каждом кувшине, если в одном из них на 3, 6 л больше, чем в другом?
Вариант 2.
Выберите правильный ответ:
А1. Найдите весь путь, если 9% пути составляет 54 км
А2. Укажите формулу, по которой находите периметра прямоугольника:
1 .S = v*t 2. P = 2a + 2b 3. P= 4a 4. S= v*T
А3. Назовите вид угла, изображенного на рисунке:
А4. Выразите в килограммах 45 г.
А5. Умножьте 3,04 на 100
А6. Найдите объем прямоугольного параллелепипеда, если длина равна 5 см, ширина –15 см, высота - 6 см.
Запишите краткий ответ:
В1. В первой коробке 7,38 кг яблок, во второй – в два раза меньше. Сколько яблок в двух корзинах вместе.
В2. Скорость автомобиля 67, 8 км/ч. Какой путь пройдет автомобиль за 4, 1 часа?
Запишите полное решение:
С1. Автобус должен 1400 км проехать за 20 часов. Оказалось, что первые 45% пути он преодолел за 9 часов. С какой скоростью ему надо двигаться дальше, чтобы прибыть в пункт назначения по расписанию?
С2. Кот Леопольд поймал леща и карпа общей массой 2, 4 кг, причем карп оказался на 0, 8 кг тяжелее леща. Найдите массу каждой из пойманных рыб.
infourok.ru
Контрольная работа № 7
«Уравнение. Решение задач алгебраическим способом»
Вариант 1
Упростите выражение 126 + 𝒙 + 474 и найдите его значение при 𝒙 =278
Упростите выражения:
1) 24а + 16 + 13а; 2) 25 т 16.
Решите уравнение: 1) 𝑥 +37 = 81; 2) 150 – 𝑥 = 98;
3) (34 + 𝑥) – 83 = 42; 4) 45 – (𝑥 – 16) = 28;
5) 19𝑥 - 12𝑥 = 126; 6) 2,4 (𝑥 + 0,98) = 4,08.
На двух машинах привезли 11,7 т угля. На первой – в два раза меньше, чем на второй. Сколько тонн угля привезли на каждой машине?
Найдите значение выражения: (4,1 – 0,66 : 1,2) ∙ 0,6.
Какое число надо подставить вместо 𝑎, чтобы корнем уравнения
52 – (𝑎 – 𝑥) = 24 было число 40?
Контрольная работа № 7
«Уравнение. Решение задач алгебраическим способом»
Вариант 2
Упростите выражение 235 + y + 465 и найдите его значение при y =153.
Упростите выражения:
1) 37k + 13 + 22k; 2) 50 п 12.
Решите уравнение: 1) 21 + 𝑥 = 58; 2) 𝑥 – 135 = 76;
3) (96 – 𝑥) – 15 = 64; 4) 31 – (𝑥 + 11) = 18;
5) 16𝑥 - 11𝑥 = 225; 6) 0,084 : (6,2 – 𝑥) = 1,2.
Турист проехал в 7 раз больше расстояния, чем прошел пешком. Весь путь туриста составил 33,6 км. Какое расстояние турист проехал?
Найдите значение выражения: (0,49 : 1,4 – 0,325) ∙ 0,8.
Какое число надо подставить вместо 𝑎, чтобы корнем уравнения
64 – (𝑎 – 𝑥) = 17 было число 16?
Контрольная работа № 7
«Уравнение. Решение задач алгебраическим способом»
Вариант 3
Упростите выражение 433 + 𝑎 + 267 и найдите его значение при 𝑎=249.
Упростите выражения:
1) 34b + 26 + 17b; 2) 18 р 50.
Решите уравнение: 1) 𝑥 + 42 = 94; 2) 284 – 𝑥 = 121;
3) (41 + 𝑥) – 12 = 83; 4) 62 – (𝑥 – 17) = 31;
5) 19𝑥 - 7𝑥 = 144; 6) 1,6 (𝑥 + 0,78) = 4,64.
В двух ящиках было 24,6 кг абрикосов. Сколько килограммов абрикосов было в каждом ящике, если в одном из них было в 3 раза больше, чем в другом
Найдите значение выражения: (5,25 – 0,63 : 1,4) ∙ 0,4.
Какое число надо подставить вместо 𝑎, чтобы корнем уравнения
(69 – 𝑎) – 𝑥 = 23 было число 12?
Контрольная работа № 7
«Уравнение. Решение задач алгебраическим способом»
Вариант 4
Упростите выражение 561 + 𝑏 + 139 и найдите его значение при 𝑏 =165.
Упростите выражение
1) 59 + х + 141, 2) у ·16 · 25.
Решите уравнение: 1) 𝑥 + 53 = 97; 2) 142 – 𝑥 = 76;
3) (58 + 𝑥) – 23 = 96; 4) 54 – (𝑥 – 19) = 35;
5) 22𝑥 - 14𝑥 = 112; 6) 0,144 : (3,4 – 𝑥) = 2,4.
В двух пакетах 3,3 кг муки. Сколько муки было в каждом пакете, если в одном из них было в 2 раза меньше муки, чем в другом
Найдите значение выражения: (4,4 – 0,63 :1,8) ∙ 0,8.
. Какое число надо подставить вместо 𝑎, чтобы корнем уравнения
(𝑎 – 𝑥) – 14 = 56 было число 5?
compedu.ru
