Проверочная работа
по теме Логические функции и схемы – основа элементной базы компьютера. Логические выражения и таблицы истинности. 10 класс.
Уважаемый ученик! Работа состоит из 8 вопросов по теории и 1 рефлексивный всего вопросов 9. Максимальное количество баллов можно набрать 19.
Время выполнения работы – 15 минут без учёта времени, отведённого на инструктаж учащихся и заполнение титульного листа бланка ответа.
Проверка выполненных работ осуществляется следующим способом:
- варианты ответов, указанные в бланке ответов, проверяют по «ключам».
1). каждое правильное выполненное задание оценивается в 1 балл вопрос 1, 4;
- каждое невыполненное задание (не выполнявшееся или выполненное с ошибкой) оценивается в 0 баллов;
- задание считается выполненным, если учащийся указал все правильные варианты ответов;
2). каждое правильное выполненное задание 2 оцениваются в 2 балла,
2 балла если верно указаны все элементы ответа,
1,5 балл, если правильно указано два домика со всеми элементами,
1 балл если правильно указан один домик со всеми элементами,
0 баллов, если ответ не содержит элементов правильного ответа.
3). каждое правильное выполненное задание 3, 5, 6, оценивается в 3 балла
3 балла если правильно указано все элементы,
2 балл, если правильно указано хотя 4-5 элемента ответа,
1 балл, если правильно указано хотя 2-3 элемента ответа,
0 баллов, если ответ не содержит элементов правильного ответа или 1 элемент правильного ответа.
4). каждое правильное выполненное задание 7, оценивается в 3 балла
3 балла если правильно указано все элементы,
2 балл, если правильно указано хотя 2 элемента ответа,
1 балл, если правильно указано хотя 1 элемент ответа,
0 баллов, если ответ не содержит элементов правильного ответа.
5). каждое правильное выполненное задание 8, оценивается в 3 балла
3 балла, если приведено полное решение, включающее следующие элементы, верно записаны формулы, выполнены логические операции, предоставлен ответ, оформление в таблице.
2 балла, представлено правильное решение только в общем виде, без каких-либо расчетов, записаны формулы, применение которых необходимо и достаточно для решения задачи выбранным способом, но допущена ошибка.
1 балл, записаны и использованы не все исходные формулы, необходимые для решения задачи.
0 балл, если все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок.
Для выставления отметок за тестирование можно воспользоваться таблицей пересчета:
для перевода числа правильных ответов в оценку по пятибалльной шкале
| Оценка | «2» | «3» | «4» | «5» |
| Число набранных баллов | 10-12 б. | 13-16 баллов | 17-18 б. | 19 |
Литература:
М.С. Цветкова, Л.С. Великович Информатика и ИКТ учебник для сред. Проф. Образования. М.: Издательский центр «Академия», 2016.-336с.
Бланк ответов
Фамилия, имя__________________________________
Предмет__________________________________________
Класс _____________________________________________
Количество баллов___________________
Оценка____________________
1. Выберите верный ответ, что присуще для: 1) алгебры; 2) алгебры логики
1. 1) числа 2) события
2. 1) события 2) числа
3. 1) 2) только числа
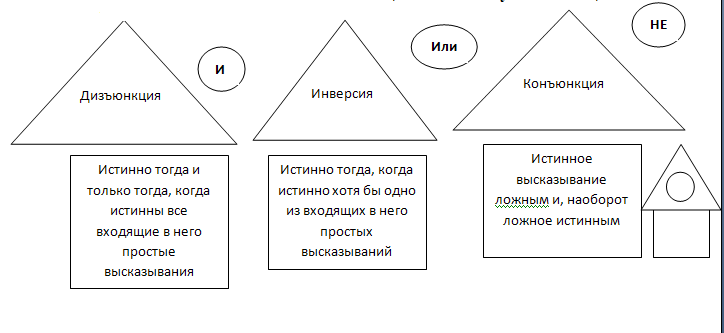
2. Собери домик: логическое сложение, логическое умножение, логическое отрицание.
3. Напишите ответ (Ложь, Истина) утверждениям с которыми вы согласны или нет.
1 Логическое умножение называется – конъюнкцией
2 Логическое сложение называется – инверсией
3 Логическое отрицание называется – дизъюнкцией
4 Логическое сложение называется – дизъюнкцией
5 Логическое отрицание называется – инверсией
6 Логическое сложение называется – конъюнкцией
4. Как обозначают логические операнды : 1. Ложь, 2. Истина.
1. 1) 1, 2) 0
2. 1) 0, 2) 1
3. 1) 0 2) 0
5. Напишите полученные ответы в задании 3 для переменной А логическими операндами.
| А | В |
6. Обозначьте логическими операндами следующие утверждения.
1. Гранатовый сок полезен.
2. Заниматься различными видами спорта вредно.
3. Чистить зубы утром и вечером полезно.
4. Сидеть за компьютером играя в игры целый день полезно.
5. Свежий воздух не приносит пользы для человека.
6. Сахар является сладким продуктом.
Напишите полученные логические операнды в задании 6 для переменной В и заполните таблицу в задании 5.
7. Напишите логические операции этим элементам.
1) & 2) ٧ 3) ¬
8. Составьте и решите таблицу истинности логического выражения переписывая переменные из задания 5:
F = ¬A & В ٧ ¬ (А & В)
9. На какой процент Вы можете оценить свои знания по теме
40-60%
61-80%
81-100%
Ключи
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | Рис. | истина ложь ложь истина истина ложь | 2 | 1 0 0 1 1 0 | 1 0 1 0 0 1 | 1).конъюнкция 2) дизъюнкция 3) инверсия |
8.
| А | В | (А & В) | ¬ (А & В) | ¬A | ¬A & В | ¬A & В ٧ ¬ (А & В) |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 |
xn--j1ahfl.xn--p1ai
ФИО________________________________________________________________________________
Контрольная работа_Логика_№1
В-1
Логическая операция с использованием связки «и», называется -
а) дизъюнкция;
б) инверсия;
в) конъюнкция
г) импликация
д) эквивалентность
Знаком «» обозначается -
а) инверсия;
б) конъюнкция;
в) эквивалентность
г) импликация
д) дизъюнкция;
Определите какой логической операции соответствует таблица истинности:
| А | Результат |
| 0 | 1 |
| 1 | 0 |
б) дизъюнкция;
в) импликация;
г) эквивалентность
д) инверсия
Постройте таблицу истинности для логической операции «эквивалентность»
| А | В | |
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
Приведите 1 пример сложного высказывания, построенного с использованием логической операции «импликация»
__________________________________________________________________________________________________________________________
Запиши высказывания в виде логической формулы:
Если в кинотеатре идет неинтересный фильм или у меня нет денег, то я останусь дома.
Пришла весна, и растаял снег.
a___________________________b_________________________
Укажите порядок вычисления значения логического выражения: (К Ā) А → К
Сколько строк в таблице истинности для выражения: (К Ā) А → К
Сколько столбцов в таблице истинности для выражения: (К Ā) А → К
Постройте таблицу истинности выражения (К Ā) → К
ФИО________________________________________________________________________________
Контрольная работа_Логика_№1
В-2
Логическая операция с использованием связки «или», называется -
а) инверсия;
б) дизъюнкция;
в) конъюнкция;
г) эквивалентность
д) импликация
Таким образом: «Ā» обозначается -
а) эквивалентность
б) конъюнкция;
в) импликация
г) дизъюнкция;
д) инверсия;
| А | В | Результат |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
а) конъюнкция;
б) дизъюнкция;
в) импликация;
г) эквивалентность
д) инверсия
Постройте таблицу истинности для логической операции «конъюнкция»
| А | В | Результат |
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
Приведите 1 пример сложного высказывания, построенного с использованием логической операции «эквивалентность»
__________________________________________________________________________________________________________________________
Запиши высказывание в виде логической формулы:
Мы сегодня пойдем с друзьями в кино или я завтра пойду в театр.
Если не купили вам пирожное и в кино не взяли вечером, то нужно на родителей обидеться.
a___________________________b_________________________
Укажите порядок вычисления значения логического выражения: (Ā С) ↔А С
Сколько строк в таблице истинности для выражения: (Ā С) ↔А С
Сколько столбцов в таблице истинности для выражения: (Ā С) ↔А С
Постройте таблицу истинности выражения: Ā (С→А)
ФИО________________________________________________________________________________
Контрольная работа_Логика_№1
В-3
Логическая операция с использованием связки «тогда и только тогда, когда…», называется -
а) инверсия;
б) конъюнкция;
в) дизъюнкция;
г) импликация
д) эквивалентность
Знаком «» обозначается -
а) инверсия;
б) конъюнкция;
в) дизъюнкция;
г) импликация
д) эквивалентность
| А | В | Результат |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
а) конъюнкция;
б) дизъюнкция;
в) импликация;
г) эквивалентность
д) инверсия
Постройте таблицу истинности для логической операции «импликация»
| А | В | |
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
Приведите 1 пример сложного высказывания построенного, с использованием логической операции «инверсия»
______________________________________________________________________________________
_________________________________________________________________________________
Запиши высказывание в виде логической формулы:
Обычно вечером я иду на тренировку или гуляю с собакой.
Если в расписании на завтра нет первого уроа, то я высплюсь.
a___________________________b_________________________
Укажите порядок вычисления значения логического выражения: (К А) Ā → К
Сколько строк в таблице истинности для выражения: (К А) Ā → К
Сколько столбцов в таблице истинности для выражения: (К А) Ā → К
Постройте таблицу истинности выражения: (К Ā) → К
ФИО________________________________________________________________________________Контрольная работа_Логика_№1
В-4
Логическая операция с использованием связки «если…, то…», называется -
а) импликация
б) конъюнкция;
в) дизъюнкция;
г) инверсия;
д) эквивалентность
Знаком «» обозначается -
а) эквивалентность
б) конъюнкция;
в) дизъюнкция;
г) импликация
д) инверсия;
| А | В | Результат |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
а) конъюнкция;
б) дизъюнкция;
в) импликация;
г) эквивалентность
д) инверсия
Постройте таблицу истинности для логической операции «инверсия»
| А | Результат |
| 0 | |
| 1 |
Приведите 1 пример сложного высказывания, построенного с использованием логической операции «дизъюнкция»
__________________________________________________________________________________
Запиши высказывание в виде логической формулы:
Если за мной зайдут друзья, и мы пойдем гулять, тоя весело проведу время.
Если с другом вышел в путь, то веселей дорога.
a___________________________b_________________________
Укажите порядок вычисления значения логического выражения: (А С) ↔ Ā С
Сколько строк в таблице истинности для выражения: (А С) ↔ Ā С
Сколько столбцов в таблице истинности для выражения: (А С) ↔ Ā С
Постройте таблицу истинности выражения: С ↔ Ā С
ФИО________________________________________________________________________________Контрольная работа_Логика_№1
В-5
Логическая операция с использованием связки «не», называется -
а) инверсия;
б) конъюнкция;
в) дизъюнкция;
г) импликация
д) эквивалентность
Знаком «» обозначается -
а) инверсия;
б) конъюнкция;
в) дизъюнкция;
г) импликация
д) эквивалентность
| А | В | Результат |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
а) конъюнкция;
б) дизъюнкция;
в) импликация;
г) эквивалентность
д) инверсия
Постройте таблицу истинности для логической операции «дизъюнкции»
| А | В | |
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
Приведите 1 пример сложного высказывания построенного, с использованием логической операции «конъюнкция»
____________________________________________________________________________________
___________________________________________________________________________________________
Запиши высказывание в виде логической формулы:
Сегодня я буду участвовать в кроссе и если пробегу дистанциюбыстрее всех, то получу медаль.
Прозвенел звонок, и все побежали на перемену.
a___________________________b_________________________
Укажите порядок вычисления значения логического выражения: (Ā ) ↔А С
Сколько строк в таблице истинности для выражения: (Ā ) ↔А С
Сколько столбцов в таблице истинности для выражения: (Ā ) ↔А С
Постройте таблицу истинности выражения: (Ā )
xn--j1ahfl.xn--p1ai
КОНТРОЛЬНАЯ РАБОТА
«РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ. ЛОГИЧЕСКИЕ ОСНОВЫ ПОСТРОЕНИЯ ПК»
Вариант №1.
1
A
Y
B
. Записать логическую функцию, описывающую состояние логической схемы. Составить таблицу истинности.
&
2. По заданной таблице истинности записать логическую функцию (СДНФ). Упростить полученную логическую функцию. Составить логическую схему.
| A | B | C | F(a,b,c) |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
3. Экзамен сдавали четыре абитуриента: Агафонов, Веткин, Сараев и Киреев. Известно, что:
1) Для того, чтобы Агафонов не сдал или Веткин сдал, необходимо, чтобы Сараев сдал и Киреев не сдал экзамен.
2) Для того, чтобы не сдал Сараев, а Веткин сдал, необходимо, чтобы Агафонов не сдал или Киреев сдал экзамен.
3) Неверно, что для того, чтобы не сдал Агафонов, достаточно, чтобы сдал Киреев.
Кто сдал экзамен?
КОНТРОЛЬНАЯ РАБОТА
«РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ. ЛОГИЧЕСКИЕ ОСНОВЫ ПОСТРОЕНИЯ ПК»
Вариант №2.
1
. Записать логическую функцию, описывающую состояние логической схемы. составить таблицу истинности.
2. По заданной таблице истинности записать логическую функцию (СДНФ). Упростить полученную логическую функцию. Составить логическую схему.
| a | b | c | F(a, b, c) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
3. Семья состоит из пяти человек: Алексей, Вера, Глеб, Даша, Евгений.
1) Если телевизор смотрит Алексей, то смотрит и Вера;
2) смотрят либо Даша, либо Евгений, либо оба вместе;
З) смотрят либо Вера, либо Глеб, но не вместе;
4) Даша и Глеб либо смотрят вместе, либо вовсе не смотрят;
5) если смотрит Евгений, то смотрят Алексей и Даша.
Кто смотрит телевизор?
КОНТРОЛЬНАЯ РАБОТА
«РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ. ЛОГИЧЕСКИЕ ОСНОВЫ ПОСТРОЕНИЯ ПК»
Вариант №3.
1
. Записать логическую функцию, описывающую состояние логической схемы. Составить таблицу истинности.
2. По заданной таблице истинности записать логическую функцию (СДНФ). Упростить полученную логическую функцию. Составить логическую схему.
| A | B | C | F(a,b,c) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
3. На вопрос о погоде на завтра синоптик ответил:
1) Если будет мороз, то пойдет снег и будет пасмурно.
2) Если не будет мороза и пойдет снег, то будет пасмурно.
3) Пойдет снег, если будет пасмурно.
4) Неверно, что если не будет мороза, то будет пасмурно.
Какая будет погода завтра?
КОНТРОЛЬНАЯ РАБОТА
«РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ. ЛОГИЧЕСКИЕ ОСНОВЫ ПОСТРОЕНИЯ ПК»
Вариант №4.
1
A
.Записать логическую функцию, описывающую состояние логической схемы. Составить таблицу истинности.
2. По заданной таблице истинности записать логическую функцию (СДНФ). Упростить полученную логическую функцию. Составить логическую схему.
| A | B | C | F(a,b,c) |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
3. В нарушении правил обмена валюты подозреваются четыре работника банка — Крымов, Нестеренко, Романова, Тимофеева. Известно, что:
1) Если Крымов нарушил, то и Нестеренко нарушил правила обмена валюты.
2) Если Нестеренко нарушил, то и Романова нарушила или Крымов не нарушал.. 3) Если Тимофеева не нарушила, то Крымов нарушил, а Романова не нарушала.
4) Если Тимофеева нарушила, то и Крымов нарушил.
Кто из подозреваемых нарушил правила обмена валюты?
Решение контрольной работы.
Вариант №1.
№1.
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
№2.
№3.
I. Запишем логические формулы, соответствующие высказываниям:
1) 
(1)
2) 
(2)
3) 
(3)
II. Умножим (1) на (3), получим:
(4)
III. Умножим (4) на (2), получим:
Ответ:
, А и К сдали, В – не сдал, С мог сдать и не сдать.
Вариант №2.
№1.
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
№2.
№3.
I. Запишем логические формулы, соответствующие высказываниям:
1) 
(1)
2) 
(2)
3) 
(3)
4) 
(4)
5) 
(5)
II. Умножим (1) на (3), получим:
(6)
III. Умножим (6) на (4) и получим формулу (7):
IV. Умножим (7) на (5) и получим формулу:
(8)
V. Умножим (8) на (2) и получим формулу:
Ответ:
, Телевизор смотрят Г и Д.
Вариант №3.
№1.
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
№2.
№3.
А: «Будет мороз»; В: «Пойдет снег»; С: «Будет пасмурно».
I. Запишем логические формулы, соответствующие высказываниям:
1) 
(1)
2) 
(2)
3) 
(3)
4) 
(4)
II. Умножим (1) на (2), получим:
(5)
III. Умножим (5) на (3) и получим формулу (6):
(6)
IV. Умножим (6) на (3) и получим формулу:
Ответ: 
, будет ясно, тепло и снег не пойдет.
Вариант №4.
№1.
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
№2.
№3.
I. Запишем логические формулы, соответствующие высказываниям:
1) 
(1)
2) 
(2)
3) 
(3)
4) 
(4)
II. Умножим (3) на (4), получим:
(5)
III. Умножим (5) на (1) и получим формулу (6):
(6)
IV. Умножим (6) на (2) и получим формулу:
Ответ: 
, виноватыКрымов, Нестеренко, Романова, Тимофеева.
Резерв.
3. Четыре ученицы: Мария, Нина, Ольга, Поля участвовали в соревновании и заняли первые 4 места. На вопрос, кто из них какое место занял, 3 девушки ответили: 1. Ольга была вторая, Поля - третья; 2. Ольга была первая, Нина - вторая; 3. Мария была вторая, Поля - четвертая.
В каждом из этих ответов одна часть верна, другая нет. Кто какие места занял в соревнования?
3. При составлении расписания на понедельник в 9-а классе преподаватели высказали просьбы завучу: 1. Учитель математики: “Желаю иметь первый или второй урок” 2. Учитель истории: “Желаю иметь первый или третий урок” 3. Учитель литературы: “Желаю иметь второй или третий урок”
Какое расписание будет составлено?
3. Предстоят спортивные соревнования между четырьмя восьмыми классами одной школы. В учительской живо обсуждаются возможные результаты и высказываются прогнозы. 1). Первое место займет 8-А, а второе - 8-Б,- сказал учитель математики. 2). Да что вы! - сказал учитель географии. - Я недавно ходил с ними в поход и знаю их возможности. 8-А займет второе место, а 8-Г-только третье. 3). А я думаю, что на втором месте будет 8-В,- сказала завуч школы,- а 8-Г будет на последнем месте.
Оказалось, что прогнозы их сбылись только наполовину. Какое место занял каждый класс?
3. Четыре марсианки, оказавшиеся на Земле в 2... году, на вопрос об их возрасте дали ответы: 1. МИ - 22 года, МЕ - 21 год 2. МО - 19 лет, МИ - 21 год 3. МА - 21 года, МО - 18 лет
Все марсианки - разных возрастов, притом только данных: 18, 19, 21 и 22. В каждом ответе одна часть верна, другая - нет. Сколько лет каждой?
studfiles.net
Контрольная работа № 2
«Упрощение логических функций»
1 вариант
1. Упростите выражение:
а) 
б) 
в) 
г) 
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
2 вариант
1. Упростите выражение:
а)
б) 
в) 
г) 
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
3 вариант
1. Упростите выражение:
а) 
б) 
в) 
г) 
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
4 вариант
1. Упростите выражения:
а) 
б) 
в) 
г) 
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
5 вариант
1. Упростите выражения:
а) 
б) 
в) 
г) 
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
6 вариант
1. Упростите выражения:
а) 
б) 
в) 
г) 
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
7 вариант
1. Упростите выражения:
а) 
б) 
в) 
г) 
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
8 вариант
1. Упростите выражения:
а) 
б) 
в) 
г) 
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
9 вариант
1. Упростите выражения:
а) 
б) 
в) 
г) 
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
10 вариант
1. Упростите выражения:
а) 
б) 
в) 
г) 
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
1 вариант
1. Упростите выражение:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
2 вариант
1. Упростите выражение:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
3 вариант
1. Упростите выражение:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
4 вариант
1. Упростите выражения:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
5 вариант
1. Упростите выражения:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
6 вариант
1. Упростите выражения:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
7 вариант
1. Упростите выражения:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
8 вариант
1. Упростите выражения:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
9 вариант
1. Упростите выражения:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Контрольная работа № 2
«Упрощение логических функций»
10 вариант
1. Упростите выражения:
а)
б)
в)
г)
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г)
Ответы:
1 а) 
2 а) 
3 а) 
б) 
б) 
б) 
в) 
в) 
в) В
г) 
г) 
г) 
4 а) 
5 а) 
6 а) 
б) 
б) 
б) 
в) 
в) АВ в)
А
г) г) 
г) 
7 а) 
8 а) 
9 а) 
10 а) 
б) 
б) 
б) 
б) 
в) 
в) в) АВ в)
А
г) 
г) г) 
г) 
Таблицы истинности:
1 в)
1 г)
botana.cc
Контрольная работа «Логические основы компьютеров»
Вариант 1
1. Упростите логическое выражение:
2.
4. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
5. Используя логические элементы постройте схему соответствующую логическому выражению:
6. Постройте выражение для логической функций, заданной таблицей истинности.
Контрольная работа «Логические основы компьютеров»
Вариант 2
1. Упростите логическое выражение:
2.
4. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
5. Используя логические элементы постройте схему соответствующую логическому выражению:
6. Постройте выражение для логической функций, заданной таблицей истинности.
Контрольная работа «Логические основы компьютеров»
Вариант 3
1. Упростите логические выражения:
2.
4. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
5. Используя логические элементы постройте схему соответствующую логическому выражению:
6. Постройте выражение для логической функций, заданной таблицей истинности.
Контрольная работа «Логические основы компьютеров»
Вариант 4
1. Упростите логические выражения:
2.
4. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
5. Используя логические элементы постройте схему соответствующую логическому выражению:
6. Постройте выражение для логической функций, заданной таблицей истинности.
Контрольная работа «Логические основы компьютеров»
Вариант 5
1. Упростите логическое выражение:
2.
4. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
5. Используя логические элементы постройте схему соответствующую логическому выражению:
6. Постройте выражение для логической функций, заданной таблицей истинности.
Контрольная работа «Логические основы компьютеров»
Вариант 6
1. Упростите логическое выражение:
2.
4. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
5. Используя логические элементы постройте схему соответствующую логическому выражению:
6. Постройте выражение для логической функций, заданной таблицей истинности.
Контрольная работа «Логические основы компьютеров»
Вариант 7
1. Упростите логические выражения:
2.
4. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
5. Используя логические элементы постройте схему соответствующую логическому выражению:
6. Постройте выражение для логической функций, заданной таблицей истинности.
Контрольная работа «Логические основы компьютеров»
Вариант 8
1. Упростите логические выражения:
2.
4. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
5. Используя логические элементы постройте схему соответствующую логическому выражению:
6. Постройте выражение для логической функций, заданной таблицей истинности.
infourok.ru
