Контрольная работа
Вариант 1
Решите неравенство:
а) х2-25≥0
б) х2+7х 0
в) х2-6х+7≤0
г) х2+4х+110
д) 

е) 
2. При каких значениях х имеет смысл выражение:

Решите неравенство:

Контрольная работа
Вариант 1
Решите неравенство:
а) х2-25≥0
б) х2+7х 0
в) х2-6х+7≤0
г) х2+4х+110
д) 

е) 
2. При каких значениях х имеет смысл выражение:

Решите неравенство:

Контрольная работа
Вариант 1
Решите неравенство:
а) х2-25≥0
б) х2+7х 0
в) х2-6х+7≤0
г) х2+4х+110
д) 

е) 
2. При каких значениях х имеет смысл выражение:

3. Решите неравенство:

Контрольная работа
Вариант 2
Решите неравенство:
а) х2-16≥0
б) х2-5х 0
в) х2-3х-4≤0
г) х2-3х+100
д) 

е) 
2. При каких значениях х имеет смысл выражение:

3. Решите неравенство:

Контрольная работа
Вариант 2
Решите неравенство:
а) х2-16≥0
б) х2-5х 0
в) х2-3х-4≤0
г) х2-3х+100
д) 

е) 
2. При каких значениях х имеет смысл выражение:

3. Решите неравенство:

multiurok.ru
Административная контрольная работа по алгебре.
« Обобщённый метод интервалов ».
Вариант I.
Решите неравенства:
(х2+ 2х)(х – 7)2≤ 0;
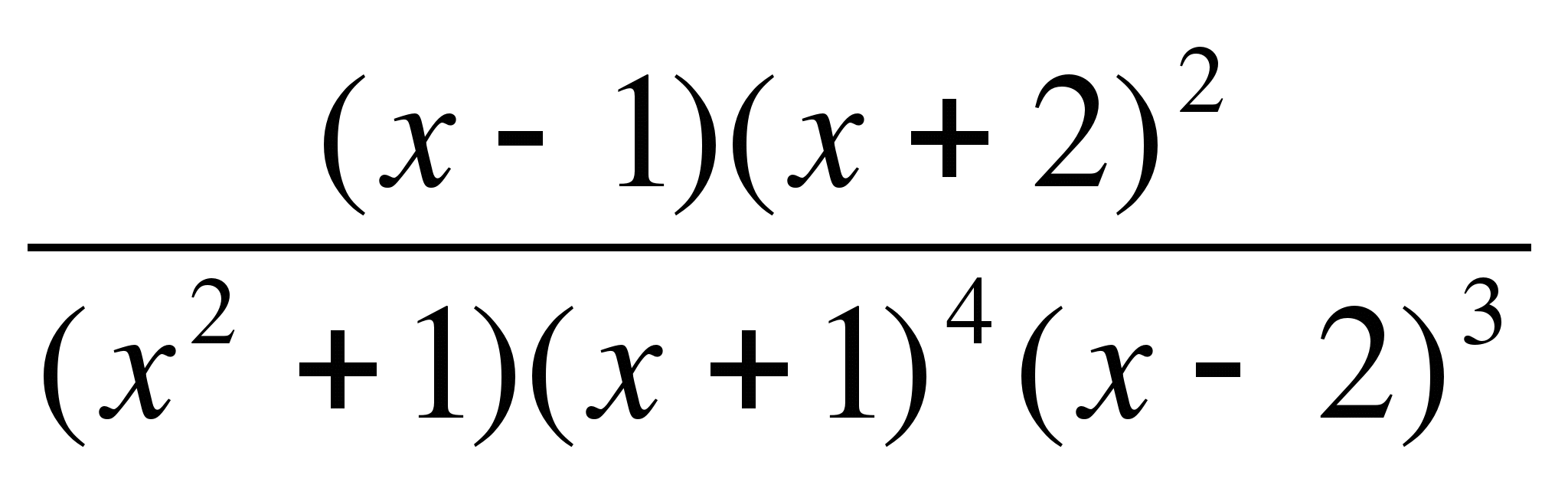 ≤ 0;
≤ 0;
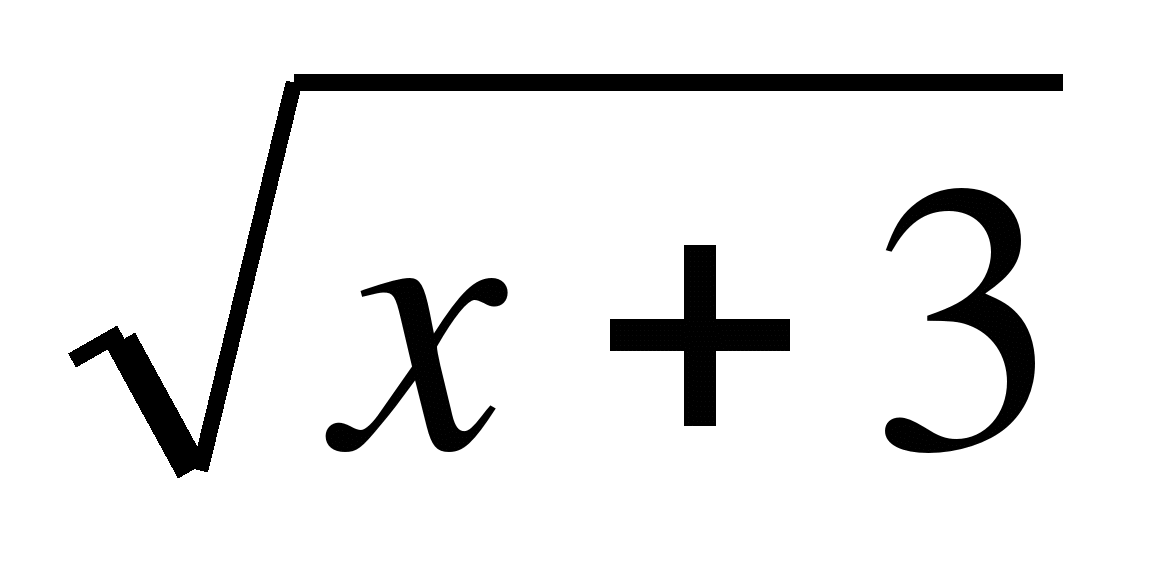 (х2- 16) > 0;
(х2- 16) > 0;
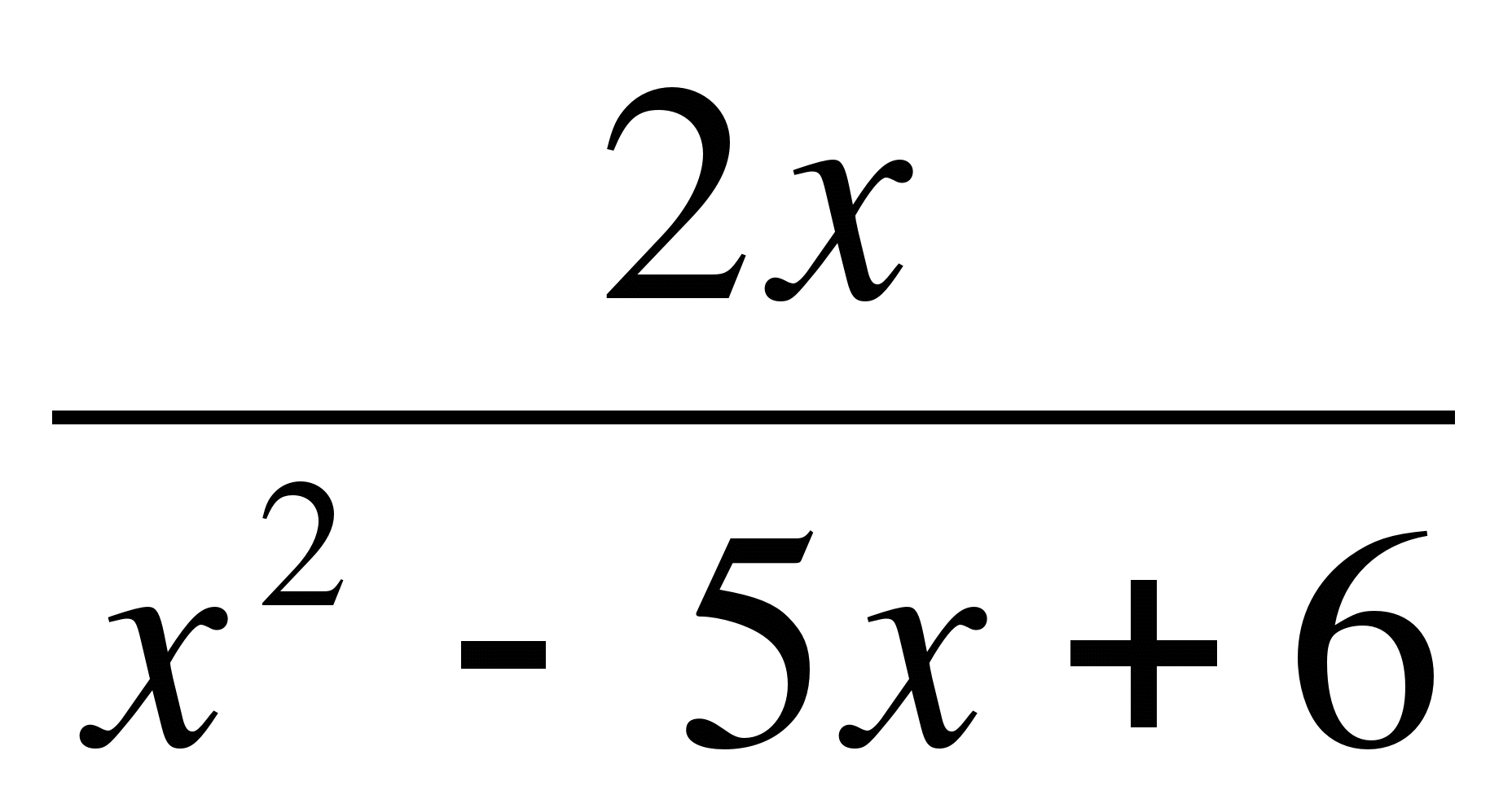 ≥ 1;
≥ 1;
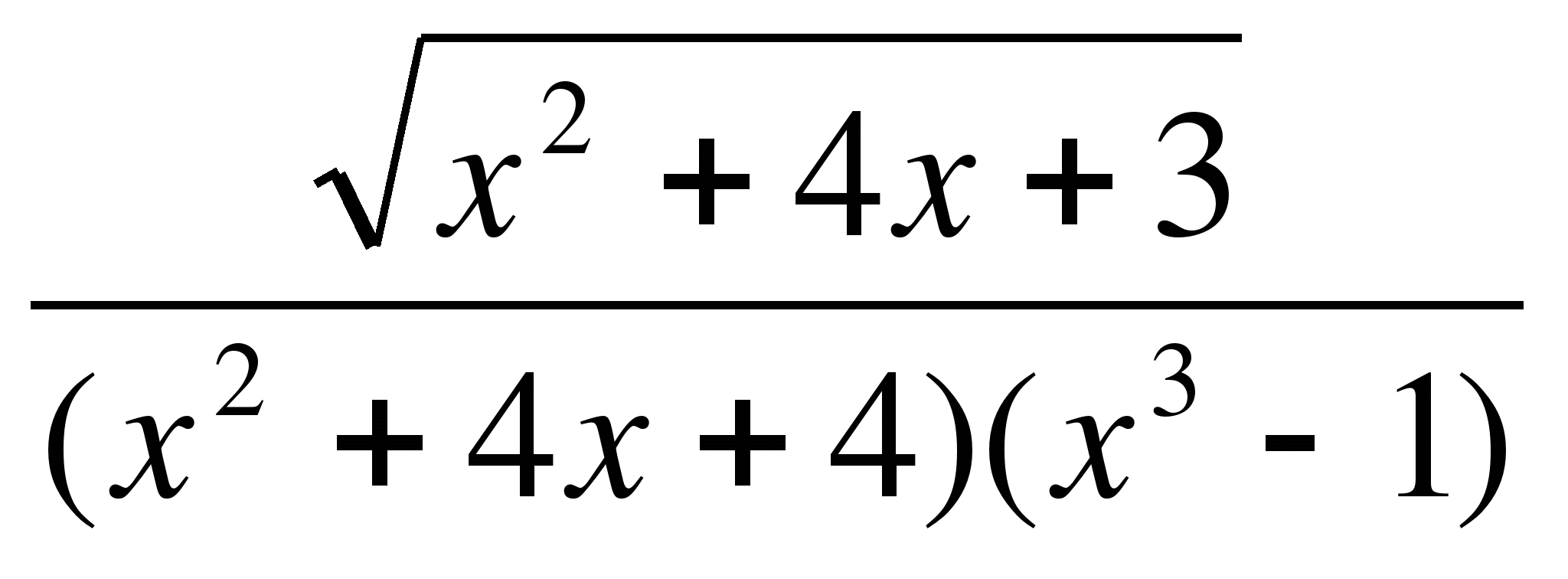 ≤ 0;
≤ 0;
х+3 > 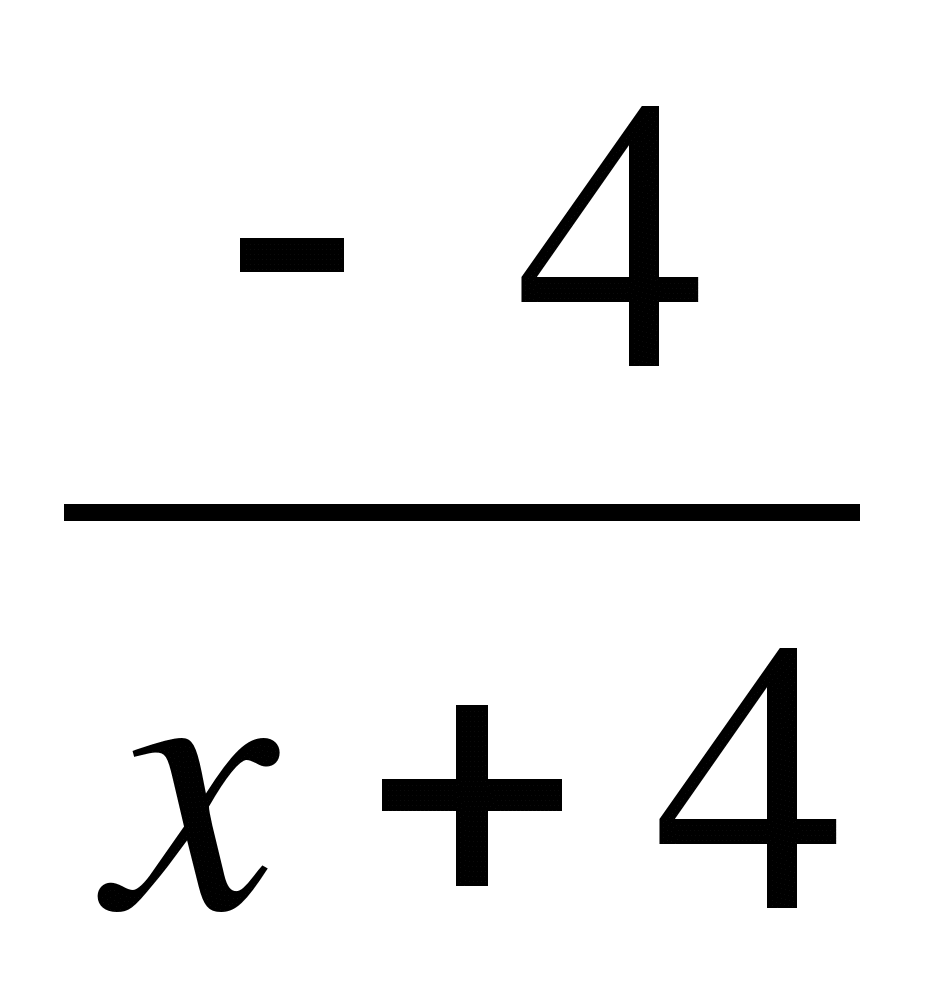 ;
;
7) 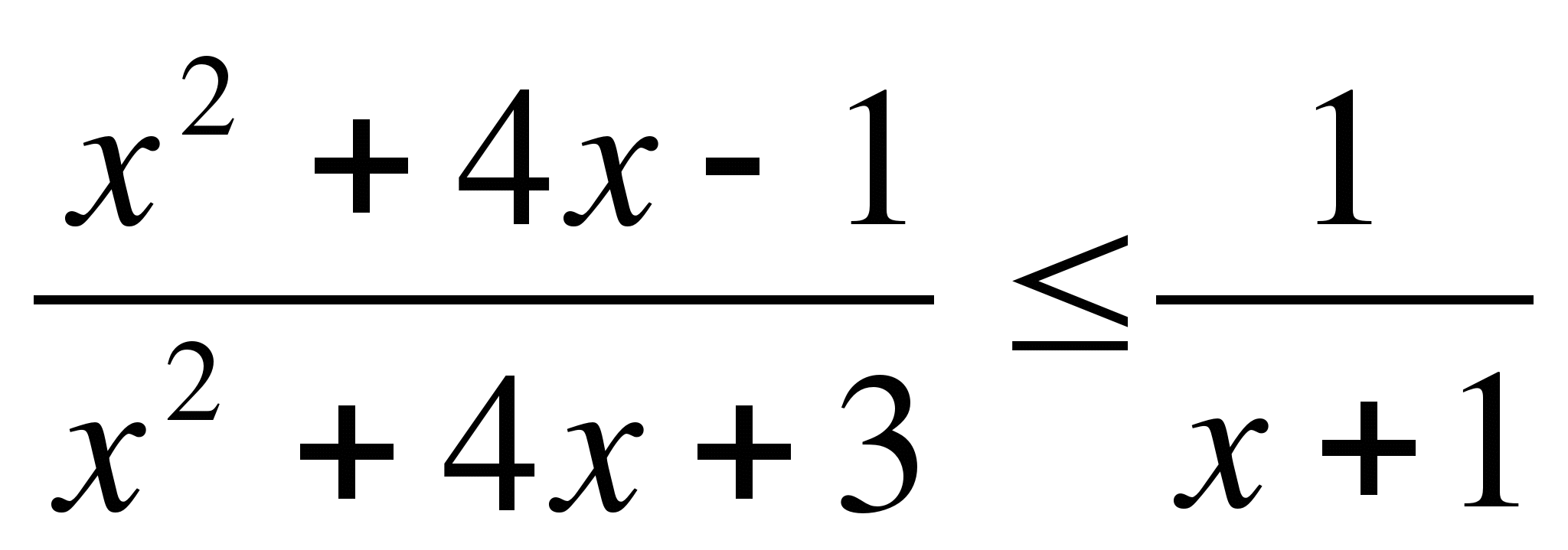

8) 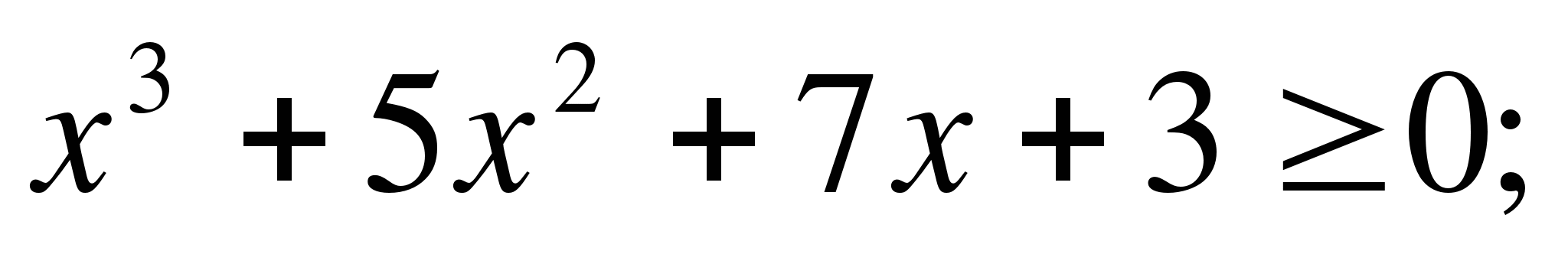

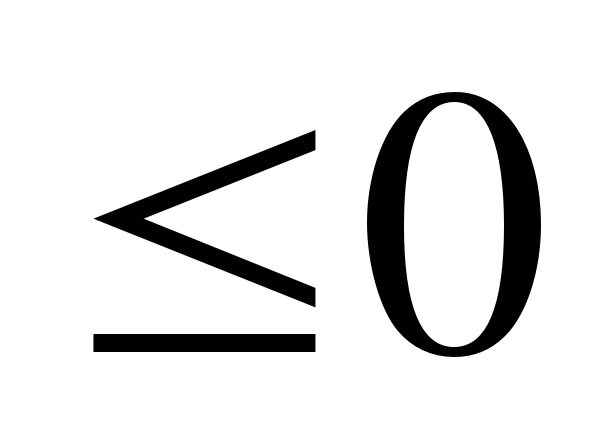
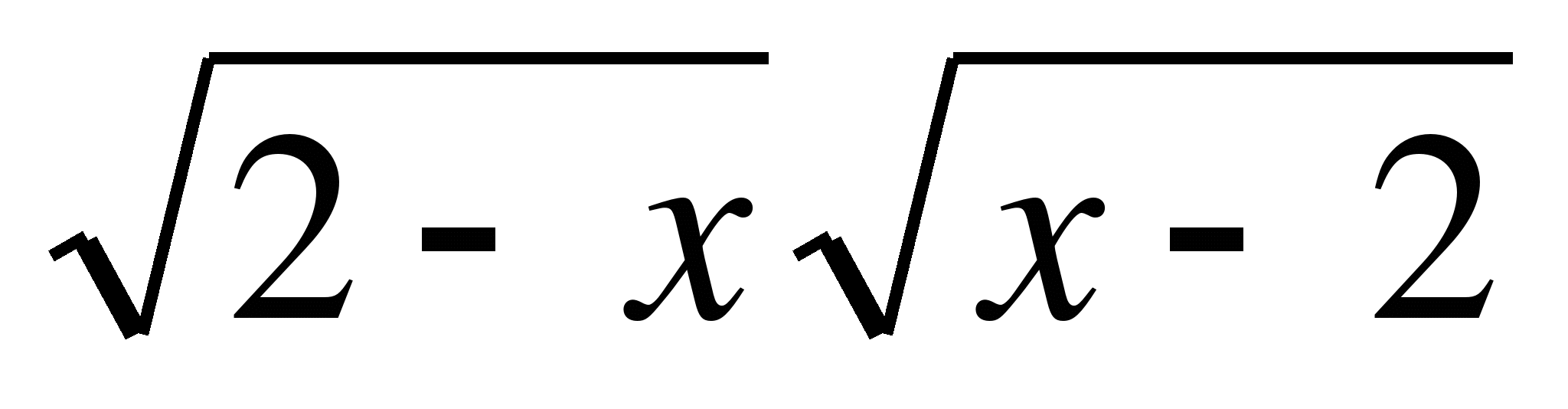 .
. х2- 4
Критерии оценки:
Оценка «5» ставится за любые шесть верно решённых неравенств из первой (обязательной) части.
Вторая часть ( профильный уровень) оценивается отдельно.
Административная контрольная работа по алгебре.
« Обобщённый метод интервалов ».
Вариант II.
Решите неравенства:
1) (х2-7х)(х+2)2≥ 0;
2) 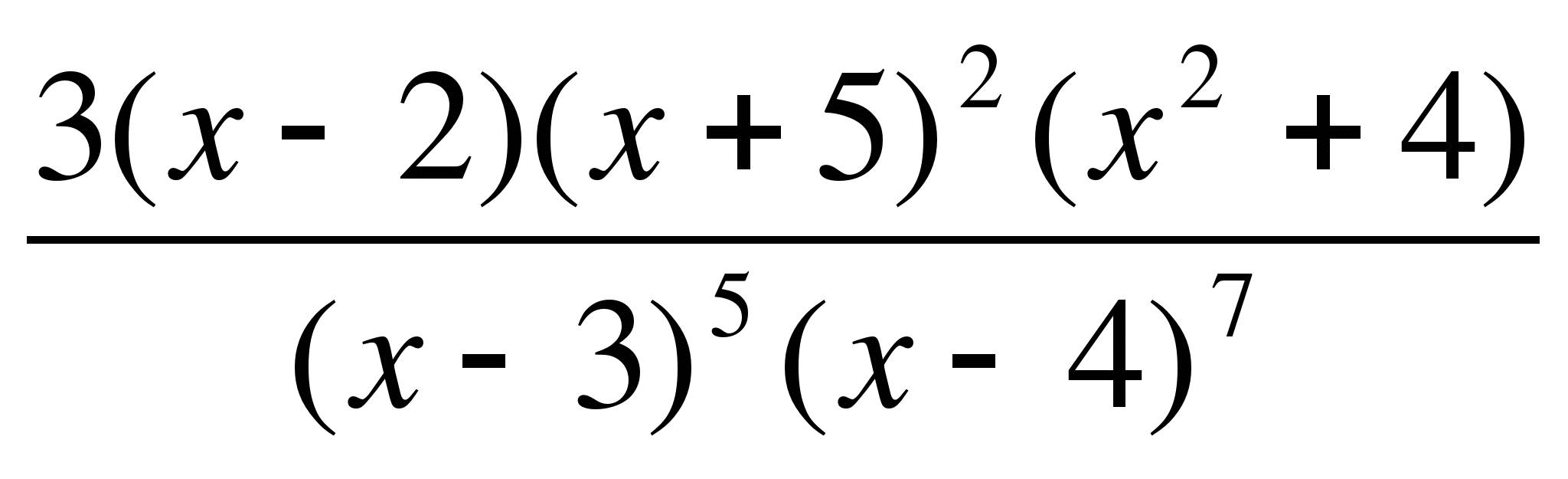 ≤ 0.
≤ 0.
3)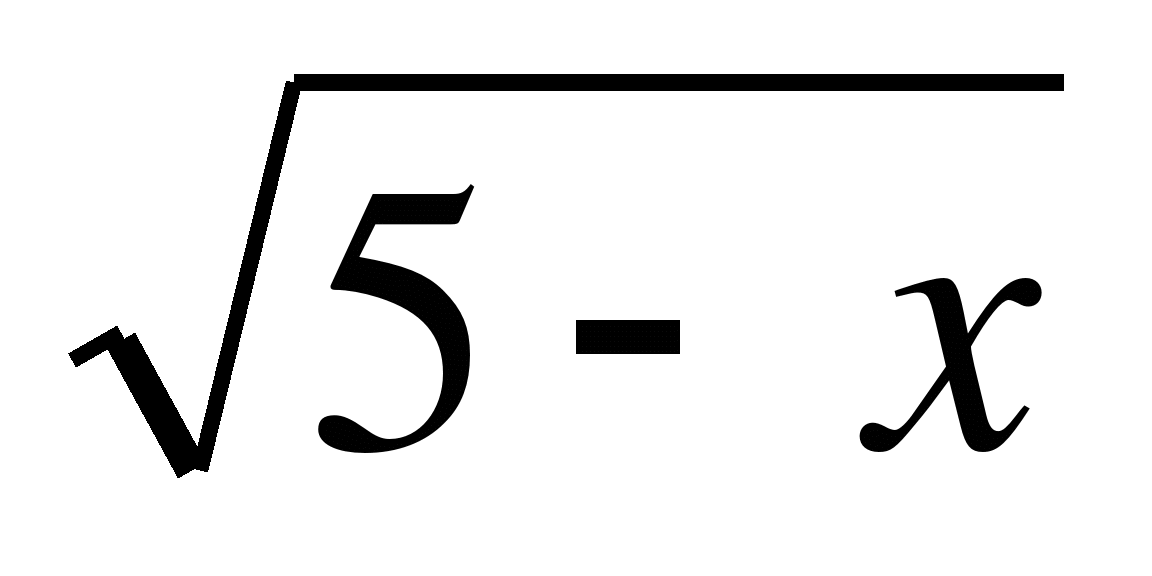 (х2-36) < 0;
(х2-36) < 0;
4)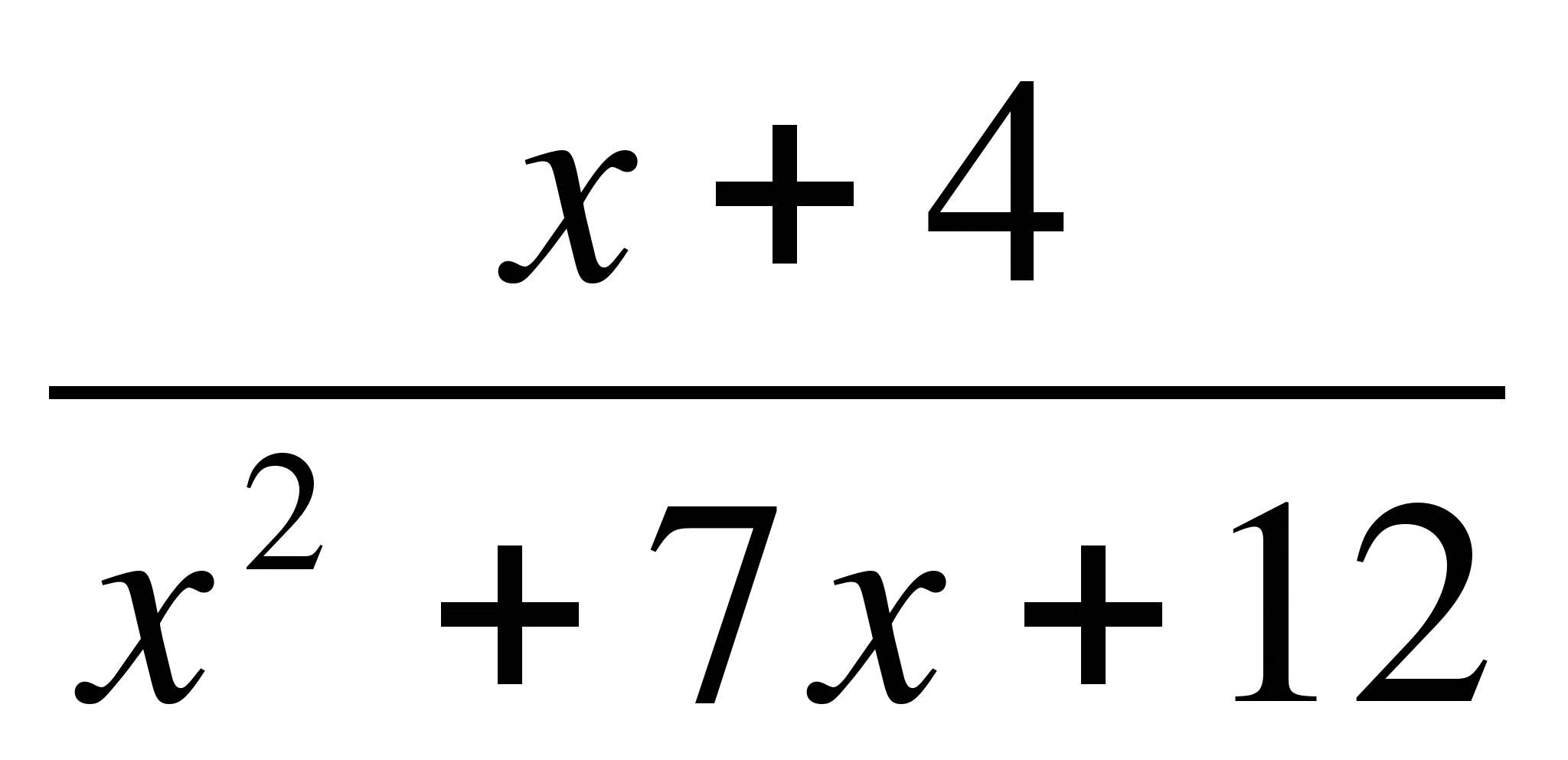 ≤ 1;
≤ 1;
5)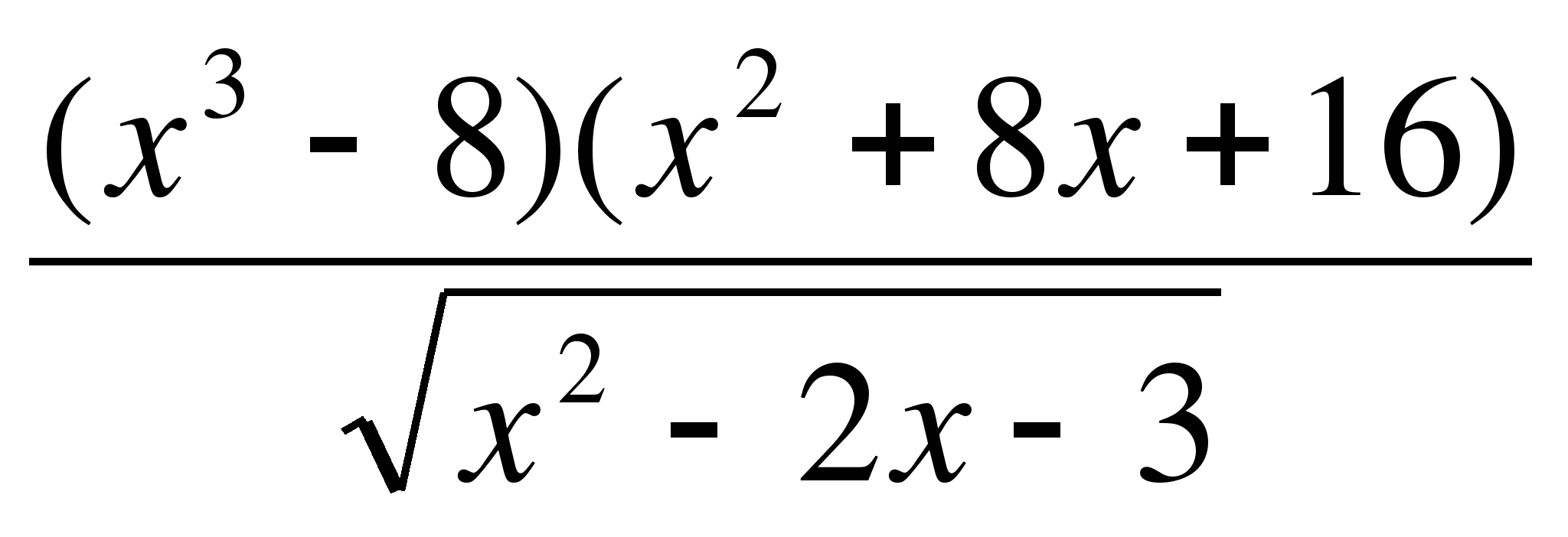 ≥ 0;
≥ 0;
6)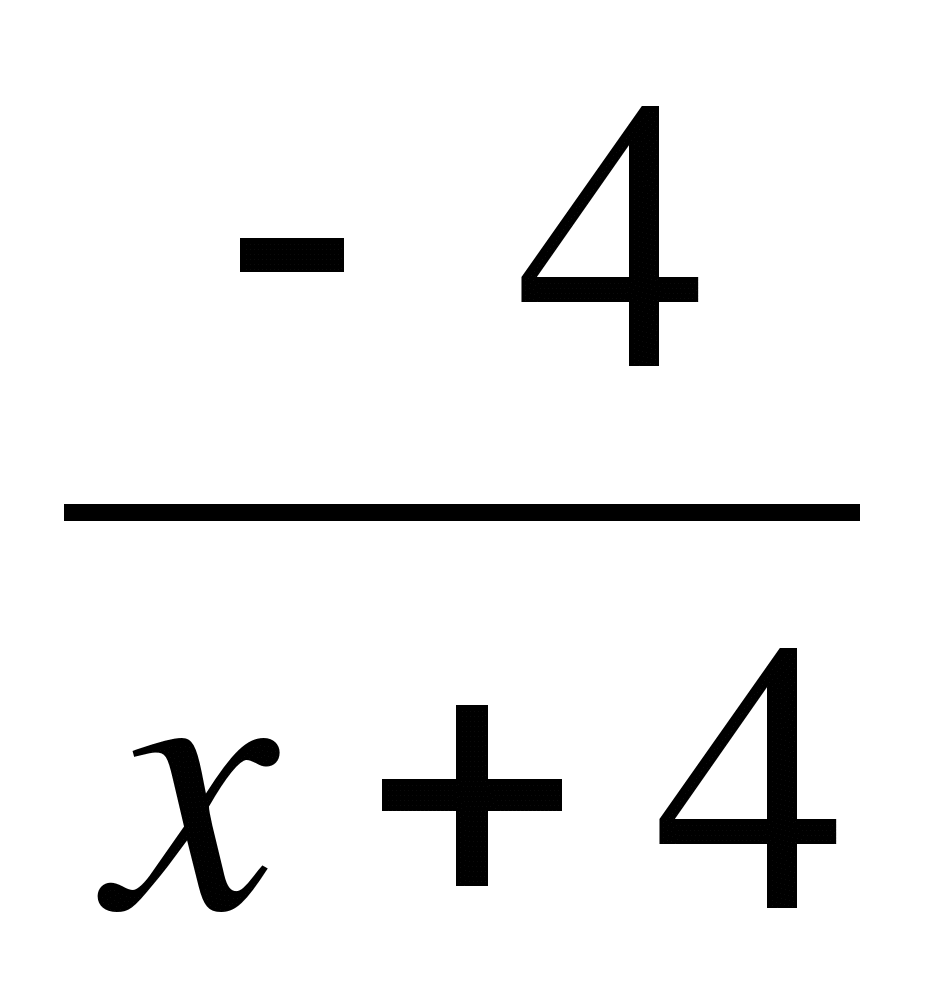 > х+2;
> х+2;
7) 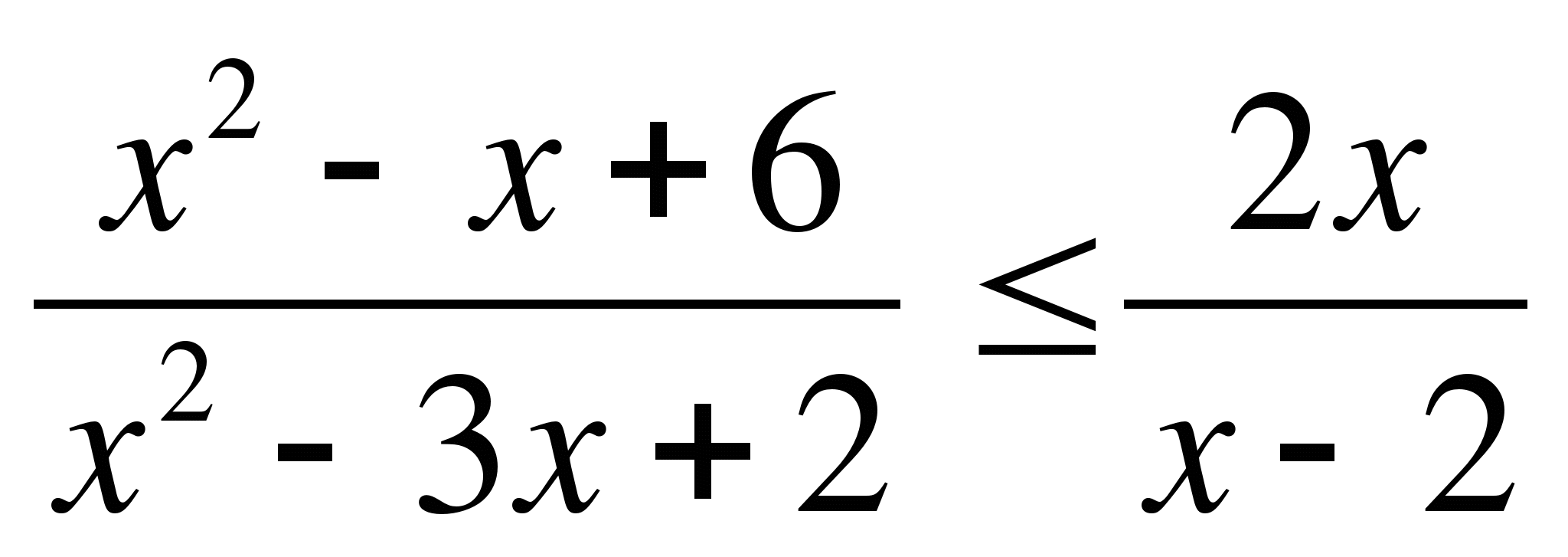

8) 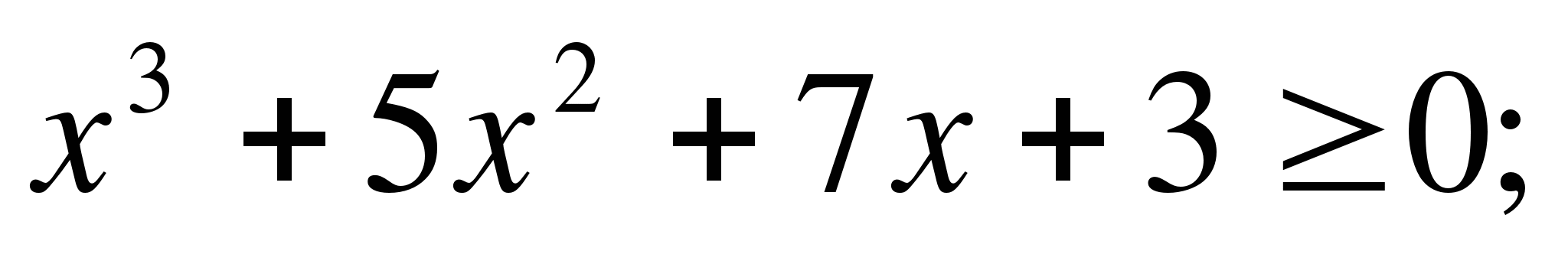
9
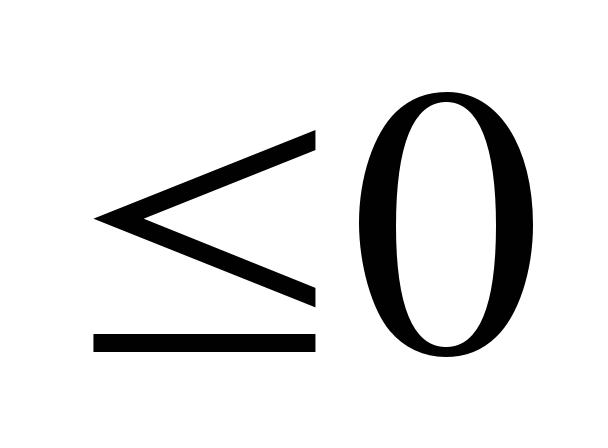 .
.
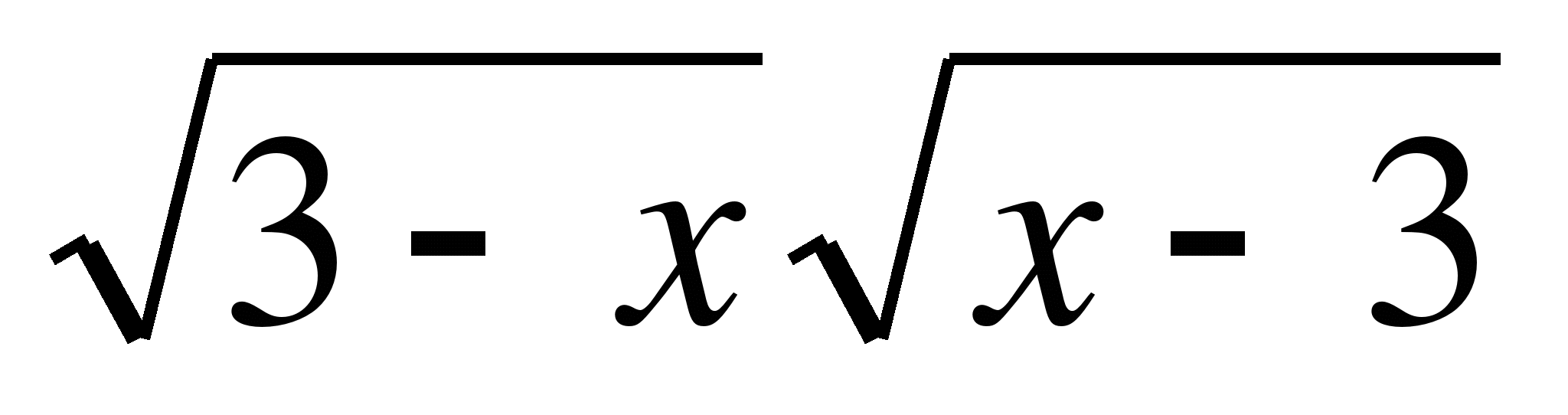
х2- 9
Критерии оценки:
Оценка «5» ставится за любые шесть верно решённых неравенств из первой (обязательной) части.
Вторая часть ( профильный уровень) оценивается отдельно.
infourok.ru
Вариант 1
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)=2x2-4x+1,х0=1
Вариант 2
1. Решите неравенство методом интервалов:
≤
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)=4x2-2x+1,х0=2
Вариант 3
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)= x2-x+4,х0=3
Вариант 4
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)=2x2-6x+1,х0=1
Вариант 5
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)=2x2-5x+1,х0=2
Вариант 6
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)=2x2-4x+1,х0=4
Вариант 7
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)=2x2+x+1,х0=1
Вариант 8
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)=2x2-4x+1,х0=1
Вариант 9
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0:f(x)= x2+х+2,х0=-3
Вариант 10
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)= x2-6x+3,х0=2
Вариант 12
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)=3x2-2x+1,х0=1
Вариант 11
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)=4x2-x+3,х0=2
Вариант 13
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)=5x2-2x+1,х0=2
Вариант 14
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0:f(x)= x2-10x+1,х0=2
Вариант 15
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)=3x2-3x+3,х0=2
Вариант 17
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)=3x2-4x+2,х0=3
Вариант 16
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)= x2-7x+5,х0=4
Вариант 18
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)=2x2-9x+1,х0=4
Вариант 19
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)= x2-x+5,х0=2
Вариант 20
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)=2x2-2x+1,х0=2
Вариант 21
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)=3x2-2x+1,х0=1
Вариант 22
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)=2x2-x+1,х0=4
Вариант 23
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)= x2+3x+2,х0=4
Вариант 24
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)= x2-5x+4,х0=1
Вариант 25
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)= 3x2-x+3,х0=5
Вариант 26
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)= x2-3x+9,х0=1
Вариант 27
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)=3x2-3x+1,х0=5
Вариант 28
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0:f(x)= x2-2x+1,х0=7
Вариант 29
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0: f(x)=2x2-2x+2,х0=2
Вариант 30
1. Решите неравенство методом интервалов:
2. Напишите уравнение касатель-ной к графику функции f в точке с абсциссой х0:f(x)= 2x2-x+1,х0=-5
xn--j1ahfl.xn--p1ai
Административная контрольная работа по алгебре.
« Обобщённый метод интервалов ».
Вариант I.
Обязательная часть
Решите неравенства:
(х2+ 2х)(х – 7)2≤ 0;
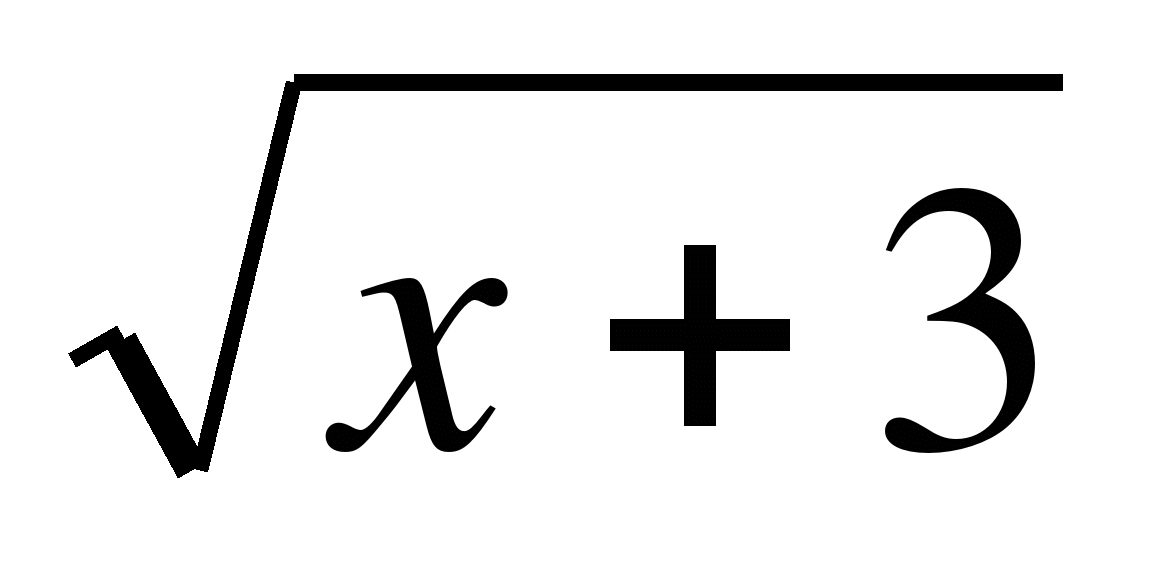 (х2- 16) > 0;
(х2- 16) > 0;
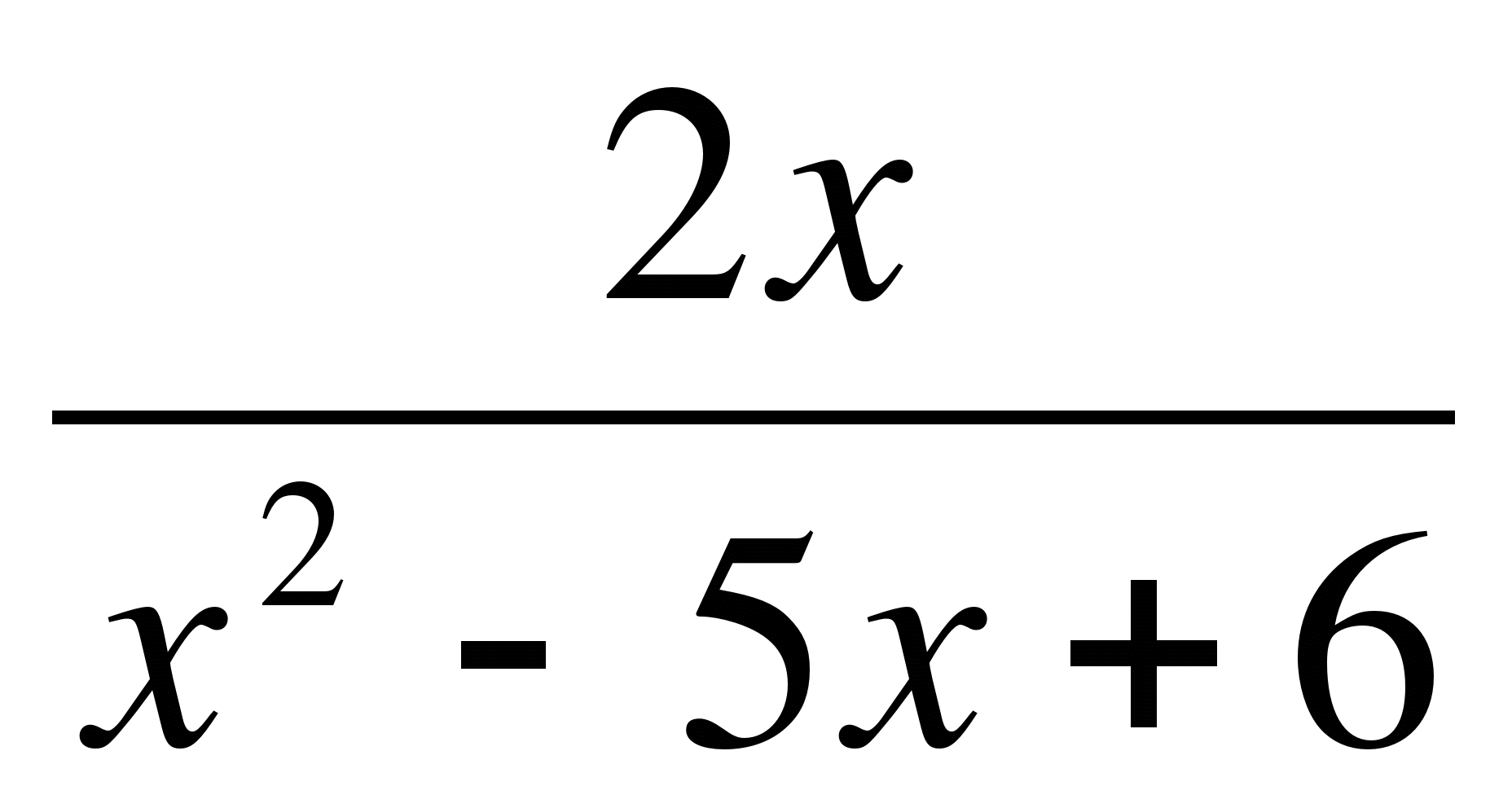 ≥ 1;
≥ 1;
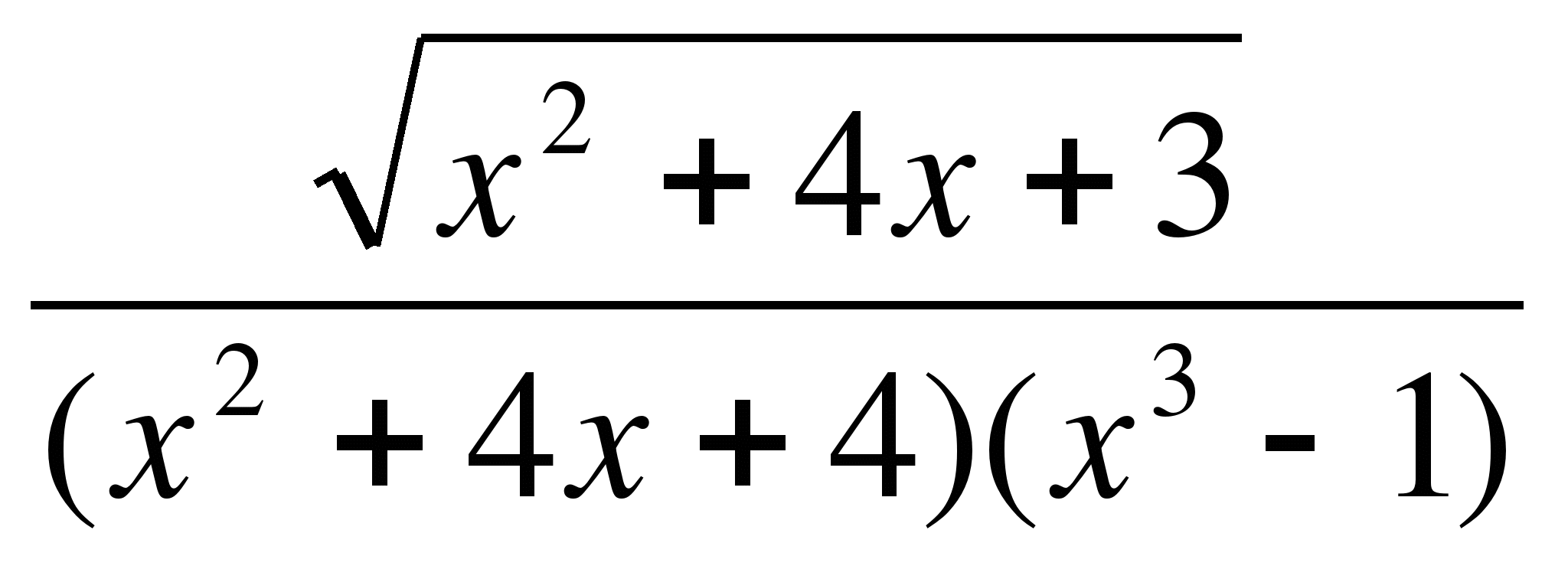 ≤ 0;
≤ 0;
х+3 > 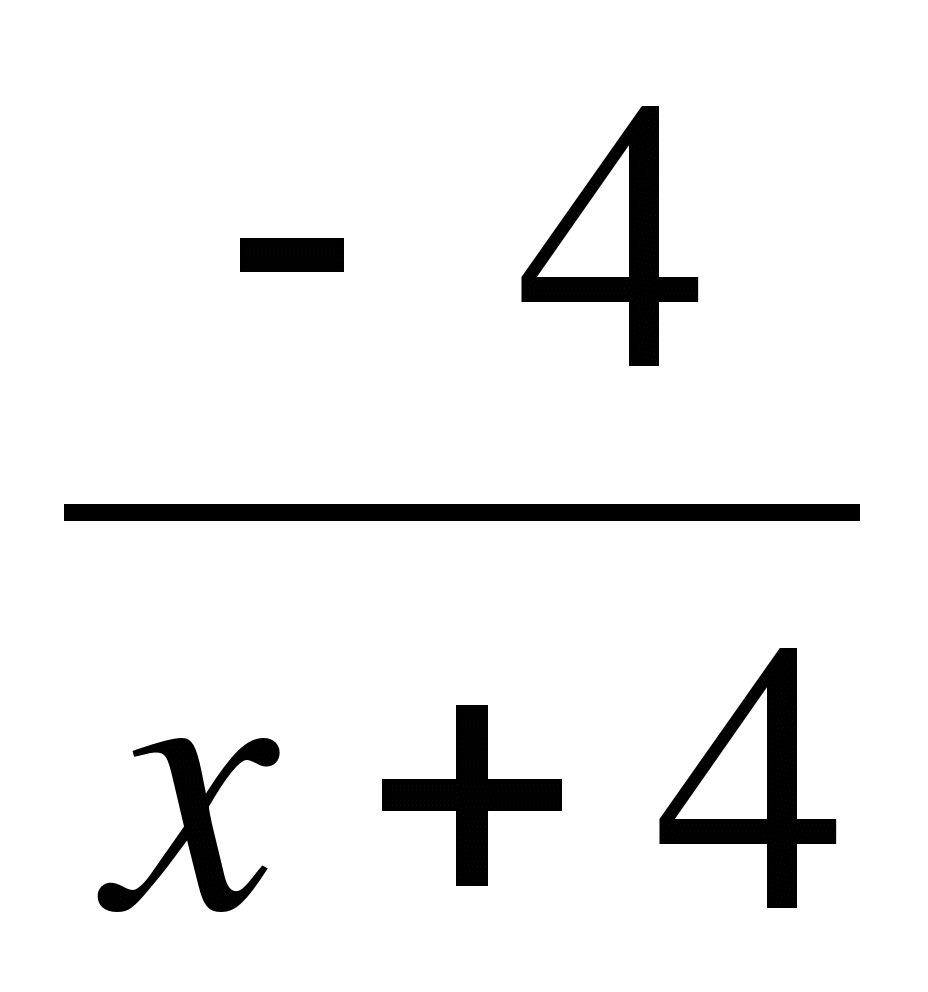 ;
;
х12+ х9- х4– х ≥ 0;
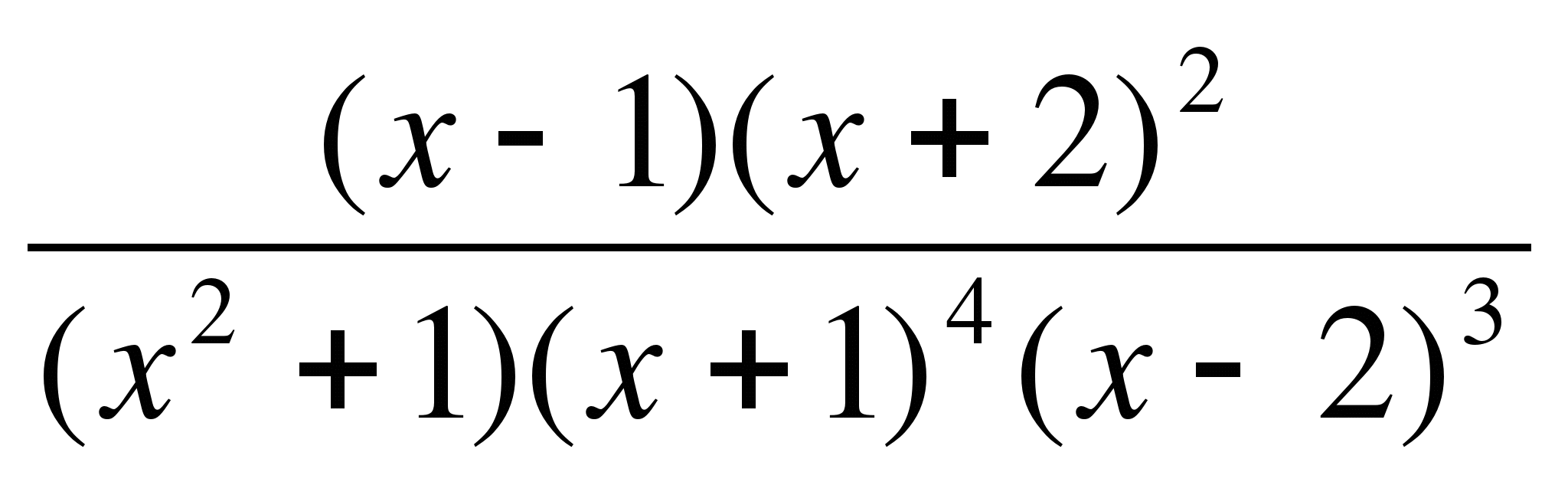 ≤ 0.
≤ 0.
8) 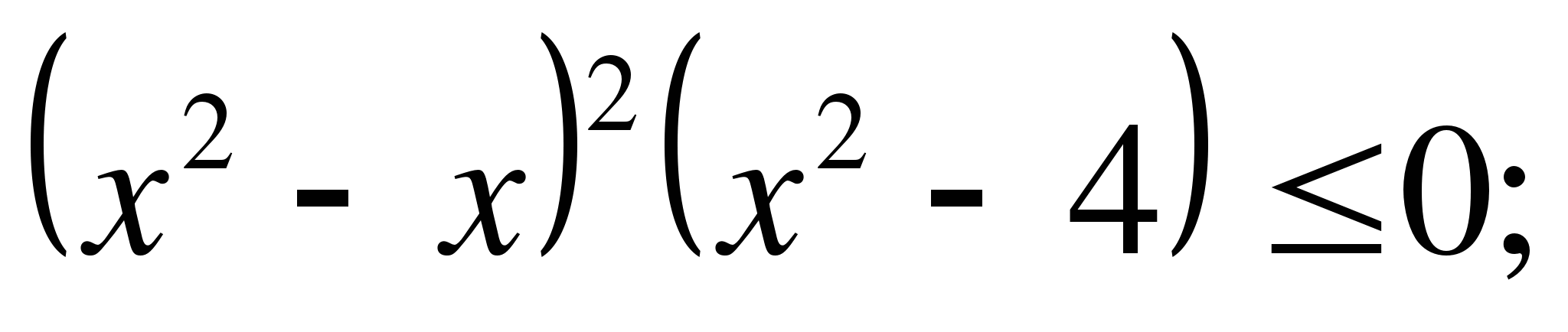
Дополнительное задание.
Найти все решения неравенств:
1) 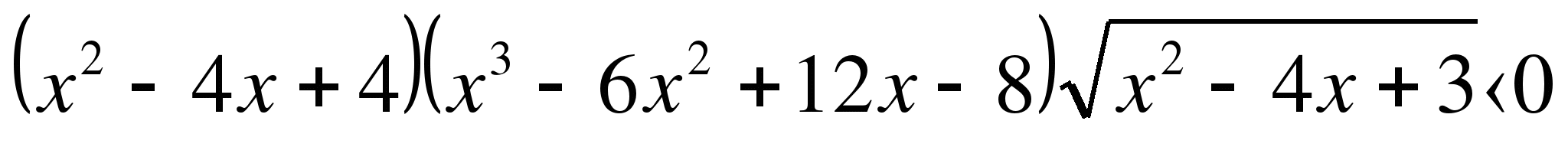 ;
;
2) 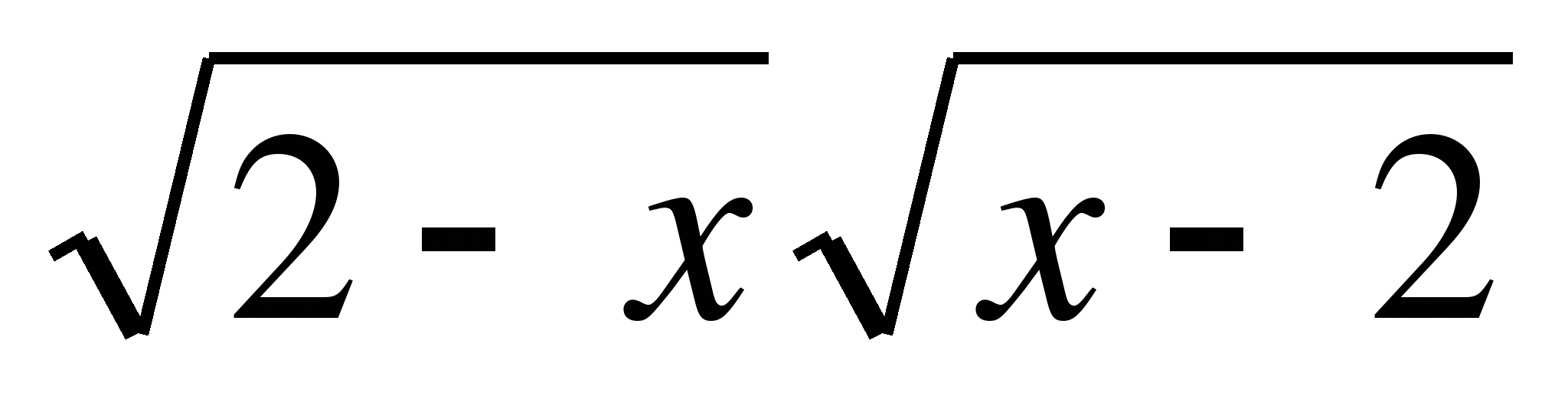
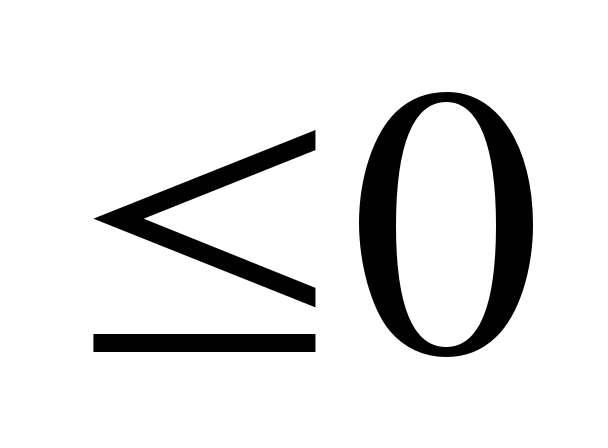 ;
;
3) 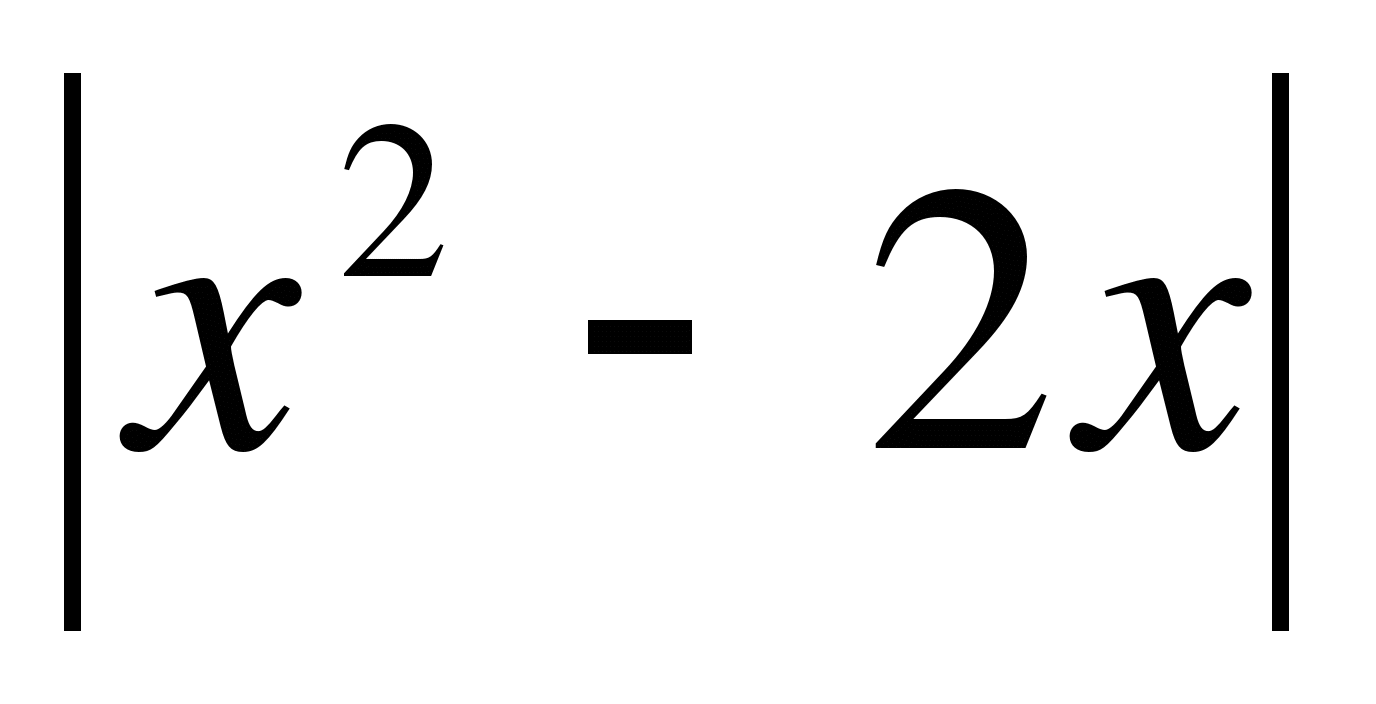 ≤ х;
≤ х;
4)(х+1)(х+2)(х+3)(х+5) >100.
Критерии оценки:
Оценка «5» ставится за любые семь верно решённых неравенств из обязательной части.
Дополнительное задание оценивается отдельно.
Административная контрольная работа по алгебре.
« Обобщённый метод интервалов ».
Вариант II.
Обязательная часть
Решите неравенства:
1)(х2-7х)(х+2)2≥ 0;
2)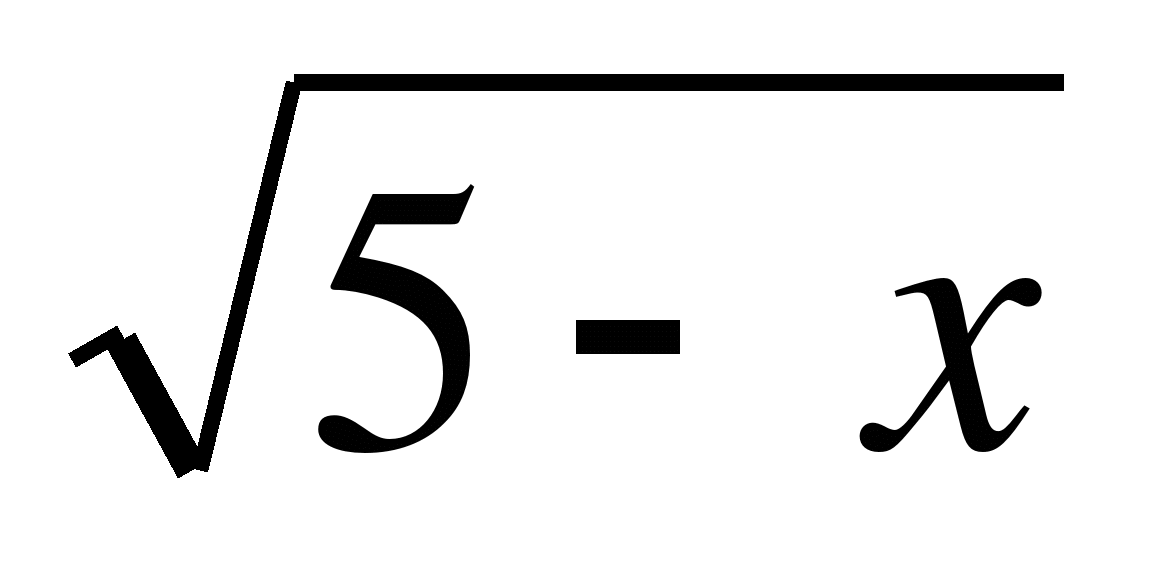 (х2-36) < 0;
(х2-36) < 0;
3)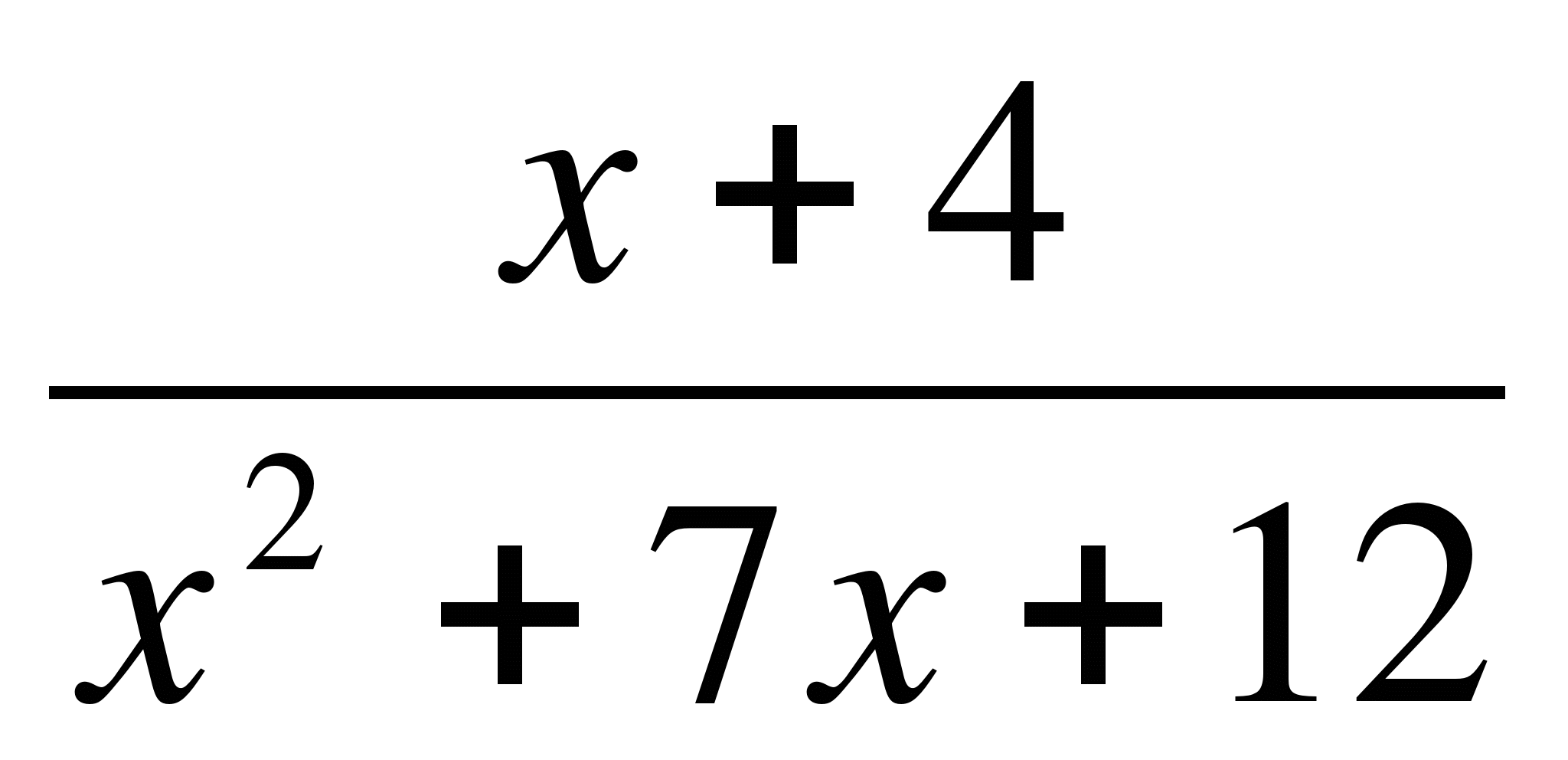 ≤ 1;
≤ 1;
4)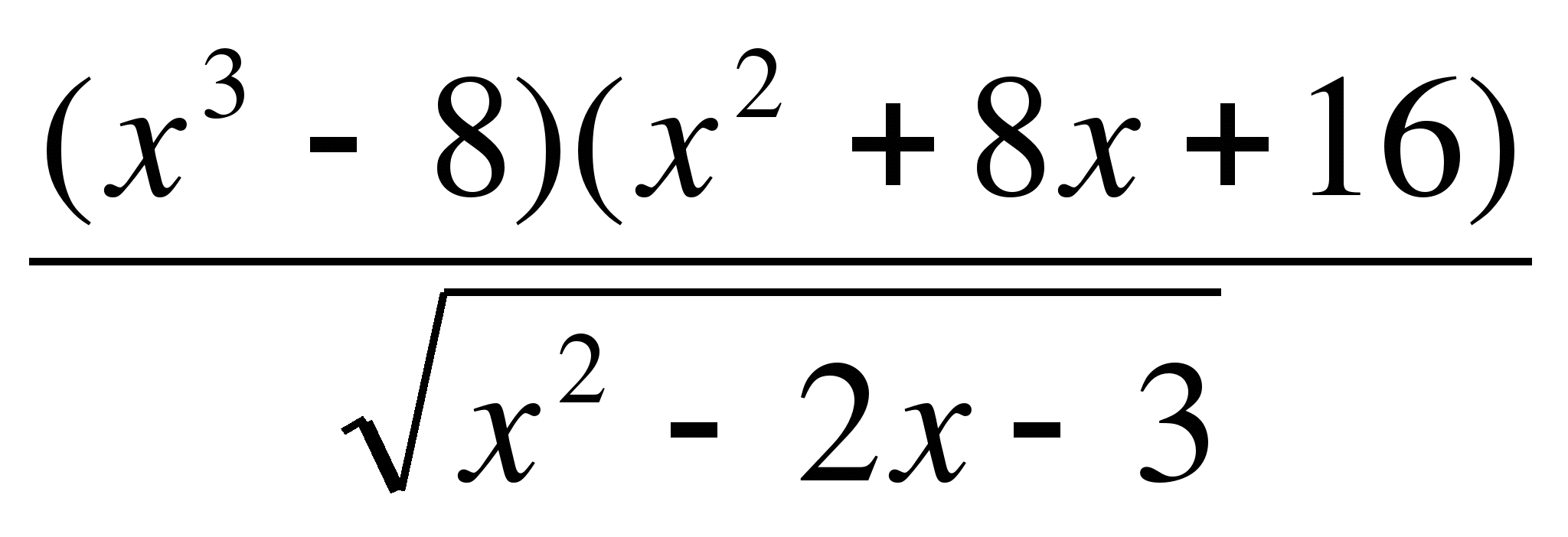 ≥ 0;
≥ 0;
5)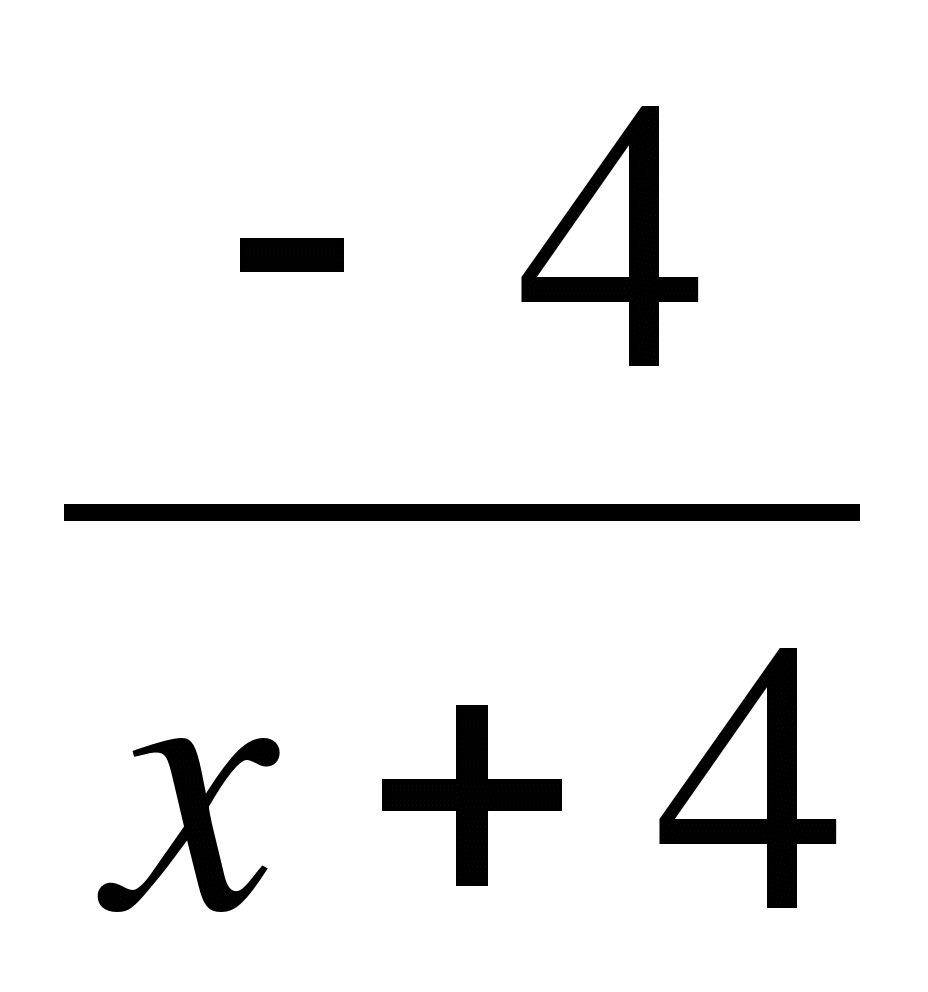 > х+2;
> х+2;
х12+ х9- х4– х ≥ 0;
7)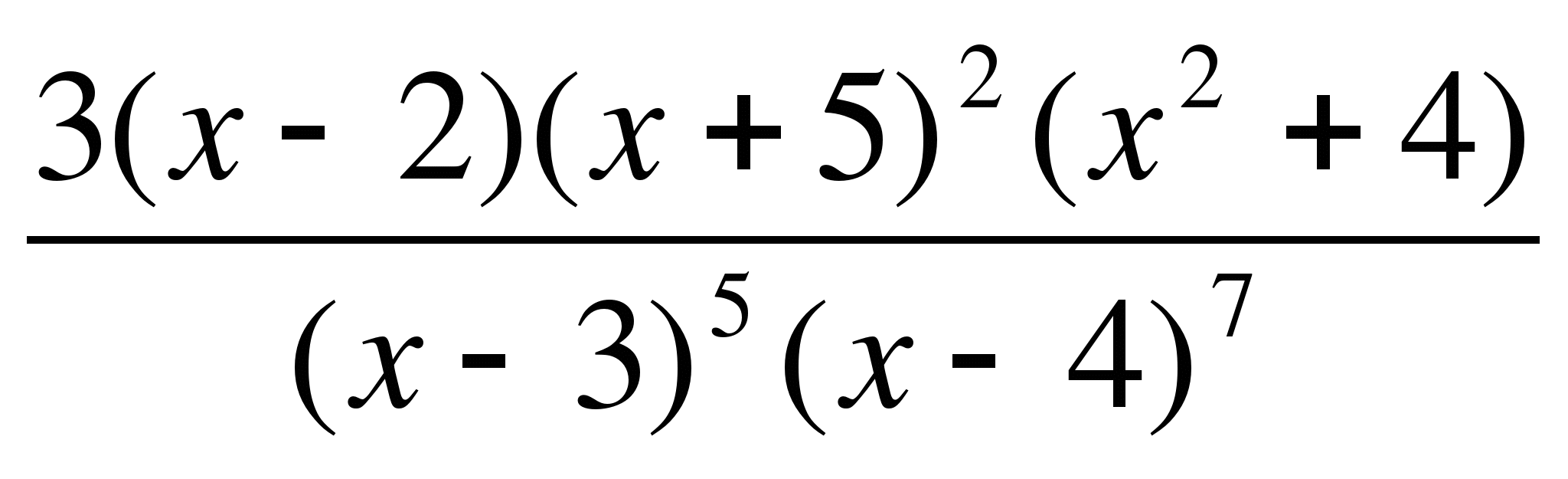 ≤ 0.
≤ 0.
8) 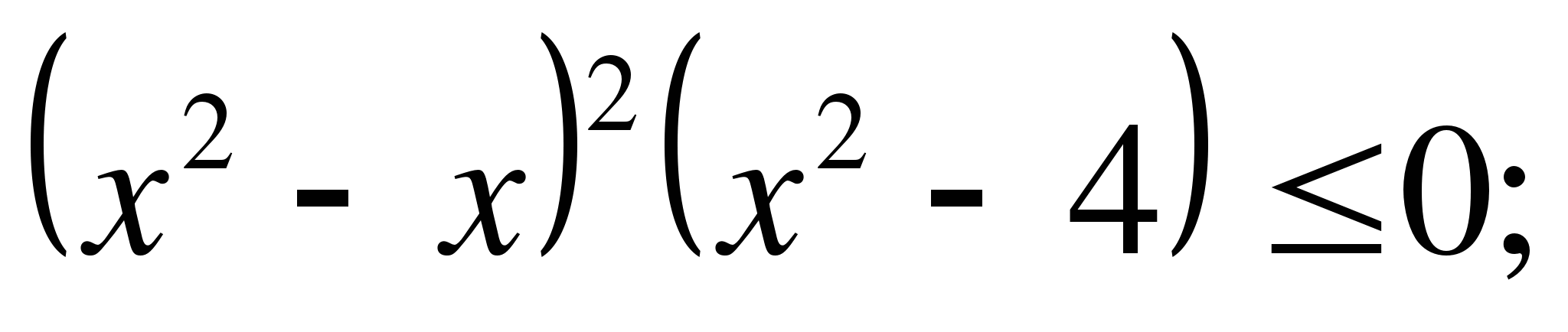
Дополнительное задание.
Найти все решения неравенств:
1) 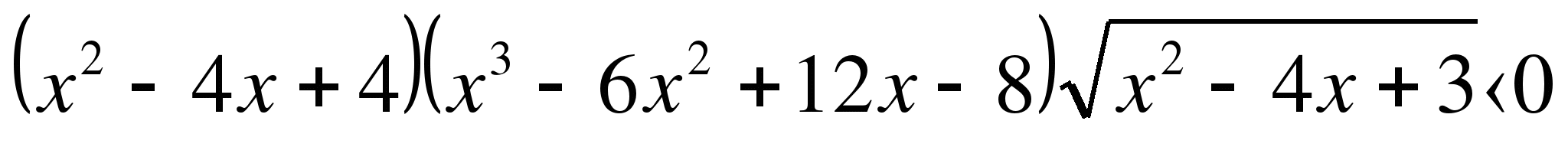 ;
;
2) 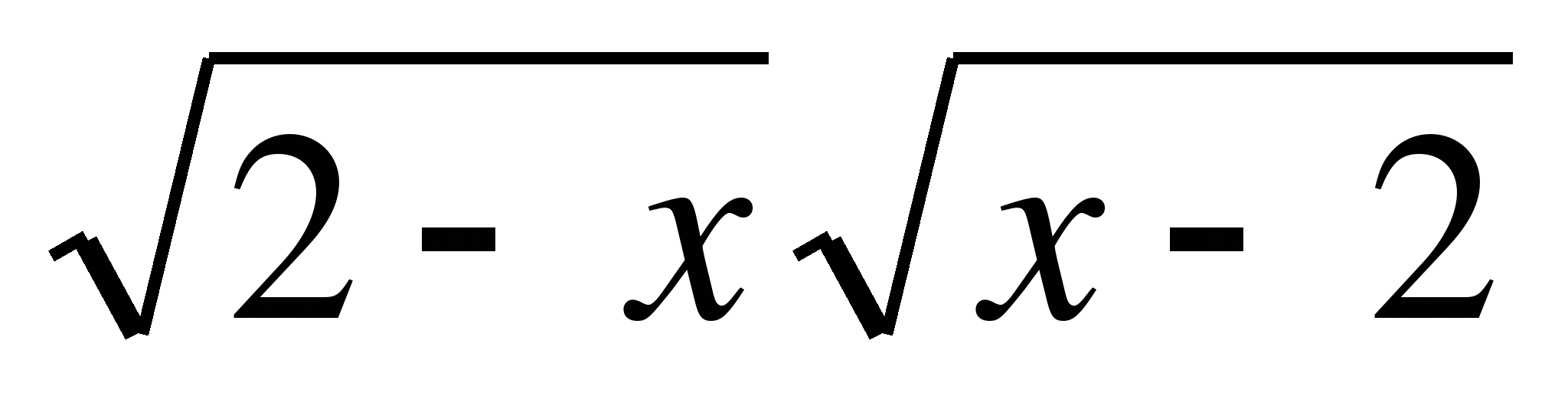
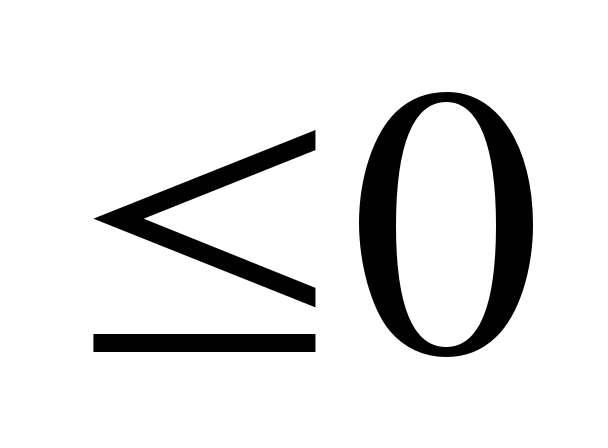 ;
;
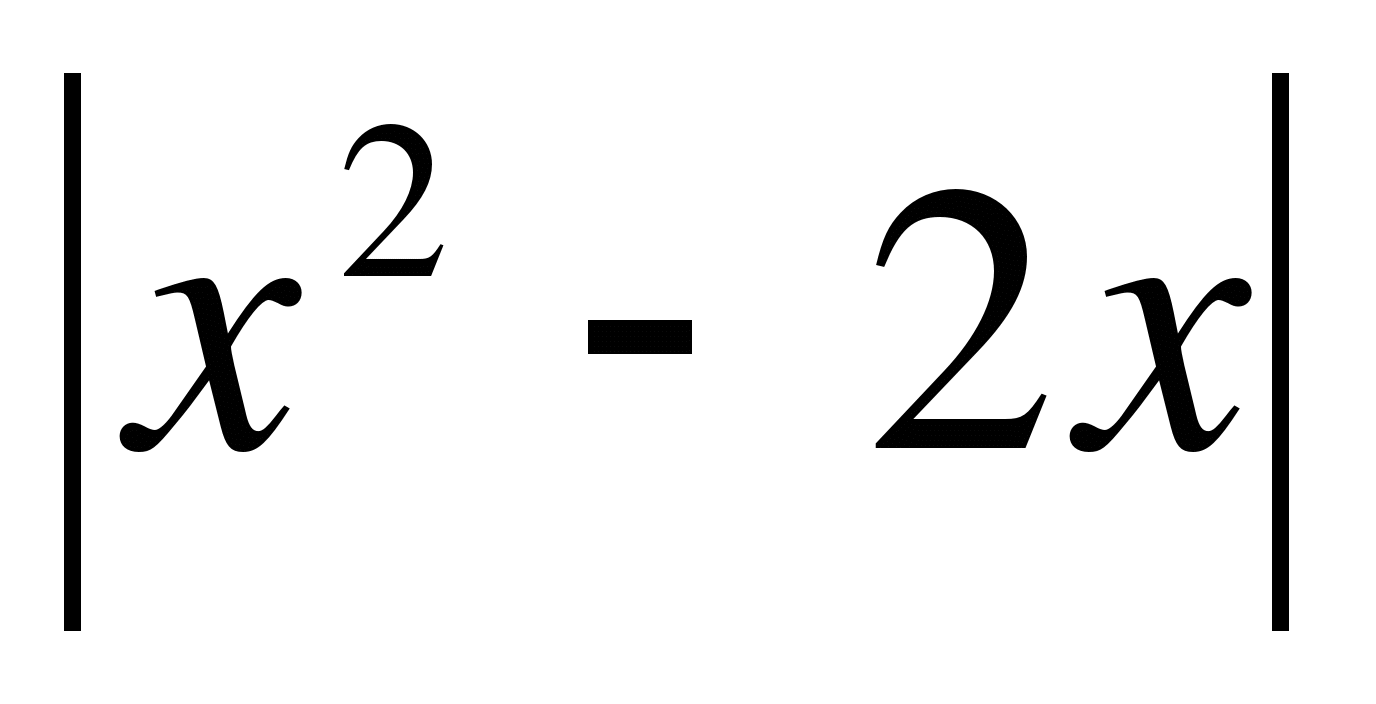 ≤ х;
≤ х;
(х+1)(х+2)(х+4)(х+5) <40.
Критерии оценки:
Оценка «5» ставится за любые семь верно решённых неравенств из обязательной части.
Дополнительное задание оценивается отдельно.
infourok.ru

Разделы: Математика, Конкурс «Презентация к уроку»
Загрузить презентацию (303 кБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
 ,
,  ,
,  ,
,  методом интервалов.
методом интервалов.Тип урока: комбинированный урок.
Методы обучения: объяснительно-иллюстративный, практический, частично-поисковый.
Формы обучения: коллективная, самостоятельная.
Технология: личностно-ориентированная.
Оборудование: компьютер, проектор.
(Слайд 1, 2)
«Ребята, вы уже умеете решать неравенства методом интервалов. Сегодня вы научитесь решать методом интервалов неравенства вида  ,
,  ,
,  ,
,  .
.
Домашнее задание ― разобрать пример №4 учебника. Кто готов объяснить решение этого неравенства?»
Один ученик выходит к доске и готовится.
(Слайд 3, 4)
Устные упражнения:
Разложить на множители.а) x2 − 16, б) x2 − 121, в) 3x − 48, г) 6x + 8x2, д) x2 − 5x + 6, е) x2 + 7x + 10.

Отвечает ученик, готовившийся у доски:
 ,
(x − 7)(x + 2)>0. Нули функции y = (x − 7)(x + 2): x = 7, x = −2.
,
(x − 7)(x + 2)>0. Нули функции y = (x − 7)(x + 2): x = 7, x = −2.

Ответ: (−∞; −2)∪(7; ∞)
«А будут ли равносильны неравенства: и (7 − x)(x + 2)≤0?» (Слайд 5)
и (7 − x)(x + 2)≤0?» (Слайд 5)
Учащиеся отвечают, что нет, так как число –2 является решением второго неравенства, но не является решением первого неравенства.
«Как записать равносильность?» (Слайд 6)

«Давайте решим это неравенство».
(x − 7)(x + 2)≥0. Нули функции y = (x − 7)(x + 2): x = 7, x = − 2

Ответ: (−∞; −2)∪[7; ∞)
Таким образом, строгие рациональные неравенства решаются переходом к равносильному неравенству, а не строгие ― переходом к системе, в которой нужно исключить значения переменной, при которой знаменатель обращается в нуль. (Слайд 7)
(Слайд 8)
1. Решить неравенство  .
.
Один ученик решает у доски, остальные учащиеся записывают решение в тетрадь.

(x − 2)(x + 6)≤0. Нули функции y = (x − 2)(x + 6): x = 2, x = −6.

Ответ: (−6; 2].
2. Решить неравенство .
.

Нули функции y = (x + 4)(x + 5)(x − 3): x = −5, x = −4, x = 3.

Ответ: (−5; −4) ∪(3; ∞)
(Слайд 9)
Тест по вариантам (см. Приложение 1). Учащиеся записывают ответы теста на двух листах, один лист сдают учителю, другой лист оставляют у себя для проверки. По истечении времени, отведенного на тест, учащимся предлагаются ответы для самоконтроля.
Учащиеся, справившиеся с тестом, получают задание для самостоятельной работы (см. Приложение 1). Не справившиеся с тестом учащиеся, работают вместе с учителем ― у доски решаются неравенства.
1.  .
Ответ: (−5; 2).
.
Ответ: (−5; 2).
2.  Ответ: (−∞;−2)∪(0; 3].
Ответ: (−∞;−2)∪(0; 3].
 .
Ответ: (−4;−3]∪(2; ∞].
.
Ответ: (−4;−3]∪(2; ∞].
Ответы самостоятельной работы учащиеся также выписывают на отдельном листе, который оставляют у себя, а работы сдают учителю для проверки. После сдачи работ учителю, учащиеся получают ответы для самоконтроля.
(Слайд 11)
Домашнее задание: П9, №202, №2.  .
.
Если осталось время урока, то учащимся можно предложить слайд с шутками на тему математики. (Слайд 12)
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Контрольная работа
Вариант 1
Решите неравенство:
а) х2-25≥0
б) х2+7х 0
в) х2-6х+7≤0
г) х2+4х+110
д) 

е) 
2. При каких значениях х имеет смысл выражение:

Решите неравенство:

Контрольная работа
Вариант 1
Решите неравенство:
а) х2-25≥0
б) х2+7х 0
в) х2-6х+7≤0
г) х2+4х+110
д) 

е) 
2. При каких значениях х имеет смысл выражение:

3. Решите неравенство:

Контрольная работа
Вариант 2
Решите неравенство:
а) х2-16≥0
б) х2-5х 0
в) х2-3х-4≤0
г) х2-3х+100
д) 

е) 
2. При каких значениях х имеет смысл выражение:

3. Решите неравенство:

Контрольная работа
Вариант 2
Решите неравенство:
а) х2-16≥0
б) х2-5х 0
в) х2-3х-4≤0
г) х2-3х+100
д) 

е) 
2. При каких значениях х имеет смысл выражение:

3. Решите неравенство:

multiurok.ru