
Государственное образовательное учреждение высшего профессионального образования «ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ» Кафедра «Теплотехника и теплосиловые
установки»
Контрольные работы №1 и №2
по теплотехнике и теплопередаче
| Шифр варианта | 21 | |||
| Выполнил студент | Харькин А. В. | |||
| Факультет | заочный | группа | 14ЛТк-351 | |
| Работу проверил | ||||
Санкт-Петебург 2016
Содержание
КОНТРОЛЬНЫЕ РАБ 3
КОНТРОЛЬНЫЕ РАБОТЫ №1, 2 3
Контрольная работа №1 3
Контрольная работа №2 6
СПИСОК ЛИТЕРАТУРЫ 7
КОНТРОЛЬНЫЕ РАБОТЫ №1, 2
Контрольная работа №1
Номер контрольных вопросов 10
В чём состоит содержание второго закона термоинамики?
Приведите основные формулировки этого закона (две формулировки).
Направленность процессов и условия их протекания устанавливаются в самом общем виде вторым законом термодинамики. Например химических реакций.
Второй закон термодинамики применительно к теплотехнике устанавливает условия, при которых превращение теплоты в механическую работу. При этом, должны соблюдаться количественные соотношения между теплотой и работой, вытекающие из первого закона
Теплота не может самопроизвольно переходить от менее нагретого тела к более нагретому без компенсации процесса затратой работы.
По Клаузису [1]. Теплота не может никогда сама собой переходить от тела с меньшей к телу с большей температурой (без компенсации).
Томсон (там же) сформулровал этот закон таким образом: «Невозможно осуществление цикла теплового двигателя без переноса некоторого количества теплоты от источника теплоты более высокой температуры к холодильнику более низкой температуры.
Задача
Для окисления топлива в цилиндры двигателя внутреннего сгорания всасывается 200 кг атмосферного воздуха в час при давлении В=745 мм рт. ст., температуре t и относительной влажности φ.
Какое количество воды всасывается двигателем в час?
| Таблица 1. Исходные данные к задаче 1 | |
| Дано: | Пояснение: |
| t=12˚С | Температура воздуха |
| φ=85% | Относительная влажность |
| B=745=99,33 кПа | Атмосферное давление |
| M=200 кг | Масса всасываемого воздуха за час. |
Для решения указанной задачи используется Id-диаграмма (рис. Рисунок) влажного воздуха. По заданным значениям t и φ находится влагосодержание d т. е. сколько водяного пара содержится в 1 кг сухого воздуха, а затем количество влаги, всасываемой в цилиндр двигателя с 200 кг воздуха в час.

Таким образом, вычислим количество всасываемой воды. Поскольку в одном килограмме сухого воздуха содержится 5,2 г влаги, то:
|
| (1) |
где v – количество (в граммах) водяного пара на 200 кг потребляемого двигателем в час воздуха.
Ответ: v=26,7 г.
Рисунок  2 – Общий вид id диаграммы
2 – Общий вид id диаграммы
Контрольная работа №2
1. Объясните физическую сущность трёх основных способов переноса теплоты.
Три основных способа передачи теплоты.
1. ТЕПЛОПРОВОДНОСТЬ.
Способ передачи теплоты за счет взаимодействия микрочастиц тела (атомов, молекул, ионов в электролитах и электронов в металлах) в переменном поле температур.
Температурным полем называется совокупность мгновенных значений температуры во всех точках рассматриваемого тела в данный момент времени. Если температура в любой точке тела с течением времени не изменяется и, следовательно, она является функцией только пространственных координат точки (x, y, z), то такое температурное поле называется установившимся или стационарным.
2. КОНВЕКТИВНЫЙ ТЕПЛООБМЕН.
Процесс передачи теплоты конвекцией происходит при движении жидкостей и газов, частицы которых могут перемещаться относительно друг друга или относительно поверхности твердого тела. Одновременно с теплообменом конвекцией происходит также теплообмен теплопроводностью. Этот совместный процесс переноса теплоты называется конвективным теплообменом.
3. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ.
способ передачи теплоты за счет распространения электромагнитных волн, согласно выводам Макса Планка.[2]
Задача
Определить температуру поверхности трубы с наружным диаметром d, если линейная плотность результирующего потока излучением от неё составляет q1, а интегральная степень черноты поверхности ε.
Температура окружающего воздуха tв=17
Диаметр трубы d=0.4
q1 = 13
ε = 0.5
Температура излучающей поверхности может быть найдена из следующего уравнения:
|
| (2) |
Где C0=5,67 – коэффициент излучения абсолютно черного тела, Вт/(м2К4).
Поскольку рассматривается закон Стефана-Больцмана, то теплоотдача Qл=ql
Ниже приведены расчёты:
|
|
Ответ: Температура стенки трубы T=293 К или t=293-273 = 20оС
СПИСОК ЛИТЕРАТУРЫ
1. Хазен М. М., Матвеев Г. А., Грицевский Ф. П., и др. «Теплотехника» стр. 49 // «Высшая школа 1981– 480 с.
2. Хазен М. М., Матвеев Г. А., Грицевский Ф. П., и др. «Теплотехника» стр. 164 // «Высшая школа 1981– 480 с.
studfiles.net
Контрольная работа № 1
Задача 6
До какой температуры будет нагрет углекислый газ  объемом
объемом  , если сообщить ему теплоту Q при постоянном, абсолютном давлении? Начальная температура газа
, если сообщить ему теплоту Q при постоянном, абсолютном давлении? Начальная температура газа  . Определить объем газа в конце процесса, а также удельные значения изменения внутренней энергии, энтальпии и энтропии в процессе. Теплоемкость принять не зависящей от температуры.
. Определить объем газа в конце процесса, а также удельные значения изменения внутренней энергии, энтальпии и энтропии в процессе. Теплоемкость принять не зависящей от температуры.
Дано:

 МПа
МПа
 МПа
МПа
Решение:
Определяем температуру конца процесса из формулы для количества теплоты в данном процессе:

где:  объем газа при нормальных условиях
объем газа при нормальных условиях

 - теплоемкость
- теплоемкость

 для двухатомного газа
для двухатомного газа

Определяем объем газа в конце процесса:


Определяем работу процесса:


Определяем изменение внутренней энергии процесса:


Определяем изменение энтальпии

 для двухатомного газа
для двухатомного газа

Определяем изменение энтропии


Задача 16
Определить теоретическую скорость адиабатического истечения и массовый расход воздуха из сужающегося сопла площадью выходного сечения  , если абсолютное давление перед соплом
, если абсолютное давление перед соплом  , а давление среды в которую вытекает воздух
, а давление среды в которую вытекает воздух  . Температура воздуха перед соплом
. Температура воздуха перед соплом  . Скорость воздуха на входе в сопло и потерями на трение пренебречь. Будет ли полное расширение в сопле, если при прочих равных условиях давление за соплом понизится до 400 кПа? Как при этом изменится расход и скорость истечения воздуха?
. Скорость воздуха на входе в сопло и потерями на трение пренебречь. Будет ли полное расширение в сопле, если при прочих равных условиях давление за соплом понизится до 400 кПа? Как при этом изменится расход и скорость истечения воздуха?
Дано:

 МПа
МПа
 МПа
МПа
Решение:
Записываем уравнение сплошности:

 - массовый расход газа кг/с;
- массовый расход газа кг/с;
 - скорость потока в рассматриваемом сечении м/с.
- скорость потока в рассматриваемом сечении м/с.

Так как


применяем формулу:

 м/с.
м/с.
 кг/с
кг/с
при понижении давление за до 400 кПа


 кг/с
кг/с
Расход и скорость газа в сопле увеличились
Задача 18
Влажный насыщенный водяной пар с начальным параметром  ,
,  дросселируется до давления
дросселируется до давления  . Определить состояние пара в конце процесса дросселирования и его конечные параметры, а также изменение его внутренней энергии и энтропии. Условно изобразить процесс дросселирования на h-s диаграмме.
. Определить состояние пара в конце процесса дросселирования и его конечные параметры, а также изменение его внутренней энергии и энтропии. Условно изобразить процесс дросселирования на h-s диаграмме.
Дано:



Решение:
Используем для определения конечных параметров h-s диаграмму
Таблица результатов h – s диаграммы
| Параметры | Р, МПа | t, К |
| h кДж/кг | S кДж/кг |
| 1 | 5 | 263 | 0,038 | 2273 | 5,9 |
| 2 | 0,3 | 160 | 0,48 | 2273 | 6,17 |
Определяем изменение внутренней энергии


Определяем изменение энтропии 

Задача 26
Одноступенчатый поршневой компрессор всасывает воздух в количестве V при давлении  и
и  и сжимает его до давления по манометру
и сжимает его до давления по манометру  . Определить секундную работу сжатия и теоретическую мощность привода компрессора для случаев изотермического, адиабатного и политропного процессов (с показателем политропы n = 1,2) сжатия. Определить температуру воздуха в конце адиабатного и политропного сжатия. Сделать вывод по данным процесса.
. Определить секундную работу сжатия и теоретическую мощность привода компрессора для случаев изотермического, адиабатного и политропного процессов (с показателем политропы n = 1,2) сжатия. Определить температуру воздуха в конце адиабатного и политропного сжатия. Сделать вывод по данным процесса.
Дано:

 МПа
МПа
Решение:
а) Изотермический процесс


Работа изотермического процесса:

Мощность:

 Вт
Вт
б) Адиабатный  при к = 1,4
при к = 1,4
Определяем температуру в конце сжатия





Мощность:
 Вт
Вт
в) Политропный процесс n = 1,2





Мощность:
 Вт
Вт


Вывод: наибольшей работой сжатия при данных условиях обладает изотермический процесс и соответственно он будет наиболее выгодный.
Контрольная работа № 2
Задача 2
По данным тепловых измерений средний удельный тепловой поток через ограждение изотермического вагона при температуре наружного воздуха  и температуру воздуха в вагоне
и температуру воздуха в вагоне  составил q. На сколько процентов изменится количество тепла, поступающего в вагон за счет теплопередачи через ограждение, если на его поверхность наложить дополнительный слой изоляции из пиатерма толщиной
составил q. На сколько процентов изменится количество тепла, поступающего в вагон за счет теплопередачи через ограждение, если на его поверхность наложить дополнительный слой изоляции из пиатерма толщиной  и с коэффициентом теплопроводности
и с коэффициентом теплопроводности  ?
?
Дано:



Решение:
Определяем из уравнения термическое сопротивление теплопередачи:


Так как в данном примере члены  и
и  постоянны выразим R
постоянны выразим R


Если на его поверхность наложить дополнительный слой изоляции из пиатерма, то


Подставляем:


Таким образом, количество тепла уменьшиться на

Задача 12
По трубе диаметром  мм, течет вода со средней скоростью
мм, течет вода со средней скоростью  . Температура трубы на входе в трубу
. Температура трубы на входе в трубу  средняя температура внутренней поверхности трубы
средняя температура внутренней поверхности трубы  . На каком расстоянии от входа температура нагреваемой воды достигнет
. На каком расстоянии от входа температура нагреваемой воды достигнет 
Дано:


Решение:
Средняя разность температур 
Если  , тогда
, тогда
 .
.

2. Движущая сила процесса теплопередачи:
 С
С
Физические константы нагреваемой жидкости:
 - коэффициент теплопроводности
- коэффициент теплопроводности
 - коэффициент теплоемкости
- коэффициент теплоемкости
 - кинематический коэффициент вязкости
- кинематический коэффициент вязкости
 - динамический коэффициент вязкости
- динамический коэффициент вязкости
Определяем среднее значение конвективной передачи использую следующие зависимости:


где:  критерий Рейнольдса
критерий Рейнольдса
 - Критерий Прандтля
- Критерий Прандтля

 - коэффициент температуропроводности
- коэффициент температуропроводности
Определяем Нуссельта

Отсюда: 
Удельная тепловая нагрузка со стороны нагреваемой жидкости

Ориентировочная площадь поверхности теплообмена:

Задаемся коэффициентом теплопередачи  из ряда
из ряда

Из формулы для поверхности теплообмена определяем длину трубы:
 м
м
Задача 19
Определить тепловой поток излучением и конвекцией от боковой поверхности цилиндра диаметром  и длиной
и длиной  , со степенью черноты
, со степенью черноты  в окружающую среду имеющую температуру
в окружающую среду имеющую температуру  , если температура поверхности
, если температура поверхности  , а коэффициент теплопередачи конвекцией
, а коэффициент теплопередачи конвекцией  . Каково значение суммарного коэффициента теплопередачи?
. Каково значение суммарного коэффициента теплопередачи?
Дано:



Решение:
Определяем тепловой поток конвекцией:


Определяем тепловой поток излучением:

 - излучательная способность абсолютно черного тела.
- излучательная способность абсолютно черного тела.

Суммарного коэффициента теплопередачи определяется по формуле:



Задача 24
В пароводяном рекуперативном теплообменнике с площадью поверхности F вода нагревается насыщенным паром с абсолютным давлением р. Температура воды на входе  , расход ее G = 1 кг/с. Определить конечную температуру нагрева воды
, расход ее G = 1 кг/с. Определить конечную температуру нагрева воды  , если коэффициент теплопередачи
, если коэффициент теплопередачи 
Дано:

Р = 0,6 МПа
Решение:
Уравнение теплового баланса:

Определяем температурный напор по формуле:

где  = 1 для прямоточной и противоточной схеме
= 1 для прямоточной и противоточной схеме
при давлении Р = 0,5 МПа температура греющего пара 
Предварительно принимаем конечную температуру 
 С
С
 С
С
Если  , тогда
, тогда

3. Расход теплоты на нагрев:

 кВт
кВт
Расход теплоты на нагрев:

где:  - теплоемкость воды.
- теплоемкость воды.
 кВт
кВт
Разность большая принимаем 
 С
С

 кВт
кВт
 кВт
кВт
Определяем разность найденных значений теплоты:

Выбранная конечная температура верна: 
topref.ru
1. Контрольная работа выполняется на листах формата А4. Вариант (шифр) задания даётся преподавателем каждому студенту на установочном занятии. Числовые значения исходных данных берутся из прилагаемых таблиц в соответствии с индивидуальным вариантом.
2. Выполнению контрольной работы должно предшествовать тщательное изучение соответствующих разделов курса.
3. Вычисление всех величин производится в развёрнутом виде с указанием всех используемых формул и единиц измерения тех величин, которые входят в формулу (точность расчёта до 0,001).
4. Графическая часть работы выполняется на миллиметровой бумаге с дополнительным расчётом двух-трёх промежуточных точек в каждом процессе между характерными точками цикла.
5. Ответы на контрольные вопросы должны быть прямыми и чёткими. Их необходимо сопровождать рисунками и схемами.
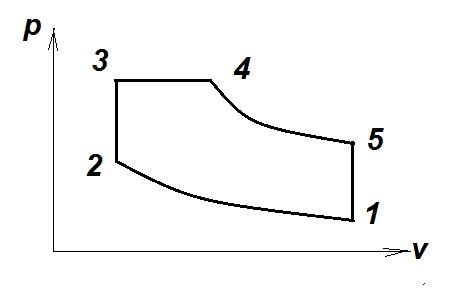
Рис. Схема цикла в координатах P,v.
Газовая трёхкомпонентная смесь, имеющая массовый состав m1,m2,m3(в кг), совершает в тепловом двигателе круговой процесс (цикл) по преобразованию теплоты в механическую работу. Значения параметров состояния смеси в отдельных точках цикла заданы в таблицах 1, 2, 3, 4.
Таблица 1. Состав газовой смеси
| Первая цифра шифра задания | Компоненты смеси mi, кг | ||||||||||
| O2 | N2 | CO | CO2 | Воздух | h3O | ||||||
| 0 | 7 | 2 | 5 | 3 | - | - | - | ||||
| 1 | 6 | - | - | - | 5 | 2,5 | 0,5 | ||||
| 2 | 8 | - | 5 | 1 | 3 | - | - | ||||
| 3 | 9 | - | 4 | - | 3,5 | - | 1,5 | ||||
| 4 | 5 | - | - | 1 | 4 | - | 3 | ||||
Таблица 2. Параметры состояния (точки 1 и 5)
| Вторая цифра шифра задания | P1, бар | T1, К | P5, бар | T5, К | |
| 0 | 4 | 1,4 | 370 | 4,8 | - |
| 1 | 5 | 2,5 | 300 | - | 935 |
| 2 | 6 | 3,0 | - | 3,0 | 1050 |
| 3 | 8 | - | 320 | 3,9 | 760 |
| 7 | 9 | 1,9 | 340 | - | 640 |
Таблица 3. Параметры состояния (точки 2 и 3)
| Третья цифра шифра задания | P2, бар | T2, К | P3, бар | T3, К | ||||
| 0 | 8 | 5,6 | 370 | 5,6 | - | |||
| 1 | 7 | 8,1 | 410 | - | 550 | |||
| 2 | 4 | 7,2 | - | 11,2 | 570 | |||
| 3 | 5 | - | 520 | 11,7 | 610 | |||
| 6 | 9 | 5,6 | 340 | 12,2 | - | |||
Таблица 4. Параметры состояния (точка 4)
| Четвёртая цифра шифра задания | T4, К | v4, м3/кг | |
| 0 | 7 | - |
|
| 1 | 8 | 935 | - |
| 2 | 9 | - |
|
| 3 | 5 | 810 | - |
| 4 | 6 | - |
|
Предполагается, что в цикле процессы:
(2-3) и (5-1) изохорные,
(3-4) – изобарный,
(1-2) и (4-5) – политропные.
Однако, при соответствующих значениях показателя политропы n (определяемых расчётом) эти процессы, в частном случае, могут оказаться изотермическими или адиабатными.
Если по условиям варианта P2=P3и (или)P5=P1, то в цикле отсутствуют, соответственно, процессы 2-3 и (или) 5-1.
studfiles.net
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Ухтинский государственный технический университет»
(УГТУ)
«Теплотехника»
Методические указания
УДК 621.1.01:536 (075.8)
М 69
Михайленко Е. В.
Методические указания к выполнению контрольной работы по дисциплине «Теплотехника» для студентов профиля Лесоинженерное дело направления 250400.62 Технология лесозаготовительных и деревообрабатывающих производств [Текст] / Е.В. Михайленко – Ухта: УГТУ, 2013. – 18 с.
Методические указания содержат контрольные задания и методику расчета задач для выполнения контрольной работы по дисциплине «Теплотехника» для студентов профиля Лесоинженерное дело направления 250400.62 Технология лесозаготовительных и деревообрабатывающих производств.
Содержание контрольных заданий соответствует рабочей программе.
Методические указания рассмотрены и одобрены заседанием кафедры теплотехники, теплогазоснабжения и вентиляции от 12 февраля 2013 пр. № 6.
Рецензент: Манжиков Анатолий Васильевич, доцент кафедры теплотехники теплогазоснабжения и вентиляции Ухтинского государственного университета.
Редактор: Артеева Л.В., доцент кафедры теплотехники теплогазоснабжения и вентиляции Ухтинского государственного технического университета.
В контрольных заданиях учтены предложения рецензента и редактора.
План 2013 г., позиция ____.
Подписано в печать ___________. Компьютерный набор Объем 18 с. Тираж 100 экз. Заказ № _____.
© Ухтинский государственный технический университет, 2013 169300, Республика Коми, г. Ухта, ул. Первомайская, д. 13.
Типография УГТУ.
169300, Республика Коми, г. Ухта, ул. Мира д. 3
Содержание
1.Состав контрольной работы…………………………………………………… 4
2.Задания и методические указания к выполнению контрольной работы ...… 5 Библиографический список……………………………………………………15
Приложение А…………………………………………………………………..16 Приложение Б…………………………………………………………………..17 Приложение В…………………………………………………………………..18
1. Состав контрольной работы
Целью контрольной работы является закрепление знаний полученных при изучении курса, а также проработка вопросов выделенных под самостоятельную работу студента.
Контрольную работу необходимо выполнить на листах формата А4 в печатном или рукописном варианте. Поля: слева - 3см, справа - 1см, сверху – 1,5 см, снизу – 2 см. Необходимо выполнить нумерацию страниц, расположение номера страницы – внизу по центру. Шрифт Times New Roman, размер – 14 кегль, начертание шрифта – обычный, междустрочный интервал – полуторный.
На титульном листе контрольной работы необходимо указать: название вуза, кафедры, учебной дисциплины, фамилию и инициалы студента, номер его зачетной книжки, курс, номер группы.
При оформлении задач полностью переписывается условие с выбранными числовыми данными. Производится расчет с указанием формул и расшифровкой входящих в них обозначений и указанием единиц международной системы (СИ).
Защита контрольной работы производится после возвращения ее преподавателем с пометкой «к защите».
2. Задания и методические указания к выполнению контрольной работы
Задача № 1
Определить газовую постоянную, кажущуюся молекулярную массу, плотность и удельный объем при нормальных условиях для смеси идеальных газов, объемное содержание которых задано.
Также определить количество теплоты для изобарного нагревания газовой смеси от t1 доt2, если задан общий начальный объем этой смесиVсм.
Исходные данные для расчета представлены в таблице 1.
Таблица 1 – Исходные данные к задаче № 1
| Последняя | P1, | Vсм, | t1, | t2, |
| Предпоследняя | Объемный состав |
| |||
| цифра |
|
| смеси |
|
| ||||||
| бар | м3 | °С | °С |
| цифра шифра |
|
|
| |||
| шифра |
|
|
|
|
|
| |||||
| N2 | O2 | h3 | CO2 |
| |||||||
|
|
|
|
|
|
|
| |||||
| 0 | 1 | 50 | 100 | 500 |
| 0 | 70 | 20 | 10 | - |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 | 3 | 60 | 200 | 600 |
| 1 | 70 | - | 10 | 20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 | 5 | 70 | 300 | 700 |
| 2 | 60 | 10 | - | 30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 3 | 7 | 80 | 400 | 600 |
| 3 | 50 | - | 10 | 40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 4 | 8 | 90 | 100 | 400 |
| 4 | 40 | 5 | - | 55 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 5 | 2 | 40 | 200 | 500 |
| 5 | 30 | 20 | - | 50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 6 | 4 | 30 | 300 | 600 |
| 6 | 20 | 10 | - | 70 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 7 | 6 | 20 | 400 | 700 |
| 7 | 50 | - | 5 | 45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 8 | 8 | 10 | 100 | 500 |
| 8 | 45 | 5 | 50 | - |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 9 | 10 | 100 | 200 | 600 |
| 9 | 10 | - | 20 | 70 |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
| Методика решения задачи № 1 |
|
|
|
|
| ||||
| Молекулярная масса природного газа μm , кмоль, определяется по урав- | |||||||||||
нению |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
| n |
|
|
|
|
|
|
|
|
|
|
| μmriμi, |
|
|
| (1) | ||
|
|
|
|
|
|
| i 1 |
|
|
|
|
|
где i − молекулярная масса компонентов смеси;
ri − молярная (объемная) концентрация компонентов смеси. Газовая постоянная смеси определяется по уравнению
см μm
Из уравнения Клапейрона при нормальных условиях tн.у = 0°C иРн.у = 0,1013 МПа определяем удельный объемvсм, м3/кг и плотность смесиρсм, кг/м3
v |
| RсмTн. у | , | (3) | |||
|
|
| |||||
см |
|
|
| Pн. у |
| ||
|
|
|
|
| |||
ρ |
|
| 1 | . | (3/) | ||
|
| ||||||
см |
|
| vсм |
| |||
|
|
|
|
| |||
Определяем количество теплоты Q, Дж, для изобарного нагревания массы газовой смеси отt1 доt2
|
|
| t2 |
|
| ||
Q mсм·cpm·(t2 | t1 ) . | (4) | |||||
|
|
| t1 |
|
| ||
Из уравнения Клапейрона определяем массу газовой смеси mсм, кг |
| ||||||
m |
| RсмTсм | . | (5) | |||
|
| ||||||
см |
|
| PсмVсм |
|
| ||
|
|
|
|
| |||
Температуру газовой смеси Тсм, °С определяем как среднее значение | |||||||
начальной t1, °С и конечнойt2,°С температур |
|
| |||||
T |
| t1t2 | . |
| (6) | ||
|
| ||||||
см | 2 |
|
|
|
| ||
|
|
|
|
| |||
|
|
| t2 |
|
| ||
Массовая изобарная теплоемкость смеси cpm , Дж/кг·К, в интервале температур
|
|
|
|
|
|
|
|
|
| t1 |
|
|
|
|
от t1 доt2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| t2 |
| t1 |
|
|
|
|
|
|
|
| t | 2 |
| c pm t2 | c pm t1 |
|
|
| ||
|
|
| c pm |
| 0 |
| 0 | , |
| (7) | ||||
|
|
|
| t2 | t1 |
| ||||||||
|
|
|
|
| t1 |
|
|
|
|
| ||||
|
| t1 | n |
|
|
| t1 |
| t2 | n |
| t2 |
| |
| с | pm | g | i | cpm | и с | pm | g | i | cpm. | (8) | |||
|
| i 1 |
|
|
| i |
| i 1 | i |
| ||||
|
| 0 |
|
|
| 0 |
|
| 0 |
| 0 |
| ||
t1 | t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
где cpm , | cpm − массовая изобарная теплоемкость смеси газа при начальной | |||||||||||||
0 | 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
температуре t1 и конечной температуреt2, Дж/кг·К; |
| |||||||||||||
t1 | t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
cpm | , cpm − с массовые изобарные теплоемкости компонентов смеси га- | |||||||||||||
i | i |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 | 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
за при начальной температуре t1 | и конечной температуре t2, Дж/кг·К (При- | |||||||||||||
ложение А) [2]; |
|
|
|
|
|
|
|
|
|
|
|
|
| |
gi − массовая концентрация компонентов смеси. |
| |||||||||||||
Массовая концентрация компонентов смеси определяется по уравнению
g | i |
| μi | r . | (9) |
| |||||
|
|
| i |
| |
|
|
| μm |
| |
Задача № 2
Газ массой m,кг, расширяется политропно, с показателем политропыn от начального состояния с параметрамиР1, МПа иt1, °С, до конечного давленияР2, МПа. Определить теплотуQ, Дж, работуL, Дж, изменение внутренней энергии ∆U, Дж, энтальпии ∆H, Дж, и энтропии ∆S, Дж, в процессе. Считать, что теплоемкость в процессе остается неизменной (сп = const).
Исходные данные для расчета представлены в таблице 2.
Таблица 2 – Исходные данные к задаче № 2
Последняя |
|
|
|
| Предпоследняя |
| Р1, |
| Р2, |
цифра | Газ | m, кг | n |
|
| t1, °С | |||
| цифра шифра |
| МПа | МПа | |||||
шифра |
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
0 | N2 | 10 | 1,0 |
| 0 |
| 0,2 | 10 | 0,8 |
|
|
|
|
|
|
|
|
|
|
1 | O2 | 20 | 1,1 |
| 1 |
| 0,4 | 15 | 2,0 |
2 | h3 | 30 | 1,2 |
| 2 |
| 0,6 | 20 | 3,0 |
|
|
|
|
|
|
|
|
|
|
3 | CO2 | 40 | 1,3 |
| 3 |
| 0,8 | 25 | 6,4 |
4 | N2 | 50 | 1,4 |
| 4 |
| 1,0 | 30 | 8,0 |
5 | O2 | 60 | 1,0 |
| 5 |
| 1,2 | 50 | 12,0 |
6 | h3 | 70 | 1,1 |
| 6 |
| 1,4 | 70 | 14,0 |
|
|
|
|
|
|
|
|
|
|
7 | CO2 | 80 | 1,2 |
| 7 |
| 1,6 | 100 | 16,0 |
8 | N2 | 90 | 1,3 |
| 8 |
| 1,8 | 120 | 18,0 |
9 | O2 | 100 | 1,4 |
| 9 |
| 2,0 | 140 | 20,0 |
|
| Методика решения задачи № 2 |
|
|
| ||||
Определяем количество теплоты Q1,2, Дж, для политропного нагревания | |||||||||
массы газа от t1 доt2 |
|
| Q mCn T2 T1 . |
|
|
| |||
|
|
|
|
|
| (10) | |||
Температуру газа в конечном состоянии Т2, °С, определяем из уравнения политропного процесса
7

|
|
|
|
| n 1 | |
|
|
| P |
| n |
|
T | T |
| 2 |
| (11) | |
| ||||||
2 | 1 |
| P |
|
|
|
|
|
|
|
|
| |
|
| 1 |
|
| ||
Теплоемкость политропного процесса Cn, Дж/кг·К определяем по формуле
где k − показатель адиабаты,k = 1,4.
Массовую изохорную теплоемкость Cvm, Дж/кг·К определяем из уравнения Майера
где Сpm − массовая изобарная теплоѐмкость газа, Дж/кг·К (Приложение А.1)[2];
R − газовая постоянная, Дж/кг·К.
Работу расширения политропного процесса L, Дж определяем по формуле
|
|
| T1T2 |
|
|
L | mR | . | (14) | ||
|
| ||||
|
|
| n 1 |
| |
Изменение внутренней энергии в процессе ∆U, Дж, определяем по фор-
муле
Изменение энтальпии в процессе ∆H, Дж, определяем по формуле
H mCvm T1 T2 . | (16) | ||||
Изменение энтропии в процессе ∆S, Дж, определяем по формуле |
| ||||
S mC |
| ln | T2 | . | (17) |
n |
| ||||
|
| T1 |
| ||
|
|
|
| ||
Задача № 3
1 кг воздуха совершает работу в цикле Карно при температурах верхнего t1 и нижнегоt3 источника тепла. Наивысшее давление составляетР1, а наинизшее –Р3. Определить параметры в характерных точках цикла, работу циклаlц, количество подведеннойq1 и отведеннойq2 теплоты и термический к.п.д. цикла (ηц). Показатель адиабаты для воздуха принять равнымk =1,41. Изобразить цикл наPv- иТs-диаграммах.
Исходные данные для расчета представлены в таблице 3.

Таблица 3 – Исходные данные к задаче № 3
Последняя |
|
| Предпоследняя |
|
| |
цифра | t1, °С | t3, °С | P1, МПа | P3, МПа | ||
цифра шифра | ||||||
шифра |
|
|
|
| ||
|
|
|
|
| ||
|
|
|
|
|
| |
0 | 600 | 25 | 0 | 5 | 0,10 | |
|
|
|
|
|
| |
1 | 700 | 24 | 1 | 5 | 0,11 | |
|
|
|
|
|
| |
2 | 800 | 23 | 2 | 7 | 0,12 | |
|
|
|
|
|
| |
3 | 900 | 22 | 3 | 8 | 0,13 | |
|
|
|
|
|
| |
4 | 1000 | 21 | 4 | 9 | 0,12 | |
|
|
|
|
|
| |
5 | 1100 | 20 | 5 | 10 | 0,11 | |
|
|
|
|
|
| |
6 | 1200 | 19 | 6 | 11 | 0,10 | |
|
|
|
|
|
| |
7 | 1300 | 180 | 7 | 12 | 0,12 | |
|
|
|
|
|
| |
8 | 1400 | 170 | 8 | 13 | 0,11 | |
|
|
|
|
|
| |
9 | 1500 | 160 | 9 | 14 | 0,10 | |
|
|
|
|
|
|
Методика решения задачи № 3
P |
| T |
|
1 | 2 | q=0 |
|
|
| ||
|
| 1 | 2 |
|
| 4 | 3 |
| 4 | 3 |
|
|
|
| S |
Рисунок 1. Цикл Карно на Pv- иТs-диаграммах
Прямой цикл Карно состоит из двух изотермических и двух адиабатных процессов. Определение параметров в характерных точках цикла будет опираться на расчетные уравнения, описывающие эти термодинамические процессы.
Определяем термодинамические параметры P, T, v в точке 1. Согласно условия задачи в данной точке известны давление и температура. Следовательно, необходимо определить удельный объем.
Удельный объем v1, м3/кг, определяем из уравнения Клайперона
|
|
|
|
|
| |
v | RT1 | . | (18) | |||
| ||||||
1 |
|
| P |
| ||
|
|
|
| |||
| 1 |
|
| |||
| 9 |
|
|
|
|
|

Характеристическую газовую постоянную R , Дж/кг, определяем из урав-
нения
|
|
| R | . | (19) | |
R | ||||||
|
| |||||
|
|
| μ |
| ||
Определяем термодинамические параметры P, T, v в точке 2. Так как процесс1-2изотермический (T=const), поэтомуТ2=Т1.
Процесс 2-3является адиабатным (q2,3=0), поэтомуР2, МПа находим из уравнения адиабатного процесса
|
|
|
|
|
|
|
|
|
|
| k |
|
|
|
| |
|
|
|
| T |
|
|
|
|
|
|
| |||||
| P |
|
| k 1 |
|
| ||||||||||
| 2 |
|
| 2 |
|
|
|
|
|
|
| , | (20) | |||
|
|
|
|
|
|
|
|
| ||||||||
| P3 |
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
| T3 |
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
| k |
|
|
|
| |
|
|
|
| T |
|
| k 1 |
|
|
|
| / | ||||
P P |
| 2 |
|
|
|
|
| . |
| 20 ) | ||||||
|
|
|
| |||||||||||||
2 | 3 |
|
|
|
|
|
|
|
|
| ||||||
|
|
|
| T3 |
|
|
|
|
|
|
|
| ||||
Удельный объем v2, м3/кг определяем из уравнения изотермического | ||||||||||||||||
процесса 1-2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| Pv P v , |
|
|
| (21) | |||||||||||
1 | 1 |
| 2 |
| 2 |
|
|
|
|
| ||||||
|
|
|
| Pv |
|
|
|
|
|
|
|
| / | |||
v |
| 1 1 |
| . |
|
|
|
|
| (21 ) | ||||||
|
|
|
|
|
|
|
|
|
|
| ||||||
2 |
|
| P2 |
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
Определяем термодинамические параметры P, T, v в точке 3. Согласно условия задачи в данной точке известны давление и температура. Следовательно, необходимо определить удельный объем.
Удельный объем v3, м3/кг, определяем из уравнения Клайперона
|
|
|
|
|
|
v | RT3 | . | (22) | ||
| |||||
3 |
| P3 |
| ||
|
|
| |||
Определяем термодинамические параметры P,T,v в точке 4. Так как процесс3-4изотермический (T=const), поэтомуТ4=Т3.
Процесс 4-1является адиабатным (q4,1=0), поэтомуР3, МПа находим из уравнения адиабатного процесса:
|
|
|
|
|
|
|
|
|
| k |
|
| |
| P |
|
| T |
|
|
|
|
| ||||
|
|
| k 1 | . | (23) | ||||||||
| 1 |
|
|
|
| 1 |
|
| |||||
| P4 |
|
|
|
|
|
|
|
| ||||
|
|
| T4 |
|
|
| |||||||
|
|
|
|
|
| P |
|
|
| . | / | ||
P4 |
|
|
|
| 1 |
|
|
| (23 ) | ||||
|
|
|
|
|
| k |
|
| |||||
|
|
|
|
| T |
| k 1 |
|
|
| |||
|
|
|
|
| 1 |
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
| T4 |
|
|
|
|
|
| |||
studfiles.net
Методические указания и задание
к контрольной работе
Контрольное задание должно выполняться студентом после изучения всегокурса дисциплины. Студенту выдается индивидуальное задание, согласно которому он должен решить две задачи. В каждой задаче исходные данные выбираются из соответствующих таблиц по последней и предпоследней цифре зачётной книжки студента. При выполнении задания необходимо соблюдать следующие требования:
На первой странице тетради привести в табличной форме исходные данные для решения каждой задачи согласно шифру - номеру зачетной книжки студента.
Обязательно перед решением записать условие задачи и содержание контрольного вопроса в тетрадь.
Решение сопровождать кратким пояснительным текстом, в котором должно быть указано: какая величина определяется и по какой формуле, какие величины подставляются в формулу (из условия задачи, из учебника, задачника, определена ранее и т.д.).
Вычисления давать в развернутом виде.
Обязательно проставлять размерности всех заданных и рассчитанных величин в международной системе СИ.
Графический материал должен быть выполнен четко, в масштабе и на миллиметровой бумаге, как исключение можно использовать бумагу в клеточку.
При изучении настоящего курса следует пользоваться литературой, которая приведена в программе дисциплины. Решение типовых задач можно найти в учебниках и задачниках. При использовании таблиц, формул и других справочных материалов, необходимо непосредственно при решении задачи указывать ссылку на литературный источник в квадратных скобках, например - [6].
После решения задачи должен быть произведен краткий анализ полученных результатов и сделаны соответствующие выводы
В конце работы дать перечень использованной литературы, указать дату окончания работы и подписать ее.
Задача 1. Смесь, состоящая из М1 кило-молей азота и М2 кило-молей кислорода с начальными параметрами p1 = 1 Мпа и Т1 = 1000 К расширяется до давления p2. Расширение может осуществляться по изотерме, адиабате и политропе с показателем n. Определить газовую постоянную смеси, ее массу и начальный объем, конечные параметры смеси, работу расширения и теплоту, участвующую в процессе.
Дать сводную таблицу результатов и анализ ее. Показать процессы в pv и Ts- диаграммах. Данные, необходимые для решения задачи выбрать из таблицы.
Указание. Показатель адиабаты, а следовательно, и теплоемкости Сp и Сv следует принять постоянными, не зависящими от температуры.
Таблица
| Последняя цифра шифра | М1 | М2 | Предпоследняя цифра шифра | p2, МПа | n |
| к-моль | |||||
| 0 | 0,1 | 0,9 | 0 | 0,43 | 1,2 |
| 1 | 0,2 | 0,8 | 1 | 0,40 | 1,3 |
| 2 | 0,3 | 0,7 | 2 | 0,35 | 1,5 |
| 3 | 0,4 | 0,6 | 3 | 0,33 | 1,6 |
| 4 | 05 | 0,5 | 4 | 0,31 | 1,7 |
| 5 | 0,6 | 0,4 | 5 | 0,47 | 1,1 |
| 6 | 0,7 | 0,3 | 6 | 0,54 | 0,5 |
| 7 | 0,8 | 0,2 | 7 | 0,57 | 0,8 |
| 8 | 0,9 | 0,1 | 8 | 0,62 | 0,7 |
| 9 | 0,5 | 0,5 | 9 | 0,66 | 0,6 |
Задача 2. Определить потребную поверхность рекуперативного теплообменника, в котором вода нагревается горячими газами. Расчет произвести для прямоточной и противоточной схем. Привести график изменения температур для обеих схем движения. Значения температур газа t1, и t1,,, воды t2, и t2,,, расхода воды М и коэффициента передачи К выбрать из таблицы:
Таблица
| Последняя цифра шифра | t1,,˚С | t1,,,˚С | t2,,˚С | t2,,,˚С | Предпоследняя цифра шифра | М, кг/с | К, Вт/(м2 К) |
| 0 | 300 | 150 | 10 | 80 | 0 | 1,4 | 30 |
| 1 | 325 | 175 | 15 | 80 | 1 | 1,3 | 32 |
| 2 | 350 | 200 | 20 | 100 | 2 | 1,2 | 34 |
| 3 | 375 | 225 | 25 | 110 | 3 | 1,1 | 36 |
| 4 | 400 | 250 | 30 | 120 | 4 | 1,0 | 38 |
| 5 | 425 | 275 | 25 | 130 | 5 | 0,9 | 40 |
| 6 | 450 | 300 | 20 | 140 | 6 | 0,8 | 42 |
| 7 | 475 | 325 | 15 | 130 | 7 | 0,7 | 44 |
| 8 | 500 | 350 | 10 | 120 | 8 | 0,6 | 46 |
| 9 | 525 | 375 | 20 | 110 | 9 | 0,5 | 48 |
studfiles.net
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РФ
Федеральное государственное бюджетное образовательное учреждение
Высшего профессионального образования
«Пермская государственная сельскохозяйственная академия
имени академика Д.Н. Прянишникова»
Кафедра Тракторы и автомобили
Контрольная работа
по дисциплине “Теплотехника”
Вариант № 23
Задание № 1: вопросы 2, 6,11, 21, 24; задача № 1.6 Задание № 2: вопросы 3, 8,13,18, 23; задача № 2.23 Задание № 3: вопросы 2, 7,13,16, 23; задача № 3.4 Задание № 4: вопросы 4, 9,13,19, 21; задача № 4.23 |
Выполнила: студентка 3-го курса
факультета заочного обучения
специальности «Безопасность
жизнедеятельности в техносфере»
Проверил:
Пермь 2012
СОДЕРЖАНИЕ | |
Задание 1 | Стр. |
Вопрос № 2…………………………………………………... | 2 |
Вопрос № 6……...………………………………………….... | 3 |
Вопрос № 11............................................................................. | 4 |
Вопрос № 21............................................................................. | 5 |
Вопрос № 24............................................................................. | 7 |
Задача 1.6................................................................................. | 7 |
Задание 2 | |
Вопрос № 3............................................................................... | 11 |
Вопрос № 8............................................................................... | 12 |
Вопрос № 13 ............................................................................ | 12 |
Вопрос № 18............................................................................. | 14 |
Вопрос № 23 ............................................................................ | 15 |
Задача 2.23............................................................................... | 17 |
Задание 3 | |
Вопрос № 2............................................................................... | 18 |
Вопрос № 7............................................................................... | 18 |
Вопрос № 13 ............................................................................ | 20 |
Вопрос № 16............................................................................. | 21 |
Вопрос № 23 ........................................................................... | 23 |
Задача 3.4.................................................................................. | 24 |
Задание 4 | |
Вопрос № 4............................................................................... | 27 |
Вопрос № 9............................................................................... | 28 |
Вопрос № 13 ............................................................................ | 29 |
Вопрос № 19............................................................................. | 30 |
Вопрос № 21 ........................................................................... | 32 |
Задача 4.23................................................................................ | 34 |
Список использованной литературы...................................... | 37 |
Задание № 1
2. Раскройте сущность понятия энергии и ее составляющих для термодинамической системы.
Понятие энергии неразрывно связано с материей. Все, что нас окружает, что воспринимается человеком и существует независимо от него – это материя. Необходимым условием существования материи является движение. И если масса служит количественной характеристикой материи, то энергия является физической мерой ее движения.
Э н е р г и я – это общая количественная мера движения и взаимодействия всех видов материи.
Энергию классифицируют по формам движения. Механической форме движения соответствует кинетическая энергия; соединению и разложению молекул – химическая энергия; перемещению электронов в проводниках – электрическая энергия и т.д. Такое разделение энергии на виды удобно для исследования и анализа явлений природы.
Совокупность материальных тел, которые находятся в тепловом и механическом взаимодействии одно с другим и с окружающими систему внешними телами (последние составляют окружающую среду), называют термодинамической системой. Всякая термодинамическая система обладает определенной энергией, которая, независимо от конкретных форм проявления, обозначается Е. За единицу энергии в СИ принят джоуль (Дж) – производная единица, определяемая через основные величины. Джоуль – это энергия, затраченная системой при перемещении точки приложения силы 1 Н на расстояние 1 м в направлении действия силы, т.е. 1 Дж = 1 Н ٠ 1 м .
Вычислить абсолютное значение энергии термодинамической системы невозможно, нет нуля отсчета энергии. Такое положение не играет существенной роли для практики, потому что при исследовании энергообмена важна не абсолютная величина энергии, а ее изменение. Для отдельных же форм энергии с целью количественной оценки их изменений в процессах устанавливается условное “начало отсчета”.
В общем случае энергия термодинамической системы Е включает в себя кинетическую энергию механического движения тела или тел внутри нее Ек , потенциальную энергию системы во внешнем поле (гравитационном, электромагнитном, сил давления) Еп и в н у т р е н н ю ю энергию (связанную с энергией микрочастиц тел, входящих в систему) Ев:
Е = Ек + Еп + Ев
В технической термодинамике, как правило, рассматривают неподвижную в окружающей среде термодинамическую систему, форма и размеры которой могут изменяться. Однако может иметь место и перемещение тел или тела внутри системы со скоростью с. В большинстве случаев гравитационной и электромагнитной составляющими потенциальной энергии пренебрегают. Существенной в таких системах будет потенциальная энергия в поле сил давления, которая выражается через объем и давление:
Еп = pV (1.4)
Величина pV представляет собой энергию, которую нужно было затратить для того, чтобы ввести тело объемом V во внешнюю среду, имеющую повсюду одинаковое давление p.
Внутреннюю энергию Ев в технической термодинамике обозначают U.
Таким образом, энергия системы, рассматриваемой технической термодинамикой, равна кинетической энергии, потенциальной энергии в поле сил давления и внутренней энергии:
Е = m + pV + U (1.5)
6. Запишите аналитическое выражение второго закона термодинамики и поясните величины, входящие в него.
Второй закон термодинамики устанавливает полноту преобразования теплоты в работу. Кроме того, он указывает на качественное различие между теплотой и работой. Если работа может вся без остатка преобразовываться в теплоту, то теплота никогда полностью не может быть преобразована в работу.
dQ = T×dS
Здесь: dQ – изменение теплоты, подведенной к системе;
T –температура, величина- необходимая, но еще не достаточная для того, что бы говорить о том, подводится тепло к системе или отводится от неё. Так, в адиабатном процессе система не обменивается теплотой с окружающей средой, а температура изменяется существенно. Остается один параметр, который должен обладать свойством достаточности, и этот параметр: dS – энтропия. Только по изменению энтропии можно судить о теплообмене системы с окружающей средой. Отсюда:
Энтропия есть калорический параметр состояния термодинамической системы, характеризующий направление протекания процесса теплообмена между системой и внешней средой.
Можно сказать, что энтропия – это единственная физическая величина, изменение которой в процессе однозначно указывает на наличие энергообмена в форме теплоты.
Данное аналитическое выражение второго закона термодинамики устанавливает как качественную, так и количественную связь между теплотой и энтропией: если изменяется энтропия тела или системы, то в том и другом случае подводится энергия в форме теплоты; если энтропия неизменна, то процесс протекает без энергообмена в форме теплоты, дает возможность установить единицу энтропии, которая равна Дж/К.
11. Дайте определение теплоемкости и поясните особенности теплоемкости газов.
Теплоемкость – термодинамическая величина, определяемая выражением:
С =
где ΔQ - количество теплоты, сообщенное системе и вызвавшее изменение ее температуры на ΔT. Отношение конечных разностей ΔQ/ΔТ называется средней теплоемкостью, отношение бесконечно малых величин dQ/dT - истинной теплоемкостью. Поскольку dQ не является полным дифференциалом функции состояния, то и теплоемкость зависит от пути перехода между двумя состояниями системы. Различают теплоемкость системы в целом (Дж/К), удельную теплоемкость [Дж/(г·К)], молярную теплоемкость [Дж/(моль·К)].
Кардинальным отличием понятия теплоемкости газа от теплоемкости жидких и твердых тел является то, что на величину теплоемкости газа специфическое влияние оказывает характер процесса, в котором она вычисляется. Так, в адиабатном процессе, где dQ = 0, теплоемкость равна нулю. В процессе с постоянной температурой (T = const) теплоемкость равна бесконечности (c = ± ∞). Теплоемкость газа, присущую тому или иному процессу, принято обозначать индексом, характеризующим конкретный процесс. Если теплоемкость определяется в процессе при постоянном давлении, то ее обозначают cp и т.д.
21. Поясните особенности распределения энергии в характерных группах термодинамических процессов.
Термодинамические процессы – это процессы расширения или сжатия рабочего тела, процессы подвода и отвода теплоты, процессы истечения газов и паров, процессы дросселирования, смешения и др.
Все реальные процессы изменения состояния системы, происходящие в различных теплотехнических устройствах, являются неравновесными и необратимыми процессами. В технической термодинамике реальные процессы заменяют равновесными обратимыми процессами. Реальные газы заменяют идеальным газом.
К основным термодинамическим процессам относятся: изохорный (V = const), изобарный (р = const), изотермический (Т = const) и адиабатный (dQ = 0).
Преобразование энергии происходит в процессах взаимодействия системы и внешней среды при непрерывном изменении состояния системы.
Для всех процессов изменение внутренней энергии определяется по формуле:
или при постоянной теплоемкости .
Работа изменения объема газа .
Количество теплоты, участвующее в процессе .
Адиабатный процесс.
Процесс, протекающий без подвода и отвода теплоты, т.е. при отсутствии теплообмена с окружающей средой, называется адиабатным. Для получения адиабатноого процесса необходимым и обязательным условием является
dQ и, следовательно, Q
Из первого начала термодинамики dQ = dU + dL для адиабатного процесса следует, что
dL = – dU
т. е. внешняя работа совершается за счет изменения внутренней энергии системы.
Изохорный процесс.
Процесс, протекающий при постоянном объеме, называют изохорным.
Если газ нагревается при постоянном объеме, то работа внешних сил равна нулю (dV = 0)) и сообщаемая газу извне теплота идет только на увеличение его внутренней энергии:
dQ = dU.
Изобарный процесс.
Процесс, протекающий при постоянном давлении, называют изобарным. Часть сообщенной теплоты dQ, равная р(V2 – V1), переходит в работу расширения, а другая часть идет на увеличение внутренней энергии тела.
Изотермический процесс.
Процесс, протекающий при постоянной температуре, называют изотермическим. В изотермическом процессе внутренняя энергия газа не меняется, т.е.
dU = 0.
24. Поясните, от чего зависит расход газа через сечение канала.
Если перемещение газа по каналу происходит его расширение с уменьшением давления и увеличением скорости, то такой канал называется соплом. Если в канале происходит сжатие рабочего тела с увеличением его давления и уменьшением скорости, то такой канал называют диффузором. В каналах при небольшой разности давлений газа и внешней среды скорость течения рабочего тела достаточно большая. В большинстве случаев длина канала небольшая и процесс теплообмена между стенкой и газом незначителен, поэтому процесс истечения газа можно считать адиабатным.
Скорость истечения (на выходе канала) определяется из уравнения:
w = w2 = v 2(h2 – h3) ,
или
w = v 2Ö/(g - 1)·P1·х 1 [1 – (P2/P1)(g-1)/g] ,
Массовый секундный расход газа, [кг/с]:
m = f·w/х 2 ,
где: f – площадь сечения канала на выходе. Так как процесс истечения адиабатный, то:
m = f·Ö 2g/(g - 1)·P1/х 1·[(P2/P1)2/g – (P2/P1)(g+1)/g].
Таким образом, массовый секундный расход идеального газа зависит от площади выходного канала, начального состояния газа и степени его расширения.
З а д а ч а
1.6 Воздух из начального состояния 1 (р1 = 4 МПа и t1 = 1600 0C) изохорно охлаждается до температуры t2 = 200 0C, а затем изотермически сжимается до состояния 3, в котором р3 = р1. Определить недостающие параметры состояния в точках 1, 2 и 3 и показать процесс 1-2-3 в pv и Ts – координатах.
Решение:
Процесс, протекающий при постоянном объеме, называется изохорным.
Дано:
р1 = р3 = 4 МПа
t1 = 1600 0C; Т1= 1600+273,15= 1873,15 К
t2 = 200 0C ; Т1= 200+273,15= 473,15 К
Rвозд= 287,1 Дж/кг∙К [1] табл. 4 стр.172
При постоянном объеме: сν = 717 Дж/кг∙К [4]
_________________________________________________________________________
ν1-?; ν 2-?; р2-?; Δsизх-?; Δsизт-?; qизх-?; qизт-?;
stud24.ru
Задачи 2. Рассчитать смешанный цикл двигателя внутреннего сгорания, т.е. найти параметры Р, v и t для характерных точек цикла, изменение внутренней энергии, энтальпии, энтропии, а также работу в отдельных процессах и цикле. Определить также степень предварительного расширения, степень повышения давления и термический КПД цикла. Параметры выбрать из табл. 2.
Исходные данные:
Qр = 1,05 кДж - количество теплоты, подводимой в изобарном процессе
= 0,001 м3 начальный объем
Qv = 0,65 кДж - количество теплоты, подводимой в изохорном процессе
- cредняя теплоемкость
- показатель адиабаты
- газовая постоянная
- степень сжатия
Решение:
1. Найдем параметры в характерных точках:
Точка 2
м3
МПа
Точка 3
Для определения температуры в третьей точке воспользуемся уравнением:
- степень повышения давления
МПа
Точка 4
МПа
Для определения температуры в четвертой точке воспользуемся уравнением:
степень предварительного расширения
Точка 5
МПа
= 0,001
С учетом найденных значений температур формула для КПД имеет вид:
Работа в изобарном процессе определяется по формуле:
Дж
Работа в изохорном процессе определяется по формуле:
Дж
Таблица результатов
| Точка | Р, МПа | Т, К | |
| 1 | 0,085 | 350 | 0,001 |
| 2 | 3,94 | 1047,6 | |
| 3 | 6,82 | 1812 | |
| 4 | 6,82 | 2725 | |
| 5 | 0,085 | 1068 | 0,001 |
Определяем изменение внутренней энергии процесса:
Определяем изменение энтальпии
Определяем изменение энтропии
Задача 3. Определить индикаторную и эффективную мощности (кВт) и производительность V м3/с одноцилиндрового поршневого компрессора по следующим данным: диаметр цилиндра D, ход поршня S, частота вращения вала компрессора п, среднее индикаторное давление , механический КПД компрессора = 0,85, коэффициент подачи = 0,75. Параметры выбрать из табл. 3.
Исходные данные:
D = 240 мм
S = 240 мм
n = 500 об/мин
МПа
Решение:
В одноступенчатом компрессоре степень повышения давления обычно не превышает:
Дальнейшее повышение давления приводит к чрезмерному росту температуры газа в конце сжатия, что вызывает ухудшение качества смазки цилиндров (вплоть до ее самовоспламенения).
В процессе нагнетания, когда поршень доходит до верхней мертвой точки, в цилиндре остается газ, занимающий объем между крышкой цилиндра и днищем поршня. Этот объем называется вредным. При обратном ходе поршня, прежде чем начнется всасывание очередной порции воздуха, происходит расширение газа, оставшегося во вредном объеме, до давления несколько ниже атмосферного. Только после этого откроется всасывающий клапан и, следовательно, свежая порция воздуха будет меньше рабочего объема цилиндра, описываемого поршнем. С увеличением давления сжатия р; эффективная часть хода поршня, соответствующая заполнению цилиндра новой порцией воздуха, уменьшается и, значит, снижается производительность компрессора.
1. Мощность привода идеального компрессора.
При одинаковых степенях повышения давления газа в каждой ступени, мощности привода каждой ступени одинаковы. Для расчета можно воспользоваться формулой:
(1)
кВт
м3
Расход воздуха определяется
Задача 4. Определить термический КПД цикла двигателя внутреннего сгорания с изобарным подводом теплоты, если начальное давление МПа, количество подведенной теплоты составляет , температура рабочего тела (воздуха) и конце сжатия , степень сжатия . Сжатие и расширение происходит по адиабатам.
Как изменится термический КПД цикла, если при том же общем количестве подведенной теплоты, часть , (в %) подвести по изохоре? Цикл изобразить в Р-V и Т-S диаграммах. Данные для решения задачи выбрать из табл. 4.
Исходные данные:
Решение:
1. Найдем параметры в характерных точках:
Точка 2 и 1
м3
м3
МПа
Точка 3
МПа
Для определения температуры в 3 точке воспользуемся уравнением:
степень предварительного расширения
Точка 4
МПа
= 0,11
Таблица результатов
| Точка | Р, МПа | Т, К | |
| 1 | 0,98 | 369 | 0,11 |
| 2 | 31,8 | 997 | 0,093 |
| 3 | 31,8 | 2180 | 0,02 |
| 4 | 2,95 | 1112 | 0,11 |
С учетом найденных значений температур формула для КПД имеет вид:
Если 24% тепла подводить по изохорном процессе
Количество теплоты МДж
Термический КПД при изохорном процессе
Термический КПД при изобарном процессе
Термический КПД при 24% вводе теплоты при изохоре
Таким образом, термический КПД системы уменьшился на 7,2 %
Задача 5. Поверхность нагрева состоит из плоской стальной стенки толщиной . По одну сторону стенки движется горячая вода, средняя температура которой , по другую - вода со средней температурой или воздух, средняя температура которого . Определить для обоих случаев удельный тепловой поток q Вт/м2 и коэффициент теплопередачи, а также значения температур на обеих поверхностях стенки. Найти изменение удельного теплового потока для первого случая, если с каждой стороны стальной стенки появится накипь толщиной в 1 мм. Коэффициенты теплопроводности стали = 45 Вт/(м-К), а накипи = 0,6 Вт/(м-К). Коэффициенты теплоотдачи для горячей воды к стенке для обоих случаев , от стенки к воде , а от стенки к воздуху . Параметры выбрать из табл. 5.
freepapers.ru