Контрольная работа по сопромату, тех.механике. Контрольная по сопромату
Контрольные работы по сопромату и гидравлике для ВУЗов с примерами решения задач.
Контрольные работы по сопромату с решениями
На этой странице приведены примеры выполнения контрольных работ по сопромату, прикладной механике и гидравлике для студентов технических специальностей Алтайского Государственного технического университета им. И. И. Ползунова (АлтГТУ).  Представленные варианты заданий выполнены с решениями и подробными пояснениями, т. е. выполняемые по приведенным примерам контрольные работы готовы к защите и сдаче.
По приведенным ниже ссылкам можно скачать варианты контрольных работ в формате Word с графиками, эпюрами и иллюстрациями.
Страничка будет особенно полезна студентам, обучающимся по заочной форме в качестве учебно-методического материала.
Представленные варианты заданий выполнены с решениями и подробными пояснениями, т. е. выполняемые по приведенным примерам контрольные работы готовы к защите и сдаче.
По приведенным ниже ссылкам можно скачать варианты контрольных работ в формате Word с графиками, эпюрами и иллюстрациями.
Страничка будет особенно полезна студентам, обучающимся по заочной форме в качестве учебно-методического материала.
Примечание: файлы (печатные документы, схемы, графики, иллюстрации), представленные по ссылкам с этой страницы, являются интеллектуальной собственностью автора, и не подлежат использованию в коммерческих целях.
Материалы, представленные для скачивания с этой странички, имеют целью ознакомить студентов технических специальностей с методикой решения контрольных заданий, поскольку методические указания, предлагаемые обучающимся соответствующими кафедрами ВУЗа, содержат сложные для понимания логические построения и пояснения, не всегда понятные студентам. Это нередко приводит к коррупционным действиям со стороны преподавателей, тьюторов и других работников ВУЗа и его филиалов, продающих студентам выполненные контрольные работы, причем, как правило, одни и те же варианты заданий (в том числе - и с этой странички).
Если сотрудники соответствующих кафедр АлтГТУ считают, что информация, представленная на этом сайте, затрудняет выдачу студентам контрольных заданий, вопрос решается достаточно просто - не следует в качестве контрольных заданий использовать варианты, представленные на этой страничке. Так, например, контрольная работа по Сопромату, предлагаемая для выполнения студентам в соответствии с Методическими указаниями, одобренными кафедрой прикладной механики в 2003 году, предусматривает возможность выделения 100 вариантов заданий, а на этой странице представлено лишь несколько из них.
Удалять ссылки не имеет смысла, поскольку заинтересованные лица, наверняка, уже скачали все файлы.
Скачивание файлов с контрольными работами совершенно бесплатно, не требуется никакой регистрации и других побочных процедур.
Рекомендация: если Вы хотите распечатать какой-либо вариант контрольной работы на принтере, необходимо сначала скачать файлы на компьютер, и лишь после этого отправить в печать. Если печатать непосредственно с браузера, возможно смещение текста, иллюстраций и графиков при печати.
Поскольку файлы представлены в формате Word, при скачивании вирусы Вашему компьютеру не грозят.
Здесь же можно скачать варианты контрольных работ по Гидравлике с примерами решения задач, поскольку методические указания для этой контрольной работы кафедра ВУЗа, как правило, студентам не представляет.
По этой ссылке можно изучить пример решения контрольной работы по Метрологии (в качестве примера приведен вариант 24).
Рассмотрены примеры решения задач по расчету подшипникового, резьбового и цилиндрического соединения, а также расчет нониуса штангенциркуля. Приведены примеры ответов на теоретические вопросы контрольного задания по метрологии.
***
Перечень задач, приведенных в контрольных работах
Задачи по сопромату и прикладной механике
Задача 1.1. Расчет стержня Условие задачи:
Стержень, жестко закрепленный одним концом, состоящий из трех участков длиной l1…l3, и площадью А1…А3, находится под действием собственного веса и силы F, приложенной на координате lF. Материал стрежня – сталь Ст.3.
Требуется:
Построить эпюры продольных сил N, нормальных напряжений σ и перемещений δ.
***
Задача 2.1. Расчет вала Условие задачи:
К стальному валу, состоящему из 4-х участков длиной l1…l4 приложено четыре сосредоточенных момента М1…М4.
Требуется: - построить эпюру крутящих моментов МКР;
- подобрать диаметр d вала из расчета на прочность;
- построить эпюру максимальных касательных напряжений τmax;
- построить эпюру углов φ закручивания вала;
- определить наибольший относительный угол Θmax закручивания вала.
***
Задача 4.1. Расчет балки Условие задачи:
На горизонтально расположенную балку, закрепленную на двух шарнирных опорах, действуют активные нагрузки М, F и q. Материал стержня – сталь Ст.3.
Требуется:
Построить эпюры поперечных сил QY и изгибающих моментов МX и подобрать сечение балки из расчета на прочность.
***
Задача 4.3. Расчет статически неопределимой балки Условие задачи:
На статически неопределимую балку, имеющую две опоры: жесткую заделку и шарнирно-подвижную опору, действуют внешние нагрузки: сила F и распределенная нагрузка q.
Требуется:
Определить опорные реакции, построить эпюры поперечных сил, изгибающих моментов и линейных перемещений.
***
Задача 5.3. Изгиб с кручением Условие задачи:
На валу круглого сечения, вращающемся с угловой частотой ω, расположены два шкива ременной передачи диаметрами D1 и D2, через которые передается мощность Nэд.
Вал закреплен в подшипниковых опорах А и В. Ветви первого шкива расположены под углом α1, а второго шкива – под углом α2 к горизонтали.
Требуется:
Подобрать диаметры вала по III теории прочности при заданном предельном напряжении [σ].
***
Задачи по гидравлике
Задача 1 Автоклав объемом 25,0 литров наполнен жидкостью и закрыт герметически. Коэффициент температурного расширения жидкости α, ее модуль упругости Е.Определить повышение давления ∆p в автоклаве при увеличении температуры жидкости на величину ∆Т.
Объемной деформацией автоклава пренебречь.
***
Задача 2 Определить скорость v равномерного скольжения прямоугольной пластины (a × b × c) по наклонной плоскости под углом α, если между пластиной и плоскостью находится слой масла толщиной δ. ***
Задача 3 Центробежный насос, перекачивающий жидкость при температуре t, развивает подачу Q.Определить допустимую высоту всасывания hв, если длина всасывающего трубопровода l, диаметр d, эквивалентная шероховатость ∆э, коэффициент сопротивления обратного клапана ζк, а показание вакуумметра не превышало бы р1.
***
Контрольные работы по сопротивлению материалов (прикладной механике) и гидравлике (примеры выполнения):
Скачать варианты заданий с решениями в формате Word по ссылкам:
***
Пример расчета вала на кручение
Сопротивление материалов
Методические указания
по вычерчиванию электрических схем
при выполнении контрольной работы по Инженерной графике
(архив ZIP, 4 Мб)
k-a-t.ru
Задание к контрольной работе по сопромату
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ПЕРМСКИЙ ИНСТИТУТ (ФИЛИАЛ)
федерального государственного бюджетного образовательного учреждения высшего профессионального образования
«Российский экономический университет им. Г.В. Плеханова»
Кафедра информационных технологий и математики
(название кафедры)
Одобрено кафедрой:
Протокол № 3
«6» ноября 2014_г.
Зав. кафедрой
Катанова Т.Н.
МЕХАНИКА
(название дисциплины)
Методические указания по выполнению контрольных работ для студентов заочной формы обучения
КОНТРОЛЬНАЯ РАБОТА ПО РАЗДЕЛУ «СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ»
Для специальности или (направления): 260800 Технология продуктов и организация общественного питания
Пермь 2014
КОНТРОЛЬНАЯ РАБОТА ПО РАЗДЕЛУ «СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ»
Расчетно-графическая работа «Растяжение и сжатие бруса».
Расчетные формулы











7
9
0




7
9
0




Пример решения задачи
Дана схема нагружения и размеры бруса до деформации. Брус защемлен, определить перемещения свободного конца.




Расчетно-графическая работа «Кручение. Расчеты на прочность и жесткость»
Расчетные формулы








Задание









Примеры решения задачи
Пример 1.
Для заданного бруса построить эпюры крутящих моментов, рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента. Построить эпюру крутящих моментов при рациональном расположении шкивов.

















Пример 2.


Расчетно-графическая работа «Расчет на прочность при изгибе»
Расчетные формулы




Задание
Для двухопорной балки, нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах. Найти максимальный изгибающий момент и, используя условия прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 Мпа. Сечение – швеллер.
При подборе сечения балки воспользоваться Приложением 1.


1
2
3
4
5
6
7
8
9
0


Пример решения задачи


















studfiles.net
Примеры решения задач по сопромату.
Решение задач по сопромату
Примеры решения задач по сопротивлению материалов
Как и в предыдущей статье, на этой странице приведены основные принципы решения задач технической механики на примере простейших заданий, в которых необходимо определить какие-либо силовые факторы, возникающие в конструкциях и телах напряжения, построить эпюры и т. п. Сопротивление материалов является базовой основой для решения вопросов наиболее практического раздела технической механики - "Детали машин".
Решение задачи на растяжение и сжатие Построить эпюру напряжений в ступенчатом круглом брусе, нагруженном продольными силами и указать на наиболее напряженный участок.
Весом бруса пренебречь.

Исходные данные:
Силы: F1 = 100 кН;F2 = 400 кН;
Площадь сечения бруса: А = 0,1 м2.
Решение:
При построении эпюры напряжений используем метод сечений, рассматривая отдельные участки бруса, как самостоятельные его элементы, находящиеся в состоянии равновесия под действием реальных и условных нагрузок. При этом исследование сечений начинаем со стороны свободного конца бруса, т. е. со стороны, где приложены известные нам силы.
Сначала разбиваем весь брус на однородные участки, границами которых служат точки приложения силовых факторов и (или) изменение размеров сечения. Для нашего бруса можно выделить три таких однородных участка - I, II, III (см. схему 2).
Для каждого из участков определяем нормальные напряжения в сечениях по формуле σ = F/A, где: F - величина продольной силы в сечении, А - площадь сечения. При этом следует учитывать знаки: если сила растягивающая, то ее условно считают положительной, если сжимающая - отрицательной. Соответственно, напряжения будут иметь такие же знаки, как и силы.
После подсчетов получим: σI = F1/A = -100×103/0,1 = -1000000 Па (-1 МПа), σII = F1/2A = -100×103/2×0,1 = -500000 Па (-0,5 МПа), σIII = (F2 - F1)/A = (400 - 100)×103/0,1 = 3000000 Па (3 МПа).
Построение эпюры напряжений начинаем с проведения линии, параллельной оси бруса (эта линия условно изображает брус и является нулевой ординатой графика эпюры). Затем, начиная от свободного конца бруса, откладываем от линии, как от нулевой ординаты, величины напряжений по каждому участку с учетом их знаков.
На брусе, приведенном в задании, величина напряжений в каждом сечении отдельных участков будет одинакова, и лишь в граничных (расположенных между соседними участками) сечениях появится скачок напряжения в виде ступени (здесь используется принцип Сен-Венана, условно полагающий, что в месте приложения нагрузки напряжение изменяется скачкообразно).
Построение эпюры завершается указанием на ее площадках знаков напряжения в кружках, проведением тонких линий перпендикулярно оси (нулевой ординаты) эпюры (эти линии условно изображают сечения бруса) и расстановкой величины напряжений на внешних углах графика (на внутренних углах цифровые обозначения не наносятся). Слева от эпюры указывается, что на ней изображено (в нашем случае - Эпюра σ)
В результате построений мы получим график (эпюру) распределения напряжений по каждому сечению бруса, визуальное исследование которого позволяет определить наиболее напряженный участок. Для бруса, представленного в задаче, максимальные напряжения возникают в сечениях участка III (см. схему). Поскольку эти напряжения положительны, они являются растягивающими
Задача решена.
***
Решение задачи с использованием закона Гука Определить величину растягивающей силы F, если известно, что под ее действием брус удлинился на величину ΔL.

Исходные данные:
Удлинение бруса ΔL = 0,005 мм;
Модуль продольной упругости балки Е = 2,0×105 МПа;
Площадь сечения бруса A = 0,01 м2;
Размеры бруса и точка приложения силы F приведены на схеме.
Решение:
Решить задачу можно, используя известную зависимость между линейными удлинениями и нагрузками (закон Гука).
Согласно закону Гука, представленному в расширенном виде:
ΔL = FL/(EA), откуда: F = (ΔLEA)/L.
Поскольку сила F приложена не к крайнему сечению бруса, а к его середине, то удлинился лишь участок между жесткой заделкой и сечением, к которому приложена растягивающая сила, имеющий длину L1 = 2 м.
Учитывая это, определяем силу, вызвавшую удлинение бруса (не забываем привести все величины к единицам системы СИ):
F = (ΔLEA)/L1 = (0,005×10-3×2×1011×0,01)/2 = 5000 Н = 5,0 кН.
Задача решена.
***
Решение задачи на срез и смятие Венец зубчатого колеса прикреплен к ступице болтовыми соединениями из шести болтов с гайками, размещенными равномерно по окружности диаметром D. Определить касательные напряжения сдвига (среза), действующие в каждом из болтов при номинальной нагрузке.
При расчете не учитывать ослабление стержня болта впадинами резьбы.
Определить касательные напряжения сдвига (среза), действующие в каждом из болтов при номинальной нагрузке.
При расчете не учитывать ослабление стержня болта впадинами резьбы.
Исходные данные:
Номинальный крутящий момент на валу шестерни: Мкр = 10 Нм;
Диаметр окружности, на которой размещены болтовые соединения D = 0,4 м;
Диаметр стержня болта d = 10 мм.
Решение:
Для решения задачи воспользуемся зависимостью между напряжением среза, внешней нагрузкой и площадью сечения по плоскости среза:
τср = Fокр /A,
где: τср - касательное напряжение среза, Fокр - окружная сила на расстоянии от оси вращения до центра болта, A - площадь сечения (в нашем случае - площадь поперечного сечения 6 болтов).
Окружную силу можно определить, зная крутящий (вращающий) момент на валу зубчатого колеса и расстояние от оси вращения зубчатого колеса до центра болта: Fокр = 2Мкр/D. Площадь сечения одного болта: А(1) = πd2/4, шести болтов: А = 3πd2/2 .
Подставив эти значения в исходную формулу, определим касательное напряжение сдвига (среза) болта:
τср = Fокр /A = (2Мкр/D) / (3πd2/2) = (2×10/0,4) / (3×3,14 0,012/2) ≈ 106 000 Па (или 0,106 МПа).
Задача решена.
***
Решение задачи на срез и смятие шпонки Произвести проверочный расчет призматической шпонки на смятие.

Исходные данные:
Вращающий момент на валу Т = 120 Нм;
Радиус сечения вала r = 30 мм;
Высота шпонки h = 6 мм;
Рабочая длина шпонки lр= 30 мм;
Допускаемое напряжение на смятие [σ]см = 200 МПа
Решение:
Решение задачи сводится к определению напряжения смятия, возникающего в продольном сечении шпонки, выступающем над канавкой вала (рабочая площадь шпонки). Это напряжение можно определить из формулы:
σсм = Fокр /Aраб (1)
где: σсм - искомое напряжение смятия, Fокр - окружная сила, действующая на рабочую поверхность шпонки: Fокр = Т/r.
Учитывая, что высота рабочей поверхности шпонки невелика, можно принять для расчета напряжения окружную силу, действующую на расстоянии r от оси вращения вала (радиус вала). Если необходимо выполнить более точный расчет, следует к радиусу вала прибавить половину высоты рабочей поверхности шпонки (в нашем случае - h/4).
Aраб - площадь шпонки, подвергаемая смятию: Aраб = hlр /2 (здесь lр - рабочая длина шпонки).
Подставив полученные значения окружной силы и площади шпонки, работающей на смятие, в формулу (1), получим:
σсм = Fокр /Aраб = (Т/r) / (hlр /2) = (120/0,03) / (0,003×0,03/2) = 88 900 000 Па (или 88,9 МПа).
Полученное напряжение сравниваем с допускаемым напряжением смятия [σсм] = 200 МПа, и делаем вывод, что шпонка выдержит нагрузку.
Задача решена.
***
Решение задачи на кручение Построить эпюру вращающих моментов для круглого однородного бруса, представленного на схеме. Указать наиболее нагруженный участок бруса и определить напряжение в его сечениях.

Исходные данные:
Вращающие моменты:Т1 = 150 Нм;Т2 = 400 Нм;Т3 = 50 Нм;
Диаметр бруса d = 0,05 м.
Решение:
Построение эпюр вращающих (крутящих моментов) начинаем со стороны свободного конца бруса, откладывая величины крутящих моментов от оси абсцисс (нулевой ординаты) бруса с соблюдением знаков моментов (см. схему).
Из эпюры очевидно, что максимальный крутящий момент возникает в сечениях участка I: Мкр = 500 Нм. Для определения напряжения (при кручении возникает касательное напряжение), воспользуемся зависимостью, полученной ранее:
τmax = Мкр / Wr ,
где: Wr ≈ 0,2d3 - момент сопротивления круглого сечения кручению (или полярный момент сопротивления круглого сечения).
Подставив полученные зависимости и их числовые значения в формулу, получим максимальное напряжение τmax, возникающее в сечениях участка I при кручении бруса:
τmax ≈ Мкр / 0,2d3 ≈ 500/0,2×0,053 ≈ 200 000 000 Па (или 200 МПа).
Задача решена.
С правилами и примерами построения эпюр при деформации кручения можно ознакомиться здесь.
***
Решение задачи на изгиб Определить максимальное нормальное напряжение, возникающее в сечении круглого бруса, расположенном рядом с жесткой заделкой, если к свободному концу бруса приложена поперечная сила F.
Вес бруса не учитывать.
 Исходные данные:
Исходные данные:Поперечная сила F = 1000 Н;
Длина бруса L = 5 м;
Диаметр бруса d = 0,1 м.
Решение:
Изгибающий момент силы F и возникающие в сечениях бруса напряжения зависят от расстояния между линией приложения (вектором) силы и плоскостью рассматриваемого сечения (очевидно, что величина изгибающего момента находится в прямо пропорциональной зависимости от расстояния до вектора силы). Поэтому для данного бруса изгибающий момент достигает максимального значения в сечении рядом с жесткой заделкой:
Миmax = FL = 1000×5 = 5000 Нм.
Максимальные нормальные напряжения в этом сечении можно определить по формуле:
σmax = Миmax / W,
где: W ≈ 0,1d3 - момент сопротивления круглого сечения изгибу (или осевой момент сопротивления круглого сечения). Подставив зависимости и их величины в формулу, получим:
σmax ≈ Миmax / 0,1d3≈ 5000/0,1х0,13 ≈ 50 000 000 Па (или 50 МПа).
Задача решена.
***
Решение задачи на изгиб с построением эпюр Построить эпюру поперечных сил и изгибающих моментов, действующих на защемленный одним концом брус (см. схему).

Исходные данные:
Поперечная сила F = 50 Н;
Распределенная нагрузка q = 10 Н/м;
Длина бруса L = 12 м;
Вес бруса не учитывать.
Решение:
Для построения эпюр определим границы участков бруса, в пределах которых внешние нагрузки и размеры сечений одинаковы. Для данного бруса можно выделить два таких участка (см. схему).
Далее, используя метод сечений, строим эпюру поперечных сил, учитывая знаки. Очевидно, что на первом участке поперечная сила будет постоянной во всех сечениях, и эпюра представляет собой горизонтальную линию, отстоящую от оси эпюры на величину -F (сила отрицательная).
В среднем сечении бруса начинает действовать распределенная нагрузка, которая линейно увеличивается и суммируется с поперечной силой F в каждом последующем сечении бруса по направлению к жесткой заделке. Поскольку эпюра поперечных сил на втором участке представляет собой отрезок наклонной прямой, то для ее построения достаточно определить величину поперечной силы в середине бруса (очевидно, что здесь F = 50 Н) и величину поперечной силы в сечении рядом с жесткой заделкой: F2 = -FL - 6q = -50 - 10×6 = -110 Н.
По полученным значениям строим эпюру поперечных сил F (см. схему).
Построение эпюры изгибающих моментов строится аналогично эпюре поперечных сил - при помощи метода сечений. При этом учитывается расстояние от сечения, в котором приложена поперечная сила, до рассматриваемого сечения (плечо силы).
Очевидно, что изгибающий момент от силы F будет увеличиваться прямо пропорционально по мере удаления от сечения, к которому она приложена, причем в крайнем сечении (где приложена сила) момент этой силы равен нулю (поскольку плечо силы равно нулю).
В среднем сечении бруса изгибающий момент достигает значения: Ми = FL/2 = -50×6 = -300 Нм .
Начиная с середины бруса начинает действовать изгибающий момент от распределенной нагрузки q, который в каждом сечении определяется, как произведение приведенной силы Fпр = ql на половину расстояния l (здесь l - расстояние от рассматриваемого сечения до начала действия распределенной нагрузки).
Очевидно, что по мере удаления от среднего сечения к жесткой заделке изгибающий момент от распределенной нагрузки q изменяется по квадратичной зависимости, и линия эпюры изгибающих моментов на втором участке представляет собой параболу.
Чтобы построить параболу недостаточно двух точек, необходимо определить величину изгибающего момента в нескольких сечениях бруса (на втором участке). При этом следует учитывать изгибающий момент от силы F, который суммируется с изгибающим моментом от распределенной нагрузки q на данном участке бруса.
Максимальной величины изгибающий момент достигает в сечении рядом с жесткой заделкой:
Миmax = - FL + [-q×(L/2)×(L/4)] = -50×12 + [-10×(12/2)×(12/4)] = -780 Нм.
Выполнив необходимые подсчеты, строим эпюру изгибающих моментов, начиная со свободного конца бруса (см. схему).
Задача решена.
***
Пример расчета бруса (стержня)
Сопротивление материалов
k-a-t.ru
Контрольная работа №2 по разделу «Сопротивление материалов»
Тема 2.2. Расчеты на прочность и жесткость при растяжении и сжатии
Знатьпорядок расчетов на прочность и жесткость, и расчетные формулы.
Уметь проводить проектировочные и проверочные расчеты на прочность и жесткость при растяжении и сжатии.
Необходимые формулы
Нормальное напряжение:
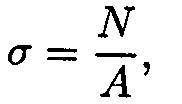
гдеN- продольная сила; А - площадь поперечного сечения.
Удлинение (укорочение) бруса:
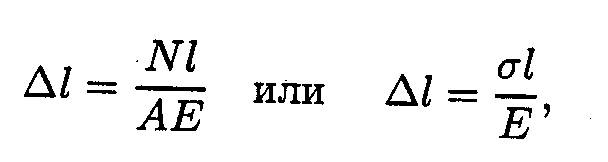
Е-модуль упругости; l - начальная длина стержня.
Допускаемое напряжение:
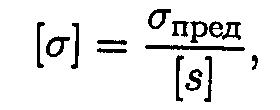
[s] - допускаемый запас Прочность
Условие прочности при растяжении и сжатии:
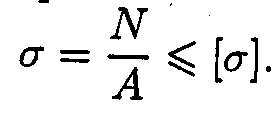
Примеры расчетов на прочность и жесткость
Пример 1.Груз закреплен на стержнях и находится в равновесии (рис. П6.1). Материал стержней - сталь, допускаемое напряжение 160 МПа. Вес груза 100 кН. Длина стержней: первого - 2 м, второго - 1 м. Определить размеры поперечного сечения и удлинение стержней. Форма поперечного сечения - круг.
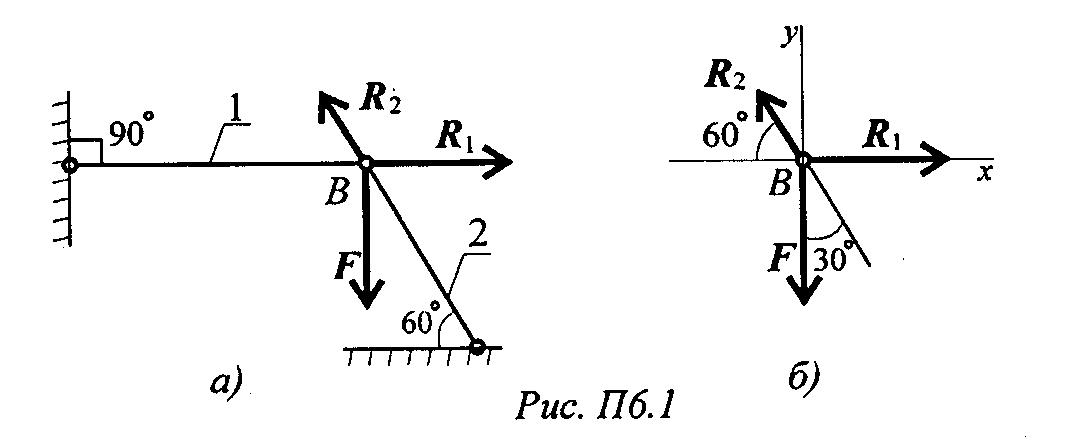
Решение
1. Определить нагрузку на стержни. Рассмотрим равновесие точки В, определим реакции стержней. По пятой аксиоме статистики (закону действия и противодействия) реакция стержня численно равна нагрузке на стержень.
Наносим реакции связей, действующих в точке В. Освобождаем точку В от связей (рис. П6.1).
Выбираем систему координат так, чтобы одна из осей координат совпала с неизвестной силой (рис. П6.1б).
Составим систему уравнений равновесия для точки В:
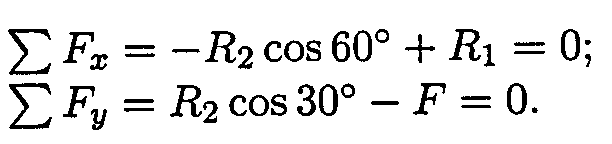
Решаем систему уравнений и определяем реакции стержней.
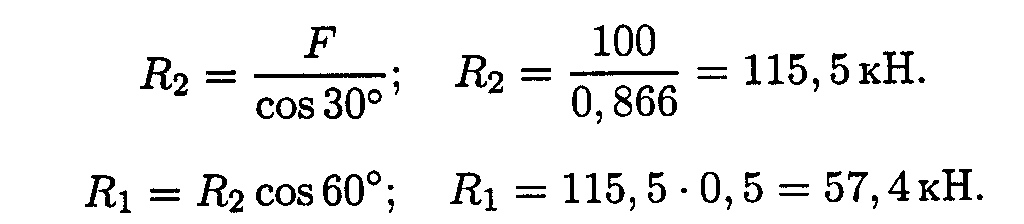
Направление реакций выбрано, верно. Оба стержня сжаты. Нагрузки на стержни:F1 = 57,4 кН; Р2 = 115,5 кН.
2. Определяем потребную площадь поперечного сечения стержней из условий прочности.
Условие прочности на сжатие: 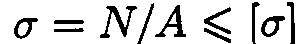
откуда 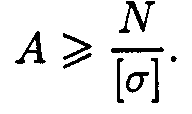
Стержень 1 (N1 = Рl):
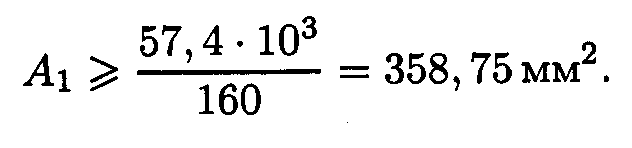
Для круга
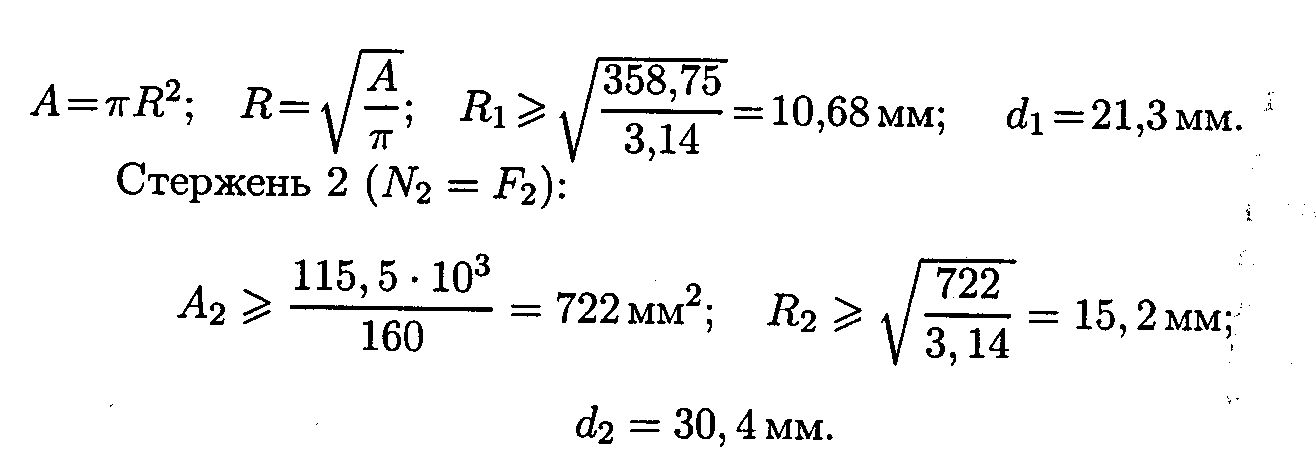
Полученные диаметры округляем.
3. Определяем удлинение стержней
Укорочение стержня 1:
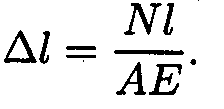
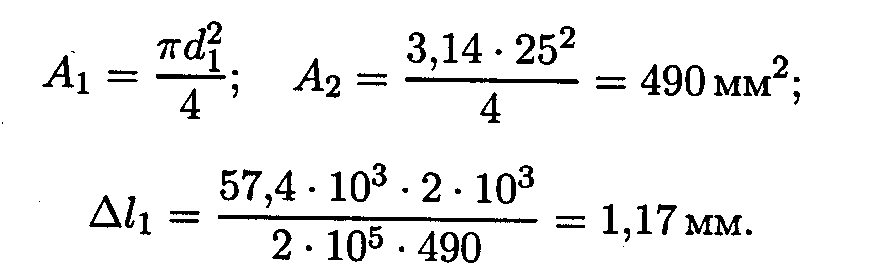
Укорочение стержня 2:
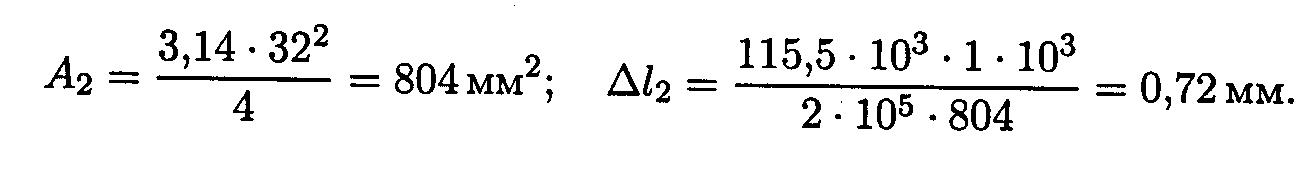
Пример 2.Однородная жесткая плита с силой тяжести 10 кН, нагруженная силой F = 4,5кН и моментом т = 3КН'м, оперта в точке А и подвешена на стержне Ее (рис. П6.2). Подобрать сечение стержня в виде швеллера и определить его удлинение, если длина стержня 1 м, материал - сталь, предел текучести 570 МПа, запас прочности для материала 1,5.
Решение:
1. Определить усилие в стержне под действием внешних сил. Система находится в равновесии, можно использовать уравнение равновесия для плиты:
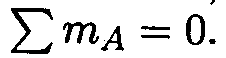
RB - реакция стержня реакции шарнира А не рассматриваем,
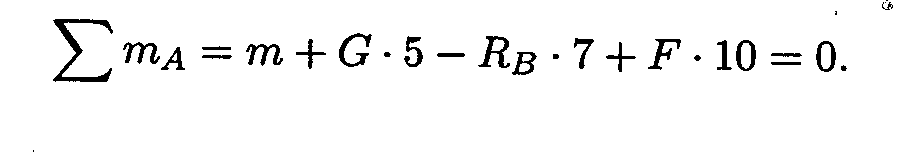
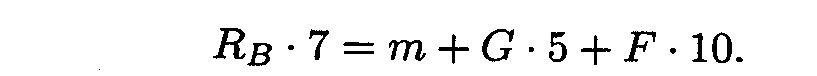
Откуда
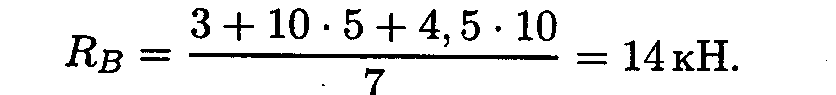
По третьему закону динамики ре акция в стержне равна силе, действующей от стержня на плиту. Усилие в стержне равно 14кН.
2. По условию прочности определяем потребную величину площади попе речного сечения: 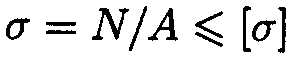
откуда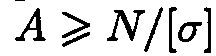
Допускаемое напряжение для материала стержня
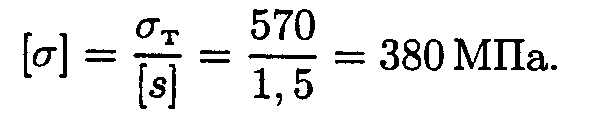
Следовательно,
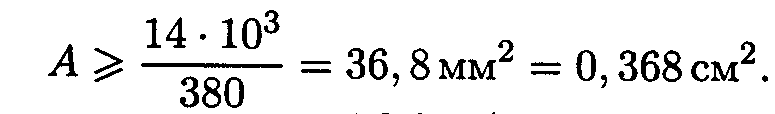
3. Подбираем сечение стержня по ГОСТ (Приложение 1). Минимальная площадь швеллера 6,16 см^2 (№ 5; ГОСТ 8240-89). Целесообразнее использовать равнополочный уголок № 2 (d = 3 мм), площадь поперечного сечения, которого 1,13 см^2 (ГОСТ 8509-86)
4. Определить удлинение стержня:
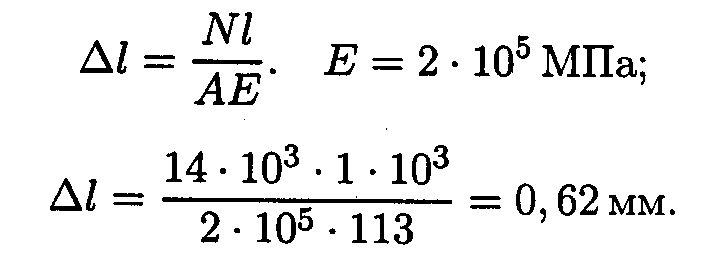
Задание 1.Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить перемещение свободного конца бруса. Двухступенчатый стальной брус нагружен силами Р1, Р2; РЗ· Площади поперечных сечений А1 и А2.
Принять 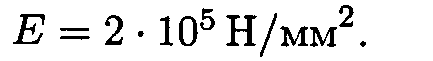
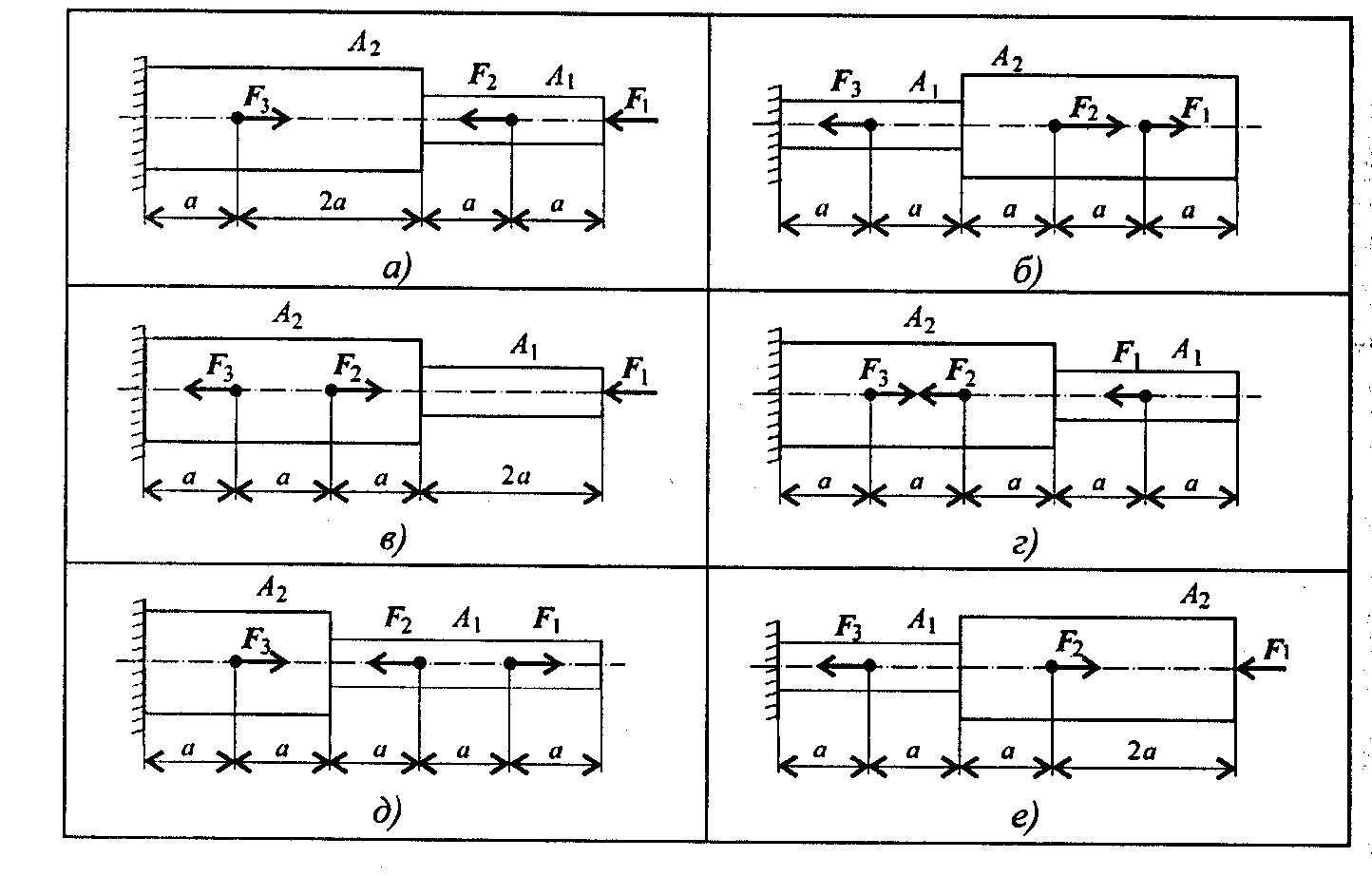
| Параметр | Вариант |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| F1, кН | 20 | 26 | 20 | 17 | 16 | 10 | 26 | 40 | 14 | 28 |
| F2, кН | 10 | 20 | 8 | 13 | 25 | 12 | 9 | 55 | 16 | 14 |
| F3, кН | 5 | 10 | 4 | 8 | 28 | 13 | 3 | 24 | 10 | 5 |
| А1, см2 | 1,8 | 1,6 | 1 | 2 | 1,2 | 0,9 | 1,9 | 2,8 | 2,1 | 1,9 |
| А2, см2 | 3,2 | 2,4 | 1,5 | 2,5 | 2,8 | 1,7 | 2,6 | 3,4 | 2,9 | 2,4 |
| а, м | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,4 | 0,3 | 0,2 | 0,5 | 0,6 |
| Рис. | а | б | в | г | д | е | а | б | в | г |
| Параметр | Вариант |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| F1, кН | 15 | 12 | 14 | 10 | 13 | 15 | 17 | 16 | 13 | 15 |
| F2, кН | 6 | 8 | 10 | 15 | 10 | 10 | 12 | 11 | 13 | 15 |
| F3, кН | 5 | 3 | 4 | 6 | 8 | 4 | 5 | 6 | 7 | 8 |
| А1, см2 | 1 | 2 | 2 | 2 | 1 | 1,9 | 1,5 | 1,7 | 0,9 | 0,7 |
| А2, см2 | 3 | 2 | 2 | 3 | 3 | 3 | 3,1 | 3,2 | 3,3 | 2,9 |
| а, м | 0,4 | 0,2 | 0,3 | 0,5 | 0,2 | 0,2 | 0,1 | 0,3 | 0,4 | 0,5 |
| Рис. | д | е | д | е | г | а | б | в | г | д |
| Параметр | Вариант |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| F1, кН | 12 | 10 | 5 | 10 | 12 | 16 | 20 | 25 | 23 | 24 |
| F2, кН | 14 | 16 | 18 | 19 | 20 | 21 | 22 | 20 | 24 | 16 |
| F3, кН | 9 | 10 | 10 | 9 | 8 | 6 | 2 | 5 | 7 | 8 |
| А1, см2 | 0,5 | 1,8 | 1,9 | 2 | 2,1 | 2,2 | 2 | 1,8 | 1,9 | 1,4 |
| А2, см2 | 2,8 | 2,7 | 2,6 | 2,7 | 2,8 | 2,9 | 1,1 | 1,2 | 1,3 | 1,5 |
| а, м | 0,6 | 0,3 | 0,4 | 0,2 | 0,1 | 0,6 | 0,4 | 0,5 | 0,7 | 0,3 |
| Рис. | е | а | б | в | г | д | е | д | е | г |
ТЕСТ ДЛЯ САМОКОНТРОЛЯ
studfiles.net
Контрольная работа по сопромату - Studentoff
Что представляют собой контрольные работы по сопромату? Сопромат расшифровывается как сопротивление материалов. Данное направление связано с технической механикой, а значит для нее будут характерны основы теорий, расчеты и изучение различных конструкций. Решение задач сопромата является основной задачей дисциплин, связанных с инженерной специальностью.
Контрольные работы по сопромату имеют аналогичные с контрольными по другим дисциплинам структуры. То есть контрольная работа состоит из нескольких теоретических вопросов и нескольких (чаще всего двух) задач. Преподаватель также вправе задать дополнительные вопросы для повышения или проверки знаний студента. Как же подготовиться к решению задач по сопромату? Для того, чтобы решение задач было легким, необходимо не только прочитать и проанализировать весь материал и конспекты, но и решать большое количество задач, так как именно они и служат основой данной дисциплины.
Решение задач по сопротивлению материалов – дело непростое, но подготовка позволит вам легче запомнить материал, а также потренироваться в решении задач.
Если вы хотите углубиться в более подробное изучение, то попросите вашего преподавателя посоветовать вам необходимую литературу.
Какие вопросы могут быть предоставлены на контрольной работе по сопромату? В основном на контрольной работе могут быть предоставлены следующие вопросы:
 />
/> Вопросы связаны с тематикой сопротивления материалов.
Вопросы связаны с тематикой сопротивления материалов.
 />
/> Рассказать о понятиях деформации, закона Гука и напряжениях.
Рассказать о понятиях деформации, закона Гука и напряжениях.
 />
/> Вопросы, связанные с напряжением, внутренними силами и сжатием.
Вопросы, связанные с напряжением, внутренними силами и сжатием.
 />
/> Описать механические характеристики различных материалов и напряжения.
Описать механические характеристики различных материалов и напряжения.
Начинать подготовку к контрольной работе по решению механики необходимо с теоретических вопросов. Для начала разберите сложные темы, в которых вы неуверенно себя чувствуете. Если же вам трудно дается решение данных тем, посетите лекции, где преподаватель сможет помочь вам разобраться.
За несколько дней до экзамена, попробуйте снова перечитать все вопросы и вспомнить сначала основные ответы, а затем дополнительные. Не стоит избегать посещения консультации – на ней можно уточнить у преподавателя все, что осталось непонятным. При повторении запоминайте формулы. Если запомнить не удастся, попробуйте сделать небольшие шпаргалки.
 />
/> В данном случае, рекомендуем обратиться к профессионалам в этой области – нашим специалистам, которые помогут выполнить любые контрольные по сопромату, тех. механике и другим смежным дисциплинам, таким как машиностроение, метрология, детали машин и.т.п. Задачи разбираются подробно для того, чтобы студент мог самостоятельно без специальных знаний объяснить ход решений преподавателю. Вы можете задать любой вопрос нашим преподавателям, мы с радостью вам поможем. Заказать контрольную работу по сопромату или заказать контрольную по тех. механике можно через форму заявки или Вконтакте.
В данном случае, рекомендуем обратиться к профессионалам в этой области – нашим специалистам, которые помогут выполнить любые контрольные по сопромату, тех. механике и другим смежным дисциплинам, таким как машиностроение, метрология, детали машин и.т.п. Задачи разбираются подробно для того, чтобы студент мог самостоятельно без специальных знаний объяснить ход решений преподавателю. Вы можете задать любой вопрос нашим преподавателям, мы с радостью вам поможем. Заказать контрольную работу по сопромату или заказать контрольную по тех. механике можно через форму заявки или Вконтакте.
 />
/>
studentoff.su
 Представленные варианты заданий выполнены с решениями и подробными пояснениями, т. е. выполняемые по приведенным примерам контрольные работы готовы к защите и сдаче.
По приведенным ниже ссылкам можно скачать варианты контрольных работ в формате Word с графиками, эпюрами и иллюстрациями.
Страничка будет особенно полезна студентам, обучающимся по заочной форме в качестве учебно-методического материала.
Представленные варианты заданий выполнены с решениями и подробными пояснениями, т. е. выполняемые по приведенным примерам контрольные работы готовы к защите и сдаче.
По приведенным ниже ссылкам можно скачать варианты контрольных работ в формате Word с графиками, эпюрами и иллюстрациями.
Страничка будет особенно полезна студентам, обучающимся по заочной форме в качестве учебно-методического материала. 






















































































 Определить касательные напряжения сдвига (среза), действующие в каждом из болтов при номинальной нагрузке.
При расчете не учитывать ослабление стержня болта впадинами резьбы.
Определить касательные напряжения сдвига (среза), действующие в каждом из болтов при номинальной нагрузке.
При расчете не учитывать ослабление стержня болта впадинами резьбы.

 Исходные данные:
Исходные данные:
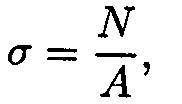
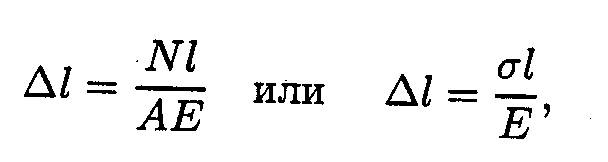
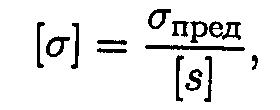
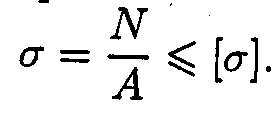

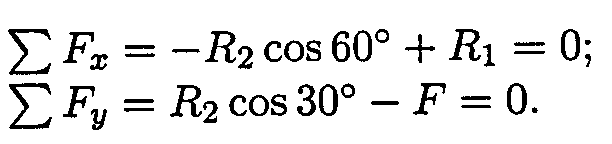
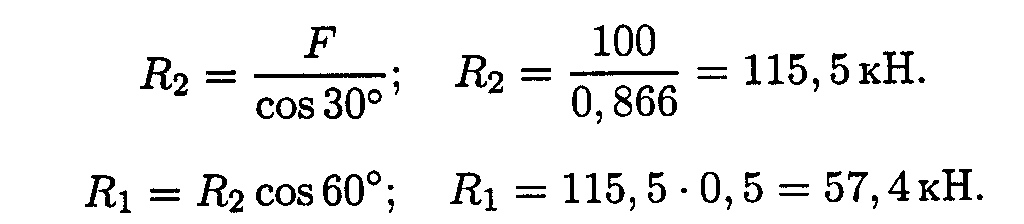
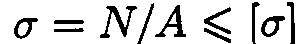
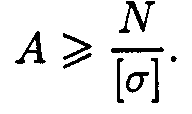
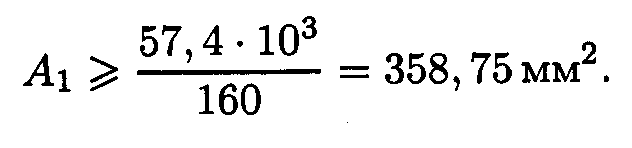
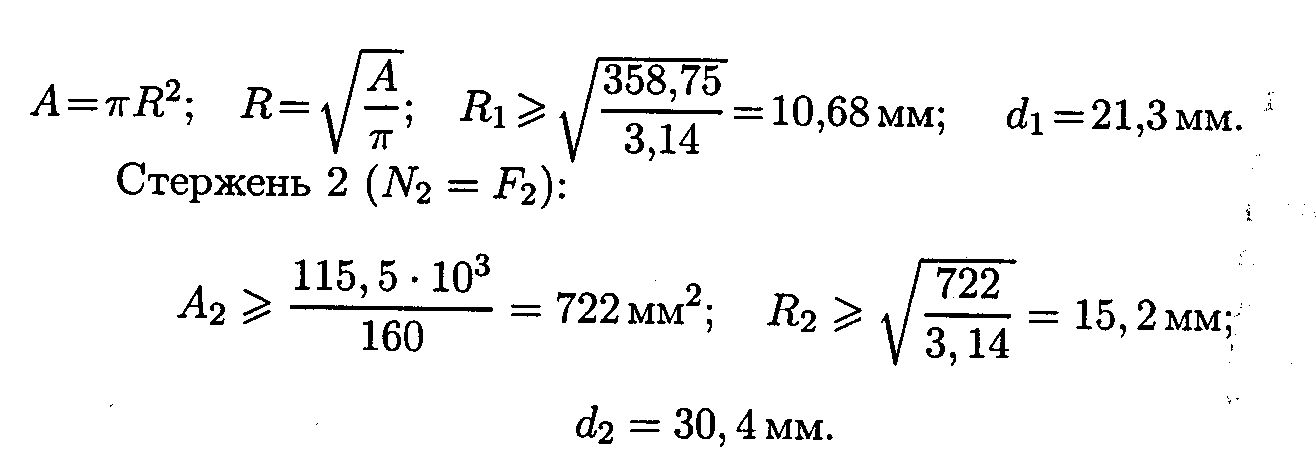
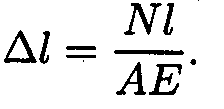
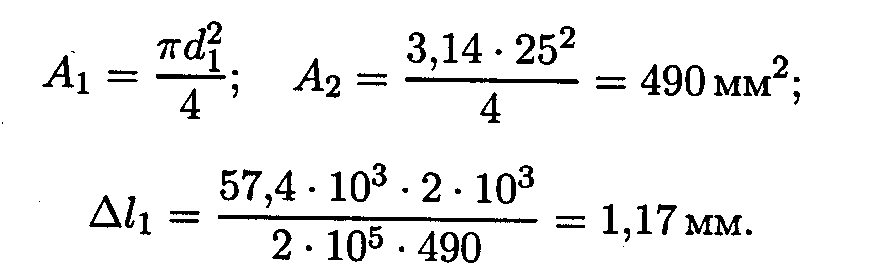
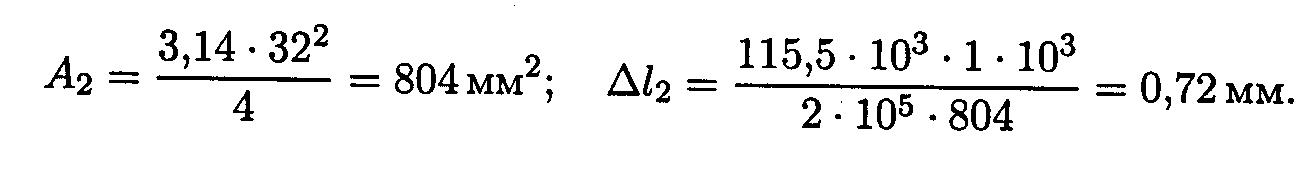
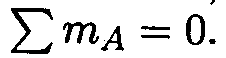
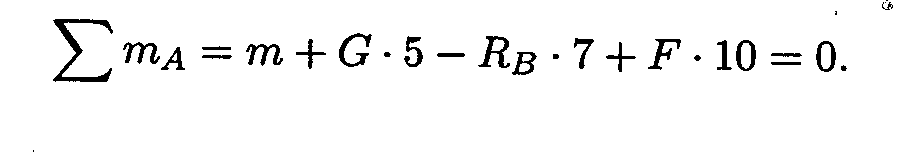
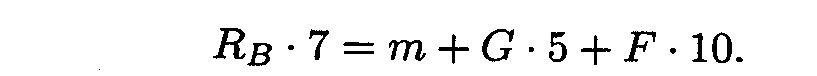
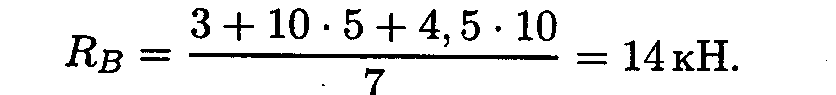
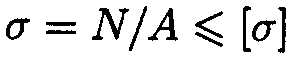
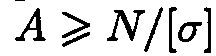
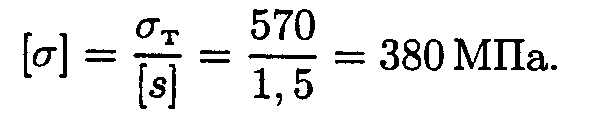
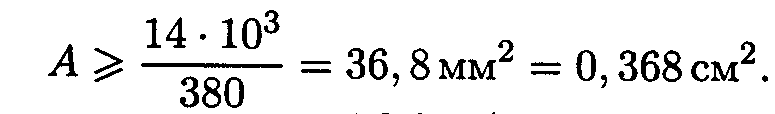
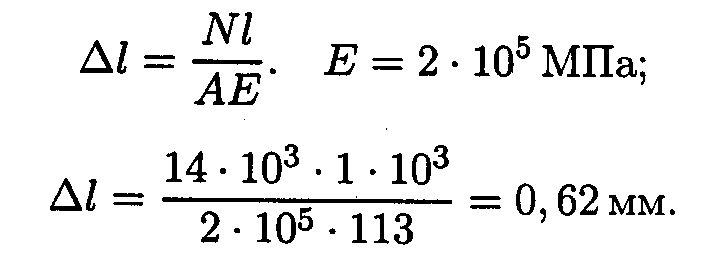
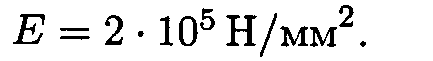

 />
/> />
/> />
/>








