
УРОК 9
Контрольная работа № 1
по теме: « Матрицы и определители »
ЦЕЛЬ:
Применение полученных знаний и умений, приобретенных во время лекций и практических занятий на уроках, в процессе выполнения контрольной работы по теме: «Матрицы и определители».
Вариант № 1
1. Найти значение матричного многочлена f (A) :
A =
f (x) = - х3 + 2x2 - x + 3

-1 0
3 2
-2 0 8 1
3 -1 7 2
-8 2 -6 -3
2. Найти ранг матрицы методом окаймляющих миноров.
А =

3. Вычислить определитель с помощью «правила треугольников»
-2 3 5
7 -1 4
9 -8 -6
Δ =

-2 3 5
7 -1 4
9 -8 -6

4
А =
. Найти обратную матрицу для матрицы5. Найти матрицу Х , удовлетворяющую уравнению. Сделать проверку.

3 -1
2 4
1 -2
-3 4
Х =


Вариант № 2
1. Найти значение матричного многочлена f (A) :
f (x) = х3 + 3x2 + 2x - 1
0 3
-1 -2
A =

2. Найти ранг матрицы методом окаймляющих миноров.
-2 3 -1 1
3 -1 7 4
8 -3 2 0

А =
3. Вычислить определитель с помощью «правила треугольников»
Δ =
-1 9 5
-4 6 2
3 7 8

4. Найти обратную матрицу для матрицы
-1 9 5
-4 6 2
3 7 8

А =
5. Найти матрицу Х , удовлетворяющую уравнению. Сделать проверку.

4 -2
3 1
3 0
4 2
Х


=
Решение контрольной работы по вариантам
Вариант № 1
1. Найти значение матричного многочлена f (A) :
f (x) = - х3 + 2x2 - x + 3
A =
-1 0
3 2
f (А) = - А3 + 2А2 - А + 3Е, где Е – единичная матрица

A2 = А. А =
-1 0
3 2


-1 0
3 2
1+0 0+0
-3+6 0+4
=
=

1 0
3 4
.

1 0
3 4
-1 0
3 2


-1+0 0+0
-3+12 0+8
-1 0
9 8

A3 = А 2 . А =
=
=
Е =

1 0
0 1
1 0
3 4
A =

-1 0
9 8


1 0
3 4

-1 0
3 2

1 0
0 1
f (А) = -
+ 2
-
+ 3
=
=

+

-

+

1 0
-9 -8
2 0
6 8
-1 0
3 2
3 0
0 3
=
1+2+1+3 0+0-0+0
-9+6-3+0 -8+8-2+3

7 0
-6 1

=
=
f (А) =

7 0
-6 1
Ответ:
2. Найти ранг матрицы методом окаймляющих миноров.
А =
-2 0 8 1
3 -1 7 2
-8 2 -6 -3

3 х 4
Решение
ШАГ 1. Рассмотрим миноры 1-го порядка матрицы А
М 11 = 8 = 8 ( условие выполнено )
11 = 8 = 8 ( условие выполнено )
ШАГ 2. Рассмотрим миноры 2-го порядка матрицы А

-2 0
3 -1
М
= 2 – 0 = 2
21 =( условие выполнено )
ШАГ 3. Рассмотрим миноры 3-го порядка матрицы А
-2 0 8
3 -1 7
-8 2 -6
М31 = = -12 +0 +48 – 64 +28 – 0 = 0
( условие не выполнено )
-2 0 1
3 -1 2
-8 2 -3

М 32 = = - 6 + 0 +6 – 8 + 8 + 0 = 0
32 = = - 6 + 0 +6 – 8 + 8 + 0 = 0
( условие не выполнено )
-2 8 1
3 7 2
-8 -6 -3

М33 = = - 56 +24 – 72 – 42 + 18 + 128 = 0
( условие не выполнено )
0 8 1
-1 7 2
2 -6 -3

М34 = = 0 + 6 +32 – 14 – 0 – 24 = 0
( условие не выполнено )
Ответ: rang ( A ) = 2
3. Вычислить определитель с помощью «правила треугольников»
-2 3 5
7 -1 4
9 -8 -6

Δ =
= - 12 – 280 + 108 + 45 – 64 + 126 = - 77
О
-2 3 5
7 -1 4
9 -8 -6
 твет: Δ = - 77
твет: Δ = - 77 А =
4. Найти обратную матрицу Α-1 для матрицы
ШАГ 1. Найти определитель матрицы А
Δ = - 77 ( см. решение – задание 3)
 ( условие выполнено )
( условие выполнено )
А – невырожденная матрица, значит, А-1 существует и определяется по формуле А-1 = А*/Δ, где А* - союзная матрица
А11 А21 А31
А12 А22 А32
А13 А23 А33

А* =
ШАГ 2. Найти алгебраические дополнения для всех элементов матрицы А
-1 4
-8 -6

А11 = + = 6+32=38
7 4
9 -6

А12 = - = - ( - 42 – 36) = 78
А
7 -1
9 -8
 13 = + = - 56 + 9 = - 47
13 = + = - 56 + 9 = - 47 3 5
-8 -6

А
-2 5
9 -6
 21 = - = - ( - 18 + 40 ) = -22
21 = - = - ( - 18 + 40 ) = -22 А
-2 3
9 -8
 22 = + = 12 – 45 = - 33
22 = + = 12 – 45 = - 33 А
3 5
-1 4
23 = - = - (16 – 27) = 11
А31 = + = 12 + 5 = 17
-2 5
7 4

А
-2 3
7 -1
32 = - = - ( -8 – 35) = 43
А33 = + = 2 – 21= - 19
ШАГ 3. Полученные значения подставить в основную формулу и найдём А-1
А11 А21 А31
А12 А22 А32
А13 А23 А33


38 -22 17
78-33 43
-47 11 -19
1
Δ

А-1 =
1
77

= -

-38 22 -17
-7833 -43
47 -1119
1
77

Ответ: А-1 =
5. Найти матрицу Х , удовлетворяющую уравнению
3 -1
2 4
1 -2
-3 4
Х =



З апишем матричное уравнение в виде АХ = В Х = А-1 В
апишем матричное уравнение в виде АХ = В Х = А-1 В
Найдём определитель матрицы А
3 -1
2 4

detA = = 12 + 2 = 14 ( условие выполнено )
А – невырожденная матрица, значит, А-1 существует и определяется по формуле А-1 = А*/Δ, где А* - союзная матрица
Н
4 1
-2 3

1
14

Α-1 =
айдём обратную матрицу А-14 1
-2 3

1
14

Х = А-1В =
1 -2
-3 4

Найдём матрицу
1
14

4-3 -8+4 -2-9 4+12

1 -4
-11 16

1
14

Х =
=
Проверка
3 -1
2 4

1 -4
-11 16

1
14

1
14

3+11 -12-16
2-44 -8+64

1
14

14 -28
-42 72

=
=

=
= В
1 -2
-3 4

А
Х
Ответ: Х =
1 -4
-11 16

1
14

Вариант № 2
1. Найти значение матричного многочлена f (A) :
f (x) = х3 + 3x2 + 2x - 1
0 3
-1 -2
A =

f (А) = А3 + 3А2 +2А - 1Е, где Е – единичная матрица
A2 = А. А =
0 3
-1 -2


0-3 0-6
0+2 -3+4
=

=

A3 = А 2 . А =


=

=

6 3
-1 4
Е =

1 0
0 1
A =
-3 -6
2 1
-3 -6
2 1
0 3
-1 -2
0+6 -9+12
0-1 6-2

0 3
-1 -2
0 3
-1 -2
f (А) =

+ 3

+ 2

- 1

1 0
0 1
=
=

+

-

-

-9 -18
6 3
0 6
-2 -4
1 0
0 1
=
=
6-9-0-1 3-18-6-0
-1+6+4-0 4+3+4-1
=

-4 -21
9 10

6 3
-1 4
-3 -6
2 1
0 3
-1 -2
6 3
-1 4
f (А) =

-4 -21
9 10
Ответ:
2. Найти ранг матрицы методом окаймляющих миноров.
А =
-2 3 -1 1
3 -1 7 4
8 -3 2 0

ШАГ 1. Рассмотрим миноры 1-го порядка матрицы А
М 11 = 8 = 8 ( условие выполнено )
11 = 8 = 8 ( условие выполнено )
ШАГ 2. Рассмотрим миноры 2-го порядка матрицы А

-2 3
3 -1
М
= 2 – 9 = -7
21 =( условие выполнено )
ШАГ 3. Рассмотрим миноры 3-го порядка матрицы А
-2 3 -1
3 -1 7
8 -3 2

М31 = = 4 + 168 + 9 – 8 – 42 – 18 = 113
( условие выполнено )
Ответ: rang ( A ) = 3
3. Вычислить определитель с помощью «правила треугольников»
Δ =
-1 9 5
-4 6 2
3 7 8

= - 48 – 140 + 54 – 90 + 14 + 288 = 78
Ответ: Δ = 78
А =
-1 9 5
-4 6 2
3 7 8

4. Найти обратную матрицу Α-1 для матрицы
ШАГ 1. Найти определитель матрицы А
Δ = 78 ( см. решение – задание 3)
( условие выполнено )

А – невырожденная матрица, значит, А-1 существует и определяется по формуле А-1 = А*/Δ, где А* - союзная матрица
А11 А21 А31
А12 А22 А32
А13 А23 А33

А* =
6 2
7 8

А11 = + = 48-14 = 34

-4 2
3 8
А12 = - = - ( - 32 – 6) = 38
-4 6
3 7
А 13 = + = - 28 - 18 = - 46
13 = + = - 28 - 18 = - 46

9 5
7 8
А 21 = - = - ( 72-35 ) = - 37
21 = - = - ( 72-35 ) = - 37
-1 5
3 8
А 22 = + = -8 – 15 = - 23
22 = + = -8 – 15 = - 23
-1 9
3 7
А23 = - = - (-7 - 27) = 34
9 5
6 2

А31 = + = 18 - 30 = - 12

-1 5
-4 2
А32 = - = - ( -2 + 20) = - 18
А
-1 9
-4 6
33 = + = - 6 + 36 = 30ШАГ 3. Полученные значения подставить в основную формулу и найдём А-1
А11 А21 А31
А12 А22 А32
А13 А23 А33


1
Δ

А-1 =
1
78

=
34 -37 12
38-23- 18
-46 34 30

1
78

34 -37 12
38-23-18
-46 34 30
Ответ: А-1 =
5. Найти матрицу Х , удовлетворяющую уравнению
4 -2
3 1
3 0
4 2
Х

=


З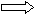 апишем матричное уравнение в виде ХА = В Х = ВА-1
апишем матричное уравнение в виде ХА = В Х = ВА-1
Найдём определитель матрицы А
4 -2
3 1

detA = = 4 + 6 = 10 ( условие выполнено )
А – невырожденная матрица, значит, А-1 существует и определяется по формуле А-1 = А*/Δ, где А* - союзная матрица
Н
1 2
-3 4

1
10

Α-1 =
айдём обратную матрицу А-1
1
10

Х = ВА-1 =

1 2
-3 4
3 0
4 2
Найдём матрицу Х
Х =
1
10

3+0 6+0 4-6 8+8

=
3 6
-2 16

1
10

Проверка


1
10

=
1
10

12+18 - 6+6
-8+48 4+16

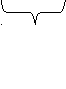

=
В
3 0
4 2

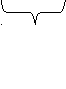
А
Х
3 6
-2 16
4 -2
3 1
Ответ: Х =
3 6
-2 16

1
10

Критерий выставления оценок:
Контрольная работа № 1
«Матрицы и определители»
№ задания
1
2
3
4
5
БАЛЫ
5
4
2
4
5
∑
20 балов, что составляет 100%
В работе максимальное количество балов - 20 , что составляет - 100%
от всей выполненной работы
« 5 » - не менее 85% от максимального бала
« 4 » - не менее 70% от максимального бала
« 3 » - не менее 50% от максимального бала
infourok.ru
Контрольная работа
«Матрицы и определители»
1). Дано: A,B. Найти:
1
а) 3A+B
б) AB
в)A -1
г)A -1A
2).Найти def A: а) методом треугольников;
б) приведением к каноническому виду
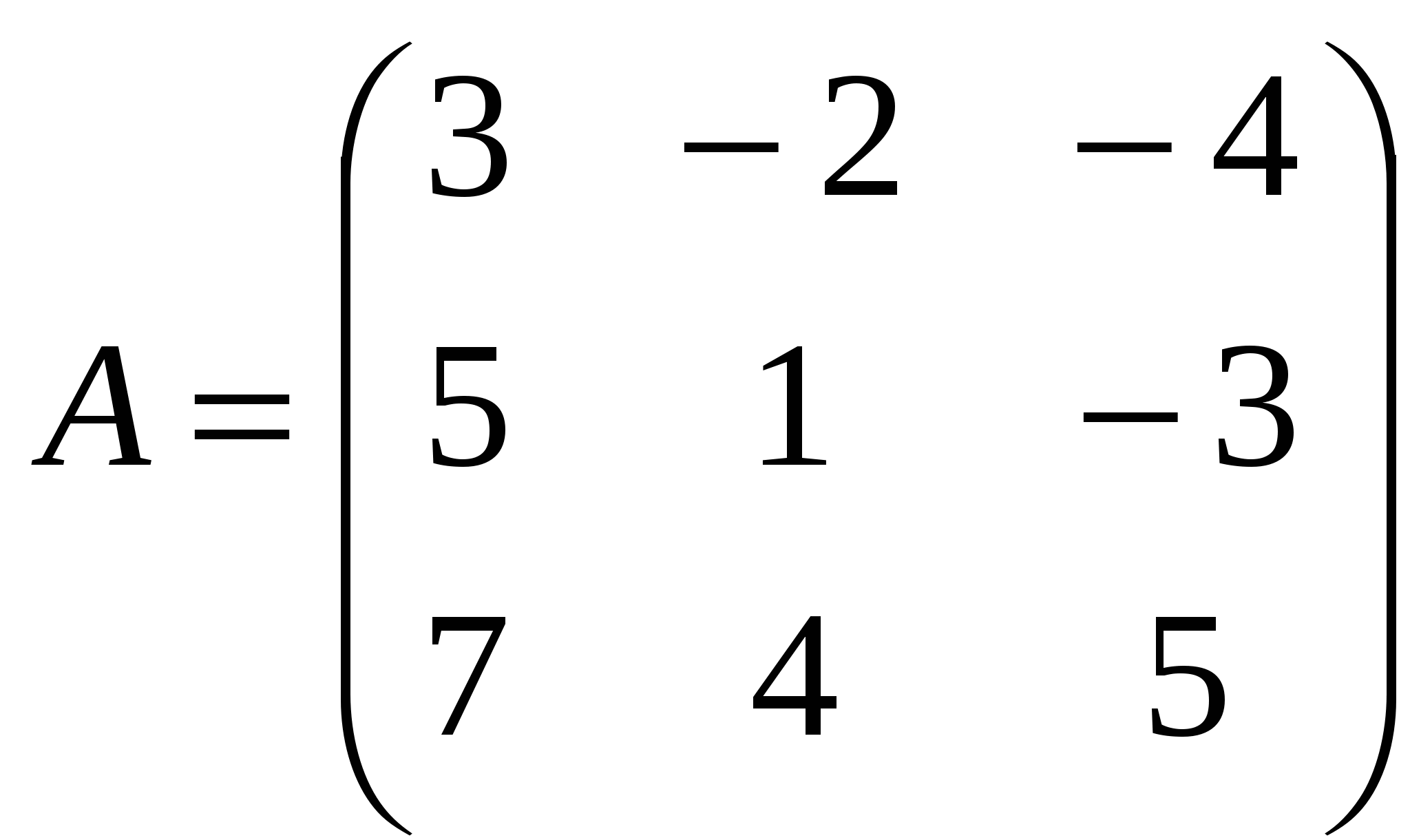
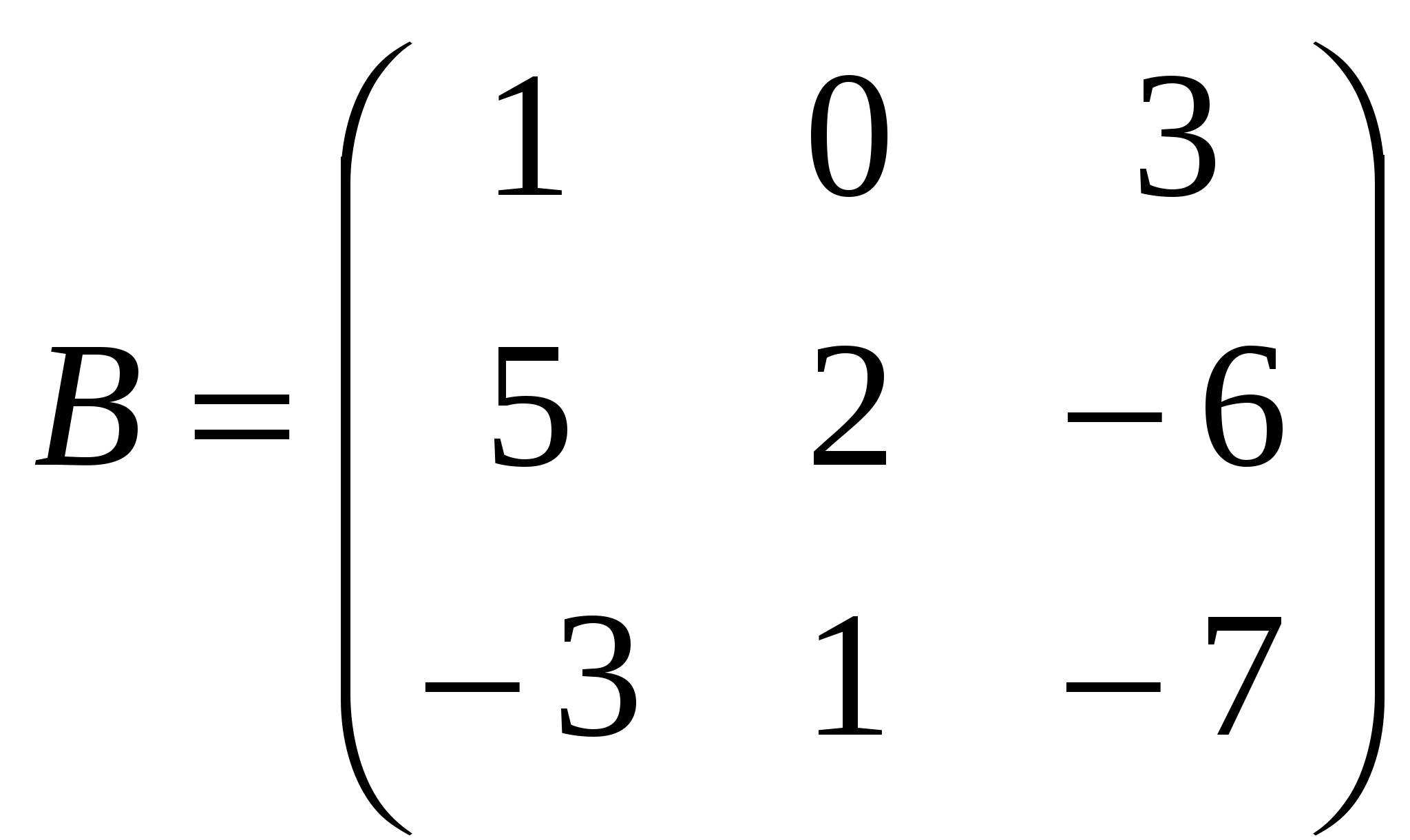
1). Дано: A,B. Найти:
2
а) -2A-B
б) BA
в)B -1
г) B -1B
2).Найти def A: а) приведением к каноническому виду;
б) методом треугольников;
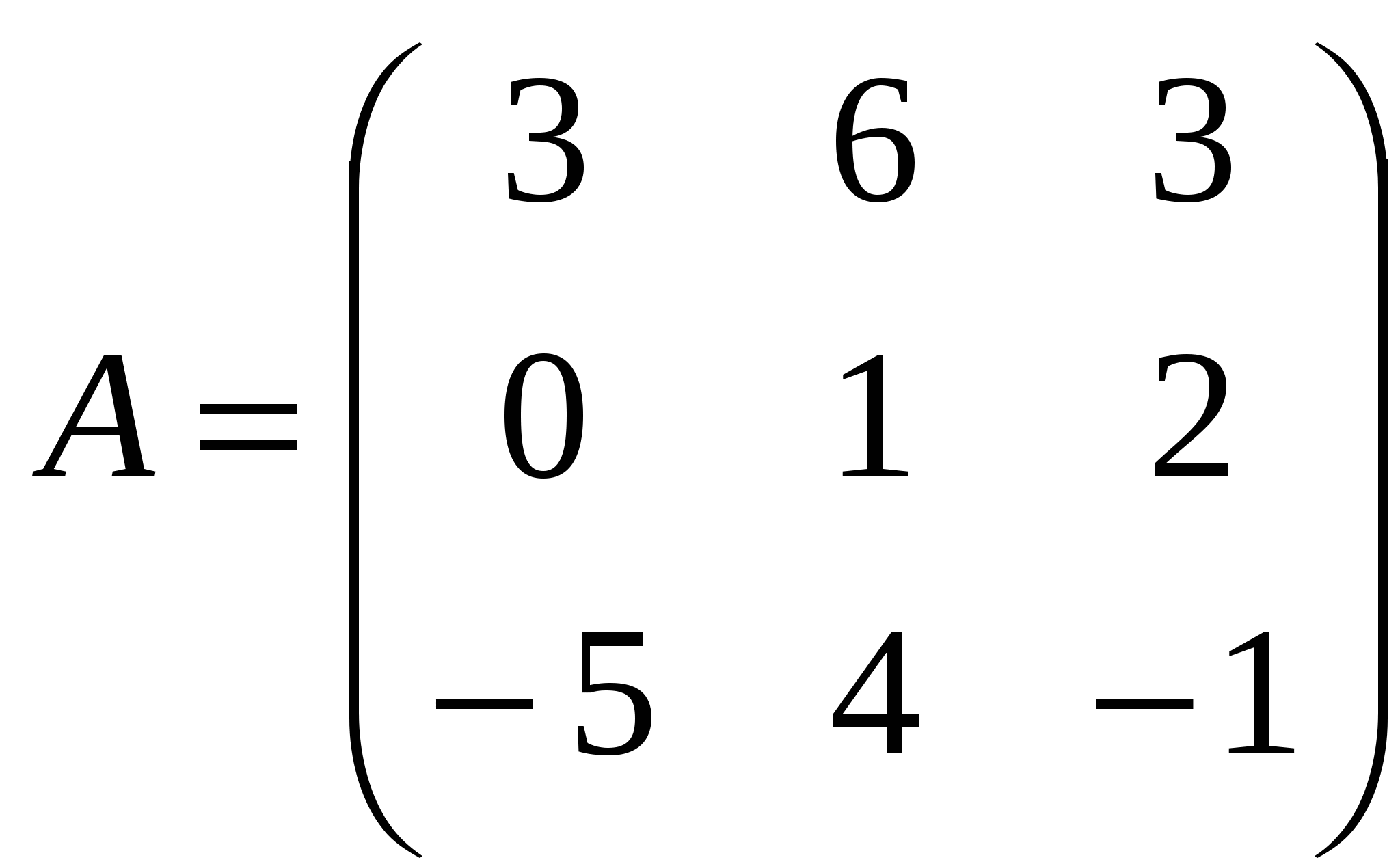
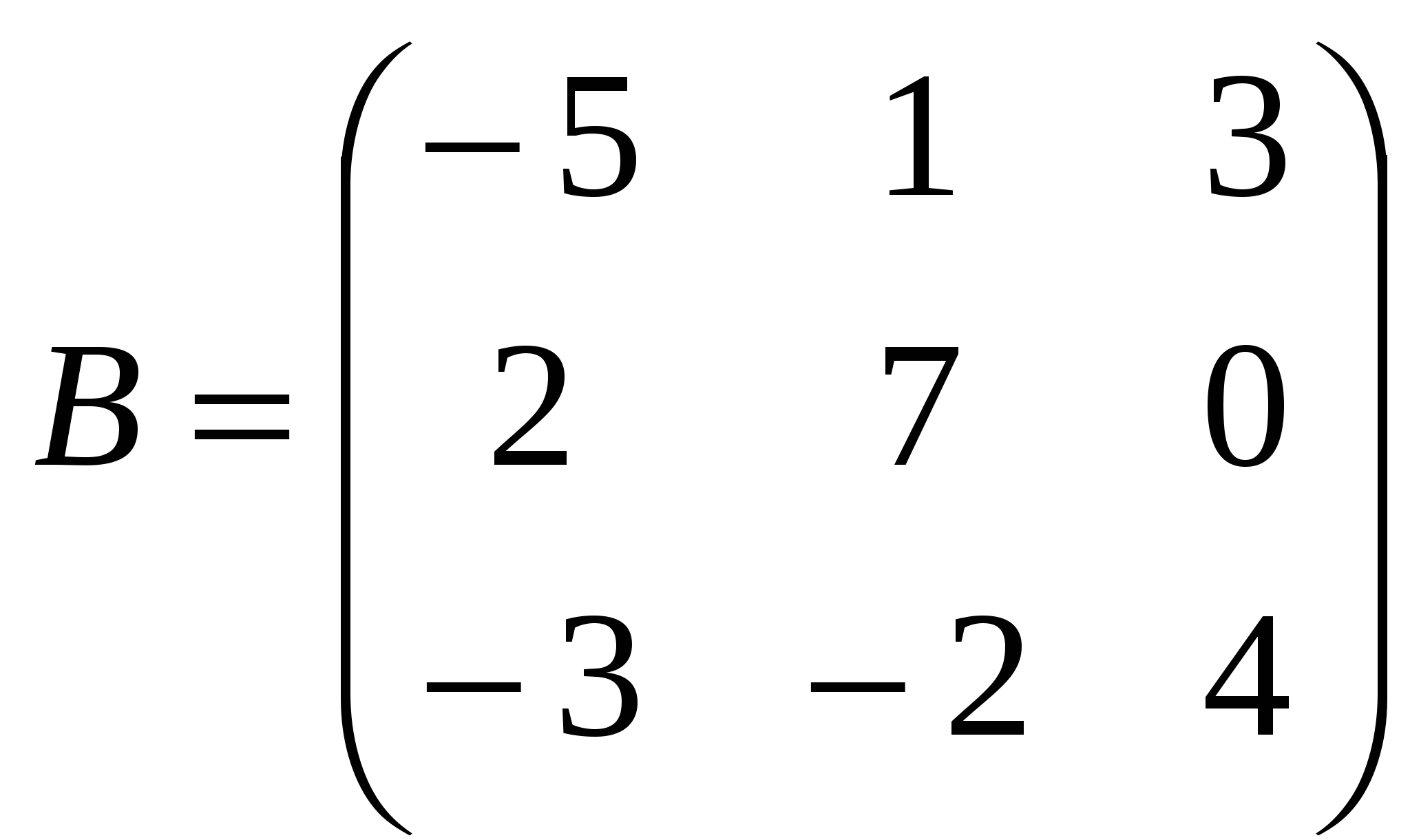
1). Дано: A,B. Найти:
3
а) 3B+A
б) BA
в)B -1
г)BB -1
2).Найти∆B: а) методом треугольников;
б) приведением к треугольному виду
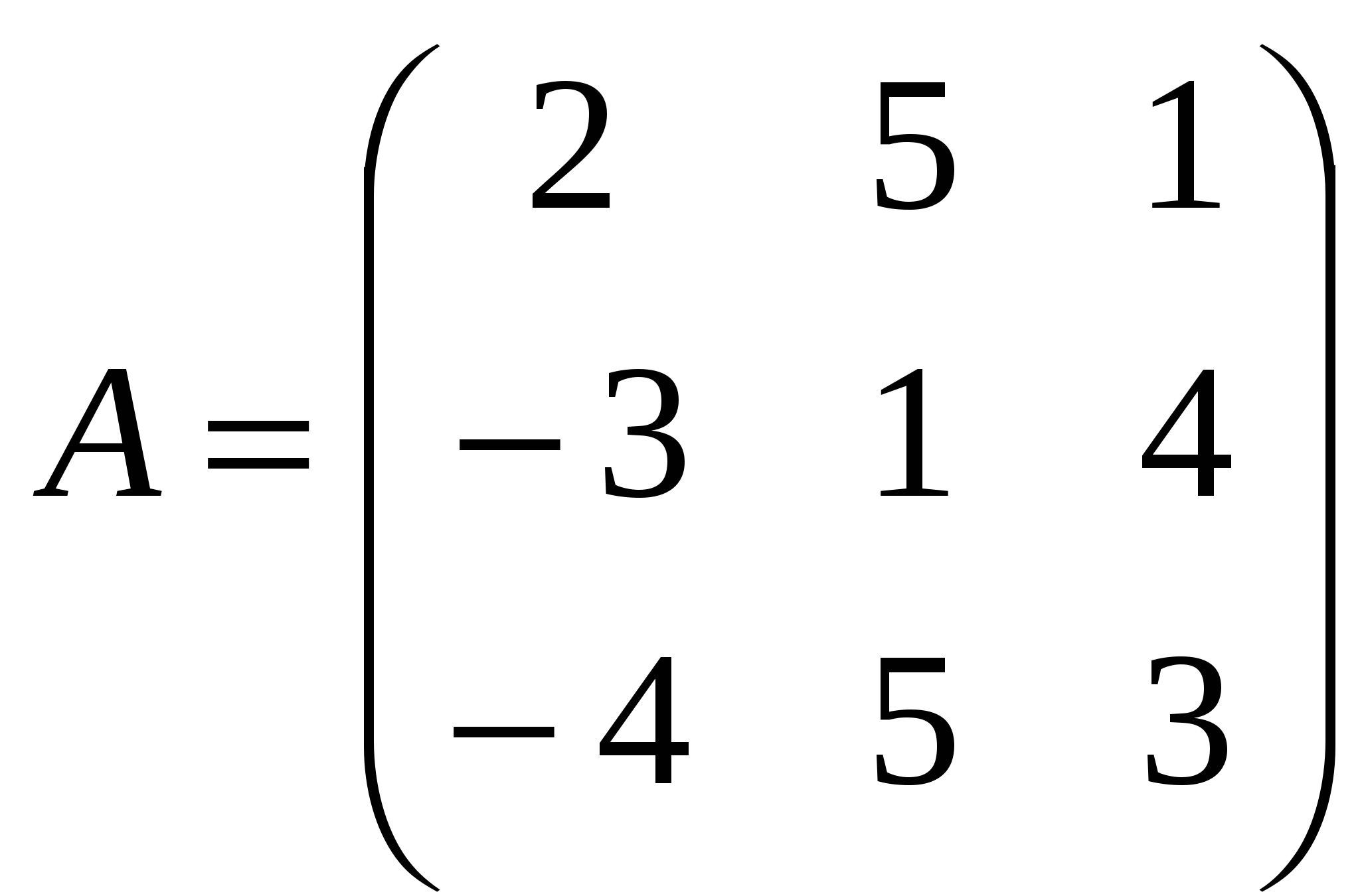
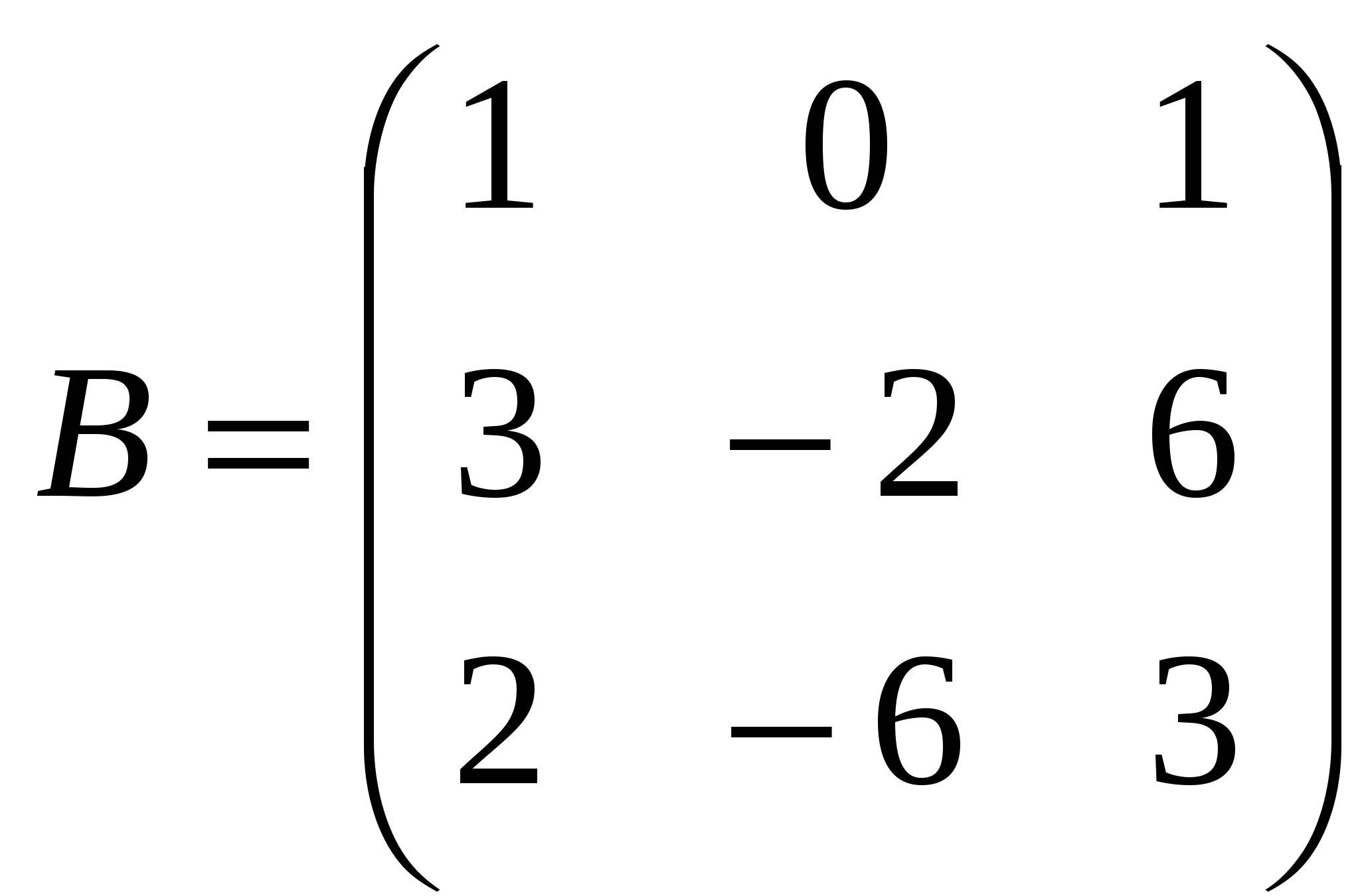
1). Дано: A,B. Найти:
4
а) 3A+B
б) AB
в)A -1
г)A -1A
2).Найти def B: а) методом треугольников;
б) приведением к каноническому виду
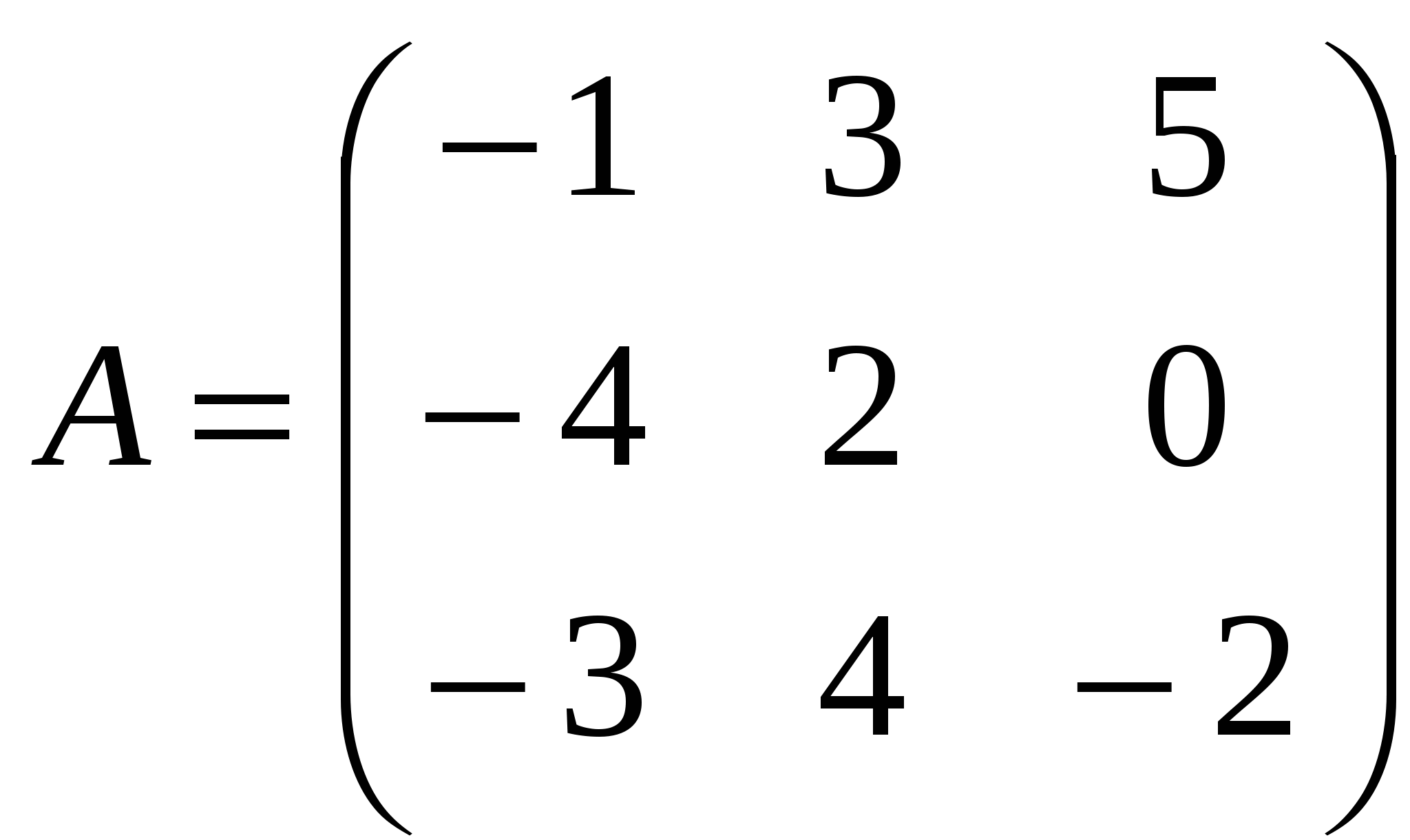
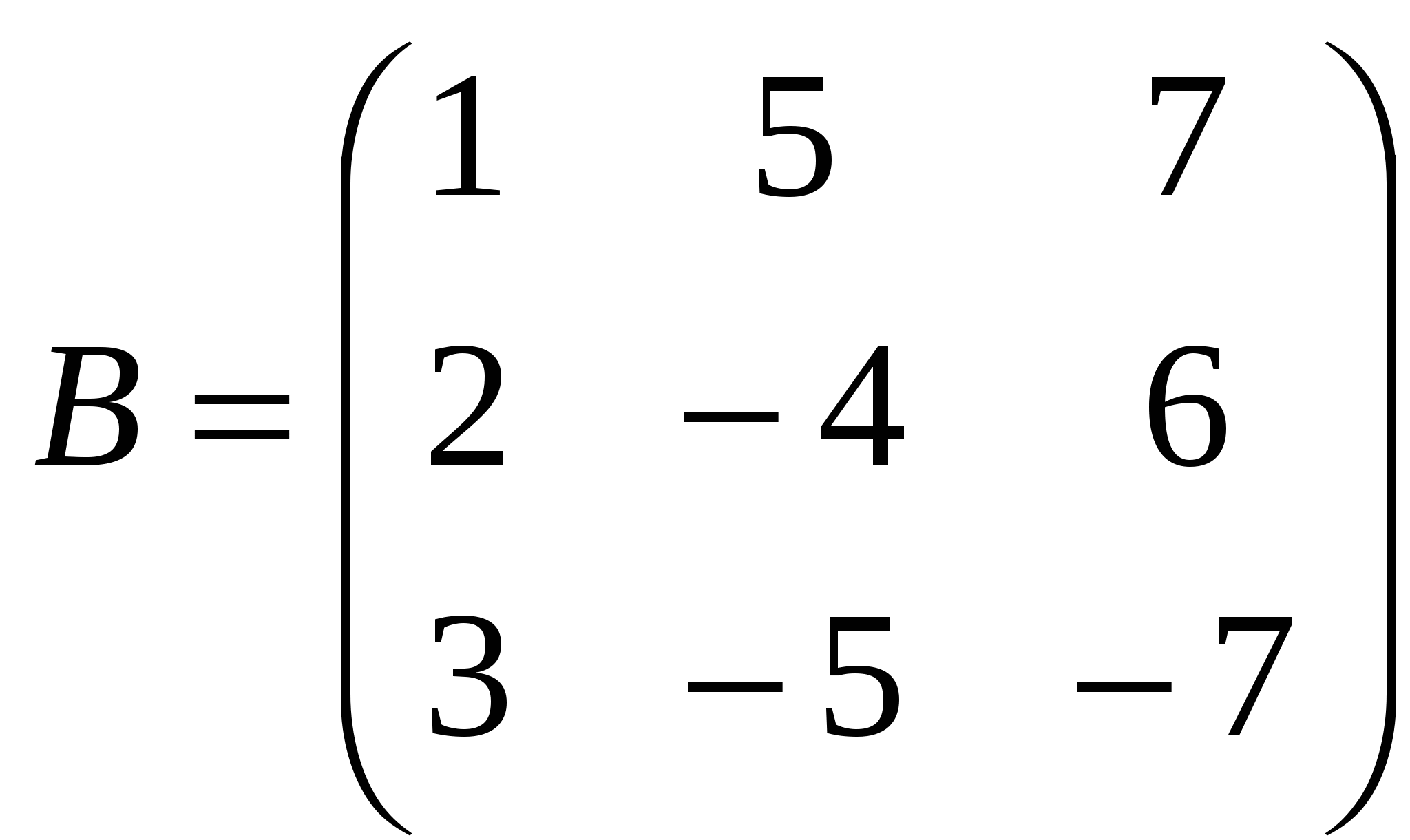
1). Дано: A,B. Найти:
5
а) 2A+B
б) AB
в)B -1
г) BB -1
2).Найти def A: а) методом треугольников;
б) приведением к треугольному виду;
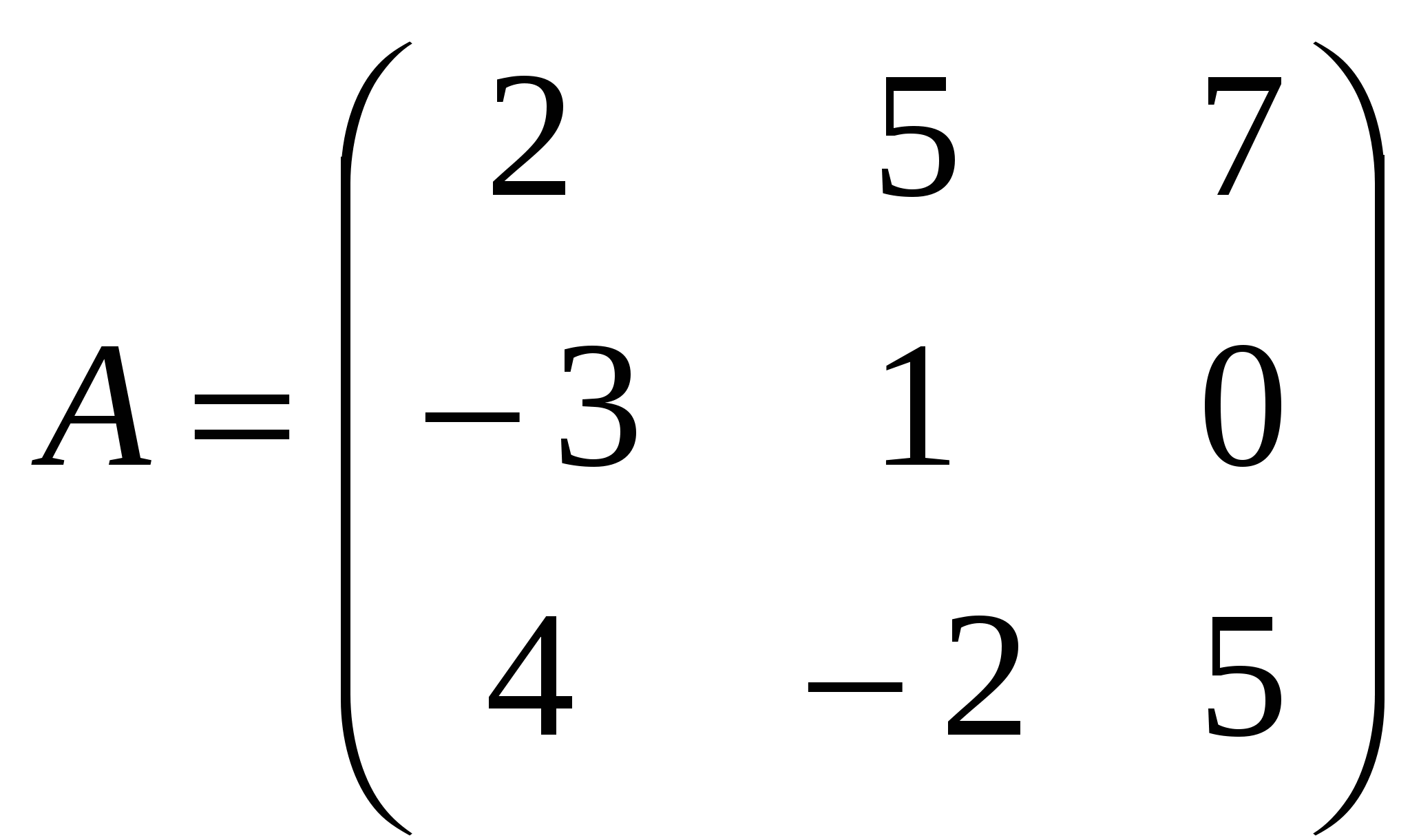
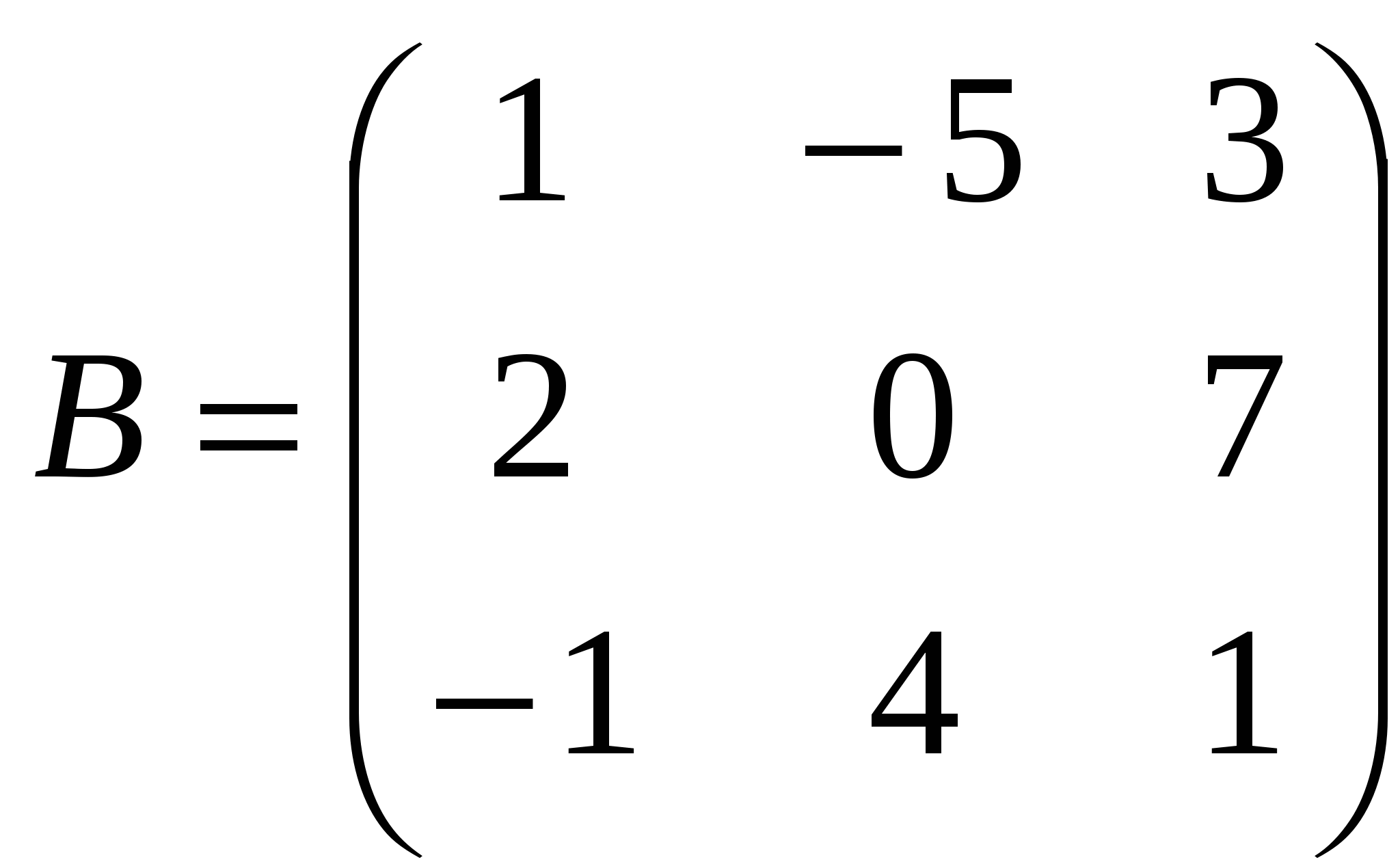
Контрольная работа № 1
1). Дано: A,B. Найти:
6
а) 3B-A
б) AB
в)A -1
г) AA -1
2).Найти ∆B: а) методом треугольников;
б) приведением к треугольному виду
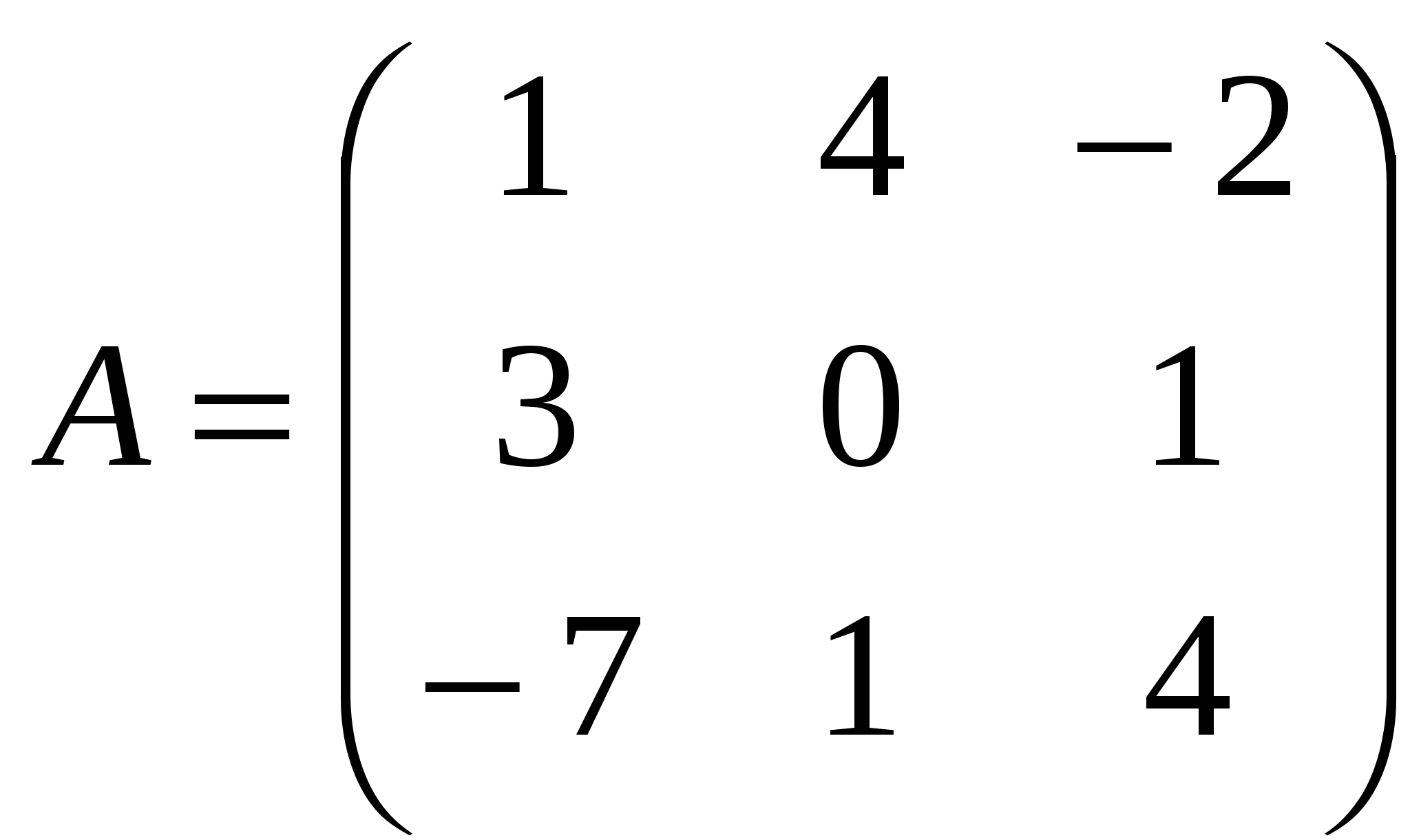
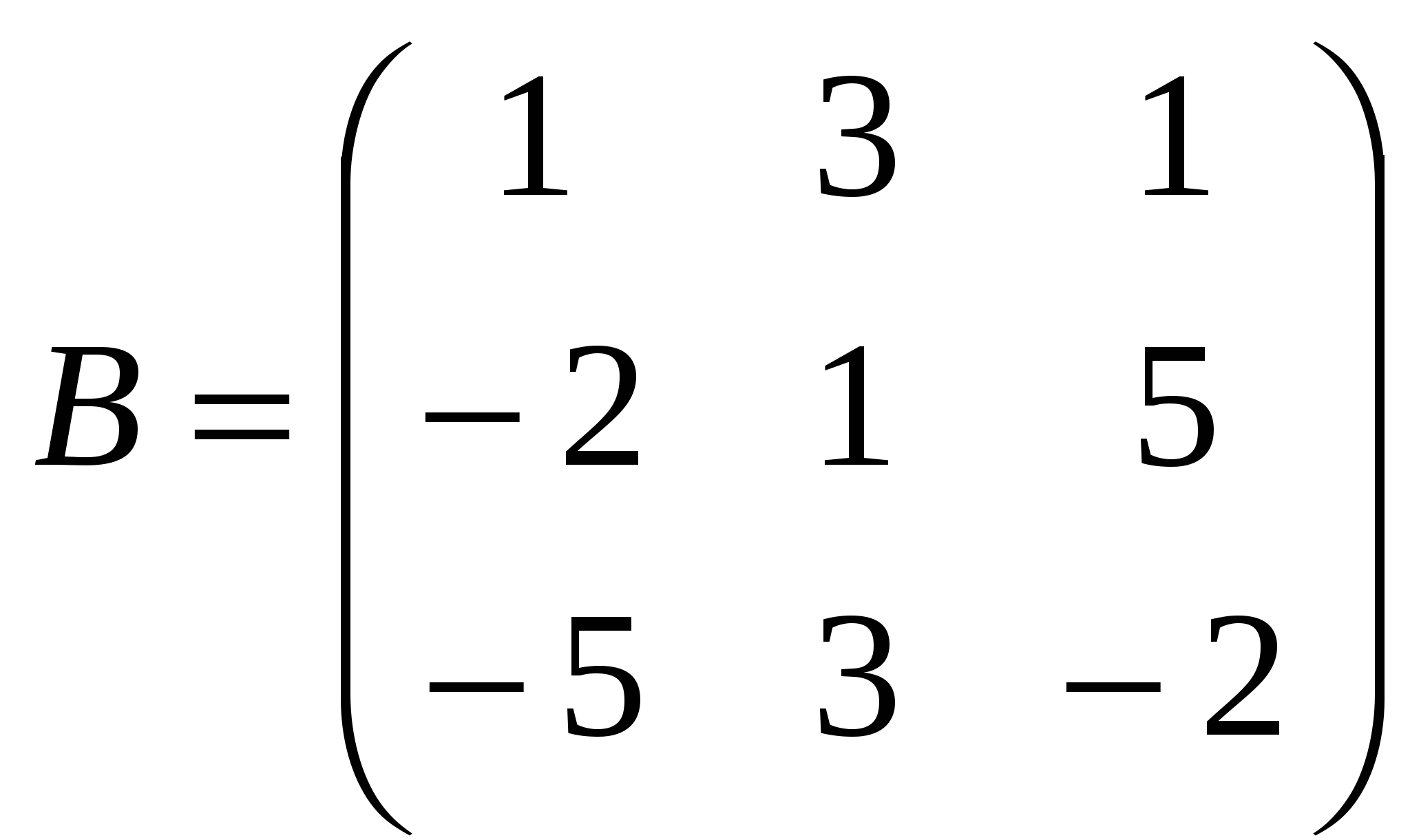
1). Дано: A,B. Найти:
7
а) 2B+3A
б) BA
в)A -1
г)A -1A
2).Найти∆B: а) методом треугольников;
б) приведением к треугольному виду
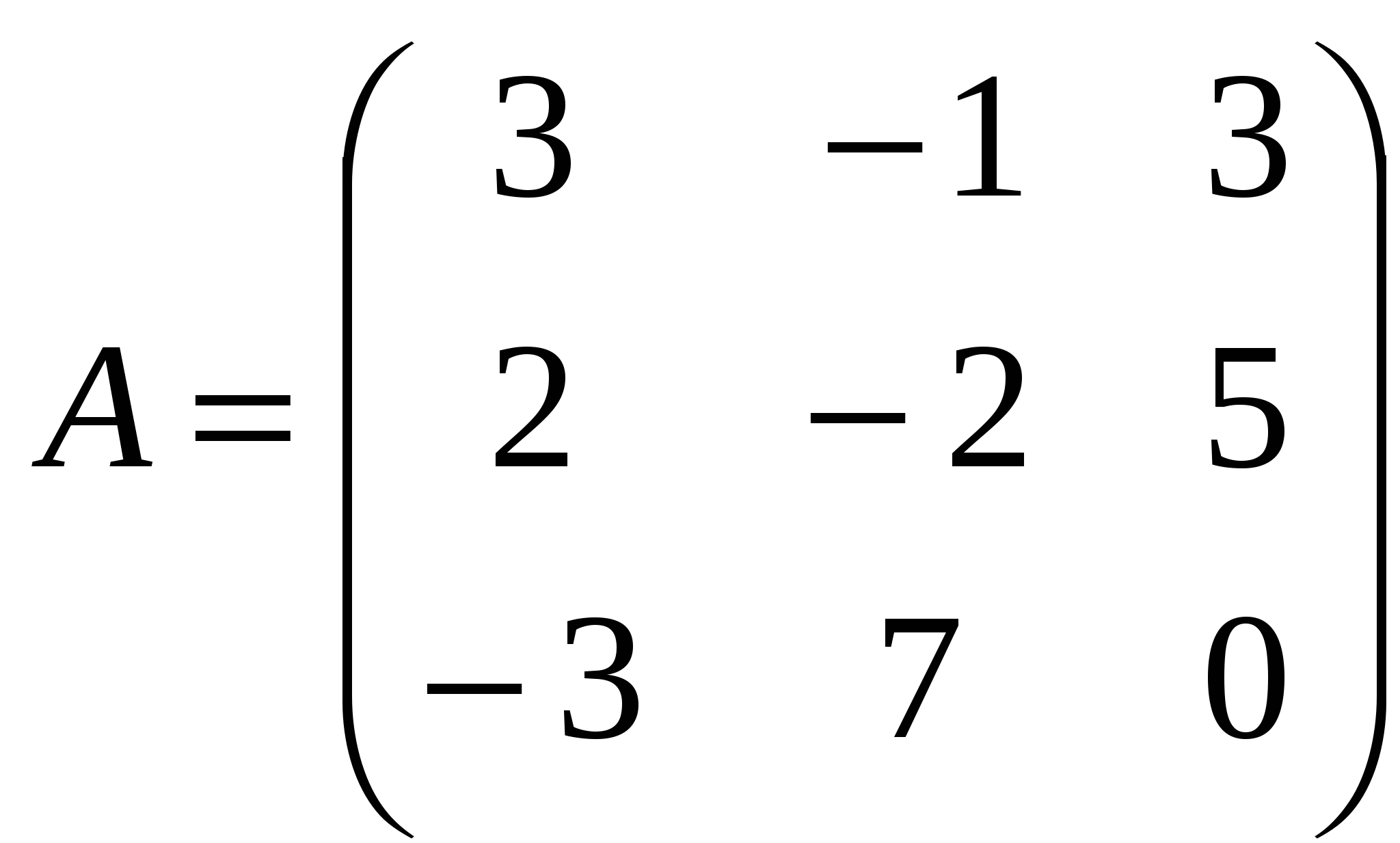
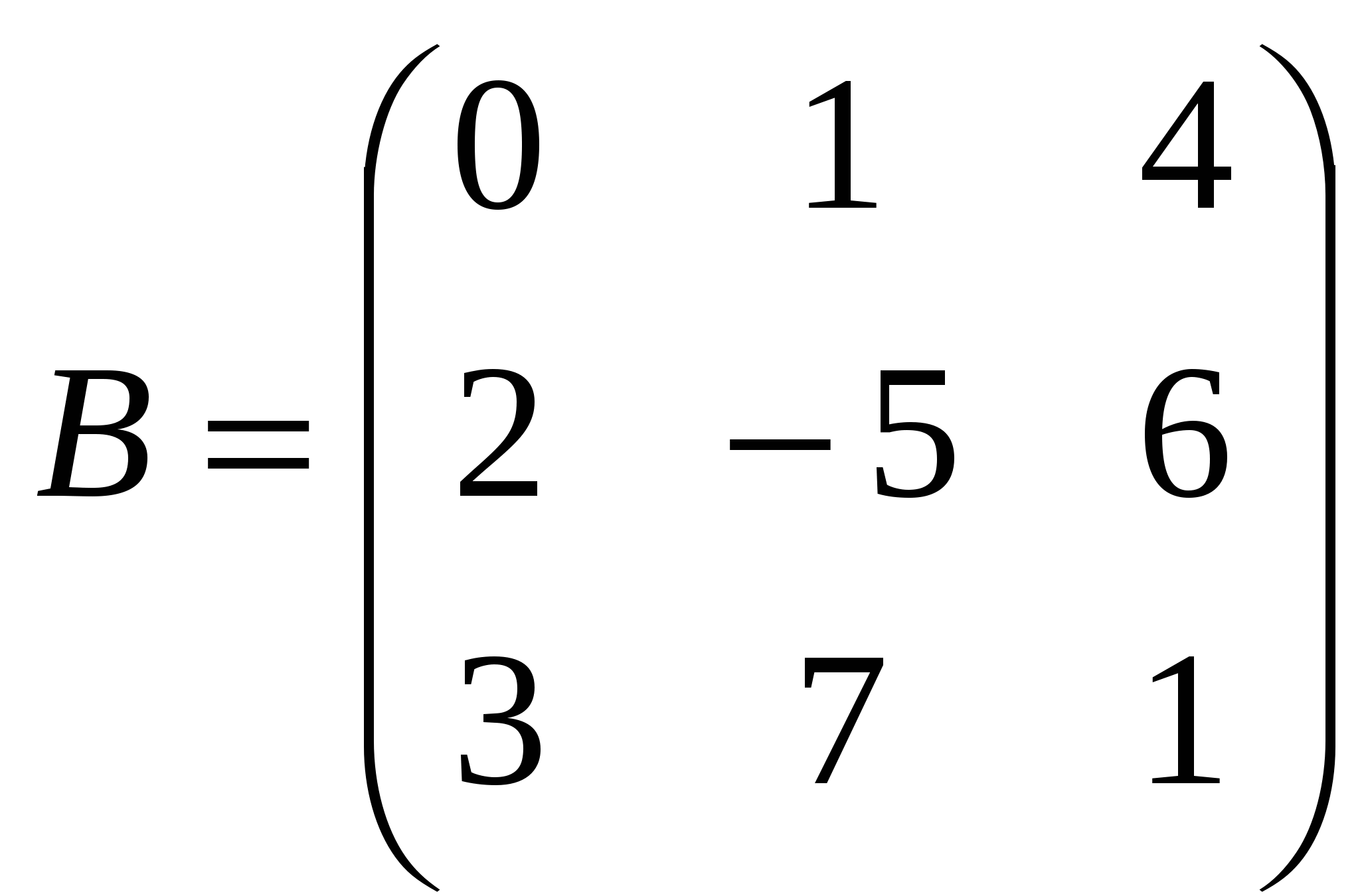
1). Дано: A,B. Найти:
8
а) 3B-A
б) AB
в)A -1
г)A -1A
2).Найти def B: а) методом треугольников;
б) приведением к треугольному виду
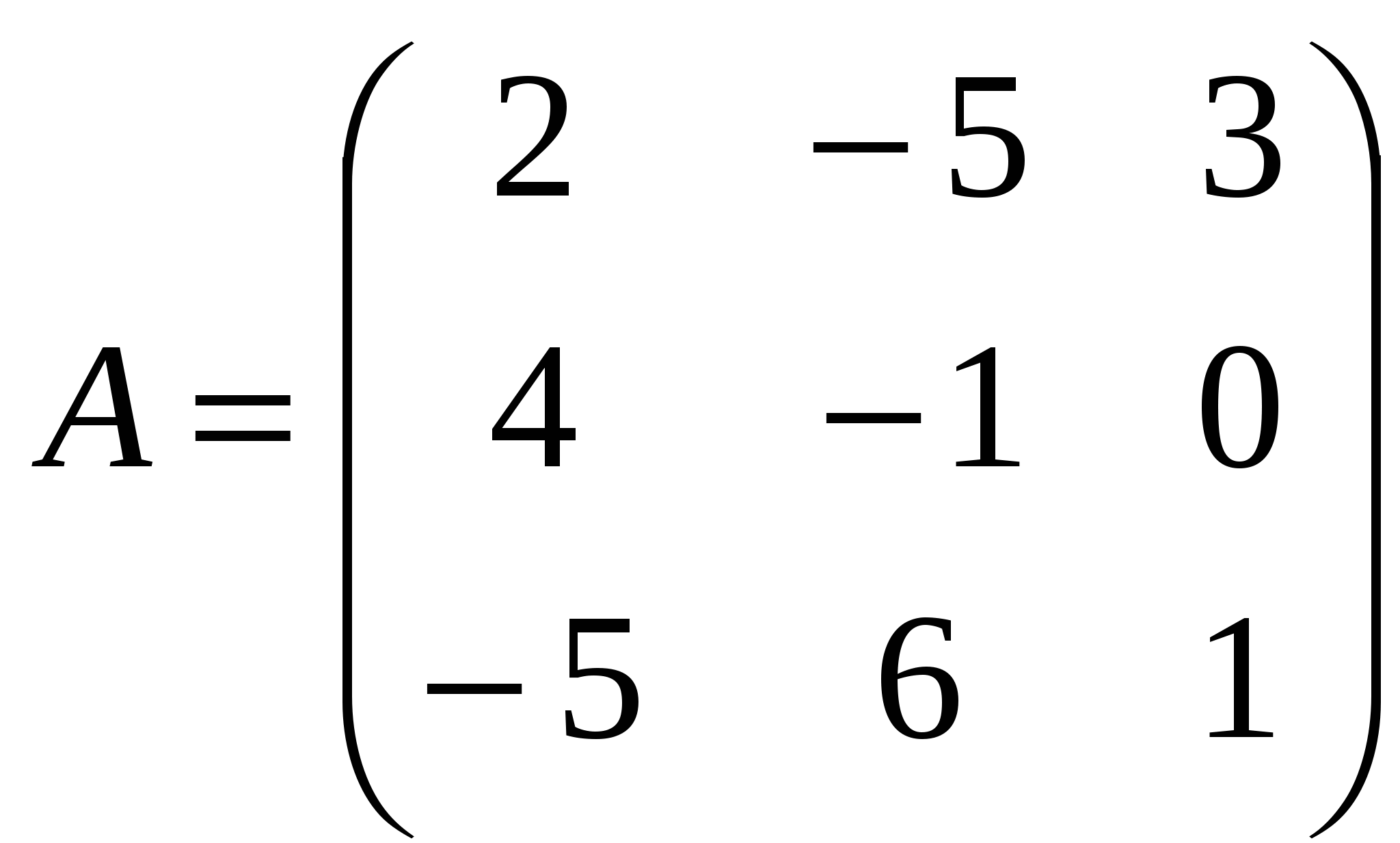
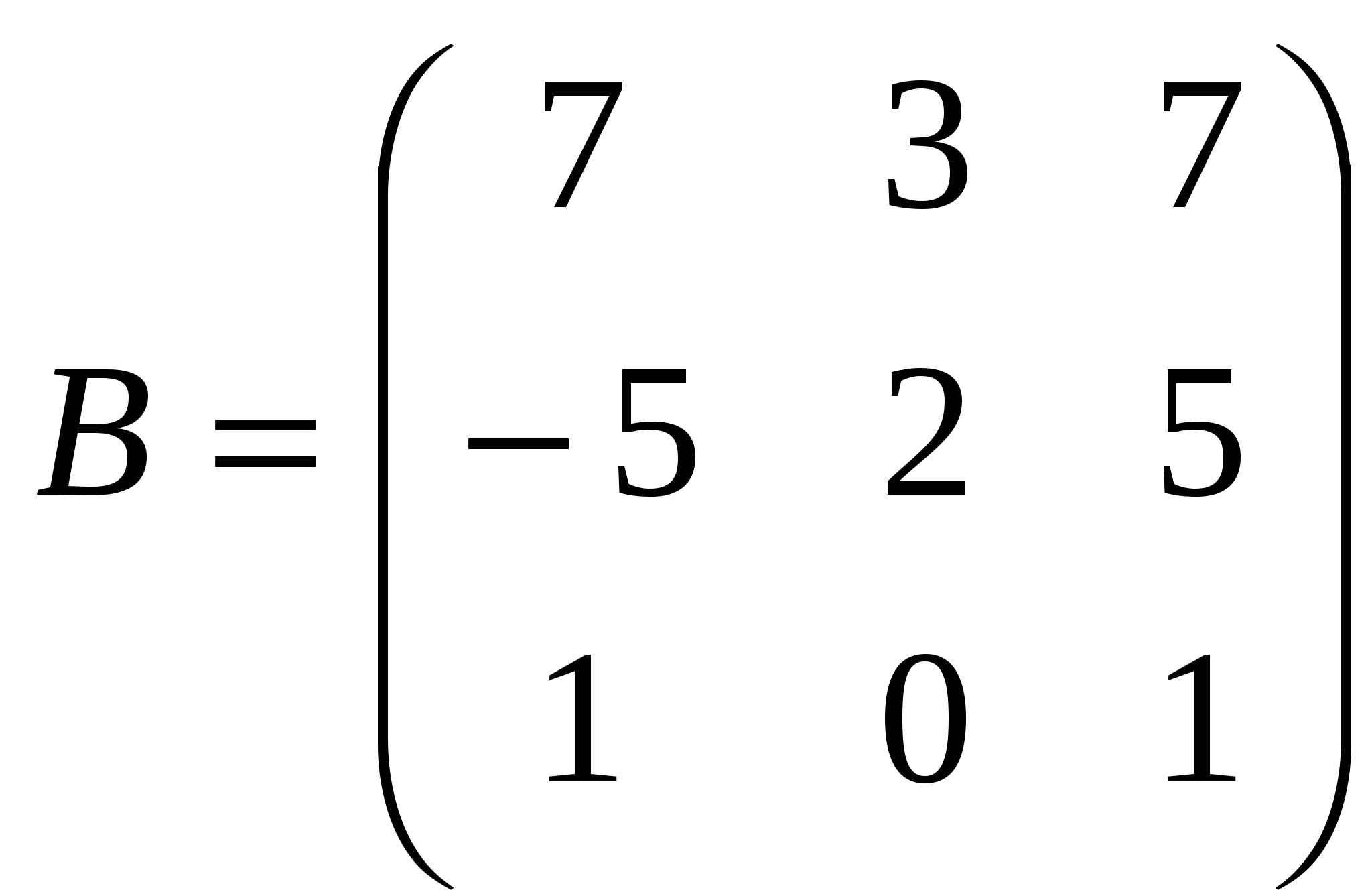
1). Дано: A,B. Найти:
9
а) 3B-A
б) AB
в)B -1
г) B -1B
2).Найти ∆ A: а) методом треугольников;
б) приведением к треугольному виду;
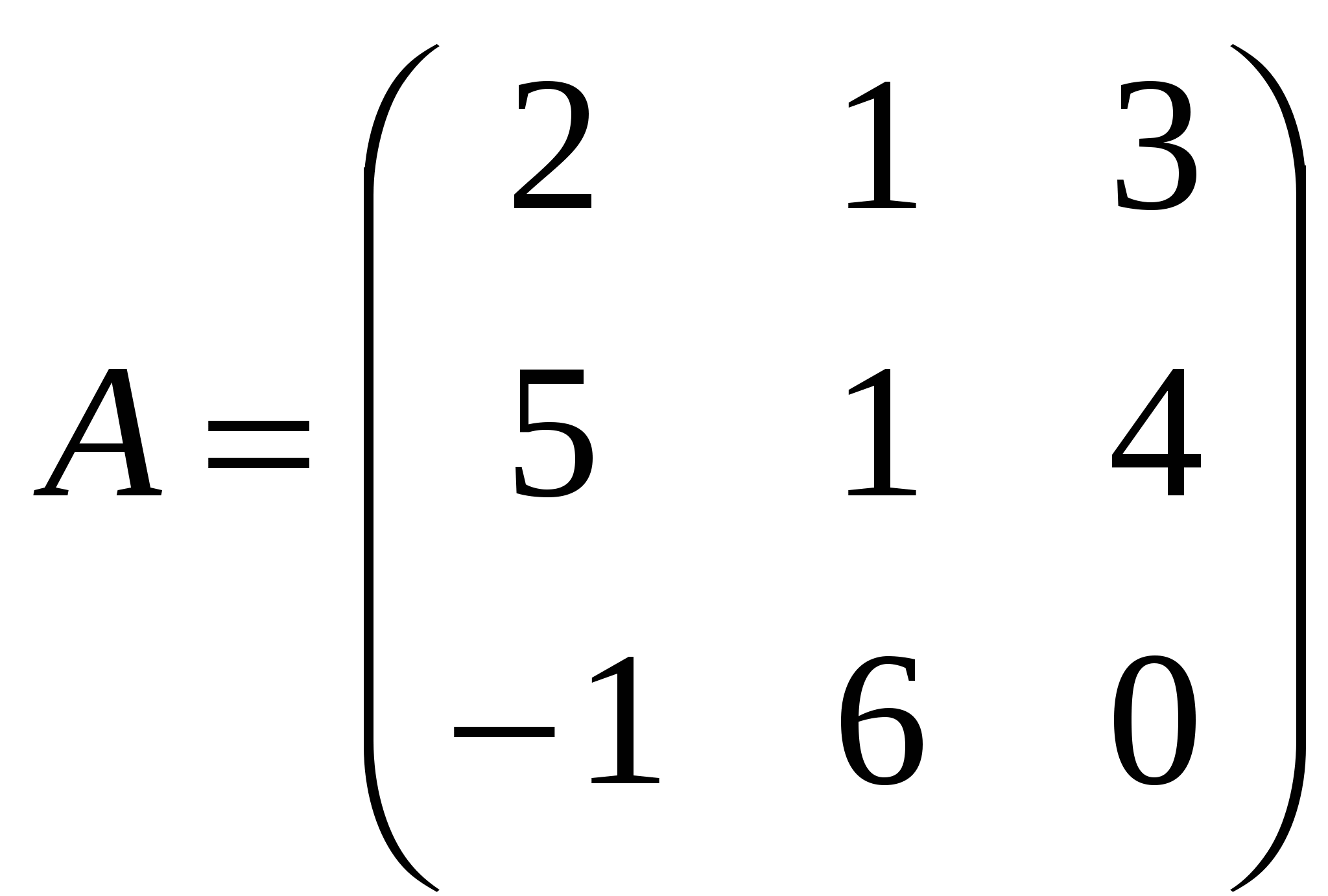
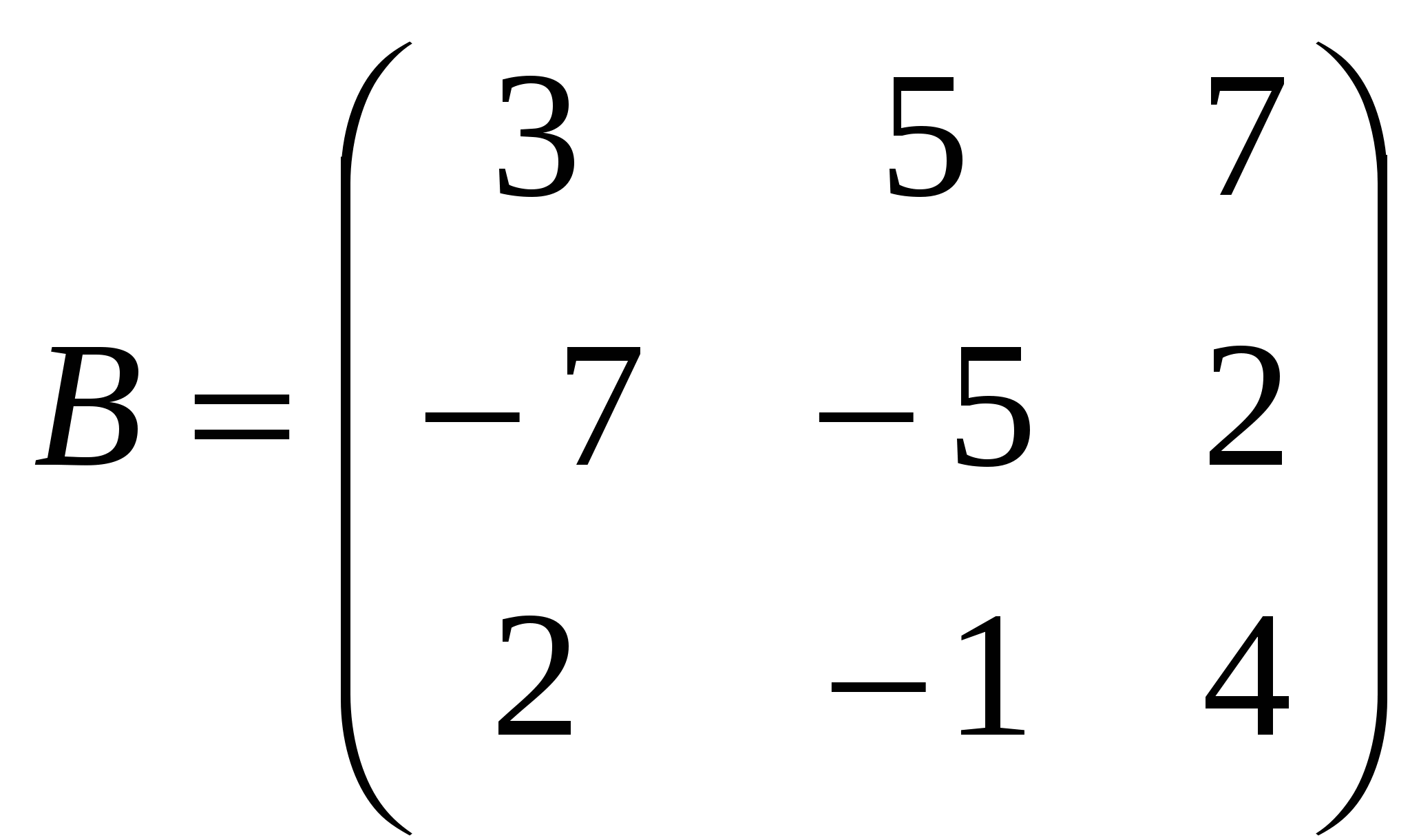
1). Дано: A,B. Найти:
10
а) 2B+2A
б) BA
в)A -1
г) AA -1
2).Найти ∆A: а) методом треугольников;
б) приведением к треугольному виду
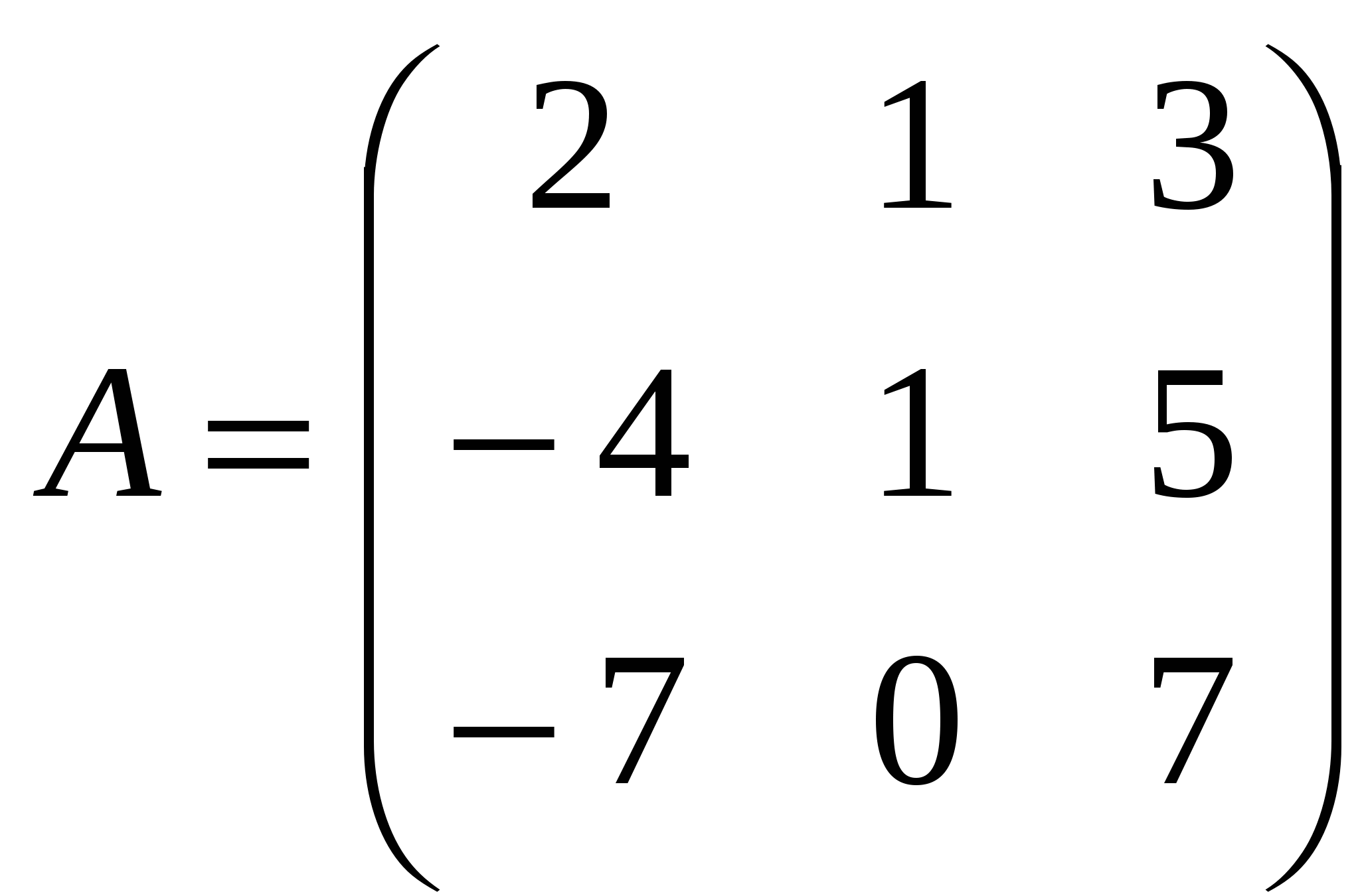
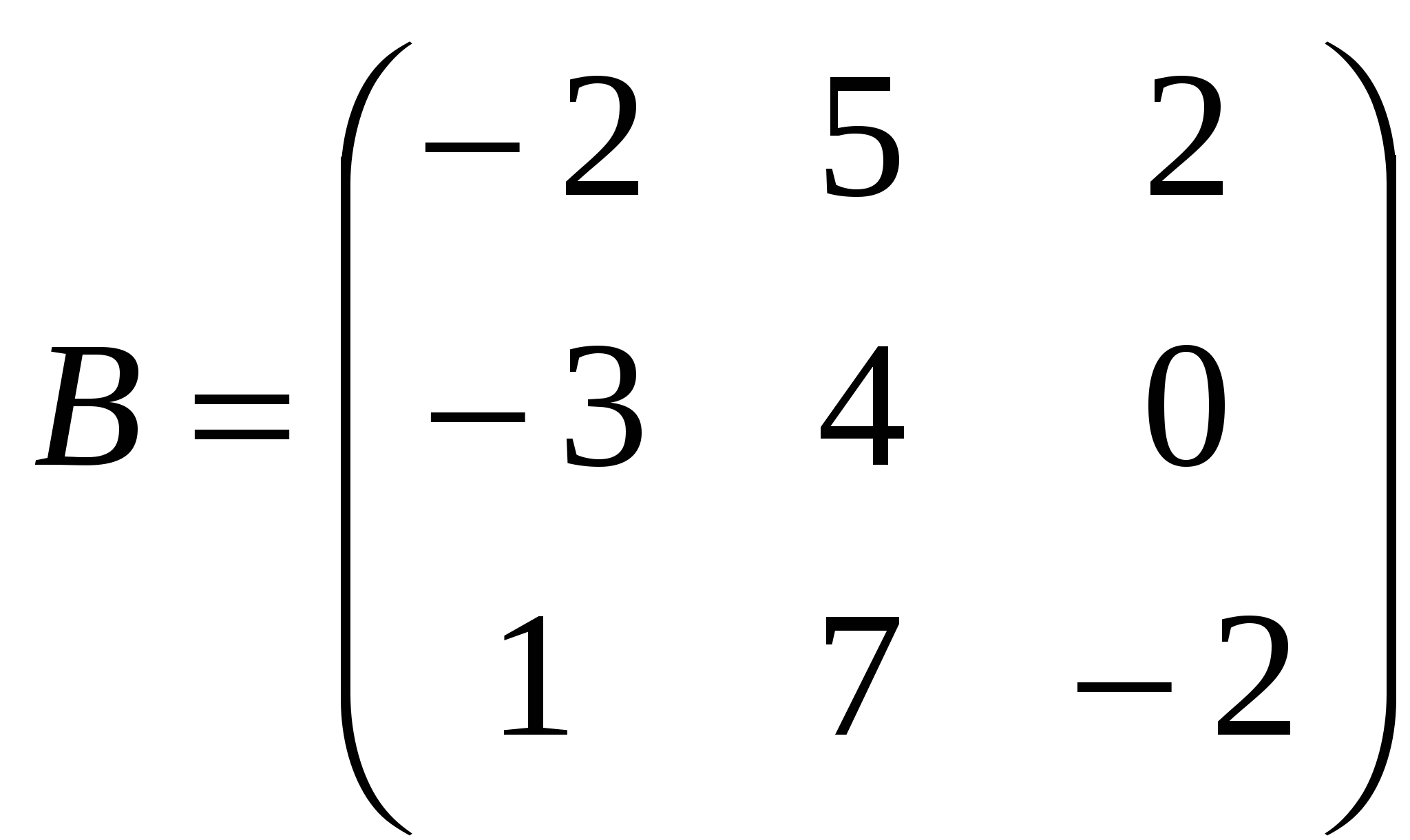
Контрольная работа № 1
1). Дано: A,B. Найти:
11
а) 2B-A
б) BA
в)B -1
г)B -1B
2).Найти def B: а) методом треугольников;
б) приведением к каноническому виду
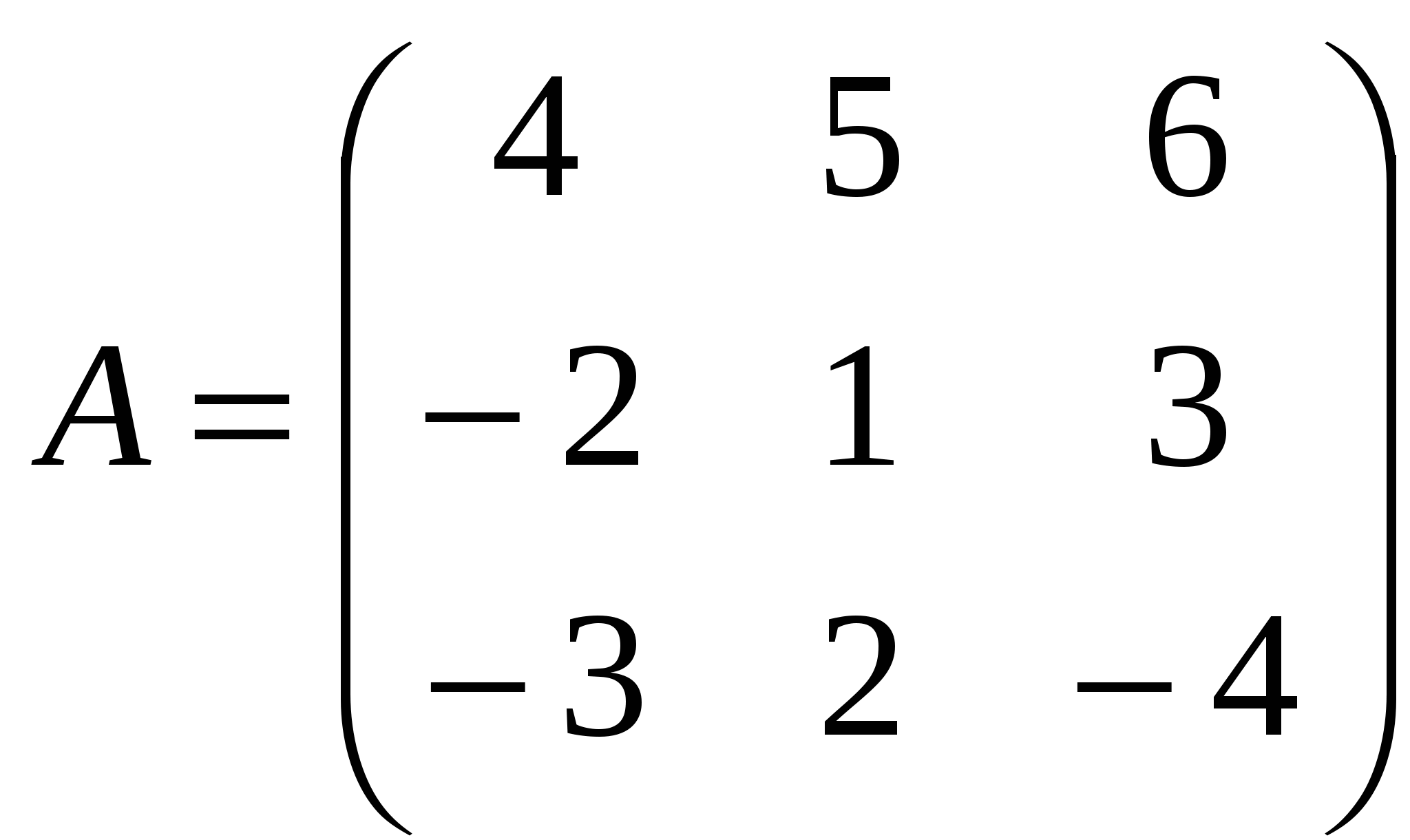
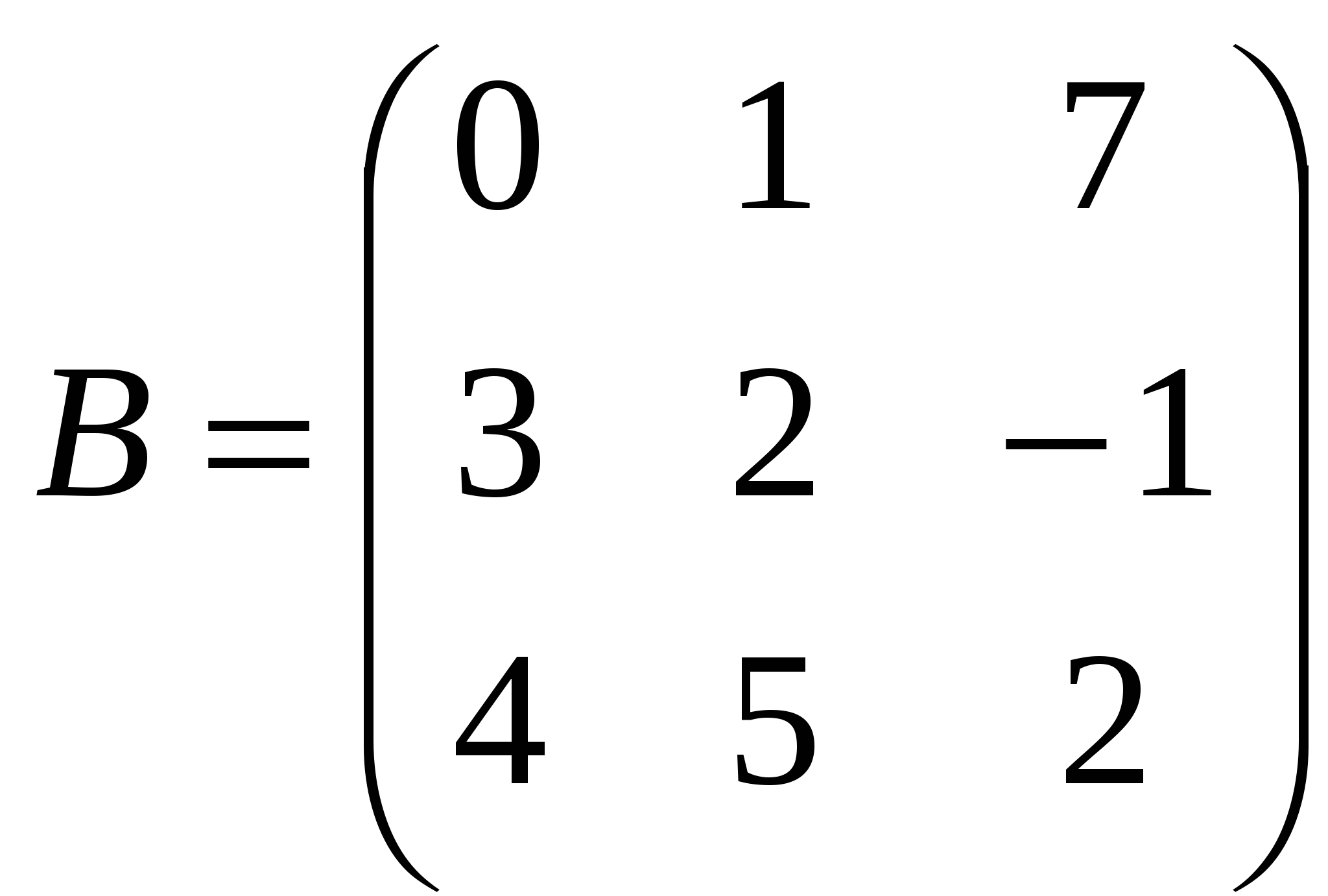
1). Дано: A,B. Найти:
12
а) 2B+A
б) AB
в)A -1
г)A -1A
2).Найти ∆ B: а) приведением к треугольному виду;
б) методом треугольников;
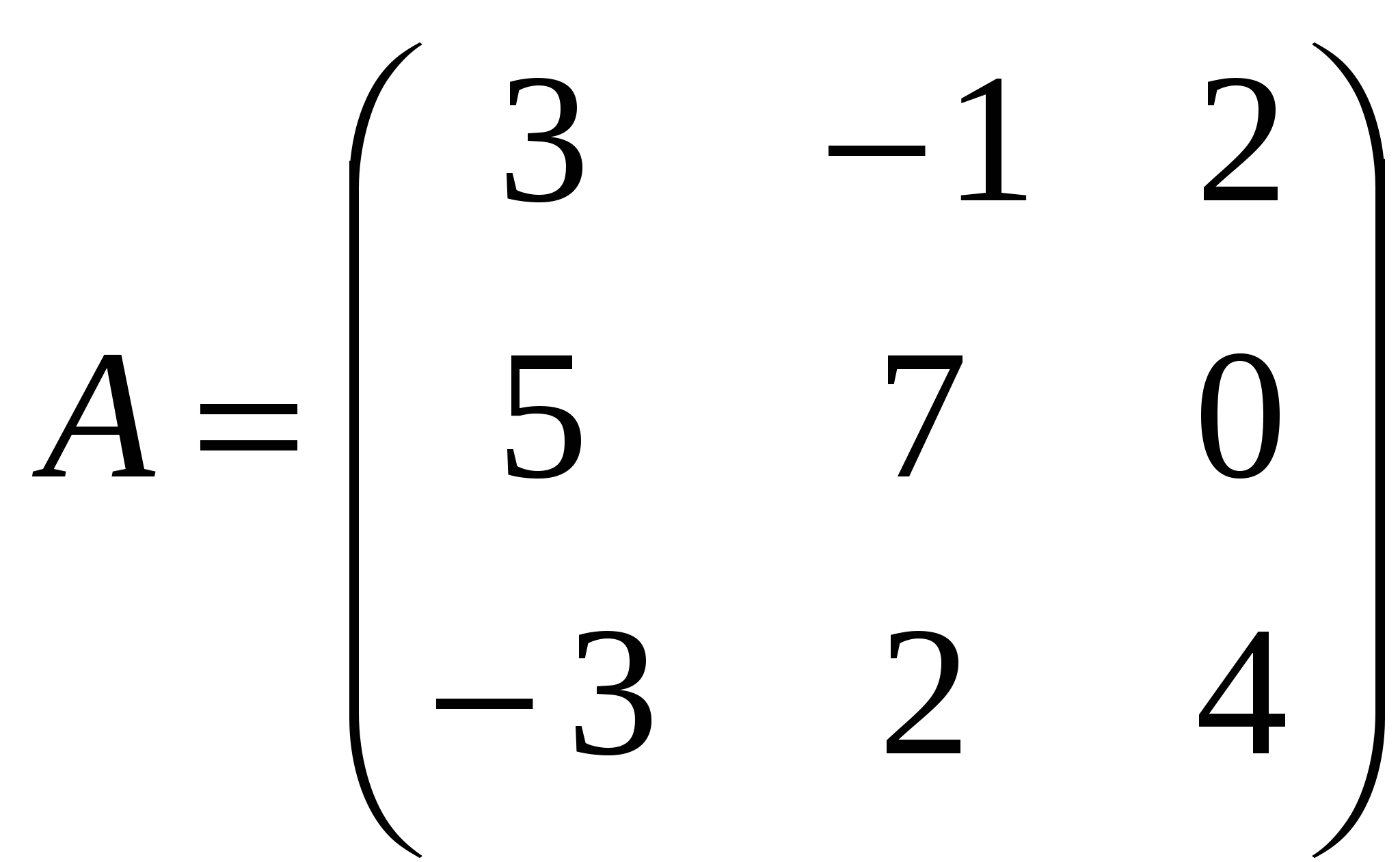
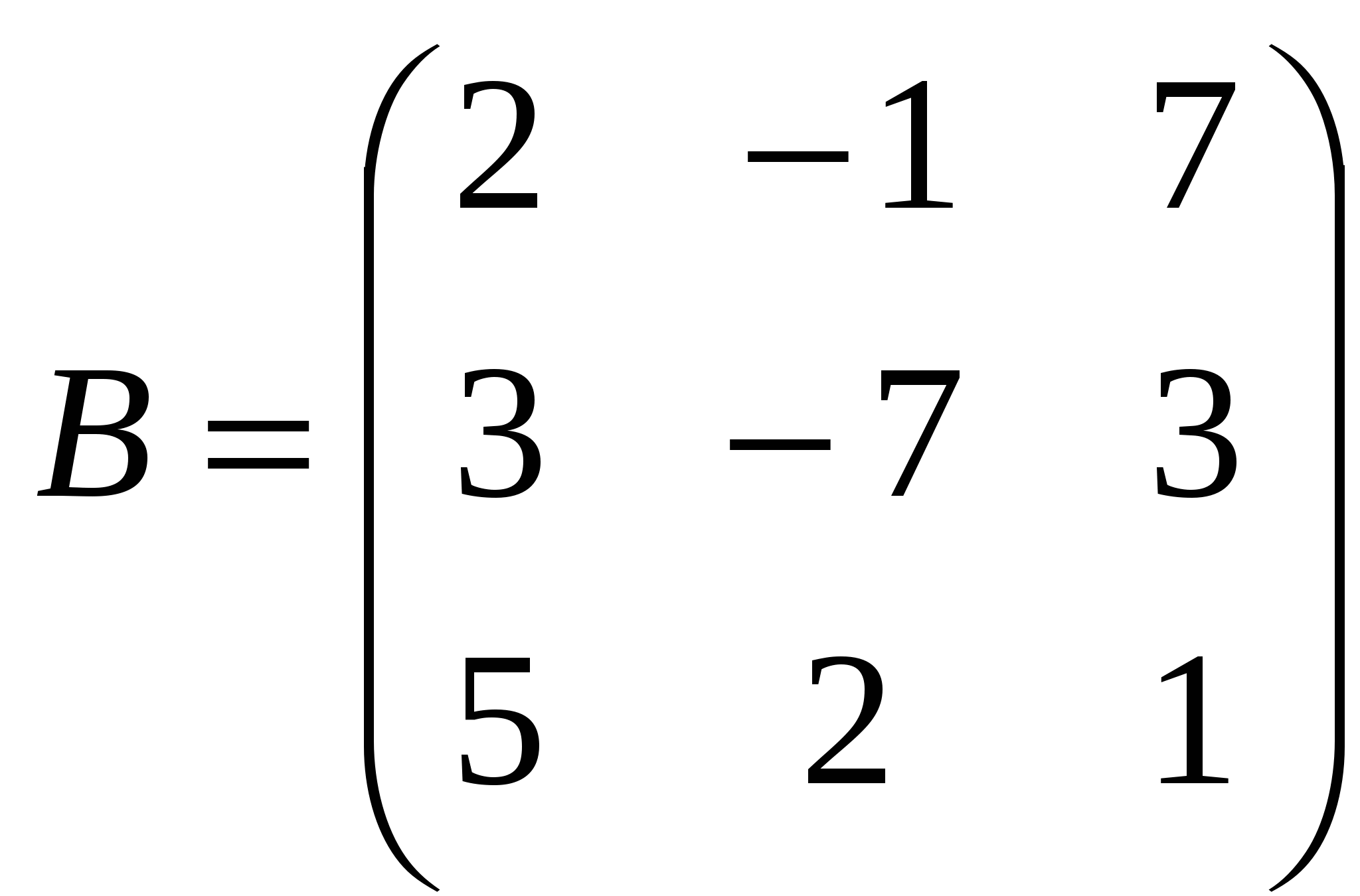
1). Дано: A,B. Найти:
13
а) 3A+B
б) AB
в)A -1
г) A -1A
2).Найти def B: а) методом треугольников;
б) приведением к треугольному виду
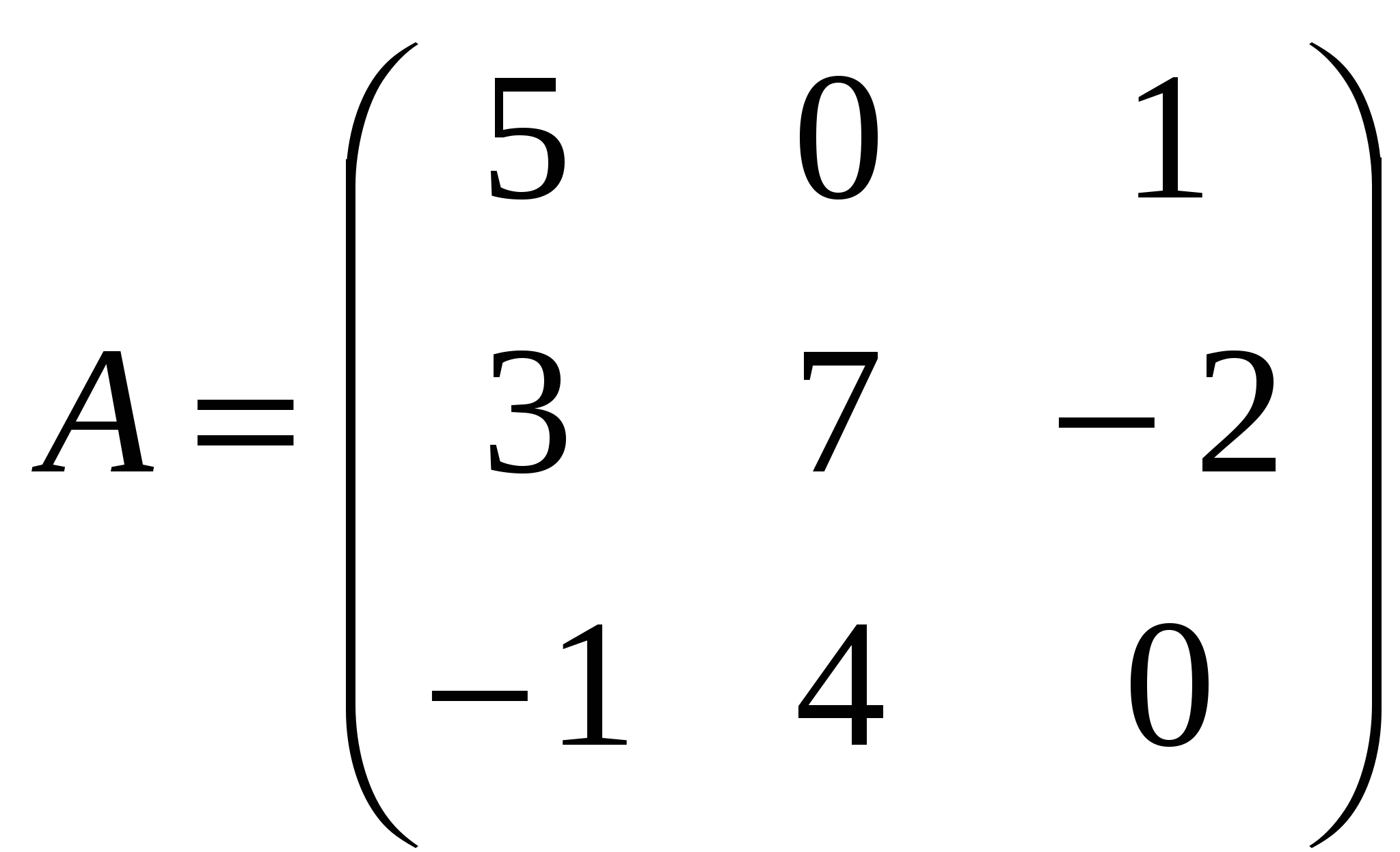
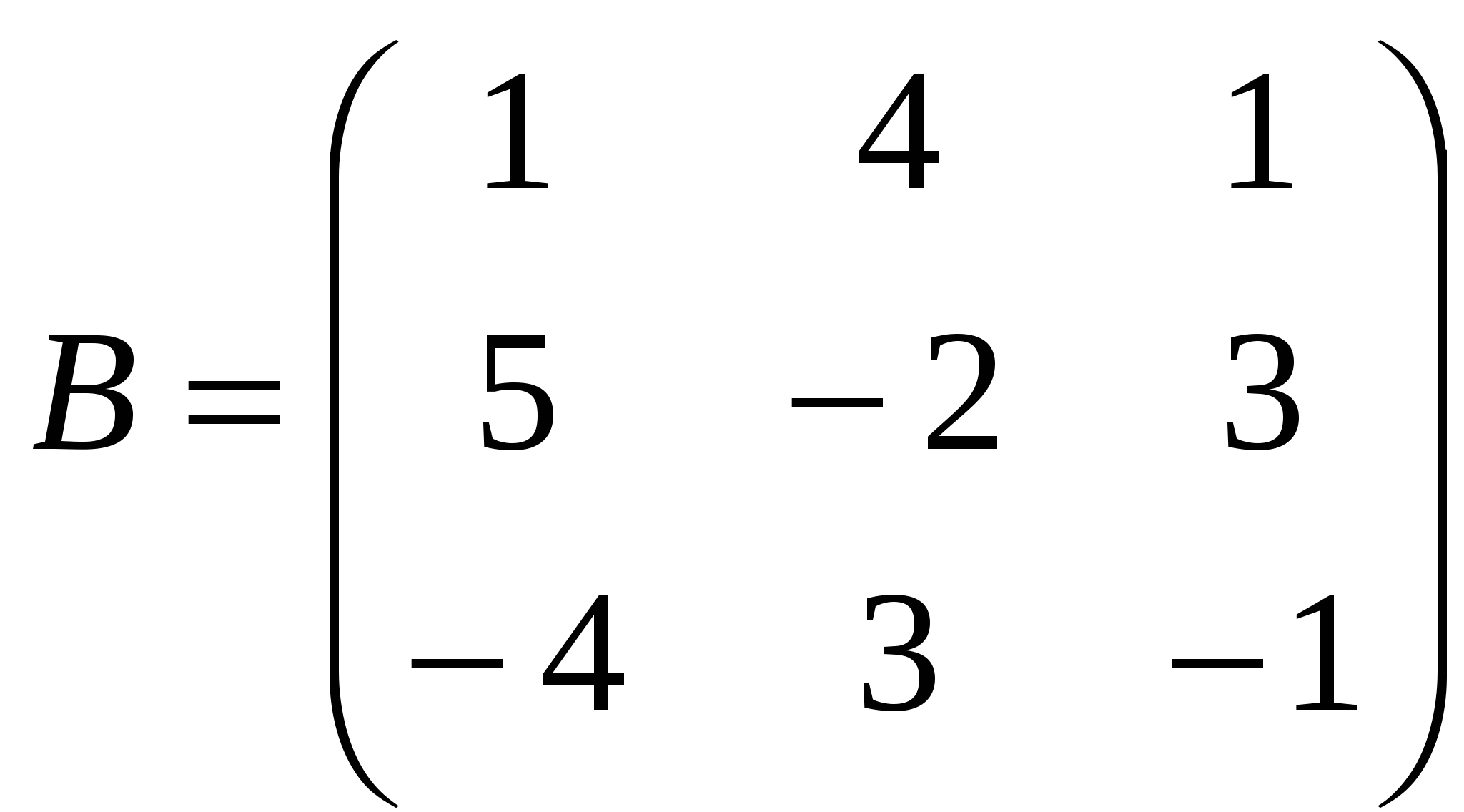
1). Дано: A,B. Найти:
14
а) 2B+3A
б) BA
в)B -1
г)B -1B
2).Найти ∆A: а) методом треугольников;
б) приведением к треугольному виду
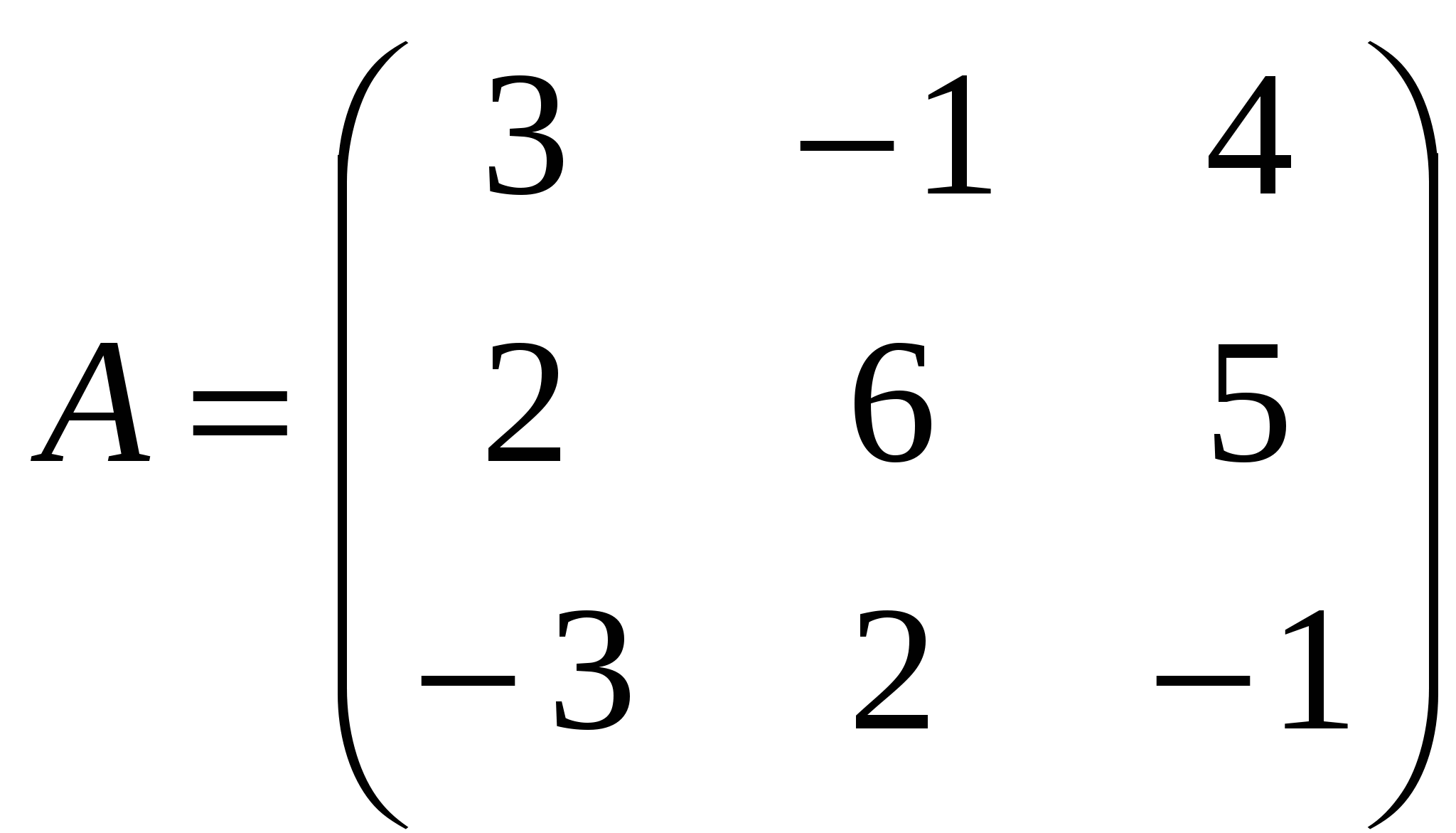
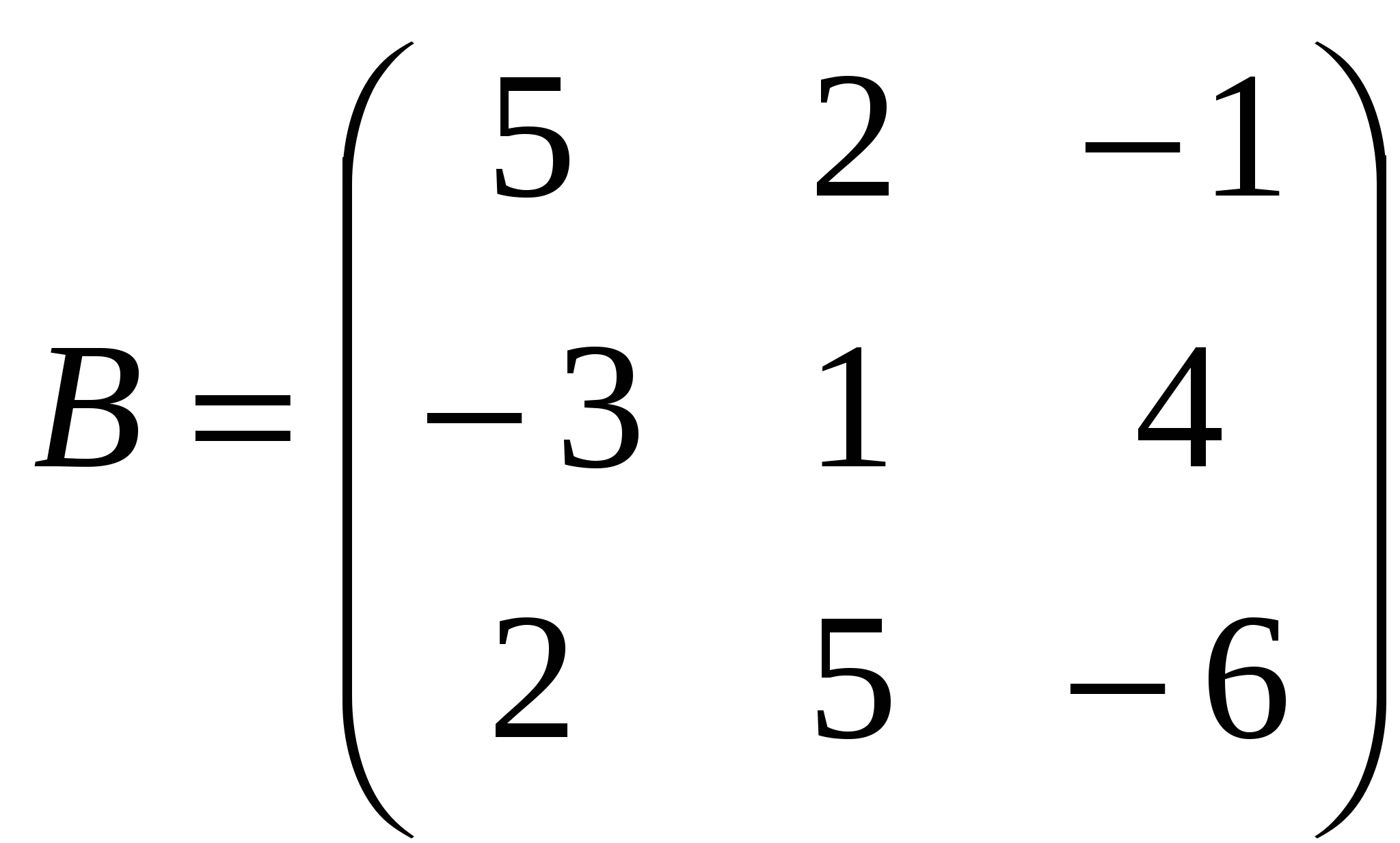
1). Дано: A,B. Найти:
15
а) 3A+B
б) BA
в)B -1
г)B -1B
2).Найти │A│: а) методом треугольников;
б) приведением к каноническому виду
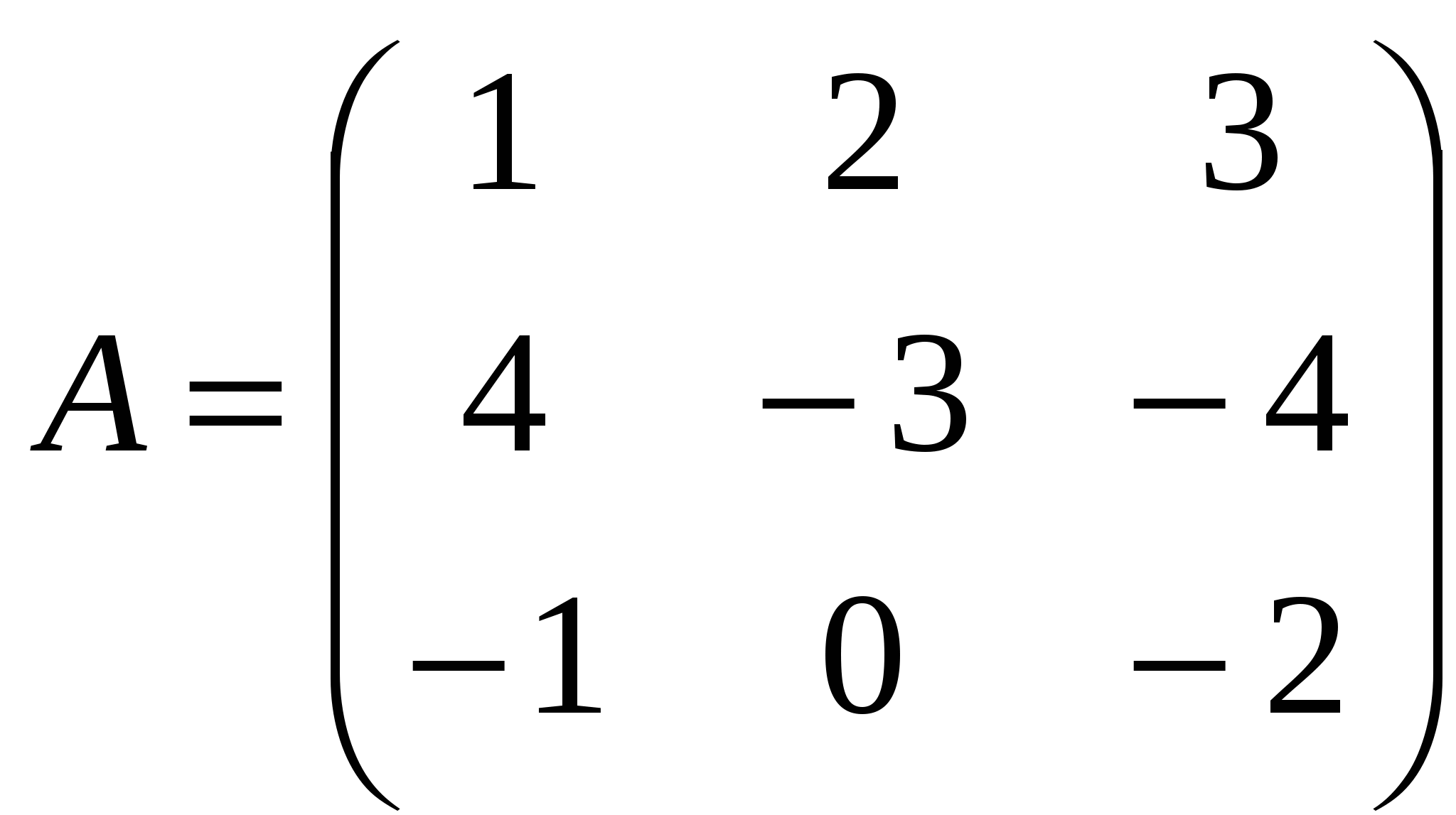
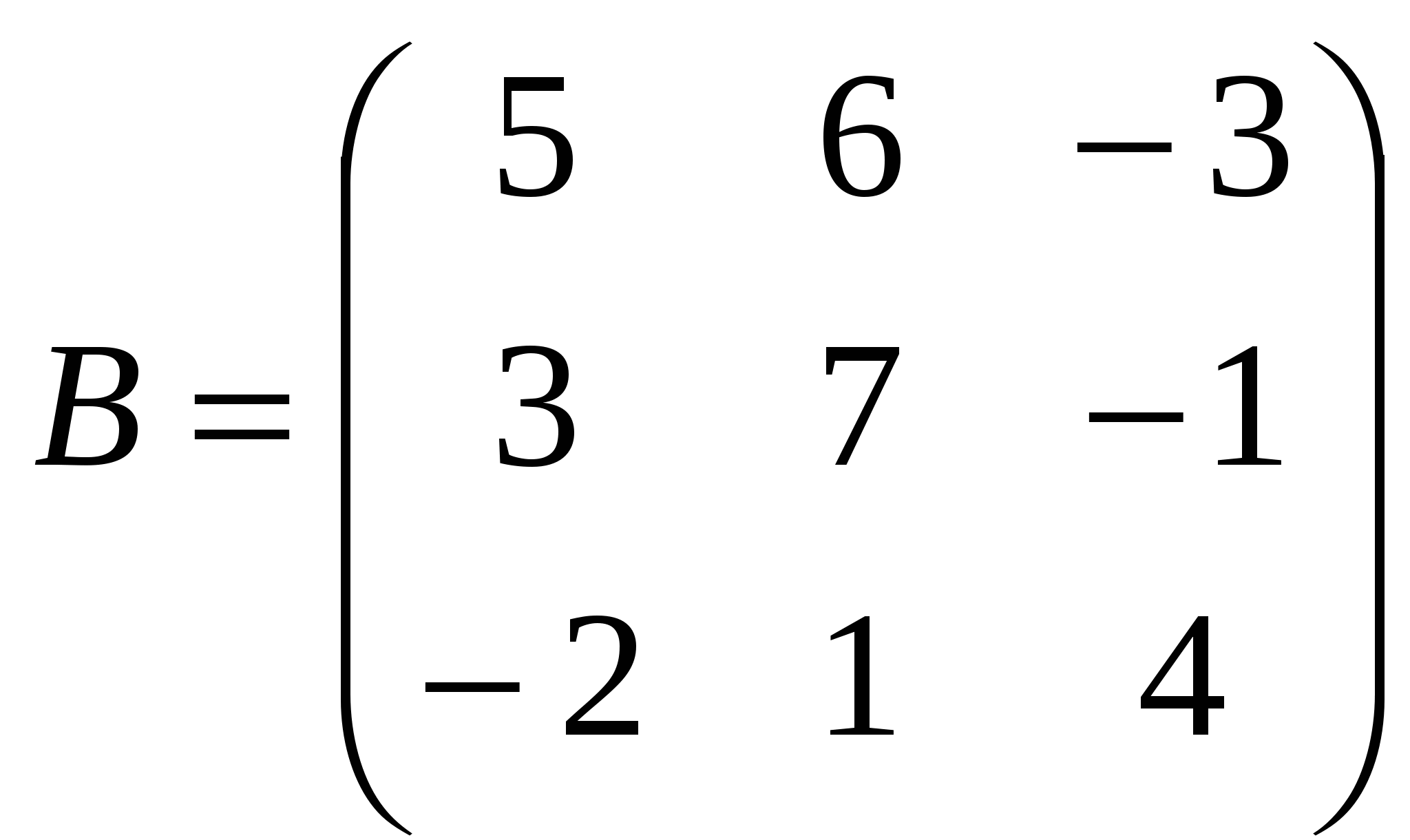
Контрольная работа № 1
1). Дано: A,B. Найти:
16
а) 2A+B
б) AB
в)A -1
г) AA -1
2).Найти def A: а) методом треугольников;
б) приведением к треугольному виду;
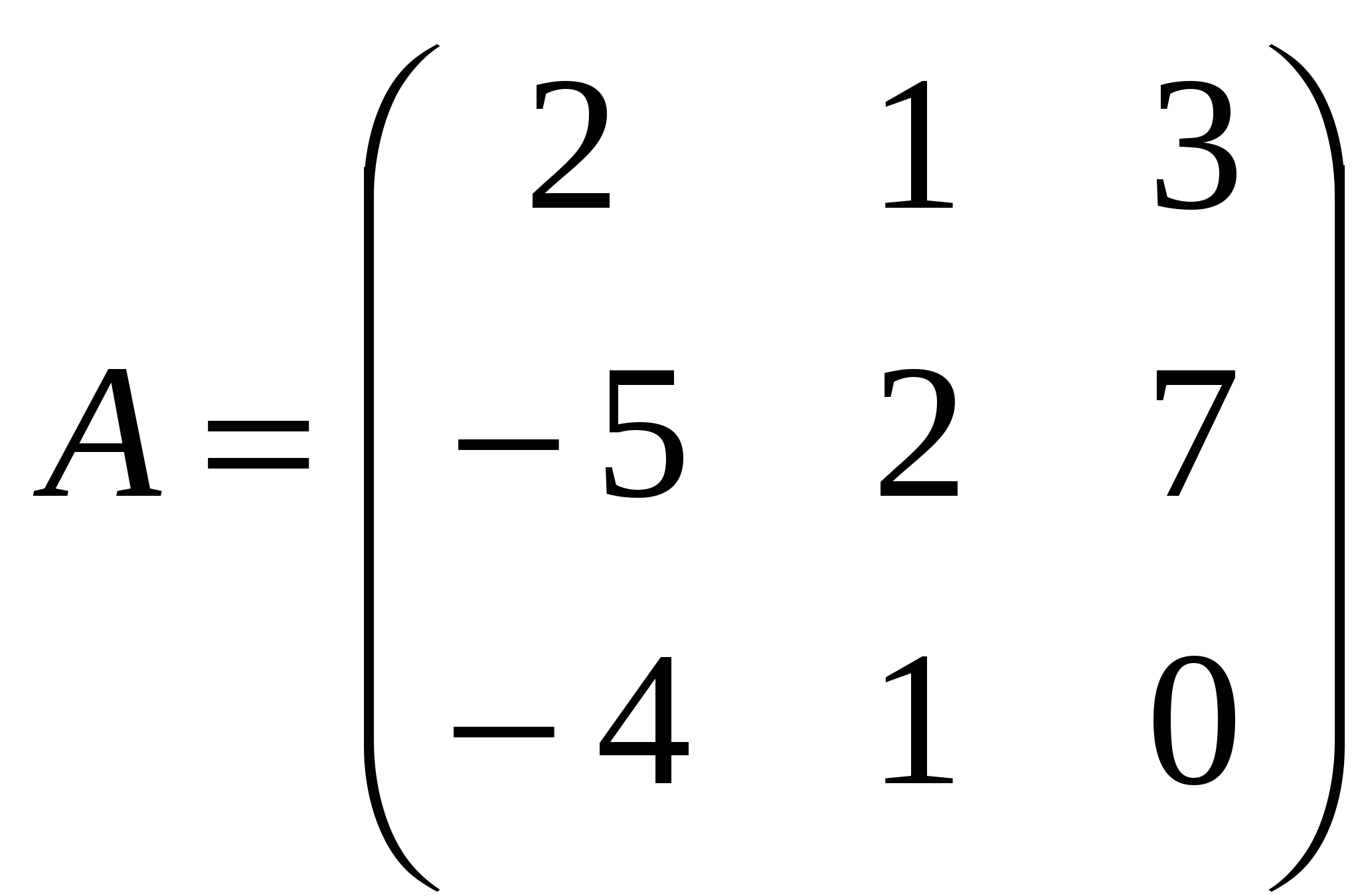
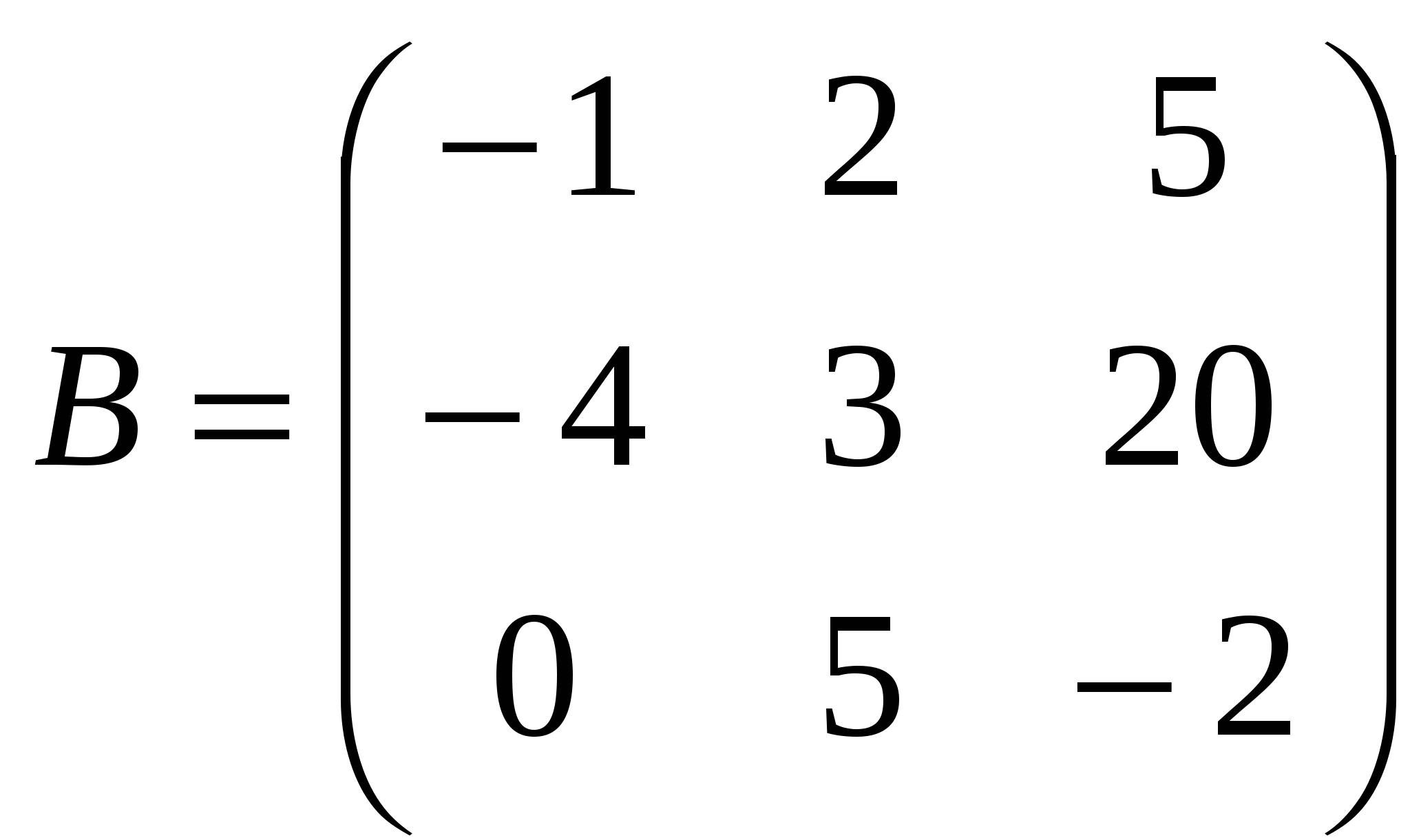
1). Дано: A,B. Найти:
17
а) 3A-B
б) AB
в)B -1
г) BB -1
2).Найти ∆A: а) методом треугольников;
б) приведением к треугольному виду
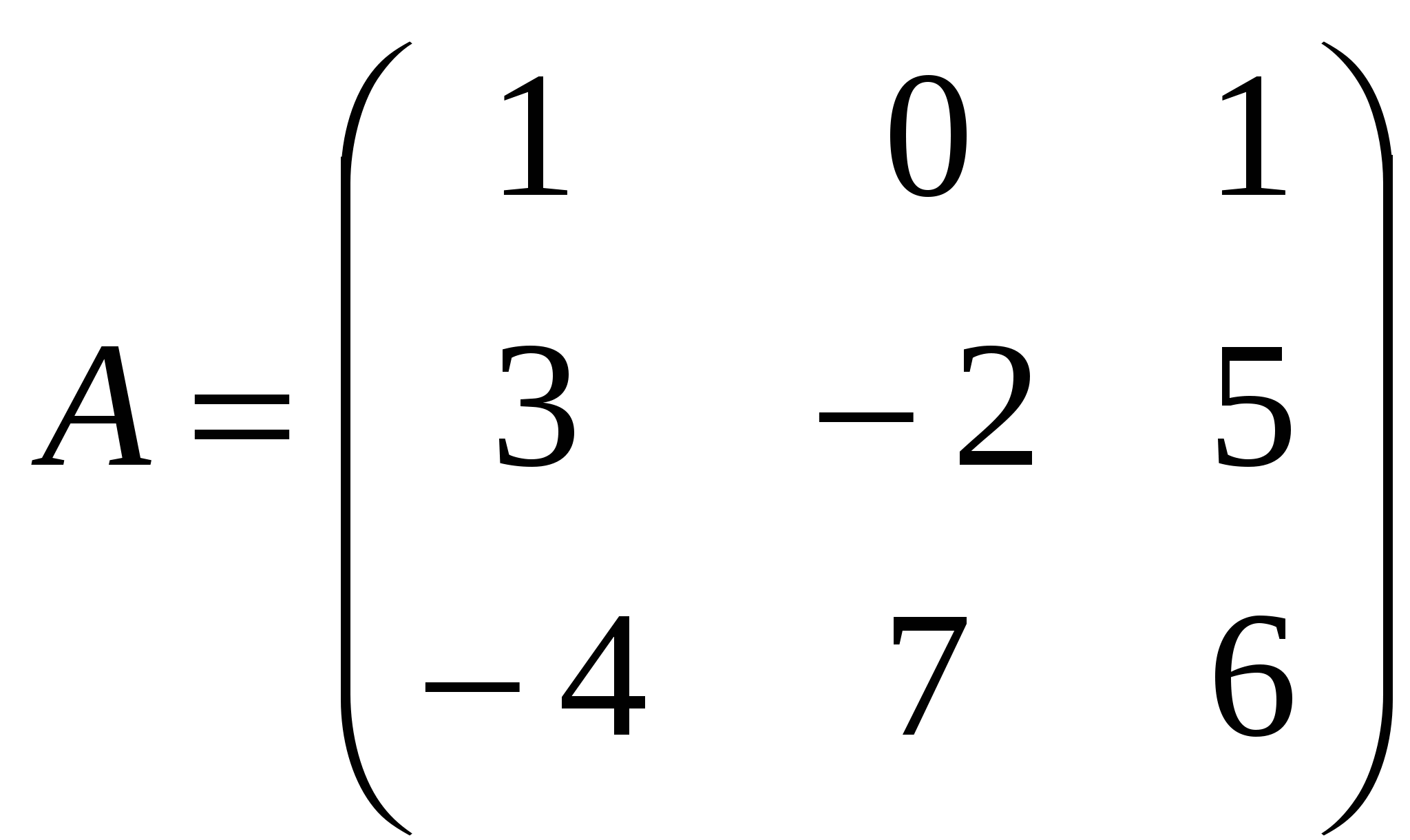
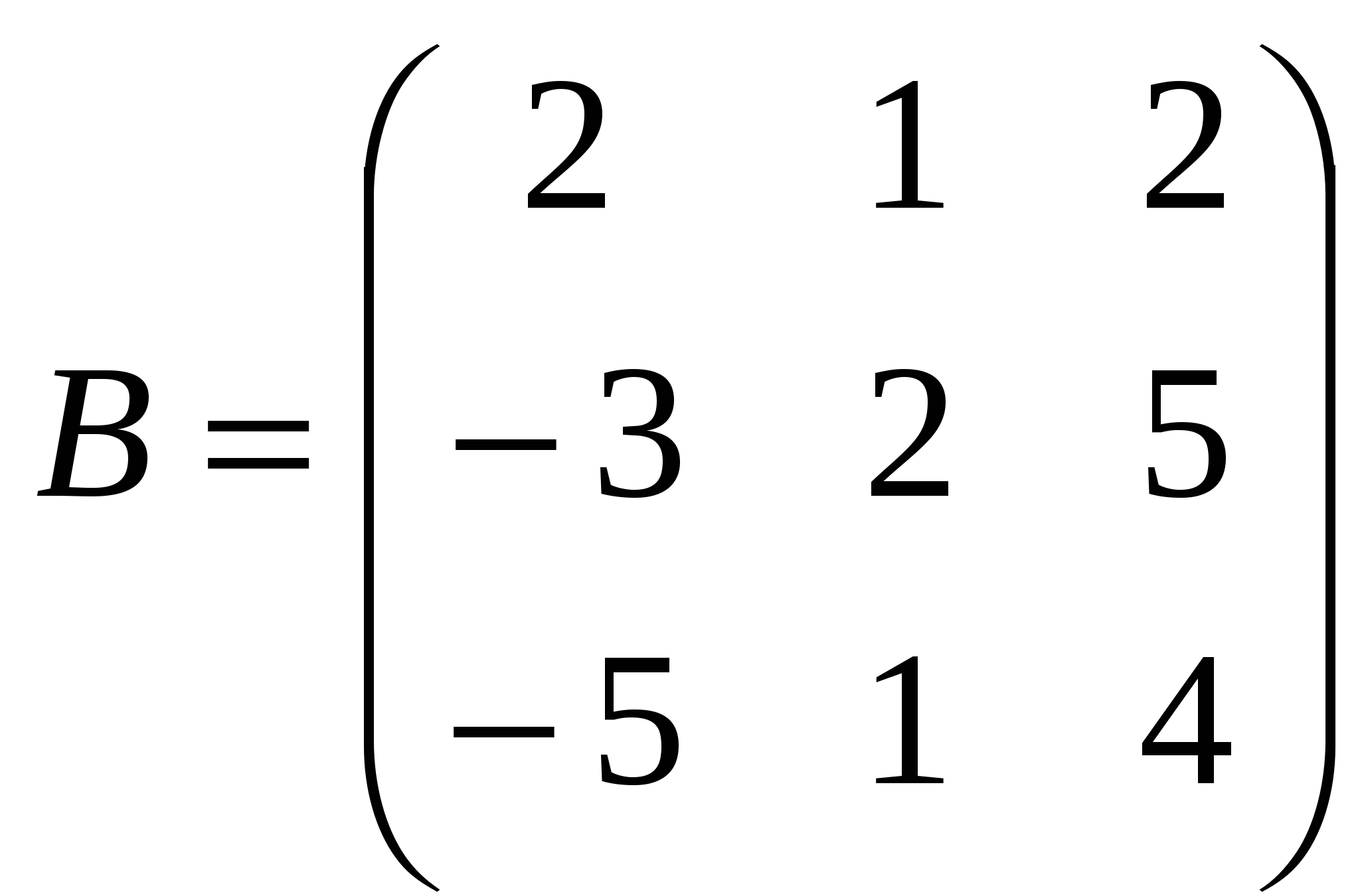
1). Дано: A,B. Найти:
18
а) A+2B
б) AB
в)B -1
г) B -1B
2).Найти def A: а) методом треугольников;
б) приведением к треугольному виду;
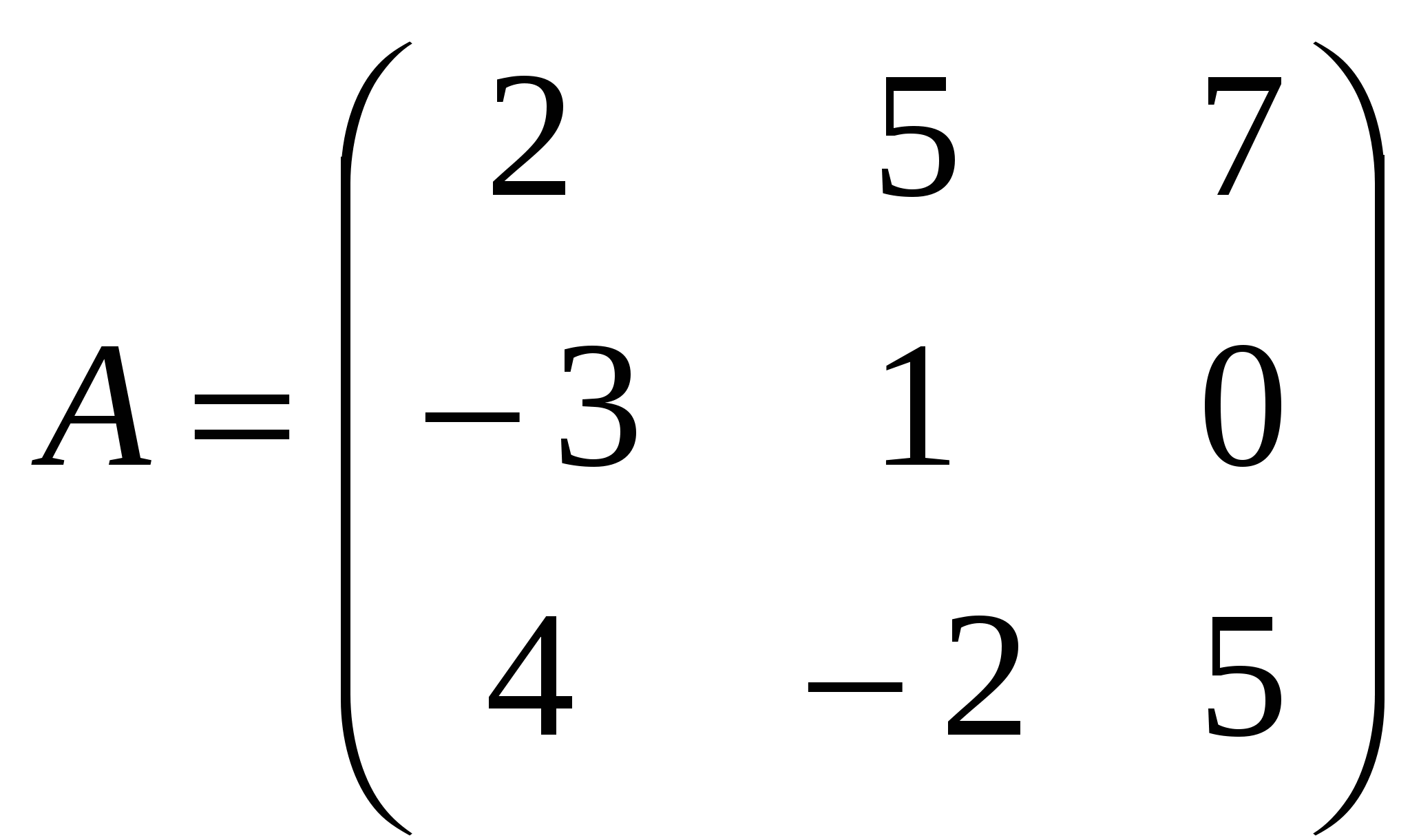
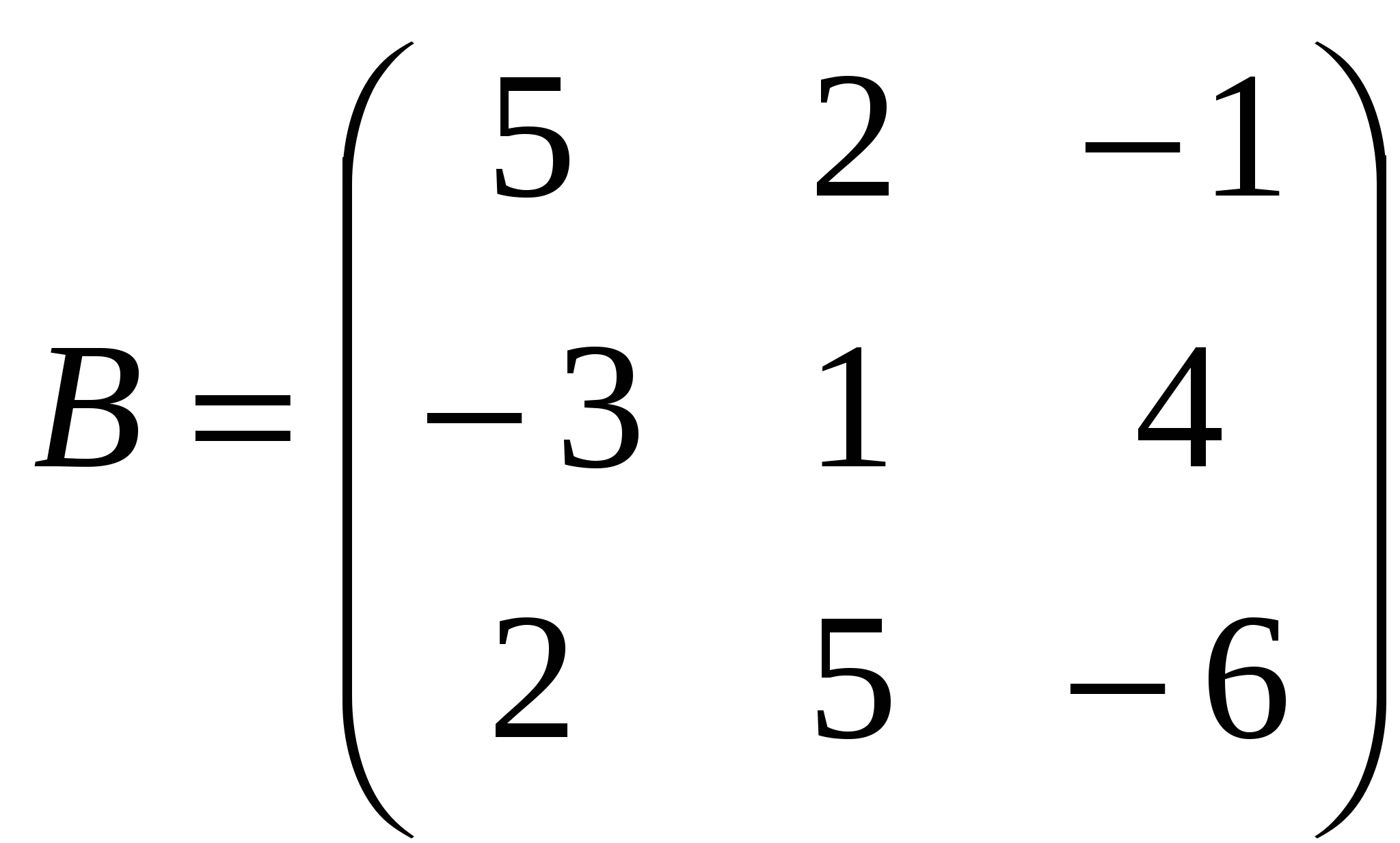
1). Дано: A,B. Найти:
19
а) B+3A
б) AB
в)B -1
г) BB -1
2).Найти def B: а) методом треугольников;
б) приведением к каноническому виду
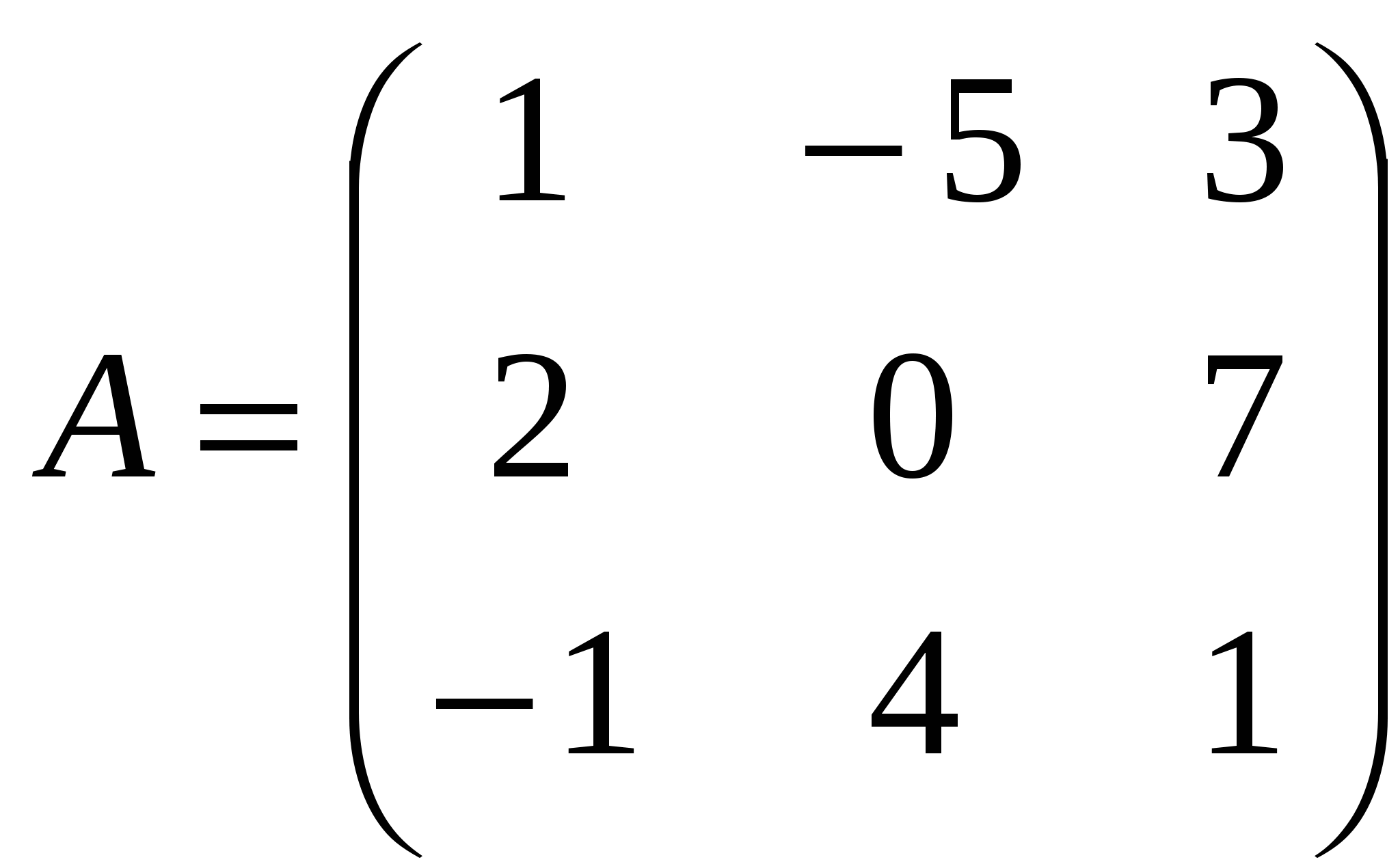
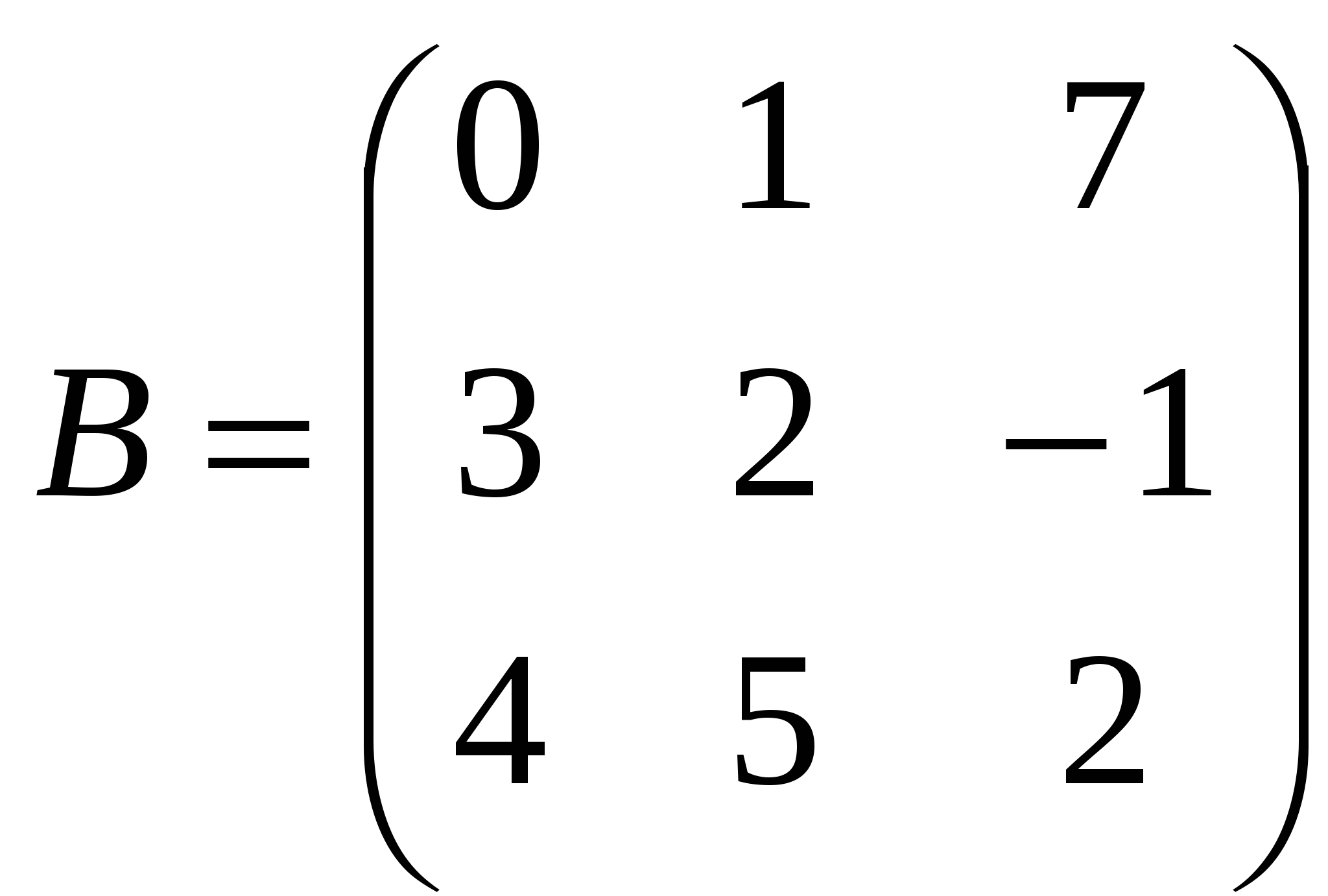
1). Дано: A,B. Найти:
20
а) 2A-B
б) AB
в)A -1
г) A -1A
2).Найти def A: а) методом треугольников;
б) приведением к треугольному виду;
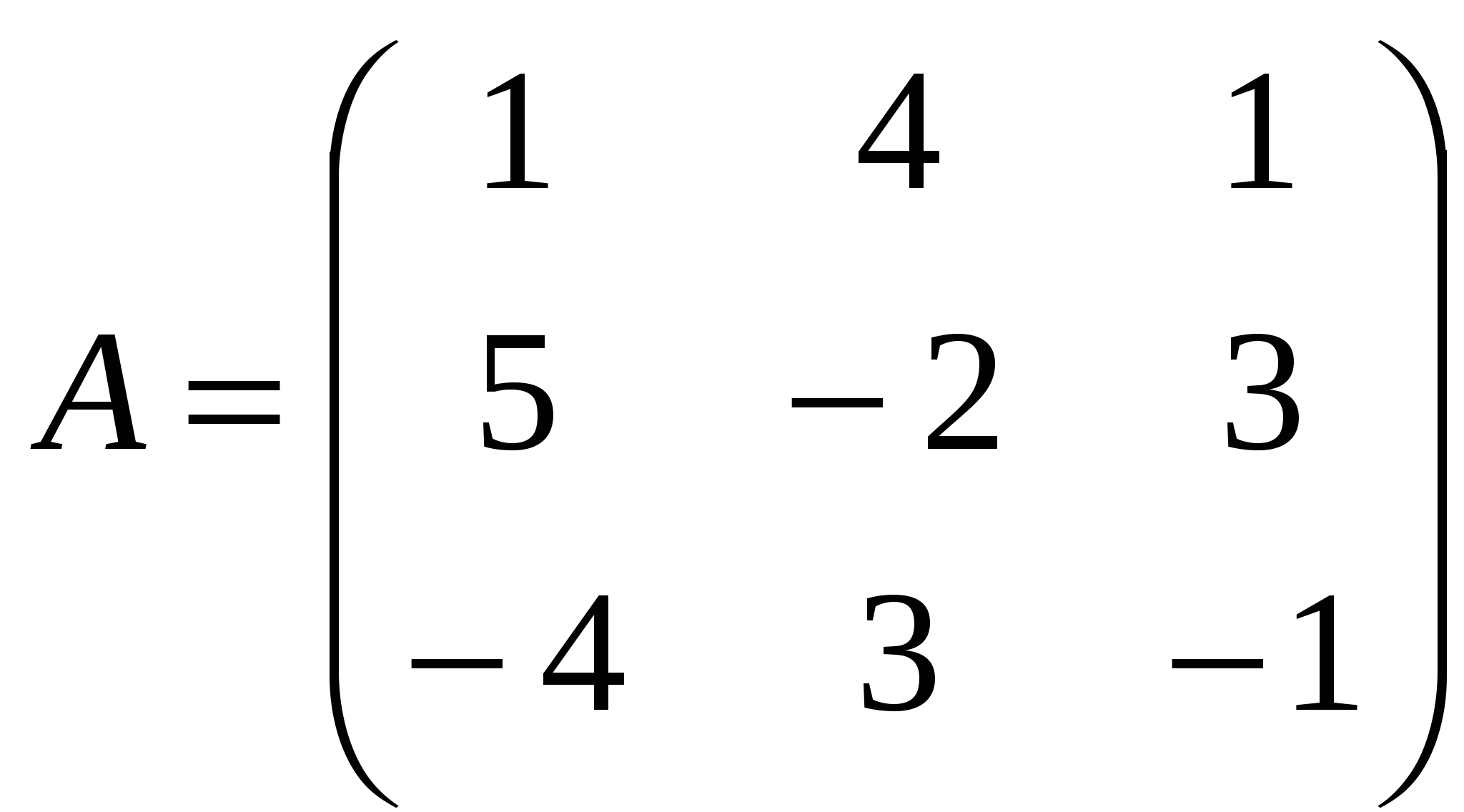
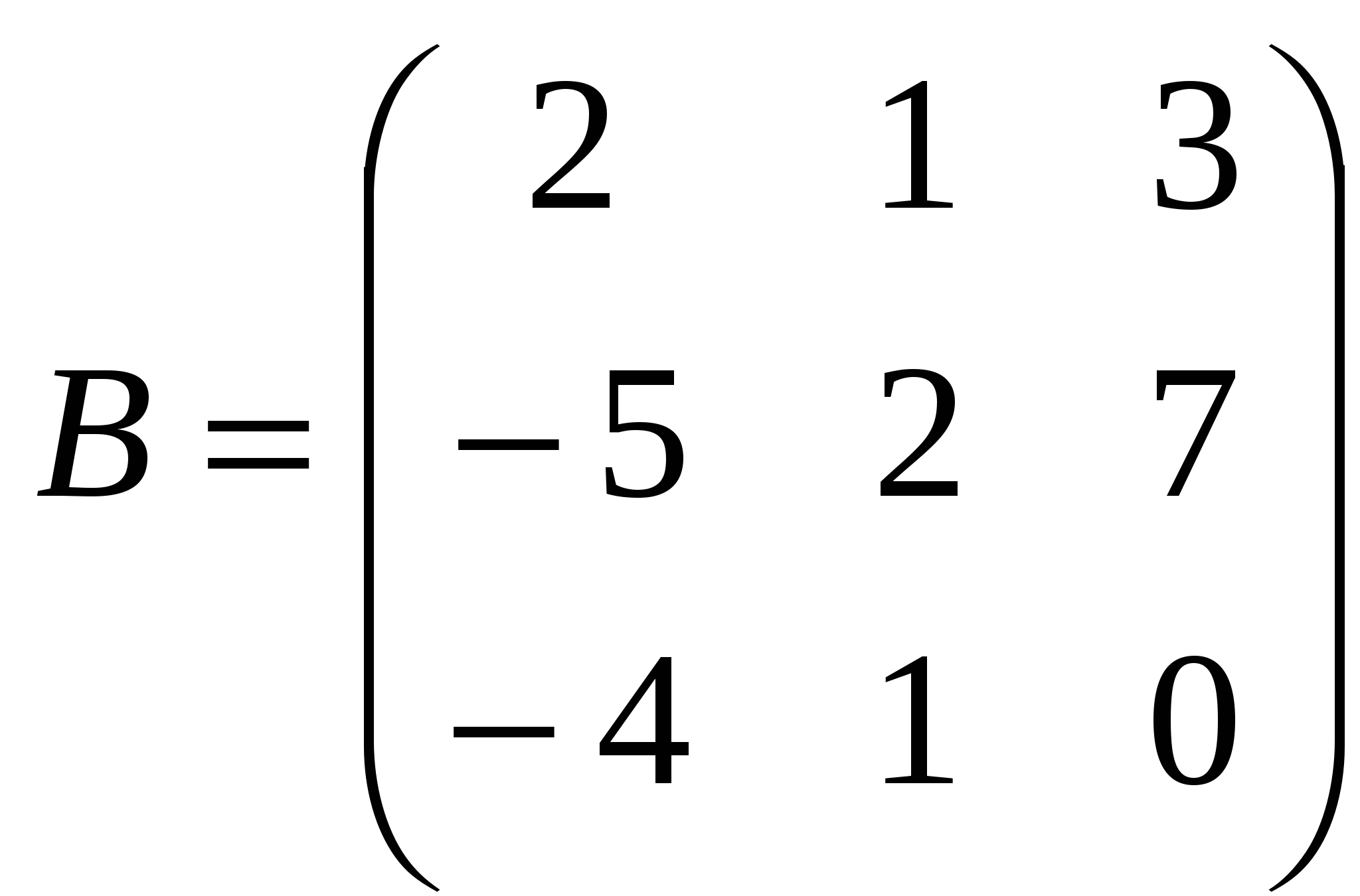
Контрольная работа № 1
infourok.ru
КОНТРОЛЬНАЯ МАТРИЦА (от лат. matrix – источник, начало).
В тестировании: специальная таблица с прорезями на месте правильных ответов, которая накладывается на заполненную учащимися рабочую матрицу с целью быстрой проверки правильности выполнения теста.Новый словарь методических терминов и понятий (теория и практика обучения языкам). — М.: Издательство ИКАР. Э. Г. Азимов, А. Н. Щукин. 2009.
Порождающая матрица — В области математики и теории информации линейный код это важный тип блокового кода, использующийся в схемах определения и коррекции ошибок. Линейные коды, по сравнению с другими кодами, позволяют реализовывать более эффективные алгоритмы… … Википедия
Проверочная матрица — В области математики и теории информации линейный код это важный тип блокового кода, использующийся в схемах определения и коррекции ошибок. Линейные коды, по сравнению с другими кодами, позволяют реализовывать более эффективные алгоритмы… … Википедия
Контроль в обучении — абитуриент тест, айзенка тест, анализ ошибок, анализ речи компьютером, анализ урока, анкета, анкетирование, баллы оценочные, валидность теста, векслера тест, гиперкоррекция, грамматико морфологические ошибки, грамматико синтаксические ошибки,… … Новый словарь методических терминов и понятий (теория и практика обучения языкам)
ГОСТ 15895-77: Статистические методы управления качеством продукции. Термины и определения — Терминология ГОСТ 15895 77: Статистические методы управления качеством продукции. Термины и определения оригинал документа: 2.30. k я порядковая статистика x(k) Определения термина из разных документов: k я порядковая статистика 2.44.… … Словарь-справочник терминов нормативно-технической документации
Линейный код — В области математики и теории информации линейный код это важный тип блокового кода, использующийся в схемах определения и коррекции ошибок. Линейные коды, по сравнению с другими кодами, позволяют реализовывать более эффективные алгоритмы… … Википедия
карта — карта: Картографическое листовое издание, содержащее карту, занимающую всю площадь листа. Источник: ГОСТ 7.60 2003: Система стандартов по информации, библиотечному … Словарь-справочник терминов нормативно-технической документации
ГОСТ Р ИСО/МЭК 19794-5-2006: Автоматическая идентификация. Идентификация биометрическая. Форматы обмена биометрическими данными. Часть 5. Данные изображения лица — Терминология ГОСТ Р ИСО/МЭК 19794 5 2006: Автоматическая идентификация. Идентификация биометрическая. Форматы обмена биометрическими данными. Часть 5. Данные изображения лица оригинал документа: 4.17 JPEG (JPEG): Стандарт сжатия цифрового… … Словарь-справочник терминов нормативно-технической документации
2: — Терминология 2: : Активирующее излучение Излучение, после воздействия которого материал становится радиоактивным Определения термина из разных документов: Активирующее излучение 4.27 антропометрическая точка (anthropometric landmark): Контрольная … Словарь-справочник терминов нормативно-технической документации
MD2 — Криптографическая хеш функция Название MD2 Создан 1989 г. Опубликован апрель 1992 г. Размер хеша 128 бит Число раундов 18 Тип хеш функция MD2 (The MD2 Message Diges … Википедия
Список выпусков телепередачи «Большая разница» — Содержание 1 Первый сезон 2 Второй сезон 3 Третий сезон … Википедия
methodological_terms.academic.ru
Понятие матрицы.
При изучении вопросов, связанных с действием над векторами,а также при изучении систем линейных уравнений приходится иметь дело стаблицами из чисел, которые называются матрицами.
Определение. Матрицей называется прямоугольная таблица изчисел, содержащая /> строк и /> столбцов.
Числа /> и /> называются порядкамиматрицы. Если />, то матрицаназывается квадратной. Для обозначения матрицы пользуются либо вертикальнымидвойными черточками, либо круглыми скобками:
/> или />.
Для краткого обозначения матрицы может быть использована иодна буква, например, />. Кроме того,вместо всей таблицы может быть написано:
/>, где />; />.
Числа /> называютсяэлементами матрицы, /> - номер строки, /> - номер столбца.
Для квадратной матрицы вводится понятие главной и побочнойдиагонали: главная диагональ идет из верхнего левого угла в нижний правый; побочная- из верхнего правого в нижний левый.
Ранг матрицы. Эквивалентные матрицы.
Дана прямоугольная матрица:
/>
Выделим в этой матрице k произвольных строк и kпроизвольных столбцов (k Ј m, k Ј n).
Определение. Определитель k-го порядка, составленныйиз элементов матрицы A, расположенных на пересечении выделенных строк истолбцов, называется минором k-го порядка матрицы A. Матрица Aимеет C km*C kn миноров k-гопорядка.
Определение. Рассмотрим всевозможные миноры матрицы A,отличные от нуля. Рангом матрицы A называется наибольший порядокотличных от нуля миноров этой матрицы. Если все элементы матрицы равны нулю, торанг этой матрицы принимают равным нулю.
Определение. Всякий отличный от нуля минор матрицы, порядоккоторого равен рангу этой матрицы, называется базисным минором матрицы.
Ранг матрицы A будем обозначать через r (A). Еслиr (A) = r (B), то матрицы A и B называются эквивалентными.
Полезно иметь ввиду, что ранг матрицы не изменяется отэлементарных преобразований. Под элементарными преобразованиями понимаются:
1) замена строк столбцами, а столбцов соответствующимистроками;
2) перестановка строк матрицы;
3) вычеркивание строки, все элементы которой равны нулю;
4) умножение какой-либо строки на число, отличное от нуля;
5) прибавление к элементам одной строки соответствующихэлементов другой строки.
Действия над матрицами.
Определение. Две матрица называются равными, если ониимеют одинаковые порядки и все их соответствующие элементы совпадают.
Определение. Суммой двух матриц /> (/>) и /> (/>) одинаковых порядков /> называется матрица /> (/>) того же порядка, элементыкоторой равны />.
На письме это действие может быть записано так: />. Операция сложенияобладает, очевидно, обычными свойствами: перестановочным />; сочетательным />.
Определение. Произведением матрицы /> на число /> называется матрица />, элементы которой равны />.
Умножение матрицы на число может быть записано: /> или />.
Эта операция обладает следующими свойствами: сочетательнымотносительно числового множителя />; распределительнымотносительно суммы матриц />; распределительнымотносительно суммы чисел />.
После первых двух действий необходимо отметить, чтовычитание матриц производится аналогично сложению, а деление матрицы на числоможет быть определено как умножение на обратное число.
Определение. Произведением матрицы /> (/>), имеющей порядок />, на матрицу /> (/>), имеющую порядок />, называется матрица /> (/>), имеющая порядок />, элементы которой равны />, где />.
Записывается это действие так />.Из сказанного выше следует, что для нахождения элемента />, в произведении /> необходимо попарноперемножить все соответствующие элементы />-ойстроки матрицы /> на элементы />-го столбца матрицы />, а затем все это сложить. Изопределения также следует, что для умножения двух матриц необходимо, чтобычисло столбцов матрицы /> было равно числустрок матрицы />. Отсюда следует,что одновременно произведение /> и /> существует только лишь втом случае, когда число столбцов /> равночислу строк />, а число столбцов /> равно числу строк />. В этом случае /> и /> будут квадратнымиматрицами, но разных порядков. Чтобы оба произведения были одинакового порядка,необходимо, чтобы /> и /> были квадратными матрицамиодинакового порядка.
Произведение матриц /> имеетсвойства: сочетательное />; распределительное/>. Перестановочным свойствомв общем случае произведение матриц не обладает. Оно выполняется лишь внекоторых случаях.
Среди квадратных матриц необходимо выделить важный классдиагональных матриц.
Определение. Диагональной называется квадратная матрица,все элементы которой, расположенные вне главной диагонали, равны 0:
/>.
В том случае, если />,то для любой квадратной матрицы /> порядка/> справедливо />. Действительно, для /> получаем />. Для /> - />. Отсюда, />.
Среди диагональных матриц с равными друг другу элементамиособое место занимают две матрицы: единичная и нулевая. У единичной матрицы />, обозначается она — />, у нулевой />, обозначается она — />.
Как было показано />, />. Перемножив эти матрицы,можно убедиться, что />; />. Таким образом, матрицы /> и /> выполняют ту же роль, чтои 1 и 0 среди чисел. Вообще нулевой называют любую матрицу, элементы которойравны нулю.
Понятие определителя.
Выше было показано, что матрица — это прямоугольная таблица,составленная из чисел. Особое место среди матриц занимают квадратные матрицы. Рассмотримпроизвольную квадратную матрицу порядка /> илипросто />:
/> (3.1.1)
Оказывается, что с такой матрицей всегда можно связатьвполне определенную численную характеристику.
Определение. Численная характеристика квадратной матрицыназывается ее определителем.
Рассмотрим матрицу первого порядка />.
Определение. Численной характеристикой матрицы первогопорядка, то есть определителем первого порядка, называется величина ее элемента/>.
Обозначается определитель одним из символов />.
Рассмотрим матрицу второго порядка
/>.
Определение. Определителем второго порядка,соответствующим матрице второго порядка, называется число, равное />.
Обозначается определитель одним из символов
/> (3.1.2)
Очевидно, что для составления определителя второго порядка,необходимо найти разность произведения элементов, стоящих на главной диагоналиматрицы, и произведения элементов, стоящих на побочной диагонали этой матрицы.
Поскольку одна из форм обозначения определителя иобозначения матрицы имеют много общего (записывается таблица из чисел), то также, как и у матрицы, говорят о столбцах, строках и элементах определителя.
После того как рассмотрены определители 1-го и 2-гопорядков, можно перейти к понятию определителя любого порядка. Но перед этимвведем понятие минора.
Определение. Минором любого элемента /> квадратной матрицы порядка/> называется определительпорядка />, соответствующий тойматрице, которая получается из первоначальной в результате вычеркивания />-ой строки и />-го столбца, на пересечениикоторых стоит элемент />.
Обычно минор элемента /> обозначается/>.
Определение. Определителем порядка />, соответствующим матрицепорядка />, называется число, равное
/>.
Обозначается определитель одним из символов
/>
(3.1 3)Приведенное выражение представляет собой правило вычисленияопределителя />-го порядка по элементампервой строки соответствующей ему матрицы и по минорам элементов этой строки,которые являются определителями порядка />.Для /> это правило дает:
/>.
В приведенном правиле вычисления определителя фигурируетлишь первая строка. Возникает вопрос, а нельзя ли вычислить определитель,используя элементы других строк?
Теорема. Каков бы ни был номер строки /> (/>), для определителя />-го порядка справедливаформула
/>,
называемая разложением этого определителя по />-ой строке.
Нетрудно заметить, что в этой формулировке степень при (-1) равнасумме номеров строки и столбца, на пересечении которых стоит элемент />.
Докажем эту теорему для />.В этом случае /> может быть равно только 2,так как /> входит в основноеопределение величины определителя. Итак:
/>.
Полученное выражение совпадает с тем, которое было дано вопределении, следовательно, для определителя 2-го порядка теорема доказана.
Для произвольного /> даннаятеорема доказывается методом математической индукции.
Итак, показано, что определитель может быть разложен полюбой строке. Возникает вопрос, а нельзя ли сделать то же самое, использовавпроизвольный столбец.
Теорема. Каков бы ни был номер столбца /> (/>), для определителя />-го порядка справедливаформула />, называемая разложениемэтого определителя по />-му столбцу.
Докажем теорему для />:
/>.
Данное выражение равно величине определителя, введенной поопределению.
Итак, на основании теорем можно сказать, что для вычисленияопределителя />-го порядка необходимо егоразложить по произвольной строке или столбцу.
В заключение введем еще одно определение.
Определение. Алгебраическим дополнением данного элемента /> определителя />-го порядка называетсячисло, равное />, котороеобозначается />.
Значит, алгебраическое дополнение отличается отсоответствующего минора только лишь знаком. Теперь величину определителя можновычислить с помощью формул:
/>.
Литература1. Лобоцкая Н.Л. Основы высшей математики. Минск, «Высшая школа»,1973.
2. Минорский В.П. Сборник задач по высшей математики.
3. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М.,«Наука», 1986.
4. Гмурман В.Е. Теория вероятностей и математическая статистика. М., «Высшаяшкола» изд. 5, 1977.
5. Гмурман В.Е. Руководство к решению задач по теории вероятностей иматематической статистике. М., «Высшая школа» изд.2.
6. Баврин И.И. Высшая математика — 1980 г.3
7. Дж. Голуб, Ч. Ван Лоун Матричные вычисления. — М.: Мир, 1999.
8. Беллман Р. Введение в теорию матриц. — М.: Мир, 1969.
9. Гантмахер Ф.Р. Теория матриц (2-е издание). — М.: Наука, 1966.
10. Ланкастер П. Теория матриц. — М.: Наука, 1973.
11. Соколов Н.П. Пространственные матрицы и их приложения. — М.: ГИФМЛ, 1960.
www.ronl.ru
Самостоятельная работа №3
Системы линейных уравнений
ТЕМА 1. Системы линейных уравнений.
Матрицы и действия с ними.
Определители и их основные свойства.
Методы решения систем линейных уравнений.
Ильин В. А., Позняк Э. Г. Линейная алгебра: Учеб. для вузов.-5-е изд., стер. - М.: Физматлит, 2002. – 317 с.
Беклемишев Д. В. Курс линейной алгебры и аналитической геометрии: - М.: Физматлит, 2003. – 303 с.
Клетеник Д. В. Сборник задач по аналитической геометрии: Учеб. пособие для втузов / ред. Ефимов Н. В. – 17-е изд., стер. – СПб: Профессия, 2001. – 199 с.
Бугров Я.С., Никольский С.М. Высшая математика: Учеб.для вузов: в 3т.-5-е изд., стер.-М.:Дрофа.- (Высшее образование. Современный учебник). т.1. Элементы линейной алгебры и аналитической геометрии.-2003.-284 с.
Данко П.Е. и др. Высшая математика в упражнениях и задачах (с решениями): в 2 ч./ Данко П.Е., Попов А.Г., Кожевникова Т.Я -6-е изд..-М.: ОНИКС 21 век, ч.1. -2002.-304 с.
Решение типового варианта контрольной работы.
Задача 1. Вычислить определитель  .
.
Решение. Для вычисления определителя третьего порядка будем использовать известную формулу Саррюса (правило треугольников), которое может быть записано следующей формулой: 

Ответ: 0.
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Решение:
Решим систему матричным способом, для этого вычислим обратную матрицу  , где
, где - алгебраические дополнения к элементам матрицы.
- алгебраические дополнения к элементам матрицы.

 - матрица невырожденная.
- матрица невырожденная.











Решим систему методом Крамера. Главный определитель системы:
 . Разложим определитель по элементам первой строки, пользуясь формулой
. Разложим определитель по элементам первой строки, пользуясь формулой  .
.

Запишем и вычислим вспомогательные определители


 Тогда
Тогда 


Ответ: 
Решим систему методом Гаусса, для этого составим расширенную матрицу системы и упростим ее приведением к треугольному виду.




Таким образом, система равносильна системе

Находим 


Ответ:  ,
, ,
,
При решении всеми методами одной и той же системы, мы получим один ответ.
Задача 3. Выполнить действия:

Решение. Выполним решение по действиям.
 =
=
 .
.
 .
.

Ответ:  .
.
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Если  ,
, , то произведением матрицы
, то произведением матрицы называется матрица
называется матрица , такая, что
, такая, что , где
, где .
.
Пример: 

Произведение  не определено, так как число столбцов матрицыА (3) не совпадает с числом строк матрицы В (2).
не определено, так как число столбцов матрицыА (3) не совпадает с числом строк матрицы В (2).
Произведение  определено.
определено.

Контрольная работа №1.
Вариант 1
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 2
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 3
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 4
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 5
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 6
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 7
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 8
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 9
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 10
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 11
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 12
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 13
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 14
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 15
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 16
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 17
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 18
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 19
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 20
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 21
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 22
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 23
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 24
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 25
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 26
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 27
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 28
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 29
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера

Задача 3. Выполнить действия:

Контрольная работа №1.
Вариант 30
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера

Задача 3. Выполнить действия:

studfiles.net
Содержание
Введение 2
1. Постановка задачи 3
2. Математические и алгоритмические основы решения задачи 5
2.1 Определитель матрицы 5
2.2 Метод Гаусса для решения систем линейных уравнений 6
2.3 Метод Гаусса для вычисления определителя 8
3. Функциональные модели и блок-схемы решения задачи 9
4. Программная реализация решения задачи 11
5. Пример выполнения программы 16
Заключение 18
Список использованных источников и литературы 19
Введение
Многие проблемы, возникающие в экономических исследованиях, планировании и управлении, будучи сформулированными математически, представляют собой задачи, в которых необходимо решить систему алгебраических уравнений.
Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной.
При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности. Этот метод (который также называют методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.
Помимо аналитического решения СЛАУ, метод Гаусса также применяется для нахождения матрицы, обратной к данной, определения ранга матрицы и нахождения определителя.
Целью данной курсовой работы является реализация вычисления определителя методом исключения Гаусса.
1. Постановка задачи
Пусть дана квадратная матрица A размером NxN. Требуется вычислить её определитель.
Вычисление определителя матрицы заключается в выполнении над матрицей алгоритма Гаусса для решения систем линейных алгебраических уравнений. В результате выполнения алгоритма получаем диагональную матрицу, её определитель равен произведению элементов, стоящих на диагонали.
Пример 1.
Вычислить определитель матрицы методом A исключения Гаусса.

Решение:
Приведем матрицу к диагональному виду методом Гаусса.


Тогда определитель матрицы равен произведению ее элементов, стоящих на диагонали:

Знак определяется количеством обменов строк, следовательно определитель матрицы 
Пример 2.
Вычислить определитель матрицы методом A исключения Гаусса.

Решение:
Приведем матрицу к диагональному виду методом Гаусса.


Тогда определитель матрицы равен произведению ее элементов, стоящих на диагонали:

Знак определяется количеством обменов строк, следовательно определитель матрицы 
2. Математические и алгоритмические основы решения задачи
2.1 Определитель матрицы
Введем определение определителя квадратной матрицы любого порядка. Это определение будет рекуррентным, то есть чтобы установить, что такое определитель матрицы порядка n, нужно уже знать, что такое определитель матрицы порядка n-1. Отметим также, что определитель существует только у квадратных матриц.
Определитель квадратной матрицы A будем обозначать 
Определение. Определителем квадратной матрицы
второго порядка называется число

Определителем
квадратной матрицы порядка n, 
где 
2.2 Метод Гаусса для решения систем линейных уравнений
Пусть дана квадратная матрица A размером NxN. Требуется вычислить её определитель.
Воспользуемся идеями метода Гаусса решения систем линейных уравнений.
Дана система:
a11 x1 + a12 x2 + ... + a1n xn = b1
a21 x1 + a22 x2 + ... + a2n xn = b2
...
an1 x1 + an2 x2 + ... + ann xn = bn
Выполним следующий алгоритм.
На первом шаге найдём в первом столбце наибольший по модулю элемент, поставим уравнение с этим элементом на первую строчку (обменяв две соответствующие строки матрицы A и два соответствующих элемента вектора B), а затем будем отнимать это уравнение от всех остальных, чтобы в первом столбце все элементы (кроме первого) обратились в ноль. Например, при прибавлении ко второй строке будем домножать первую строку на -a21/a11, при добавлении к третьей - на -a31/a11, и т.д.
На втором шаге найдём во втором столбце, начиная со второго элемента, наибольший по модулю элемент, поставим уравнение с этим элементом на вторую строчку, и будем отнимать это уравнение от всех остальных (в том числе и от первого), чтобы во втором столбце все элементы (кроме второго) обратились в ноль. Понятно, что эта операция никак не изменит первый столбец - ведь от каждой строки мы будем отнимать вторую строку, домноженную на некоторый коэффициент, а во второй строке в первом столбце стоит ноль.
Т.е. на i-ом шаге найдём в i-ом столбце, начиная с i-го элемента, наибольший по модулю элемент, поставим уравнение с этим элементом на i-ю строчку, и будем отнимать это уравнение от всех остальных. Понятно, что это никак не повлияет на все предыдущие столбцы (с первого по (i-1)-ый).
В конце концов, мы приведём систему к так называемому диагональному виду:
c11 x1 = d1
c22 x2 = d2
...
cnn xn = dn
Т.е. мы нашли решение системы.
Замечание 1. На каждой итерации найдётся хотя бы один ненулевой элемент, иначе система бы имела нулевой определитель, что противоречит условию.
Замечание 2. Требование, что на каждом шаге мы выбираем наибольший по модулю элемент, очень важно в смысле численной устойчивости метода. Если выбирать произвольный ненулевой элемент, то это может привести к гигантской погрешности, когда получившееся решение будет отличаться в разы от правильного.
2.3 Метод Гаусса для вычисления определителя
Будем выполнять те же самые действия, что и при решении системы линейных уравнений, исключив только деление текущей строки на a[i][i] (точнее, само деление можно выполнять, но подразумевая, что число выносится за знак определителя). Тогда все операции, которые мы будем производить с матрицей, не будут изменять величину определителя матрицы, за исключением, быть может, знака (мы только обмениваем местами две строки, что меняет знак на противоположный, или прибавляем одну строку к другой, что не меняет величину определителя).
Но матрица, к которой мы приходим после выполнения алгоритма Гаусса, является диагональной, и определитель её равен произведению элементов, стоящих на диагонали. Знак, как уже говорилось, будет определяться количеством обменов строк (если их нечётное, то знак определителя следует изменить на противоположный). Таким образом, мы можем с помощью алгоритма Гаусса вычислять определитель матрицы за O(N3).
Осталось только заметить, что если в какой-то момент мы не найдём в текущем столбце ненулевого элемента, то алгоритм следует остановить и вернуть 0.
3. Функциональные модели и блок-схемы решения задачи
Блок-схема решения задачи представлена на рисунке 1.
Рисунок 1 – Блок-схема решения задачи для функции DETERMINATE
4 Программная реализация решения задачи
;ФУНКЦИЯ, ВЫЧИСЛЯЮЩАЯ ОПРЕДЕЛИТЕЛЬ
(DEFUN DETERMINANT (MATRIX SIZE)
;ОБЪЯВЛЕНИЕ ПЕРЕМЕННЫХ
;ОПРЕДЕЛИТЕЛЬ
(DECLARE (SPECIAL DET))
;ВСПОМОГАТЕЛЬНЫЕ МАССИВЫ И ПЕРЕМЕННЫЕ
(DECLARE (SPECIAL PAR))
(DECLARE (SPECIAL R))
(DECLARE (SPECIAL T_))
(DECLARE (SPECIAL I))
(DECLARE (SPECIAL II))
;*********************
(SETQ R (MAKE-ARRAY SIZE :ELEMENT-TYPE 'FLOAT :INITIAL-ELEMENT 0))
(SETQ T_ 1)
(SETQ DET 1)
(DO
((J 0))
((>= J (- SIZE 1)))
;ИСКЛЮЧАЕМ ДЕЛЕНИЕ НА 0
(IF (= (AREF MATRIX J J) 0)
(PROGN
(SETQ II (+ J 1))
;ИЩЕМ СТРОКУ В КОТОРОЙ J-Й ЭЛЕМЕНТ НЕ 0
(DO
(())
((OR (/= (AREF MATRIX II J) 0) (= II (- SIZE 1))))
(SETQ II (+ II 1))
)
;ЕСЛИ НЕТ ТАКОЙ СТРОКИ ОПРЕДЕЛИТЕЛЬ РАВЕН 0
(IF (AND (= (AREF MATRIX II J) 0) (= II (- SIZE 1))) (SETQ T_ 0))
;МЕНЯЕМ J СТРОКУ И НАЙДЕННУЮ
(DO
((K 0))
((>= K SIZE))
(SETF (AREF R K) (AREF MATRIX J K))
(SETF (AREF MATRIX J K) (AREF MATRIX II K))
(SETF (AREF II K) (AREF R K))
(SETQ K (+ K 1))
)
)
)
;ПРЯМОЙ ХОД
;ПРИВЕДЕНИЕ К ТРЕУГОЛЬНОМУ ТИПУ
(DO
((I (+ J 1)))
((>= I SIZE))
;ЕСЛИ (AREF MATR I J)=0 ДЕЛАТЬ НИЧЕГО НЕ НАДО
(IF (/= (AREF MATRIX I J) 0)
(PROGN
(SETQ PAR (/ (AREF MATRIX I J) (AREF MATRIX J J)))
(DO
((JJ J))
((>= JJ SIZE))
(SETF (AREF MATRIX J JJ) (* (AREF MATRIX J JJ) PAR))
(SETF (AREF MATRIX I JJ) (- (AREF MATRIX I JJ) (AREF MATRIX J JJ)))
(SETF (AREF MATRIX J JJ) (/ (AREF MATRIX J JJ) PAR))
(SETQ JJ (+ JJ 1))
)
)
)
(SETQ I (+ I 1))
)
(SETQ J (+ J 1))
)
(IF (/= T_ 0)
(PROGN
(DO
((I 0))
((>= I SIZE))
(SETQ DET (* DET (AREF MATRIX I I)))
(SETQ I (+ I 1))
)
)
;ИНАЧЕ
(SETQ DET 0)
)
;ВОЗВРАЩАЕМ ОПРЕДЕЛИТЕЛЬ
DET
)
(SETQ N 0)
(SETQ INPUT_STREAM (OPEN " D:\MATRIX.TXT" :DIRECTION :INPUT))
;РАЗМЕР МАТРИЦЫ
(SETF N (READ INPUT_STREAM))
(SETQ MATR (MAKE-ARRAY (LIST N N) :ELEMENT-TYPE 'FLOAT :INITIAL-ELEMENT 0))
(SETF MATR (READ INPUT_STREAM))
(CLOSE INPUT_STREAM)
(SETQ DETERM (DETERMINANT MATR N))
;РЕЗУЛЬТАТ
(SETQ OUTPUT_STREAM (OPEN " D:\DETERMINANT.TXT" :DIRECTION :OUTPUT))
;ЗАПИСЫВАЕМ ОПРЕДЕЛИТЕЛЬ
(PRINT 'DETERMINANT OUTPUT_STREAM)
(PRINT DETERM OUTPUT_STREAM)
;ЗАКРЫВАЕМ ФАЙЛ
(TERPRI OUTPUT_STREAM)
(CLOSE OUTPUT_STREAM)
5 Пример выполнения программы
Пример 1.
Рисунок 2 – Входные данные
Рисунок 3 – Выходные данные
Пример 2.
Рисунок 4 – Входные данные
Рисунок 5 – Выходные данные
Пример 3.
Рисунок 6 – Входные данные
Рисунок 7 – Выходные данные
Заключение
Проблема повышения качества вычислений, как несоответствие между желаемым и действительным, существует и будет существовать в дальнейшем. Ее решению будет содействовать развитие информационных технологий, которое заключается как в совершенствовании методов организации информационных процессов, так и их реализации с помощью конкретных инструментов – сред и языков программирования.
Итогом работы можно считать созданную функциональную модель для вычисления определителя методом исключения Гаусса. Созданная функциональная модель и ее программная реализация могут служить органической частью решения более сложных задач.
Список использованных источников и литературы
Бронштейн, И.Н. Справочник по математике для инженеров и учащихся втузов [Текст] / И.Н. Бронштейн, К.А. Семендяев. – М.: Наука, 2007. – 708 с.
Васильев, Ф.П. Численные методы решения экстремальных задач. [Текст] / Ф.П. Васильев – М.: Наука, 2002. C. 415.
Калиткин, Н.Н. Численные методы. [Электронный ресурс] / Н.Н. Калиткин. – М.: Питер, 2001. С. 504.
Кнут, Д.Э. Искусство программирования. Основные алгоритмы [Текст] / Д.Э. Кнут. – М.: Вильямс, 2007. Т.1. – 712 с.
Метод Гаусса [Электронный ресурс] – Режим доступа: http://www.wikipedia.org/wiki/Метод_Гаусса.
Степанов, П.А. Функциональное программирование на языке Lisp. [Электронный ресурс] / П.А.Степанов, А.В. Бржезовский. – М.: ГУАП, 2003. С. 79.
Симанков, В.С. Основы функционального программирования [Текст] / В.С. Симанков, Т.Т. Зангиев, И.В. Зайцев. – Краснодар: КубГТУ, 2002. – 160 с.
Хювенен Э. Мир Лиспа [Текст] / Э. Хювенен, Й. Сеппянен. – М.: Мир, 1990. – 460 с.
bukvasha.ru
Сумма (разность) определяется только для матриц одинаковой размерности. Пусть
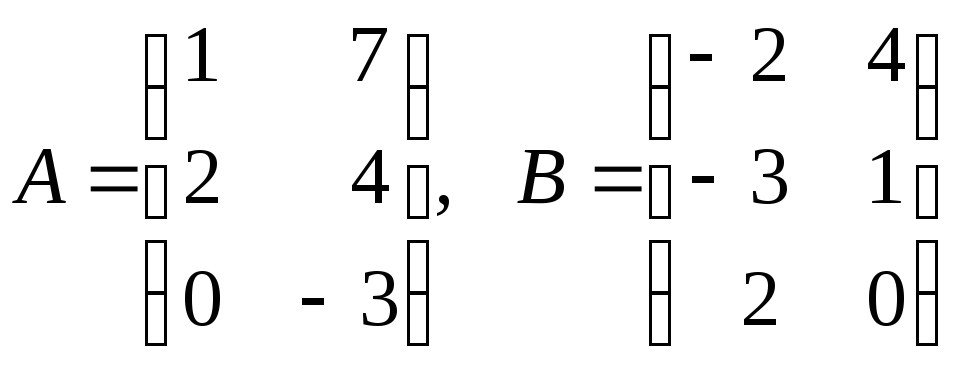 . Тогда
. Тогда 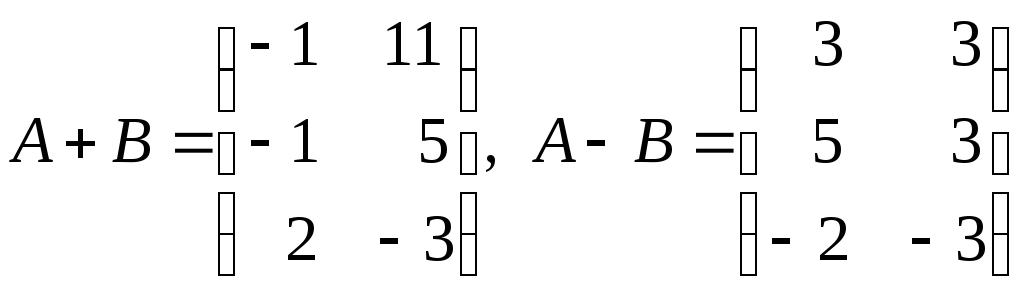 .
.
При умножении матрицы А на число 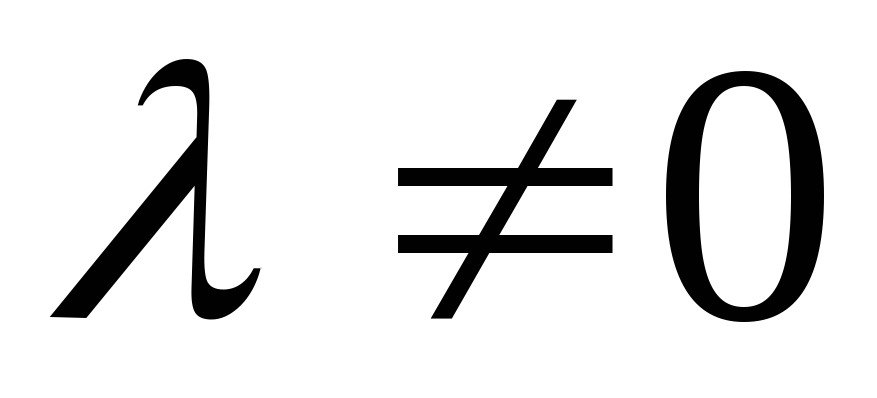 нужно все элементы матрицыА умножить на это число.
нужно все элементы матрицыА умножить на это число.
Если 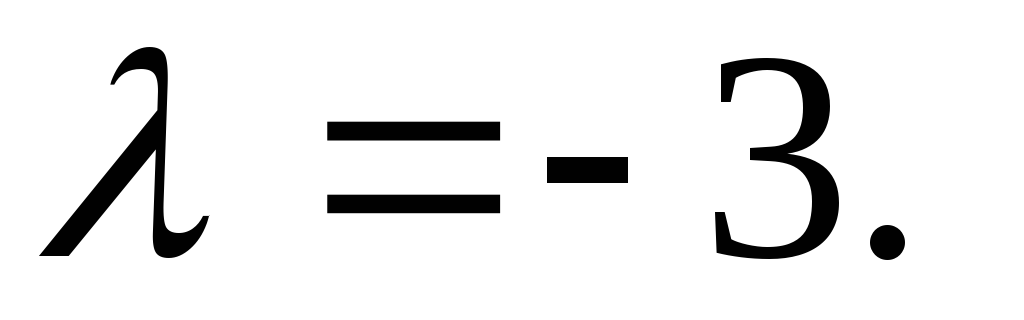
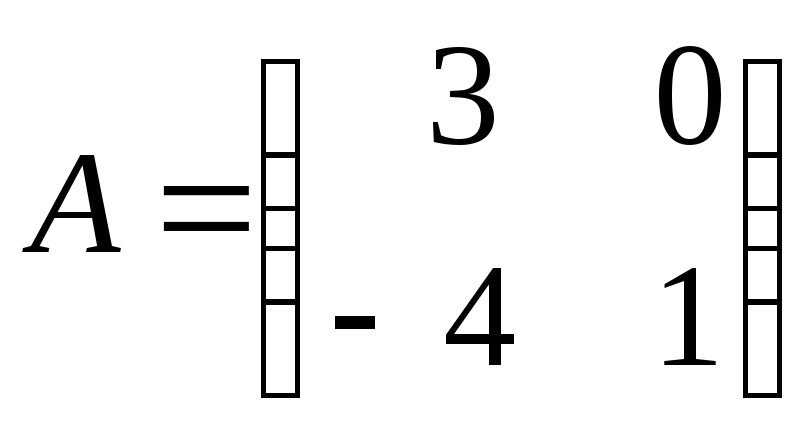 , то
, то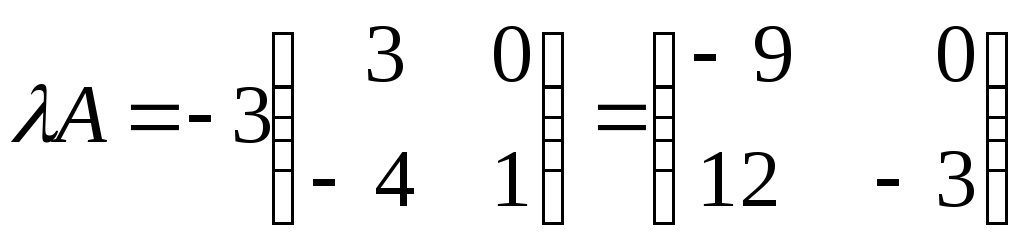 .
.
Произведением матрицы 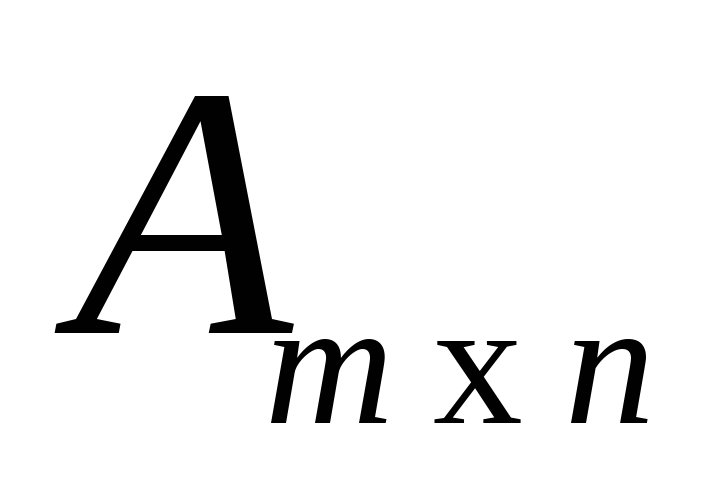 на матрицу
на матрицу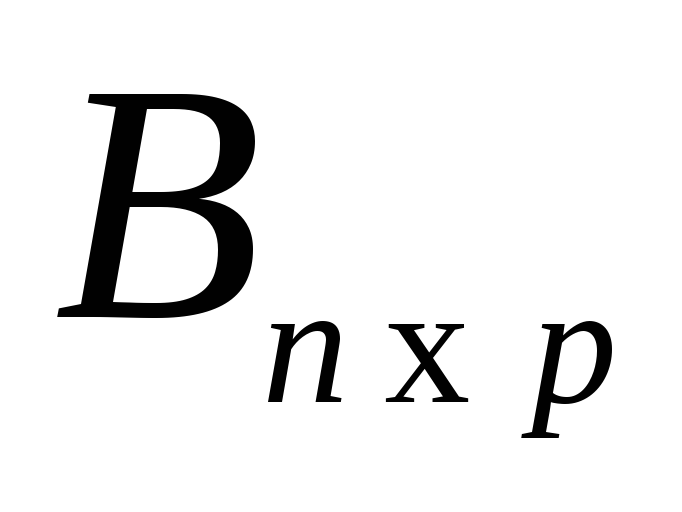 называется матрица
называется матрица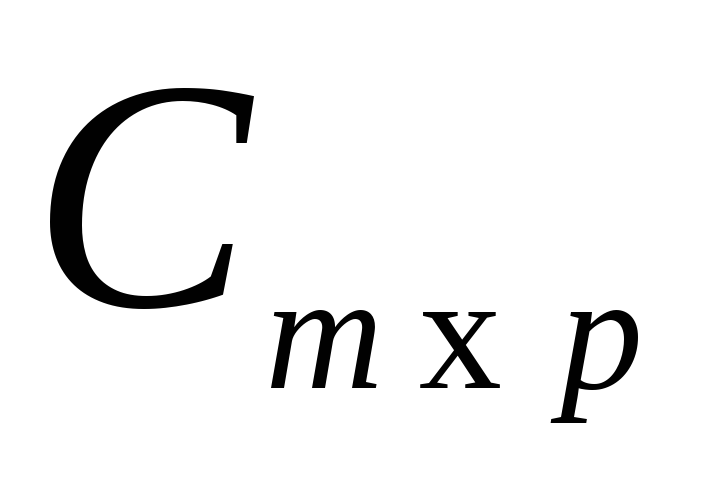 , элементы которой находятся по формуле
, элементы которой находятся по формуле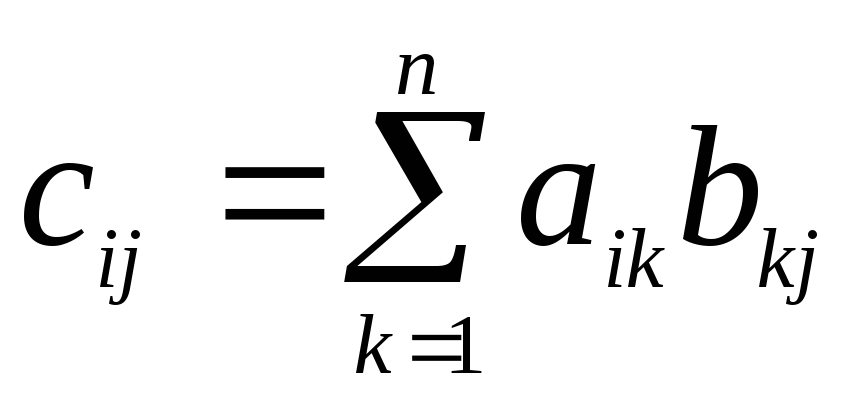 . В общем случае
. В общем случае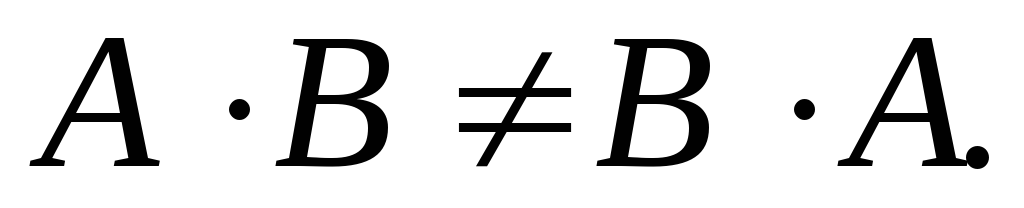
Пусть 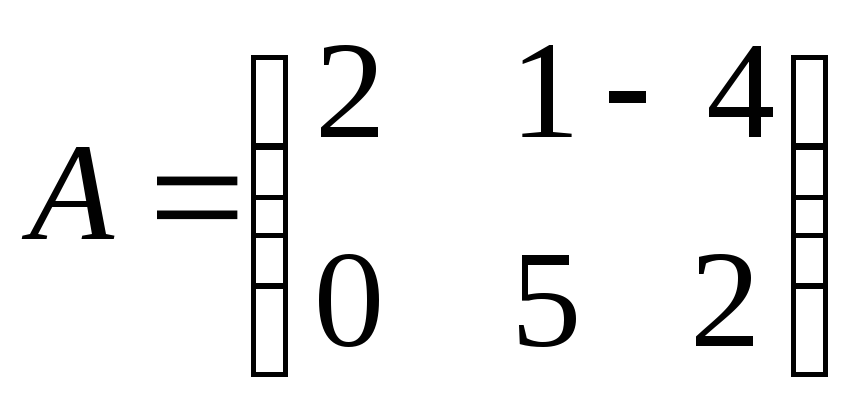 ,
,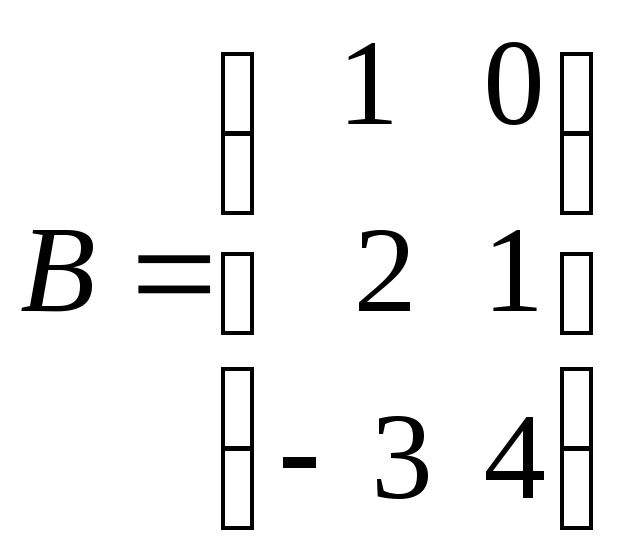 .
.
Имеем: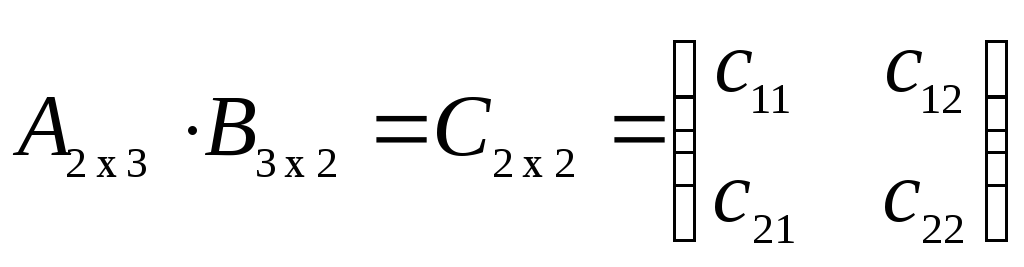 , где
, где
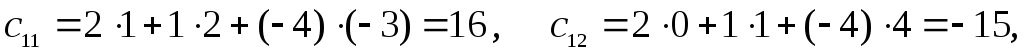
 следовательно
следовательно
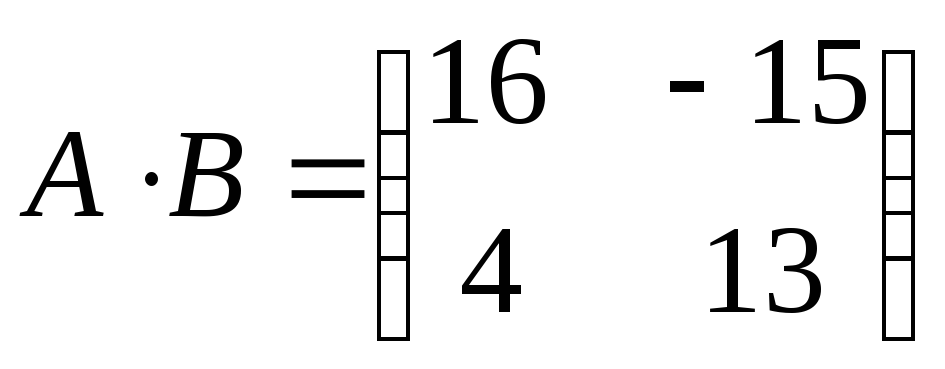 .
.
Определителем второго порядка называется число, равное 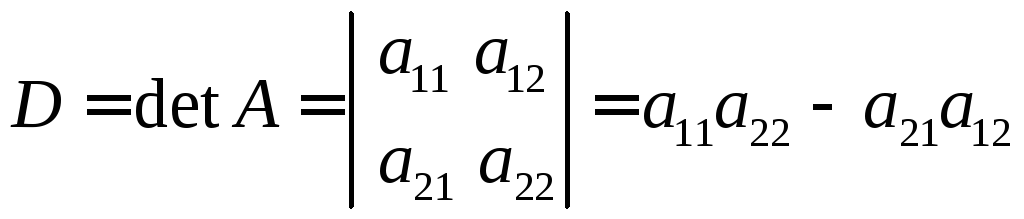 . (1.1)
. (1.1)
Примеры.
1) 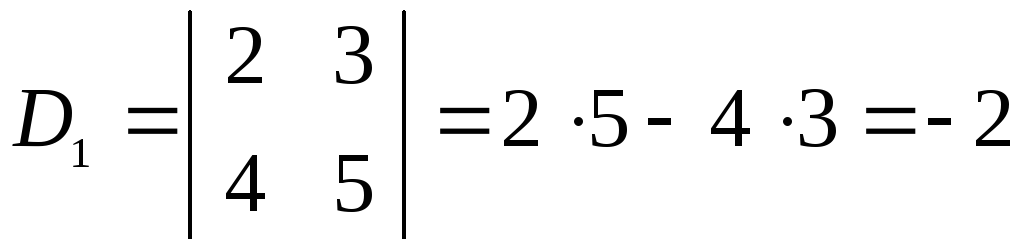 ; 2)
; 2)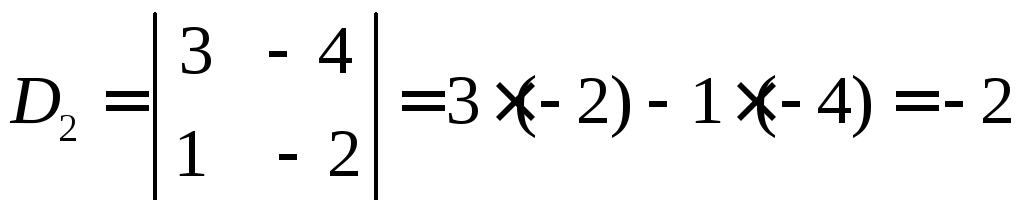 .
.
Определителем третьего порядка называется число, равное сумме произведений элементов его первой строки на их алгебраические дополнения.
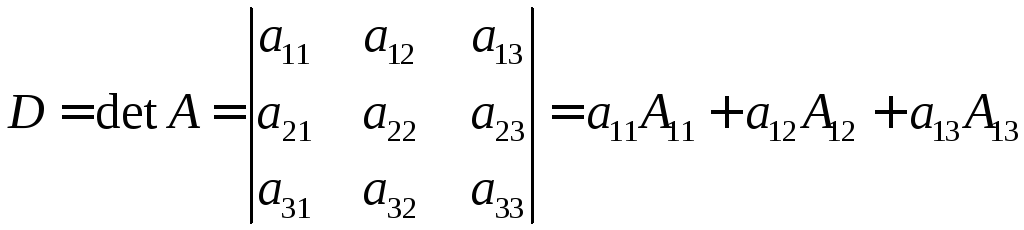 . (1.2)
. (1.2)
Аналогично определяются определители более высоких порядков.

Вычислим определитель, разложив его по элементам первой строки:
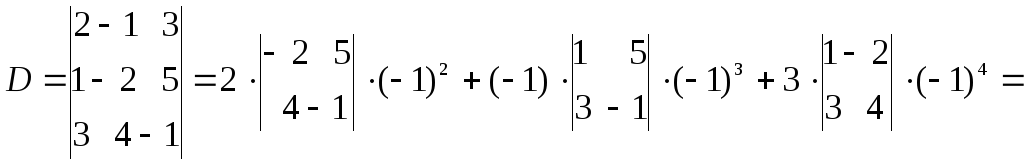
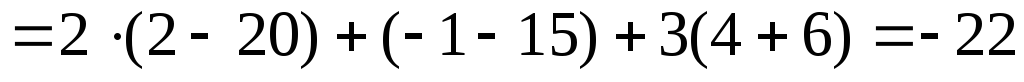 .
.
Определители третьего порядка можно вычислить и по правилу треугольников (правилу Саррюса) по схеме:
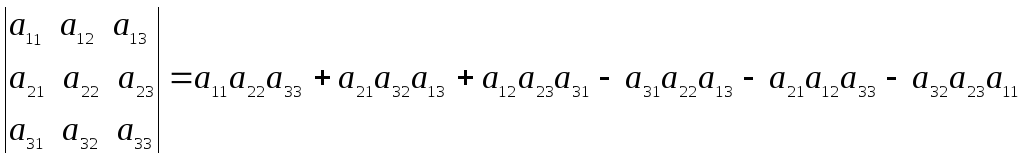 . (1.3)
. (1.3)
Пример.
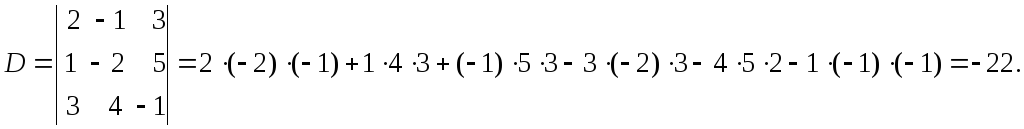
Метод Крамера
Пример. Решить систему линейных уравнений по формулам Крамера
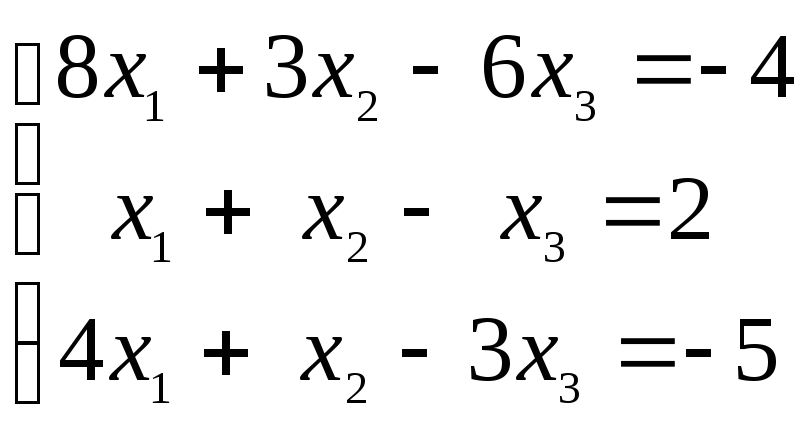 .
.
Вычислим определитель системы 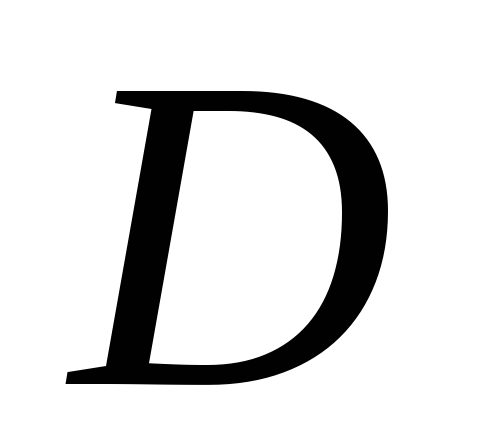
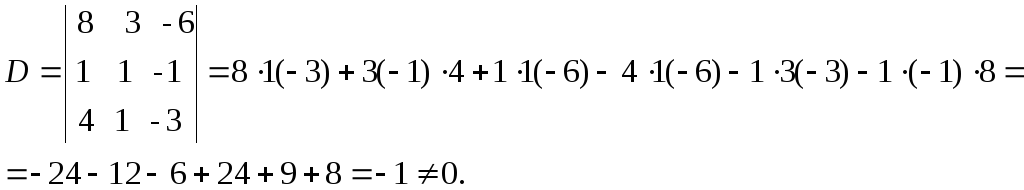
Вычислим определители D1, D2, D3, заменяя в определителе D элементы первого, второго и третьего столбцов соответственно элементами столбца из свободных членов.
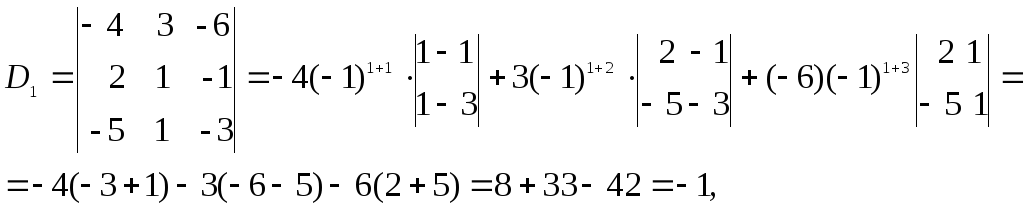
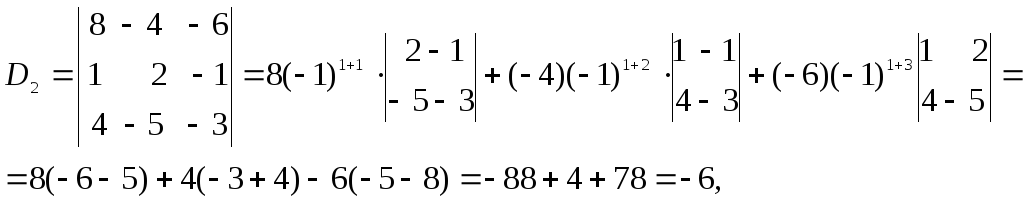
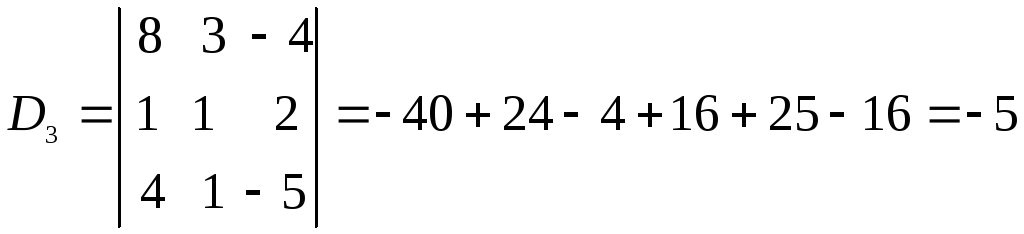 .
.
Таким образом,
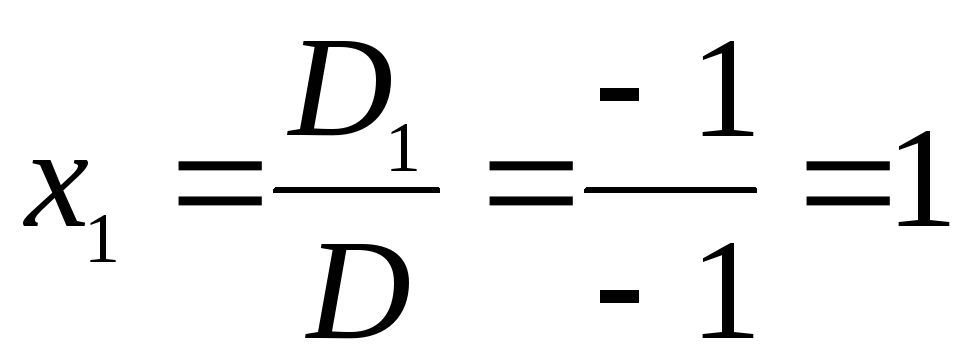 , х2=
, х2=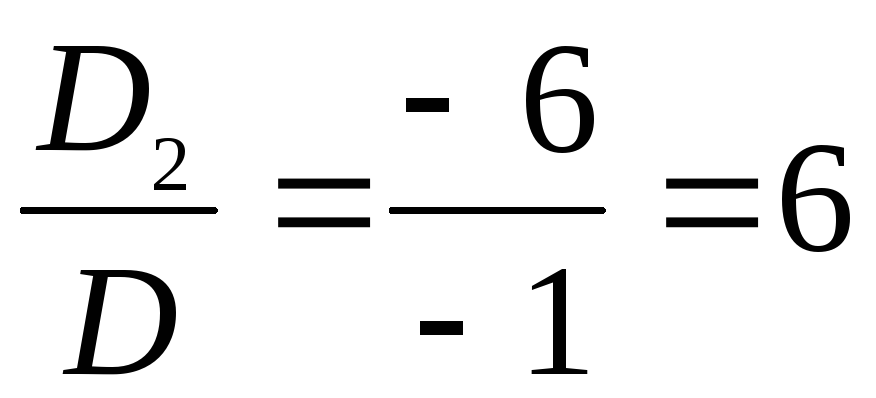 ,
,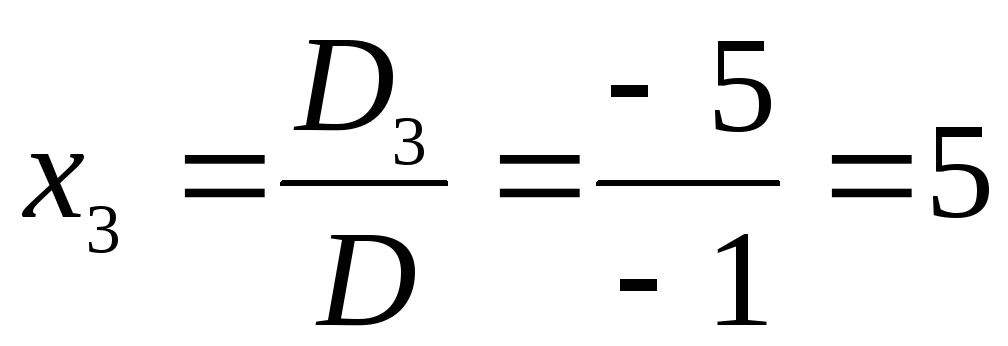 .
.
Итак,
х1=1, х2=6, х3=5.
Определение. Матрица А называется невырожденной, если D=det А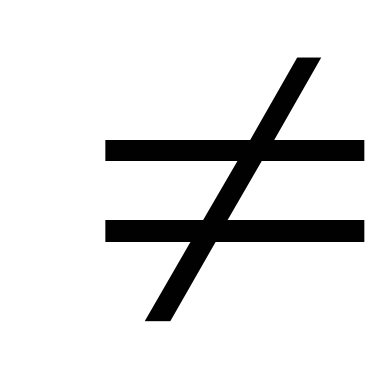 0.
0.
Каждая невырожденная матрица А имеет обратную 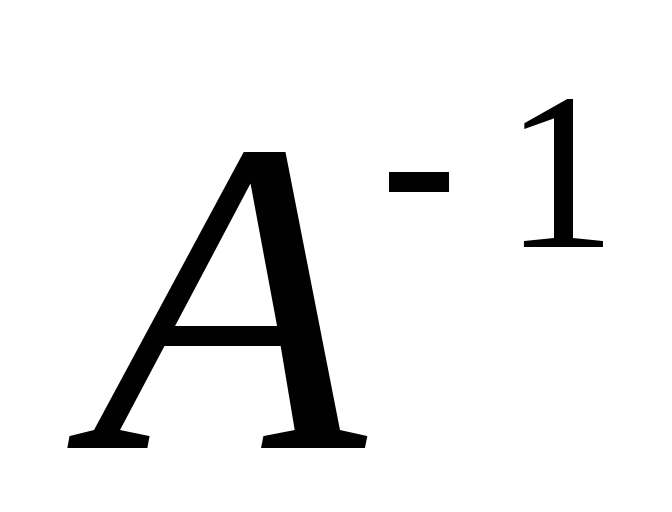 , причем для матрицы
, причем для матрицы третьего порядка с элементами
третьего порядка с элементами :
: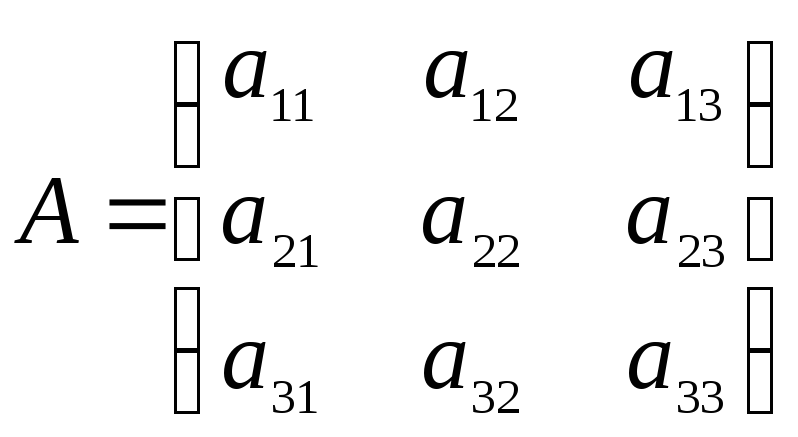 обратная матрица
обратная матрица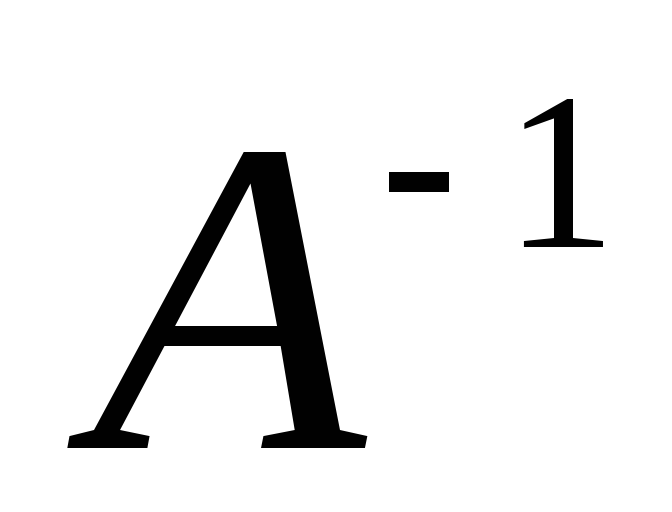 имеет вид:
имеет вид:
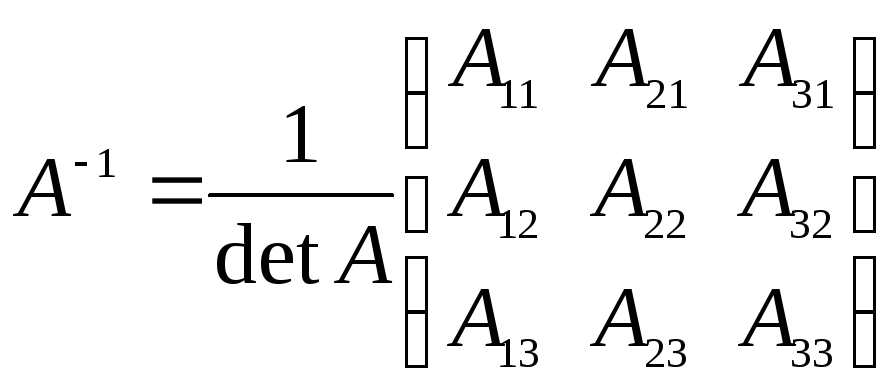 , (1.4)
, (1.4)
где А11, А12 ,…, А33 – алгебраические дополнения соответствующих элементов  матрицы
матрицы , располагаемые по столбцам в новой матрице.
, располагаемые по столбцам в новой матрице.
Пример. Решить систему уравнений матричным методом:
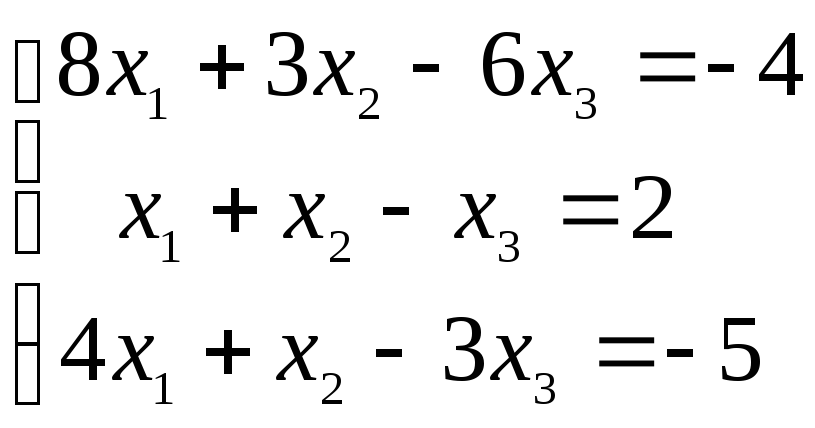 . Имеем: А=
. Имеем: А=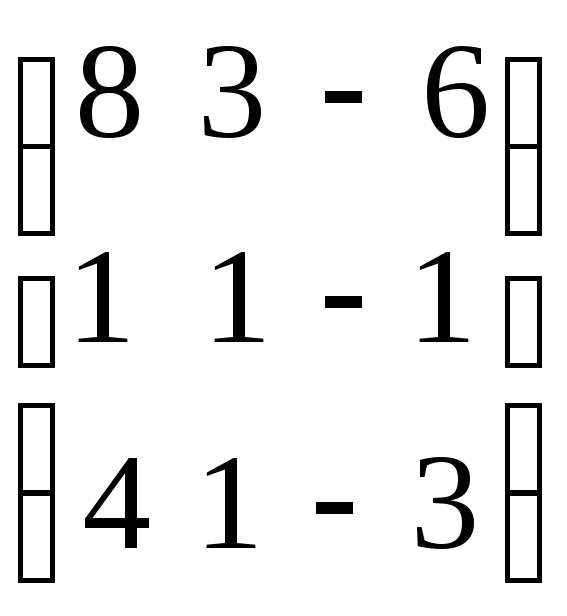 ,Х=
,Х=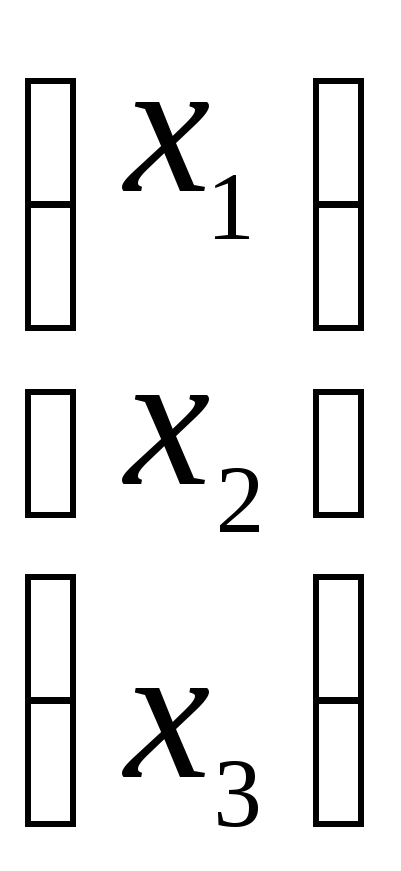 ,Н=
,Н=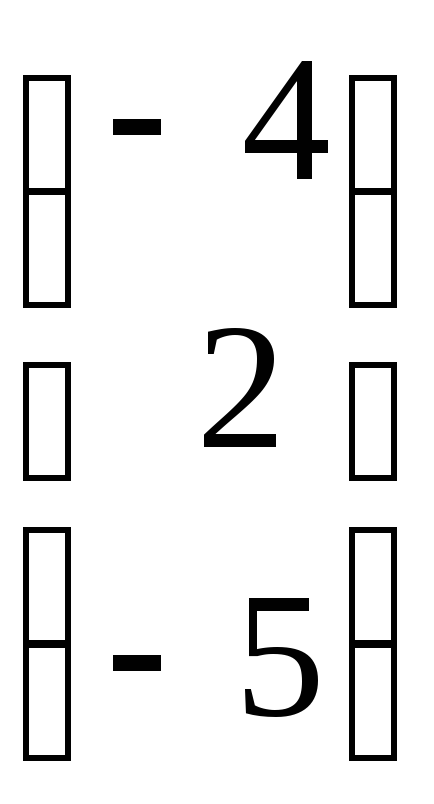 .
.
 ,
, 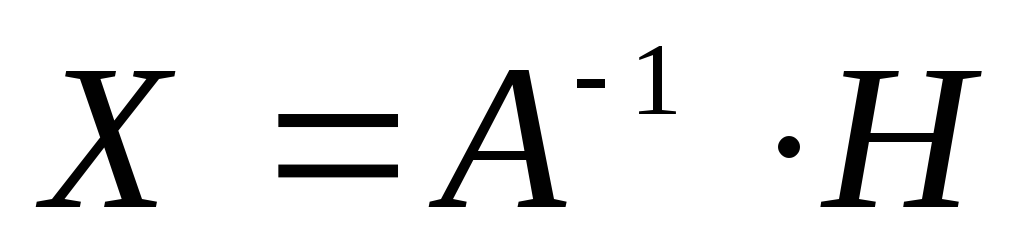 .
.
Для нахождения обратной матрицы А-1 вычисляем все алгебраические дополнения элементов матрицы А:
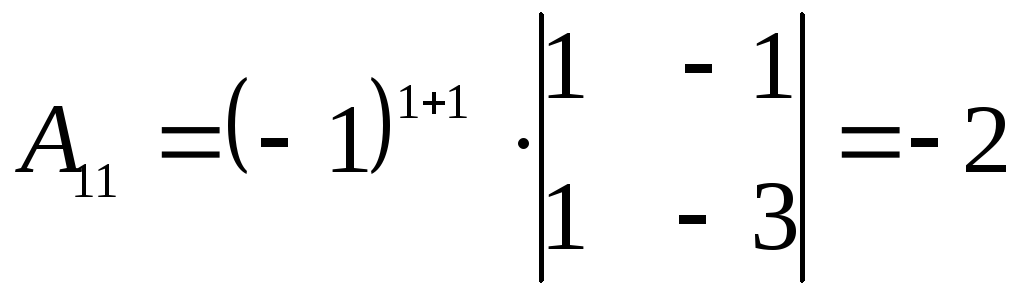 ,
, 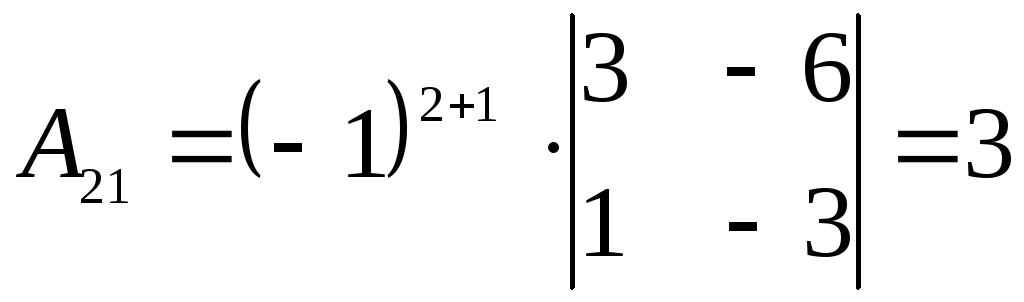 ,
,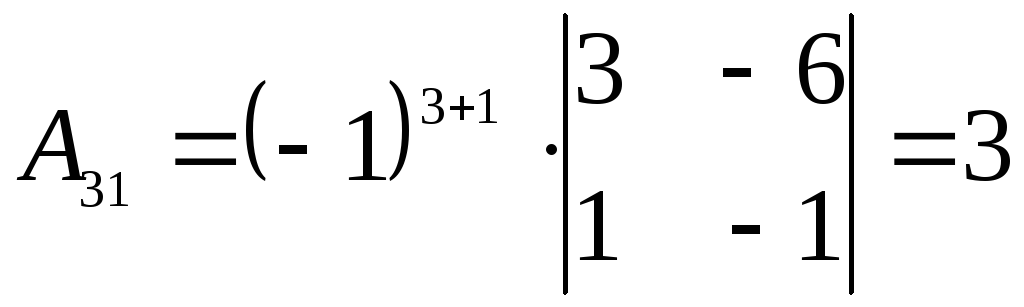 ,
,
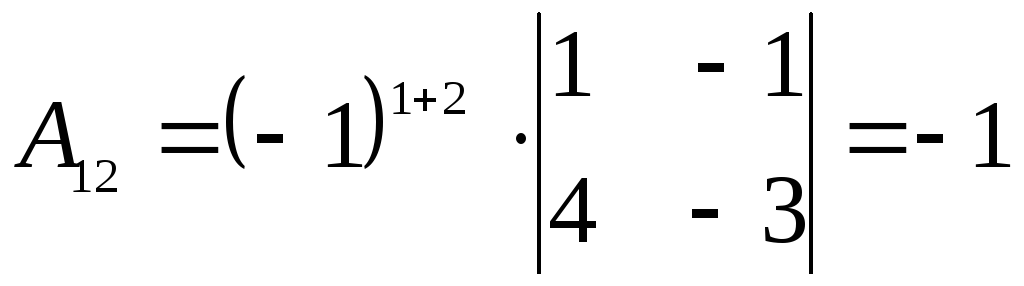 ,
, 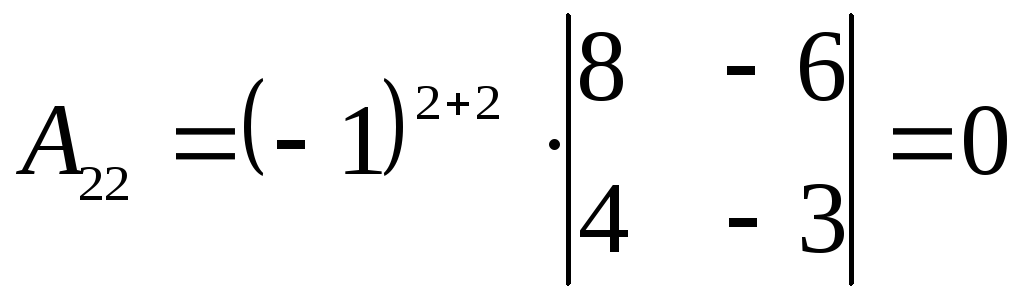 ,
,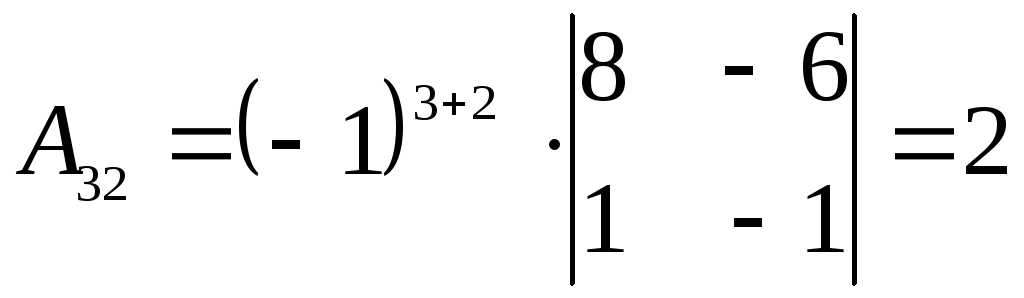 ,
,
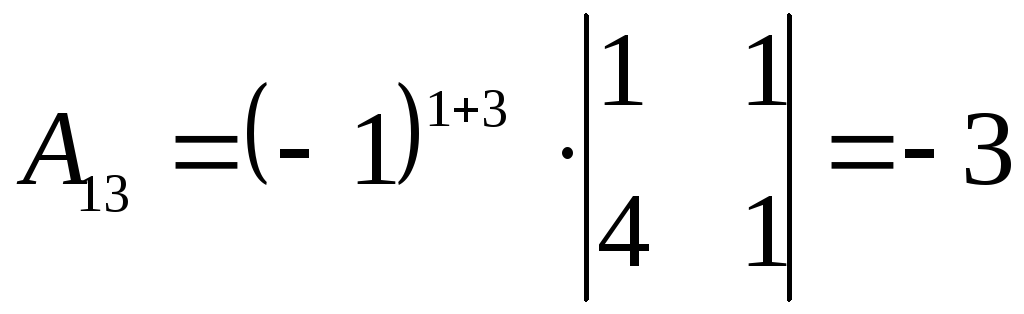 ,
, 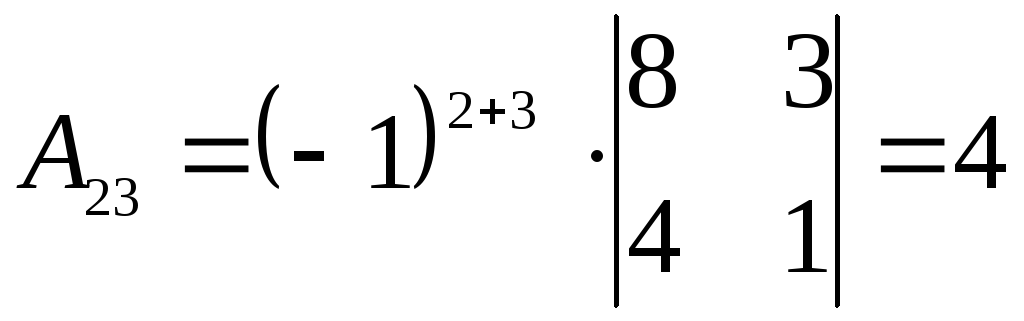 ,
,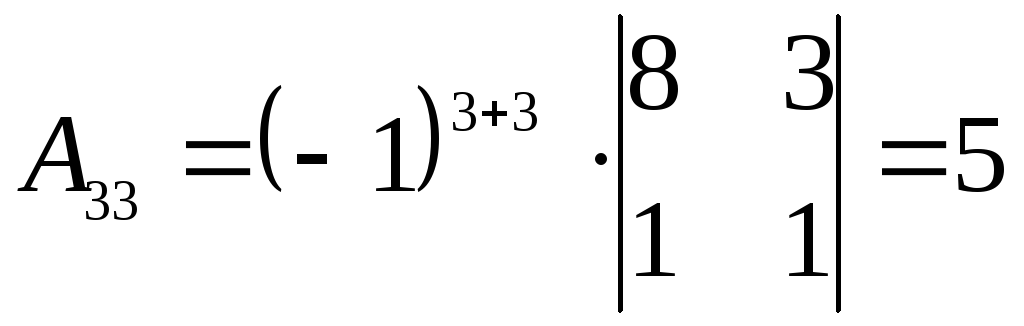 .
.
Составляем обратную матрицу (1.4):
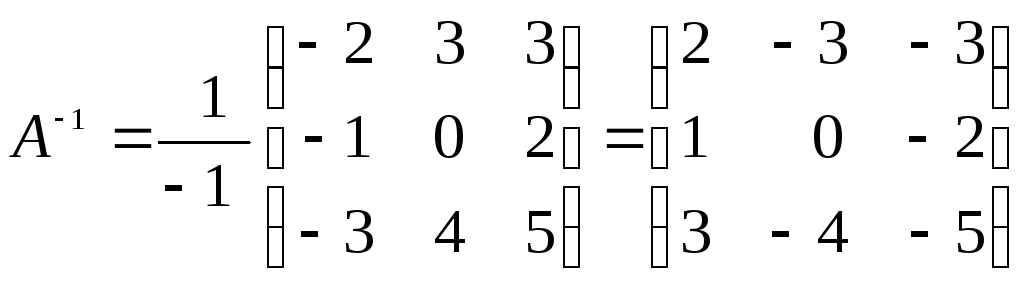 .
.
Тогда
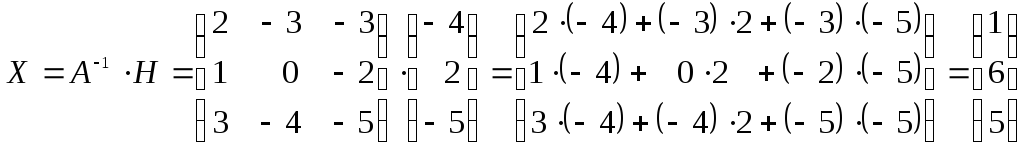 .
.
Таким образом, х1=1, х2=6, х3=5.
Пример. Решить систему методом Жордана-Гаусса. Найти общее, частное и базисное решение системы.
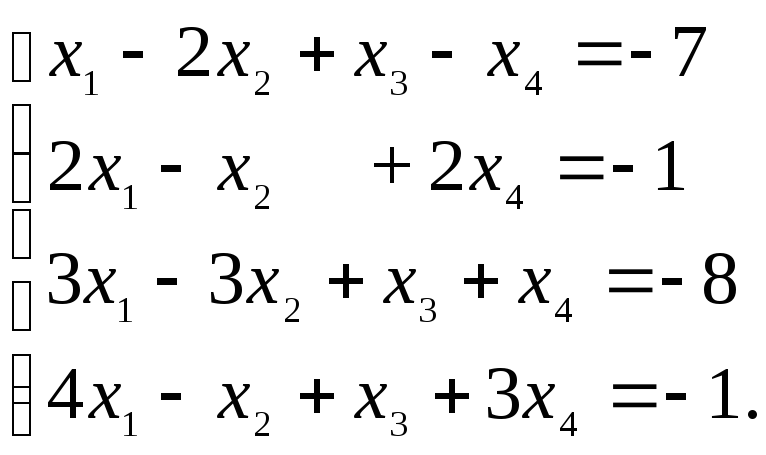
Составляем расширенную матрицу системы и проводя элементарные преобразования над строками матрицы исключаем переменные в соответствующих этой матрице системах линейных уравнений. В результате преобразований исходная матрица сводится к трапецеидальному виду. Преобразуем расширенную матрицу системы:
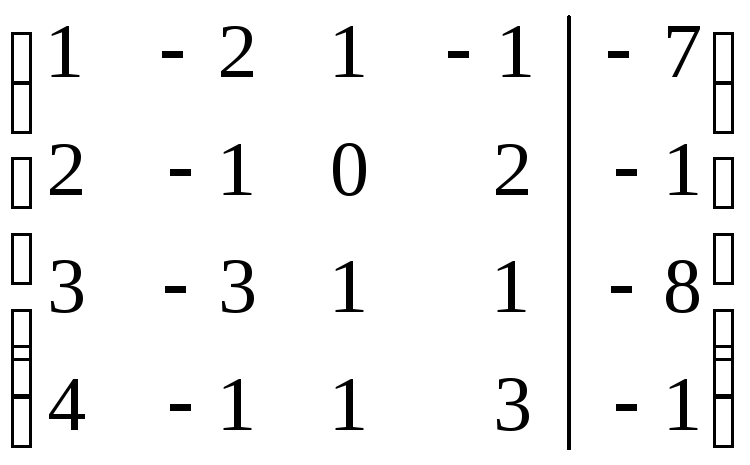
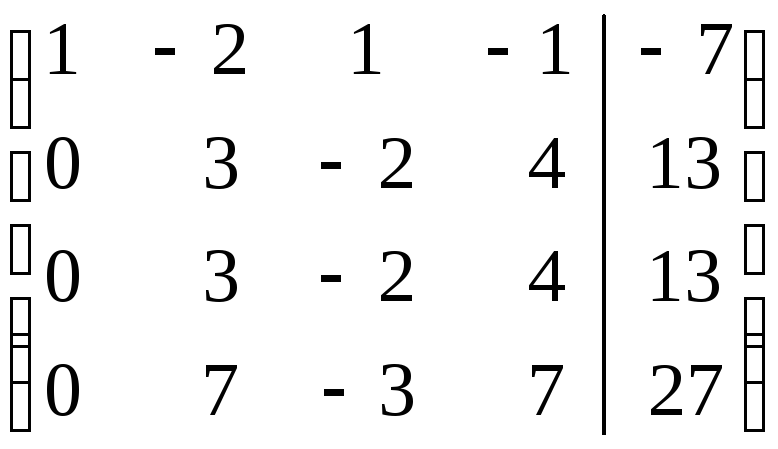
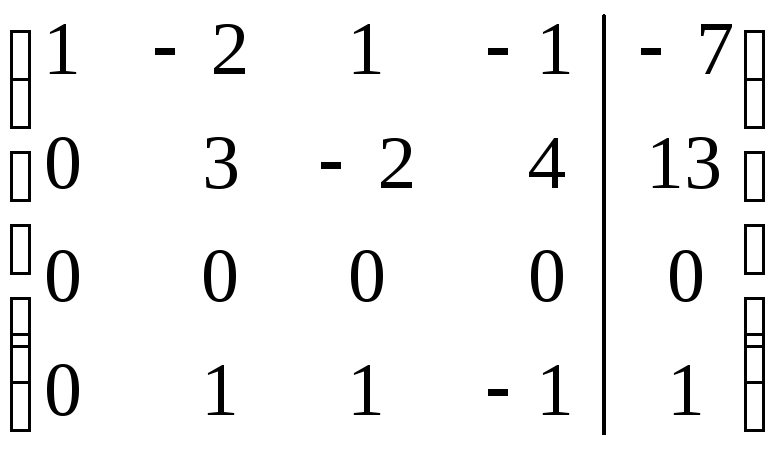

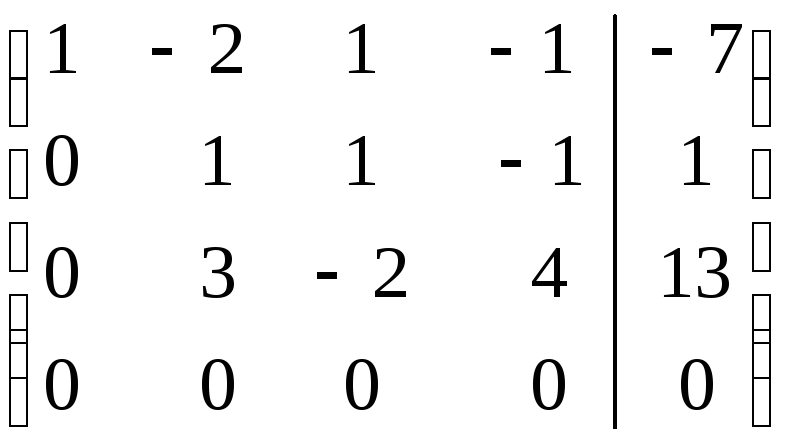
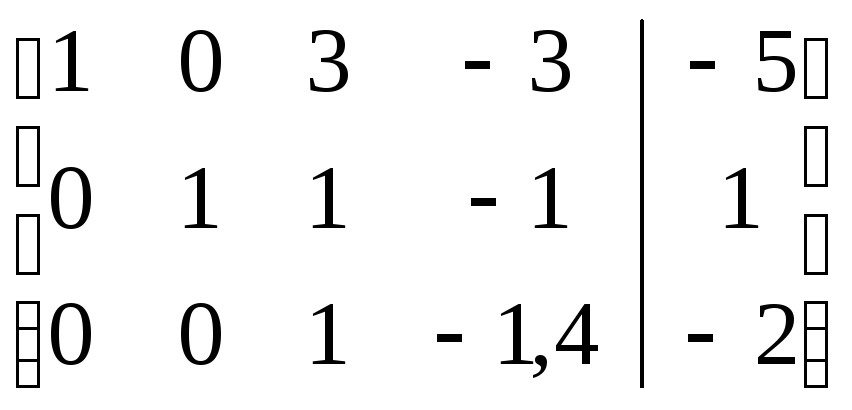

Поясним сделанные преобразования:
Первую строку умножим последовательно на (- 2), (-3), (-4) и прибавим ко второй, третьей и четвертой строкам соттветственно.
Вторую строку умножаем на (-1), (-2) и прибавим к третьей и четвертой строке соответственно.
Поменяем местами вторую и четвертую строчку.
Вторую строку умножаем на 2 и на (-3) и прибавим к первой и третьей строке соответственно. Удаляем четвертую – нулевую строку.
Третью строку умножаем на на (-1) и на (-3) и прибавляем ко второй и первой строке соответственно.
Используя последнюю матрицу, эквивалентную исходной, получаем равносильную систему уравнений следующего вида:

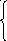 х1+
х1+ +1,2х4 = 1
+1,2х4 = 1
х2+ +0,4х4 = 3
х3+ −1,4х4 =− 2.
Переменные х1, х2, х3
х1, х2, х3 назовём базисными, переменную х4 − свободной. Полагая х4=0, непосредственно находим базисное решение: х1=1, х2=3, х3=−2.При х4=5, получим частное решение: х3=5, х2=1, х1=−5. При х4= t, где t
назовём базисными, переменную х4 − свободной. Полагая х4=0, непосредственно находим базисное решение: х1=1, х2=3, х3=−2.При х4=5, получим частное решение: х3=5, х2=1, х1=−5. При х4= t, где t R, получим общее решение системы:
R, получим общее решение системы:
х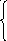 1=1-1,2 t
1=1-1,2 t
х2=3-0,4 t
х3=-2+1,4 t.
studfiles.net