a2 an2 ,По дисциплине «Безопасность жизнедеятельности»
Теоретическая часть.
Вариант № 8
Выполнил ст. гр 2ПГ
Иванцова Е.Г.
7. Цель науки эргономики? Приведите пример положительного решения задач эргономики в Вашей организации.
Эргономика (от греческого ergon – «работа», nomos – «закон», или «закон работы») – это область знаний, которая комплексно изучает трудовую деятельность человека в системе «человек – техника – среда» с целью обеспечения эффективности, безопасности и комфорта трудовой деятельности. Поэтому исследования эргономики базируются на определении закономерностей психических и физиологических процессов, которые лежат в основе определенных видов трудовой деятельности, изучающие особенности взаимодействия человека с орудием и предметами труда.
Современная эргономика выступает как интегральная наука о трудовой деятельности, которая позволяет повысить трудовую эффективность путем оптимизации условий труда и всех процессов, с ним связанных. Под эффективностью труда в данном случае выступает не только высокая производительность труда, но и положительное влияние на личность рабочего, удовлетворенность своим трудом. Данные, полученные с помощью эргономики, используются при разработке рекомендаций в системе научной организации труда. Эргономика решает задачи оптимизации трудовой деятельности, способствует охране труда, обеспечивая его гигиену и безопасность труда. И если гигиена труда в эргономике организуется на основе требований физиологии и медицины, то эргономический аспект безопасности труда решается, главным образом, при непосредственном вмешательстве психологии.
Нужно отметить, что эргономика занимается не только усовершенствованием условий труда при существующей технике, но и разработкой рекомендаций по проектированию новой техники и новой организации труда с позиций требований этой науки. Исходя из психологических, гигиенических и прочих условий труда, она вырабатывает соответствующие требования к технике, в том числе и к техническим средствам безопасности труда.
Современная эргономика исследует не только усовершенствование условий труда при существующей технической оснащенности, но и разработку рекомендаций новой организации труда с позиций требований этой науки.
Инструкции могут разрабатываться для работников как по профессиональному признаку (преподаватели, слесари, уборщицы, лаборанты и т.д.), так и на отдельные виды работ (проведение лабораторных работ, на токарном станке, на высоте, ремонтные работы и т.д.) с учетом специфики работы, оборудования и технологических процессов.
Методическое руководство разработкой инструкций осуществляет служба охраны труда (инженер по охране труда).
После составления инструкция согласовывается службой охраны труда, в случае необходимости и с другими заинтересованными службами и должностными лицами по усмотрению службы охраны труда.
Инструкции должны утверждаться руководителем учреждения с учетом мнения выборного органа профсоюзной организации или иного уполномоченного работниками органа в порядке, установленном ст.372 Трудового кодекса РФ для принятия локальных нормативных актов.
Изучение инструкций для работников обеспечивается руководителем учреждения. При этом требования инструкций являются обязательными для работников. Невыполнение этих требований должно рассматриваться как нарушение трудовой дисциплины.
Инструкции по охране труда являются нормативным документом, устанавливающим требования по охране труда при выполнении работ работниками на рабочих местах в производственных помещениях, на территории учреждения и в других местах, где работники выполняют порученную им работу или служебные обязанности.
При разработке инструкции должны учитываться требования:
• Трудового кодекса РФ;
• законодательства Российской Федерации об охране труда;
• Единого тарифно-квалификационного справочника работ и профессий рабочих и Квалификационного справочника должностей руководителей, специалистов и других служащих;
• государственных нормативных требований охраны труда;
• специальных правил безопасности по пожарной, промышленной, электроэнергетической, технологической, санитарно-гигиенической, радиационной, транспортной, физической и т.п.;
• паспортов, инструкций по эксплуатации и техническому обслуживанию оборудования;
• руководящих материалов и другой организационно-технической документации, характеризующей специфику работ;
• руководства по эксплуатации данного вида техники: прибора, агрегата, оборудования, машины, станка и т.п.;
• технологической документации;
• материалов расследования несчастных случаев, актов по форме Н-1, имеющих отношение к данной профессии или виду работы;
положения о разработке инструкций по охране труда.
Инструкция по охране труда для работника разрабатывается на основе межотраслевой или отраслевой типовой инструкции по охране труда (а при ее отсутствии - межотраслевых или отраслевых правил по охране труда), требований безопасности, изложенных в эксплуатационной и ремонтной документации организаций - изготовителей оборудования, а также в технологической документации организации с учетом конкретных условий производства. Эти требования излагаются применительно к должности, профессии работника или виду выполняемой работы.
Инструкции не должны содержать требований, противоречащих содержанию нормативных документов.
Инструкции для работников, требования безопасности труда которых установлены в нормативных актах, утвержденных федеральными надзорами России, разрабатываются на основе указанных актов и утверждаются в порядке, установленном этими органами.
Так как инструкция является важным документом повседневного пользования, она должна быть оформлена удобно и практично и в соответствии с установленными требованиями.
Первая страница оригинала инструкции должна быть использована для размещения подписей утверждающих должностных лиц, последняя – для подписей разработчиков и согласующих должностных лиц.
Инструкции должны быть подписаны ее разработчиком и руководителем подразделения – разработчика, согласованы с отделом охраны труда. Инструкции, содержащие требования безопасности при работе с вредными веществами, можно согласовать с санитарными врачами, а при работе с легковоспламеняющимися и горючими жидкостями с пожарной охраной.
Инструкции по работам, поднадзорным федеральным органам надзора и контроля, должны быть согласованы с их представителями.
Инструкции после утверждения должны поступать в отдел охраны труда образовательного учреждения для регистрации, размножения и хранения.
Инструкции вводятся в действие со дня их утверждения приказом или распоряжением руководителя.
Инструкции выдаются на руки или вывешиваются (разрешается вывешивать выписки из инструкций) на видном месте в рабочей зоне, или хранятся в доступном и известном для работающих месте.
Содержание инструкций пересматривают не реже 1 раза в 5 лет. Кроме того, инструкции по охране труда должны быть пересмотрены в случае:
• изменения или внедрения нового технологического процесса;
• установки нового или модернизации действующего оборудования;
• внедрения новых материалов;
• при изменении условий труда;
• по результатам расследования производственного травматизма, аварий, катастроф;
• при изменении действующих или издании новых правил по безопасности и охране труда;
• пересмотра межотраслевых и отраслевых правил и типовых инструкций по охране труда;
• требования представителей органов исполнительной власти субъектов Российской Федерации в области охраны труда или органов федеральной инспекции труда.
Инструкция должна сохранять ранее присвоенный номер (отделом охраны труда или подразделением) при ее пересмотре или внесении дополнений и изменений.
Если при пересмотре и переутверждении инструкции не были внесены какие-либо изменения, то срок ее действия продлевается на 5 лет выпуском "Листка продления срока действия инструкции". Листок продления оформляет структурное подразделение – разработчик инструкции. Листок продления срока действия инструкции по охране труда прикладывается к оригиналу инструкции.
На титульном листе оригинала пересматриваемой инструкции ставится штамп (или пишется от руки) "Пересмотрено" и дата со ссылкой на листок продления. На общих для учреждения инструкциях отметку делает служба охраны труда, на всех других – разработчики инструкции.
Переработанные, пересмотренные инструкции согласовываются и утверждаются в таком же порядке, как и вновь разработанные.
До переработки инструкции допускается вносить в нее изменения на основании оформления листка регистрации изменений к инструкции или распоряжения главного инженера или другого должностного лица, полномочия которого в области охраны труда подтверждены приказом по предприятию. Изменения в инструкции должны оформляться ее разработчиками. Лист регистрации изменений прикладывается к оригиналу инструкции и копиям. Копии измененных инструкций должны рассылаться службой охраны труда в соответствующие подразделения по заявке подразделения разработчика.
Аннулирование действий инструкций оформляется приказом или распоряжением соответствующего руководителя. В отдельных случаях допускается введение в действие или аннулирование инструкций предписанием (служебным письмом, запиской) за подписью главного инженера (или приравненного по должностным обязанностям лица) или другого лица, ответственного за охрану труда или начальника Службы охраны труда.
studfiles.net
Министерство образования и науки Российской Федерации
Уральский федеральный университет
имени первого Президента России Б. Н. Ельцина
Физика
Механика. Молекулярная физика и термодинамика.
Электростатика
Методические указания и задания к контрольной работе № 1
по трех- и четырехсеместровому курсам физики для студентов технических специальностей заочной формы обучения
Екатеринбург
УрФУ
2010
1
УДК 530(075.8)
Составитель Н. А. Звездина
Научный редактор доц., канд. физ.-мат.наук А. Г. Андреева
ФИЗИКА. Механика. Молекулярная физика и термодинамика.
Электростатика : метод. указания и задания к контрольной работе № 1 / сост. Н. А. Звездина. Екатеринбург : УрФУ, 2010. 66 с.
Приведены методические указания к решению задач, примеры решения типичных задач, задания и таблица вариантов контрольной работы № 1.
Задания составлены в соответствии с действующей рабочей программой по физике для студентов технических специальностей заочной формы обучения (трех- и четырехсеместровый курс). Они могут быть использованы также студентами очной формы обучения в качестве домашних заданий.
Библиогр.: 10 назв.
Подготовлено кафедрой физики.
© УрФУ, 2010
2
ВВЕДЕНИЕ
Целью настоящих методических указаний является оказание помощи студентам-заочникаминженерно-техническихспециальностей высших учебных заведений в изучении курса физики.
Учебный материал программы курса разделен на четыре раздела.
Каждому разделу соответствует определенная контрольная работа.
По каждой теме заданий контрольной работы приведены основные формулы и законы, необходимые для решения задач, а также подробные решения типичных задач и примеры их оформления.
Даны таблицы вариантов и тексты задач контрольных работ.
Кроме того, здесь же приведены общие методические указания, которые необходимо учитывать при выполнении и оформлении контрольных заданий.
Обязательно внимательно прочитайте указания, приведенные ниже, и
учтите все рекомендации по оформлению и срокам выполнения работ!
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Основной формой обучения студента-заочникаявляется самостоятельная работа над учебным материалом. Для облегчения этой работы в периоды экзаменационных сессий читаются лекции и проводятся лабораторные работы.
Процесс изучения физики состоит из следующих этапов:
I. Самостоятельная работа над учебниками и учебными пособиями
[1 – 10]. О правилах самостоятельной работы студентов над учебными пособиями подробно говорится на установочных лекциях, которые обычно читаются в УрФУ перед началом изучения каждой части курса физики;
3
сроки этих лекций сообщаются студентам-заочникамдеканатом заочного факультета.
II. Выполнение контрольных работ.
III. Прохождение лабораторного практикума.
IV. Сдача зачетов и экзаменов.
Самостоятельная работа
При самостоятельной работе над учебным материалом необходимо:
1. Изучать курс физики систематически в течение всего семестра. Изуче-
ние материала курса только лишь перед экзаменом не позволит получить глубокие и прочные знания.
2. В качестве основного учебного пособия использовать один из рекомен-
дованных учебников, чтобы не утрачивалась логическая связь между отдельными вопросами. В конце методического пособия приведен список литературы для самостоятельной работы над материалом курса.
3.Составлять конспект при работе над учебным материалом, в котором записывать законы и формулы, выражающие эти законы, определения основных физических величин и сущность физических явлений и методов исследования.
4.Решить контрольные работы. Контрольные работы призваны закрепить теоретический материал и позволить более глубоко разобраться в материале при решении конкретных задач.
5.Прослушать курс обзорных лекций по физике для студентов-заочников,
организуемый в начале каждой сессии. Пользоваться очными консультациями преподавателей.
Выполнение контрольных работ
При выполнении контрольных работ студенту необходимо руководствоваться следующим:
4
1.Номер варианта контрольной работы определяется последней цифрой его шифра. Шифр – номер зачетной книжки. Номера задач каждого варианта определяются таблицей вариантов, приведенной в указаниях.
2.Контрольные работы выполняются в обычной школьной тетради, на лицевой стороне которой (на обложке) приводятся сведения по следующему образцу:
Студент заочного факультета УрФУ специальность Андреев И. В.
Шифр 253720 Адрес: 620460, г. Верхняя Салда,
ул. Восточная, д. 16, кв. 54 Контрольная работа № 1 по физике
3. Условия задач в контрольной работе переписываются полностью без сокращений. На страницах тетради оставляются поля для замечаний преподавателя и после каждой решенной задачи необходимо оставлять место для замечаний преподавателя и для ответа на эти замечания. Каждая следующая задача должна начинаться с новой страницы.
4.В конце контрольной работы указывается, каким основным учебником или учебным пособием пользовался студент при изучении курса физики (название, автор, год издания).
5.На рецензию следует высылать одновременно не более одной работы во избежание одних и тех же ошибок. Очередную работу нужно высылать только после получения рецензии на предыдущую работу.
6.Если контрольная работа при первой проверке не зачтена, то студент обязан представить ее на повторную проверку не позднее чем за две недели до начала сессии, включив в нее те задачи, решение которых оказалось неверным. Зачтенные задачи заново переписывать не надо. Если работа для повторной
5
проверки переписана заново, то ее надо представлять вместе с уже проверенной
работой.
7.Защита выполненных, но незачтенных работ производится во время экзаменационной сессии в форме собеседования с преподавателем (дни и часы защиты работ указываются в расписании).
8.В том случае, когда работа зачтена, студенту отсылается только обложка работы с отметкой преподавателя и его росписью.
Обложка зачтенной контрольной работы предъявляется экзаменатору
перед началом экзамена.
Указания к решению и оформлению задач
1.Записать условие задачи полностью.
2.Выписать численные данные и перевести их в Международную систему измерения физических величин (СИ).
3.Выполнить чертеж или рисунок, поясняющий содержание задачи, показав на нем соответствующие обозначения физических величин, используемых при решении именно этой задачи.
4.Проанализировать условия задачи и указать основные законы, которые нужно применить для решения, указать, почему их можно применить и записать их аналитическую форму. Пояснить буквенные обозначения физических величин, входящих в эти формулы. Если величины векторные, то на рисунке показать их направления и пояснить, как определяются эти направления.
Если при решении задач применяется частная формула, не выражающая какой-нибудьзакон или не являющаяся определениемкакой-либофизической величины, то ее следует вывести.
5.Необходимо сопровождать весь ход решения задачи краткими, но исчер-
пывающими пояснениями. Результатом анализа и решения задачи является
составление системы уравнений, которая включает в себя все искомые
величины.
6
6.Получить решение задачи в аналитическом виде, т. е. выразить искомые величины через заданные величины в буквенном виде и стандартные физические постоянные.
7.Подставить в полученную формулу численные значения всех величин,
выраженных в системе СИ. Произвести вычисления и получить искомый результат. Записать ответ, указав единицы измерения искомой величины.
Проанализировать полученный результат.
Чтобы разобраться в предложенных задачах и выполнить контрольную работу правильно, следует после изучения теории очередного раздела учебника внимательно разобрать помещенные в настоящих указаниях примеры решения типовых задач, близких по уровню сложности к задачам контрольной работы.
Выполнение лабораторных работ
Лабораторные работы выполняются студентами-заочникамив лабораториях кафедры физики УрФУ в периоды экзаменационных сессий, часы и даты этих занятий указываются в сессионном расписании.
Сдача зачетов и экзаменов
После выполнения всех видов работ, предусмотренных учебным планом,
студенты сдают экзамен или зачет. Расписание контрольных мероприятий составляется деканатом заочного факультета.
На экзамен или зачет студент должен явиться, имея при себе зачетную книжку, в которой должна быть запись преподавателя о том, что лабораторные работы студент выполнил. Кроме этого, на руках у него должна быть корочка зачтенной контрольной работы (одной или двух, согласно учебному плану).
Расписание пересдач в межсессионный период вывешивается около деканата заочного факультета и на доске объявлений на кафедре физики.
7
КОНТРОЛЬНАЯ РАБОТА №1
(для специальностей, учебным планом которых предусмотрены 4 контрольные
работы в течение трех семестров)
Основные формулы и примеры решения задач
1.Механика
1.1.Кинематика и динамика материальной точки
Для освоения материала этой темы и решения задач по теме «Кинематика и динамика материальной точки» необходимо ознакомиться со следующими
понятиями и законами: |
|
|
|
|
|
|
Материальная точка, абсолютно | твердое тело, система отсчета, | |||||
перемещение, путь, траектория движения. |
|
|
|
|
| |
Скорость и ускорение материальной точки определяются | ||||||
формулами |
|
|
|
|
|
|
|
|
|
|
|
| |
dr |
|
| dV | |||
V |
| ; | a |
|
| . |
dt | dt | |||||
Перемещение в случае прямолинейного равнопеременного движения по оси ОХ
sx | V0 x t | a | x | t 2 |
| ||
|
|
| . |
| |||
| 2 |
|
| ||||
|
|
|
|
|
| ||
В случае движения материальной |
| точки по | криволинейной | ||||
траектории полное ускорение складывается из двух составляющих:
нормального ускорения и тангенциального.
Модуль полного ускорения равен
a a2 an2 ,
где a – модуль тангенциального ускорения иan – модуль нормального ускорения, причем
8
|
|
| a |
|
| dV | , |
|
|
|
| a |
|
| V 2 | , | |
|
|
|
|
|
|
|
|
|
| n |
| ||||||
|
|
|
|
|
| dt |
|
|
|
|
|
| R |
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
где V – модуль скорости движения точки, | R – радиус кривизны траектории в | ||||||||||||||||
данной точке, в заданный момент времени. |
|
|
|
|
| ||||||||||||
| Инерциальные системы отсчета. Первый закон Ньютона. Инерция. | ||||||||||||||||
Масса. Сила. Силы в механике. |
|
|
|
|
|
|
|
|
|
|
| ||||||
|
| Основной закон динамики поступательного движения (второй | |||||||||||||||
закон Ньютона). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
2-йзакон Ньютона может быть записан следующим образом : | |||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
| Fdt d (mV) . |
|
|
| |||||||
Если масса m постоянна, то |
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
| dV |
| dp |
|
|
|
|
| ||||
|
|
| F | m |
|
|
|
|
| ma , |
|
|
| ||||
|
| dt | dt |
|
|
| |||||||||||
|
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
где a | – | ускорение, | которое приобретает | тело | массой т под действием | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
результирующей силы, | p – импульс тела или системы тел. | ||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
| Третий закон Ньютона. |
| F12 | F21. |
| |||||||||||
1.2. Кинематика и динамика вращательного движения
Угловая скорость |
| и угловое ускорение , их связь с | |||||
линейными характеристиками. |
|
|
|
|
| ||
При вращательном движении вокруг неподвижной оси угловая | |||||||
скорость и угловое ускорение определяются формулами | |||||||
| d |
|
|
| d | ||
| , |
|
|
| . | ||
dt |
|
| dt | ||||
Модуль угловой скорости вращательного движения связан с частотой | |||||||
вращения следующим образом: |
|
|
|
|
| ||
|
| 2 | 2 n , | ||||
| T | ||||||
| t |
|
|
|
| ||
|
|
|
|
| 9 |
|
|
где Т – период вращения,п – линейная частота вращения, т. е. число оборотов в единицу времени.
Модуль угловой скорости связан с модулем V линейной скорости точки соотношением
V R ,
где R – расстояние от точки до оси вращения. Тангенциальное и нормальное ускорения могут быть выражены в виде
a R, | a 2 R. |
|
|
|
| n |
|
|
|
Момент силы и момент импульса. Момент инерции тела | ||||
относительно закрепленной оси вращения. |
|
|
| |
|
|
|
|
|
Момент силы относительно оси вращения определяется как |
| F , | ||
M r | ||||
или модуль момента силы M rFsin , где α – угол междурадиус-вектором,
проведенным от оси вращения к точке приложения силы, и вектором силы.
Момент импульса относительно оси вращения для материальной точки
|
|
| L J . |
определяется как L r | p , а для абсолютно твердого тела – | ||
Момент инерции материальной точки определяется следующим образом:
J mr2 , гдеm – масса движущейся точки,r – кратчайшее расстояние от точки до оси вращения.
Моменты инерции некоторых тел массой m относительно оси,
проходящей через центр масс:
а) тонкого стержня длиной l относительно оси, перпендикулярной стержню и проходящей через его середину, –
J 121 ml2 ;
б) обруча (тонкостенного цилиндра) радиуса R относительно оси, перпендику-
лярной плоскости обруча (совпадающей с осью цилиндра), –
J mR2 ;
в) диска радиуса R относительно оси, перпендикулярной плоскости диска и проходящей через его центр, –
10
studfiles.net
Контрольные работы 1(семестр 1), 2(семестр 2) по теоретической механике
для студентов заочной формы обучения
Контрольное задание № 1: задачи С1, К1, К2.
Контрольное задание № 2 :задачи Д1, Д3, Д5.
Число вариантов каждой задачи равно 100. Методические указания студентам и примеры решения задач представлены в методических разработках № 168-2006 и № 169-2006.
Выбор варианта: номер рисунка – предпоследняя цифра номера зачетке;
строка исходных данных в таблице - последняя цифра номера зачетке.
Контрольная работа №1
Задача С1
Жесткая рама закреплена в точке А шарнирно, а точке В прикреплена или к невесомому стержню ВВ, или к шарнирной опоре на катках; стержень прикреплен к раме и к неподвижной опоре шарнирами. На раму действует пара сил с моментом М=100 н.м и две силы, значения, направления и точки приложения которых указаны в таблице.
Определить реакции связей в точках А и В, вызываемые действующими нагрузками.
Задача К1
Точка движется в плоскости xy,закон движения точки задан в координатной форме.
Найти уравнение траектории точки; для момента времени t= 1 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Задача К2
Плоский механизм состоит из стержней 1-4 и ползуна В, соединенных друг с другом и с неподвижными опорами шарнирам .Длины стержней известны. Положение механизма определяется углами, которые вместе с другими величинами заданы в таблице.
Определить величины, указанные в столбце «Найти», а также определить ускорение точки А стержня 1 при заданном угловом ускорении этого стержня.
Контрольная работа №2
Задача Д1
Груз Dмассойm,получив в точке А начальную скорость, движется в изогнутой трубе АВС, расположенной в вертикальной плоскости; на участке АВ на груз кроме силы тяжести действует постоянная силаQи сила сопротивления среды, зависящая от скорости. В точке В груз, не изменяя значения своей скорости, переходит на участок ВС трубы, где на него действует переменная сила, проекция которой на ось x задана в таблице.
Считая груз материальной точкой , найти закон движения на участке ВС.
Задача Д3
Механизм состоит из грузов 1 и 2 , цилиндрического сплошного однородного катка 3 и ступенчатых шкивов 4 и 5 с заданными радиусами ступеней. Тела системы соединены друг с другом нитями, намотанными на шкивы. Под действием силы F, зависящей от перемещения точки приложения силы, механизм приходит в движение из состояния покоя. При движении механизма на шкивы 4 и 5 действуют постоянные моменты сил сопротивления , равные М.
Определить значение кинематической величины, указанной в таблице, в тот момент времени, когда перемещение точки приложения силы Fравноs.
Задача Д5
Механизмы, состоящие из пяти звеньев , представлены на рисунке. Кроме сил тяжести на одно из тел системы действует постоянная сила F, а на шкивы при их вращении действуют постоянные моменты сил сопротивления М
Определить ускорение указанное в таблице в столбце «Найти» .
Исследовать движение системы и найти ускорение используя уравнения Лагранжа.
Контрольная работа №1
Рисунки и таблицы к задачам
Задача С1
Задача К1
Задача К2
Контрольная работа № 2
Задача Д1
Задача Д3
Задача Д5
13
studfiles.net
Математика 2 класс
Задачи для 2 класса
Контрольные работы
| 8 + 9 = | 4 + 7 = | 11 - 9 = | 12 - 7 = |
| 26 - 6 = | 79 + 1 = | 45 - 40 = | 90 - 1 = |
| 8 + 5 - 9 = | 13 - 4 + 6 = | 16 - (12 - 3) = |
| 8 + 9 = 17 | 4 + 7 = 11 | 11 - 9 = 2 | 12 - 7 = 5 |
| 26 - 6 = 20 | 79 + 1 = 80 | 45 - 40 = 5 | 90 - 1 = 89 |
| 8 + 5 - 9 = 4 | 13 - 4 + 6 = 15 | 16 - (12 - 3) = 7 |
В магазине было 12 телевизоров. До обеда продали 4 телевизора, а после обеда в магазин привезли еще 6 таких телевизоров. Сколько телевизоров стало в магазине?
Найди длину ломаной, составленной из трех звеньев такой длины: 7 дм, 6 дм и 3 дм.
В левом кармане у мальчика 3 монеты, а в правом — 7. Сколько монет надо переложить в левый карман из правого, чтобы монет в двух этих карманах стало поровну?
| 7 + 7 = | 6 + 9 = | 13 - 4 = | 15 - 6 = |
| 69 + 1 = | 96 - 90 = | 80 - 1 = | 74 - 4 = |
| 11 - 2 - 5 = | 14 - (3 + 7) = | 17 - (13 - 5) = |
| 7 + 7 = 14 | 6 + 9 = 15 | 13 - 4 = 9 | 15 - 6 = 9 |
| 69 + 1 = 70 | 96 - 90 = 6 | 80 - 1 = 79 | 74 - 4 = 70 |
| 11 - 2 - 5 = 4 | 14 - (3 + 7) = 4 | 17 - (13 - 5) = 9 |
| 81см...8дм | 30мм...Зсм |
Решение:
| 81см > 8дм | 30мм = Зсм |
Найди длину ломаной, составленной из трех звеньев такой длины: 4 см, 7 см и 6 см.
В большом пакете было 11 морковок, а в маленьком — 7. Сколько морковок надо переложить из большого пакета в маленький, чтобы морковок в двух этих пакетах стало поровну?
На странице использованы материалы из книги С. И. Волковой «Математика. Контрольные работы. 1-4 классы» 2008г.
Составные задачи
Простые задачи
mat-zadachi.ru
102. Уравнения движения двух материальных точек по прямой: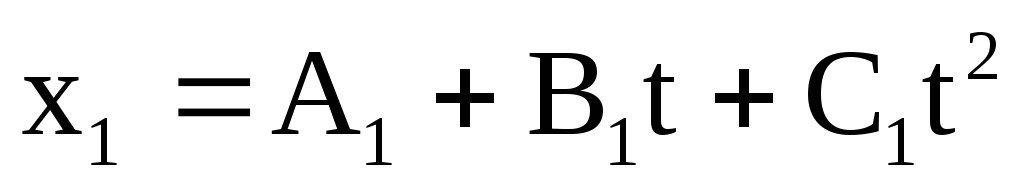 
, где
= 12 м/с,
,
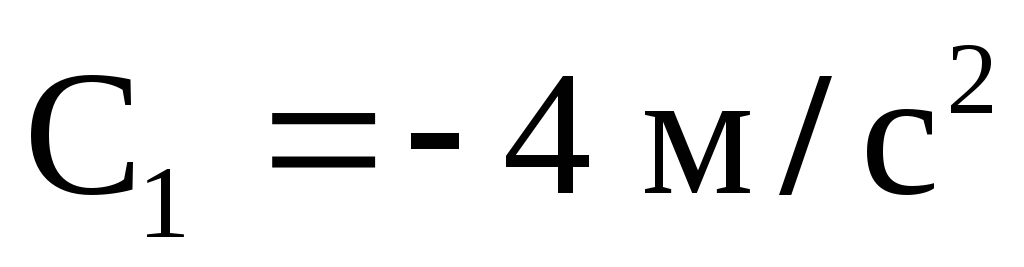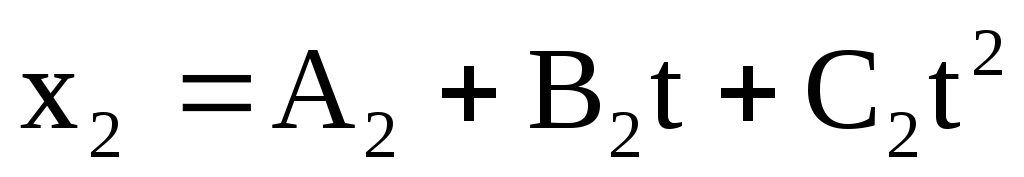, где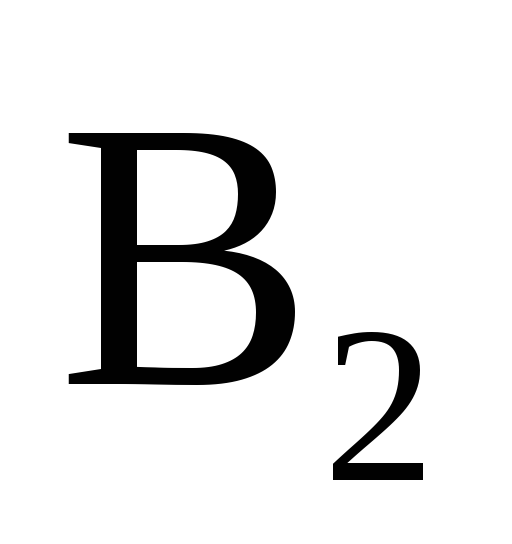
= 2 м/с,
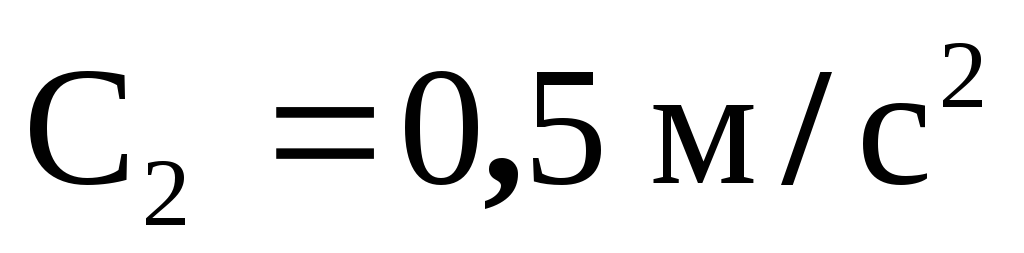. В какой момент времени скорости этих точек будут одинаковыми? Чему равны скорости и ускорения точек в этот момент?
Дано:
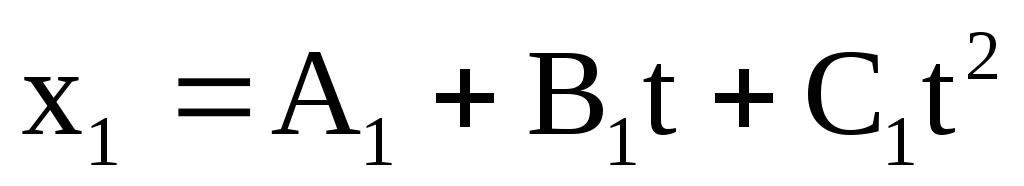
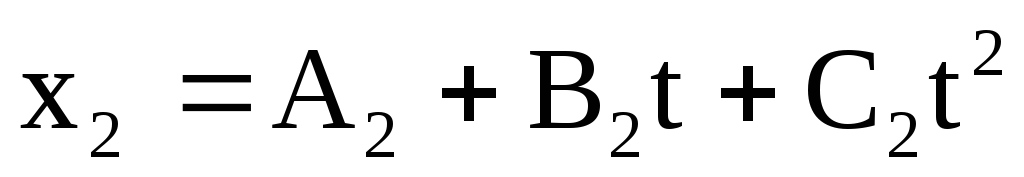
= 12 м/с
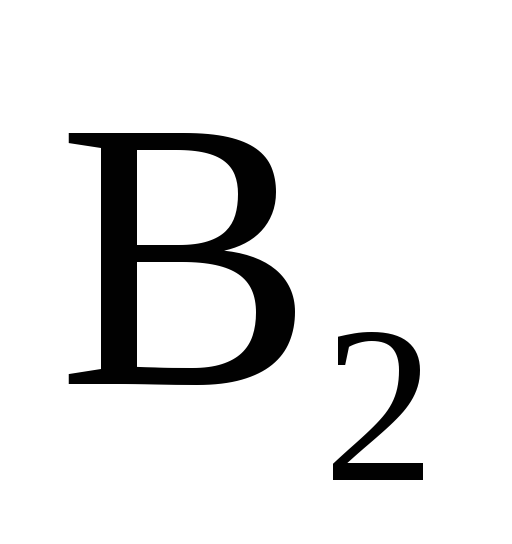= 2 м/с
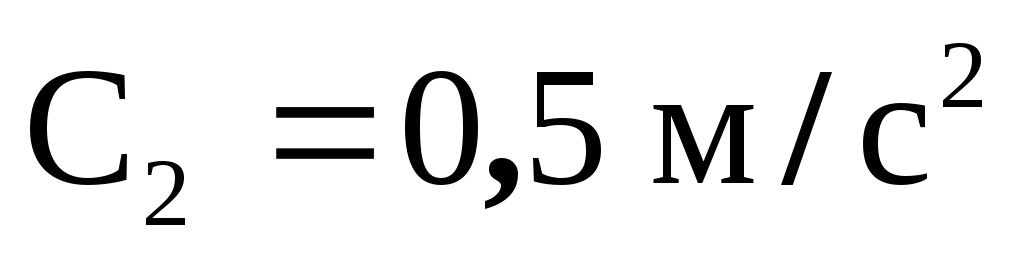
v1 = v2 = v
t=? v=? a1 =? а2 = ?
Решение:
Модуль мгновенной скорости находим как производную от координаты по времени:
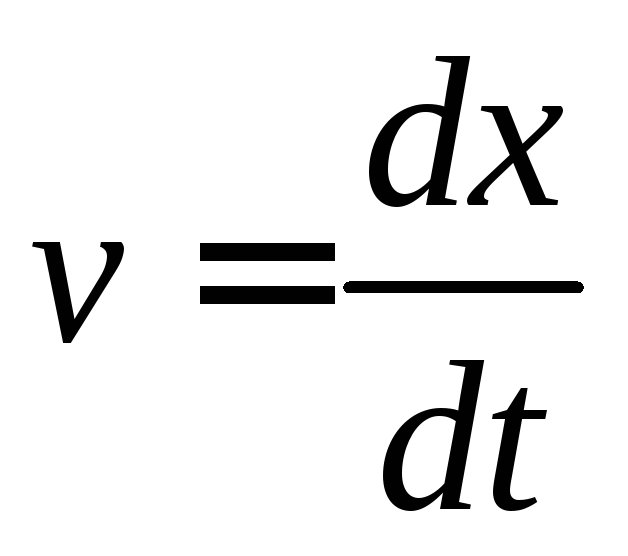
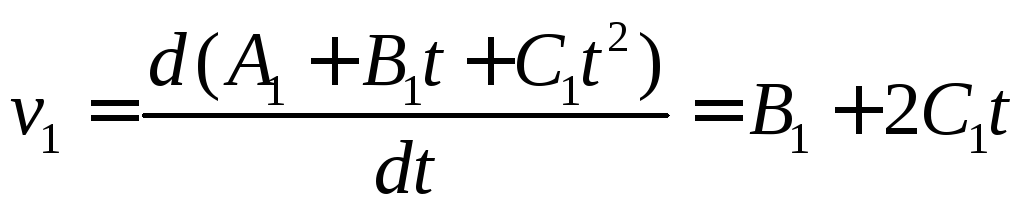
Приравниваем скорости двух точек и находим в какой момент времени это произойдет
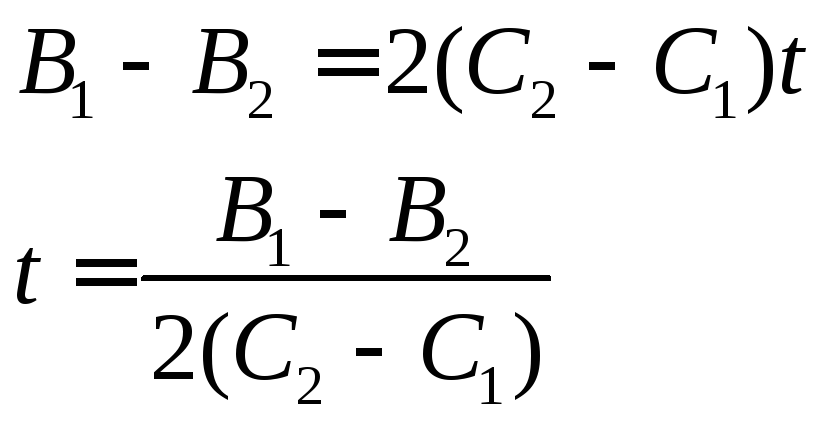
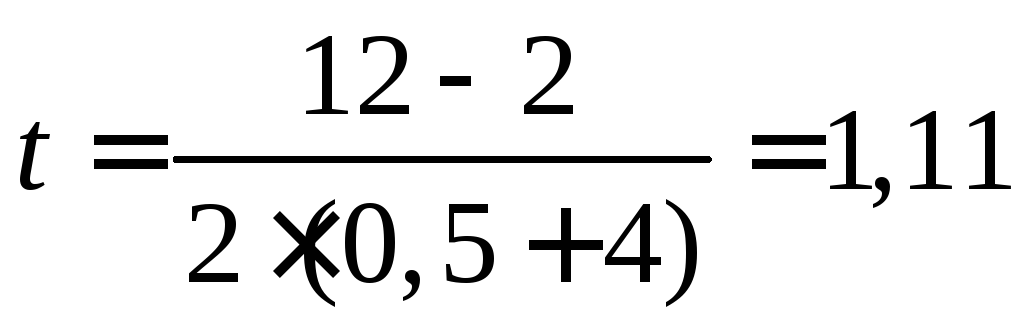с
Скорости в этот момент будут равны
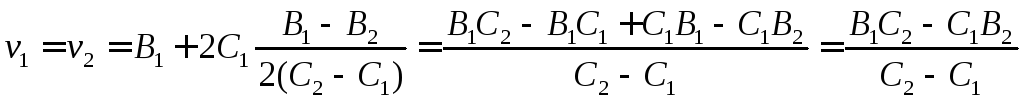
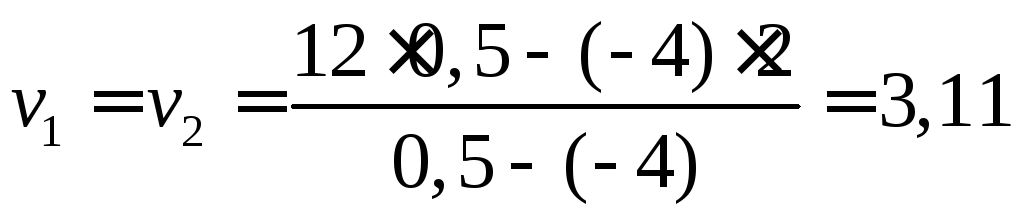м/с
Ускорение есть производная скорости по времени
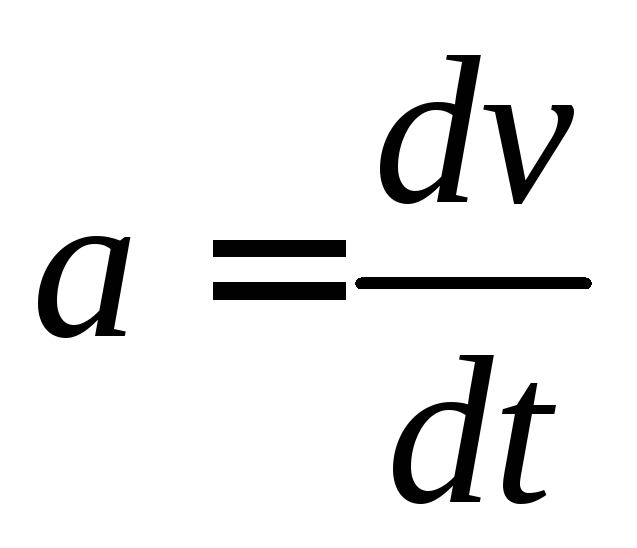
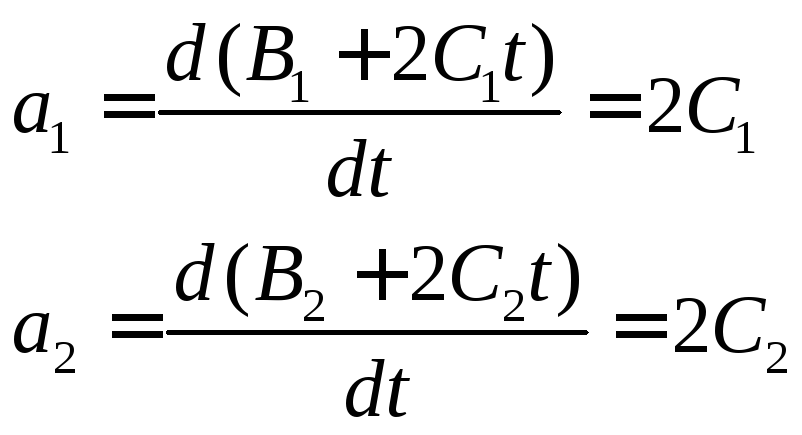
Таким образом, ускорения точек постоянны во времени и равны
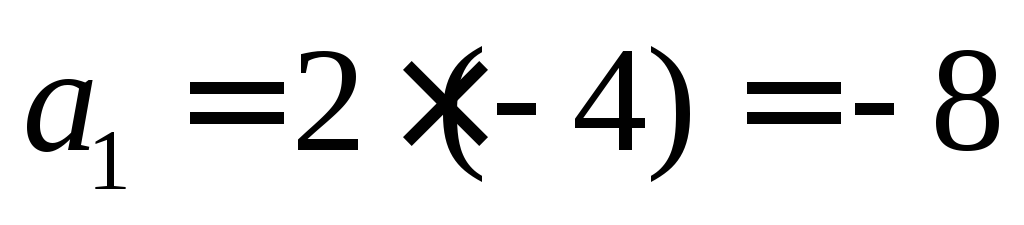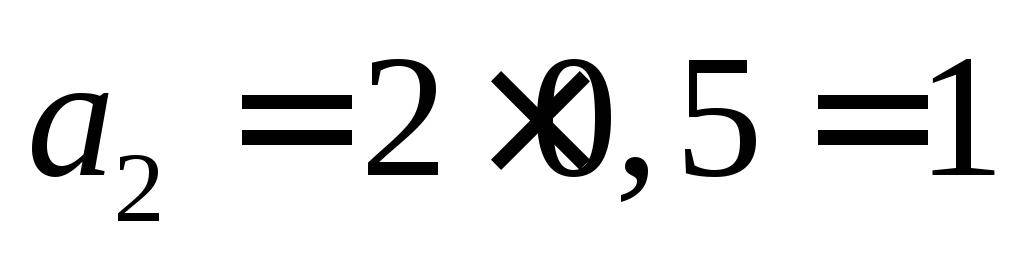м/с2
м/с2
Ответ: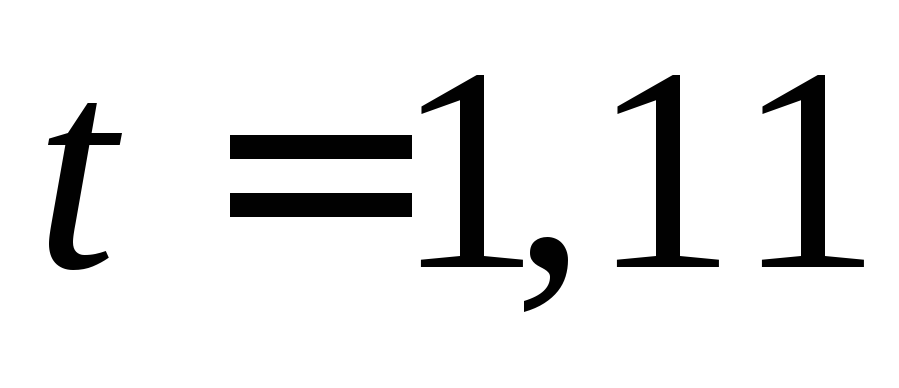 
с,
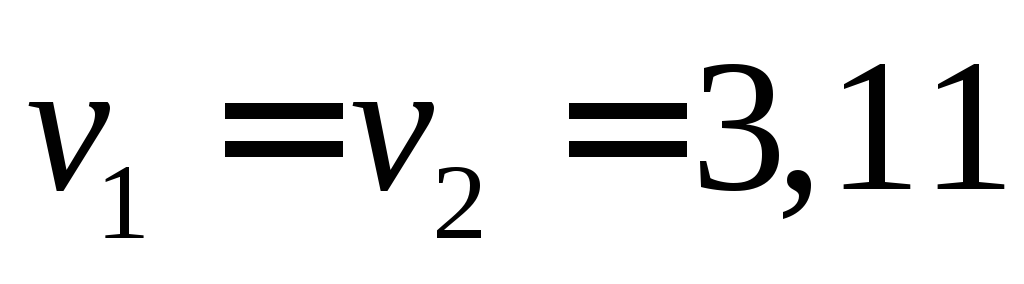м/с,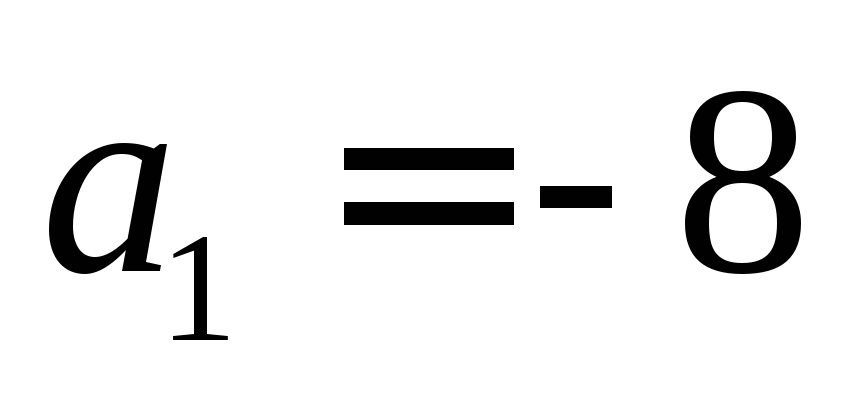
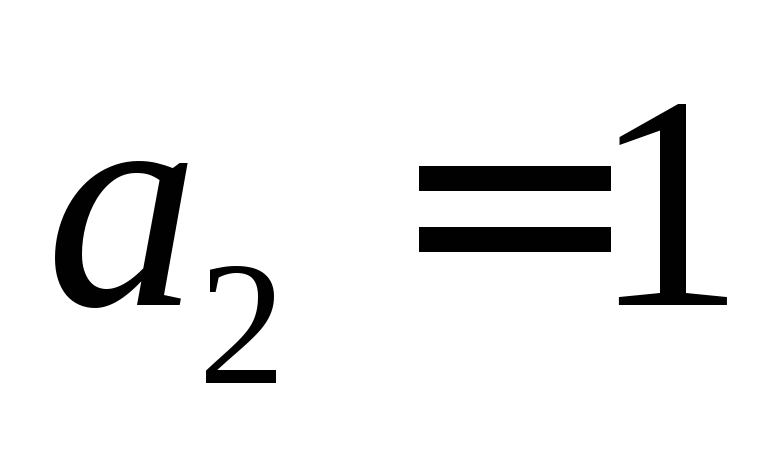м/с2, 
м/с2.
112. На горизонтальной поверхности лежит тело массой 5 кг. Какой путь пройдет это тело за 1 с, если к нему приложить силу 50 Н, образующую угол 60 с горизонтом? Коэффициент трения между телом и поверхностью принять равным 0,2.
Дано:
m = 5 кг
t = 1 c
F = 50 H
α = 60
μ = 0,2
L=?
Решение:
На тело действуют силы: сила тяжести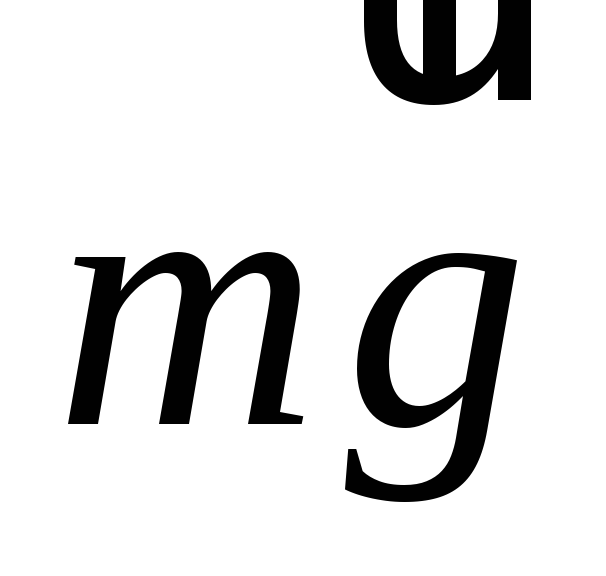 
, сила реакции опоры
, сила трения
, сила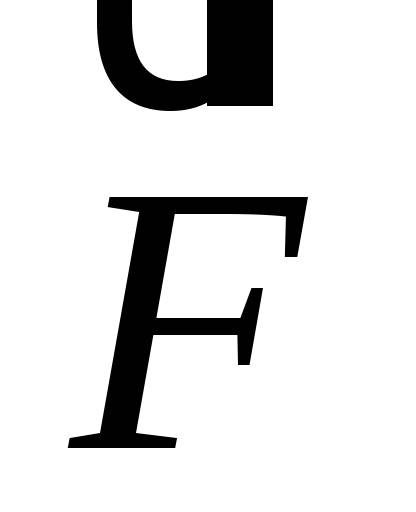
. Изобразим их на чертеже, направим оси координат – х – вдоль плоскости горизонта в сторону направления проекции силыF, у – перпендикулярно плоскости вверх.
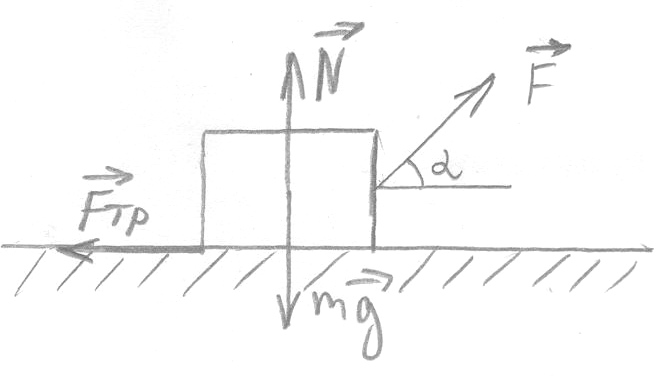
По второму закону Ньютона
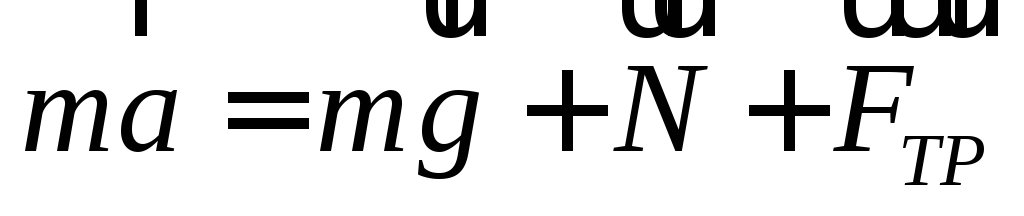
Спроецируем равенство на оси координат
Х: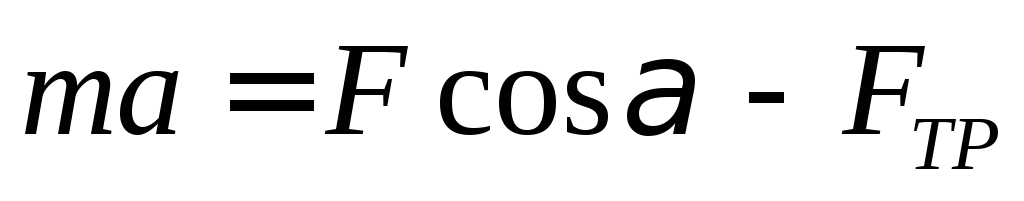 
(1)
Y: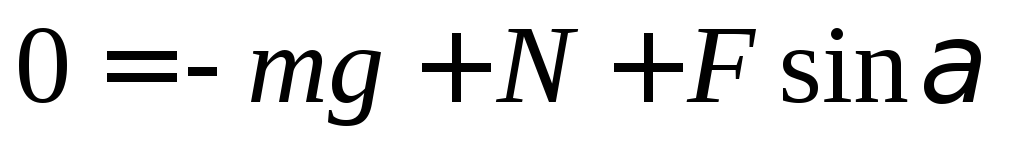 
Из последнего равенства имеем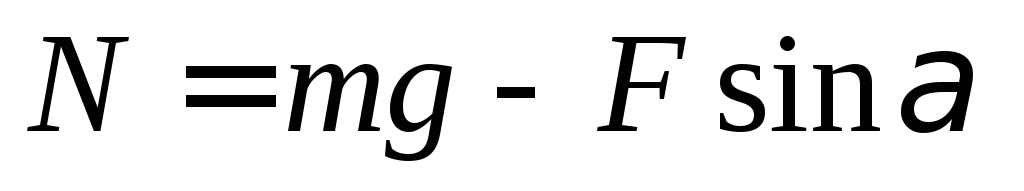 
.
Сила трения равна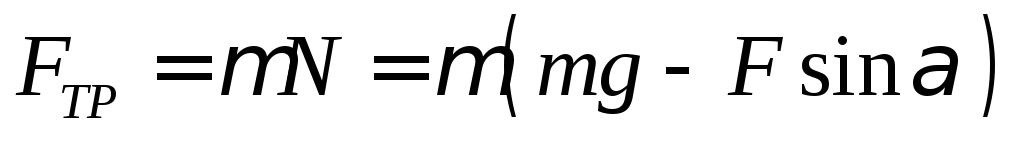 
Подставим в (1)
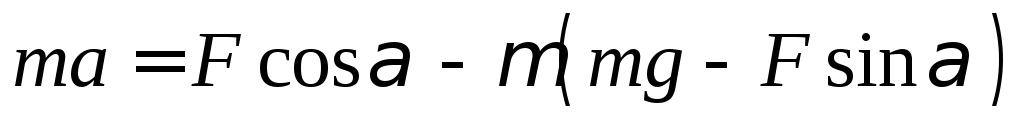
Выразим ускорение
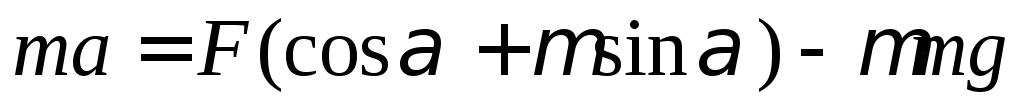
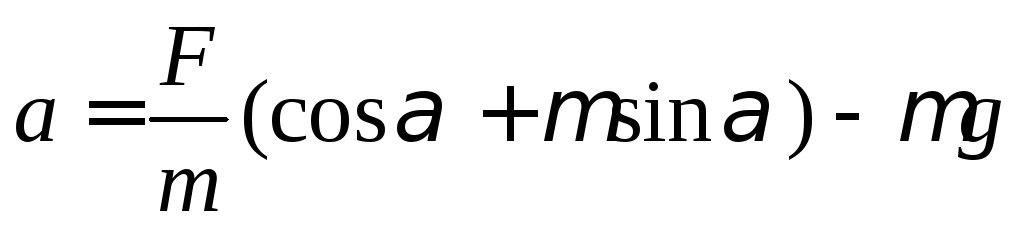
Найдем пройденный путь. Движение равноускоренное. Начальная скорость и расстояние равны 0. Тогда скорость равна
Пройденное расстояние
Проверим размерность
[L]= с2·[(кг·м/с2)/кг - м/с2] = м
Вычисли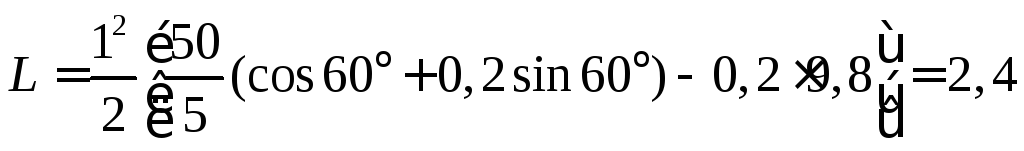м
м
Ответ: 2,4 м.
122. Снаряд, летевший со скоростью 400 м/с, разорвался на два осколка. Меньший осколок, масса которого составляет 40% от массы снаряда, полетел в противоположном направлении со скоростью 150 м/с. Определить скорость большого осколка (по величине и направлению).
Дано:
v = 400 м/с
m1 = 0,4m
u1 = 150 м/с
u2=?
Решение:
Сопротивлением воздуха пренебрежем. Считаем, что снаряд находится в горизонтальном полете, появлением вертикальной составляющей скорости в результате действия силы тяжести также пренебрежем. В этом случае система замкнутая, суммарный импульс сохраняется. Запишем закон сохранения импульса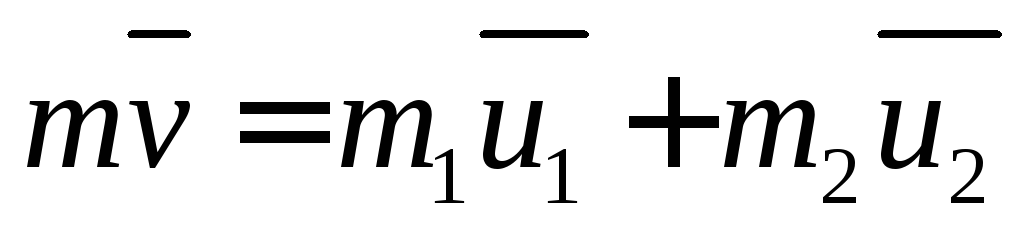 
. Исходя из того, что векторы скоростей
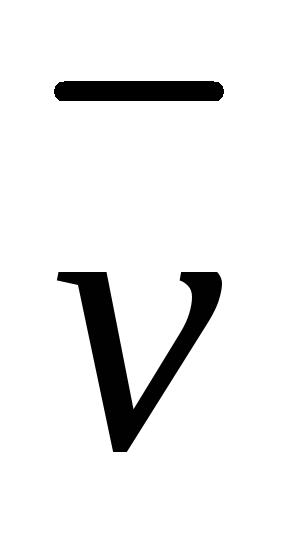и
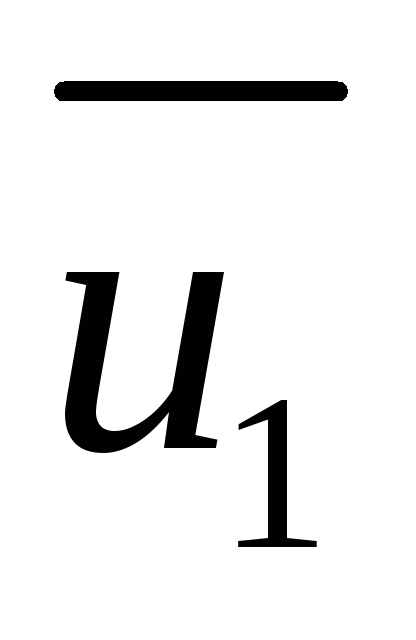противонаправлены, очевидно, что вектор скорости
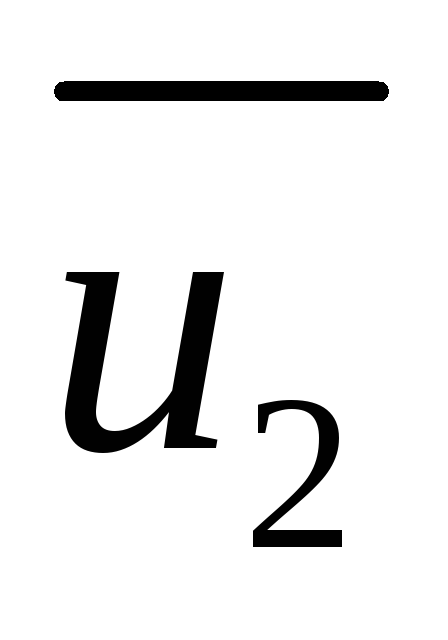также параллелен первым двум векторам. Примем, что он сонаправлен
.
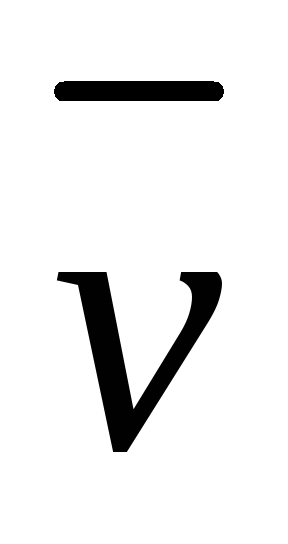Сделаем чертеж
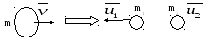
Спроецируем закон сохранения импульса на направление скорости полета снаряда.
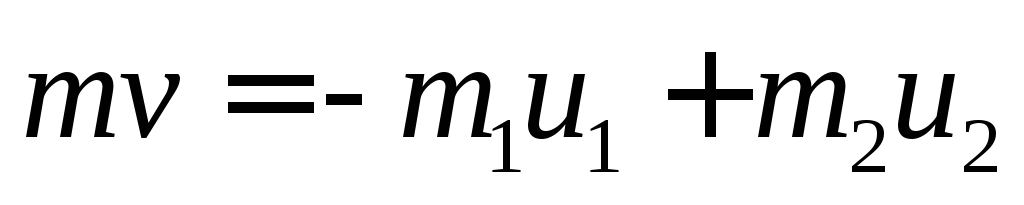
Найдем выражение для скорости большей части снаряда.
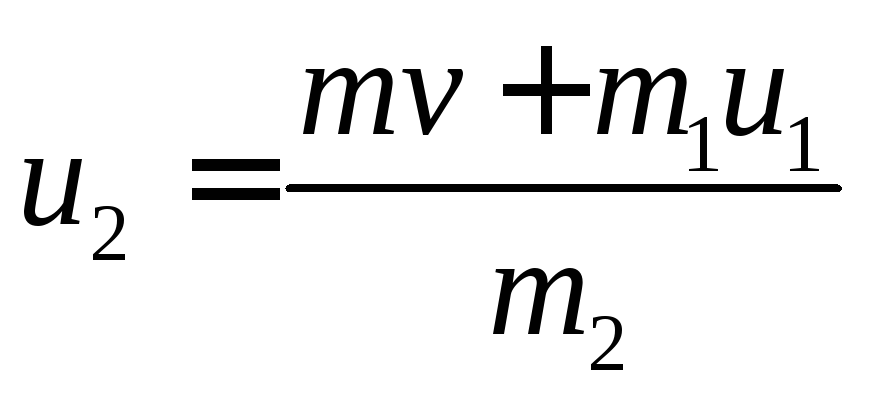
Учтем, что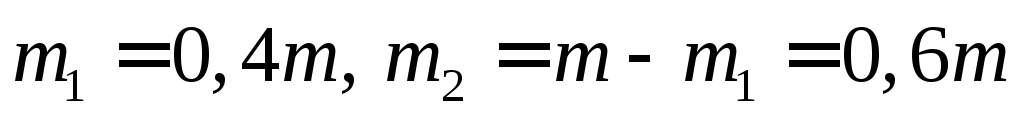 
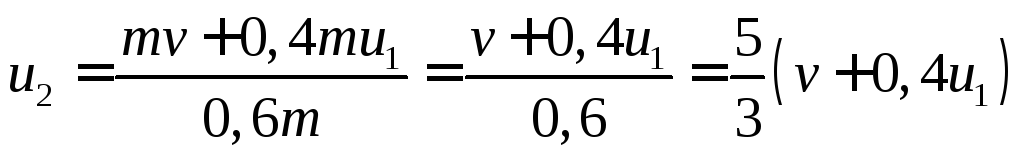
Вычислим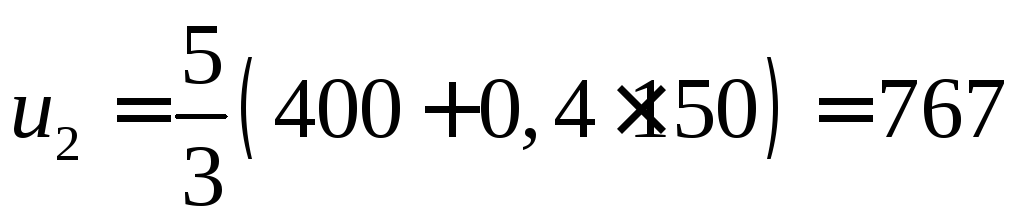 
м/с
Поскольку скорость получилась положительной, следовательно, направление вектора скорости выбрано верно.
Ответ: 767 м/с.
132. Найти работу, совершаемую при подъеме груза массой 10 кг по наклонной плоскости с углом наклона 45 на расстояние 2 м, если время подъема – 2 с, а коэффициент трения = 0,1.
Дано:
m = 10 кг
α = 45
L = 2 м
t = 2 с
= 0,1
А = ?
Решение:
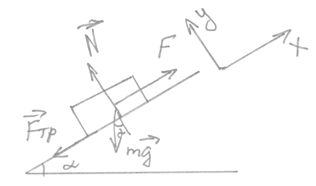
На тело действуют силы: сила тяжести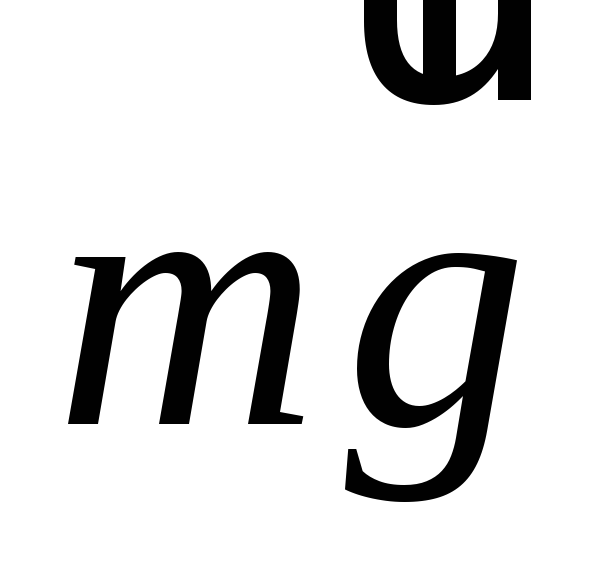 
, сила реакции опоры
, сила трения
и внешняя сила
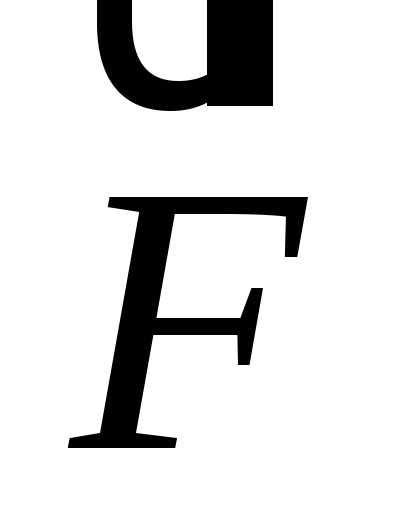, которая и будет совершать работу. Изобразим их на чертеже, направим оси координат –х – вдоль плоскости вверх, у – перпендикулярно плоскости вверх.
Тогда по второму закону Ньютона
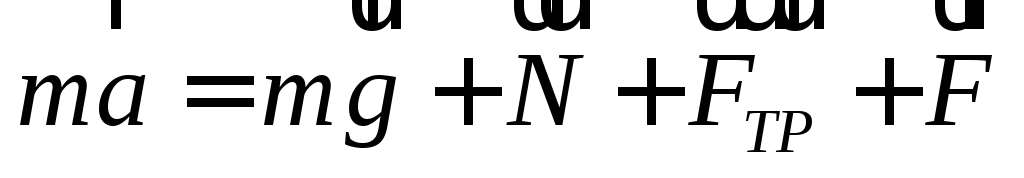
Спроецируем равенство на оси координат
Х: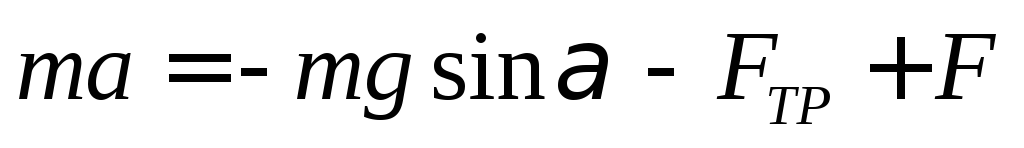 
Y: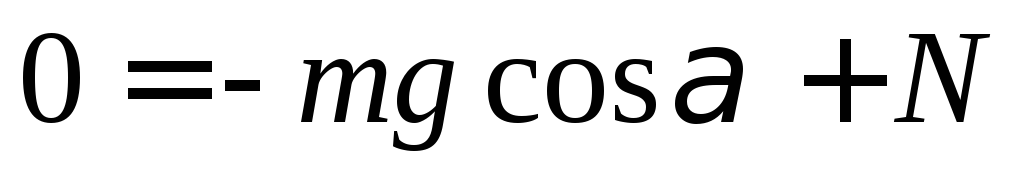 
Из последнего равенства имеем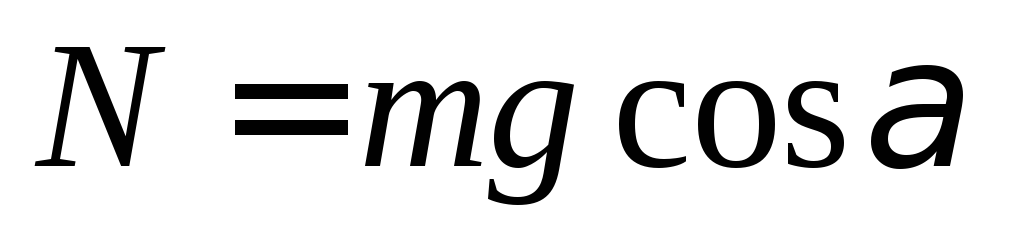 
.
Подставим в первое уравнение и выразим ускорение тела
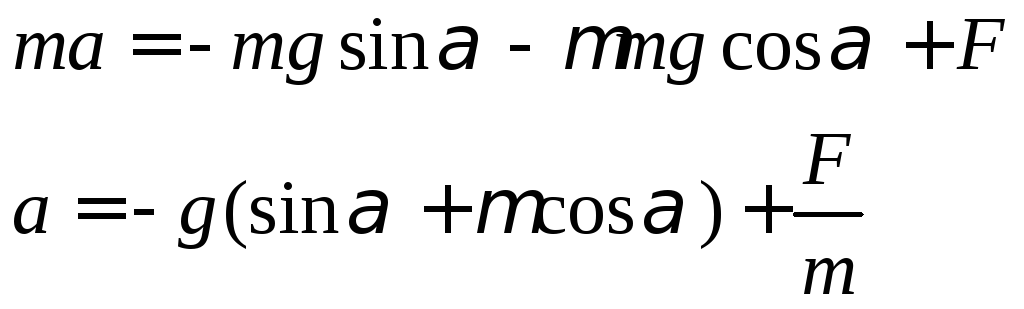
Ускорение, с котором будет двигаться тело, найдем из условия для времени подъема. Для равноускоренного движения
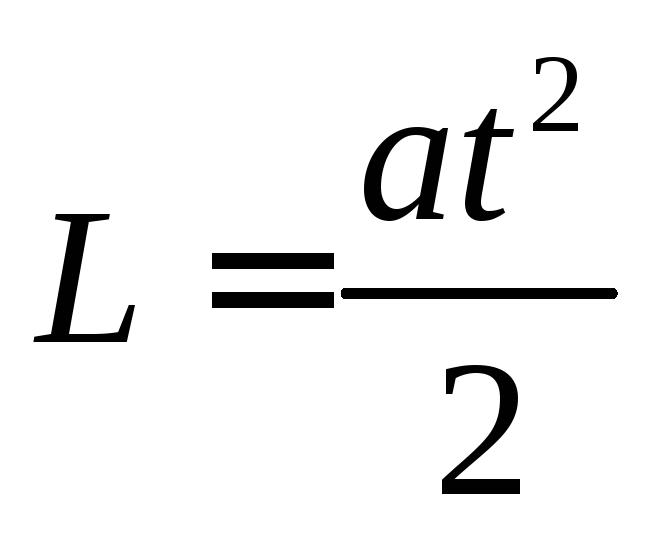
Отсюда ускорение тела равно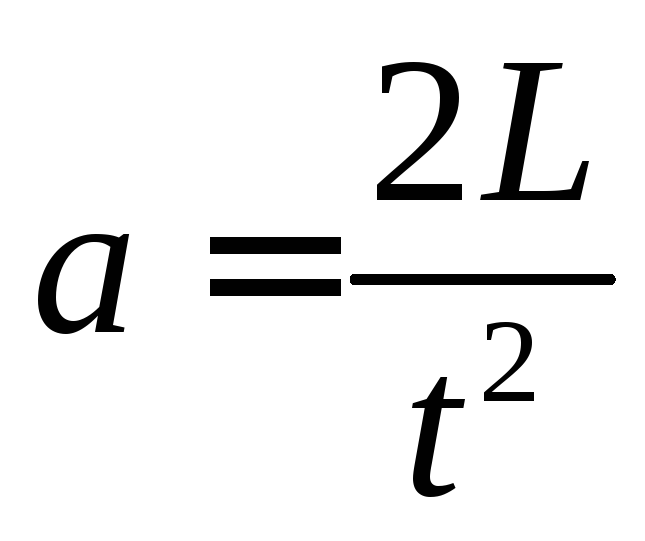 
.
Приравняем выражения для ускорения и выразим действующую на тело силу.
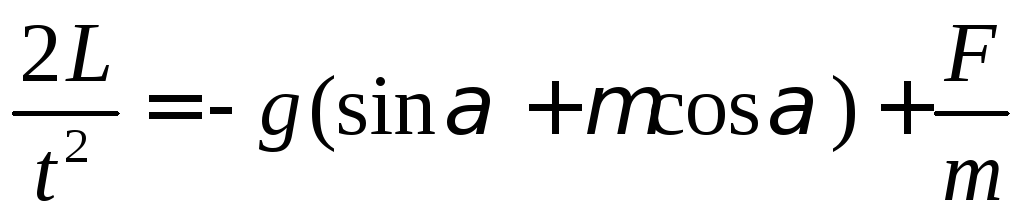
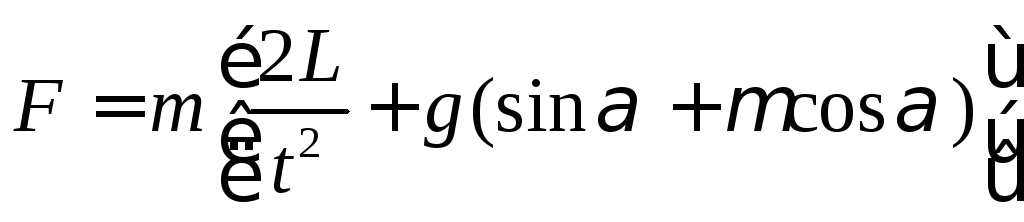
По определению работа силы F равна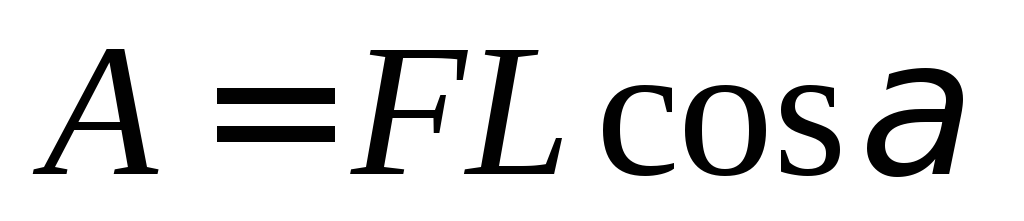 
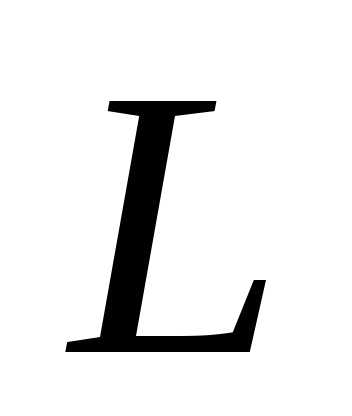- перемещение тела, 
- направление между вектором силы и вектором перемещения.
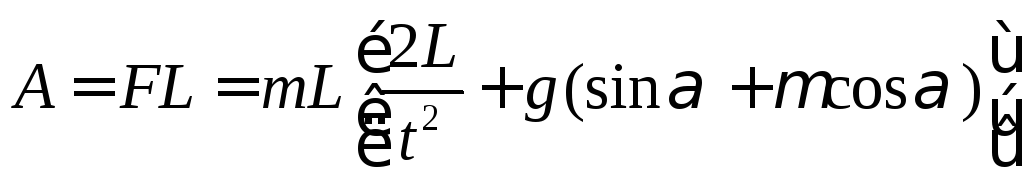
Проверим размерность
[А]=кг·м·м/с2 = Дж
Дж
Ответ: 172 Дж.
142. На барабан радиусом 20 см, момент инерции которого равен 0,1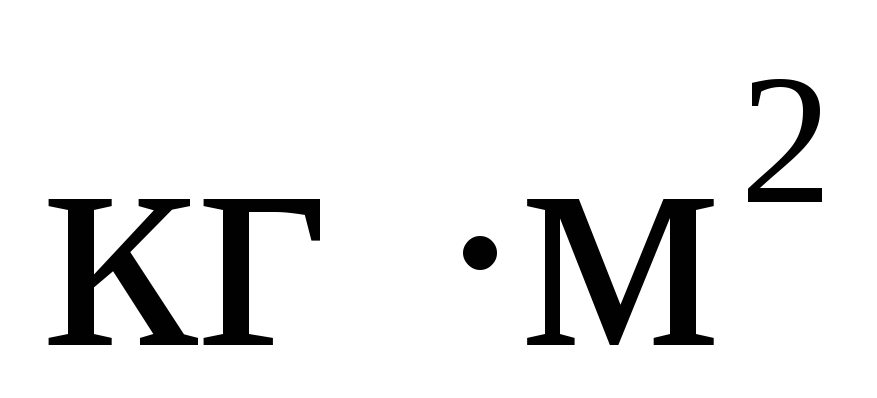 
, намотан шнур, к которому привязан груз массой 0,5 кг. До начала вращения барабана высота груза над полом равна 1 м. Найти: 1) через сколько времени груз опустится до пола; 2) кинетическую энергию груза в момент удара о пол. Трением пренебречь.
Дано:
R = 20 см = 0,2 м
I = 0,1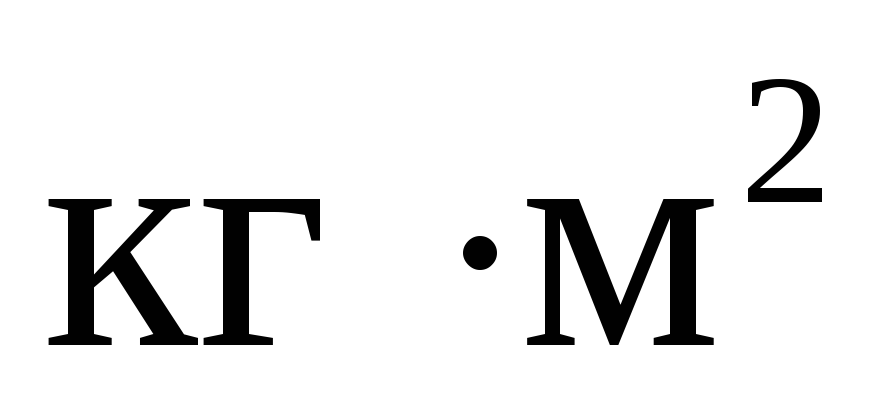 
m=0,5 кг
Н = 1 м
t = ? WK = ?
Решение:
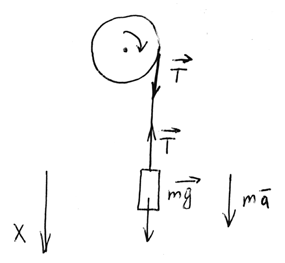
Считаем шнур невесомым и нерастяжимым, тогда сила натяжения шнура Т одинакова во всех точках
Второй закон Ньютона для груза (проецируем на ось ox):
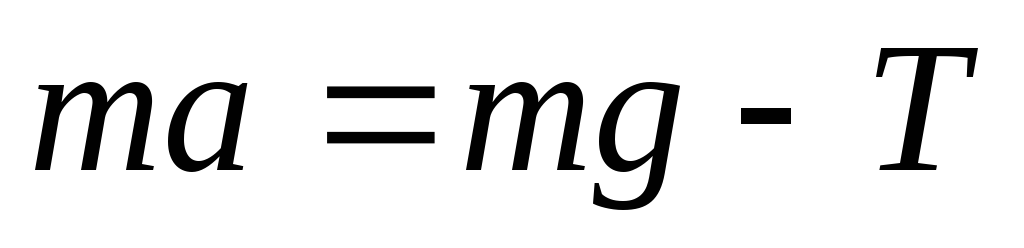(1)
Угловое ускорение маховика будет равно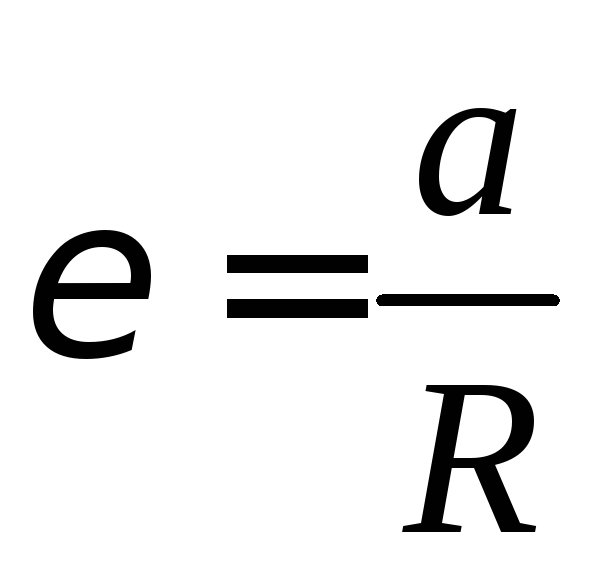 
, (2) гдеR-радиус маховика.
По закону изменения момента импульса системы
,
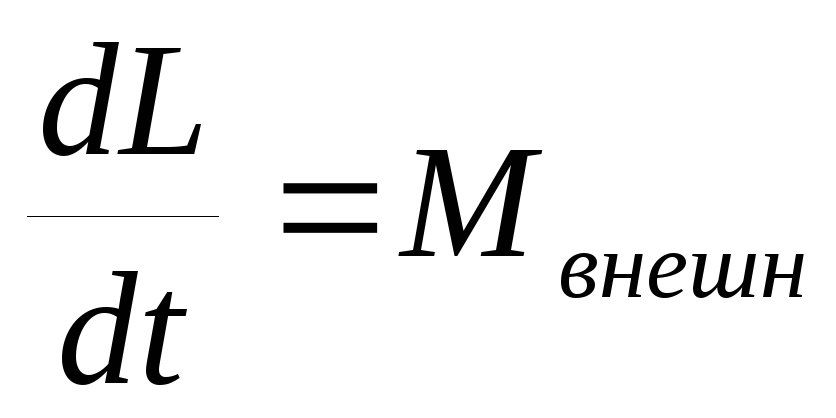где L- момент импульса системы,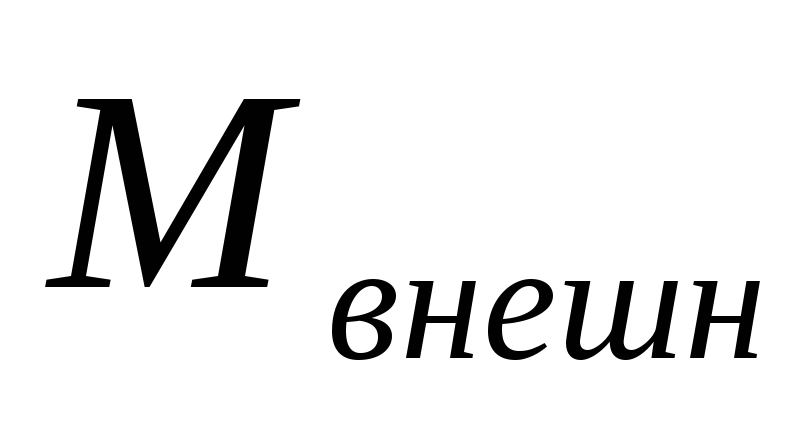 
- момент внешних сил, действующих на систему (силаT)
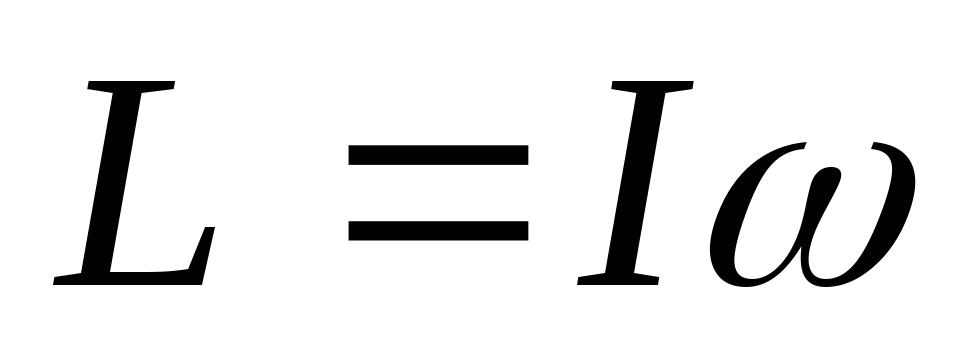, где 
- угловая скорость маховика. С учетом того, чтоI постоянно
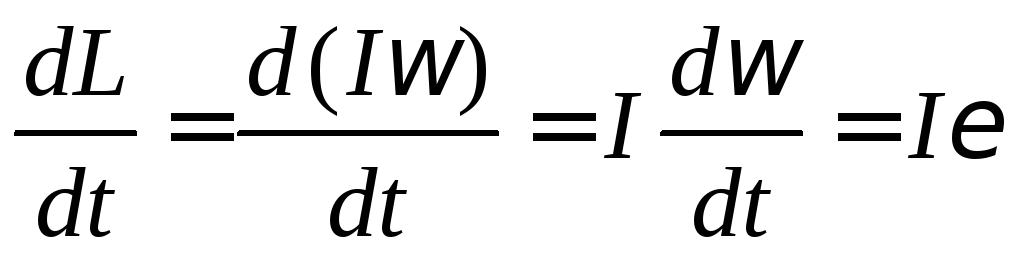
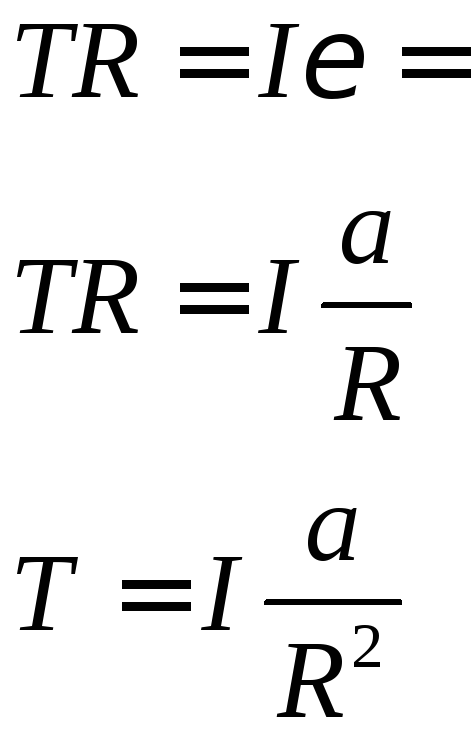
Подставляем в (1) и находим ускорение
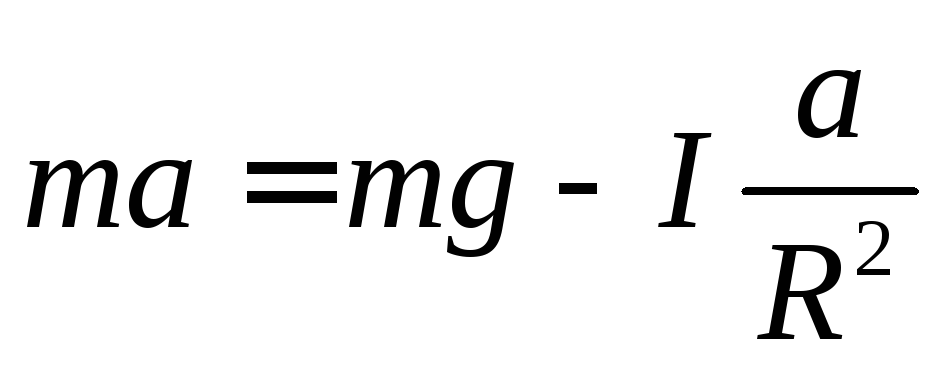
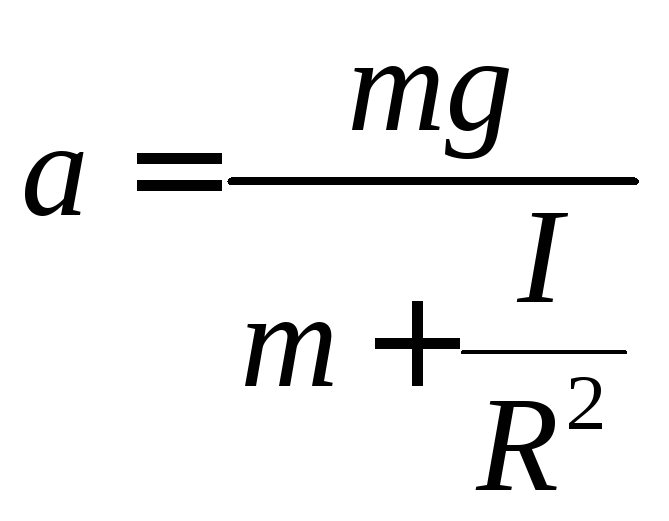
Для равноускоренного движения зависимость пройденного расстояния от времени
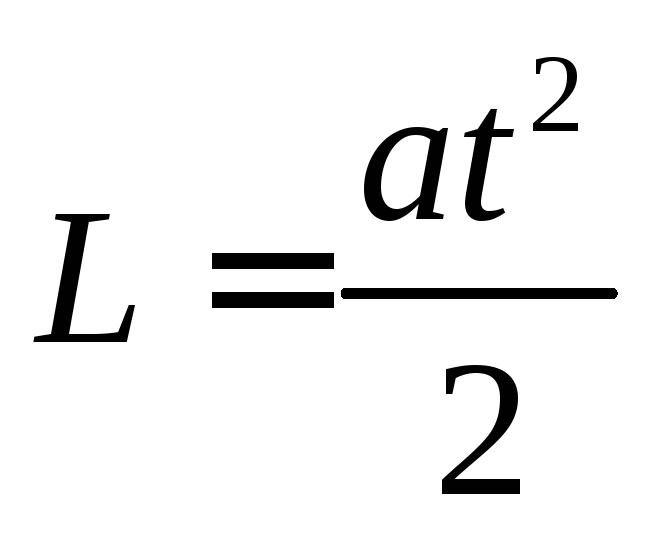
Отсюда находим время опускания груза
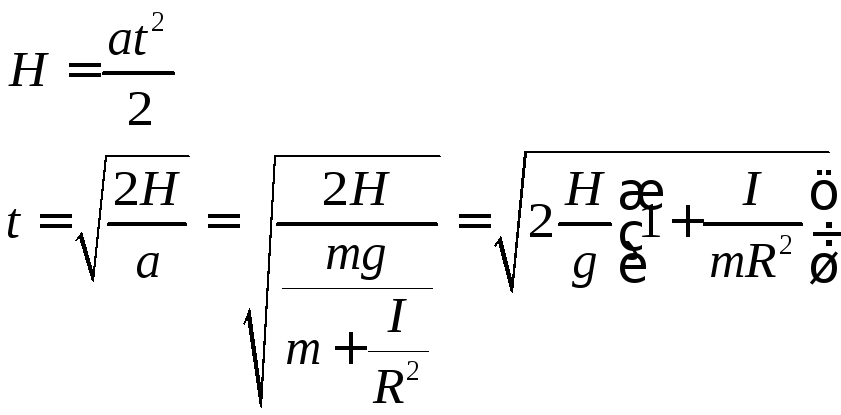
Вычислим
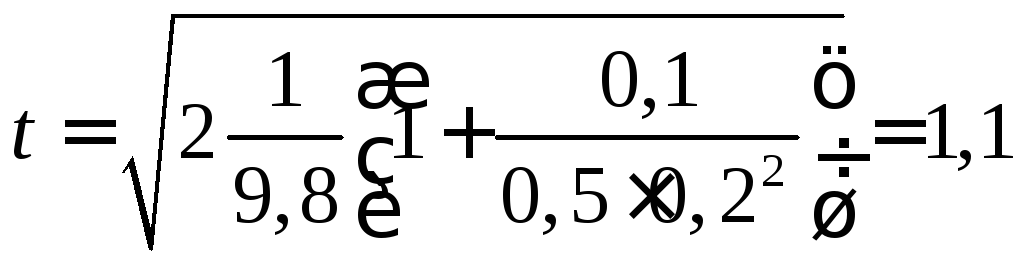с
Если скорость груза в начальный момент времени равна нулю, то в момент касания пола она будет равна
.
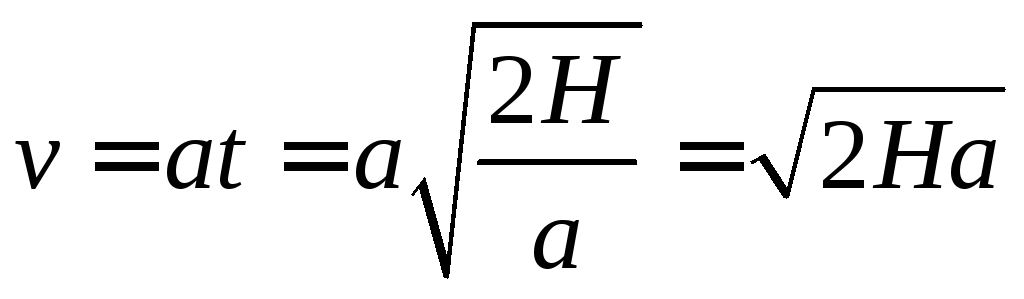Кинетическая энергия груза в момент касания
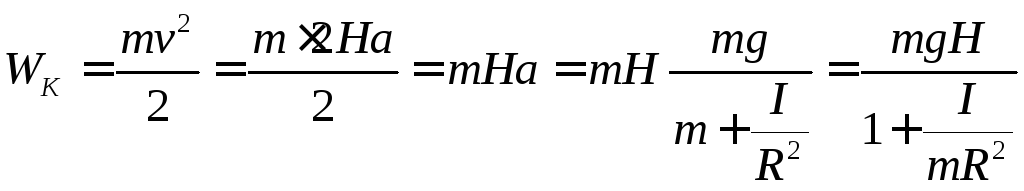
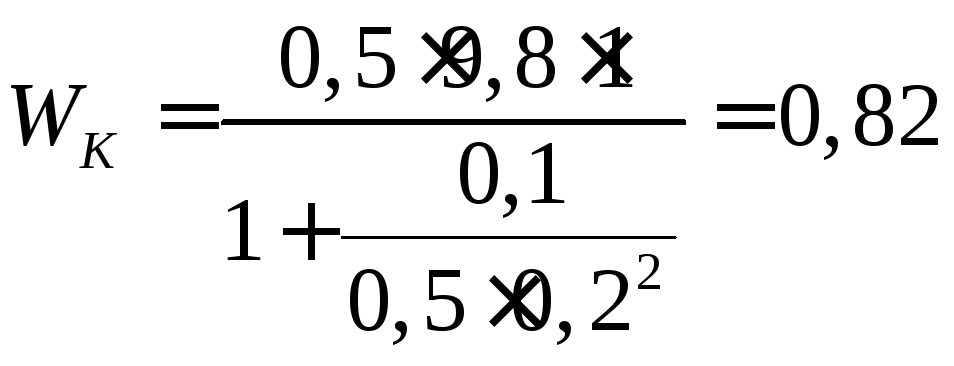Дж
Ответ: 0,82 Дж.
152. Определить высоту наклонной плоскости, если линейная скорость центра шара, скатившегося без скольжения с наклонной плоскости равна 2,65 м/с. Начальная скорость шара равна нулю.
Дано:
v= 2,65 м/с
h =?
Решение:
Движение шара складывается из поступательного и вращательного движения шара. Следовательно,
Wk= Wk пост+ Wk вр
Кинетическая энергия поступательного движения
Wk пост =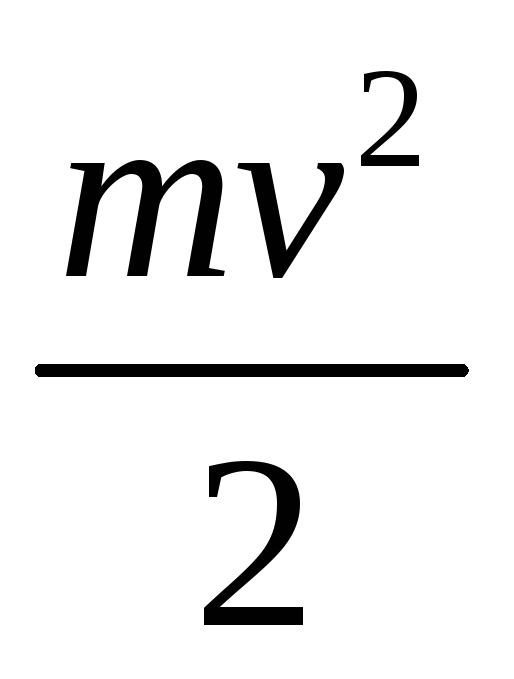 
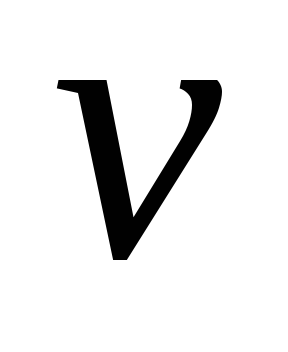- скорость центра масс, т.е. центра шара, 
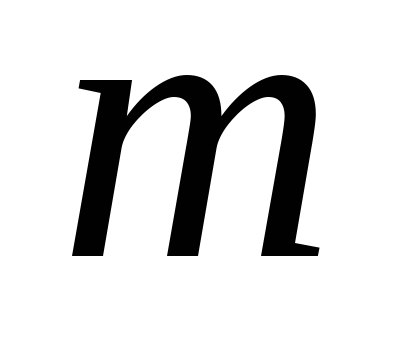- масса шара.
Кинетическая энергия вращательного движения
Wk вр =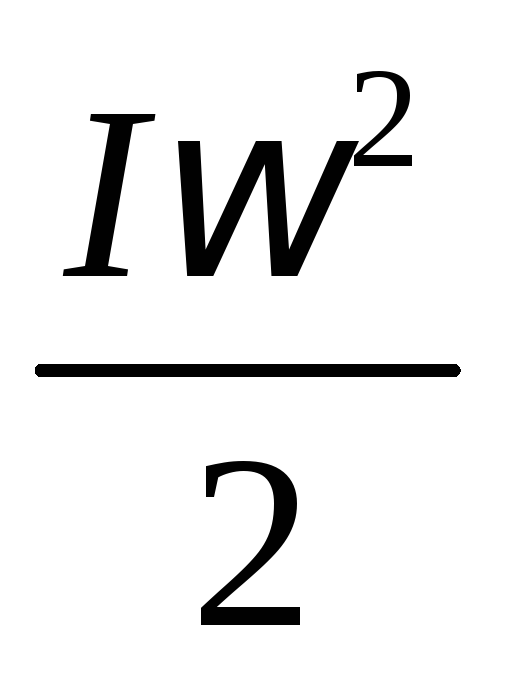 
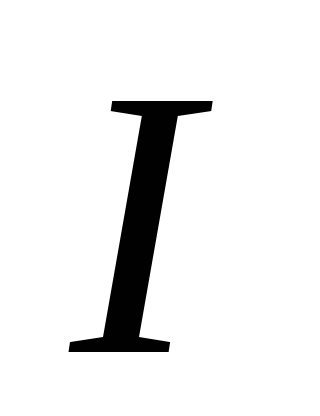- момент инерции шара, 
- угловая скорость вращения.
Изобразим движение шара. Линейная скорость движения точек шара, которые попеременно соприкасаются с поверхностью, одинакова. Тогда суммарные мгновенные значения скоростей равны:
Обозначим радиус шара R. Тогда
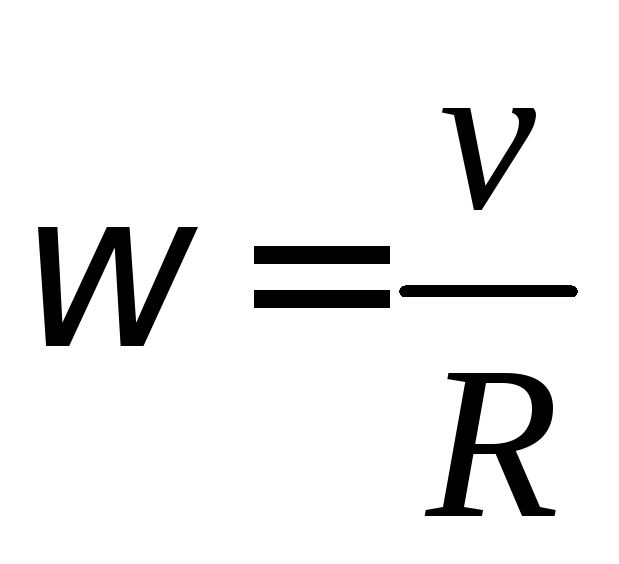
Для сплошного шара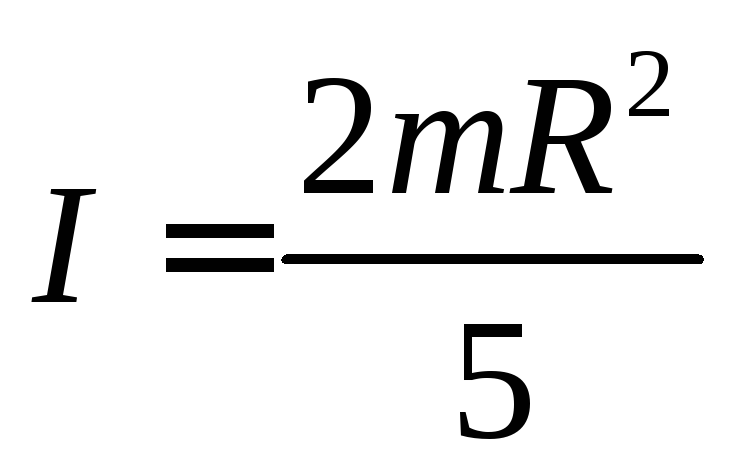 
Wk=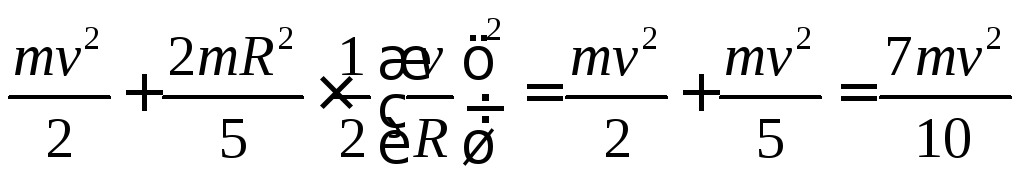 
Система замкнутая. По закону сохранения энергии
Wk =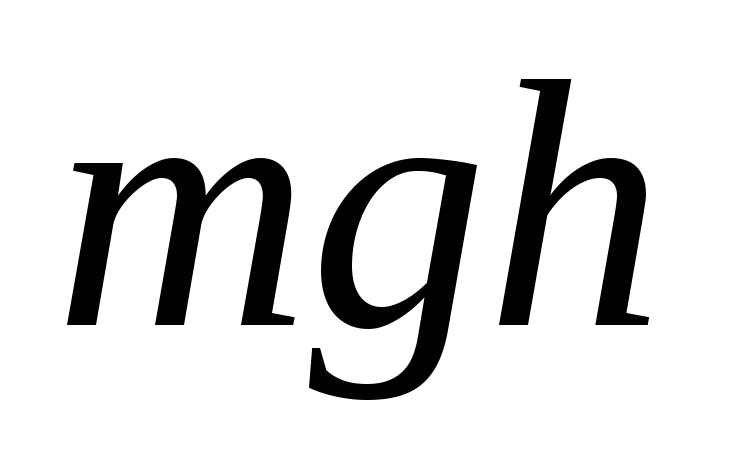
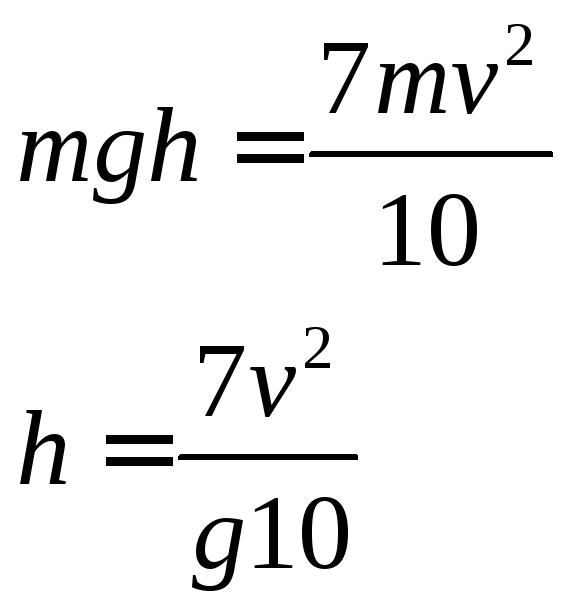
Проверим размерность
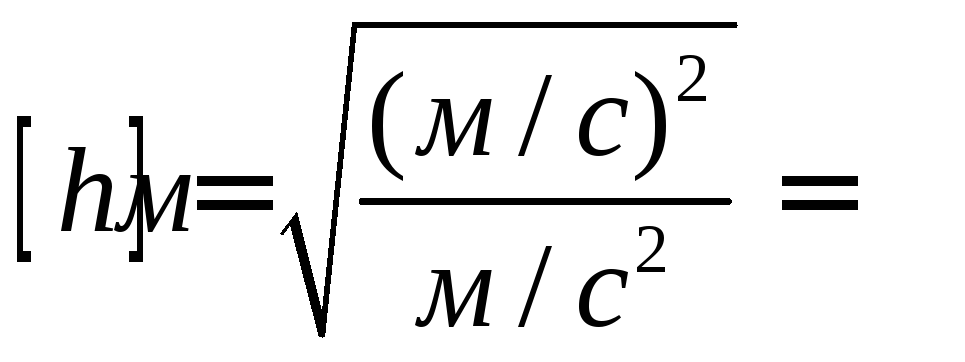
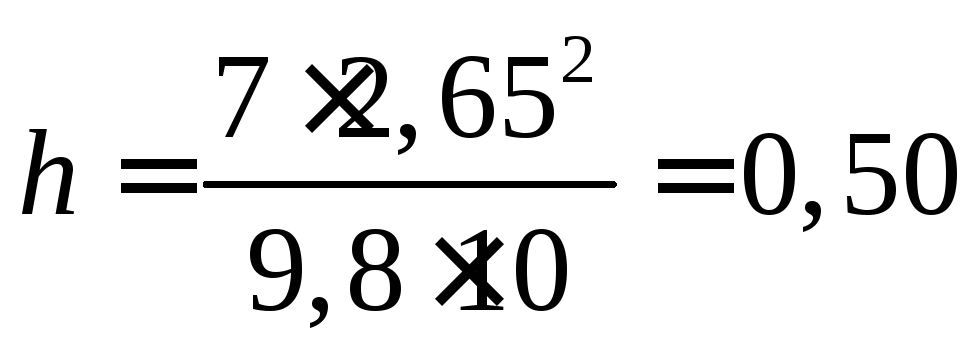м
Ответ: 0,50 м.
studfiles.net
Что должен знать дошкольник по предмету математика перед поступлением в 1 класс?Будущий первоклассник должен знать:1. цифры от 1 до 9;2. геометрические фигуры: круг, квадрат, треугольник, прямоугольник, многоугольник;3. знаки сравнения: больше, меньше, равно и уметь ими пользоваться;4. знаки арифметических действий: пляс, минус и уметь ими пользоваться.
Также будущий первоклассник должен уметь:1. считать от 1 до 10;2. сравнивать цифры, сопоставлять цифры с количеством предметов;3. формулировать и решать простейшие задачи на сложение и вычитание;4. четко различать простейшие геометрические фигуры;5. различать типы линий: ломанные, прямые, кривые.
Как проводить данный тест (подсказки для родителей).Каждый ученик должен понимать, как правильно работать с математическим тестом. Для этого, рекомендуется наглядно продемонстрировать и совместно решить несколько различных тестовых примеров.Необходимо четко и не торопясь прочитать тестовые задания ребёнку, при этом следует обратить внимание на следующие моменты:1. Объясните ребенку, что необходимо каким-либо образом отметить правильный вариант ответа (подчеркнуть, зачеркнуть или обвести). Поясните, что вариантов ответа несколько, но правильный – только один.2. Необходимо, чтобы ребенок понял условия задачи, если же возникают вопросы, то ребенок должен попросить помощи у взрослых.3. Поясните, что если ребенок сделал ошибку и понял это, то нужно исправить эту ошибку и выбрать другой вариант ответа. Как это делать, лучше показать на примере.4. Объясните, что не стоит тратить на одну задачу слишком много времени. Если не удается решить задачу, то лучше перейти к следующему заданию.5. Заострите внимание, что необходимо еще раз проверить работу после завершения выполнения всех тестовых заданий.
После того как все поняли, как нужно работать с тестом, можно приступать к выполнению входного тестового задания из данного раздела.
1. Сколько груш на картинке? Выберете правильный ответ.
2. Выдели ряд, в котором все числа больше ШЕСТИ.
5, 7, 8, 9 1, 5, 6, 8 7, 8, 9, 10 4, 6, 8, 9 2, 5, 8, 93. Внимательно посмотри на числовой ряд. Какое число расположено левее числа 8? Выбери это число.
4. Выбери число, к которому надо прибавить ЕДИНИЦУ, чтобы получить число 8. Выбери правильный ответ.
5. Какая из этих линий называется кривая? Выбери правильный ответ.
6. Сколько яблок надо добавить, чтобы на картинке оказалось семь яблок? Выберите правильный ответ.
7. Какая фигура называется квадрат? Выберите правильный ответ.
Вариант II.
1. Сколько абрикосов висит на ветке? Выбери правильный ответ.
2. Выдели числовой ряд, в котором все числа больше СЕМИ.
5, 7, 8, 9 4, 5, 6, 8 8, 8, 9, 10 4, 6, 8, 9 2, 3, 4, 53. Внимательно посмотри на числовой ряд. Какое число расположено правее числа 4? Выбери это число.
4. Выбери число, от которого надо отнять ЕДИНИЦУ, чтобы получить число 5. Выбери правильный ответ.
5. Какая из этих линий называется прямая? Выбери правильный ответ.
6. Сколько лимонов надо добавить, чтобы на картинке оказалось 8 лимонов? Выбери правильный ответ.
7. Какая фигура называется круг?
Вариант III.
1. Сколько слив нарисовано на картинке? Выбери правильный ответ.
2. Выдели числовой ряд, в котором все числа больше ЧЕТЫРЕХ.
5, 7, 8, 9 1, 5, 6, 8 3, 5, 9, 1 4, 6, 8, 9 3, 5, 8, 93. Внимательно посмотри на числовой ряд. Какое число расположено правее числа 5? Выбери правильный ответ.
4. Выбери число, к которому надо прибавить ЕДИНИЦУ, чтобы получить число 9. Выбери правильный ответ.
5. Какая из этих линий называется ломаная? Выбери правильный ответ.
6. Сколько ягод надо добавить, чтобы на картинке оказалось 8 клубничек? Выбери правильный ответ.
7. Какая из нарисованных фигур называется треугольник? Выбери правильный ответ.
Вариант II.1. 4 абрикоса.2. 3 ряд.3. 6.4. 6.5. 1.6. 3 лимона.7. 1 фигура - круг.
Вариант III.1. 3 сливы.2. 1 ряд .3. 7.4. 8.5. 3.6. 5 ягод.7. 4 фигура - треугольник.
mathematics-tests.com
Министерство образования Республики Беларусь
Учреждение образования
«Белорусский государственный университет
информатики и радиоэлектроники»
Специальность ИСиТвЭ
КОНТРОЛЬНАЯ РАБОТА
По курсу «Высшая математика »
Вариант № 11
Студент-заочник 1 курса
Группы: № 282324
ФИО: BET
Адрес:
Тел. 8 044
Минск 2012
Контрольная работа № 1
Задание 1.
Даны три комплексных числа 
и
1) выполните действия над ними в алгебраической, тригонометрической и показательной формах;
2) найдите расстояние между точками 
и
на комплексной плоскости.
Решение задания 1.
1) выполните действия над ними в алгебраической, тригонометрической и показательной формах;
Вычислим в алгебраической форме
(a-b)4= a4-4a3b+6a2b2-4ab3+b4
Следовательно
(a-b)2=a2-2ab+b2
Следовательно
Представим заданные Z1,Z2,Z3 в тригонометрической форме
Используем формулы
Получим
По формуле найдем значение 
Подставим в
Представим заданные Z1,Z2,Z3 в показательной форме
По формуле найдем значение 
Примем экспоненты e равною своему алгебраическому значению ~ 2.7182
2) найдите расстояние между точками 
и
на комплексной плоскости.
Расстояние между точками Z1 и Z3 есть модуль их разности
Задание 3
Решите систему уравнений тремя способами:
1) методом Крамера;
2) методом обратной матрицы;
3) методом Гаусса.
Решение задания 3.
Метод Крамера
Запишем систему в виде:
BT = (-6,6,-4)
Найдем главный определитель:
∆ = 2 х (-1 х 1-(-1 х (-2)))-3 х (-2 х 1-(-1 х 1))+1 х (-2 х (-2)-(-1 х 1)) = 2 = 2
Заменим 1-ый столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы.
∆1 = -6 х (-1 х 1-(-1 х (-2)))-6 х (-2 х 1-(-1 х 1))+(-4 х (-2 х (-2)-(-1 х 1))) = 4
Заменим 2-ый столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы.
∆2 = 2 х (6 х 1-(-4 х (-2)))-3 х (-6 х 1-(-4 х 1))+1 х (-6 х (-2)-6 х 1) = 8
Заменим 3-ый столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы.
∆3 = 2 х (-1 х (-4)-(-1 х 6))-3 х (-2 х (-4)-(-1 х (-6)))+1 х (-2 х 6-(-1 х (-6))) = -4
Ответ: найденные переменные: ; ; .
2. Методом обратной матрицы;
Обозначим через А — матрицу коэффициентов при неизвестных; X — матрицу-столбец неизвестных; B - матрицу-столбец свободных членов:
Вектор B:
BT=(-6,6,-4)
С учетом этих обозначений данная система уравнений принимает следующую матричную форму: А*Х = B.
Найдем главный определитель.
∆=2•(-1•1-(-1•(-2)))-3•(-2•1-(-1•1))+1•(-2•(-2)-(-1•1))=2 ≠ 0
Транспонированная матрица
Вычислим алгебраические дополнения.
∆1,1=(-1•1-(-2•(-1)))=-3
∆1,2=-(-2•1-1•(-1))=1
∆1,3=(-2•(-2)-1•(-1))=5
∆2,1=-(3•1-(-2•1))=-5
∆2,2=(2•1-1•1)=1
∆2,3=-(2•(-2)-1•3)=7
∆3,1=(3•(-1)-(-1•1))=-2
∆3,2=-(2•(-1)-(-2•1))=0
∆3,3=(2•(-1)-(-2•3))=4
Обратная матрица
Вектор результатов X
X=A-1 • B
XT=(2,4,-2)
x1=4 / 2=2
x2=8 / 2=4
x3=-4 / 2=-2
Ответ: найденные переменные: x1=4 / 2=2; x2=8 / 2=4; x3=-4 / 2=-2
3) методом Гаусса.
Запишем систему в виде расширенной матрицы:
Умножим 1-ую строку на (3). Умножим 2-ую строку на (-2). Добавим 2-ую строку к 1-ой:
Умножим 3-ую строку на (-3). Добавим 3-ую строку к 2-ой:
Умножим 2-ую строку на (2). Добавим 2-ую строку к 1-ой:
Теперь исходную систему можно записать как:
x3 = 6/(-3)
x2 = [18 - ( - 5x3)]/2
x1 = [-4 - ( - x2 + x3)]/1
Из 1-ой строки выражаем x3
Из 2-ой строки выражаем x2
Из 3-ой строки выражаем x1
Ответ: найденные переменные: x1=2; x2=4; x3=-2
Задание 4
Даны три вектора 
и
Докажите, что векторы
образуют базис, и определите, какая это тройка векторов: правая или левая.
Решение задания 4.
Найдем смежное произведение векторов
Следовательно вектора некомпланарные и образуют базис, так как 
≠-19, то тройка левая.
Ответ: вектора образуют базис , тройка левая.
Задание 5
Даны координаты вершин треугольной пирамиды 
Найдите:
1) угол между ребрами 
и
2) площадь грани 
3) длину высоты, опущенной из вершины 
на грань
4) уравнение прямой, проходящей через ребро 
5) уравнение плоскости, которой принадлежит грань 
6) массу материальной треугольной пирамиды 
изготовленной из меди плотностью
(считая, что 1 масштабная единица в системе координат равна 1 см).
Решение задания 5.
1. ) угол между ребрами 
и
Угол между векторами 
и
можно найти по формуле:
где A1B2 = X1X2 + Y1Y2 + Z1Z2
Найдем угол между ребрами AB и AD
γ = arccos(0.55) = 123.370
Ответ: угол между ребрами 127,37 градуса.
2. ) площадь грани 
Площадь грани можно найти по формуле:
где
Найдем площадь грани 
Найдем угол между ребрами A1A2 и A1A3:
Площадь грани ABC=
Ответ: площадь грани равна 3,83 см2.
3 .) длину высоты, опущенной из вершины 
на грань
Проекцию вектора b на грань b можно найти по формуле:
Найдем проекцию вектора A4h на грань 
Ответ: высота, опущенная из вершины 
на грань
равна 1,34 см.
4 .) уравнение прямой, проходящей через ребро 
Прямая, проходящая через точки A1(x1; y1; z1) и A2(x2; y2; z2), представляется уравнениями:
Уравнение прямой 
; уравнение1
Ответ: уравнение прямой имеет вид «уравнение 1».
5 .) уравнение плоскости, которой принадлежит грань 
Если точки A1(x1; y1; z1), A2(x2; y2; z2), A3(x3; y3; z3) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:
Уравнение плоскости 
(x-2)(2 • 2-(-3) • 1) - (y-1)((-1) • 2-1 • 1) + (z+3)((-1) • (-3)-1 • 2) = 7x + 3y + 1z-14 = 0
Ответ: уравнение плоскости, которой принадлежит грань 
имеет вид 7x + 3y + 1z-14 = 0
.
6 .) массу материальной треугольной пирамиды 
изготовленной из меди плотностью
(считая, что 1 масштабная единица в системе координат равна 1 см).
Масса материальной точки определяется по формуле
,
где µ-плотность равная 8,9 г/см3, V-объем
Следовательно m=8.9x2.17=19.313 г
Ответ: масса материальной треугольной пирамиды равна 19,313 грамма.
studfiles.net
